- 1Division of Cognitive Sciences, Department of Psychology, University of Potsdam, Potsdam, Germany
- 2Department of Behavioral Sciences, Ariel University, Ariel, Israel
A Commentary on
The mental representation of integers: An abstract-to-concrete shift in the understanding of mathematical concepts
by Varma, S., and Schwartz, D. L. (2011). Cognition 121, 363–385. doi: 10.1016/j.cognition.2011.08.005
Decision times during processing of positive number symbols (1, 2, 3 etc.) inform our understanding of mental representations of integers (Holyoak, 1978; Dehaene et al., 1993; Fischer and Shaki, 2014). Effects of number magnitude on cognition include distance effects (faster discrimination for larger numerical differences in a number pair), size effects (faster processing of smaller numbers), Spatial-Numerical Association of Response Codes (SNARC; faster left/right responses to small/large numbers), linguistic markedness (MARC; faster left/right responses to odd/even numbers) and semantic congruity effects (faster smaller/larger decisions over smaller/larger number pairs). Results converge on the notion of a spatially oriented mental number line (MNL) where numerically smaller number concepts exist to the left of larger number concepts. How do these performance signatures help us to understand the cognitive representation of negative number symbols (−1, −2, −3 etc.)? Unlike natural number symbols, negative number symbols lack corresponding real entities that support sensory-motor learning. We discuss a recent proposal by Varma and Schwartz (2011) with implications for developmental research.
Terminological Clarification
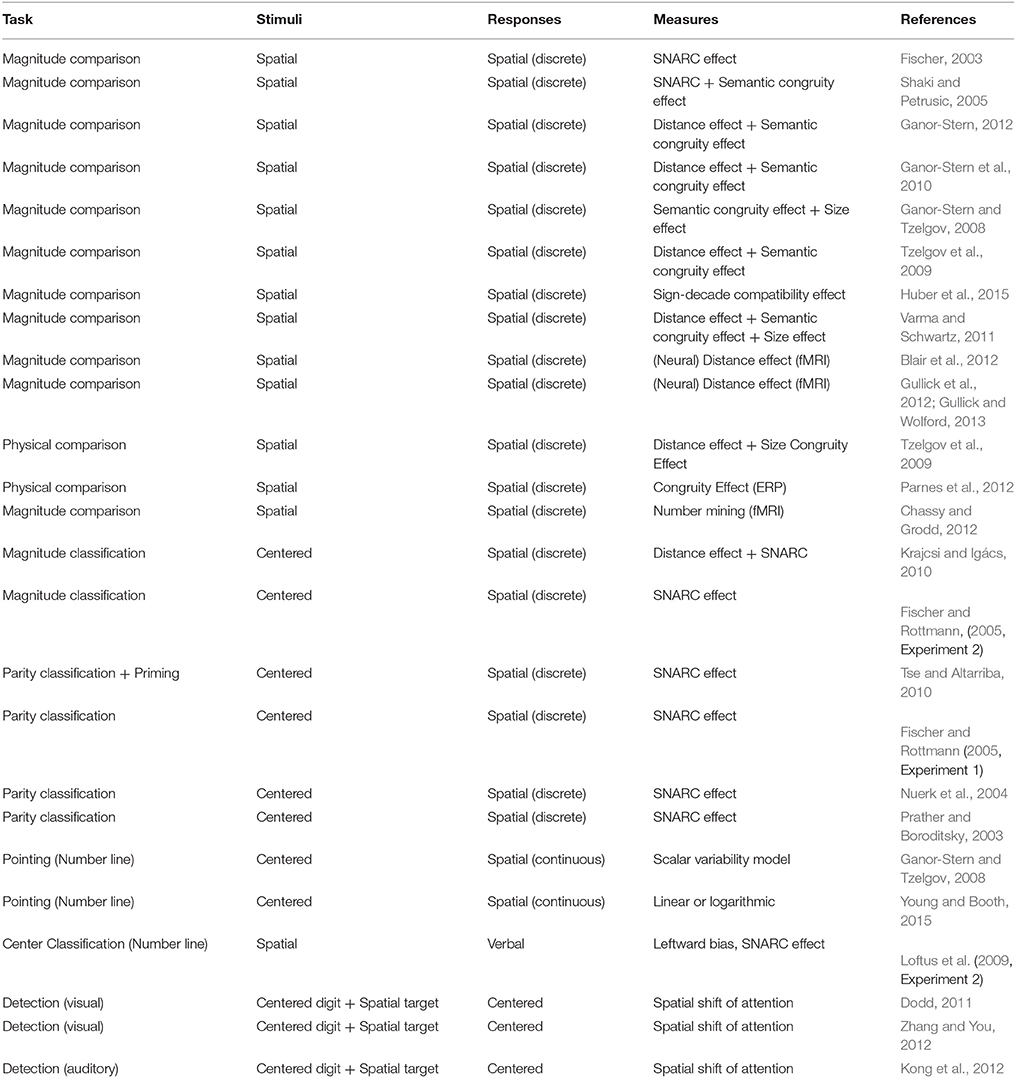
Different terms distinguish two fundamentally different views regarding the cognitive representation of negative numbers: The first view states that negative numbers are cognitively represented to the left of positive numbers, thereby extending the MNL infinitely leftward (henceforth called “extended MNL account”). The second view states that negative numbers have no cognitive representations but are understood through augmenting positive entries of the MNL (henceforth called “rule-based MNL account”). This dichotomy reflects identical distinctions made by Fischer (2003: ontogenetic vs. phylogenetic), Shaki and Petrusic (2005: extended number line vs. magnitude polarity), Ganor-Stern and Tzelgov (2008: holistic vs. components) and Varma and Schwartz (2011: analog+ vs. symbol+). Evidence from magnitude comparisons was used to support either account (see Table 1 for more studies) so we review it before recommending methodological improvements.
Evidence from Magnitude Comparison
Magnitude comparison was first used by Fischer (2003) to report a cognitive processing signature for negative numbers: Adults identified the larger of two digits ranging from −9 to +9 and shown in pairs with constant numerical distance (to control both distance and MARC effects). Faster decisions obtained when the spatial arrangement of digits on screen matched a leftward-extended mental number line, thus supporting the extended MNL account. However, Shaki and Petrusic (2005) identified a confound with semantic congruity and showed that results depend on whether positive and negative numbers are blocked or mixed.
Ganor-Stern and Tzelgov (2008) found similar size effects for positive and negative numbers in the comparison task and a systematic decrease of localization variability with increasing number magnitude in a number-to-position task (where adults localized the position of numbers with a mouse cursor on a horizontal line). They inferred a rule-based MNL account.
Varma and Schwartz (2011) found an inverse distance effect in magnitude comparison with adults, inconsistent with a rule-based MNL which predicted no distance effect at all in mixed comparisons (with one positive and one negative integer), due to superficial sign comparisons. The authors augmented the extended MNL account by postulating additional knowledge about the relationship between positive and negative number concepts which is not available yet to 6th graders because they showed no inverse distance effect and thus used a rule-based MNL.
Evidence from other Methods
This conclusion is surprising, given the wide consensus for a concrete-to-abstract shift in knowledge development. Why are conclusions so heterogeneous, even when using a single task? Other methods assessed negative number representation, including pointing, parity judgments, brain activation, eye movement recording and computer simulation (see Table 1 for details). For example, Gullick and Wolford (2013) investigated neural distance effects in children. They found that IPS activity increased with age while parietal, frontal and precentral activity decreased, consistent with an anterior-posterior shift during maturation (Rivera et al.,2005). They concluded that practice and experience help to integrate negative numbers into an extended mental number line. In addition, Young and Booth (2015) found results both in line with an extended MNL and in line with a rule-based MNL account in two pointing experiments with middle school students. The authors concluded that this conflicting pattern could reflect under-developed number knowledge and differences in previous number exposure. In summary, previous findings in adult and children studies are highly controversial. The lack of consistent effects in adults does not provide a sufficient basis for firm developmental interpretations, thus distorting current conclusions about the development of negative number processing.
Methodological Comment
We believe that this ongoing debate benefits from a methodological comment. Specifically, we note that all published studies on negative number processing either presented spatially distributed stimuli or recorded response speed with lateralized keys (see Table 1). This use of spatially distributed stimuli or responses permits participants different strategies (e.g., selective attending to the sign or “mirroring” cf. Varma and Schwartz, 2011) and induces extraneous biases (e.g., the semantic congruity effect), all of which contaminates number processing (Fischer and Rottmann, 2005; Shaki and Petrusic, 2005; Gevers et al., 2010; Fischer and Shaki, 2016).
To address this concern, we recently developed a method where positive and negative numbers are interleaved with spatially oriented objects. Participants only ever see a single stimulus (number or object) and respond with a single button only if the relevant part of a conjunction rule was fulfilled (Fischer and Shaki, 2017). Examples are “respond only if the number is larger than −5 or the car is facing left” (incongruent rule) or “respond only if the number is smaller than−5 or the car is facing left” (congruent rule). We found that negative numbers are associated with space according to their signed magnitude, thus resolving the long-standing debate about the cognitive representation of negative numbers (Fischer, 2003; Shaki and Petrusic, 2005): Once the task prevents strategies, an extended mental number line prevails. This conclusion is based on results from a paradigm free of spatial or reporting biases. It can, in turn, inform our studies of the development of negative number concepts (Shaki and Fischer, 2018).
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Blair, K. P., Rosenberg-Lee, M., Tsang, J. M., Schwartz, D. L., and Menon, V. (2012). Beyond natural numbers: negative number representation in parietal cortex. Hum. Neurosci. 6, 1–17. doi: 10.3389/fnhum.2012.00007
Chassy, P., and Grodd, W. (2012). Comparison of quantities: core and format-dependent regions as revealed by fMRI. Cereb. Cortex 22, 1420–1430. doi: 10.1093/cercor/bhr219
Dehaene, S., Bossini, S., and Giraux, P. (1993). The mental representation of parity and number magnitude. J. Exper. Psychol. 122, 371–396. doi: 10.1037/0096-3445.122.3.371
Dodd, M. D. (2011). Negative numbers eliminate, but do not reverse, the attentional SNARC effect. Psychol. Res. 75, 2–9. doi: 10.1007/s00426-010-0283-6
Fischer, M. H. (2003). Cognitive representation of negative numbers. Psychol. Sci. 14, 278–282. doi: 10.1111/1467-9280.03435
Fischer, M. H., and Rottmann, J. (2005). Do negative numbers have a place on the mental number line? Psychology Science 47, 22–32.
Fischer, M. H., and Shaki, S. (2014). Spatial associations in numerical cognition—From single digits to arithmetic. Q. J. Exper. Psychol. 67, 1461–1483. doi: 10.1080/17470218.2014.927515
Fischer, M. H., and Shaki, S. (2016). Measuring spatial–numerical associations: evidence for a purely conceptual link. Psychol. Res. 80, 109–112. doi: 10.1007/s00426-015-0646-0
Fischer, M. H., and Shaki, S. (2017). Implicit spatial-numerical associations: negative numbers and the role of counting direction. J. Exp. Psychol. 43, 639–643. doi: 10.1037/xhp0000369
Ganor-Stern, D. (2012). Fractions but not negative numbers are represented on the mental number line. Acty Psychol. 139, 350–357. doi: 10.1016/j.actpsy.2011.11.008
Ganor-Stern, D., Pinhas, M., Kallai, A., and Tzelgov, J. (2010). Holistic representation of negative numbers is formed when needed for the task. Q. J. Exp. Psychol. 63, 1969–1981. doi: 10.1080/17470211003721667
Ganor-Stern, D., and Tzelgov, J. (2008). Negative numbers are generated in the mind. Exp. Psychol. 55, 157–163. doi: 10.1027/1618-3169.55.3.157
Gevers, W., Santens, S., Dhooge, E., Chen, Q., Van den Bossche, L., Fias, W., et al. (2010). Verbal-spatial and visuospatial coding of number–space interactions. J.Exper. Psychol. 139, 180. doi: 10.1037/a0017688
Gullick, M. M., and Wolford, G. (2013). Understanding less than nothing: children's neural response to negative numbers shifts across age and accuracy. Front. Psychol. 4, 1–17. doi: 10.3389/fpsyg.2013.00584
Gullick, M. M., Wolford, G., and Temple, E. (2012). Understanding less than nothing: neural distance effects for negative numbers. Neuroimage 62, 542–554. doi: 10.1016/j.neuroimage.2012.04.058
Holyoak, K. J. (1978). Comparative judgments with numerical reference points. Cogn. Psychol. 10, 203–243. doi: 10.1016/0010-0285(78)90014-2
Huber, S., Cornelsen, S., Moeller, K., and Nuerk, H. C. (2015). Toward a model framework of generalized parallel componential processing of multi-symbol numbers. J. Exp. Psychol. Learn. Mem. Cogn. 41, 732–745. doi: 10.1037/xlm0000043
Kong, F., Zhao, J., and You, X. (2012). Components representation of negative numbers: evidence from auditory stimuli detection and number classification tasks. Q. J. Exper. Psychol. 65, 691–701. doi: 10.1080/17470218.2011.622048
Krajcsi, A., and Igács, J. (2010). Processing negative numbers by transforming negatives to positive range and by sign shortcut. Eur. J. Cog. Psychol. 22, 1021–1038. doi: 10.1080/09541440903211113
Loftus, A. M., Nicholls, M. E., Mattingley, J. B., Chapman, H. L., and Bradshaw, J. L. (2009). Pseudoneglect for the bisection of mental number lines. Q. J. Exp. Psychol. 62, 925–945. doi: 10.1080/17470210802305318
Nuerk, H. C., Iversen, W., and Willmes, K. (2004). Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect. Q. J. Exp. Psychol. Sect. A 57, 835–863. doi: 10.1080/02724980343000512
Parnes, M., Berger, A., and Tzelgov, J. (2012). Brain representations of negative numbers. Can. J. Exper. Psychol. 66:251. doi: 10.1037/a0028989
Prather, R. W., and Boroditsky, L. (2003, January). “Left of zero: Representing negative numbers on the mental number line,” in 25th Annual Meeting of the Cognitive Science Society (Boston, MA).
Rivera, S. M., Reiss, A. L., Eckert, M. A., and Menon, V. (2005). Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb. Cortex 15, 1779–1790. doi: 10.1093/cercor/bhi055
Shaki, S., and Petrusic, W. M. (2005). On the mental representation of negative numbers: context-dependent SNARC effects with comparative judgments. Psychonomic Bull. Rev. 12, 931–937. doi: 10.3758/BF03196788
Tse, C. S., and Altarriba, J. (2010). The revelation of the negative side of a mental number line depends on list context: evidence from a sign priming paradigm. Eur. J. Cogn. Psychol. 22, 1248–1260. doi: 10.1080/09541440903427495
Tzelgov, J., Ganor-Stern, D., and Maymon-Schreiber, K. (2009). The representation of negative numbers: exploring the effects of mode of processing and notation. Q. J. Exp. Psychol. 62, 605–624. doi: 10.1080/17470210802034751
Varma, S., and Schwartz, D. L. (2011). The mental representation of integers: an abstract-to-concrete shift in the understanding of mathematical concepts. Cognition 121, 363–385. doi: 10.1016/j.cognition.2011.08.005
Young, L. K., and Booth, J. L. (2015). Student magnitude knowledge of negative numbers. J. Num. Cogn. 1, 38–55. doi: 10.5964/jnc.v1i1.7
Keywords: cognitive development, mental number line, negative numbers, embodied cognition, abstract concepts
Citation: Mende MA, Shaki S and Fischer MH (2018) Commentary: The mental representation of integers: An abstract-to-concrete shift in the understanding of mathematical concepts. Front. Psychol. 9:209. doi: 10.3389/fpsyg.2018.00209
Received: 17 November 2017; Accepted: 07 February 2018;
Published: 27 February 2018.
Edited by:
Frank Domahs, Philipps University of Marburg, GermanyReviewed by:
Ken Hiraiwa, Meiji Gakuin University, JapanSashank Varma, University of Minnesota, United States
Daniel L Schwartz, Stanford University, United States
Copyright © 2018 Mende, Shaki and Fischer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martin H. Fischer, bWFydGluZkB1bmktcG90c2RhbS5kZQ==
 Melinda A. Mende
Melinda A. Mende Samuel Shaki
Samuel Shaki Martin H. Fischer
Martin H. Fischer