- 1China Academy of Big Data for Education, Qufu Normal University, Qufu, China
- 2Department of Psychology, School of Education, Qufu Normal University, Qufu, China
- 3Collaborative Innovation Center of Assessment toward Basic Education Quality, Beijing Normal University, Beijing, China
- 4School of Economics and Management, Taishan University, Tai'an, China
As a class of discrete latent variable models, cognitive diagnostic models have been widely researched in education, psychology, and many other disciplines. Detecting and eliminating differential item functioning (DIF) items from cognitive diagnostic tests is of great importance for test fairness and validity. A Monte Carlo study with varying manipulated factors was carried out to investigate the performance of the Mantel-Haenszel (MH), logistic regression (LR), and Wald tests based on item-wise information, cross-product information, observed information, and sandwich-type covariance matrices (denoted by Wd, WXPD, WObs, and WSw, respectively) for DIF detection. The results showed that (1) the WXPD and LR methods had the best performance in controlling Type I error rates among the six methods investigated in this study and (2) under the uniform DIF condition, when the item quality was high or medium, the power of WXPD, WObs, and WSw was comparable with or superior to that of MH and LR, but when the item quality was low, WXPD, WObs, and WSw were less powerful than MH and LR. Under the non-uniform DIF condition, the power of WXPD, WObs, and WSw was comparable with or higher than that of LR.
Introduction
Cognitive diagnostic models (CDMs) as a class of discrete latent variable models have been developed to provide finer-grained and multidimensional diagnostic feedback information about examinees' strengths and weaknesses on a set of attributes. However, inferences based on CDMs are invalid when an item functions unequally for examinees with the same attribute mastery pattern but from different population groups. In CDMs, an item is assumed to function differently when subjects from different groups but with the same attribute mastery pattern nevertheless have different probabilities of answering the item correctly. Manifest group characteristics (e.g., gender, age, and race/ethnicity) are typically treated as proxy variables that may lead to DIF, and several studies tried to explore underlying sociological and psychological reasons why DIF occurred in practice (see e.g., Svetina et al., 2017; George and Robitzsch, 2018). The occurrence of differential item functioning (DIF) in CDMs could possibly lead to severe consequences, such as inaccurate and imprecise item and attribute mastery pattern estimates (Hou et al., 2014). Given that, great importance has been attached to detecting and eliminating DIF items from cognitive diagnostic tests, DIF should be routinely detected to ensure the fairness and validity of the tests in practice applications.
Several DIF detection methods have been proposed and investigated in the framework of CDMs (Zhang, 2006; Li, 2008; Hou et al., 2014; Wang et al., 2014; Li and Wang, 2015; Liu et al., 2016b), which can be classified into two types, CDM based and not. For example, the modified higher-order DINA (Li, 2008) and log-linear cognitive diagnosis models for DIF assessment (Li and Wang, 2015), for which the model parameters were estimated using the Markov chain Monte Carlo (MCMC) algorithm, and the Wald test, for which MCMC or maximum likelihood estimation was used for estimating the item parameters (Hou et al., 2014; Li and Wang, 2015) are the CDM-based method. The Mantel-Haenszel (MH; Mantel and Haenszel, 1959; Mantel, 1963) test, the simultaneous item bias test (SIBTEST; Shealy and Stout, 1993), and logistic regression (LR; Swaminathan and Rogers, 1990) are non-parametric methods that are not based on CDMs. Zhang (2006) investigated the performance of MH and SIBTEST for DIF detection using attribute mastery profiles as the matching variables; however, the attribute mastery profiles were estimated under the assumption that the item parameters for the reference and focal groups were the same, and both tests exhibited very low power to detect non-uniform DIF. Although the modified higher-order DINA model for DIF analysis proposed by Li (2008) had acceptable Type I error rate control, one of the limitations of Li's method was that the author imposed a very strong assumption on the attribute mastery patterns. Hou et al. (2014) proposed that the Wald statistic can be used to detect DIF, and they found that the performance of the Wald test was comparable with or superior to that of MH and SIBTEST in detecting uniform DIF. However, Hou et al. (2014) and Wang et al. (2014) found that the Wald statistic (Wd) based on the information matrix estimation method developed by de la Torre (2011) yielded inflated Type I error rates. Li and Wang (2015) compared the empirical performance of the LCDM-DIF method with the Wald method for two and three groups using the MCMC algorithm, and they found that the Type I error rates of the LCDM-DIF were better controlled than the Wald statistic under most conditions, however, for the three-group conditions, the power of the Wald method was slightly better than that of the LCDM-DIF. Svetina et al. (2018) evaluated the impact of Q-matrix misspecification on the performance of LR, MH, and Wd for detecting DIF in CDMs. They found that the Type I error rate control of LR and MH was better than that of Wd; LR and Wd had greater power than MH and the performance of LR, MH, and Wd was affected by Q-matrix misspecification.
The Wd test for DIF detection that was used in previous studies (Hou et al., 2014; Svetina et al., 2018) was based on item-wise information matrix. However, Liu et al. (2016a) pointed out that because the item and the structural model parameters are simultaneously estimated from the item response data, the information matrix of CDMs should contain both item and structural parameters. The item-wise information matrix underestimate the variance-covariance matrix of item parameters (Philipp et al., 2018). As alternatives, cross-product (XPD) information, observed (Obs) information, and sandwich-type (Sw) covariance matrices have been proposed for estimating asymptotic covariance matrices of item parameters (Liu et al., 2016b, 2019; Philipp et al., 2018). That is, the item parameter covariance matrix used to compute the Wald statistic can be estimated using XPD, Obs, or Sw matrix (statistics denoted as WXPD, WObs, and WSw, respectively). Liu et al. (2016b) evaluated the empirical performance of WXPD and WObs for detecting DIF in CDMs following Hou et al.'s (2014) simulation design. They found that when the sample size was 1,000 and the attribute correlation was 0, following Bradley's (1978) liberal criteria (1978), WXPD and WObs had accurate Type I error rates.
In summary, the main focus of this study was to investigate the empirical behavior of the Wald statistic based on the XPD, Obs, Sw, and item-wise information matrices for DIF detection and to compare these Wald statistics with MH and LR using DINA model as an example. The remainder of this article is organized as follows. Firstly, we introduce the DINA model and item parameter covariance matrix estimation procedures as the basis of the estimation of the Wald statistics for DIF detection. Secondly, we outline the DIF detection methods investigated in this study. Thirdly, we present the results of simulation studies conducted to systematically evaluate the DIF detection methods under various conditions. Finally, a discussion of the findings is provided.
Background
Assume that there are N examinees responding to J dichotomous items, in which K binary attributes are diagnosed. The number of the possible attribute mastery patterns is L = 2K, , and is the structural parameter vector that describes the probability of a randomly selected examinee belonging to the lth attribute mastery pattern,
note that ηL is fixed at zero for purposes of model identification (Rupp et al., 2010; Liu et al., 2016a). A J × K binary Q-matrix specifies the relationships between items and attributes; ; qjk = 1 when the jth item requires mastery of the kth attribute; and qjk = 0 otherwise. According to the DINA model, the probability of endorsing item j for the nth examinee given αn and qj is
where is a binary indicator function, the guessing parameter gj denotes the probability that an examinee who lacks at least one of the required attributes gives a correct response, and the slipping parameter sj is the probability that an examinee who has mastered all the required attributes gives an incorrect response.
Although the maximum marginal likelihood with the expectation–maximization (EM) algorithm provides an elegant solution to estimating the model parameters of CDMs, computing the variance-covariance matrix for item parameters is a challenging process under the EM framework. Calculating the matrix requires the inverse of the information matrix in which the item and structural parameters should be simultaneously considered (Liu et al., 2016b). Denote the marginal likelihood of the nth examinee's response pattern xn as
where β = (λ′, η′)′ denotes model parameters, denotes item parameters, and . Then, the log-likelihood function of the observed item response data matrix is
Under the necessary regularity conditions (Bishop et al., 1975), the XPD information matrix is the cross-product of the first-order derivatives of the ℓ(β|x) with respect to the model parameters β:
The Obs information matrix is the negative of the second-order derivatives of the ℓ(β|x) with respect to the model parameters β:
Finally, the Sw matrix can be expressed as
The detailed derivation process can be found in Liu et al.'s (2018) study. For the DINA model, the XPD and Obs matrices can be expressed as
Wald Statistics for DIF Detection
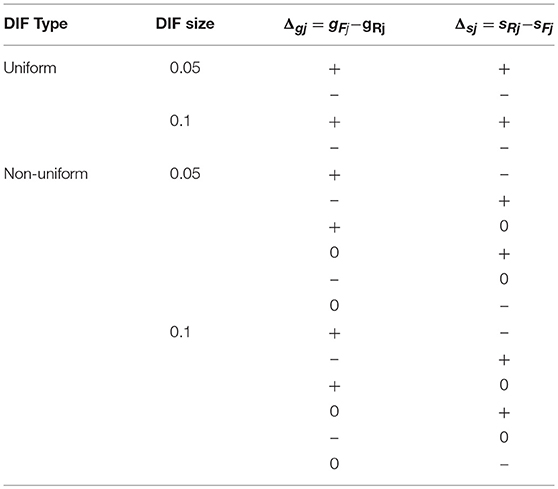
In CDMs, DIF refers to the differences in the probabilities of correctly answering an item for examinees from different groups with the same attribute mastery pattern (Hou et al., 2014; Li and Wang, 2015). Uniform DIF refers to cases when the probabilities of correctly answering an item are uniformly higher or lower for one group across all attribute mastery patterns. Non-uniform DIF occurs if the differences in the probabilities of correctly answering an item between groups depend on the attribute mastery patterns. Theoretically, in the DINA model DIF occurs in item j when
and/or
where subscript “F” refers to the focal group and “R” refers to the reference group. Item j exhibits uniform DIF if Δgj and Δsj have the same signs:
On the other hand, non-uniform DIF occurs.
The Wald test for DIF detection proposed by Hou et al. (2014) in the DINA model evaluates the significance of the joint differences between the item parameters of two groups:
where , is the asymptotic variance-covariance matrix associated with the item parameter estimates for both groups, and C is a contrast matrix:
Under the null hypothesis of H0: Cvj = 0, Wd asymptotically follows a chi-square distribution with 2 degrees of freedom. However, authors of previous studies (Hou et al., 2014; Svetina et al., 2018) showed that Wd tended to have inflated Type I errors and the WXPD and WObs performed better than that for Wd with regard to Type I error control (Liu et al., 2016b).
MH and LR
MH and LR are non-CDM-based DIF detection methods. MH evaluates if the examinees' item responses are independent of group membership after conditioning on the observed total score (Mantel and Haenszel, 1959; Mantel, 1963). Let Nm denote the number of examinees with observed total test score m from the focal and reference groups. The Nm examinees are cross classified into a 2 × 2 contingency table according to their group membership and their responses to item j. Let Am and Bm denote the numbers of correct and incorrect responses to item j in the reference group, respectively. Let Cm and Dm be the corresponding numbers of correct and incorrect responses in the focal group, respectively. The numbers of examinees in the reference group and the focal group are NmR = Am + Bm and NmF = Cm + Dm, respectively; the numbers of correct and incorrect responses are Nm1 = Am + Cm and Nm0 = Bm + Dm, respectively. The MH statistic can be computed by
where
and
Under the null hypothesis that the examinees' responses are independent of group membership, the MH statistic asymptotically follows a chi-square distribution with 1 degree of freedom.
The LR approach (Swaminathan and Rogers, 1990) is based on the logistic regression model for predicting the probability of a correct response to item j from group membership, total test score, and the interaction of these two factors. The full logistic regression model is given by
where πn is the probability that examinee n correctly answers item j, Mn is examinee n's total score, Gn is the group membership, and τ0, τ1, τ2, and τ3 are the regression coefficients. If item j does not exhibit any DIF, then τ2 = τ3 = 0; if item j presents uniform DIF, then τ2 ≠ 0 and τ3 = 0; and if τ3 ≠ 0, item j shows non-uniform DIF.
Simulation Design
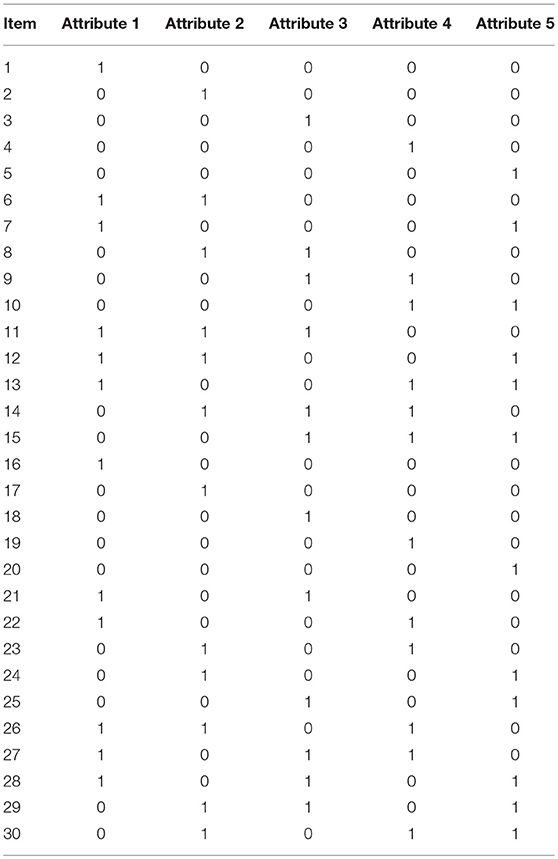
The purpose of this simulation study was to systematically investigate the Type I error and power performances of Wd, WXPD, WObs, WSw, MH, and LR for detecting DIF. The settings of the simulation draw on those of previous real data analyses and simulations on DIF detection methods in CDMs (e.g., de la Torre and Douglas, 2004; Hou et al., 2014; Li and Wang, 2015; Svetina et al., 2018). The test length, sample size, and number of attributes were fixed to J = 30, N = 1, 000, and K = 5, respectively, and the binary item response data sets were generated from the DINA model. The Q-matrix is presented in Table 1.
Five factors that might affect the performance of these methods were manipulated, namely, item quality, attribute correlation, percentage of DIF items, DIF effect size, and DIF type. In the CDM literature (e.g., de la Torre and Douglas, 2004), the guessing and slip parameters of DINA model were typically in the range of (0.1, 0.3), and previous simulation studies (Hou et al., 2014; Liu et al., 2016b) showed that the Type I error rate control of Wald statistics was affected by the item reference slip and guessing parameter values. In this study, the item parameters of the reference group for the high, medium, and low item quality conditions were fixed to 0.1, 0.2, and 0.3, respectively. In previous DIF simulation studies (e.g., Hou et al., 2014; Liu et al., 2016b) the correlation coefficient between two attributes was fixed to 0, however, according to Kunina-Habenicht et al. (2012), attribute correlation coefficient was typically in the range of (0.5, 0.8). In this study, three attribute correlation coefficient levels ρ = 0, 0.5, and 0.8 were considered, which allowed for a more realistic depiction of the attribute correlation between attributes seen in practical cognitive diagnostic assessments. The percentage of DIF items had two levels, 10 and 30%. The DIF effect size had two levels, 0.05 (small DIF) or 0.1 (large DIF). There were also two DIF types, uniform or non-uniform. The summary of DIF conditions are shown in Table 2. Note that to ensure that the item parameters for the focal group would be larger than zero, for the λj = 0.1 condition, only the small DIF size was considered. This yielded 240 conditions for data generation. For each simulation condition, 200 converged replications were used to evaluate the performance of DIF detection methods. The simulation study was implemented in R (R Core Team, 2018), the R packages CDM (Robitzsch et al., 2018) and dcminfo (Liu and Xin, 2017) were used to estimate the model parameters and the asymptotic covariance matrices of item parameter estimates, respectively, the R functions for Wald statistic calculation were modified from the CDM package, the MH and LR tests were performed using the R package difR (Magis et al., 2010). The R codes in this study are available upon request from the corresponding author.
For the purpose of this study, the performance of the Wd, WXPD, WObs, WSw, MH, and LR methods was evaluated in terms of Type I error rate and power. Type I error rate was computed as the proportion of non-DIF items incorrectly flagged as DIF items. On the other hand, empirical power was computed as the proportion of DIF items that were correctly identified. The empirical Type I error rate of the DIF detection method in the interval [0.025, 0.075] for the nominal level of 0.05 was considered to be accurate (Bradley, 1978).
Results
The averaged Type I error rate control results for these six methods under the uniform and non-uniform DIF conditions for different percentages of DIF items, attribute correlations, and reference item parameters across the 200 replications showed similar patterns; thus, only the Type I error rate results for the uniform DIF condition are shown graphically in Figure 1. In general, the empirical Type I error rates for WXPD, WObs, and WSw were better than those for Wd under all conditions. Consistent with the results reported in previous studies (e.g., Hou et al., 2014; Wang et al., 2014; Svetina et al., 2018), the Type I error rates for Wd were somewhat inflated under most of the conditions. Moreover, although the performances of WXPD, WObs, and WSw seemed to be influenced by the attribute correlation, the Type I error rates for those methods were reasonably close to the nominal Type I rate of 0.05 under most of the simulation conditions. For most conditions, WXPD had good performance in controlling Type I error rates; the only exceptions were for conditions ρ = 0.8 and λRj = 0.1, for which the Type I error rates were slightly higher than the nominal level. The Type I error rates were close to the nominal level for WObs and WSw on most occasions except when λRj = 0.1, or λRj = 0.2 under the ρ = 0.8 condition. The performance of the WXPD was found to perform slightly better than WObs and WSw in controlling Type I error rates when ρ = 0.8. It was found that under the null hypothesis, MH and LR tended to be somewhat conservative, with Type I error rates consistently below the nominal level when λRj = 0.1. The Type I error rates for WXPD and LR were in the range of [0.025, 0.075] under most of the simulation conditions, which suggested that WXPD and LR had the best performance in controlling Type I error rates among the six methods investigated in this study.
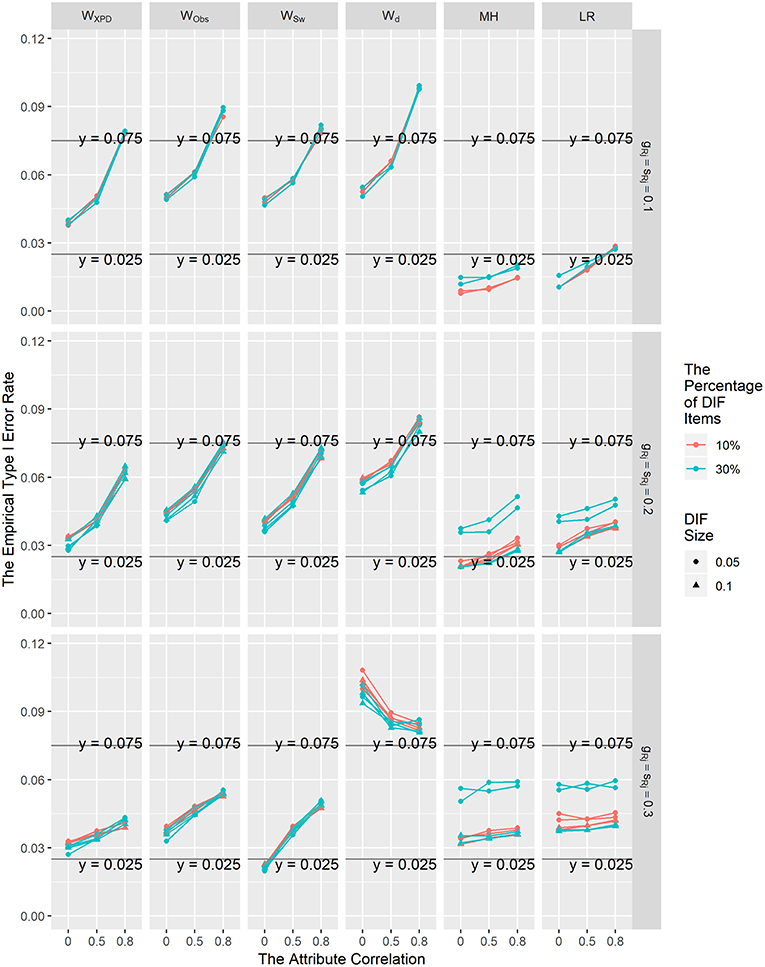
Figure 1. The Type I error rates for the Wd, WXPD, WObs, WSw, MH, and LR methods under the uniform DIF condition.
The empirical power results for WXPD, WObs, WSw, MH, and LR for detecting uniform DIF are shown in Figure 2. The power results for Wd method are not reported, due to its inflated Type I error rates. In Figure 2, it is clear that the DIF size and reference item parameter values influenced the power rates of the WXPD, WObs, WSw, MH, and LR; as the DIF effect size increased, the power rates of these five methods increased. Specifically, when DIF size was 0.1, the power rates were all above 0.8, and when DIF size was 0.05, the power of these methods decreased as item parameter values increased. The power for WXPD, WObs, and WSw was comparable with or superior to that for MH and LR under λRj = 0.1 and λRj = 0.2 condition; in contrast, WXPD, WObs, and WSw were less powerful than MH and LR under λRj = 0.3. The power for WXPD, WObs, and WSw increased as attribute correlation values increased when DIF size was .05. Figure 2 demonstrates that for the MH and LR methods, when DIF size was 0.05, the power increased as the proportion of DIF items decreased or the attribute correlation increased. In contrast, for WXPD, WObs, and WSw, the power decreased as the attribute correlation increased when DIF size was 0.05 and λRj = 0.3. Similar to the results reported by Hou et al. (2014), we found that the power for WXPD, WObs, and WSw was not affected by the percentage of DIF items.
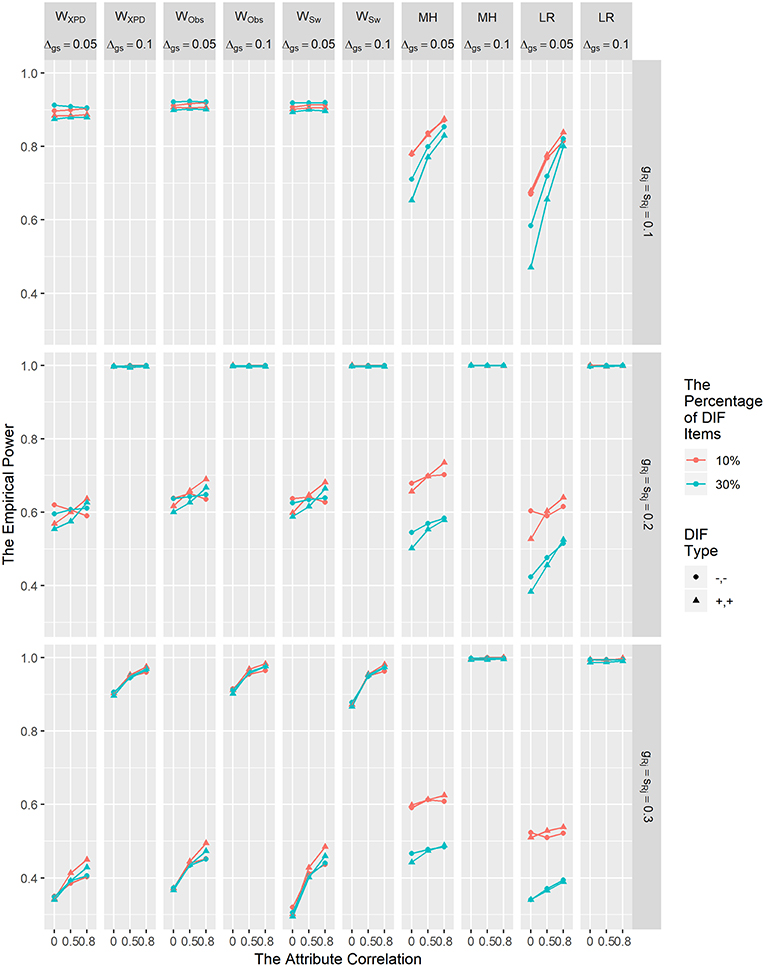
Figure 2. The empirical power results of the WXPD, WObs, WSw, MH, and LR methods under the uniform DIF condition.
Figure 3 depicts the power results for WXPD, WObs, WSw, and LR for detecting non-uniform DIF. The power results for MH are not presented in Figure 3, since MH is only capable of detecting uniform DIF. In general, the power of WXPD, WObs, and WSw was comparable with or higher than that of LR under all conditions. As shown in Figure 3, the power rates for the non-uniform DIF conditions were similar to those for the uniform DIF conditions in that the power increased with larger DIF size, and smaller reference item parameter values regardless of other factors. Close inspection of the results in Figures 2, 3 reveals that the power of the MH and LR methods decreased with more DIF items under most of the conditions; in contrast, the power of the Wald statistics was not affected by the percentage of DIF items.
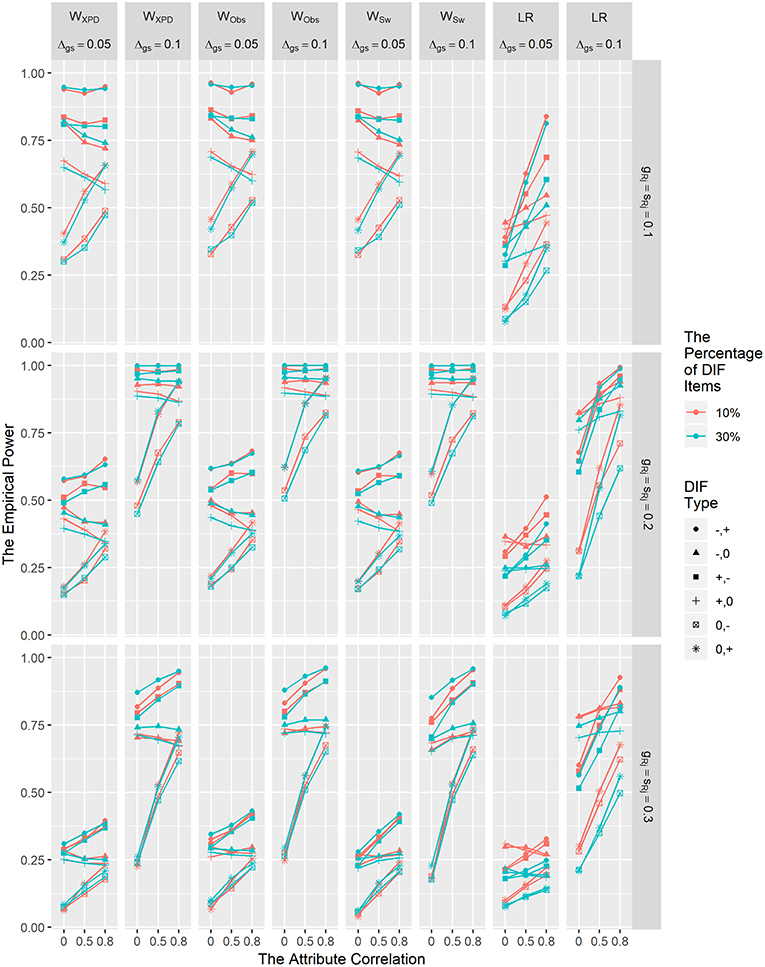
Figure 3. The empirical power results of the WXPD, WObs, WSw, and LR methods under the non-uniform DIF condition.
Summary and Discussion
Given the fact that detecting and eliminating DIF items from cognitive diagnostic tests is important for test fairness and validity, researchers have proposed a number of CDM-based and non-CDM-based DIF detection methods. Previous studies (Hou et al., 2014; Svetina et al., 2018) found that although the power of Wd was comparable with or better than that of LR and MH, the Type I error rate for Wd can be inflated under certain conditions because of the method's underestimated item parameter covariance matrix. Alternative information matrix estimation methods such as XPD, Obs, and Sw have been proposed to calculate item parameter covariance matrices in CDMs in which the item parameters and structural model parameters are simultaneously considered (Liu et al., 2016b, 2018; Philipp et al., 2018). Motivated by these findings, in the current study we sought to systematically evaluate the performance of the Wald tests based on item-wise, XPD, Obs, and Sw matrices and to compare the behavior of the CDM-based DIF detection methods Wd, WXPD, WObs, and WSw and the non-CDM-based DIF methods MH and LR under various simulation conditions.
In this study, it was found that the Type I error rate control of WXPD, WObs, and WSw was generally better than that of Wd. WXPD had slightly better performance in controlling Type I error rates than did WObs or WSw under most conditions. The power of WXPD, WObs, and WSw was generally better than that for LR and MH, especially when the item quality was medium or high under most of the simulation conditions. As far as we are aware, this study is the first to compare the Wald statistic based on the XPD, Obs, or Sw matrix with LR and MH. The results provide strong evidence that among the six DIF detection methods investigated in this study, WXPD performed best in terms of Type I errors and power under most of the conditions. We believe the current study contributes valuable information regarding the DIF detection methods in CDMs for practical implications.
In spite of the encouraging results, there are, of course, a number of limitations that should be noted here. First, it should be noted that in CDM-based DIF detection, the good performance of the Wald statistic depends highly on the accuracy of the item parameter estimates; for example the Type I error for WXPD was somewhat high when λRj = 0.1 and ρ = 0.8, and its power decreased as the item quality decreased.
Second, the test length, sample size, and number of attributes in this study were fixed. To further generalize the simulation results, future studies that involve a wider range of conditions are needed. Third, even though this simulation was carefully designed to mimic those of CDM practices and simulations on DIF detection methods (de la Torre and Douglas, 2004; Hou et al., 2014; Li and Wang, 2015; Svetina et al., 2018), the findings of this study rely on the assumptions that the fitted model and the corresponding Q-matrix were correctly specified, which may limit the generalizability of our findings. For example, in the present study, the DINA model, which has been frequently used in applications, was taken as an example to compare the performance of the DIF detection methods. However, DINA is one of, if not the most restrictive, simplest model, and previous studies (Ma et al., 2016; Liu et al., 2018) have shown that no single CDM suits all the test items in many, if not all, diagnostic applications. It would be useful to examine the empirical behavior of the DIF detection methods in the in the context of general CDMs, such as the general diagnostic model (von Davier, 2008), the log-linear cognitive diagnosis model (Henson et al., 2009) and the generalized DINA model (de la Torre, 2011). Fourth, model misspecification is virtually unavoidable in real-world data analyses (Liu et al., 2016a), further studies are needed to investigate the performance of the DIF detection methods under varying degree of misspecified models, especially with real data examples. Since we believe more simulations are needed before researchers can be sure how to use DIF detection methods safely in CDMs, real data analyses were not conducted in this study.
In conclusion, the simulation study shows that WXPD, WObs, and WSw perform better than Wd, LR, and MH in terms of Type I errors and power.
Author Contributions
YL and TX developed the original idea, carried out the simulations and analyses. YL, HY, LS, and LY were involved in drafting and revising the manuscript. All authors approve the final manuscript submitted.
Funding
This work was supported by the Cultural Experts, and “Four Groups of Talented People” Foundation of China and Natural Science Foundation of Shandong Province, China (Grant No. ZR2019BC084).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Bishop, Y. M., Fienberg, S. E., and Holland, P. W. (1975). Discrete Multivariate Analysis: Theory and Practice. Cambridge, MA: MIT Press.
Bradley, J. V. (1978). Robustness?. Br. J. Math. Stat. Psychol. 31, 144–152. doi: 10.1111/j.2044-8317.1978.tb00581.x
de la Torre, J. (2011). The generalized DINA model framework. Psychometrika 76, 179–199. doi: 10.1007/s11336-011-9207-7
de la Torre, J., and Douglas, J. A. (2004). Higher-order latent trait models for cognitive diagnosis. Psychometrika 69, 333–353. doi: 10.1007/BF02295640
George, A. C., and Robitzsch, A. (2018). Focusing on interactions between content and cognition: a new perspective on gender differences in mathematical sub-competencies. Appl. Meas. Educ. 31, 79–97. doi: 10.1080/08957347.2017.1391260
Henson, R. A., Templin, J. L., and Willse, J. T. (2009). Defining a family of cognitive diagnosis models using log-linear models with latent variables. Psychometrika 74, 191–210. doi: 10.1007/s11336-008-9089-5
Hou, L., de la Torre, J. D., and Nandakumar, R. (2014). Differential item functioning assessment in cognitive diagnostic modeling: application of the Wald test to investigate DIF in the DINA model. J. Educ. Meas. 51, 98–125. doi: 10.1111/jedm.12036
Kunina-Habenicht, O., Rupp, A. A., and Wilhelm, O. (2012). The impact of model misspecification on parameter estimation and item-fit assessment in log-linear diagnostic classification models. J. Educ. Meas. 49, 59–81. doi: 10.1111/j.1745-3984.2011.00160.x
Li, F. (2008). A Modified Higher-Order DINA Model for Detecting Differential Item Functioning and Differential Attribute Functioning. Doctoral dissertation, University of Georgia, Athens, GA.
Li, X., and Wang, W. C. (2015). Assessment of differential item functioning under cognitive diagnosis models: the DINA model example. J. Educ. Meas. 52, 28–54. doi: 10.1111/jedm.12061
Liu, Y. L., Andersson, B., Xin, T., Zhang, H. Y., and Wang, L. L. (2018). Improved Wald statistics for item-level model comparison in diagnostic classification models. Appl. Psychol. Meas. doi: 10.1177/0146621618798664. [Epub ahead of print].
Liu, Y. L., Tian, W., and Xin, T. (2016a). An Application of M2 Statistic to Evaluate the Fit of Cognitive Diagnostic Models. J. Educ. Behav. Stat. 41, 3–26. doi: 10.3102/1076998615621293
Liu, Y. L., and Xin, T. (2017). dcminfo: Information Matrix for Diagnostic Classification Models. R package version 0.1.7. Retrieved from the Comprehensive R Archive Network [CRAN]: https://CRAN.R-project.org/package=dcminfo (accessed December 15, 2018).
Liu, Y. L., Xin, T., Andersson, B., and Tian, W. (2019). Information matrix estimation procedures for cognitive diagnostic models. Br. J. Math. Stat. Psychol. 72, 18–37. doi: 10.1111/bmsp.12134
Liu, Y. L., Xin, T., Li, L., Tian, W., and Liu, X. (2016b). An improved method for differential item functioning detection in cognitive diagnosis models: an application of Wald statistic based on observed information matrix. Acta Psychol. Sin. 48, 588–598. doi: 10.3724/SP.J.1041.2016.00588
Ma, W. C., Iaconangelo, C., and de la Torre, J. (2016). Model similarity, model selection, and attribute classification. Appl. Psychol. Meas. 40, 200–217. doi: 10.1177/0146621615621717
Magis, D., Béland, S., Tuerlinckx, F., and Boeck, P. D. (2010). A general framework and an R package for the detection of dichotomous differential item functioning. Behav. Res. Methods 42, 847–862. doi: 10.3758/BRM.42.3.847
Mantel, N. (1963). Chi-square tests with one degree of freedom; extensions of the mantel-haenszel procedure. J. Am. Stat. Assoc. 58, 690–700.
Mantel, N., and Haenszel, W. (1959). Statistical aspects of the analysis of data from retrospective studies of disease. J. Natl. Cancer Inst. 22, 719–748. doi: 10.2307/2282717
Philipp, M., Strobl, C., de la Torre, J., and Zeileis, A. (2018). On the estimation of standard errors in cognitive diagnosis models. J. Educ. Behav. Stat. 43, 88–115. doi: 10.3102/1076998617719728
R Core Team (2018). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Robitzsch, A., Kiefer, T., George, A. C., and Uenlue, A. (2018). CDM: Cognitive Diagnosis Modeling. R package version 7.1–20. Retrieved from the Comprehensive R Archive Network [CRAN]: http://CRAN.R-project.org/package=CDM (accessed December 15, 2018).
Rupp, A. A., Templin, J., and Henson, R. A. (2010). Diagnostic Measurement: Theory, Methods, and Applications. New York, NY: Guilford Press.
Shealy, R., and Stout, W. (1993). A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF. Psychometrika 58, 159–194. doi: 10.1007/BF02294572
Svetina, D., Dai, S., and Wang, X. (2017). Use of cognitive diagnostic model to study differential item functioning in accommodations. Behaviormetrika 44, 313–349. doi: 10.1007/s41237-017-0021-0
Svetina, D., Feng, Y., Paulsen, J., Valdivia, M., Valdivia, A., and Dai, S. (2018). Examining DIF in the context of CDMs when the Q-matrix is misspecified. Front. Psychol. 9:696. doi: 10.3389/fpsyg.2018.00696
Swaminathan, H., and Rogers, H. J. (1990). Detecting differential item functioning using logistic regression procedures. J. Educ. Meas. 27, 361–370. doi: 10.1111/j.1745-3984.1990.tb00754.x
von Davier, M. (2008). A general diagnostic model applied to language testing data. Br. J. Math. Stat. Psychol. 61, 287–307. doi: 10.1348/000711007X193957
Wang, Z. R., Guo, L., and Bian, Y. F. (2014). Comparison of DIF detecting methods in cognitive diagnostic test. Acta Psychol. Sin. 46, 1923–1932. doi: 10.3724/SP.J.1041.2014.01923
Keywords: cognitive diagnostic model, Wald statistics, differential item functioning, information matrix, logistic regression method
Citation: Liu Y, Yin H, Xin T, Shao L and Yuan L (2019) A Comparison of Differential Item Functioning Detection Methods in Cognitive Diagnostic Models. Front. Psychol. 10:1137. doi: 10.3389/fpsyg.2019.01137
Received: 04 November 2018; Accepted: 30 April 2019;
Published: 17 May 2019.
Edited by:
Yanyan Sheng, Southern Illinois University Carbondale, United StatesReviewed by:
Dubravka Svetina, Indiana University Bloomington, United StatesRaman Grover, British Columbia Ministry of Education, Canada
Copyright © 2019 Liu, Yin, Xin, Shao and Yuan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tao Xin, eGludGFvQGJudS5lZHUuY24=
 Yanlou Liu
Yanlou Liu Hao Yin
Hao Yin Tao Xin
Tao Xin Laicheng Shao
Laicheng Shao Lu Yuan
Lu Yuan