- 1School of Education, Faculty of Humanities, Arts, Social Sciences and Education, University of New England, Armidale, NSW, Australia
- 2Institute for Positive Psychology and Education, Australian Catholic University, Sydney, NSW, Australia
One notable concept that is of interest is a person’s state of optimal functioning. Achieving optimal functioning (e.g., subjective well-being at school), aside from personal autonomy, requires some form of “optimization.” Optimization, we argue, is more than just an “enhancement,” a “predictive effect,” and/or a “causal flow” between an independent variable (IV) and a dependent variable (DV). We note from existing literature that optimization has often been referred to without a clear, definitive explanation of what this term actually entails. At the same time, we acknowledge that unlike other areas of development (e.g., engagement), no theoretical article is available to explain the concept of optimization. This article considers a number of theoretical tenets for advancement: (1) the tenet of three major criteria that could assist in the explanation, assessment, and measurement of optimization, (2) the tenet of the development of a methodological conceptualization that could measure and assess optimization, and (3) the tenet of the “quantification” of optimization, and in particular, a proposed index of optimization and a corresponding scientific notation of “γ”, which we coin as an “optimizing effect.” Overall, we contend that this examination is insightful and holistic, seeking clarity into an important topical theme in psychology.
Introduction
One notable line of research in psychology that has recently received considerable interest is the operational nature of optimal functioning. Optimal functioning, which may be in physical, cognitive, emotional, and/or social terms, emphasizes the importance of a person’s inner strength, state of resilience, virtue, and the maximization in capability (Source: Applied Psychology: Health and Well-being). Optimal functioning reflects the paradigm of positive psychology (Seligman and Csikszentmihalyi, 2000; Seligman, 2010), and may in the context of academia, involve the experience of mastery, and/or the achievement of an exceptional academic result. Optimal functioning in a nonacademic arena, likewise, may indicate a football player’s exceptional achievement to score 50 goals in one season, for example. This theoretical concept of optimal functioning is in direct contrast to personal experiences of stagnation and pessimism, highlighting weakness, sub-optimal performance, and minimal potential. The concept of optimal functioning therefore takes a positive perspective. However, what optimal functioning constitutes and how optimization of human functioning operates are not clearly defined and understood. The aim of this article is to conduct an in-depth examination of the theories related to the concept of optimization and to propose future directions for research advancement.
Understanding Optimization
Relating to the concept of optimal functioning is a question that we, as researchers, have made concerted attempts to address: how does a person reach an optimal state of functioning? This important question has led to our numerous empirical and conceptual undertakings, which specifically focus on the complexity of the operational mechanism of optimal functioning. What causes an exceptional state of functioning? What actually occurs as a state of functioning improves from one level to that of another level? How does the cause of optimal functioning associate with a level of optimal functioning? These three major questions have, to date, formed the central premise of existing research inquiries and our own contributions. Understanding this complexity of optimal functioning (e.g., how a person reaches a state of optimal cognitive functioning) is innovative, especially in terms of educational and social practices for implementation. From the context of successful schooling, for example, we could capitalize on this line of research development and design appropriate educational programs and/or pedagogical strategies, which may closely align with the optimization of students’ learning experiences.
The study of the processes of optimal functioning, from our point of view, is emerging and has received moderate attention. We recognize there are some prominent theoretical tenets that have, likewise, considered the improvement of cognitive functioning. For example, Vygotsky’s (1978, 1981) sociocultural theory of cognitive development stipulates the potent impact of the contextual environment to shape a person’s cognitive development. Psychological tools and cultural artifacts, such as mathematical symbols and notations may mediate a student’s progress in his/her understanding of problem solving. In particular, Vygotsky (1978) makes reference to an important term, coined as the “zone of proximal development,” which depicts the difference between what a person can do without help and what he/she can do with help (e.g., scaffolding). Piaget’s (1963) theory of personal constructivism, somewhat different from Vygotsky’s (1978) theory, contends that cognitive growth arises from a person’s experience resolution of disequilibrium via means of adaptation. In school contexts, according to Piaget’s (1963) theory, effective learning occurs when a child experiences a mental state of cognitive conflict. Learning outcomes that do not stimulate intellectual challenges or “flow” (Csíkszentmihályi, 1990; Seligman and Csikszentmihalyi, 2000) are more likely, in this analysis, to limit enriched cognitive experiences.
In sum then, our brief introduction contends that an optimal state of functioning indicates personal growth, improvement, and exceptional performance. Achieving this optimal state of functioning requires some form of scaffolding from the external world. Notwithstanding existing theoretical contributions (Piaget, 1963; Vygotsky, 1978), one element that has gone amiss is an in-depth examination of the actual operation involved in the achievement of optimal functioning. This operation, from our point of view and proposition, is known as the process of “optimization” (Phan et al., 2019a, b). The term optimization, extensively used in the academic literature (e.g., Freund and Baltes, 1998; Fraillon, 2004; Ziegelmann and Lippke, 2007) is inconsistently explained, and has not been adequately addressed. The true nature of optimization, we argue, is relatively unknown at present in terms of analysis and understanding. What actually occurs during the process of optimization? How does the process of optimization explain a person’s optimal best practice? Can the process of optimization be “quantified” and be represented by a scientific notation? These questions indicate the totality of our understanding of optimal functioning.
Optimal Functioning: An Introduction
Optimal functioning is a perceived positive theoretical concept that emphasizes the importance of improved competence, personal best or exceptionality, and a strong sense of motivation and resilience. Optimal functioning situated within the context of academia is also analogously termed as optimal best practice (Phan et al., 2016, 2018a) and personal best (Martin, 2006, 2011). An analysis of the literature indicates that, likewise, educators and researchers have often referred to the notion of an “optimal condition” for effective learning and enriched schooling experiences. An educator, for example, may consider strategies and/or programs that could stimulate and foster a positive social climate for learning, which in turn could instill a perceived sense of school belonging for students (Goodenow, 1993; Goodenow and Grady, 1993).
Optimal functioning is a central feat of human agency and may apply to different complex contexts in life (Straszewski and Siegel, 2018; Wiese et al., 2018). Optimal functioning, in this case, may consist of different facets – for example, optimal physical functioning, optimal cognitive functioning, optimal emotional functioning, etc. In the areas of health and subjective well-being, researchers have, for example, explored the concept of optimal subjective well-being (Fraillon, 2004; ACU and Erebus International, 2008). This research inquiry, indeed, has led to the propositions of a number of definitions and views about the nature of optimal functioning. The literature review published by the Australian Catholic University (ACU) in 2004 specifically elucidated the essence of optimal functioning, which the researchers expressed their understanding – “maximizing one’s potential” (Dunn, 1961; Ryff, 1995), “pursuit of excellence in physical, mental, emotional, and spiritual realm” (Ardell, 1982), “an active process of fulfillment” (Hettler, 1984), “living and working effectively” (Corbin, 1997), “living fully in the natural community” (Witmer and Sweeney, 1998), “resilience and successful community participation” (Weisner, 1998), “holistic, positive emotions” (Stewart-Brown, 2000), “positive emotions, life satisfaction, and absence of negative emotions” (Diener and Biswas-Diener, 2002), “positive feelings and positive psychosocial functioning” (Keyes, 2002), “resilience, satisfaction, and maximizing one’s potential” (Bornstein et al., 2003), “positive feelings and life satisfaction” (Headey and Wooden, 2004), “positive state and satisfaction of needs” (Prilleltensky and Prilleltensky, 2006), and “resilience and maximizing one’s potential” (WHO, 2007).
From this theoretical overview (ACU and Erebus International, 2008), a person’s achievement of optimal functioning indicates numerous attributes that are positive – for example, self-fulfillment and inner satisfaction, exceptional accomplishment, and enrichment and personal growth. Depending on the nature of the context, a person may experience different types of attributes when he/she achieves optimal functioning. From an educational perspective, optimal functioning in an academic subject may reflect different learning experiences: a student’s ability to continuously perform and achieve outstanding results in Year-8 mathematics and receiving an “A” grade at the end of the school term (Phan et al., 2017), or a student’s seeking of mastery to know the different pedagogical approaches that could enable in-depth understanding of a topical theme (i.e., ability to solve challenging transfer percentage problems) (Ngu et al., 2018). At the same time, aside from mastery and performance-based accomplishments, optimal functioning may indicate a student’s heightened state of motivation (e.g., intrinsic) to persist with his/her studies (Church et al., 2001; Elliot and Murayama, 2008). From a noneducational point of view, likewise, optimal functioning on a daily basis may indicate a person’s positive outlook about life, and his/her strong state of personal resolute and resilience to combat health-related matters. Low optimal functioning, in this case, may result in feelings of pessimism and helplessness, and a belief that existing health issues are not worth combatting.
Overall then, from the aforementioned description, we contend that optimal functioning is an important element of a person’s development. Optimal functioning, in its simplistic summation, is concerned with an individual state of “change” that a person experiences for the better. Job satisfaction, combatting health, a positive outlook of life, personal best in sports performance, and successful schooling are some examples of a person’s positive experience of optimal functioning. Of relevance and significance in this discussion, which we next discuss, is an in-depth analysis and understanding of how an optimal level of functioning is accomplished. For example, within the context of academia, we want to consider in-class pedagogical strategies, school-based educational programs, and/or the use of intellectual capitals to enhance and optimize students’ cognitive functioning. This feat concerning the nature of achievement of optimal functioning has not been adequately addressed. We do not have clear evidence at present, both conceptually and empirically, to explain how a state of optimal best is ascertained. What are the underlying processes, which may govern our drive to achieve a state of exceptionality?
Our proposition of a detailed conceptualization of optimization, which may explain the intricate processes of achievement of optimal functioning, draws from existing theorizations (e.g., Csíkszentmihályi, 1990; Fraillon, 2004; Phan et al., 2017) and empirical research findings (Martin, 2011; Liem et al., 2012; Phan et al., 2018a,b,c). Optimization, as we conceptualize, is not an outcome or a relationship, but rather depicts an underlying process that in turn “optimizes” an entity in question (e.g., a person’s academic learning experience in a subject matter). In addition, we have also recently considered a related theoretical matter, namely, the conceptualization and development of appropriate methodologies that could enable the assessment and validation of optimization. This research-based discourse is innovative as emphasis is placed on researchers’ theoretical contributions to the study of a conceptualized inquiry.
The Operational Nature of Optimization
What is optimization? In the preceding sections, we mentioned that optimization is an intricate process that closely aligns with the achievement of optimal functioning. An examination of the literature indicates that researchers have extensively used the term optimization in their researches (e.g., Freund and Baltes, 1998; Fraillon, 2004; Ziegelmann and Lippke, 2007). We contend there is ambiguity as to what optimization actually entails as a process. From a generic, simple point of view, optimization may be perceived as a “vehicle” that operates to maximize a person’s state of functioning from T1 to T2. In recent years, researchers in the areas of subjective well-being (Fredrickson, 2000; Keyes et al., 2002) and healthcare and aging for senior citizens (Freund and Baltes, 1998; Ziegelmann and Lippke, 2007) have made extensive reference to the concept of optimization. For example, in relation to healthcare for senior citizens, a number of researchers have theorized that optimization serves as a process of engagement in goal-directed actions and means to pursue and maintain personally relevant goals (e.g., a goal of adopting and maintaining a physically active lifestyle). In relation to the study of positive psychology, likewise, Noble and McGrath (2008) proposed a Positive Educational Practices (PEPs) Framework that focuses on five specific foundations of well-being, namely: (1) social and emotional competency, (2) positive emotions, (3) positive relationships, (4) engagement through strengths, and (5) a sense of meaning and purpose. This framework, according to the authors, provides guidance to educators, school administrators, and researchers in the optimization of positive educational initiatives. The PEPs Framework, in this case, facilitates and encourages students to find a sense of meaning at school, and a purpose in life. In a similar vein, Seligman’s (e.g., Seligman and Csikszentmihalyi, 2000; Seligman, 2010, 2011) work on the PERMA Framework has also acknowledged the importance of happiness, resilience, and personal growth. One central aspect of human endeavor encompasses an inner desire and striving for one to lead and live a meaningful and enriching life.
Other researchers, similarly, have explored other comparable concepts that we believe reflect the relatedness to the process of optimization. Diener (e.g., Diener et al., 2009, 2010) and other colleagues (e.g., Keyes, 2002; Huppert and So, 2013) have explored the concept of flourishing, which is defined as a person’s experience that life is going well. In a similar vein, a research focus on the proactivity and enrichment of life has led to the propositions of theoretical constructs such as thriving (Su et al., 2014; Wiese et al., 2018), defined as “a state of positive functioning at its fullest range” (Su et al., 2014), and personal striving (Phan and Ngu, 2015; Phan et al., 2018a,b,c), defined as “a person’s effort attempt to seek out realistic and/or ambitious endeavor for accomplishment” (Phan et al., 2018a,b,c). Flourishing, thriving, and personal striving are in accord with the paradigm of positive psychology (Seligman and Csikszentmihalyi, 2000; Seligman, 2010), and place emphasis on a person’s seeking to achieve optimal endeavors.
Understanding the true mechanism of optimization, theoretically and/or empirically, is relatively unknown at this stage. This consideration, in particular, depicts the finer detail of the “steps” involved in the achievement of optimal functioning. A few researchers have, in this instance, provided comparable explanations of the operational nature of optimization. Fraillon’s (2004) discussion paper on the subject of student well-being, for example, described an interesting tenet – namely a person’s actual best functioning (ABF) and his/her subsequent notional best functioning (NBF). Optimization, for the author, is defined as the difference between ABF and NBF. From Fraillon’s (2004) brief account, Phan et al. (2017) presented an elaborated conceptualization of the relationship between two levels of functioning – realistic best (RB) and optimal best (OB). Importantly, the authors’ conceptualization proposes an important element coined as the “zone of optimization,” which is defined as the difference or range between RB and OB. The zone of optimization varies in the magnitude of the difference or range between the two levels of functioning. Moreover, as a point for consideration, the zone of optimization seeks to explain the “amount” of optimization that would be needed to help optimize the achievement of OB from RB.
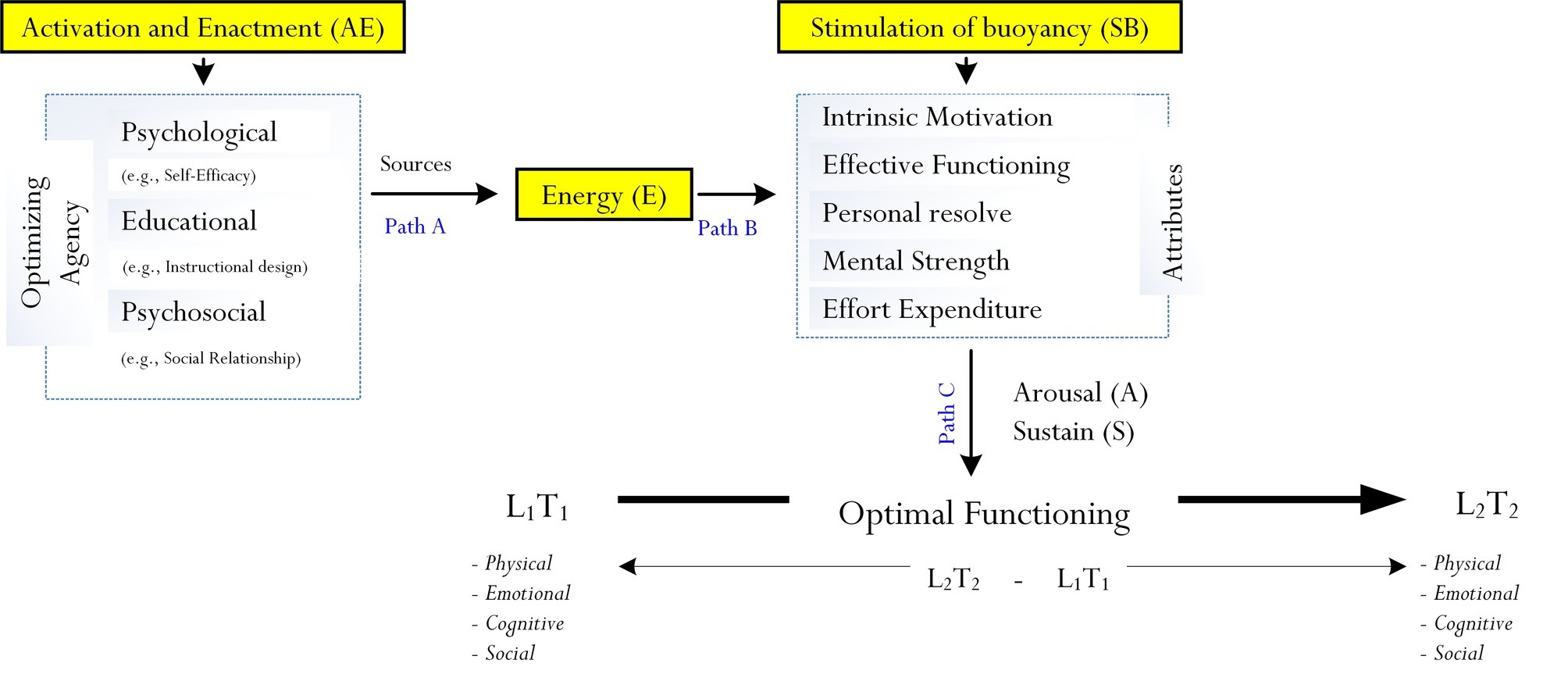
Fraillon’s (2004) initial, but brief description of optimization and Phan et al.’s (2017) subsequent analysis both have provided theoretical grounding for further development. In our own recent research inquiries pertaining to the nature and scope of mindfulness (Phan et al., 2019a,b), we offered an expanded perspective and explanation of optimization. Our conceptualization, as shown in Figure 1, is more detailed and technical. In terms of different levels of functioning (e.g., RB: Phan et al., 2017), we argue that time precedence is an important element for incorporation – in other words, different levels of functioning cannot take place simultaneously.
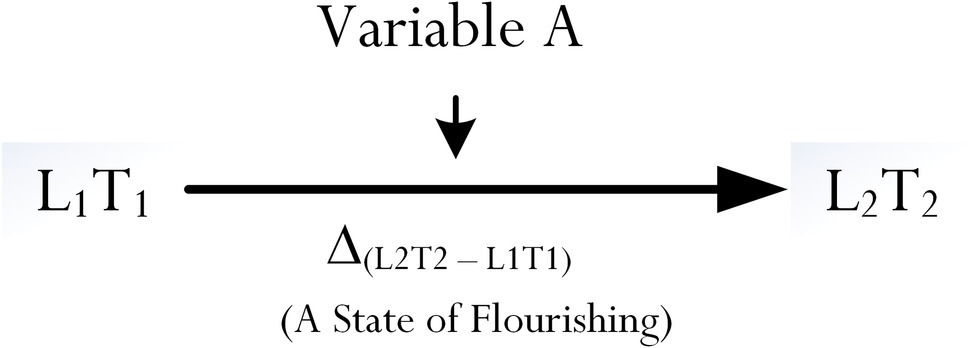
From Figure 1, we propose that optimal functioning is the result of a progression from an existing level of functioning, denoted as L1, to a level that is more exceptional, denoted as L2. Mathematically, in this analysis, a person’s progression from L1 to L2 is denoted as Δ(L2–L1). We argue for the inclusion of time difference because, as Fraillon (2004) and Phan et al. (2017) concur, L1 is indicative of a what person is capable of at present, whereas L2 is concerned with his/her maximum outcome. Being able to achieve L2 from L1 does not occur instantaneously, but rather requires an adequate timeframe for completion. Hence, from our conceptualization, we equate L1 to situate at T1 and L2 to situate at T2 – hence, overall, the achievement of optimal functioning may be defined as Δ(L2T2–L1T1).
Methodologically, from a quantitative point of view (Tabachnick and Fidell, 2007), we may consider the assessment, measurement, and validation of Δ(L2T2–L1T1). Social science’s research has used complex quantitative methodological designs to investigate associative and predictive effects of psychological and educational variables. Nonexperimentally, in this instance, we could consider the introduction of a variable A, which is then proposed to help “optimize” the improvement in score of L1 to L2 (Figure 2). Moreover, we expect to find that Δ(L2T2–L1T1) would be positive in value. This proposition, in this case, stipulates an association between Variable A and Δ(L2T2–L1T1).
Baron and Kenny’s (1986) seminal publication has resulted in extensive research development into the importance of mediating effects of variables (e.g., Grice et al., 2015; Kline, 2015; Tate, 2015; Trafimow, 2015). In this analysis, referring to our explanation, a central variable A could operate to mediate the effect of L1 at T1 onto L2 at T2 which can be tested in a series of path models: (1) Test 1: estimates a model in which only L1 predicts L 2, (2) Test 2: estimates a model in which only Variable A predicts L2, (3) Test 3: estimates a model in which only L1 predicts Variable A, and (4) Test 4: assesses the reduction in the path from L1 to L2 with the introduction of Variable A as a mediator. Importantly though, in order to determine a true mediating effect and the potency of a mediator, we need to have evidence of causal effects, which in this case requires an experimental treatment or treatments, and the precedence of time difference.
Referring to Figure 2, and in tandem with Baron and Kenny’s (1986) criteria, it is poignant for us to consider the use of an intervention between T1 and T2. Referring to our previous discussion, Variable A could be considered as an “optimizing variable” between a determinant, L1, and an outcome, L2 – that is: L1 at T1 (determinant) → Variable A (optimizing variable) → L2 at T2 (outcome). In sum, from this introduction of a simple methodological design of optimal functioning, we propose three major criteria:
1. L1 as an informational source, which then serves as a point of reference for the achievement of L2.
2. The requirement of timeframe in order for a person to develop and experience an “increase” in optimal functioning (e.g., emotional functioning) – that is, the existence of multiple time points, which correspond with different levels of functioning – for example, L1 at T1, L2 at T2, etc.
3. The introduction of an intervention, which could operate as an “optimizing agent” in order to enhance and optimize L1 to L2.
Aside from a methodological account, we also need to consider the nature of Variable A. How does Variable A operate in order to facilitate an improvement of L2 from L1? The operational nature of Variable A, we contend, is intricate for its variation, which closely associates with the complexity of the Δ(L2T2–L1T1). This proposition is similar to Phan et al.’s (2017) zone of optimization, whereby this “zone” differs and connotes a magnitude in strength for the process of optimization. What does this actually mean? For example, in relation to optimal health functioning, a person may require a substantial time period to combat an illness. An optimizing agent (i.e., Variable A) to improve the person’s health, in this case, may consist of an effective therapy, varying in intensity in accordance with the difference between L1 and L2. In a similar vein, a secondary school student wishing to achieve an optimal level of best practice in the topical theme of essay composition, based on his/her previous experiences, may require a lesser amount of time in terms of optimization. An optimizing agent to address Δ(L2T2–L1T1) for writing composition may consist of an academic skills program that also vary in intensity.
An In-Depth Analysis of the Operational Nature of Optimization
Variable A, as depicted in Figure 2, is proposed to operate as an optimizing agent, which then optimizes and enhances the achievement of L1 to L2. This proposition has been extensively detailed in Phan et al.’s (2017) theorization of optimization. From a methodological point of view, we could treat Variable A as a mediator between L1 and L2, and that there is a direct predictive path from L1 to L2. However, aside from its assessment and measurement, we contend that the totality and operational nature of Variable A is much more complex than it being viewed and treated as a mediator. Phan et al. (2017), in this case, proposed an underlying process encompassing this complexity, which comprises of two major sub-processes:
1. Sub-process 1 concerns the “enactment” of different types of psychological (e.g., the positive impact of hope: Snyder, 2004), educational (e.g., an appropriate pedagogical practice: Ngu et al., 2014), and psychosocial (e.g., the complexity of the home environment: Daulta, 2008) agencies, which then initiate sub-process 2.
2. Sub-process 2 involves the activation of the attributes of persistence, effort expenditure, and effective functioning, which then operate to optimize a state of functioning.
Both Fraillon’s (2004) consideration and Phan et al.’s (2017) theoretical model of optimization suggests that the process of optimization is more than just a directional association between sub-process 1 and sub-process 2. The “totality” of optimization, we propose, encompasses the stimulation and enrichment of experience of vitality and buoyancy. In this analysis, the enactment of optimization is likely to result in an enriched state of energy, strength, and liveliness, which would then enable a person to engage in proactive functioning. This complexity, we contend, is more accurately indicative of what actually occurs within the process of optimization. As shown in Figure 1, there are three pathways: Path A, Path B, and Path C. These paths tend to operate in a sequential manner, following these steps:
1. Step 1: This step, in line with Phan et al.’s (2017) theorization, is concerned with the activation and enactment (i.e., denoted as “AE”) of different psychological (e.g., the impact of hope: Snyder et al., 2000), educational (e.g., an appropriate instructional design: Ngu and Yeung, 2013), and/or psychosocial (e.g., the impact of teacher-student relationship: Roorda et al., 2011) agencies that then serve as sources of a person’s state of “energy” (we denote this as “E”). We argue that the activation and enactment of a particular agent (e.g., psychological agency) does not necessarily influence cognitive or motivational processes directly. Rather, the execution (i.e., activation and enactment) of an optimizing agent (e.g., psychological agent) serves to produce an experience of high “energy.” Energization is therefore an underlying sub-process of optimization, which in this case entails the experience and indication of vitality and buoyancy, assisting a person to stay focused on task.
Vitality, from our conceptualization, forms a central element of the process of optimization. Personal experience of vitality (e.g., “I feel very energized at the moment”) is positive and enriching, predisposing a person to strife for the achievement of an optimal state of functioning. Importantly, of course, vitality is concerned with the observation and reporting of “stamina and liveliness” in cognition, behavior, and/or emotion, contrasting to a state of pessimism and procrastination, which correspondingly associate with a low level of energy. The selection, activation, and enactment of a specific optimizing agent (e.g., the use of hope as a psychological agent), in this case, depend upon the type of optimal functioning that a person is striving to achieve (e.g., optimal cognitive functioning in the area of mathematics).
2. Step 2: Personal experience of energization from Step 1 is postulated to stimulate the buoyancy of five comparable psychological attributes: intrinsic motivation (i.e., defined as a person’s intrinsic motive to persist a course of action – for example, learning Calculus), personal resolve (i.e., defined as a person’s internal state of decisiveness and resolute to strive for optimal functioning), effective functioning (i.e., defined as a person’s purposive state of organization, structured thoughts, and behavioral patterns and a deliberate intent to succeed), mental strength (i.e., defined as a person’s mindset of having the capacity to deal with obstacles, stressors, and pressure – for example, a tennis player is able to bounce back after losing two out of three games in competition tournament), and effort expenditure (i.e., a person’s conscious attempt to invest effort in order to achieve a particular outcome).
Further to Fraillon’s (2004) brief description and Phan et al.’s (2017) subsequent conceptualization of optimization, we offer an expanded analysis where the sub-process of energization positively influences the operational nature of different types of psychological attributes (e.g., the stimulation of buoyancy of effort) that we perceive as being positive in nature. For example, one psychological attribute that we propose as being potent is a person’s internal mental strength to persevere, whereas another notable and related attribute is that of effort expenditure. Our recent correlational research, likewise, has attested to the direct and mediating effects of personal resolve and effective functioning (e.g., Phan et al., 2018a,b,c, 2019a).
3. Step 3: The stimulation of buoyancy of intrinsic motivation, personal resolve, effective functioning, mental strength, and effort expenditure via positive energy is postulated to arouse a person’s state of functioning at T1 at and sustain it to T2 (e.g., optimal cognitive functioning) (i.e., denoted as “AS”). For example, within the context of secondary schooling, the stimulation of buoyancy of intrinsic motivation may arouse a student’s interest in understanding Calculus, which could then help sustain a state of cognitive functioning. The student’s aroused state of cognitive functioning of mathematics learning, sustaining in progress from T1 to T2, may also involve the stimulation of buoyancy of effort expenditure, personal resolve, etc.
A person’s aroused and sustained state of functioning within a particular context (e.g., academic learning in a subject matter) reflects the effectiveness of the stimulation of buoyancy of different types of psychological attributes. The effective stimulation is facilitated by an enriching state of energy, which arises from the activation and enactment of a relevant educational, psychological, and/or psychosocial agent. A low level of energy, in contrast, is likely to produce the inaction of different types of psychological attributes, resulting in sub-optimal functioning.
In summary, the pivotal components of optimization consist of the activation and enactment of psychological, educational, and psychosocial agencies, which then serve as sources of energy in order to stimulate the buoyancy of the five mentioned comparable attributes. Intrinsic motivation, personal resolve, effective functioning, mental strength, and effort expenditure in turn would individually, and/or in tandem, arouse and sustain a person’s progress in functioning from T1 to T2. In its simplistic term then, we can summarize the operational nature of optimization as follows: AE + E + SB.
Our methodological conceptualization of optimization, which we theoretically derive from previous inquiries (Fraillon, 2004; Phan et al., 2017), partially reflects Vygotsky’s (1978, 1981) sociocultural theory of cognitive development as well as other theories. For example, aligning to Vygotsky’s (1978, 1981) sociocultural theory of cognitive development, our conceptualization highlights three major facets: (1) extensive contributions from an external agent, especially in terms of the provision of opportunities of different types of agency for achievement of optimal functioning (e.g., a child’s exposure to different instructional designs/pedagogical practices from a teacher: Ngu et al., 2014), (2) the “internalization” of a particular agent and its “transformation” into a form of positive energy, and (3) the progress in a person’s state of functioning (e.g., cognitive functioning), consequently, as a result of external scaffolding. Other researchers, in contrast, have been less clear in their explanatory accounts and descriptions of optimal functioning and optimization-related entities.
Methodological Development of Optimization
Our theoretical development of optimization has also led us to consider an important inquiry – namely, the development of what we coin as “methodological conceptualization,” which places an emphasis on the measurement, assessment, and evaluation of optimal functioning, and more importantly, the process of optimization. This methodological inquiry has theoretical, methodological, and empirical implications for consideration. From the perspective of quantitative methodology in the social sciences, there is acknowledgment that researchers may use both experimental and nonexperimental research designs to study associative patterns between variables (Bordens and Abbott, 2008; Gravetter and Forzano, 2009; Babbie, 2014). An important question for discussion then, is how do we measure, assess, and quantify the process of optimization?
Assessing Optimal Functioning
From the preceding sections, the concept of optimal functioning reflects a number of analogous attributes, such as “personal best,” “maximization in capability,” “fullest potential,” and “exceptionality.” Our previous discussion has emphasized a reference point (e.g., T1) for benchmarking and comparison – this reference point may be denoted as L1T1, where L1 = initial level of functioning (e.g., cognitive functioning), T1 = time 1. For example, in the area of mathematics learning, we could consider a student’s current cognitive competence to solve linear equations with one unknown, x (e.g., solve for x: 5x – 11 = 4), as L1. This initial level of cognitive functioning (i.e., L1), known as actual functioning in Fraillon’s (2004) terms, or realistic achievement best in Phan et al.’s (2017), is postulated to act as a focal point for benchmarking. The student’s optimal level, denoted as L2 and benchmarked against L1, may consist of a competence to solve quadratic equations with one unknown, x [e.g., solve for x: (x – 5)2 = 20]. L2 (i.e., learning quadratic equations), compared to L1 (i.e., learning linear equations), is more advanced in terms of quality and cognitive complexity.
The achievement of optimal functioning from a current state of functioning, reflecting personal growth (i.e., “increase in a state of functioning”), may be defined as follows: ΔL21 = L2 T2 – L1 T1. From a quantitative point of view, we need to equate L1 and L2 with actual numerical values in order to determine what ΔL21 is. The “equating” of L1, L2, etc., with specific numerical values is subjective – that is, a student may equate L1 (i.e., knowing how to solve for x: 5x – 11 = 4) with an arbitrary value of 12 (e.g., out of 20), say, and L2 (i.e., knowing how to solve x: (x – 5)2 = 20) with an arbitrary value of 15 (e.g., out of 20), etc. Why do we want to quantify L1, L2, etc.? We contend that quantifying L1, L2, etc. with numerical values (e.g., 9, 10, 11, …, etc.) makes it relatively easy for researchers to rationalize the meaning of ΔL21, ΔL32, etc. In other words, quantitatively, an optimal level of functioning is more meaningful when it is denoted by a definitive numerical value.
Quantifying different levels of functioning with numerical values (e.g., “Provide an arbitrary score that you believe best describes your current level of emotional functioning”), of course, may pose a few problems for researchers, such as inconsistency, subjective bias, and miscalibration. A student’s inexperience in personal reflection, for example, may result in unintentional biased alignment of L1 (e.g., 3 out of 20), L2 (e.g., 12 out of 20), etc. when, in fact, this is not the case. Researchers focusing on students’ self-efficacy for academic learning (Bandura, 1986, 1997), likewise, have reported on the problem of underestimation and overestimation of judgments of perceived competence (Pajares and Kranzler, 1995; Pajares, 1996a,b). This problem of miscalibration of competence beliefs (e.g., underestimation), we contend, may arise from a student’s lack of focus, lack of concentration, and misunderstanding of instruction.
Aside from instructing a person to equate his/her level of an internal state of functioning with a corresponding numerical value, it is also possible to use Likert-scale measures and/or open-ended surveys. In the broad area of subjective well-being, for example, a number of researchers have developed different Likert-scale measures, such as the Comprehensive Inventory of Thriving (CIT) Scale (Su et al., 2014), the Flourishing Scale (Diener et al., 2010), and the Academic Striving Subscale (Phan et al., 2018a,b,c). The use of Likert-scale measures, administered to subjects on multiple occasions, is straightforward and may provide fruitful information about their current state of functioning and the potential of achieving optimal functioning. For example, consider a participant’s response to the Flourishing Scale (Diener et al., 2010) on two occasions, denoted as: Response-FT1 to Response-FT2. A positive change in scores from Response-FT1 and Response-FT2 (Δ(Response-FT2 – Response-FT1) = +ve), in this analysis, would indicate an improvement in personal flourishing from T1 to T2. A negative difference (Δ(Response-FT2 – Response-FT1) = −ve), in contrast, would suggest a decline in a person’s state of flourishing. It is possible, too, for us to explore and identify linear and/or nonlinear trajectories of a person’s subject well-being. The use of latent growth modeling (LGM) procedures, in particular, may also enable researchers to test for effects of extraneous influences on growth trajectories (Bollen and Curran, 2006; Hancock and Lawrence, 2006).
More recently, in an attempt to study the process of optimization (Fraillon, 2004; Phan et al., 2017), Phan et al. (2016) developed a Likert-scale questionnaire to measure and assess current level and optimal level of subjective academic well-being. The Realistic Achievement Best Subscale (e.g., “I am content with what I have accomplished so far for this subject”), according to the authors, explores a person’s actual functioning, whereas the Optimal Achievement Best Subscale (e.g., “I can achieve much more in this subject than I have indicated through my work so far”) reflects the person’s notional best functioning. The Optimal Outcome Questionnaire, as Phan et al. (2016) proposed, may serve as a diagnostic tool to assess students’ “profiles” of cognitive competence in their academic learning (Phan et al., 2018a,b,c). Furthermore, in their detailed theorization of optimization, Phan et al. (2016) postulate the forming of two subscale scores [i.e., the Realistic Achievement Best (RAB) Subscale and the Optimal Achievement Best (OAB) Subscale scores] that would assist in the assessment, measurement, and evaluation of the process of optimization. What is unclear though, from this consideration, is how we could use the RAB and OAB scores to measure and assess the operational nature of optimization.
From an educational perspective then, measuring and assessing a current level of cognitive functioning and an optimal level of cognitive functioning may involve the use of comparable quantitative methodologies, such as Likert-scale measures and cognitive competence tests (e.g., quiz). A robust methodological approach, in this case, may consist of an integration of three comparable measures: Likert-scale measures, the Optimal Outcome Questionnaire (Phan et al., 2016), and standardized testing (Phan et al., 2019a,b). This methodological conceptualization is depicted as follows:
Note: the Likert-scale measure X = Comprehensive Inventory of Thriving (CIT) Scale (Su et al., 2014), the Flourishing Scale (Diener et al., 2010), the Academic Striving Subscale (Phan et al., 2018a,b,c), etc.
The above methodological conceptualization is insightful as it enables us to cross-validate the three comparable measures. The Optimal Outcome Questionnaire is administered to participants at a particular time point (Phan et al., 2016, 2017), and measures and assesses a person’s current level of functioning (i.e., the RAB Subscale) and his/her optimal level of functioning (i.e., the OAB Subscale). Of concern, from our viewpoint, is whether the OAB score actually indicates a person’s optimal best, or whether it is simply an indication of “miscalibrated” and potential optimal best (Phan et al., 2018a,b,c). On this basis, it would be appropriate to cross-validate the Optimal Outcome Questionnaire with another comparable Likert-scale measure (e.g., coined as “X”), administered to a participant on multiple occasions. Longitudinal research designs emphasize the importance of time precedence, stipulating the administration of the same Likert-scale measure on multiple occasions (Rogosa, 1979; MacCallum and Austin, 2000) – for example, a current time point, T1, and a future time point, T2. Hence, considering the Optimal Outcome Questionnaire and Likert-scale measure X, we propose a first iteration (Iteration 1) where there are two associations: (1) rXT1-RAB, which depicts the association between a Likert-scale measure X administered at T1 and the RAB Subscale, and (2) rXT2-OAB, which depicts the association between the same Likert-scale measure X administered at T2 and the OAB Subscale. In this analysis then, in terms of consistency and accuracy, we would expect similar rating scores for the RAB Subscale and the Likert-scale measure X at T1, and for the OAB Subscale and the same Likert-scale measure X at T2, respectively.
A scrutiny of the possibility of miscalibration is important (e.g., Pajares and Miller, 1994; Pajares and Kranzler, 1995; Pajares, 1996a,b) because miscalibration may result in either inflated (e.g., overconfidence of optimal level of cognitive functioning) or deflated (e.g., underconfidence of current level of cognitive functioning) responses. In a similar vein, the use of an identical Likert-scale measure on multiple occasions also poses problems such as identification of familiarity of items, and evidence of autocorrelated errors between items – for example, Item 1 at T1 and Item 1 at T2, Item 2 at T1 and Item 2 at T2, etc. (Bandalos et al., 1995; Marsh and Yeung, 1997; Guay et al., 1999). Addressing these potential problems, we propose a second iteration (Iteration 2), namely: (1) rXT1-STT1, which depicts the association between the Likert-scale measure X administered at T1 and a standardized performance test, denoted as STT1, and (2) rXT2-STT2, which depicts the association between the same Likert-scale measure X administered at T2 and a different standardized performance test, denoted as STT2. Again, in terms of consistency and accuracy, we would expect a similar rating score for the Likert-scale measure X at T1 and the performance score of the standardized test at T1, and for the same Likert-scale measure X at T2 and the performance score of the standardized test at T2.
Finally, in order to validate the nature of the Optimal Outcome Questionnaire (Phan et al., 2016) and taking into account the possible shortcomings of Likert-scale measures, we consider a third iteration (Iteration 3), which emphasizes the potential associations between the Optimal Outcome Questionnaire and standardized testing at T1 and T2: (1) rRAB-STT1, which depicts the association between the RAB Subscale and a standardized test administered at T1, and (2) rOAB-STT2, which depicts the association between the OAB Subscale and a standardized test administered at T2. Similar to the two previous iterations, in terms of consistency and accuracy, we would expect a similar rating score for the RAB Subscale and the performance score of the standardized test at T1, and the OAB Subscale and the performance score of the standardized test at T2.
We contend that the three iterations outlined, in their totality, make substantive contributions to the study of measurement and assessment of optimal functioning. From our rationalization, rXT1-RAB, rRAB-STT1, and rXT1-STT1 would provide theoretical understanding of a current level of functioning [i.e., X(T1) ≈ RAB ≈ ST(T1)], whereas rXT2-OAB, rOAB-STT2, and rXT2-STT2 would provide theoretical understanding of an optimal level of functioning [i.e., X(T2) ≈ OAB ≈ ST(T2)]. The use of any of the three measures alone is somewhat limited, whereas a combination of two or all three measures is more stringent in terms of elucidating the complex nature of optimal functioning. One notable inquiry that has, to date, remained elusive is our theoretical inference and interpretation of Δ [i.e., Δ(XT2 − XT1), Δ(OAB-RAB), and Δ(STT2-STT1)]. For example, given a participant’s response to a Likert-scale measure X at T1 and T2, the Optimal Outcome Questionnaire at T1, and a cognitive competence test at T1 and T2, can we use this information to explain the process of optimization?
The Quantification of Optimization: A Proposed Index of Optimization?
The preceding discussion pertaining to the assessment and measurement of optimal functioning is insightful for the purpose of our proposition: the potential “quantitative” measure of the process of optimization. Referring to our previous mentioning of the three comparable iterations of optimal functioning, we have X(T1), RAB, and ST(T1) as indicators of a current level of functioning, and X(T2), OAB, and ST(T2) as indicators of an optimal level of functioning. Of interest, in this analysis, is whether and/or to what extent the derivative of Δ notation (e.g., Δ(XT2 − XT1)) could align with, and/or fit in with out proposed conceptualization (i.e., activation and enactment of an agent → the sub-process of energization → stimulation of buoyancy of psychological attributes; Figure 1). Empirical validation of optimization (OB), as an underlying process, does not equate to a “predictive effect,” an “enhancement,” and/or a “causal flow.” In other words, at this stage, methodologically and statistically, very little is known about the “quantitative representation” of the process of optimization. A predictive effect, denoted as a beta value (i.e., β), may simply inform us of a positive association between an educational, psychological, or psychosocial agent and an adaptive outcome. For example, in a recent longitudinal, nonexperimental study, Phan et al. (2018a,b,c) found that effective functioning exerted a positive effect on school experience (β = 0.62, p < 0.001) and academic achievement (β = 0.30, p < 0.001). Likewise, in an earlier research, McCartney et al. (2007) reported the positive effect of high quality child care, as an index of a psychosocial agent, on school readiness (β = 0.21, p < 0.01).
A complex issue then relates to the “transformation” of an r value (i.e., an association) or a β value (i.e., a predictive effect) into an “optimizing effect.” What is an “optimizing” effect, and how do we define and/or calculate this optimizing effect? We postulate that an optimizing effect, denoted as “γ,” is derived from three “pathways,” as shown in Figure 1: (1) Path A describes the result of the activation and enactment of psychological, educational, and psychosocial agents, which then results in the process of energization (i.e., AE → E), (2) Path B describes the result of energization, which consequently leads to the stimulation of buoyancy of different psychological attributes (i.e., E → SB), and (3) Path C describes the arousal of an internal state of functioning and its sustained positioning from T1 to T2 (i.e., SB → AS).
Having identified these specific paths, we need to conceptualize the “intensity” of optimization by assigning a numerical value to each effect (e.g., 0 for minimal optimizing effect to 1 for maximal optimizing effect). The quantification of γ, in this instance, would reflect the totality of effects (i.e., the combined effects of Path A, Path B, and Path C). In other words, as a point of summary: γ = Path A + Path B + Path C. An important question for us to consider then, is why would γ vary in its magnitude? Referring back to our conceptualization of optimization, one notable aspect is the difference between L1T1 and L2T2. The Δ(L2T2–L1T1), we argue, is likely to vary in accordance with a person’s current level of functioning (L1T1) and his/her subsequent level of optimal functioning (L2T2). For example, consider mathematics learning for the topic of Algebraic expressions with two different scenarios:
Scenario 1.
L1T1 = knowing how to solve equations with one unknown, x: x + 8 = 10, evaluate x?
L2T2 = knowing how to solve quadratic equations with one unknown, x: (x – 10)2 = 20, evaluate x?
Scenario 2.
L1T1 = knowing how to solve equations with one unknown, x: x + 8 = 10, evaluate x?
L2T2 = knowing how to solve simultaneous equations with two unknowns, x and y: (2x + y) = 9 and (5x – 10y) = 20, solve for x and y.
An analysis of the two mentioned scenarios indicates that L2 cognitive functioning is more complex for Scenario 2 (i.e., simultaneous equations that have two unknowns) than that for Scenario 1 (i.e., equations that have one unknown), suggesting that Δ(L2T2–L1T1) is “larger” in scale or amount for the former. Achieving L2 (i.e., an optimal level) from L1 for Scenario 2 requires “more” effort in terms of optimization. This example, interestingly, emphasizes the potential interrelations between the magnitude (i.e., intensity or strength) of the process of optimization and the range or difference between L1T1 and L2T2. On this basis, the magnitude of the quantification of γ (i.e., reflecting the totality of the process of optimization) is postulated to associate with the “complexity” of L2, and how this optimal level of functioning differs from L1. In formulating a quantitative derivative of this consideration, we recently proposed a theoretical concept, which we coined as the “index of optimization” (i.e., denoted as IO) (Phan et al., 2019a,b). The IO is defined as: Δ(L2T2–L1T1) × γ, where γ = Path A + Path B + Path C.
The index of optimization is the combination (i.e., multiplication) of the difference between L1T1 and L2T2 and the magnitude of the optimizing effect of an educational, psychological, or psychosocial agent. How does the IO help us in our understanding of optimal functioning and optimization? A quantified numerical value of IO, which we propose to range from 0 (e.g., minimal IO) to 1, may elucidate the complexity of Δ(L2T2–L1T1), and the amount of resources that would be needed for optimization to achieve L2 (e.g., ability to solve simultaneous equations with two unknowns)? Importantly, the quantification of IO (close to 1) may also reveal a person’s energy level. A high value of IO, for example, would indicate a person is completely energized, and that the stimulation of buoyancy of different psychological attributes is more likely. A low value of IO (close to 0), in contrast, would indicate a low level of vitality and liveliness.
How do we standardize the measurement and assessment of the IO? Aside from the complexity of Δ(L2T2–L1T1), it is important to highlight that the “combination” in effects of Path A (i.e., AE → E), Path B (i.e., E → SB), and Path C (i.e., SB → AS) in the process of optimization is not easily measured and/or computed. Consider the personal experience of energization, which arises from the activation and enactment of educational, psychological, and psychosocial agents. Measurement and assessment of the sub-process of energization, along with the delving into the subsequent arousal and sustaining of an internal state of functioning is a difficult feat to ascertain. It would be of interest for future research to focus on the development of appropriate methodological designs and measurements that could validate and standardize the proposed IO. For example, the level of optimization to assist a person’s optimal level of emotional functioning (e.g., a positive state of happiness) would differ from that of the level of optimization to facilitate optimal physical functioning (e.g., being able to score 50 goals in one football season). A γ value of “0.4” for the achievement of optimal cognitive functioning would not, in our view, equate to the same γ value of 0.4 for the achievement of optimal physical functioning. In other words, from this comparison, we contend that the index of optimization would vary in accordance with a particular type of functioning (e.g., cognitive functioning versus physical functioning).
Differential Influences of Human Agencies: An Example of Optimal Cognitive Functioning
One notable component of our conceptualization of optimization that is worthy for discussion is the activation and enactment of different agencies to serve as sources of energy. We argue that the differential influences of psychological, educational, and psychosocial agencies are subject to the contextual situation at hand, as well as the timely opportunity that may arise. For example, the optimization of physical functioning (e.g., a football player’s scoring of goals) may benefit more from psychological (e.g., the use of self-efficacy beliefs to convince the football player’s resolve) and/or psychosocial (e.g., the provision of an adequate environment for training) agencies. However, educational agencies (e.g., the teaching of an effective instructional design) could be more appropriate in the optimization of cognitive functioning (e.g., a student’s academic performance in mathematics). In a similar vein, we argue that on a daily basis, the provision of opportunities for optimization purposes may vary in accordance with the contextual situation. What this means is that at any point in time, there are variations in the exposure of psychological, educational, and psychosocial agencies.
Personal energy, we postulate, differentially influence intrinsic motivation, personal resolve, effective functioning, mental strength, and effort expenditure. The stimulation of buoyancy of the five personal attributes that serve to arouse and sustain a person’s progress is likely to vary in accordance with the contextual subject matter. For example, in the context of academic learning, a student may show personal resolve as he or she seeks achievement of optimal best (e.g., achieving mastery of a particular concept). Likewise, an academic subject matter that is of interest and has authentic relevance may energize a student’s intrinsic motivation. In a nonacademic sense, in contrast, an athletic may exhibit a high level of mental strength as he makes attempts to achieve optimal best in long-distance running. The impact of a psychosocial agency (e.g., the provision of emotional and social support) may, in contrast, serve to energize the person’s effort expenditure as she seeks to adjust to a new social environment.
Hence, from our conceptualization, the process of optimization is dynamic in terms of the availability of different agencies. The dynamic of the process of optimization is postulated to intricately link with the contextual matter or situation, at hand – for example, a senior citizen’s seeking to achieve optimal health after surgery, or a student’s fulfillment of mastery competence in Calculus. The contextual matter or situation, from our point of view, then corresponds with a related agency for the personal experience of energization. This consideration places an emphasis on different “pathways” of optimization: (1) psychological agency (e.g., the impact of personal self-efficacy: Bandura, 1997) → energization → stimulation of buoyancy of intrinsic motivation, or (2) educational agency (e.g., an appropriate instructional design: Ngu and Yeung, 2013) → energization → stimulation of buoyancy of effort expenditure, or (3) psychosocial agency (e.g., the impact of teacher-student relationship: Roorda et al., 2011) → energization → stimulation of buoyancy of mental strength.
For this final section of the article, we discuss the comparable influences of psychological, educational, and psychosocial agencies on the optimization of cognitive functioning. From previous research development, we consider the importance of personal self-efficacy (Rosenberg, 1965; Bandura, 1997; Trautwein et al., 2006), effective instructional designs (Ngu et al., 2014; Star et al., 2015), and social relationships at school (Cornelius-White, 2007; Roorda et al., 2011) as psychological, educational, and psychosocial agencies, respectively. Optimal cognitive functioning, within the contexts of schooling, may consist of a student’s academic performance in a subject area, his or her willingness to show mastery competence in a topical theme, or successful school adjustment.
An Example of Psychological Agency: The Impact of Personal Self-Efficacy
Personal self-efficacy (Bandura, 1997), which forms part of the self-beliefs system, is a notable construct that serves as a strong predictor of educational and noneducational outcomes. Personal self-efficacy, according to Bandura (1997), refers to “beliefs in one’s capabilities to organize and execute the course of action required to produce given attainments” (p. 3). This definition contends that self-efficacy is not concerned with a person’s actual capability, but rather his/her self-judgment of perceived competence (e.g., regardless of my current ability, do I believe that I have the capability to complete this mathematics task?) Self-efficacy is a potent predictor of different types of adaptive outcomes (e.g., academic performance), as it mobilizes a person’s state of persistence and effort expenditure, governs his or her choices in life, and regulates appropriate emotional responses. In accordance with Bandura’s (1997) theory, a high level of academic self-efficacy is likely to assist a student to choose an appropriate course of action (e.g., choosing a mathematics-related career pathway: Betz and Hackett, 1983, 1986).
We contend that personal self-efficacy is analogously related to the paradigm of positive psychology (Seligman and Csikszentmihalyi, 2000; Seligman, 2010). As existing research has shown, a heightened state of self-efficacy is associated with improvement in corresponding outcomes (Schunk, 1995; Pajares, 1996a,b;Bandura, 1997). A weakened state of self-efficacy, in contrast, is more likely to result in engagement of maladaptive functioning (e.g., orientation toward performance-avoidance goals: Liem et al., 2008). From the perspective of schooling, in terms of optimization of enjoyable learning experiences, we could use academic self-efficacy as a source of energy to stimulate the buoyancy of intrinsic motivation, personal resolve, effective functioning, mental strength, and/or effort expenditure. To our knowledge, to date, no research has yet considered the conceptualization of academic self-efficacy as an operator of a person’s energy that manifests in his or her stamina and liveliness.
How does academic self-efficacy instill a level of stamina and liveliness in the teaching and learning processes? Our conceptualization, in this case, considers the “potency” of academic self-efficacy to not only predict different types of future educational outcomes (e.g., Fast et al., 2010; Martin et al., 2010; Yailagh et al., 2013), but to also yield a corresponding level of “energy” (i.e., self-efficacy → level of energy). In this analysis, from the characteristics and nature of self-efficacy (Bandura, 1997), we propose that a high level of perceived competence would instill confidence, “feel-good” experiences, and a state of deliberate focus, all of which then transform into a source of energy, acting as an intermediary outcome to stimulate the buoyancy of intrinsic motivation, personal resolve, effective functioning, mental strength, and effort expenditure (i.e., energy → intrinsic motivation, etc.). This postulation of optimization gives a noteworthy positioning of academic self-efficacy (Bandura, 1997) as a source of energy for further prediction.
The proposition regarding a person’s experience of energy, which results from a heightened level of self-efficacy, is an interesting tenet and requires further consideration and development. The main emphasis, in this case, is the saliency of an “interjection” of energy between self-efficacy and a corresponding criterial outcome (i.e., self-efficacy → energy → outcome). Previous correlational studies, in contrast, have attested to the interjecting role of other educational and/or psychological variables. For example, in one of their studies, Pajares and Johnson (1996) used path analysis techniques to highlight the “in-between” role of apprehension between self-efficacy and academic performance. Statistically, taking into account Baron and Kenny’s (1986) writing, it is also appropriate for us to infer that energy could serve as a mediator between self-efficacy and different types of educational outcomes. In the context of optimization, we contend that energy, as an in-between variable, would mediate the effect of academic self-efficacy on intrinsic motivation, personal resolve, effective functioning, mental strength, and/or effort expenditure. An important focus of inquiry, in this case, considers the specific pathways that originate from self-efficacy to intrinsic motivation, personal resolve, effective functioning, mental strength, and effort expenditure, via a level of energy. We purport that the stimulation of buoyancy of the five mentioned attributes and their subsequent effects to arouse and sustain progress would vary in accordance with a student’s experience, and the contextual nature of the subject matter. In other words, from this theoretical account, personal experience of energy may selectively influence some but not all of the five attributes. For example, a topical theme that is of interest is more likely to yield a student’s experience of energy that gears toward intrinsic motivation and effort expenditure, whereas another student’s previous experience of repeated successes in a subject matter could energize a high level of personal resolve, effective functioning, and mental strength.
An Example of an Educational Agency: An Instructional Design
Cognitive load theory (Sweller et al., 2011; Sweller, 2012), for example, has assisted the design and implementation of different instructional designs for effective mathematics learning (e.g., Ngu et al., 2016; Ngu and Phan, 2016). Situating within our explanatory account of optimization, we argue that an instructional design may optimize a student’s mathematics learning experience (e.g., better comprehension and understanding of instructional materials). We consider cognitive load theory as a basis to determine to what extent an instructional design could act as a source of energy during the process of optimization. By this account, a question then is how an instructional design could cultivate positive emotions, which in turn energize a student and stimulates the buoyancy of intrinsic motivation, effective functioning, personal resolve, mental strength, and effort expenditure.
Cognitive Load Theory and Element Interactivity
Cognitive load theory (Sweller et al., 2011; Sweller, 2012) highlights the interaction between the acquisition of schemas and a person’s human cognitive architecture. Basically, it focuses on the management of the limited working memory load to process complex cognitive tasks in order to facilitate acquire acquisition. It also seeks to capitalize on the unlimited capacity of the long-term memory that stores a huge number of schemas. Processing schemas retrieved from the long-term memory reduces working memory load.
Sweller (2010) argued that element interactivity is a common factor across the three types of cognitive loads (i.e., extraneous cognitive load, intrinsic cognitive load and germane cognitive load). Element interactivity refers to the interaction between elements within a learning task, which must be processed simultaneously in working memory to allow understanding to occur. An element refers to any item that requires learning (e.g., a number, a symbol, a concept, a procedure, etc.) (Chen et al., 2017). Investing cognitive resources to process interacting elements that hampers learning constitutes extraneous cognitive load, which can be reduced by altering the design of the instruction. Investing cognitive resources to process element interactivity that arises from the inherent complexity of material constitutes intrinsic cognitive load. There is an inverse relation between the amount of intrinsic cognitive load and learners’ expertise in a domain. The intrinsic cognitive load of the material is fixed with a given level of the learner’s expertise in the domain. Investing cognitive resources to process element interactivity of the material that contributes toward learning constitutes germane cognitive load. The germane cognitive load depends on the intrinsic cognitive load because the level of element interactivity that determines germane cognitive load is associated with the intrinsic cognitive load of the material.
Instructional Design, Cognitive Load, and Emotion
Research has indicated that negative emotions (e.g., anxiety) increase cognitive load imposition and decrease working memory capacity for processing information, resulting in reduced learning (Fraser et al., 2014). However, less is known about the relation between cognitive load imposition, positive emotions, and learning outcomes (Fraser et al., 2012). It is possible an effective instruction that imposes low cognitive load would cultivate positive emotions, which in turn increase a student’s energy level. Based on cognitive load theory, we propose the benefit of acquiring a higher level schema by building on a lower level of schema in learning linear equations.
Element Interactivity and Instructional Design
The concept of element interactivity (Sweller, 2010) may provide information that could help us understand the relation between the varying levels of schemas (e.g., lower level schema versus higher level schema). According to Sweller (2010), element interactivity acts as an index of complexity of learning material – in other words, the extent to which elements within the learning material interact determines the level of element interactivity. Estimation of the level of element interactivity is made by noting the number of elements involved, as well as assessing the interaction between the elements. Interestingly, in terms of instructional designs, a level of element interactivity accounts for the efficiency of a particular design – for example, a high level of element interactivity imposes high cognitive load and, likewise, vice versa.
Researchers (Blayney et al., 2009; Ngu et al., 2014) have advocated sequencing complex materials to allow the building of a higher level schema upon a lower level schema (i.e., prior knowledge). In relation to linear equations, capitalizing prior knowledge of one-step equations (Figure 3A) in order to learn two-step equations (Figure 3B) would help ease the burden of the working memory. The learning of the two-step equations can occur in two stages. In the first stage, we can instruct the learner to review the solution procedure of the one-step equation (i.e., Lines 1, 2, and 3, Figure 3A). In the second stage, the learner will learn the solution procedure of the two-step equation (i.e., Lines 1, 2, 3, 4 and 5, Figure 3B). The recall of prior knowledge, in this case, ensures that the learner is able to identify that 3x = 12 (i.e., one-step equation) is similar to that of 4x = 8 (i.e., Line 3, two-step equation) in terms of problem structure, and therefore both share the same solution procedure. Accordingly, the learning of the two-step equation becomes the learning of Lines 1 and 2 only, thus alleviating working memory load. From this understanding, the acquisition of a higher level schema (i.e., two-step equation) is built upon a lower level schema (i.e., one-step equation), which then reduces the working memory load. Based on the same rationale, we can acquire a higher level schema of a multi-step equation (i.e., 5x – 2 = 3x + 8) by building on the prior knowledge of a lower level schema of a two-step equation (i.e., 4x – 5 = 11).
Our emphasis of the acquisition of a higher level of schema (i.e. complex equations) by building on a lower level of schema (i.e., simple equations) is expected to generate positive emotions, which, in our view, could serve as a source of energy for students. Nonetheless, the prior knowledge level of students may differentially stimulate the buoyancy of the five or a subset of the mentioned attributes in varying degrees of magnitude. In accordance with research in the area of expertise reversal effect (Kalyuga et al., 2003), low prior knowledge students need greater instructional support to strengthen their prior knowledge (e.g., one-step equations). Therefore, instructional design that highlights the capitalization of prior knowledge for learning linear equations would have greater impact on the process of optimization for high rather than low prior knowledge students.
It should be noted that popular mathematics textbooks (e.g., Vincent et al., 2012) advocate the learning of linear equations in a hierarchical order of complexity without explicitly indicating the connection between a lower level schema (e.g., one-step equations) and a higher level schema (e.g., two-step equations). This manner of learning linear equations would impose high cognitive load and cultivate negative emotions. Consequently, this would lower the student’s energy level, which is likely to dampen the stimulation of buoyancy of the five mentioned attributes, leading to limited positive arousal and sustainability in the optimization progress.
An Example of Psychosocial Agency: The Importance of Social Relationships
School is a complex place that may impart conflicting, but yet important information and influences on students, teachers, and school administrators. The school social milieu, in this sense, may influence and shape students’ cognitive, social, moral, and emotional development. This premise places emphasis on the “situational placement” of a student within a larger sociocultural system of change (Okagaki and Sternberg, 1993; Okagaki, 2001). Okagaki’s (2001) proposed triarchic model of student achievement, similar to that of Bronfenbrenner’s (1989) bioecological systems theory, is interesting as it contends that improvement in cognitive development (e.g., academic performance) is not isolated, but rather depends on extraneous social and educational influences.
Our proposition, described in the preceding sections, considers the school social milieu as a possible agency of optimization. The point of contention is that different individual and/or sociocultural attributes within the social milieu, and not the social milieu itself, would act as optimizing agencies. For example, from Goodenow’s (1993) research, we note that teachers’ attitudes toward students and/or school-based philosophical beliefs could influence the perceptions of cultural acceptance and diversity, resulting in some students’ negative experiences of school belonging. One notable facet of the school social environment, which could impart meaningful contributions to students’ academic adjustment and learning experiences is that of teacher-student relationships (Cornelius-White, 2007; Bergeron et al., 2011; Allen et al., 2013), commonly known as TSRs (Roorda et al., 2011). What is so unique about the concept of TSR as a potential optimizing agency for change?
Roorda et al.’s (2011) theoretical review delves into an interesting tenet, namely, the explanatory account of the concept of TSR in school settings. According to the authors, there are two interesting perspectives that could account and explain the quality of TSRs: extended attachment and social-motivational perspectives (Note: consult Roorda et al., 2011 for further detail). The extended attachment perspective postulates that teachers, like caregivers, may provide a security base (e.g., emotional security) from which children feel free, and can explore the school environment and engage in different learning and extracurricular activities (Birch and Ladd, 1997; Pianta et al., 1997; Pianta, 1999). Social-motivational perspectives (e.g., self-determination theory: Deci et al., 1991; Ryan and Powelson, 1991), in contrast, contend that children become motivated when they are able to fulfill three fundamental needs: the needs for relatedness, for competence, and for autonomy. Teachers play a major role, according to Roorda et al. (2011), by showing “involvement (i.e., caring for and expressing interest in the student), providing structure (i.e., setting clear rules and being consequent), and supporting autonomy (i.e., giving students freedom to make their own choices and showing connections between schoolwork and students’ interests)”. Regardless of which theoretical perspective we align to, it is obvious that teachers play a central role in the schooling process.
Teacher-student relationships, consequently, form an important basis at school for social functioning (e.g., Ladd et al., 1999), school adjustment (e.g., Buyse et al., 2009), academic achievement (e.g., Valiente et al., 2008), and engagement in learning activities (Skinner et al., 1990). We expand on this research testament by proposing that a teacher’s role at school could yield a number of meaningful outcomes, which would then transform into a source of energy to differentially stimulate the buoyancy of intrinsic motivation, personal resolve, effective functioning, mental strength, and effort expenditure. In this analysis, from our previous discussion into the operational nature of quality TSRs (Roorda et al., 2011), we consider the importance of the following: (1) a teacher’s persona in-class that conveys messages of warmth, care, and nurturing, (2) a teacher’s attempts to provide opportunities, pathways, and means for student growth, and (3) a teacher’s willingness to facilitate a school social milieu that fosters acceptance, cultural diversity, and a sense of belonging. This development in school, similar to that of self-efficacy and instructional designs, would create a positive learning environment and a strong emotional base for students to learn.
However, the nature of stimulation is subject to different contextual and personal situations. For example, a student’s favorable response to a teacher’s warmth and caring nature may lead to mental strength whereas another student’s response to a teacher’s provision of opportunities and pathways may lead to intrinsic motivation that facilitates effective cognitive functioning and personal resolve. In contrast, a student’s negative experience of school, especially in the relationship with a number of teachers, may result in a low level of mental strength that thwarts learning.
Conclusion
The study of optimal functioning, which emphasizes the maximization of a person’s capability, requires understanding into the process of optimization. The theoretical concept of optimization has received some research interests, both theoretically and empirically. A synthesis of the literature in the areas of education, psychology, health, and subjective well-being indicates a number of comparable constructs such as cognitive flow, academic buoyancy, and personal thriving. To date, there is no satisfactory account or explanation as to what constitutes optimization. Capitalizing on recent research progress (e.g., Fraillon, 2004; Phan et al., 2017, 2019a), we develop an in-depth account of optimization for further development. We conceptualize optimization as an “underlying process” that could facilitate the achievement of optimal functioning. Optimization, we contend, is more than just a statistical prediction of a psychological variable (e.g., self-efficacy: Bandura, 1997); rather, optimization reflects the experience of “energy,” which then stimulates the buoyancy of intrinsic motivation, effective functioning, personal resolve, mental strength, and effort expenditure.
An important advancement for investigation includes the development of appropriate methodological designs that could test and validate our theoretical contribution of optimization. Our proposed quantification of optimization is useful for assessing a person’s level of optimal functioning, self-referenced against his/her current level of functioning. From our theorization, the index of optimization, quantified as a numerical value, helps us to address specific types of functioning that a person may develop over time (e.g., optimal cognitive functioning versus optimal emotional functioning).
In sum, our theoretical contribution into the study of optimal functioning has potential to facilitate specific positive outcomes, academically and nonacademically. The three major optimizing agencies (psychological, educational, and psychosocial) are prevalent as sources of information that enable a person’s experience of energization. What practitioners need to consider are specific pathways and means that could instill and sustain a state of energization to achieve optimal functioning.
Despite the aforementioned theoretical account of optimization, we do acknowledge that more progress is needed to truly understand the nature of optimization. Our proposition (e.g., the concept of “optimizing effect”), as described, is theoretical and conceptual, providing grounding for further empirical development. As Merrotsy (2017) recently noted in his book, titled Pedagogy for creative problem solving, there are similar theories such as flow (Csíkszentmihályi, 1990, 2014) that lack empirical support – “…It is interesting to note that Thomas (2011) conducted a comprehensive search, using every available database search engine, and was unable to locate any independent research on the existence of flow” (p. 163). This testament, in tandem with our own writing, suggests an important need for researchers to consider pathways and means by which we could soundly “measure, assess, and validate” optimization and, hence, the quantification of flourishing. Importantly too, from this analysis, is a focus on the positive association between optimization and academic performance in school contexts. Our previous description proposes a potential correlation between a child’s experience of optimal best and his/her achievement of a cognitive test (e.g., a quiz in mathematics). It is achievable, in this case, for us to validate this relationship via means of factorial and/or regression techniques. What is of perplexity, however, is how does the totality of optimization, as detailed in Figure 1, explain a child’s academic performance? At present, we are investigating the operational nature of energy using a quantitative, nonexperimental approach. We encourage readers, likewise, to undertake robust scientific inquiries to support our proposed theoretical-conceptual model of optimization. We are mindful of Merrotsy’s (2017) caution that we do not simply accept and use a theory and/or a concept in a “passing” manner without concrete, established grounding.
Author Contributions
HP was responsible for the original conceptualization and write-up of the manuscript. BN was responsible for the original conceptualization and write-up of the manuscript. AY assisted in the revision of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
ACU and Erebus International (2008). Scoping study into approaches to student wellbeing: Literature review. Report to the Department of Education, Employment and Workplace Relations. (Sydney, Australia: Australian Catholic University).
Allen, J., Gregory, A., Mikami, A., Lun, J., Hamre, B., and Pianta, R. (2013). Observations of effective teacher-student interactions in secondary school classrooms: predicting student achievement with the classroom assessment scoring system-secondary. Sch. Psychol. Rev. 42, 76–98. ISSN: 0279-6015.
Bandalos, D. L., Yates, K., and Thorndike-Christ, T. (1995). Effects of math self-concept, perceived self-efficacy, and attributions for failure and success on text anxiety. J. Educ. Psychol. 87, 611–623. doi: 10.1037/0022-0663.87.4.611
Bandura, A. (1986). Social foundations of thought and action: A social cognitive theory. (Englewood Cliffs, NJ: Prentice-Hall).
Baron, R. M., and Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J. Pers. Soc. Psychol. 51, 1173–1182. doi: 10.1037/0022-3514.51.6.1173
Bergeron, J., Chouinard, R., and Janosz, M. (2011). The impact of teacher-student relationships and achievement motivation on students’ intentions to dropout according to socio-economic status. US-China Educ. Rev. B 2, 273–279. ISSN: 1548-6613.
Betz, N. E., and Hackett, G. (1983). The relationship of mathematics self-efficacy expectations to the selection of science-based majors. J. Vocat. Behav. 23, 329–345. doi: 10.1016/0001-8791(83)90046-5
Betz, N. E., and Hackett, G. (1986). Applications of self-efficacy theory to understand career choice behavior. J. Soc. Clin. Psychol. 4, 279–289. doi: 10.1521/jscp.1986.4.3.279
Birch, S. H., and Ladd, G. W. (1997). The teacher-child relationship and children’s early school adjustment. J. Sch. Psychol. 35, 61–79. doi: 10.1016/S0022-4405(96)00029-5
Blayney, P., Kalyuga, S., and Sweller, J. (2009). Interactions between the isolated–interactive elements effect and levels of learner expertise: experimental evidence from an accountancy class. Instr. Sci. 38, 277–287. doi: 10.1007/s11251-009-9105-x
Bollen, K. A., and Curran, P. J. (2006). Latent curve models: A structural equation perspective. (Hoboken, NJ: Wiley).
Bordens, K. S., and Abbott, B. B. (2008). Research design and methods: A process approach. (New York, NY: McGraw-Hill).
Bornstein, M. H., Davidson, L., Keyes, C. L. M., and Moore, K. A. (2003). Well-being positive development across the life course. (Lawrence, Erlbaum Associates: Mahwah).
Bronfenbrenner, U. (1989). “Ecological systems theory” in Annals of child development: Theories of child development: Revised formulations and current issues. ed. R. Vasta, vol. 6 (Greenwich, CT: JAI Press), 187–251.
Buyse, E., Verschueren, K., Verachtert, P., and Van Damme, J. (2009). Predicting school adjustment in early elementary school: impact of teacher-child relationship quality and relational classroom climate. Elem. Sch. J. 110, 119–141. doi: 10.1086/605768
Chen, O. H., Kalyuga, S., and Sweller, J. (2017). The expertise reversal effect is a variant of the more general element interactivity effect. Educ. Psychol. Rev. 29, 393–405. doi: 10.1007/s10648-016-9359-1
Church, M. A., Elliot, A. J., and Gable, S. L. (2001). Perceptions of classroom environment, achievement goals, and achievement outcomes. J. Educ. Psychol. 93, 43–54. doi: 10.1037/0022-0663.93.1.43
Corbin, C. L. R. (1997). Concepts of fitness and wellness: With laboratories. (Madison, WI: Brown and Benchmark Publishers).
Cornelius-White, J. (2007). Learner-centered teacher-student relationships are effective: a meta-analysis. Rev. Educ. Res. 77, 113–143. doi: 10.3102/003465430298563
Csíkszentmihályi, M. (1990). Flow: The psychology of optimal experience. (New York: Harper Perennial).
Daulta, M. S. N. (2008). Impact of home environment on the scholastic achievement of children. J. Hum. Ecol. 23, 75–77. doi: 10.1080/09709274.2008.11906058
Deci, E. L., Vallerand, R. J., Pelletier, L. G., and Ryan, R. M. (1991). Motivation and education–the self-determination perspective. Educ. Psychol. 26, 325–346. doi: 10.1080/00461520.1991.9653137
Diener, E., and Biswas-Diener, R. (2002). Will money increase subjective well-being? A literature review and guide to needed research. Soc. Indic. Res. 57, 119–169. doi: 10.1023/A:1014411319119
Diener, E., Wirtz, D., Biswas-Diener, R., Tov, W., Kim-Prieto, C., Choi, D.-W., et al. (2009). “New measures of well-being” in Assessing well-being: The collected works of Ed Diener. ed. E. Diener (Netherlands: Springer Science+Business Media B.V.), 247–266.
Diener, E., Wirtz, D., Tov, W., Kim-Prieto, C., Choi, D. W., Oishi, S., et al. (2010). New well-being measures: short scales to assess flourishing and positive and negative feelings. Soc. Indic. Res. 97, 143–156. doi: 10.1007/s11205-009-9493-y
Elliot, A. J., and Murayama, K. (2008). On the measurement of achievement goals: critique, illustration, and application. J. Educ. Psychol. 100, 613–628. doi: 10.1037/0022-0663.100.3.613
Fast, L. A., Lewis, J. L., Bryant, M. J., Bocian, K. A., Cardullo, R. A., Rettig, M., et al. (2010). Does math self-efficacy mediate the effect of perceived classroom environment on standardized math performance? J. Educ. Psychol. 102, 729–740. doi: 10.1037/a0018863
Fraillon, J. (2004). Measuring student well-being in the context of Australian schooling: Discussion paper. (Carlton South, Victoria: The Australian Council for Research).
Fraser, K., Huffman, J., Ma, I., Sobczak, M., McIlwrick, J., Wright, B., et al. (2014). The emotional and cognitive impact of unexpected simulated patient death: a randomized controlled trial. Chest J. 145, 958–963. doi: 10.1378/chest.13-0987
Fraser, K., Ma, I., Teteris, E., Baxter, H., Wright, B., and McLaughlin, K. (2012). Emotion, cognitive load and learning outcomes during simulation training. Med. Educ. 46, 1055–1062. doi: 10.1111/j.1365-2923.2012.04355.x
Fredrickson, B. L. (2000). Cultivating positive emotions to optimize health and well-being. Prevent. Treat. 3, 1. doi: 10.1037/1522-3736.3.1.31a
Freund, A. M., and Baltes, P. B. (1998). Selection, optimization, and compensation as strategies of life management: correlations with subjective indicators of successful aging. Psychol. Aging 13, 531–543. doi: 10.1037/0882-7974.13.4.531
Goodenow, C. (1993). The psychological sense of school membership among adolescents–scale development and educational correlates. Psychol. Sch. 30, 79–90. doi: 10.1002/1520-6807(199301)30:1<79::AID-PITS2310300113>3.0.CO;2-X
Goodenow, C., and Grady, K. (1993). The relationship of school belonging and friends’ values to academic motivation among urban adolescent students. J. Exp. Educ. 60, 60–71.
Gravetter, F. J., and Forzano, L.-A. B. (2009). Research methods for the behavioral sciences. (Belmont, CA: Wadsworth Cengage Learning).
Grice, J. W., Cohn, A., Ramsey, R. R., and Chaney, J. M. (2015). On muddled reasoning and mediation modeling. Basic Appl. Soc. Psychol. 37, 214–225. doi: 10.1080/01973533.2015.1049350
Guay, F., Boivin, M., and Hodges, E. V. E. (1999). Predicting change in academic achievement: a model of peer experiences and self-system processes. J. Educ. Psychol. 91, 105–115. doi: 10.1037/0022-0663.91.1.105
Hancock, G. R., and Lawrence, F. R. (2006). “Using latent growth models to evaluate longitudinal change” in Structural equation modeling: A second course. eds. G. R. Hancock and R. O. Mueller (Greenwich, Connecticut: Information Age Publishing), 171–196.
Headey, B., and Wooden, M. (2004). The effects of wealth and income on subjective well-being and ill-being. Econ. Rec. 80, S24–S33. doi: 10.1111/j.1475-4932.2004.00181.x
Huppert, F. A., and So, T. T. (2013). Flourishing across Europe: application of a new conceptual framework for defining well-being. Soc. Indic. Res. 110, 837–861. doi: 10.1007/s11205-011-9966-7
Kalyuga, S., Ayres, P., Chandler, P., and Sweller, J. (2003). The expertise reversal effect. Educ. Psychol. 38, 23–31. doi: 10.1207/S15326985EP3801_4
Keyes, C. L. (2002). The mental health continuum: from languishing to flourishing in life. J. Health Soc. Behav. 43, 207–222. doi: 10.2307/3090197
Keyes, C. L., Shmotkin, D., and Ryff, C. D. (2002). Optimizing well-being: the empirical encounter of two traditions. J. Pers. Soc. Psychol. 82, 1007–1022. doi: 10.1037/0022-3514.82.6.1007
Kline, R. B. (2015). The mediation myth. Basic Appl. Soc. Psychol. 37, 202–213. doi: 10.1080/01973533.2015.1049349
Ladd, G. W., Birch, S. H., and Buhs, E. S. (1999). Children’s social and scholastic lives in kindergarten: related spheres of influence? Child Dev. 70, 1373–1400. doi: 10.1111/1467-8624.00101
Liem, G. A. D., Ginns, P., Martin, A. J., Stone, B., and Herrett, M. (2012). Personal best goals and academic and social functioning: a longitudinal perspective. Learn. Instr. 22, 222–230. doi: 10.1016/j.learninstruc.2011.11.003
Liem, A. D., Lau, S., and Nie, Y. (2008). The role of self-efficacy, task value, and achievement goals in predicting learning strategies, task disengagement, peer relationship, and achievement outcome. Contemp. Educ. Psychol. 33, 486–512. doi: 10.1016/j.cedpsych.2007.08.001
MacCallum, R. C., and Austin, J. T. (2000). Applications of structural equation modeling in psychological research. Annu. Rev. Psychol. 51, 201–226. doi: 10.1146/annurev.psych.51.1.201
Marsh, H. W., and Yeung, A. S. (1997). Causal effects of academic self-concept on academic achievement: structural equation models of longitudinal data. J. Educ. Psychol. 89, 41–54. doi: 10.1037/0022-0663.89.1.41
Martin, A. J. (2006). Personal bests (PBs): a proposed multidimensional model and empirical analysis. Br. J. Educ. Psychol. 76, 803–825. doi: 10.1348/000709905X55389
Martin, A. J. (2011). Personal best (PB) approaches to academic development: implications for motivation and assessment. Educ. Pract. Theory 33, 93–99. doi: 10.7459/ept/33.1.07
Martin, A. J., Colmar, S. H., Davey, L. A., and Marsh, H. W. (2010). Longitudinal modelling of academic buoyancy and motivation: do the 5Cs hold up over time? Br. J. Educ. Psychol. 80, 473–496. doi: 10.1348/000709910X486376
McCartney, K., Dearing, E., Taylor, B. A., and Bub, K. L. (2007). Quality child care supports the achievement of low-income children: direct and indirect pathways through caregiving and the home environment. J. Appl. Dev. Psychol. 28, 411–426. doi: 10.1016/j.appdev.2007.06.010
Merrotsy, P. (2017). Pedagogy for creative problem solving. (Abingdon, United Kingdom: Taylor & Francis Ltd).
Ngu, B. H., and Phan, H. P. (2016). Comparing balance and inverse methods on learning conceptual and procedural knowledge in equation solving: a cognitive load perspective. Pedagogiesl 11, 63–83. doi: 10.1080/1554480X.2015.1047836
Ngu, B. H., Phan, H. P., Hong, K. S., and Hasbee, U. (2016). Reducing intrinsic cognitive load in percentage change problems: the equation approach. Learn. Individ. Differ. 51, 81–90. doi: 10.1016/j.lindif.2016.08.029
Ngu, B. H., and Yeung, A. S. (2013). Algebra word problem solving approaches in a chemistry context: equation worked examples versus text editing. J. Math. Behav. 32, 197–208. doi: 10.1016/j.jmathb.2013.02.003
Ngu, B. H., Yeung, A. S., Phan, H. P., Hong, K. S., and Usop, H. (2018). Learning to solve challenging percentage-change problems: a cross-cultural study from a cognitive load perspective. J. Exp. Educ. 86, 362–385. doi: 10.1080/00220973.2017.1347774
Ngu, B. H., Yeung, A. S., and Tobias, S. (2014). Cognitive load in percentage change problems: unitary, pictorial, and equation approaches to instruction. Instr. Sci. 42, 685–713. doi: 10.1007/s11251-014-9309-6
Noble, T., and McGrath, H. (2008). The positive educational practices framework: A tool for facilitating the work of educational psychologists in promoting well-being. Educ. Child Psychol. 25, 119–134.
Okagaki, L. (2001). Triarchic model of minority children’s school achievement. Educ. Psychol. 36, 9–20. doi: 10.1207/S15326985EP3601_2
Okagaki, L., and Sternberg, R. J. (1993). Parental beliefs and children’s school performance. Child Dev. 64, 36–56. doi: 10.2307/1131436
Pajares, F. (1996a). Self-efficacy beliefs and mathematical problem-solving of gifted students. Contemp. Educ. Psychol. 21, 325–344.
Pajares, F., and Johnson, M. J. (1996). Self-efficacy beliefs and the writing performance of entering high school students. Psychol. Sch. 33, 163–175.
Pajares, F., and Kranzler, J. (1995). Self-efficacy beliefs and general mental-ability in mathematical problem-solving. Contemp. Educ. Psychol. 20, 426–443. doi: 10.1006/ceps.1995.1029
Pajares, F., and Miller, M. D. (1994). Role of self-efficacy and self-concept beliefs in mathematical problem-solving: a path analysis. J. Educ. Psychol. 86, 193–203. doi: 10.1037/0022-0663.86.2.193
Phan, H. P., and Ngu, B. H. (2015). Validating personal well-being experiences: a quantitative approach. Education 136, 34–52. ISSN: 0013-1172.
Phan, H. P., Ngu, B. H., and Alrashidi, O. (2018a). Contextualised self-beliefs in totality: an integrated framework from a longitudinal perspective. Educ. Psychol. 38, 411–434. doi: 10.1080/01443410.2017.1356446
Phan, H. P., Ngu, B. H., Wang, H.-W., Shih, J.-H., Shi, S.-Y., and Lin, R.-Y. (2018b). “Introducing the theoretical concept of ‘profiling’: a cross-cultural perspective” in Progress in education. ed. R. V. Nata, vol. 53 (New York, NY: Nova Science), 43–74.
Phan, H. P., Ngu, B. H., Wang, H.-W., Shih, J.-H., Shi, S.-Y., and Lin, R.-Y. (2018c). Understanding levels of best practice: an empirical development. PLoS One 13:e0198888. doi: 10.1371/journal.pone.0198888
Phan, H. P., Ngu, B. H., Wang, H.-W., Shih, J.-H., Shi, S.-Y., and Lin, R.-Y. (2019a). Achieving optimal best practice: an inquiry into its nature and characteristics. PLoS One 14:e0215732. doi: 10.1371/journal.pone.0215732
Phan, H. P., Ngu, B. H., and Williams, A. (2016). Introducing the concept of optimal best: theoretical and methodological contributions. Education 136, 312–322. ISSN: 0013-1172.
Phan, H. P., Ngu, B. H., and Yeung, A. S. (2017). Achieving optimal best: instructional efficiency and the use of cognitive load theory in mathematical problem solving. Educ. Psychol. Rev. 29, 667–692. doi: 10.1007/s10648-016-9373-3
Phan, H. P., Wang, H.-W., Shih, J.-H., Shi, S.-Y., Lin, R.-Y., and Ngu, B. H. (2019b). “The importance of mindfulness in the achievement of optimal best: conceptualization for research development” in Educational psychology – Between certitudes and uncertainties. ed. V. Trif (Rijeka, Croatia: Intech Publishing).
Pianta, R. C. (1999). Enhancing relationships between children and teachers. (Washington, DC: American Psychological Association).
Pianta, R. C., Nimetz, S. L., and Bennett, E. (1997). Mother-child relationships, teacher-child relationships, and school outcomes in preschool and kindergarten. Early Child. Res. Q. 12, 263–280. doi: 10.1016/S0885-2006(97)90003-X
Prilleltensky, I., and Prilleltensky, O. (2006). Promoting well-being: Linking personal, organizational, and community change. (Hoboken, NJ: John Wiley & Sons, Inc).
Rogosa, D. (1979) in Causal models in longitudinal research: Rationale, formulation, and interpretation. Longitudinal research in the study of behaviour and development. eds. J. R. Nesselroade and P. B. Balles (New York: Academic Press), 263–302.
Roorda, D. L., Koomen, H. M. Y., Spilt, J. L., and Oort, F. J. (2011). The influence of affective teacher-student relationships on students’ school engagement and achievement: a meta-analytic approach. Rev. Educ. Res. 81, 493–529. doi: 10.3102/0034654311421793
Rosenberg, M. (1965). Society and the adolescent child. (Princeton, NJ: Princeton University Press).
Ryan, R. M., and Powelson, C. L. (1991). Autonomy and relatedness as fundamental to motivation and education. J. Exp. Educ. 60, 49–66.
Schunk, D. H. (1995) in Self-efficacy and education and instruction. Self-efficacy, adaptation, and adjustment: Theory, research and application. ed. J. E. Maddux (New York: Plenum Press), 283–301.
Seligman, M. (2010). Flourish: Positive psychology and positive interventions. The Tanner Lectures on human values at the University of Michigan. (Ann Arbor, Michigan: The University of Michigan).
Seligman, M., and Csikszentmihalyi, M. (2000). Positive psychology: an introduction. Am. Psychol. 55, 5–14. doi: 10.1037/0003-066X.55.1.5
Skinner, E. A., Wellborn, J. G., and Connell, J. P. (1990). What it takes to do well in school and whether I’ve got it: a process model of perceived control and children’s engagement and achievement in school. J. Educ. Psychol. 82, 22–32. doi: 10.1037/0022-0663.82.1.22
Snyder, C. R. (2004). Hope and depression: a light in the darkness. J. Soc. Clin. Psychol. 23, 347–351. doi: 10.1521/jscp.23.3.347.35458
Snyder, C. R., Ilardi, S. S., Cheavens, J., Michael, S. T., Yamhure, L., and Sympson, S. (2000). The role of hope in cognitive-behavior therapies. Cogn. Ther. Res. 24, 747–762. doi: 10.1023/A:1005547730153
Star, J. R., Pollack, C., Durkin, K., Rittle-Johnson, B., Lynch, K., Newton, K., et al. (2015). Learning from comparison in algebra. Contemp. Educ. Psychol. 40, 41–54. doi: 10.1016/j.cedpsych.2014.05.005
Stewart-Brown, S. (2000) in Parenting, well-being, health and disease. Promoting children’s emotional well-being. eds. A. Buchanan and B. Hudson (New York: Oxford University Press), 28–47.
Straszewski, T., and Siegel, J. T. (2018). Positive emotion infusions: can savoring increase help-seeking intentions among people with depression? Appl. Psychol. Health Well Being 10, 171–190. doi: 10.1111/aphw.12122
Su, R., Tay, L., and Diener, E. (2014). The development and validation of the comprehensive inventory of thriving (CIT) and the brief inventory of thriving (BIT). Appl. Psychol. Health Well Being 6, 251–279. doi: 10.1111/aphw.12027
Sweller, J. (2010). Element interactivity and intrinsic, extraneous, and germane cognitive load. Educ. Psychol. Rev. 22, 123–138. doi: 10.1007/s10648-010-9128-5
Sweller, J. (2012). “Human cognitive architecture: why some instructional procedures work and others do not” in APA educational psychology handbook. eds. K. Harris, S. Graham, and T. Urdan, Vol. 1 (Washington DC: American Psychological Association), 295–325.
Tabachnick, B. G., and Fidell, L. S. (2007). Using multivariate statistics. (Boston, MA: Pearson Education, Inc).
Tate, C. U. (2015). On the overuse and misuse of mediation analysis: it may be a matter of timing. Basic Appl. Soc. Psychol. 37, 235–246. doi: 10.1080/01973533.2015.1062380
Thomas, J. (2011). In search of the optimal learning experience: flow theory and its implications for talent development. TalentEd 27, 31–38.
Trafimow, D. (2015). Introduction to the special issue on mediation analyses: what if planetary scientists used mediation analysis to infer causation? Basic Appl. Soc. Psychol. 37, 197–201. doi: 10.1080/01973533.2015.1064290
Trautwein, U., Ludtke, O., Koller, O., and Baumert, J. (2006). Self-esteem, academic self-concept, and achievement: how the learning environment moderates the dynamics of self-concept. J. Pers. Soc. Psychol. 90, 334–349. doi: 10.1037/0022-3514.90.2.334
Valiente, C., Lemery-Chalfant, K., Swanson, J., and Reiser, M. (2008). Prediction of children’s academic competence from their effortful control, relationships, and classroom participation. J. Educ. Psychol. 100, 67–77. doi: 10.1037/0022-0663.100.1.67
Vincent, J., Price, B., Caruso, N., McNamara, A., and Tynan, D. (2012). MathsWorld 8 Australian curriculum edition. (South Yarra, VIC: Macmillan).
Vygotsky, L. (1978). Mind in society: The development of higher psychological processes. (Cambridge, MA: Harvard University Press).
Vygotsky, L. (1981). “The genesis of higher mental functions” in The concept of activity in Soviet Psychology. ed. J. V. Wertsch (Armonk, NY: Sharpe), 144–188.
Weisner, T. S. (1998). Human development, child well-being, and the cultural project of development. New Dir. Child Dev. 81, 69–85.
WHO. (2007). Fact sheet no. 220. Retrieved 15th December, 2014. Available at: http://www.who.int/mediacentre/factsheets/fs220/en/
Wiese, C. W., Tay, L., Su, R., and Diener, E. (2018). Measuring thriving across nations: examining the measurement equivalence of the comprehensive inventory of thriving (CIT) and the brief inventory of thriving (BIT). Appl. Psychol. Health Well Being 10, 127–148. doi: 10.1111/aphw.12119
Witmer, J. M., and Sweeney, T. J. (1998). “Toward wellness: the goal of counseling” in Adlerian counseling: A practioner’s approach. ed. T. J. Sweeney (Philadelphia: Accelerated Development, Taylor & Francis Group), 43–99.
Yailagh, M. S., Birgani, S. A., Boostani, F., and Hajiyakhchali, A. (2013). The relationship of self-efficacy and achievement goals with metacognitiion in female high school students in Iran. Procedia Soc. Behav. Sci. 84, 11–119. doi: 10.1016/j.sbspro.2013.06.520
Keywords: optimal functioning, optimization, index of optimization, energization, subjective well-being, positive psychology, cognitive load theory, optimizing effect
Citation: Phan HP, Ngu BH and Yeung AS (2019) Optimization: In-Depth Examination and Proposition. Front. Psychol. 10:1398. doi: 10.3389/fpsyg.2019.01398
Edited by:
Juan Luis Castejon, University of Alicante, SpainReviewed by:
Shi Yongchuan, Wenzhou University, ChinaPeter Merrotsy, University of Western Australia, Australia
Copyright © 2019 Phan, Ngu and Yeung. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huy Phuong Phan, aHBoYW4yQHVuZS5lZHUuYXU=
 Huy Phuong Phan
Huy Phuong Phan Bing Hiong Ngu
Bing Hiong Ngu Alexander Seeshing Yeung2
Alexander Seeshing Yeung2