- 1Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming, China
- 2Department of Physics, Chongqing University of Arts and Sciences, Chongqing, China
- 3Department of Physics, School of Chemical Engineering and Physical Sciences, Lovely Professional University, Phagwara, India
The search for new topological materials that are realistic to synthesize has attracted increasing attention. In this study, we systematically investigated the electronic, mechanical, and topological semimetallic properties, as well as the interesting surface states, of the tetragonal monoxide of platinum, which is realistic to synthesize, via a first-principles approach. Our calculated results indicate that PtO is a novel topological semimetal with double nodal lines in the kz = 0 plane and a pair of triple topological nodal points along the A'-M-A directions. Obvious surface states, including Fermi arc and drum-head-like surfaces, could be found around nodal points and nodal lines. The dynamic and mechanical stabilities of P42/mmc-type PtO were examined in detail via calculation of the phonon dispersion and determination of elastic constants, respectively. Some other mechanical properties, including the bulk modulus, Young's modulus, shear modulus, Poisson's ratio, and Pugh's index, were considered in this study. P42/mmc-type PtO provides a good research platform for investigation of novel behaviors that combine mechanical properties and rich topological elements.
Introduction
As rising stars in the topological material family, topological semimetals (Fang et al., 2012, 2016; Chiu and Schnyder, 2014; Yan and Felser, 2017; Gao et al., 2019), whose band crossing points form 0-D nodal point, 1-D nodal line, or 2-D nodal surface states in momentum space, have recently attracted extensive attention. Topological nodal point semimetals (Hosur et al., 2012; Zyuzin and Burkov, 2012; Hosur and Qi, 2013; Vazifeh and Franz, 2013; Liu et al., 2014; Lundgren et al., 2014; Kobayashi and Sato, 2015; Miransky and Shovkovy, 2015; Xu et al., 2015a; Young and Kane, 2015) enjoy 0-D nodal points in momentum space. Topological nodal line semimetals (Cai et al., 2018; Chen et al., 2018; Gao et al., 2018; Zhou et al., 2018; He et al., 2019; Jin et al., 2019a; Pham et al., 2019; Yi et al., 2019; Zou et al., 2019; Zhao et al., 2020) host 1-D topological nodal lines in momentum space via band crossing along a line in momentum space. Topological nodal surface semimetals (Wu et al., 2018; Zhang et al., 2018; Fu et al., 2019a; Qie et al., 2019; Yang et al., 2020) host 2-D nodal surface states that are composed of continuous band crossing points.
In addition, topological semimetals exhibit many types of band crossing points based on degeneracy. Weyl and Dirac semimetals feature 2-fold and 4-fold degenerate 0-D band crossing points, respectively. In detail, Weyl semimetals (Hosur et al., 2012; Zyuzin and Burkov, 2012; Hosur and Qi, 2013; Vazifeh and Franz, 2013; Lundgren et al., 2014; Yan and Felser, 2017) have nodal points that are protected by inversion (P) or time-reversal symmetries (T). Dirac semimetals (Liu et al., 2014; Lundgren et al., 2014; Kobayashi and Sato, 2015; Miransky and Shovkovy, 2015; Young and Kane, 2015) host quadruple degenerate nodal points that are protected by crystalline symmetry. Furthermore, topological semimetals with 3-, 6-, and 8-fold degenerate band crossing points have been considered (Weng et al., 2016a,b; Cai et al., 2018; Kumar et al., 2020) by researchers. Of these, triply degenerate nodal point-type semimetals (Weng et al., 2016a,b) are well-studied due to their novel topological elements and related surface states. Triple nodal points can appear both in isolation and at nodal line connections.
Many topological semimetals that are realistic to synthesize and have various types of band crossing points have been proposed. Unfortunately, these band crossing points are usually disturbed by other trivial bands near the Fermi level, which covers novel physics behaviors from the band crossing points. Hence, to search for topological behaviors of topological semimetals with rich topological elements, it is necessary to find topological semimetals with clean band structures near the Fermi level. Thus far, there are few potential clean topological semimetals with more than one topological element. This greatly impedes further investigation of realistic topological semimetals with rich topological elements.
In this work, we focus on an old realistic material, tetragonal PtO with ICSD IDs1 164290 and 26599. In 1941, Moore Jr and Pauling (Moore Pauling, 1941) synthesized PdO and PtO by the method of Shriner and Adams, involving fusing palladous chloride and potassium nitrate, and platinous oxide by a similar method. Based on previous powder photographic X-ray data, the tetragonal crystal PtO (Moore Pauling, 1941) exhibits a P42/mmc type structure with lattice constants a = b = 3.04 ± 0.03 and c = 5.34 ± 0.05Ǻ. In this paper, we use a first-principles analysis to investigate its electronic and mechanical properties, as well as its phase stability, systematically. We report its interesting 0-D and 1-D topological elements and the related surface states.
Computational Details
First-principles calculations were performed using the Vienna ab initio simulation package (VASP) (Hafner, 2007) with density functional theory (DFT) (Lejaeghere et al., 2016). The generalized gradient approximation (GGA) (Perdew et al., 1996) of the Perdew–Burke–Ernzerhof (PBE) functional (Ernzerhof and Scuseria, 1999) was selected for the exchange-correlation potential. The projector augmented wave (PAW) (Kresse and Joubert, 1999) pseudo-potential was employed with a cutoff energy of 600 eV for plane-wave expansions. The energy and force convergence criteria were set to 10−6 eV per atom and 0.0005 eV/Ǻ, respectively. The surface states were obtained using the Wannier-tools package (Villanova and Park, 2018). The phonon dispersion of 2 × 2 × 2 supercell of PtO monolayer was checked based on density functional perturbation theory (DFPT).
Results and Discussion
Structural Model and Dynamic Stability
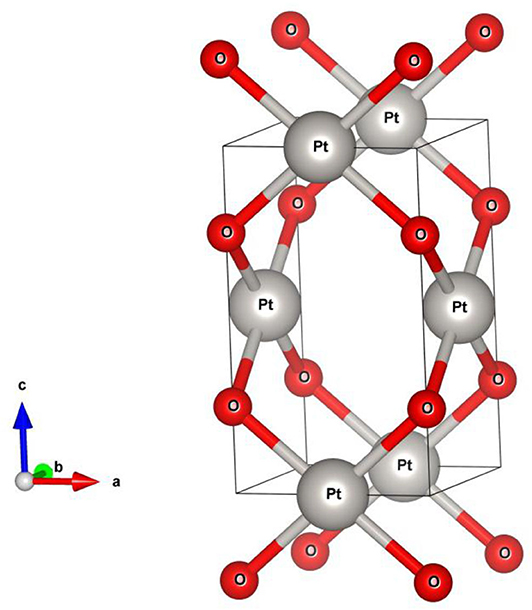
PtO (Moore Pauling, 1941) crystallizes in a tetragonal structure (as shown in Figure 1) with space group P42/mmc (no. 131). The minimum energy approach was used for structural optimization. The PtO primitive cell contains two O and two Pt atoms. The atomic positions and equilibrium lattice constants were determined after complete relaxation. The resulting lattice constants are a = b = 3.15 and c = 5.37Ǻ, and are in a good agreement with the experimental data. In their relaxed atomic positions, the Pt and O atoms occupy the 2c (0.0, 0.5, 0.0) and 2e (0.0, 0.0, 0.25) Wyckoff sites, respectively. We would like to point out that the results of current study will retain if the experimental lattice constants are selected, as shown in Figure S1.
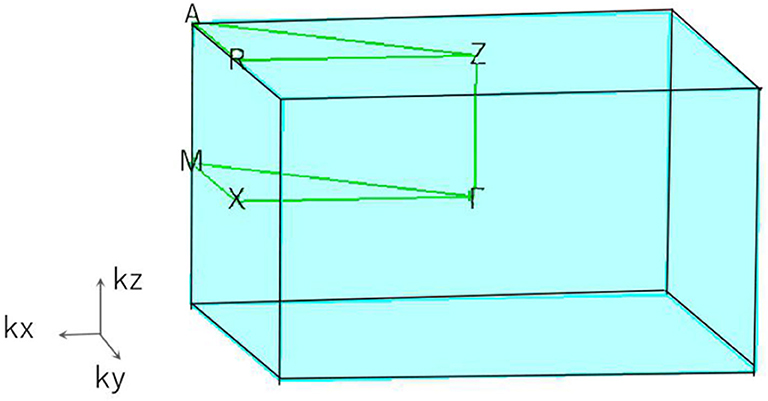
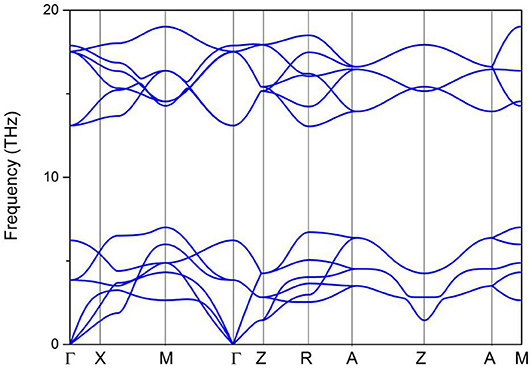
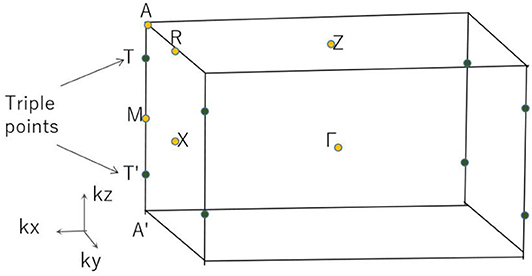
Based on the 3-D bulk Brillouin zone (BZ) selected in Figure 2, the phonon dispersion (Sultana et al., 2018; Abutalib, 2019; Ding et al., 2019; Fu et al., 2019b; Han et al., 2019; Jia et al., 2019) was determined in order to examine the dynamic stability of tetragonal PtO. It is well-known that materials are dynamically stable when no imaginary phonon modes exist in their phonon dispersion curves. Figure 3 shows the calculated phonon dispersion along the Γ-X-M-Γ-Z-R-A-Z-A-M directions. Since only positive frequencies appear in Figure 3, PtO is a dynamically stable material.
Mechanical Properties and Mechanical Stability
By analyzing the elastic constants, we can obtain information about the mechanical stability of PtO. In this paper, we use the energy-strain method to compute six independent elastic constants. The results are shown in Table 1.
Tetragonal PtO has six independent elastic constants, C11, C12, C13, C33, C44, and C66. We can use the Born–Huang criteria (see criteria i, ii, and iii) to test the mechanical stability of tetragonal PtO:
Criteria (i) C11 > |C12|;
Criteria (ii) 2C132<C33(C11 + C12); and
Criteria (iii) C44 > 0.
The Born–Huang criteria indicate that PtO is mechanically stable. Other useful mechanical parameters, including the bulk modulus (B), shear modulus (G), Young's modulus (E), Poisson's ratio (v), and Pugh's index (B/G) are shown in Table 2.
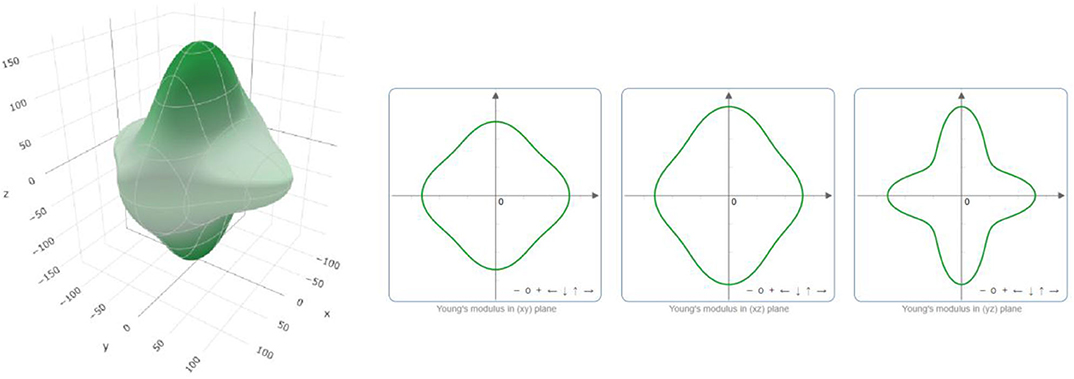
The critical value B/G that is used to distinguish between brittle and ductile crystals is 1.75. Obviously, PtO is in hand elastically ductile. Moreover, the critical value of v that distinguishes between the ionic and covalent chemical band natures is ~0.25. The chemical bonds in a PtO tetragonal crystal are mainly ionic. We use the ELATE program to determine the directional dependence anisotropy of PtO on the Young's modulus, shear modulus, and Possion's ratio in Figures 4–6, respectively. The elastic anisotropy of PtO can be determined from these figures. This is quite important for future practical applications of this material.
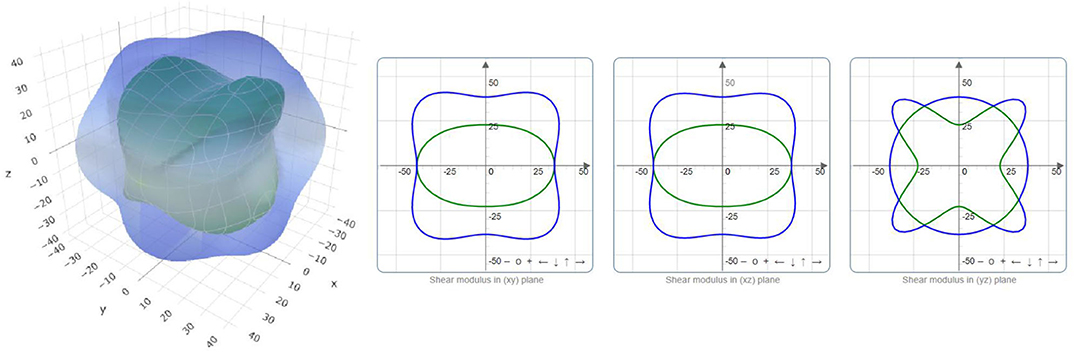
Figure 5. Directional dependence of the shear modulus: blue and green indicate the maximum and minimum values, respectively.
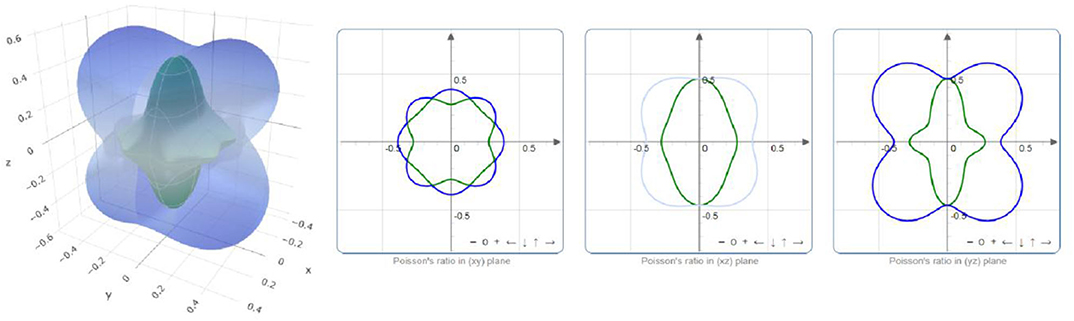
Figure 6. Directional dependence of Poisson's ratio: blue and green indicate the maximum and minimum values, respectively.
Topological Elements and Novel Surface States
Without considering the spin–orbit coupling effect, the band structure of PtO at its equilibrium lattice constants along the Γ-X-M-Γ-Z-R-A-Z-A-M directions was calculated using the GGA method, and the result is given in Figure 7. PtO is a typical semimetal (Wang et al., 2020a,b; Yalameha and Nourbakhsh, 2020) with clean band crossing points, These band-crossing points are located around the Fermi level and far from other trivial bands. Interestingly, these band crossing points are concentrated mainly in the R1 and R2 regions. We will discuss each band crossing point in R1 and R2. To confirm the band crossing points near the Fermi level further, one type of meta-GGA method, Tao–Perdew–Staroverov–Scuseria (TPSS) (Sun et al., 2011), was selected to prove the occurrence of the band crossing points in the R1 and R2 regions. The PtO band structure along the X-M-Γ-A-M directions as determined via the TPSS-meta-GGA method is shown in Figure 8. Obviously, the band crossing points in both regions are retained.
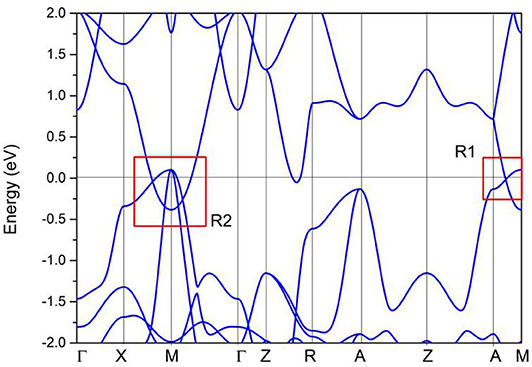
Figure 7. Calculated band structure of PtO along the Γ-X-M-Γ-Z-R-A-Z-A-M directions, as determined using the GGA method.
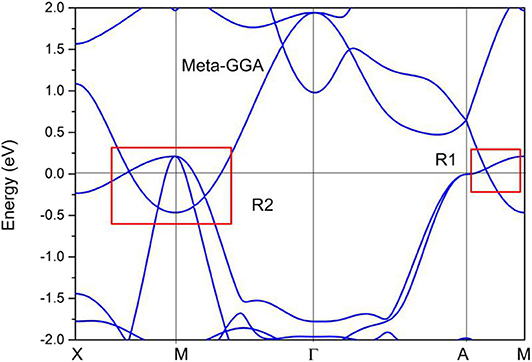
Figure 8. Calculated band structure of PtO along the X-M-Γ-A-M directions, as determined using the TPSS-meta-GGA method.
In R1, we can see that the band crossing point along the A-M direction induces a pair of triple nodal points. Symmetry analysis (with the help of Quantum ESPRESSO) shows that the two bands (conduction and valence bands), respectively, belong to irreducible representations Γ2 and Γ2 of the C4v symmetry for the A-M path (in R1). This pair of triple nodal points is generated by one non-degenerate band and one doubly degenerate band. The triple nodal point locations are given in Figure 9. The Fermi arc surface state (Xu et al., 2015b; Jin et al., 2019b, 2020) can be seen as strong evidence for the appearance of triple nodal points. In Figure 10, we show the projected spectrum on the (010) PtO tetragonal crystal surface. The triple nodal points are highlighted as yellow balls and the obvious Fermi arc non-trivial surface states, which are located inside the band crossing points and marked by black arrows, are near the Fermi level.
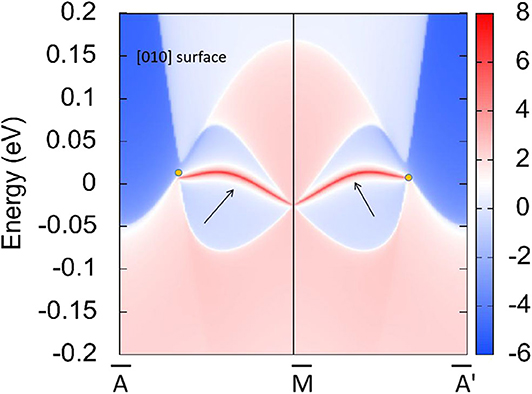
Figure 10. Projected spectrum on the (010) PtO tetragonal crystal surface. The band crossing points are marked as yellow balls and the Fermi arc surface states are highlighted using black arrows.
As shown in Figure 11, there are four band crossing points along the X-M-Γ directions and near the Fermi level in R2. Band crossing points 1 and 4 are generated by crossing bands 1 and 2. However, band crossing points 2 and 3 are formed by overlaps between bands 1 and 3. Since PtO hosts both P and T symmetries, these four band crossing points along the X-M-Γ directions in the kz = 0 plane cannot be treated as isolated points (Gao et al., 2018; He et al., 2019; Zhao et al., 2020). To further verify that these four band crossing points in R2 belong to nodal lines, 3-D and 2-D plots of bands 1 and 3 in the kz = 0 plane are given in Figure 12. One M-point-centered closed nodal line, marked as a white line, occurs in the kz = 0 plane. Similarly, the 3-D and 2-D plots of bands 1 and 2 in the kz = 0 plane are shown in Figure 13. The other M-point-centered nodal line with a closed shape appears in the kz = 0 plane. However, these two closed nodal lines exhibit different shapes and sizes, and are located at different energies. The closed nodal line shown in Figure 13 is larger than that in Figure 12. An overall illustration of the M-point-centered double closed nodal lines in the kz = 0 plane is shown in Figure 14.
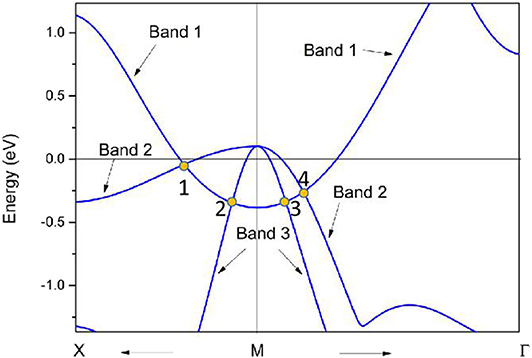
Figure 11. Calculated PtO band structure along the X-M-Γ directions, as determined using the GGA method. The band crossing points, labeled 1, 2, 3, and 4, are marked by yellow balls.
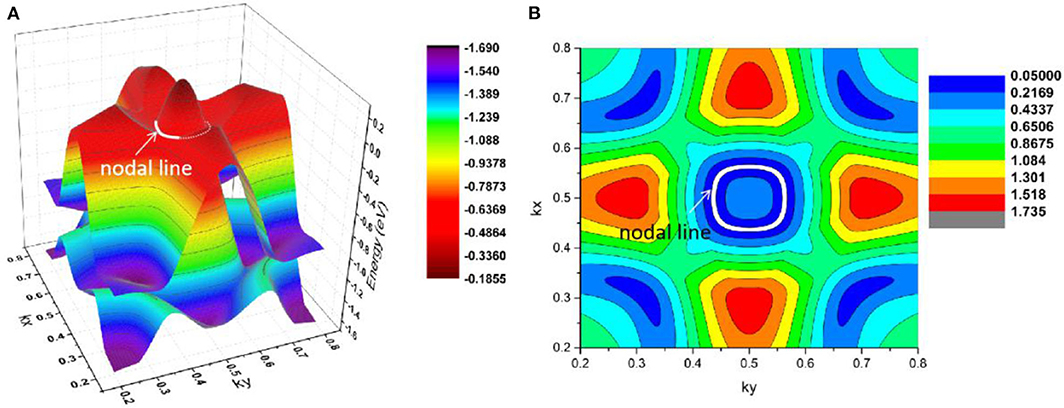
Figure 12. M-point-centered (A) 3-D and (B) 2-D plots of bands 1 and 3 in the kz = 0 plane in R2. The white line indicates the nodal line in this plane.
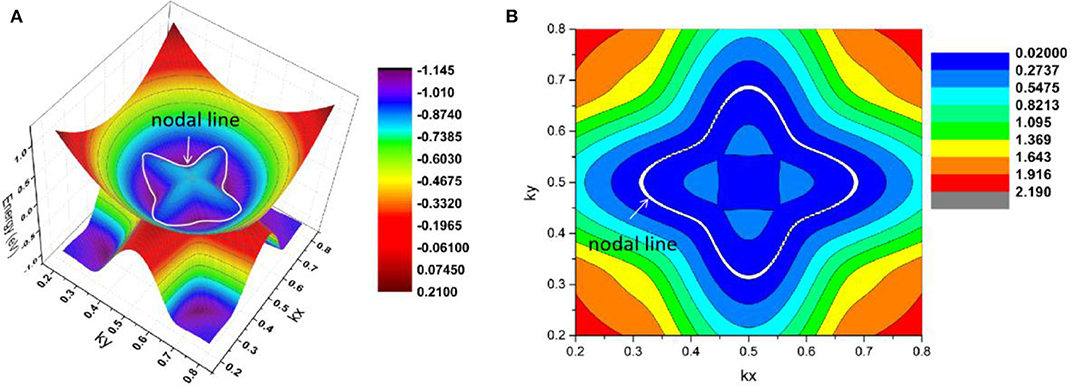
Figure 13. M-point-centered (A) 3-D and (B) 2-D plots of bands 1 and 2 in the kz = 0 plane in R2. The nodal line is marked as a white line.
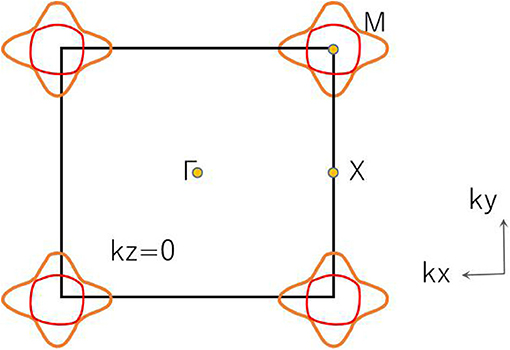
Figure 14. Illustration of M-point-centered double closed nodal lines in the kz = 0 plane. Double nodal lines are marked using different colors.
Typically, drum-head-like surface states that originate from the bulk band crossing points can be observed (Zhou et al., 2018; Yi et al., 2019). To further prove this argument, the spectrum is projected on the (001) PtO tetragonal crystal surface in Figure 15. The drum-head-like surface states clearly appear outside and inside band crossing points 1, 2, 3, and 4.
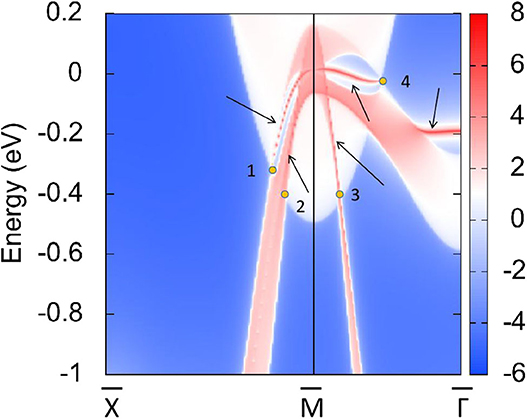
Figure 15. Projected spectrum on the (001) PtO tetragonal crystal surface. Band crossing points 1, 2, 3, and 4 are marked as yellow balls and the drum-head-like surface states are highlighted using black arrows.
Conclusions
In summary, we have systematically used first-principles calculations to study the electronic, mechanical, and topological properties of tetragonal phase PtO, which is a realistic material. PtO is an excellent topological semimetal with pairs of triple nodal points and double closed nodal lines in the kz = 0 plane when the spin–orbit coupling effect is ignored. The 0-D triple nodal points and 1-D closed nodal lines are further confirmed by the exotic Fermi arc surface states and drum-head-like surface states, respectively. The mechanical properties and phonon dispersion of this material allowed us to determine that PtO is mechanically stable, elastically ductile, and dynamically stable. These results demonstrate that PtO is an interesting material, which can be used to achieve experimental detection of nodal points and nodal lines or to further practical applications.
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Author Contributions
YL: software, supervision, and conceptualization. JX and VS: reviewing and editing. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by the first batch of post-doctoral research fund projects in Yunnan Province (Serial No. 9), the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN201801346), and the Chongqing University of Arts and Sciences Foundation (Grant No. Z2011Rcyj05).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2020.00704/full#supplementary-material
Footnotes
1. ^Available online at: https://www.materialsproject.org/materials/mp-7947/.
References
Abutalib, M. M. (2019). A DFT based prediction of a new 2D zirconium disulfide Pmmm-ZrS2 monolayer: A quasi direct band gap semiconductor. Res. Phys. 12, 903–907. doi: 10.1016/j.rinp.2018.10.028
Cai, J., Xie, Y., Chang, P., Kim, H., and Chen, Y. (2018). Nodal-chain network, intersecting nodal rings and triple points coexisting in nonsymmorphic Ba3Si4. Phys. Chem. Chem. Phys. 20, 21177–21183. doi: 10.1039/C8CP02810A
Chen, H., Zhang, S., Jiang, W., Zhang, C., Guo, H., Liu, Z., et al. (2018). Prediction of two-dimensional nodal-line semimetals in a carbon nitride covalent network. J. Mater. Chem. C 6, 11252–11259. doi: 10.1039/C8TA02555J
Chiu, C. K., and Schnyder, A. P. (2014). Classification of reflection-symmetry-protected topological semimetals and nodal superconductors. Phys. Rev. B 90:205136. doi: 10.1103/PhysRevB.90.205136
Ding, G., Hu, Y., Li, D., and Wang, X. (2019). A comparative study of thermoelectric properties between bulk and monolayer SnSe. Res. Phys. 15:102631. doi: 10.1016/j.rinp.2019.102631
Ernzerhof, M., and Scuseria, G. E. (1999). Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 110, 5029–5036. doi: 10.1063/1.478401
Fang, C., Gilbert, M. J., Dai, X., and Bernevig, B. A. (2012). Multi-Weyl topological semimetals stabilized by point group symmetry. Phys. Rev. Lett. 108:266802. doi: 10.1103/PhysRevLett.108.266802
Fang, C., Lu, L., Liu, J., and Fu, L. (2016). Topological semimetals with helicoid surface states. Nat. Phys. 12, 936–941. doi: 10.1038/nphys3782
Fu, B. B., Yi, C. J., Zhang, T. T., Caputo, M., Ma, J. Z., Gao, X., et al. (2019a). Dirac nodal surfaces and nodal lines in ZrSiS. Sci. Adv. 5:eaau6459. doi: 10.1126/sciadv.aau6459
Fu, J., Song, T., Liang, X., and Zhao, G. (2019b). Composition dependence of phonon and thermodynamic properties of the ternary AlGaN mixed crystal. Res. Phys. 14:102505. doi: 10.1016/j.rinp.2019.102505
Gao, H., Venderbos, J. W., Kim, Y., and Rappe, A. M. (2019). Topological semimetals from first-principles. Ann. Rev. Mater. Res. 49, 153–183. doi: 10.1146/annurev-matsci-070218-010049
Gao, Y., Xie, Y., Chen, Y., Gu, J., and Chen, Z. (2018). Spindle nodal chain in three-dimensional α′ boron. Phys. Chem. Chem. Phys. 20, 23500–23506. doi: 10.1039/C8CP03874K
Hafner, J. (2007). Materials simulations using VASP—a quantum perspective to materials science. Comp. Phys. Commun. 177, 6–13. doi: 10.1016/j.cpc.2007.02.045
Han, Y., Wu, M., Feng, Y., Cheng, Z., Lin, T., Yang, T., et al. (2019). Competition between cubic and tetragonal phases in all-d-metal Heusler alloys, X2−xMn1+xV (X = Pd, Ni, Pt, Ag, Au, Ir, Co; x = 1, 0): a new potential direction of the Heusler family. IUCrJ 6, 465–472. doi: 10.1107/S2052252519004007
He, T., Zhang, X., Meng, W., Jin, L., Dai, X., and Liu, G. (2019). Topological nodal lines and nodal points in the antiferromagnetic material β-Fe2PO5. J. Mater. Chem. C 7, 12657–12663. doi: 10.1039/C9TC04046C
Hosur, P., Parameswaran, S. A., and Vishwanath, A. (2012). Charge transport in Weyl semimetals. Phys. Rev. Lett. 108:046602. doi: 10.1103/PhysRevLett.108.046602
Hosur, P., and Qi, X. (2013). Recent developments in transport phenomena in Weyl semimetals. Comptes Rendus Phys. 14, 857–870. doi: 10.1016/j.crhy.2013.10.010
Jia, K., Yang, C., Wang, M., Ma, X., and Yi, Y. (2019). First-principles insight on elastic, electronic, and thermoelectric transport properties of BAgX (X =Ti, Zr, Hf). Res. Phys. 15:102563. doi: 10.1016/j.rinp.2019.102563
Jin, L., Zhang, X., Dai, X., Liu, H., Chen, G., and Liu, G. (2019b). Centrosymmetric Li2NaN: a superior topological electronic material with critical-type triply degenerate nodal points. J. Mater. Chem. C 7, 1316–1320. doi: 10.1039/C8TC05930F
Jin, L., Zhang, X., He, T., Meng, W., Dai, X., and Liu, G. (2019a). Topological nodal line state in superconducting NaAlSi compound. J. Mater. Chem. C 7, 10694–10699. doi: 10.1039/C9TC03464A
Jin, L., Zhang, X., He, T., Meng, W., Dai, X., and Liu, G. (2020). Electronic structure, doping effect and topological signature in realistic intermetallics Li3−xNaxM (x = 3, 2, 1, 0; M = N, P, As, Sb, Bi). Phys. Chem. Chem. Phys. 22, 5847–5854. doi: 10.1039/C9CP06033B
Kobayashi, S., and Sato, M. (2015). Topological superconductivity in Dirac semimetals. Phys. Rev. Lett. 115:187001. doi: 10.1103/PhysRevLett.115.187001
Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59:1758. doi: 10.1103/PhysRevB.59.1758
Kumar, N., Yao, M., Nayak, J., Vergniory, M. G., Bannies, J., Wang, Z., et al. (2020). Signatures of sixfold Degenerate Exotic Fermions in a superconducting Metal PdSb2. Adv. Mater. 32:1906046. doi: 10.1002/adma.201906046
Lejaeghere, K., Bihlmayer, G., Björkman, T., Blaha, P., Blügel, S., Blum, V., et al. (2016). Reproducibility in density functional theory calculations of solids. Science 351:aad3000. doi: 10.1126/science.aad3000
Liu, Z. K., Zhou, B., Zhang, Y., Wang, Z. J., Weng, H. M., Prabhakaran, D., et al. (2014). Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 343, 864–867. doi: 10.1126/science.1245085
Lundgren, R., Laurell, P., and Fiete, G. A. (2014). Thermoelectric properties of Weyl and Dirac semimetals. Phys. Rev. B 90:165115. doi: 10.1103/PhysRevB.90.165115
Miransky, V. A., and Shovkovy, I. A. (2015). Quantum field theory in a magnetic field: from quantum chromodynamics to graphene and Dirac semimetals. Phys. Rep. 576, 1–209. doi: 10.1016/j.physrep.2015.02.003
Moore and Pauling 1941~Moore, W. J. Jr, and Pauling, L. (1941). The crystal structures of the tetragonal monoxides of lead, tin, palladium, and platinum. J. Am. Chem. Soc. 63, 1392–1394. doi: 10.1021/ja01850a074
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865. doi: 10.1103/PhysRevLett.77.3865
Pham, A., Klose, F., and Li, S. (2019). Robust topological nodal lines in halide carbides. Phys. Chem. Chem. Phys. 21, 20262–20268. doi: 10.1039/C9CP04330F
Qie, Y., Liu, J., Wang, S., Sun, Q., and Jena, P. (2019). Tetragonal C24: a topological nodal-surface semimetal with potential as an anode material for sodium ion batteries. J. Mater. Chem. A 7, 5733–5739. doi: 10.1039/C8TA11276B
Sultana, F., Uddin, M. M., Ali, M. A., Hossain, M. M., Naqib, S. H., and Islam, A. K. M. A. (2018). First principles study of M2InC (M = Zr, Hf and Ta) MAX phases: the effect of M atomic species. Res. Phys. 11, 869–876. doi: 10.1016/j.rinp.2018.10.044
Sun, J., Marsman, M., Csonka, G. I., Ruzsinszky, A., Hao, P., Kim, Y. S., et al. (2011). Self-consistent meta-generalized gradient approximation within the projector-augmented-wave method. Phys. Rev. B 84:035117. doi: 10.1103/PhysRevB.84.035117
Vazifeh, M. M., and Franz, M. (2013). Electromagnetic response of Weyl semimetals. Phys. Rev. Lett. 111:027201. doi: 10.1103/PhysRevLett.111.027201
Villanova, J. W., and Park, K. (2018). Magnetic field induced Weyl semimetal from Wannier-function-based tight-binding model. Phys. Rev. B 98:075123. doi: 10.1103/PhysRevB.98.075123
Wang, X., Ding, G., Cheng, Z., Surucu, G., Wang, X. L., and Yang, T. (2020a). Novel topological nodal lines and exotic drum-head-like surface states in synthesized CsCl-type binary alloy TiOs. J. Adv. Res. 22, 137–144. doi: 10.1016/j.jare.2019.12.001
Wang, X., Ding, G., Cheng, Z., Surucu, G., Wang, X. L., and Yang, T. (2020b). Rich topological nodal line bulk states together with drum-head-like surface states in NaAlGe with anti-PbFCl type structure. J. Adv. Res. 23, 95–100. doi: 10.1016/j.jare.2020.01.017
Weng, H., Fang, C., Fang, Z., and Dai, X. (2016a). Topological semimetals with triply degenerate nodal points in θ-phase tantalum nitride. Phys. Rev. B 93:241202. doi: 10.1103/PhysRevB.93.241202
Weng, H., Fang, C., Fang, Z., and Dai, X. (2016b). Coexistence of Weyl fermion and massless triply degenerate nodal points. Phys. Rev. B 94:165201. doi: 10.1103/PhysRevB.94.165201
Wu, W., Liu, Y., Li, S., Zhong, C., Yu, Z. M., Sheng, X. L., et al. (2018). Nodal surface semimetals: theory and material realization. Phys. Rev. B 97, 115125. doi: 10.1103/PhysRevB.97.115125
Xu, S. Y., Belopolski, I., Alidoust, N., Neupane, M., Bian, G., Zhang, C., et al. (2015a). Discovery of a Weyl fermion semimetal and topological fermi arcs. Science 349, 613–617. doi: 10.1126/science.aaa9297
Xu, S. Y., Liu, C., Kushwaha, S. K., Sankar, R., Krizan, J. W., Belopolski, I., et al. (2015b). Observation of Fermi arc surface states in a topological metal. Science 347, 294–298. doi: 10.1126/science.1256742
Yalameha, S., and Nourbakhsh, Z. (2020). Coexistence of type-I and critical-type nodal line states in intermetallic compounds ScM (M = Cu, Ag, Au). J. Phys. Condensed Matter 32:295502. doi: 10.1088/1361-648X/ab80f4
Yan, B., and Felser, C. (2017). Topological materials: weyl semimetals. Ann. Rev. Condensed Matter Phys. 8, 337–354. doi: 10.1146/annurev-conmatphys-031016-025458
Yang, T., Khenata, R., and Wang, X. (2020). Predicted remarkably topological nodal surface states in P63/m type Sr3WN3 from first-principles. Res. Phys. 17:103026. doi: 10.1016/j.rinp.2020.103026
Yi, X., Li, W. Q., Li, Z. H., Zhou, P., Ma, Z., and Sun, L. Z. (2019). Topological dual double node-line semimetals NaAlSi(Ge) and their potential as cathode material for sodium ion batteries. J. Mater. Chem. C 7, 15375–15381. doi: 10.1039/C9TC04096J
Young, S. M., and Kane, C. L. (2015). Dirac semimetals in two dimensions. Phys. Rev. Lett. 115:126803. doi: 10.1103/PhysRevLett.115.126803
Zhang, X., Yu, Z. M., Zhu, Z., Wu, W., Wang, S. S., Sheng, X. L., et al. (2018). Nodal loop and nodal surface states in the Ti3Al family of materials. Phy. Rev. B 97:235150. doi: 10.1103/PhysRevB.97.235150
Zhao, Z., Zhang, Z., and Guo, W. (2020). A family of all sp2-bonded carbon allotropes of topological semimetals with strain-robust nodal-lines. J. Mater. Chem. C 8, 1548–1555. doi: 10.1039/C9TC05470G
Zhou, P., Ma, Z., and Sun, L. Z. (2018). Coexistence of open and closed type nodal line topological semimetals in two dimensional B2C. J. Mater. Chem. C 6, 1206–1214. doi: 10.1039/C7TC05095J
Zou, Z. C., Zhou, P., Ma, Z., and Sun, L. Z. (2019). Strong anisotropic nodal lines in the TiBe family. Phys. Chem. Chem. Phys. 21, 8402–8407. doi: 10.1039/C9CP00508K
Keywords: double nodal lines, fermi arc and drum-head-like surface states, triple point, DFT, phonon dispersion, mechanical behaviors
Citation: Li Y, Xia J and Srivastava V (2020) The Tetragonal Monoxide of Platinum: A New Platform for Investigating Nodal-Line and Nodal-Point Semimetallic Behavior. Front. Chem. 8:704. doi: 10.3389/fchem.2020.00704
Received: 19 June 2020; Accepted: 08 July 2020;
Published: 14 August 2020.
Edited by:
Zhenxiang Cheng, University of Wollongong, AustraliaReviewed by:
Junjie He, University of Bremen, GermanyYong-Chun Gao, North China University of Science and Technology, China
Copyright © 2020 Li, Xia and Srivastava. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Li, bGl5YW5nQGNxd3UuZWR1LmNu; bGl5YW5nX3BoeXNpY3NAMTI2LmNvbQ==
 Yang Li
Yang Li Jihong Xia2
Jihong Xia2