Mini Review: Quantum Confinement of Atomic and Molecular Clusters in Carbon Nanotubes

Abstract

We overview our recent developments on a computational approach addressing quantum confinement of light atomic and molecular clusters (made of atomic helium and molecular hydrogen) in carbon nanotubes. We outline a multi-scale first-principles approach, based on density functional theory (DFT)-based symmetry-adapted perturbation theory, allowing an accurate characterization of the dispersion-dominated particle–nanotube interaction. Next, we describe a wave-function-based method, allowing rigorous fully coupled quantum calculations of the pseudo-nuclear bound states. The approach is illustrated by showing the transition from molecular aggregation to quasi-one-dimensional condensed matter systems of molecular deuterium and hydrogen as well as atomic ⁴He, as case studies. Finally, we present a perspective on future-oriented mixed approaches combining, e.g., orbital-free helium density functional theory (He-DFT), machine-learning parameterizations, with wave-function-based descriptions.

1 Introduction

The cylindrical confinement provided by carbon nanotubes has offered the possibility of studying the pronounced quantum behaviour of ⁴He atoms and H₂ molecules at reduced dimensionality. Recent measurements have demonstrated the formation of two-dimensional (2D) ⁴He layers on the outer surface of single-walled carbon nanotubes (SWCNTs) (Noury et al., 2019). Also, an experimental study (Ohba, 2016) of gas adsorption at low (2–5 K) temperature revealed a quenched propagation of ⁴He atoms through carbon nanopores with diameters below 7 Å despite of their small kinetic diameter. The application of orbital-free helium density functional theory (He-DFT) to carbon nanotubes immersed in a helium nanodroplet provided theoretical explication that the experimental observations stem from the exceptionally high zero-point energy of ⁴He as well as its tendency to form two-dimensional (2D) layers upon adsorption at low temperatures (Hauser and de Lara-Castells, 2016). These conclusions were further confirmed by applying more accurate ab initio potential modelling along with a wave-function (WF)-based approach (Hauser et al., 2017). This study also showed that SWCNTs are filled by more molecules of N₂ than ⁴He atoms, due to the higher zero-point energy of the latter. More generally, the interaction of small atomic and molecular systems with carbon-based nanostructures has attracted a lot of attention recently (see, e.g. Deb et al., 2016; Deb et al., 2019; Paul et al., 2019; Paul et al., 2020 and references therein).

GRAPHICAL ABSTRACT

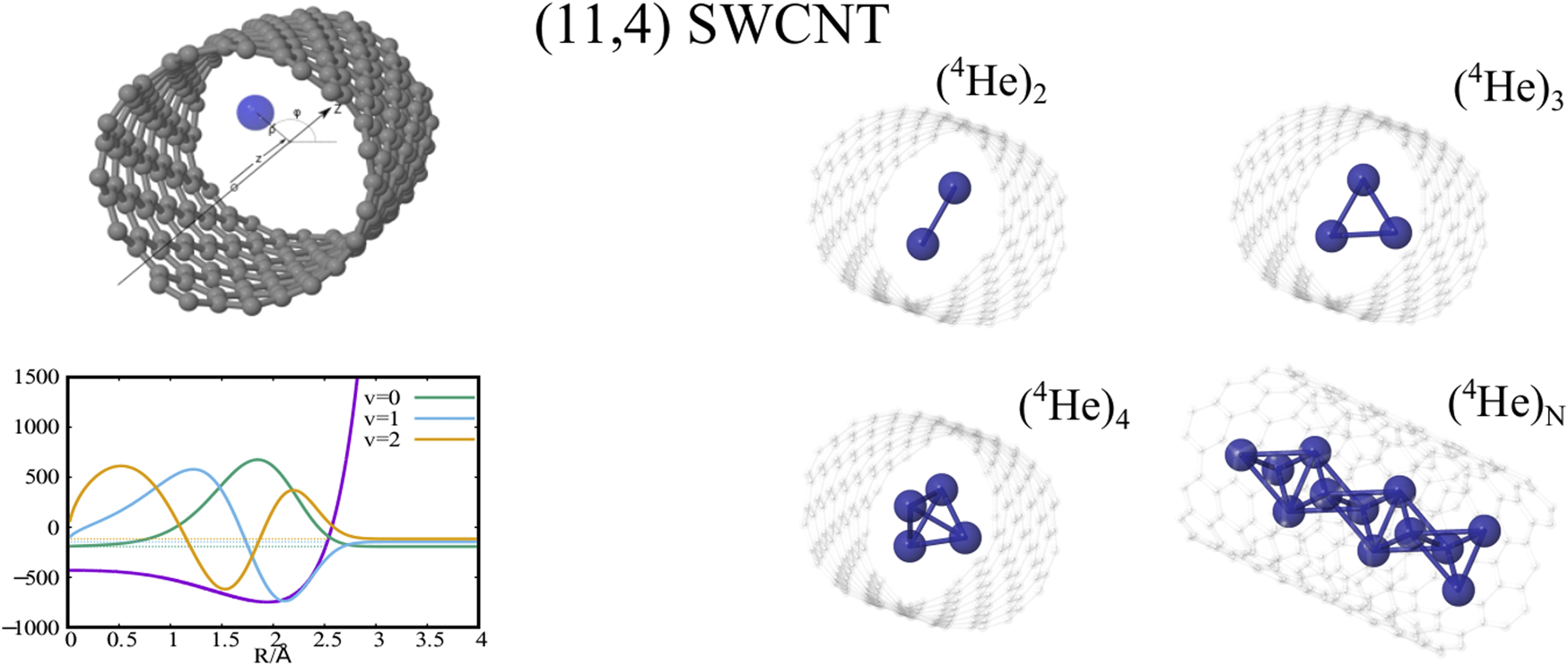
For the case of molecular deuterium, our recent theoretical work has provided conclusive evidence for the transition from molecular aggregation to quantum solid-like packing in a SWCNT of 1 nm diameter (de Lara-Castells and Mitrushchenkov, 2020; de Lara-Castells and Mitrushchenkov, 2021), confirming a previous study using an embedding approach in a broader (ca. 1.4 nm) SWCNT (de Lara-Castells et al., 2017). Experimental evidence, using neutron scattering, on the formation of one-dimensional D₂ crystals under carbon nanotube confinement has been reported as well (Cabrillo et al., 2021). Altogether, these studies have confirmed the key role played by the quantum nature of the nuclear degrees of freedom in the confined atomic helium, molecular hydrogen, or molecular deuterium motion.

The quest for the understanding of the aggregation of molecular H₂ in carbon nanotubes is also application-oriented as it is being actively used as a clean energy source, substituting fossil fuels. In fact, its combustion produces only heat and water, and it can be efficiently combined with oxygen in a fuel cell to produce electricity. Yet, the usage of hydrogen as a profit fuel requires a substantial development of efficient storage materials (Schlapbach and Züttel, 2001; Züttel, 2003; Zheng et al., 2021) such as metal organic frameworks, Rosi et al. (2003) covalent organic frameworks (Zheng et al., 2021), and carbon-based nanoporous materials (Cheng et al., 2001; Liu et al., 2010). Hydrogen storage methods are aimed to pack hydrogen molecules as close as possible, existing direct experimental evidences for solid-like packing of hydrogen at temperatures of industrial importance (Ting et al., 2015). Actually, the question on the nature of the hydrogen packing in carbon nanotubes is truly fundamental. Thus, the possible existence of either a superfluid (Rossi and Ancilotto, 2016) or a crystalline phase (Del Maestro and Boninsegni, 2017; Ferré et al., 2017) for para-H₂ molecules inside carbon nanotubes at zero (Rossi and Ancilotto, 2016; Ferré et al., 2017) or ultra-low temperatures (Del Maestro and Boninsegni, 2017) have been addressed as well (see also (Cazorla and Boronat, 2017) for a recent review). Specially appealing in regards to the impact of quantum effects on the diffusion of H₂ and D₂ along carbon nanotubes is the experimental finding of reserved trends in their rates upon cooling (Nguyen et al., 2010), with the D₂ isotope becoming the faster inspite of its higher mass (Nguyen et al., 2010). The impact of quantum effects in confined H₂ and D₂ motion has been theoretically confirmed as well (Mondelo-Martell and Huarte-Larrañaga, 2016; Mondelo-Martell et al., 2017; Mondelo-Martell and Huarte-Larrañaga, 2021).

The high interest on the confinement of clusters of atomic ⁴He is also related to the superfluid nature of ⁴He droplets at a temperature close to absolute zero (0.4 K) (Mudrich and Stienkemeier, 2014) and, more specifically, to the onset of such fascinating property in doped clusters made of just a few ⁴He atoms (Toennies and Vilesov, 2004). Then, the question is whether the confinement provided by SWCNTs can favour the emergence of such feature at reduced dimensionality. The effect of carbon nanotube confinement has been also shown to be remarkable for the ³He isotope inside a SWCNT of 1 nm diameter. Thus, as opposed to the free dimer case, the confined ³He dimer is predicted to be bound, mainly as a consequence of the strong localization along the radial ³He–SWCNT direction (de Lara-Castells and Mitrushchenkov, 2021).

This overview article is organized as follows. The next section presents the computational approach addressing the modeling of intermolecular adsorbate–SWCNT interactions as well as fully coupled quantum calculations of the corresponding pseudo-nuclear wavefunctions. Section 3 presents an illustrative application of the computational approach to the transition from molecular aggregation to quasi-one-dimensional (1D) matter systems composed by either D₂/H₂ molecules or ⁴He atoms. Finally, Section 4 closes with a summary of concluding remarks and a few future prospects.

2 Computational Approach

2.1 Ab Initio Modelling of the Adsorbate-Nanotube Interaction

Achieving a correct description of the interaction of the lightest atomic and molecular clusters in nature (i.e., made of He or H₂) with its confining SWCNT environment is a challenge even for expensive ab initio methods since they are dominated by long-range dispersion forces (van der Waals forces). Extended dispersion-corrected DFT methods are applicable including confinement effects in extended SWCNT structures but they bear a tendency to overshoot when applied to ultimate cases of dispersion-dominated (e.g., He-surface) interactions. One key idea has consisted in designing a functional [the so-called dlDF functional (Pernal et al., 2009)] which accounts for the dispersionless interaction energy only so that the dispersion corrections can be safely added later. Within a practical implementation of this idea, the incremental method (Stoll, 1992) is applied on non-periodic (small) cluster models of extended systems and combined with periodic dispersionless DFT calculations (de Lara-Castells et al., 2014b; de Lara-Castells et al., 2014a). This approach has been shown to be particularly successful when describing the interaction of atomic helium (de Lara-Castells et al., 2014a) as well as heavier noble gases (de Lara-Castells et al., 2015) with coronene/graphene/graphite surfaces. Very recently, it has been also demonstrated how modern ab initio intermolecular perturbation theory allows a cost-effective and accurate characterization of van der Waals-dominated He-SWCNT and H₂-SWCNT interactions using small clusters models of the SWCNTs. The use of small cluster models is justified as complicated, dispersionless contributions are mostly of short-range nature. Dispersion, on the other hand, is long-range, but the corresponding parameters show excellent transferability properties upon increasing the size of the surface cluster models (de Lara-Castells et al., 2014a; de Lara-Castells et al., 2015). Therefore, these parameters can be calculated at high level of ab initio theory on small clusters and then scaled to the actual SWCNT system. As previously emphasized (de Lara-Castells and Hauser, 2020), detailed energy decomposition schemes, an intrinsic feature of methods such as density functional theory (DFT)-based symmetry-adapted perturbation theory [SAPT(DFT)] (Hesselmann and Jansen, 2003; Misquitta et al., 2003; Heßelmann et al., 2005; Misquitta et al., 2005) has been shown to be particularly useful in this respect.

In our most recent works (de Lara-Castells and Mitrushchenkov, 2020; de Lara-Castells and Mitrushchenkov, 2021), the SAPT(DFT) method has been used to derive by fitting the dispersionless and dispersion SAPT(DFT) energy contributions to an additive pairwise potential model (PPM) (de Lara-Castells et al., 2016; Hauser and de Lara-Castells, 2017; de Lara-Castells et al., 2017; Hauser et al., 2017), which is a modified version of that proposed by Carlos and Cole (Carlos and Cole, 1980). For the illustrative cases presented in this work, these terms were calculated for the interaction between a single H₂ molecule (He atom) and a hydrogen-saturated (unsaturated) nanotube SWCNT(5, 5) tube made of 62 (40) atoms, considering two transverse sections of the tube. The SAPT(DFT) MOLPRO (Heßelmann et al., 2005; Werner et al., 2012) implementation was applied, using the Perdew-Burke-Ernzerhof (PBE) density functional (Perdew et al., 1996) and the augmented polarized correlation-consistent triple-zeta basis (Woon et al., 1994) for all atoms but the hydrogen atoms saturating the dangling bonds, for which the correlation-consistent double-zeta basis was used instead.

The PPM functional form (de Lara-Castells et al., 2016; Hauser and de Lara-Castells, 2017; de Lara-Castells et al., 2017; Hauser et al., 2017) for the dispersionless energy contribution accounts for the typical exponential growth of the dominant dispersionless term, the exchange-repulsion, but also including a Gaussian-type “cushion” to describe weakly attractive tails stemming from other dispersionless termswhere R_c is a cut-off distance, R_A-C stands for the distance between the adsorbate center-of-mass and one carbon atom of the SWCNT, and θ_C is the angle between the radial vector going from the SWCNT center to one carbon atom and the vector R_A-C pointing from the adsorbate center-of-mass to the same C atom. The dimensionless factor γ_R in the first term accounts for the anisotropy of the C − C bonds. The sum in Eq. (1) runs over all carbon atoms of the nanotube. For the dispersion part, we apply the typical C₆/C₈ expansion with the damping functions of Tang and Toennies f_n (n = 6, 8) (Tang and Toennies, 1984)where γ_A is also a dimensionless anisotropy parameter. The inclusion of γ_A and γ_R anisotropy terms has been found to be important when modelling potential corrugation effects on both curved carbon and metallic surfaces (de Lara-Castells et al., 2016; Hauser and de Lara-Castells, 2017; Hauser et al., 2017).

2.2 The Pseudo-Nuclear Wave-Function Problem

Our method has been designed to allow bound-state calculations for N identical atoms or molecules (referred to as “pseudo-nuclei”, PNs) inside a SWCNT. Using cylindrical coordinates (x_i, y_i, z_i → ρ_i, ϕ_i, z_i) for each PN (see left panel of Figure 1), together with a Jacobian transformation of the volume to keep the Hamiltonian “explicitly Hermitian”, , the Hamiltonian describing a motion of N PN’s takes the formwhere the distance r_ij is explicitly given by

FIGURE 1

We note that, in order to preserve the cylindrical symmetry of the system, the very small corrugation appearing along the azimuthal degree of freedom ϕ is not accounted for. Considering long nanotubes, it is thus assumed that the interaction potential depends only on ρ. The atomic structure of the SWCNT, however, is implicitly considered through the SAPT(DFT) calculations used to fit the parameters of our PPM (see Section 3.1). These potentials are used within the Discrete Variable Representation (DVR) approach (Bačic̀ and Light, 1989) upon fitting them to polynomials of ρ:

To separate the overall Z-translation and overall rotational motions, we introduce relative coordinates as t_i = z_i − z_N and χ_i = ϕ_i − ϕ_N, for i = 1 … N − 1. The overall Z-translation and overall rotation coordinates are conveniently defined as and Φ = ϕ_N. The overall rotation quantum number reads Λ = m₁ + m₂ + ⋯ + m_N, where m_i is the integer standing for the projection of the angular momentum of the i-th particle onto the nanotube axis. Since both PN–SWCNT and PN–PN interactions do not depend on Φ, the coordinate Φ can be separated via the factor . Finally, the full kinetic energy is written as whereand

We note that the internal Hamiltonian does not account explicitly for the bosonic permutation symmetry of all N particles. The symmetry is automatically included for the particles labelled as 1 … N − 1 since it is equivalent to a simple exchange of the corresponding coordinates t_i, ρ_i, χ_i. The exchange of the particles labelled as i and N, however, results in linear transformations of the coordinates t_i and χ_i. The symmetry with respect to the i ↔ N exchange is analyzed a posteriori by defining a “bosonic symmetry factor” Q as the matrix element:

The Q factor is unity for true bosonic solutions. This test is used as a criteria to evaluate the wavefunction accuracy.

To calculate the eigenvalues of the internal Hamiltonian, we use the DVR approach (Bačic̀ and Light, 1989; de Lara-Castells and Mitrushchenkov, 2020; de Lara-Castells and Mitrushchenkov, 2021). This approach allows an easy and quick evaluation of the pair interaction potential V₂, with the basis set being obtained as a direct product of functions for the different coordinates. Sinc-DVR functions are conveniently employed for the t and χ coordinates. When dealing with the polar radii ρ, however, it is necessary to explicitly treat the singular kinetic energy term , which stems from the Jacobian transformation to cylindrical coordinates. For this purpose, we use the DVR basis obtained for the finite basis set representation (FBR) built from the radial functions of two-dimensional (2D) Harmonic oscillator functions. However, this basis renders the grid size too large for clusters with, e.g., 4 PNs since the internal Hamiltonian becomes 10-dimensional (10 D). This problem is efficiently solved by using potential-optimized DVR (PO-DVRs) functions (Echave and Clary, 1992), allowing for a very fast energy convergence as well. The diagonalization of the resulting Hamiltonian matrix is carried out using the Jacobi-Davidson algorithm (Sleijpen and van der Vorst, 1996). This technique has been very successful even for characterizing ill-behaved interactions such as, e.g., the “hard-core” interaction problem of doped helium clusters (de Lara-Castells et al., 2009a; de Lara-Castells et al., 2009b).

3 Illustrative Applications

In the first subsection, we will illustrate how the interaction of molecular hydrogen with various SWCNTs can be modelled at ab initio level. In the second subsection, we will show how our computational approach has allowed to reveal the transition from van-der-Waals-type molecular aggregation to quasi-1D condensed matter systems for atomic ⁴He and molecular H₂ and D₂ inside a SWCNT of 1 nm diameter.

3.1 H₂-Nanotube Interaction Potentials for SWCNTs of Increasing Diameter

As an illustrative case, the top (left-hand) panel of Figure 1 shows the total H₂/CNT interaction potential as a function of the radial distance r between the molecule center-of-mass and the SWCNT(5,5) center, along with the electrostatic E_elec, exchange-repulsion E_exch-rep, induction E_ind, and dispersion contributions E_disp. Upon applying the pairwise PPM presented in Section 3.1, the radial scans of interaction energies shown in the upper (right-hand) panel of Figure 1 are obtained for SWCNTs of increasing diameter.

As can be observed in the top panel of Figure 1 (left-hand side), the H₂/CNT attractive interaction is dispersion-dominated, with the exchange-repulsion dominating the whole dispersionless term. This repulsive energy contribution grows exponentially as the molecule-surface distance decreases although such behaviour is somewhat smoothed out by the attractive electrostatic contribution. The induction term contributes very little at the potential minimum but considerably at the SWCNT cage. The potential minimum is located at the center of the narrowest nanotube (diameter of 6.74 Å), where the adsorbates benefit from the dispersion interaction with carbon atoms at both sides of the carbon cage. However, upon increasing the nanotube diameter (see right-hand panel at the top of Figure 1), the dispersion becomes very small at the nanotube center and the potential minima shift towards the carbon cage. For a nanotube of diameter of 27.21 Å, the value of the well-depth (−56 meV) is already close to that obtained for a graphene sheet and measured for the H₂ molecule adsorbed onto graphite (−51.7 meV from Ref. 29). From the top (left-hand side) panel of Figure 1 it can also be observed that the pairwise potential model closely reproduces the results obtained with the SAPT(DFT) method. Similar conclusions hold for the case of the He/SWCNT interaction (Hauser et al., 2017), also emphasizing the usefulness of the SAPT(DFT)-derived PPM (see Section 3.1).

3.2 From van-der-Waals Aggregation to Quasi-One-Dimensional Chains

Considering a SWCNT of 1 nm diameter and helicity index (11, 4), the He-SWCNT and H₂-SWCNT one-particle potentials V₁(ρ) are shown in the bottom (right-side) panels of Figure 1 along with a few supported bound states of a single ⁴He atom or H₂ molecule. Figure 2 presents the plots of the ground-state two-dimensional (2D) densities of PN₄ clusters (PN = ⁴He, para-H₂, and ortho-D₂).

FIGURE 2

As previously reported (de Lara-Castells and Mitrushchenkov, 2020; de Lara-Castells and Mitrushchenkov, 2021) the structuring of PN_N clusters, with N = 1 − 3, is characterized by a high pseudo-nuclear delocalization. Thus, the triangular-like structure exhibited by confined (⁴He)₃ clusters (see graphical abstract) freely rotates inside the nanotube. However, as can be observed in Figure 2, whatever the bosonic particle be, the most probable structure is pyramidal-like. This confinement effect is specially remarkable for the case of ⁴He, due to the high delocalization of the bare PN–PN dimer (see bottom panel (d) of Figure 1). Yet, it features an increasing spatial delocalization when going from molecular ortho-D₂ through molecular para-H₂ to atomic ⁴He. Inspite of para-H₂ molecules being twice as light as ⁴He atoms, the three times deeper attractive well of the pair potential (see bottom panels (a) and (b) of Figure 1) causes a much more compact structuring of the (para-H₂)₄ cluster when compared with the ⁴He counterpart. Particularly, we note that the extended profile of the 2D densities in the χ coordinates reflects a quasi-independent relative rotational motion of two (⁴He)₂ dimers lying orthogonal to the tube axis. Since ortho-D₂ molecules are twice as heavy as para-H₂ molecules, the solid-like nature of the (ortho-D₂)₄ structure (a regular tetrahedron) becomes even more apparent than for the (para-H₂)₄ counterpart. The formation of (vibrationally averaged) tetrahedral structures of (para-H₂)₄ clusters is not a special effect from the SWCNT confinement. In fact, the same feature has also been revealed in clathrate hydrate cages (Sebastianelli et al., 2008; Witt et al., 2010). These similarities indicate that the aggregation of multiple light PNs are driven by quantum nuclear effects and very weak dispersive PN–PN interaction forces rather than the much more stronger PN–SWCNT (or PNT-cage) energy contribution (see bottom panels (a) and (b) of Figure 1). As discussed in detail in our previous work (de Lara-Castells and Mitrushchenkov, 2020), the onset of solid-like packing for molecular deuterium is explained by analyzing the potential minima landscape, allowing also to predict the formation of a one-dimensional chain of tetrahedral structures along the tube axis when the number of D₂ molecules increase. Similar conclusions holds for the cases of ⁴He atoms and H₂ molecules (de Lara-Castells and Mitrushchenkov, 2021). Moreover, these special structures feature stabilization of collective rotational motion resembling the behaviour of quantum rings exhibiting persistent current (charged particles) or persistent flow (neutral particles). This characteristic has been connected with the onset of superfluid motion and persistent flow in quantum rings made of ⁴He atoms by Bloch (Bloch, 1973). It is remarkable that such feature occurs already in clusters made of four ⁴He atoms at the reduced dimensionality offered by the confining medium.

4 Concluding Remarks and Future Directions

Summarizing, this mini review shows how a challenging case of confined molecular system can be accurately characterized using multi-scale first-principles modelling. In order to emphasize the key role of quantum effects, we have chosen the lightest atomic and molecular species in nature as the confined object and SWCNTs as the confining medium. In the first part, we have overviewed how an ab initio-derived pairwise potential model can accurately characterize the intermolecular interaction between the confining medium and the confined object. In the second part, we have illustrated how a computational approach, allowing for rigorous fully coupled quantum calculations of the pseudo-nuclear bound states, has been capable of revealing the transition from van der Waals-type molecular aggregation to quasi-1D condensed matter systems under cylindrical carbon nanotube confinement. Remarkably, it has been also shown that the structuring is driven by purely dispersive PN-PN interactions together with quantum pseudo-nuclear effects and not the much more stronger PN-tube interaction forces. In this way, it can be also understood why, inspite of its weak cohesive PN-PN interaction, neutron scattering experimental measurements have very recently shown the formation of quasi-one-dimensional structures of molecular D₂ corresponding to cylindrical sections of the hexagonal close-packed bulk crystal (Cabrillo et al., 2021).

As a future perspective, we are aimed to adapt our Full Configuration Interaction Nuclear Orbital (FCI-NO) approach (de Lara-Castells et al., 2009b), originally developed for doped helium clusters, to the present case in which the carbon nanotube acts as the “dopant” species. The essential advantage of this ansatz is that the wave function is expanded using products of nuclear orbitals, allowing the employment of second quantization techniques, an automatic inclusion of Fermi–Dirac and Bose–Einstein nuclear spin statistical effects, and, then, a characterization of ³He and ⁴He isotopes on an equal footing. The second future prospect is the creation of embedding approaches linking our wave-function-based description with orbital free He-DFT (Dalfovo et al., 1995; Ancilotto et al., 2017), following previous efforts (Hauser et al., 2017). In this sense, the highly accurate method presented in our latest work (de Lara-Castells and Mitrushchenkov, 2021) is expected to provide benchmark results guiding new, machine-learning driven, parameterizations in He-DFT, as already illustrated in electronic structure theory (Meyer et al., 2020).

References

• 1

  Ancilotto F. Barranco M. Coppens F. Eloranta J. Halberstadt N. Hernando A. et al (2017). Density Functional Theory of Doped Superfluid Liquid Helium and Nanodroplets. Int. Rev. Phys. Chem.36, 621–707. 10.1080/0144235X.2017.1351672

  • CrossRef
  • Google Scholar

• 2

  Bačić Z. Light J. C. (1989). Theoretical Methods for Rovibrational States of Floppy Molecules. Annu. Rev. Phys. Chem.40, 469–498. 10.1146/annurev.pc.40.100189.002345

  • CrossRef
  • Google Scholar

• 3

  Bloch F. (1973). Superfluidity in a Ring. Phys. Rev. A.7, 2187–2191. 10.1103/PhysRevA.7.2187

  • CrossRef
  • Google Scholar

• 4

  Cabrillo C. Fernández-Perea R. Bermejo F. J. Chico L. Mondelli C. González M. A. et al (2021). Formation of One-Dimensional Quantum Crystals of Molecular Deuterium inside Carbon Nanotubes. Carbon175, 141–154. 10.1016/j.carbon.2020.12.067

  • CrossRef
  • Google Scholar

• 5

  Carlos W. E. Cole M. W. (1980). Interaction between a He Atom and a Graphite Surface. Surf. Sci.91, 339–357. 10.1016/0039-6028(80)90090-4

  • CrossRef
  • Google Scholar

• 6

  Cazorla C. Boronat J. (2017). Simulation and Understanding of Atomic and Molecular Quantum Crystals. Rev. Mod. Phys.89, 035003. 10.1103/RevModPhys.89.035003

  • CrossRef
  • Google Scholar

• 7

  Cheng H.-M. Yang Q.-H. Liu C. (2001). Hydrogen Storage in Carbon Nanotubes. Carbon39, 1447–1454. 10.1016/s0008-6223(00)00306-7

  • CrossRef
  • Google Scholar

• 8

  Dalfovo F. Lastri A. Pricaupenko L. Stringari S. Treiner J. (1995). Structural and Dynamical Properties of Superfluid Helium: A Density-Functional Approach. Phys. Rev. B52, 1193–1209. 10.1103/PhysRevB.52.1193

  • CrossRef
  • Google Scholar

• 9

  Deb J. Bhattacharya B. Paul D. Sarkar U. (2016). Interaction of Nitrogen Molecule with Pristine and Doped Graphyne Nanotube. Phys. E84, 330–339. 10.1016/j.physe.2016.08.006

  • CrossRef
  • Google Scholar

• 10

  Deb J. Paul D. Sarkar U. (2019). Donor-acceptor Decorated Graphyne: A Promising Candidate for Nonlinear Optical Application. Dae Solid State Phys. Symp.10.1063/1.5113008

  • CrossRef
  • Google Scholar

• 11

  de Lara-Castells M. P. Bartolomei M. Mitrushchenkov A. O. Stoll H. (2015). Transferability and Accuracy by Combining Dispersionless Density Functional and Incremental post-Hartree-Fock Theories: Noble Gases Adsorption on Coronene/Graphene/Graphite Surfaces. J. Chem. Phys.143, 194701. 10.1063/1.4935511

  • CrossRef
  • Google Scholar

• 12

  de Lara-Castells M. P. Fernández-Perea R. Madzharova F. Voloshina E. (2016). Post-Hartree-Fock Studies of the He/Mg(0001) Interaction: Anti-corrugation, Screening, and Pairwise Additivity. J. Chem. Phys.144, 244707. 10.1063/1.4954772

  • CrossRef
  • Google Scholar

• 13

  de Lara-Castells M. P. Hauser A. W. Mitrushchenkov A. O. Fernández-Perea R. (2017). Quantum Confinement of Molecular Deuterium Clusters in Carbon Nanotubes: Ab Initio Evidence for Hexagonal Close Packing. Phys. Chem. Chem. Phys.19, 28621–28629. 10.1039/C7CP05869A

  • CrossRef
  • Google Scholar

• 14

  de Lara-Castells M. P. Hauser A. W. (2020). New Tools for the Astrochemist: Multi-Scale Computational Modelling and Helium Droplet-Based Spectroscopy. Phys. Life Rev.32, 95–98. 10.1016/j.plrev.2019.08.001

  • CrossRef
  • Google Scholar

• 15

  de Lara-Castells M. P. Mitrushchenkov A. O. (2021). A Nuclear Spin and Spatial Symmetry-Adapted Full Quantum Method for Light Particles inside Carbon Nanotubes: Clusters of ³He, ⁴He, and Para-H₂. Phys. Chem. Chem. Phys.23, 7908–7918. 10.1039/d0cp05332e

  • CrossRef
  • Google Scholar

• 16

  de Lara-Castells M. P. Mitrushchenkov A. O. Delgado-Barrio G. Villarreal P. (2009a). Using a Jacobi-Davidson "Nuclear Orbital" Method for Small Doped ³He Clusters. Few-body Syst.45, 233–236. 10.1007/s00601-009-0035-6

  • CrossRef
  • Google Scholar

• 17

  de Lara-Castells M. P. Mitrushchenkov A. O. (2020). From Molecular Aggregation to a One-Dimensional Quantum crystal of Deuterium inside a Carbon Nanotube of 1 nm Diameter. J. Phys. Chem. Lett.11, 5081–5086. 10.1021/acs.jpclett.0c01432

  • CrossRef
  • Google Scholar

• 18

  de Lara-Castells M. P. Stoll H. Civalleri B. Causà M. Voloshina E. Mitrushchenkov A. O. et al (2014a). Communication: A Combined Periodic Density Functional and Incremental Wave-Function-Based Approach for the Dispersion-Accounting Time-Resolved Dynamics of ⁴He Nanodroplets on Surfaces: ⁴He/Graphene. J. Chem. Phys.141, 151102. 10.1063/1.4898430

  • CrossRef
  • Google Scholar

• 19

  de Lara-Castells M. P. Stoll H. Mitrushchenkov A. O. (2014b). Assessing the Performance of Dispersionless and Dispersion-Accounting Methods: Helium Interaction with Cluster Models of the TiO₂(110) Surface. J. Phys. Chem. A.118, 6367–6384. 10.1021/jp412765t

  • CrossRef
  • Google Scholar

• 20

  de Lara-Castells M. P. Villarreal P. Delgado-Barrio G. Mitrushchenkov A. O. (2009b). An Optimized Full-Configuration-Interaction Nuclear Orbital Approach to a "Hard-Core" Interaction Problem: Application to (³He_N)-Cl₂(B) Clusters (N≤4). J. Chem. Phys.131, 194101. 10.1063/1.3263016

  • CrossRef
  • Google Scholar

• 21

  Del Maestro A. Boninsegni M. (2017). Absence of Superfluidity in a Quasi-One-Dimensional Parahydrogen Fluid Adsorbed inside Carbon Nanotubes. Phys. Rev. B95, 054517. 10.1103/PhysRevB.95.054517

  • CrossRef
  • Google Scholar

• 22

  Echave J. Clary D. C. (1992). Potential Optimized Discrete Variable Representation. Chem. Phys. Lett.190, 225–230. 10.1016/0009-2614(92)85330-D

  • CrossRef
  • Google Scholar

• 23

  Ferré G. Gordillo M. C. Boronat J. (2017). Luttinger parameter of quasi-one-dimensional para−H₂. Phys. Rev. B95, 064502. 10.1103/PhysRevB.95.064502

  • CrossRef
  • Google Scholar

• 24

  Sleijpen G. L. van der Vorst H. A. (1996). A Jacobi-Davidson Iteration Method for Linear Eigenvalue Problems. SIAM J. Matrix Anal. Appl.17, 401–425. 10.1137/s0895479894270427

  • CrossRef
  • Google Scholar

• 25

  Hauser A. W. de Lara-Castells M. P. (2016). Carbon Nanotubes Immersed in Superfluid Helium: The Impact of Quantum Confinement on Wetting and Capillary Action. J. Phys. Chem. Lett.7, 4929–4935. 10.1021/acs.jpclett.6b02414

  • CrossRef
  • Google Scholar

• 26

  Hauser A. W. de Lara-Castells M. P. (2017). Spatial Quenching of a Molecular Charge-Transfer Process in a Quantum Fluid: the C^sx-C₆₀ Reaction in Superfluid Helium Nanodroplets. Phys. Chem. Chem. Phys.19, 1342–1351. 10.1039/C6CP06858H

  • CrossRef
  • Google Scholar

• 27

  Hauser A. W. Mitrushchenkov A. O. de Lara-Castells M. P. (2017). Quantum Nuclear Motion of Helium and Molecular Nitrogen Clusters in Carbon Nanotubes. J. Phys. Chem. C121, 3807–3821. 10.1021/acs.jpcc.6b12959

  • CrossRef
  • Google Scholar

• 28

  Hesselmann A. Jansen G. (2003). Intermolecular Dispersion Energies from Time-dependent Density Functional Theory. Chem. Phys. Lett.367, 778–784. 10.1016/S0009-2614(02)01796-7

  • CrossRef
  • Google Scholar

• 29

  Heßelmann A. Jansen G. Schütz M. (2005). Density-functional Theory-Symmetry-Adapted Intermolecular Perturbation Theory with Density Fitting: A New Efficient Method to Study Intermolecular Interaction Energies. J. Chem. Phys.122, 014103. 10.1063/1.1824898

  • CrossRef
  • Google Scholar

• 30

  Liu C. Chen Y. Wu C.-Z. Xu S.-T. Cheng H.-M. (2010). Hydrogen Storage in Carbon Nanotubes Revisited. Carbon48, 452–455. 10.1016/j.carbon.2009.09.060

  • CrossRef
  • Google Scholar

• 31

  Mattera L. Rosatelli F. Salvo C. Tommasini F. Valbusa U. Vidali G. (1980). Selective Adsorption of ¹H₂ and ²H₂ on the (0001) Graphite Surface. Surf. Sci.93, 515–525. 10.1016/0039-6028(80)90279-4

  • CrossRef
  • Google Scholar

• 32

  Meyer R. Weichselbaum M. Hauser A. W. (2020). Machine Learning Approaches toward Orbital-free Density Functional Theory: Simultaneous Training on the Kinetic Energy Density Functional and its Functional Derivative. J. Chem. Theor. Comput.16, 5685–5694. 10.1021/acs.jctc.0c00580

  • CrossRef
  • Google Scholar

• 33

  Misquitta A. J. Jeziorski B. Szalewicz K. (2003). Dispersion Energy from Density-Functional Theory Description of Monomers. Phys. Rev. Lett.91, 033201. 10.1103/PhysRevLett.91.033201

  • CrossRef
  • Google Scholar

• 34

  Misquitta A. J. Podeszwa R. Jeziorski B. Szalewicz K. (2005). Intermolecular Potentials Based on Symmetry-Adapted Perturbation Theory with Dispersion Energies from Time-dependent Density-Functional Calculations. J. Chem. Phys.123, 214103. 10.1063/1.2135288

  • CrossRef
  • Google Scholar

• 35

  Mondelo-Martell M. Huarte-Larrañaga F. (2021). Competition of Quantum Effects in H2/D2 Sieving in Narrow Single-Wall Carbon Nanotubes. Mol. Phys.119, e1942277. 10.1080/00268976.2021.1942277

  • CrossRef
  • Google Scholar

• 36

  Mondelo-Martell M. Huarte-Larrañaga F. (2016). Diffusion of H₂ and D₂ Confined in Single-Walled Carbon Nanotubes: Quantum Dynamics and Confinement Effects. J. Phys. Chem. A.120, 6501–6512. 10.1021/acs.jpca.6b00467

  • CrossRef
  • Google Scholar

• 37

  Mondelo-Martell M. Huarte-Larrañaga F. Manthe U. (2017). Quantum Dynamics of H₂ in a Carbon Nanotube: Separation of Time Scales and Resonance Enhanced Tunneling. J. Chem. Phys.147, 084103. 10.1063/1.4995550

  • CrossRef
  • Google Scholar

• 38

  Mudrich M. Stienkemeier F. (2014). Photoionisaton of Pure and Doped Helium Nanodroplets. Int. Rev. Phys. Chem.33, 301–339. 10.1080/0144235X.2014.937188

  • CrossRef
  • Google Scholar

• 39

  Nguyen T. X. Jobic H. Bhatia S. K. (2010). Microscopic Observation of Kinetic Molecular Sieving of Hydrogen Isotopes in a Nanoporous Material. Phys. Rev. Lett.105, 085901. 10.1103/PhysRevLett.105.085901

  • CrossRef
  • Google Scholar

• 40

  Noury A. Vergara-Cruz J. Morfin P. Plaçais B. Gordillo M. C. Boronat J. et al (2019). Layering Transition in Superfluid Helium Adsorbed on a Carbon Nanotube Mechanical Resonator. Phys. Rev. Lett.122. 10.1103/physrevlett.122.165301

  • CrossRef
  • Google Scholar

• 41

  Ohba T. (2016). Limited Quantum Helium Transportation through Nano-Channels by Quantum Fluctuation. Sci. Rep.6. 10.1038/srep28992

  • CrossRef
  • Google Scholar

• 42

  Paul D. Deb J. Sarkar U. (2019). Influence of Noble Gas Atoms on B12N12 Fullerene: A DFT Study. Dae Solid State Phys. Symp. 10.1063/1.5113010

  • CrossRef
  • Google Scholar

• 43

  Paul D. Dua H. Sarkar U. (2020). Confinement Effects of a Noble Gas Dimer inside a Fullerene Cage: Can it Be Used as an Acceptor in a DSSC?. Front. Chem.8. 10.3389/fchem.2020.00621

  • CrossRef
  • Google Scholar

• 44

  Perdew J. P. Burke K. Ernzerhof M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett.77, 3865–3868. 10.1103/physrevlett.77.3865

  • CrossRef
  • Google Scholar

• 45

  Pernal K. Podeszwa R. Patkowski K. Szalewicz K. (2009). Dispersionless Density Functional Theory. Phys. Rev. Lett.103, 263201. 10.1103/physrevlett.103.263201

  • CrossRef
  • Google Scholar

• 46

  Rosi N. L. Eckert J. Eddaoudi M. Vodak D. T. Kim J. O'Keeffe M. et al (2003). Hydrogen Storage in Microporous Metal-Organic Frameworks. Science300, 1127–1129. 10.1126/science.1083440

  • CrossRef
  • Google Scholar

• 47

  Rossi M. Ancilotto F. (2016). Superfluid Behavior of Quasi-One-dimensionalp−H₂ inside a Carbon Nanotube. Phys. Rev. B94, 100502. 10.1103/PhysRevB.94.100502

  • CrossRef
  • Google Scholar

• 48

  Schlapbach L. Züttel A. (2001). Hydrogen-Storage Materials for Mobile Applications. Nature414, 353–358. 10.1038/35104634

  • CrossRef
  • Google Scholar

• 49

  Sebastianelli F. Xu M. Bačić Z. (2008). Quantum Dynamics of Small H₂ and D₂ Clusters in the Large Cage of Structure II Clathrate Hydrate: Energetics, Occupancy, and Vibrationally Averaged Cluster Structures. J. Chem. Phys.129, 244706. 10.1063/1.3049781

  • CrossRef
  • Google Scholar

• 50

  Stoll H. (1992). On the Correlation Energy of Graphite. J. Chem. Phys.97, 8449–8454. 10.1063/1.463415

  • CrossRef
  • Google Scholar

• 51

  Tang K. T. Toennies J. P. (1984). An Improved Simple Model for the Van Der Waals Potential Based on Universal Damping Functions for the Dispersion Coefficients. J. Chem. Phys.80, 3726–3741. 10.1063/1.447150

  • CrossRef
  • Google Scholar

• 52

  Ting V. P. Ramirez-Cuesta A. J. Bimbo N. Sharpe J. E. Noguera-Diaz A. Presser V. et al (2015). Direct Evidence for Solid-like Hydrogen in a Nanoporous Carbon Hydrogen Storage Material at Supercritical Temperatures. ACS Nano9, 8249–8254. 10.1021/acsnano.5b02623.PMID:26171656

  • CrossRef
  • Google Scholar

• 53

  Toennies J. P. Vilesov A. F. (2004). Superfluid Helium Droplets: A Uniquely Cold Nanomatrix for Molecules and Molecular Complexes. Angew. Chem. Int. Ed.43, 2622–2648. 10.1002/anie.200300611

  • CrossRef
  • Google Scholar

• 54

  Werner H. J. Knowles P. J. Knizia G. Manby F. R. Schütz M. Celani P. et al (2012). Molpro, Version 2012.1, a Package of Ab Initio Programs, See Available at: http://www.molpro.net [Dataset].

  • Google Scholar

• 55

  Witt A. Sebastianelli F. Tuckerman M. E. Bačić Z. (2010). Path Integral Molecular Dynamics Study of Small H₂ Clusters in the Large Cage of Structure II Clathrate Hydrate: Temperature Dependence of Quantum Spatial Distributions. J. Phys. Chem. C114, 20775–20782. 10.1021/jp107021t

  • CrossRef
  • Google Scholar

• 56

  Woon D. E. Dunning Jr. Dunning T. H. (1994). Gaussian Basis Sets for Use in Correlated Molecular Calculations. IV. Calculation of Static Electrical Response Properties. J. Chem. Phys.100, 2975–2988. 10.1063/1.466439

  • CrossRef
  • Google Scholar

• 57

  Zheng J. Wang C.-G. Zhou H. Ye E. Xu J. Li Z. et al (2021). Current Research Trends and Perspectives on Solid-State Nanomaterials in Hydrogen Storage. Research. 10.34133/2021/3750689

  • CrossRef
  • Google Scholar

• 58

  Züttel A. (2003). Materials for Hydrogen Storage. Mater. Today6, 24–33. 10.1016/S1369-7021(03)00922-2

  • CrossRef
  • Google Scholar