Abstract
Introduction:
Pneumonia is the primary cause of mortality in preterm infants in developing nations; yet, early detection and treatment can significantly reduce mortality rates. Pharmaceutical researchers are diligently striving to identify avariety of drugs that might effectively cure pneumonia.
Method:
We are motivated to examine the quantitative structureproperty relationships (QSPR) of anti-pneumonia pharmaceuticals. We employed K-Banhatti topological descriptors and analyzed the findings to achieve this. For estimation of physicochemical properties of pneumonia treatment drugs we utilized linear, quadratic, cubic, and biquadratic regression analyses.
Results and Conclusion:
The drugs comprise linezolid, ceftabiprole, and clarithromycin, among others. Topological descriptors enable the exploration of the complexity, connectivity, and other essential attributes of molecules. The quantitative structure-property relationship (QSPR) analysis of pharmaceuticals for illness treatment employing K-Banhatti topological descriptors is an economical approach utilised by pharmaceutical researchers. We performed a QSPR analysis on 20 anti-pneumonia drugs to ascertain the most precise predictions for five properties: enthalpy, flash point, molecular weight, molar volume, and molar refractivity, employing five K-Banhatti indices. To do this, we used linear, quadratic, cubic, and biquadratic regression analyses to find links between molecules and the physical and chemical properties of drugs used to treat pneumonia. Employing molecular descriptors and regression models to investigate chemical patterns is a cost-effective and theoretical methodology.
1 Introduction
Pneumonia is an infectious disease and is frequently induced by bacterial, viral, or fungal infections that specifically affect the lungs, leading to inflammation of the alveoli (Scotta et al., 2019). Common bacterial agents include Streptococcus pneumoniae and Haemophilus influenzae, while viral agents may include the influenza virus, respiratory syncytial virus (RSV), and coronaviruses (Marangu and Zar, 2019). Pneumonia transmission occurs via inhalation of airborne droplets from coughs or sneezes, direct contact with infected individuals, or by touching contaminated objects and then contacting the face.
Each year, around two million children under 5 years old succumb to pneumonia in developing countries, primarily due to infections caused by streptococcus or the influenza virus (Singh and Aneja, 2011; Leung et al., 2018). Pneumonia ranks among the primary causes of mortality and morbidity in children globally. Pneumonia is a sudden respiratory infection caused by various organisms, impacting management strategies in the developing world (Shann, 1995). Lungs exhibit swelling of the airway sacs and pleural effusion, which occurs when the lung is infiltrated with fluid. Pneumonia impacts 10 to 15 percent of children with respiratory issues. Underdeveloped and rising nations are predisposed to elevated pneumonia rates due to factors such as overcrowding, pollution, unsanitary environmental conditions, and restricted access to healthcare (Wojsyk-Banaszak and Breeborowicz, 2013; Wardlaw et al., 2006).
Pneumonia in toddlers under the age of two is especially perilous. The lack of adequate immunizations and limited access to healthcare services in several impoverished communities in developing and underdeveloped nations results in undetected pneumonia, thereby exacerbating respiratory conditions (Rudan et al., 2004). Over the past 10 years, the number of cases and severity of pneumonia in children, as well as their death rates, have gone down significantly. This is because the economy is better, care is better, more effective treatment and prevention strategies are used, and more vaccinations are made available, especially the combination vaccines against pneumococcal disease (PCV) and hepatitis B. Survival rates have markedly improved since the 20th century due to advancements in immunisations and pharmaceuticals (Madhi et al., 2008; Scelfo et al., 2021). Moreover, increasing evidence associates childhood pneumonia and lower respiratory tract infections (LRTIs) with diminished lung capacity in early childhood and an escalation of long-term, latent respiratory conditions in both children and adults, such as asthma and chronic bronchitis (Munywoki et al., 2013). The illness can be classified based on its origin, such as community-acquired or hospital-acquired pneumonia (Venditti et al., 2009).
Pneumonia is treatable with various medications. Potentially appropriate medications include beta-lactams such as penicillin and amoxicillin in combination with a macrolide, or fluoroquinolone antibiotics like Levaquin (Garau, 2005). Macrolide antibiotics, including tetracycline, azithromycin, and clarithromycin, may serve as initial treatment options (Alvarez-Elcoro and Enzler, 1999; Sood, 1999). Adverse events associated with ceftobiprole in patients indicated that the medication demonstrated an acceptable safety profile (Liapikou et al., 2015).
Despite the discovery of antibiotics, the prevalence of pneumonia has likely remained relatively stable over the past century; however, the overall mortality rate has significantly decreased. Determining the responsible pathogen may present challenges. Diagnosis may be confirmed through blood tests, sputum culture, and chest X-rays (Parveen and Sathik, 2011). Symptoms and a physical examination are commonly employed to establish a diagnosis. Potential symptoms include (Harari et al., 1991): Expectoration of greenish or yellow mucus, or potentially bloody mucus, may occur. Productive cough with phlegm production, Dyspnoea, Fever and anorexia. Figure 1 shows the pneumonia infection.
FIGURE 1

Pneumonia in children.
According to the chemical theory of graphs, atoms are represented as vertices of a graph, and the bonds that bind them together are described as edges (Khan et al., 2024a). A graph is characterized as a pair of is a set of connected vertices with components known as edges, and is a collection of items known as vertices (Khan et al., 2023a). The degree of any vertex , denoted by the symbol , is expressed as the number of vertices that are close to it. One type of structural descriptor that may be determined using a chemical substance’s molecule network is a topological indicator (Dehmer et al., 2010; Khan et al., 2025). Chemical graph theory is a branch of graph theory that combines chemical models mathematically (Khan et al., 2024b). It emphasizes topological aspects that are directly associated with molecular chemical properties (Galvez et al., 2011).
A topological descriptor is a distinctive number that characterizes the intrinsic structure of the molecular graph. In QSPR and QSAR, scientists use numerical parameters from a chemical graph network. Its uses are increasing in medication design. Wiener pioneered the concept of topological descriptors with the distance base topological descriptor (Hayat, 2017). Husin et al. (2015) discuss Zagreb polynomials and topological indices for a synthesized molecule composed of branched units known as monomers. In Vijay et al. (2023), the study focused on the vertex version of the distance-based topological indices, the entropy of the topological indices and their numerical analysis of aluminophosphates. Fathi et al. (2024) examined topological indices based on valency, induced by quantitative structural relationships, to predict the structural properties of Ni tetrathiafulvalene tetrathionate (NiTTFtt) in a 2D sheet configuration.
A molecular structure’s topological index gives numerical values that are useful for property prediction. Topological descriptors are useful tools for researchers who want to figure out the different topological properties of drugs (Hakami et al., 2024), networks (Chu et al., 2023; Khan et al., 2024c), and materials (Imran et al., 2023; Khan et al., 2023b). Numerous researchers have investigated different topological descriptors of material-related networks in Hakami et al. (2025), Khan et al. (2024d), Khan et al. (2024e) and the estimation of physical and chemical properties of various drugs in Husin et al. (2024). Nadeem et al. put forward the QSPR idea on babesiosis drugs (Awan et al., 2025) and antimalarial compounds modeling results depict the clear picture (Awan et al., 2024) said disease efficiently. Fozia made a great contribution to cardiac (Bashir Farooq et al., 2022) drugs and blood cancer (Nasir et al., 2022) and Sobia done QSPR application of infertility Drugs (Sultana, 2023) modeling is done.
2 Material and methodology
The current study examines the following anti-pneumonia drugs: Linezolid , Tetracycline , Tazobactam , Amoxicillin , Cefaclor , Ceftriaxone, Avibactam , Lefamulin , Clarithromycin , Levaquin Cefpodoxime , Doxycycline , Omadacycline , Penicillin , Cefuroxime, Carbapenem , Erythromycin, Ceftobiprole , Moxifloxacin and Unasyn are examined. Additionally, we sourced the drugs, their chemical formulas, and their physical and chemical properties from https://www.chemicalbook.com/. In this study, anti-pneumonia medications are shown by plain graphs in Figure 2. The drug’s topological indices are computed using vertex division, edge division, and edge degree algorithms. The degree of edge is represented by and
FIGURE 2
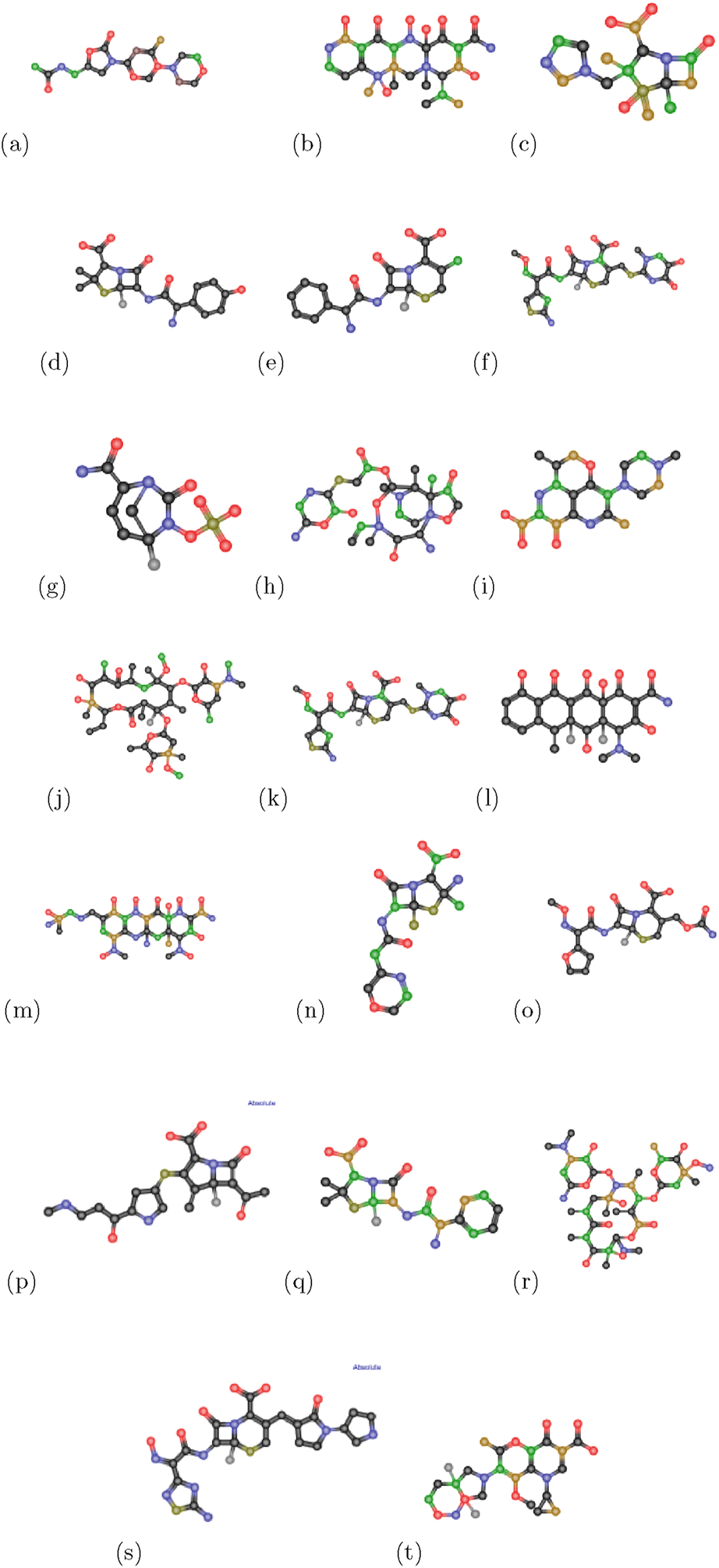
Chemical structures of anti-pneumonia drugs (a) linezolid (b) tetracycline (c) tazobactam (d) amoxicillin (e) cefaclor (f) ceftriaxone (g) avibactam (h) lefamulin (i) levaquine (j) clarithromycin (k) cefpodoxime (l) doxycycline (m) omadacycline (n) penicillin (o) cefuroxime (p) carbapenem (q) unasyn (r) erythromycin (s) ceftabiprole (t) moxifloxacin.
The graph’s greatest and lowest degree can be expressed by and . Equations 1–5 offer formulae for descriptors which will be used in the sequel.
The first -Banhatti descriptor is defined as (Mahboob et al., 2022)
The second -Banhatti descriptor is defined as (Ghani et al., 2022)
The first Hyper -Banhatti descriptor (Kulli, 2016)
The second Hyper -Banhatti descriptor (Almalki and Tabassum, 2024)
The -Banhatti Harmonic descriptor (Anjum and Safdar, 2019)
3 Results
In this study, we compute topological descriptor values using two-dimensional graphs of pneumonia treatment drugs. We used various methods, including edge dividing, vertex degree evaluation, and edge degree methodology, to calculate the -Banhatti descriptors. Edge division and edge degree of Linezolid are presented in Table 1. -Banhatti descriptors may be calculated as indicated below.
TABLE 1
| Edge division | ||||
|---|---|---|---|---|
| Edge degree | 2 | 2 | 3 | 4 |
| Cardinality | 4 | 6 | 12 | 4 |
Edge division and edge degree of Linezolid.
3.1 -Banhatti descriptors for linezolid
The following linezolid results were obtained by utilizing
Equations 1–
5;
Table 1.
• First -Banhatti descriptor
• Second -Banhatti descriptor
• First Hyper -Banhatti descriptor
• Second Hyper -Banhatti descriptor
• Harmonic -Banhatti descriptor
3.2 -Banhatti descriptors for Unasyn
The following Unasyn results were obtained by utilizing Equations 1–5; Table 2.
TABLE 2
| Edge division | |||||||
|---|---|---|---|---|---|---|---|
| Edge degree | 2 | 3 | 2 | 3 | 4 | 4 | 5 |
| Cardinality | 5 | 3 | 4 | 4 | 6 | 2 | 3 |
Edge division and edge degree of Unasyn.
3.3 -Banhatti descriptors for Cefuroxime
The following Cefuroxime results were obtained by utilizing Equations 1–5; Table 3
TABLE 3
| Edge division | ||||||||
|---|---|---|---|---|---|---|---|---|
| Edge degree | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 3 |
| Cardinality | 1 | 6 | 6 | 10 | 5 | 2 | 1 | 1 |
Edge division and edge degree of Cefuroxime.
3.4 -Banhatti descriptors for Avibactam
The following Avibactam results were obtained by utilizing Equations 1–5; Table 4.
TABLE 4
| Edge division | |||||||
|---|---|---|---|---|---|---|---|
| Edge degree | 2 | 3 | 2 | 3 | 4 | 4 | 5 |
| Cardinality | 3 | 4 | 1 | 3 | 4 | 3 | 1 |
Edge division and edge degree of Avibactam.
Remark 1. Other -Banhatti topological descriptors of pneumonia treatment drugs are computed in a similar way as computed above, and their values are presented in Table 5.
TABLE 5
| Drugs | |||||
|---|---|---|---|---|---|
| Linezolid | 268 | 356 | 1,452 | 2,908 | 21.364 |
| Omadacycline | 520 | 850 | 3,326 | 10,566 | 33.453 |
| Moxifloxacin | 406 | 616 | 2,536 | 6,964 | 26.569 |
| Ceftriaxone | 440 | 634 | 2,604 | 6,406 | 31.675 |
| Unasyn | 312 | 474 | 1,960 | 5,498 | 20.6357 |
| Lefamulin | 453 | 716 | 2,966 | 9,504 | 30.213 |
| Carbapanem | 336 | 500 | 2,058 | 4,282 | 24.055 |
| Cefuroxime | 337 | 466 | 1,919 | 4,465 | 26.696 |
| Cefaclor | 342 | 440 | 1,810 | 4,724 | 21.392 |
| Tetracycline | 458 | 752 | 3,122 | 10,372 | 27.054 |
| Amoxicillin | 326 | 496 | 2052 | 5,708 | 21.83 |
| Ceftabiprole | 454 | 658 | 2,698 | 6,678 | 37.376 |
| Doxycycline | 446 | 710 | 2,934 | 8,834 | 27.69 |
| Avibactam | 224 | 340 | 1,414 | 3,852 | 14.06 |
| Tazobactam | 280 | 454 | 1,886 | 6,354 | 16.911 |
| Clarithromycin | 626 | 944 | 3,912 | 10,880 | 43.984 |
| Levaquin | 322 | 462 | 1890 | 4,386 | 22.462 |
| Erythromycin | 598 | 886 | 3,666 | 9,678 | 46.817 |
| Cefpodoxima | 344 | 516 | 2,124 | 6,184 | 26.907 |
| Pencillin | 298 | 448 | 1,852 | 5,116 | 19.905 |
Computational values of -Banhatti Descriptors of Anti-Pneumonia Drugs.
4 Quantitative structure-property relation analysis of anti-pneumonia drugs
The QSPR analysis and Topological descriptor exhibit a significant association, indicating a strong connection between the disease’s physical and chemical attributes. To forecast the relationship between a molecule’s structure and its behaviour or characteristics, algorithms are utilized. Several methods have been developed and used in research during the last few decades. By the use of the statistical factors ( and ), the prediction will be verified. In real life, topological descriptors that have an actual coefficient of correlation below 0.8 are regarded as worthless. Applying linear, quadratic, cubic, and bi-quadratic regression analyses, we demonstrate the strong relationship between the attributes derived from associated topological descriptors and the physical qualities of the medications. The regression model’s quality is demonstrated by the greater value, which is very near to 1. Models Like Linear Models are shown in Figures 3–5, quadratic models are shown in Figures 6–8, cubic models are shown in Figures 9, 10, and in Figure 11 and biquadratic models are shown in Figures 12–14.
FIGURE 3
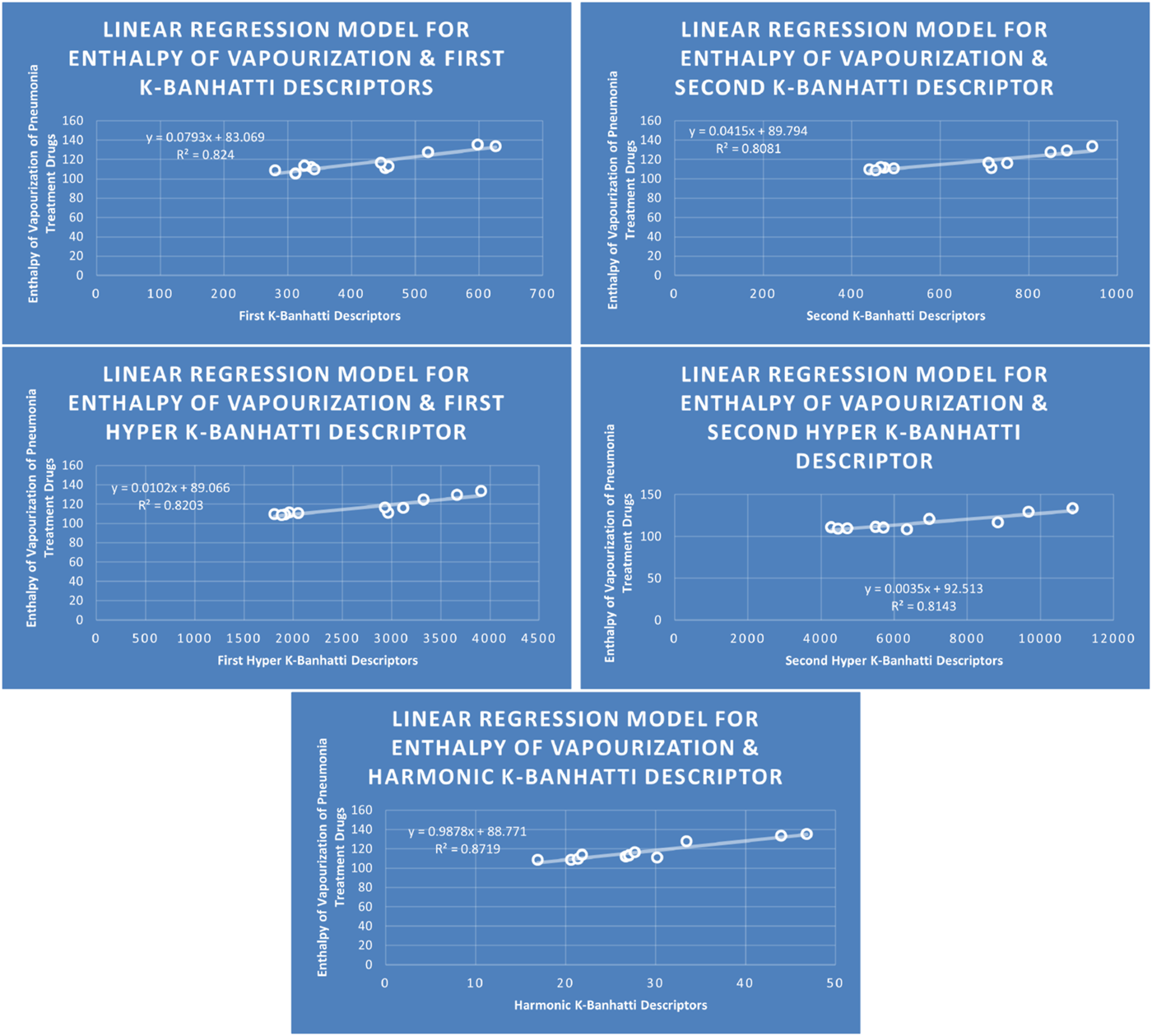
Models of Enthalpy of Vaporization for Pneumonia Treatment Drugs.
FIGURE 4
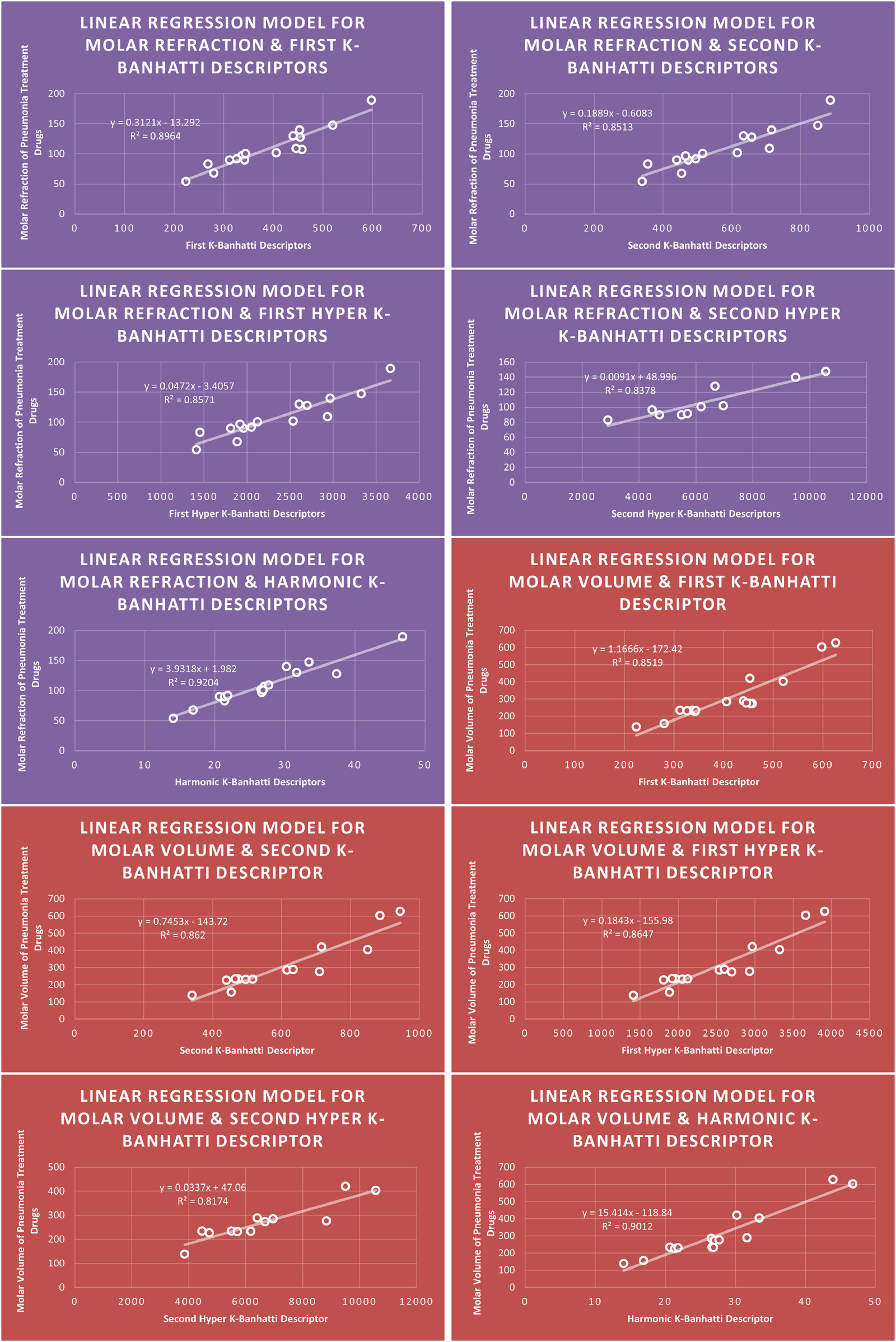
models of molar refraction and molar volume for pneumonia treatment drugs.
FIGURE 5
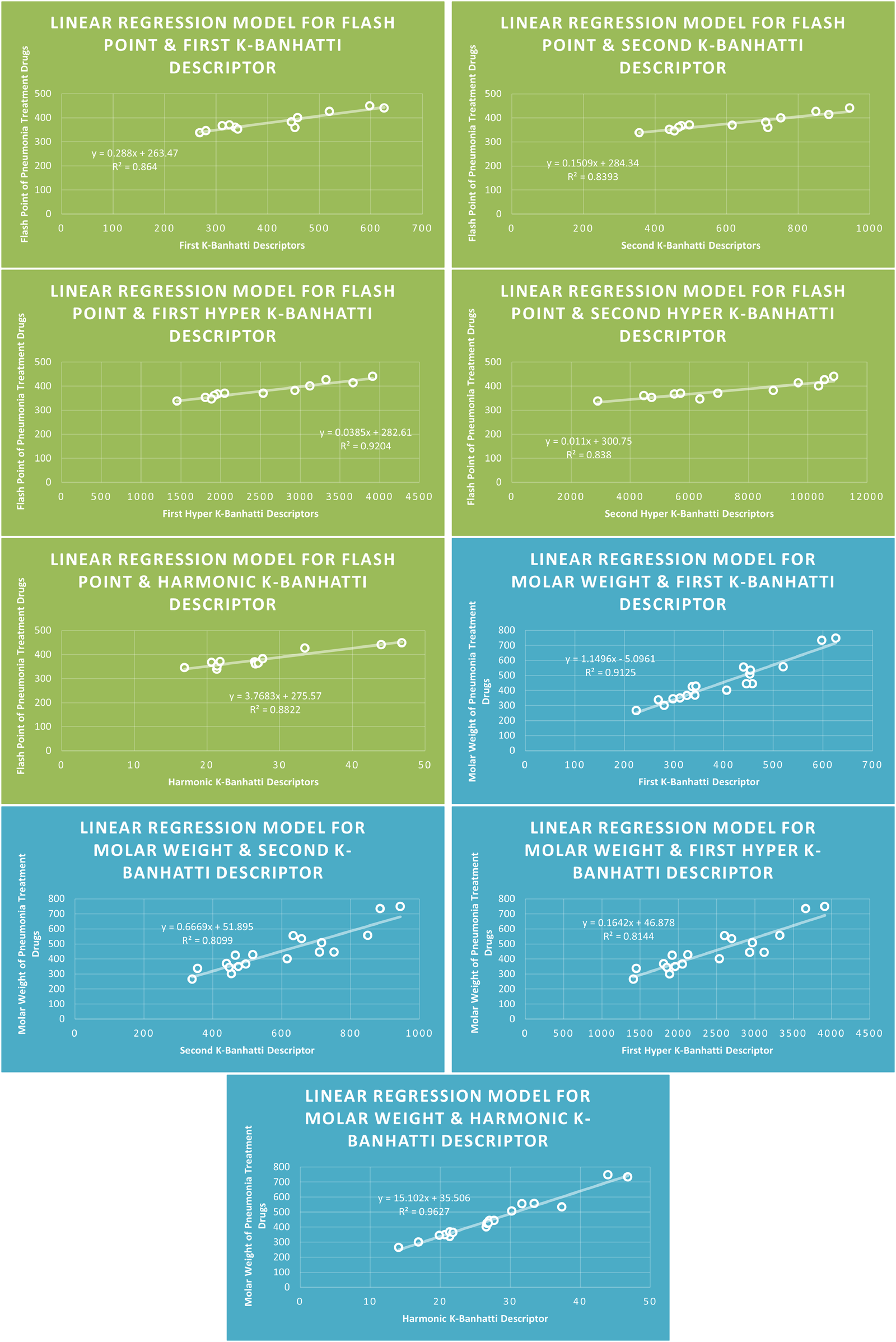
LR models of flash point and molar weight for pneumonia treatment drugs.
FIGURE 6
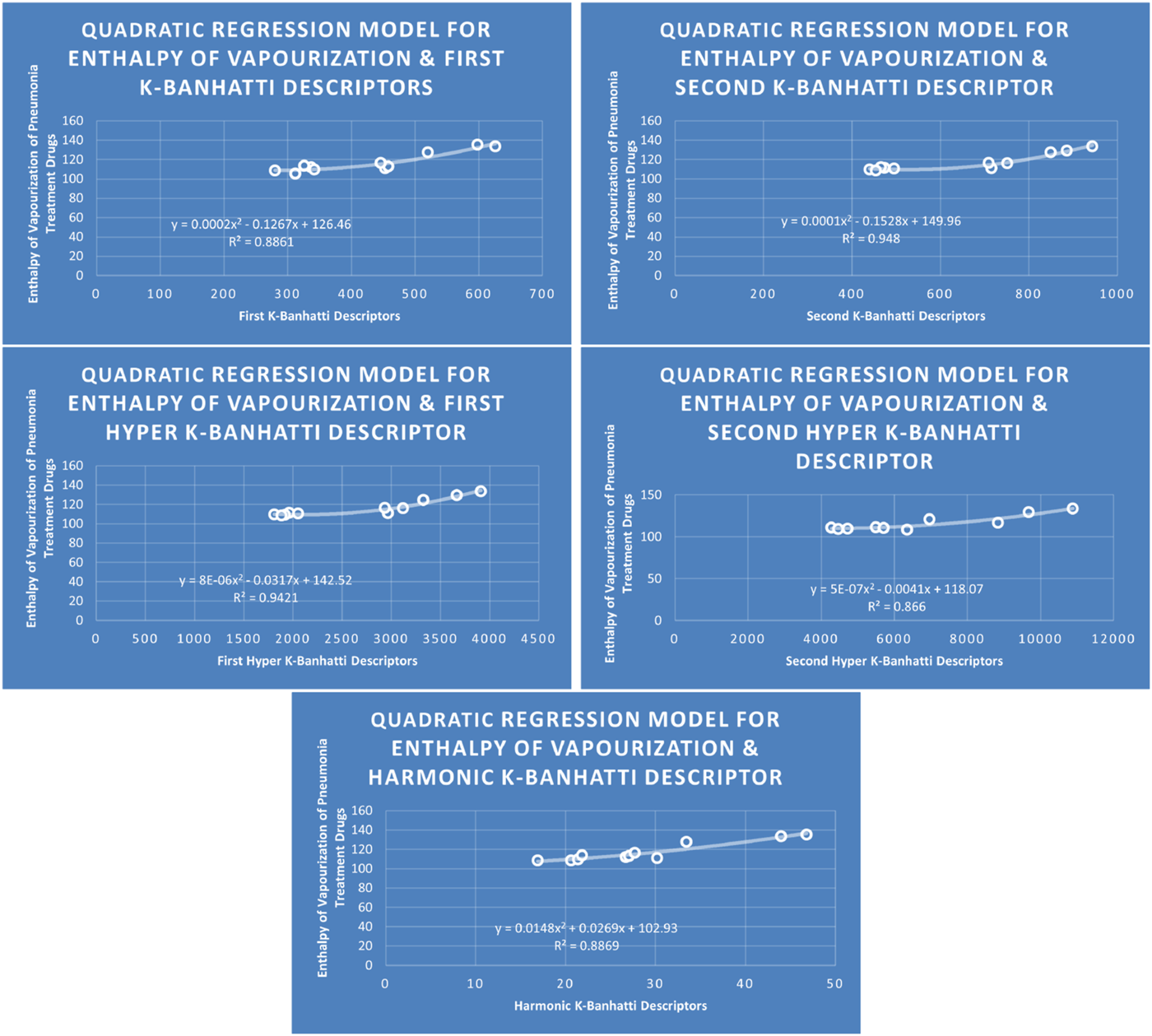
models of enthalpy of vaporization for pneumonia treatment drugs.
FIGURE 7
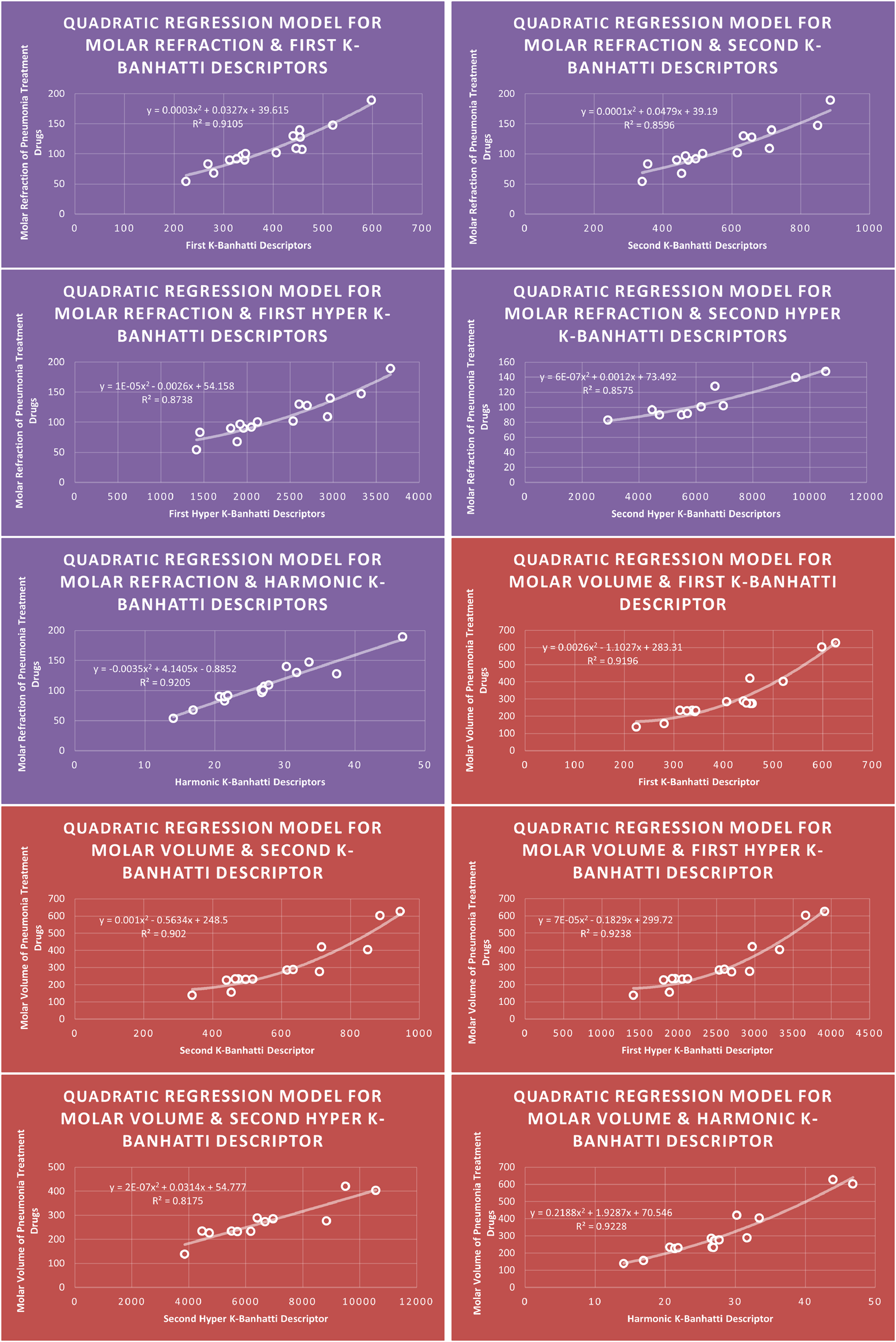
QR models of molar refraction and molar volume for pneumonia treatment drugs.
FIGURE 8
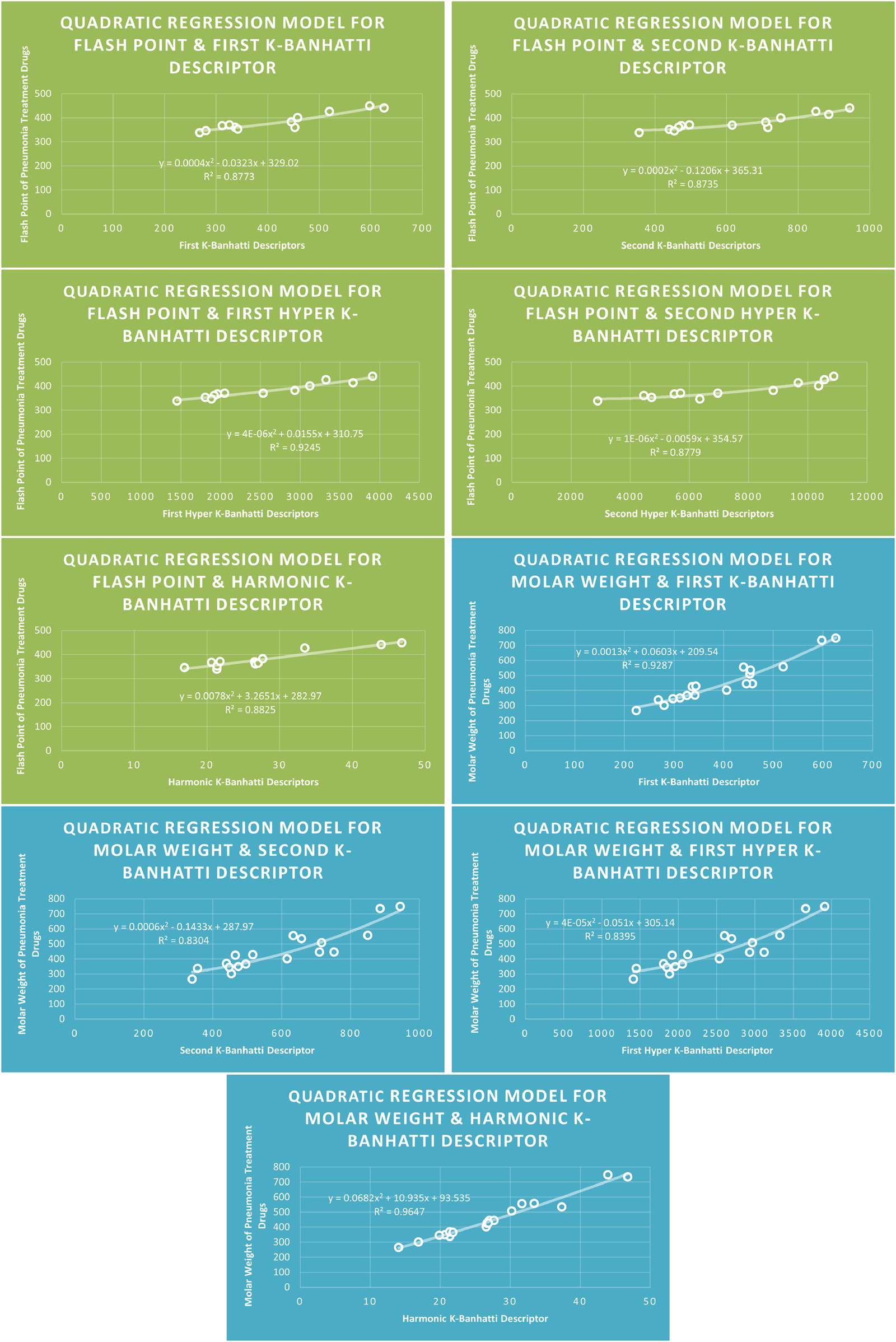
QR models of flash point and molar weight for pneumonia treatment drugs.
FIGURE 9
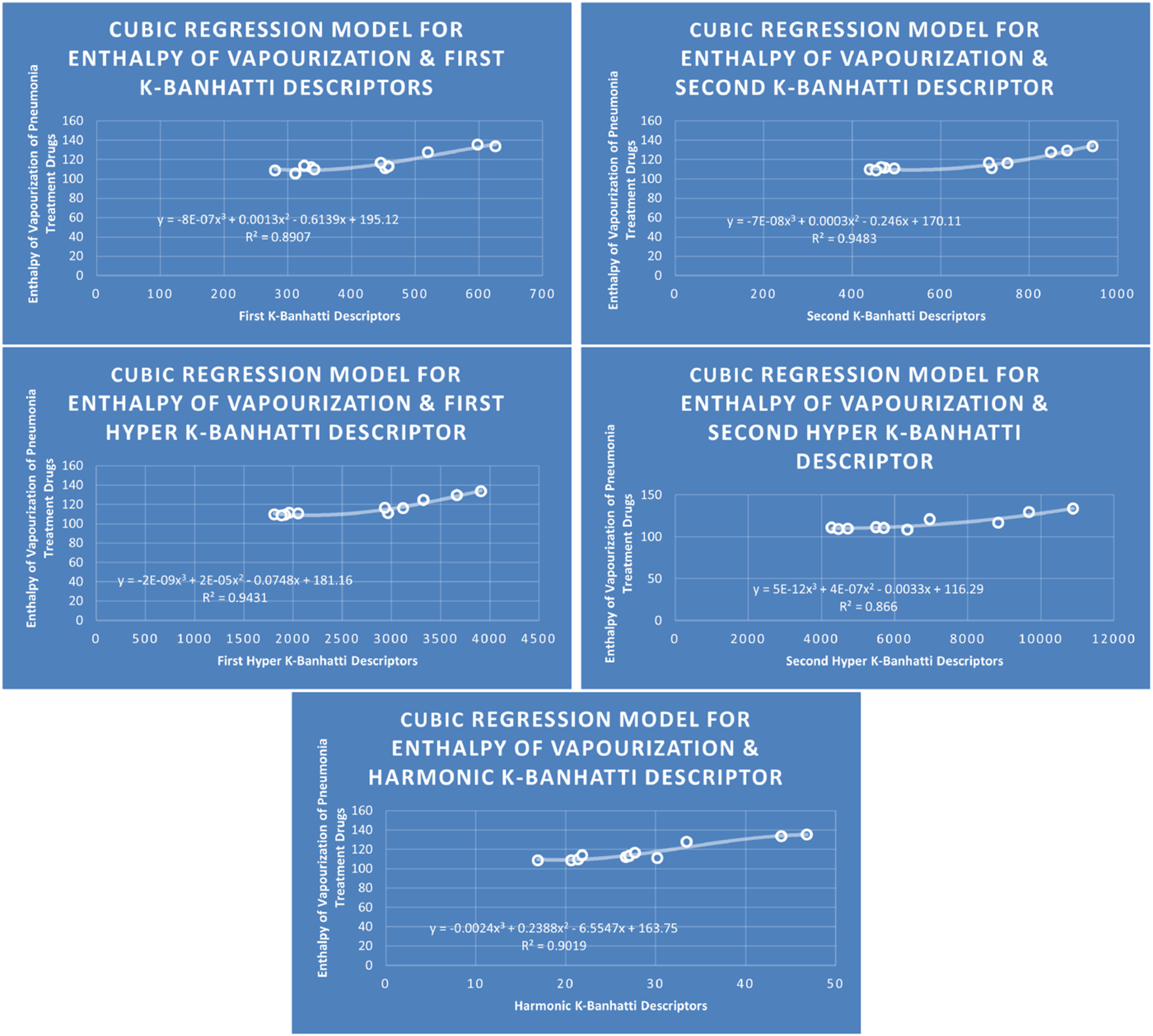
CR models of enthalpy of vapourization for pneumonia treatment drugs.
FIGURE 10
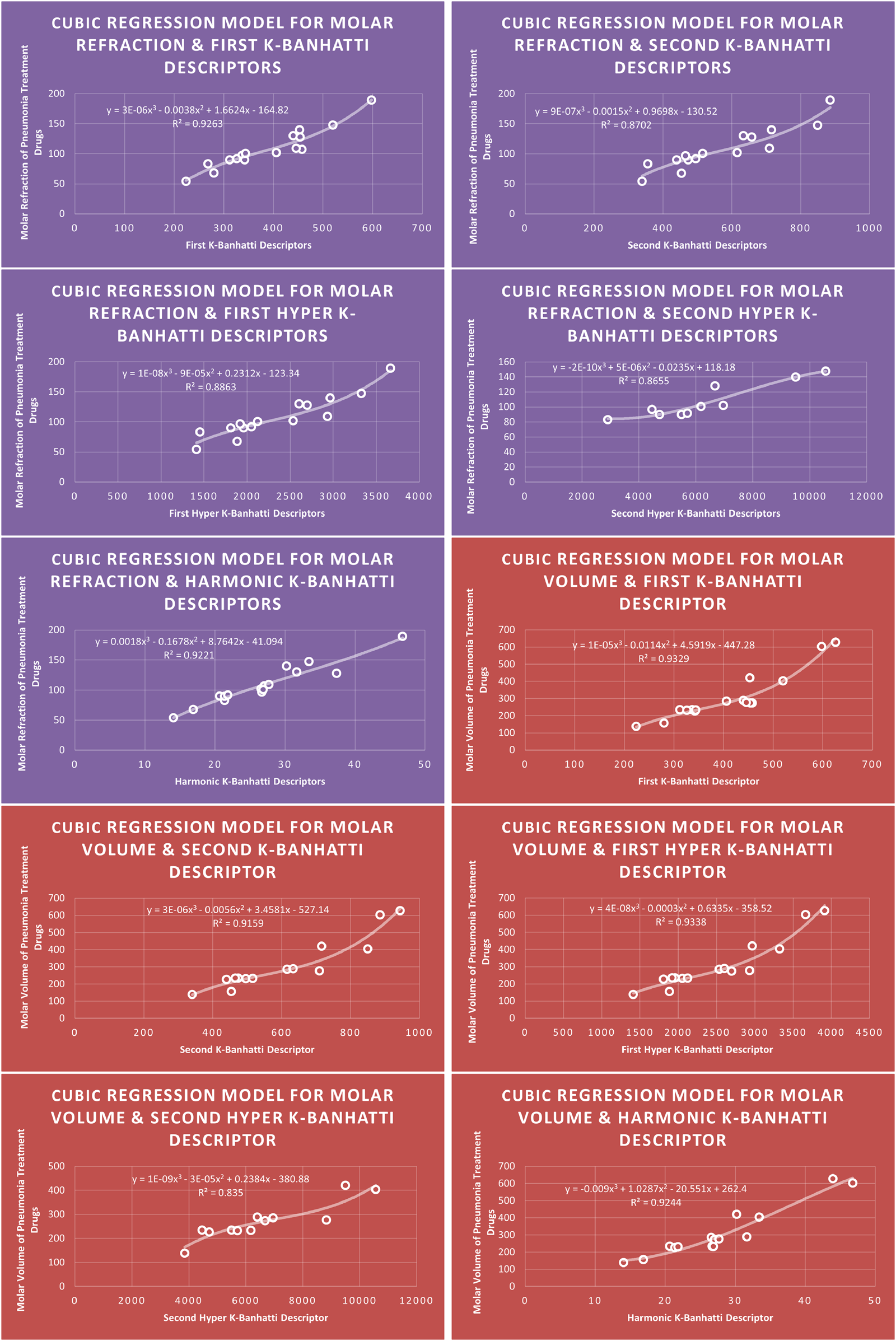
CR models of molar refraction and molar volume for pneumonia treatment drugs.
FIGURE 11
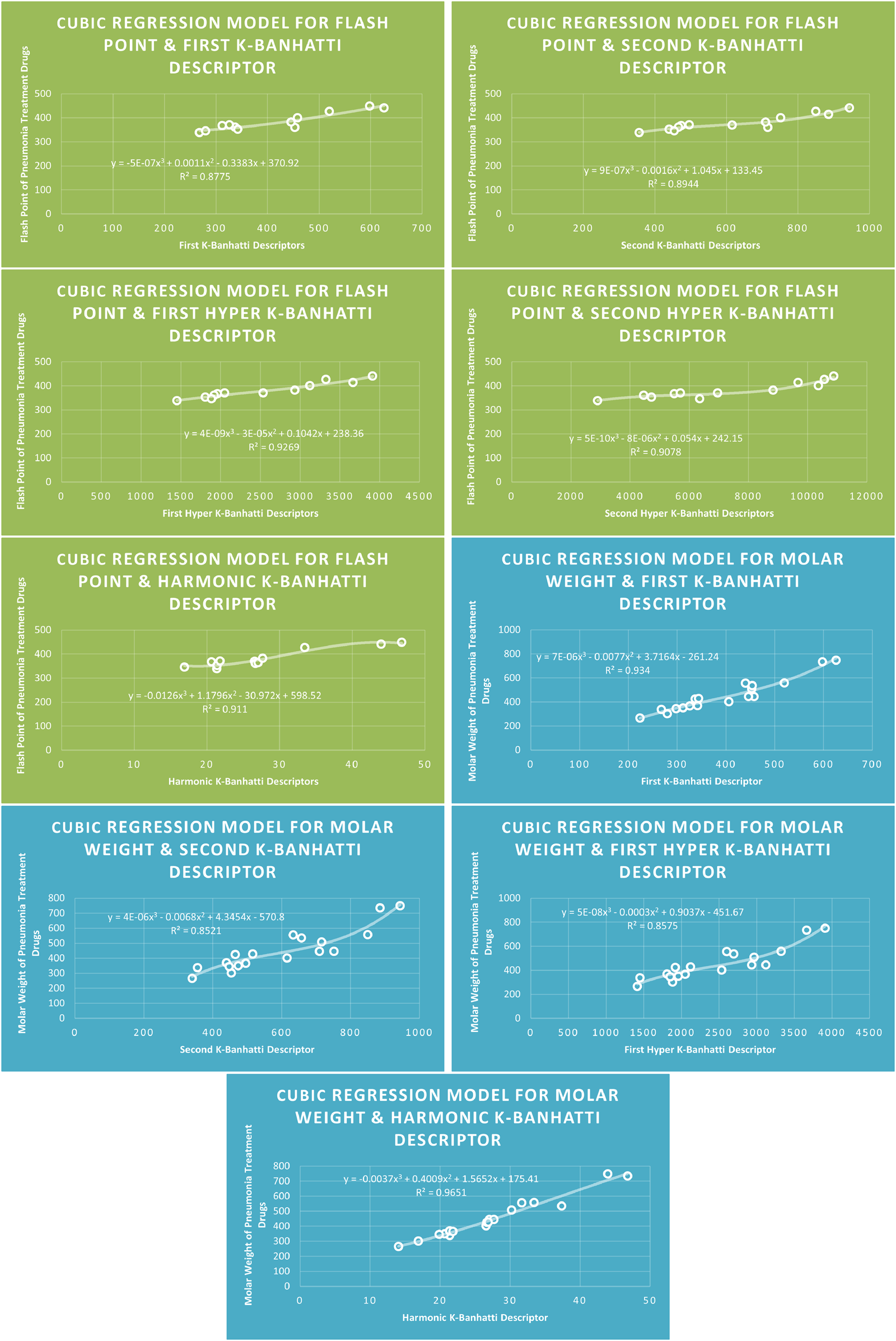
CR models of flash point and molar weight for pneumonia treatment drugs.
FIGURE 12
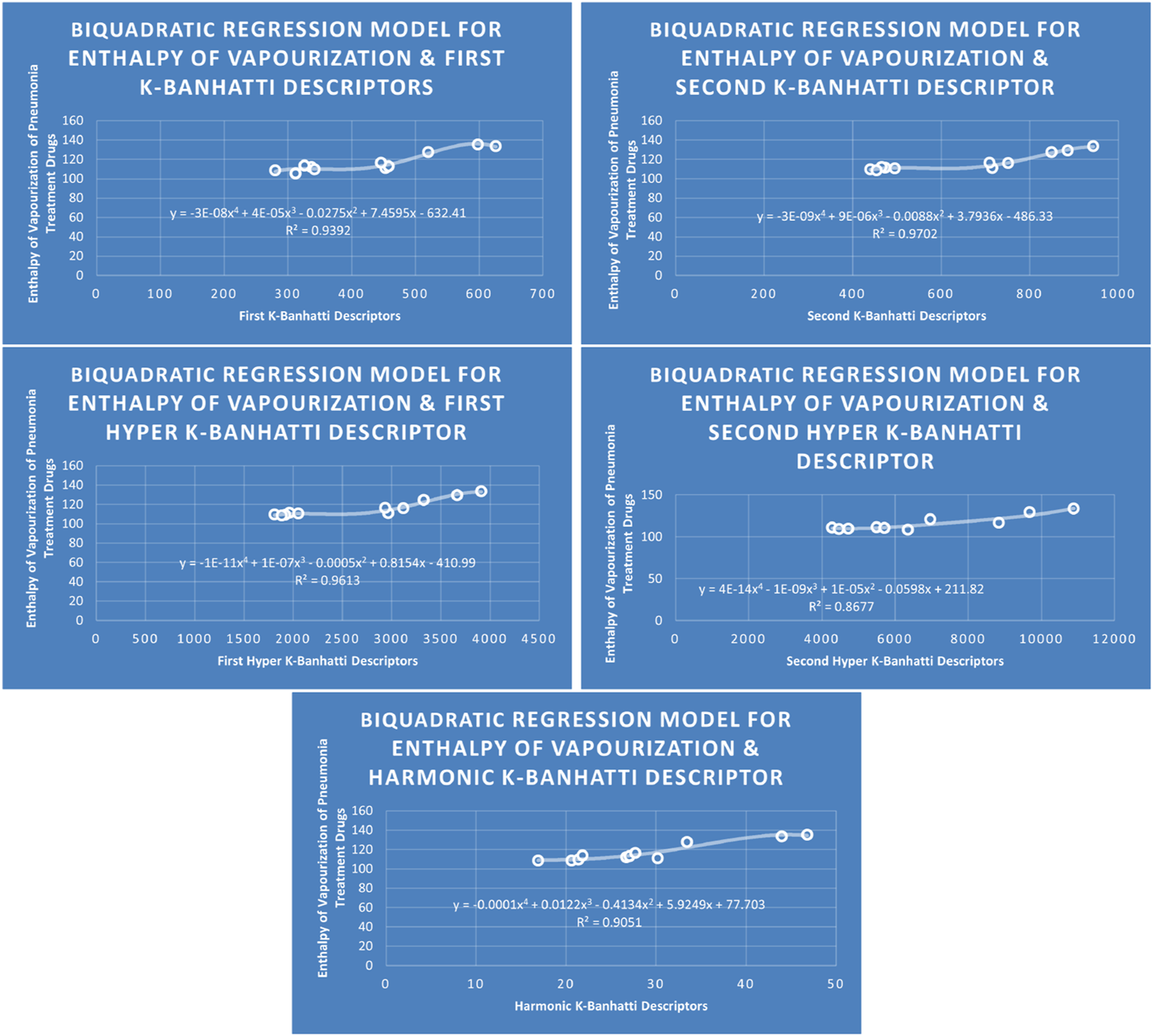
models of enthalpy of vaporization for pneumonia treatment drugs.
FIGURE 13
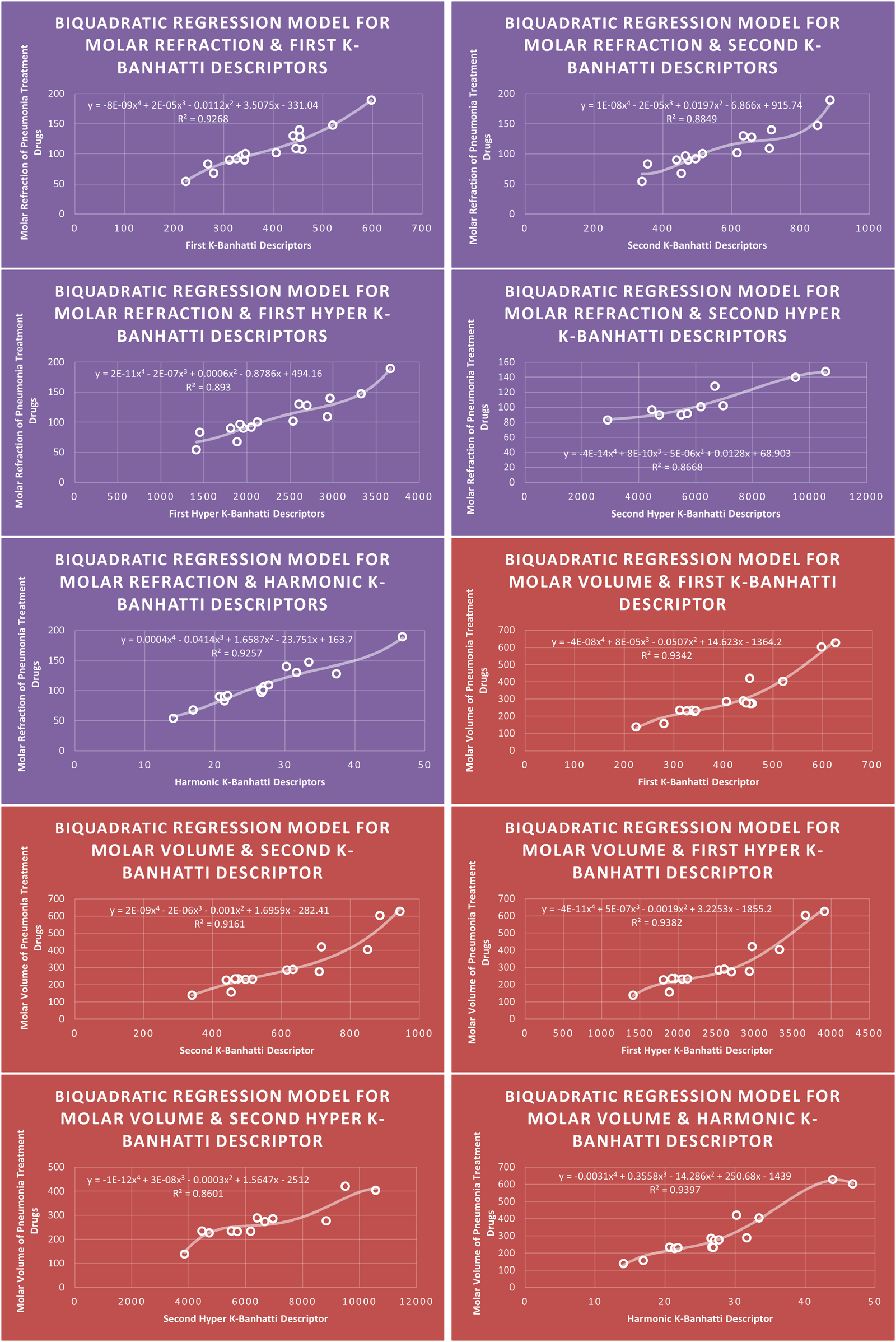
models of molar refraction and molar volume for pneumonia treatment drugs.
FIGURE 14
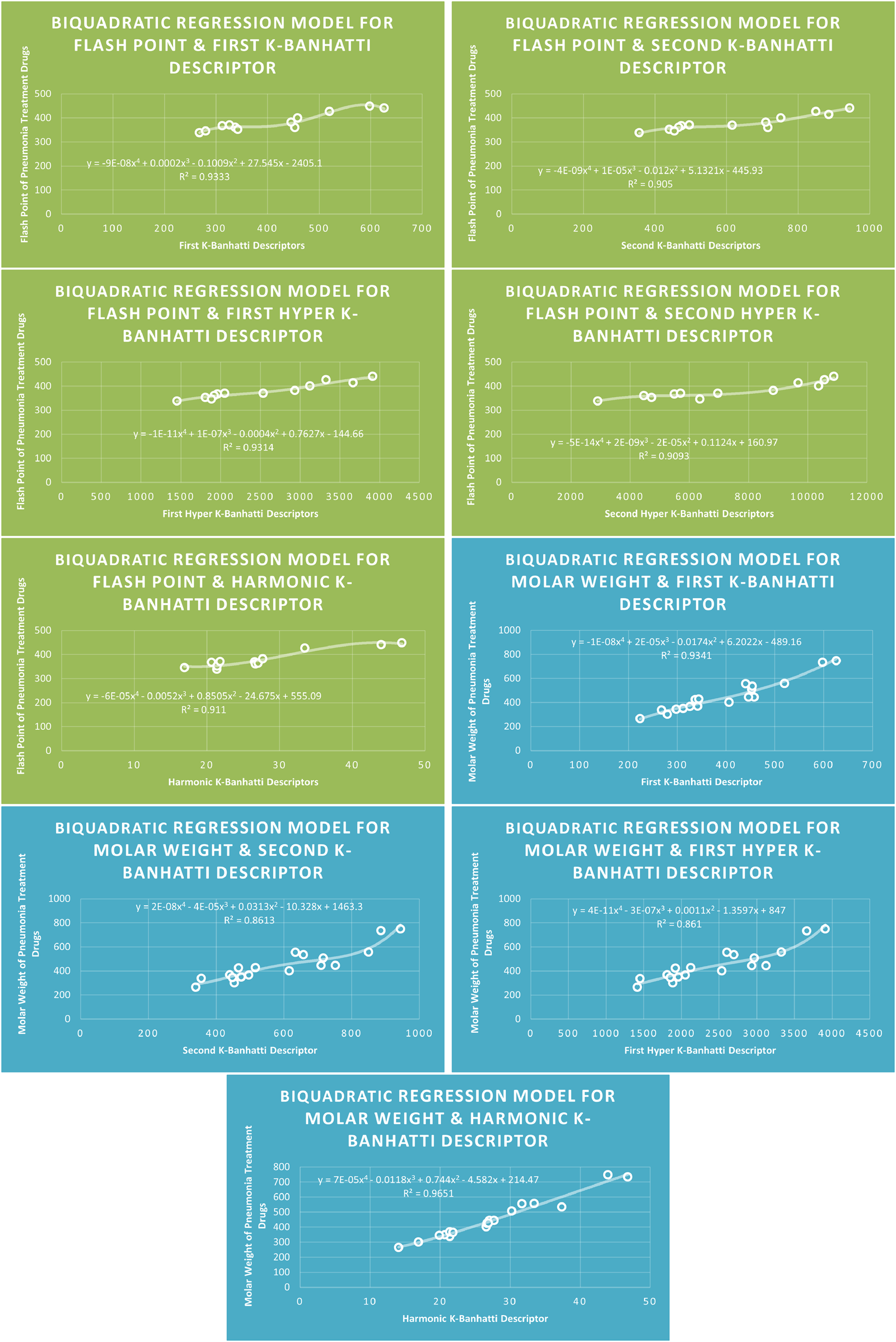
models of flash point and molar weight for pneumonia treatment drugs.
4.1 Linear regression analysis
The correlation between some -Banhatti topological descriptors and the physical characteristics of different medications taken to treat pneumonia, as shown in Table 6, is obtained by employing the Linear regression framework:While is the drug’s physical attribute is constant, the value of the regression coefficient, and is the topological descriptor. Using Equation 6, the linear regression models for the given -Banhatti topological descriptors and physicochemical properties are formulated as follows:
TABLE 6
| Drugs | MW | FP | |||
|---|---|---|---|---|---|
| Linezolid | 87.53 | 337.346 | 2593 | 307.930.1 | 830.3 |
| Omadacycline | 127.63 | 556.651 | 398.45 | 460.434.3 | 147.50.4 |
| Moxifloxacin | 98.83 | 401.431 | 2853 | 338.731.5 | 101.80.3 |
| Ceftriaxone | 554.580 | 281.77 | 1300.5 | ||
| Unasyn | 105.43 | 349.4 | 239.35 | 367.431.5 | 89.94 |
| Lefamulin | 105.16 | 507.726 | 424.85 | 327.931.5 | 139.80.4 |
| Carbapanem | 74.66 | 153.135 | 99.35 | 210.922.9 | 35.70.4 |
| Cefuroxime | 112.13 | 424.385 | 2417 | 396.335.7 | 96.70.5 |
| Cefaclor | 109.53 | 367.807 | 226.55 | 385.232.9 | 89.60.4 |
| Tetracycline | 1133 | 444.435 | 266.37 | 400.235.7 | 106.90.5 |
| Amoxicillin | 113.73 | 365.404 | 236.25 | 403.332.9 | 91.50.4 |
| Ceftabiprole | 534.569 | 266.17 | 127.80.5 | ||
| Doxycycline | 116.53 | 444.435 | 271.15 | 41532.9 | 1090.4 |
| Avibactam | 265.244 | 143.15 | 540.4 | ||
| Tazobactam | 108.63 | 300.291 | 155.87 | 381.435.7 | 67.70.5 |
| Clarithromycin | 133.46 | 747.953 | 631.95 | 440.934.3 | |
| Levaquin | 361.367 | 24475 | 91.170.4 | ||
| Erythromycin | 135.46 | 733.927 | 607.25 | 448.834.3 | 189.20.4 |
| Cefpodoxima | 427.455 | 239.57 | 100.50.5 | ||
| Penicillin | 344.390 |
Physicochemical properties of anti-pneumonia drugs.
4.2 Quadratic regression analysis
The correlation between some -Banhatti topological descriptors and the physical characteristics of different medications taken to treat pneumonia as shown in Table 6, is obtained by employing the quadratic regression framework:While is the drug’s physical attributes are constants, is the value of the regression coefficient is the topological descriptor. Using Equation 7, the quadratic regression models for the topological descriptors given -Banhatti and the physicochemical properties are formulated as follows:
4.3 Cubic regression analysis
The correlation between some -Banhatti topological descriptors and the physical characteristics of different medications taken to treat pneumonia, as shown in Table 6, are obtained by employing the cubic regression framework:While the drug’s physical attribute, are constants, is a constant, the value of the regression coefficient, and is the topological descriptor. Using Equation 8, the cubic regression models for the given -Banhatti topological descriptors and physicochemical properties are formulated as follows:
4.4 Biquadratic regression analysis
The correlation between some -Banhatti topological descriptors and the physical characteristics of different medications taken to treat pneumonia, as shown in Table 6, is obtained by employing the biquadratic regression framework:While is the drug’s physical attributes are constants, is the value of the regression coefficient is the topological descriptor. Using Equation 9, the biquadratic regression models for the given -Banhatti topological descriptors and physicochemical properties are formulated as follows:
4.5 Mathematical models for linear regression
This subsection provides mathematical models obtained after incorporating QSPR analysis.
• First -Banhatti Descriptor
• Second -Banhatti descriptor
• First Hyper -Banhatti descriptor
• Second Hyper -Banhatti Descriptor
• Harmonic -Banhatti Descriptor
4.6 Mathematical models for quadratic regression
This subsection provides mathematical models obtained after incorporating QSPR analysis.
• First -Banhatti Descriptor
• Second -Banhatti descriptor
• First Hyper -Banhatti descriptor
• Second Hyper -Banhatti Descriptor
• Harmonic -Banhatti Descriptor
4.7 Mathematical models for cubic regression
This subsection provides mathematical models obtained after incorporating QSPR analysis.
• First -Banhatti Descriptor
• Second -Banhatti descriptor
• First Hyper -Banhatti descriptor
• Second Hyper -Banhatti Descriptor
• Harmonic -Banhatti Descriptor
4.8 Mathematical models for biquadratic regression
This subsection provides mathematical models obtained after incorporating
analysis.
• First -Banhatti Descriptor
• Second -Banhatti Descriptor
• First Hyper -Banhatti Descriptor
• Second Hyper -Banhatti Descriptor
• Harmonic -Banhatti Descriptor
5 Discussions
The correlation evaluation specifies the proportion of the connection and offers additional details regarding the association of parameters. Squaring the correlation coefficient yields the correlation of determination . In Table 7 correlation coefficients are given. The descriptor for molecular weight is not best fitted for any model because for this desriptor correlation value is below 0.8. The descriptor provides the highest correlation coefficient for Enthalpy of vaporization for Biquadratic regression, descriptor provides the highest correlation coefficient for molar Refraction for biquadratic regression, descriptor provides the highest correlation coefficient for molar volume for biquadratic regression. The descriptor has the strongest correlation coefficient for flash point (0.9661) for Biquadratic regression, and the descriptor provides the highest correlation coefficient for Cubic and Biquadratic regression. Moreover, Table 7 highlights the highest correlation value against each property and descriptor for every model for ready reference.
TABLE 7
| Model | Descriptor | MV | FP | MW | ||
|---|---|---|---|---|---|---|
| Linear | 0.9077 | 0.9468 | 0.9230 | 0.9295 | 0.9552 | |
| 0.8989 | 0.9227 | 0.9284 | 0.9161 | 0.8999 | ||
| 0.9057 | 0.9258 | 0.9299 | 0.9024 | |||
| 0.9024 | 0.9153 | 0.9041 | 0.9154 | |||
| 0.9393 | ||||||
| 0.9413 | 0.9542 | 0.9590 | 0.9366 | 0.9637 | ||
| 0.9271 | 0.9497 | 0.9346 | 0.9113 | |||
| Quadratic | 0.9706 | 0.9348 | 0.9162 | |||
| 0.9306 | 0.9260 | 0.9042 | 0.9370 | |||
| 0.9418 | 0.9606 | 0.9394 | ||||
| 0.9438 | 0.9659 | 0.9367 | 0.9664 | |||
| 0.9328 | 0.9570 | 0.9457 | 0.9231 | |||
| Cubic | 0.9711 | 0.9414 | 0.9260 | |||
| 0.9306 | 0.9303 | 0.9138 | 0.9528 | |||
| 0.96497 | 0.9603 | 0.9615 | 0.9545 | |||
| 0.9691 | 0.9665 | 0.9665 | ||||
| 0.9407 | 0.9571 | 0.9513 | 0.9281 | |||
| Biquadratic | 0.9805 | 0.9450 | 0.9686 | 0.9651 | 0.9279 | |
| 0.9315 | 0.9310 | 0.9274 | 0.9536 | |||
| 0.9514 | 0.9621 | 0.9544 |
Correlation coefficient () of physicochemical properties for Linear, Quadratic, Cubic, and Biquadratic regression model for Banhatti Descriptors.
6 Concluding remarks
This research employs
-Banhatti topological descriptors derived from pharmaceutical chemical graphs to develop QSPR models for pneumonia therapeutics. The testing of our model shows that it can make predictions, which suggests that it could be a useful tool for guiding the research into drug therapies for pneumonia. In this paper, the
-Banhatti descriptors were computed. We utilized the quantitative method by expanding the
-Banhatti topological descriptors for the estimation of the physicochemical properties of medications for pneumonia. This work employed linear, quadratic, cubic, and biquadratic regressions to evaluate the relationship between properties and the
-Banhatti descriptors. The correlation between physicochemical properties and our findings is represented in
Table 7, which implies that every model for properties was determined to be valid and provide a good correlation. The findings give an economical and scientific basis for developing novel medicines having comparable designs for greater effect and therapy. The study suggests that pharmacists and scientists can build anti-pneumonia medications based on such topological descriptors. We have discovered that topological descriptors have a correlation coefficient, suggesting that we can combine medications with an elevated correlation to create novel medications. Below are some of the best approximations from this study.
• Best approximated result for Linear, Quadratic, Cubic, and Biquadratic regression for Enthalpy of vaporization
• Best approximated result for Linear, Quadratic, Cubic, and Biquadratic regression for Flash point
• Best approximated result for Linear, Quadratic, Cubic, and Biquadratic regression for Molar refraction
• Best approximated result for Linear, Quadratic, Cubic, and Biquadratic regression for Molar volume
• Best approximated result for Linear, Quadratic, Cubic, and Biquadratic regression for Molar weight
For this study, the cubic and Biquadratic regressions give more reliable results as compared to linear and quadratic. From these models and Table 7, we have oder of reliability:
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
AK: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. IN: Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft. FT: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – review and editing. FT: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review and editing. SH: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. Researchers Supporting Project number (RSP2025R401), King Saud University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Almalki N. Tabassum H. (2024). On K-banhatti, revan indices and entropy measures of MgO (111) nanosheets via linear regression. Mathematics12 (4), 561. 10.3390/math12040561
2
Alvarez-Elcoro S. Enzler M. J. (1999). The macrolides: erythromycin, clarithromycin, and azithromycin. Mayo Clin. Proc.74 (6), 613–634. 10.4065/74.6.613
3
Anjum M. S. Safdar M. U. (2019). K Banhatti and K hyper-Banhatti indices of nanotubes. Eng. Appl. Sci. Lett.2(1), 19–37. 10.30538/psrp-easl2019.0013
4
Awan N. U. H. Ghaffar A. Tawfiq F. M. Mustafa G. Bilal M. (2024). QSPR analysis for physiochemical properties of new potential antimalarial compounds involving topological indices. Int. J. Quantum Chem.124 (11), e27391. 10.1002/qua.27391
5
Awan N. U. H. Ghani M. U. Bibi S. Kirmani S. A. K. Abdalla M. E. M. (2025). A paradigmatic approach to the topological measure of babesiosis drugs and estimating physical properties via QSPR analysis. Heliyon11 (1), e41615. 10.1016/j.heliyon.2024.e41615
6
Bashir Farooq F. Awan N. U. H. Parveen S. Idrees N. Kanwal S. Abdelhaleem T. A. (2022). Topological indices of novel drugs used in autoimmune disease vitiligo treatment and its QSPR modeling. J. Chem.2022 (1), 6045066. 10.1155/2022/6045066
7
Chu Y. M. Khan A. R. Ghani M. U. Ghaffar A. Inc M. (2023). Computation of zagreb polynomials and zagreb indices for benzenoid triangular and hourglass system. Polycycl. Aromat. Compd.43 (5), 4386–4395. 10.1080/10406638.2022.2090970
8
Dehmer M. M. Barbarini N. N. Varmuza K. K. Graber A. A. (2010). Novel topological descriptors for analyzing biological networks. BMC Struct. Biol.10, 18–17. 10.1186/1472-6807-10-18
9
Fathi A. Vijay J. S. Husin M. N. Augustine T. (2024). Valency-based molecular descriptor on structural property relationship of Ni tetrathiafulvalene tetrathionate. Malays. J. Fundam. Appl. Sci.20 (6), 1398–1409. 10.11113/mjfas.v20n6.3831
10
Galvez J. Villar V. Galvez-Llompart M. Amigo J. (2011). Chemistry explained by topology: an alternative approach. Comb. Chem. and High Throughput Screen.14 (4), 279–283. 10.2174/138620711795222464
11
Garau J. (2005). Role of beta-lactam agents in the treatment of community-acquired pneumonia. Eur. J. Clin. Microbiol. Infect. Dis.24, 83–99. 10.1007/s10096-005-1287-9
12
Ghani M. U. Sultan F. Tag El Din E. S. M. Khan A. R. Liu J. B. Cancan M. (2022). A paradigmatic approach to find the valency-based K-banhatti and redefined Zagreb entropy for niobium oxide and a metal–organic framework. Molecules27 (20), 6975. 10.3390/molecules27206975
13
Hakami K. H. Khan A. R. Bhatti S. A. (2025). Computation of differential, integral operators and quantitative structure–property analysis of boron α-icosahedral nanosheet. J. Math.2025 (1), 5607620. 10.1155/jom/5607620
14
Hakami K. H. Khan A. R. Zia I. (2024). Bicubic regression analysis a novel approach for estimation of physicochemical properties of skin cancer drugs through degree based entropy. Heliyon10 (20), e39084. 10.1016/j.heliyon.2024.e39084
15
Harari M. Spooner V. Meisner S. Carney M. Shann F. De Campo J. (1991). Clinical signs of pneumonia in children. Lancet338 (8772), 928–930. 10.1016/0140-6736(91)91785-s
16
Hayat S. (2017). Computing distance-based topological descriptors of complex chemical networks: new theoretical techniques. Chem. Phys. Lett.688, 51–58. 10.1016/j.cplett.2017.09.055
17
Husin M. N. Hasni R. Arif N. E. (2015). Zagreb polynomials of some nanostar dendrimers. J. Comput. Theor. Nanosci.12 (11), 4297–4300. 10.1166/jctn.2015.4354
18
Husin M. N. Khan A. R. Awan N. U. H. Campena F. J. H. Tchier F. Hussain S. (2024). Multicriteria decision making attributes and estimation of physicochemical properties of kidney cancer drugs via topological descriptors. Plos one19 (5), e0302276. 10.1371/journal.pone.0302276
19
Imran M. Khan A. R. Husin M. N. Tchier F. Ghani M. U. Hussain S. (2023). Computation of entropy measures for metal-organic frameworks. Molecules28 (12), 4726. 10.3390/molecules28124726
20
Khan A. R. Awan N. U. H. Ghani M. U. Eldin S. M. Karamti H. Jawhari A. H. et al (2023a). Fundamental aspects of skin cancer drugs via degree-based chemical bonding topological descriptors. Molecules28 (9), 3684. 10.3390/molecules28093684
21
Khan A. R. Awan N. U. H. Tchier F. Alahmari S. D. Khalel A. F. Hussain S. (2025). An estimation of physiochemical properties of bladder cancer drugs via degree-based chemical bonding topological descriptors. J. Biomol. Struct. Dyn.43 (4), 1665–1673. 10.1080/07391102.2023.2292792
22
Khan A. R. Bhatti S. A. Imran M. Tawfiq F. M. Cancan M. Hussain S. (2024e). Computation of differential and integral operators using M-polynomials of gold crystal. Heliyon10 (14), e34419. 10.1016/j.heliyon.2024.e34419
23
Khan A. R. Bhatti S. A. Tawfiq F. Siddiqui M. K. Hussain S. Ali M. A. (2024d). On degree-based operators and topological descriptors of molecular graphs and their applications to QSPR analysis of carbon derivatives. Sci. Rep.14 (1), 21543. 10.1038/s41598-024-72621-7
24
Khan A. R. Ghani M. U. Ghaffar A. Asif H. M. Inc M. (2023b). Characterization of temperature indices of silicates. Silicon15 (15), 6533–6539. 10.1007/s12633-023-02298-6
25
Khan A. R. Mutlib A. Campeña F. J. H. Tchier F. Karim M. Hussain S. (2024b). Investigation of reduced reverse degree based polynomials and indices of gold crystals. Phys. Scr.99 (7), 075259.10.1088/1402-4896/ad5648
26
Khan A. R. Ullah Z. Imran M. Malik S. A. Alamoudi L. M. Cancan M. (2024c). Molecular temperature descriptors as a novel approach for QSPR analysis of Borophene nanosheets. PloS one19 (6), e0302157. 10.1371/journal.pone.0302157
27
Khan A. R. Zia A. Campeña F. J. H. Siddiqui M. K. Tchier F. Hussain S. (2024a). Investigations of entropy double and strong double graph of silicon carbide. Silicon, 164187–4197. 10.1007/s12633-024-02975-0
28
Kulli V. R. (2016). On K Banhatti indices of graphs. J. Comp. Mat. Sci., 7(4), 213–218.
29
Leung A. K. Wong A. H. Hon K. L. (2018). Community-acquired pneumonia in children. Recent Pat. Inflamm. and allergy drug Discov.12 (2), 136–144. 10.2174/1872213x12666180621163821
30
Liapikou A. Cillóniz C. Torres A. (2015). Ceftobiprole for the treatment of pneumonia: a European perspective. Drug Des. Dev. Ther.9, 4565–4572. 10.2147/dddt.s56616
31
Madhi S. A. Levine O. S. Hajjeh R. Mansoor O. D. Cherian T. (2008). Vaccines to prevent pneumonia and improve child survival. Bull. world Health Organ.86, 365–372. 10.2471/blt.07.044503
32
Mahboob A. Muhiuddin G. Siddique I. Alam S. M. (2022). A view of Banhatti and Revan indices in chemical graphs. J. Math.2022 (1), 5680712. 10.1155/2022/5680712
33
Marangu D. Zar H. J. (2019). Childhood pneumonia in low-and-middle-income countries: an update. Paediatr. Respir. Rev.32, 3–9. 10.1016/j.prrv.2019.06.001
34
Munywoki P. K. Ohuma E. O. Ngama M. Bauni E. Scott J. A. G. Nokes D. J. (2013). Severe lower respiratory tract infection in early infancy and pneumonia hospitalizations among children, Kenya. Emerg. Infect. Dis.19 (2), 223–229. 10.3201/eid1902.120940
35
Nasir S. Farooq F. B. Parveen S. (2022). Topological indices of novel drugs used in blood cancer treatment and its QSPR modeling. AIMS Math.7 (7), 11829–11850. 10.3934/math.2022660
36
Parveen N. Sathik M. M. (2011). Detection of pneumonia in chest X-ray images. J. X-ray Sci. Technol.19 (4), 423–428. 10.3233/xst-2011-030400304
37
Rudan I. Tomaskovic L. Boschi-Pinto C. Campbell H. (2004). Global estimate of the incidence of clinical pneumonia among children under five years of age. Bull. World Health Organ.82 (12), 895–903.
38
Scelfo C. Menzella F. Fontana M. Ghidoni G. Galeone C. Facciolongo N. C. (2021). Pneumonia and invasive pneumococcal diseases: the role of pneumococcal conjugate vaccine in the era of multi-drug resistance. Vaccines9 (5), 420. 10.3390/vaccines9050420
39
Scotta M. C. Marostica P. J. Stein R. T. (2019). “Pneumonia in children,” in Kendig’s disorders of the respiratory tract in children (Elsevier), 427–438.
40
Shann F. (1995). The management of pneumonia in children in developing countries. Clin. Infect. Dis.21 (Suppl. 3), S218–S225. 10.1093/clind/21.supplement_3.s218
41
Singh V. Aneja S. (2011). Pneumonia–management in the developing world. Paediatr. Respir. Rev.12 (1), 52–59. 10.1016/j.prrv.2010.09.011
42
Sood S. K. (1999). Macrolides: clarithromycin and azithromycin. Semin. Pediatr. Infect. Dis. (Vol. 10, No. 1, pp. 23–30). 10.1016/s1045-1870(99)80006-5
43
Sultana S. (2023). Chemical application of topological indices in infertility treatment drugs and QSPR analysis. Int. J. Anal. Chem.2023 (1), 1–11. 10.1155/2023/6928167
44
Venditti M. Falcone M. Corrao S. Licata G. Serra P. (2009). Outcomes of patients hospitalized with community-acquired, health care–associated, and hospital-acquired pneumonia. Ann. Intern. Med.150 (1), 19–26. 10.7326/0003-4819-150-1-200901060-00005
45
Vijay J. S. Roy S. Beromeo B. C. Husin M. N. Augustine T. Gobithaasan R. U. et al (2023). Topological properties and entropy calculations of aluminophosphates. Mathematics11 (11), 2443. 10.3390/math11112443
46
Wardlaw T. Salama P. Johansson E. W. Mason E. (2006). Pneumonia: the leading killer of children. Lancet368 (9541), 1048–1050. 10.1016/s0140-6736(06)69334-3
47
Wojsyk-Banaszak I. Breeborowicz A. (2013). “Pneumonia in children,” in Respiratory disease and infection-A new insight (IntechOpen).
Summary
Keywords
molecular structure, anti-pneumonia drugs, physicochemical properties, topological descriptors, K-Banhatti descriptors, regression models, QSPR testing, chemical graph theory
Citation
Khan AR, Naeem I, Tchier F, Tolasa FT and Hussain S (2025) Mathematical modeling and estimation of physicochemical characteristics of pneumonia treatment drugs through a novel approach K-Banhatti topological descriptors. Front. Chem. 13:1564809. doi: 10.3389/fchem.2025.1564809
Received
22 January 2025
Accepted
10 March 2025
Published
02 May 2025
Volume
13 - 2025
Edited by
Rachelle J. Bienstock, RJB Computational Modeling LLC, United States
Reviewed by
Joseph Clement, VIT University, India
Nadeem Ul Hassan Awan, Gazi University, Türkiye
Mohamad Nazri Husin, University of Malaysia Terengganu, Malaysia
Updates
Copyright
© 2025 Khan, Naeem, Tchier, Tolasa and Hussain.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Abdul Rauf Khan, khankts@gmail.com; Fikadu Tesgera Tolasa, fikadu@dadu.edu.et
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.