- 1Materials Science and Technology Division, Los Alamos National Laboratory, Los Alamos, NM, USA
- 2Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM, USA
- 3Department of Materials Science and Engineering, Institute of Materials Science, University of Connecticut, Storrs, CT, USA
Advanced materials with improved properties have the potential to fuel future technological advancements. However, identification and discovery of these optimal materials for a specific application is a non-trivial task, because of the vastness of the chemical search space with enormous compositional and configurational degrees of freedom. Materials informatics provides an efficient approach toward rational design of new materials, via learning from known data to make decisions on new and previously unexplored compounds in an accelerated manner. Here, we demonstrate the power and utility of such statistical learning (or machine learning, henceforth referred to as ML) via building a support vector machine (SVM) based classifier that uses elemental features (or descriptors) to predict the formability of a given ABX3 halide composition (where A and B represent monovalent and divalent cations, respectively, and X is F, Cl, Br, or I anion) in the perovskite crystal structure. The classification model is built by learning from a dataset of 185 experimentally known ABX3 compounds. After exploring a wide range of features, we identify ionic radii, tolerance factor, and octahedral factor to be the most important factors for the classification, suggesting that steric and geometric packing effects govern the stability of these halides. The trained and validated models then predict, with a high degree of confidence, several novel ABX3 compositions with perovskite crystal structure.
1. Introduction
The materials community is currently witnessing a fundamental change in the way novel materials are designed and discovered. A steady increase in computational power, accompanied by developments in quantum theory and algorithmic breakthroughs that allow for efficient yet accurate quantum mechanical computations, opens the door to computing properties of a wide range of materials that once seemed prohibitively expensive. As a result, high-throughput explorations of the vast chemical space are increasingly being pursued and have significantly aided our intuition and knowledge-base of material properties (Ceder et al., 2011; Jain et al., 2011; Yu and Zunger, 2012; Curtarolo et al., 2013; Pilania et al., 2013, 2016; Sharma et al., 2014; Balachandran et al., 2016; Kim et al., 2016; Mannodi-Kanakkithodi et al., 2016). Massive open source databases of materials properties (including electronic structure, thermodynamic, and structural properties) are now available on the web (Curtarolo et al., 2012; Computational Materials Repository, 2015; Materials Project – A Materials Genome Approach, 2015). Big-data materials infrastructure (Service, 2012) is increasingly being built with the intent of knowledge extraction and rule-mining to identify candidate materials for next-generation materials breakthroughs.
To illustrate the efficacy and utility of the informatics route to materials discovery, we here take-up a specific example of predicting the formability of perovskite halides – a class of technologically relevant materials (Mitchell, 2002) possessing a number of interesting properties, including high resistivity and breakdown field, electron-acceptor behavior, a large optical transmission domain, photoluminescence, ionic conductivity over a wide temperature range, antiferromagnetism, ferroelectricity, and piezoelectricity (Muller and Roy, 1974; Sarukura et al., 2007; Zhang et al., 2008; Pilania and Lookman, 2014; Pilania and Uberuaga, 2015).
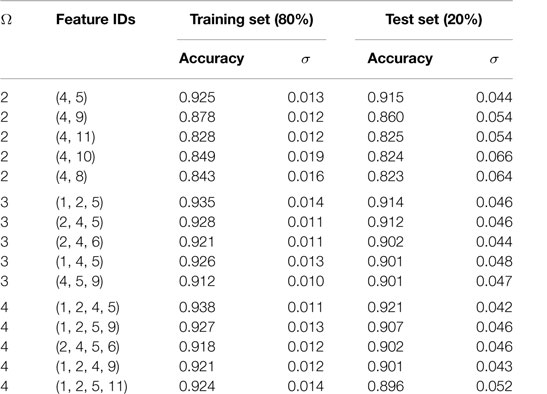
A typical cubic crystal structure adopted by ABX3 perovskite halides [with three-dimensional arrangement of corner-sharing octahedral BX6 units (Muller and Roy, 1974)] is depicted in Figure 1A, where A and B cations are 12- and 6-fold coordinated, and have +1, +2 nominal charge states, respectively, while X ∈ {F, Cl, Br, I} represents a halide. However, non-perovskite structures with edge sharing octahedral arrangement are also common in compounds with ABX3 stoichiometry (for instance, CsNiF3 and CsCoCl3 compounds) (Muller and Roy, 1974). The central focus of this paper is a basic task: from available data on formability of ABX3 solids (i.e., known compounds with perovskite or non-perovskite labels), can we construct a ML model and predict with a high degree of accuracy whether a proposed solid with given choices of A, B, and X should be a perovskite or a non-perovskite?
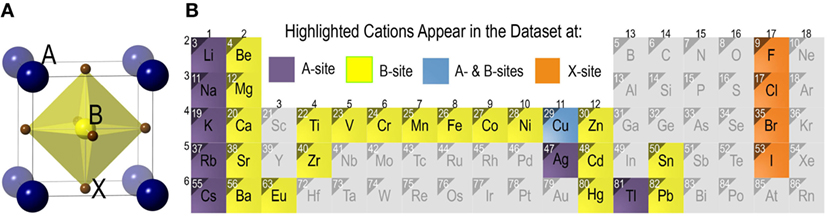
Figure 1. (A) The prototypical cubic perovskite halide crystal structure of ABX3 compounds with corner sharing octahedra of halide anions (X) housing B-site cations. A-site cations occupy a 12-fold coordination site surrounding BX6 octahedra (shown explicitly in the figure). (B) Chemical space of the ABX3 halide chemistries explored in the present study. Cations appearing at the A-site and/or the B-site are highlighted. X site can be occupied by four halides in group 17.
Given the technological importance of perovskites, formability of both oxides (Li et al., 2004; Zhang et al., 2007; Feng et al., 2008; Kumar et al., 2008) and halides (Li et al., 2008) falling in this class has been previously studied. These studies performed a classification into perovskite or non-perovskite in the traditional way by using a structure map. A structure map is defined as a two-dimensional plot of the values of two features of the known solids and with lines drawn using ad hoc principles (including by hand) that separate the data points into the different classes of crystal structures (Mooser and Pearson, 1959). The tolerance and octahedral factors are the two most widely used structure governing features in these plots (Li et al., 2004, 2008; Zhang et al., 2007; Feng et al., 2008; Kumar et al., 2008). Our work is a departure from these earlier publications: we consider a large number of potential features that are known to govern the crystal structures of inorganic solids (beyond tolerance and octahedral factors), utilize state-of-the-art ML methods to rationally establish the decision boundaries (based on available data and cross-validation methods) that separate perovskites from non-perovskites and accurately quantify prediction accuracies. By exploring a vast number of different feature combinations, we identify new classifiers, previously unknown, that complement (or could even potentially substitute) the two popular geometric factors used in the past.
While drawing that the standard structure map is not possible with more than two features, ML provides an alternative, more rigorous, and automated method of classification. Unlike the traditional approach adopted for structure maps, where decision boundaries are drawn by hand, in the ML approach model parameters govern the position of decision boundaries and optimal parameters are selected by evaluating the model performance (or prediction accuracy) on unseen data (Pilania et al., 2015a,b).
For ML, we used the support vector classification (SVC) method, which is commonly used in binary classification problems (Vapnik, 1995, 1998; Flach, 2012). An additional advantage of using this method is that besides returning a classification model, it also provides probabilistic estimates of confidence in those predictions that can be very useful in forecasting new candidates, which are yet to be synthesized. In fact, after performing training and testing steps on the available 185 compounds, we employ the best performing model to predict formability of 455 ABX3 chemistries falling within the same chemical space spanned by the training data. The top 20 new ABX3 compounds with high prediction probability of forming perovskite-type crystal structure are, thus, identified. In what follows, we describe the details of our study.
2. Dataset, Features, and Chemical Space
This section describes the details of features and perovskite halide formability dataset that were used to train and test the prediction performance of the ML models developed here. Besides the tolerance and octahedral factor feature pairs, we also considered the A, B, and X ionic radii (denoted as , , and , respectively), the bond valence distances of A and B from X (denoted as and ) (Zhang et al., 2007), and the ratio of the sum of the s and p orbital radii of the A and B atoms relative to that of the X atom (i.e., and ) (Rabe et al., 1992). Finally, differences in the Martynov–Batsanov electronegativity scales of A–X and B–X atoms pairs (i.e., and ) were also included. Initial tests, however, showed that these last two features when multiplied, respectively, by the ionic radii ratios and perform slightly better and, therefore, and were included as features instead of just the differences in the Martynov–Batsanov electronegativity scales of A–X and B–X atoms pairs. Rabe et al. (1992) have shown that the pseudopotential core radii sum and Martynov–Batsanov electronegativity are widely transferable across crystal classes and capture important trends essential to describe the electronic charge distribution, crystal geometry, and bond lengths. We explore the relevance of these features for classifying perovskite and non-perovskite halides.
Bond valence radii that we have used in this work refers particularly to the bond valence parameter R0 in the equation, Sij = exp((R0 − Rij)/b) (Brown, 1978), where Rij is the length and Sij is the valence of the bond between atoms i and j; R0 and b are the empirically determined bond valence parameters, whose values are compiled in crystallographic databases. Note that R0 has the unit of bond distances and has unique values for a given cation and anion pair.
The s and p orbital radii refers to the Zunger’s pseudopotential core radii sum (Zunger and Cohen, 1979), which, in sharp contrast to the empirical R0 parameter, is derived directly from quantum-mechanical calculations. They refer to the core distance of the wave function at which the pseudopotential crosses zero for a given angular momentum of an orbital. Here, we considered s and p-orbitals for our classification. In Table 1, we list all features that were considered in this study.

Table 1. A summary of various geometric and electronic properties used in constructing features for the binary classification.
We started with the ABX3 perovskite halide formability dataset used by Li et al. (2008) consisting of 186 labeled compounds. From this dataset, five compounds (viz., KSmCl3, CsGeCl3, LiCoBr3, KCoBr3, and KCoI3) were omitted since the bond valence features were not available for these compounds. Furthermore, we augmented the dataset with four tin fluorides, namely NaSnF3, KSnF3, RbSnF3, and CsSnF3, for which formability labels became available only recently (Tran and Halasyamani, 2014). Thus, the final dataset contained 185 ABX3 compounds with known labels and 11 features.
The chemical space covered by the compounds in the training dataset is depicted in Figure 1B. The 185 ABX3 perovskite halides contain eight different A-site cations (viz. Ag, Cs, Cu, K, Li, Na, Rb, and Tl) and twenty B-site cations (viz. Ba, Be, Ca, Cd, Co, Cr, Cu, Eu, Fe, Hg, Mg, Mn, Ni, Pb, Sn, Sr, Ti, V, Zn, and Zr). Cu appears on either A- or B-sites. The X-site has four different possible choices of F, Cl, Br, and I.
Owing to the inherent interpolative nature of ML approaches, we confined our exploration to the above restricted chemical space of perovskite halides throughout this study. Within this space, a total of 640 unique compounds exist, out of which 185 (<30%) are known from previous experiments. The remaining 455 are not explored in the literature and our objective is learned from 185 known compounds via ML and infer or predict the formability of the remaining 455 compositions for rationally guiding the experimental synthesis efforts.
3. Machine Learning Model
For the binary classification problem at hand, each instance of our data is described by an Ω-dimensional feature vector = ( f1, f2, f3, …, fΩ) and a label y. The label has a value of +1, say for perovskites, and −1, for non-perovskites. A support vector machine aims to find a function that for any given has a value of ±1. Ideally, it is desired to generate a decision boundary in the space of features that maximizes the distance (also known as margin) of the closest instance from either class from it. Instances are defined as points in the hyperspace of features that lie on one side or the other of this hypersurface.
Often a clear separation of the data via a finite margin is not possible. In such cases, a soft margin support vector machine is constructed instead. This classifier allows misclassification of instances; in other words, points in the margin are allowed. If we represent our input data by the set of labeled instances {()}, then a soft margin support vector classifier determines the hypersurface in the space of features by solving
subjected to the following constraints:
Here, the parameter C controls the number of misclassifications. In the minimization, the competition is between the size of the margin and the degree of misclassification acceptable. The support vectors are identified as those points for which 0 < αi < C.
The term is known as the kernel, for which there are several choices, for example, linear kernels, polynomial kernels, or Gaussian kernels (also known as radial basis functions or RBFs) (Pedregosa et al., 2011). If the kernel is linear, the decision boundary is always a hyperplane. With two features, the linear kernel support vector machine draws a straight line through the data and, hence, is analogous to drawing a structure map. This was another reason that we choose support vector machine over other classification methods as a linear kernel with just two features mimics what has been done in the past.
In this work, however, after testing a number of kernels for their classification accuracies, we chose to go forward with a Gaussian kernel, defined as:
To use a support vector machine as a classifier, we first need to select a kernel and set its parameters. For the RBF kernel, the number of parameters that need to be set are two, namely C and γ. To aid in selecting these parameters, we used grid-search cross-validation (Pedregosa et al., 2011) that generates a two-dimensional grid. For each grid point, we used five-fold cross-validation on a 0.8/0.2 training/testing split of the dataset. Our metric of success is the accuracy, that is, the number of instances in the test set predicted correctly divided by the total number of instances in the test set. For this metric, the grid for C often had a number of points with nearly identical values. In many cases, repeating the analysis with a different random number sequence produced variations nearly comparable. For γ, the best results were obtained when the parameter was varied inversely with number of features; i.e., when γ ∝ 1/Ω. Instead of choosing the parameter values at the grid point with the best value of the metric for a given kernel, we simply choose C = 1 and γ = 1/Ω to define the model. With these parameters, we tested all possible combination of the features going up to four features. These results are discussed in the next section.
4. Results and Discussion
Using the SVC model, we tested all possible models built by taking two (11C2 = 55 models with Ω = 2), three (11C3 = 165 models with Ω = 3), and four features at a time (11C4 = 330 models with Ω = 4). Performances of these models were ranked by evaluating their prediction accuracy (i.e., fraction of the correctly predicted formability labels) on a 20% independent test set that was not used for model training. Performance of the top-5 models for each of the cases with Ω = 2, 3, and 4 is summarized in Table 2 and Figure 2. We also tested each model for its stability by evaluating prediction variability over 500 different randomly selected test sets. The SDs on test set prediction accuracies for the top performing models are provided in Table 2.
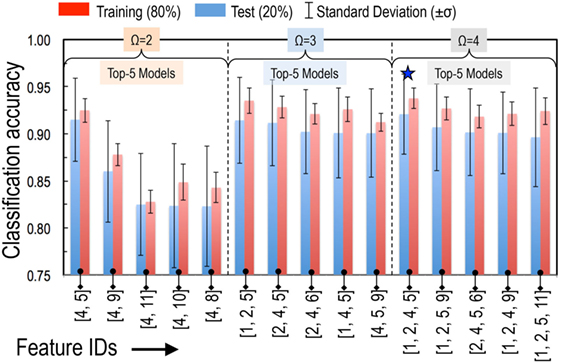
Figure 2. Performance of top-5 models for each of the cases with two features (Ω = 2), three features (Ω = 3), and four features (Ω = 4). Models were ranked by their prediction accuracy defined as fraction of the correctly predicted formability labels on a 20% test set that was not used for model training. To obtain reliable statistics of our model performance, we performed 500 such trials of randomly choosing 80% for training and 20% for testing. At the end of each trial, we have an estimate for the accuracy of the model performance on each test set. Error bars represent the SD (σ) of those 500 accuracy estimates. The best performing model is identified with a ★.
The top performing model with Ω = 2 is the classical tolerance- and octahedral-factor pair (tf, of). While tf appears in all five top-performing models with Ω = 2, performance of the tf, of pair was found to be remarkably better than the other models. This pair leads to classification accuracies of 92.5% on the training set and 91.5% on the test set. It was also interesting to compare the classification performance of this feature pair when individual features were used with and without normalization. For normalization, we scaled each of the features to have a zero mean and unit variance. Figure 3 compares the results of the structure map. We find that the model with normalized features not only results in superior prediction performance but also leads to a more physically meaningful finite formability region for perovskites. In light of this result, we used normalized features for all SVC models in our study.
Figure 3. A comparison of classification performance for the SVC models with tf–of feature pair (A) when both features used as is and (B) when both features were normalized with a zero mean and unit variance.
The models with Ω = 3 and Ω = 4 provide only slight improvements in the prediction accuracies. For example, our best performing model with Ω = 4 (i.e., with features , , tf, and of) led to improvements to both the training set and test set prediction accuracies by about 1%. We were able to classify training and test sets formabilities with 93.8 and 92.1% accuracies, respectively. Ninety-five percent confidence intervals (i.e., ±1.96 σ) on these predictions were within 4.3 and 16.5%, respectively. Going beyond Ω = 4 did not improve the prediction accuracies and, therefore, we used our best performing model with the four features for subsequent analysis and to make formability predictions on the compounds in the target chemical space which have not yet been synthesized.
Before moving on to new predictions, we also analyzed compounds that were misclassified. The results are presented in Figure 4. While all four features were used in the classification model, here we plot the results in tf and of feature space for visualization purposes. It can be seen that most of the misclassifications occur at the boundary of the perovskite and non-perovskite regions. Furthermore, model-predicted probabilities of formation for most of these compounds were close to 50% for both the classes. For instance, the predicted probabilities of RbEuCl3 and RbSrCl3 for being a perovskite were 58 and 52%, respectively. Given that many non-perovskite oxides can be synthesized in a long-lived metastable perovskite phase through non-equilibrium high pressure synthesis routes, it will not be unreasonable to contemplate that such possibilities may also exist for these border-line halide ABX3 chemistries as well. Finally, a compound that comes forth as clear exception is CsMnF3, which was labeled as non-perovskite but predicted to be a perovskite with a 96% probability. Not surprisingly, we found that that the hexagonal antiferromagnetic structure of CsMnF3 can be easily transformed to cubic perovskite at high pressures (Kafalas and Longo, 1972). Therefore, such misclassifications should be looked at, not so much as learning model failures, but rather as indicators of possibilities for alternative synthesis routes (such as high temperature, pressure, or epitaxial strain) toward perovskite crystal structures (Balachandran et al., 2015).
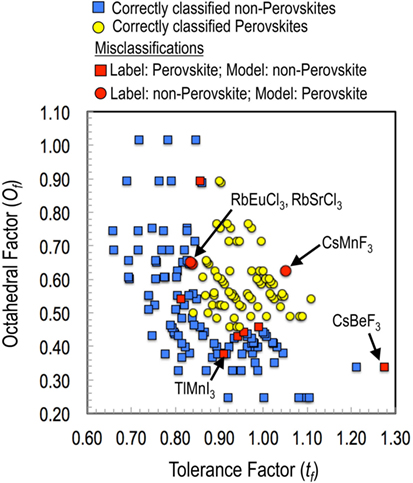
Figure 4. Analysis of the training set misclassifications for the best performing model with Ω = 4 (i.e., with features , , tf, and of). While all of the four features were used in the classification model; here, the results are plotted in a two-dimensional plot with the tf and the of for better intelligibility.
Having demonstrated classification using known data, we now use the ML model to predict formability (i.e., perovskite vs. non-perovskite) of the unlabeled ABX3 chemistries. While, in principle, we were able to classify all of the 455 chemical compositions, going forward, we focus our attention on the top-40 ABX3 chemistries, all of which were classified as a perovskite with a probability ≥85%. These systems are listed in Table 3 along with the predicted probability of formation in a perovskite structure. A complete list of predictions on the entire dataset of 455 compounds can be found in Supplementary Material. It is interesting to note that some of these compounds [such as TlCaF3 and TlHgF3 have also been predicted to be stable in the perovskite crystal structure by a recent independent study (Körbel et al., 2016)].

Table 3. Model predicted novel ABX3 chemistries with a probability of ≥85% to form a perovskite structure.
Finally, we note that our ML-based formability prediction model has only considered structural factors and other easily accessible attributes for the ABX3 systems. This is a reasonable first screening step that allows us to efficiently down-select a small fraction of the overall unlabeled dataset (i.e., 40 out of a total of 455 possibilities, viz., <10%). However, to make reliable predictions relative thermodynamic stability of the identified ABX3 chemistries has to be rigorously tested against all potential chemical combinations that may combine to form the composition of interest. More specifically, this requires computation of relative stability with respect to a set of most stable known materials (including elemental, binaries, and ternaries chemistries) at that chemical composition for each of the top-40 ABX3 chemistries identified here. Furthermore, one has to confirm the absence of any soft mode instabilities over the entire Brillouin zone in order to establish the dynamical stabilities of these systems. Such efforts are currently underway.
5. Conclusion
Perovskite halides (hybrid and inorganic) have garnered significant interest because of their outstanding photovoltaic properties. One of the outstanding challenges that concern experimental efforts in this direction is in successfully synthesizing phase pure perovskite compounds. We attempted to address this by employing a ML approach, which allows us to rapidly screen and identify candidate ABX3 perovskite compounds for experimental evaluation. From our analysis, we identified a combination of features that best represent the description of a hard-sphere model (ionic radii, tolerance factor, and octahedral factors) in classifying perovskites from non-perovskites. The key insight is that, in halides, interactions that govern geometric packing and steric effects are important for classification, in spite of the fact that there were transition metal cations in our training set. However, we anticipate that additional electronic effects, such as crystal-field stabilization energy, might emerge as critical features to accurately describe different octahedral tilt patterns within a perovskite sub-class, which we do not discuss here. Furthermore, the ability to rationally establish decision boundaries and assign uncertainties with predictions and misclassifications makes this approach highly attractive for predictive materials design. We demonstrated this by identifying 40 new ABX3 compounds that show potential for forming stable perovskite structure-type and, to the best of our knowledge, have not been reported previously. A detailed study targeted to assess thermodynamic and dynamical stabilities of these compounds is currently underway.
Author Contributions
GP, PB assembled the halide formability dataset and the feature set used in learning. GP performed the machine learning. All authors analyzed the results and contributed in writing the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer XW and handling Editor declared their shared affiliation, and the handling Editor states that the process nevertheless met the standards of a fair and objective review.
Funding
GP, PB and TL acknowledge support from the Los Alamos National Laboratory (LANL) Laboratory Directed Research and Development (LDRD). Los Alamos National Laboratory is operated by Los Alamos National Security, LLC, for the National Nuclear Security Administration of the (U.S.) Department of Energy under contract DE-AC52-06NA25396.
Supplementary Material
The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/fmats.2016.00019
References
Balachandran, P. V., Theiler, J., Rondinelli, J. M., and Lookman, T. (2015). Materials prediction via classification learning. Sci. Rep. 5, 13285. doi: 10.1038/srep13285
Balachandran, P. V., Xue, D., Theiler, J., Hogden, J., and Lookman, T. (2016). Adaptive strategies for materials design using uncertainties. Sci. Rep. 6, 19660. doi:10.1038/srep19660
Brown, I. D. (1978). Bond valences? A simple structural model for inorganic chemistry. Chem. Soc. Rev. 7, 359. doi:10.1039/CS9780700359
Ceder, G., Hauthier, G., Jain, A., and Ong, S. P. (2011). Recharging lithium battery research with first-principles methods. Mater. Res. Soc. Bull 36, 185. doi:10.1557/mrs.2011.31
Curtarolo, S., Hart, G. L. W., Nardelli, M. B., Mingo, N., Sanvito, S., and Levy, O. (2013). The high-throughput highway to computational materials design. Nat. Mater. 12, 191. doi:10.1038/nmat3568
Curtarolo, S., Setyawan, W., Wang, S., Xue, J., Yang, K., Taylor, R. H., et al. (2012). AFLOWLIB.ORG: a distributed materials properties repository from high-throughput ab initio calculations. Comput. Mater. Sci. 58, 227. doi:10.1016/j.commatsci.2012.02.002
Feng, L., Jiang, L., Zhu, M., Liu, H., Zhou, X., and Li, C. (2008). Formability of ABO3 cubic perovskites. J. Phys. Chem. Solids 69, 967. doi:10.1016/j.jpcs.2007.11.007
Flach, P. (2012). Machine Learning: The Art and Science of Algorithms that Make Sense of Data. Cambridge: Cambridge University Press.
Jain, A., Hautier, G., Moore, C. J., Ong, S. P., Fischer, C. C., Mueller, T., et al. (2011). A high-throughput infrastructure for density functional theory calculations. Comput. Mater. Sci. 50, 2295. doi:10.1016/j.commatsci.2011.02.023
Kafalas, J. A., and Longo, J. M. (1972). High pressure synthesis of (ABX3) (AX)n compounds. J. Solid State Chem. 4, 55. doi:10.1016/0022-4596(72)90132-6
Kim, C., Pilania, G., and Ramprasad, R. (2016). From organized high-throughput data to phenomenological theory using machine learning: the example of dielectric breakdown. Chem. Mater 28, 1304–1311. doi:10.1021/acs.chemmater.5b04109
Körbel, S., Marques, M. A. L., and Botti, S. (2016). Stability and electronic properties of new inorganic perovskites from high-throughput ab initio calculations. J. Mater. Chem. C doi:10.1039/c5tc04172d
Kumar, A., Verma, A. S., and Bhardwaj, S. R. (2008). Prediction of formability in perovskite-type oxides. Open Appl. Phys. J. 1, 11. doi:10.2174/1874183500801010011
Li, C., Lu, X., Ding, W., Feng, L., Gao, Y., and Guo, Z. (2008). Formability of ABX3 (X = F, Cl, Br, I) halide perovskites. Acta Cryst. B 64, 702. doi:10.1107/S0108768108032734
Li, C., Soh, K. C. K., and Wu, P. (2004). Formability of ABO3 perovskites. J. Alloys Compd. 372, 40. doi:10.1016/j.jallcom.2003.10.017
Mannodi-Kanakkithodi, A., Pilania, G., Huan, T. D., Lookman, T., and Ramprasad, R. (2016). Machine learning strategy for accelerated design of polymer dielectrics. Sci. Rep. 6, 20952. doi:10.1038/srep20952
Mooser, E., and Pearson, W. B. (1959). On the crystal chemistry of normal valence compounds. Acta Cryst. 12, 1015. doi:10.1107/S0365110X59002857
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825.
Pilania, G., Balachandran, P. V., Gubernatis, J. E., and Lookman, T. (2015). Classification of ABO3 perovskite solids: a machine learning study. Acta Cryst. B 71, 507. doi:10.1107/S2052520615013979
Pilania, G., Gubernatis, J. E., and Lookman, T. (2015a). Structure classification and melting temperature prediction in AB solids via machine learning. Phys. Rev. B 91, 214302. doi:10.1103/PhysRevB.91.214302
Pilania, G., Gubernatis, J. E., and Lookman, T. (2015b). Classification of octet AB-type binary compounds using dynamical charges: a materials informatics perspective. Sci. Rep. 5, 17504. doi:10.1038/srep17504
Pilania, G., and Lookman, T. (2014). Electronic structure and biaxial strain in RbHgF3 perovskite and hybrid improper ferroelectricity in (Na,Rb)Hg2F6 and (K,Rb)Hg2F6 superlattices. Phys. Rev. B 90, 115121. doi:10.1103/PhysRevB.90.115121
Pilania, G., Mannodi-Kanakkithodi, A., Gubernatis, J. E., Ramprasad, R., and Lookman, T. (2016). Machine learning bandgaps of double perovskites dielectrics. Sci. Rep. 6, 19375. doi:10.1038/srep19375
Pilania, G., and Uberuaga, B. P. (2015). Cation ordering and effect of biaxial strain in double perovskite CsRbCaZnCl6. J. Appl. Phys 117, 114103. doi:10.1063/1.4915938
Pilania, G., Wang, C., Jiang, X., Rajasekaran, S., and Ramprasad, R. (2013). Accelerating materials property predictions using machine learning. Sci. Rep. 3, 2810. doi:10.1038/srep02810
Rabe, K. M., Phillips, J. C., Villars, P., and Brown, I. D. (1992). Global multinary structural chemistry of stable quasicrystals, high-TC ferroelectrics, and high-T-c superconductors. Phys. Rev. B 45, 7650. doi:10.1103/PhysRevB.45.7650
Sarukura, N., Murakami, H., Estacio, E., Ono, S. G., El Ouenzerfi, R., Cadatal, M., et al. (2007). Proposed design principle of fluoride-based materials for deep ultraviolet light emitting devices. Opt. Mater. 30, 15. doi:10.1016/j.optmat.2006.11.031
Service, R. F. (2012). Materials scientists look to a data-intensive future. Science 335, 1434. doi:10.1126/science.335.6075.1434
Sharma, V., Wang, C., Lorenzini, R. G., Ma, R., Zhu, Q., Sinkovits, D. W., et al. (2014). Rational design of all organic polymer dielectrics. Nat. Commun. 5, 4845. doi:10.1038/ncomms5845
Tran, T. T., and Halasyamani, P. S. (2014). Effect of SiO2, NaCl, Al2O3, and FeCl3 on phase change behavior of supported and unsupported TiO2. J. Solid State Chem. 210, 213. doi:10.1006/jssc.1993.1282
Computational Materials Repository. (2015). Available at: https://wiki.fysik.dtu.dk/cmr/(Documentation); https://cmr.fysik.dtu.dk/
Materials Project – A Materials Genome Approach. (2015). Available at: http://materialsproject.org/
Yu, L., and Zunger, A. (2012). Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials. Phys. Rev. Lett. 108, 068701. doi:10.1103/PhysRevLett.108.068701
Zhang, F., Mao, Y., Park, T.-J., and Wong, S. S. (2008). Green synthesis and property characterization of single-crystalline perovskite fluoride nanorods. Adv. Funct. Mater. 18, 103. doi:10.1002/adfm.200700655
Zhang, H., Li, N., Li, K., and Xue, D. (2007). Structural stability and formability of ABO3-type perovskite compounds. Acta Cryst. B 63, 812. doi:10.1107/S0108768107046174
Keywords: perovskites, informatics, support vector machines, formability, materials discovery
Citation: Pilania G, Balachandran PV, Kim C and Lookman T (2016) Finding New Perovskite Halides via Machine Learning. Front. Mater. 3:19. doi: 10.3389/fmats.2016.00019
Received: 29 February 2016; Accepted: 06 April 2016;
Published: 26 April 2016
Edited by:
Zhenyu Li, University of Science and Technology of China, ChinaReviewed by:
Xiaojun Wu, University of Science and Technology of China, ChinaLiang Chen, Chinese Academy of Sciences, China
Jun-Wei Luo, Chinese Academy of Sciences, China
Copyright: © 2016 Pilania, Balachandran, Kim and Lookman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ghanshyam Pilania, Z3BpbGFuaWFAbGFubC5nb3Y=
 Ghanshyam Pilania
Ghanshyam Pilania Prasanna V. Balachandran
Prasanna V. Balachandran Chiho Kim
Chiho Kim Turab Lookman
Turab Lookman