A Multiscale Perspective on Misfit Dislocations in Oxide Films

Since misfit dislocations were first conceived by Jan H. van der Merwe in 1949 (Frank and van der Merwe, 1949), their appreciation by the scientific community has evolved from being considered a drawback to being recognized as a challenging opportunity. However, taking full advantage of all their potential sets out issues that, despite being well-established in semiconductor or metals, remain poorly understood in transition metal oxides. In this Perspective contribution we select recent findings on misfit dislocations in La_0.7Sr_0.3MnO₃ under compressive strain to illustrate effects spanning a range of length scales like the coupling between strain and defect chemistry in and around their cores, the impact of kinetics on the morphology of dislocated films, or the subtle sensitivity of oxide properties to dislocation strain fields.

Introduction

Dislocations are linear crystal defects that store their elastic energy at comparatively large distances (several nanometers) from their sub-nanometer core, and therefore can modify the properties of the host material at different length scales. Similarly to ferroic domain walls two decades ago (Catalan et al., 2012), dislocations in transition metal oxides constitute a class of topological defect which is rapidly catching interest owing to their distinct chemical and physical properties. For instance, non-superconducting dislocation cores have been shown to act as efficient pinning centers for the magnetic flux lines in type-II superconductors (Sandiumenge et al., 2000), conducting dislocations have been reported in insulating Ti doped Al₂O₃ and in TiO₂ (Nakamura et al., 2003; Sun R. et al., 2015), ferromagnetic dislocations have been observed in antiferromagnetic NiO (Sugiyama et al., 2013), or dislocations in SrTiO₃ exhibit redox-based resistive switching behavior (Szot et al., 2006; Metlenko et al., 2014; Marrocchelli et al., 2015b). In the latter case, moreover, flexoelectric polarization induced by the strong strain gradients has been recently reported (Gao et al., 2018). Such a rich behavior stems, on the one hand, from a high susceptibility of electronic degrees of freedom to strain, and, particularly at dislocation cores, from a strong coupling between strain and defect chemistry. The ease of formation of oxygen vacancies at the strained core, in turn, results in electrostatic interactions having a strong influence in their structure and properties. Notably, in insulating materials, such accumulation of oxygen vacancies has been shown to promote the formation of vacancy depleted space charge zones that, in turn, modify the properties of the host crystal on length scales ranging from several tens to hundreds of nanometers (Metlenko et al., 2014; Marrocchelli et al., 2015b; Waldow and De Souza, 2016; Adepalli et al., 2017).

Besides such ionic effects, dislocations entail long-range strains that can alter the material's properties within several nanometers around the subnanometric core. Epitaxial thin films provide an ideal playground to investigate such elastic effects through the generation of misfit dislocations (MDs). Repulsive interactions between individual MDs provide a driving force for the formation of self-organized misfit relief patterns at length scales of 10–20 nm, and can be manipulated through an appropriate choice of the substrate and the thickness of the film. Despite this concept has been used to produce strain guided patterned surfaces in semiconductor (Häusler et al., 1996; Shiryaev et al., 1997) and metal (Brune et al., 1998; Lee and Clemens, 2005) systems, to date, its extension to oxide epitaxy has received little interest.

The perspective presented in this work is constructed around recent results on misfit dislocations in the La_0.7Sr_0.3MnO₃/LaAlO₃ (LSMO/LAO) system (Sandiumenge et al., 2016; Santiso et al., 2016; Bagués et al., 2018), providing insightful elements to understand their behavior in a single system at different lengths scales, ranging from the subnanometer core to their impact on the properties of the film surface.

Structure and Defect Chemistry of Misfit Dislocations Cores

MDs are located at the interface bridging two different compounds and therefore their structure and chemical composition is expected to combine both of them. Here, we restrict ourselves to the simplifying situation where both the film and the substrate have the same crystal structure, namely that of ABO₃ perovskites, but with different cuboctahedral (A) and octahedral (B) site compositions. Although the atomic structure of MDs in perovskite systems has been intensively investigated (Ernst et al., 1999), it is not until recently that the detailed core configuration and its associated defect chemistry have been accessed by combining different spectroscopic and imaging techniques using aberration corrected transmission electron microscopy (Chang et al., 2014; Bagués et al., 2018). In fact, MDs do not decorate a sharp boundary between the two compounds: Interfaces are typically affected by cation inter-diffusion within a few unit cells as a response to misfit strain or polar discontinuity effects (Nakagawa et al., 2006; Krishnan et al., 2014), as well as MDs, tend to shift their position toward the softer material (Wu and Weatherly, 2003). This diffusive scenario is, in turn, altered by the dislocation strain field. Particularly, steric effects associated with the formation of oxygen vacancies may play a critical role in the structure and chemistry of dislocations in oxides: Their preferential accumulation at the under-coordinated core can, for instance, cause the dissociation of the Burgers vector (Metlenko et al., 2014); they can, as well, transfer electrons to the d orbitals of neighboring transition metal cations inducing chemical expansion (Aschauer et al., 2013), create electrostatic interactions governing dopant distributions around the core (Sun L. et al., 2015), or generate a net charge around the core (Metlenko et al., 2014; Sun L. et al., 2015; Bagués et al., 2018).

All those effects are captured by the [100] dislocation formed at the interface between LSMO thin films and LAO substrates (Bagués et al., 2018). Figure 1A shows a cross section high resolution high-angle annular dark-field image of the interface viewed along the [100] edge of the (pseudo)cubic structure. MDs, indicated by red arrows, are clearly seen as dark contrasts. The bottom panel is a (010)-Fourier filtered image pointing out the positions of the MDs. As seen on the filtered image, the extra half-plane resides in the substrate to accommodate the −2.3% biaxial compressive mismatch. Elemental concentration profiles determined by energy dispersive x-ray analysis (EDX) showed cation intermixing between LSMO and LAO over 4 and 2 nm for A and B cations, respectively, suggesting that the polar discontinuity existing between LSMO and LAO is screened by chemical intermixing (Bagués et al., 2018).

FIGURE 1

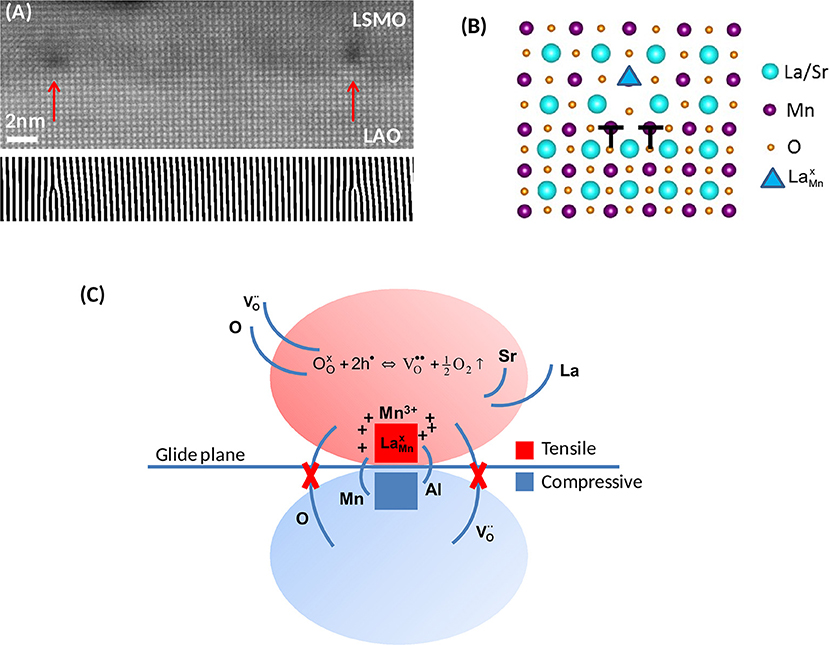
Figure 1. (A) High resolution cross-sectional HAADF image, viewed along the [100] direction, of a 6 nm thick LSMO/LAO film. Vertical arrows indicate the position of misfit dislocations, seen as dark contrasts. Bottom Panel: Fourier filtered image using the (010) frequency to reveal the extra half-planes. (B) Atomic model of the dislocation core. (C) Schematic illustration of the basic mechanisms governing the defect chemistry in the vicinity of the MD core. Tensile and compressive regions are indicated by red and blue colors, respectively. The redox reaction indicated in the tensile region is displaced to the right, favoring the formation of electron donor oxygen vacancies, $V_O^{··}$. Modified from Bagués et al. (2018).

The atomic structure of the MD, shown in Figure 1B, is similar to that experimentally observed for the [100] edge dislocation found in SrTiO₃ bicrystals (Zhang et al., 2002; Du et al., 2015) and other perovskite thin films like SrZrO₃ and BiFeO₃ (Ernst et al., 1999; Lubk et al., 2013), thus suggesting a model configuration for perovskite on perovskite systems. The core is dissociated in two partials, b = 1/2[010] + 1/2[010], corresponding to the two B-site half extra planes, as indicated in the schematics. Atomistic simulations show that this dissociation is driven by the accumulation of oxygen vacancies (Metlenko et al., 2014; Waldow and De Souza, 2016). Therefore, the observation of a dissociated configuration strongly suggests an oxygen deficient core. It can be observed in Figure 1B that the extended core contains an A-site/B-site antiphase boundary on the glide plane. The B-sites next to the antiphase contact, on the film side, exhibit partial occupancy by larger La³⁺ cations, forming ${\text{La}}_{\text{Mn}}^{\text{x}}$ antisite defects, as indicated by a triangle (Kröger-Vink notation is used in this text, taking Mn³⁺ as reference state, Kröger and Vink, 1956). According to the Shannon's ionic radii of La³⁺ and Mn³⁺ in octahedral coordination, 1.032 and 0.645 Å, respectively (Shannon, 1976), such antisite defects yield a huge localized positive dilatational strain of 60%, with an associated shear strain field rapidly decaying as 1/r³ with distance, r, from the defect (Mott and Nabarro, 1940). Therefore, ${\text{La}}_{\text{Mn}}^{\text{x}}$ antisite defects, by themselves, are in principle not expected to fully accommodate the tensile strain above the dislocation glide plane.

From a pure elastic perspective, atomic scale chemical mapping by EDX yields a rather counterintuitive picture of the distribution of ions around the MD core. According to Bagués et al. (2018), there is a clear La enrichment relative to Sr which, comparing the ionic radii of La³⁺ and Sr²⁺ in cuboctahedral coordination, 1.36 and 1.44 Å (Shannon, 1976), would work against the accommodation of the tensile strain above the glide plane. Again counterintuitively, the compressive zone exhibits a preferential substitution of smaller Al³⁺ (ionic radius, 0.535 Å) by larger Mn³⁺ (0.645 Å) cations (Shannon, 1976). Significantly, however, this anomalous behavior is accompanied by a preferential accumulation of oxygen vacancies at the tensile zone. These results contrast with atomistic simulations of the behavior of diluted dopants and oxygen vacancies at edge dislocations in CeO₂, showing clear “size accommodating” and charge compensating tendencies, respectively (Sun L. et al., 2015). In the present case, however, the concentration of divalent Sr cations, 33% of A-sites, is much higher than the doping level employed in the simulations and the chemical behavior of the system very likely cannot be properly described by individual point defect interactions.

According to Marrocchelli et al. (2015a), oxygen vacancies in the perovskite structure can be considered similar in size, or even slightly smaller, to oxide ions. Therefore, their accumulation in the tensile zone, by itself, is expected to have a negligible effect on the accommodation of MD strain. Nevertheless, atomic scale electron energy loss spectroscopy results by Bagués et al. (2018) clearly reveal a spatial correlation between the concentration of oxygen vacancies and the reduction of Mn ions. The point defect reaction describing the reduction process can be expressed as (Poulsen, 2000),

$\begin{array}{rc}{\text{O}}_{\text{O}}^{\text{x}}+{2\text{Mn}}_{\text{Mn}}^{·}\leftrightarrow {\text{V}}_{\text{O}}^{··}+{2\text{Mn}}_{\text{Mn}}^{\text{x}}+\frac{1}{2}{\text{O}}_2\uparrow & (1)\end{array}$

where ${\text{V}}_{\text{O}}^{··}$ are doubly charged oxygen vacancies, and Mn³⁺ is used as the reference state for the host B-site. According to Equation (1), each ${\text{V}}_{\text{O}}^{··}$ leaves two free carriers, that are transferred to the Mn d band (Yamada and Miller, 1973). Therefore, each oxygen vacancy can reduce two neighboring Mn⁴⁺ cations. Now, comparing the ionic radius of the ${\text{Mn}}_{0.7}^{3+}$${\text{Mn}}_{0.3}^{4+}$ “average B-site cation” of the LSMO structure, 0.610 Å, with that of Mn³⁺, 0.645 Å, one finds that the formation of oxygen vacancies is associated with a chemical expansion of ~6% that efficiently contributes to minimize the elastic energy above the glide plane of the MD. In agreement with those considerations, atomistic simulations show a reduction of the oxygen vacancy formation energy in other manganese perovskites under tensile strain (Aschauer et al., 2013).

As schematically illustrated in Figure 1C, in accordance with the discussion above, the driving force governing the overall chemical behavior of the MD can be identified as the decrease in the oxygen vacancy formation energy induced by the tensile strain above the glide plane. This coupling displaces the oxygen vacancy equilibrium reaction indicated in Figure 1C toward the right, thus favoring the reduction of neighboring Mn ions following Equation (1). The unbalance between the rate of Sr diffusion out of the core region and the concentration of ${\text{V}}_{\text{O}}^{··}$ results in a net positive charge in the tensile region, as indicated in the schematics (Bagués et al., 2018). Despite the counterintuitive decrease of the Sr/La ratio is not clearly understood, the concurrent formation of ${\text{La}}_{\text{Mn}}^{\text{x}}$ antisite defects localized on the axial plane, between the two partials, and the chemical expansion implicit in Equation (1), should minimize the elastic energy in the tensile zone. It is worthy to note that since the glide plane separates tensile and compressively strained regions, as a consequence of the selective formation of oxygen vacancies in the tensile zone, at the position of the MD the glide plane becomes a sharp boundary between oxygen deficient and fully oxygenated material.

Long Range Impact of Misfit Dislocations: Surface Patterning

The view of MDs as distinct infinite filamentary phases –infinite relative to the size of the crystal; recall that a dislocation cannot end within a periodic structure (see for instance Hull and Bacon, 2001)- immediately raises the question of whether they could be ideally self-organized into functional nanodevices. When the interface plane coincides with the dislocation glide plane, as the distance between MDs decreases repulsive forces drive their arrangement into ordered interfacial networks (Springholz and Wiesauer, 2002). This is, in fact, a common situation in perovskite epitaxial systems, as exemplified in the preceding section. In the LSMO/LAO case considered above, however, dislocation glide on the interface plane requires the synchronized movement of the two ½[100] partials of the dissociated core. Nevertheless, this circumstance does not appear to hinder much the mobility of the MDs under proper kinetic growth conditions (Sandiumenge, 2017); the standard deviation of the MD spacing distribution (which reflects the degree of order), decreases from 10 nm down to 3 nm when the mean dislocation spacing decreases from 25 to 16 nm (Santiso et al., 2016). These variations take place in a range of film thicknesses comprised between 3.5 and 14 nm, illustrating the possibility to efficiently tune, though not independently, the degree of order and the density of the MD network.

The impact of MDs in oxide heteroepitaxy has been extensively studied in ferroelectric systems, were their strain field has been shown to depress the spontaneous polarization eventually leading to the formation of dead layers (Misirlioglu et al., 2005). Beyond their impact at interfaces, MD networks, also produce surface strain-relief patterns that have been extensively investigated in semiconductor and metal films to generate low-dimensional nanostructures (Häusler et al., 1996; Shiryaev et al., 1997; Brune et al., 1998; Springholz and Wiesauer, 2002; Lee and Clemens, 2005; Zeljkovic et al., 2015). However, despite their interest, MDs have been mostly considered detrimental by the oxide film community. This may be partly due to the fact that strain and MDs are more difficult to control in oxide systems than in semiconductor and metal films (Sandiumenge, 2017). However, the feasibility of extending this concept to perovskite oxide epitaxy has been recently demonstrated in the PbZr_0.2Ti_0.8O₃/SrRuO₃/STO and LSMO/LAO systems (Pandya et al., 2016; Sandiumenge et al., 2016). These studies observe a growth mode transition from two-dimensional layer-by-layer growth to three-dimensional island growth upon the introduction of MDs. The coupling between the surface strain resulting from the introduction of MDs and the morphology of the free surface of the film, is mediated by the surface chemical potential, according to Srolovitz (1989),

$\begin{array}{rc}\mu (x)={\mu }_0+{\gamma }_s\Omega \kappa (x)+\Omega w(x)& (2)\end{array}$

where μ₀ is the chemical potential of the stress free surface, γ_s is the surface energy density, Ω is the volume of a growth unit, κ(x) is the surface curvature, and w(x) is the local surface strain energy density. For a flat surface κ ~ 0 and the variation of the chemical potential relative to the position of a MD is given by Δμ_d(x) = μ(x)–μ_d (μ_d is the chemical potential of a growth unit located above a buried MD). The result is a modulation of the binding energy of growth units with the same periodicity as the MDs. Figure 2A shows Δμ_d(x) for 3.5 (red) and 6 nm (blue) thick films. For the 3.5 nm one, the fluctuation features two minima centered on the MD, corresponding to the maximum misfit relaxation (Sandiumenge et al., 2016). At these points the chemical potential is reduced by 17 meV. This abrupt depression should promote the preferential nucleation of growth units at each side of the dislocation. The lower panel in Figure 2A is a high resolution electron micrograph of a 3.5 nm thick film showing an MD indicated by a white circle. There can be clearly seen two mounds grown at each side of the dislocation, at positions corresponding to the two minima in Δμ_d(x). These mounds give rise to ridges aligned with the MDs, as seen in the atomic force microscopy image corresponding to a 3.5 nm thick film shown in Figure 2B. The height of the ridges becomes kinetically limited as their surface curvature increases due to the competition between the surface energy, γκ(x), and strain energy, w(x), terms in Equation 2 (Yang et al., 2004). As shown by Sandiumenge et al. (2016), see Figure 2A, the amplitude of the Δμ_d(x) fluctuation is rapidly smoothed out as the film thickens and the distance between MDs is reduced. This results in the disappearance of the nanostructure, as observed in the atomic force microscopy image of the 6 nm thick film shown in Figure 2B. Unfortunately, the degree of order of the MD network and the amplitude of the fluctuation in chemical potential follow opposite dependencies on the film thickness: The former is enhanced with increasing thickness (MD density), whereas the later rapidly vanishes as the film surface moves apart from the strain source and the strain field of individual MDs overlap. The balance between both effects is determined by the Burgers vector, the misfit strain and the elastic constants, although the growth kinetics can profoundly alter the equilibrium dislocation configurations. Therefore, a compromise must be found in each specific case.

FIGURE 2

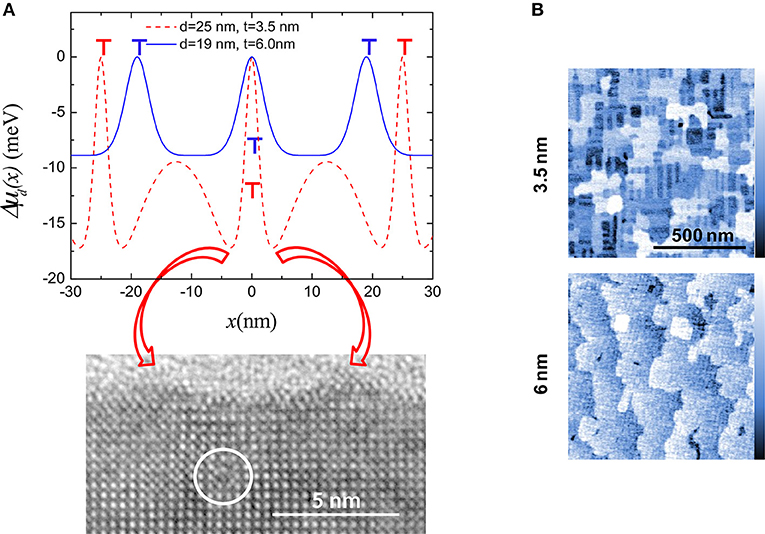
Figure 2. (A) Strain induced modulation of the surface chemical potential relative to the position of the MDs, Δμ_d(x), for different values of the MD spacing, d, and film thickness, t, as indicated. The location of dislocations for each film thickness is indicated by T symbols. Bottom panel: Cross-section high resolution transmission electron micrograph image corresponding to a 3.5 nm thick film, exhibiting a MD (inside the white circle). Two mounds are seen on the film surface, at each side of the MD. Red arrows highlight the correspondence between the minima in Δμ_d(x) and the positions of the mounds. (B) Atomic force microscopy images showing the topography of 3.5 nm (upper panel) and 6 nm (Bottom) thick films. The surface of the 3.5 nm thick film features a nanostructure consisting of ridges aligned with the [100] and [010] directions, and the 6 nm thick film shows flat terraces. The color scale bar corresponds to a full range of 1.5 nm. Modified from Sandiumenge et al. (2016).

Besides such topographic effects, the modulation of the lattice distortion induced by the MD network also causes an increase of the film resistivity along the locus of the MDs (Sandiumenge et al., 2016). This effect persists at larger thicknesses than the topographic instability. This behavior can be well-described by the lateral modulation of the c/a axial ratio, controlling the balance between selective Mn d orbital occupation, in-plane Mn 3d- O 2p orbital overlapping, and antiferromagnetic interactions (Fang et al., 2000).

Concluding Remarks and Future Prospects

The oxide thin film community has devoted, so far, a lot of interest to the investigation of fascinating and conceptually new film-substrate interfacial structures driven by octahedral tilting mechanisms in perovskite systems (Huijben et al., 2017). Whatever their electronic or structural origin, such mechanisms may bypass energetically costly dislocation mechanisms (Sandiumenge et al., 2013; Gazquez et al., 2017). As exemplified by the LSMO system, where the sign of the misfit allows switching between two opposite relaxation mechanisms (Sandiumenge, 2017), MDs in oxides could become a question of choice. Nevertheless, taking full advantage of MDs in oxide films is challenged by the complex relaxation behavior of epitaxial octahedral framework structures. As highlighted in this work, MDs in oxides are much more than an accidental relaxation mechanism: They carry a distinct phase confined at their cores, with strong potential as active functional element, as well as they are associated with long range strains driving their self-organization and the creation of surface nanostructures.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work is dedicated to Prof. Emeritus Jacques Rabier (SFA-Laboratoire Pprime, University of Poitiers) for inspiring and feeding my interest in dislocations when, by the early 1990s, dislocations were nothing to me but just intriguing lines in electron micrographs. This research was funded by the Spanish MINECO through the Severo Ochoa Programme for Centers of Excellence in R&D (SEV-2015-0496) and MAT2015-71664-R.

References

Adepalli, K. K., Yang, J., Maier, J., Tuller, H. L., and Yildiz, B. (2017). Tunable oxygen diffusion and electronic conduction in SrTiO₃ by dislocation-induced space charge fields. Adv. Funct. Mater. 27:1700243. doi: 10.1002/adfm.201700243

CrossRef Full Text | Google Scholar

Aschauer, U., Pfenninger, R., Selbach, S. M., Grande, T., and Spaldin, N. A. (2013). Strain-controlled oxygen vacancy formation and ordering in CaMnO₃. Phys. Rev. B 88:054111. doi: 10.1103/physrevb.88.054111

CrossRef Full Text | Google Scholar

Bagués, N., Santiso, J., Esser, B. D., Williams, R. E. A., McComb, D. W., Konstantinovic, Z., et al. (2018). The misfit dislocation core phase in complex oxide heteroepitaxy. Adv. Funct. Mater. 28:1704437. doi: 10.1002/adfm.201704437

CrossRef Full Text | Google Scholar

Brune, H., Giovannini, M., Bromann, K., and Kern, K. (1998). Self-organized growth of nanostructure arrays on strain-relief patterns. Nature 394, 451–453. doi: 10.1038/28804

CrossRef Full Text | Google Scholar

Catalan, G., Seidel, J., Ramesh, R., and Scott, J. F. (2012). Domain wall nanoelectrics. Revs. Mod. Phys. 84, 119–155. doi: 10.1103/RevModPhys.84.119

CrossRef Full Text | Google Scholar

Chang, C.-P., Chu, M.-W., Jeng, H. T., Cheng, S.-L., Lin, J. G., Yang, J.-R., et al. (2014). Condensation of two-dimensional oxide-interfacial charges into one-dimensional electron chains by the misfit-dislocation strain field. Nat. Commun. 5:3522. doi: 10.1038/ncomms4522

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, H., Jia, C.-L., Houben, L., Metlenko, V., De Souza, R. A., Waser, R., et al. (2015). Atomic structure and chemistry of dislocation cores at low-angle tilt grain boundary in SrTiO₃ bicrystals. Acta Mater. 89, 344–350. doi: 10.1016/j.actamat.2015.02.01

CrossRef Full Text | Google Scholar

Ernst, F., Rečnik, A., Langjahr, P. A., Nellist, P. D., and Rühle, M. (1999). Atomic structure of misfit dislocations in SrZrO₃/SrTiO₃ interfaces. Acta Mater. 47, 183–198. doi: 10.1016/S1359-6454(98)00334-6

CrossRef Full Text | Google Scholar

Fang, Z., Solovyev, I., and Terakura, K. (2000). Phase diagram of tetragonal manganites. Phys. Rev. Lett. 84, 3169–3172. doi: 10.1103/PhysRevLett.84.3169

PubMed Abstract | CrossRef Full Text | Google Scholar

Frank, F. C., and van der Merwe, J. H. (1949). One-dimensional dislocations. I and II. Proc. R. Soc. Lond. A. 198, 205–216, 216–225.

Google Scholar

Gao, P., Yang, S., Ishikawa, R., Li, N., Feng, B., Kumamoto, A., et al. (2018). Atomic-scale measurement of flexoelectric polarization at SrTiO₃ dislocations. Phys. Rev. Lett. 120:267601. doi: 10.1103/physrevlett.120.267601

PubMed Abstract | CrossRef Full Text | Google Scholar

Gazquez, J., Stengel, M., Mishra, R., Scigaj, M., Varela, M., Roldan, M. A., et al. (2017). Competition between polar and nonpolar lattice distortions in oxide quantum wells: new critical thickness at polar interfaces. Phys. Rev. Lett. 119:106102. doi: 10.1103/physrevlett.119.106102

PubMed Abstract | CrossRef Full Text | Google Scholar

Häusler, K., Eberl, K., Noll, F., and Trampert, A. (1996). Strong alignment of self-assembling InP quantum dots. Phys. Rev. B 54, 4913–4918. doi: 10.1103/PhysRevB.54.4913

PubMed Abstract | CrossRef Full Text | Google Scholar

Huijben, M., Koster, G., Liao, Z. L., and Rijnders, G. (2017). Interface-engineered oxygen octahedral coupling in manganite heterostructures. Appl. Phys. Rev. 4:041103. doi: 10.1063/1.4985770

CrossRef Full Text | Google Scholar

Hull, D., and Bacon, D. J. (2001). Introduction to Dislocations. Oxford: Elsevier.

Google Scholar

Krishnan, P. S. S. R., Morozovska, A. N., Eliseev, E. A., Ramasse, Q. M., Kepaptsoglou, D., Liang, W.-I., et al. (2014). Misfit strain driven cation inter-diffusion across an epitaxial multiferroic thin film interface. J. Appl. Phys. 115:054103. doi: 10.1063/1.4862556

CrossRef Full Text | Google Scholar

Kröger, F. A., and Vink, H. J. (1956). “Relations between concentrations of imperfections in crystalline solids” in Solid State Physics, Vol. 3, eds F. Seitz and D. Turnbull (New York, NY: Academic Press), 307–435.

Lee, Y.-W., and Clemens, B. M. (2005). Strong alignment of self-assembling InP quantum dots. Phys. Rev. B 71:245416. doi: 10.1103/PhysRevB.71.245416

CrossRef Full Text

Lubk, A., Rossell, M. D., Seidel, J., Chu, Y. H., Ramesh, R., Hýtch, M. J., et al. (2013). Electromechanical coupling among edge dislocations, domain walls, and nanodomains in BiFeO₃ revealed by unit-cell-wise strain and polarization maps. Nano. Lett. 13, 1410–1415. doi: 10.1021/nl304229k

PubMed Abstract | CrossRef Full Text | Google Scholar

Marrocchelli, D., Perry, N. H., and Bishop, S. R. (2015a). Understanding chemical expansion in perovskite-structured oxides. Phys. Chem. Chem. Phys. 17, 10028–10039. doi: 10.1039/C4CP05885B

PubMed Abstract | CrossRef Full Text | Google Scholar

Marrocchelli, D., Sun, L., and Yildiz, B. (2015b). Dislocations in SrTiO₃: Easy to reduce but not so fast for oxygen transport. J. Am. Chem. Soc. 137, 4735–4748. doi: 10.1021/ja513176u

CrossRef Full Text | Google Scholar

Metlenko, V., Ramadan, A. H. H., Gunkel, F., Du, H., Schraknepper, H., Hoffmann-Eifert, S., et al. (2014). Do dislocations act as atomic autobahns for oxygen in the perovskite oxide SrTiO₃. Nanoscale 6, 12864–12876. doi: 10.1039/c4nr04083j

PubMed Abstract | CrossRef Full Text | Google Scholar

Misirlioglu, I. B., Vasiliev, A. L., Aindow, M., and Alpay, S. P. (2005). Strong degradation of physical properties and formation of a dead-layer in ferroelectric films due to interfacial dislocations. Integr. Ferroelectrics 71, 67–80. doi: 10.1080/10584580590964709

CrossRef Full Text | Google Scholar

Mott, N. F., and Nabarro, F. R. N. (1940). An attempt to estimate the degree of precipitation hardening, with a simple model. Proc. Phys. Soc. 52, 86–89. doi: 10.1088/0959-5309/52/1/312

CrossRef Full Text | Google Scholar

Nakagawa, N., Hwang, H. Y., and Muller, D. A. (2006). Why some interfaces cannot be sharp. Nat. Mater. 5, 204–209. doi: 10.1038/nmat1569

CrossRef Full Text | Google Scholar

Nakamura, A., Matsunaga, K., Tohma, J., Yamamoto, T., and Ikuhara, Y. (2003). Conducting nanowires in insulating ceramics. Nat. Mater. 2, 453–456. doi: 10.1038/nmat920

PubMed Abstract | CrossRef Full Text | Google Scholar

Pandya, S., Damodaran, A. R., Xu, R., Hsu, S.-L., Agar, J. C., and Martin, L. W. (2016). Strain-induced growth instability and nanoscale surface patterning in perovskite thin films. Sci. Rep. 6:26075. doi: 10.1038/srep26075

PubMed Abstract | CrossRef Full Text | Google Scholar

Poulsen, F. W. (2000). Defect chemistry modelling of oxygen-stoichiometry, vacancy concentrations, and conductivity of (La_1−xSr_x)_yMnO_3±δ. Sol. State Ionics 129, 145–162. doi: 10.1016/S0167-2738(99)00322-7

CrossRef Full Text | Google Scholar

Sandiumenge, F. (2017). Strain landscapes and self-organization of free surfaces in complex oxide epitaxy. J. Mater. Res. 32, 3958–3976. doi: 10.1557/jmr.2017.317

CrossRef Full Text | Google Scholar

Sandiumenge, F., Bagués, N., Santiso, J., Paradinas, M., Pomar, A., Konstantinovic, Z., et al. (2016). Misfit dislocation guided topographic and conduction patterning in complex oxide epitaxial thin films. Adv. Mater. Interfaces 3:1600106. doi: 10.1002/admi.201600106

CrossRef Full Text | Google Scholar

Sandiumenge, F., Puig, T., Rabier, J., Plain, J., and Obradors, X. (2000). Optimization of flux pinning in bulk melt textured 1-2-3 superconductors: bringing dislocations under control. Adv. Mater. 12, 375–381. doi: 10.1002/(SICI)1521-4095(200003)12:5<375::AID-ADMA375>3.0.CO;2-9

CrossRef Full Text | Google Scholar

Sandiumenge, F., Santiso, J., Balcells, L.l., Konstantinovic, Z., Roqueta, J., Pomar, A., et al. (2013). Competing misfit relaxation mechanisms in epitaxial correlated oxides. Phys. Rev. Lett. 110:107206. doi: 10.1103/physrevlett.110.107206

PubMed Abstract | CrossRef Full Text | Google Scholar

Santiso, J., Roqueta, J., Bagués, N., Frontera, C., Konstantinovic, Z., Lu, Q., et al. (2016). Self-arranged misfit dislocation network formation upon strain release in La_0.7Sr_0.3MnO₃/LaAlO₃(100) epitaxial films under compressive strain. ACS Appl. Mater. Interfaces 8, 16823–16832. doi: 10.1021/acsami.6b02896

CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomie distances in halides and chaleogenides. Acta Cryst. A 32, 751–767. doi: 10.1107/S0567739476001551

CrossRef Full Text | Google Scholar

Shiryaev, S. Y., Jensen, F., Hansen, J. L., Petersen, J. W., and Larsen, A. N. (1997). Nanoscale structuring by misfit dislocations in Si_1−xGe_x/Si epitaxial systems. Phys. Rev. Lett. 78, 503–506. doi: 10.1103/PhysRevLett.78.503

CrossRef Full Text | Google Scholar

Springholz, G., and Wiesauer, K. (2002). Nanoscale dislocation patterning in PbTe/PbSe(001) lattice-mismatched heteroepitaxy. Phys. Rev. Lett. 88:015507. doi: 10.1103/physrevlett.88.015507

PubMed Abstract | CrossRef Full Text | Google Scholar

Srolovitz, J. D. (1989). On the stability of surfaces of stressed solids. Acta Metall. 37, 621–625. doi: 10.1016/0001-6160(89)90246-0

CrossRef Full Text | Google Scholar

Sugiyama, I., Shibata, N., Wang, Z., Kobayashi, S., Yamamoto, T., and Ikuhara, Y. (2013). Ferromagnetic dislocations in antiferromagnetic NiO. Nat. Nanotechnol. 8, 266–270. doi: 10.1038/nnano.2013.45

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, L., Marrocchelli, D., and Yildiz, B. (2015). Edge dislocation slows down oxide ion diffusion in doped CeO₂ by segregation of charged defects. Nat. Commun. 6:6294. doi: 10.1038/ncomms7294

CrossRef Full Text | Google Scholar

Sun, R., Wang, Z., Shibata, N., and Ikuhara, Y. (2015). A dislocation core in titanium dioxide and its electronic structure. RSC Adv. 5, 18506–18510. doi: 10.1039/C4RA15278F

CrossRef Full Text | Google Scholar

Szot, K., Speier, W., Bihlmayer, G., and Wasser, R. (2006). Switching the electrical resistance of individual dislocations in single-crystalline SrTiO₃. Nat. Mater. 5, 312–320. doi: 10.1038/nmat1614

PubMed Abstract | CrossRef Full Text | Google Scholar

Waldow, S. P., and De Souza, R. A. (2016). Computational study of oxygen diffusion along a[100] dislocations in the perovskite oxide SrTiO₃. ACS Appl. Mater. Interfaces 8, 12246–12256. doi: 10.1021/acsami.5b12574

CrossRef Full Text | Google Scholar

Wu, X., and Weatherly, G. C. (2003). Equilibrium position of misfit dislocations in thin epitaxial films. Semicond. Sci. Technol. 18, 307–311. doi: 10.1088/0268-1242/18/4/320

CrossRef Full Text | Google Scholar

Yamada, H., and Miller, G. R. (1973). Point defects in reduced strontium titanate. J. Solid State Chem. 6, 169–177. doi: 10.1016/0022-4596(73)90216-8

CrossRef Full Text | Google Scholar

Yang, B., Liu, F., and Lagally, M. G. (2004). Local strain-mediated chemical potential control of quantum dot self-organization in heteroepitaxy. Phys. Rev. Lett. 92:025502. doi: 10.1103/physrevlett.92.025502

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeljkovic, I., Walkup, D., Assaf, B. A., Scipioni, K. L., Sankar, R., Chou, F., et al. (2015). Strain engineering Dirac surface states in heteroepitaxial topological crystalline insulator thin films. Nat. Nanotech. 10, 849–853. doi: 10.1038/nnano.2015.177

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Sigle, W., and Rühle, M. (2002). Atomic and electronic characterization of the a[100] dislocation core in SrTiO₃. Phys. Rev. B 66:094108. doi: 10.1103/PhysRevB.66.094108

CrossRef Full Text | Google Scholar