- 1BitWrex, LLC, Morton, IL, United States
- 2Department of Bioengineering and Therapeutic Sciences, UCSF, San Francisco, CA, United States
- 3Lawrence Berkeley National Laboratory, Molecular Foundry, Berkeley, CA, United States
Observations in crystal growth and assembly from recent in situ methods suggest alternative, non-classical crystallization pathways play an important role in the determination of the micro- and meso- structures in crystalline systems. These processes display parallels that cross-cut multiple disciplines investigating crystallization across four orders of magnitude in size scales and widely differing environments, hinting that alternative crystal growth pathways may be a fundamental scheme in natural crystal formation. Using a system of short-range attractive microbeads, we demonstrate that the addition of a small concentration of sub-species incommensurate with the lattice spacing of the dominant species results in a stark change in crystal size and morphology. These changes are attributed to the presence of fleeting, amorphous-like configurations of beads that ultimately change the melting and growth dynamics in preferred directions. From these real-time observations, we hypothesize the amorphous mineral precursors present in biological mineralized tissues undergo similar non-classical crystallization processes resulting in the complex structures found in biomineralization.
Introduction
Functional biological materials possess a myriad of intricate architectures and material properties, brought about by similarly diverse and complex formation processes (Coelfen and Antonietti, 2008; Noorduin et al., 2013). Biology has adapted mechanisms to sequester and organize local environments to provide the conditions necessary for growth of these materials while the organism exists in a global environment unsuited for growth or development of these materials. Local environments have shown to be controlled in numerous ways, such as regulation of pH, material concentration, protein concentration, and cellular density (Fritz et al., 1994; Aizenberg, 2004; Seto et al., 2004; Dunlop and Fratzl, 2010; Schenk et al., 2012; Seto, 2012; Rao et al., 2017). For example, organic scaffolds can template inorganic mineral components to create hierarchical composites such as teeth, sea shells, and bones (Lowenstam, 1981; Ashby et al., 1995; Weiner and Wagner, 1998; Fratzl and Weinkamer, 2007; Huang et al., 2019). Crystallization plays an essential role in the development of these materials, though the exact physical processes governing this process are not well understood. However, there is intense interest in these fundamental mechanisms (Gasser, 2009; Dalmaschio et al., 2010; Vekilov, 2010; Weiner and Addadi, 2011; Vekilov and Vorontsova, 2014), and the results of recent studies have produced valuable insights that may enable better understanding of these processes. Important among these insights is that classical nucleation and crystal growth paradigms cannot sufficiently explain the existence of certain phases, structures, or properties of various materials developed in solution, many of which are found in biological materials. Thus, alternative pathways for the structure and growth of these crystalline materials must be considered (Auer and Frenkel, 2001; Filion et al., 2010).
Many of these crystallization processes relevant to formation and structuring in biological materials can now be studied at the single-particle level even at the nanoscale in situ due to advances in computational and experimental methods. Thus, a growing body of evidence showing the importance of non-classical nucleation and growth mechanisms utilizing intermediate, metastable or kinetically-determined states can arise that considerably alter the resulting crystal growth (DeYoreo and Vekilov, 2003; Ivanov et al., 2014; Deyoreo et al., 2015). For example, crystal growth assisted by structured pre-crystalline states (Gebauer et al., 2008; Dey et al., 2010; Demichelis et al., 2011), nucleation from metastable phases (Chung et al., 2009; Washington et al., 2012; Baumgartner et al., 2013; Maes et al., 2015), oriented attachment of crystallites (Banfield et al., 2000; Li et al., 2012; Nielsen et al., 2014), and growth emerging out of amorphous phases (Weiss et al., 2002; Politi et al., 2004; Killian et al., 2009; Savage and Dinsmore, 2009; Mahamid et al., 2010; Lechner et al., 2011; Salvalaglio et al., 2014; Ma et al., 2017; Pendola et al., 2018) have all been shown to alter growth in non-trivial ways, often resulting in complex structure formation that appear to defy the evolution of the system toward its ultimate lowest energy configuration. Moreover, these types of alternative growth mechanisms have been suggested in systems with widely different environmental conditions, from biological context such as protein crystal nucleation (Vekilov and Vorontsova, 2014), calcite growth (Weiss et al., 2002; Politi et al., 2004; Killian et al., 2009; Seto et al., 2012), tissue mineralization (Wang et al., 2012; Weaver et al., 2012; Tao et al., 2019), magnetite nucleation and growth (Kuhrts et al., 2019; Mirabello et al., 2019; Rawlings et al., 2019), as well as inorganic contexts like cadmium selenide quantum dot growth (Washington et al., 2012), iron oxide growth (Banfield et al., 2000; Baumgartner et al., 2013; Dideriksen et al., 2015), and colloidal microparticle crystallization (Savage et al., 2006; Savage and Dinsmore, 2009), just to name a few examples. The vast range of systems exhibiting these behaviors is paralleled by the span of the size scales of the crystallizing components, from the micro to the atomic scale.
Looking at tissue mineralization in particular, intermediate mineral phases in mineralization have been shown to exist and form metastable assemblies that eventually undergo a transition to high crystallinity over time (Mahamid et al., 2010; Seto et al., 2013, 2014). Several groups have shown that interactions with these intermediate phases drive mineralization along diverse paths (Teng et al., 1998; De Yoreo et al., 2015; Mass et al., 2017; Zhou et al., 2019). The presence of these mineralization precursors across such a diverse range of systems implies that there are underlying universal mechanisms at play (Figure 1). From previous work, specific macromolecules are known in nature to interact with minerals and form metastable phases as well as select specific crystalline polymorphs and form unique bulk crystalline arrangements (Zou et al., 2017) as measured by select in situ techniques such as Raman, electron microscopy and X-ray scattering methods (Figure 1). In perturbing such organic-inorganic interactions through physiochemical and microfluidic methods, it can be shown that local ion supersaturation can be altered to drive mineralization along specific mineral-organic assemblies (Wang et al., 2012; Seto et al., 2014). The characteristics of these assemblies are crucial in changing the local chemical environments as they stabilize/destabilize neighboring assemblies (Noorduin et al., 2009). Thus, neighboring non-crystalline assemblies have an indirect effect on nucleation, crystal growth mechanisms, and subsequently, final structure. By delineating the basic components and parameters (both thermodynamic and kinetic) that drive some of these crystallization processes, an improved understanding of nucleation and crystal growth events can be updated in the context of recent observations with advanced methods.
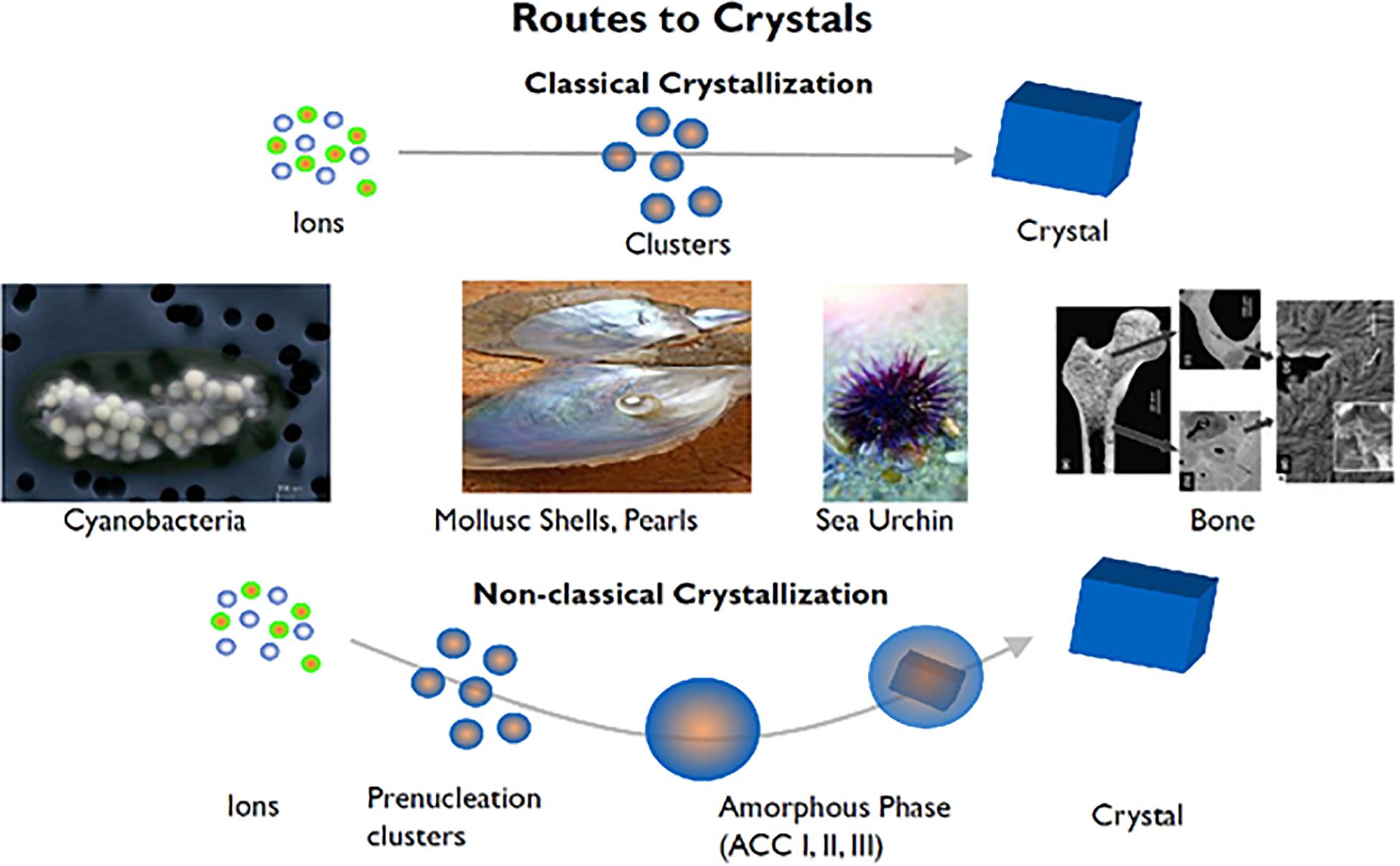
Figure 1. Biological crystallization of diverse mineralized tissues ranging from sea urchin spines to bones and teeth demonstrate a non-classical crystallization pathway. From calcium carbonate (CaCO3) to hydroxyapatite (Ca10(PO4)6(OH)), these divergent mineralization systems have been found to contain intermediates mineral phases not explained by classical crystallization theories. Adapted from Coelfen and Antonietti (2008) with permission from John Wiley and Sons.
In the case of biomineralization, specialized cells lay the groundwork for the mineralized tissue by secreting an organic scaffold that serves as a template for crystal growth, regardless of mineral type (Politi et al., 2004; Seto et al., 2004; Jee et al., 2010; Gong et al., 2012; Cho et al., 2016; de Melo Pereira and Habibovic, 2018). Using the developing sea urchin larval spine as an example organism, we extracted the proteinaceous extracellular matrix and performed remineralization to determine the roles of constituent proteins in the mineralization of the highly crystalline larval spicule. Of specific interest is understanding the organization and the specific components involved in stabilization of an amorphous mineral precursor phase in the growing spicule. As shown in Figure 2, physio-chemical selective domains of these scaffolds initially bind directly to nascent intermediate phases and amorphous precursors to create localized layer-by-layer arrangements of mineral on/within an organic layer. The mineral precursors in this case are promoted and cover an organic layer in order to start an initial epitaxial growth process (Figures 2B,C,E,F). Eventually, this isotropic epitaxy of stabilized mineral precursors and their organic counterparts fill voids and spaces not already occupied (Figures 2A,D). Through this biological control of mineral precursors, subsequent assemblies are arranged such that crystallinity and organization of the organic and mineral constituents in the forming mineralized material are highly regulated.

Figure 2. High spatial and temporal arrangement of organic and mineral islands of CaCO3 intermediate phases of crystallization found in the developing sea urchin larval spine. (A–C) Transmission electron micrographs (TEM) of CaCO3 remineralized proteinaceous scaffolds from sea urchin spine at increasing magnification insets in panels (B,C) show diffraction patterns of crystalline and amorphous regions, respectively. (D–F) A schematic diagram demonstrates a biphasic behavior found in protein mediated biological CaCO3 mineralization systems among the organic and mineral components. Subsequent panels are corresponding higher magnification zoom-ins of the previous panel.
To simplify these interactions and crystalline states found in biological crystallization, we utilize a model system of attractive polystyrene microbeads to focus on the interactions of the mineral phases involved in the early formation processes in mineralized tissues. With the ability to fine-tune the strength of the interaction between microspheres, we can investigate crystal nucleation, growth, and melting with single-particle precision. This technique is well-suited for investigating the effects of phenomena that occur on short timescales or within rare assemblies, because the individual particles can be imaged in real-time (Crocker and Grier, 1996; Larsen and Grier, 1996; Ganapathy et al., 2010; Zeravcic et al., 2014; Mergo, 2017). Through use of this system, assembly and dissociation kinetics can be observed without the added complexity of material properties or solution chemistry, allowing us to relate the effects of kinetics to the final crystal state on the single-particle scale. These direct observations enable for the investigation of events immediately before and after nucleation as well as during crystal growth in order to observe intermediate and “exotic” states altering particle dynamics that are difficult to observe on smaller scales and only now becoming noticed as important for driving growth along specific pathways (Gebauer et al., 2008; Dey et al., 2010; Picker et al., 2017). Of specific interest are questions related to amorphous precursors, neighboring crystal domains, and their effects on the resulting material structure as observed by previous work in biological materials and systems (Aizenberg, 2004; Politi et al., 2004; Munch et al., 2008; Meyers et al., 2013; Fischer et al., 2017; Tao et al., 2019). Similar model systems of attractive microbeads have revealed that island formation, step-edge barriers (Ganapathy et al., 2010), and even multi-layer growth on heavily strained substrates (Lechner et al., 2011; Savage et al., 2013) arise even when the length scale of the interparticle interaction is far shorter than a particle radius. In all these cases, the particles’ dynamics are slowed via interactions with their neighbors, creating a dynamic analog to structures often attributed to the influence of a particle’s next-nearest-neighbors. The ability to identify individual particles allows us the ability to measure changes to crystal morphology via controlled variation of the microbead population itself (i.e., slight variations in bead population like: 100% small beads, 0% large beads or 90% small beads, 10% large beads, lead to drastic changes in morphology)—perturbations that are prevalent in the formation of biological tissues.
In this microbead system, we observe the evolution of a bidisperse quasi-2D colloidal system during crystal nucleation, growth, and coarsening. In a monodisperse system, crystallization and growth occur in a manner consistent with prior observations representative of that which is expected of particles with short-range attractive interactions (Dinsmore et al., 1997; Dullens et al., 2006; Palberg, 2014). In our bidisperse system consisting of microbeads of two different diameters, crystal growth results in a fundamentally different final morphology. During growth, crystals of the more numerous particle species slows and reverses while a second layer nucleates and grows on most islands. The intermixing of this secondary species with the primary species in the regions between crystal islands, before eventual separation into crystals of similar species, determines the time scales over which they can act as either promoters of crystallization or intermediate phase stabilizers—corresponding to natural interactions of proteins and metals found in the mineralization of sea urchin larval spicule.
We can not only observe sequences of events as a function time, but also can quantify the energetic states found in certain configurations of bead assemblies. This uniquely enables an opportunity to fill in gaps left behind by Ostwald’s theory on classical nucleation as these diverse states form (Ostwald, 1897). These states include the immediate events after nucleation processes when a nucleate reaches a specific size, classical nucleation theory states that the nucleate continues to grow larger from the nucleated state, however, it does not reconcile observations from in situ cryo-Transmission Electron Microscopy (TEM) and X-ray studies that demonstrate that neighboring nucleates can also predominantly shrink, divide, and merge at the sake of growing nucleates (Noorduin et al., 2009; Nielsen et al., 2014; Smeets et al., 2015; Zhou et al., 2019). Recent experiments using in situ TEM of iron-palladium composite nanoparticles composed of only 10s of atoms to seed nucleation and observe crystallization processes (Zhou et al., 2019) while in dissolution experiments with glucose isomerase crystallization, the density of mesoscopic clusters are found to control the rate of nucleation (Sleutel and Van Driessche, 2014). Like the microbeads, these nanoparticles and protein crystals show intermediate states that are not explainable in the framework of classical nucleation theory. We show a system that can concisely describe inter-bead interactions on a time scale that is manipulatable as well as containing enough accuracy to attribute kinetic and thermodynamic parameters in order to expand on recent findings of non-classical nucleation behaviors occurring in nucleation and crystallization processes on a non-infinite time-scale.
With these observations, we can begin to characterize the configuration states of rare physical states along the crystallization pathway (i.e., prenucleation and intermediate phases) recently observed with in situ techniques at the molecular level (Gebauer et al., 2008; Mahamid et al., 2010; Demichelis et al., 2011; Habraken et al., 2013; Hedges and Whitelam, 2013; Zou et al., 2017). It is also noteworthy that these observations can detail how nascent states develop and translate into the final microstructural configurations in the mineralized tissue over time despite possessing the same assumed final configurations on an infinite timescale. Although these mixed states are not stable, their presence creates a long-lasting effect on the final structures of these biomineralized materials as found in nature. This improved understanding about nucleation and crystallization processes involved in the growth and development of mineralized tissues over multiple scales not only provides a window how biological regulation and control can take root at tissue formation, but encourages inspiration to search for novel approaches that utilize these biological strategies in creating synthetic, bulk functional crystalline materials with tunable materials properties and structures.
Materials and Methods
Remineralization of Sea Urchin Larval Spine
Organic extracellular matrices (ECM) were precipitated from demineralized sea urchin larval spines collected after 48 h of fertilization. The ECM were resuspended in ddH2O and aliquoted onto copper TEM grids (Quantifoil, Ted Pella, Inc.). Supersaturated solutions of 10 mM CaCl2 and 10 mM Na2CO3 and 10 mM NaHCO3 were added to initiate remineralization as described elsewhere (Seto et al., 2013). A TEM (Libra 120, Zeiss SMT) examined the remineralized structures after subsequent ddH2O washes and air-drying.
Bead-Bead Interactions
The solvent used in these experiments consisted of 2 mM NaCl in H2O (Millipore). The non-ionic surfactant hexaethylene glycol monododecyl ether (C12E6), 2.5 mM, was added to induce an attraction between microparticles via depletion and was gently shaken until the surfactant was dissolved. Colloidal microspheres were introduced by adding an additional 2% of sample volume of polystyrene microbeads suspended in water. Bidisperse samples were prepared using a mixture of polystyrene microbeads with radii of rl = 0.6 and rs = 0.5 μm and less than 4% size polydispersity, mixed 1:10 by volume, both drawn from stock solutions of 8% solids by volume from Sigma Aldrich. Monodisperse samples used as a control were prepared using the 0.5 μm spheres.
Samples were pipetted into glass chambers that had been cleaned with a strong base and rinsed with methanol and deionized (DI) water. The chambers were sealed and loaded onto an inverted optical microscope. Because of the temperature sensitivity of the depletant, the microscope was thermally isolated from its surroundings using an extruded polystyrene box 5 cm in thickness (Owens Corning). The target temperature of the sample was controlled using two PID heating elements placed above and below the sample. Colloids sedimented for about 12 h at 22°C before undergoing a temperature ramp of+0.1°C every 30 min until failed nucleation events were observed. The temperature ramp was halted, and images of the sample were captured at one frame per minute for 78 h.
Particle locations were extracted from the video data using custom software based on previously developed particle tracking methods (Seto et al., 2014). Significant effort went into implementing additional segmentation and featuring algorithms, as well as manual checks to account for optical artifacts that arise from setting the focal plane at the second layer (Mahamid et al., 2010).
Free Energy Computation
A heatmap of the bond energy states of the microbeads shows the energy landscape presented to small particles due to the presence of particles on the glass substrate. This is computed by generating two sparse binary matrices, one for each particle size, marking the pixels containing a particle center-of-mass. The images are convolved with a thin annulus representing the extent of the depletion interaction at the height of the crystals’ second layer and scaled by the relative bond strength of the small-small and large-small bonds. The images are then superimposed and summed, resulting in a heatmap depicting the bond energy for a small test particle placed at the corresponding location.
Results
We observe that monodisperse solutions form single layer islands that display previously observed growth behaviors (Dinsmore et al., 1997; Savage and Dinsmore, 2009). Remarkably, bidisperse samples form crystals consisting of two full layers of small particles in the same time span. A characteristic image of the crystals formed at the end of the experiments on the monodisperse and bidisperse samples are shown in Figures 3A,B, respectively. Microbeads that reside on the glass substrate of the sample chamber appear as black circles, while microbeads at the height of the top layer appear white. To illustrate the evolution of the bilayer crystal morphology, we display a time lapse image of the bidisperse sample in the four panels that make up Figure 3C. Within the first 400 min, the sample transitions from a quasi-2D gas composed of mixed large and small particles to a gas crystal coexistence of small particles and a gas of large particles. The large particles are excluded from the solid phase of small particles and can be seen near the crystal edges. Rather than continuing to grow and coarsen, the crystal islands melt from their periphery while a second layer nucleates and grows on a subset of the islands. This simultaneous melting of the bottom layer and growth of the top layer continues until all crystal islands have either evaporated or have grown two full layers of small particles.

Figure 3. Characteristic images of crystallizing mixtures of attractive colloidal hard spheres. Dark particles reside on the glass sample chamber. White particles are in focus, about 1 μm above the black particles. Crystals formed from panel (A) monodisperse and (B–F) bidisperse mixtures show distinctly different “final” morphologies, 20 h after initial nucleation. The monodisperse sample forms monolayer crystals, while the bidisperse sample forms bilayer crystals of small particles. To illustrate the formation of bilayer crystals in the bidisperse sample, we show one image every 400 min (scale bar = 10 μm). (C) At 0 min, the system is a gas of bidisperse particles (scale bar = 10 μm). (D) After 400 min, the nucleation and growth of the monolayer crystals of small particles has completed, with the larger particles displaced to the periphery of the islands. In addition, we observe the nucleation and growth of a second crystal layer as indicated by the white particles (scale bar = 10 μm). (E) The top layers continue to grow through 800 min, while the exposed monolayer regions shrink. The large particles have formed monolayers of their own species at the crystal edges (scale bar = 10 μm). (F) The final panel shows the final configuration of the system after 1200 min. We see that all islands throughout the sample chamber consist of two full layers (scale bar = 10 μm). Furthermore, we find that the largest crystal island in the field of view completely melts during the transition to a two-layer system, while the smallest two-layer islands persist.
For clarity, we will refer to the top layer as the second layer, and the bottom as the first layer. To quantify the growth behavior of the two crystalline layers, we measure the total number of particles in the first and second layers of the crystals and plot these in Figure 4. A particle is considered part of a layer if it has at least two neighbors and a bond orientational order parameter ψ6 value greater than 0.8, where ψ6 is defined as | 1/Nj Pk exp(6iθjk)|, Nj is the particle’s total number of nearest neighbors, and θjk is the angle between the particle and its kth neighbor relative to a reference axis (Mergo, 2017).
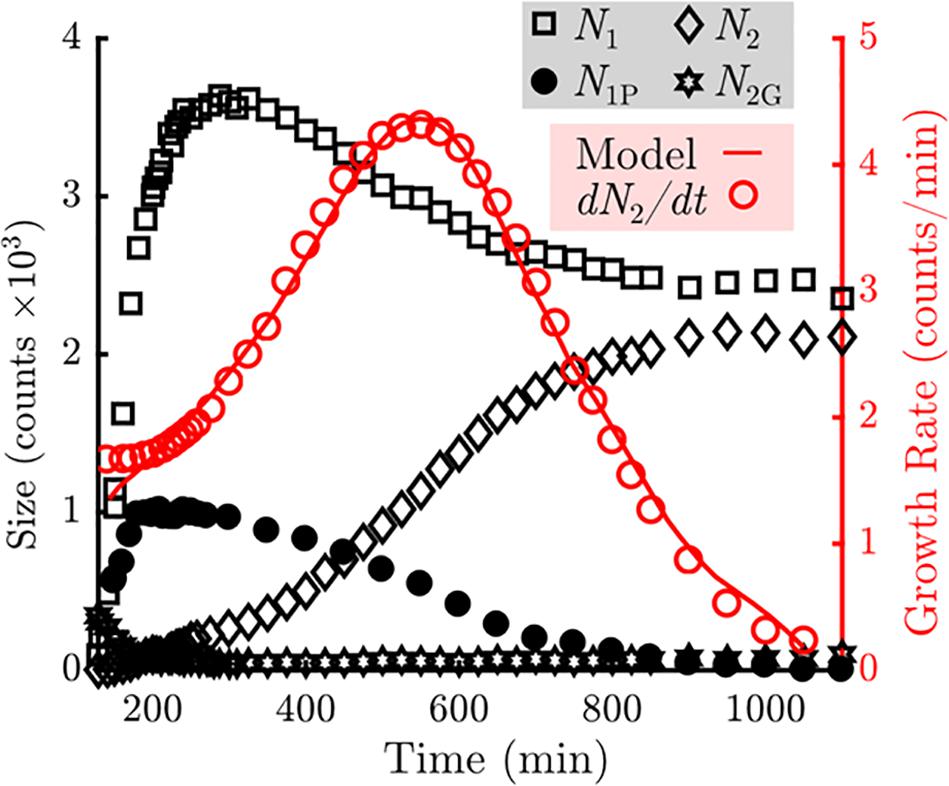
Figure 4. Measurement of the counts of particles in various states in the sample (Left axis, black). The number of particles in the bottom (N1) layers are indicated by the squares. The number of particles in the top (N2) layers are indicated by the diamonds. The number of unblocked perimeter particles (N1P) are indicated by the closed circles. The number of gaseous particles promoted off of the sample floor (N2G) are indicated by the stars. Measurement of the growth rate of the top layer as a function of time is indicated by the open circles (Right axis, red). A fit using the model described in Eq. 1 is overlaid as a solid red line.
We observe that the number of particles incorporated into the first crystal layer, N1 (black squares), rises rapidly during the first 200 min, during which nucleation and subsequent growth of monolayers occur. The number of particles in the first layer peaks at 300 min and then declines by roughly one-third at later times. Meanwhile the number of particles in the second crystal layer, N2 (black diamonds), increases monotonically. The growth rate of the second layer (red open circles) peaks at roughly 550 min and decays to zero when all second layer positions are filled. In addition, we observe that particles are never promoted to the top layer from the interior of an island during the span of the experiment (Figure 3). We also observe that any adatoms atop a monolayer that nucleate or join a second layer edge remain bound to the second layer.
Collectively, these observations indicate that to model the top layer growth, incorporation into the top layer crystal can be treated as a permanent adsorbing state. Thus, the top-layer growth rate should only depend on the number of particles elevated off of the substrate that may resediment onto a crystal island, N2G, and the number of particles at the perimeter of the first layer that are able to take a neighboring position above the first layer. This restriction is critical: in addition to gaining another bond to the crystal, particles on the first layer’s perimeter become geometrically blocked from vertical motion by neighboring second layer particles. It is this “mobile perimeter,” N1P, that is free to participate directly in growth of the second layer. N1P is plotted in Figure 4 and follows a similar trend to N1, while N2G contains about 300 particles at the onset of monolayer nucleation but nearly vanishes by 200 min. This level is held for the majority of the experiment, and slowly increases to about 100 particles at the end of the experiment.
We fit the growth rate data for the top layer with a simple model of the form
where k1 and k2 are fit constants and each term represents the contribution from one of the two pathways described in the previous paragraph. While we assume the simplest relationship for N2G particles to contribute to second-layer growth, the same cannot be true for particles along the mobile perimeter. Once promoted to the top layer, the rate of capture into second layer must depend on the fraction of sites adjacent to the growing layer. N2/N1 represents a rough but useful approximate to this fraction (personal communication with Peter Harrowell). We find a good qualitative fit for the second layer growth rate with k1 = 2 × 10–2min–1 and k1/k2 = 3.1. The results are plotted in Figure 4.
Discussion
We have identified two major contributions to the growth of the bilayer of beads in this system. The initial top-layer growth is heavily influenced by the resedimenting gas (N2G), above the plane of the bottom layer particles. During this time, there are no attachment sites for particles promoted onto the top layer, and the number of perimeter particles is small due to the relatively small number of crystals and crystal sizes. The elevated gas particles contribute to the top layer growth by increasing the particle density, encouraging nucleation of a new layer. After the onset of new layer growth, these particles are captured faster than they are created, causing a decrease in N2G. Promotion from the island edges becomes the dominant contribution to total top-layer growth once N2G is depleted. This does not hold true for every individual island. An island that does not nucleate a second layer after N2G is depleted has a vastly reduced chance to capture an adatom on its surface, as multiple adatoms must converge to nucleate a new layer. As a result, first-layer melting is observed, decreasing the footprint of islands over time. To illustrate this effect, the position of a large monolayer crystal – the largest crystal in the field of view – is highlighted in Figures 3D–F. Adatoms are promoted to the surface of this crystal, where they diffuse and detach without participating in a nucleation event. The island eventually evaporates, along with noticeably fast melting of large monolayer regions, as seen in Supplementary Video S1.
Assuming an island has nucleated a bilayer before N2G has depleted, second-layer growth accelerates as the top layer becomes larger until the top layer begins to stabilize the perimeter. Top layer growth slows as the sizes of the top and bottom layers begin to converge.
It would be reasonable to conclude that the growth model is applicable for both monodisperse and bidisperse samples, as the model has no explicit dependence on particle size. In either system, the lowest energy position that a particle can assume is inside the interior of a multilayer crystal. Thus, the energetically preferred structures are large, 3D, close-packed crystals of microparticles. Nevertheless, only samples containing bidisperse particles exhibit 3D growth during the course of the experiment. The nucleation and growth of these crystals spanned 15 h, while the monodisperse samples showed no second-layer growth after 78 h. This indicates that large particles are enabling an accelerated pathway to the promotion of small particles onto the crystal islands. We hypothesize that this is due to a combination of effects: the observed inability of the large particles to incorporate into crystals of small particles, and the energetic preference of a bond between a large and small particle over the bond between two small particles.
The preference for small particles to bond with larger particles arises from the linear dependence of the depletion interaction’s strength on the diameter of the particles experiencing the depletion force (Asakura and Oosawa, 1954; Lekkerkerker and Tuinier, 2011). Combined with relegation of large particles to the crystal exterior, this leads to intermixing of large and small particles and the formation of short-lived amorphous clusters in the regions unoccupied by crystals. Examples of such arrangements are shown from our experiment in Figure 5A. The energetic differences associated with 2D clusters consisting of small particles versus similar clusters with one large particle replacing the central small particle are shown to scale in Figure 5B. Keeping the number of particles constant, a cluster containing a large particle is energetically favored until the central particle is close-packed and has six nearest neighbors. Interstitial sites involving a large particle also present a stronger bond site as shown schematically in Figure 5C.
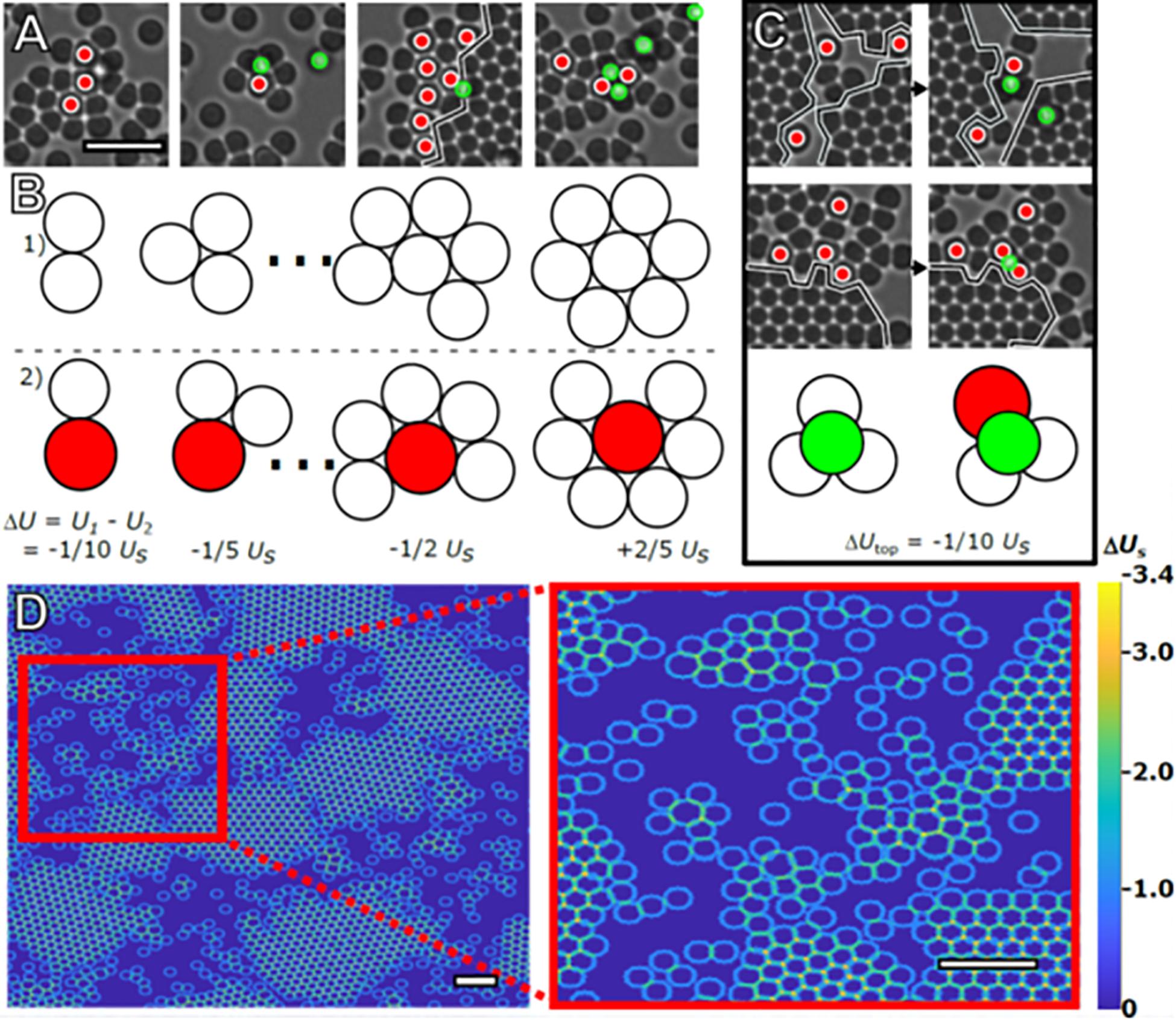
Figure 5. Stabilization of amorphous clusters. Four representative images of the intermixing of large and small particles taken from the same time frame (A). Red circles mark large particles. The black line marks the boundary of crystal islands (scale bar = 4 μm). Using Usas the bond energy between two small particles in contact due to depletion, the effect of the increased bond strength on total cluster bond energy is illustrated in (B). 2D clusters of small particles (Row 1) have a higher total bond energy, U, compared to clusters containing a large particle (Row 2), and until close-packed clusters of seven particles are formed. Particles are drawn to scale. Images of promotion and/or capture events occurring between subsequent frames are displayed in (C). The illustration demonstrates the energetic preference, ΔUtop, for adatoms (green) occupying interstitials formed with large particles vs. those formed with only small particles. These configurations are commonly observed in the experiment, with examples also visible in (A). (D) Heat map demonstrating the different energetic configurations presented to a hypothetical small particle that takes up residence on the second layer due to the presence of particles present on the substrate. Although there are relatively strong bonding locations located at the interstitial sites (orange) and troughs (teal), there are stronger bonding locations in the amorphous areas near large particles (scale bar = 4 μm, inset scale bar = 4 μm).
In the absence of a second crystal layer, these interstitials are the energetically preferred top-layer sites. In addition to being present in amorphous configurations, these interstitials are always formed by large particles at a crystal’s edge, effectively halting monolayer growth while simultaneously presenting advantageous bonding sites for small particles in- and out-of-plane. A particle at a preferred site may take up residence on the monolayer surface but will eventually leave the crystal if it does not participate in a nucleation event. Thus, the second layer growth depends on the prior nucleation of the layer. Once a second layer has formed on the island, the lowest energy sites are always interstitial sites that border a second layer.
Given these energetic arguments, we hypothesize that the mechanism by which large particles accelerate promotion of particles onto crystal islands is intricately related to their role in the formation of amorphous clusters of particles. In a true 2D system, particles in these mixed regions of neighbors and crystal interfaces have no means to reduce their free energy by rearrangement. In our quasi-2D system, small particles have access to a unique option: promotion off of the substrate. Promoted particles retain contact with the strongly interacting large particles as well as any surrounding small particles. In this model, the promotion is driven by the exchange of a strained or frustrated interfacial environment on the lower layer with a less constrained environment on the upper layer. Once promoted, the presence of a surface particle atop this interface constrains any further local promotion until the particle eventually moves away, allowing the interface to participate in another promotion. Once promoted, these particles are elevated gas particles, which were the drivers of initial top-layer nucleation in our experiment. The overall effect of the large particles is to catalyze second-layer growth by enabling the formation of temporary low-energy sites that cannot form in a monodisperse system, while also geometrically inhibiting crystal growth of the smaller particle species, forcing the system to evolve along a different pathway.
When these interactions between bidisperse particles are allowed an infinite amount of time to react, we will observe complete phase separation between the large and small particles as homogenous bonding (between large-on-large and small-on-small particles) begins to occur more frequently. While heterogeneous bonding is common, the presence of incommensurate particles at crystal boundaries inhibits growth at nearby lattice positions while also restricting the ability of compatible particles to diffuse away from the growing crystal. In biological systems, the amorphous and intermediate phase assemblies are often stabilized by an accompanying organic component at the interface and energetically stabilized, with the ultimate effect of “jamming” the pathway to initiate and complete phase separation. In the case of bacterial S layer formation, the nucleation and growth of carbonate minerals on organic template surfaces is widespread, such that at the subsurface organic constituents directly promote carbonate mineralization through an amorphous transition (Chung et al., 2010). All of these organic mediated interactions are short ranged and provide local stability to maximize the energy input and material output ratio. We observe these interactions with an organic component in the formation of mollusk shells where compartmentalization of these assemblies is partitioned away from the larger milieu of mineral particles. In sea urchin larval spicules, a similar sequestration route occurs within a syncytial membrane that enables for local regulation for tissue growth (Seto et al., 2004; Killian et al., 2009). A similar parallel with hydroxyapatite mineral is found with the periosteum in bone in the formation and growth of bone tissue (Weiner and Wagner, 1998; Fratzl and Weinkamer, 2007). It is interesting to note, all the organic interacting components in all these biomineralization cases have similar structural effects and chemical characteristics, but are very different in amino acid sequence and kinetic behaviors when compared independently. Unlike the bead experiments, none of the mineralized tissues formed from intermediate phases occur in a “clean, non-interacting” chamber but within biological environments that skew the pathways of mineralized tissue formation and growth. This makes it exceedingly difficult to ascertain underlying causes for growth pathway selection, especially when structure formation may depend on rare but important events.
Further experiments altering the size ratios and concentration of these secondary particles should determine the parameter space where such mechanisms most strongly alter the crystallization pathways. Additionally, tailoring future experiments to focus on the various growth regimes we have identified in this work would enable identification and better characterization of the various mechanisms at play. During the onset of accelerated second-layer growth, high frame-rate imaging of the interface between amorphous clusters and the crystal edge would elucidate mechanisms for particle detachment and promotion to the second layer via the types of intermediary structures seen in Figure 5, providing direct measurement of interfacial fluctuations and rearrangements occurring in these regions. Similar imaging techniques could be used to measure the evolution of the free energy of amorphous clusters in these bidisperse, attractive colloidal systems based on analysis methods outlined in Dullens et al. (2006). In addition, using total internal reflection microscopy or scanning probe methods it should be possible to identify the direct effects of the large particles on the detachment of small particles from the substrate (Ganapathy et al., 2010; Chen et al., 2019). We anticipate that the lessons learned by extensive study of these colloidal systems will ultimately shed light on molecular processes where crystallization occurs in the presence of unwanted impurities in solution.
Conclusion
Biological mineralization has provided examples of materials with a diversity of morphologies and functions found in the biological world. Contrary to studies on crystal nucleation and growth from the last century, biology utilizes mechanisms where regulation of crystallite size and distribution takes on intermediate phases and metastable clusters as precursors to crystalline assemblies. From recent in situ investigations on a diversity of biomineralization model systems, we find common themes in the construction of strong, tough biological materials from their nano-scale constituents. Specifically, many of these model systems involve the utility of a proteinaceous scaffold to interact with nascent mineral precursors and the formation of intermediate mineral states like amorphous phases, and subsequently, the assembly and growth of crystallization states. As shown here in this work, we describe mechanistic behaviors from a simple colloidal system that parallel biological mineralization showing insights into biological materials utilizing 2D pathways to form 3D materials at molecular length-scales. This biphasic model concisely shows the energetic and kinetic advantages of intermediate states and non-classical crystallization paths to crystallization states. These intermediate states, like their biological equivalents, are templated by an organic component and their utility is to aid in the pre-programed construction of larger, complex assemblies required to build the hierarchical architectures observed in biological materials. By manipulating the unit assemblies and local parameters, the same mechanistic behaviors can be utilized and lead to drastic divergence in morphology (Etinger-Geller et al., 2017; Zhao et al., 2018; Kartha et al., 2019) and subsequently materials properties. Biological control of substrate chemistry is vital and determines the energetic barriers of the following layers of assemblages. With these constraints, the designing of bio-inspired hierarchically architecture materials with high toughness and strength can be realized from the presence of specific constituents at the molecular scale and the control of their interactions at interfaces for bottom-up, bioinspired materials engineering.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
Both authors contributed to the experimentation, analyses of data, discussion of data, and writing of the resulting manuscript.
Funding
Funding for this work was supported by NSF DMR-CMP Award No. 1507607 and NSF DGE Award No. 0654193. We also acknowledge Aperion Information Technologies for student funding, computational resources for simulations and data analysis. Data was acquired at the Cohen laboratory (Cornell University). JS was currently on sabbatical at Berkeley Labs and supported by the user programs at the Advanced Light Source (ALS) and Molecular Foundry (MF) (ALS-10280, MF-0088, and MF-0090). This work is supported by the Office of Science, Office of Basic Energy Sciences, of the United States Department of Energy under Contract No. De-AC02-05CH11231.
Conflict of Interest
JM was currently affiliated with BitWrex.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Drs. Megan Comins, Brian Leahy, James Sethna, and Matthew Warkentin for helpful conversations and guidance. Professor Peter Harrowell (University of Sydney) was thanked for their technical expertise and theoretical contributions to this work.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.00075/full#supplementary-material
VIDEO S1 | A compressed video of the microparticle system outlined in the experimental methods which demonstrates the initial monolayer growth, melting, and simultaneous second-layer growth of crystal islands. The video is accelerated in time by 1500x, such that 1 s of video playback spans 25 min in real time.
References
Aizenberg, J. (2004). Crystallization in patterns: a bio-inspired approach. Adv. Mater. 16, 1295–1302. doi: 10.1002/adma.200400759
Asakura, S., and Oosawa, F. (1954). On interaction between two bodies immersed in a solution of macromolecules. J. Chem. Phys. 22, 1255–1256. doi: 10.1063/1.1740347
Ashby, M., Gibson, L., Wegst, U., and Olive, R. (1995). The mechanical properties of natural materials I. Material property charts. Proc. R. Soc. A 450, 123–140. doi: 10.1098/rspa.1995.0075
Auer, S., and Frenkel, D. (2001). Prediction of absolute crystal-nucleation rate in hard-sphere colloids. Nature 409, 1020–1023. doi: 10.1038/35059035
Banfield, J., Welch, S., Zhang, H., Ebert, T., and Penn, R. (2000). Aggregation-based crystal growth and microstructure development in natural iron oxyhydroxide biomineralization products. Science 289, 751–754. doi: 10.1126/science.289.5480.751
Baumgartner, J., Dey, A., Bomans, P., Le Coadou, C., Fratzl, P., Sommerdijk, N., et al. (2013). Nucleation and growth of magnetite from solution. Nat. Mater. 12, 310–314. doi: 10.1038/nmat3558
Chen, J., Zhu, E., Liu, J., Zhang, S., Lin, Z., Duan, X., et al. (2019). Building two-dimensional materials one row at a time: avoiding the nucleation barrier. Science 362, 1135–1139. doi: 10.1126/science.aau4146
Cho, K., Kim, Y., Yang, P., Cai, W., Kulak, P. H. A., Lau, J., et al. (2016). Direct observation of mineral-organic composite formation reveals occlusion mechanism. Nat. Commun. 7, 1–7. doi: 10.1038/ncomms10187
Chung, S., Kim, Y., Kim, J., and Kim, Y. (2009). Multiphase transformation and Ostwald’s rule of stages during crystallization of a metal phosphate. Nat. Phys. 5, 68–73. doi: 10.1038/nphys1148
Chung, S., Shin, S., Bertozzi, C., and De Yoreo, J. (2010). Self-catalyzed growth of S layers via an amorphous-to-crystalline transition limited by folding kinetics. PNAS 107, 16536–16541. doi: 10.1073/pnas.1008280107
Coelfen, H., and Antonietti, M. (2008). Mesocrystals and Nonclassical Crystallization. Ltd. Berlin: John Wiley and Sons.
Crocker, J., and Grier, D. (1996). Methods of digital video microscopy for colloidal studies. J. Coll Interf Sci. 179, 298–310. doi: 10.1006/jcis.1996.0217
Dalmaschio, C., Ribeiro, C., and Leite, E. (2010). Impact of the colloidal state on the oriented attachment growth mechanism. Nanoscale 2, 2336–2345. doi: 10.1039/c0nr00338g
de Melo Pereira, D., and Habibovic, P. (2018). Biomineralization-inspired material design for bone regeneration. Adv. Health Mater 7, 1–18. doi: 10.1002/adhm.201800700
De Yoreo, J., Gilbert, P., Sommerdijk, N., Penn, R., Whitelam, S., Joester, D., et al. (2015). Crystallization by particle attachment in synthetic, biogenic, and geological environments. Science 349, 6760–6769. doi: 10.1126/science.aaa6760
Demichelis, R., Raiteri, P., Gale, J., Quigley, D., and Gebauer, D. (2011). Stable prenucleation mineral clusters are liquid-like ionic polymers. Nat. Commun. 2, 1–8. doi: 10.1038/ncomms1604
Dey, A., Bomans, P., Mueller, F., Will, J., Frederik, P., de With, G., et al. (2010). The role of prenucleation clusters in surface-induced calcium phosphate crystallization. Nat.Mater 9, 1010–1014. doi: 10.1038/nmat2900
Deyoreo, J., Gilbert, P., Sommerdijk, N., Penn, R., Whitelam, S., Joester, D., et al. (2015). Crystallization by particle attachment in synthetic, biogenic, and geologic environments. Science 349:aaa6760. doi: 10.1126/science.aaa6760
DeYoreo, J., and Vekilov, P. (2003). Principles of crystal nucleation and growth. Rev. Mineral. Geochem. 54, 57–93.
Dideriksen, K., Frandsen, C., Bovet, N., Wallace, A., Sel, O., Arbour, T., et al. (2015). Formation and transformation of a short range ordered iron carbonate precursor. Geochim. Cosmochm. Acta 164, 94–109. doi: 10.1016/j.gca.2015.05.005
Dinsmore, A., Warren, P., Poon, W., and Yodh, A. (1997). Fluid-solid transitions on walls in binary hard-sphere mixtures. Europhys. Lett. 40, 337–342. doi: 10.1209/epl/i1997-00468-4
Dullens, R., Aarts, D., and Kegel, W. (2006). Direct measurement of the free energy by optical microscopy. PNAS 103, 529–531. doi: 10.1073/pnas.0507052103
Etinger-Geller, Y., Katsman, A., and Pokroy, B. (2017). Density of nanometrically thin amorphous films varies by thickness. Chem. Mater 29, 4912–4919. doi: 10.1021/acs.chemmater.7b01139
Filion, L., Hermes, M., Ni, R., and Dijkstra, M. (2010). Crystal nucleation of hard spheres using molecular dynamics, umbrella sampling, and forward flux sampling: a comparison of simulation techniques. J. Chem. Phys. 133, 1–15. doi: 10.1063/1.3506838
Fischer, F., Kolednik, O., Predan, J., Razi, H., and Fratzl, P. (2017). Crack driving force in twisted plywood structures. Acta Biomaterialia 55, 349–359. doi: 10.1016/j.actbio.2017.04.007
Fratzl, P., and Weinkamer, R. (2007). Nature’s hierarchical materials. Prog. Mater Sci. 52, 1263–1334.
Fritz, M., Belcher, A., Radmacher, M., Walters, D., Hansma, P., Stucky, G., et al. (1994). Flat pearls from biofabrication of organized composites on inorganic substrates. Nature 371, 49–51. doi: 10.1038/371049a0
Ganapathy, R., Buckley, M., Gerbode, S., and Cohen, I. (2010). Direct measurements of island growth and step-edge barriers in colloidal epitaxy. Science 327, 445–448. doi: 10.1126/science.1179947
Gasser, U. (2009). Crystallization in three- and two- dimensional colloidal suspensions. J. Phys: Condensed Matter 21, 1–24.
Gebauer, D., Voelkel, A., and Coelfen, H. (2008). Stable prenucleation calcium carbonate clusters. Science 322, 1819–1822. doi: 10.1126/science.1164271
Gong, Y., Killian, C., Olson, I., Appathurai, N., Amasino, A., Martin, M., et al. (2012). Phase transitions in biogenic amorphous calcium carbonate. PNAS 109, 6088–6093. doi: 10.1073/pnas.1118085109
Habraken, W., Tao, J., Brylka, L., Friedrich, H., Bertinetti, L., Schenk, A., et al. (2013). Ion-association complexes unite classical and non-classical theories for the biomeimetic nucleation of calcium phosphate. Nat. Commun. 4, 1–12. doi: 10.1038/ncomms2490
Hedges, L., and Whitelam, S. (2013). Selective nucleation in porous media. Soft. Matter 8, 9763–9766.
Huang, W., Restrepo, D., Jung, J., Su, F., Liu, Z., Ritchie, R., et al. (2019). Multiscale toughening mechanisms in biological materials and bioinspired designs. Adv. Mater 1901561, 1–37. doi: 10.1002/adma.201901561
Ivanov, V., Fedorov, P., Baranchikov, A., and Osiko, V. (2014). Oriented aggregation of particles: 100 years of investigations of non-classical crystal growth. Russian Chem. Rev. 83, 1204–1222. doi: 10.1070/rcr4453
Jee, S., Culver, L., Li, Y., Douglas, E., and Gower, L. (2010). Biomimetic mineralization of collagen via an enzyme-aided PILP process. J. Crystal. Growth 312, 1249–1256. doi: 10.1016/j.jcrysgro.2009.11.010
Kartha, K., Allampally, N., Politi, A., Prabhu, D., Ouchi, H., Albuquerque, R., et al. (2019). Influence of metal coordination and light irradiation on hierarchical self-assembly processes. Chem. Sci. 10, 752–760. doi: 10.1039/c8sc03875a
Killian, C., Metzler, R., Gong, Y., Olson, I., Aizenberg, J., and Politi, Y. (2009). Mechanism of Calcite Co-orientation in the sea urchin tooth. J. Am. Chem. Soc. 131, 18404–18409. doi: 10.1021/ja907063z
Kuhrts, L., Macias-Sanchez, E., Tarakina, N., and Hirt, A. (2019). Shaping magnetite with Poly-L-arginine and pH: from small single crystals to large mesocrystals. J. Phys. Chem. Lett. 10, 5514–5518. doi: 10.1021/acs.jpclett.9b01771
Larsen, A., and Grier, D. (1996). Melting of metastable crystallites in charge-stabilized colloidal suspensions. PRL 76, 3862–3865. doi: 10.1103/physrevlett.76.3862
Lechner, W., Dellago, C., and Bolhuis, P. (2011). Role of the prestructured surface cloud in crystal nucleation. PRL 106, 1–4.
Lekkerkerker, H., and Tuinier, R. (2011). Colloids and the Depletion Interaction. Heidelberg: Springer.
Li, D., Nielsen, M., Lee, J., Frandsen, C., Banfield, J., and De Yoreo, J. (2012). Direction-specific interactions control crystal growth by oriented attachment. Science 336, 1014–1018. doi: 10.1126/science.1219643
Lowenstam, H. (1981). Minerals formed by organisms. Science 211, 1126–1131. doi: 10.1126/science.7008198
Ma, X., Zhang, S., Jiao, F., Newcomb, C., Zhang, Y., and Prakash, A. (2017). Tuning crystallization pathways through sequence engineering of biomimetic polymers. Nat. Mater 16, 767–774. doi: 10.1038/nmat4891
Maes, D., Vorontsova, M., Potenza, M., Sanvito, T., Sleutel, M., Giglio, M., et al. (2015). Do protein crystals nucleate within dense liquid clusters? Acta Crystallo F Struct. Biol. Commun. 71(Pt 7), 815–822. doi: 10.1107/S2053230X15008997
Mahamid, J., Aichmayer, B., Shimoni, E., Ziblat, R., Li, C., Siegel, S., et al. (2010). Mapping amorphous calcium phosphate transformation into crystalline mineral from the cell to the bone in zebrafish fin rays. PNAS 107, 6316–6321. doi: 10.1073/pnas.0914218107
Mass, T., Giuffre, A., Sun, C., Stifler, C., Frazier, M., Neder, M., et al. (2017). Amorphous calcium carbonate particles form coral skeletons. PNAS 114, E7670–E7678. doi: 10.1073/pnas.1707890114
Mergo, J. (2017). Statistical Dynamics of Multicomponent Quasi-Two-Dimensional Colloidal Systems. Applied Physics. Ithaca, NY.: Cornell University, 100.
Meyers, M., Mckittrick, J., and Chen, P. (2013). Structural biological materials: critical mechanics-materials connections. Science 339, 773–779. doi: 10.1126/science.1220854
Mirabello, G., Keizer, A., Bomans, P., Kovacs, A., Dunin-Borkowski, R., Sommerdijk, N., et al. (2019). Understanding the formation mechanism of magnetic mesocrystals with (Cryo-)electron microscopy. Chem. Mater 31, 7320–7328. doi: 10.1021/acs.chemmater.9b01836
Munch, E., Launey, M., Alsem, D., Saiz, E., Tomsia, A., and Ritchie, R. (2008). Tough, bio-inspired hybrid materials. Science 322, 1516–1520. doi: 10.1126/science.1164865
Nielsen, M., Aloni, S., and DeYoreo, J. (2014). In situ TEM imaging of CaCO3 nucleation reveals coexistence of direct and indirect pathways. Science 345, 158–162. doi: 10.1126/science.1254051
Noorduin, W., Grinthal, A., Mahadevan, L., and Aizenberg, J. (2013). Rationally designed complex, hierarchical microarchitectures. Science 340, 832–837. doi: 10.1126/science.1234621
Noorduin, W., Vlieg, E., Kellogg, R., and Kaptein, B. (2009). From ostwald ripening to single chirality. Angew Chem.Int. Ed. 48, 9600–9606. doi: 10.1002/anie.200905215
Ostwald, W. (1897). Studies on the formation and transformation of solid bodies. Z.Phys. Chem. 22, 289–330.
Palberg, T. (2014). Crystallization kinetics of colloidal model suspensions: recent achievements and new perspectives. J. Phys. Condensed Matter 26, 1–23. doi: 10.1088/0953-8984/26/33/333101
Pendola, M., Jain, G., Huang, Y., Gebauer, D., and Evans, J. (2018). Secrets of the sea urchin spicule revealed: protein cooperativity is responsible for ACC transformation, intracrystalline incorporation, and guided mineral particle assembly in biocomposite material formation. ACS Omega 3, 11823–11830. doi: 10.1021/acsomega.8b01697
Picker, A., Nicoleau, L., Burghard, Z., Bill, J., Zlotnikov, I., Labbez, C., et al. (2017). Mesocrystalline calcium silicate hydrate: a bioinspired route toward elastic concrete materials. Sci. Adv. 3, 1–6. doi: 10.1126/sciadv.1701216
Politi, Y., Arad, T., Klein, E., Weiner, S., and Addadi, L. (2004). Sea urchin spine calcite forms via a transient amorphous calcium carbonate phase. Science 306, 1161–1164. doi: 10.1126/science.1102289
Rao, A., Arias, J., and Coelfen, H. (2017). On mineral retrosynthesis of a complex biogenic scaffold. Inorganics 5, 1–16.
Rawlings, A., Somner, L., Fitzpatrick-Milton, M., Roebuck, T., Gwyn, C., Liravi, P., et al. (2019). Artificial coiled coil biomineralisation protein for the synthesis of magnetic nanoparticles. Nat. Commun. 10, 1–9. doi: 10.1038/s41467-019-10578-2
Salvalaglio, M., Perego, C., Giberti, F., Mazzotti, M., and Parrinello, M. (2014). Molecular-dynamics simulations of urea nucleation from aqueous solution. PNAS 112, 1–14.
Savage, J., Blair, D., Levine, A., Guyer, R., and Dinsmore, A. (2006). Imaging the sublimation dynamics of colloidal crystallites. Science 314, 795–798. doi: 10.1126/science.1128649
Savage, J., and Dinsmore, A. (2009). Experimental evidence for two-step nucleation in colloidal crystallization. PRL 102, 1–4.
Savage, J., Hopp, S., Ganapathy, R., Gerbode, S., Heuer, A., and Cohen, I. (2013). Entropy-driven crystal formation on highly strained substrates. PNAS 110, 9301–9304. doi: 10.1073/pnas.1221529110
Schenk, A., Zlotnikov, I., Pokroy, B., Gierlinger, N., Masic, A., Zaslansky, P., et al. (2012). Hierarchical calcite crystals with occlusions of a simple polyeletrolyte mimic complex biomineral structures. Adv Func Mater 22, 4668–4676. doi: 10.1002/adfm.201201158
Seto, J., Azais, T., and Coelfen, H. (2013). Formation of aragonitic layered structures from kaolinite and amorphous calcium carbonate precursors. Langmuir 29, 7521–7528. doi: 10.1021/la400442j
Seto, J., Ma, Y., Davis, S., Meldrum, F., Gourrier, A., Kim, Y., et al. (2012). Structure-property relationships of a biological mesocrystal in the adult sea urchin spine. PNAS 109, 3699–3704. doi: 10.1073/pnas.1109243109
Seto, J., Picker, A., Chen, Y., Rao, A., Evans, J., and Coelfen, H. (2014). nacre protein sequence compartmentalizes mineral polymorphs in solution. Crystal. Growth and Des. 14, 1501–1505. doi: 10.1021/cg401421h
Seto, J., Zhang, Y., Hamilton, P., and Wilt, F. (2004). The localization of occluded matrix proteins in calcareous spicules of sea urchin larvae. J. Struc. Biol. 148, 123–130. doi: 10.1016/j.jsb.2004.04.001
Sleutel, M., and Van Driessche, A. (2014). Role of clusters in nonclassical nucleation and growth of protein crystals. PNAS 111, E546–E553. doi: 10.1073/pnas.1309320111
Smeets, P., Cho, K., Kempen, R., Sommerdijk, N., and DeYoreo, J. (2015). Calcium carbonate nucleation driven by ion binding in a biomimetic matrix revealed by in situ electron microscopy. Nat. Mater 14, 394–399. doi: 10.1038/nmat4193
Tao, J., Shin, Y., Jayasinha, R., Buchko, G., Burton, S., Dohnalkova, A., et al. (2019). The energetic basis for hydroxyapatite mineralization by amelogenin variants provides insights into the origin of amelogenesis imperfect. PNAS 116, 13867–13872. doi: 10.1073/pnas.1815654116
Teng, H., Dove, P., Orme, C., and DeYoreo, J. (1998). Thermodynamics of calcite growth: baseline for understanding biomineral formation. Science 282, 724–727. doi: 10.1126/science.282.5389.724
Vekilov, P. (2010). The two-step mechanism of nucleation of crystals in solution. Nanoscale 2, 2346–2357. doi: 10.1039/c0nr00628a
Vekilov, P., and Vorontsova, M. (2014). Nucleation precursors in protein crystallization. Acta Crystallo F Struct. Biol. Commun. 70, 271–282.
Wang, Y., Azais, T., Robin, M., Vallee, A., Catania, C., Legriel, P., et al. (2012). The predominant role of collagen in the nucleation, growth, structure and orientation of bone apatite. Nat.Mater 11, 724–733. doi: 10.1038/nmat3362
Washington, A. II, Foley, M., Cheong, S., Quffa, L., Breshike, C., Watt, J., et al. (2012). Ostwald’s Rule of Stages and its role in CdSe quantum dot crystallization. J. Am. Chem. Soc. 134, 17046–17052. doi: 10.1021/ja302964e
Weaver, J., Milliron, G., Miserez, A., vans-Lutterodt, K. E., Herrera, I. Gallana, and Mershon, W. (2012). The stomatopod dactyl club: a formidable damage-tolerant biological hammer. Science 336, 1275–1280. doi: 10.1126/science.1218764
Weiner, S., and Addadi, L. (2011). Crystallization Pathways in Biomineralization. Ann. Rev. Mater Res. 41, 21–40. doi: 10.1146/annurev-matsci-062910-095803
Weiner, S., and Wagner, H. (1998). The material bone: structure-mechanical function relations. Ann. Rev. Mater Sci. 28, 271–298. doi: 10.1016/j.bone.2013.10.023
Weiss, I., Tuross, N., Addadi, L., and Weiner, S. (2002). Mollusc larval shell formation: amorphous calcium carbonate is a precursor phase for aragonite. J. Exp. Zool. 293, 478–491. doi: 10.1002/jez.90004
Zeravcic, Z., Manoharan, V., and Brenner, M. (2014). Size limits of self-assembled colloidal structures made using specific interactions. PNAS 111, 15918–15923. doi: 10.1073/pnas.1411765111
Zhao, R., Li, M., Ren, Z., Zhu, Y., and Han, G. (2018). Three-dimensional oriented attachment growth of single-crystal pre-perovskite PbTiO3 hollowed fibers. Cryst. Eng. Commun. 20, 448–453. doi: 10.1039/c7ce01780d
Zhou, J., Yang, Y., Yang, Y., Kim, D., Yuan, A., Tian, X., et al. (2019). Observing crystal nucleation in four dimensions using atomic electron tomography. Nature 570, 500–503. doi: 10.1038/s41586-019-1317-x
Keywords: non-classical crystallization pathways, biological mineralization, multiscale interactions, bead-bead interactions, amorphous precursors, colloidal crystallization
Citation: Mergo JC III and Seto J (2020) On Simulating the Formation of Structured, Crystalline Systems via Non-classical Pathways. Front. Mater. 7:75. doi: 10.3389/fmats.2020.00075
Received: 07 October 2019; Accepted: 12 March 2020;
Published: 08 April 2020.
Edited by:
Admir Masic, Massachusetts Institute of Technology, United StatesReviewed by:
Lucas Kuhrts, Max Planck Institute of Colloids and Interfaces, GermanyThierry Azaïs, Sorbonne Universités, France
Copyright © 2020 Mergo and Seto. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jong Seto, Sk1TZXRvQGxibC5nb3Y=
 John C. Mergo III
John C. Mergo III Jong Seto
Jong Seto