- 1Graduate School of Engineering, Toyota Technological Institute, Nagoya, Japan
- 2Nuclear Science and Engineering Center, Japan Atomic Energy Agency, Tokai-mura, Japan
The stress state at an atomic level and its governing physics inside a random alloy are essential elements in developing a model for solid solution strengthening in random alloys, which is one of the primary strengthening mechanisms of high-entropy alloys (HEAs). Through first-principles calculation, we investigated the atomic stress in fcc and bcc random alloys that were subsets of CrMnFeCoNi and VNbMoTaW HEAs, respectively. The results showed a correlation between the atomic pressure dispersion and the experimental yield stress for the bcc random alloys, as observed in a previous study on fcc alloys. By focusing on the charge transfer and volume change with respect to a bulk crystal, we examined whether the internal stress fields in the fcc and bcc alloys could be interpreted from a unified viewpoint in terms of these physical quantities. Regression analyses using the random forest method revealed that the charge transfer and volume change simultaneously govern the stress state inside an alloy, albeit with varying degrees of intensity.
1 Introduction
In modern materials science, the search for structural materials with excellent mechanical properties involves target materials whose micron- and atomic-level structures are diverse and complex. A high-entropy alloy (HEA) is a type of advanced material that has attracted much attention because of unique properties including a high yield strength and toughness, and excellent high-temperature capabilities (Zhang et al. (2014); Pickering and Jones (2016); Toda-Caraballo et al. (2017); Ikeda et al. (2019); George et al. (2020)). The structural characteristic of HEAs is that they are single-phase solid solution alloys that generally contain five or more primary elements with an atomic ratio that is equimolar or close to it. This characteristic means that these alloys have a vast design space, with a considerable number of element combinations and resulting short- and medium-range ordered structures (Antillon et al. (2020); Zhang et al. (2020); Yu et al. (2022)). Accordingly, HEAs present the possibility of obtaining novel, unexplored material functions.
A typical HEA alloy phase has a relatively simple face-centered cubic (fcc) or body-centered cubic (bcc) crystal structure. Nevertheless, large lattice distortions occur inside HEAs (Oh et al. (2016); Tong et al. (2018); Ye et al. (2018); Zhao et al. (2019); Lee et al. (2020); Roy et al. (2021)). The reason is that they are composed of various elements with different atomic sizes and electronic states. The solid solution strengthening induced by these differences is onemechanisms of HEAs and is believed to be responsible for their excellent mechanical properties (Okamoto et al. (2016); Tian (2017); Keil et al. (2021); Lugovy et al. (2021); Wen et al. (2021)). In conventional dilute alloys, it is easy to distinguish the solute and solvent. Accordingly, physical models that incorporate the elastic interactions between dislocations and solute atoms, such as the Labusch and Fleischer models (Fleischer (1961); Labusch (1970)), have been applied to explain the solution strengthening mechanism in those alloys. In contrast, it is difficult to distinguish the solute and solvent in HEAs because of the multiple constituent elements and the variety of their sizes and electronic properties; thus, the conventional solution strengthening model cannot be applied.
This limitation and the growing interest in HEAs have given rise to a new field of research on solid solution strengthening models for random alloys. Senkov et al. (2011a) made a pioneering attempt to extend the Labusch model to such complex alloys. Using the idea of a pseudo-binary alloy, they constructed a solution strengthening model for a TiZrNbHfTa bcc alloy by estimating the atomic size misfit and elastic modulus misfit. Rao et al. (2016) extended Senkov’s work to fcc HEAs of Fe0.4Cr0.4NiMnxCu (0 ≤ x ≤ 1.4). Toda-Caraballo and Rivera-Díaz-Del-Castillo (2015) further extended Labusch’s theory to a model for multicomponent alloys by considering the variation of the interatomic spacing inside the alloys. Varvenne et al. (2016) developed a model in which the solute atoms are assumed to exist in a homogenized effective medium of a random alloy. They applied their model to fcc random alloys, in which the strain field generated by the solute atoms in the effective medium affects the motion of dislocations. Maresca and Curtin (2020) leveraged Varvenne et al.’s model to develop a solid solution strengthening model for refractory bcc HEAs.
The solution strengthening models mentioned above are extensions of the conventional theory, which attempts to infer the elastic state inside an alloy from the bulk properties of the constituent atoms. An alternative approach is to use first-principles calculations to directly reveal the elastic state inside a random alloy. By using the locally self-consistent multiple scattering method, Oh et al. (2019) calculated the atomic stresses in fcc random alloys based on the constituent atoms of the Cantor HEA. Their results showed a correlation between the variation of the atomic pressure and the experimental yield stress. They also found that the yield strength could be assessed via the differences in the electronegativity of the constituent elements. Ishibashi et al. (2020) evaluated the atomic stress fields of 15 bcc random alloys, including refractory HEAs, by using the projector augmented wave (PAW) method with Bader analysis. They found that the atomic pressure correlated linearly with the average valence electron concentration in the alloy. These approaches, which use atomic stress to evaluate the elastic field, are direct and provide a bottom-up view of the elastic interaction of dislocations with the elastic field inside a crystal. Both of these studies found that the atomic-level elastic state of the constituent atoms differs greatly depending on the surrounding environment of the atom.
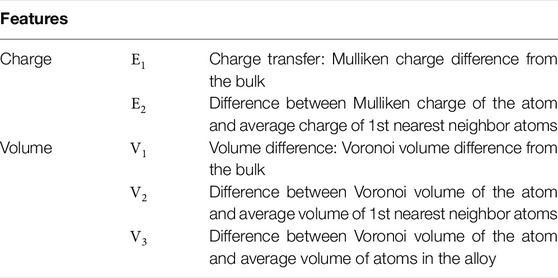
In this study, we applied first-principles calculations to investigate the atomic stress in random alloys that were subsets of CrMnFeCoNi and VNbMoTaW HEAs. We calculated the atomic stress by using the linear combination of atomic orbitals (LCAO) method implemented in the OpenMX software package (Ozaki and Kino (2005); Ozaki (2006)). Whereas Oh et al. (2019) and Ishibashi et al. (2020) investigated fcc and bcc random alloys, respectively, this study used the same framework to deal with both types. As Oh et al. (2019) did for only the fcc case, we examined the relationship between the atomic pressure dispersion and the experimental yield stress for both fcc and bcc random alloys. The elemental species in these types are different: the fcc alloys contain 3d late transition metal elements, while the bcc alloys contain 3d, 4d, and 5d early transition metal elements. Therefore, the main physics governing the internal stress state may be different between the two types of alloys. Here, by focusing on the charge transfer estimated from the Mulliken atomic charge and the volume change estimated via the Voronoi volume, we analyzed whether the internal stress fields in the fcc and bcc alloys could be interpreted from a unified viewpoint in terms of these physical quantities. To analyze the multiple dominant factors governing the stress in detail, we applied a data science approach, namely, the random forest method. In addition to regression analyses using the charge transfer and volume change as features, analyses using the numbers of first-nearest neighbor atoms for each element were conducted to draw a connection between the stress field and atomic environment in random alloys including the fcc and bcc HEAs.
2 Computational Methods and Models
2.1 Atomic Stress
In this study, the stress field at the atomic level was calculated by using density-functional theory (DFT) (Hohenberg and Kohn (1964); Kohn and Sham (1965)), in which the macroscopic stress of a supercell
where Vcell is the volume of the supercell. The atomic stress is calculated by using the decomposed atomic energy for individual atoms, Ei (Shiihara et al. (2010); Nicholson et al. (2013); Kohyama et al. (2021)):
where Vi is the Voronoi volume of atom i. The method to calculate the atomic stress depends on how this decomposition is performed. In this study, the LCAO method was used to decompose the total energy, and the macroscopic stress was then incorporated as in Lobzenko et al. (2020). In the LCAO method, a wave function is expressed by using the atomic orbital as the basis function. In DFT, most of the components of the total energy, the forces acting on the atoms, and the macroscopic stress are calculated via the wave function and the atomic orbital. Accordingly, these quantities can be decomposed into the contributions from individual atomic orbitals. By collecting these contributions atom by atom, we can obtain the atomic stress, which is a decomposition of the cell stress into individual atoms. The details of the formulation can be found elsewhere (Y. Shiihara et al., to be submitted). The atomic hydrostatic pressure is calculated from the trace of the atomic stress:
The atomic stress field inside random alloys is analyzed via the atomic pressure. Note that the atomic pressure in this study is positive in compression and negative in tension.
2.2 Atomic Volume and Charge
In random alloys, the environment surrounding an atom is different, even for the same element. Hence, the atomic volume spreads, and there are also differences in charge transfer. To find a relationship between these inhomogeneities and the inhomogeneity of the stress field, we can calculate the physical properties at the atomic level. Among these properties, this paper focuses on the atomic volume and charge.
In general, there are multiple ways to calculate per-atom physical quantities, including the Voronoi and Bader decompositions (Bader (1990)) used in Oh et al. (2019) or Ishibashi et al. (2020). In the Voronoi decomposition, the space is filled with Voronoi polyhedra. The boundary of a Voronoi polyhedron consists of a set of the perpendicular bisectors of line segments connecting two control points, with each atom as a control point. Under periodic boundary conditions, one Voronoi polyhedron (with its Voronoi volume) is assigned to each atom. The Voronoi volume is a geometric quantity that is determined only by the atomic coordinates and is suitable for incorporating the effects of volume misfit and lattice distortion, which are important for modeling solid solution strengthening. Thus, we adopted the Voronoi volume as the atomic volume. The volume difference was calculated by subtracting the volume in a bulk crystal corresponding to the basic lattice of the alloy structure (fcc or bcc) from the volume in a random alloy.
There are also multiple ways to calculate atomic charges, such as the Bader and Voronoi charges. We used the Mulliken charge, which is computed from density and overlap matrices based on the LCAO method. Because the approach is similar to the approach used for atomic stresses in this study, Mulliken charges are considered comparable with atomic stresses. We thus evaluated the charge transfer in an atom in a similar way to the volume changes: by subtracting the Mulliken charge in a bulk crystal from the charge in a random alloy.
2.3 DFT Settings and Random Alloy Models
The DFT calculations were performed with OpenMX, a first-principles software package based on the LCAO method and the norm-conserving pseudopotential (Morrison et al. (1993)), to investigate the atomic stress and other atomic-level properties. The spin-polarized generalized gradient approximation with the Perdew-Burke-Ernzerhof functional (Perdew et al. (1996)) was used. Table 1 lists the set of basis functions in OpenMX. For integration over the Brillouin zone, a 4 × 4 × 4 Monkhorst-Pack k-point mesh (Monkhorst and Pack (1976)) was used.
Table 2 lists the random alloys containing HEAs that were evaluated in this study. A supercell containing 60 atoms was adopted as the atomic model for all alloys. To approximate a random solid solution under periodic boundary conditions, we modeled the atomic structure by the special quasirandom structure (SQS) approach (Zunger et al. (1990)) based on a simulated annealing Monte Carlo method implemented in the Alloy Theoretic Automated Toolkit (ATAT) software (Van de Walle et al. (2002)). The atomic structure model was constructed as follows: first, 60 particles arranged in fcc or bcc structures were prepared with an appropriately chosen lattice constant, then the SQS method was used to determine the elemental species of each particle so that chemical disorder in random alloys is approximately satisfied. Finally, the density functional theory was used to relax the size and internal coordinates of the supercell. To encompass various atomic environments in the calculations, five calculation cases with a different SQS were performed for each alloy model. Table 2 also lists the mean and variance of the calculated lattice parameters for each alloy.
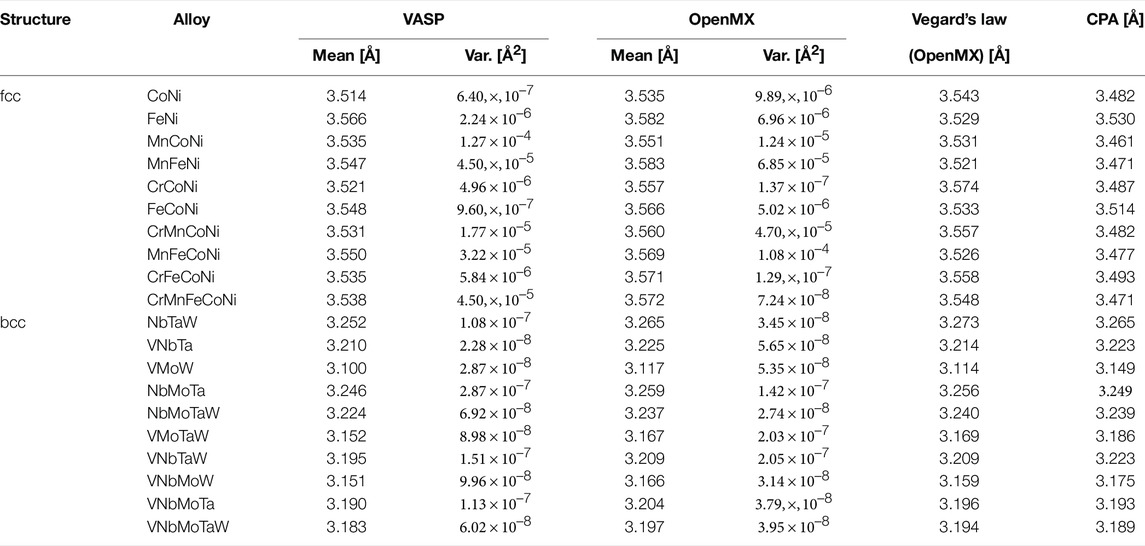
TABLE 2. Lattice constants in angstroms for the fcc and bcc random alloys, obtained from VASP and OpenMX. The listed means and variances were obtained in calculations on five SQS structures. For reference, the table also lists lattice constants that were estimated by Vegard’s law from their bulk values and obtained from AkaiKKR with the coherent potential approximation (CPA).
One of the characteristics of HEAs is the “cocktail effect” (Miracle and Senkov (2017)), which refers to the fact that unexpected properties can be obtained by mixing many elements. At the same time, this characteristic implies the complexity of the physics of HEAs. In this study, we applied the random forest method as a data science approach to tackle this complexity. Specifically, the atomic stresses were estimated from the atomic properties of individual atoms and their neighboring atoms as listed in Table 3, or from features that represent the atomic environment, such as the first neighboring atomic species. By using this approach, the factors that affect atomic stress were extracted for each elemental species, and the differences between elements were clarified.
3 Results and Discussion
Table 2 compares the lattice constants obtained with the software packages OpenMX and VASP (Kresse and Joubert (1999)) for the alloys. For reference, the results obtained with the software package AkaiKKR (Akai (1981)) and by Vegard’s law are also listed. The calculation conditions for VASP were the same, except that the plane-wave basis functions (with the plane-wave cutoff set to 520 eV) and the PAW method (Blöchl (1994)) were used. Because the means obtained by OpenMX and VASP over the five cases were sufficiently close (the maximum error was nearly 1%), we considered the calculations by OpenMX to be reasonable. The table also lists the variances obtained by OpenMX and VASP over the five cases. If the supercell size was too small, these variances could be large; however, the largest variance was only about 1.3 × 10–4. Accordingly, the supercell of 60 atoms in this study was assumed to be sufficient.
This study focuses on the differences in charge and volume from the bulk as the quantities characterizing the stress state inside a random alloy. Oh et al. (2019) reported the charge difference to dominate the internal stress in fcc random alloys. The volume difference reflects the lattice distortion, which significantly affects solid solution strengthening. Figure 1 shows a plot of the electronegativity versus the atomic volume at equilibrium in bulk for the elemental species. Because we are interested in these properties inside an fcc or bcc structure, for example, the atomic volume of Fe, which is inherently stable in the bcc structure, was calculated in the fcc bulk case. While the constituent elements of fcc random alloys have minor volume differences, their electronegativities have a specific range. In order of their electronegativities, these elements have the same order as in Period 4, but with Cr and Mn reversed. As for the constituents of the bcc alloys, the electronegativities of W and Mo in Group 6 are relatively large. In addition, we can categorize these elements into three groups according to their atomic volumes: (Nb, Ta), (Mo, W), and V. Note that V has a lower electronegativity and smaller atomic volume than the other constituent elements. We will refer to these inherent differences among the elements in the following discussion.
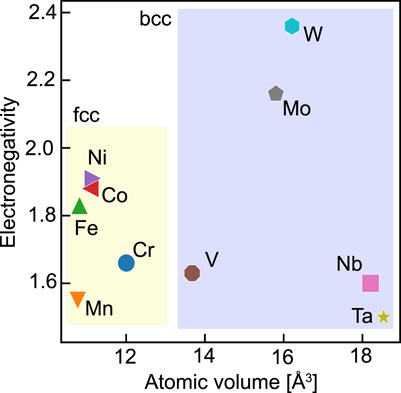
FIGURE 1. Electronegativity versus atomic volume for the constituent elements in the case of a pure bulk crystal.
Solid solution strengthening occurs when the stress field inside an alloy hampers or traps the movement of dislocations. Assuming that dislocations are firmly trapped if the stress field oscillates intensely, it is natural to assume that the first characteristic of the atomic stress field to describe the yield stress should be its dispersion. Oh et al. (2019) found a correlation between the experimental yield stress and the standard deviation of the atomic pressure in fcc random alloys. As shown in Figure 2, we found a similar correlation here, although we used a different method to calculate the atomic stress. The alloys containing Cr and Mn tend to have a higher yield stress. For alloys containing more than three elements, there is a clear difference in the experimental yield stress between the Cr-containing and Mn-containing groups; however, the standard deviation of the atomic stress does not reflect this difference. This result suggests that the strengthening mechanism of random alloys involves factors that cannot be described only in terms of the dispersion of atomic pressure.
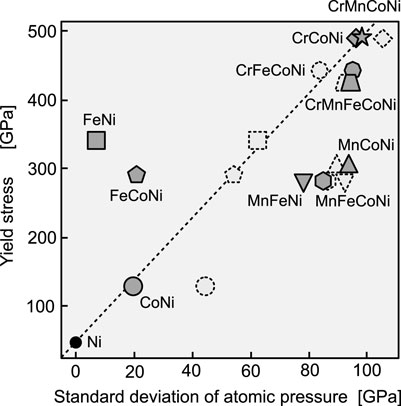
FIGURE 2. Experimental yield stress versus standard deviation of atomic pressure in various fcc random alloys. The experimental yield stress data were obtained from the friction stress (without its athermal portion) estimated at 0 K in Wu et al. (2014). For Ni, the Peierls friction stress is shown as the zero-temperature stress value, as in Oh et al. (2019). The broken symbols represent data obtained in Oh et al. (2019). The broken line connecting Ni and CrMnFeCoNi is an eye guide.
Next, Figure 3 plots the experimental yield stress and stress dispersion for bcc random alloys. The yield stress at room temperature was used for comparison, assuming that there is only a moderate change in yield stress from room temperature to 0 K. As with the fcc alloys, the effects of grain size and precipitation strengthening were treated as negligible. We found a similar correlation here to the case of the fcc random alloys. As supposed in the theory of Fleischer and Labusch, even in bcc alloys with a high Peierls stress, dislocations are subject to friction from the elastic field created by solid solution atoms during their motion. The relationship found here shows the significance of examining the yield stress in terms of the stress state inside the alloy. From Figure 3, it is difficult to grasp the tendency of the constituent element species to increase the yield stress in some cases. Hence, the following discussion will explore the dominant factors in internal stress variation.
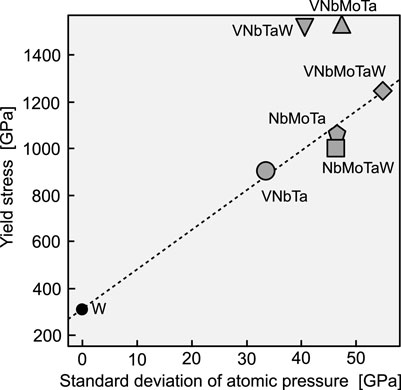
FIGURE 3. Yield stress versus standard deviation of atomic pressure in various bcc random alloys. The experimental yield stresses were obtained from room-temperature data (Senkov et al. (2011b); Nguyen et al. (2019); Li et al. (2020)). The data point for W represents the critical resolved shear stress that was experimentally observed at 77 K in Argon and Maloof (1966). The broken line connecting W and VNbMoTaW is an eye guide.
Figure 4 shows the relationship between the atomic hydrostatic pressure and the charge transfer or volume change for each atom in the fcc and bcc random alloys listed in Table 2. As in other studies on atomic stress, a large spread of atomic pressure is observed even for the same element. Previous studies that modeled a solid solution based on the Labusch model and did not consider atomic stresses expected similar behavior for the same element. In contrast, the results here indicate that the atoms are embedded in a diverse environment.
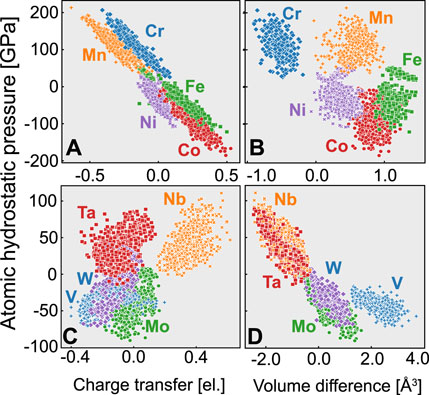
FIGURE 4. Relationship between atomic hydrostatic pressure and the atomic quantities of charge transfer and volume difference, for (A,B) fcc random alloys and (C,D) bcc random alloys.
First, Figures 4A,B show the results for the fcc random alloys. The volume differences indicate that Fe, Co, Mn, and Ni expand, while Cr contracts. Most of these atoms expand because most of the fcc alloys do not follow Vegard’s law, as seen in Table 2. Although Cr atoms with a large volume are under compression, it is difficult to find a relationship between the atomic pressure and the atomic volume difference. For example, although Mn occupies a larger volume than in the bulk fcc crystal, its atomic pressure indicates compression. In contrast, there is a strong inverse correlation between the atomic pressure and charge transfer: Cr and Mn, which have relatively small electronegativities, are under compression, while Fe, Co, and Ni, which have large electronegativities, are under tension. Oh et al. (2019) concluded that the electronegativity is a physical quantity that controls the internal stress states of fcc random alloys, thus increasing the yield stress due to solid solution strengthening.
Second, Figures 4C,D show the results for the bcc random alloys. In this case, there is no significant bias in the number of atoms between expansion and compression because the lattice constants are close to the values estimated by Vegard’s law (Table 2), unlike in the case of the fcc alloys. Also in contrast to the fcc case, there is no strong correlation between the atomic pressure and charge transfer. On the other hand, there is a weak inverse correlation between the atomic pressure and volume: Nb and Ta, which have large atomic radii, are under compression, while V, Mo, and W, which have small atomic radii, are under tension. Because the Voronoi volume change corresponds to the lattice distortion, this result is consistent with previous studies showing that the lattice distortion significantly affects the frictional stress in bcc random alloys (Zhao et al. (2019); Lee et al. (2020)).
Figure 5 shows the relationship between charge transfer and electronegativity; and the relationship between volume difference and atomic volume in bulk. There is a weak inverse correlation between volume change and atomic volume in bulk in the fcc alloys, while charge transfer correlates with electronegativity. In contrast, the bcc alloys do not show a relationship between charge transfer and electronegativity. However, we observed a correlation between the volume change and the atomic volume in bulk. This result justifies that the main factors governing the atomic stress state inside fcc and bcc random alloys are electronegativity and bulk atomic volume, respectively.
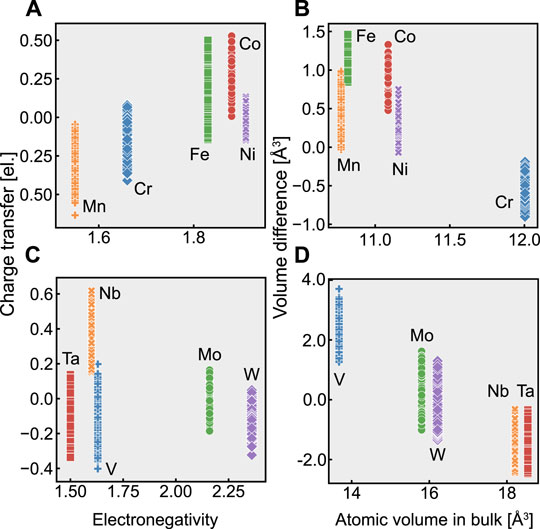
FIGURE 5. Relationships between charge transfer and electronegativity; and between volume difference and atomic volume in bulk, for (A,B) fcc random alloys and (C,D) bcc random alloys.
In Figure 4D, the change in the atomic pressure with respect to the volume change is smaller for V than for the other elements. This shallow slope implies that the bulk modulus of V is low. However, the experimental bulk modulus of pure V in a bcc bulk crystal is 162 GPa, which is close to the bulk modulus of Nb (170 GPa) (Tran et al. (2016)). We should thus consider the effect of other factors besides the volume change on the atomic pressure of V.
In this study, it is confirmed that the charge transfer in fcc random alloys and the atomic volume difference in bcc random alloys are the primary factors governing the atomic hydrostatic pressure, respectively. However, rather than assuming that only one of them determines the stress field, it is more natural to assume that both of them can work simultaneously with a certain degree of strength. Hence, we used the random forest method to regress the atomic pressure via features determined by the atomic charge and volume as listed in Table 3. The features described in this table can be calculated for each atom in the supercell, indicating that we have a data set for every atom: the features as the input and the atomic pressure as the output. Using 80% of this data set, we trained the regressor, whose performance was evaluated by using the remaining 20%. Figure 6A shows the results of regressing the atomic pressure on all elements simultaneously. The coefficient of determination (R2) and the root-mean-square error (RMSE), which are two measures of the accuracy of regression, are 0.96 and 13.3 GPa, respectively, which are comparable to the values in Ishibashi et al. (2020). This performance justifies using the random forest method to determine which feature acts as the dominant factor governing the atomic hydrostatic pressure. Note that all of the random alloys, both fcc and bcc, were regressed simultaneously here, whereas previous studies treated the fcc and bcc cases separately.

FIGURE 6. Regression results for the atomic hydrostatic pressure by the random forest method with the features listed in Table 3. (A) Comparison of the regressed pressure and that obtained by the DFT calculations. The data for all of the constituent elements were regressed at the same time. (B) Importance of features obtained by the random forest method. Here, the regression was performed individually for each element.
The random forest approach enabled us to evaluate the importance of each feature in the regression. Specifically, to investigate the determinants of the atomic hydrostatic pressure for each element, we applied the random forest method to each element’s data and regressed the atomic pressure. R2 and the importance of the features obtained from the regression are shown in Figure 6B. The R2 value averages 0.93 for the fcc alloy constituents, which indicates that the regression was performed successfully and that the atomic pressure in those alloys can largely be explained by charge transfer. This result strongly supports the conclusion of Oh et al. (2019) that the charge transfer and thus the electronegativity, as well, are the dominant factors governing the atomic pressure of fcc random alloys.
As for the bcc alloys, R2 was not as high as for the fcc alloys. Although high R2 values of 0.95 and 0.88 were obtained for W and Mo, respectively, the accuracy of the regression for V was relatively low at about 0.6. It is possible that the regression did not work well for V, Nb, and Ta because they are located at both ends of the pressure distribution. Alternatively, there may be another, underlying factor in the case of V. Regarding the overall trend, most of the atomic pressure in the bcc case is determined by the volume difference, especially for Mo and W, while a contribution from charge transfer is also observed for V, Nb, and Ta. The latter tendency is especially strong for V. This result indicates that charge transfer can contribute to the atomic pressure even in bcc random alloys.
Next, Figure 7A shows the same results when the features were the physical quantities obtained from the first-principles calculations. Specifically, for each atom, the number of its first-nearest neighbor atoms and its element were used as the features. The number of first-nearest neighbor atoms is 12 in the fcc case and eight in the bcc case. Figure 7A shows the results of simultaneous regression of the atomic pressure for all of the elements. The R2 and RMSE values are 0.99 and 6.4 GPa, respectively, which indicate good performance of the regression. Note that these results are not necessarily inconsistent with the results of Ishibashi et al. (2020), which required the influence of the second-nearest neighbor atoms. Because we used the SQS method, which does incorporate the second-nearest neighbor atoms, elements that are not located in the first neighbor shell are likely included in the second neighbor shell. We should thus assume that the information of the second-nearest neighbor atoms is partly involved in this regression.
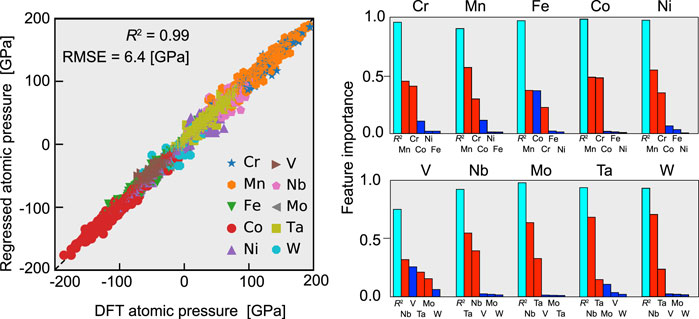
FIGURE 7. Regression results for the atomic hydrostatic pressure by the random forest method with the features consisting of the numbers of atoms for each element located in the first neighbor shell.
As in the previous case for the results shown in Figure 6B, the random forest method was also applied separately for each element, and Figure 7B shows the results. In this figure, elements that are roughly on the compressive side are shown in red, while those on the tensile side are shown in blue. Both the fcc and bcc alloys have a high R2 above 0.9 on average. Although the physics governing the atomic pressure is different between the two types of alloys, the constituent elements can be classified according to the physics for both types. This classification should strongly affect the regression of the atomic pressure. In the fcc case, the feature importance is high for Cr and Mn, which have relatively low electronegativities. For example, Ni is under strong tension when there are many Mn or Cr atoms in its first-nearest neighbor shell, whereas Cr is under strong compression when Mn or Cr is abundant in the first neighbor shell. In particular, the effect of Mn is significant, which follows from the fact that Mn has the lowest electronegativity, as shown in Figure 1.
For the bcc alloys, the number of Ta or Nb atoms in the first neighbor shell is a significant feature because of the large atomic volumes of Nb and Ta. For example, when a W atom is surrounded by Nb atoms, its atomic volume should be comparable to that of Nb, which thus puts it under tension. On the other hand, when there are many small atoms in the first-nearest neighbor shell, e.g., V, Mo, or W, Nb must enter a cage surrounded by them and is thus strongly compressed. In contrast, V does not show this tendency due to volume. Looking more closely at the information for the first-nearest neighbor atoms, we find that a V atom surrounded by many other V atoms has an atomic pressure near zero. Charge transfer occurs between V and Mo or W due to its difference in their electro-negativities, which may make a V atom unstable if there is many Mo or W in the first neighbor shell of the V atom. Hence, we believe that the atomic pressure approaches zero when V is abundant in the first-nearest neighbor shell of a V atom.
4 Conclusion
This study applied first-principles calculations to investigate the atomic stress in various fcc and bcc random alloys, which were subsets of CrMnFeCoNi and VNbMoTaW HEAs. We found a correlation between the pressure dispersion and the experimentally estimated yield stress for the fcc random alloys, as in Oh et al. (2019), although we used a different method to calculate the atomic stress. A similar correlation was also observed for the bcc random alloys, which confirms the significance of examining the yield stress in terms of an alloy’s internal stress state.
By comparing the atomic pressure to certain atomic quantities, namely, the charge transfer and volume change, it is confirmed that the pressure was primarily governed by the charge transfer in the fcc random alloys and by the atomic volume difference in the bcc random alloys. Furthermore, a successful regression by the random forest method showed that the atomic pressure in the fcc alloys can almost entirely be explained by the charge transfer. This result strongly supports the conclusion of Oh et al. (2019). As for the bcc alloys, most of the atomic pressure is determined by the volume difference, although a charge transfer contribution was also observed for some elements. In summary, we confirmed that the stress states inside fcc and bcc random alloys are simultaneously governed by the charge transfer and the volume difference. This conclusion was supported by another regression in which the features were the number of first-nearest neighbor atoms for each atom and its element.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
YS, IL, and TT contributed to the conception and design of the study. YI performed the DFT calculations. YS and IL developed and examined the local stress calculations. YS and YI performed the regressions using the random forest method. YS wrote the first draft of the manuscript. All authors contributed to revision of the manuscript, and they all read and approved the submitted version.
Funding
This work was supported by JSPS KAKENHI grants (Nos. 21H00154 and 18H05453). The DFT calculations were performed on the large-scale parallel computer system with SGI 8600 at JAEA and the Fujitsu PRIMERGY CX600M1/CX1640M1 (Oakforest-PACS) system at the Information Technology Center of The University of Tokyo.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akai, H. (1981). Electronic Structure of Ni-Pd Alloys Calculated by the Self-Consistent KKR-CPA Method. J. Phys. Soc. Jpn. 51, 468–474.
Antillon, E., Woodward, C., Rao, S. I., Akdim, B., and Parthasarathy, T. A. (2020). Chemical Short Range Order Strengthening in a Model FCC High Entropy alloy. Acta Mater. 190, 29–42. doi:10.1016/j.actamat.2020.02.041
Argon, A. S., and Maloof, S. (1966). Plastic Deformation of Tungsten Single Low Temperatures. Acta Metall. 14, 1449–1462. doi:10.1016/0001-6160(66)90165-9
Blöchl, P. E. (1994). Projector Augmented-Wave Method. Phys. Rev. B 50, 17953–17979. doi:10.1103/physrevb.50.17953
Fleischer, R. L. (1961). Solution Hardening. Acta Metall. 9, 996–1000. doi:10.1016/0001-6160(61)90068-2
George, E. P., Curtin, W. A., and Tasan, C. C. (2020). High Entropy Alloys: A Focused Review of Mechanical Properties and Deformation Mechanisms. Acta Mater. 188, 435–474. doi:10.1016/j.actamat.2019.12.015
Hohenberg, P., and Kohn, W. (1964). Inhomogeneous Electron Gas. Phys. Rev. 136, B864. doi:10.1103/physrev.136.b864
Ikeda, Y., Grabowski, B., and Körmann, F. (2019). Materials Characterization Ab Initio Phase Stabilities and Mechanical Properties of Multicomponent Alloys : A Comprehensive Review for High Entropy Alloys and Compositionally Complex Alloys. Mater. Charact. 147, 464–511. doi:10.1016/j.matchar.2018.06.019
Ishibashi, S., Ikeda, Y., Körmann, F., Grabowski, B., and Neugebauer, J. (2020). Correlation Analysis of Strongly Fluctuating Atomic Volumes , Charges , and Stresses in Body-Centered Cubic Refractory High-Entropy Alloys. Phys. Rev. Mater. 4, 023608. doi:10.1103/PhysRevMaterials.4.023608
Keil, T., Utt, D., Bruder, E., Stukowski, A., Albe, K., and Durst, K. (2021). Solid Solution Hardening in CrMnFeCoNi-Based High Entropy alloy Systems Studied by a Combinatorial Approach. J. Mater. Res. 36, 2558–2570. doi:10.1557/s43578-021-00205-6
Kohn, W., and Sham, L. J. (1965). Self-consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 140, A1133. doi:10.1103/physrev.140.a1133
Kohyama, M., Tanaka, S., and Shiihara, Y. (2021). Ab Initio Local-Energy and Local-Stress Calculations for Materials Science and Engineering. Mater. Trans. 62, 1–15. doi:10.2320/matertrans.mt-m2020291
Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758
Labusch, R. (1970). A Statistical Theory of Solid Solution Hardening. Physica Status Solidi (B) 41, 659–669. doi:10.1002/pssb.19700410221
Lee, C., Chou, Y., Kim, G., Gao, M. C., An, K., Brechtl, J., et al. (2020). Lattice-Distortion-Enhanced Yield Strength in a Refractory High-Entropy Alloy. Adv. Mater. 32, 1–9. doi:10.1002/adma.202004029
Li, Q., Zhang, H., Li, D., Chen, Z., and Qi, Z. (2020). The Effect of Configurational Entropy on Mechanical Properties of Single BCC Structural Refractory High-Entropy Alloys Systems. Int. J. Refractory Met. Hard Mater. 93, 105370. doi:10.1016/j.ijrmhm.2020.105370
Lobzenko, I., Shiihara, Y., Iwashita, T., and Egami, T. (2020). Shear Softening in a Metallic Glass : First-Principles Local-Stress Analysis. Phys. Rev. Lett. 124, 85503. doi:10.1103/PhysRevLett.124.085503
Lugovy, M., Slyunyayev, V., and Brodnikovskyy, M. (2021). Solid Solution Strengthening in Multicomponent Fcc and Bcc Alloys: Analytical Approach. Prog. Nat. Sci. Mater. Int. 31, 95–104. doi:10.1016/j.pnsc.2020.11.006
Maresca, F., and Curtin, W. A. (2020). Theory of Screw Dislocation Strengthening in Random BCC Alloys from Dilute to ”High-Entropy” Alloys. Acta Mater. 182, 144–162. doi:10.1016/j.actamat.2019.10.007
Miracle, D. B., and Senkov, O. N. (2017). A Critical Review of High Entropy Alloys and Related Concepts. Acta Mater. 122, 448–511. doi:10.1016/j.actamat.2016.08.081
Monkhorst, H. J., and Pack, J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B 13, 5188–5192. doi:10.1103/physrevb.13.5188
Morrison, I., Bylander, D. M., and Kleinman, L. (1993). Nonlocal Hermitian Norm-Conserving Vanderbilt Psendopotential. Phys. Rev. B 47, 6728–6731. doi:10.1103/physrevb.47.6728
Nguyen, V. T., Qian, M., Shi, Z., Song, T., Huang, L., and Zou, J. (2019). Compositional Design of strong and Ductile ( Tensile ) Ti-Zr-Nb-Ta Medium Entropy Alloys ( MEAs ) Using the Atomic Mismatch Approach. Mater. Sci. Eng. A 742, 762–772. doi:10.1016/j.msea.2018.11.054
Nicholson, D. M., Ojha, M., and Egami, T. (2013). First-principles Local Stress in Crystalline and Amorphous Metals. J. Phys. Condensed Matter 25, 435505. doi:10.1088/0953-8984/25/43/435505
Oh, H. S., Kim, S. J., Odbadrakh, K., Ryu, W. H., Yoon, K. N., Mu, S., et al. (2019). Engineering Atomic-Level Complexity in High-Entropy and Complex Concentrated Alloys. Nat. Commun. 10, 2090. doi:10.1038/s41467-019-10012-7
Oh, H. S., Ma, D., Leyson, G. P., Grabowski, B., Park, E. S., Körmann, F., et al. (2016). Lattice Distortions in the FeCoNiCrMn High Entropy alloy Studied by Theory and experiment. Entropy 18, 1–9. doi:10.3390/e18090321
Okamoto, N. L., Fujimoto, S., Kambara, Y., Kawamura, M., and George, E. P. (2016). Size Effect , Critical Resolved Shear Stress , Stacking Fault Energy , and Solid Solution Strengthening in the CrMnFeCoNi High-Entropy alloy. Sci. Rep. 6, 35863. doi:10.1038/srep35863
Ozaki, T., and Kino, H. (2005). Efficient Projector Expansion for the Ab Initio LCAO Method. Phys. Rev. B 72, 045121. doi:10.1103/PhysRevB.72.045121
Ozaki, T. (2006). O(N) Krylov-Subspace Method for Large-Scale Ab Initio Electronic Structure Calculations. Phys. Rev. B 74, 1–16. doi:10.1103/PhysRevB.74.245101
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865
Pickering, E. J., and Jones, N. G. (2016). High-entropy Alloys : a Critical Assessment of Their Founding Principles and Future Prospects. Int. Mater. Rev. 61, 183–202. doi:10.1080/09506608.2016.1180020
Rao, Z. Y., Wang, X., Zhu, J., Chen, X. H., Wang, L., Si, J. J., et al. (2016). Affordable FeCrNiMnCu High Entropy Alloys with Excellent Comprehensive Tensile Properties. Intermetallics 77, 23–33. doi:10.1016/j.intermet.2016.06.011
Roy, A., Sreeramagiri, P., Babuska, T., Krick, B., Ray, P. K., and Balasubramanian, G. (2021). Lattice Distortion as an Estimator of Solid Solution Strengthening in High-Entropy Alloys. Mater. Charact. 172, 110877. doi:10.1016/j.matchar.2021.110877
Senkov, O. N., Scott, J. M., Senkova, S. V., Miracle, D. B., and Woodward, C. F. (2011a). Microstructure and Room Temperature Properties of a High-Entropy TaNbHfZrTi alloy. J. Alloys Compd. 509, 6043–6048. doi:10.1016/j.jallcom.2011.02.171
Senkov, O. N., Wilks, G. B., Scott, J. M., and Miracle, D. B. (2011b). Mechanical Properties of Nb 25 Mo 25 Ta 25 W 25 and V 20 Nb 20 Mo 20 Ta 20 W 20 Refractory High Entropy Alloys. Intermetallics 19, 698–706. doi:10.1016/j.intermet.2011.01.004
Shiihara, Y., Kohyama, M., and Ishibashi, S. (2010). Ab Initio local Stress and its Application to Al (111) Surfaces. Phys. Rev. B 81, 075441. doi:10.1103/PhysRevB.81.075441
Tian, F. (2017). A Review of Solid-Solution Models of High-Entropy Alloys Based on Ab Initio Calculations. Front. Mater. 23, 00036. doi:10.3389/fmats.2017.00036
Toda-Caraballo, I., and Rivera-Díaz-Del-Castillo, P. E. (2015). Modelling Solid Solution Hardening in High Entropy Alloys. Acta Mater. 85, 14–23. doi:10.1016/j.actamat.2014.11.014
Toda-Caraballo, I., Wróbel, J., Nguyen-Manh, D., Pérez, P., and Rivera-Díaz-del Castillo, P. (2017). Simulation and Modeling in High Entropy Alloys. JOM 69, 2137–2149. doi:10.1007/s11837-017-2524-2
Tong, Y., Zhao, S., Jin, K., Bei, H., Ko, J. Y., Zhang, Y., et al. (2018). A Comparison Study of Local Lattice Distortion in Ni80Pd20binary alloy and FeCoNiCrPd High-Entropy alloy. Scr. Mater. 156, 14–18. doi:10.1016/j.scriptamat.2018.07.002
Tran, F., Stelzl, J., and Blaha, P. (2016). Rungs 1 to 4 of DFT Jacob’s Ladder: Extensive Test on the Lattice Constant, Bulk Modulus, and Cohesive Energy of Solids. J. Chem. Phys. 144, 204120. doi:10.1063/1.4948636
Van de Walle, A., Asta, M., and Ceder, G. (2002). The alloy Theoretic Automated Toolkit: A User Guide. Calphad: Comput. Coupling Phase Diagrams Thermochem. 26, 539–553. doi:10.1016/S0364-5916(02)80006-2
Varvenne, C., Luque, A., and Curtin, W. A. (2016). Theory of Strengthening in Fcc High Entropy Alloys. Acta Mater. 118, 164–176. doi:10.1016/j.actamat.2016.07.040
Wen, C., Wang, C., Zhang, Y., Antonov, S., Xue, D., Lookman, T., et al. (2021). Modeling Solid Solution Strengthening in High Entropy Alloys Using Machine Learning. Acta Mater. 212, 116917. doi:10.1016/j.actamat.2021.116917
Wu, Z., Bei, H., Pharr, G. M., and George, E. P. (2014). Temperature Dependence of the Mechanical Properties of Equiatomic Solid Solution Alloys with Face-Centered Cubic crystal Structures. Acta Mater. 81, 428–441. doi:10.1016/j.actamat.2014.08.026
Ye, Y. F., Zhang, Y. H., He, Q. F., Zhuang, Y., Wang, S., Shi, S. Q., et al. (2018). Atomic-scale Distorted Lattice in Chemically Disordered Equimolar Complex Alloys. Acta Mater. 150, 182–194. doi:10.1016/j.actamat.2018.03.008
Yu, P., Du, J. P., Shinzato, S., Meng, F. S., and Ogata, S. (2022). Theory of History-dependent Multi-Layer Generalized Stacking Fault Energy - A Modeling of the Micro-substructure Evolution Kinetics in Chemically Ordered Medium-Entropy Alloys. Acta Mater. 224, 117504. doi:10.1016/j.actamat.2021.117504
Zhang, R., Zhao, S., Ding, J., Chong, Y., Jia, T., and Ophus, C. (2020). Short-range Order and its Impact on the CrCoNi Medium-Entropy alloy. Nature 581, 283–287. doi:10.1038/s41586-020-2275-z
Zhang, Y., Zuo, T. T., Tang, Z., Gao, M. C., Dahmen, K. A., Liaw, P. K., et al. (2014). Microstructures and Properties of High-Entropy Alloys. Prog. Mater. Sci. 61, 1–93. doi:10.1016/j.pmatsci.2013.10.001
Zhao, Y. Y., Lei, Z. F., Lu, Z. P., Huang, J. C., and Nieh, T. G. (2019). A Simplified Model Connecting Lattice Distortion with Friction Stress of Nb-Based Equiatomic High-Entropy Alloys. Mater. Res. Lett. 7, 340–346. doi:10.1080/21663831.2019.1610105
Keywords: random alloys, high entropy alloys, first-principles calculation, solid solution strengthening, atomic stress
Citation: Shiihara Y, Itai Y, Lobzenko I and Tsuru T (2022) Atomic Stress State Inside fcc and bcc Random Alloys: A First-Principles Approach. Front. Mater. 9:895626. doi: 10.3389/fmats.2022.895626
Received: 14 March 2022; Accepted: 24 March 2022;
Published: 02 May 2022.
Edited by:
Yue Fan, University of Michigan, United StatesReviewed by:
Jiro Kitagawa, Fukuoka Institute of Technology, JapanShijun Zhao, City University of Hong Kong, Hong Kong SAR, China
Copyright © 2022 Shiihara, Itai, Lobzenko and Tsuru. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yoshinori Shiihara, c2hpaWhhcmFAdG95b3RhLXRpLmFjLmpw
 Yoshinori Shiihara
Yoshinori Shiihara Yuki Itai1
Yuki Itai1 Tomohito Tsuru
Tomohito Tsuru