- Departamento de Física and CICECO—Aveiro Institute of Materials, University of Aveiro, Aveiro, Portugal
Magnetocaloric materials are recognized as one of the major classes of magnetic materials for energy applications, and can be either employed as refrigerants in heat-pumping devices, or in thermomagnetic generators for energy conversion/harvesting. For both applications, having a material that presents a first-order magnetic phase transition is advantageous, as this typically leads to enhanced values of magnetization change in temperature (relevant to energy conversion) and of the magnetocaloric effect (relevant to heat-pumping). We present a brief overview of selected models applied to the simulation of applied magnetic field and temperature-dependent magnetization and magnetic entropy change of first-order magnetic phase transition systems, covering mean-field models such as the Landau theory of phase transitions and the Bean-Rodbell model, up to more recent developments using a Ising-like microscopic model with magnetovolume coupling effects. We highlight the fundamental and practical limitations of employing these models and compare predicted thermodynamic properties.
1 Introduction
Magnetic materials have had, for several decades, wide-spread use in energy applications, including power generation, conditioning, conversion and transportation (Gutfleisch et al., 2011). Since the discovery of the giant magnetocaloric effect (GMCE) in the late 1990s (Pecharsky and Gschneidner, 1997), the use of magnetic materials for room-temperature refrigeration has been gathering the attention from both the scientific and industrial communities (Pecharsky and Gschneidner, 2008). The GMCE is typically observed only for first-order magnetic phase transition (FOMPT) materials, where a strong magnetovolume coupling is present. As the designation implies, the GMCE is considerably larger than the MCE of second-order magnetic phase transition (SOMPT) systems. While technologically challenging, the development and use of FOMPT materials for use in refrigeration devices is now commonplace, as seen from the number of current prototypes using these materials as refrigerants (Kitanovski et al., 2015). More recently, the use of magnetocaloric materials for energy generation from near room temperature thermal energy harvesting has also gathered attention (Waske et al., 2019). In this case, the sharp dependence of magnetization (M) on temperature (T) near the Curie temperature TC of a FOMPT material enhances the energy-harvesting potential of a device, in a tunable operating temperature window. In short, for both refrigeration and thermal energy harvesting, the use of a first-order magnetic phase transition (FOMPT) material presents considerable advantages. The search for new and optimized magnetocaloric materials for these applications is an on-going effort from the community. In this context, the use of magnetism models to both interpret experimental data and predict the magnetic and magnetocaloric performance of materials are valuable tools. Naturally, correctly describing the thermodynamics of a FOMPT is required to ensure the physical soundness of calculations. Nevertheless, when choosing a model to use, practical questions come into play, and in the end, the choice of a particular model becomes the result of the balance between the complexity of the model, the information being sought, and the computational cost.
In this work, we consider three distinct models which have been employed to describe quantitatively describe FOMPT materials, from mean-field models such as the Landau theory of phase transitions, the Bean-Rodbell model, and a microscopic Ising-like model with magnetovolume interactions. We employ these models to simulate both SOMPT and FOMPT systems with similar thermodynamic properties, such as a TC ∼ 300 K for the SOMPT, same spin values and saturation magnetization, and a similar value of critical field for the FOMPT system. Both magnetic field (H) and T dependent M and magnetic entropy change (ΔSM) are simulated for the three considered models. The aim is to compare the obtained results both qualitatively and quantitatively, highlighting the fundamental and practical limitations of employing these models to describe real materials.
2 The Landau theory of phase transitions
The Landau theory of phase transitions has been previously employed to describe the GMCE of FOMPT systems, from describing the magnetoelastic coupling influence on the magnetocaloric effect in ferromagnetic materials (Amaral and Amaral, 2004), and the effect of magnetic irreversibility on estimating the magnetocaloric effect from magnetization measurements (Amaral and Amaral, 2009). The model starts from an expansion of the (Gibbs) Free Energy G on even powers of M, together with an Zeeman-like external field interaction term.
where A, B, and C are the temperature-dependent Landau coefficients. Typically A is assumed to be linear in temperature, establishing the Curie temperature TC of the system: A(T) = A′(T − TC). This linear relation is valid in the susceptibility regime, obeying the Curie law:
where CCurie is the Curie constant of the system. For low M values, the A′ parameter is then equal to the inverse Curie constant. Minimizing the free energy expression of Eq 1, an equation of state is derived:
with a structure that allows fitting the well-known isothermal Arrott plot (H/M versus M2) construction to determine the Landau coefficients’ dependence on temperature from magnetization data. This approach was employed for both FOMPT (Amaral and Amaral, 2004) and SOMPT (Amaral et al., 2005) systems.
Here, we consider a trial system with A′ = 1.5 × 102, and constant B and C coefficients, ±5 × 10−1 and 1 × 10−4 respectively in cgs units, with TC = 300 K. The A′ value was chosen to correspond to the inverse Curie constant of a molecular mean-field system with spin S = 1/2, and a saturation magnetization of 100 emu/g. The chosen B value leads, when negative, to a critical field of ∼ 25 kOe which is within values achievable in commercially available magnetometers with superconducting coils as applied field source.
The M(H, T) and ΔSM(H, T) data of Figure 1, using a positive B coefficient, show how a system with thermomagnetic behavior comparable to real SOMPT systems is obtained, with M around 40 emu/g at 50 kOe near TC, and a maximum value of ΔSM around 12 J/(K.kg) for a field change from 0 to 50 kOe.
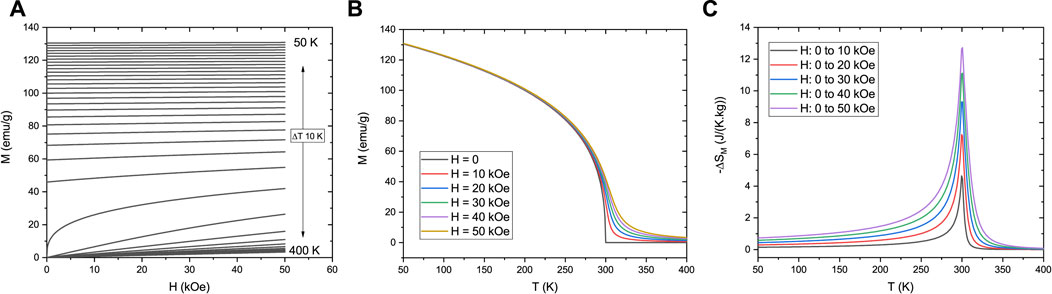
FIGURE 1. (A) Isothermal magnetization M versus applied magnetic field H, of a SOMPT system simulated by the Landau theory of phase transitions. Simulation parameters where chosen to correspond to a magnetic material with spin 1/2 and a saturation magnetization value of 100 emu/g. (B) Isofield M versus temperature T behavior, for H between 0 and 50 kOe. (C) Magnetic entropy change ΔSM dependence on H change and T.
When considering a negative B coefficient value, the system now shows a FOMPT, where discontinuities are present in both the magnetization and magnetic entropy change dependence in T and H, as shown in Figure 2.
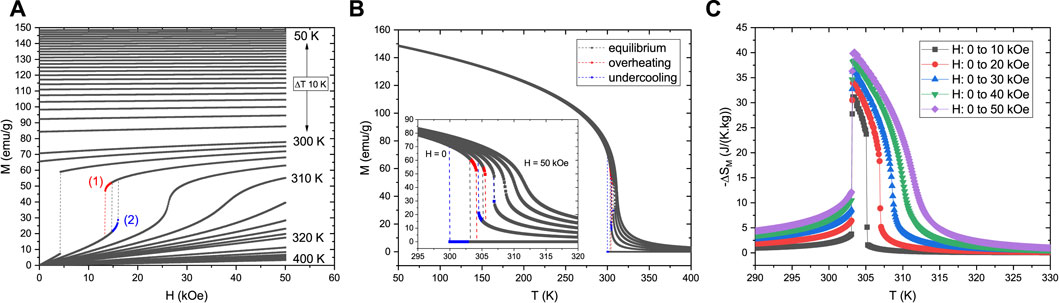
FIGURE 2. (A) Isothermal magnetization M versus applied magnetic field H, of a FOMPT system simulated by the Landau theory of phase transitions. Simulation parameters where chosen to correspond to a magnetic material with spin 1/2 and a saturation magnetization value of 100 emu/g, with a critical field value ∼ 25 kOe. (B) Isofield M versus temperature T behavior, for H between 0 and 50 kOe. (C) Magnetic entropy change ΔSM dependence on H change and T.
As expected, the maximum ΔSM increases considerably, up to values ∼ 40 J/(K.kg). The FOMPT nature is clearly visible in the discontinuities in both M(H, T) and ΔSM(H, T) data. One of the main limitations of the Landau theory of phase transitions, in this context, is visible when the system reaches higher values of M. Due to the equation of state originating from a power expansion in M, the validity of this expansion fails for high M values, and the magnetization does not saturate even at very low T. This is an important fact that is often overlooked when fitting or extrapolating Arrott plots of experimental data in the high-magnetization regime. There is also no deep physical insight from the values of the B and C Landau parameters. One can observe a negative B value and justify its occurrence with effects such as magnetovolume coupling and electron condensation, depending on the particular physics of the system under study, but a quantitative analysis is typically not the objective of employing this model. As we will see in the next section, the use of the Bean-Rodbell model, overcomes some of these limitations.
3 The Bean-Rodbell model
The Bean-Rodbell model is an extention to the Weiss molecular field model, and was first reported in a study on the magnetic properties of MnAs, a system well-known to have strong magneto-volume coupling (Bean and Rodbell, 1962). The model imposes a linear relation between TC and volume, as shown in Eq. 4.
where β is positive and constant, v is volume, v0 the equilibrium volume with no magnetic interactions, and T0 the Curie temperature of the rigid system with v = v0.
For a sufficiently large linear dependence of TC on volume (large β value), the magnetic transition becomes first-order. The crossover point is established via the η parameter, which is defined for a system with compressibility K:
where S is the spin quantum number, N the spin density and kB the Boltzmann constant. The transition is second-order for 0 < η ≤ 1, while for η > 1 the transition is first-order.
For a comparable system with the previous simulations using the Landau theory of phase transitions, we consider the following parameters for our Bean-Rodbell model calculations: S = 1/2, T0 = 300 K, and a N value of 1.077 × 1022 spins/g, which corresponds to a saturation magnetization of 100 emu/g. For simulating a SOMPT, a null η value is used, with data for magnetization and magnetic entropy change shown in Figure 3.
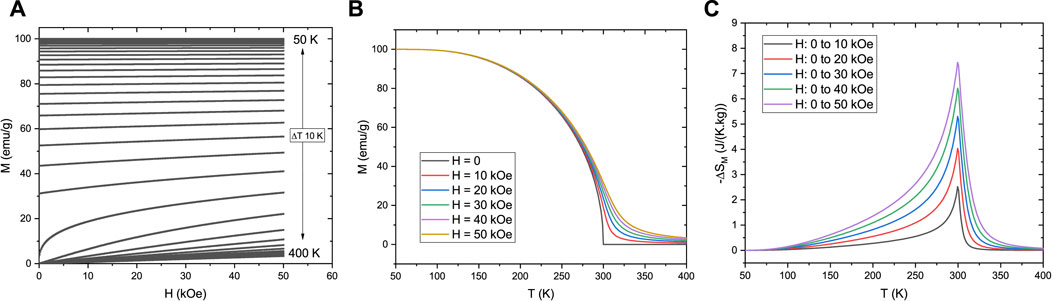
FIGURE 3. (A) Isothermal magnetization M versus applied magnetic field H, of a SOMPT system (η = 0) simulated by the Bean-Rodbell model, with spin 1/2 and a saturation magnetization value of 100 emu/g. (B) Isofield M versus temperature T behavior, for H between 0 and 50 kOe. (C) Magnetic entropy change ΔSM dependence on H change and T.
For simulating a FOMPT, an η value of 1.35 is used, which increases the TC to around 304 K, and leads to a critical field around 2.5 kOe, together with an increase in magnetic entropy change, as shown in Figure 4.
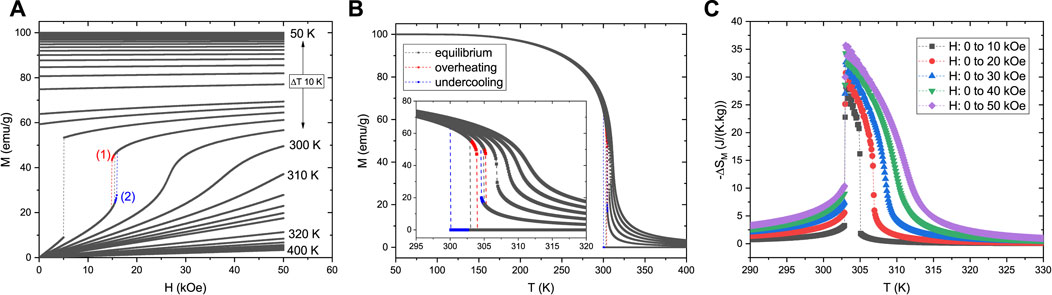
FIGURE 4. (A) Isothermal magnetization M versus applied magnetic field H, of a FOMPT system (η = 1.35) simulated by the Bean-Rodbell model, with spin 1/2 and a saturation magnetization value of 100 emu/g. (B) Isofield M versus temperature T behavior, for H between 0 and 50 kOe. (C) Magnetic entropy change ΔSM dependence on H change and T.
The Bean-Rodbell model simulation results are quite similar to those obtained by the Landau theory of phase transitions, for both the SOMPT and FOMPT. This could only be achieved by establishing comparable systems with the same Curie constant, and adjusting the values of the Landau B and the Bean-Rodbell η parameters to lead to similar values of the critical field. Note, however, how for the Bean-Rodbell data, the M(H, T) data clearly saturates. The use of the model in the high-M region was useful in the simulation of mixed-phase FOMPT materials, and the validity of the use of the Maxwell relation in estimating ΔSM in strongly first-order systems (Amaral and Amaral, 2009; Amaral and Amaral, 2010). It is also worth highlighting that, as opposed to the Landau theory of phase transitions, the fact that physically meaningful parameters such as spin and compressibility are defined in the model, a quantitative analysis of experimental data using the Bean-Rodbell model is possible, for both FOMPT and SOMPT systems (Amaral et al., 2007). Simulations using this model are computationally inexpensive, and it is possible to consider smooth distributions of TC values, with hundreds of points, to describe disordered SOMPT (Amaral et al., 2008; Bahl et al., 2012) and FOMPT (Amaral and Amaral, 2014; Nielsen et al., 2017) systems.
While widely employed in the study of both SOMPT and FOMPT materials, the Bean-Rodbell model is not the right model for predicting a given material’s magnetic and magnetocaloric performance. For this, an ab initio approach is required, which can start from using Density Functional Theory (DFT) to estimate relevant magnetic and physical properties of a given system. DFT calculations are typically performed at 0 K, so it is required to feed this parameters to a given model for estimating thermodynamic properties. A relatively straightforward approach is to estimate the Heisenberg exchange parameter J of a given material using DFT, and then use the calculated value in an Ising or Heisenberg model. Naturally, for describing a magneto-volume driven FOMPT, the model needs to include this coupling. In the next section, we will consider an Ising-like microscopic model with magnetovolume interactions.
4 Microscopic model with magnetovolume interactions
A FOMPT system can be described in simple microscopic models, such as the Ising and Heisenberg models, by including an explicit dependence of the magnetic exchange parameter J, together with a volume energy potential (Amaral et al., 2016):
where J is the magnetic exchange parameter between Si and Sj nearest-neighbour spins, v volume and K compressibility.
All the parameters required to simulate a given (real) magnetic system using this approach can be readily obtained by existing DFT packages. Estimating J for multi-component alloys is particularly relevant in the study of magnetocaloric materials, so the use of the Liechtenstein method (Liechtenstein et al., 1987) in systems where fractional site occupancy is accurately described by the Coherent Potential Application (Yonezawa and Morigaki, 1973) is a practical approach. These capabilities are available in the SPR-KKR (Ebert, 2005) and openmx (Ozaki et al., 2013) DFT packages. The estimate of the full M(H, T) and ΔSM(H, T) dependencies can be challenging using the standard Monte Carlo Metropolis method (Metropolis et al., 1953), as each (H, T) pair will require an independent calculation, and for the case of FOMPT the stabilization of the two order parameters, M and v is difficult and time-consuming. Another approach is to obtain the thermodynamic properties of the system with previously calculated Joint Density of States (JDOS) estimates. The JDOS of a given model (discrete or continuous) and of a given lattice (e. g. 2D, 3D) can be calculated by Monte Carlo methods such as the Wang-Landau method (Wang and Landau, 2001; Zhou et al., 2006), Random Path Sampling (Amaral et al., 2014) and the recently reported Flat Scan Sampling method (Inácio et al., 2022). As the JDOS is T, H and v independent, the full calculation of M(H, T) and ΔSM(H, T) dependencies for both SOMPT and FOMPT systems is robust and quickly achievable using a regular personal computer.
For describing a comparable system to the previous mean-field simulations, we consider the Ising model of 512 spin 1/2 particles in a 3D lattice. In the case of the rigid system with a SOMPT, the J value is chosen to lead to a TC of 300 K. The field interaction is calculated with a magnetic moment value of 1 μB per spin. Imposing a 100 emu/g saturation magnetization, a similar behavior compared to the previous mean-field models is obtained for magnetization and magnetic entropy change, as seen in Figure 5.
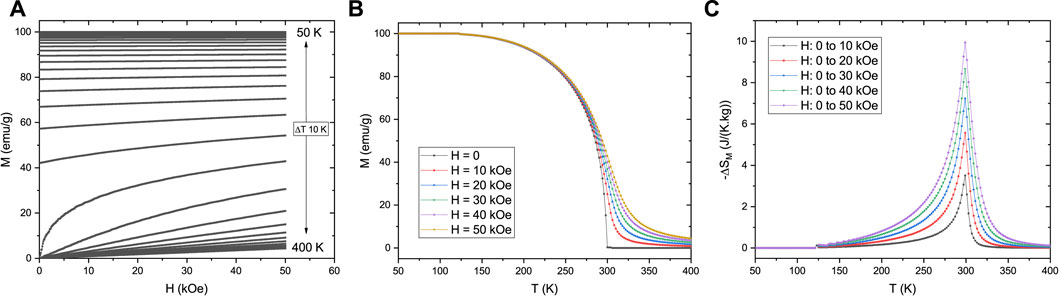
FIGURE 5. (A) Isothermal magnetization M versus applied magnetic field H, of a SOMPT system (J′ = 0) from a Ising spin 1/2 3D lattice with 512 spins, considering a saturation magnetization of 100 emu/g and a magnetic moment value of 1 μB per spin. (B) Isofield M versus temperature T behavior, for H between 0 and 50 kOe. (C) Magnetic entropy change ΔSM dependence on H change and T.
Considering now a compressible system, with a linear dependence of J on volume, J(v) = J0 + J′(v − v0)/v0 and a K value of 50, a J′ value of 2.8 (in units of J0) leads to a FOMPT with a critical field of ∼ 25 kOe, comparable to the previous simulations of the Landau Theory of phase transitions and the Bean-Rodbell model, as shown in Figure 6.
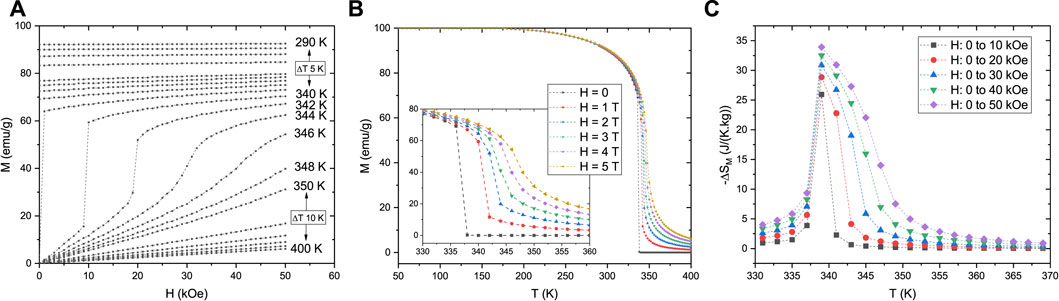
FIGURE 6. (A) Isothermal magnetization M versus applied magnetic field H, of a FOMPT system (J′ = 2.8) from a compressible Ising spin 1/2 3D lattice with 512 spins, considering a saturation magnetization of 100 emu/g and a magnetic moment value of 1 μB per spin. (B) Isofield M versus temperature T behavior, for H between 0 and 50 kOe. (C) Magnetic entropy change ΔSM dependence on H change and T.
While qualitatively the behavior of the Ising model simulations for both SOMPT and FOMPT systems are similar to the results of the mean-field models, a quantitative comparison highlights some differences. While for the mean-field models the change of TC between the SOMPT and FOMPT is relatively small at around 3 K (∼ 1% of TC), for the case of the microscopic model, this value is substantially higher at ∼ 40 K (∼ 13% of TC). In terms of the observed maximum values of −ΔSM for an applied field of 50 kOe, for both SOMPT and FOMPT systems the obtained results are similar for all the considered models. These increase from ∼ 10 J/(K.kg) of the SOMPT systems, to values ∼ 35 J/(K.kg) for the FOMPT systems. These results highlight how these fundamentally different models can lead to quantitatively similar behaviors for both the M(H, T) and ΔSM(T, H) dependencies, with results comparable to real SOMPT and FOMPT materials.
5 Overview
In this work, we have explored three distinct magnetic models that can simulate the relevant thermodynamic properties of both SOMPT and FOMPT systems for application in magnetic refrigeration and thermal energy harvesting. One of the main objectives was to consider equivalent SOMPT and FOMPT magnetic systems with TC values around room temperature, and to compare the simulated results, particularly M(H, T) and ΔSM(H, T), which are the main thermodynamic properties for these applications.
Landau theory allows to easily interpret experimental magnetization data by fitting the isothermal Arrott plots. The observation of negative values of the B coefficient (negative slopes in the Arrott plots) is a sign of a FOMPT. With a full description of the temperature dependence of the A, B and C coefficients, it is straightforward to smooth, interpolate and, away for saturation, to extrapolate the (H, T) dependence of magnetization and magnetic entropy change data. Still, while it is possible to qualitatively interpret the values of the model parameters, they do not have a straightforward or quantitative physical interpretation. Nevertheless, the obtained M(H, T) and ΔSM(H, T) data are physically and quantitatively sound.
The Bean-Rodbell model, as an extension of the Weiss molecular mean-field model, while also a phenomenological model, has physical meaning to all its parameters. This allows to interpret experimental data of both SOMPT and FOMPT systems and estimate fundamental system properties such as spin value and quantify magnetovolume coupling. The validity of the simulations near M saturation, in contrast to the Landau theory, allows for accurate description of GMCE systems in a wider temperature range, including disordered and mixed phase systems. While the Bean-Rodbell simulation parameters have physical meaning, it is impossible to directly obtain input values of TO and β from ab initio calculations at 0 K. To allow the prediction of the properties of a given material from DFT calculations at 0K, then a different approach is required.
A microscopic model approach, while typically more expensive in terms of computational cost, allows for more intricate and detailed simulation of model systems. As the main simulation parameter J, together with its dependence on system volume J(v), are obtainable via DFT calculations, an in silico approach to predict the thermo-magnetic properties of new and optimized magnetic materials is possible. The use of prior JDOS of models such as the Ising and Heisenberg models, lowers computational cost for simulation of materials for arbitrary values of J and J(v), and allows the description of the full M(H, T) and ΔSM(H, T) dependencies.
Our simulation results for the three models, for both SOMPT and FOMPT systems are both qualitatively and quantitatively in agreement. The M(H, T) and ΔSM(H, T) behaviors are similar, particularly the increase of the maximum ΔSM value due to the change of a SOMPT to a FOMPT. The most notable difference between our obtained results is the larger change of TC of the FOMPT system compared to the SOMPT, in the case of the compressible Ising model simulations. We highlight that all three models are physically sound, and the choice of which one to use will depend if the purpose is to interpret experimental data, or the in silico prediction of the performance of new and optimized magnetic refrigerants and ferromagnets for thermal energy harvesting.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was developed within the scope of the project CICECO-Aveiro Institute of Materials, UIDB/50011/2020, UIDP/50011/2020 and LA/P/0006/2020, financed by national funds through the FCT/MEC (PIDDAC).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Amaral, J. S., and Amaral, V. S. (2014). Disorder effects in giant magnetocaloric materials. Phys. Stat. Sol. A 211, 971–974. doi:10.1002/pssa.201300749
Amaral, J. S., and Amaral, V. S. (2010). On estimating the magnetocaloric effect from magnetization measurements. J. Magn. Magn. Mat. 322, 1552–1557. doi:10.1016/j.jmmm.2009.06.013
Amaral, J. S., and Amaral, V. S. (2009). The effect of magnetic irreversibility on estimating the magnetocaloric effect from magnetization measurements. Appl. Phys. Lett. 94, 042506. doi:10.1063/1.3075851
Amaral, J. S., Fortunato, N. M., Amorim, C. O., Gonçalves, J. N., and Amaral, V. S. (2016). “Giant magnetocaloric effect of compressible ising and heisenberg lattices,” in Proceedings of the 7th International Conference on Magnetic Refrigeration at Room Temperature (Thermag VII), Turin, Italy, 11 - 14 September 2016, 30019341. doi:10.18462/iir.thermag.2016.0200
Amaral, J. S., Gonçalves, J. N., and Amaral, V. S. (2014). Thermodynamics of the 2-D ising model from a random path sampling method. IEEE Trans. Magn. 50, 1–4. doi:10.1109/tmag.2014.2326713
Amaral, J. S., Reis, M. S., Amaral, V. S., Mendonça, T. M., Araújo, J. P., Sá, M. A., et al. (2005). Magnetocaloric effect in Er- and Eu-substituted ferromagnetic La-Sr manganites. J. Magn. Magn. Mat. 290-291, 686–689. doi:10.1016/j.jmmm.2004.11.337
Amaral, J. S., Silva, N. J. O., and Amaral, V. S. (2007). A mean-field scaling method for first- and second-order phase transition ferromagnets and its application in magnetocaloric studies. Appl. Phys. Lett. 91, 172503. doi:10.1063/1.2801692
Amaral, J. S., Tavares, P. B., Reis, M. S., Araújo, J. P., Mendonça, T. M., Amaral, V. S., et al. (2008). The effect of chemical distribution on the magnetocaloric effect: A case study in second-order phase transition manganites. J. Non-cryst. Sol. 354, 5301–5303. doi:10.1016/j.jnoncrysol.2008.05.078
Amaral, V. S., and Amaral, J. S. (2004). Magnetoelastic coupling influence on the magnetocaloric effect in ferromagnetic materials. J. Magn. Magn. Mat. 272-276, 2104–2105. doi:10.1016/j.jmmm.2003.12.870
Bahl, C. R. H., Bjørk, R., Smith, A., and Nielsen, K. K. (2012). Properties of magnetocaloric materials with a distribution of curie temperatures. J. Magn. Magn. Mat. 324, 564–568. doi:10.1016/j.jmmm.2011.08.044
Bean, C. P., and Rodbell, D. S. (1962). Magnetic disorder as a first-order phase transformation. Phys. Rev. 126, 104–115. doi:10.1103/PhysRev.126.104
Gutfleisch, O., Willard, M. A., Brück, E., Chen, C. H., Sankar, S. G., and Liu, J. P. (2011). Magnetic materials and devices for the 21st century: Stronger, lighter, and more energy efficient. Adv. Mater. 23, 821–842. doi:10.1002/adma.201002180
Inácio, J. C., Ferreira, A. L., and Amaral, J. S. (2022). Accurate estimate of the joint density of states via flat scan sampling. arXiv arXiv:2203.02718. doi:10.48550/arXiv.2203.02718
Kitanovski, A., Tušek, J., Tomc, U., Plaznik, U., Ošbolt, M., and Poredoš, A. (2015). Magnetocaloric energy conversion - from theory to applications. Berlin: Springer.
Liechtenstein, A. I., Katsnelson, M. I., Antropov, V. P., and Gubanov, V. A. (1987). Local spin density functional approach to the theory of exchange interactions in ferromagnetic metals and alloys. J. Magn. Magn. Mat. 67, 65–74. doi:10.1016/0304-8853(87)90721-9
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E. (1953). Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1092. doi:10.1063/1.1699114
Nielsen, K. K., Bahl, C. R. H., Smith, A., and Bjørk, R. (2017). Spatially resolved modelling of inhomogeneous materials with a first order magnetic phase transition. J. Phys. D. Appl. Phys. 50, 414002. doi:10.1088/1361-6463/aa86e2
Ozaki, T., Kino, H., and Yu, J. (2013) Openmx (open source package for material explorer). ver. 3.7.
Pecharsky, V. K., and Gschneidner, K. A. (1997). Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 78, 4494–4497. doi:10.1103/PhysRevLett.78.4494
Pecharsky, V. K., and Gschneidner, K. A. (2008). Thirty years of near room temperature magnetic cooling: Where we are today and future prospects. Int. J. Refrig. 31, 945–961. doi:10.1016/j.ijrefrig.2008.01.004
Wang, F., and Landau, D. P. (2001). Efficient, multiple-range random walk algorithm to calculate the density of states. Phys. Rev. Lett. 86, 2050–2053. doi:10.1103/physrevlett.86.2050
Waske, A., Dzekan, D., Sellschopp, K., Berger, D., Stork, A., Nielsch, K., et al. (2019). Energy harvesting near room temperature using a thermomagnetic generator with a pretzel-like magnetic flux topology. Nat. Energy 4, 68–74. doi:10.1038/s41560-018-0306-x
Yonezawa, F., and Morigaki, K. (1973). Coherent potential approximation. basic concepts and applications. Prog. Theor. Phys. Suppl. 53, 1–76. doi:10.1143/PTPS.53.1
Keywords: magnetic materials, magnetic refrigeration, energy harvesting, first-order phase transitions, magnetovolume coupling
Citation: Amaral JS and Amaral VS (2023) Simulating the giant magnetocaloric effect-from mean-field theory to microscopic models. Front. Mater. 10:1037396. doi: 10.3389/fmats.2023.1037396
Received: 05 September 2022; Accepted: 23 January 2023;
Published: 03 February 2023.
Edited by:
Sidney JL Ribeiro, São Paulo State University, BrazilReviewed by:
Kalipada Das, University of Calcutta, IndiaCopyright © 2023 Amaral and Amaral. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: V. S. Amaral, dmFtYXJhbEB1YS5wdA==
 J. S. Amaral
J. S. Amaral V. S. Amaral
V. S. Amaral