Thermal transport of glasses via machine learning driven simulations

Accessing the thermal transport properties of glasses is a major issue for the design of production strategies of glass industry, as well as for the plethora of applications and devices where glasses are employed. From the computational standpoint, the chemical and morphological complexity of glasses calls for atomistic simulations where the interatomic potentials are able to capture the variety of local environments, composition, and (dis)order that typically characterize glassy phases. Machine-learning potentials (MLPs) are emerging as a valid alternative to computationally expensive ab initio simulations, inevitably run on very small samples which cannot account for disorder at different scales, as well as to empirical force fields, fast but often reliable only in a narrow portion of the thermodynamic and composition phase diagrams. In this article, we make the point on the use of MLPs to compute the thermal conductivity of glasses, through a review of recent theoretical and computational tools and a series of numerical applications on vitreous silica and vitreous silicon, both pure and intercalated with lithium.

1 Introduction

The pursuit of improving the thermal conductivity properties of amorphous solids is central to contemporary materials science and engineering (Mauro, 2014). Glasses, characterized by their lack of crystalline order, possess unique attributes that make them invaluable across a wide range of applications. One of the prominent features of this class of materials is a inherently low thermal conductivity, a result of their disordered structure. This property is useful in various fields, such as aerospace engineering (Kotz et al., 2017; Hu et al., 2020), electronics (Pasquarello et al., 1998), and pharmaceutical industries (Niu et al., 2018). In contrast, specific industrial applications demand a nuanced balance in the thermal properties of glasses. For example, nuclear reactors and nuclear weapon decommissioning generate radioactive waste (Ewing, 2015) that must be safely stored for exceptionally long time. This waste can be solidified through vitrification, preventing accidental radionuclide release thanks to the amorphous structure of glasses, which provides radiation protection and outstanding chemical durability, thus enabling thousands of years of safe storage (Ojovan et al., 2019). Here, effective heat management is crucial, as high thermal conductivity enhances vitrification efficiency, influencing melt rate and glass homogeneity (Sugawara et al., 2014; Kim et al., 2015). Moreover, in long-term storage, elevated heat conductivity rapidly dissipates decay-generated heat, avoiding issues like high-temperature-assisted crystallization, porosity, and cracks (Matzke and Vernaz, 1993). During the last decades, a huge effort has been put forward to access the structural and thermodynamical properties of the glasses employed for nuclear waste vitrification, mainly (boro)silicates, from both the experimental (Matzke and Vernaz, 1993; Sugawara et al., 2014; Kim et al., 2015; Kim and Morita, 2017) and the computational sides (Pedesseau et al., 2015; Sørensen et al., 2019; Sørensen et al., 2021; Pedone et al., 2022; Sørensen et al., 2022; Bertani et al., 2023; Pallini et al., 2023). Nevertheless, a microscopic description of thermal conduction in these materials beyond the celebrated Cahill-Pohl model (Cahill and Pohl, 1988), as a function of temperature and composition, is still missing. The lack of computational studies on thermal conduction is shared by another important application, namely, solid-state batteries, where several designs leverage amorphous solid electrolytes (Manthiram et al., 2017; Zhao et al., 2020; Fujita et al., 2023; Janek and Zeier, 2023; Landry et al., 2023). Here, the glassy phase is also characterized by a diffusive species (like Li⁺ or Na⁺ ions) which poses further challenges for the microscopic simulation of heat transport, since lattice methods cannot be formally applied due to the lack of well defined positions of mechanical equilibrium.

Machine-learning (ML) is an increasingly popular tool in materials modeling due to its ability to train on extensive datasets precise models able to match a wide array of target properties. One route is to leverage datasets of mechanical and functional glass properties to discover new materials (Mauro et al., 2016; Onbaşlı et al., 2020), or to predict end-properties such as solubilities (Brauer et al., 2007), dissolution rates (Anoop Krishnan et al., 2018), or transition temperatures (Cassar et al., 2018), to name a few (Liu et al., 2021). By taking a microscopic approach, one can build surrogate models of ab initio interatomic potentials able to drive simulations to sample all kinds of properties of amorphous materials that can be accessed by atomistic simulations (Allen and Feldman, 1989; Sosso et al., 2012; Deringer and Csányi, 2017; Paruzzo et al., 2018; Sosso et al., 2018; Sivaraman et al., 2020; Deringer et al., 2021; Islam et al., 2021; Brorsson et al., 2022; Guo et al., 2022; Langer et al., 2023; Liu et al., 2023; Xie et al., 2023).

In this article, we provide an overview of the microscopic theory of heat transport in glasses. Our focus is on methods that effectively utilize ML potentials (MLPs) for computing thermal conductivity. We explore two primary approaches: lattice dynamics, suitable for solids at temperatures significantly below their melting point, enabling the incorporation of quantum-mechanical effects in heat transport; and equilibrium molecular dynamics (EMD) simulations, a versatile tool for sampling material properties, which however is limited in its ability to account for the aforementioned quantum effects. While the basic theoretical grounds on the use of MLPs for thermal transport are well known (Sosso et al., 2012), the effects of the finite size of samples, the applicability of lattice methods, and spurious effects due to particle diffusion have not been extensively tested, even on simple systems. The methods, described in Section 2, are showcased via MLPs trained on an empirical force-field for vitreous silica in Section 3.1. Section 3.2 discusses the existing challenges and limitations of MLPs in lattice-dynamics calculations, due to unphysically large scattering rates exhibited by low-frequency normal modes. Finally, the need for large-scale simulations is investigated in Section 3.3 on vitreous Li_xSi_1−x at different Li concentrations and system sizes.

2 Materials and methods

2.1 Thermal transport in glasses

Heat transport is characterized by the value of the thermal conductivity, κ, whose linear-response value is given by the Green-Kubo (GK) formula, whose classical expression reads (Green, 1952; Kubo, 1957; Kubo et al., 1957; Baroni et al., 2020)

$\kappa =\frac{1}{3\mathrm{\Omega }{k}_{\text{B}}{T}^2}{\int }_0^{\infty }⟨{\mathbf{J}}_q\left(t\right)\cdot {\mathbf{J}}_q\left(0\right)⟩dt,(1)$

where Ω is the system’s volume, k_B the Boltzmann constant, T the temperature, and J_q the heat flux. The factor 1/3 comes from the assumption of isotropy. The temperature-dependent behavior of κ in glasses exhibits three distinctive, universally recognized patterns (Beltukov et al., 2013). At extremely low temperatures, specifically when T ≲ 2K, the predominant scattering mechanism involves quantum tunneling between various local minima within the glass energy landscape, resulting in κ ∼ T² (Phillips, 1987; Buchenau et al., 1992; Lubchenko and Wolynes, 2003). As the temperature reaches a few tens of kelvins, thermal conductivity increases and eventually reaches a plateau value. Despite the absence of a firmly established theoretical consensus in the literature, this phenomenon appears to be linked to the transition from a regime dominated by quantum processes to one where propagating waves are scattered by random disorder (Buchenau et al., 1992; Lubchenko and Wolynes, 2003; Schirmacher, 2006; Beltukov et al., 2013). Beyond the plateau, the behavior of the thermal conductivity is governed by the anharmonic decay of normal modes (Isaeva et al., 2019; Simoncelli et al., 2019), and κ starts increasing again until it saturates to its high-temperature value. We focus here on the latter range of temperatures, which is relevant for applications and can be investigated by means of atomistic simulations.

There are different techniques for computing κ. Equilibrium methods require the calculation of the heat flux appearing in Eq. 1 (Baroni et al., 2020), or the energy density (Drigo et al., 2023). Equivalently, one can compute the energy flux along with other relevant mass fluxes, as discussed below. A versatile approach for obtaining these fluxes is through EMD simulations, which allow to sample the energy flux at all orders within anharmonic perturbation theory. A downside of EMD simulations is that it is currently impossible to sample the energy flux including nuclear quantum effects (Habershon et al., 2013), despite extensive efforts are being made in this direction [see, e.g., (Sutherland et al., 2021; Siciliano et al., 2023; Wang et al., 2023) and citations therein]. In solids, an alternative approach lies in exploiting lattice dynamics, at the cost of neglecting high-order anharmonic interactions. At temperatures well below the melting point, atomic nuclei undergo small oscillations around well-defined equilibrium positions. This behavior allows us to represent the dynamics with harmonic normal modes, which, in crystals, are described as phonon quasiparticles. In the harmonic approximation, the normal modes feature infinite lifetimes, resulting in infinite thermal conductivity, regardless of the presence of (harmonic) perturbations, such as disorder (Fiorentino et al., 2023a). However, when anharmonic interactions are appropriately accounted for, e.g., through perturbation theory (Isaeva et al., 2019; Simoncelli et al., 2019), they induce temperature-dependent frequency shifts and broadenings, impacting phonon lifetimes and ultimately determining the thermal conductivity of materials.

Using lattice dynamics to express the heat flux in Eq. 1 in terms of phonon creation and annihilation operators, one can compute the GK formula for κ in the quasi-harmonic Green-Kubo (QHGK) approximation (Isaeva et al., 2019; Fiorentino and Baroni, 2023) as

$\kappa =\frac{1}{3\mathrm{\Omega }}{\displaystyle \sum _{\mu \nu }}{C}_{\mu \nu }{\left|v_{\mu \nu }\right|}^2\frac{{\gamma }_{\mu }+{\gamma }_{\nu }}{{\left({\omega }_{\mu }-{\omega }_{\nu }\right)}^2+{\left({\gamma }_{\mu }+{\gamma }_{\nu }\right)}^2},(2)$

where ω_μ and γ_μ are the angular frequency and anharmonic linewidth of the μth normal mode, respectively; v_μν is a generalized velocity matrix, and

$C_{\mu \nu }=\frac{{\hslash }^2{\omega }_{\nu }{\omega }_{\mu }}{T}\frac{n\left({\omega }_{\nu }\right)-n\left({\omega }_{\mu }\right)}{\hslash \left({\omega }_{\mu }-{\omega }_{\nu }\right)}(3)$

is a generalized two-mode isochoric heat capacity, $n(\omega )={[{\mathrm{e}}^{\hslash \omega /(k_{\text{B}}T)}-1]}^{-1}$ being the Bose-Einstein (BE) occupation function.

The QHGK approach employs two interconnected approximations (Caldarelli et al., 2022; Fiorentino and Baroni, 2023). The first is the dressed bubble approximation, where four-point correlation functions among phonon creation and annihilation operators are factorized into products of two-point correlation functions, neglecting vertex corrections (Fiorentino and Baroni, 2023). This implies that normal modes decay independently, each interacting with a common heat bath. The second approximation, termed Markovian, disregards memory effects in the heat bath-normal mode interaction (Fiorentino and Baroni, 2023). The combination of these approximations leads to four-point correlation functions being expressed using single-body greater Green’s functions, denoted by $g_{\mu }^{>}(t)=-\mathrm{i}(n_{\mu }+1){\mathrm{e}}^{-\mathrm{i}{\omega }_{\mu }t-{\gamma }_{\mu }|t|}$. The quasi-harmonic hypothesis requires ${\gamma }_{\mu }^2/{\omega }_{\mu }^2\ll 1$, implying that only nearly-degenerate modes with |ω_μ − ω_ν|≲ γ_μ + γ_ν significantly contribute to heat conductivity. The QHGK approximation works on crystals and glasses alike, reducing to the result of the Boltzmann Transport Equation in the former case, and—at the expense of neglecting anharmonic effects—to the Allen-Feldman (AF) model of harmonic disordered solids in the latter (Isaeva et al., 2019; Barbalinardo et al., 2020; Fiorentino and Baroni, 2023). Neglecting anharmonic effects is no trivial matter—it remarkably transforms the finite bulk thermal conductivity of a glass into an infinite quantity, thereby emphasizing the AF calculations’ qualitative accuracy driven solely by size effects (Fiorentino et al., 2023a; Fiorentino et al., 2023b).

If compared with crystals, glasses present an additional complexity in numerical computations due to their inherent aperiodic nature (Fiorentino et al., 2023b). The customary application of periodic boundary conditions (PBC) to finite simulation cells, from which quantities in Eq. 2 are derived, requires cautious consideration of size effects. While the physical symmetry of crystals allows for calculations on a fine mesh in reciprocal space, in glasses the same approach is not feasible without introducing spurious contributions to the thermal conductivity (Fiorentino et al., 2023b). Nonetheless, size extrapolation remains possible by leveraging the asymptotic Debye expression of the thermal conductivity of propagons—the low-frequency normal modes in glasses characterized by wave-like properties, including well-defined dispersion with small broadening (Allen et al., 1999; Fiorentino et al., 2023b).

Using lattice dynamics requires to be able to compute second and third-order interatomic force constants, i.e., the second and third partial derivatives of the potential energy with respect to nuclear coordinates at equilibrium (Barbalinardo et al., 2020). This can be achieved through finite differences (Narasimhan and Vanderbilt, 1991; Tang et al., 2010) or perturbation theory (Paulatto et al., 2013), with the former method being more common. For large systems (i.e., containing tens of thousands of atoms) calculating interatomic force constants is computationally feasible using empirical force fields, but becomes impractical when pursued ab initio due to the $N_{\text{atoms}}^2$ scaling of second and $N_{\text{atoms}}^3$ scaling of third-order force constants. In principle, MLPs offer a partial remedy, significantly expediting interatomic force computations. Regrettably, practical implementation is often spoiled by pronounced numerical noise in interatomic force constants, impeding the computation of anharmonic linewidths through Fermi’s golden rule (Barbalinardo et al., 2020), as it will be showcased below by a toy example involving vitreous silica. Inaccurate anharmonic linewidths severely hinder the computation of heat conductivities, thereby rendering the entire lattice dynamical workflow unfeasible. This concern is particularly relevant at low frequencies (Bruns et al., 2022), even for MLPs with good performances within the medium to high-frequency range. A potential strategy to mitigate this issue entails substituting finite-difference third-order derivatives with analytical ones, exploiting the differentiabilty of MLP descriptors through, e.g., automatic differentiation (Langer et al., 2023).

Therefore, while the challenge of deriving interatomic force constants from MLPs is under scrutiny, their accuracy in reproducing ab initio results can be leveraged in MD simulations through the GK equation, Eq. 1.

2.2 Thermal conductivity from molecular dynamics simulations

The GK formula requires an expression for the heat flux. Equivalently, one can combine the energy flux with all the independent mass fluxes of the chemical species in the material (Bertossa et al., 2019; Baroni et al., 2020). The latter option is often preferable, since all the needed fluxes are readily available from EMD simulations, while the heat flux also necessitates computing partial enthalpies (De Groot and Mazur, 1962) through post-processing (Debenedetti, 1988).

The energy flux is the first spatial moment of the time derivative of the energy density (Baroni et al., 2020):

$\begin{array}{ll}\hfill {\mathbf{J}}_E\left(t\right)& =\int \mathbf{r}\dot{e}\left(\mathbf{r},t\right){\mathrm{d}}^{3}r\hfill \\ \hfill & =\int \mathbf{r}{\displaystyle \sum _{\ell =1}^N}\left[\frac{\partial e\left(\mathbf{r},t\right)}{\partial {\mathbf{R}}_{\ell }}\cdot {\dot{\mathbf{R}}}_{\ell }+\frac{\partial e\left(\mathbf{r},t\right)}{\partial {\mathbf{P}}_{\ell }}\cdot {\mathbf{f}}_{\ell }\right]{\mathrm{d}}^{3}r,\hfill \end{array}(4)$

where R_ℓ and P_ℓ are the position and linear momentum of the ℓth atom, respectively, and f_ℓ is force acting on it. There is no a priori correct way to define the energy density of a condensed matter system. However, this ambiguity does not pose an issue, as this quantity is not directly measurable in experiments. Moreover, quantities dependent on it, such as thermal conductivity, remain unaffected by the precise expression of local densities. This concept is referred to as the gauge invariance of transport coefficients (Baroni et al., 2020; Grasselli and Baroni, 2021).

The explicit expression of the energy flux depends on the Hamiltonian of the system, which, for a classical system of N particles, takes the general form:

$\mathcal{H}={\displaystyle \sum _{\ell =1}^N}\frac{P_{\ell }^2}{2M_{\ell }}+\mathcal{V}\left({\mathbf{R}}_1,\dots ,{\mathbf{R}}_N\right),(5)$

where $\mathcal{V}$ denotes the potential energy. Given the gauge-invariance principle, any local breakdown of the energy density into atomic contributions is suitable for computing the energy flux (Baroni et al., 2020; Grasselli and Baroni, 2021). A valid choice is thus

$e\left(\mathbf{r},t\right)={\displaystyle \sum _{\ell =1}^N}{ϵ}_{\ell }\left(t\right)\delta \left(\mathbf{r}-{\mathbf{R}}_{\ell }\left(t\right)\right),(6)$

where each atomic energy, ϵ_ℓ, is concentrated on the respective atom and can be expressed as:

${ϵ}_{\ell }=\frac{P_{\ell }^2}{2M_{\ell }}+{\mathcal{V}}_{\ell },(7)$

with the first term representing atomic kinetic energy and the second indicating the portion of potential energy assigned to the ℓth atom, such that $\mathcal{V}={\sum }_{\ell }{\mathcal{V}}_{\ell }$. These atomic energies are phase-space variables dependent on time through atomic positions and momenta. Consequently, the energy flux in Eq. 4 becomes

${\mathbf{J}}_E\left(t\right)={\displaystyle \sum _{\ell =1}^N}\left[{ϵ}_{\ell }{\dot{\mathbf{R}}}_{\ell }-{\displaystyle \sum _{{\ell }^{\prime }=1}^N}\frac{\partial {\mathcal{V}}_{{\ell }^{\prime }}}{\partial {\mathbf{R}}_{\ell }}\cdot {\dot{\mathbf{R}}}_{\ell }\left({\mathbf{R}}_{\ell }-{\mathbf{R}}_{{\ell }^{\prime }}\right)\right].(8)$

This equation is well-defined in PBC, as it solely depends on interatomic distances calculated using the minimum-image convention. As such, the formula proves suitable for MD simulations involving bulk systems.

The concepts discussed thus far are applicable to both empirical force fields (FFs) and MLPs, regardless of the number of chemical species in the system (Bertossa et al., 2019). In the case of the latter, it is possible to generate MD simulations of ab initio quality to sample the relevant fluxes, including the energy flux of Eq. 8, thus leading to the computation of κ. This approach becomes especially significant for glasses, where, as previously mentioned, challenges arise in lattice-dynamical calculations involving MLPs. While for semi-empirical FFs assigning the atomic energies in Eq. 7 might seem reasonable and simple, especially in the case of pairwise potentials, it is less so in the case of MLPs. MLPs typically rely on a decomposition of the global target quantity into local, atom-centered contributions. This approach offers several advantages, such as computational scalability and the possibility of retrospective interpretation of patterns of local contributions, provided that local predictions are sufficiently “rigid”, i.e., that their value is robust under perturbations of the training set and/or model parameters (Chong et al., 2023).

3 Results

In this Section we first develop, for demonstration purposes, a dataset for the paradigmatic amorphous solid vitreous silica (v-SiO₂) based on a referece semi-empirical FF. We train different MLPs on this dataset, and analyze their ability in reproducing thermal conductivity calculations. We then discuss the current limitations of lattice dynamics in thermal conductivity calculations with MLPs, and how these are absent in EMD simulations. We finally apply GKMD to an amorphous alloy useful in the context of solid-state electrolytes.

3.1 Toy model of vitreous silica

The reference potential is a Tersoff FF developed in Munetoh et al. (2007) as a short-range potential able to describe the amorphous phase of silica with relatively good accuracy. We choose a short-range reference potential in order to keep the model simple; moreover, the MLP to be trained is rigorously short-range, even if strategies to incorporate bona fide long-range interactions exist and are being developed (Grisafi and Ceriotti, 2019; Veit et al., 2020; Xie et al., 2020; Ko et al., 2021; Zhang et al., 2022; Huguenin-Dumittan et al., 2023). The dataset is generated starting from 100 independently quenched glassy samples, equilibrated at 10 different temperatures ranging from 300 to 7,000 K. From each of the 100 simulations, 500 uncorrelated configurations are drawn once every 10 ps. The dataset thus comprises 50,000 glassy and molten configurations. Further details can be found in the Supplementary Material.

We trained a committee of four deep neural network DeePMD potentials (DPs) (Wang et al., 2018; Lu et al., 2021; Zeng et al., 2023) smooth edition (Zhang et al., 2018) and a neuroevolution potential (NEP) (Fan et al., 2021) to reproduce energies, forces and virials of the dataset. All the MLPs have a cutoff of 3 Å, and are trained for more than 400 epochs to ensure the proper minimization of the loss function. The optimization of the loss function for the DPs is performed through the Adam stochastic gradient descent (Kingma and Ba, 2017), while for the NEP via a genetic algorithm (Fan et al., 2021). Each model within the DP committee differs from the others based on the initial random seed used in the minimization. The NEP features instead a different architecture and slightly different descriptors with respect to DPs (Fan et al., 2021).

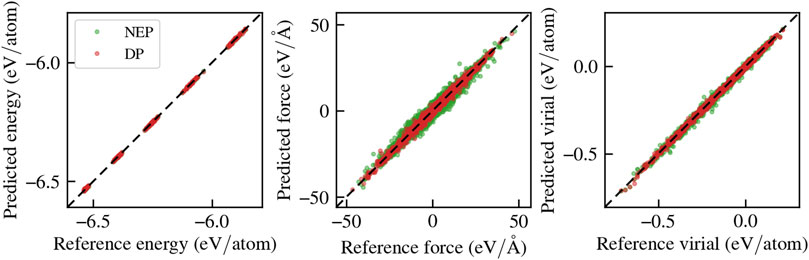
We assess the performance of these models on a validation set, which consists of an additional 2,500 configurations produced using the same methodology as the training set. Figure 1 presents parity plots comparing the reference and predicted potential energies, forces, and virials for the four DP models in the committee. All the DPs exhibit comparable accuracy. The root mean square errors (RMSEs) and relative error with respect of the standard deviation of the test set (in parentheses), are 2.86 ± 0.09 meV/atom for the energy (1%), 237.04 ± 0.14 meV/A for the force (8%), and 6.96 ± 0.04 meV for the virial (5%). In Figure 1 the performance of a selected member of the DP committee is shown (red) for simplicity. The NEP features RMSEs and relative errors of 0.9 meV/atom for the energy $(<1\%)$, of 311 meV/A for the force (11%), and of 13 meV for the virial (8%).

FIGURE 1

FIGURE 1. Parity plots of the committee of MLPs trained on the vitreous silica Tersoff dataset.

3.2 Lattice dynamics vs. molecular dynamics

Subsequently, we test the models’ performance in replicating the reference thermal conductivity. We compute the thermal conductivity of vitreous silica as determined by Eq. 1. To do so, we sample the energy flux and the atomic mass fluxes through EMD simulations on a system with 648 atoms. Given that the Tersoff FF is a many-body potential, particular care needs to be taken when computing the energy flux (Fan et al., 2015). A correct implementation of the Tersoff energy flux can be found in gpumd (Fan et al., 2022). As reference, we carried out a 1 ns-long EMD simulation at 300 K using gpumd, collecting the energy and mass fluxes every 5 fs. Further computational details can be found in the Supplementary Material. We use the same trajectory to sample these quantities using the committee of DPs and the NEP, utilizing the DeePMD and NEP implementations in lammps (Plimpton et al., 2021; Tisi et al., 2021; Fan et al., 2022). Using the same trajectory to test the models allows us to isolate the effects of gauge invariance, eliminating subtle differences that may arise when employing independent EMD runs to sample different trajectories. The thermal conductivity is finally obtained through cepstral analysis of the fluxes’ time series (Ercole et al., 2017; Bertossa et al., 2019), as implemented in SporTran (Ercole et al., 2022). The total energy decomposition into local contributions is in general different for different models, since the latter is a task arbitrarily performed by the ML algorithm. Thus, also the fluxes differ among the pool of models. Nevertheless, what must remain consistent is the physical observable, namely, the thermal conductivity, as commanded by gauge invariance (Grasselli and Baroni, 2021).

In Figure 2, we show the distributions (normalized histograms) of the deviation of the atomic energies per species with respect to their average value, sampled along the trajectory, as computed by the available MLPs. The DPs feature similar distributions of such quantity, so only one member of the committee is shown, while the NEP results are quite different. Nonetheless, even within the DP committee, the average values of the atomic energies are significantly different. In particular, the set of mean energies for the Tersoff FF, the DPs, and the NEP is reported in Table 1.

FIGURE 2

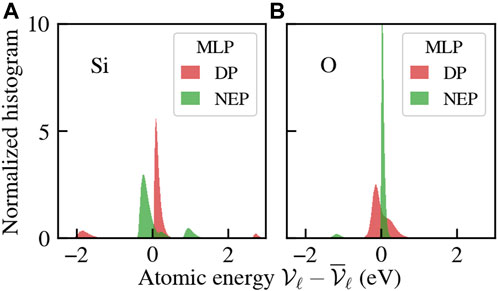
FIGURE 2. Distribution of the atomic energies of Si (A) and O (B) for the committee of MLPs. Simulations are carried out at T =300 K and ambient pressure.

TABLE 1

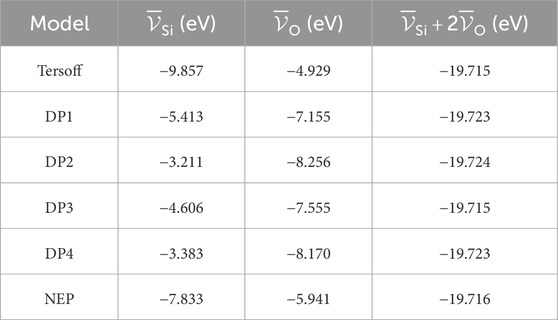
TABLE 1. Average atomic energies for the different models. The last column is the stoichiometry-weighted sum of average energies. It coincides for all the models, as it should, it being a physical observable. The discrepancy among this quantity’s reported values is well below the threshold of chemical accuracy ($\sim 40$meV).

We stress again that such a difference is expected, as the atomic energies are not target quantities in the learning scheme, and only the total energy is physically observable. The difference in atomic energies predicted by the different models is translated into a difference in energy fluxes, as shown in Figure 3A. Crucially, the thermal conductivity, as represented by the zero-frequency value of the fluxes’ power spectral density (Ercole et al., 2017; Bertossa et al., 2019), remains unchanged, as reported in Figure 3B.

FIGURE 3

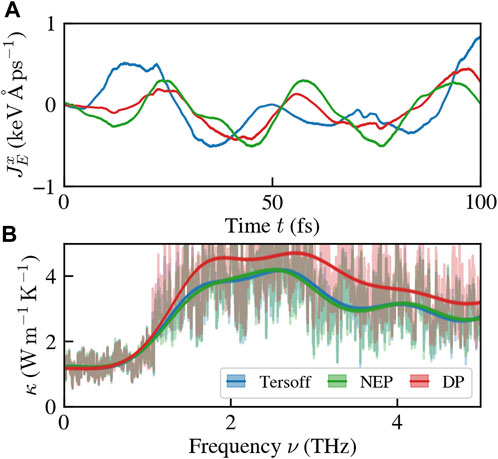
FIGURE 3. Gauge invariance of the thermal conductivity. Simulations are carried out at 300 K and ambient pressure. (A) the reference (Tersoff) energy flux and the DP committee ones are different, in general. (B) cepstral analysis of the fluxes’ time series. The thermal conductivity, given by the zero-frequency value of the curve, is the same for different models, as commanded by gauge invariance.

We now assess the models’ performance in reproducing quantities relevant for lattice-dynamical calculations. We compute the second and third-order interatomic force constants with lammps and obtain normal-mode frequencies and linewidths using κALDo (Barbalinardo et al., 2020). We use these quantities to compute the QHGK thermal conductivity with the Tersoff FF, a DP, and the NEP. Figure 4 showcases the results, including the vibrational density of states (VDOS), normal-mode linewidths, γ, and QHGK thermal conductivity. While the VDOS outcomes in Figure 4A exhibit agreement, the same cannot be said for anharmonic normal-mode linewidths (Figure 4B), which appear to be accurately captured only by the NEP. In contrast, the DP results considerably overestimate the linewidths, even surpassing the quasi-harmonic regime, denoted by the dashed black line. These disparities have direct implications for the computed QHGK thermal conductivities, as evident in Figure 4C. Specifically, while the NEP and Tersoff results align with each other, the DP results do not share this agreement.

FIGURE 4

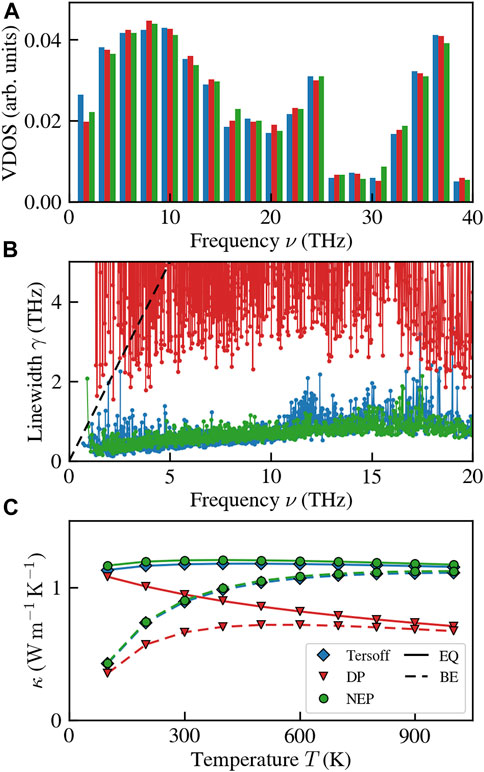
FIGURE 4. Results based on lattice dynamics of vitreous silica computed with the Tersoff FF, the DP, and the NEP. (A) vibrational density of states computed with the three models. (B) normal-mode linewidths. (C) QHGK thermal conductivity. EQ stands for the classical equipartition, while BE for the Bose-Einstein occupation.

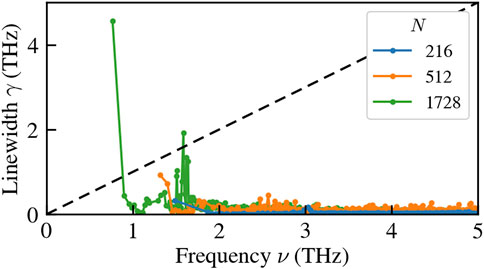
It is essential to recognize that the apparently satisfactory performance of the NEP leads to potentially misleading outcomes. Upon closer examination of Figure 4B, a notable issue emerges: at low frequencies (in this instance, the first available finite frequency) there are disproportionately large linewidths. This stark contrast with the expected decrease in linewidths as frequencies decrease, as dictated by the hydrodynamics of solids (Griffin, 1968; Fiorentino et al., 2023b), precludes the hydrodynamic extrapolation the NEP results to obtain a size-converged value for bulk thermal conductivity (Fiorentino et al., 2023a; Fiorentino et al., 2023b). As a further proof that MLPs still present some issues with lattice dynamics, we compute the anharmonic linewidths of a more complex NEP for vitreous silicon (v-Si) developed in Wang et al. (2023) and based on the dataset of Bartók et al. (2018). As shown in Figure 5, increasing the size of the sample exacerbates the issue of the low-frequency peak in the linewidths, which hinders the possibility of carrying out size-converged thermal conductivity calculations (Fiorentino et al., 2023a; Fiorentino et al., 2023b). This issue persists even when manually imposing acoustic sum rules due to global translational invariance and symmetry under Cartesian-direction permutation.

FIGURE 5

FIGURE 5. Anharmonic linewidths of a NEP model for v-Si at 300K, for samples of different sizes.

Due to these limitations, lattice-dynamical calculations prove to be of limited utility when employing MLPs. Consequently, the alternative approach is to resort to GKMD simulations, albeit at the cost of neglecting the quantum BE occupation. It is worth noting that in specific instances, like vitreous silica, this omission remains notable even at room temperature (Lv and Henry, 2016; Zhu and Shao, 2022). Conversely, for other simple glasses like vitreous silicon, this concern does not apply (Fiorentino et al., 2023b; Wang et al., 2023).

3.3 Thermal conductivity of Li-intercalated silicon

To exemplify the GKMD methodology within the context of MLPs, we conduct a thermal conductivity assessment of a PBE-accurate model describing amorphous LiSi, as developed by Fu et al. (2023). This MLP was employed to investigate the properties of silicon, encompassing both crystalline and amorphous phases, as an anode material for Li-based electrolytes (Fu et al., 2023). Thermal transport plays a pivotal role in the design of electrolytes, especially for solid-state systems (Feng et al., 2018). Indeed, an exceedingly low thermal conductivity can lead to excessive heat generation, especially during rapid charging processes, thereby posing the risk of critical incidents such as material melting or explosions. Moreover, the management of thermal dissipation is crucial to optimizing energy conservation and utilization, requiring a delicate equilibrium between minimizing heat dissipation and maximizing electric flux throughout the charging cycle (Feng et al., 2018). In addition, in situations involving materials where ionic diffusion is not only expected but also a desired attribute, such as solid-state electrolytes, one is forced to use methods that do not rely on the presence of well-defined atomic equilibrium positions (Pegolo et al., 2022).

We conduct EMD simulations on Li_xSi_1−x with varying concentration of intercalated lithium, denoted as x, under room temperature conditions (T = 300K, p = 0bar). Amorphous samples are prepared through a melt-quench-anneal procedure as outlined in Fu et al. (2023). The samples so obtained are used as initial configurations for EMD simulations that sample the relevant fluxes in canonical runs (Bussi et al., 2007) carried out for 3 ns at 300 K. The simulations are performed with gpumd using a NEP trained on the dataset of Fu et al. (2023). Further details can be found in the Supplementary Material.

Results for the thermal conductivity as a function of Li concentration are presented in Figure 6. Size effects are important for low Li concentrations, where the system is close to pure vitreous silicon. v-Si is known for being severely affected by size effects (Fiorentino et al., 2023b) due to its high local order (Bartók et al., 2018). Thus, samples with 3,000 atoms are not converged in size, while 70,000 atoms appear to be enough, when compared to calculations on systems with 150,000 atoms.

FIGURE 6

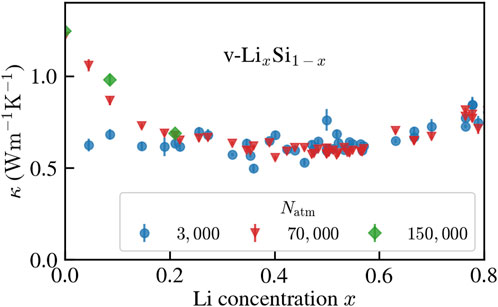
FIGURE 6. Thermal conductivity of v-Li_xSi_{1− x} as a function Li concentration at room-temperature conditions for different system sizes.

At higher Li concentrations, even 3,000 atoms are sufficient to achieve convergence. The behavior of κ(x) features a minimum at x ≈ 0.5, followed by an increase for larger values of x. Pure v-Si features κ = 1.24 ± 0.03 W m⁻¹ K⁻¹. This value can be compared with calculations (Wang et al., 2023) done on structure of similar size that use a NEP trained on a dataset relying on PW91 DFT calculations (Bartók et al., 2018), rather than PBE. The results are compatible at high quenching rate, while we report a value which is $\approx 30$% lower than the one of Wang et al. (2023) at the lowest quenching rate. Experimental data on the thermal conductivity of v-Si severely depend on the experimental sample size, due to the high relevance of propagons in this material. At 300 K, they can range from less than 1 W m⁻¹ K⁻¹ (Zink et al., 2006) to around 4 W m⁻¹ K⁻¹ (Liu et al., 2009; Yang et al., 2010). While measurements exist for (poly)crystalline Li-Si alloys (Swift, 2011), we are not aware of any experimental data on the thermal conductivity of Li-intercalated amorphous silicon.

The qualitative behavior of the thermal conductivity as a function of Li concentration aligns with calculations on crystalline alloys (Garg et al., 2011), where the distinctive U-shape of κ(x) is interpreted in terms of phonon scattering due to isotopic mass disorder (Tamura, 1983) at the perturbative level. Conversely, in glasses the thermal conductivity reduction with increasing concentration of different-species atoms is mostly due to the increased localization of low- and mid-frequency vibrational modes, together with the broadening of the respective linewidths, which hinders their ability to transport heat (Lundgren et al., 2021).

4 Conclusion

In this work, we have reviewed the theory of thermal transport in amorphous solids, focusing on the role of MLPs as a tool to expedite and, in some cases, allow for thermal-transport characterization of glasses from atomistic simulations. We have build an example of MLP for vitreous silica able to reproduce the potential energy surface of a Tersoff FF, and used it to highlight some challenges still present when dealing with lattice dynamics, leaving Green-Kubo molecular dynamics as a valuable alternative to carry out calculations with MLPs. We then applied such methodologies to the Li-concentration dependence of the thermal conductivity of lithium-intercalated amorphous silicon, finding that κ features a minimum at half concentration, coherent with analogous calculations made on other amorphous alloys and interpreted in terms of the localization of propagating modes due to chemical disorder.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.5281/zenodo.10225316.

Author contributions

PP: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. FG: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially supported by the European Commission through the MaX Centre of Excellence for supercomputing applications (grant number 101093374) and by the Italian MUR, through the PRIN project FERMAT (grant number 2017KFY7XF) and the Italian National Centre from HPC, Big Data, and Quantum Computing (grant number CN00000013). FG acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Action IF-EF-ST, grant agreement number 101018557 (TRANQUIL).

Acknowledgments

We thank A. Fiorentino and D. Tisi for fruitful discussions. We are grateful to S. Baroni for his valuable guidance.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2024.1369034/full#supplementary-material

References

Allen, P. B., and Feldman, J. L. (1989). Thermal conductivity of glasses: theory and application to amorphous si. Phys. Rev. Lett. 62, 645–648. doi:10.1103/physrevlett.62.645

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, P. B., Feldman, J. L., Fabian, J., and Wooten, F. (1999). Diffusons, locons and propagons: character of atomic vibrations in amorphous Si. Philos. Mag. B 79, 1715–1731. doi:10.1080/13642819908223054

CrossRef Full Text | Google Scholar

Anoop Krishnan, N., Mangalathu, S., Smedskjaer, M. M., Tandia, A., Burton, H., and Bauchy, M. (2018). Predicting the dissolution kinetics of silicate glasses using machine learning. J. Non-Crystalline Solids 487, 37–45. doi:10.1016/j.jnoncrysol.2018.02.023

CrossRef Full Text | Google Scholar

Barbalinardo, G., Chen, Z., Lundgren, N. W., and Donadio, D. (2020). Efficient anharmonic lattice dynamics calculations of thermal transport in crystalline and disordered solids. J. Appl. Phys. 128, 135104. doi:10.1063/5.0020443

CrossRef Full Text | Google Scholar

Baroni, S., Bertossa, R., Ercole, L., Grasselli, F., and Marcolongo, A., Heat transport in insulators from ab initio green-kubo theory, Handbook of materials modeling: applications: Current and emerging materials, 809 (2020).

CrossRef Full Text | Google Scholar

Bartók, A. P., Kermode, J., Bernstein, N., and Csányi, G. (2018). Machine learning a general-purpose interatomic potential for silicon. Phys. Rev. X 8, 041048. doi:10.1103/physrevx.8.041048

CrossRef Full Text | Google Scholar

Beltukov, Y. M., Kozub, V. I., and Parshin, D. A. (2013). Ioffe-regel criterion and diffusion of vibrations in random lattices. Phys. Rev. B 87, 134203. doi:10.1103/physrevb.87.134203

CrossRef Full Text | Google Scholar

Bertani, M., Bisbrouck, N., Delaye, J.-M., Angeli, F., Pedone, A., and Charpentier, T. (2023). Effects of magnesium on the structure of aluminoborosilicate glasses: NMR assessment of interatomic potentials models for molecular dynamics. J. Am. Ceram. Soc. 106, 5501–5521. doi:10.1111/jace.19157

CrossRef Full Text | Google Scholar

Bertossa, R., Grasselli, F., Ercole, L., and Baroni, S. (2019). Theory and numerical simulation of heat transport in multicomponent systems. Phys. Rev. Lett. 122, 255901. doi:10.1103/physrevlett.122.255901

PubMed Abstract | CrossRef Full Text | Google Scholar

Brauer, D. S., Rüssel, C., and Kraft, J. (2007). Solubility of glasses in the system P2O5–CaO–MgO–Na2O–TiO2: experimental and modeling using artificial neural networks. J. Non-Crystalline Solids 353, 263–270. doi:10.1016/j.jnoncrysol.2006.12.005

CrossRef Full Text | Google Scholar

Brorsson, J., Hashemi, A., Fan, Z., Fransson, E., Eriksson, F., Ala-Nissila, T., et al. (2022). Efficient calculation of the lattice thermal conductivity by atomistic simulations with ab initio accuracy. Adv. Theory Simulations 5, 2100217. doi:10.1002/adts.202100217

CrossRef Full Text | Google Scholar

Bruns, D., Nojeh, A., Phani, A. S., and Rottler, J. (2022). Comment on “ultrahigh convergent thermal conductivity of carbon nanotubes from comprehensive atomistic modeling”. Phys. Rev. Lett. 128, 259601. doi:10.1103/physrevlett.128.259601

PubMed Abstract | CrossRef Full Text | Google Scholar

Buchenau, U., Galperin, Y. M., Gurevich, V. L., Parshin, D. A., Ramos, M. A., and Schober, H. R. (1992). Interaction of soft modes and sound waves in glasses. Phys. Rev. B 46, 2798–2808. doi:10.1103/physrevb.46.2798

PubMed Abstract | CrossRef Full Text | Google Scholar

Bussi, G., Donadio, D., and Parrinello, M. (2007). Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101. doi:10.1063/1.2408420

PubMed Abstract | CrossRef Full Text | Google Scholar

Cahill, D. G., and Pohl, R. O. (1988). Lattice vibrations and heat transport in crystals and glasses. Annu. Rev. Phys. Chem. 39, 93–121. doi:10.1146/annurev.pc.39.100188.000521

CrossRef Full Text | Google Scholar

Caldarelli, G., Simoncelli, M., Marzari, N., Mauri, F., and Benfatto, L. (2022). Many-body Green’s function approach to lattice thermal transport. Phys. Rev. B 106, 024312. doi:10.1103/physrevb.106.024312

CrossRef Full Text | Google Scholar

Cassar, D. R., de Carvalho, A. P. L. F., and Zanotto, E. D. (2018). Predicting glass transition temperatures using neural networks. Acta Mater. 159, 249–256. doi:10.1016/j.actamat.2018.08.022

CrossRef Full Text | Google Scholar

Chong, S., Grasselli, F., Ben Mahmoud, C., Morrow, J. D., Deringer, V. L., and Ceriotti, M. (2023). Robustness of local predictions in atomistic machine learning models. J. Chem. Theory Comput. 19, 8020–8031. doi:10.1021/acs.jctc.3c00704

PubMed Abstract | CrossRef Full Text | Google Scholar

Debenedetti, P. G. (1988). Fluctuation-based computer calculation of partial molar properties. II. A numerically accurate method for the determination of partial molar energies and enthalpies. J. Chem. Phys. 88, 2681–2684. doi:10.1063/1.453996

CrossRef Full Text | Google Scholar

De Groot, S. R., and Mazur, P. (1962). Non-equilibrium thermodynamics. Amsterdam: North-Holland Publishing Company.

Google Scholar

Deringer, V. L., Bernstein, N., Csányi, G., Ben Mahmoud, C., Ceriotti, M., Wilson, M., et al. (2021). Origins of structural and electronic transitions in disordered silicon. Nature 589, 59–64. doi:10.1038/s41586-020-03072-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Deringer, V. L., and Csányi, G. (2017). Machine learning based interatomic potential for amorphous carbon. Phys. Rev. B 95, 094203. doi:10.1103/physrevb.95.094203

CrossRef Full Text | Google Scholar

Drigo, E., Izzo, M. G., and Baroni, S. (2023). Heat conductivity from energy-density fluctuations. J. Chem. Phys. 159, 184107. doi:10.1063/5.0168732

PubMed Abstract | CrossRef Full Text | Google Scholar

Ercole, L., Bertossa, R., Bisacchi, S., and Baroni, S. (2022). Sportran: a code to estimate transport coefficients from the cepstral analysis of (multivariate) current time series. Comput. Phys. Commun. 280, 108470. doi:10.1016/j.cpc.2022.108470

CrossRef Full Text | Google Scholar

Ercole, L., Marcolongo, A., and Baroni, S. (2017). Accurate thermal conductivities from optimally short molecular dynamics simulations. Sci. Rep. 7, 15835. doi:10.1038/s41598-017-15843-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ewing, R. C. (2015). Long-term storage of spent nuclear fuel. Nat. Mater. 14, 252–257. doi:10.1038/nmat4226

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Z., Pereira, L. F. C., Wang, H.-Q., Zheng, J.-C., Donadio, D., and Harju, A. (2015). Force and heat current formulas for many-body potentials in molecular dynamics simulations with applications to thermal conductivity calculations. Phys. Rev. B 92, 094301. doi:10.1103/physrevb.92.094301

CrossRef Full Text | Google Scholar

Fan, Z., Wang, Y., Ying, P., Song, K., Wang, J., Wang, Y., et al. (2022). GPUMD: a package for constructing accurate machine-learned potentials and performing highly efficient atomistic simulations. J. Chem. Phys. 157, 114801. doi:10.1063/5.0106617

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Z., Zeng, Z., Zhang, C., Wang, Y., Song, K., Dong, H., et al. (2021). Neuroevolution machine learning potentials: combining high accuracy and low cost in atomistic simulations and application to heat transport. Phys. Rev. B 104, 104309. doi:10.1103/physrevb.104.104309

CrossRef Full Text | Google Scholar

Feng, X., Ouyang, M., Liu, X., Lu, L., Xia, Y., and He, X. (2018). Thermal runaway mechanism of lithium ion battery for electric vehicles: a review. Energy Storage Mater. 10, 246–267. doi:10.1016/j.ensm.2017.05.013

CrossRef Full Text | Google Scholar

Fiorentino, A., and Baroni, S. (2023). From Green-Kubo to the full Boltzmann kinetic approach to heat transport in crystals and glasses. Phys. Rev. B 107, 054311. doi:10.1103/physrevb.107.054311

CrossRef Full Text | Google Scholar

Fiorentino, A., Drigo, E., Baroni, S., and Pegolo, P., Unearthing the foundational role of anharmonicity in heat transport in glasses, preprint at. doi:10.48550/arXiv.2307.093702023a).

CrossRef Full Text | Google Scholar

Fiorentino, A., Pegolo, P., and Baroni, S. (2023b). Hydrodynamic finite-size scaling of the thermal conductivity in glasses. npj Comput. Mater. 9, 157. doi:10.1038/s41524-023-01116-2

CrossRef Full Text | Google Scholar

Fu, F., Wang, X., Zhang, L., Yang, Y., Chen, J., Xu, B., et al. (2023). Unraveling the atomic-scale mechanism of phase transformations and structural evolutions during (de)lithiation in si anodes. Adv. Funct. Mater. 33, 2303936. doi:10.1002/adfm.202303936

CrossRef Full Text | Google Scholar

Fujita, Y., Kimura, T., Deguchi, M., Motohashi, K., Sakuda, A., Tatsumisago, M., et al. (2023). Structural investigation of li2o–lii amorphous solid electrolytes. J. Phys. Chem. C 127, 14687–14693. doi:10.1021/acs.jpcc.3c03876

CrossRef Full Text | Google Scholar

Garg, J., Bonini, N., Kozinsky, B., and Marzari, N. (2011). Role of disorder and anharmonicity in the thermal conductivity of silicon-germanium alloys: a first-principles study. Phys. Rev. Lett. 106, 045901. doi:10.1103/physrevlett.106.045901

PubMed Abstract | CrossRef Full Text | Google Scholar

Grasselli, F., and Baroni, S. (2021). Invariance principles in the theory and computation of transport coefficients. Eur. Phys. J. B 94, 160. doi:10.1140/epjb/s10051-021-00152-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Green, M. S. (1952). Markoff random processes and the statistical mechanics of time-dependent phenomena. J. Chem. Phys. 20, 1281–1295. doi:10.1063/1.1700722

CrossRef Full Text | Google Scholar

Griffin, A. (1968). Brillouin light scattering from crystals in the hydrodynamic region. Rev. Mod. Phys. 40, 167–205. doi:10.1103/revmodphys.40.167

CrossRef Full Text | Google Scholar

Grisafi, A., and Ceriotti, M. (2019). Incorporating long-range physics in atomic-scale machine learning. J. Chem. Phys. 151, 204105. doi:10.1063/1.5128375

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, H., Wang, Q., Urban, A., and Artrith, N. (2022). Artificial intelligence-aided mapping of the structure–composition–conductivity relationships of glass–ceramic lithium thiophosphate electrolytes. Chem. Mater. 34, 6702–6712. publisher: American Chemical Society. doi:10.1021/acs.chemmater.2c00267

PubMed Abstract | CrossRef Full Text | Google Scholar

Habershon, S., Manolopoulos, D. E., Markland, T. E., and Miller, T. F. (2013). Ring-polymer molecular dynamics: quantum effects in chemical dynamics from classical trajectories in an extended phase space. Annu. Rev. Phys. Chem. 64, 387–413. doi:10.1146/annurev-physchem-040412-110122

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y.-J., Zhao, G., Zhang, M., Bin, B., Del Rose, T., Zhao, Q., et al. (2020). Predicting densities and elastic moduli of SiO2-based glasses by machine learning. npj Comput. Mater. 6, 25. doi:10.1038/s41524-020-0291-z

CrossRef Full Text | Google Scholar

Huguenin-Dumittan, K. K., Loche, P., Haoran, N., and Ceriotti, M. (2023). Physics-inspired equivariant descriptors of nonbonded interactions. J. Phys. Chem. Lett. 14, 9612–9618. doi:10.1021/acs.jpclett.3c02375

PubMed Abstract | CrossRef Full Text | Google Scholar

Isaeva, L., Barbalinardo, G., Donadio, D., and Baroni, S. (2019). Modeling heat transport in crystals and glasses from a unified lattice-dynamical approach. Nat. Commun. 10, 3853. doi:10.1038/s41467-019-11572-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Islam, S. M., Sangwan, V. K., Bruce Buchholz, D., Wells, S. A., Peng, L., Zeng, L., et al. (2021). Amorphous to crystal phase change memory effect with two-fold bandgap difference in semiconducting K2Bi8Se13. J. Am. Chem. Soc. 143, 6221–6228. doi:10.1021/jacs.1c01484

PubMed Abstract | CrossRef Full Text | Google Scholar

Janek, J., and Zeier, W. G. (2023). Challenges in speeding up solid-state battery development. Nat. Energy 8, 230–240. doi:10.1038/s41560-023-01208-9

CrossRef Full Text | Google Scholar

Kim, Y., and Morita, K. (2017). Temperature dependence and cation effects in the thermal conductivity of glassy and molten alkali borates. J. Non-Crystalline Solids 471, 187–194. doi:10.1016/j.jnoncrysol.2017.05.034

CrossRef Full Text | Google Scholar

Kim, Y., Yanaba, Y., and Morita, K. (2015). The effect of borate and silicate structure on thermal conductivity in the molten na2o–b2o3–sio2 system. J. Non-Crystalline Solids 415, 1–8. doi:10.1016/j.jnoncrysol.2015.02.008

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. (2017). Adam: a method for stochastic optimization. arXiv:1412.6980 [cs.LG].

Google Scholar

Ko, T. W., Finkler, J. A., Goedecker, S., and Behler, J. (2021). A fourth-generation high-dimensional neural network potential with accurate electrostatics including non-local charge transfer. Nat. Commun. 12, 398. doi:10.1038/s41467-020-20427-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kotz, F., Arnold, K., Bauer, W., Schild, D., Keller, N., Sachsenheimer, K., et al. (2017). Three-dimensional printing of transparent fused silica glass. Nature 544, 337–339. doi:10.1038/nature22061

PubMed Abstract | CrossRef Full Text | Google Scholar

Kubo, R. (1957). Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 12, 570–586. doi:10.1143/jpsj.12.570

CrossRef Full Text | Google Scholar

Kubo, R., Yokota, M., and Nakajima, S. (1957). Statistical-mechanical theory of irreversible processes. II. Response to thermal disturbance. J. Phys. Soc. Jpn. 12, 1203–1211. doi:10.1143/jpsj.12.1203

CrossRef Full Text | Google Scholar

Landry, A.-K., Bayzou, R., Benayad, A., Trébosc, J., Pourpoint, F., Lafon, O., et al. (2023). Unveiling the origins of high ionic conductivity in lithium phosphorus oxynitride amorphous electrolytes. Chem. Mater. 35, 9313–9324. doi:10.1021/acs.chemmater.3c02099

CrossRef Full Text | Google Scholar

Langer, M. F., Knoop, F., Carbogno, C., Scheffler, M., and Rupp, M. (2023). Heat flux for semilocal machine-learning potentials. Phys. Rev. B 108, L100302. doi:10.1103/physrevb.108.l100302

CrossRef Full Text | Google Scholar

Liu, H., Fu, Z., Yang, K., Xu, X., and Bauchy, M. (2021). Machine learning for glass science and engineering: a review. J. Non-Crystalline Solids 557, 119419. doi:10.1016/j.jnoncrysol.2019.04.039

CrossRef Full Text | Google Scholar

Liu, X., Feldman, J. L., Cahill, D. G., Crandall, R. S., Bernstein, N., Photiadis, D. M., et al. (2009). High thermal conductivity of a hydrogenated amorphous silicon film. Phys. Rev. Lett. 102, 035901. doi:10.1103/physrevlett.102.035901

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Liang, H., Yang, L., Yang, G., Yang, H., Song, S., et al. (2023). Unraveling thermal transport correlated with atomistic structures in amorphous gallium oxide via machine learning combined with experiments. Adv. Mater. 35, 2210873. doi:10.1002/adma.202210873

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, D., Wang, H., Chen, M., Lin, L., Car, R., W, E., et al. (2021). 86 pflops deep potential molecular dynamics simulation of 100 million atoms with ab initio accuracy. Comput. Phys. Commun. 259, 107624. doi:10.1016/j.cpc.2020.107624

CrossRef Full Text | Google Scholar

Lubchenko, V., and Wolynes, P. G. (2003). The origin of the boson peak and thermal conductivity plateau in low-temperature glasses. PNAS 100, 1515–1518. doi:10.1073/pnas.252786999

PubMed Abstract | CrossRef Full Text | Google Scholar

Lundgren, N. W., Barbalinardo, G., and Donadio, D. (2021). Mode localization and suppressed heat transport in amorphous alloys. Phys. Rev. B 103, 024204. doi:10.1103/physrevb.103.024204

CrossRef Full Text | Google Scholar

Lv, W., and Henry, A. (2016). Non-negligible contributions to thermal conductivity from localized modes in amorphous silicon dioxide. Sci. Rep. 6, 35720. doi:10.1038/srep35720

PubMed Abstract | CrossRef Full Text | Google Scholar

Manthiram, A., Yu, X., and Wang, S. (2017). Lithium battery chemistries enabled by solid-state electrolytes. Nat. Rev. Mater. 2, 16103. doi:10.1038/natrevmats.2016.103

CrossRef Full Text | Google Scholar

Matzke, H., and Vernaz, E. (1993). Thermal and physicochemical properties important for the long term behavior of nuclear waste glasses. J. Nucl. Mater. 201, 295–309. doi:10.1016/0022-3115(93)90186-3

CrossRef Full Text | Google Scholar

Mauro, J. C. (2014). Grand challenges in glass science. Front. Mater. 1. doi:10.3389/fmats.2014.00020

CrossRef Full Text | Google Scholar

Mauro, J. C., Tandia, A., Vargheese, K. D., Mauro, Y. Z., and Smedskjaer, M. M. (2016). Accelerating the design of functional glasses through modeling. Chem. Mater. 28, 4267–4277. doi:10.1021/acs.chemmater.6b01054

CrossRef Full Text | Google Scholar

Munetoh, S., Motooka, T., Moriguchi, K., and Shintani, A. (2007). Interatomic potential for si–o systems using tersoff parameterization. Comput. Mater. Sci. 39, 334–339. doi:10.1016/j.commatsci.2006.06.010

CrossRef Full Text | Google Scholar

Narasimhan, S., and Vanderbilt, D. (1991). Anharmonic self-energies of phonons in silicon. Phys. Rev. B 43, 4541–4544. doi:10.1103/physrevb.43.4541

PubMed Abstract | CrossRef Full Text | Google Scholar

Niu, H., Piaggi, P. M., Invernizzi, M., and Parrinello, M. (2018). Molecular dynamics simulations of liquid silica crystallization. Proc. Natl. Acad. Sci. 115, 5348–5352. doi:10.1073/pnas.1803919115

PubMed Abstract | CrossRef Full Text | Google Scholar

Ojovan, M. I., Lee, W. E., and Kalmykov, S. N. (2019). An introduction to nuclear waste immobilisation. 3rd ed. Elsevier.

Google Scholar

Onbaşlı, M. C., Tandia, A., and Mauro, J. C. (2020). “Mechanical and compositional design of high-strength corning Gorilla®Glass,” in Handbook of materials modeling: applications: current and emerging materials. Editors W. Andreoni, and S. Yip (Cham: Springer International Publishing), 1997–2019.

Google Scholar

Pallini, A., Bertani, M., Rustichelli, D., Ziebarth, B., Mannstadt, W., and Pedone, A. (2023). Comparison of five empirical potential models for aluminosilicate systems: albite and anorthite as test cases. J. Non-Crystalline Solids 615, 122426. doi:10.1016/j.jnoncrysol.2023.122426

CrossRef Full Text | Google Scholar

Paruzzo, F. M., Hofstetter, A., Musil, F., De, S., Ceriotti, M., and Emsley, L. (2018). Chemical shifts in molecular solids by machine learning. Nat. Comm. 9, 4501. doi:10.1038/s41467-018-06972-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pasquarello, A., Hybertsen, M. S., and Car, R. (1998). Interface structure between silicon and its oxide by first-principles molecular dynamics. Nature 396, 58–60. doi:10.1038/23908

CrossRef Full Text | Google Scholar

Paulatto, L., Mauri, F., and Lazzeri, M. (2013). Anharmonic properties from a generalized third-order ab initio approach: theory and applications to graphite and graphene. Phys. Rev. B 87, 214303. doi:10.1103/physrevb.87.214303

CrossRef Full Text | Google Scholar

Pedesseau, L., Ispas, S., and Kob, W. (2015). First-principles study of a sodium borosilicate glass-former. ii. the glass state. Phys. Rev. B 91, 134202. doi:10.1103/physrevb.91.134202

CrossRef Full Text | Google Scholar

Pedone, A., Bertani, M., Brugnoli, L., and Pallini, A. (2022). Interatomic potentials for oxide glasses: past, present, and future. J. Non-Crystalline Solids X 15, 100115. doi:10.1016/j.nocx.2022.100115

CrossRef Full Text | Google Scholar

Pegolo, P., Baroni, S., and Grasselli, F. (2022). Temperature- and vacancy-concentration-dependence of heat transport in Li₃ClO from multi-method numerical simulations. NPJ Comput. Mater. 8, 24. doi:10.1038/s41524-021-00693-4

CrossRef Full Text | Google Scholar

Pegolo, P., and Grasselli, F., Data for “Thermal transport of glasses via machine learning driven simulations”, doi:10.5281/zenodo.102253162023).

CrossRef Full Text | Google Scholar

Phillips, W. A. (1987). Two-level states in glasses. Rep. Prog. Phys. 50, 1657–1708. doi:10.1088/0034-4885/50/12/003

CrossRef Full Text | Google Scholar

Plimpton, S., Kohlmeyer, A., Thompson, A., Moore, S., and Berger, R. (2021). Lammps stable release 29 september 2021.

Google Scholar

Schirmacher, W. (2006). Thermal conductivity of glassy materials and the boson peak. Europhys. Lett. 73, 892–898. doi:10.1209/epl/i2005-10471-9

CrossRef Full Text | Google Scholar

Siciliano, A., Monacelli, L., Caldarelli, G., and Mauri, F. (2023). Wigner Gaussian dynamics: simulating the anharmonic and quantum ionic motion. Phys. Rev. B 107, 174307. doi:10.1103/physrevb.107.174307

CrossRef Full Text | Google Scholar

Simoncelli, M., Marzari, N., and Mauri, F. (2019). Unified theory of thermal transport in crystals and glasses. Nat. Phys. 15, 809–813. doi:10.1038/s41567-019-0520-x

CrossRef Full Text | Google Scholar

Sivaraman, G., Krishnamoorthy, A. N., Baur, M., Holm, C., Stan, M., Csányi, G., et al. (2020). Machine-learned interatomic potentials by active learning: amorphous and liquid hafnium dioxide. npj Comput. Mater. 6, 104. doi:10.1038/s41524-020-00367-7

CrossRef Full Text | Google Scholar

Sørensen, S. S., Bødker, M. S., Johra, H., Youngman, R. E., Logunov, S. L., Bockowski, M., et al. (2021). Thermal conductivity of densified borosilicate glasses. J. Non-Crystalline Solids 557, 120644. doi:10.1016/j.jnoncrysol.2021.120644

CrossRef Full Text | Google Scholar

Sørensen, S. S., Cielecki, P. P., Johra, H., Bockowski, M., Skovsen, E., Yue, Y., et al. (2022). Thermal conduction in a densified oxide glass: insights from lattice dynamics. Mater. Today Commun. 32, 104160. doi:10.1016/j.mtcomm.2022.104160

CrossRef Full Text | Google Scholar

Sørensen, S. S., Johra, H., Mauro, J. C., Bauchy, M., and Smedskjaer, M. M. (2019). Boron anomaly in the thermal conductivity of lithium borate glasses. Phys. Rev. Mater. 3, 075601. doi:10.1103/physrevmaterials.3.075601

CrossRef Full Text | Google Scholar

Sosso, G. C., Deringer, V. L., Elliott, S. R., and Csányi, G. (2018). Understanding the thermal properties of amorphous solids using machine-learning-based interatomic potentials. Mol. Simul. 44, 866–880. doi:10.1080/08927022.2018.1447107

CrossRef Full Text | Google Scholar

Sosso, G. C., Donadio, D., Caravati, S., Behler, J., and Bernasconi, M. (2012). Thermal transport in phase-change materials from atomistic simulations. Phys. Rev. B 86, 104301. doi:10.1103/physrevb.86.104301

CrossRef Full Text | Google Scholar

Sugawara, T., Katsuki, J., Shiono, T., Yoshida, S., Matsuoka, J., Minami, K., et al. (2014). High-temperature heat capacity and density of simulated high-level waste glass. J. Nucl. Mater. 454, 298–307. doi:10.1016/j.jnucmat.2014.07.055

CrossRef Full Text | Google Scholar

Sutherland, B. J., Moore, W. H. D., and Manolopoulos, D. E. (2021). Nuclear quantum effects in thermal conductivity from centroid molecular dynamics. J. Chem. Phys. 154, 174104. doi:10.1063/5.0051663

PubMed Abstract | CrossRef Full Text | Google Scholar

Swift, G. A. (2011). Thermophysical properties of lithium alloys for thermal batteries. Int. J. Thermophys. 32, 2102–2111. doi:10.1007/s10765-011-1081-0

CrossRef Full Text | Google Scholar

Tamura, S.-i. (1983). Isotope scattering of dispersive phonons in ge. Phys. Rev. B 27, 858–866. doi:10.1103/physrevb.27.858

CrossRef Full Text | Google Scholar

Tang, X., Li, C. W., and Fultz, B. (2010). Anharmonicity-induced phonon broadening in aluminum at high temperatures. Phys. Rev. B 82, 184301. doi:10.1103/physrevb.82.184301

CrossRef Full Text | Google Scholar

Tisi, D., Zhang, L., Bertossa, R., Wang, H., Car, R., and Baroni, S. (2021). Heat transport in liquid water from first-principles and deep neural network simulations. Phys. Rev. B 104, 224202. doi:10.1103/physrevb.104.224202

CrossRef Full Text | Google Scholar

Veit, M., Wilkins, D. M., Yang, Y., DiStasio, J., Robert, A., and Ceriotti, M. (2020). Predicting molecular dipole moments by combining atomic partial charges and atomic dipoles. J. Chem. Phys. 153, 024113. doi:10.1063/5.0009106

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Zhang, L., Han, J., and W, E. (2018). Deepmd-kit: a deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 228, 178–184. doi:10.1016/j.cpc.2018.03.016

CrossRef Full Text | Google Scholar

Wang, Y., Fan, Z., Qian, P., Caro, M. A., and Ala-Nissila, T. (2023). Quantum-corrected thickness-dependent thermal conductivity in amorphous silicon predicted by machine learning molecular dynamics simulations. Phys. Rev. B 107, 054303. doi:10.1103/physrevb.107.054303

CrossRef Full Text | Google Scholar

Xie, X., Persson, K. A., and Small, D. W. (2020). Incorporating electronic information into machine learning potential energy surfaces via approaching the ground-state electronic energy as a function of atom-based electronic populations. J. Chem. Theory Comput. 16, 4256–4270. pMID: 32502350. doi:10.1021/acs.jctc.0c00217

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, Y., Vandermause, J., Ramakers, S., Protik, N. H., Johansson, A., and Kozinsky, B. (2023). Uncertainty-aware molecular dynamics from Bayesian active learning for phase transformations and thermal transport in SiC. npj Comput. Mater. 9, 36. doi:10.1038/s41524-023-00988-8

CrossRef Full Text | Google Scholar

Yang, H.-S., Cahill, D. G., Liu, X., Feldman, J. L., Crandall, R. S., Sperling, B. A., et al. (2010). Anomalously high thermal conductivity of amorphous si deposited by hot-wire chemical vapor deposition. Phys. Rev. B 81, 104203. doi:10.1103/physrevb.81.104203

CrossRef Full Text | Google Scholar

Zeng, J., Zhang, D., Lu, D., Mo, P., Li, Z., Chen, Y., et al. (2023). DeePMD-kit v2: a software package for deep potential models. J. Chem. Phys. 159, 054801. doi:10.1063/5.0155600

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., Han, J., Wang, H., Saidi, W. A., Car, R., and Weinan, E. (2018). “End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems,” in Proceedings of the 32nd International Conference on Neural Information Processing Systems, NIPS’18, Red Hook, NY, USA (New York, United States: Curran Associates Inc.), 4441–4451.

Google Scholar

Zhang, L., Wang, H., Muniz, M. C., Panagiotopoulos, A. Z., Car, R., and W, E. (2022). A deep potential model with long-range electrostatic interactions. J. Chem. Phys. 156, 124107. doi:10.1063/5.0083669

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Q., Stalin, S., Zhao, C.-Z., and Archer, L. A. (2020). Designing solid-state electrolytes for safe, energy-dense batteries. Nat. Rev. Mater. 5, 229–252. doi:10.1038/s41578-019-0165-5

CrossRef Full Text | Google Scholar

Zhu, X., and Shao, C. (2022). Effect of anharmonicity on the thermal conductivity of amorphous silica. Phys. Rev. B 106, 014305. doi:10.1103/physrevb.106.014305

CrossRef Full Text | Google Scholar

Zink, B. L., Pietri, R., and Hellman, F. (2006). Thermal conductivity and specific heat of thin-film amorphous silicon. Phys. Rev. Lett. 96, 055902. doi:10.1103/physrevlett.96.055902

PubMed Abstract | CrossRef Full Text | Google Scholar