- 1Department of Industrial and Systems Engineering, College of Engineering, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia
- 2Department of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, Bangi, Selangor, Malaysia
- 3Department of Mathematics, Faculty of Science, Sakarya University, Serdivan, Türkiye
- 4Department of Computer Science and Mathematics, Lebanese American University, Byblos, Lebanon
- 5Department of Mechanics and Mathematics, Western Caspian University, Baku, Azerbaijan
- 6Department of Mathematical Sciences, Federal Urdu University of Arts, Science and Technology, Gulshan-e-Iqbal Karachi, Pakistan
- 7Department of Physics, College of Science, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia
The significant increase in thermal efficiency and the rate of energy exchange used in fuel dynamics and automobile coolants are leading to a better understanding of nanofluids. This computational analysis explores the thermal conductivity performance for radiative cross-flow of a nanofluid across an expanding/constricting sheet with a suction effect as a result of its application. To compute or calculate the magnificent point of nanofluid flow, the entropy, and asymmetrical heat source/sink effects are also elicited. The boundary layers traverse a stream-wise procedure for expanding and contracting sheets. Additionally, the study examines the features of heat transfer and cross-flow of nanofluids using numerical simulations. By employing similarity variables, the basic PDE equations of the current model are transformed into ODEs, and they are subsequently evaluated using the bvp4c method. Therefore, the effects of embedded flow variables on drag force, heat transfer rate, and entropy generation profiles have been framed using parametric research. Multiple solutions are offered for a specific range of the contracting parameter as well as the mass suction parameter. In addition, the heat transfer rate accelerates due to the heat source and decelerates due to the heat sink. The literature that is already published has been compared favorably, and it reveals many commonalities.
1 Introduction
The nanofluid has a large number of nanoparticles and nanometer-sized molecules. Tiny particles are disseminated (added) in fluids to increase their heat transfer capabilities, even though the structure and content of nano-molecules depend on carbides, metals, and carbon nanotubes. The combinations that make up the nanofluid are typically combined with particles of average nanoscale size. Nanotubes, nanofibers, nanowires, nanoparticles, nanosheets, nanorods, and other materials are routinely made with nanofluids. The most effective and practical methods have been developed and put into practice for the modeling of nanofluid flow models, while the addition of specific materials of a particular kind has increased the thermal conductivity of various fluids. Several engineering procedures use nanoparticles in fluids to improve heat transfer. Equipment like heat exchangers in heavy machinery, automobiles, and industries is highly dependent on effective energy transfer. With these applications in mind, Choi and Eastman (Choi and Eastman, 1995) developed nanofluids to enhance the heat transfer capabilities of ordinary fluids. According to Eastman et al. (Eastman et al., 2001), adding copper nanoparticles to ethylene glycol at a concentration of 0.3 volumes results in a 40% increase in thermal conductivity. Khan and Pop (Khan and Pop, 2010) have numerically addressed the issue of laminar fluid flow that develops when a flat surface is stretched in a nanofluid. It was discovered that the reduced heat transfer is a diminishing function of every single dimensionless number. The numerical solution of the boundary layer flow caused by a linearly extending sheet in a nanofluid was inspected by Makinde and Aziz (Makinde and Aziz, 2011). They observed that the convective heating, thermophoresis, and Brownian motion all get more intense as the local temperature rises, which causes the thermal boundary layer to thicken. The thermal conductivity performance of carbon nanotubes in fluid flow over a stretching sheet was discovered by Haq et al. (Haq et al., 2015). Sheikholeslami et al. (Sheikholeslami et al., 2016) discovered the impacts of Lorentz forces on free convective flow in the presence of nanofluid with thermal radiation. A two-dimensional time-independent flow conveying nanofluid toward a thin needle was deliberated by Soid et al. (Soid et al., 2017) where the existence of multiple solutions was reported. Bakar et al. (Bakar et al., 2018) looked into the stability analysis of mass suction impacts through a shrinking/stretching cylinder considering the nanoparticles. Kamal et al. (Kamal et al., 2019) investigated the flow of nanomaterial through a stretchable/shrinkable sheet with a chemical reaction effect. A two-dimensional magneto mixed convection flow induced by a shrinking/stretching plate in a nanofluid was investigated by Jumana et al. (Jumana et al., 2020). Johan and Mansur (Johan and Mansur, 2021) examined the features of dusty nanomaterial flow and thermal transport analysis past a stretchable sheet with a slip boundary. They used three kinds of particles, namely, alumina, copper, and titania. Shahzad et al. (Shahzad et al., 2022) scrutinized the influence of the slip effect on the flow and heat transport incorporated by copper nanofluid with different shape factors through a heated stretched sheet and found that the platelet shape factor particles have a greater rate of heat transfer compared to other shape factors. Shamshuddin et al. (Shamshuddin et al., 2024a) examined the ohmic and ferromagnetic effects on the flow of nanofluid through a porous rotating disk. They discovered that in normal fluid and nanofluid, the increased suction velocity suppresses the fluid velocity produced by the surface’s porosity. Recently, Shamshuddin et al. (Shamshuddin et al., 2024b) explored the impact of electromagnetic on the radiative flow of tri-hybrid nanofluid through a bidirectional stretchy surface in penetrable media. The factors of the surface frictional force of the ternary hybrid nanofluids are found to decrease with increasing the Lorentz force and number of surface pores.
The problem of sheets stretching or shrinking in a viscous fluid has caught a lot of concentration as it has numerous applications in physics, engineering, and other scientific disciplines. It frequently occurs in practical issues that have attracted a lot of research attention because of their wide range of significance in fields like the production of glass fibre, glass blowing, metal extrusion, transportation, microfluidics, paper production, hot rolling, space, and acoustics (see Fisher (Fisher, 1976)). The BLF over an ongoing solid kind surface flowing at uniform motion was initially studied by Sakiadis (Sakiadis, 1961) in light of these applications. Numerous authors (Chen and Char, 1988; Ishak et al., 2009; Mi, 2015; Guo and Fu, 2019; Wang, 2019; Zhao et al., 2019; Zi and Wang, 2019) have thought about different elements of this problem and found similarity solutions since the groundbreaking research conducted by Crane (Crane, 1970), who provided an exact solution for the 2D steady flow caused by a stretchable surface in a quiescent fluid. Instead of focusing on the scenario of a stretched sheet, researchers instead looked at the scenario of a shrinking sheet. According to Goldstein (Goldstein, 1965), this new kind of flow of shrinking sheet is fundamentally a backward flow. The steady flow across a shrinkable sheet was studied by Miklavčič and Wang (Miklavčič and Wang, 2006). They discovered that mass suction is necessary to continue the flow across a shrinkable sheet. Waini et al. (Waini et al., 2019) examined the dependency of time-varying flow along with thermal transport across a shrinking/stretching sheet incorporated with hybrid nanofluids and provided multiple solutions.
The examination of cross-flow began following the early studies by Prandtl (Prandtl, 1946a) and Blasius (Blasius, 1908) that included the flow over a smooth surface caused by thin viscosity. Prandtl (Prandtl, 1946b) is believed to be the initial researcher to publish the findings for uniform pressure gradients flowing through a finite yawed cylinder. Weidman et al. (Weidman, 2017) examined the boundary layer via cross-flow generated by transverse plate motions. The work of Weidman was recently expanded by (Roşca et al., 2021) by taking into account rotational stagnation-point flow that transports hybrid nanofluids along a permeable shrinking or stretching surface. It was discovered that both stretching and shrinking surfaces can have multiple solutions to the fundamental similarity equations.
The phenomena of an irregular heat sink or source have applications in both engineering and medicine, involving the recovery of crude oil, the construction of thrust bearings, and the cooling of metallic sheets, etc. In the presence of an irregular heat sink/source, Tawade et al. (Tawade et al., 2016) addressed the motion of the MHD unsteady thin film and heat transfer past a stretchable sheet. It was determined that irregular heat parameters are crucial to the effectiveness of heat transfer. Thumma et al. (Thumma et al., 2017) revealed that the stretching of a sheet caused the MHD convective motion of nanofluid to have a changeable heat sink or source. To obtain the solution, a well-known Keller-Box numerical approach is utilized. Kumar et al. (Kumar et al., 2020) looked at the movement of hybrid ferrofluids film and heat transfer in the inclusion of radiation and erratic heat source/sink (EHSE/EHSK). The rate of heat transfer is believed to be greater in hybrid ferrofluids than in ferrofluids. In addition, the velocity of the fluid and temperature tend to decline as film thickness parameters increase. Areekara et al. (Areekara et al., 2021) investigated the impact of an irregular heat source/sink on the fluid flow of nanofluid past a nonlinear stretching sheet. They observed that positive correlations exist between the radiative heat flux and the rate of heat transfer. A negative sensitivity to the rate of heat transfer is shown by the exponential heat source. Akram et al. (Akram et al., 2022) discussed the concepts of non-linear stretching and EHS/SHS to describe the heat transfer through the stretchable cylinder. It is discovered that the temperature distribution in the fluid region is being disrupted by the non-linear stretching rate and the source of heat.
The scrutiny of second law analysis or, EG (entropy generation) in fluid flow and heat transport is a prominent area of study. Energy losses resulting from chemical processes, diffusion, solid-surface friction, and the viscosity of fluids all contribute to the production of entropy in thermodynamic systems. As a result, the formation of entropy generation (EG) has drawn a lot of attention to applications including heat exchangers, turbo machinery, and electronics cooling. Aiboud and Sauoli (Aiboud and Saouli, 2010) scrutinized the entropy optimized in viscoelastic flow through a flexible surface subjected to the magnetic field. The effect of slip across a heated vertical surface in entropy-optimized flow was calculated by But et al. (Butt et al., 2012). Slips have been found to allow for the control and adjustment of entropy formation in thermal systems. Abolbashari et al. (Abolbashari et al., 2014) employed HAM to examine, EG in magneto nanofluid flow near an unsteady stretched surface with H2O-base liquid and several nanoparticle types. Tlau and Ontela (Tlau and Ontela, 2019) examined the role of magnetohydrodynamics on nanomaterial entropy-optimized flow from an inclined channel with a heat source/sink embedded in a porous media. Entropy optimization of nanomaterials flow across two stretchable rotating disks with effects of bioconvection was examined by Khan et al. (Khan et al., 2020). Mondal et al. (Mondal et al., 2021) used trapezoidal lid-driven enclosures with, EG to study the Lorentz forces on the constant buoyant flow of Al2O3 nanoparticles. According to the calculations, the average Nusselt and Sherwood numbers, and aspect ratio all decrease with increasing the percentage of nanoparticle volume.
The literature that is currently accessible indicates that no exploration has been performed on the entropy generation of the radiative cross-flow stimulated with nanofluid from a porous expanding/contracting sheet with an asymmetrical heat source/sink. The present investigation fills a research gap by demonstrating cross-flow and heat transfer towards a stagnation point of nanofluid via an expanding/contracting sheet with asymmetrical heat sink/source and thermal radiation. The proposed model is originally described via a highly nonlinear system of PDEs. The PDEs are rehabilitated into ODEs by using the proper similarity variables and then solved by employing a bvp4c solver. Multiple solutions are provided for certain values of the parameters such as mass suction and shrinking sheet. The study described in this paper was driven by the following research questions.
• What impact does have on the skin friction and Nusselt number by raising the suction parameter against the stretching/shrinking parameter?
• How can the separation of the boundary layer be controlled in the presence of nanoparticles and stretching/shrinking parameters along with suction?
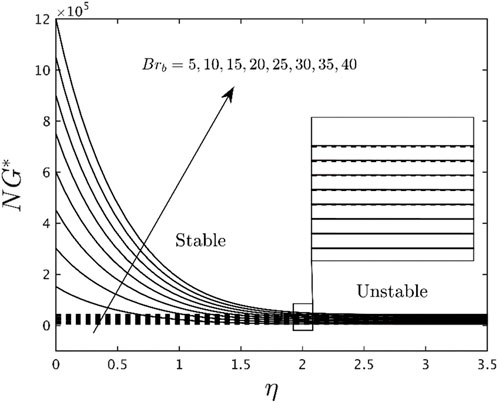
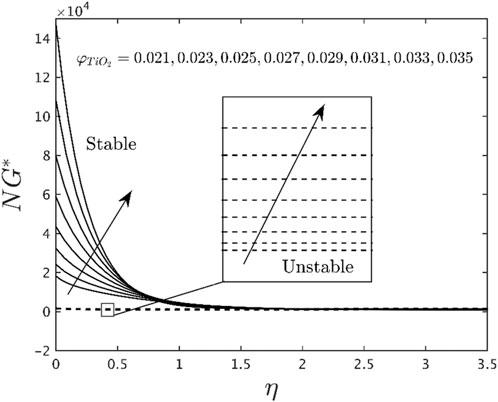
• What influence do Brinkman, temperature difference parameters, and TiO2 nanoparticles have on the entropy profiles?
2 Description of the flow problem
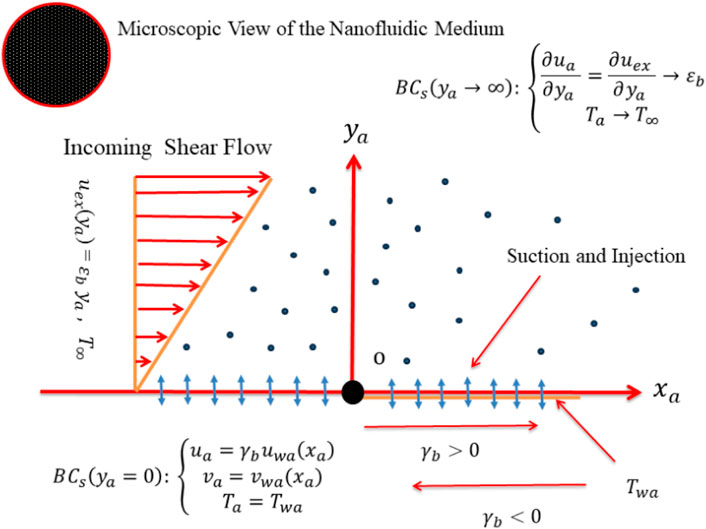
The nanofluids’ stagnation points radiative cross flow and thermal system characteristics past a contracting/expanding surface with the mutual influence of mass suction and EHSE/EHSK are taken in this study. As portrayed in Figure 1,
with boundary conditions (BCs) are:
In Eqs 1–4,
The radiation heat flux
Here, the Stefan Boltzmann constant and the mean absorption coefficient are denoted by
In addition, executing Eqs 5, 6 into Eq 3 yields the final form:
where
Furthermore,
Here,
For the considered model, the similarity transformations that can be expressed to further simplify the procedure for mathematical analysis are as follows:
which provides the opportunity to describe flows extremely broadly, regardless of the system size. Also, the prime corresponds to the derivative with respect to
In Eq. 10,
With the help of similarity transformations (9), the continuity Eq 1 of the governing model is satisfied while the rest of Eqs 2, 7 equations change to the resulting known ordinary (similarity) differential equations (ODEs) as:
along with border conditions:
In addition, Eq 11 for the case of
2.1 Gradients
The two vital physical aspects, namely, heat transfer rate and shear stress of the assumed model are of practical significance to apply by scientists or engineers. They are defined as follows:
By incorporating Eq 9 into Eq 14, the following dimensionless form yields:
Hence,
3 Second law analysis
Entropy generation (E.G.,), also known as the second law analysis, is a necessary instrument for measuring energy loss and depreciation in the effectiveness of engineering and industrial systems, such as rate and transport operations. As a result, the systems expend less energy, making, E.G., analysis and comprehension crucial. Taking into account the scenario of, E.G., for the viscous Newtonian liquid with the inclusion of nanoparticles (Abolbashari et al., 2014; Tlau and Ontela, 2019).
Two fundamental elements are principally responsible for the, E.G., in the contemplated cross-flow of viscous Newtonian nanofluid. The first term in the statement, which is on the right-hand side, denotes the ensuing local heat transfer, and the final term, the consequent fluid friction or viscous dissipation. The second law analysis is defined as follows in the dimensionless form:
The following formulas are obtained by incorporating the similarity transformations from Eq 9 into Eq 16. Hence,
where
4 Methodology
This section demonstrates the analysis of the assumed cross-flow and the suspension of nanofluid for heat transfer. The requisite model equations are expressed as highly nonlinear ODEs (11) and (12) along with BCs (13) using similarity variables (9). A built-in function named bvp4c included in the MATLAB software is used to work out these equations numerically. It ought to be noted that the scheme of the finite difference is the foundation for the bvp4c package, which is further highlighted by the 3-stage Lobatto IIIA procedure. To instigate the bvp4c method, the transmuted ODEs are modified into a first-order system by launching new-fangled variables. By establishing this process, let
Substituting Eq. 20 into Eqs 11, 12 along with BCs Eq. 13 we obtain the set of first-order ODEs as follows:
with BCs
The code desired initial estimations at the posited mesh point to solve Eq 21 and the corresponding conditions Eq. 22. The polynomial used in the collective type yields a continuous result. A fourth order accuracy set that is equally distributed over the spatial intervals where the function is integrated provides the result. The limitation at a distance
4.1 Validation of the MATLAB bvp4c solver
This subsection of the work specifies the rationality or validity, accuracy, and correctness of the considered MATLAB bvp4c solver for the special limiting case. To confirm this rationality, the friction factor outcomes for both branches (stable and unstable) results owing to several values of the shrinking constraint with prior research work when
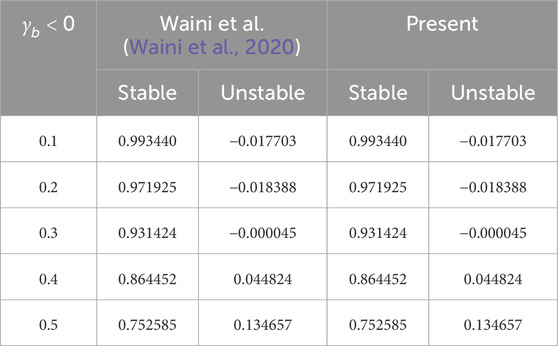
Table 2. Numerical comparison of outcomes for friction factor owing to several values of the shrinking parameter when
5 Analysis of the results
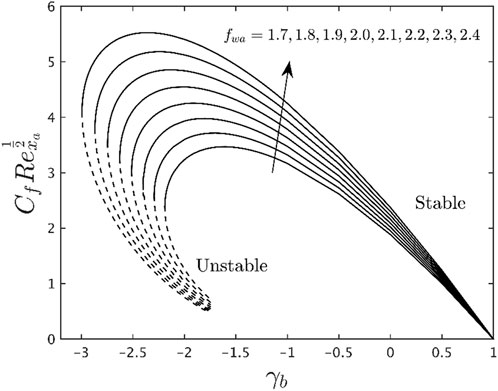
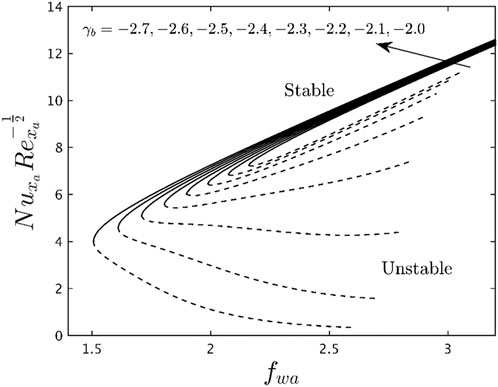
The current portion of the work describes the binary (stable and unstable) solutions for a certain region or area of the dimensionless mass suction parameter as well as the contracting parameter
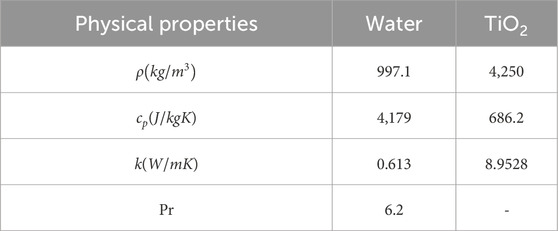
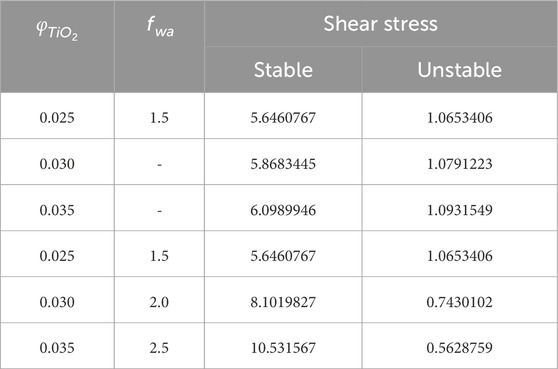
The numerical data of the gradients (skin friction and heat transfer rate) with the impression of the several distinguished factors corresponding to water-based Titania nanofluid are illustrated in Tables 3, 4 for the SBSE and USBES, respectively. Upshots divulge that the friction factor upsurges for the SBSE owed to the superior values of
Figures 2, 3 show the impact of
The impressions of
With the assistance or support of entropy generation or second law analysis (SLA), the thermodynamic system performance of water-based Titania nanoparticles can be improved. Figures 6–8 describe the consequence of parameters
6 Conclusion
The theoretical inspection on radiative cross flow and heat transfer incorporated water-based TiO2 nanofluid through a permeable stretching/shrinking sheet with irregular heat source/sink have been explored. The entropy generation was used to analyze the heat transfer process after the development of a computational model. Combined impacts of pertaining governing parameters like suction, expanding/contracting parameter, irregular heat source/sink parameter, radiation parameter, and volume fraction of the nanoparticles on shear stress and the heat transfer have been analyzed. The important conclusions of our research can be summed up as follows.
• The results suggest that the shear stress enhances due to
• The heat transfer rate accelerates due to the heat source
• The entropy generation increases in the presence of Brinkman number and nanoparticle volume fraction in both solutions, while decreasing due to the higher impacts of the difference of temperature parameter in both solutions.
7 Future work
Further, this problem can also be studied by incorporating unsteady flow or mixed convection flow in addition to incorporating various physical elements such as the slip effect, chemical reaction viscous dissipation, etc. Also, this model can be extended to any non-Newtonian models of the problem along with several other impacts like shape factors of the nanoparticles, waste discharge concentration, and thermophoresis particle deposition effects.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
SE: Writing–review and editing, Writing–original draft, Validation, Software, Project administration, Investigation, Funding acquisition, Formal Analysis. UK: Writing–review and editing, Visualization, Software, Methodology, Investigation, Conceptualization. AZ: Writing–original draft, Validation, Methodology, Data curation, Conceptualization. AI: Writing–review and editing, Validation, Supervision, Investigation, Formal Analysis. NA: Writing–review and editing, Writing–original draft, Validation, Resources, Funding acquisition. HA: Writing–original draft, Visualization, Validation, Resources, Funding acquisition.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University, through the Research Groups Program Grant no. (RGP-1444-0060).
Acknowledgments
This work was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University, through the Research Groups Program Grant no. (RGP-1444-0060).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abolbashari, M. H., Freidoonimehr, N., Nazari, F., and Rashidi, M. M. (2014). Entropy analysis foran unsteady MHD flow past a stretching permeable surface in nanofluid. Powder Technol. 267, 256–267. doi:10.1016/j.powtec.2014.07.028
Aiboud, S., and Saouli, S. (2010). Entropy analysis for viscoelastic magneto-hydrodynamic flow over a stretching surface. Int. J. Nonlinear Mech. 45, 482–489. doi:10.1016/j.ijnonlinmec.2010.01.007
Akram, M., Jamshed, W., Goud, B. S., Pasha, A. A., Sajid, T., Rahman, M. M., et al. (2022). Irregular heat source impact on carreau nanofluid flowing via exponential expanding cylinder: a thermal case study. Eng 36, 102171. doi:10.1016/j.csite.2022.102171
Areekara, S., Mackolil, J., Mahanthesh, B., Mathew, A., and Rana, P. (2021). A study on nanoliquid flow with irregular heat source and realistic boundary conditions: a modified Buongiorno model for biomedical applications. Z. für Angew. Math. Mech. 102 (3), e202100167. doi:10.1002/zamm.202100167
Bakar, N. A. A., Bachok, N., Arifin, N. M., and Pop, I. (2018). Stability analysis on the flow and heat transfer of nanofluid past a stretching/shrinking cylinder with suction effect. Res. Phys. 9, 1335–1344. doi:10.1016/j.rinp.2018.04.056
Butt, A. S., Munawar, S., Ali, A., and Mehmood, A. (2012). Entropy generation in hydrodynamic slip flow over a vertical plate with convective boundary. J. Mech. Sci. Technol. 26, 2977–2984. doi:10.1007/s12206-012-0701-3
Chen, C. K., and Char, M. I. (1988). Heat transfer of a continuous, stretching surface with suction or blowing. J. Math. Anal. Appl. 135, 568–580. doi:10.1016/0022-247x(88)90172-2
Choi, S. U., and Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29). IL (United States): Argonne National Lab.
Crane, L. J. (1970). Flow past a stretching plate. Z. Angew. Math. Phys. 21, 645–647. doi:10.1007/bf01587695
Eastman, J. A., Choi, S. U. S., Li, S., Yu, W., and Thompson, L. J. (2001). Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 78 (6), 718–720. doi:10.1063/1.1341218
Goldstein, S. (1965). On backward boundary layers and flow in converging passages. J. Fluid Mech. 21, 33–45. doi:10.1017/s0022112065000034
Guo, X., and Fu, Z. (2019). An initial and boundary value problem of fractional Jeffreys’ fluid in a porous half space. Comput. Math. Comp. 78 (6), 1801–1810. doi:10.1016/j.camwa.2015.11.020
Haq, R. U., Nadeem, S., Khan, Z. H., and Noor, N. F. M. (2015). Convective heat transfer in MHD slip flow over a stretching surface in the presence of carbon nanotubes. Phys. B Condens. Matter 457, 40–47. doi:10.1016/j.physb.2014.09.031
Ishak, A., Nazar, R., and Pop, I. (2009). Boundary layer flow and heat transfer over an unsteady stretching vertical surface. Meccanica 44, 369–375. doi:10.1007/s11012-008-9176-9
Johan, N. A., and Mansur, S. (2021). Boundary layer flow of dusty nanofluid over stretching sheet with partial slip effects. J. Advan. Res. Fluid Mech. Therm. Sci. 87 (2), 118–126. doi:10.37934/arfmts.87.2.118126
Jumana, S. A., Murtaza, M. G., Ferdows, M., Makinde, O. D., and Zaimi, K. (2020). Dual solutions analysis of melting phenomenon with mixed convection in a nanofluid flow and heat transfer past a permeable stretching/shrinking sheet. J. Nanofluids 9 (4), 313–320. doi:10.1166/jon.2020.1761
Kamal, F., Zaimi, K., Ishak, A., and Pop, I. (2019). Stability analysis of MHD stagnation-point flow towards a permeable stretching/shrinking sheet in a nanofluid with chemical reactions effect. Sains Malay 48 (1), 243–250. doi:10.17576/jsm-2019-4801-28
Khan, N. S., Shah, Q., Bhaumik, A., Kumam, P., Thounthong, P., and Amiri, I. (2020). Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. Sci. Rep. 10, 4448. doi:10.1038/s41598-020-61172-2
Khan, W. A., and Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat. Mass Transf. 53 (11-12), 2477–2483. doi:10.1016/j.ijheatmasstransfer.2010.01.032
Kumar, K. A., Sandeep, N., Sugunamma, V., and Animasaun, I. L. (2020). Effect of irregular heat source/sink on the radiative thin film flow of MHD hybrid ferrofluid. J. Therm. Anal. Calorim. 139, 2145–2153. doi:10.1007/s10973-019-08628-4
Makinde, O. D., and Aziz, A. (2011). Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 50 (7), 1326–1332. doi:10.1016/j.ijthermalsci.2011.02.019
Merkin, J. H. (1986). On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 20, 171–179. doi:10.1007/bf00042775
Mi, L. (2015). Boundary behavior for the solutions to Dirichlet problems involving the infinity-Laplacian. J. Math. Anal. Appl. 425 (2), 1061–1070. doi:10.1016/j.jmaa.2014.12.070
Miklavčič, M., and Wang, C. Y. (2006). Viscous flow due to a shrinking sheet. Q. Appl. Math. 64, 283–290. doi:10.1090/s0033-569x-06-01002-5
Mondal, P., Mahapatra, T. R., and Parveen, R. (2021). Entropy generation in nanofluid flow due to double diffusive MHD mixed convection. Heliyon 7, e06143. doi:10.1016/j.heliyon.2021.e06143
Prandtl, L. (1946a). Über Flüssigkeitsbewegung bei sehr kleiner Reibung, Verh. III. Int. Math. Kongr. Heidelberg. Leipzig: Teubner, 484–491.
Prandtl, L. (1946b). On boundary layers in three-dimensional flow. Rep. Aero. Res. Coun. Lond. No. 9829.
Roşca, N. C., Roşca, A. V., Jafarimoghaddam, A., and Pop, I. (2021). Cross flow and heat transfer past a permeable stretching/shrinking sheet in a hybrid nanofluid. Int. J. Numer. Meth. Heat. Fluid Flow. 31, 1295–1319. doi:10.1108/hff-05-2020-0298
Sakiadis, B. C. (1961). Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. Am. Inst. Chem. Eng. J. 7, 26–28. doi:10.1002/aic.690070108
Shahzad, A., Liaqat, F., Ellahi, Z., Sohail, M., Ayub, M., and Ali, M. R. (2022). Thin film flow and heat transfer of Cu-nanofluids with slip and convective boundary condition over a stretching sheet. Sci. Rep. 12, 14254. doi:10.1038/s41598-022-18049-3
Shamshuddin, M. D., Panda, S., Pattnaik, P. K., and Mishra, S. R. (2024a). Ferromagnetic and ohmic effects on nanofluid flow via permeability rotative disk: significant interparticle radial and nanoparticle radius. Phys. Scr. 99, 055206. doi:10.1088/1402-4896/ad35f8
Shamshuddin, M. D., Salawu, S. O., Panda, S., Mishra, S. R., Alanazy, A., and Eid, M. R. (2024b). Thermal case exploration of electromagnetic radiative tri-hybrid nanofluid flow in Bi-directional stretching device in absorbent medium: SQLM analysis. Case Stud. Therm. Eng. 60, 104734. doi:10.1016/j.csite.2024.104734
Sheikholeslami, M., Hayat, T., and Alsaedi, A. (2016). MHD free convection of Al2O3-water nanofluid considering thermal radiation: a numerical study. Int. J. Heat. Mass Transf. 96, 513–524. doi:10.1016/j.ijheatmasstransfer.2016.01.059
Soid, S. K., Ishak, A., and Pop, I. (2017). Boundary layer flow past a continuously moving thin needle in a nanofluid. Appl. Therm. Eng. 114, 58–64. doi:10.1016/j.applthermaleng.2016.11.165
Tawade, J., Abel, M. S., Metri, P. G., and Koti, A. (2016). Thin film flow and heat transfer over an unsteady stretching sheet with thermal radiation, internal heating in the presence of external magnetic field. Int. J. Adv. Appl. Math. Mech. 3, 29–40.
Thumma, T., Beg, O. A., and Kadir, A. (2017). Numerical study of heat source/sink effects on dissipative magnetic nanofluid flow from a non-linear inclined stretching/shrinking sheet. J. Mol. Liq. 232, 159–173. doi:10.1016/j.molliq.2017.02.032
Tlau, L., and Ontela, S. (2019). Entropy generation in MHD nanofluid flow with heat source/sink. SN Appl. Sci. 1, 1672. doi:10.1007/s42452-019-1733-4
Waini, I., Ishak, A., and Pop, I. (2019). Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat. Mass Transf. 136, 288–297. doi:10.1016/j.ijheatmasstransfer.2019.02.101
Waini, I., Ishak, A., and Pop, I. (2020). Transpiration effects on hybrid nanofluid flow and heat transfer over a stretching/shrinking sheet with uniform shear flow. Alex. Eng. J. 59, 91–99. doi:10.1016/j.aej.2019.12.010
Wang, Y. (2019). Multiple positive solutions for mixed fractional differential system with p-Laplacian operators. Value Probl. 2019, 144. doi:10.1186/s13661-019-1257-2
Weidman, P. (2017). Further solutions for laminar boundary layers with cross flows driven by boundary motion. Acta Mech. 228, 1979–1991. doi:10.1007/s00707-017-1810-y
Weidman, P. D., Kubitschek, D. G., and Davis, A. M. J. (2006). The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 44, 730–737. doi:10.1016/j.ijengsci.2006.04.005
Zhao, Y., Sun, Y., Liu, Z., and Bai, Z. (2019). Basic theory of differential equations with mixed perturbations of the second type on time scales. Adv. Differ. Equ. 2019, 268. doi:10.1186/s13662-019-2212-3
Zi, Y., and Wang, Y. (2019). Positive solutions for Caputo fractional differential system with coupled boundary conditions. Adv. Differ. Equ. 2019, 80. doi:10.1186/s13662-019-2016-5
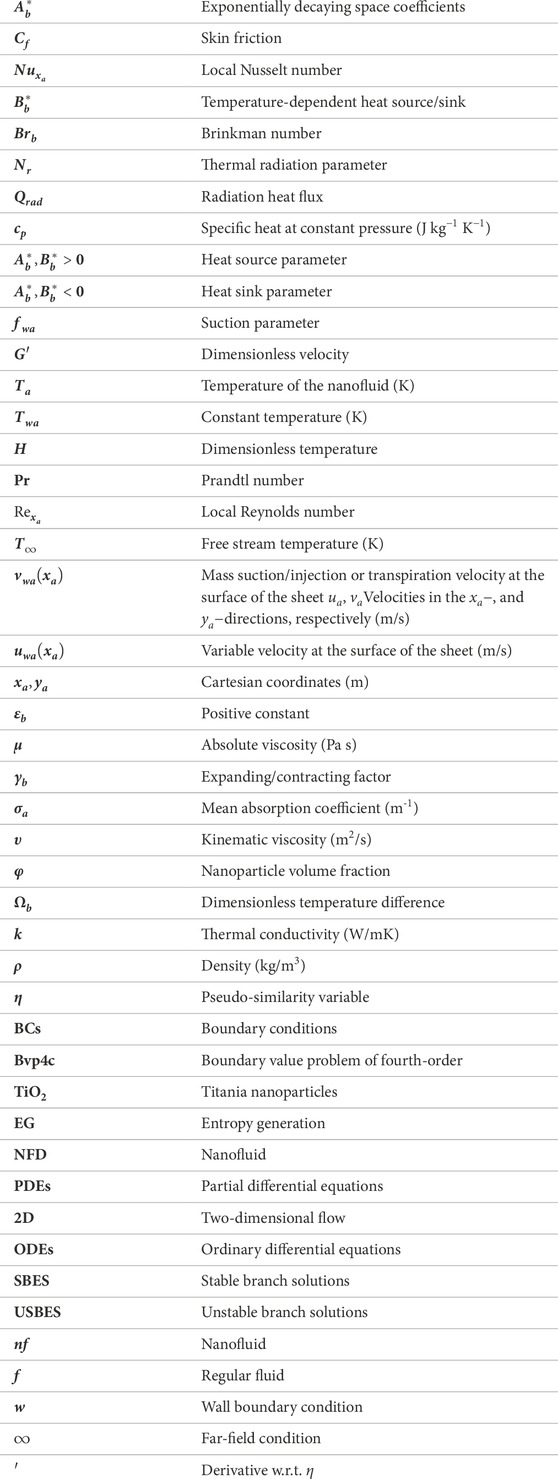
Nomenclature
Keywords: cross flow, entropy generation, expanding/contracting sheet, irregular heat source/sink, nanofluid
Citation: Elattar S, Khan U, Zaib A, Ishak A, Alwadai N and Albalawi H (2024) Irreversible mechanism and thermal cross-radiative flow in nanofluids driven along a stretching/shrinking sheet with the existence of possible turning/critical points. Front. Mater. 11:1391066. doi: 10.3389/fmats.2024.1391066
Received: 24 February 2024; Accepted: 23 July 2024;
Published: 08 August 2024.
Edited by:
Adebowale Martins Obalalu, Augustine University Ilara Epe, NigeriaCopyright © 2024 Elattar, Khan, Zaib, Ishak, Alwadai and Albalawi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Umair Khan, dW1haXIua2hhbkBsYXUuZWR1Lmxi
 Samia Elattar
Samia Elattar Umair Khan
Umair Khan Aurang Zaib
Aurang Zaib Anuar Ishak2
Anuar Ishak2