Low-velocity impact resistance of double arrowhead triangular structure with negative Poisson’s ratio

Negative Poisson’s ratio (NPR) structures, known for their high specific strength, high specific stiffness, high impact resistance, etc., have broad applications in aerospace, medical equipment, transportation, shipping, sports, and other fields. Among them, the double arrowhead triangular structure with NPR effect has been proposed and designed, showing great potential for practical use. To study the properties of the double arrowhead triangular structure, Poisson’s ratio and low-velocity impact resistance of this structure have been calculated by numerical theory and finite element analysis. These methods provide a reliable way to evaluate the mechanical behavior of the structure under different conditions. The analysis of the double arrowhead triangular board structure has revealed the impact failure mode, impact velocity history curves, and the distribution of the first principal stress. Importantly, the results show that when the specific angles are α = 20° and β = 50°, the Poisson’s ratio of the double arrowhead triangular structure reaches − 2.1, and the low-velocity impact resistance of the structure is found to be the strongest at this angle combination. The findings of this study reveal the mechanism of low-velocity impact resistance of the double arrowhead triangular board structure and the influence of angle parameters on its impact performance. This understanding not only contributes to the theoretical knowledge of NPR structures but also broadens the engineering applications of double arrowhead triangular structures and NPR structures as a whole.

1 Introduction

In the natural world, biological structures have evolved unique mechanical characteristics to adapt to environmental challenges. For instance, Yang and Yang (2021) revealed that the vascular bundle structure of Moso bamboo enables uniform stress distribution and efficient energy dissipation under tensile loads. Similarly, Jiang et al. (2020) demonstrated that the concentric hierarchical arrangement of coconut palm stems enhances impact energy absorption through layered deformation. These structural features, often exhibiting negative Poisson’s ratio (NPR) effects, provide inspiration for engineering materials with superior mechanical performance. NPR structures, characterized by lateral expansion under axial compression, have garnered significant attention due to their exceptional energy absorption, vibration damping, and impact resistance (Chen J. et al., 2020; Yu et al., 2018; Wang T. et al., 2021; Lu et al., 2016; Lu et al., 2021; Li et al., 2018). They are broadly classified into re-entrant (Chen M. M. et al., 2020; Hu et al., 2019; Nkansaht et al., 1994), rotational (Grima and Evans, 2006), chiral (Pasternak and Dyskin, 2012), and origami-inspired (Mahadevan and Rica, 2005; Alderson and Evans, 1997) types, with applications spanning aerospace, biomedical devices, and protective engineering.

Recent advances in NPR structure design emphasize bio-inspired principles and additive manufacturing. Chen and Pugno (2013) reviewed biomimetic mechanisms in hierarchical materials, such as the crack-resistant microstructure of turtle shells. Concurrently, Zhang et al. (2020), Zhang and Lu (2020), Zhang and Lu (2023) explored energy absorption in re-entrant honeycombs under dynamic loading, highlighting the synergy between geometric design and mechanical optimization. However, existing studies predominantly focus on conventional honeycomb configurations (Jiang and Hu, 2017; Xu et al., 2021; Yang et al., 2015; Zhang et al., 2014), with limited exploration of angle-parameterized NPR structures. For example, Shen et al. (2020) established that honeycomb structures’ impact resistance correlates with speed and arc angle, while Nakamoto et al. (2009) examined honeycomb structures with random rigid inclusions under in-plane impact. He et al. (2016) further linked low-speed impact resistance to energy absorption and top-plate dent depth. Despite these efforts, a comprehensive understanding of the impact resistance of non-hexagonal NPR geometries, such as the double arrowhead triangular structure, remains elusive.

To address this gap, this study proposes a double arrowhead triangular structure with an NPR effect, inspired by the boomerang’s geometry—an engineered design integrating bio-inspired principles. Unlike previous work (Li et al., 2017; Larsen et al., 1997), we systematically investigate the angle-dependent NPR mechanism and its relationship to impact resistance through theoretical modeling and finite element analysis. The novelty lies in: deriving an analytical Poisson’s ratio formula for double arrowhead units, identifying optimal angle parameters (α = 20°, β = 50°) for maximal NPR effect (ν = −2.1), and elucidating low-velocity impact failure modes and stress distribution patterns. Through numerical derivation and finite element simulation, the relationship between unit angles and Poisson’s ratio is analyzed, and the NPR effect mechanism is explained. Furthermore, the low-speed impact load of the double arrowhead triangular plate structure is numerically simulated, with impact resistance assessed using the destruction mode of the impactor, stress distribution, and velocity history curve as evaluation indicators.

In addition, while static compression tests can reveal material deformation and the NPR effect, low-velocity impact simulations are crucial for understanding real-world performance in fields like aerospace and automotive applications (He et al., 2016). The correlation between static and dynamic responses is vital for optimizing NPR structure design, as it enables prediction of material behavior under different loading conditions (Yang and Yang, 2021). This study investigates both the static compression behavior and low-velocity impact resistance of the double arrowhead triangular structure, providing a comprehensive understanding of its mechanical performance. These findings bridge the gap between bio-inspired design and impact-resistant engineering, offering a paradigm for optimizing NPR structures in protective applications.

2 Double arrowhead triangular structure

2.1 Design of double arrowhead triangular structure

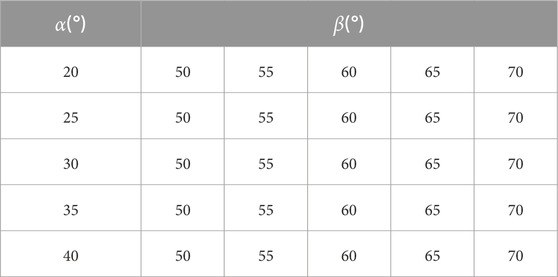
Inspired by the boomerang, the double arrowhead triangular structure was obtained by simplifying the boomerang as shown in Figure 1a. The selection of angle parameters α and β was initially based on the need to achieve a negative Poisson’s ratio (NPR) effect while maintaining structural integrity. These parameters were chosen after a series of preliminary studies and simulations indicated they would yield the desired mechanical properties.The angle parameters α and β are crucial for determining the structure’s response to external loads. Specifically, is the angle between sides AB and AD, while is the angle between side BO and OD. The fundamental reason for selecting these parameters was to explore the range of angles that would result in the most pronounced NPR effect, characterized by a negative Poisson’s ratio. This effect is known to enhance the structure’s energy absorption capability upon impact, a key characteristic for applications in industries such as aerospace, automotive, and personal protective equipment. Our preliminary screening of the angle parameters was guided by theoretical considerations and computational simulations. The aim was to identify angles that would not only result in a negative Poisson’s ratio but also strike a balance between structural strength and flexibility. This balance is essential for withstanding impact forces without catastrophic failure.Furthermore, the chosen angles were also intended to facilitate the manufacturing and assembly processes. Simpler angles often lead to more straightforward construction, which in turn can affect the cost-effectiveness and scalability of the structure’s production.In summary, the angle parameters α and β were selected based on their potential to provide the required mechanical properties, their performance in preliminary simulations, and their practical implications for manufacturing. The unit cells are periodically arranged to obtain the double arrowhead triangular structure as shown in Figure 1b. The double arrowhead triangular structure consists of three unit cells connected by dots horizontally and longitudinally. To ensure structural integrity, beams have been added to the top and bottom of the model. The values of the parameters of Figure 1 are shown in Table 1.

Figure 1

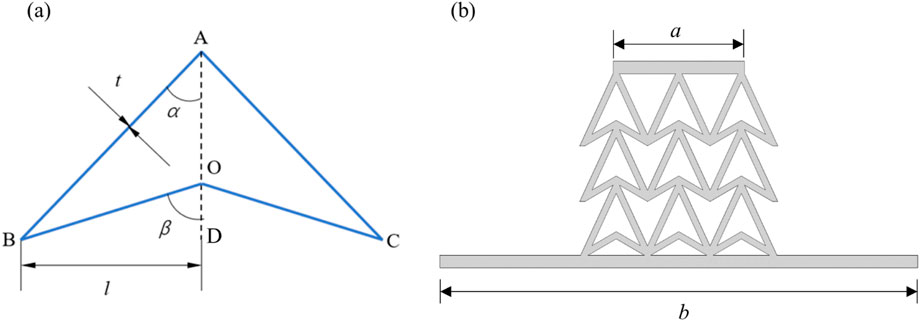
Figure 1. Schematic diagram of the double arrowhead triangular structure. (a) The configuration of double arrowhead triangular structure unit cell. (b) The model of double arrowhead triangular structure.

Table 1

Table 1. Figure 1 of the parameter values.

2.2 Numerical calculation

In order to describe the NPR mechanism of the structure, based on the concept and definition of Poisson’s ratio, a mechanical analysis and deformation analysis of the double arrowhead triangular structure cell have been conducted. Considering the particularity of the Y-axis symmetry of the cell structure, we only need to analyze half of the model. For the diagram of unit cell structure shown in Figure 2a, α is the angle between side AB and side AD, while β is the angle between side BO and side OD. According to the configuration characteristics of the cell structure, the following is obtained:

$l=l_2·\mathit{sin}\mathrm{\alpha }(1)$

$l_2=\frac{l_1\sin \mathrm{\beta }}{\sin \mathrm{\alpha }}(2)$

$h=l_2·\cos \mathrm{\alpha }-l_1·\cos \mathrm{\beta }(3)$

Figure 2

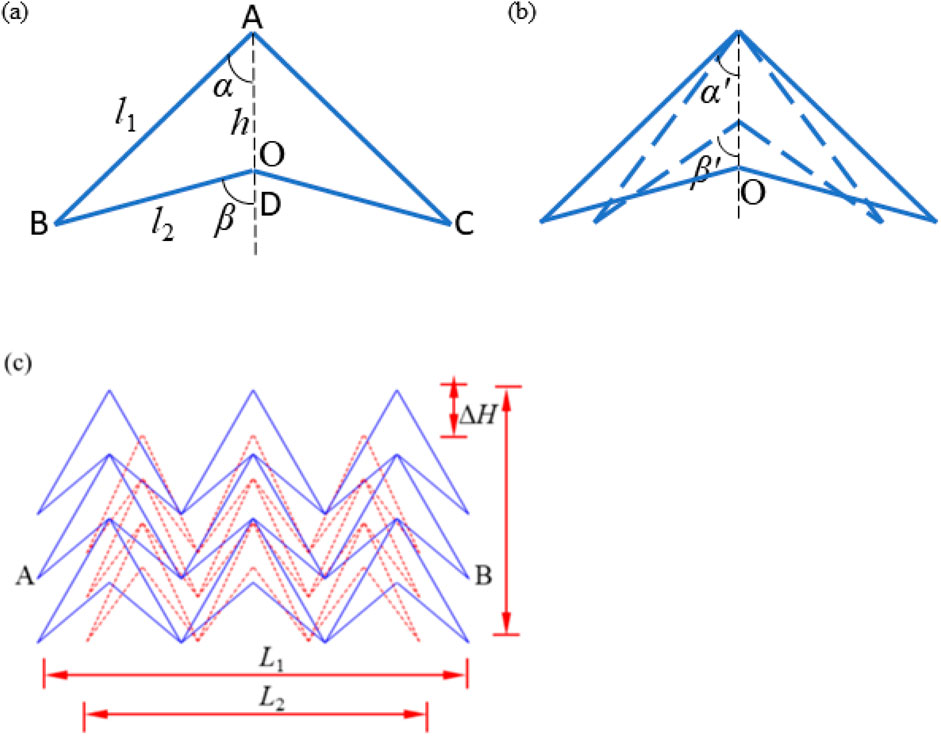
Figure 2. Deformation analysis of a double-arrow triangular structure. (a) Schematic diagram of the unit cell unit structure. (b) Schematic diagram of the compression deformation of the unit cell structure. (c) Compression deformation diagram of a double-arrow triangular structure.

According to previous studies, the strain can be calculated from the displacement corresponding to the deformation mechanism (Zhang et al., 2018; Gao et al., 2018).

As shown in Figure 2b, points B and C move along the X-axis direction, and point O can move along the Y-axis direction. The angles α and β correspond to angles α′ and β′ after compression deformation. Therefore, considering the particularity of the Y-axis symmetry of the cell structure, we only need to calculate half of the model. Assuming that AB and OB are always in the linear elastic stage during the deformation process, the horizontal displacement components of point B and the vertical displacement components of point O can be obtained using the methods of theoretical mechanics.

$∆l=l_2·\sin \mathrm{\alpha }-l_2·\cos \mathrm{\alpha }\tan {\alpha }^{\prime }(4)$

$∆h=\frac{l_2·\cos \mathrm{\alpha }\tan {\alpha }^{\prime }}{\tan {\mathrm{\beta }}^{\prime }}-l_1·\cos \mathrm{\beta }(5)$

where is the horizontal displacement component of point B, which is the vertical displacement component of point O, and according to Equations 4, 5, the strain increment of the unit cell structure along the X and Y-axes can be obtained.

${\mathrm{\epsilon }}_x=\frac{∆l}{l}(6)$

${\mathrm{\epsilon }}_y=\frac{∆h}{h}(7)$

Equations 1–5 are substituted into Equations 6, 7, respectively, to obtain the Poisson’s ratio expression for the unit cell structure.

$\mathrm{\nu }=\frac{{\mathrm{\epsilon }}_{\mathrm{x}}}{{\mathrm{\epsilon }}_{\mathrm{y}}}=\frac{\left(\sin \mathrm{\alpha }-\cos \mathrm{\alpha }\tan {\mathrm{\alpha }}^{\prime }\right)\left(\frac{\sin \mathrm{\beta }}{\sin \mathrm{\alpha }}\cos \mathrm{\alpha }-\cos \mathrm{\beta }\right)}{\sin \mathrm{\alpha }\left(\frac{\sin \mathrm{\beta }\cot \mathrm{\alpha }\tan {\mathrm{\alpha }}^{\prime }}{\tan {\mathrm{\beta }}^{\prime }}-\cos \mathrm{\beta }\right)}(8)$

According to Equation 8, the Poisson’s ratio of the unit cell structure is only related to the angular parameter and. Due to and and α′ and β′ values range from 0° to 90° and α are less than β, α′ is less than α, and β′ is less than β,Therefore, $\sin \mathrm{\alpha }-\cos \mathrm{\alpha }\tan {\alpha }^{\prime }$ is greater than 0, $\frac{\sin \mathrm{\beta }}{\sin \mathrm{\alpha }}\cos \mathrm{\alpha }-\cos \mathrm{\beta }$ is greater than 0, $\frac{\sin \mathrm{\beta }\cot \mathrm{\alpha }\tan {\alpha }^{\prime }}{\tan {\mathrm{\beta }}^{\prime }}-\cos \mathrm{\beta }$ is less than 0, and because $\sin \mathrm{\alpha }$ is greater than 0, $\mathrm{\nu }$ can be obtained less than 0.Hence the Poisson’s ratio of the unit cell structure is always negative, and the unit cell structure is NPR structure. With the increase of $\mathrm{\alpha }$ or $\mathrm{\beta }$, the Poisson’s ratio increases correspondingly, while the NPR effect decreases, indicating that the NPR of the unit cell structure is positively correlated with $\mathrm{\alpha }$ and $\mathrm{\beta }$.

In order to accurately measure the NPR characteristics of double arrowhead triangular structure, the concept of material Poisson’s ratio has been used to define the NPR of double arrowhead triangular structure. The distance above and below the beam of the longitudinal strain of the double arrowhead triangular structure has been taken as the original length standard, and the two points on the outermost edge of the second row of unit cells have been selected as the characteristic points. The initial transverse distance of the two feature points is the original length, and the variation value of the transverse distance of the two points is the transverse deformation value. As demonstrated in Figure 2c, two points A and B are characteristic points of transverse strain calculation of the structure. The distance between the two points before the model deformation is $L_1$ and the distance between the two points after the model deformation is $L_2$. The initial height of the model is $H$, and the height of the compression is $\Delta H$. Poisson’s ratio has been obtained by deducing transverse and longitudinal strains of double arrowhead triangular structure as shown in Equations 9–11.

${\mathrm{\epsilon }}_x=\frac{L_1-L_2}{L_1}(9)$

${\mathrm{\epsilon }}_y=\frac{\Delta H}{H}(10)$

$\mathrm{\nu }=-\frac{{\mathrm{\epsilon }}_x}{{\mathrm{\epsilon }}_y}=-\frac{H·\left(L_1-L_2\right)}{\Delta H·L_1}(11)$

2.3 Finite element modeling

2.3.1 NPR effect

The finite element analysis software ABAQUS has been utilized for the static compression analysis of the double arrowhead triangular structure. Polylactic acid (PLA) has been selected as the material for the double arrowhead triangular structure, with a density of 1.22 g/cm³, an elastic modulus of 413 MPa, and a Poisson’s ratio of 0.3. The double arrowhead triangular structure is meshed using solid elements with a 0.5 mm seed distribution. A fixed constraint has been applied to the lower boundary of the model, and a vertical downward displacement load of 1 mm has also been applied to the upper boundary. The selected angular parameters of the double arrowhead triangular structure are shown in Table 2.

Table 2

Table 2. Angle parameters of double arrowhead triangular structure.

In the construction of the finite element model, we meticulously designed the meshing strategy. A structured approach was adopted for meshing the model, with finer meshes applied to areas of stress concentration and potential damage to ensure that key details were captured, while coarser meshes were used in other areas to optimize computational efficiency. The mesh density was determined based on mesh independence tests, where the mesh was gradually refined and the analysis results were compared to find the optimal balance between computational accuracy and cost. For element selection, we prioritized the use of a 0.5 mm seed distribution for meshing solid elements to ensure the accuracy of the simulation. The material properties of each mesh element involved selecting polylactic acid (PLA) as the material, with a density of 1.22 g/cm³, an elastic modulus of 413 MPa, and a Poisson’s ratio of 0.3 (Suresh et al., 2024). Boundary conditions and loading were applied to strictly simulate actual working conditions, including the application of fixed constraints and various mechanical loads. Fixed constraints were applied at the bottom of the model, and a 1 mm vertical downward displacement load was applied at the top. Finally, by comparing with experimental data and computational results from other literature, as well as conducting a sensitivity analysis, we verified the accuracy and reliability of the mesh model, ensuring the validity of the model for subsequent analysis. In this way, the structural performance under different angular parameters was investigated.

2.3.2 Low-velocity impact

In order to accurately simulate the impact dynamic response, cracking behavior and crack development of double arrowhead triangular structure, the cracking of PLA is simulated by ABAQUS/EXPLICIT module. Impact model consists of impactor and double arrowhead triangular board structure as shown in Figure 3a. The impactor is hammerhead, in which the diameter of hammerhead hemisphere is 16 mm, the cylinder height is 8 mm, located in the center of the double arrowhead triangular board structure. The length and width of double arrowhead triangular board structure is 9 cm, the thickness of the upper and lower boards is 2 mm, and the height is controlled by unit angle parameters.

Figure 3

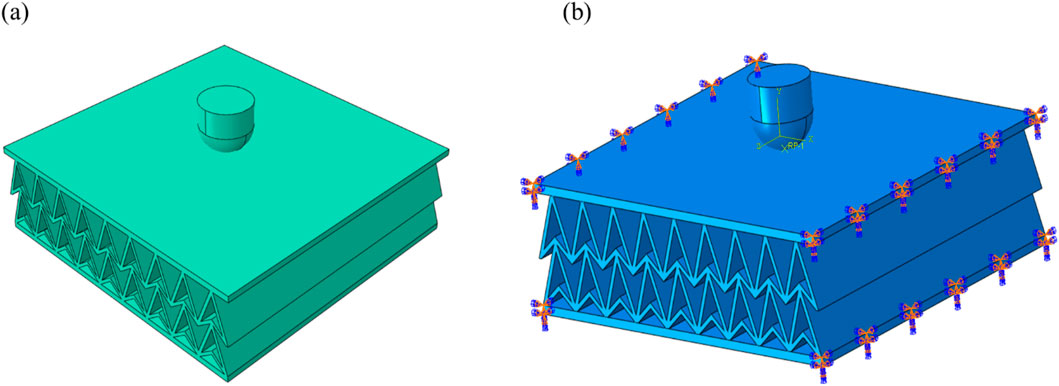
Figure 3. Schematic of the low-velocity impact tests finite element model for double arrowhead triangular board structure. (a) Finite element model of double arrowhead triangular board structure. (b) The boundary condition of double arrowhead triangular board structure.

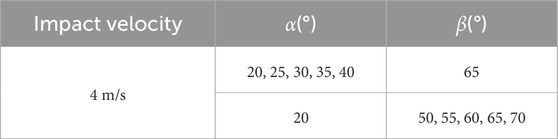
In order to deeply analyze the low-velocity impact resistance of different unit cell structures, nine different unit cell structures of double arrowhead triangular board structure have been designed as shown in Table 3. At the same time, the low-velocity impact computational work has been conducted to fully explore the internal law of angle parameters and low-velocity impact resistance. The physical and mechanical parameters of the impactor and the double arrowhead triangular board structure material PLA are shown in Table 4. To satisfy the vertical impact of hammerhead on the double arrowhead triangular board structure, the displacement and angle constraints are imposed on the impactor, and only the displacement freedom in the Y direction is retained. Complete constraints are added on the two outer surfaces of the double arrowhead triangular board structure, as shown in Figure 3b.

Table 3

Table 3. Nine numerical simulation schemes of double arrowhead triangular board structures.

Table 4

Table 4. Elastic and strength properties of the steel and PLA.

3 Results and discussions

3.1 Poisson’s ratio

Figure 4 illustrates that the double arrowhead triangular structure exhibits significant NPR effect under vertical compression load. Under the vertical compression load, the hypotenuse and underside of the two sides of the unit cell produce bending deformations and in-plane rotation, and at the same time the unit cells contract inward. From the color shades of the legend, it is obvious that the contraction degree of the unit cell group gradually decreases from top to bottom.

Figure 4

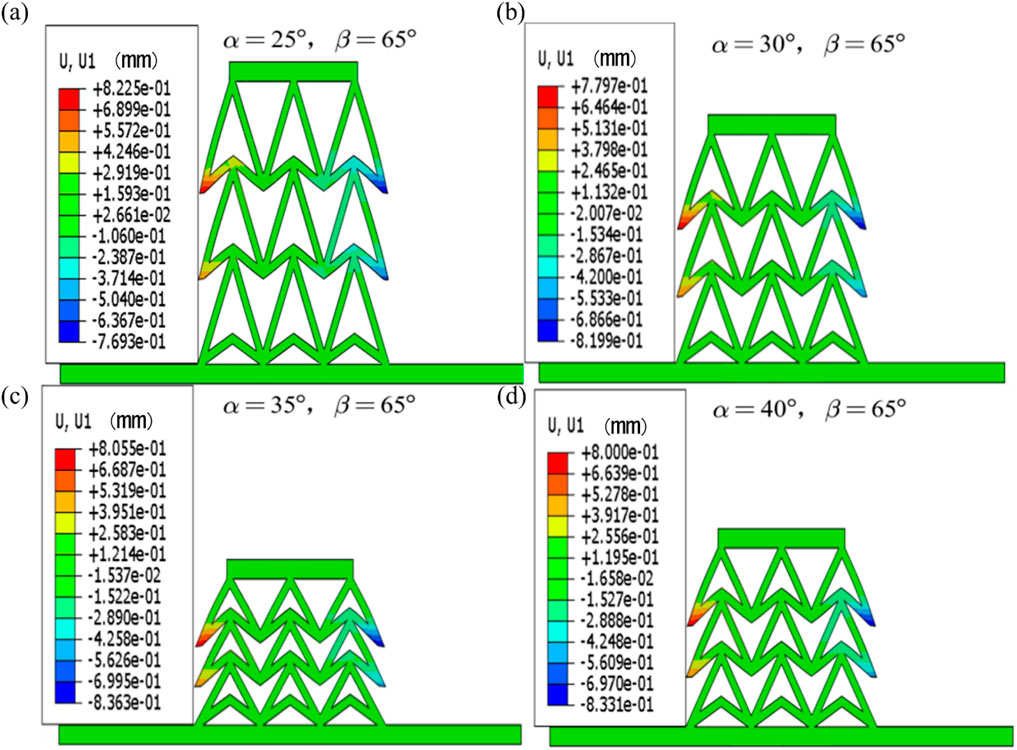
Figure 4. Lateral displacement distribution of double arrowhead triangular structure. (a) α = 25°, β = 65°. (b) α = 30°, β = 65°. (c) α = 35°, β = 65°. (d) α = 40°, β = 65°.

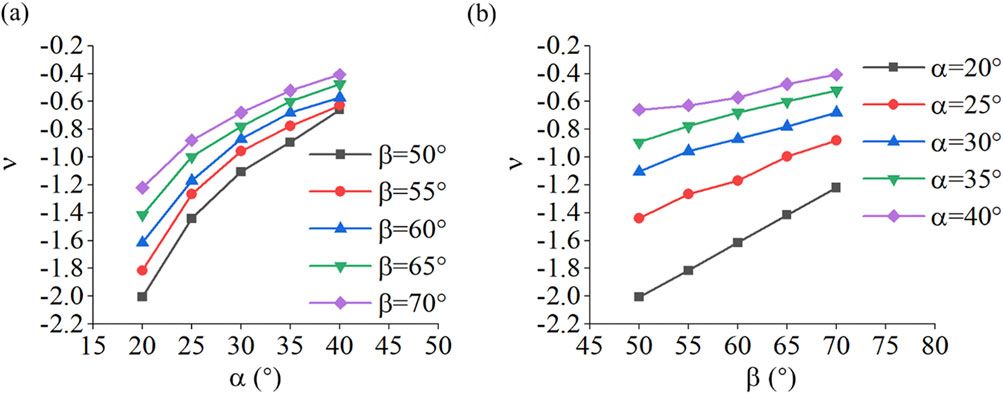
Figure 5 shows the Poisson ratio of double arrowhead triangular structure under different angle combinations. The Poisson’s ratio of double arrowhead triangular structures are related to the angle parameter, and the Poisson’s ratio has obvious difference under different angle parameter combination. The angle parameters α and β are positively correlated with Poisson’s ratio, and Poisson’s ratio increases with the increase of angle parameters. With the increase of α or β, the Poisson’s ratio increases slowly, and the gain effect of angle parameters on Poisson’s ratio decreases gradually. The Poisson’s ratio of double arrowhead triangular structure has upper and lower limits due to the limited value of the angle parameters α and β. It can be roughly judged from the direction of the curves that the Poisson’s ratio of double arrowhead triangular structure is always in the negative range, presenting continuous NPR effect. The NPR of dart structures depends on the concave structure of unit cell structure. The NPR effect can be increased by reducing α and β. When α = 20° and β = 50°, the minimum Poisson’s ratio of double arrowhead triangular structure is −2.1.

Figure 5

Figure 5. Poisson’s ratio of double arrowhead triangular structure.

3.2 Failure modes of double arrowhead triangular board structure

Figure 6 clearly shows the top and bottom failure modes of three double arrowhead triangular board structures at 4 m/s impact velocity when α = 65°. From the perspective of failure mode, the three models are all penetrating failures, and all cracks are generated, and the crack propagation direction is roughly horizontal and vertical. There are a lot of massive material fragments in the crack and the phenomenon of partial lifting of material exists. The top surface of each model is directly cracked, and the shape of the crack is approximately circular.

Figure 6

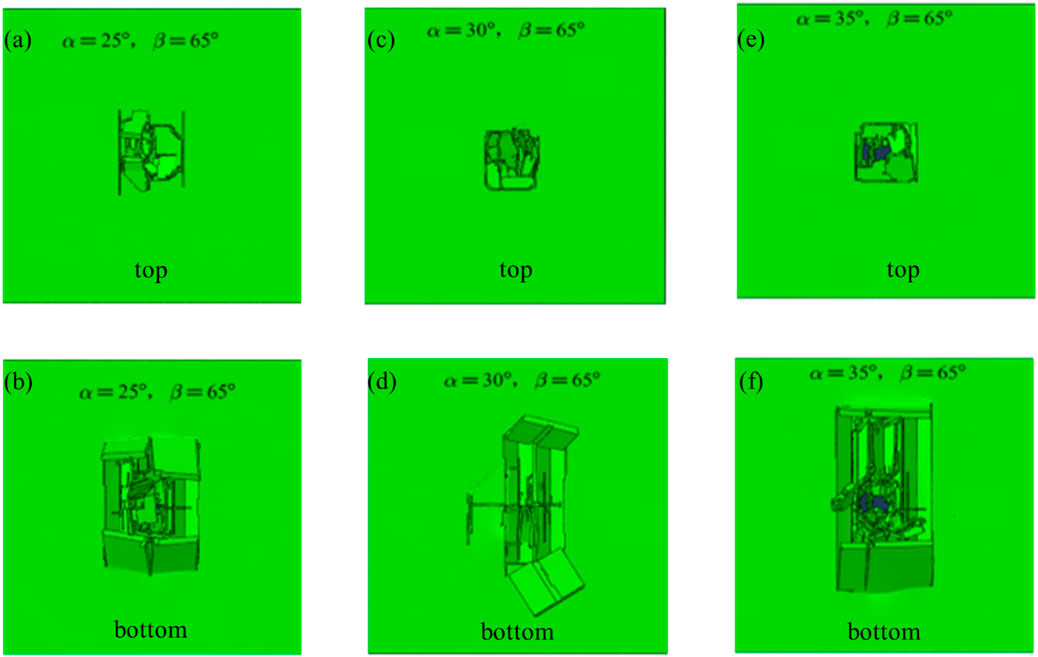
Figure 6. The top and bottom impact damage pattern of double arrowhead triangular board structure. (a) and (b) α = 25°, β = 65°. (c, d) α = 30°, β = 65°. (e, f) α = 35°, β = 65°.

3.3 Velocity history curves of impactor

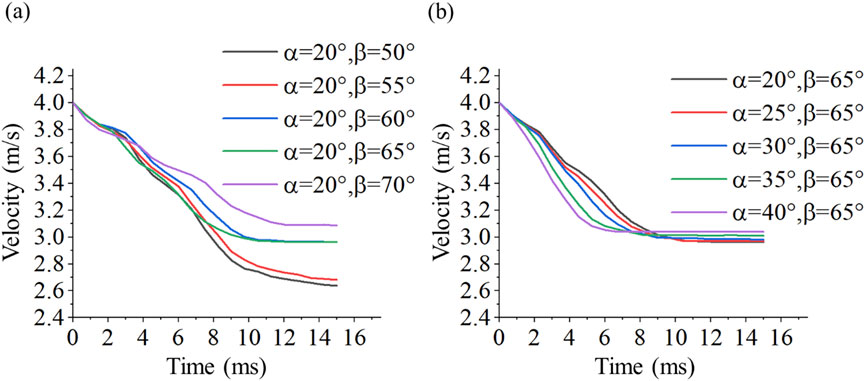
Figure 7 clearly reflects the changing trend of the impactor’s velocity history. The velocity variation trend of impactor under different models has obvious difference. The velocity history of the impactor is roughly divided into two stages: descending and smooth. In the velocity decline stage, part of the kinetic energy of the impactor is converted into the internal energy of the double arrowhead triangular board structure, and the velocity of the impactor decreases. In the velocity decline stage, part of the kinetic energy of the impactor is converted into the internal energy of the double arrowhead triangular board structure, and the velocity of the impactor decreases. In the stable velocity stage, the impactor penetrates the double arrowhead triangular board structure. Therefore, the impactor is no longer affected by the impedance of the double arrowhead triangular board structure, and the speed remains basically stable.

Figure 7

Figure 7. Velocity history curves of impactor.

Figure 7 shows that depending on the angle parameters, the rate and amplitude of the velocity drop are also different. Comprehensive analysis shows that the decline amplitude is negatively correlated with angle parameters, that is, the smaller α or β is, the larger the decline amplitude of impactor velocity is. The decrease amplitude of impactor velocity directly reflects the loss of kinetic energy and indirectly reflects the impact resistance of the double arrowhead triangular board structure. The larger the drop amplitude of impactor velocity is, the stronger the impact resistance of the double arrowhead triangular board structure is. Reducing α or β is beneficial to improving the impact resistance of the double arrowhead triangular board structure. The double arrowhead triangular board structure with angle parameters of α = 20° and β = 50° has the strongest impact resistance, and its velocity decrease amplitude reaches 1.4 m/s, and the reduction rate is 35%.

In this study, the velocity history curves of the impactor we observed show similar trends compared to the results from previous research. For instance, He et al. (2016) found that the impact resistance of honeycomb structures is positively correlated with impact velocity and arc angle. In our study, the variation in the velocity drop amplitude also directly reflects the structure’s impact energy absorption capability. These findings echo the energy absorption performance optimization of sinusoidal NPR honeycomb structures mentioned by He et al. (2016).

The velocity drop amplitude holds significant engineering importance for energy absorption and impact protection. As Lu et al. (2021) stated, shape optimization can significantly enhance a structure’s bending stiffness and specific energy absorption capacity. In our study, structures with a larger velocity drop amplitude exhibit better energy absorption performance, which can be translated into improved design guidelines to optimize the impact response of NPR structures. For example, by adjusting the angle parameters to control the velocity drop amplitude, the impact protection performance of the structure in practical applications can be optimized.

3.4 Impact deformation of double arrowhead triangular board structure

In the current study, the impact deformation patterns we observed are similar to the findings of previous research. For instance, Zhang et al. (2018) found in their low-velocity impact study of foam-core composite sandwich structures that the structural deformation behavior is positively correlated with impact energy and the dent depth of the top panel. Similar trends were observed in our study, where the impact deformation patterns are significantly influenced by the angle parameters. These findings are consistent with the impact dynamics research on honeycomb structures with NPR effects by He et al. (2016), who discovered that the deformation patterns of these structures are related to the impact velocity and arc angle.

Impact deformation has long-term implications for the integrity and functionality of a structure. As Chen M. M. et al. (2020) stated, structures with NPR effects exhibit better energy absorption under impact loads, which helps maintain the integrity of the structure. In our study, we found that impact deformation can be controlled by adjusting the angle parameters, thereby enhancing the structure’s impact resistance. For example, when the angle parameters are 20° and 50°, the structure demonstrates the best impact resistance, indicating that optimizing the angle parameters can significantly improve the structure’s impact resistance.

To provide a more detailed description of the impact deformation process, we utilized charts and finite element analysis results. Figure 8a presents the curve of the impactor’s velocity change over time, which can be roughly divided into two stages: the velocity decline stage and the stable stage. During the velocity decline stage, part of the impactor’s kinetic energy is transformed into the internal energy of the structure, causing the impactor’s velocity to decrease. In the stable stage, the impactor penetrates the structure and is no longer hindered by it, so the velocity remains essentially stable.

Figure 8

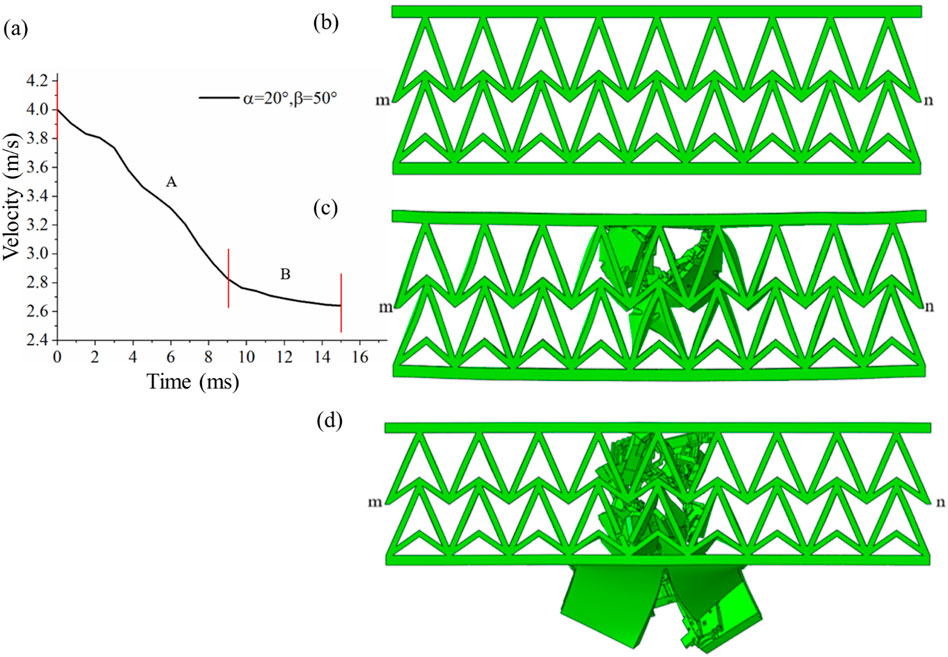
Figure 8. Impact damage diagram of double arrowhead triangular board structure during different period. (a) Velocity history of impactor when α = 20°, β = 50°. (b) Initial time. (c) At the end of period A. (d) At the end of period B.

Figures 8b–d illustrate the impact deformation at different time points. At the initial moment, the impactor comes into contact with the top of the structure. During Phase A, the model is subjected to the impact load, resulting in the formation of a small hole at the top. Over time, the PLA gradually reaches its strength limit and deforms. Disregarding the axial displacement of the PLA and considering the longitudinal displacement as the dominant factor, the small hole gradually enlarges, and the structure is extruded around along the longitudinal axis. As the hole expands, radial cracks form around the circumference of the hole, the circumferential stress is unloaded and gradually extends outward, forming a circular orifice on the top surface. During the impact process, the impactor enters the shear area of the structure, and the shear resistance additionally consumes the kinetic energy of the impactor. Meanwhile, the heat transfer caused by the impact friction between the impactor and the structure also consumes part of the kinetic energy. The structure exhibits transverse and longitudinal compression behavior macroscopically, demonstrating the NPR effect.In Phase B, the impactor contacts the bottom plate and is subjected to the impact load. The PLA within the structure gradually reaches its strength limit and deforms, forming a small hole. As time progresses, the orifice material is extruded longitudinally, and the orifice enlarges. During the expansion of the orifice, radial cracks gradually develop. The stress around the PLA gradually reaches the cracking stress, causing partial cracking of the bottom plate, energy release, and stress redistribution. In this process, the interaction between the impactor and the structure gradually weakens, and the velocity of the impactor tends to stabilize. The decrease in the impactor’s velocity is influenced by the material. The material in the weak action areas on both sides of the structure exhibits a rebound behavior and returns to its original position. The slopes of Phases A and B indicate that the NPR effect significantly influences the decrease in the impactor’s velocity.

3.5 The first principal stress distribution

Figures 9–11 clearly show the distribution of the first principal stress of the double arrowhead triangular board structures at the end of the impact. Figures 9, 10a illustrate that when β = 65°, as α increases, the maximum tensile stress of the double arrowhead triangular board structures first decreases and then increases, and the damage resistance first decreases and then increases. It is obvious that when α = 20°, β = 65°, double arrowhead triangular board structure has the strongest damage resistance. Combined with the velocity history curves of the impactor and the first principal stress distribution of the double arrowhead triangular board structure, comprehensively judged from the aspects of damage resistance and impact resistance, reducing α is beneficial to increase the impact safety of the structure.

Figure 9

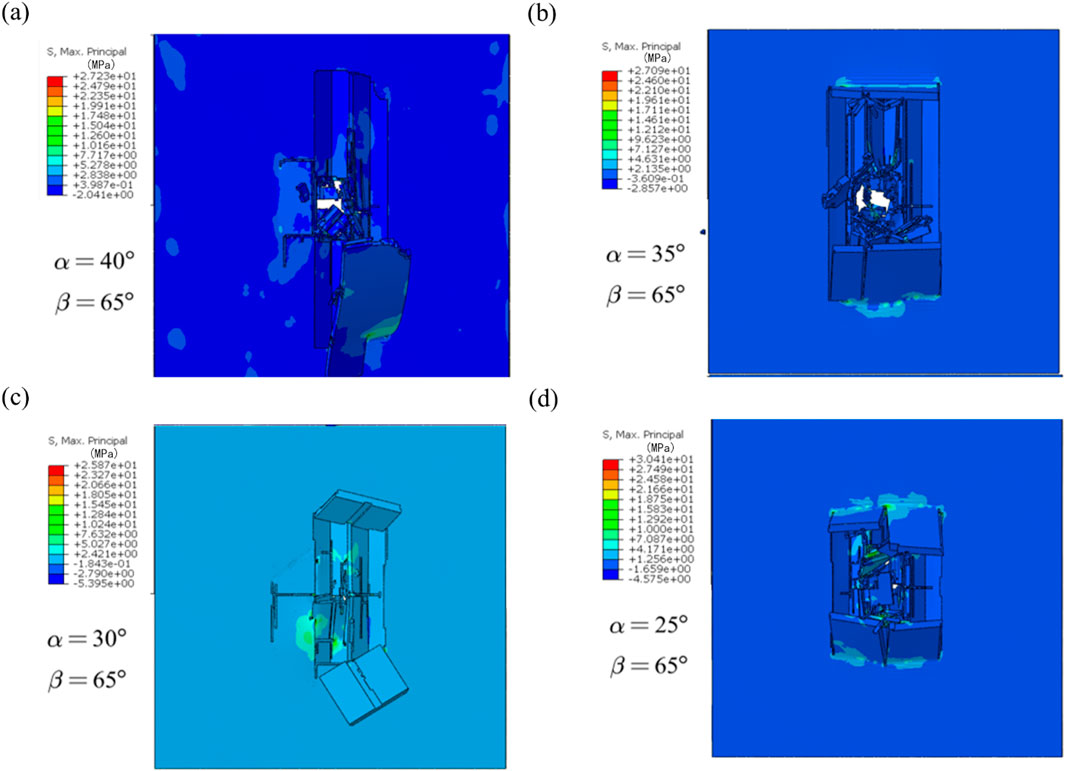
Figure 9. The distribution of first principal stress of double arrowhead triangular board structures. (a) α = 40°, β = 65°. (b) α = 35°, β = 65°. (c) α = 30°, β = 65°. (d) α = 25°, β = 65°.

Figure 10

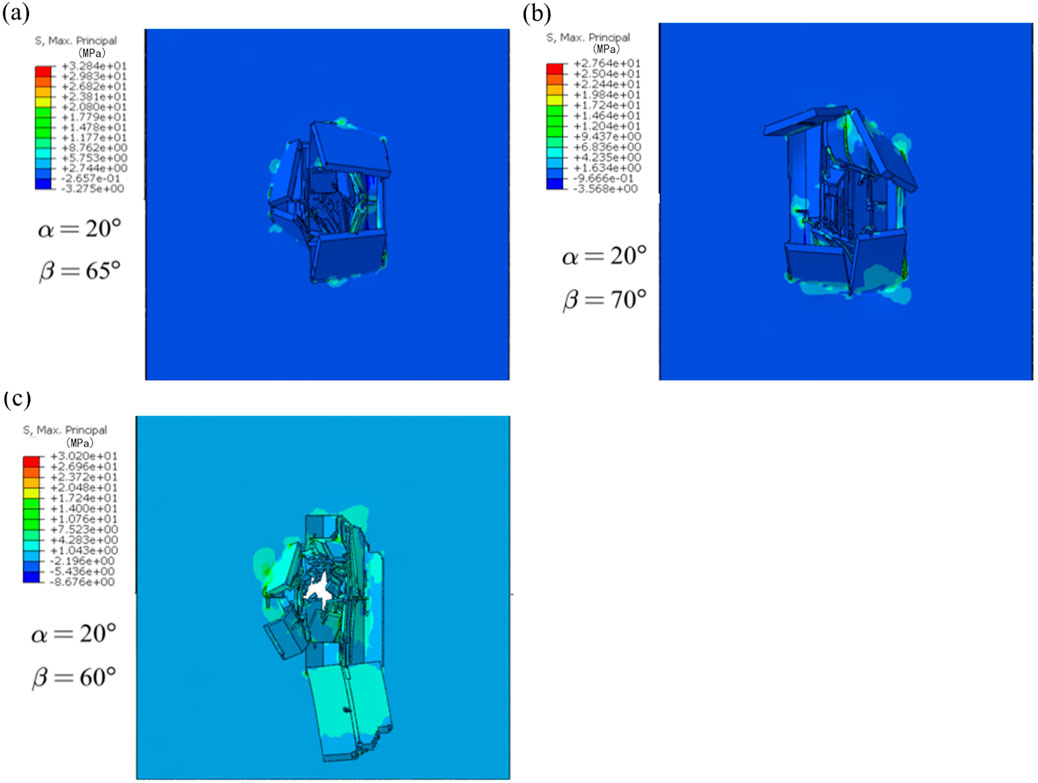
Figure 10. The distribution of first principal stress of double arrowhead triangular board structures. (a) α = 20°, β = 65°. (b) α = 20°, β = 70°. (c) α = 20°, β = 60°.

Figure 11

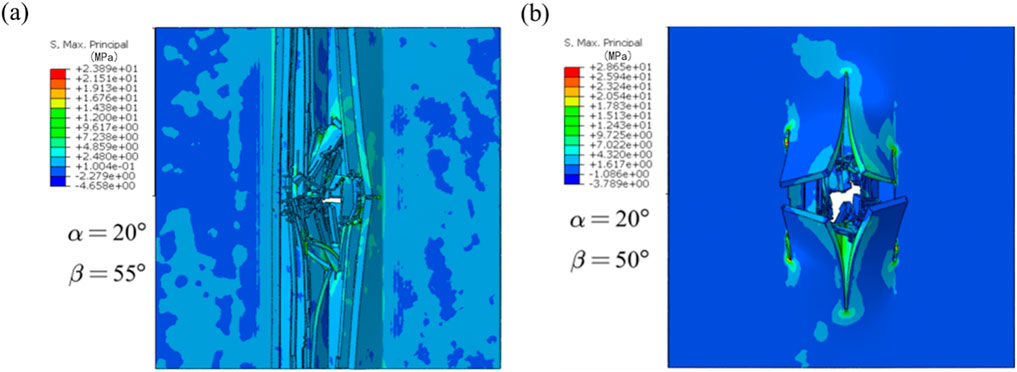
Figure 11. The distribution of first principal stress of double arrowhead triangular board structures. (a) α = 20°, β = 55°. (b) α = 20°, β = 50°.

Figures 10b, c, 11 show when α = 20°, as β increases, the maximum tensile stress of the double arrowhead triangular board structures first decreases and then increases, and the damage resistance of the model first decreases and then increases. From the comprehensive judgment of impact resistance abilities and impact performance, the structural impact safety can be improved by reducing β.

3.6 Correlation between static compression and low-velocity impact resistance

To address the correlation between static compression and low-velocity impact resistance, we conducted a series of simulations to analyze the deformation behavior of the double arrowhead triangular structure under both loading conditions. The static compression tests revealed that the structure exhibits a pronounced NPR effect, with a Poisson’s ratio of −2.1 when α = 20° and β = 50°. This negative Poisson’s ratio indicates that the structure expands laterally when compressed, a characteristic that enhances its energy absorption capability.In the low-velocity impact simulations, we observed that the structure’s ability to absorb energy is directly related to its NPR effect. The lateral expansion observed during static compression allows the structure to distribute impact forces more evenly, reducing the likelihood of localized failure. This behavior is particularly evident in the stress distribution patterns, where the first principal stress is uniformly distributed across the structure, minimizing stress concentrations. Furthermore, the impact velocity history curves show that the structure’s resistance to low-velocity impact is influenced by its static compression behavior. The structure’s ability to maintain its integrity under impact is a direct result of its NPR effect, which allows it to absorb and dissipate energy more effectively. This correlation between static and dynamic responses highlights the importance of considering both loading conditions when designing NPR structures for impact-resistant applications.

4 Conclusion

In summary, inspired by boomerang, a double arrowhead triangular structure with NPR effect has been designed. The influences of different angle parameters on Poisson’s ratio have been explored by changing angle parameters α and β. Poisson’s ratio expressions of unit cell structure and dart structure have been derived from numerical analysis. The NPR effect and low-velocity impact resistance of double arrowhead triangular board structure have been analyzed by finite element analysis. In conclusion, our study demonstrates that the double arrowhead triangular structure exhibits excellent low-velocity impact resistance, which is directly correlated with its NPR effect observed during static compression. The structure’s ability to expand laterally under compression allows it to distribute impact forces more evenly, enhancing its energy absorption capability. This correlation between static and dynamic responses provides valuable insights for the design of NPR structures in impact-resistant applications. Future research should focus on further optimizing the geometric parameters of the structure to maximize its performance under both static and dynamic loading conditions. The failure patterns, impact deformations, distribution of first principal stress and velocity history curves of the double arrowhead triangular board structure reveal the dynamic response and failure mechanism of the double arrowhead triangular structure. The results show that the Poisson’s ratio is positively correlated with the angle parameters α and β, and the low-velocity impact resistance is negatively correlated with the α and β. When α = 20° and β = 50°, the minimum NPR of the double arrowhead triangular structure is −2.1, and the structure has the best low-velocity impact resistance. This discovery provides a new idea for the design of structures with NPR and its impact resistance. The results of this study are in agreement with the findings of Zeng et al. (2023) and Wang Y. et al. (2021), demonstrating that innovative structural designs can significantly improve the energy absorption efficiency of lightweight structures during impact. The introduction of auxetic structures, which have a negative Poisson’s ratio, offers new possibilities for enhancing the impact performance of structures. Moreover, the research by Gao et al. (2022) and Gao and Liao. (2021) supports the conclusions of this study, highlighting that the integration of gradient design and composite materials can effectively increase a structure’s energy absorption capacity. The following work focuses on the unit cell density of double arrowhead triangular structure and the performance of 0buffering energy dissipation and impact resistance.

5 Limitations and future work

While this study has provided valuable insights into the behavior of double arrowhead triangular structures with a negative Poisson’s ratio, it is essential to acknowledge the limitations of the current research to guide future studies. The finite element analysis conducted in this study involved several simplifications and assumptions that may have influenced the results. These include:

(1) Material Homogeneity and Isotropy: The PLA material was assumed to be homogeneous and isotropic, which may not fully represent the behavior of real materials, especially under dynamic loading conditions where inhomogeneities and anisotropies can play a significant role.

(2) Geometric Simplifications: The model of the double arrowhead triangular structure was simplified to ideal geometric shapes, which may not capture the complexity of real-world manufacturing processes that could introduce irregularities and defects.

(3) Loading Conditions: The low-velocity impact simulations were conducted under idealized impact conditions. Real-world impacts can be more complex, involving oblique impacts, varying impact energies, and non-uniform contact areas.

(4) Failure Criteria: The study relied on visual inspection and stress distribution to determine failure modes. More advanced failure criteria, such as damage mechanics models, could provide a more accurate prediction of material failure under impact.

(5) Model Scale: The simulations were performed on a specific scale of the double arrowhead triangular structure. Scaling up or down may lead to different results due to changes in the structural response and stress distribution.

(6) Dynamic Effects: Although ABAQUS/EXPLICIT was used to simulate the dynamic response, the model did not account for all possible dynamic effects, such as inertial forces, which could influence the impact resistance.

Future research should aim to address these limitations by incorporating more complex material models, conducting experiments to validate the numerical findings, and exploring a wider range of impact scenarios. Additionally, the influence of manufacturing processes on the structural performance should be investigated to better understand the practical implications of the current findings.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LX: Methodology, Writing – original draft. LW: Software, Writing – review and editing. XF: Methodology, Writing – review and editing. YY: Formal Analysis, Writing – original draft. LY: Methodology, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alderson, A., and Evans, K. E. (1997). Modelling concurrent deformation mechanisms in auxetic microporous polymers. J. Mater. Sci. 32, 2797–2809. doi:10.1023/a:1018660130501

CrossRef Full Text | Google Scholar

Chen, J., Lin, Y., Du, L., Kang, M., Chi, X., Wang, Z., et al. (2020a). The comparison of HHHFNC and NCPAP in extremely low-birth-weight preterm infants after extubation: a single-center randomized controlled trial. Compos. Struct. 8, 250. doi:10.3389/fped.2020.00250

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, M.-M., Fu, M.-H, Lan, L.-H., and Sheshenin, S. (2020b). A novel 3D structure with tunable Poisson’s ratio and tailorable coefficient of thermal expansion based on a tri-material triangle unit. Compos. Struct., 253, 112803.

CrossRef Full Text | Google Scholar

Chen, Q., and Pugno, N. M. (2013). Bio-mimetic mechanisms of natural hierarchical materials: a review. J. Mech. Behav. Biomed. Mater 19, 3–33. doi:10.1016/j.jmbbm.2012.10.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Q., Ding, Z., and Liao, W. H. (2022). Effective elastic properties of irregular auxetic structures. Compos. Struct. 287, 115269, doi:10.1016/j.compstruct.2022.115269

CrossRef Full Text | Google Scholar

Gao, Q., and Liao, W. H. (2021). Energy absorption of thin walled tube filled with gradient auxetic structures-theory and simulation. Int. J. Mech. Sci. 201, 106475, doi:10.1016/j.ijmecsci.2021.106475

CrossRef Full Text | Google Scholar

Gao, Q., Wang, L., Zhou, Z., Ma, Z., Wang, C., and Wang, Y. (2018). Theoretical, numerical and experimental analysis of three-dimensional double-V honeycomb. Mater. & Des. 139, 380–391. doi:10.1016/j.matdes.2017.11.024

CrossRef Full Text | Google Scholar

Grima, J. N., and Evans, K. E. (2006). Auxetic behavior from rotating triangles. J. Mater. Sci. 41 (10), 3193–3196. doi:10.1007/s10853-006-6339-8

CrossRef Full Text | Google Scholar

He, Y., Zhang, X., Long, S., Yao, X., and He, L. (2016). Dynamic mechanical behavior of foam-core composite sandwich structures subjected to low-velocity impact. Archive Appl. Mech. 86 (9), 1605–1619. doi:10.1007/s00419-016-1138-4

CrossRef Full Text | Google Scholar

Hu, L. L., Luo, Z., Zhang, Z., Lian, M., and Huang, L. (2019). Mechanical property of re-entrant anti-trichiral honeycombs under large deformation. Compos. Part B Eng. 163, 107–120. doi:10.1016/j.compositesb.2018.11.010

CrossRef Full Text | Google Scholar

Jiang, H., Ren, Y., Jin, Q., Zhu, G., Hu, Y., and Cheng, F. (2020). Crashworthiness of novel concentric auxetic reentrant honeycomb with negative Poisson's ratio biologically inspired by coconut palm. Thin-Walled Struct. 154, 106911. doi:10.1016/j.tws.2020.106911

CrossRef Full Text | Google Scholar

Jiang, L., and Hu, H. (2017). Low-velocity impact response of multilayer orthogonal structural composite with auxetic effect. Compos. Struct. 169, 62–68. doi:10.1016/j.compstruct.2016.10.018

CrossRef Full Text | Google Scholar

Larsen, U. D., Sigmund, O., and Bouwstra, S. (1997). Design and fabrication of compliant micromechanisms and structures with negative Poisson’s ratio. J. Microelectromechanical 6(2), 99–106.

Google Scholar

Li, D., Ma, J., Dong, L., and Lakes, R. S. (2017). Stiff square structure with a negative Poisson's ratio. Mater. Lett. 188, 149–151. doi:10.1016/j.matlet.2016.11.036

CrossRef Full Text | Google Scholar

Li, T., Chen, Y., Hu, X., Li, Y., and Wang, L. (2018). Exploiting negative Poisson's ratio to design 3D-printed composites with enhanced mechanical properties. Mater. & Des. 142, 247–258. doi:10.1016/j.matdes.2018.01.034

CrossRef Full Text | Google Scholar

Lu, H., Wang, X., and Chen, T. (2021). In-plane dynamics crushing of a combined auxetic honeycomb with negative Poisson's ratio and enhanced energy absorption. Thin-Walled Struct. 160, 107366. doi:10.1016/j.tws.2020.107366

CrossRef Full Text | Google Scholar

Lu, Z. X., Li, X., Yang, Z. Y., and Xie, F. (2016). Novel structure with negative Poisson’s ratio and enhanced Young’s modulus. Compos. Struct. 138, 243–252. doi:10.1016/j.compstruct.2015.11.036

CrossRef Full Text | Google Scholar

Mahadevan, L., and Rica, S. (2005). Self-organized origami. Science 307 (5716), 1740. doi:10.1126/science.1105169

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamoto, H., Adachi, T., and Araki, W. (2009). In-plane impact behavior of honeycomb structures randomly filled with rigid inclusions. Int. J. Impact Eng. 36 (1), 73–80. doi:10.1016/j.ijimpeng.2008.04.004

CrossRef Full Text | Google Scholar

Nkansaht, M. A., Evanst, K. E., and Hutchinsont, I. J. (1994). Modelling the mechanical properties of an auxetic molecular network. Model. Simul. Mater. Sci. Eng. 2 (3), 337.

CrossRef Full Text | Google Scholar

Pasternak, E., and Dyskin, A. V. (2012). Materials and structures with macroscopic negative Poisson’s ratio. Int. J. Eng. Sci. 52, 103–114. doi:10.1016/j.ijengsci.2011.11.006

CrossRef Full Text | Google Scholar

Shen, J., Ge, J., Xiao, J., and Liang, J. (2020). In-plane impact dynamics of honeycomb structure containing curved reentrant sides with negative Poisson’s ratio effect. Mech. Adv. Mater. Struct. 29 (10), 1489–1497. doi:10.1080/15376494.2020.1824285

CrossRef Full Text | Google Scholar

Suresh, A., Aljafari, B., and Thanikanti, S. B. (2024). Investigations of the performance of 3D printed micro wind turbine composed of PLA material. Heliyon 10(3), e25356. doi:10.1016/j.heliyon.2024.e25356

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, T., An, J., He, H., Wen, X., and Xi, X. (2021). A novel 3D impact energy absorption structure with negative Poisson’s ratio and its application in aircraft crashworthiness. Compos. Struct.262, 113663

CrossRef Full Text | Google Scholar

Wang, Y., Zeng, H., Nie, B., Jia, F., and Gao, Q. (2021). Energy absorption characteristics of carbon fiber reinforced plastic/aluminum hybrid materials double arrow-head auxetic structure. J. Sandw. Struct. & Mater. 26 (4), 490–506. doi:10.1177/10996362241226980

CrossRef Full Text | Google Scholar

Xu, F., Yu, K., and Hua, L. (2021). In-plane dynamic response and multi-objective optimization of negative Poisson's ratio (NPR) honeycomb structures with sinusoidal curve. Compos. Struct., 269.

Google Scholar

Yang, S., Qi, C., Wang, D., Gao, R., Hu, H., and Shu, J. (2015). A comparative study of ballistic resistance of sandwich panels with aluminum foam and auxetic honeycomb cores. Adv. Mech. Eng. 5. doi:10.1155/2013/589216

CrossRef Full Text | Google Scholar

Yang, T.-C., and Yang, H.-Y. (2021). Strain analysis of Moso bamboo (Phyllostachys pubescens) subjected to longitudinal tensile force. Mater. Today Commun. 28, 102491. doi:10.1016/j.mtcomm.2021.102491

CrossRef Full Text | Google Scholar

Yu, X., Zhou, J., Liang, H., Jiang, Z., and Wu, L. (2018). Mechanical metamaterials associated with stiffness, rigidity and compressibility: a brief review. Prog. Mater. Sci. 94, 114–173. doi:10.1016/j.pmatsci.2017.12.003

CrossRef Full Text | Google Scholar

Zeng, H., Shi, W., Lv, H., Qiu, N., Ma, C., and Gao, Q. (2023). Crashworthiness analysis and optimization of a novel “cake-cutting” multi-cell tube. Thin-Walled Struct. 192, 111160. doi:10.1016/j.tws.2023.111160

CrossRef Full Text | Google Scholar

Zhang, J., and Lu, G. (2020). Dynamic tensile behaviour of re-entrant honeycombs. Int. J. impact Eng. 139, 103497. doi:10.1016/j.ijimpeng.2019.103497

CrossRef Full Text | Google Scholar

Zhang, J., and Lu, G. (2020). Energy absorption of re-entrant honeycombs in tension and compression. Eng. Struct. 288, 116237, doi:10.1016/j.engstruct.2023.116237

CrossRef Full Text | Google Scholar

Zhang, J., Lu, G., Ruan, D., and Wang, Z. (2018). Tensile behavior of an auxetic structure: analytical modeling and finite element analysis. Int. J. Mech. Sci. 136, 143–154. doi:10.1016/j.ijmecsci.2017.12.029

CrossRef Full Text | Google Scholar

Zhang, J., Lu, G., and You, Z. (2020). Large deformation and energy absorption of additively manufactured auxetic materials and structures: a review. Compos. Part B Eng. 201, 108340. doi:10.1016/j.compositesb.2020.108340

CrossRef Full Text | Google Scholar

Zhang, X.-C., Ding, H. M., Zhu, X. Y., and El-Rich, M. (2014). The influence of cell micro-structure on the in-plane dynamic crushing of honeycombs with negative Poisson’s ratio. J. Sandw. Struct. & Mater. 17 (1), 26–55. doi:10.1177/1099636214554180

CrossRef Full Text | Google Scholar