Analytical investigation on resolution calculation method for nonlinear temperature load of steel-concrete composite girders

This study establishes a thermo-mechanical coupling framework to elucidate the contribution mechanisms of nonlinear thermal loads in composite girders through thermal effect decomposition. A novel decomposition methodology for nonlinear temperature fields is developed based on the thermal effect equivalence principle, integrating cross-sectional deformation compatibility conditions to characterize the dynamic coupling between thermal responses and temperature loads. The proposed approach enables systematic decomposition of actual nonlinear temperature fields into three equivalent components: uniform, linear, and nonlinear temperature gradients. A computational framework incorporating statically indeterminate structural effects is subsequently formulated for comprehensive thermal response analysis. Four thermal loading models are comparatively investigated: field-measured temperature gradients, two theoretical thermal loading models (TLM-I and TLM-II), and the standardized gradient in Chinese Code JTG D60-2015. The analysis encompasses temperature-induced self-restraint stresses, secondary stresses, and axial deformation in variable-section continuous composite girders. Key findings reveal that code-specified thermal stresses exhibit opposing polarity characteristics at specific locations compared to other models. Quantitative decomposition demonstrates that self-restraint stresses primarily derive from equivalent uniform and nonlinear temperature components, while secondary stresses predominantly originate from equivalent linear and uniform temperature contributions. Axial deformations show 89%–94% dependence on equivalent uniform temperature effects. The developed methodology provides theoretical foundations for refined thermal design of composite bridge structures, addressing critical limitations in current code-specified thermal analysis approaches.

1 Introduction

Steel-concrete composite girders take full advantage of the combined strengths of steel and concrete. This not only offers a new option for innovative bridge structure with long spans, high heights, and heavy loads, but also significantly enhances economic benefits. In recent years, the investigation on the static and dynamic behaviour of composite girders has witnessed significant advancements (Zhang et al., 2023; Wang and Zhang, 2024; Wang et al., 2023; Yu, 2023).

Under the periodic temperature loading, the steel composite girder can experience the temperature self-restrained stress, secondary stress, as well as temperature variation, and all of these effects may cause the damage to the bridge structure (Fan et al., 2022; He et al., 2021; Zhang et al., 2020). The linear expansion coefficients of steel and concrete are 1.0 × 10⁻⁵/°C and 1.2 × 10⁻⁵/°C, respectively, which are comparable. It is worth noting, however, that the concrete has only 1/50 of the thermal conductivity of steel. In addition, in the ambient temperature field, the concrete bridge panels may experience temperature change hysteresis phenomena, leading to significant temperature differences between steel and concrete sections, thereby resulting in a pronounced nonlinear temperature gradient (Chen et al., 2021; Zhou et al., 2023; Wang et al., 2023). In steel-concrete composite girders, the unrestricted deformation of a single material, whether steel or concrete, is constrained by the presence of another material. This constraint causes a redistribution of sectional stress within the composite girders, which may result in the interface slip and significant temperature-induced self-stress (Lawson et al., 2020; Han et al., 2021). The combined influence of temperature and vehicle load can potentially lead to structural failure (Zhang et al., 2022a; Zhang et al., 2022b), with temperature response surpassing even that of live load effects and becoming a primary factor in design considerations (Zhao and Ye, 2019; Xia et al., 2017; Guo et al., 2008a).

Currently, there have been numerous studies on the self-stress behavior of bridges under extreme temperature distributions across various regions (Silveira et al., 2000; Westgate et al., 2015; Liu et al., 2016; Hottel, 1976). A numerical analysis of the temperature distributions on the bridges was conducted, and found that the spatial thermal profile could be reduced to linear thermal distributions under given conditions (Mirambell and Aguado, 1990). The experimental analysis demonstrated that the temperature-induced self-stress in concrete box-sectional girders primarily depended on the form of thermal profile distributions (Roberts-Wollman et al., 2002). The experiments and analysis indicated that temperature effects have a typical nonlinear characteristic (Liu, 1986). The vertical temperature gradient effect of composite girder bridges in Chinese, American, and European standards was compared through the numerical analysis, and found that the standard temperature gradient modes and parameter values mentioned above exhibited significant differences (Wang et al., 2016). In addition, in order to further streamline the temperature gradient, the multi-parabola model (Gottsäter et al., 2018) and the multi-linear segment model (MOT, 2015; ASHTO, 2017; Guo et al., 2008b) were proposed. The temperature gradient of composite girder in China was modified based on the thermal grads model of AASHTO considering the climatic characters. However, it should be noted that the AASHTO temperature model was derived through statistical analysis on the temperatures of concrete bridges. As a result, there may be uncertainties regarding the accuracy of the temperature action model for composite girder bridges in China (Fan et al., 2020). Recently, the bridge health monitoring system and probabilistic limit state method were used to determine the representative value of temperature action during the design base period, and a temperature action model for composite girders that incorporates distinctive Chinese characteristics was proposed (Yan et al., 2022; Wang et al., 2015). However, whether using the previous standard or the latest temperature action mode proposed by scholars, only the probability and statistical analysis of the cross-section temperature are used to obtain the uniform temperature and nonlinear gradient temperature in the design reference period. The approach used to construct this temperature action mode does not consider the cross-section characteristics of the bridge and the one-to-one correspondence between different temperature actions and responses. Therefore, it is critical to propose a practical nonlinear temperature gradient decomposition calculation method using temperature response classification.

In terms of the temperature effect, a simplified mechanical model for an inclined concrete box girder was developed (Zhang, 2009), and examined the effect of the slope and flexo-torsional stiffness ratio on the temperature response of both single-span and multi-span inclined box girders. A uniform distribution of temperature difference is assumed by the traditional method for calculating temperature-induced stress in steel-concrete composite girders. By incorporating the strain coordination between the steel beam and concrete bridge deck at the joint interface, the impact of temperature difference was equivalent to the tension-bending or compression-bending effect of steel-concrete composite girder when calculating the temperature stress (JTG 3362, 2018; BS EN, 2003; Ye, 2016). The proposed method posits that the distribution of bending moment between the concrete deck slab and steel beam is determined by their respective distances from the joint surface to their center of gravity axis, which contradicts the principle of distributing bending moment based on structural stiffness. Consequently, its analytical solution increases stress on the bridge panel while decreasing stress on the steel beam, thereby causing potential risks in design.

While existing research on thermal behavior of steel-concrete composite girders has established fundamental temperature-stress relationships, two critical limitations persist: (1) The intrinsic coupling mechanisms between thermal excitation and sectional deformation remain underexplored, particularly regarding system-level structural interactions; (2) Conventional thermal effect analyses predominantly employ simplified temperature patterns with restrictive assumptions, lacking generalized computational frameworks for arbitrary thermal environments. To bridge these knowledge gaps, this study makes three pivotal contributions: proposes a novel temperature-equivalent decomposition method that enables accurate resolution of nonlinear thermal loads through mathematical decoupling techniques; develops a system-sensitive thermal response formulation incorporating structural constraint effects; and systematically elucidates the load-transfer mechanisms of nonlinear temperature fields, quantitatively distinguishing between membrane and bending components in thermal stress generation. The proposed methodology establishes a theoretical framework for precisely characterizing thermo-structural interactions in composite systems, offering both analytical tools for complex thermal condition assessments and fundamental insights for code specification improvements.

2 Nonlinear temperature decomposition

Taking the centroid of the transformed section in the steel concrete composite girder as the origin of coordinates, the temperature action deformation is shown in Figure 1. If the vertical thermal profile of the section is $T\left(y\right)$, the stress ${\sigma }_{\mathrm{T}}\left(y\right)$ of the free-form deformation of the section is as follows:

${\sigma }_{\mathrm{T}}\left(y\right)=E\left(y\right)\alpha \left(y\right)T\left(y\right)(1)$

where $E\left(y\right)$ is the elastic modules of the material at cross-section $y$ position, and $\alpha \left(y\right)$ represents the thermal expansion ratio of the material at the cross-section $y$ position. When the cross-sectional deformation of the composite girder is constrained by the presence of fibers, the cross-sectional stress ${\sigma }_{\text{sum}}\left(y\right)$ and strain ${\epsilon }_{\text{sum}}\left(y\right)$ have a linear relationship, as expressed in Equation 2.

${\sigma }_{\text{sum}}\left(y\right)=E\left(y\right){\epsilon }_{\text{sum}}\left(y\right)(2)$

Figure 1

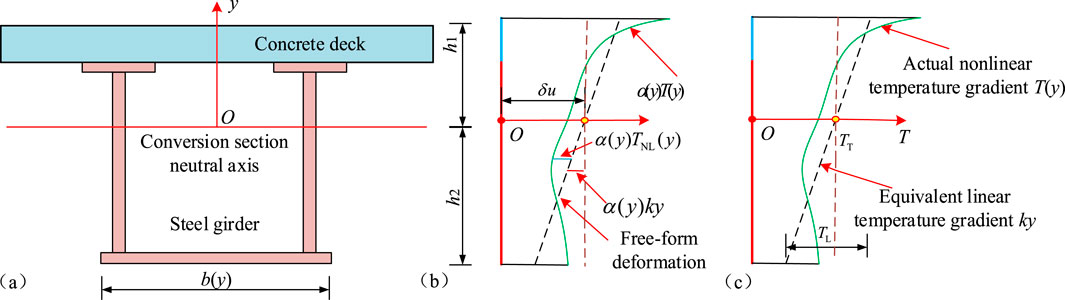
Figure 1. Temperature reaction and thermal-induced deformation; (a) Cross-section of composite girder, (b) Thermal-induced deformation, and (c) Temperature effect.

Then the total stress at any position of the composite girder section can be expressed as follows:

$\sigma \left(y\right)=E\left(y\right)\left({\epsilon }_0+\phi y\right)(3)$

where ${\epsilon }_0$ is the axial deformation at the centroid position of the whole section considering both cross-section fiber constraints and structural boundary constraints. $\phi$ represents the bending curvature of the entire section taking into account constraints imposed by cross-sectional fibers and structural boundaries.

In addition, the total stress at any position of the composite girder section can be expressed as follows:

$\sigma \left(y\right)={\sigma }_{\mathrm{T}}\left(y\right)+{\sigma }_{\text{sum}}\left(y\right)(4)$

By simultaneously solving Equation 3 and Equation 4, the relationship between the aggregate thermal stress ${\sigma }_{\text{sum}}\left(y\right)$ of the composite girder and cross-section temperature $T\left(y\right)$ can be derived as follows:

${\sigma }_{\text{sum}}\left(y\right)=E\left(y\right)\left[{\epsilon }_0+\phi y-\alpha \left(y\right)T\left(y\right)\right](5)$

According to Hooke’s law, the cross-sectional axial force (N) and bending moment (M) caused by the nonlinear temperature are shown by Equations 6, 7, respectively.

$N={\int }_{h_1}^{h_2}{\sigma }_{\text{sum}}\left(y\right)b\left(y\right)dy(6)$

$M={\int }_{h_1}^{h_2}{\sigma }_{\text{sum}}\left(y\right)yb\left(y\right)dy(7)$

In current study, the axial load ($N_{\mathrm{T}}$)and the bending moment ($M_{\mathrm{T}}$) of the free-form deformation of the composite girder section under the effect of any vertical nonlinear temperature $T\left(y\right)$ are defined as the nominal axial force and the nominal bending moment of the steel, respectively, which can be expressed as follows:

$N_{\mathrm{T}}={\int }_A{\sigma }_{\mathrm{T}}dA={\int }_{h_1}^{h_2}E\left(y\right)\alpha \left(y\right)T\left(y\right)b\left(y\right)dy(8)$

$M_{\mathrm{T}}={\int }_{A}y{\sigma }_{\mathrm{T}}dA={\int }_{h_1}^{h_2}E\left(y\right)\alpha \left(y\right)T\left(y\right)b\left(y\right)ydy(9)$

where $h_1$ and $h_2$ are the distances from the centroid of the converted section to the upper surface of the bridge deck and the lower surface of the lower flange of the steel beam, respectively.

The Chinese specification (MOT, 2015) clearly stipulates that the values of the linear expansion coefficients for concrete and steel materials when calculating temperature effects are ${\alpha }_{\mathrm{c}}=1.0\times {10}^{-5}$ and ${\alpha }_{\mathrm{s}}=1.2\times {10}^{-5}$, respectively. The disparity in linear expansion coefficients between concrete and steel beams is relatively insignificant. Therefore, the average value of the linear expansion coefficients of steel and concrete is determined as the conversion factor for composite girder cross-sectional linear expansion coefficient, as presented in Equation 10.

${\alpha }_0=\frac{\left({\alpha }_{\mathrm{s}}+{\alpha }_{\mathrm{c}}\right)}{2}(10)$

According to the equivalent principle of temperature effect, the connection between the nominal axial load $N_{\mathrm{T}}$ and equivalent homogenous temperature $T_{\mathrm{T}}$ of the composite girder under any nonlinear temperature load can be calculated as follows:

$N_{\mathrm{T}}=E_{\mathrm{s}}{\alpha }_0{T}_{\mathrm{T}}{A}_0(11)$

where $T_{\mathrm{T}}$ is the equivalent homogenous temperature, and $A_0$ is the conversion section area of composite girder; $A_0=A_{\mathrm{c}}/{\alpha }_{\text{Es}}+A_{\mathrm{s}}$; A_c and $A_{\mathrm{s}}$ are the area of the concrete bridge panel and the steel beam, respectively; ${\alpha }_{\text{Es}}=E_{\mathrm{s}}/E_{\mathrm{c}}$; $E_{\mathrm{s}}$ and $E_{\mathrm{c}}$ represent the elastic modulus of steel and concrete, respectively.

Under the influence of the nonlinear temperature, the transformed section curvature ($\phi$) induced by the nominal curved moment M_T and converted section curvature generated by the equivalent linearity temperature load T_L must be equal, as shown as follows:

$\phi =\frac{{\alpha }_0{T}_{\mathrm{L}}}{H}=\frac{M_{\mathrm{T}}}{E_{\mathrm{s}}{I}_0}(12)$

where $T_{\mathrm{L}}$ is the equivalent linearity temperature load, and I₀ represents the converted moment of inertia; $I_0=I_{\mathrm{c}}/{\alpha }_{\text{Es}}+I_{\mathrm{s}}+A_{\mathrm{s}}{A}_{\mathrm{c}}/\left[A_0{\alpha }_{\text{Es}}{\left(y_{\mathrm{s}}-y_{\text{cs}}\right)}^2\right]$; y_s and y_cs are the vertical offsets from the centroids of the steel beam section and concrete deck section to the lower surface of the lower flange plate of the steel beam, respectively; where H is the cross-sectional height of steel-concrete composite girders.

By substituting Equations 3, 6 into Equations 8, 9, the T_T and T_L can be expressed as follows:

$T_{\mathrm{T}}=\frac{{\int }_{h_1}^{h_2}E\left(y\right)T\left(y\right)b\left(y\right)dy}{E_{\mathrm{s}}{A}_0}(13)$

$T_{\mathrm{L}}=\frac{H{\int }_{h_1}^{h_2}E\left(y\right)T\left(y\right)yb\left(y\right)dy}{E_{\mathrm{s}}{I}_0}(14)$

As shown in Figure 1c, the equivalent uniform temperature (T_T) is uniformly distributed across the composite beam section. Meanwhile, the equivalent linear temperature exhibits a straight-line distribution with a specific slope (k) extending from the top surface of the concrete bridge deck to the bottom surface of the lower flange of the steel beam. The k can be calculated by Equation 15.

$k=\frac{{\int }_{h_1}^{h_2}E\left(y\right)T\left(y\right)yb\left(y\right)dy}{E_{\mathrm{s}}{I}_0}(15)$

The equivalent linear thermal gradient of composite girder cross-section is denoted as $G\left(y\right)$, as expressed in Equation 16.

$G\left(y\right)=ky(16)$

As shown in Figure 1b, the equivalent uniform thermal reaction ($\delta u$), equivalent linear thermal reaction ($\delta w$), as well as the actual nonlinear thermal reaction ($\delta v$) are presented as follows, respectively,

$\delta u=\alpha \left(y\right)T_{\mathrm{T}}(17)$

$\delta w=\alpha \left(y\right)ky(18)$

$\delta v=\alpha \left(y\right)T\left(\mathrm{y}\right)(19)$

Temperature self-strain ($\delta l$)of composite girder section is expressed as follows:

$\delta l=\alpha \left(y\right)T_{\text{NL}}\left(y\right)(20)$

where ${T_{\mathrm{N}}}_{\mathrm{L}}\left(y\right)$ is the equivalent nonlinear temperature at any height of the composite girder section.

The stress-strain behavior of the composite girder under temperature loading satisfies the linear elastic relationship, and Equation 21 can be derived from the principle of strain superposition:

$\delta v=\delta u+\delta w+\delta l(21)$

From Equation 21, it can be seen that compared with the actual nonlinear temperature effect, the overall effect produced by the equivalent uniform temperature load and the linear temperature is bound to lack the effect produced by the equivalent nonlinear temperature. Therefore, the T_NL (y) at the vertical y position of the composite girder section is defined as follows:

${T_{\mathrm{N}}}_{\mathrm{L}}\left(y\right)=T\left(y\right)-T_{\mathrm{T}}-ky(22)$

In summary, the actual nonlinear temperature gradient $T\left(y\right)$ at any height of the composite beam section can be expressed by three temperature decomposition indexes ($T_{\mathrm{T}}$; $G\left(y\right)$, ${T_{\mathrm{N}}}_{\mathrm{L}}\left(y\right)$), as shown in Equation 23.

$T\left(y\right)=T_{\mathrm{T}}+G\left(y\right)+{T_{\mathrm{N}}}_{\mathrm{L}}\left(y\right)(23)$

3 Temperature response based on decomposition index

3.1 Temperature self-restrained stress and secondary stress

When ignoring the influence of the linear expansion coefficient, the temperature self-stress ${\sigma }_{\mathrm{s}}\left(y\right)$ of steel-concrete composite girders can be calculated by the T_NL, as shown in Equation 24.

${\sigma }_{\mathrm{s}}\left(y\right)=E\left(y\right)\delta l=E\left(y\right)\alpha \left(y\right)T_{\text{NL}}(24)$

Taking the centroid of the transformed section of the composite girder as the origin of the coordinate, there are:

${\int }_{h_1}^{h_2}E\left(y\right)yb\left(y\right)dy=0(25)$

The extra axial force and the additional bending moment caused by the constrained deformation of the composite girder structure system and cross-section fiber are denoted as N_con and M_con, respectively. By making $N=N_{\text{con}}$ and $M=M_{\text{con}}$ in Equations 6, 7, and then by combining Equations 2–5, the calculation formula for the axial strain ${\epsilon }_0$ and section curvature ${\phi }_0$ of the transformed section of the composite girders under the combined action of temperature self-stress and secondary stress can be derived, as presented in Equations 26, 27, respectively.

${\epsilon }_0=\frac{N_{\text{con}}+N_0}{EA}(26)$

${\phi }_0=\frac{M_{\text{con}}+M_0}{EI}(27)$

in which, $N_0=E_{\mathrm{c}}{\alpha }_{\mathrm{c}}{T}_1+E_{\mathrm{s}}{\alpha }_{\mathrm{s}}{T}_2$; $M_0=E_{\mathrm{c}}{\alpha }_{\mathrm{c}}{T}_3+E_{\mathrm{s}}{\alpha }_{\mathrm{s}}{T}_4$; $EA=E_{\mathrm{c}}{A}_{\mathrm{c}}+E_{\mathrm{s}}{A}_{\mathrm{s}}$; $EI=E_{\mathrm{c}}{I}_{\mathrm{c}}+E_{\mathrm{s}}{I}_{\mathrm{s}}$; $T_1={\int }_{A_{\mathrm{c}}}T\left(y\right)dA$; $T_2={\int }_{A_{\mathrm{s}}}T\left(y\right)dA$; $T_3={\int }_{A_{\mathrm{c}}}T\left(y\right)ydA$; $T_4={\int }_{A_{\mathrm{s}}}T\left(y\right)ydA$. ${\alpha }_{\mathrm{c}}$ and ${\alpha }_{\mathrm{s}}$ are the linear expansion coefficients of concrete and steel, respectively; $E_{\mathrm{c}}$ and $E_{\mathrm{s}}$ represent the elastic modulus of concrete and steel, respectively; $I_{\mathrm{c}}$ and $I_{\mathrm{s}}$ are the moments of inertia of concrete and steel girders with respect to the centroid of the converted section, respectively.

In general, the conventional bridges allow for unrestricted axial expansion and contraction of beams due to the temperature changes, resulting in $N_{\text{con}}=0$. By substituting Equations 6, 7 in Equation 5, the overall temperature-induced stress at any height can be expressed by Equation 28:

$\begin{array}{l}{\sigma }_{\text{sum}}\left(y\right)=\frac{E\left(y\right)N_0}{EA}+\frac{E\left(y\right)y\left(M_0+M_{\text{con}}\right)}{EI}-E\left(y\right)\alpha \left(y\right)T\left(y\right)\end{array}(28)$

In Equation 28, by making $M_{\text{con}}=0$, the expression of the temperature self-stress can be obtained as follows:

${\sigma }_{\mathrm{s}}\left(y\right)=\frac{E\left(y\right)N_0}{EA}+\frac{E\left(y\right)y{M}_0}{EI}-E\left(y\right)\alpha \left(y\right)T\left(y\right)(29)$

In Equations 28, 29, by making $T\left(y\right)$ is $G\left(y\right)$, $T_{\mathrm{T}}$ and $T_{\text{NL}}\left(y\right)$, respectively. The temperature secondary stress of the continuous composite beam is calculated by difference calculation, as shown in Equation 30:

${\sigma }_{\text{con}}=\frac{E\left(y\right)M_{\text{con}}y}{EI}(30)$

In Equation 30, the temperature secondary bending moment (M_con) can be determined according to the method of structural mechanics. Assume a composite beam with (n + 1) spans, which is a statically indeterminate structure with n degrees of freedom, and the excess constraining moment due to the temperature deformation is $P_i\left(i=1,2,...,n\right)$. Then the restrained bending moment of the (n + 1)-span continuous beam can be calculated by Equation 31.

$M_{\text{con}}={\displaystyle \sum _{i=1}^n}{P}_i\overline{M_i}(31)$

Based on the principle of virtual work, the relative change angle of the arbitrary incision position of (n + 1) continuous beam along the direction of excess binding force is given as follows:

${\Delta }_P={\int }_L\overline{M_P}{\phi }_{0}dx(32)$

Combining Equations 27, 30 to Equation 32, and considering the deformation compatibility equation ${\Delta }_P=0$, Equation 33 can be determined.

$\begin{array}{l}{\Delta }_P={\displaystyle \sum _i^n}{\int }_L\frac{\overline{M_i}\overline{M_P}}{EI}{P}_{i}dx+{\int }_L\frac{M_0\overline{M_P}}{EI}dx=0\\ \left(i=1,2,...,n\right)\end{array}(33)$

Equation 33 is a n-order linear equation sets, which can solve $P_i\left(i=1,2,...,n\right)$, and it is substituted into Equation 31 to solve the secondary bending moment $M_{\text{con}}$. According to Equations 27, 28, it is evident that $M_0$ possesses a non-zero value due to the disparate linear expansion coefficients of concrete and steel. As a result, even when subjected to the equivalent uniform and linear temperature, the composite girder experiences the stress redistribution as a result of the mutual restraint between these two materials, leading to the secondary stresses induced by temperature. Therefore, by replacing the variable $T\left(y\right)$ in $N_0$ and $M_0$ with $T_{\mathrm{T}}$, $G\left(y\right)$, and $T_{\text{NL}}\left(y\right)$, the temperature self-restraint stress and secondary stress generated by the equivalent uniform, linear and nonlinear temperatures can be determined using Equations 28, 29.

3.2 Beam expansion amount

According the tested results on the long-term monitoring of a large number of existing bridges (Zhou et al., 2021; Zhou et al., 2020), the beam expansion and section average temperature has the statistically significant linear relationship. However, it should be noted that this specific functional relationship is only applicable to certain bridges and cannot be extrapolated to general bridge structures when separated from the bridge health monitoring system. As a result, based on the equivalent temperature derived from actual nonlinear temperature decomposition, a quantitative calculation method for predicting beam expansion in any given bridge is proposed in current study.

Taking the centroid of the composite cross-section as the origin, the longitudinal direction of the bridge span is designated as the X-axis, and the coordinate x represents the distance between the section and the fixed bearing. From Equation 17, the equivalent uniform temperature strain $\delta u$ corresponds to the axial strain at the center of form in the composite girder. If the axial strain ${\epsilon }_0$ at the initial time at the center of the composite girder is known, the strain variation $\delta \epsilon \left(x\right)$ invoked by the temperature change can be expressed as,

$\delta \epsilon \left(x\right)=\delta u-{\epsilon }_0(34)$

According to Equation 13, the calculation formula of the equivalent uniform temperature $T_0$ at the initial moment can be calculated as follows:

$T_0=\frac{{\int }_{h_1}^{h_2}E\left(y\right)T\left(y\right)b\left(y\right)dy}{E_{\mathrm{s}}{A}_0}(35)$

The axial direction strain ${\epsilon }_0$ at the initial moment of composite girders cross-section is a function related to the equivalent uniform temperature $T_0\left(y\right)$ at the initial moment, as shown in Equation 36:

${\epsilon }_0=\alpha \left(y\right)T_0\left(y\right)(36)$

Combining Equation 13, Equations 34–36, the axial strain variation $\delta \epsilon \left(x\right)$ of composite girders induced by the temperature change is calculated by Equation 37.

$\delta \epsilon \left(x\right)=\alpha \left(y\right)\left[T_{\text{Tt}}\left(y\right)-T_0\left(y\right)\right](37)$

where $T_{\text{Tt}}\left(y\right)$ is the equivalent uniform temperature at the calculation time of cross-section.

For the (N + 1)-span continuous composite beam with variable cross-section, as presented in Figure 2, the unit load method can be adopted to solve the beam expansion amount, that is, an axial unit load is applied at the centroid position of the beam end while neglecting the moment and shear caused by the unit load on the eccentric cross-section. Consequently, the axial expansion amount ($\Delta$) of the beam end can be calculated as follows:

$\Delta ={\int }_0^l\overline{N}\delta \epsilon \left(x\right)dx(38)$

where $\overline{N}=1$ is the unit load.

Figure 2

Figure 2. Unit-load method of (n+1) span variable cross-section continuous composite girder.

In the case of the variable cross-section composite girder, the equivalent uniform temperature is proportional to both the vertical coordinate y and the distance x between the section and the fixed bearing. Therefore, the integral operation of Equation 38 is complex. In this study, the layered element weight method is proposed for converting the integral operation of Equation 38 into algebraic operation. Taking solving the equivalent uniform temperature T_Tt as an example, the specific process is as follows:

(1) Assume the section width is b(y) when the vertical coordinate is y on the section at the x position of the fixed bearing. From the top surface of the concrete deck to the bottom of the composite girder, the composite girder section is vertically divided into n layered units with each unit's area recorded as A₁、A₂、……A_n-1、A_n respectively. When the cross-section width b(y) is large, the division of layered elements is denser, while that is sparser when b(y) is small.

(2) If the temperatures of the upper and lower surfaces of the ith layered unit are $T_{\mathrm{A}i}$ and $T_{\mathrm{B}i}$, respectively, then the temperature $T_{\mathrm{C}i}$ at the centroid of the ith layered unit is as follows:

$T_{\mathrm{C}i}=0.5\left(T_{\mathrm{A}i}+T_{\mathrm{B}i}\right)(39)$

Taking $E_i{A}_i$ as the calculation weight, the equivalent uniform temperature T_Tt on the cross-section at the x position of the fixed bearing can be expressed as,

$T_{\text{Tt}}=\frac{{\displaystyle \sum _{i=1}^n}{E}_i{T}_{\mathrm{C}i}{A}_i}{{\displaystyle \sum _{i=1}^n}{E}_i{A}_i}(40)$

where E_i is the elastic modulus of the ith element.

Similarly, the equivalent uniform temperature $T_0$ at the initial time can be obtained. Substituting $T_0$ and $T_{\text{Tt}}$ into Equation 37, the axial strain variation $\delta \epsilon \left(x\right)$ at the position x from the fixed bearing can be solved, and the axial expansion of the beam end can be further determined by Equation 38. For the equal cross-section composite beam, the equivalent uniform temperature is only related to the vertical coordinate y, but not to the distance x from the cross-section to the fixed bearing. The axial expansion amount of the beam end can be expressed as follows:

$\Delta ={\alpha }_{0}l\left(T_{\text{Tt}}-T_0\right)(41)$

4 Method validation and analysis

4.1 Nonlinear temperature decomposition

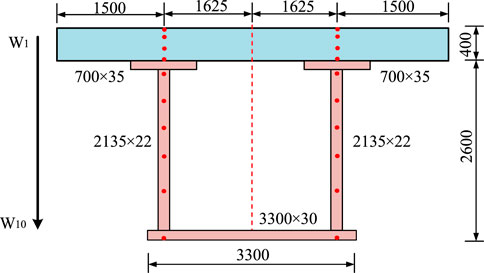
The approach presented in this paper is used for decomposing the nonlinear temperature effect of the measured composite girders and analyze the temperature effect. The continuous steel-concrete composite beam bridge with a span of 3 × 30 m (Chen et al., 2021) is set as an example for the further analysis. The bridge has a deck of 2.65 m and a height of 0.4 m. The width and height of the steel beam baseplate are 3.3 m and 2.6 m, respectively, with the total height of 3.0 m for the composite girder, as shown in Figure 3. Along the vertical direction of the beam, 10 temperature measuring points are labeled from W1 to W10, and are located at distances from the top edge of the bridge slab ranging from 0 m to 2.6 mm (at intervals of: 0m, 0.1m, 0.25m, 0.4m, 0.5m, 0.7m, 0.9m, 1.5m, 2.1m and 2.6 m).

Figure 3

Figure 3. Cross section diagram of the composite girder (unit: mm).

The moment when the maximum temperature difference presents during the monitoring period is 18:00 in summer. Figure 4 presents the measured distribution curves of the nonlinear, equivalent nonlinear and equivalent linear temperatures. The quasi-function of the measured nonlinear temperature curve ($T$) is expressed as follows:

$\begin{array}{ll}\hfill T& =11.3h^4+38.2h^3+49.9h^2+36.6h+45\hfill \\ \hfill & \left(-1.5\le h\le 0\right)T=30.6\left(h\le -1.5\right)\hfill \end{array}(42)$

where $h$ is the distance from the calculated point to the top surface of the bridge slab.

Figure 4

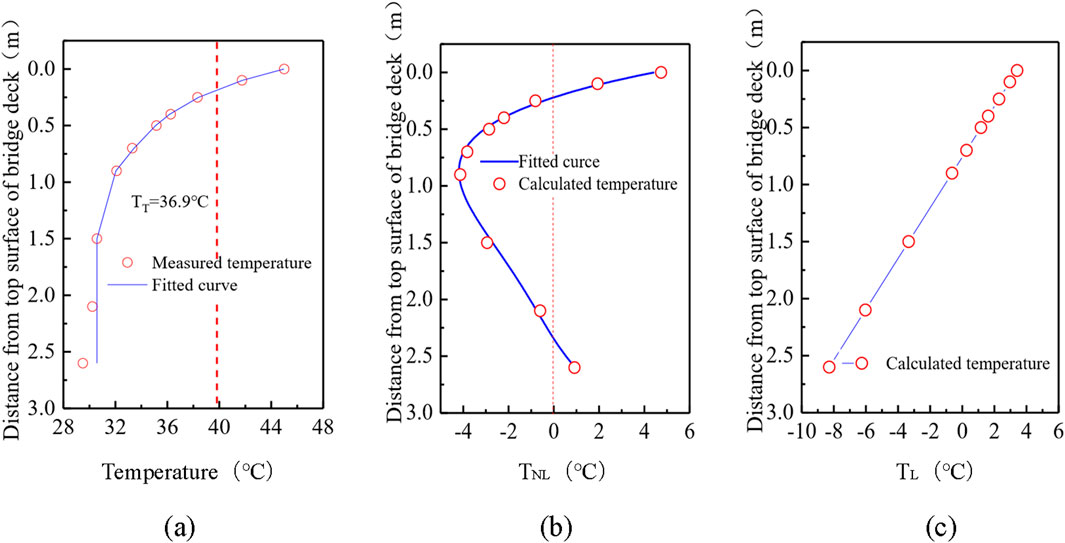
Figure 4. Temperature distribution of the composite girder; (a) Measured nonlinear temperature distribution, (b) Equivalent nonlinear temperature distribution, and (c) Equivalent linear temperature distribution.

The slope coefficient of the equivalent linear temperature curve k = 4.6 C/m, then the equivalent linearity thermal profile fitting function is as follows:

$T_{\mathrm{L}}\left(y_{\text{oi}}\right)=k{y}_{\text{oi}}=4.6y_{\text{oi}}(43)$

where $y_{\text{oi}}$ is the distance from the calculated point to the neutral axis of the converted section. The quasi-function of the equivalent nonlinear temperature curve (T_NL) can be expressed in Equation 44.

$\begin{array}{l}{T}_{\text{NL}}\left(h,y_{\text{oi}}\right)=11.3h^4+38.2h^3+49.9h^2+36.6h+8-k{y}_{\text{oi}}\left(-1.5\le h\le 0\right)\\ T_{\text{NL}}\left(h,y_{\text{oi}}\right)=-6.4-k{y}_{\text{oi}}\left(h\le -1.5\right)\end{array}(44)$

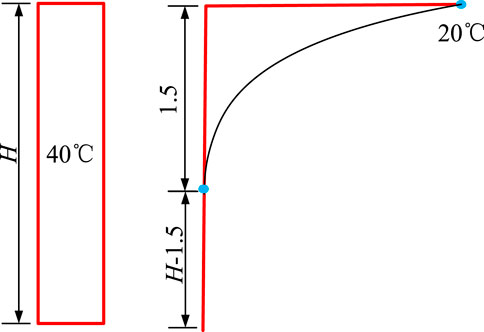
The calculated equivalent uniform temperature is 36.9°C, and the measured maximum temperature deviation between bridge deck and steel girder is 15°C. Because the measured temperature is in sunny weather status, and the maximum temperature difference and distribution pattern of the composite beam along the height direction of the beam are relatively stable due to solar radiation. So, the maximum temperature difference of the cross-section can be taken as 20°C, and the equivalent uniform standard temperature is 40°C, due to the complexity of the weather conditions in the actual project. Therefore, the temperature action model 1 (TLM-I) of the composite girder is shown in Figure 5, where H means the height, which can be expressed as follows:

$T=11.3h^4+38.2h^3+49.9h^2+36.6h+20(45)$

where $h$ is the height between the calculated point and the top edge of bridge slab.

Figure 5

Figure 5. Thermal load model 1 (TLM-Ⅰ) of the composite girder.

It can be observed from Equation 13 that the equivalent uniform temperature is associated to the cross-section characteristics, so the equivalent uniform temperature proposed in this paper is the reference value when there is a lack of actual investigation data. The Chinese Specification (MOT, 2015) stipulates that the uniform temperature of steel-concrete composite girder is 39°C, which is basically consistent with the equivalent uniform temperature proposed in TLM-I. In addition, the equivalent uniform thermal is taken as 36.9°C, the equivalent nonlinear thermal gradient $T_{\text{NL}}\left(h,y_{\text{oi}}\right)$ and the equivalent linear thermal gradient $T_{\mathrm{L}}\left(y_{\text{oi}}\right)$ are used to form the thermal action model 2 (TLM-Ⅱ).

Both the model of TLM-I and TLM-II can express the action form of temperature load, but TLM-I mixes the temperature action that causes temperature self-stress and temperature secondary stress together, making it difficult for engineers to distinguish the category of temperature action. TLM-II will cause the temperature effect of temperature self-stress and temperature sub-stress to be separated, so that engineers can distinguish the type of temperature effect, so as to calculate the temperature effect more conveniently.

4.2 Thermal effect analysis

4.2.1 Thermal stress analysis

Figure 6 shows the distribution curves of temperature self-stress, secondary stress and overall stress along the height direction in the intermediate span cross-section of continuous composite beam under the four temperature action modes, including the TLM-I, TLM-II, measured temperature distribution, as well as bridge specifications temperature modes, respectively. It shows that the temperature stress difference of the bridge deck under the four temperature action modes is observed to be minimal, while the stress distribution in the steel beam varies significantly. Compared with the three temperature action models of TLM-I, TLM-II and measured temperature distribution, the stress distribution form caused by the temperature mode specified in the bridge specification is obviously different. In terms of stress nature, it may even exhibit an opposite trend to the tensile and compressive stress symbols observed in the other three modes. The stress based on the measured temperature distribution can effectively represent the actual stress state of the composite girder section. It should be mentioned, nonetheless, that in certain scenarios, the temperature stress calculated using the temperature action mode specified by the bridge specification may not accurately reflect the temperature stress state in the actual environment. The stress properties of TLM-I and TLM-II are consistent with the measured values, and the stress form is the same as the measured results. However, there is a large deviation between the stress value of TLM-I and measured values. The maximum deviations of temperature self-stress, secondary stress and overall stress are 89.5%, 57.3% and 78.6%, respectively. The temperature stress values of TLM-II match well with the measured values, with the maximum deviations of 5.386%, 0.143% and 1.556% for the temperature self-stress, secondary stress and overall stress, respectively. Therefore, TLM-II can be used as the most suitable temperature action mode for steel-concrete composite girders. Meanwhile, the nonlinear temperature decomposition method has great advantages in obtaining the temperature action model.

Figure 6

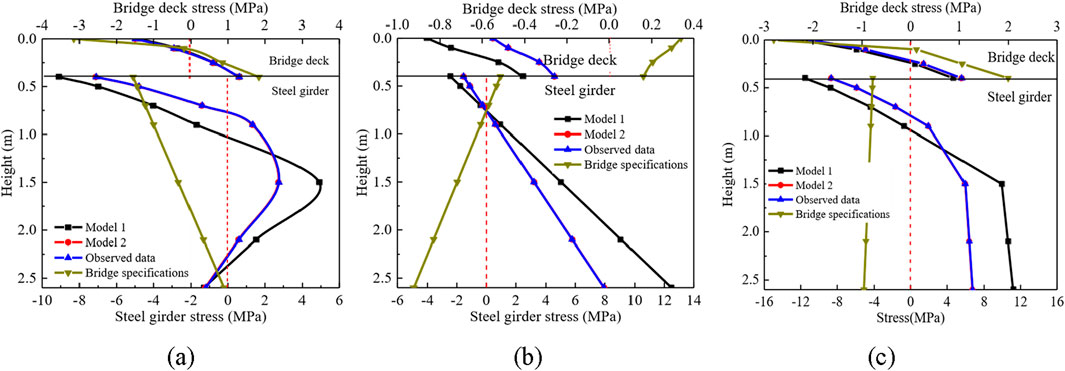
Figure 6. Thermal stress of the mid-span section; (a) Temperature self-stress, (b) Temperature secondary stress, and (c) Total temperature stress.

To investigate the mechanism action of the equivalent linearity, nonlinear and uniform temperatures of the thermo-response of steel-concrete composite girders, Figure 7 illustrates the distribution curves of temperature self-stress and secondary stress along the height direction in the mid-span section of continuous composite girders under the action of TLM-II model. It shows that the maximum temperature self-stress induced by the equivalent linearity and uniform temperatures appear at the upper flange of the steel girder at the interface between steel and concrete, with the values of −0.850 MPa and −11.939 MPa, respectively. The maximum temperature self-restrained stress resulted from the equivalent nonlinear temperature occurs near the centroid of the composite girder, with a value of 10.707 MPa. Furthermore, the maximum values of temperature secondary stress (caused by equivalent linear, nonlinear, and uniform temperatures) are all located at the lower flange of composite girder, with the maximum values of −23.583 MPa, −1.612 MPa and −14.020 MPa, respectively.

Figure 7

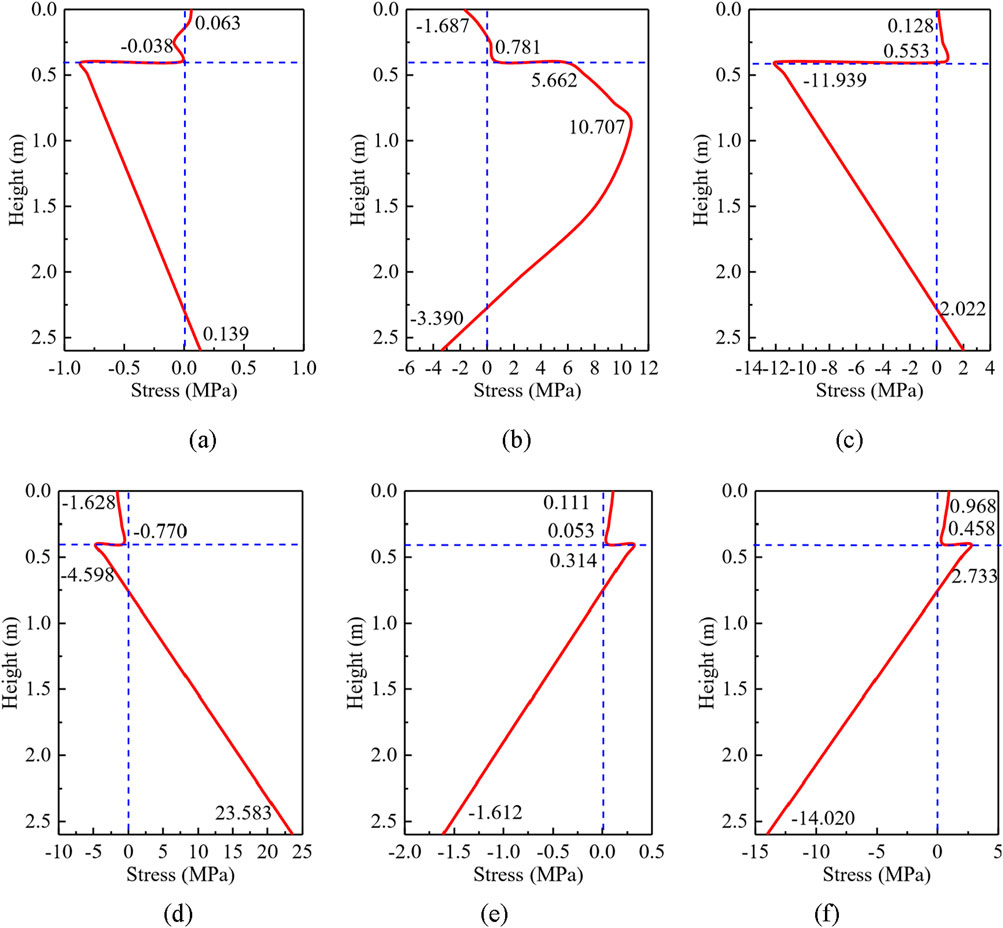
Figure 7. Thermal stress of the TLM-Ⅱ; (a) Linear temperature self-restrained stress, (b) Nonlinear temperature self-stress, (c) Uniform thermal self-stress, (d) Linear thermal secondary stress, (e) Nonlinear temperature self-stress, and (f) Uniform temperature secondary stress.

As a result, under the temperature loads of equivalent linear, nonlinear and uniform temperature, the temperature self-restrained stress and secondary stress exist in the cross-section. In terms of the temperature self-stress, the equivalent uniform and nonlinear temperature are the dominant temperature loads, but the contribution of the equivalent linear temperature is negligible. For the temperature secondary stress, the equivalent linear and uniform temperature are the dominant temperature loads, and the influence of the equivalent nonlinear thermal is neglected. Due to the different linear expansion coefficients of concrete and steel, even under the action of equivalent uniform and linear thermal, the amount of fiber expansion of different materials is not the same, resulting in self-balanced stress on the cross section. However, because the cross-section deformation satisfies the plane section assumption, the difference of linear expansion coefficient has a greater effect on the self-stress of equivalent uniform temperature than the linear temperature. As seen in Equations 27, 32, once the self-balanced stress exists in the statically indeterminate structure, the constraint force can be generated at the redundant constraint, resulting in the temperature secondary stress.

However, for concrete girder bridges or steel bridges, Equation 24 shows that neither the equivalent uniform temperature nor the equivalent linear temperature in a statically indeterminate structure induces cross-sectional stress, but only the axial expansion deformation or vertical deflection. In the hyperstatic composite girders, the equivalent uniform thermal produces the longitudinal expansion deformation and temperature secondary stress. The equivalent linear temperature causes the vertical deflection deformation and temperature secondary stress, while the equivalent nonlinear temperature only results in the temperature self-stress.

Therefore, in engineering practice, it is particularly necessary to pay attention to the stress redistribution phenomenon of composite beams under temperature action resulting from the difference in steel and concrete materials, and to emphasize that the temperature self-restrained and secondary stress values generated by equivalent uniform temperature of composite girders cannot be ignored. However, with concrete and steel bridges, the equivalent uniform temperature solely causes axial deformation and not stress.

To sum up, the nonlinear temperature decomposition method based on temperature response classification proposed in this paper is more conducive to understanding the temperature effect from the two aspects of bridge temperature self-balance effect and secondary effect. So far, both domestic and foreign scholars have obtained numerous bridge temperature action models with a certain return period. Although the temperature distribution and temperature values vary based on the monitoring object and bridge site environment, the obtained design temperature action models exhibit relatively consistent. They are uniformly expressed as a combination of uniform temperature and nonlinear temperature gradient, that is, the form of TLM-I in this study. Similarly, the temperature load model for design that combines uniform temperature and nonlinear temperature gradient is also used in Chinese bridge design specification. However, based on the aforementioned analysis, it is possible to conclude that, in comparison to the TLM-I model derived from traditional analytical methods, which combines the equivalent linear and nonlinear thermal gradient, as well as the equivalent uniform thermal, more effectively captures the correlation between the temperature response and the temperature effect in actual composite constructions.

4.2.2 Analysis of beam expansion amount

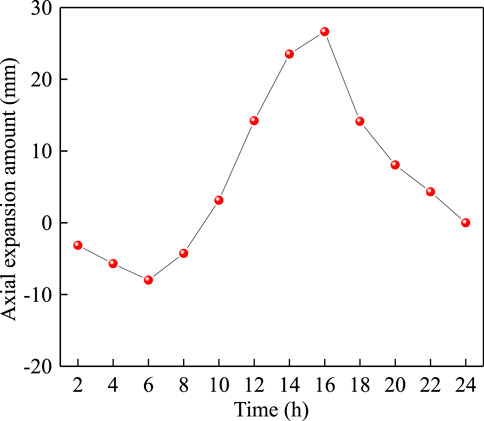
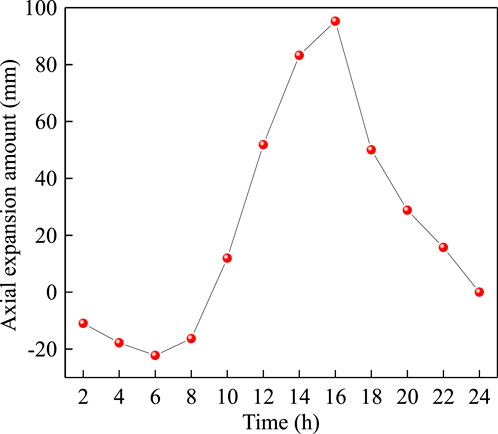
Based on the reference point of 0 h in summer (Chen et al., 2021), the longitudinal expansion deformation in equal section composite constructions (Figure 3) within a 24 h period during summer is calculated by using Equation 38, as illustrated in Figure 8. It shows that the axial expansion of the equal-section beam varies as the time increases, exhibiting a similar trend to the temperature curve and having a consistent change magnitude with the beam expansion deformation specified by the Specifications for Chinese code (JTG 3362, 2018).

Figure 8

Figure 8. Axial expansion deformation.

In order to investigate the axial expansion deformation of variable cross-section continuous steel-concrete composite girders, the equivalent uniform temperature and axial expansion deformation of variable cross-section steel-concrete composite girders with span arrangement of 250 m (65 m + 120 m + 65 m) are calculated. The cross-section arrangement is shown in Figure 9, and the beam height and baseplate thickness change from the central bearing point to the mid-span according to the quadratic parabola.

Figure 9

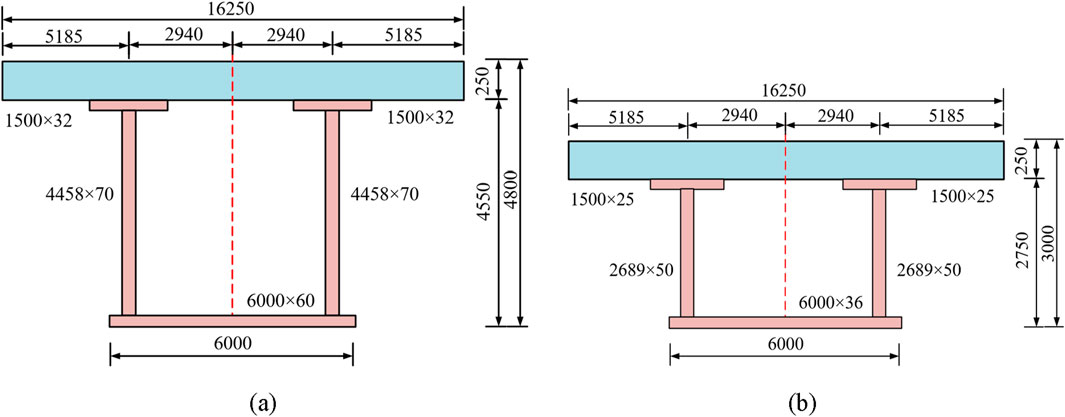
Figure 9. Transverse section of composite girder (unit: mm); (a) Middle fulcrum cross section, and (b) Mid-span section.

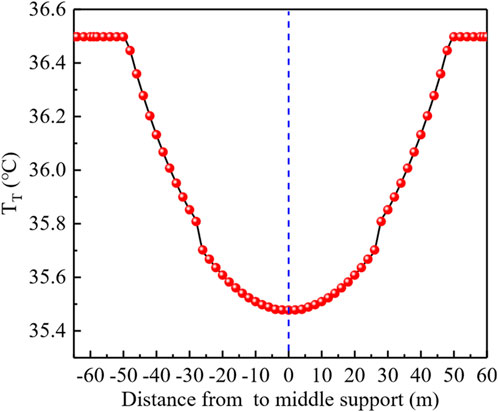
In this paper, it is assumed that the variable cross-section composite beam still satisfies the summer temperature distribution (Chen et al., 2021) within the range of 1.5 m from the bridge deck, and the temperature outside the range of 1.5 m from the bridge deck is consistent with the temperature at 1.5 m. The distribution of the equivalent temperature of the variable cross-section continuous composite beam along the span direction can be determined using Equation 13, as illustrated in Figure 10. It shows that the equivalent temperature of the variable cross-section composite beam is a variable value along the span direction, which distinguishes it from a uniform cross-section composite beam. The equivalent uniform temperature gradually increases from the central bearing point to both the side branch and mid-span directions, indicating that the equivalent uniform temperature is closely related to the cross-section characteristics.

Figure 10

Figure 10. Equivalent uniform temperature.

According to Equations 38, 40, the longitudinal expansion deformation in variable cross-section composite constructions within 24 h in summer can be calculated, as depicted in Figure 11. It presents that the variation trend of the axial expansion of the variable cross-section steel-concrete composite girder and equal cross-section is essentially identical, but there is a considerable numerical difference between them. Hence, it is debatable to take the uniform temperature along the span in the design on expansion joint of the variable cross-section steel-concrete composite girder according to the bridge specification.

Figure 11

Figure 11. Time histories of energy dissipation of specimen SRCFST-T1 during the impact process.

5 Conclusion

Based on the analytical research on resolution calculation method for nonlinear temperature load of steel-concrete composite girders presented in this study, the following conclusion can be drawn:

(1) Based on thermal response principles and equivalency of temperature effects for composite buildings, an analytical approach of disintegrating non-linear temperature load is proposed in this study. By considering the influence of statically indeterminate structural systems and utilizing the derived practical formula for temperature response, this method offers a novel perspective towards establishing a design temperature load model for composite girders.

(2) The bridge gauge yields significantly different temperature stress calculations than the observed temperature distribution, TLM-Ⅰ, and TLM-Ⅱ temperature load models. Even in the stress properties, the tensile and compressive stress symbols are opposite to those of the other three modes. TLM-Ⅰ calculates the self-stress, secondary stress, and total stress with maximum variances of 89.5%, 57.3%, and 78.6% compared to measured temperature distribution, respectively, and the maximum deviations for those corresponding stress values derived using TLM-Ⅱ are 5.39%, 0.14%, and 1.56%, respectively.

(3) In the context of a composite girder, the temperature self-stress is primarily governed by the equivalent uniform and nonlinear thermal, while the temperature secondary stress is mainly influenced by the equivalent linear and uniform thermal. The equivalent uniform temperature has a significant effect on the axial expansion deformation.

(4) The equivalent uniform thermal of composite girders with equal cross-sections remains constant throughout its span, while that of the composite girder with varying sections fluctuates. The design of bridge gauge typically assumes uniform temperature along the span as the bridge expansion joint, with no attention for the influence of cross-sectional characteristics on uniform temperature, but this study presents a method for calculating the expansion quantity of any bridge beam.

Based on the research of this paper, the classification of temperature effects and the calculation of temperature effects can be easily carried out. However, there are still some deficiencies: the temperature load values in different design reference periods are not considered, and the influence of temperature load values in different reference periods on temperature effect is not analyzed; the probabilistic reliability theory of temperature effect is not combined with the calculation method in this paper to formulate a more scientific temperature load model. The next step will be to carry out relevant research on the above deficiencies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

C-MZ: Writing – original draft, Writing – review and editing. W-HW: Writing – original draft, Writing – review and editing. WX: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by Gansu Provincial Department of Transport’s Science and Technology Innovation Unveiling and Leading System Project (No. 2021-02), and Gansu Provincial Talent Project (No. KY24CHX-001).

Conflict of interest

Authors C-MZ, and WX were employed by Gansu Province Transportation Planning Survey & Design Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

ASHTO. (American Association of State Highway and Transportation Officials) (2017). “AASHTO LRFD bridge design specifications,”. Washington, DC.

Google Scholar

BS EN (2003). Eurocode 1: actions on structures-Part 2: traffic loads on bridges.

Google Scholar

Chen, S. L., Su, Y. H., and Ban, X. L. (2021). Study on solar radiation temperature field of steel-concrete composite girder in high altitude area. Railw. Eng. 61 (4), 12–16.

Google Scholar

Fan, J., Li, B., Liu, C., and Liu, Y. F. (2022). An efficient model for simulation of temperature field of steel-concrete composite beam bridges. Structures 43, 1868–1880. doi:10.1016/j.istruc.2022.05.079

CrossRef Full Text | Google Scholar

Fan, J. S., Liu, C., Liu, Y. F., et al. (2020). Review of temperature distribution and temperature effects of steel-concrete composite girder bridges in China. China J. Highw. Transp. 33 (4), 1–13.

Google Scholar

Gottsäter, E., Larsson Ivanov, O., Molnár, M., and Plos, M. (2018). Validation of temperature simulations in a portal frame bridge. Structures 15, 341–348. doi:10.1016/j.istruc.2018.07.007

CrossRef Full Text | Google Scholar

Guo, T., Li, A., and Li, J. (2008b). Fatigue life prediction of welded joints in orthotropic steel decks considering temperature effect and increasing traffic flow. Struct. Health Monit. 7 (3), 189–202. doi:10.1177/1475921708090556

CrossRef Full Text | Google Scholar

Guo, T., Li, A., and Wang, H. (2008a). Influence of ambient temperature on the fatigue damage of welded bridge decks. Int. J. Fatigue 30 (6), 1092–1102. doi:10.1016/j.ijfatigue.2007.08.004

CrossRef Full Text | Google Scholar

Han, Q., Ma, Q., Xue, J., and Liu, M. (2021). Structural health monitoring research under varying temperature condition: a review. J. Civ. Struct. Health Monit. 11, 149–173. doi:10.1007/s13349-020-00444-x

CrossRef Full Text | Google Scholar

He, Z., Ma, Z., Zhang, S., and Liu, Z. (2021). Temperature gradients and stress distributions in concrete box-girder bridges during hot-mix asphalt paving. Structures 33, 1954–1966. doi:10.1016/j.istruc.2021.05.078

CrossRef Full Text | Google Scholar

Hottel, H. C. (1976). A simple model for estimating the transmittance of direct solar radiation through clear atmospheres. Sol. Energy 18, 129–134. doi:10.1016/0038-092x(76)90045-1

CrossRef Full Text | Google Scholar

JTG 3362-2018 (2018). Specification for design of high-way reinforced concrete and prestressed concrete bridges. People's Communications Publishing House Co., Ltd.

Google Scholar

Lawson, L., Ryan, K. L., and Buckle, I. G. (2020). Bridge temperature profiles revisited: thermal analyses based on recent meteorological data from Nevada. J. Bridge Eng. 25 (1), 04019124. doi:10.1061/(asce)be.1943-5592.0001498

CrossRef Full Text | Google Scholar

Liu, X. F. (1986). Computation of temperature stresses for prestressed concrete box girders. China Civ. Eng. J. 19 (1), 44–54.

Google Scholar

Liu, Y., Qian, Z., and Hu, H. (2016). Thermal field characteristic analysis of steel bridge deck during high-temperature asphalt pavement paving. KSCE J. Civ. Eng. 20 (7), 2811–2821. doi:10.1007/s12205-016-0027-2

CrossRef Full Text | Google Scholar

Mirambell, E., and Aguado, A. (1990). Temperature and stress distributions in concrete box girder bridges. J. Struct. Eng. 116 (9), 2388–2409. doi:10.1061/(asce)0733-9445(1990)116:9(2388)

CrossRef Full Text | Google Scholar

MOT (Ministry of Transport of the People’s Republic of China) (2015). General specifications for design of highway bridges and culverts. Beijing, China.

Google Scholar

Roberts-Wollman, C. L., Breen, J. E., and Cawrse, J. (2002). Measurements of thermal gradients and their effects on segmental concrete bridge. J. Bridge Eng. 7 (3), 166–174. doi:10.1061/(asce)1084-0702(2002)7:3(166)

CrossRef Full Text | Google Scholar

Silveira, A. P., Branco, F. A., and Castanheta, M. (2000). Statistical analysis of thermal actions for concrete bridge design. Struct. Eng. Int. 10, 33–38. doi:10.2749/101686600780621008

CrossRef Full Text | Google Scholar

Wang, D., Liu, H. Z., and Liu, Y. (2016). In comparison with vertical temperature gradient effects of steel-concrete composite bridge deck in Chinese. Ind. Constr. 46 (10), 163–173.

Google Scholar

Wang, D., Zhang, Y. J., Liu, Y., et al. (2015). Vertical temperature gradient effect analysis of steel-concrete composite deck system on steel truss stiffening girder with health monitoring. China J. Highw. Transp. 28 (11), 29–36.

Google Scholar

Wang, R., Ji, W., Li, X., Peng, K., Peng, C., and Wang, C. (2023). Thermal load models for the static design of steel-concrete composite girders. Structures 51, 1004–1018. doi:10.1016/j.istruc.2023.03.029

CrossRef Full Text | Google Scholar

Wang, R. Z., and Zhang, Y. H. (2024). Distortion effect of simply supported curved steel box composite girders with corrugated webs and flexible diaphragms. J. Jilin Univ. Eng. Technol. Ed. doi:10.13229/j.cnki.jdxbgxb.20240260

CrossRef Full Text | Google Scholar

Westgate, R., Koo, K. Y., and Brownjohn, J. (2015). Effect of solar radiation on suspension bridge performance. J. Bridge Eng. 20 (5), 04014077. doi:10.1061/(asce)be.1943-5592.0000668

CrossRef Full Text | Google Scholar

Xia, Q., Chen, Y., Zhang, J., and Zhu, F. (2017). In-service condition assessment of a long-span suspension bridge using temperature-induced strain data. J. Bridge Eng. 22 (3), 04016124. doi:10.1061/(asce)be.1943-5592.0001003

CrossRef Full Text | Google Scholar

Yan, X. K., Liu, Y. J., Liu, J., et al. (2022). Extreme value statistical model of temperature action of steel plate composite girder. J. Southeast Univ. Nat. Sci. Ed. 52 (5), 856–865.

Google Scholar

Ye, J. S. (2016). Principles of structural design[M]. Beijing: China Communications Press.

Google Scholar

Yu, Y. (2023). Natural frequency analysis of beam bridge structure under temperature and vehicle action. J. Jilin Univ. Eng. Technol. Ed. 53 (6), 1702–1710.

Google Scholar

Zhang, C., Liu, Y., Ye, F., Yuan, Z., Zhang, G., and Ma, Z. (2020). Validation of long-term temperature simulations in a steel-concrete composite girder. Structures 27, 1962–1976. doi:10.1016/j.istruc.2020.07.070

CrossRef Full Text | Google Scholar

Zhang, H., Li, L., Ma, W., Luo, Y., Li, Z., and Kuai, H. (2022a). Effects of welding residual stresses on fatigue reliability assessment of a PC beam bridge with corrugated steel webs under dynamic vehicle loading. Structures 45, 1561–1572. doi:10.1016/j.istruc.2022.09.094

CrossRef Full Text | Google Scholar

Zhang, H., Yang, Z., and Li, L. (2022b). Numerical study on welding residual stress distribution of corrugated steel webs. Metals 12 (11), 18–31.

Google Scholar

Zhang, Y. H. (2009). Computation of temperature stresses for prestressed concrete box girders. Eng. Mech. 26 (1), 131–136.

Google Scholar

Zhang, Y. H., Ma, Y. L., and Liu, Z. X. (2023). Analysis on distortion effect of thin-walled box girders considering coupling between torsion and distortion. J. Southeast Univ. Nat. Sci. Ed. 53 (3), 418–424.

Google Scholar

Zhao, P., and Ye, J. S. (2019). Analysis of transverse temperature effects on the deck of box girder with corrugated steel webs. J. Harbin Eng. Univ. 40 (5), 974–978.

Google Scholar

Zhou, Y., Xia, Y., Chen, B., et al. (2021). Analytical formulas of beam deflection due to vertical temperature difference. Eng. Struct. 240, 112366. doi:10.1016/j.engstruct.2021.112366

CrossRef Full Text | Google Scholar

Zhou, Y., Xia, Y., Chen, B., and Fujino, Y. (2020). Analytical solution to temperature-induced deformation of suspension bridges. Mech. Syst. Signal Process. 139, 106568. doi:10.1016/j.ymssp.2019.106568

CrossRef Full Text | Google Scholar

Zhou, Y., Zheng, J. Y., and Hao, G. W. (2023). A temperature effect prediction method for long-span bridges based on meteorological big data. J. Hunan Univ. Nat. Sci. 43 (7), 1674–1682.

Google Scholar

Glossary

E_c elastic modules of the concrete

E_s elastic modules of the steel girder

E(y) elastic modules of the material at cross-section $y$ position

α(y) thermal expansion ratio of the material at the cross-section $y$ position.

${\mathit{\sigma }}_{\mathbf{\text{sum}}}\left(\mathit{y}\right)$ the cross-sectional stress

${\mathit{\epsilon }}_{\mathbf{\text{sum}}}\left(\mathit{y}\right)$ the cross-sectional strain

${\mathit{\epsilon }}_{\mathbf{0}}$ the axial deformation at the centroid position

$\mathit{\phi }$ bending curvature

T(y) the vertical thermal profile of the section

N cross-sectional axial force caused by the nonlinear temperature

M bending moment caused by the nonlinear temperature

N_T cross-sectional axial force the free-form deformation

M_T cross-sectional bending moment the free-form deformation

h₁ distances from the centroid of the converted section to the upper surface of the bridge deck

h₂ distances from the centroid of the converted section to the lower surface of the lower flange

A_c area of concrete bridge deck

As area of steel girder

A₀ converted cross-sectional area of composite girder

T_L equivalent linearity temperature load

T_NL equivalent nonlinear temperature load

T_T equivalent uniformly y temperature load

k a straight-line distribution with a specific slope

I₀ the converted moment of inertia

H the cross-sectional height of steel-concrete composite girders.

G(y) equivalent linear thermal gradient

y_s distance from centroid of transformed section to upper concrete deck surface

y_cs distance from centroid of transformed section to lower steel flange surface

α_c linear expansion coefficient of concrete

α_s linear expansion coefficient of steel

b(y) cross-sectional width at vertical coordinate y

n number of spans in continuous composite girder system