Development of micromechanical model of asphalt mixture in complex form for dynamic modulus characterization

Asphalt mixture is a multiphase composite viscoelastic material, with its fundamental viscoelastic properties primarily determined by its material composition and internal microstructure. The application of composite micromechanics and the development of mathematical models to predict the mechanical performance of asphalt mixtures are of great significance. However, existing self-consistent micromechanics models primarily focus on the magnitude of the complex modulus of asphalt mixtures, often neglecting the phase angle. To more comprehensively evaluate the viscoelastic mechanical properties of asphalt mixtures, this study extends the self-consistent model to its complex form. By predicting the storage modulus and loss modulus of the mixture, the goal of simultaneously predicting the dynamic modulus and phase angle is achieved. The effectiveness of the model was validated using four types of asphalt mixtures through forward and inverse modeling approaches. By integrating inverse and forward solutions within the complex micromechanical model, the dynamic modulus and phase angle can be accurately predicted. The coefficients of determination between the predicted results and the measured data are all above 0.9, demonstrating the model’s robust predictive capabilities.

1 Introduction

The objective of asphalt mixture material design is to determine the proportion of coarse and fine aggregates, the amount of asphalt, and the most reasonable skeleton structure, internal void distribution, and mortar content, so that the mixture exhibits favorable mechanical properties (ARA and ERES Consultants Division, 2004). Currently, the Marshall design method and the Superpave design method are the two commonly used approaches for mixture design (Kandhal and Koehler, 1985; Lytton et al., 1993; Chakroborty et al., 2010; D’Angelo, 2001). These methods differ in terms of gradation design, compaction methods, equipment used, and the approach to determining asphalt content (Kandhal and Koehler, 1985; Lytton et al., 1993; Chakroborty et al., 2010; D’Angelo, 2001). However, for performance evaluation, both methods rely on empirical and macroscopic mechanical testing to reflect the actual pavement performance of the mixture, and corresponding macro-mechanical indicators are proposed to assess the quality of the mixture design (Kandhal and Koehler, 1985; Lytton et al., 1993). Nevertheless, years of engineering practice have shown that these seemingly reasonable mechanical indicators often exhibit poor correlation with the actual pavement performance (ARA and ERES Consultants Division, 2004). There are instances where asphalt mixtures with excellent laboratory macro-mechanical indicators develop rutting, moisture damage, and other distresses shortly after paving, significantly compromising the service life of the asphalt pavement (ARA and ERES Consultants Division, 2004). While insufficient construction quality may contribute to such issues, the primary reason lies in the design phase’s failure to accurately link laboratory test indicators with pavement serviceability. At present, neither the Marshall design method nor the Superpave design method considers the mechanical properties of the mixture from a microstructural perspective during the design process. Factors such as the size, shape, surface characteristics of aggregates, the contact characteristics between aggregates, and the spatial distribution of voids and asphalt all influence the serviceability of the mixture in various ways (Karki et al., 2015).

At present, the macroscopic pavement performance of asphalt mixtures is a key research focus, with most research methods relying on two approaches: one being empirical formula methods (ARA and ERES Consultants Division, 2004; Lytton et al., 2010), and the other being laboratory testing methods (AASHTO, 2022; A ASHTO, 2020; Zeng et al., 2021; Zeng et al., 2023a). Empirical formulas are derived from extensive laboratory test data through numerical analysis and mathematical fitting, resulting in models with high fitting accuracy to predict the fundamental mechanical properties of mixtures (Christensen et al., 2003; Zhang et al., 2020). For example, one of the most well-known dynamic modulus prediction equations, the Witczak model shown in Equation 1, was developed under the National Cooperative Highway Research Program (NCHRP) Project 1-40D (Zhang et al., 2020). As shown, it is essentially a regression model built on a large dataset. However, the validity of such empirical formulas depends on extensive laboratory data obtained under specific experimental conditions. As a result, when applied to environments different from those in which the formulas were originally developed, the prediction results may deviate significantly (Zeng et al., 2021). For instance, Zhang et al. reported that the Witczak 1-40D model achieved an R² value of only 0.66 (Zhang et al., 2020).

$\begin{array}{l}\log \left|E^{*}\right|=-0.349+0.754{\left(\left|G^{*}\right|\right)}^{-0.0052}\\ \left[\begin{array}{l}6.65-0.032p_{200}+0.0027p_{200}^2+0.011p_4-0.0001p_4^2\\ +0.006p_{38}-0.00014p_{38}^2-0.08V_a-1.06\left(\frac{V_{beff}}{V_a+V_{beff}}\right)\end{array}\right]\\ +\frac{2.558+0.032V_a+0.713\left(\frac{V_{beff}}{V_a+V_{beff}}\right)+0.0124p_{38}-0.0001p_{38}^2-0.0098p_{34}}{1+\exp \left(-0.7814-0.5785\log \left|G^{*}\right|+0.8834\log {\delta }_b\right)}\end{array}(1)$

where: $\left|E^{*}\right|$ is the dynamic modulus predicted by the Witczak’s 1-40D model; $\left|G^{*}\right|$ is the dynamic shear modulus of asphalt binder measured by dynamic shear rheometer; p₂₀₀, p₄, p₃₈, p₃₄ are measured parameters related to aggregate gradation; $V_a$ is the air voids of asphalt mixture; $V_{beff}$ is the effective asphalt volume of asphalt mixture; ${\delta }_b$ is the measured phase angle of asphalt binder.

Laboratory testing methods involve testing specimens formed under controlled conditions to evaluate their mechanical properties under specific loads and environmental conditions, yielding highly accurate results. For instance, AASHTO T 378 was developed to measure the dynamic modulus using the Asphalt Mixture Performance Tester (AMPT) (AASHTO, 2022). This test not only requires a dynamic modulus testing system and data processing software, but also a conditioning chamber, balance, and specimen fabrication equipment, making it difficult to operate in practice. Additionally, each specimen must be compacted, cored, and cut to dimensions of 100 mm in diameter and 150 mm in height for a single test (AASHTO, 2022). As a result, laboratory testing is both time-consuming and costly.

Furthermore, both empirical formulas and laboratory methods are based on the macroscopic mechanical behavior of the mixture, which prevents an understanding of its mechanical response mechanisms from the standpoint of its constituent materials and internal structure. Asphalt mixtures can be regarded as composites composed of aggregates, asphalt, air, and other materials with different properties. These materials are discretely and non-uniformly distributed within the mixture, resulting in a distinctly heterogeneous structure (Underwood and Kim, 2013). The inherent anisotropy of the mixture is a significant manifestation of this heterogeneity, which is also the primary reason why traditional continuum mechanics theories fail to accurately describe the damage mechanisms of asphalt mixtures (Zhang et al., 2011). It is evident that the properties of the constituent materials and their structural distribution within the mixture are decisive factors for the macroscopic mechanical properties of the mixture. By applying micromechanics theory to investigate the influence mechanisms of material composition on the mechanical properties of the mixture and establishing quantitative analysis models, the goal of efficiently obtaining the mechanical parameters of the mixture can be achieved (You and Buttlar, 2006; Abbas et al., 2007). This approach lays the foundation for developing design methods grounded in mechanical theories, making asphalt mixture design more scientific, rational, and economical, while ensuring its stability and durability.

Dynamic modulus and phase angle are two critical viscoelastic parameters of asphalt mixtures (Zeng et al., 2023b). These two properties are primarily influenced by the material composition and internal structure of the mixture (Zeng et al., 2024; Shu and Huang, 2008). Therefore, analyzing the structural composition of asphalt mixtures and establishing mechanical models that link the properties of the constituent materials to the macroscopic mechanical properties (dynamic modulus and phase angle) of the mixture enable the prediction of dynamic modulus and phase angle values under different conditions. This approach allows for the quick and straightforward acquisition of fundamental mechanical parameters during the initial design phase of the mixture, providing mechanical guidance for material design. The fundamental idea of studying composite materials through micromechanics is to homogenize the constituent phases, establishing the relationship between the properties, composition, and structure of each phase and the macroscopic mechanical properties of the composite material, thereby constructing the material’s constitutive model (Kachanov and Sevostianov, 2018; Hashin, 1960).

2 Modulus characterization using self-consistent micromechanics

In the 1950s, Eshelby proposed the equivalent inclusion theory, which largely addressed the homogenization of heterogeneous materials and laid the foundation for the study of micromechanics in composite materials (Eshelby, 1957; Eshelby, 1959). Building on Eshelby’s inclusion theory, extensive exploration and derivation by numerous scholars led to the development of classical micromechanical theories for composite materials (Böhm, 1998; Molladavoodi and RahimiRezaei, 2018; Tan et al., 2005; Hill, 1965; Huang et al., 1994). Among these, the self-consistent micromechanics model has gained significant attention in the asphalt community due to its rigorous formulation and practical applicability (Yin et al., 2008; Luo et al., 2011; Alam and Hammoum, 2015; Nguyen et al., 2024). The self-consistent micromechanics model was initially established for simple two-phase composite materials (Luo et al., 2011). During the homogenization process, one material is designated as the matrix phase, and the other as the inclusion phase (Yin et al., 2008; Luo et al., 2011; Alam and Hammoum, 2015; Nguyen et al., 2024). In the 1970s, Hashin and Shriskman, while studying the equivalent mechanical parameters of composite materials, derived boundary expressions for the effective modulus of multiphase composite materials based on the average strain energy theory (Hashin and Shtrikman, 1962; Hashin and Shtrikman, 1963). As shown in Equations 2–5, they established the lower and upper bounds for the bulk modulus and shear modulus of composite materials (Hashin and Shtrikman, 1962; Hashin and Shtrikman, 1963). The rationale behind these bounds is that for a two-phase composite, Equations 2, 4 represent the case where phase one forms the matrix and spherical inclusions of phase two are embedded within it. Similarly, Equations 3, 5 apply when phase two is the matrix and phase one forms the spherical inclusions. These bounds are the most restrictive limits that can be derived based on the known volume fractions and moduli of the constituent phases (Hashin and Shtrikman, 1962; Hashin and Shtrikman, 1963).

$K_{\left(-\right)}^{*}=K_1+\frac{c_2}{\frac{1}{K_2-K_1}+\frac{3c_1}{3K_1+4G_1}}(2)$

$G_{\left(-\right)}^{*}=G_1+\frac{c_2}{\frac{1}{G_2-G_1}+\frac{6\left(K_1+2G_1\right)c_1}{5G_1\left(3K_1+4G_1\right)}}(3)$

$K_{\left(+\right)}^{*}=K_2+\frac{c_1}{\frac{1}{K_1-K_2}+\frac{3c_2}{3K_2+4G_2}}(4)$

$G_{\left(+\right)}^{*}=G_2+\frac{c_1}{\frac{1}{G_1-G_2}+\frac{6\left(K_2+2G_2\right)c_2}{5G_2\left(3K_2+4G_2\right)}}(5)$

where: $K_{\left(-\right)}^{*}$ and $K_{\left(+\right)}^{*}$ are the lower and upper boundaries of the composite material’s bulk modulus, respectively; $G_{\left(-\right)}^{*}$ and $G_{\left(+\right)}^{*}$ the lower and upper boundaries of the composite material’s shear modulus, respectively; $K_1$, $K_2$ and $K^{*}$ are the bulk modulus of the inclusion phase, matrix phase, and composite material, respectively; $G_1$, $G_2$ and $G^{*}$ are the shear modulus of the inclusion phase, matrix phase, and composite material, respectively; $c_1$ and $c_2$ are volumetric fractions of the constituent materials.

In 2010, based on the modulus boundary for two-phase composite materials proposed by Hashin and Shriskman, Luo and Lytton decomposed the lower bound expression, as shown in Equations 6, 7 (Luo et al., 2011; Hashin and Shtrikman, 1963).

$K_{\left(-\right)}^{*}=K_1+\left(3K_1+G_1\right)\frac{c_2\frac{K_2-K_1}{3K_2+4G_1}}{1-3\frac{c_2\left(K_2-K_1\right)}{3K_2+4G_1}}(6)$

$G_{\left(-\right)}^{*}=G_1+5G_1\frac{3K_1+4G_1}{K_1+2G_1}\frac{\frac{c_2\left(G_2-G_1\right)}{G_1\frac{9K_1+8G_1}{K_1+G_1}+6G_2}}{1-6\frac{c_2\left(G_2-G_1\right)}{G_1\frac{9K_1+8G_1}{K_1+2G_1}+6G_2}}(7)$

Furthermore, for heterogeneous materials such as asphalt mixtures, which are composed of aggregates, asphalt, and air, the above model can be extended to three-phase composite materials, as demonstrated in Equations 8, 9. According to Luo and Lytton, the extension from a two-phase to a three-phase model follows the same homogenization principles, as each phase, such as air in asphalt mixtures, can be represented by its own volume fraction and mechanical properties. This maintains the original framework while accounting for more complex material structures (Luo et al., 2011).

$K_{\left(-\right)}^{*}=K_1+\left(3K_1+G_1\right)\frac{{\displaystyle {\sum }_{i=1}^n}{c}_i\frac{K_i-K_1}{3K_i+4G_1}}{1-{\displaystyle {\sum }_{i=1}^n}3\frac{c_i\left(K_i-K_1\right)}{3K_i+4G_1}}(8)$

$G_{\left(-\right)}^{*}=G_1+5G_1\frac{3K_1+4G_1}{K_1+2G_1}\frac{{\displaystyle {\sum }_{i=1}^n}\frac{c_i\left(G_i-G_1\right)}{G_1\frac{9K_1+8G_1}{K_1+G_1}+6G_i}}{1-6{\displaystyle {\sum }_{i=1}^n}\frac{c_2\left(G_i-G_1\right)}{G_1\frac{9K_1+8G_1}{K_1+2G_1}+6G_i}}(9)$

where: $K_i$, $G_i$, and $c_i$ are the bulk modulus, shear modulus, and volumetric fraction of the ith phase material.

By applying the ‘self-consistent’ approximation method to solve Equations 8–11, can be derived. After verification, this model has been demonstrated to effectively characterize the dynamic modulus with reasonable trends using one asphalt mixture under three different aging conditions (Luo et al., 2011).

$\frac{c_1\left(K_1-K^{*}\right)}{3K_1+G^{*}}+\frac{c_2\left(K_2-K^{*}\right)}{3K_2+G^{*}}+\frac{c_3\left(K_3-K^{*}\right)}{3K_3+G^{*}}=0(10)$

$\frac{c_1\left(G_1-G^{*}\right)}{G^{*}\frac{9K^{*}+G^{*}}{K^{*}+2G^{*}}+6G_1}+\frac{c_2\left(G_2-G^{*}\right)}{G^{*}\frac{9K^{*}+G^{*}}{K^{*}+2G^{*}}+6G_2}+\frac{c_3\left(G_3-G^{*}\right)}{G^{*}\frac{9K^{*}+G^{*}}{K^{*}+2G^{*}}+6G_3}=0(11)$

where: $K_1$, $K_2$, $K_3$ and $K^{*}$ specifically represent the bulk modulus of the aggregate, asphalt binder, air, and asphalt mixture, respectively; $G_1$, $G_2$, $G_3$ and $G^{*}$ are shear modulus of the aggregate, asphalt binder, air, and asphalt mixture, respectively; $c_1$, $c_2$ and $c_3$ are volumetric fractions of the aggregate, asphalt binder, and air, respectively.

3 Self-consistent micromechanics in complex form

Although the above self-consistent model inherits the typical advantages of the micromechanics approach and can be implemented in a relatively simple manner, it is solely focused on predicting the modulus magnitude of the mixture and does not account for the phase angle, which reflects the viscous behavior of the mixture. It is well known that asphalt mixture is a typical viscoelastic material, where a higher degree of material viscosity results in a phase angle closer to 90°, while a higher degree of material elasticity leads to a phase angle closer to 0°. Since viscoelastic materials exhibit time-dependent behavior, with a delayed response after loading, neglecting the phase angle also means ignoring the corresponding time delay inherent to viscoelasticity (Luo et al., 2011; Findley and Davis, 2013). Given the limitations of the existing model, it is necessary to develop a new model that more comprehensively describes and predicts the viscoelastic mechanical parameters of the mixture. According to viscoelastic theory, the modulus should be expressed in complex form to account for the effect of phase angle (Findley and Davis, 2013). Therefore, the bulk modulus and shear modulus in the original self-consistent micromechanical model are expressed in complex form, as shown in Equations 12, 13.

$K=K^{\prime }+\mathrm{i}{K}^{″}(12)$

$G=G^{\prime }+\mathrm{i}{G}^{″}(13)$

Substituting the above two equations into the self-consistent micromechanical model yields Equations 14, 15:

${\displaystyle \sum _{i=1}^3}{c}_i\left[\frac{\left(K_i^{\prime }+\mathrm{i}{K}_i^{″}\right)-\left(K^{\prime }+\mathrm{i}{K}^{″}\right)}{3\left(K_i^{\prime }+\mathrm{i}{K}^{″}\right)+\left(G^{\prime }+\mathrm{i}{G}^{″}\right)}\right]=0(14)$

${\displaystyle \sum _{i=1}^3}{c}_i\frac{\left(G_i^{\prime }+\mathrm{i}{G}_i^{″}\right)-\left(G^{\prime }+\mathrm{i}{G}^{″}\right)}{\frac{\left(G^{\prime }+\mathrm{i}{G}^{″}\right)\left[9\left(K^{\prime }+\mathrm{i}{K}^{″}\right)+8\left(G^{\prime }+\mathrm{i}{G}^{″}\right)\right]}{\left(K^{\prime }+\mathrm{i}{K}^{″}\right)+2\left(G^{\prime }+\mathrm{i}{G}^{″}\right)}+6\left(G_i^{\prime }+\mathrm{i}{G}_i^{″}\right)}=0(15)$

Separating the real and imaginary parts of the equation gives the following two expressions:

${\displaystyle \sum _{i=1}^3}{c}_i\left[\begin{array}{l}\frac{3\left({K^{\prime }}_i^2+{K^{″}}_i^2\right)+\left(K_i^{\prime }-K^{\prime }\right)G^{\prime }+\left(K_i^{″}-K^{″}\right)G^{″}-3\left(K_i^{\prime }{K}^{\prime }+K_i^{″}{K}^{″}\right)}{{\left(3K_i^{\prime }+G^{\prime }\right)}^2+{\left(3K_i^{″}+G^{″}\right)}^2}+\\ \mathrm{i}\frac{\left(K_i^{″}{G}^{\prime }-K_i^{\prime }{G}^{″}\right)+3\left(K_i^{″}{K}^{\prime }-K_i^{\prime }{K}^{″}\right)+\left(G^{″}{K}^{\prime }-G^{\prime }{K}^{″}\right)}{{\left(3K_i^{\prime }+G^{\prime }\right)}^2+{\left(3K_i^{″}+G^{″}\right)}^2}\end{array}\right]=0(16)$

${\displaystyle \sum _{i=1}^3}{c}_i\left[\begin{array}{l}\frac{\left(G_i^{\prime }-G^{\prime }\right)\left(A+6G^{\prime }\right)+\left(G_i^{″}-G^{″}\right)\left(B+6G_i^{″}\right)}{{\left(A+6G_i^{\prime }\right)}^2+i{\left(B+6G_i^{″}\right)}^2}+\\ \mathrm{i}\frac{\left(G_i^{″}-G^{″}\right)\left(A+6G_i^{\prime }\right)-\left(G_i^{\prime }-G^{\prime }\right)\left(B+6G^{″}\right)}{{\left(A+6G_i^{\prime }\right)}^2+i{\left(B+6G_i^{\prime }\right)}^2}\end{array}\right]=0(17)$

where: A and B are two expressions related only to the bulk modulus and shear modulus of the asphalt mixture, as shown in Equations 18, 19:

$A=\left\{\begin{array}{l}{G}^{\prime }\left[\frac{9\left({K^{\prime }}^2+{K^{″}}^2\right)+16\left({G^{\prime }}^2+{G^{″}}^2\right)+26\left(K^{\prime }{G}^{\prime }+K^{″}{G}^{″}\right)}{{\left(K^{\prime }+2G^{\prime }\right)}^2+{\left(K^{″}+2G^{″}\right)}^2}\right]-\\ G^{″}\left[\frac{10\left(K^{″}{G}^{\prime }-K^{\prime }{G}^{″}\right)}{{\left(K^{\prime }+2G^{\prime }\right)}^2+{\left(K^{″}+2G^{″}\right)}^2}\right]\end{array}\right\}(18)$

$B=\left\{\begin{array}{l}{G}^{″}\left[\frac{9\left({K^{\prime }}^2+{K^{″}}^2\right)+16\left({G^{\prime }}^2+{G^{″}}^2\right)+26\left(K^{\prime }{G}^{\prime }+K^{″}{G}^{″}\right)}{{\left(K^{\prime }+2G^{\prime }\right)}^2+{\left(K^{″}+2G^{″}\right)}^2}\right]-\\ G^{\prime }\left[\frac{10\left(K^{″}{G}^{\prime }-K^{\prime }{G}^{″}\right)}{{\left(K^{\prime }+2G^{\prime }\right)}^2+{\left(K^{″}+2G^{″}\right)}^2}\right]\end{array}\right\}(19)$

For Equations 16, 17 to hold, both the real and imaginary parts must be equal to zero, resulting in the following four equations:

${\displaystyle \sum _{i=1}^3}{c}_i\frac{3\left({K^{\prime }}_i^2+{K^{″}}_i^2\right)+\left(K_i^{\prime }-K^{\prime }\right)G^{\prime }+\left(K_i^{″}-K^{″}\right)G^{″}-3\left(K_i^{\prime }{K}^{\prime }+K_i^{″}{K}^{″}\right)}{{\left(3K_i^{\prime }+G^{\prime }\right)}^2+{\left(3K_i^{″}+G^{″}\right)}^2}=0(20)$

${\displaystyle \sum _{i=1}^3}{c}_i\frac{\left(K_i^{″}{G}^{\prime }-K_i^{\prime }{G}^{″}\right)+3\left(K_i^{″}{K}^{\prime }-K_i^{\prime }{K}^{″}\right)+\left(G^{″}{K}^{\prime }-G^{\prime }{K}^{″}\right)}{{\left(3K_i^{\prime }+G^{\prime }\right)}^2+{\left(3K_i^{″}+G^{″}\right)}^2}=0(21)$

${\displaystyle \sum _{i=1}^3}{c}_i\frac{\left(G_i^{\prime }-G^{\prime }\right)\left(A+6G_i^{\prime }\right)+\left(G_i^{″}-G^{″}\right)\left(B+6G_i^{″}\right)}{{\left(A+6G_i^{\prime }\right)}^2+{\left(B+6G^{″}\right)}^2}=0(22)$

${\displaystyle \sum _{i=1}^3}{c}_i\frac{\left(G_i^{″}-G^{″}\right)\left(A+6G_i^{\prime }\right)-\left(G_i^{\prime }-G^{\prime }\right)\left(B+6G_i^{″}\right)}{{\left(A+6G^{\prime }\right)}^2+{\left(B+6G^{″}\right)}^2}=0(23)$

Among the four equations above, there are a total of 16 modulus parameters for aggregate, asphalt binder, air, and the asphalt mixture. The modulus parameters of air are all zero, and the modulus parameters of asphalt binder can be obtained through DSR testing. Therefore, knowing the modulus parameters of either the asphalt mixture or the aggregate allows the other to be determined using these four equations. Consequently, the self-consistent approach is still used to solve these as shown in Equations 24–27.

$K^{\prime }+\mathrm{i}{K}^{″}=\frac{E^{\prime }+\mathrm{i}{E}^{″}}{3\left[1-2\left({\mu }^{\prime }+\mathrm{i}{\mu }^{″}\right)\right]}(24)$

$G^{\prime }+\mathrm{i}{G}^{″}=\frac{E^{\prime }+\mathrm{i}{E}^{″}}{2\left[1+\left({\mu }^{\prime }+\mathrm{i}{\mu }^{″}\right)\right]}(25)$

$K^{\prime }+\mathrm{i}{K}^{″}=\frac{\left(3-6{\mu }^{\prime }\right)E^{\prime }-6{\mu }^{″}{E}^{″}}{{\left(3-6{\mu }^{\prime }\right)}^2+36{{\mu }^{″}}^2}+\mathrm{i}\frac{\left(3-6{\mu }^{\prime }\right)E^{″}+6{\mu }^{″}{E}^{\prime }}{{\left(3-6{\mu }^{\prime }\right)}^2+36{{\mu }^{″}}^2}(26)$

$G^{\prime }+\mathrm{i}{G}^{″}=\frac{\left(2+2{\mu }^{\prime }\right)E^{\prime }+2{\mu }^{″}{E}^{″}}{{\left(2+2{\mu }^{\prime }\right)}^2+{\left(2{\mu }^{″}\right)}^2}+\mathrm{i}\frac{\left(2+2{\mu }^{\prime }\right)E^{″}-2{\mu }^{″}{E}^{\prime }}{{\left(2+2{\mu }^{\prime }\right)}^2+{\left(2{\mu }^{″}\right)}^2}(27)$

4 Complex Poisson’s ratio

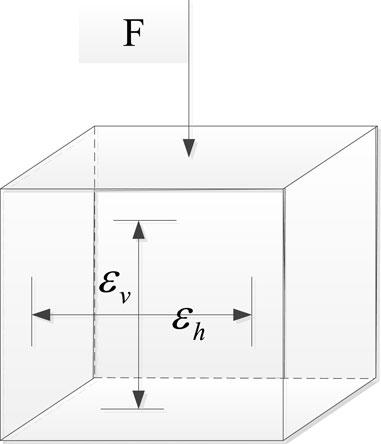
Poisson’s ratio represents the ratio of strain in the compaction direction to the strain perpendicular to the compaction direction under loading, as expressed in Equation 28.

$\mu =-\frac{{\epsilon }_h}{{\epsilon }_v}(28)$

ų is the Poisson’s ratio of the asphalt mixture; ɛ_h and ɛ_v represent the strain values in the direction perpendicular to the compaction direction and along the compaction direction, respectively.

Currently, most researchers use the recommended values provided in standards for model calculations, typically ranging from 0.25 to 0.40 (Zeng et al., 2022). However, Poisson’s ratio is an inherent material property that depends on the mechanical characteristics of the material itself. For viscoelastic materials, Poisson’s ratio varies with temperature and frequency and has both real and imaginary components.

As seen from Equation 28, obtaining Poisson’s ratio requires measuring strain values in both directions during loading. To extend this into the complex domain, the Laplace transform is commonly used to generalize material properties from the elastic domain to viscoelastic behavior. First, the axial load applied to the mixture can be modelled through Equation 29 (Ling et al., 2020). Simultaneously, axial and transverse strains of the asphalt mixture are measured using LVDTs and fitted with Equations 30, 31, respectively.

$\sigma \left(t\right)={\alpha }_{\sigma }\left(1-{\mathrm{e}}^{-b_{\sigma }t}\right)(29)$

${\epsilon }_h\left(t\right)={\alpha }_h\left(1-{\mathrm{e}}^{-b_{h}t}\right)(30)$

${\epsilon }_v\left(t\right)={\alpha }_v\left(1-{\mathrm{e}}^{-b_{v}t}\right)(31)$

where: t is time; σ is stress; ${\alpha }_{\sigma }$、 $b_{\sigma }$、 ${\alpha }_h$、 $b_h$、 ${\alpha }_v$ and $b_v$ are the model fitting coefficients.

By applying the Laplace transform to Equations 30–33, can be obtained. By substituting Equations 30, 31 into Equations 32, 33, the solution can be derived, as shown in Equations 34, 35.

${\epsilon }_h\left(s\right)={\displaystyle \underset{t=0}{\overset{t=\infty }{\int }}}{\epsilon }_h\left(t\right){\mathrm{e}}^{-st}\mathrm{d}t(32)$

${\epsilon }_v\left(s\right)={\displaystyle \underset{t=0}{\overset{t=\infty }{\int }}}{\epsilon }_v\left(t\right){\mathrm{e}}^{-st}\mathrm{d}t(33)$

${\epsilon }_h\left(s\right)=\frac{{\alpha }_h{b}_h}{s\left(s+b_h\right)}(34)$

${\epsilon }_v\left(s\right)=\frac{{\alpha }_v{b}_v}{s\left(s+b_v\right)}(35)$

where: s is a complex variable used for Laplace transform.

Thus, Poisson’s ratio can be expressed in Equation 36:

$\mu \left(t\right)=L^{-1}\left[-\frac{{\epsilon }_h\left(s\right)}{s{\epsilon }_v\left(s\right)}\right](36)$

$\mu \left(\omega \right)=\mathrm{i}\omega L{\left[\mu \left(t\right)\right]}_{s=\mathrm{i}\omega }=\mathrm{i}\omega {\left[-\frac{\frac{{\alpha }_h{b}_h}{s\left(s+b_h\right)}}{s\frac{{\alpha }_v{b}_v}{s\left(s+b_v\right)}}\right]}_{s=\mathrm{i}\omega }(37)$

According to viscoelastic theory and as shown in Equation 37, substituting the Laplace transform variable s with iω yields the viscoelastic solution (Findley and Davis, 2013). Accordingly, the real and imaginary parts of Poisson’s ratio are expressed in Equations 38, 39:

${\mu }^{\prime }\left(\omega \right)=-\frac{{\alpha }_h{b}_h\left(b_v+{\omega }^2\right)}{{\alpha }_v{b}_v\left(b_h^2+{\omega }^2\right)}(38)$

${\mu }^{″}\left(\omega \right)=\frac{\omega {\alpha }_h{b}_h\left(b_v-b_h\right)}{{\alpha }_v{b}_v\left(b_h^2+{\omega }^2\right)}(39)$

5 Material

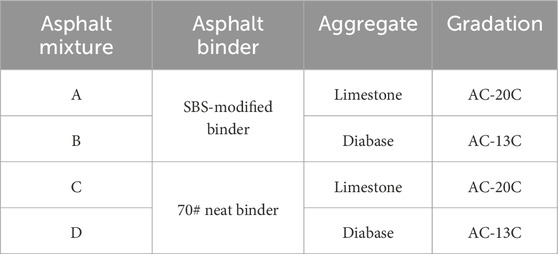
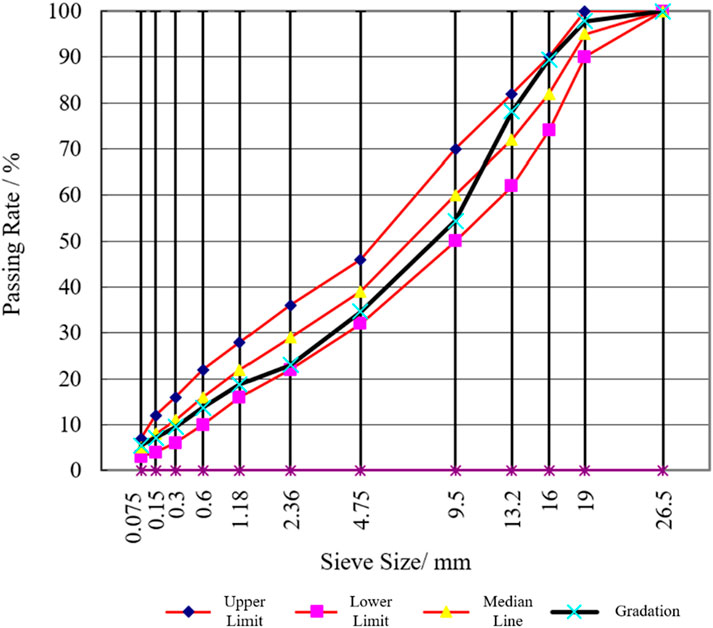
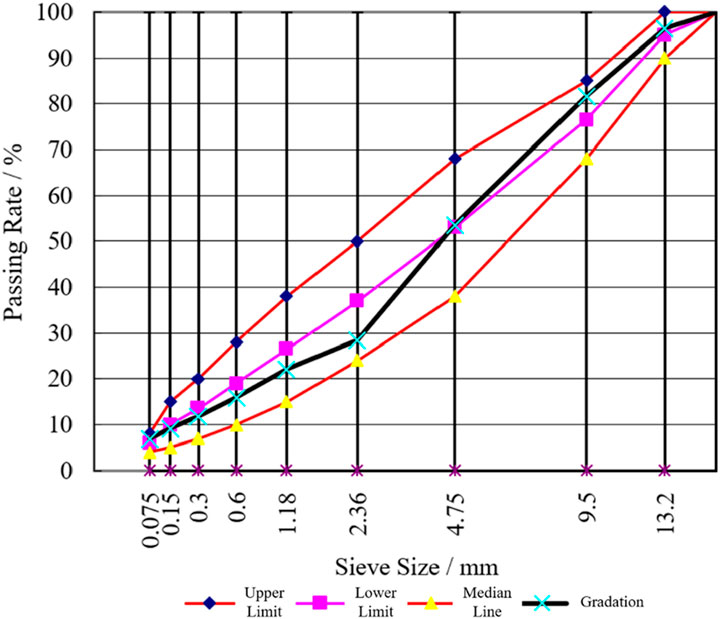
Two asphalt binders (a styrene-butadiene-styrene (SBS)-modified binder and a 70# neat binder) and two types of aggregate (limestone and diabase) were used in this study, as shown in Table 1. The gradation design follows the JTG F40-2004 specification. Two gradations were employed, with the gradation curves for the diabase AC-13C and limestone AC-20C shown in Figures 1, 2, respectively (JTG F40, 2004). The optimal asphalt-aggregate ratios for the four mixtures (A, B, C, and D) were determined to be 4.3%, 4.5%, 4.1%, and 4.4%, respectively.

Table 1

Table 1. Asphalt mixture types.

Figure 1

Figure 1. Gradation of AC-20C.

Figure 2

Figure 2. Gradation of AC-13C.

6 Complex modulus measurement

This section describes the laboratory measurement of the complex modulus of asphalt mixtures and the processing of raw data to obtain viscoelastic properties, including dynamic modulus and phase angle, which serve as the foundation for applying the self-consistent micromechanical model. In accordance with viscoelastic theory, the time–temperature superposition principle and the sigmoidal model were used to construct the master curve (Findley and Davis, 2013). The test specimens were prepared using a gyratory compactor, forming cylindrical specimens with a height of 170 mm and a diameter of 150 mm. These specimens were then cored and cut to obtain final cylindrical specimens with a height of 150 mm and a diameter of 100 mm. To ensure specimen uniformity and test repeatability, the air void content after coring and cutting was maintained at (4.0 ± 0.5)%, with at least three parallel tests conducted for each asphalt mixture.

Asphalt mixtures are viscoelastic materials, and their viscoelastic properties are typically represented by the complex modulus, as shown in Equation 40. The complex modulus consists of a real part and an imaginary part, where the real part represents the elastic component, known as the storage modulus, while the imaginary part, referred to as the loss modulus, characterizes the viscous component of the mixture.

$E^{*}\left(\omega \right)=E^{\prime }\left(\omega \right)+\mathrm{i}{E}^{″}\left(\omega \right)(40)$

where: $E^{*}\left(\omega \right)$ is complex modulus; $E^{\prime }\left(\omega \right)$ and $E^{″}\left(\omega \right)$ are storage and loss modulus, respectively; $\omega$ is angular frequency.

The dynamic modulus of the mixture is equal to the magnitude of the complex modulus, as shown in Equation 41. During the loading process, due to the viscoelastic effects of the mixture, its strain always lags behind the stress by a certain angle, known as the phase angle. The phase angle is related to the storage modulus and loss modulus as expressed in Equation 42.

$\left|E^{*}\left(\omega \right)\right|=\sqrt{{\left[E^{\prime }\left(\omega \right)\right]}^2+{\left[E^{″}\left(\omega \right)\right]}^2}(41)$

$\tan \phi =\frac{E^{″}\left(\omega \right)}{E^{\prime }\left(\omega \right)}(42)$

where: $\left|E^{*}\left(\omega \right)\right|$ is dynamic modulus of asphalt mixture; $\phi$ is phase angle.

The uniaxial compression dynamic modulus test was conducted on the specimens using a dynamic testing system (DTS). During loading, the axial deformation of the specimen was recorded by three Linear Variable Differential Transformers (LVDTs) with a gauge length of 100 mm, mounted on the surface at 120° intervals, as shown in Figure 3.

Figure 3

Figure 3. Dynamic modulus configurations.

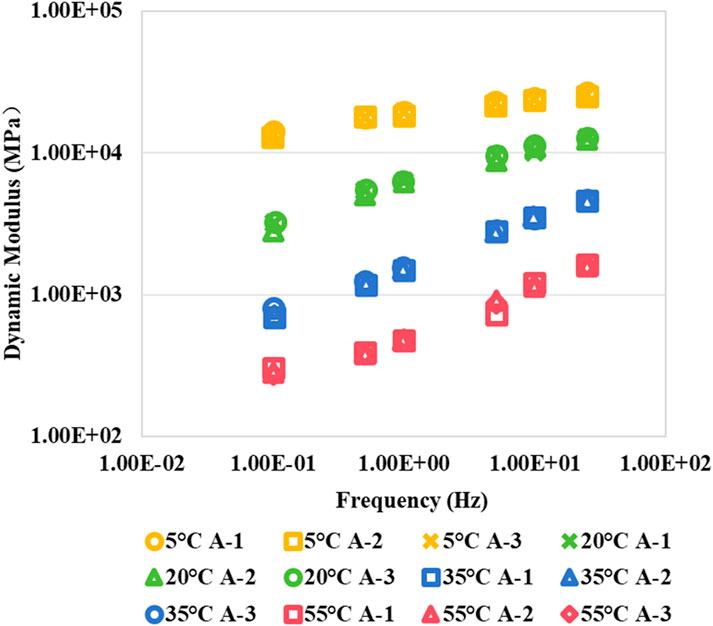
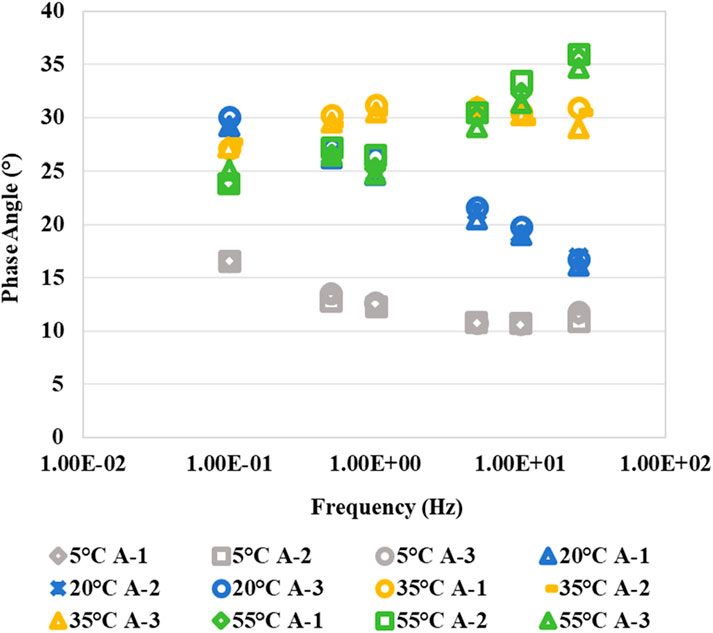
The experiment followed the AASHTO TP 79 test protocol, with loading applied at frequencies of 0.1, 0.5, 1.0, 5.0, 10, and 25 Hz at temperatures of 5, 20, 35, and 55°C. Before each test, specimens were conditioned in a temperature-controlled chamber for at least 3 h to ensure uniform internal temperature. The testing sequence proceeded from 5°C to 55°C and 25 Hz–0.1 Hz. For each asphalt mixture, three replicate specimens were tested. Taking mixture A as an example, the DTS test results are shown in Figures 4, 5. As seen in these figures, the results are highly consistent across different temperatures and frequencies, demonstrating good repeatability and representativeness. It is worth noting that other mixtures have shown similar trends but with different measured values. Therefore, only the results for mixture A are presented here for demonstration purposes.

Figure 4

Figure 4. Dynamic modulus results.

Figure 5

Figure 5. Phase angle results.

Figure 4 shows that the dynamic modulus varies with temperature and frequency. At the same frequency, the modulus is highest at 5°C and lowest at 55°C. At the same temperature, the modulus is highest at 25 Hz and lowest at 0.1 Hz. Overall, the dynamic modulus is at its minimum at 55°C and 0.1 Hz, while it reaches its maximum at 5°C and 25 Hz. As seen in Figure 5, under the conditions of 5°C and 20°C, an increase in loading frequency results in a decrease in the phase angle test results. Under the conditions of 35°C and 55°C, an increase in loading frequency leads to an increase in the phase angle test results. At the same loading frequency, the phase angle reaches its minimum value at 5°C and its maximum value at 55°C.

To process the measured dynamic modulus and phase angle shown in Figures 4, 5, a master curve was constructed by horizontally shifting the data in the log-log space (ARA and ERES Consultants Division, 2004). This is because the viscoelastic properties of asphalt mixtures follow the time-temperature equivalence principle. This principle states that for thermorheological simple materials, their mechanical properties exhibit the same trend of change in both the time domain and frequency domain. Taking the dynamic modulus as an example, the expression of its time-temperature equivalence principle is shown in Equations 43, 44.

$\left|E^{*}\left(t,f\right)\right|=\left|E^{*}\left(t_{\text{ref}},f_{\mathrm{r}}\right)\right|(43)$

$f_{\mathrm{r}}=a_{t}f(44)$

where: t is temperature; t_ref is reference temperature; f is frequency; $f_{\mathrm{r}}$ is reduced frequency; $\left|E^{*}\left(t,f\right)\right|$ is measured dynamic modulus; $\left|E^{*}\left(t_{\text{ref}},f_{\mathrm{r}}\right)\right|$ is dynamic modulus at the reference temperature and reduced frequency; $a_t$ is shift factor, as shown in Equation 45.

$\lg {\alpha }_t=\frac{-C_1\left(t-t_{\text{ref}}\right)}{C_2+\left(t-t_{\text{ref}}\right)}(45)$

where: C₁ and C₂ are the fitting constants.

For constructing the dynamic modulus master curve, the generalized Sigmoid model provides a good fit, with its expression given in Equation 46. The corresponding phase angle master curve model is derived using Equation 47, and the final phase angle master curve model is presented in Equation 48. Note that Equations 43–48 are derived from viscoelastic theory and used to construct a single smooth curve by combining data collected at different temperatures and frequencies. This process eliminates temperature and frequency dependency, enabling the application of self-consistent micromechanics (Findley and Davis, 2013). In other words, once the time–temperature superposition and master curve are established, the previously presented self-consistent model is used to fit and represent the data.

$\lg \left|E^{*}\left(f_r\right)\right|=\alpha +\frac{\beta }{{\left(1+\lambda ·{\mathrm{e}}^{\gamma +\delta \lg f_r}\right)}^{\frac{1}{\lambda }}}(46)$

$\phi \left(f_r\right)\approx \frac{\mathrm{\pi }}{2}\frac{d\ln \left|E^{*}\left(f_r\right)\right|}{d\ln \left(f_r\right)}(47)$

$\lg \phi =-\left(\frac{1}{\lambda }+1\right)\lg \left(1+\lambda {\mathrm{e}}^{\gamma +\delta \lg f_r}\right)+\left(\gamma +\delta \lg f_r\right)\lg \mathrm{e}+\lg \left(-\frac{\mathrm{\pi }}{2}\beta \delta \right)(48)$

where: $\left|E^{*}\left(f_r\right)\right|$ is dynamic modulus at reduced frequency; $\phi \left(f_r\right)$ is phase angle at reduced frequency; α is lower asymptote of the master curve in the logarithmic scale; β is the difference between the upper and lower asymptotes of the master curve in the logarithmic scale; γ is the shape parameter of the master curve, controlling the horizontal position of the inflection point; δ is the shape parameter of the master curve, controlling the steepness; λ is the shape parameter of the master curve, controlling symmetry.

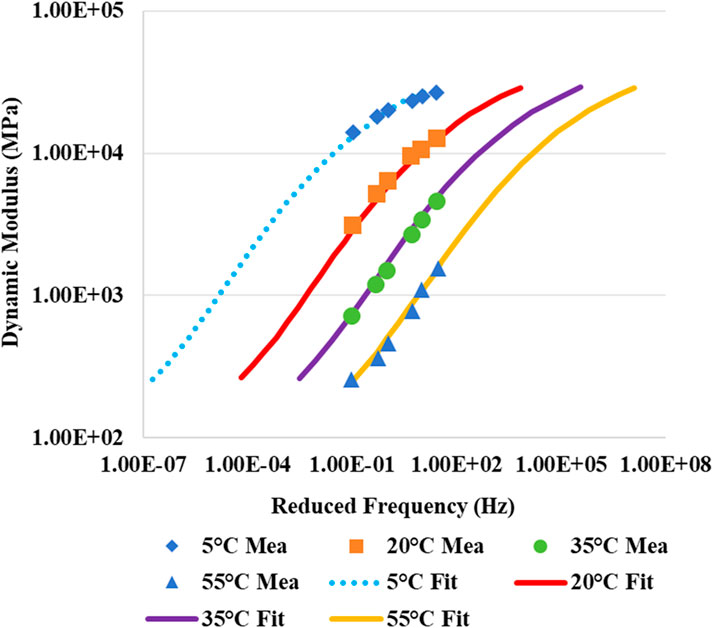
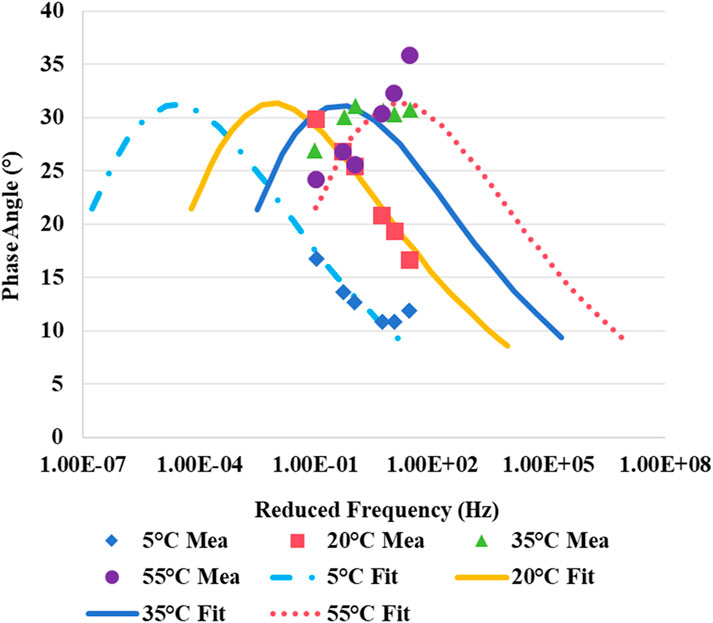
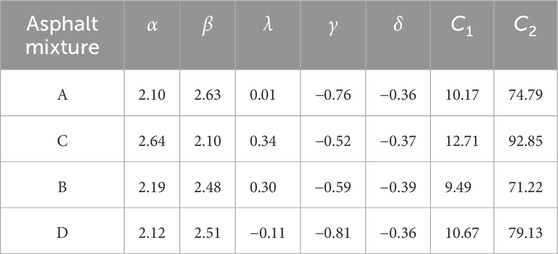
During the solving process, the objective function was set as shown in Equation 49, aiming to minimize the errors of both dynamic modulus and phase angle to achieve the optimal fitting parameters. Again, taking mixture A as one example, the dynamic modulus master curves obtained from the model are shown in Figure 6, while the phase angle master curves are presented in Figure 7. The fitting parameters for the master curves of the different mixtures are listed in Table 2.

$\begin{array}{l}Error=Erro{r}_{\left|E^{*}\right|}+Erro{r}_{\phi }=\\ \frac{1}{N}\sqrt{{\displaystyle \sum _{i=1}^N}{\left(\frac{{\left|E^{*}\right|}_{mea,i}-{\left|E^{*}\right|}_{pre,i}}{{\left|E^{*}\right|}_{mea,i}}\right)}^2}+\frac{1}{N}\sqrt{{\displaystyle \sum _{i=1}^N}{\left(\frac{{\phi }_{mea,i}-{\phi }_{pre,i}}{{\phi }_{mea,i}}\right)}^2}\end{array}(49)$

Figure 6

Figure 6. Dynamic modulus master curves for mixture A.

Figure 7

Figure 7. Phase angle master curves for mixture A.

Table 2

Table 2. Fitting coefficients for the generalized Sigmoid model.

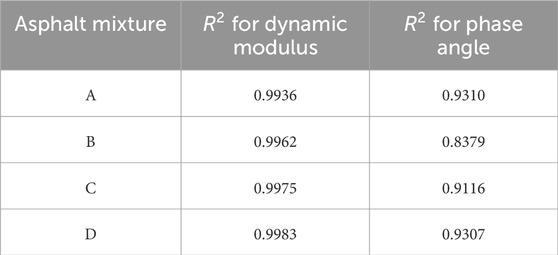
For a given asphalt mixture, the shapes of the master curves plotted at different temperatures are very similar. To evaluate the goodness of fit between the predicted data from the master curves and the indoor measured data, the coefficients of determination were calculated for the four selected mixtures, as shown in Table 3.

Table 3

Table 3. Coefficients of determination for the master curves.

The coefficients of determination for dynamic modulus of all mixtures are above 0.99, indicating that the values predicted by the master curves are very close to the measured values. For the phase angle master curves, except for mixture B, which has a coefficient of determination of 0.8379, the other three asphalt mixtures have coefficients of determination above 0.90, also demonstrating good fitting accuracy. However, compared to the dynamic modulus master curves, the fitting accuracy of the phase angle master curves is slightly lower. From the measured phase angle data, it can be observed that at a single temperature, the measured phase angle data does not exhibit a clear monotonic increasing or decreasing trend and includes abrupt changes, which is the main reason for the lower fitting accuracy.

7 Complex Poisson’s ratio measurement

Since this study developed the micromechanical model in complex form, the complex Poisson’s ratio was also considered, as it is an important property that reflects the anisotropy of the asphalt mixture (Ling et al., 2020). This section presents the measurement of the complex Poisson’s ratio and the development of its master curve. The key to testing the complex Poisson’s ratio of asphalt mixtures lies in accurately measuring the axial and transverse strains of the asphalt mixture during the loading process. Since measuring the transverse strain of cylindrical specimens is challenging, cubic specimens were chosen for the test. The specimens have dimensions of 100 mm in length, width, and height. Displacement sensors were installed on the front and side faces of the cube according to the configuration shown in Figure 8.

Figure 8

Figure 8. LVDT configuration.

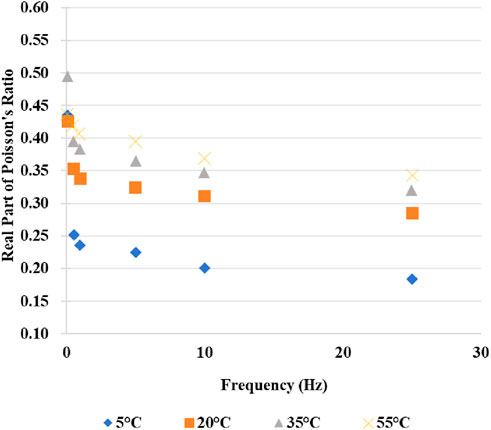
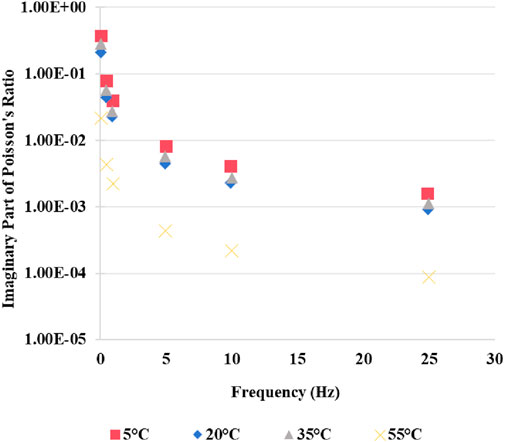
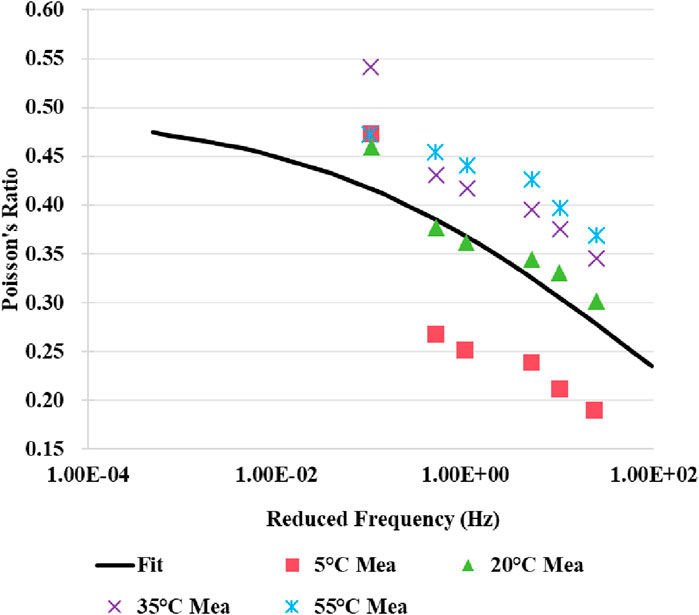
To ensure that the axial and transverse LVDTs do not interfere with each other, the fixture was designed as a rectangular block with uneven heights. This design spatially separates the LVDTs, preventing any interference, with a spacing of 70 mm between the fixtures. Cylindrical specimens were formed using a rotary compactor and then cut into cubic specimens using a cutting saw, with their void content controlled within the range of (4.0 ± 0.5)%. The specimens were installed in the Material Test System (MTS) loading frame, as shown in Figure 9, and tested at temperatures of 5°C, 20°C, 35°C, and 55°C. Pressure was applied to the specimens using the MTS testing system, with a loading duration of 100 s at each temperature. After measurement, the real and imaginary parts of the Poisson’s ratio at various temperature-frequency conditions can be determined using Equations 38, 39 shown earlier in this study. Similar to the construction of the dynamic modulus master curve, Poisson’s ratio values measured under various temperature–frequency conditions were horizontally shifted to develop the Poisson’s ratio master curve at 20°C. Using mixture A as an example, the measured results are shown in Figures 10–12.

Figure 9

Figure 9. Complex Poisson’s ratio test.

Figure 10

Figure 10. Real part of Poisson’s ratio of mixture A.

Figure 11

Figure 11. Imaginary part of Poisson’s ratio of mixture A.

Figure 12

Figure 12. Poisson’s ratio master curve of mixture A.

As shown in Figure 12, it can be observed that both the real and imaginary parts of the measured Poisson’s ratio of the mixture decrease as the loading frequency increases. With an increase in test temperature, the real part of the Poisson’s ratio gradually increases, while the imaginary part gradually decreases. Additionally, from the Poisson’s ratio master curve, it is evident that as the loading frequency increases, the Poisson’s ratio of the mixture gradually decreases, whereas it gradually increases with rising temperature.

8 Model prediction

While the previous sections present the procedures and results for determining the complex modulus and Poisson’s ratio, this section demonstrates how the derived complex self-consistent model is used to predict corresponding results for self-validation. The model validation consists of two parts: inverse modeling and forward modeling. In the inverse model, the modulus parameters of the aggregate are determined based on the volume fractions of the constituent materials in the mixture and the material parameters of the mixture, asphalt, and air. Specifically, One of the four equations (Equations 20–23) was chosen as the objective function, with the goal of driving its result to zero, while the remaining three equations were treated as constraints, also set to zero. The variables included the real and imaginary parts of the aggregate’s bulk modulus and shear modulus. Iterations were performed to determine the numerical solution that best satisfies the equations.

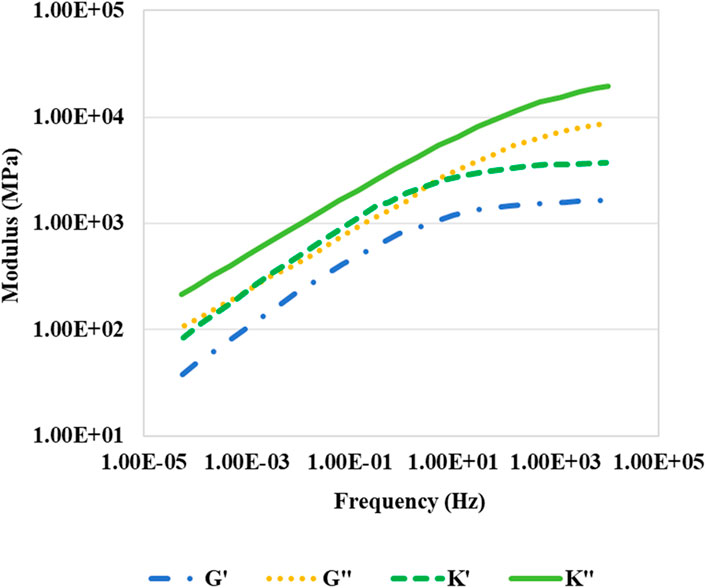
In the forward model, the material parameters of the asphalt mixture were solved using the aggregate parameters obtained from the inverse model, along with the material parameters of the asphalt and air, and the volume fractions of the constituent materials. Specifically, after determining the real and imaginary parts of the aggregate’s bulk modulus and shear modulus using the above method, these values are treated as known conditions. Taking mixture A as an example, the predicted bulk modulus and shear modulus obtained through the model are shown in Figure 13.

Figure 13

Figure 13. Predicted shear and bulk modulus of mixture A.

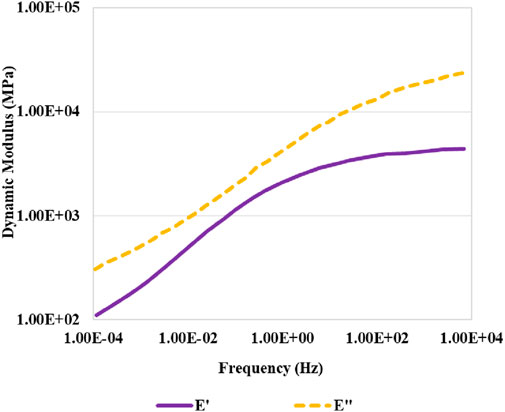
Subsequently, using Equations 50, 51, the results from the forward model can be converted into storage modulus and loss modulus. Similarly, to demonstrate the process, mixture A is taken as an example, with the calculated storage modulus and loss modulus shown in Figure 14.

$E^{\prime }=\frac{3K^{\prime }\left[{\left(1-2{\mu }^{\prime }\right)}^2+4{\mu }^{″}\right]+4G^{\prime }\left[{\left(1-{\mu }^{\prime }\right)}^2+{{\mu }^{″}}^2\right]}{3}(50)$

$E^{″}=\frac{3K^{″}\left[{\left(1-2{\mu }^{\prime }\right)}^2+4{\mu }^{″}\right]+4G^{″}\left[{\left(1-{\mu }^{\prime }\right)}^2+{{\mu }^{″}}^2\right]}{3}(51)$

Figure 14

Figure 14. Predicted compressive storage modulus and loss modulus of mixture A.

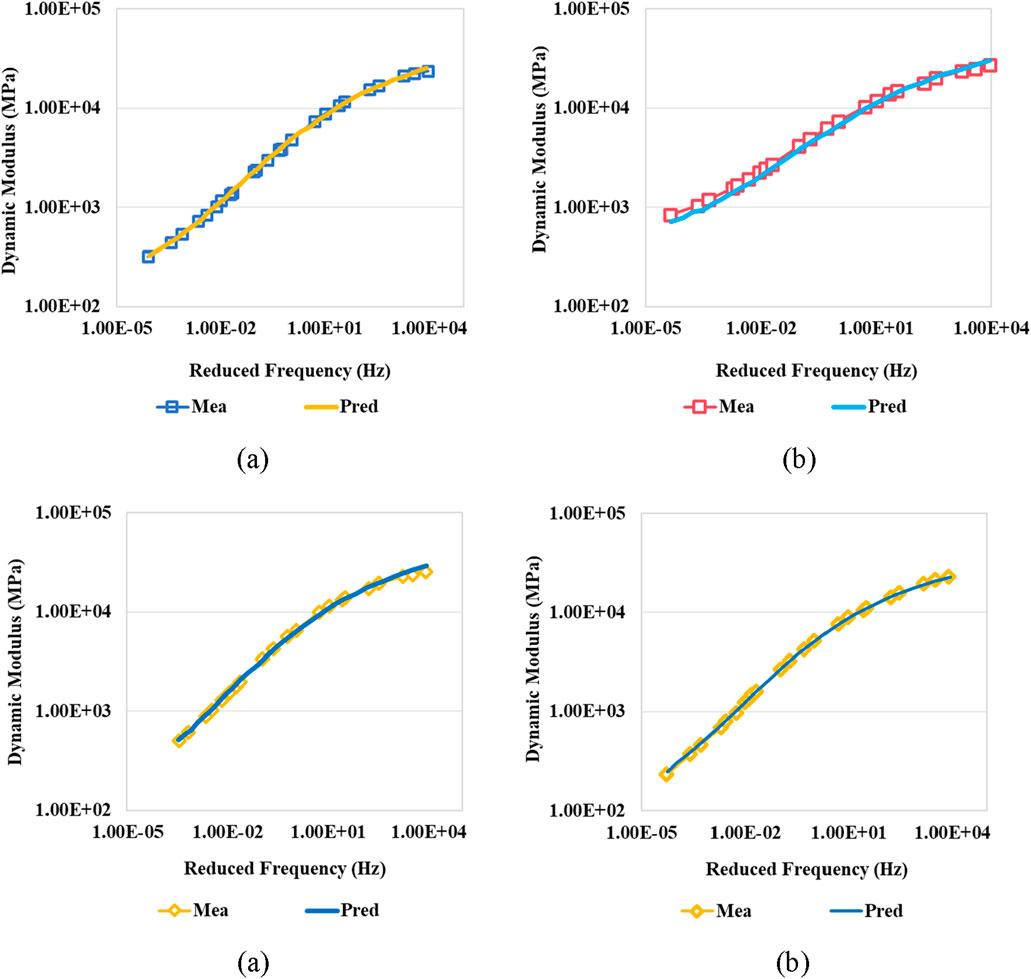
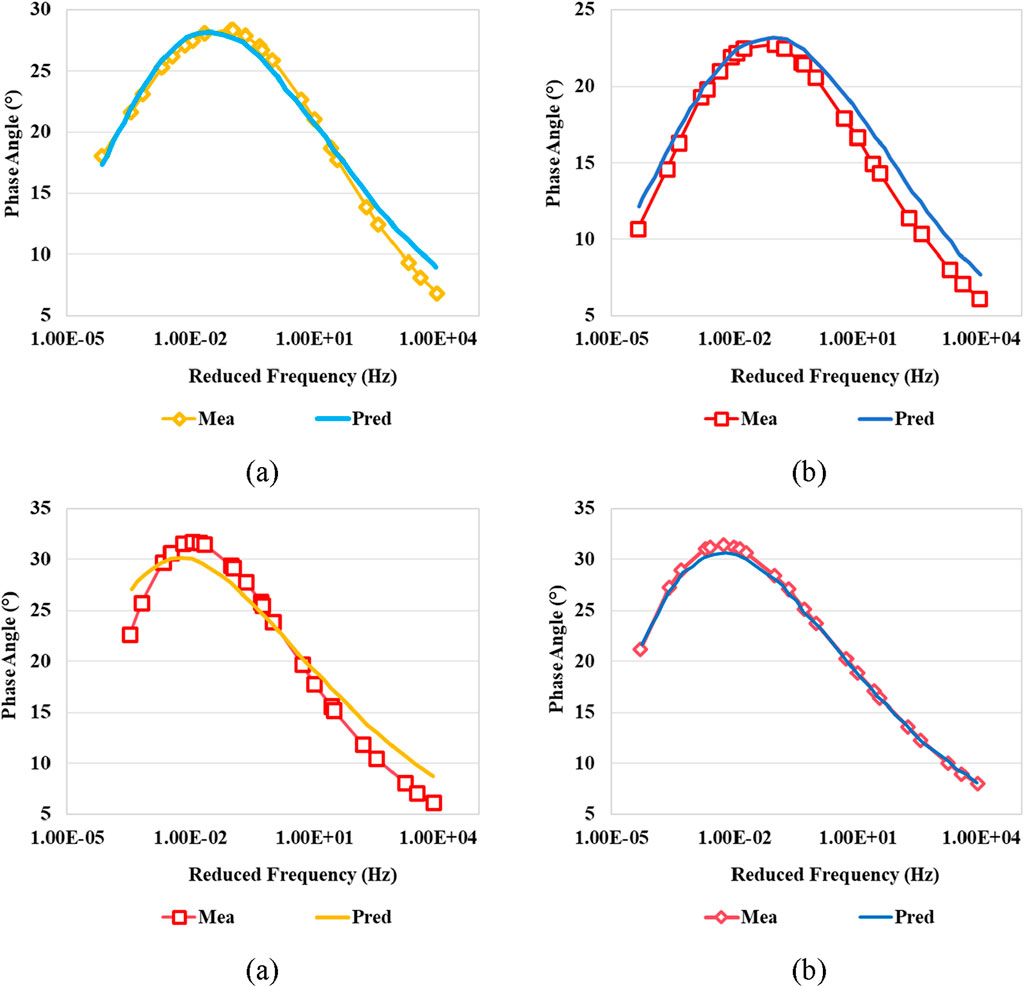
To further validate the proposed model, additional specimens of the four selected mixtures were fabricated with different volumetric compositions than those used to derive the model coefficients. The dynamic modulus master curves from both the model predictions and laboratory measurements are shown in Figure 15. Using the predicted storage modulus and loss modulus values from the model, the phase angle results of the asphalt mixtures were also calculated and plotted. These curves were then compared with the phase angle master curves obtained from laboratory measurements, as illustrated in Figure 16.

Figure 15

Figure 15. Predicted dynamic modulus versus measured dynamic modulus.

Figure 16

Figure 16. Predicted phase angle versus measured phase angle.

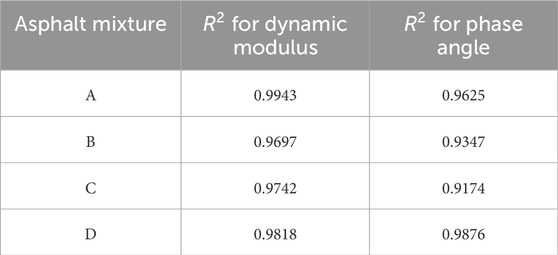
To demonstrate the accuracy of the predictions, the coefficients of determination are shown in Table 4. It can be observed that for the four types of mixtures selected, the predicted dynamic modulus values closely match the laboratory measured data across all temperature-frequency conditions, with coefficients of determination all above 0.95. The coefficients of determination for the phase angle are also above 0.90, indicating good fitting accuracy. However, Figures 15, 16 clearly show that the mismatch between the model prediction and laboratory measurement varies depending on the mixture. For instance, the dynamic modulus predictions for the other three mixtures closely match the measurements, whereas mixture B shows a certain degree of mismatch. On the other hand, for the phase angle, mixture D demonstrates the best fit, while for the other three mixtures, discrepancies tend to occur at higher or lower frequencies. This indicates that the mixture type certainly affects the accuracy of the model predictions.

Table 4

Table 4. Coefficients of determination for the predicted master curves.

From the perspective of model derivation, the discrepancy between the prediction and measurement may arise because the proposed model assumes that both asphalt and aggregate have the same influence on the mixture, regardless of whether the temperature is high or low. In reality, at low temperatures or high frequencies, the viscoelastic properties of the mixture are more significantly influenced by the properties of the asphalt. As the temperature increases or the frequency decreases, the flow ability of the asphalt gradually increases, and the properties of the mixture become more influenced by the properties of the aggregate. Despite this, the complex self-consistent model has demonstrated satisfactory and acceptable accuracy.

9 Conclusions

Within the complex domain, the self-consistent micromechanics model was extended, leading to the derivation of the model presented in this study. By designing laboratory experiments to measure the complex Poisson’s ratio of mixtures and applying it to the proposed model, the dynamic modulus and phase angle of four types of asphalt were predicted, and their accuracy was validated using laboratory-measured values. The research findings are as follows:

(1) The self-consistent model is extended to the complex domain, and a complex micromechanics model is established. By predicting the storage modulus and loss modulus of the mixture, the dynamic modulus and phase angle of the mixture can be simultaneously predicted.

(2) Compared to the dynamic modulus master curves, the fitting accuracy of the phase angle master curves is slightly lower. This is because, at a single temperature, the measured phase angle data does not exhibit a clear monotonic increasing or decreasing trend and includes abrupt changes.

(3) The Poisson’s ratio of the mixtures measured in the laboratory exhibits different patterns under varying temperatures and frequencies. As the temperature increases from 5°C to 55°C, the real part of the Poisson’s ratio gradually increases, while the imaginary part gradually decreases; however, the overall Poisson’s ratio value increases. As the frequency increases, both the real and imaginary parts of the Poisson’s ratio decrease, and the Poisson’s ratio of the mixture also decreases.

(4) The dynamic modulus and phase angle master curves predicted by the developed model are smooth curves that vary with frequency. The predicted curves closely align with the measured curves, with coefficients of determination all above 0.9, demonstrating that the model’s predictions meet the practical requirements of engineering applications. However, at low or high frequencies, some deviations in the predictions of both parameters are observed, which warrants further attention.

Overall, the prediction accuracy of the phase angle achieved by the proposed model helps improve the self-consistent micromechanics approach in obtaining the complete complex modulus properties. However, further validation is needed by using more asphalt mixtures for the proposed model. Additionally, it is believed that further consideration of the aggregate gradation would further improve the model’s prediction accuracy.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BL: Writing – original draft, Conceptualization, Writing – review and editing, Investigation, Validation, Data curation. JY: Writing – review and editing, Investigation, Methodology, Conceptualization. KZ: Investigation, Writing – review and editing, Supervision. XF: Resources, Writing – review and editing, Methodology.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors acknowledge the funding support from the Key Research and Development Program of the Jiangxi Provincial Department of Science and Technology (S20254552), the Ganpo Juncai Support Plan–Double High Leading Talents Project of Jiangxi Province, Science and Technology Project of the Jiangxi Provincial Department of Transportation (2023Z0001), and General Science and Technology Project of Jiangxi Provincial Transportation Investment Group (2024JT0017).

Conflict of interest

Authors BL, KZ, and XF were employed by Jiangxi Provincial Transportation Investment Maintenance Technology Group Co., Ltd.

Author JY was employed by Powerchina Jiangxi Electric Power Engineering Co., Ltd.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

AASHTO (2022). T 378-22: standard Method of Test for Determining the dynamic Modulus and flow Number for asphalt mixtures Using the asphalt mixture performance tester (AMPT). American Association of State Highway and Transportation Officials.

Google Scholar

AASHTO (2020). Mechanistic–empirical pavement design guide: a manual of practice. American Association of State Highway and Transportation Officials.

Google Scholar

Abbas, A., Masad, E., Papagiannakis, T., and Harman, T. (2007). Micromechanical modeling of the viscoelastic behavior of asphalt mixtures using the discrete-element method. Int. J. Geomechanics 7 (2), 131–139. doi:10.1061/(asce)1532-3641(2007)7:2(131)

CrossRef Full Text | Google Scholar

Alam, S. Y., and Hammoum, F. (2015). Viscoelastic properties of asphalt concrete using micromechanical self-consistent model. Archives Civ. Mech. Eng. 15 (1), 272–285. doi:10.1016/j.acme.2014.02.005

CrossRef Full Text | Google Scholar

ARA, I.ERES Consultants Division (2004). Guide for mechanistic-empirical design of new and rehabilitated pavement structures. Natl. Coop. Highw. Res. Program.

Google Scholar

Böhm, H. J. (1998). A short introduction to basic aspects of continuum micromechanics. CDLFMD Rep. Tech. Rep.

Google Scholar

Chakroborty, P., Das, A., and Ghosh, P. (2010). Determining reliability of an asphalt mix design: case of marshall method. J. Transp. Eng. 136 (1), 31–37. doi:10.1061/(asce)0733-947x(2010)136:1(31)

CrossRef Full Text | Google Scholar

Christensen, J. , D. W., Pellinen, T., and Bonaquist, R. F. (2003). Hirsch model for estimating the modulus of asphalt concrete. J. Assoc. Asphalt Paving Technol. 72.

Google Scholar

D’Angelo, J. A. (2001). Superpave mix design tests methods and requirements, 104. US Federal Highway Administration.

Google Scholar

Eshelby, J. D. (1957). The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 241 (1226), 376–396.

Google Scholar

Eshelby, J. D. (1959). The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 252 (1271), 561–569.

Google Scholar

Findley, W. N., and Davis, F. A. (2013). Creep and relaxation of nonlinear viscoelastic materials. Cour. Corp.

Google Scholar

Hashin, Z. (1960). The elastic moduli of heterogeneous materials. US Department of Commerce, 143–150. Office of Technical Services.

CrossRef Full Text | Google Scholar

Hashin, Z., and Shtrikman, S. (1963). A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 11 (2), 127–140. doi:10.1016/0022-5096(63)90060-7

CrossRef Full Text | Google Scholar

Hashin, Z. A., and Shtrikman, S. (1962). On some variational principles in anisotropic and nonhomogeneous elasticity. J. Mech. Phys. Solids 10 (4), 335–342. doi:10.1016/0022-5096(62)90004-2

CrossRef Full Text | Google Scholar

Hill, R. (1965). Theory of mechanical properties of fibre-strengthened materials—III. Self-consistent model. J. Mech. Phys. Solids 13 (4), 189–198. doi:10.1016/0022-5096(65)90008-6

CrossRef Full Text | Google Scholar

Huang, Y., Hu, K. X., Wei, X., and Chandra, A. (1994). A generalized self-consistent mechanics method for composite materials with multiphase inclusions. J. Mech. Phys. Solids 42 (3), 491–504. doi:10.1016/0022-5096(94)90028-0

CrossRef Full Text | Google Scholar

JTG F40 (2004). “Technical specifications for construction of highway asphalt pavements,”. Beijing, China.Ministry Transp. China

Google Scholar

Kachanov, M., and Sevostianov, I. (2018). Micromechanics of materials, with applications, 249. Cham: Springer.

CrossRef Full Text | Google Scholar

Kandhal, P. S., and Koehler, W. S. (1985). “Marshall mix design method: current practices,” in Association of asphalt paving technologists proc, 54.

Google Scholar

Karki, P., Kim, Y. R., and Little, D. N. (2015). Dynamic modulus prediction of asphalt concrete mixtures through computational micromechanics. Transp. Res. Rec. 2507 (1), 1–9. doi:10.3141/2507-01

CrossRef Full Text | Google Scholar

Ling, M., Deng, Y., Zhang, Y., Luo, X., and Lytton, R. L. (2020). Evaluation of complex Poisson’s ratio of aged asphalt field cores using direct tension test and finite element simulation. Constr. Build. Mater. 261, 120329. doi:10.1016/j.conbuildmat.2020.120329

CrossRef Full Text | Google Scholar

Luo, R., and Lytton, R. L. (2011). Self-consistent micromechanics models of an asphalt mixture. J. Mater. Civ. Eng. 23 (1), 49–55. doi:10.1061/(asce)mt.1943-5533.0000007

CrossRef Full Text | Google Scholar

Lytton, R. L., Tsai, F. L., Lee, S. I., Luo, R., Hu, S., and Zhou, F. (2010). Models for predicting reflection cracking of hot-mix asphalt overlays (No. Project 01-41).

Google Scholar

Lytton, R. L., Uzan, J., Fernando, E. G., Roque, R., Hiltunen, D., and Stoffels, S. M. (1993). Development and validation of performance prediction models and specifications for asphalt binders and paving mixes, 357. Washington, DC: Strategic Highway Research Program.

Google Scholar

Molladavoodi, H., and RahimiRezaei, Y. (2018). Heterogeneous rock simulation using DIP-micromechanics-statistical methods. Adv. Civ. Eng. 2018 (1), 7010817. doi:10.1155/2018/7010817

CrossRef Full Text | Google Scholar

Nguyen, Q. T., Tran, B. V., Nguyen, M. L., Hoang, T. T. N., Chailleux, E., and Bui, V. P. (2024). Relationships between 3D linear viscoelastic properties of bitumen, asphalt mastics and asphalt mixtures using micromechanical models. Constr. Build. Mater. 416, 135299. doi:10.1016/j.conbuildmat.2024.135299

CrossRef Full Text | Google Scholar

Shu, X., and Huang, B. (2008). Micromechanics-based dynamic modulus prediction of polymeric asphalt concrete mixtures. Compos. Part B Eng. 39 (4), 704–713. doi:10.1016/j.compositesb.2007.05.003

CrossRef Full Text | Google Scholar

Tan, H., Huang, Y., Liu, C., and Geubelle, P. (2005). The Mori–Tanaka method for composite materials with nonlinear interface debonding. Int. J. Plasticity 21 (10), 1890–1918. doi:10.1016/j.ijplas.2004.10.001

CrossRef Full Text | Google Scholar

Underwood, B. S., and Kim, Y. R. (2013). Microstructural association model for upscaling prediction of asphalt concrete dynamic modulus. J. Mater. Civ. Eng. 25 (9), 1153–1161. doi:10.1061/(asce)mt.1943-5533.0000657

CrossRef Full Text | Google Scholar

Yin, H. M., Buttlar, W. G., Paulino, G. H., and Benedetto, H. D. (2008). Assessment of existing micro-mechanical models for asphalt mastics considering viscoelastic effects. Road Mater. Pavement Des. 9 (1), 31–57. doi:10.1080/14680629.2008.9690106

CrossRef Full Text | Google Scholar

You, Z., and Buttlar, W. G. (2006). Micromechanical modeling approach to predict compressive dynamic moduli of asphalt mixtures using the distinct element method. Transp. Res. Rec. 1970 (1), 72–83. doi:10.1177/0361198106197000107

CrossRef Full Text | Google Scholar

Zeng, Z., Kim, Y. R., Underwood, B. S., and Guddati, M. (2023a). Asphalt mixture fatigue damage and failure predictions using the simplified viscoelastic continuum damage (S-VECD) model. Int. J. Fatigue 174, 107736. doi:10.1016/j.ijfatigue.2023.107736

CrossRef Full Text | Google Scholar

Zeng, Z., Liu, B., and Zhang, D. (2023b). Critical evaluation of unit response function interconversions for asphalt concrete linear viscoelastic modeling using discrete spectrum. Constr. Build. Mater. 382, 131301. doi:10.1016/j.conbuildmat.2023.131301

CrossRef Full Text | Google Scholar

Zeng, Z., Underwood, B. S., and Kim, Y. R. (2024). A state-of-the-art review of asphalt mixture fracture models to address pavement reflective cracking. Constr. Build. Mater. 443, 137674. doi:10.1016/j.conbuildmat.2024.137674

CrossRef Full Text | Google Scholar

Zeng, Z. A., Lee, K. C., and Kim, Y. R. (2021). Determination of dynamic modulus master curve of damaged asphalt pavements for mechanistic–empirical pavement rehabilitation design. Transp. Res. Rec. 2675 (8), 161–174. doi:10.1177/0361198121996708

CrossRef Full Text | Google Scholar

Zeng, Z. A., Underwood, B. S., and Castorena, C. (2022). Low-temperature performance grade characterisation of asphalt binder using the dynamic shear rheometer. Int. J. Pavement Eng. 23 (3), 811–823. doi:10.1080/10298436.2020.1774766

CrossRef Full Text | Google Scholar

Zhang, D., Birgisson, B., and Luo, X. (2020). A new dynamic modulus predictive model for asphalt mixtures based on the law of mixtures. Constr. Build. Mater. 255, 119348. doi:10.1016/j.conbuildmat.2020.119348

CrossRef Full Text | Google Scholar

Zhang, Y., Luo, R., and Lytton, R. L. (2011). Microstructure-based inherent anisotropy of asphalt mixtures. J. Mater. Civ. Eng. 23 (10), 1473–1482. doi:10.1061/(asce)mt.1943-5533.0000325

CrossRef Full Text | Google Scholar