Unconventional compute methods and future challenges for superconducting digital computing

Superconducting digital computing (SDC) based on Josephson junctions (JJs) offers significant potential for enhancing compute throughput and reducing energy consumption compared to conventional room-temperature CMOS-based approaches. Current superconducting logic families exhibit diverse characteristics in clocking strategies, power management, and information encoding techniques. This paper reviews recent advancements in unconventional computing methods specifically designed for superconducting digital circuits, emphasizing temporal computing and pulse-train representations. Notable techniques include race logic (RL), temporal pulse train computing (U-SFQ), and temporal multipliers, each offering unique performance and area advantages suited to superconducting implementations. Additionally, this paper reviews innovations in superconducting coarse-grain reconfigurable architectures (CGRA), superconducting-specific on-chip communication architectures, cryogenic sensor interfaces, and quantum computing control electronics. Finally, we highlight research challenges that should be addressed to facilitate the widespread adoption of superconducting digital computing.

1 Introduction

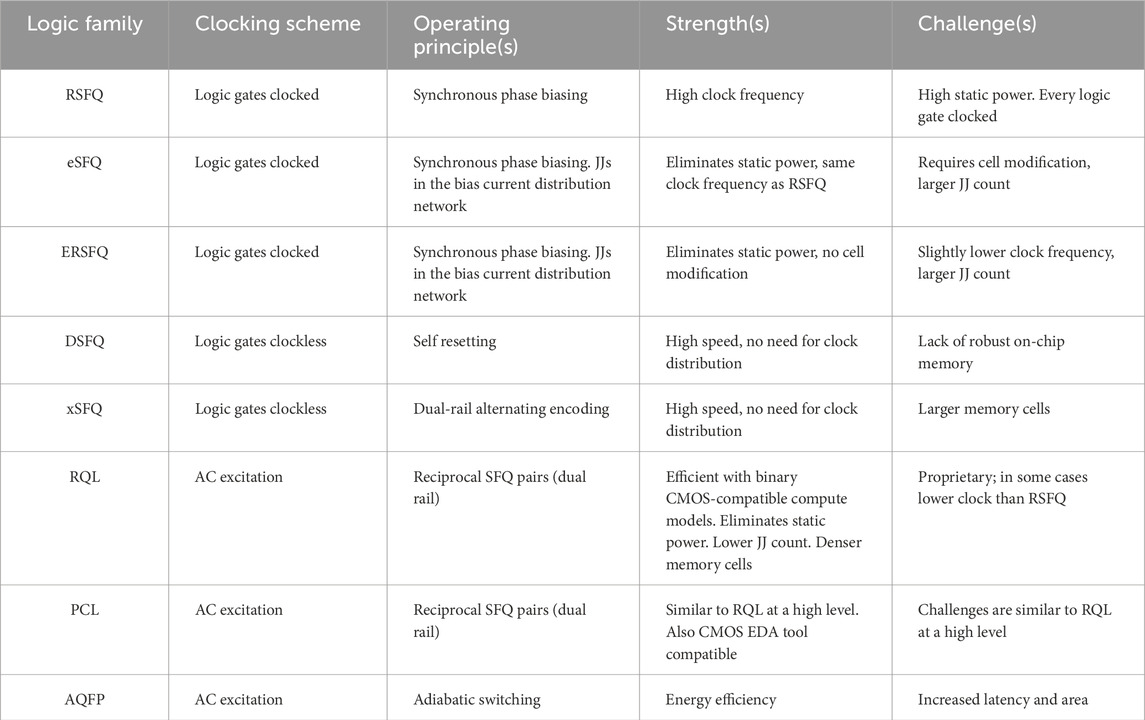
Josephson junction (JJ)-based superconducting digital computing (SDC) promises higher compute throughput combined with lower energy per bit for on-chip data movement compared to modern room-temperature CMOS (Tannu et al., 2019; Holmes, 2023). Currently, there are numerous digital superconducting logic families that differ in how they abstract information, their method or lack of clocking, their cell implementations, power delivery networks, memory cells, and other key characteristics. Notably, reciprocal quantum logic (RQL) (Herr et al., 2011) and pulse conserving logic (PCL) (Herr et al., 2023) use AC power for synchronization (clocking), xSFQ (Tzimpragos et al., 2021; Volk et al., 2024) and dynamic SFQ (DSFQ) (Rylov, 2019) use clockless and self-resetting gates, adiabatic quantum-flux-parametron (AQFP) focuses on energy-efficiency (Marakkalage et al., 2021), whereas rapid single flux quantum (RSFQ) (Likharev and Semenov, 1991) and its variants (such as ERSFQ (Krylov and Friedman, 2020; Mukhanov, 2011) and eSFQ (Volkmann et al., 2013) that reduce static power by using JJs to bias current delivery networks, typically use synchronous logic gates. RSFQ is currently the dominant logic family and has been adopted in numerous applications, including recently quantum computer control (Barbosa et al., 2024).

Because SFQ pulses last only a few picoseconds and guaranteeing that pulses arrive simultaneously at logic gates is impractical, typically RSFQ logic gates are all clocked such that they observe input pulses between clock pulses and generate an output pulse when a clock pulse arrives (Bakolo and Fourie, 2011); However, having so many clocked cells increases the size and overhead of the clock distribution network. Therefore, related work relies on compute formulations other than traditional binary as a way to increase performance per unit power or area, as well as to remove the clocking requirement from the vast majority of cells. In this paper, we provide an overview of such works. In doing so, we make the argument that CMOS-inspired compute formulations are a poor fit for the intrinsic realities of RSFQ. Therefore, the community should further invest in unconventional compute methods and drastically re-design circuit architectures, memories, and related components accordingly. We conclude this paper by outlining some immediate and important challenges towards widespread adoption of SDC.

1.1 Motivation: architectural challenges of transliterating conventional CMOS processors to SDC

Early on in the SuperTools project IARPA (2017), our team was asked to create a RISC-V microprocessor core implemented in superconducting logic to test out the SDC electronic design automation (EDA) tools that were created by the performers. As we dove into the details of what such an implementation would entail, we came to the realization that to operate at the clock rates desired would require extremely deep pipelining, which creates a lot of additional logic. Worse yet, SFQ-derived logic families that were targeted by the EDA tools of the SuperTools project used clocked gates as described above. In contrast, data in current CMOS-based designs for the RISC-V microprocessor flows from the input latches through clockless combinational logic to the next pipeline stage. In CMOS, this traversal of information takes a single clock cycle, but for SFQ-derived logic there must be multiple clocks to move data through combinational logic because each gate is self-latching. However transliterating a typical CMOS processor pipeline to self-latching logic would result in pipeline depths of a hundred or more stages. Architects have long struggled to maintain high pipeline utilization as pipelines get deeper. Some of the deepest designs ever built had depths nearing 40 stages, but the most aggressive current designs are usually only in the high twenties. The SDC EDA tools in SuperTools added automation to automatically infer latches and create hierarchical clocks to propagate data. This solved the problem of logic synthesis using self-latching gates, but this also hugely reduced the effective efficiency of the logic.

In an effort to recover efficiency, we studied the use of spatio-temporal skewing. One alternative approach to hiding deep pipeline latencies is many-threading, which has many examples that range from the CDC6600 “barrel processing” to the TeraMTA many-threaded processor to the modern GPU architectures (where a many-threaded execution is referred to as a WARP). Since the amount of instruction-level parallelism (ILP) available from a single thread is often limited, a classic solution is to use many threads simultaneously. Many-threaded processors have been successfully built, but to achieve reasonable throughput, the application must be parallelized and balanced across many threads. In general, the multi-threaded microarchitectural approach improved the utilization and throughput of the superconducting RISC-V core, but did not enable acceleration of serial kernels.

Soon we realized that an instruction processor was likely not an appropriate architecture for SDC. This forced a consideration of alternative formulations of SFQ-based SDC logic that go beyond RSFQ derivatives. We describe such formulations in this paper, including U-SFQ and race logic (RL), different applications such as ultra-fast integrated control processors for quantum computing systems, and fundamentally different architectures that are more suitable for high-speed massively pipelined operation such as dataflow and coarse-grain reconfigurable arrays (CGRAs).

2 Unconventional compute methods and building blocks

With the aforementioned motivation, we focus on past work that represents information in the time domain or through SFQ pulse trains starting from their fundamental operating principles and then describing larger compute and network blocks that build on these principles. Before diving in the details, we provide an overview of SDC logic families we discuss in this section along with some of their characteristic traits in Table 1.

Table 1

Table 1. Main attributes of SDC logic families we discuss in this paper.

2.1 Temporal computing with race logic

A pioneering effort to encode information temporally in RSFQ adapted race logic (RL) Tzimpragos et al. (2020) to RSFQ. With RL, time is divided into epochs, which are further divided internally into time slots, and each time slot is assigned a numerical value. The time of arrival of a pulse, not merely its presence, encodes the numerical value the pulse represents. For instance, if a pulse arrives in time slot $X$ within the epoch, the pulse represents the numerical value $X$. Across epochs, values reset. This is illustrated in Figure 1A where at the top we show the numerical integer assignment of each time slot, in the middle we change the numerical range to follow the unipolar representation [0,1], and in the bottom the bipolar representation [-1,1]. In all three examples, a pulse arrives in the third time slot which represents the values 3, 0.375, and $-0.25$ respectively.

Figure 1

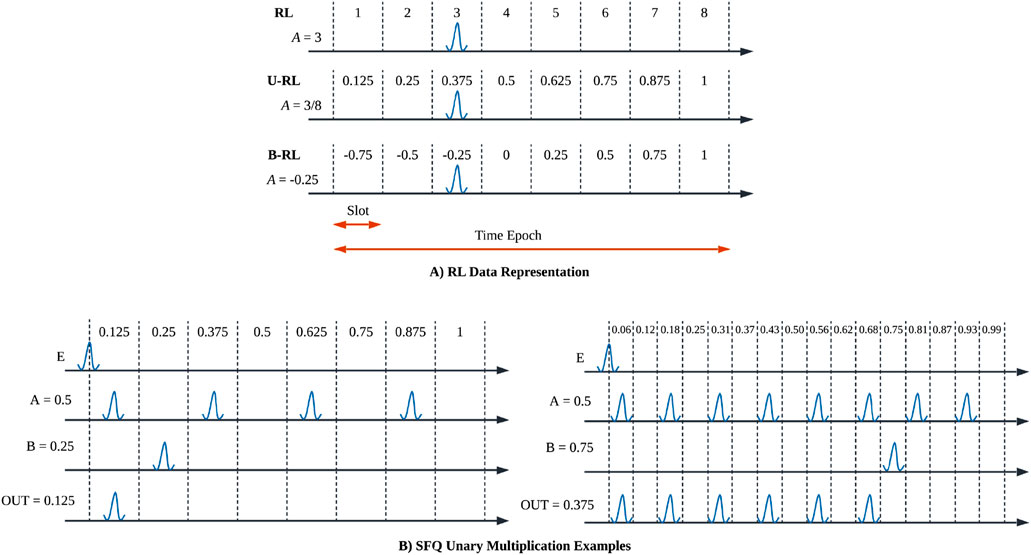
Figure 1. (A) Conventional RL data representation and our proposed unipolar (U-RL) and bipolar RL $(\text{B}-\text{R}\text{L})$ data encoding. (B) Unipolar multiplication examples combining pulse trains and RL formats. $E$ signals the beginning of the time epoch. $A$ is mapped to a pulse train, $B$ is in unipolar RL format. The first example with a 3-bit resolution $(N_{\mathit{max}}=8)$ results in 0.125 $1/N_{\mathit{max}}$. The second example with a 4-bit resolution $(N_{\mathit{max}}=16)$ results in 0.375 $6/N_{\mathit{max}}$. The multiplication occurs throughout the entire epoch.

With RL, a value that in binary would require multiple bits thus multiple parallel wires (which is typical to lower complexity instead of a serial binary representation), can be efficiently represented with just a single wire. This improves performance per unit area and power in many applications, which is an important metric in modern area-constrained SFQ fabrication processes. However, variables with a wider numerical range require more time slots, thus longer epochs, which increases computation latency. Also, time slots should be long enough to allow a pulse to propagate from the circuit’s input to the circuit’s output and remain in the same time slot plus any circuit timing margins, to avoid changing the pulse’s value simply due to propagation delay. Alternatively, in the case of larger circuits with multiple stages, the time reference (the epoch start) that time slots are derived from can be delayed (shifted) in later stages in a manner similar to wave pipelining (Krylov and Friedman, 2022).

In RL, traditional logic operations such as binary AND and OR are challenging because RL does not use binary representations. Similarly, arithmetic additions and multiplications are also complex. Recent work Gretsch et al. (2024) as well as the work we describe later address this shortcoming by proposing new temporal formulations with different tradeoffs. However, minimum (MIN) and maximum (MAX) comparisons are particularly easy with RL because they rely on the order of arrival of pulses; namely, between any number of pulses, the first to arrive represents the minimum value without the need for additional computation. Likewise, the last pulse represents the maximum value. This enables efficient implementations of decision trees Tzimpragos et al. (2020) as well as hyperdimensional computing (HDC) Huch et al. (2023). The latter is a promising result given that similarity comparison is traditionally the primary limiting factor in scaling up HDC to more stored classes and higher-dimension vectors. Thus, an RL implementation of HDC’s associative lookup allows HDC to reach larger application scales in area-constrained RSFQ circuits.

2.2 U-SFQ: combining temporal and pulse train formulations

Current superconducting technologies are hampered by area constraints and complex designs inspired by the realities of CMOS, which conflict with the inherent nature of SFQ pulses. Current binary SFQ (B-SFQ) approaches struggle with scalability due to the large number of JJs required for complex circuits. This inspired unary SFQ (U-SFQ) that leverages pulse-streams and RL data representations to create significantly more compact building blocks, including multipliers, adders, and memory cells (Gonzalez-Guerrero et al., 2022). For multiplication, U-SFQ achieves this by combining RL and pulse train operators, as illustrated in Figure 1B. As shown, operator $A$ is a pulse train and $B$ is encoded in RL. Any pulses in $A$ are propagated to the output until a pulse in $B$ arrives. The output is a pulse train of the multiplication result in the unipolar range. The same principle applies for bipolar multiplication (not shown). This allows a U-SFQ unipolar multiplier to use just a single cell, and a bipolar only 4 cells.

By drastically reducing the number of JJs required, U-SFQ offers the potential to overcome the limitations of existing superconducting prototypes, enabling larger-scale and more complex hardware accelerators like dot-product units (DPUs) (Gonzalez-Guerrero et al., 2022), fast Fourier transform (FFT) (Bautista et al., 2022), filters for signal processing, i.e., finite impulse response (FIR), and machine learning accelerators (Gonzalez-Guerrero et al., 2023). U-SFQ demonstrated compelling advantages, particularly in area efficiency, where U-SFQ processing elements for a multiply–add operation can achieve up to 200$\times$ fewer JJs compared to their B-SFQ counterparts. Similarly, U-SFQ neural processing and FIR filters exhibit superior area metrics, especially at lower bit resolutions. For example, a novel U-SFQ convolutional neural network (CNN) hardware accelerator achieves comparable peak performance to state-of-the-art B-SFQ designs in 32$\times$ less area (Gonzalez-Guerrero et al., 2023). By supporting variable bit resolutions and demonstrating substantial speedups over CMOS (up to 63$\times$) and area efficiency improvements over B-SFQ (up to 173$\times$) for lower bit precisions, U-SFQ offers a compelling solution for deploying high-performance, area-constrained CNN accelerators. While the unary approach may introduce some latency trade-offs, the significant reduction in area, coupled with inherent resilience to errors, positions U-SFQ as a promising solution for the future of high-performance and edge computing. We argue that further research and investment in U-SFQ architectures are important to realize the full benefits of superconducting technology and move beyond the limitations of current CMOS-inspired designs.

2.3 Temporal multiplier

Temporal multipliers rely on temporal encoding of operands rather than voltage levels. Here we describe a temporal decimal multiplier that encodes operands as multiple digits where each digit is encoded in the 0–9 range and in the time domain. This design mitigates a drawback of temporal logic that typically requires $N$ time delays (slots) to represent $N$ numerical values, which results in longer latency for large values of $N$. By representing numbers as parallel temporal values where each value represents a different digit (0–9) of the number, we reduce the maximum delay needed to represent the product to only 9 delay (clock) cycles for any multiplication outcome. As shown in Figure 2c, the proposed design is a hybrid by using both temporal signals and digital design blocks to build a seamless time-domain decimal multiplication architecture. Compared to the digital binary design shown in Figure 2a and the purely temporal design which requires signal domain conversions shown in Figure 2b, the proposed design enables embedding the architecture in the natural temporal signal flow; by performing computation directly in the decimal domain, the design eliminates binary-decimal conversion overhead, reducing area and energy consumption. Temporal multipliers offer application-specific advantages in power reduction and mixed-signal system integration, targeting energy-constrained edge AI, sensor fusion, and biomedical applications.

Figure 2

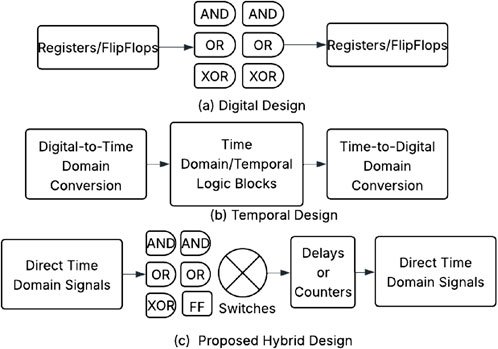
Figure 2. (a) Conventional digital binary RSFQ implemented using flip-flops and combinational gates. (b) Time-domain/temporal logic based designs require time-to-digital and digital-to-time conversions. (c) The proposed temporal hybrid design which can be built inline with time-domain signals and conventional digital blocks without requiring domain conversions.

We demonstrated a fabricated prototype of decimal multiplication using delay-based signal encoding and time-domain logic gates in Vasudevan and Michelogiannakis (2023). We showed performance and area benefits for different temporal multipliers with a fully-laid out, tapeout-ready design implemented in MIT-LL’s SFQ5ee process Schindler et al. (2022) with an area of $5m{m}^2$. Compared to a four-bit binary multiplier, this temporal decimal multiplier reduces the pin count by approximately 3$\times$ and the area by 40% for a proof-of-concept implementation. Further optimizations in this direction have potential for a lower area footprint and high throughput multiplication engines, enabling large scale high-throughput computing systems.

Current designs face challenges in maintaining arithmetic precision due to PVT (process-voltage-temperature) variations, calibration overhead, and susceptibility to timing jitter and analog noise. These limitations severely impact scalability and require robust design strategies. Research efforts should focus on improving the linearity of delay elements, developing real-time calibration techniques, and integrating time-domain multipliers with temporal analog to digital converters (ADCs) and neuromorphic computation interfaces. A chiplet-based modular architecture could allow large-scale assembly of multiple temporal arithmetic units, forming flexible, low-power processing fabrics for edge computing, real-time digital signal processing (DSP), and low-energy inference platforms.

2.4 Coarse-grain reconfigurable arrays (CGRAs)

CGRAs using superconducting RSFQ logic introduce a promising direction for high-performance, energy-efficient computing while at the same time offering reconfigurability to better customize data flow and computation to match different applications. A CGRA implemented in RSFQ logic has been fabricated in MIT-LL’s SFQ5ee process (Schindler et al., 2022) within $5m{m}^2$ chip as a proof-of-concept shown in Figure 3, showcasing a reconfigurable datapath architecture with high throughput and low energy per operation. However, limitations of current RSFQ-based CGRAs include limited integration density due to cryogenic packaging constraints, restricted on-chip memory, and complex clock distribution schemes. Furthermore, the requirement for operation at 4K presents practical challenges in large-scale deployment. Future directions involve exploring hybrid cryo-CMOS and superconducting architectures especially for denser hierarchical memory (Alam et al., 2023), improving EDA tools for SDC (Krylov et al., 2021), and co-locating small and fast memory blocks (Zokaee and Jiang, 2021) with CGRA compute components to enable more scalable and programmable CGRA systems suitable for data center and edge supercomputing applications.

Figure 3

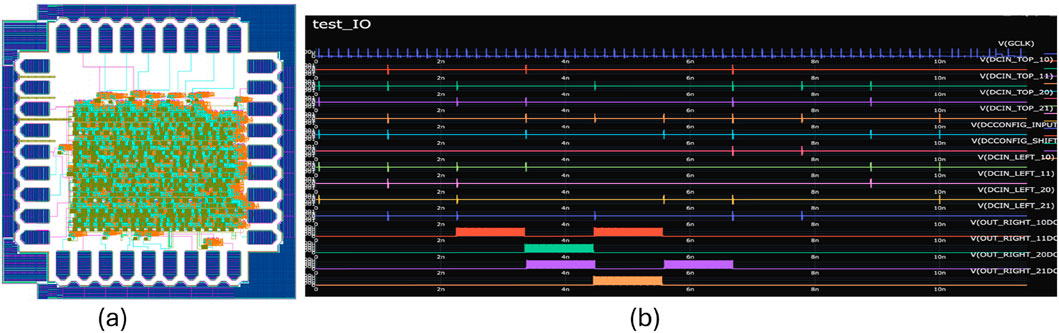
Figure 3. (a) Chip layout of a coarse-grain reconfigurable array (CGRA) implemented using RSFQ Logic in MIT-LL’s SFQ5ee process. (b) Pulse-like RSFQ signals used for testing the chip.

2.5 On-chip communication

SDC offers on-chip network design tradeoffs that are in stark contrast to those of CMOS (Michelogiannakis et al., 2010). For instance, on-chip data propagation consumes orders of magnitude lower energy per bit per mm relative to compute, compared to CMOS (Holmes, 2023). In addition, due to the low device density, storage buffers that are often used for temporary on-chip network storage, are significantly more expensive in terms of area and power efficiency compared to CMOS. Combined, these motivate high-radix topologies with long wires (assuming enough metal layers) and without buffers in routers or at network boundaries. Without buffers, networks can resolve contention either by dropping or deflecting packets. Dropping packets requires re-transmitting them that usually requires large buffers at network injection ports. In contrast, deflecting packets sends them towards a direction that takes them farther away from their destination; however, in contrast to CMOS, the relative energy overhead for such non-minimal paths is typically preferable compared to adding buffers to every router, especially considering the low on-chip propagation energy per bit.

Furthermore, on-chip networks for SDC should adapt to emerging compute models, instead of a conventional binary interface (Yorozu et al., 2004) that can increase overhead by requiring data conversions. To that end, we proposed two on-chip networks that do not use binary control paths and payloads can be readily interpreted as binary, pulse trains, or via any another formulation. The first such work is an on-chip network with a reconfigurable and dynamic connection schedule, and a variable number of parallel routers (Michelogiannakis et al., 2021); based on each router’s schedule and the current time, each router creates static connections in a circuit-switched manner between unique input–output pairs. Each network injection point, based on each packet’s destination, can determine which router, if any, has a direct connection to the desired destination. If no such direct path exists, packets can wait or use an indirect path. The second such on-chip network uses a single wire and a temporal packet format that uses a single pulse to temporally encode the packet’s destination, shown in Figure 4 (Lyles et al., 2023). Routers have two inputs and two outputs with control paths that operate entirely in the temporal domain, thus keeping routers small and energy-efficient. Contention is resolved by deflecting packets, thus without storage buffers. This network can scale up by composing butterfly, mesh or other larger network topologies out of $2\times 2$ routers.

Figure 4

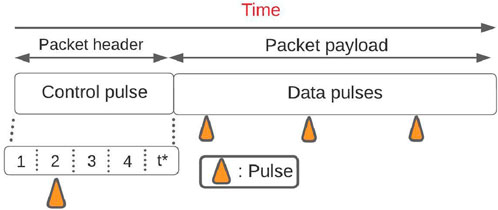
Figure 4. A temporal packet encodes the destination temporally in its header (in this example the destination is 2). The payload is a collection of pulses that can be interpreted as pulse trains, temporally, or via another formulation.

Much of this intuition for SDC on-chip networks can carry over to chiplet-to-chiplet SDC networks, which are regarded as a promising strategy for scaling up SDC (Smith et al., 2022; Egan et al., 2022). However, inter-chiplet networks face bandwidth constraints at chiplet boundaries as well as larger energy per bit overheads, which can motivate different design choices.

2.6 Neuromorphic computing

Neuromorphic computing is also rapidly emerging in SDC and predominantly RSFQ because RSFQ’s encoding of information as pulses due to the natural spiking behavior of JJs and the ability to transmit short voltage spikes without resistive capacitive are a natural fit to spiking neural networks (SNNs) (Schneider et al., 2022). Based on this observation, recent work proposes various approaches such as XOR digital gates, novel circuits (both digital and analog), and hybrid JJ devices to efficiently implement neurons that accept incoming pulses as positive or negative weight inputs and activate upon reaching their pre-defined threshold (Edwards et al., 2024; Razmkhah et al., 2024; Karamuftuoglu and Pedram, 2023; Jardine and Fourie, 2023; Bozbey et al., 2020). Coupling between neurons can be done with wires or modified Josephson transmission lines (JTLs) (Feldhoff and Toepfer, 2021). Based on these building blocks, further work designed and fabricated entire SNN architectures with optimizations such as synapse plasticity, dynamically regulating the threshold behavior of leaky integrate and fire neurons, efficient on-chip networks that can support in-network processing, simplified or custom weight processing and stateless neurons to increase area efficiency, and reinforcement learning-based local weight update rules (Schneider et al., 2025; Liu et al., 2023; Karamuftuoglu et al., 2024; Liu et al., 2025; Schneider et al., 2025). These demonstrations achieved impressive area and power efficiency. Furthermore, other work focused on further reducing the power overhead of neuromorphic computing in SDC by using AQFP to implement a binary neural network combined with processing in memory to reduce data movement (Li et al., 2023; Zhu et al., 2024).

3 Challenges and opportunities

Here we outline some challenges towards widespread adoption of SDC and some promising application domains.

3.1 EDA tools

Electronic design automation (EDA) tools have played a critical role in chip design, enabling a robust, scalable design-to-fabrication pipeline from a high-level description down to physical implementation. However, SDC presents a different design landscape and thus requires EDA tool customization. The IARPA SuperTools project (IARPA, 2017) launched in 2017 and marks a major investment in advancing SDC EDA tools, intending to enable end-to-end automation from device modeling to chip layout and manufacturing. Significant progress has been made, including through the ColdFlux program, which enabled the development of tools such as Katana, JoSIM, SPiRA, InductEx, and the qPALACE suite. These tools collectively support workflows ranging from TCAD-based process simulation to high-level logic synthesis and chip manufacturing (Fourie, 2020; Fourie et al., 2019).

Although significant progress has been made, current tool suites still impose constraints on design capabilities. Clocking in DC-biased SFQ circuits continues to pose challenges; unlike conventional CMOS logic, superconducting digital circuits depend on specialized timing mechanisms such as pulsed clocking in RSFQ or adiabatic synchronization in AQFP. These approaches introduce unique timing requirements that demand custom solutions for clock tree synthesis and timing extraction. Designing for these systems is not just a matter of adapting CMOS tools; managing clock skew, ensuring adequate timing margins, and balancing delays across the circuit become significantly more complex. As a result, precise control over timing becomes a central challenge in the design and verification of superconducting logic. Thus, an ongoing challenge remains to develop reliable and efficient clocking strategies. Similarly, synthesizing sequential logic for RSFQ remains a complex problem due to the unique timing and state encoding requirements of pulse-based logic.

Another challenge in SDC is the fragmentation of design methodologies, driven by the fundamental differences between logic families such as RSFQ, RQL, and AQFP. Each of these technologies relies on distinct physical principles, clocking strategies, and data encoding methods, requiring customized design approaches. As a result, tools developed for one logic family are often incompatible with others. This forces designers to rely on a patchwork of specialized, and often custom-built, tools tailored to each specific logic family. Addressing these challenges would help in picking with minimal effort the most suitable logic family for a particular set of design constraints, enabling scalable design methodologies beyond those practically possible with manual circuit design, and thus supporting the commercialization of SDC.

3.2 Quantum computing control

Quantum computing has gained significant attention due to its potential to solve complex scientific and practical problems that are otherwise intractable for classical computing systems. Among the various hardware platforms explored for quantum computing, superconducting qubits are currently the leading technology, primarily because of their relative maturity and promising scalability (Steffen et al., 2016). However, superconducting qubits encounter unique challenges in addition to those common to all qubit technologies, such as limited fidelity, noise, and leakage. A particular challenge for superconducting qubits is their operational requirement of a millikelvin (mK) cryogenic environment, while their control and readout electronics typically operate at room temperature as shown in Figure 5A. This spatial and thermal separation introduces substantial limitations on system integration, increases latency, and complicates scalability.

Figure 5

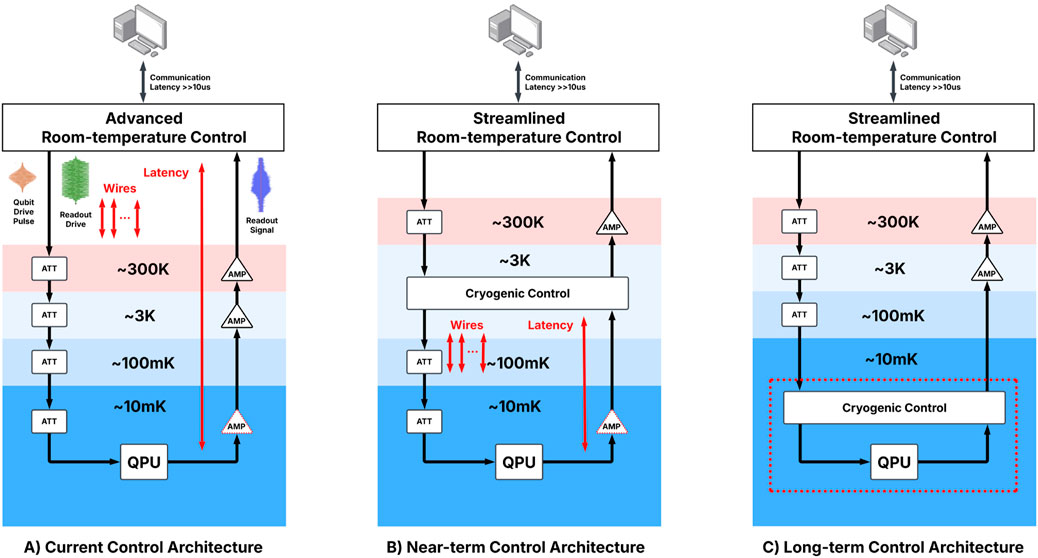
Figure 5. SDC enables us to co-locate the control systems with the quantum processing unit. (A) Modern control systems for superconducting transmon-based quantum computers have the cryo-control system external to the cryostat. This is problematic because of the latency required to make control decisions, and because space is very limited for cables to come into and out of the cryostat. (B) An improved system could have the control system residing in the middle tier of the dilution refrigerator to reduce the number of wires entering and exiting the outer tier of the cryostat. (C) The most aggressive approach is to have the classical SDC-based control system fully integrated with the superconducting quantum processing unit.

This motivates exploring quantum control and cryogenic sensor technologies integrated at cryogenic temperatures (Butko et al., 2020). Although some developments have already occurred, the amount of functionality that can realistically be integrated at mK temperatures remains limited. Most current research focuses on control electronics operating at around 4K, where superconductivity can still be achieved, particularly for scenarios where data originates from room-temperature environments as shown in Figure 5B. However, certain applications generate data directly at mK temperatures, making it advantageous to process data closer to its source to improve cable power consumption as shown in Figure 5C, reduce bit error rates, enhance bandwidth, and minimize latency. These considerations highlight the importance of advancing digital computing technologies at mK temperatures. For technologies such as RSFQ circuits, this requires adjustments in size and critical current to reduce the dynamic power JJs dissipate as well as reduce or eliminate static power by adopting ERSFQ, eSFQ, or using AQFP as an RSFQ alternative, allowing circuits to function effectively at mK temperatures (Bernhardt et al., 2025; Ohki et al., 2003). Current standards indicate that power consumption at mK temperatures should ideally remain at the microWatt level or a few milliWatts at most, yet current implementations and synthesis results using SDC EDA tools such as qPalace demonstrate that we are far from this target. Addressing this gap involves strategies such as designing smaller circuits, reducing bit widths, lowering the activity factor, and utilizing energy-efficient logic variants like ERSFQ (Mukhanov, 2011) and eSFQ (Volkmann et al., 2013).

Quantifying and presenting this performance and power gap clearly motivates ongoing research in this area. Fortunately, the stringent power budgets required at mK temperatures reduce the impact of current area constraints, providing an advantageous trade-off for further system development.

3.3 Compute models for robust computation

Superconducting logic systems, despite their considerable promise for improved computational efficiency, face several critical sources of unreliability. Key among these are cooling imperfections and thermal noise (Semenov et al., 1999) from adjacent components such as cables that raise the bit error rate (BER) (Hall et al., 2023) and introduce timing jitter (Ortlepp and Uhlmann, 2005). SDC is more likely than modern traditional CMOS to experience soft errors, whether due to technological imperfections or external factors. In particular, in many circuit designs, JJs are biased at 70% of their critical current, but thermal variations, cooling imperfections, electromagnetic or radiation fields from the environment that SDC circuits operate in [such as next to superconducting magnets (Schultz, 2002)] create a non-trivial probability that the current distribution network will be affected thus some JJs will reach their critical current unexpectedly, or will not reach their critical current when expected. In practice, this means that erroneous pulses may appear in the circuit or pulses that are expected based on the circuit’s logical operation will not appear. Unfortunately, no circuit simulation models exist to precisely model the effects of these various external factors such that we can more confidently quantify their impact and design circuits accordingly.

Additionally, superconducting circuits are sensitive to electromagnetic fields, which can inadvertently trigger or prevent expected JJ transitions, leading to logical errors (Ebert et al., 2009; Schindler et al., 2023). Variations in manufacturing processes also introduce inconsistencies in JJ parameters such as critical currents, potentially causing unpredictable logic behavior. Timing precision, essential to superconducting digital logic, is another significant vulnerability; variations in clock distribution and timing skew can lead to missed synchronization windows and errors (Bairamkulov et al., 2022), particularly for pulse-based logic families such as SFQ, which depend upon exact pulse timing for correct operation. Advancing EDA tools tailored specifically for superconducting circuits presents another essential mitigation strategy (Krylov et al., 2021). Enhanced EDA tools enable precise modeling and optimization of superconducting circuit parameters, systematically addressing issues stemming from timing skew, fabrication variability, and synchronization errors. Improvements to environmental control—-such as stabilizing cryogenic operating conditions, implementing electromagnetic shielding (Collot et al., 2016), and minimizing ambient fluctuations—-are also critical. Finally, adaptive and reconfigurable circuit designs, which dynamically adjust operational parameters such as bias currents and pulse timings in response to environmental or internal fluctuations, can further enhance reliability. Collectively, these approaches form a strategy for managing unreliability in superconducting logic systems, paving the way toward broader and more practical commercial applications.

To address these challenges, a range of mitigation strategies can be employed. One approach involves increasing critical current margins to enhance reliability (Mitrovic and Friedman, 2024), although this strategy often results in greater power consumption and reduced performance. Alternative computational paradigms, inherently robust against bit errors, such as hyperdimensional computing (Huch et al., 2023) or neural network-based methods (Razmkhah et al., 2024), offer another route, enabling systems to tolerate individual pulse-level deviations while still producing accurate outcomes. Architectural-level solutions also play a critical role, where redundancy, probabilistic computing (Chowdhury et al., 2023), or self-correcting circuits can help mask inherent variability and environmental disturbances. Employing computational representations with intrinsic bounded-error properties, such as temporal encoding (Tzimpragos et al., 2020) or pulse-train logic (Gonzalez-Guerrero et al., 2023), further supports resilience by allowing systems to gracefully handle small deviations in timing or signal integrity without catastrophic failure.

This realization presents another opportunity for unconventional models, such as those inspired by stochastic computing (Sartori et al., 2011), which provide bounds for the numerical impact of soft errors. In binary number representation, changing the value of one bit can have a numerical impact as much as half the maximum number range. In RL, a pulse unexpectedly appearing can have no effect if it appears after the original (correct) pulse, or will reduce the represented value if it appears before the original pulse. In contrast, a pulse appearing or disappearing unexpectedly in a pulse train (Section 2.2), has a deterministic numerical impact of 1 divided by the numerical range. This not only is a small error, but the determinism of this error is advantageous because it can be co-designed with error correction algorithms or with applications that can relax strict correctness constraints (Kumar, 2012). This way, we can avoid the circuit overhead of making circuits more robust to handle such internal errors, or we can bias JJs more aggressively for lower power such as with a lower critical current, simply by using compute methods that bound the impact of errors. In addition, given that data movement to and from the cryogenic environment is another major constraint, robust numerical representations allow us to configure cables at a higher bit error rate since we can quantify the expected numerical impact of those errors, because doing so enables those cables to operate at a higher bandwidth (Pintus et al., 2022).

3.4 Superconducting converters for cryogenic sensors

Readout electronics implemented using superconducting circuitry may be transformative for a number of emerging radiation detection systems. By putting the front-end readout electronics as close as possible to the sensor, the overall noise and power dissipation can be reduced and the scalability can be increased.

A superconducting analog-to-digital converter (ADC) can be used as the main vehicle in this direction: counting single magnetic flux quanta provides inherently low-noise and high-accuracy (Mukhanov et al., 2004) with superconducting ADCs being far superior to their CMOS counterparts in terms of achieved figures of merit (Gupta et al., 2011). Additionally, converting analog sensor information to the digital domain at superconducting temperatures allows the use of the robust, noise-resilient digital compute methods discussed in this paper to process the information; in turn, this has a dual benefit: (i) control feedback loops with low latency can be implemented close to the cryogenic sensors, and (ii) the overall readout system can be significantly simplified with amplifiers in the complex analog lines being replaced by digital lines carrying only meaningful, post-processed sensor data.

Calorimetry and superconducting magnet instrumentation are two cryogenic sensing applications that have great use for a superconducting readout system. For example, rare event searches such as the cryogenic underground observatory for rare events (CUORE) (Arnaboldi, 2004) could benefit from simpler readout approaches that utilize direct digitization of superconducting sensors. As a proof-of-principle, a calorimeter readout integrated circuit operating below 1K was demonstrated using cryo-compatible CMOS electronics (Huang et al., 2021). Moving towards superconducting readout electronics could further enhance the power efficiency and scalability of future calorimetry systems. Superconducting magnet instrumentation can also be greatly improved by incorporating cryogenic readout electronics, utilizing the direct quantization of magnetic flux quanta (Radparvar and Rylov, 1997). Finally, cryogenic electronics can also be used for readouts and decision making in cold diagnostics and quench detection for superconducting magnets (Buzio et al., 2024), where fast controls are necessary to avoid destructive quenching events.

4 Conclusion

Superconducting digital computing (SDC) promises to improve performance per unit power compared to today’s traditional room-temperature CMOS. This paper outlines some recent novel compute methods that adapt numerical representations and operations to the unique properties of RSFQ, instead of trying to shoe-horn CMOS-inspired architectures into RSFQ. Further research along those lines can provide higher gains thus increase the impact of SDC. This paper outlines current challenges of SDC and promising application domains that should be addressed by future research in order to increase the impact of SDC as well as increase the viability of widespread commercial SDC applications.

Author contributions

GM: Visualization, Conceptualization, Writing – review and editing, Funding acquisition, Writing – original draft, Supervision. AB: Writing – original draft, Visualization, Resources, Funding acquisition. PG-G: Methodology, Writing – original draft. DV: Visualization, Writing – original draft. MGB-J: Writing – original draft, Investigation. CG: Conceptualization, Writing – original draft. PZ: Conceptualization, Writing – original draft. JS: Writing – review and editing, Funding acquisition, Writing – original draft, Supervision, Visualization.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the IARPA supertools program, the army research office (ARO), and the laboratory for physical sciences (LPS). This work was also supported by the Director, Office of Science, and the Laboratory Directed Research and Development Program of Lawrence Berkeley National Laboratory of the U.S. Department of Energy under Contract No. DE- AC02–05CH11231.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alam, S., Hossain, M. S., Srinivasa, S. R., and Aziz, A. (2023). Cryogenic memory technologies. Nat. Electron. 6, 185–198. doi:10.1038/s41928-023-00930-2

CrossRef Full Text | Google Scholar

Arnaboldi, e. a., C., Avignone III, F., Beeman, J., Barucci, M., Balata, M., Brofferio, C., et al. (2004). Cuore: a cryogenic underground observatory for rare events. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 518, 775–798. doi:10.1016/j.nima.2003.07.067

CrossRef Full Text | Google Scholar

Bairamkulov, R., Jabbari, T., and Friedman, E. G. (2022). Qucts—single-flux quantum clock tree synthesis. IEEE Trans. Computer-Aided Des. Integr. Circuits Syst. 41, 3346–3358. doi:10.1109/TCAD.2021.3123141

CrossRef Full Text | Google Scholar

Bakolo, R. S., and Fourie, C. J. (2011). “Development of a rsfq cell library for the university of stellenbosch,” in IEEE africon ’11, 1–5. doi:10.1109/AFRCON.2011.6072026

CrossRef Full Text | Google Scholar

Barbosa, J., Brennan, J. C., Casaburi, A., Hutchings, M. D., Kirichenko, A., Mukhanov, O., et al. (2024). RSFQ all-digital programmable multi-tone generator for quantum applications. arXiv:2411.08670v1.

Google Scholar

Bautista, G., Gonzalez-Guerrero, P., Lyles, D., Huch, K., and Michelogiannakis, G. (2022). “Superconducting digital dit butterfly unit for fast fourier transform using race logic,” in 2022 20th IEEE interregional NEWCAS conference (NEWCAS), 441–445. doi:10.1109/NEWCAS52662.2022.9842221

CrossRef Full Text | Google Scholar

Bernhardt, J., Jordan, C., Rahamim, J., Kirchenko, A., Bharadwaj, K., Fry-Bouriaux, L., et al. (2025). Quantum computer controlled by superconducting digital electronics at millikelvin temperature.

Google Scholar

Bozbey, A., Karamuftuoglu, M. A., Razmkhah, S., and Ozbayoglu, M. (2020). Single flux quantum based ultrahigh speed spiking neuromorphic processor architecture. arXiv:1812.10354.

Google Scholar

Butko, A., Michelogiannakis, G., Williams, S., Iancu, C., Donofrio, D., Shalf, J., et al. (2020). “Understanding quantum control processor capabilities and limitations through circuit characterization,” in International Conference on rebooting computing, ICRC 2020 (Atlanta, GA, USA), 66–75. doi:10.1109/ICRC2020.2020.00011

CrossRef Full Text | Google Scholar

Buzio, M., Di Capua, V., Fiscarello, L., and Martinez Hernandex, U. (2024). Cryogenic tests of electronic components and sensors for superconducting magnet instrumentation. Meas. Sensors. doi:10.1016/j.measen.2024.101436

CrossRef Full Text | Google Scholar

Chowdhury, S., Grimaldi, A., Aadit, N. A., Niazi, S., Mohseni, M., Kanai, S., et al. (2023). A full-stack view of probabilistic computing with p-bits: devices, architectures, and algorithms. IEEE J. Explor. Solid-State Comput. Devices Circuits 9, 1–11. doi:10.1109/JXCDC.2023.3256981

CrossRef Full Text | Google Scholar

Collot, R., Febvre, P., Kunert, J., Meyer, H.-G., Stolz, R., and Issler, J. L. (2016). Characterization of an on-chip magnetic shielding technique for improving sfq circuit performance. IEEE Trans. Appl. Supercond. 26, 1–5. doi:10.1109/TASC.2016.2542117

CrossRef Full Text | Google Scholar

Ebert, B., Ortlepp, T., and Uhlmann, F. H. (2009). Experimental study of the effect of flux trapping on the operation of rsfq circuits. IEEE Trans. Appl. Supercond. 19, 607–610. doi:10.1109/TASC.2009.2018738

CrossRef Full Text | Google Scholar

Edwards, A. J., Krylov, G., Friedman, J. S., and Friedman, E. G. (2024). Harnessing stochasticity for superconductive multi-layer spike-rate-coded neuromorphic networks. Neuromorphic Comput. Eng. 4, 014005. doi:10.1088/2634-4386/ad207a

CrossRef Full Text | Google Scholar

Egan, J., Nielsen, M., Strong, J., Talanov, V., Rudman, E., Song, B., et al. (2022). Synchronous chip-to-chip communication with a multi-chip resonator clock distribution network. Supercond. Sci. Technol. 35, 105010. doi:10.1088/1361-6668/ac8e38

CrossRef Full Text | Google Scholar

Feldhoff, F., and Toepfer, H. (2021). Niobium neuron: rsfq based bio-inspired circuit. IEEE Trans. Appl. Supercond. 31, 1–5. doi:10.1109/TASC.2021.3063212

CrossRef Full Text | Google Scholar

Fourie, C. J. (2020). “Electronic design automation tools for superconducting circuits,” in Journal of physics: conference Series, Kyoto, Japan (IOP Publishing). 012040. doi:10.1088/1742-6596/1590/1/012040

CrossRef Full Text | Google Scholar

Fourie, C. J., Jackman, K., Botha, M. M., Razmkhah, S., Febvre, P., Ayala, C. L., et al. (2019). Coldflux superconducting eda and tcad tools project: overview and progress. IEEE Trans. Appl. Supercond. 29, 1–7. doi:10.1109/tasc.2019.2892115

CrossRef Full Text | Google Scholar

Gonzalez-Guerrero, P., Bautista, M. G., Lyles, D., and Michelogiannakis, G. (2022). “Temporal and SFQ pulse-streams encoding for area-efficient superconducting accelerators,” in Proceedings of the 27th ACM international conference on architectural support for programming languages and operating systems (New York, NY, USA: Association for Computing Machinery), 963–976. doi:10.1145/3503222.3507765

CrossRef Full Text | Google Scholar

Gonzalez-Guerrero, P., Huch, K., Patra, N., Popovici, T., and Michelogiannakis, G. (2023). “An area efficient superconducting unary cnn accelerator,” in 2023 24th international symposium on quality electronic design (ISQED), 1–8. doi:10.1109/ISQED57927.2023.10129299

CrossRef Full Text | Google Scholar

Gretsch, R., Song, P., Madhavan, A., Lau, J., and Sherwood, T. (2024). “Energy efficient convolutions with temporal arithmetic,” in Proceedings of the 29th ACM International Conference on Architectural Support for Programming Languages and Operating Systems (New York, NY, USA: Association for Computing Machinery), 354–368. doi:10.1145/3620665.3640395

CrossRef Full Text | Google Scholar

Gupta, D., Inamdar, A. A., Kirichenko, D. E., Kadin, A. M., and Mukhanov, O. A. (2011). “Superconductor analog-to-digital converters and their applications,” in 2011 IEEE MTT-S international microwave symposium (IEEE), 1–4.

Google Scholar

Hall, T., Delport, J. A., and Fourie, C. J. (2023). Determination of the bit error rate due to thermal noise using josim superconducting circuit simulator and the Monte Carlo method. IEEE Trans. Appl. Supercond. 33, 1–5. doi:10.1109/TASC.2023.3251940

CrossRef Full Text | Google Scholar

Herr, Q. P., Herr, A. Y., Oberg, O. T., and Ioannidis, A. G. (2011). Ultra-low-power superconductor logic. J. Appl. Phys. 109, 103903. doi:10.1063/1.3585849

CrossRef Full Text | Google Scholar

Herr, Q., Josephsen, T., and Herr, A. (2023). Superconducting pulse conserving logic and josephson-sram. Appl. Phys. Lett. 122, 182604. doi:10.1063/5.0148235

CrossRef Full Text | Google Scholar

Holmes, D. (2023). in Cryogenic electronics and quantum information processing, 1–93.

Google Scholar

Huang, G., Gnani, D., Grace, C., Kolomensky, Y., Mei, Y., and Papadopoulou, A. (2021). “Interfacing with cryogenic sensors via 180 nm cmos operating near 1 kelvin,” in 2021 IEEE 14th workshop on low temperature electronics (WOLTE), 1–4. doi:10.1109/WOLTE49037.2021.9555449

CrossRef Full Text | Google Scholar

Huch, K., Gonzalez-Guerrero, P., Lyles, D., and Michelogiannakis, G. (2023). Superconducting hyperdimensional associative memory circuit for scalable machine learning. IEEE Trans. Appl. Supercond. 33, 1–14. doi:10.1109/TASC.2023.3271951

CrossRef Full Text | Google Scholar

IARPA (2017). Supertools program.

Google Scholar

Jardine, M. A., and Fourie, C. J. (2023). Hybrid rsfq-qfp superconducting neuron. IEEE Trans. Appl. Supercond. 33, 1–9. doi:10.1109/TASC.2023.3248140

CrossRef Full Text | Google Scholar

Karamuftuoglu, M. A., and Pedram, M. (2023). a-Soma: single flux quantum threshold cell for spiking neural network implementations. IEEE Trans. Appl. Supercond. 33, 1–5. doi:10.1109/TASC.2023.3264703

CrossRef Full Text | Google Scholar

Karamuftuoglu, M. A., Ucpinar, B. Z., Razmkhah, S., Kamal, M., and Pedram, M. (2024). Unsupervised sfq-based spiking neural network. IEEE Trans. Appl. Supercond. 34, 1–8. doi:10.1109/TASC.2024.3367618

CrossRef Full Text | Google Scholar

Krylov, G., and Friedman, E. G. (2020). Design methodology for distributed large-scale ersfq bias networks. IEEE Trans. Very Large Scale Integration (VLSI) Syst. 28, 2438–2447. doi:10.1109/TVLSI.2020.3023054

CrossRef Full Text | Google Scholar

Krylov, G., and Friedman, E. G. (2022). Wave pipelining in dsfq circuits. IEEE Trans. Appl. Supercond. 32, 1–6. doi:10.1109/TASC.2021.3135956

CrossRef Full Text | Google Scholar

Krylov, G., Kawa, J., and Friedman, E. G. (2021). Design automation of superconductive digital circuits: a review. IEEE Nanotechnol. Mag. 15, 54–67. doi:10.1109/MNANO.2021.3113218

CrossRef Full Text | Google Scholar

Kumar, R. (2012). “Algorithmic techniques for robust applications,” in 2012 IEEE 18th international on-line testing symposium (IOLTS), 168. doi:10.1109/IOLTS.2012.6313865

CrossRef Full Text | Google Scholar

Li, Z., Yuan, G., Yamauchi, T., Masoud, Z., Xie, Y., Dong, P., et al. (2023). “Superbnn: randomized binary neural network using adiabatic superconductor josephson devices,” in Proceedings of the 56th Annual IEEE/ACM International Symposium on Microarchitecture (New York, NY, USA: Association for Computing Machinery), 584–598. doi:10.1145/3613424.3623771

CrossRef Full Text | Google Scholar

Likharev, K., and Semenov, V. (1991). Rsfq logic/memory family: a new josephson-junction technology for sub-terahertz-clock-frequency digital systems. IEEE Trans. Appl. Supercond. 1, 3–28. doi:10.1109/77.80745

CrossRef Full Text | Google Scholar

Liu, Z., Chen, S., Qu, P., Liu, H., Niu, M., Ying, L., et al. (2023). “Sushi: ultra-high-speed and ultra-low-power neuromorphic chip using superconducting single-flux-quantum circuits,” in Proceedings of the 56th Annual IEEE/ACM International Symposium on Microarchitecture (New York, NY, USA: Association for Computing Machinery), 614–627. doi:10.1145/3613424.3623787

CrossRef Full Text | Google Scholar

Liu, Z., Chen, S., Qu, P., Tang, G., and You, H. (2025). Toward superconducting neuromorphic computing using single-flux-quantum circuits. IEEE Trans. Appl. Supercond. 35, 1–14. doi:10.1109/TASC.2025.3544687

CrossRef Full Text | Google Scholar

Lyles, D., Gonzalez-Guerrero, P., Bautista, M. G., and Michelogiannakis, G. (2023). Past-noc: a packet-switched superconducting temporal noc. IEEE Trans. Appl. Supercond. 33, 1–13. doi:10.1109/TASC.2023.3236248

CrossRef Full Text | Google Scholar

Marakkalage, D. S., Riener, H., and De Micheli, G. (2021). “Optimizing adiabatic quantum-flux-parametron (aqfp) circuits using an exact database,” in 2021 IEEE/ACM international symposium on nanoscale architectures (NANOARCH), 1–6. doi:10.1109/NANOARCH53687.2021.9642241

CrossRef Full Text | Google Scholar

Michelogiannakis, G., Sanchez, D., Dally, W. J., and Kozyrakis, C. (2010). “Evaluating bufferless flow control for on-chip networks,” in 2010 fourth ACM/IEEE international symposium on networks-on-chip, 9–16. doi:10.1109/NOCS.2010.10

CrossRef Full Text | Google Scholar

Michelogiannakis, G., Lyles, D., Gonzalez-Guerrero, P., Bautista, M., Vasudevan, D., and Butko, A. (2021). “Srnoc: a statically-scheduled circuit-switched superconducting race logic noc,” in 2021 IEEE international parallel and distributed processing symposium (IPDPS), 1046–1055. doi:10.1109/IPDPS49936.2021.00113

CrossRef Full Text | Google Scholar

Mitrovic, A., and Friedman, E. G. (2024). Thermal exploration of rsfq integrated circuits. IEEE Trans. Very Large Scale Integration (VLSI) Syst. 32, 728–738. doi:10.1109/TVLSI.2023.3348452

CrossRef Full Text | Google Scholar

Mukhanov, O. A. (2011). Energy-efficient single flux quantum technology. IEEE Trans. Appl. Supercond. 21, 760–769. doi:10.1109/TASC.2010.2096792

CrossRef Full Text | Google Scholar

Mukhanov, O. A., Gupta, D., Kadin, A. M., and Semenov, V. K. (2004). Superconductor analog-to-digital converters. Proc. IEEE 92, 1564–1584. doi:10.1109/jproc.2004.833660

CrossRef Full Text | Google Scholar

Ohki, T., Habif, J., Feldman, M., and Bocko, M. (2003). Thermal design of superconducting digital circuits for millikelvin operation. IEEE Trans. Appl. Supercond. 13, 978–981. doi:10.1109/TASC.2003.814118

CrossRef Full Text | Google Scholar

Ortlepp, T., and Uhlmann, F. (2005). Noise induced timing jitter: a general restriction for high speed rsfq devices. IEEE Trans. Appl. Supercond. 15, 344–347. doi:10.1109/TASC.2005.849830

CrossRef Full Text | Google Scholar

Pintus, P., Singh, A., Xie, W., Ranzani, L., Gustafsson, M. V., Tran, M. A., et al. (2022). Ultralow voltage, high-speed, and energy-efficient cryogenic electro-optic modulator. Optica 9, 1176–1182. doi:10.1364/OPTICA.463722

CrossRef Full Text | Google Scholar

Radparvar, M., and Rylov, S. (1997). High sensitivity digital squid magnetometers. IEEE Trans. Appl. Supercond. 7, 3682–3685. doi:10.1109/77.622217

CrossRef Full Text | Google Scholar

Razmkhah, S., Karamuftuoglu, M. A., and Bozbey, A. (2024). Hybrid synaptic structure for spiking neural network realization. Supercond. Sci. Technol. 37, 065011. doi:10.1088/1361-6668/ad44e3

CrossRef Full Text | Google Scholar

Rylov, S. V. (2019). Clockless dynamic sfq and gate with high input skew tolerance. IEEE Trans. Appl. Supercond. 29, 1–5. doi:10.1109/TASC.2019.2896137

CrossRef Full Text | Google Scholar

Sartori, J., Sloan, J., and Kumar, R. (2011). “Stochastic computing: embracing errors in architectureand design of processors and applications,” in Proceedings of the 14th International Conference on Compilers, Architectures and Synthesis for Embedded Systems (New York, NY, USA: Association for Computing Machinery), 135–144. doi:10.1145/2038698.2038720

CrossRef Full Text | Google Scholar

Schindler, L., Delport, J. A., and Fourie, C. J. (2022). The coldflux rsfq cell library for mit-ll sfq5ee fabrication process. IEEE Trans. Appl. Supercond. 32, 1–7. doi:10.1109/TASC.2021.3135905

CrossRef Full Text | Google Scholar

Schindler, L., Ayala, C. L., Jackman, K., Fourie, C. J., and Yoshikawa, N. (2023). Adopting a standard track routing architecture for next-generation hybrid ac/dc-biased logic circuits. IEEE Trans. Appl. Supercond. 33, 1–5. doi:10.1109/TASC.2023.3258366

CrossRef Full Text | Google Scholar

Schneider, M., Toomey, E., Rowlands, G., Shainline, J., Tschirhart, P., and Segall, K. (2022). Supermind: a survey of the potential of superconducting electronics for neuromorphic computing. Supercond. Sci. Technol. 35, 053001. doi:10.1088/1361-6668/ac4cd2

CrossRef Full Text | Google Scholar

Schneider, M. L., Jué, E. M., Pufall, M. R., Segall, K., and Anderson, C. W. (2025). A self-training spiking superconducting neuromorphic architecture. npj Unconv. Comput. 2, 5. doi:10.1038/s44335-025-00021-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Schultz, J. (2002). Protection of superconducting magnets. IEEE Trans. Appl. Supercond. 12, 1390–1395. doi:10.1109/TASC.2002.1018662

CrossRef Full Text | Google Scholar

Semenov, V., Polyakov, Y., and Chao, W. (1999). Extraction of impacts of fabrication spread and thermal noise on operation of superconducting digital circuits. IEEE Trans. Appl. Supercond. 9, 4030–4033. doi:10.1109/77.783912

CrossRef Full Text | Google Scholar

Smith, K. N., Ravi, G. S., Baker, J. M., and Chong, F. T. (2022). Scaling superconducting quantum computers with chiplet architectures. 1092, 1109. doi:10.1109/micro56248.2022.00078

CrossRef Full Text | Google Scholar

Steffen, M., Gambetta, J. M., and Chow, J. M. (2016). “Progress, status, and prospects of superconducting qubits for quantum computing,” in 2016 46th European solid-state device research conference (ESSDERC), 17–20. doi:10.1109/ESSDERC.2016.7599578

CrossRef Full Text | Google Scholar

Tannu, S. S., Das, P., Lewis, M. L., Krick, R., Carmean, D. M., and Qureshi, M. K. (2019). “A case for superconducting accelerators,” in Proceedings of the 16th ACM international conference on computing frontiers (New York, NY, USA: Association for Computing Machinery), 67–75. doi:10.1145/3310273.3321561

CrossRef Full Text | Google Scholar

Tzimpragos, G., Vasudevan, D., Tsiskaridze, N., Michelogiannakis, G., Madhavan, A., Volk, J., et al. (2020). “A computational temporal logic for superconducting accelerators,” in Proceedings of the twenty-fifth international conference on architectural support for programming languages and operating systems (New York, NY, USA: Association for Computing Machinery), 435–448. doi:10.1145/3373376.3378517

CrossRef Full Text | Google Scholar

Tzimpragos, G., Volk, J., Wynn, A., Smith, J. E., and Sherwood, T. (2021). “Superconducting computing with alternating logic elements,” in 2021 ACM/IEEE 48th annual international symposium on computer architecture (ISCA), 651–664. doi:10.1109/ISCA52012.2021.00057

CrossRef Full Text | Google Scholar

Vasudevan, D., and Michelogiannakis, G. (2023). Efficient temporal arithmetic logic design for superconducting rsfq logic. IEEE Trans. Appl. Supercond. 33, 1–7. doi:10.1109/TASC.2023.3248003

CrossRef Full Text | Google Scholar

Volk, J., Tzimpragos, G., and Mukhanov, O. (2024). xeSFQ: clockless sfq logic with zero static power. arXiv:2411.03052.

Google Scholar

Volkmann, M. H., Sahu, A., Fourie, C. J., and Mukhanov, O. A. (2013). Experimental investigation of energy-efficient digital circuits based on esfq logic. IEEE Trans. Appl. Supercond. 23, 1301505. doi:10.1109/TASC.2013.2240755

CrossRef Full Text | Google Scholar

Yorozu, S., Hashimoto, Y., Kameda, Y., Terai, H., Fujimaki, A., and Yoshikawa, N. (2004). “A 40 ghz clock 160 gb/s 4/spl times/4 switch circuit using single flux quantum technology for high-speed packet switching systems,” in 2004 workshop on high performance switching and routing, 20–23. doi:10.1109/HPSR.2004.1303415

CrossRef Full Text | Google Scholar

Zhu, G., Kan, Y., Zhang, R., Nakashima, Y., Luo, W., Takeuchi, N., et al. (2024). Supersim: a comprehensive benchmarking framework for neural networks using superconductor josephson devices. Supercond. Sci. Technol. 37, 095022. doi:10.1088/1361-6668/ad6d9e

CrossRef Full Text | Google Scholar

Zokaee, F., and Jiang, L. (2021). “Smart: a heterogeneous scratchpad memory architecture for superconductor sfq-based systolic cnn accelerators,” in MICRO-54: 54th Annual IEEE/ACM International Symposium on Microarchitecture (New York, NY, USA: Association for Computing Machinery), 912–924. doi:10.1145/3466752.3480041

CrossRef Full Text | Google Scholar