Forced vibration of an axially functionally graded energy pile embedded in temperature-sensitive Winkler soils

In this study, forced vibration analysis of an energy pile with non-uniformity in vertically inhomogeneous soil is presented considering the non-uniform distributed temperature. In establishing the numerical model, it is assumed that the cross-sectional area of the pile remains constant throughout its length, while Young’s modulus and mass density vary along the x direction. The nonlinear soil–pile interaction is modeled with the p–y curve method. Because of the heterogeneity of the soil, the parameter in the p–y curve method changes along the depth direction. The energy pile experiences a complex mechanical load in the working process. In this study, a periodic lateral force and a constant vertical force are applied on the top of the energy pile. The governing equations and the boundary conditions are obtained based on the Hamilton principle. The vibration frequency responses are obtained numerically by using the differential quadrature method. The non-uniformity effects of the pile’s temperature and material inhomogeneity effect are analyzed in detail. Our results demonstrate that the non-uniformity for both the pile and temperature could have significant effects on the vibration frequency response.

1 Introduction

The behavior of pile or beam structures supported by an elastic foundation is a subject of engineering with practical and theoretical interests (Bai et al., 2021a; Bai et al., 2019; Bai et al., 2021b; Mohamad et al., 2014). The Winkler model is commonly used to model the pile–soil interaction (Wu et al., 2018a). Due to its simplicity, closed-form solutions could be derived for various problems by adopting the Winkler model.The static (Rui and Soga, 2019; Huang et al., 2019; Bourne-Webb et al., 2019), dynamic (Bai et al., 2019; Bourne-Webb et al., 2015; Sung et al., 2018; Bourne-Webb and Bodas-Freitas, 2020; Zhang et al., 2019; Du et al., 2018; Semmah et al., 2019; Bagheri et al., 2018; Safarpour et al., 2019; Feng et al., 2017; Wu et al., 2018b; Prendergast and Gavin, 2016), buckling (Bai et al., 2021a; Bourne-Webb et al., 2015), and post-buckling (Filipich and Rosales, 2002) problems have been extensively analyzed by researchers using the Winkler model.

The piles embedded in soils often experience thermal loads, which induce a pattern of the deformation field that differs from that induced by mechanical loads (Shen and Li, 2004; Anoyatis et al., 2019; Auersch, 2019). Thermal buckling (Karatzia and Mylonakis, 2017; Wang et al., 2020; Le et al., 2020), thermal stress analysis (Khalil et al., 2020), thermo-elastic wave propagation analysis (Tu et al., 2020), dynamic thermal analysis (Le et al., 2020; Fattah et al., 2020), and thermal transfer analysis (Moghaddasi et al., 2020) of beams, plates, or piles have been performed by researchers. However, the temperature-dependent properties of the soil’s reaction to the pile are rarely noticed by researchers. In this study, the soil’s reaction to the pile is modeled by using the Winkler model, and the temperature-dependent property is considered by introducing a temperature-dependent coefficient into the Winkler model.

Functionally graded materials (FGMs) are newly engineered materials, with smoothly and continuously varying properties in the preferred direction (Jiang et al., 2018; Bahrami and Nikraz, 2017; Zhi et al., 2025). FGMs can provide improved mechanical and thermal properties, and they are of interest in many technological fields (Mouadh et al., 2025; Jincheng et al., 2025; Chenglong et al., 2025; Lu et al., 2025; Ya et al., 2025). Structures designed by FGMs are superior to those designed by homogeneous materials composed of similar constituents (Ya et al., 2025). Abundant studies of functionally graded (FG) structures supported by the elastic foundation have been performed by researchers (Huaibo et al., 2025; Huaibo et al., 2023; Aylin et al., 2023a; Aylin et al., 2023b; Long et al., 2024; Lei et al., 2025). The axially functionally graded (AFG) beams or piles, with varying properties along the length of the beam or pile, can meet specific requirements under inhomogeneous conditions, such as a graded temperature field, suffering a non-uniformly distributed load, etc. AFG piles differ from traditional isotropic FG structures in that their material properties vary continuously along the length of the structures. This variation allows AFG piles to meet specific requirements under inhomogeneous conditions, such as graded temperature fields and non-uniformly distributed loads. The potential applications of AFG structures are also under investigation. While many studies focus on material properties of FG structures in the thickness direction, research on AFG beams (piles) is limited (Zhang et al., 2019; Yang et al., 2023; Xuanming et al., 2022; Zhechen et al., 2025; Wei et al., 2025; Mohammed et al., 2019).

This study presents forced-vibration analyses of AFG piles resting on temperature-dependent soil. The temperature dependency of the soil’s reaction to the pile is modeled by a new temperature-dependent Winkler configuration. Recent advancements in numerical methods for the pile–soil interaction, particularly the differential quadrature method (DQM), have enabled the development of efficient solutions for system inhomogeneity (Bai et al., 2021a; Bai et al., 2019; Bai et al., 2021b). However, its application to thermo-mechanically coupled energy piles remains limited. This study extends the application of DQM to address temperature-dependent Winkler foundations and non-uniform pile properties, filling a critical gap in dynamic analysis. The framework of this study is as follows: in Section 2, the mathematical formula is deduced. The temperature dependency of the soil–pile interaction is introduced. The variation of the material properties of the AFG pile is modeled based on power–law relationships. The governing equation of vibration of the pile is deduced by Hamilton’s principle. In Section 3, the numerical solution of the governing equations is obtained with the differential quadrature method. In Section 4, the forced vibrational responses are displayed for several cases, and the effects of the non-linearity of the material properties and the temperature distribution are discussed. In Section 5, some conclusions are drawn.

2 Mathematical modeling

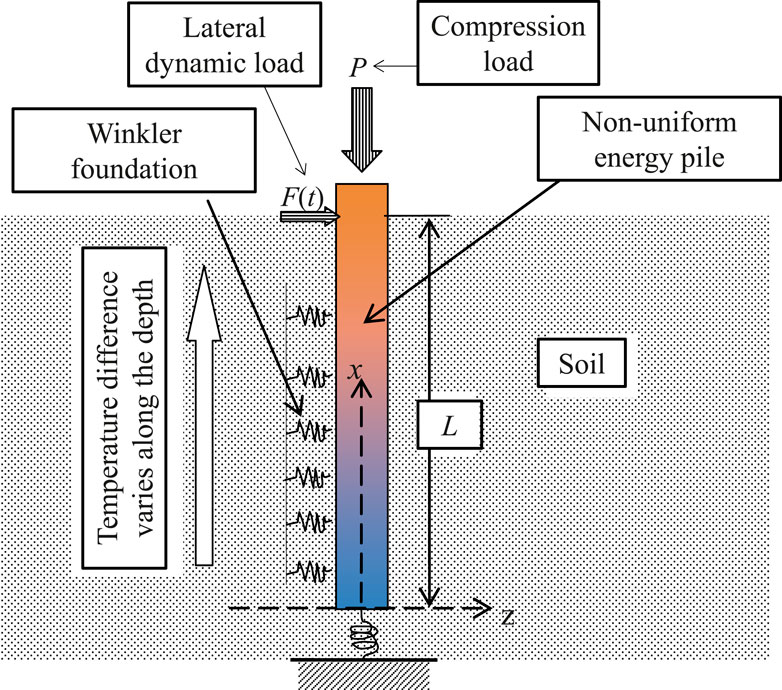
As shown in Figure 1, the sketch of a non-uniform energy pile embedded in vertically inhomogeneous soil with a non-uniform distributed temperature is presented. The length of the pile is denoted as L, and the cross-sectional area is denoted as A. The origin of the Cartesian coordinate system is set on the bottom of the pile. The x and z directions are along the depth and horizontal directions, respectively. Young’s modulus and the mass density of the pile are denoted as $E\left(x\right)$ and $\rho \left(x\right)$, respectively. It should be mentioned that the cross-sectional area is constant, while Young’s modulus and the mass density vary along the x direction. A vertical compressive load $P$ and a horizontal periodic force $F\left(t\right)$ are applied on the top of the pile. The bottom of the pile is assumed to be fixed. The pile is modeled by Euler’s beam theory, and the displacement of the neutral layer in $z$ direction is denoted as $w\left(x\right)$. The soil–pile interaction is modeled and referred to the p–y theory. The reaction of the Winkler foundation is calculated as follows:

$p\left(x\right)=kw\left(x\right).(1)$

Figure 1

Figure 1. Model of the non-uniform energy pile under forced vibration load condition.

Here, k is the Winkler foundation stiffness coefficient. The linear model for the temperature-dependence coefficient k is based on the theory of thermal elasticity, assuming a linear change in the soil response with temperature. This assumption is reasonable within a low range of temperature changes and has been validated by multiple studies. In this study, the reaction of the Winkler foundation is assumed to be temperature-dependent, and the temperature dependency of k is assumed as follows:

$k=k_0\left[1+k_1\left(T-300\right)\right],(2)$

where $k$ is the modulus of the subgrade reaction considering the temperature effect, $k_0$ is the Winkler foundation stiffness when the temperature $T=300$ K, and $k_1$ measures the temperature dependence. The reference temperature T0 = T1 = 300 K corresponds to the annual average shallow geothermal temperature in temperate zones, which is consistent with ASHRAE guidelines for geothermal structures and field data (Zhang et al., 2019). With positive $k_0$, the Winkler foundation stiffness k increases with an increase in the temperature, and vice versa.

According to Euler’s beam theory, the displacements of the pile are expressed as follows:

$\overline{u}\left(x,z\right)=-z\frac{\partial w}{\partial x}.(3)$

$\overline{w}\left(x,z\right)=w\left(x\right).(4)$

The strain of the pile can be expressed as follows:

${\epsilon }_{xx}=-z\frac{{\partial }^{2}w}{\partial x^2}.(5)$

Including the temperature effect, the stress of the pile can be written as follows:

${\sigma }_{xx}=E\left(x\right)\left[{\epsilon }_{xx}-\alpha \left(x\right)△T\left(x\right)\right].(6)$

Here, $E\left(x\right)$ is Young’s modulus, and $\alpha \left(x\right)$ is the thermal expansion coefficient. The strain energy density can be expressed as follows:

${\mathrm{U}}_{\mathrm{e}}=\frac{1}{2}{\mathrm{\sigma }}_{\text{xx}}{\mathrm{\epsilon }}_{\text{xx}}=\frac{1}{2}\mathrm{E}\left(\mathrm{x}\right)\left[-\mathrm{z}\frac{{\mathrm{\partial }}^2\mathrm{w}}{\mathrm{\partial }{\mathrm{x}}^2}-\mathrm{\alpha }\left(\mathrm{x}\right)△\mathrm{T}\left(\mathrm{x}\right)\right]\left(-\mathrm{z}\frac{{\mathrm{\partial }}^2\mathrm{w}}{\mathrm{\partial }{\mathrm{x}}^2}\right).(7)$

The total strain energy is obtained by integrating the strain energy density in the domain of the pile, which is calculated as follows:

$U={\displaystyle \underset{0}{\overset{L}{\int }}}{\int }_A{U}_{e}dAdx=\frac{1}{2}{\displaystyle \underset{0}{\overset{L}{\int }}}{\int }_{A}E\left(x\right)\left[-z\frac{{\partial }^{2}w}{\partial x^2}-\alpha \left(x\right)△T\left(x\right)\right]\left(-z\frac{{\partial }^{2}w}{\partial x^2}\right)dAdx.(8)$

The variation of the total strain energy is calculated as follows:

$\delta U={\displaystyle \underset{0}{\overset{L}{\int }}}{\int }_{A}E\left(x\right)\left[-z^2\frac{{\partial }^{2}w}{\partial x^2}\delta \frac{{\partial }^{2}w}{\partial x^2}+\frac{1}{2}z\alpha \left(x\right)△T\left(x\right)\delta \frac{{\partial }^{2}w}{\partial x^2}\right]dAdx={\displaystyle \underset{0}{\overset{L}{\int }}}E\left(x\right)I\frac{{\partial }^{2}w}{\partial x^2}\delta \frac{{\partial }^{2}w}{\partial x^2}dx,(9)$

where I is calculated as $I={\int }_A{z}^{2}dA$.

During vibration, the kinetic energy of the pile can be calculated as follows:

$V=\frac{1}{2}{\displaystyle \underset{0}{\overset{L}{\int }}}{\int }_A\rho \left(x\right)\left[{\left(-z\frac{{\partial }^{2}w}{\partial x^2}\right)}^2+{\dot{w}}^2\right]dAdx.(10)$

The variation of the kinetic energy is calculated as follows:

$\delta V={\displaystyle \underset{0}{\overset{L}{\int }}}{\int }_A\rho \left(x\right)\left[\dot{w}\delta \dot{w}+z^2\frac{\partial \dot{w}}{\partial x}\delta \frac{\partial \dot{w}}{\partial x}\right]dAdx={\displaystyle \underset{0}{\overset{L}{\int }}}\rho \left(x\right)\left[A\dot{w}\delta \dot{w}+I\frac{\partial \dot{w}}{\partial x}\delta \frac{\partial \dot{w}}{\partial x}\right]dx.(11)$

The variation of the work done by the applied force P and F (t) with the damping effect included is written as follows:

$\delta W={\displaystyle \underset{0}{\overset{L}{\int }}}\left[P\frac{\partial w}{\partial x}\delta \frac{\partial w}{\partial x}-\left[p\left(x\right)+c\dot{w}\right]\delta w+F\left(t\right)\left(L-x\right)\delta \frac{{\mathrm{\partial }}^2\mathrm{w}}{\mathrm{\partial }{\mathrm{x}}^2}\right].(12)$

The Hamilton’s principle is applied as follows:

$\delta {\displaystyle \underset{t_1}{\overset{t_2}{\int }}}\left(V-U+W\right)dt={\displaystyle \underset{t_1}{\overset{t_2}{\int }}}\left(\delta V-\delta U+\delta W\right)dt=0.(13)$

On performing the substitution and calculation, one obtains

${\displaystyle \underset{t_1}{\overset{t_2}{\int }}}{\displaystyle \underset{0}{\overset{L}{\int }}}\left[\begin{array}{c}\rho \left(x\right)A\dot{w}\delta \dot{w}\\ +I\rho \left(x\right)\frac{\partial \dot{w}}{\partial x}\delta \frac{\partial \dot{w}}{\partial x}\\ +\left[-E\left(x\right)I\frac{{\partial }^{2}w}{\partial x^2}+F\left(t\right)\left(L-x\right)\right]\delta \frac{{\partial }^{2}w}{\partial x^2}\\ +P\frac{\partial w}{\partial x}\delta \frac{\partial w}{\partial x}\\ -\left[p\left(x\right)+c\dot{w}\right]\delta w\end{array}\right]dxdt=0.(14)$

Performing the calculation, one obtains

${\displaystyle \underset{t_1}{\overset{t_2}{\int }}}{\displaystyle \underset{0}{\overset{L}{\int }}}\left\{\begin{array}{c}-\rho \left(x\right)A\ddot{w}+\frac{\partial }{\partial x}\left[\rho \left(x\right)I\frac{\partial \ddot{w}}{\partial x}\right]\\ -\frac{{\partial }^2}{\partial x^2}\left[E\left(x\right)I\frac{d^{2}w}{d{x}^2}\right]-P\frac{{\partial }^{2}w}{\partial x^2}-\left(p+c\dot{w}\right)\end{array}\right\}\delta wdxdt=0,(15)$

and

$\left\{-\rho \left(x\right)I\frac{\partial \ddot{w}}{\partial x}+\frac{\partial }{\partial x}\left[E\left(x\right)I\frac{{\partial }^{2}w}{\partial x^2}\right]+P\frac{\partial w}{\partial x}+F\left(t\right)\right\}{\left(\delta w\right)}_{x=0}^{x=L}=0.(16)$

$\left\{F\left(t\right)\left(L-x\right)-E\left(x\right)I\frac{d^{2}w}{d{x}^2}\right\}\delta {\left(\frac{dw}{dx}\right)}_{x=0}^{x=H}=0.(17)$

For Equation 10, because $\delta w$ is arbitrary, it holds that

$-\rho \left(x\right)A\ddot{w}+\frac{\partial }{\partial x}\left[\rho \left(x\right)I\frac{\partial \ddot{w}}{\partial x}\right]-\frac{{\partial }^2}{\partial x^2}\left[E\left(x\right)I\frac{{\partial }^{2}w}{\partial x^2}\right]-P\frac{{\partial }^{2}w}{\partial x^2}-\left[p\left(x\right)+c\dot{w}\right]=0,(18)$

which is the governing equation of vibration. Equation 11 and Equation 12 represent the corresponding boundary conditions.

The material property function of the pile is modeled using the power-law relation, which is given by

$E\left(x\right)={\left(\frac{x}{L}\right)}^p\left(E_1-E_0\right)+E_0,0\le x\le L,(19)$

$\rho \left(x\right)={\left(\frac{x}{L}\right)}^p\left({\rho }_1-{\rho }_0\right)+{\rho }_0,0\le x\le L,(20)$

where $E_0$ and $E_1$ are Young’s modulus at $x=0$ and $x=L$, respectively. ${\rho }_0$ and ${\rho }_1$ are the mass density at $x=0$ and $x=L$, respectively. $p$ is the power-law index, which measures the changes in the material property.

Let us consider that the temperature distribution satisfies the following formula:

$T\left(x\right)={\left(\frac{x}{L}\right)}^s\left(T_1-T_0\right)+T_0,0\le X\le L,(21)$

where $T_0$ and $T_1$ denote the temperature of the bottom and the top of the pile, respectively. The power–law index $s$ measures the temperature changes along the depth direction. As the depth changes, the temperature varies. The action of the soil on the pile is dependent on the temperature; thus, the modulus of subgrade reaction $k$ in Equation 1 is variable for different depths.

3 Solution with differential quadrature methods

The governing Equation 8 is a nonlinear differential equation with variable coefficients, and it is difficult to obtain an analytical solution. Thus, numerical solutions will be achieved in the present study. The differential quadrature method effectively obtains the numerical solution of differential equations. Boundary conditions rigorously enforce fixed-base (x = 0) and force-balanced top (x = L) constraints. The non-uniform grid setting are employed to resolve boundary layers near x = 0, which is critical for high-stress gradients. The discrete points are established by $x_i\left(i=1,2,...,N\right)$ and $0=x_1<x_2<\cdots <x_{N-1}<x_N=L$. A non-uniform grid is divided as

$x_i=\frac{L}{2}\left[1-\mathit{cos}\frac{\left(N-i\right)\pi }{N-1}\right],\left(i=1,2,...,N\right).(22)$

The Lagrangian interpolator function is written as follows:

${\chi }_j\left(x_i\right)={\displaystyle \prod _{\begin{array}{c}k=1\\ k\ne j\end{array}}^N}\frac{x_i-x_k}{x_j-x_k},j=1,2,...,N.(23)$

Thus, the displacement at $x_i$ is given by

$w\left(x_i\right)={\displaystyle \sum _{j=1}^N}{\chi }_j\left(x_i\right)w\left(x_j\right).(24)$

The deviations of $w\left(x\right)$ are written as

$\frac{d^{k}w\left(x_i\right)}{d{x}^k}={\displaystyle \sum _{j=1}^N}\frac{d^k{\chi }_j\left(x_i\right)}{d{x}^k}w\left(x_j\right)={\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{ij}^{\left(k\right)}w\left(x_j\right),(25)$

where ${\mathrm{\Psi }}_{ij}^{\left(k\right)}=\frac{d^k{\chi }_j\left(x_i\right)}{d{x}^k}$, and it holds that

$\left\{\begin{array}{l}{\mathrm{\Psi }}_{ij}^{\left(1\right)}=\frac{{\displaystyle {\prod }_{\begin{array}{c}k=1\\ k\ne i,j\end{array}}^N}\left(x_i-x_k\right)}{{\displaystyle {\prod }_{\begin{array}{c}k=1\\ k\ne j\end{array}}^N}\left(x_j-x_k\right)},\left(i,j=1,2,...,N;i\ne j\right)\\ {\mathrm{\Psi }}_{ii}^{\left(1\right)}={\displaystyle \prod _{\begin{array}{c}k=1\\ k\ne i\end{array}}^N}\frac{1}{x_i-x_k}\end{array}\right.,(26)$

and

${\mathrm{\Psi }}_{ij}^{\left(k\right)}={\displaystyle \sum _{k=1}^N}{\mathrm{\Psi }}_{ik}^{\left(1\right)}{\mathrm{\Psi }}_{kj}^{\left(k-1\right)}={\displaystyle \sum _{k=1}^N}{\mathrm{\Psi }}_{ik}^{\left(2\right)}{\mathrm{\Psi }}_{kj}^{\left(k-2\right)}=\dots ={\displaystyle \sum _{k=1}^N}{\mathrm{\Psi }}_{ik}^{\left(k-1\right)}{\mathrm{\Psi }}_{kj}^{\left(1\right)},\left(i,j=1,2,...,N\right).(27)$

On substituting Equation 19 and Equation 20 into Equation 13, and re-writing it in the matrix form, one obtains the following:

$\left[L_{ij}\right]\left\{w_j\right\}+\left[S_{ij}\right]\left\{\frac{{\partial }^2{w}_j}{\partial t^2}\right\}+\left[G_{ij}\right]\left\{\frac{\partial w_j}{\partial t}\right\}=0,(28)$

where

$\begin{array}{l}{L}_{ij}=-\frac{{\partial }^{2}E\left(x_i\right)}{\partial x^2}I{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{ij}^{\left(2\right)}w\left(x_j\right)-2\frac{\partial E\left(x_i\right)}{\partial x}I{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{ij}^{\left(3\right)}w\left(x_j\right)\\ -E\left(x_i\right)I{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{ij}^{\left(4\right)}w\left(x_j\right)-P{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{ij}^{\left(2\right)}w\left(x_j\right)-k\left(L-x_i\right){\displaystyle \sum _{j=1}^N}{\chi }_j\left(x_i\right)\\ S_{ij}=-\rho \left(x_i\right)A{\displaystyle \sum _{j=1}^N}{\chi }_j\left(x_i\right)+\frac{\partial \rho \left(x_i\right)}{\partial x}I{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{ij}^{\left(1\right)}+\rho \left(x_i\right)I{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{ij}^{\left(2\right)}\\ G_{ij}=-c{\displaystyle \sum _{j=1}^N}{\chi }_j\left(x_i\right)\frac{\partial w\left(x_j\right)}{\partial t}.\end{array}$

At boundary $x=0$ and $x=L$, i.e., $i=1$ and $i=N$, the boundary equation must hold. By substituting Equation 19 and Equation 20 into Equation 11 and Equation 12, one obtains

$\left\{\begin{array}{l}\left[B_{Nj}\right]\left\{w_j\right\}+\left[H_{Nj}\right]\left\{\frac{{\partial }^2{w}_j}{\partial t^2}\right\}+F\left(t\right)=0\\ {\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{Nj}^{\left(2\right)}w\left(x_j\right)=0\end{array}\right.\text{\hspace{0.5em}for\hspace{1em}}i=N,(29)$

and

$\left\{\begin{array}{c}{\displaystyle \sum _{j=1}^N}{\chi }_j\left(x_1\right)w\left(x_j\right)=0\\ {\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{1j}^{\left(1\right)}w\left(x_j\right)=0\end{array}\right.\text{\hspace{1em}for\hspace{1em}}i=1,(30)$

where

$B_{Nj}=\frac{\partial E\left(x_N\right)}{\partial x}I{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{Nj}^{\left(2\right)}+E\left(x_N\right)I{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{Nj}^{\left(3\right)}+P{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{Nj}^{\left(1\right)}.(31)$

$H_{Nj}=-\rho \left(x_N\right)I{\displaystyle \sum _{j=1}^N}{\mathrm{\Psi }}_{Nj}^{\left(1\right)}\frac{{\partial }^{2}w\left(x_j\right)}{\partial t^2}.(32)$

In the present case, at the boundary, Equation 23 does not hold. Therefore, by replacing the first, second, (N-1)th, and (N)th low in Equation 23 by Equation 24 and Equation 25, a governing equation with boundary equation is obtained in the following form:

$\left[{\overline{L}}_{ij}\right]\left\{w_j\right\}+\left[{\overline{S}}_{ij}\right]\left\{\frac{{\partial }^2{w}_j}{\partial t^2}\right\}+\left[{\overline{G}}_{ij}\right]\left\{\frac{\partial w_j}{\partial t}\right\}=\left\{F_i\right\}.(33)$

In Equation 28,

$\left\{\begin{array}{l}{\overline{L}}_{ij}={\chi }_j\left(x_1\right),{\overline{S}}_{ij}=0,{\overline{G}}_{ij}=0\text{\hspace{1em}when\hspace{0.17em}}i=1\\ {\overline{L}}_{ij}={\mathrm{\Psi }}_{1j}^{\left(1\right)},{\overline{S}}_{ij}=0,{\overline{G}}_{ij}=0\text{\hspace{1em}when\hspace{0.17em}}i=2\\ {\overline{L}}_{ij}=L_{ij},{\overline{S}}_{Nj}=S_{Nj},{\overline{G}}_{ij}=0\text{\hspace{1em}when\hspace{0.17em}}i=3,4,...,N-2\\ {\overline{L}}_{ij}={\mathrm{\Psi }}_{Nj}^{\left(2\right)},{\overline{S}}_{ij}=0,{\overline{G}}_{ij}=0\text{\hspace{1em}when\hspace{0.17em}}i=N-1\\ {\overline{L}}_{ij}=B_{Nj},{\overline{S}}_{Nj}=H_{Nj},{\overline{G}}_{ij}=0\text{\hspace{1em}when\hspace{0.17em}}i=N\end{array}\right.,(34)$

and $\left\{F_i\right\}={\left\{0,0,...,0,F_0\right\}}^T$. Solve the matrix Equation 28, and the solution can be obtained.

Assuming harmonic excitation, i.e., $F\left(t\right)=F_0\mathit{exp}\left(j\omega t\right)$, where $\omega$ is the excitation frequency. The response of the pile can be expressed as $w\left(x_j\right)=W\left(x_j\right)e^{j\left(\omega t-\varphi \right)}$, and substituting it into Equation 28, one obtains

$\left\{W_j\right\}={\left\{\left[{\overline{L}}_{ij}\right]-{\omega }^2\left[{\overline{S}}_{ij}\right]+j\omega \left[{\overline{G}}_{ij}\right]\right\}}^{-1}\left\{F_i\right\}\mathit{exp}\left(j\varphi \right).(35)$

The maximum deflection occurs at $x=L$, which can be expressed as

${\mathrm{W}}_{\mathrm{M}}={\left\{{\left[{\overline{\mathrm{L}}}_{\text{ij}}-{\mathrm{\omega }}^2{\overline{\mathrm{S}}}_{\text{ij}}+\mathrm{j}\omega {\overline{\mathrm{G}}}_{\text{ij}}\right]}^{-1}\right\}}_{\text{NN}}{\mathrm{F}}_0.(36)$

4 Results and discussions

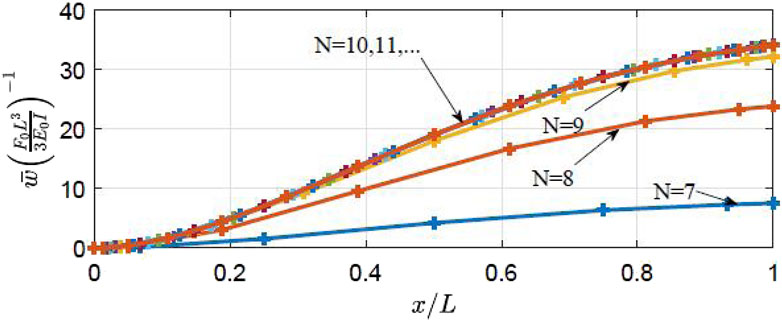
To verify the convergence of the grid division, the computational results for different numbers of nodes (N) are compared, and the convergence of the differential quadrature method is verified. The Newmark-β method is adopted for guaranteeing unconditional stability. The geometric dimensions are set as L = 1 m, b = 0.1 L, I = b⁴/12, and the vertical force P = 0. The material properties are E₀ = E₁ = 100 MPa, ρ₀ = ρ₁ = 9,870 kg/m³, k₀ = k₁ = 0, and T₀ = T₁ = 300 K. In such cases, the first-order resonance frequency is $\frac{{1.875104}^2}{L^2}\sqrt{\frac{E_{0}I}{{\rho }_{0}A}}$ . The first-order mode shapes for different node numbers (N) are shown in Figure 2. It is shown that when the node number is less than 10, the errors are relatively high, leading to unreliable results. When the node number is no less than 10, it leads to a congruent result. The node number is selected as N = 30 in the following discussions to obtain reliable results.

Figure 2

Figure 2. Convergence analysis.

In order to discuss the forced vibrational behavior, in the following contexts, the geometric dimensions are selected as $=1\mathrm{m},$ $b=h=0.1L$, and $I=b{h}^3/12$. The dimensionless excitation frequency is defined as $\overline{\omega }=\omega {\left(\frac{{1.875104}^2}{L^2}\sqrt{\frac{E_{0}I}{{\rho }_{0}A}}\right)}^{-1}$. The dimensionless amplitude is defined as $\overline{W}=W_M{\left(\frac{F_0{L}^3}{3E_{0}I}\right)}^{-1}$.

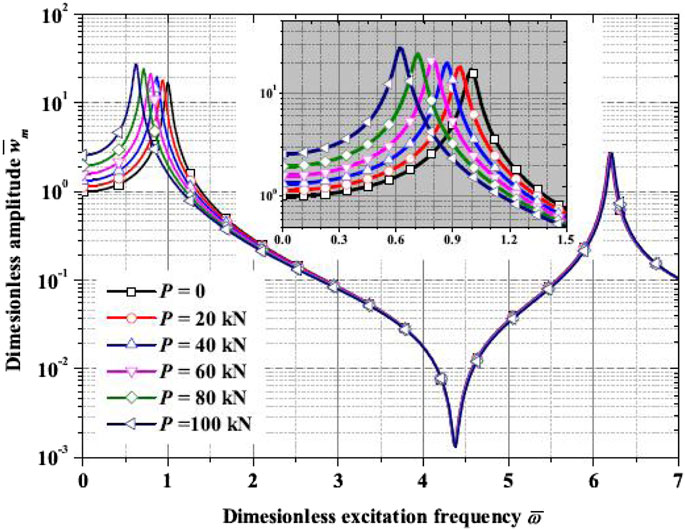
Figure 3 shows the dimensionless amplitude–excitation frequency curves for different compressive loads P in a uniform temperature field (T₀ = T₁ = 300 K, E₀ = E₁ = 100 MPa, ρ₀ = ρ₁ = 9,870 kg/m³, p = 0, and k = 0). An excitation frequency of 0 indicates static lateral force, and the amplitude reduces to a static deflection. It is observed that a larger compressive load causes a larger static deflection. It is also seen that resonance occurs when the frequency equals some specific value, and such a frequency is the so-called resonance frequency. When the compressive load P = 0, the dimensionless resonance frequency for the first-order mode equals 1. As the compressive load increases, the resonance frequency for the first-order mode decreases, whereas the resonance peak increases slightly. On the other hand, the second-order mode’s resonance frequency and resonance peak are less affected by the compressive load P. It is worth noting that axial compression primarily affects the first buckling mode of the pile, with minimal impact on higher modes. This is because the axial compressive force mainly acts at the top of the pile, resulting in less bending deformation at the fixed bottom end. Some dimensionless frequency and resonance peak values for the first-order and second-order modes are listed in Table 1.

Figure 3

Figure 3. Dimensionless amplitude–excitation frequency curves for different compressive loads P.

Table 1

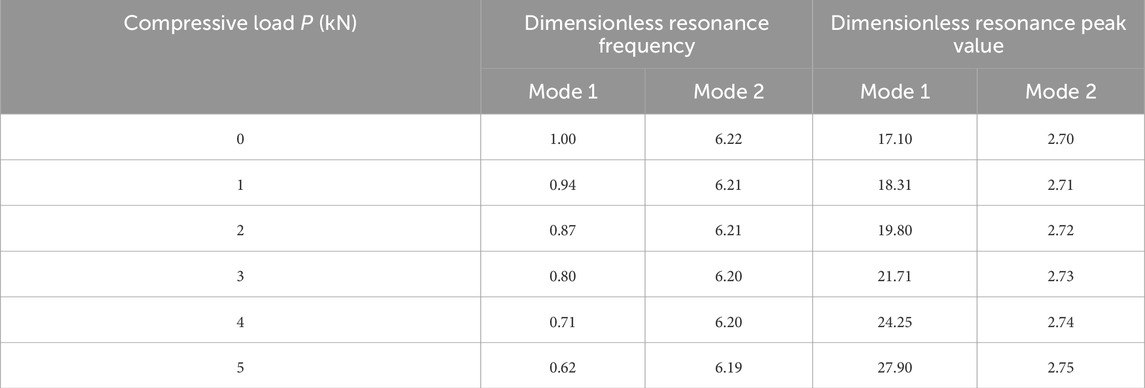
Table 1. Data of dimensionless frequencies $\omega {\left(\frac{{1.875104}^2}{L^2}\sqrt{\frac{E_{0}I}{{\rho }_{0}A}}\right)}^{-1}$ and resonance peak values $W_M{\left(\frac{F_0{L}^3}{3E_{0}I}\right)}^{-1}$ for the first-order and second-order modes with a different compressive load.

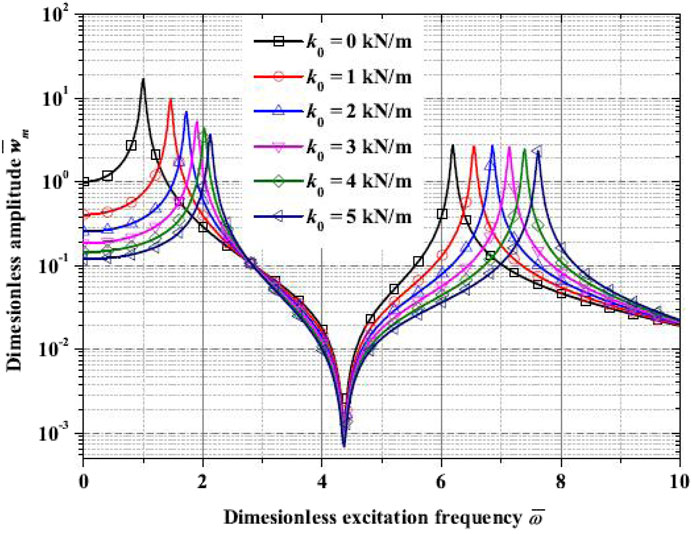
Figure 4 presents the dimensionless amplitude–excitation frequency curves for different Winkler foundation constants k₀ in a uniform temperature field (T0 = T1 = 300 K, E0 = E1 = 100 MPa, ρ0 = ρ1 = 9,870 kg/m³, and p = 0.5). When the excitation frequency is 0 (i.e., the case of a static deflection problem), if k0 is 0, the dimensionless amplitude is 1. As k0 increases, there is a reduction in static deflection. Furthermore, a higher Winkler foundation constant results in higher resonance frequencies for different modes. The resonance peak for the first-order mode decreases with a higher Winkler foundation constant, while the resonance peak for the second-order mode is rarely affected by the Winkler foundation constant. The relevant data are listed in Table 2.

Figure 4

Figure 4. Dimensionless amplitude–excitation frequency curves for different temperatures.

Table 2

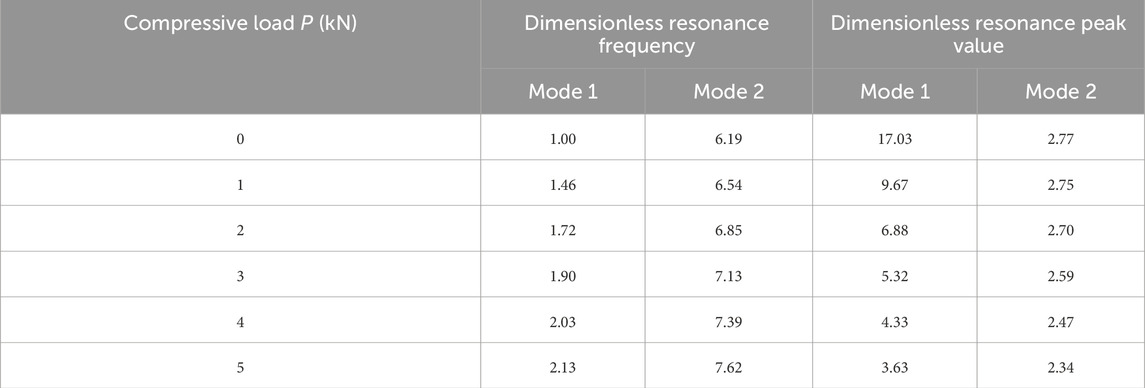
Table 2. Data of dimensionless frequencies $\omega {\left(\frac{{1.875104}^2}{L^2}\sqrt{\frac{E_{0}I}{{\rho }_{0}A}}\right)}^{-1}$ and resonance peak values $W_M{\left(\frac{F_0{L}^3}{3E_{0}I}\right)}^{-1}$ for the first-order and second-order modes with different k₀.

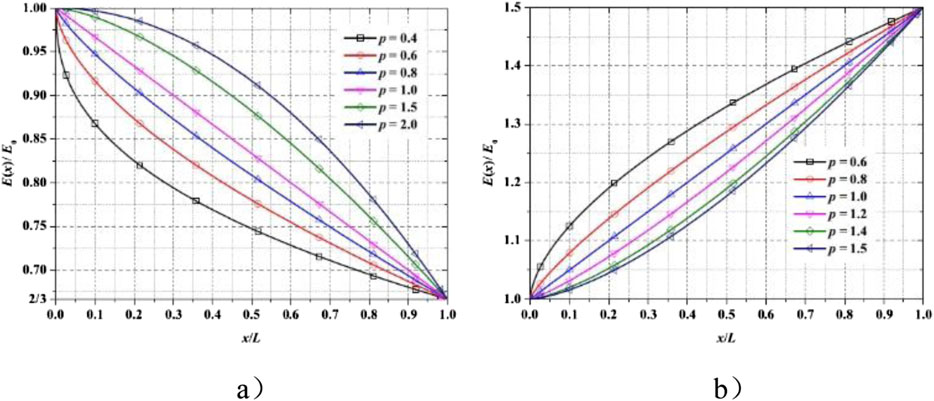
Figures 5a, b show two typical distributions of the AFG pile. For distribution 1 (shown in Figure 5a), Young’s modulus is higher at the clamped end (x = 0) and decreases when x/L increases from 0 to 1. For distribution 2 (shown in Figure 5b), Young’s modulus is smaller at the clamped end (x = 0) and increases when x/L increases from 0 to 1. If the power index p = 1, Young’s modulus varies in linearity from one end to the other. If the power index p is less than 1, the variation in Young’s modulus is more acute near the clamped end. On the contrary, if p is more significant than 1, the variation in Young’s modulus is more acute near the free end.

Figure 5

Figure 5. Two typical distributions of pile materials. (a) Distribution 1 and (b) distribution 2.

Figures 6a, b illustrate the dimensionless amplitude–excitation frequency curves with different p for distribution 1 and distribution 2, respectively (T₁ = T₂ = 300 K, k₀ = 5 kN/m). The stiffness for distribution 1 focuses on the clamped end, while the stiffness for distribution 2 focuses on the free end. It is seen in the figure that for distribution 1, the static deflection is more considerable for a low value of p, while the static deflection for distribution 2 is more considerable for higher-power indices of p. Furthermore, the resonance frequency for distribution 1 increases with p, while the resonance frequency for distribution 2 decreases with an increase in p. Furthermore, the resonance peak for distribution 1 decreases slightly as p increases, while the resonance frequency for distribution 2 increases slightly with an increase in p.

Figure 6

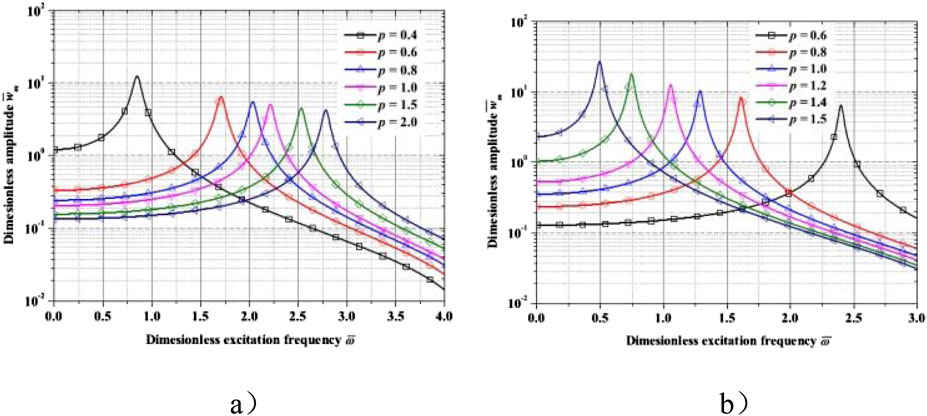
Figure 6. Dimensionless amplitude–excitation frequency curves for different pile material distribution. (a) Distribution 1 and (b) distribution 2.

Figures 7a, b illustrate the dimensionless amplitude–excitation frequency curves with different E1 for p = 0.5 and p = 1.5, respectively (T₀ = T₁ = 300 K, E₀ = E₁ = 100 MPa, and ρ₀ = 9,870 kg/m³, k₁ = 0). As shown in both the figures, Young’s modulus at the clamped end is set as E₀ = 100 MPa. It is found that for p = 0.5 (Figure 7a), the resonance frequency increases as c increases, while for p = 1.5 (Figure 7b), the resonance frequency decreases as E₁ increases.

Figure 7

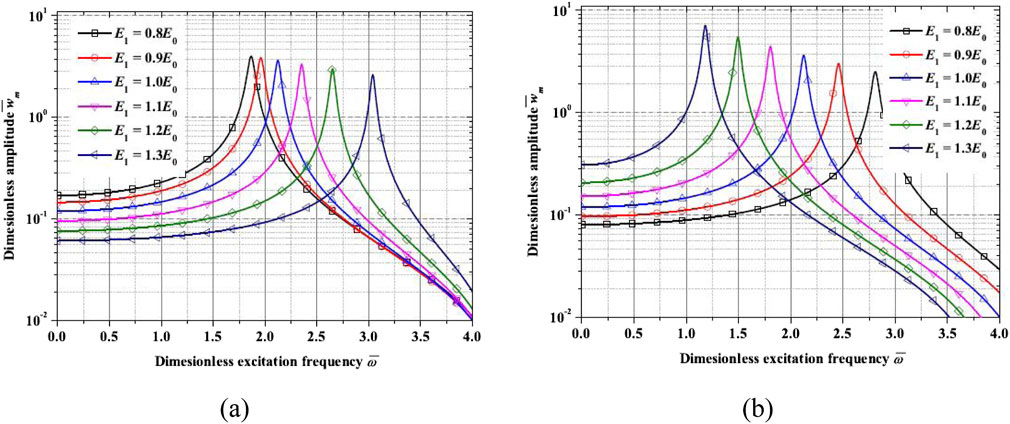
Figure 7. Dimensionless amplitude–excitation frequency curves for different parameters p. (a) k1 = 0.01, (b) k1 = −0.01.

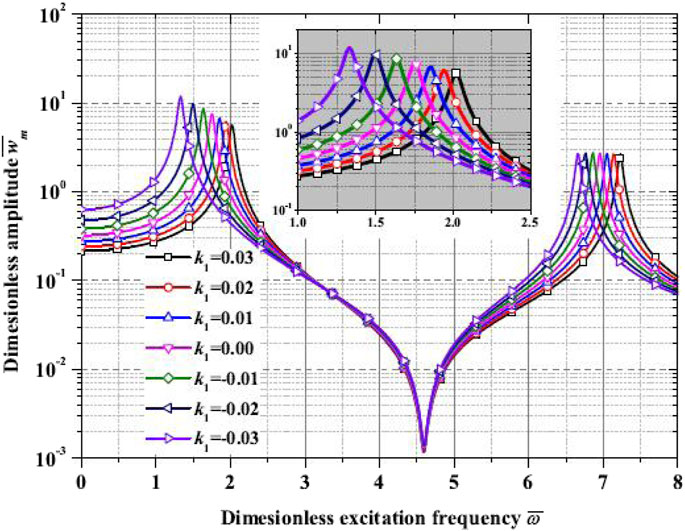
Figure 8 shows the dimensionless amplitude–excitation frequency curves with different k₁ (T₀ = 300 K, T₁ = 330 K, s = 1, k₀ = 1 kN/m, P = 20 kN, E₀ = 100 MPa, E₁ = 80 MPa, and p = 1). When the excitation frequency is 0 (i.e., the case of the static deflection problem), as k1 increases, the static deflection decreases. Furthermore, a higher value of k1 results in higher resonance frequencies for different modes. The temperature gradient affects the soil stiffness through the thermal expansion coefficient. A positive temperature gradient (k1 > 0) increases the soil stiffness as thermal expansion increases the spacing between the soil particles. Conversely, a negative temperature gradient (k1 < 0) decreases the soil stiffness as thermal contraction increases the spacing between soil particles. The resonance peak for the first-order mode decreases with an increase in the Winkler foundation constant, while the resonance peak for the second-order mode is rarely affected by k1. The relevant data are listed in Table 3. Note that k1 introduced in Equation 1 is the parameter that measures temperature dependence. A positive k1 increases the Winkler foundation stiffness as the temperature increases, and vice versa. Therefore, a positive k1 increases the stiffness of the pile, resulting in a higher resonance frequency, while a negative k1 decreases the stiffness of the pile, resulting in a lower resonance frequency.

Figure 8

Figure 8. Dimensionless amplitude–excitation frequency curves for different k1.

Table 3

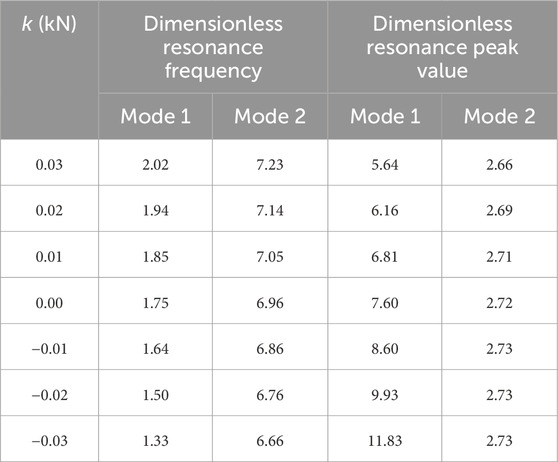
Table 3. Data of dimensionless frequencies $\omega {\left(\frac{{1.875104}^2}{L^2}\sqrt{\frac{E_{0}I}{{\rho }_{0}A}}\right)}^{-1}$ and resonance peak values $W_M{\left(\frac{F_0{L}^3}{3E_{0}I}\right)}^{-1}$ for the first-order and second-order modes with different k₁.

Figure 9 illustrates the dimensionless amplitude–excitation frequency curves with a fixed temperature at the clamped end (T₀ = 300 K) for k₁ = 0.01 and k₁ = −0.01, respectively (E₀ = 100 MPa, E₁ = 80 MPa, s = 1, P = 20 kN, and p = 1). The results illustrate the dimensionless amplitude–excitation frequency curves with a fixed temperature at the free end (T₁ = 300 K) for k₁ = 0.01 and k₁ = −0.01 (E₀ = 100 MPa, E₁ = 80 MPa, s = 1, P = 20 kN, and p = 1). It is seen that for a positive k₁, the resonance frequency increases as T₁ increases. For a negative k_1, the resonance frequency decreases as T₁ increases. Furthermore, this study explores the interaction between temperature gradients and material gradients. The results indicate that the interplay between thermal softening at the high-temperature end and the grading of E(x) significantly influences the vibration response of the pile.

Figure 9

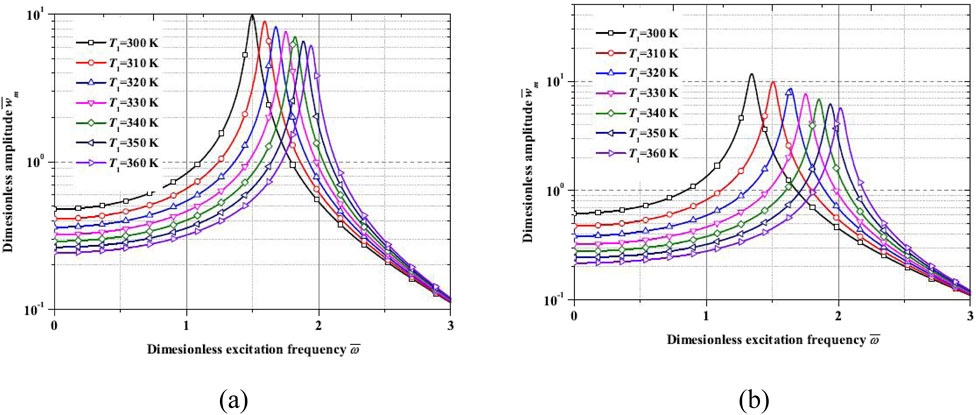
Figure 9. Dimensionless amplitude–excitation frequency curves for different temperatures. (a) k1 = 0.01, (b) k1 = −0.01.

5 Conclusion

In this study, forced vibration analysis of an energy pile resting on temperature-dependent soil is presented with consideration of a non-uniform distributed temperature. A temperature-dependent Winkler model is proposed to model the temperature dependency of the soil’s reaction to the pile. The governing equations are achieved by Hamilton’s principle. Numerical solutions are obtained with the differential quadrature method. Effects of the temperature-dependent Winkler model and the non-linearity of material properties of the pile are discussed. The investigation demonstrates that the temperature-dependent Winkler foundation significantly enhances the suppression of high-frequency vibrations in the pile. Specifically, under a positive temperature gradient, the first resonance frequency increases by approximately 15%, while the second resonance frequency remains largely unaffected. Results show that the temperature dependency of the Winkler foundation, the inhomogeneity effects of the pile, and the non-uniformity of the temperature field could significantly influence the excitation frequency and vibration amplitude of the pile.

The proposed model aids in optimizing energy pile designs for regions prone to seismic activity, where temperature fluctuations may alter soil–structure interaction. For instance, negative k values (indicating reduced soil stiffness at high temperatures) could amplify resonance risks in geothermal piles under dynamic loads (Bourne-Webb et al., 2019; Bourne-Webb and Bodas-Freitas, 2020). For a specific seismic design, temperature rise may reduce soil stiffness, lowering the system’s natural frequencies and potentially resonating with the earthquake spectra. Designers should incorporate site-specific thermal profiles into dynamic analysis. Future field validations in real energy foundations are recommended. In addition, relevant potential research studies include experimental validation of the temperature-dependent Winkler model using scaled pile–soil tests, coupled thermo-hydro-mechanical analysis incorporating pore–water effects, and prototype monitoring of energy piles in district heating systems to refine design guidelines.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

ZZ: Formal Analysis, Methodology, Validation, Writing – original draft, Investigation, Software, and Visualization. ZL: Formal Analysis, Methodology, Validation, Writing – original draft, Conceptualization, Data curation, Funding acquisition, Project administration, Resources, Supervision, and Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors acknowledge the financial support from the National Science and Technology Major Project (2024ZD1403304), the Project of Hetao Shenzhen-Hong Kong Science and Technology Innovation Cooperation Zone (HZQB-KCZYB-2020083), the Shenzhen Science and Technology Program (No.KCXFZ20230731093901003), and the National Science Foundation of China (U24B20113).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anoyatis, G., Mylonakis, G., and Tsikas, A. (2019). An analytical continuum model for axially loaded end-bearing piles in inhomogeneous soil. Int. J. Numer. Anal. Methods Geomech. 43, 1162–1183. doi:10.1002/nag.2886

CrossRef Full Text | Google Scholar

Auersch, L. (2019). Compliance and damping of piles for wind tower foundation in non-homogeneous soils by the finite-element boundary-element method. Soil Dyn. Earthq. Eng. 120, 228–244. doi:10.1016/j.soildyn.2018.12.005

CrossRef Full Text | Google Scholar

Aylin, N., Ali, N., Jean-Michel, P., and Anh-Minh, T. (2023a). Cyclically thermally-activated pile under combined axial/horizontal loads in saturated clay. Géotechnique Letters 13, 1–17. doi:10.1680/jgele.22.00079

CrossRef Full Text | Google Scholar

Aylin, N., Ali, N., Jean-Michel, P., and Anh-Minh, T. (2023b). Small-scale cyclically thermally-activated pile under inclined mechanical loads. Acta Geotechnica 18, 1–14. doi:10.1007/s11440-023-01807-6

CrossRef Full Text | Google Scholar

Bagheri, H., Kiani, Y., and Eslami, M. (2018). Asymmetric thermal buckling of temperature dependent annular FGM plates on a partial elastic foundation. Comput. Math. Appl. 75, 1566–1581. doi:10.1016/j.camwa.2017.11.021

CrossRef Full Text | Google Scholar

Bahrami, A., and Nikraz, H. (2017). Generalized Winkler support properties for far field modeling of laterally vibrating piles. Soil Dyn. Earthq. Eng. 92, 684–691. doi:10.1016/j.soildyn.2016.09.017

CrossRef Full Text | Google Scholar

Bai, B., Nie, Q., ZhangYike, W. X., and Hu, W. (2021b). Cotransport of heavy metals and SiO₂ particles at different temperatures by seepage. J. Hydrology 597, 125771. doi:10.1016/j.jhydrol.2020.125771

CrossRef Full Text | Google Scholar

Bai, B., Yang, G., Tao, Li, and Yang, G. (2019). A thermodynamic constitutive model with temperature effect based on particle rearrangement for geomaterials. Mech. Mater. 139, 103180. doi:10.1016/j.mechmat.2019.103180

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Cai, G., Hu, W., and Yang, G. (2021a). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotechnics 137 (8), 104272. doi:10.1016/j.compgeo.2021.104272

CrossRef Full Text | Google Scholar

Bourne-Webb, P., Freitas, T. B., and Assunção, R. F. (2019). A review of pile-soil interactions in isolated, thermally-activated piles. Comput. Geotech. 108, 61–74. doi:10.1016/j.compgeo.2018.12.008

CrossRef Full Text | Google Scholar

Bourne-Webb, P. J., and Bodas-Freitas, T. M. (2020). Thermally-activated piles and pile groups under monotonic and cyclic thermal loading–A review. Renew. Energy 147, 2572–2581. doi:10.1016/j.renene.2018.11.025

CrossRef Full Text | Google Scholar

Bourne-Webb, P. J., Bodas Freitas, T. M., and Freitas Assunção, R. M. (2015). Soil–pile thermal interactions in energy foundations. Géotechnique 66, 167–171. doi:10.1680/jgeot.15.T.017

CrossRef Full Text | Google Scholar

Chenglong, W., Lingfei, S., Hanlong, L., Abdelmalek, B., Gang-Qiang, K., and Xuanming, D. (2025). Analysis of energy piles under cyclic axial loads and impact of loading amplitudes. Can. Geotech. J. 62, 1–21. doi:10.1139/cgj-2024-0776

CrossRef Full Text | Google Scholar

Du, G., Wang, A., Li, L., and Zhang, D. (2018). Calculation approach for lateral bearing capacity of single precast concrete piles with improved soil surrounds. Adv. Civ. Eng. 2018, e5127927. doi:10.1155/2018/5127927

CrossRef Full Text | Google Scholar

Fattah, M. Y., Karim, H. H., and Al-Recaby, M. K. M. (2020). Dynamic response of pile group model in sandy soil to lateral excitation. IOP Conf. Ser. Mater Sci. Eng. 737, 012091. doi:10.1088/1757-899X/737/1/012091

CrossRef Full Text | Google Scholar

Feng, S., Liu, X., and Cui, H. (2017). Dynamical response of an elastic supporting pile embedded in saturated soil under horizontal vibration. Civ. Eng. J. 26, 99–113. doi:10.14311/CEJ.2017.02.0010

CrossRef Full Text | Google Scholar

Filipich, C. P., and Rosales, M. B. (2002). A further study about the behaviour of foundation piles and beams in a Winkler–Pasternak soil. Int. J. Mech. Sci. 44, 21–36. doi:10.1016/S0020-7403(01)00087-X

CrossRef Full Text | Google Scholar

Huaibo, S., Huafu, P., Jean-Michel, P., Anh-Minh, T., and Chao, Z. (2023). A simple load transfer method for energy pile groups. Computers and Geotechnics 159, 105483. doi:10.1016/j.compgeo.2023.105483

CrossRef Full Text | Google Scholar

Huaibo, S., Jean-Michel, P., Anh-Minh, T., and Huafu, P. (2025). Thermally-induced long-term behavior of energy piles under inclined load in saturated clay. Can. Geotech. J. 62, 1–23. doi:10.1139/cgj-2024-0416

CrossRef Full Text | Google Scholar

Huang, J., McCartney, J. S., Perko, H., Johnson, D., Zheng, C., and Yang, Q. (2019). A novel energy pile: the thermo-syphon helical pile. Appl. Therm. Eng. 159, 113882. doi:10.1016/j.applthermaleng.2019.113882

CrossRef Full Text | Google Scholar

Jiang, C., Li, Y., Liu, L., and Lin, H. (2018). Nonlinear analysis of flexible pile near undrained clay slope under lateral loading. Adv. Civ. Eng. 2018, 6817362. doi:10.1155/2018/6817362

CrossRef Full Text | Google Scholar

Jincheng, F., Shijin, F., Yong, Z., Wang, X., and Hong-Xin, C. (2025). Load–displacement response and interaction behavior of energy pile groups under combined mechanical and cyclic thermal loading. Can. Geotech. J. 62, 1–23. doi:10.1139/cgj-2024-0790

CrossRef Full Text | Google Scholar

Karatzia, X., and Mylonakis, G. (2017). Horizontal stiffness and damping of piles in inhomogeneous soil. J. Geotech. Geoenvironmental Eng. 143, 04016113. doi:10.1061/(ASCE)GT.1943-5606.0001621

CrossRef Full Text | Google Scholar

Khalil, M. M., Hassan, A. M., and Elmamlouk, H. H. (2020). Dynamic behavior of pile foundations under vertical and lateral vibrations: review of existing codes and manuals. HBRC J. 16, 39–58. doi:10.1080/16874048.2020.1729586

CrossRef Full Text | Google Scholar

Le, Y., Wang, N., Hu, W., Geng, D., and Jiang, Y. (2020). Torsional dynamic impedance of a stepped pile based on the wedged soil model. Comput. Geotech. 128, 103854. doi:10.1016/j.compgeo.2020.103854

CrossRef Full Text | Google Scholar

Lei, H., Zhaowei, D., and Chunyu, S. (2025). A novel three-dimensional analytical model for the thermomechanical responses of energy piles and the surrounding soil based on thermoelastic theory. Int J Numer Anal Meth Geomech. doi:10.1002/nag.4010

CrossRef Full Text | Google Scholar

Long, C., Yifan, H., Zi, Y., Yang, Z., Gang-Qiang, K., and Yonghui, C. (2024). Centrifuge modeling of end-bearing slender energy pile performance under temperature cycles. Can. Geotech. J. 62 1–13. doi:10.1139/cgj-2023-0357

CrossRef Full Text | Google Scholar

Lu, Z., Wang, L., Guo, Z., Hong, Y., and Zhang, L. (2025). The microfluidic in geo-energy resources: current advances and future perspectives. Advances in Geo-Energy Research 16.

CrossRef Full Text | Google Scholar

Moghaddasi, H., Shahbodagh, B., and Khalili, N. (2020). Lateral vibration of piles and pile groups in nonhomogeneous transversely isotropic media. Int. J. Geomech. 20, 04020124. doi:10.1061/(ASCE)GM.1943-5622.0001753

CrossRef Full Text | Google Scholar

Mohamad, H., Soga, K., and Amatya, B. (2014). Thermal strain sensing of concrete piles using brillouin optical time domain reflectometry. Geotech. Test. J. 37, 1–14. doi:10.1520/gtj20120176

CrossRef Full Text | Google Scholar

Mohammed, F., Abdelmalek, B., John, M., and Chris, H. (2019). Effects of cyclic temperature variations on thermal response of an energy pile under a residential building. J. Geotech. Geoenviron. Eng. 145, 04019066. doi:10.1061/(ASCE)GT.1943-5606.0002147

CrossRef Full Text | Google Scholar

Mouadh, R., Diana, S., and Phil, V. (2025). Energy pile displacements due to cyclic thermal loading at different mechanical load levels. Acta Geotechnica 20, 3067–3086. doi:10.1007/s11440-025-02556-4

CrossRef Full Text | Google Scholar

Prendergast, L. J., and Gavin, K. (2016). A comparison of initial stiffness formulations for small-strain soil–pile dynamic Winkler modelling. Soil Dyn. Earthq. Eng. 81, 27–41. doi:10.1016/j.soildyn.2015.11.006

CrossRef Full Text | Google Scholar

Rui, Y., and Soga, K. (2019). Thermo-hydro-mechanical coupling analysis of a thermal pile. Proc. Inst. Civ. Eng-Geotech Eng. 172, 155–173. doi:10.1680/jgeen.16.00133

CrossRef Full Text | Google Scholar

Safarpour, H., Hajilak, Z. E., and Habibi, M. (2019). A size-dependent exact theory for thermal buckling, free and forced vibration analysis of temperature dependent FG multilayer GPLRC composite nanostructures restring on elastic foundation. Int. J. Mech. Mater Des. 15, 569–583. doi:10.1007/s10999-018-9431-8

CrossRef Full Text | Google Scholar

Semmah, A., Heireche, H., Bousahla, A. A., and Tounsi, A. (2019). Thermal buckling analysis of SWBNNT on Winkler foundation by non local FSDT. Adv. Nano Res. 7, 89.

Google Scholar

Shen, H.-S., and Li, Q. (2004). Postbuckling of shear deformable laminated plates resting on a tensionless elastic foundation subjected to mechanical or thermal loading. Int. J. Solids Struct. 41, 4769–4785. doi:10.1016/j.ijsolstr.2004.02.015

CrossRef Full Text | Google Scholar

Sung, C., Park, S., Lee, S., Oh, K., and Choi, H. (2018). Thermo-mechanical behavior of cast-in-place energy piles. Energy 161, 920–938. doi:10.1016/j.energy.2018.07.079

CrossRef Full Text | Google Scholar

Tu, W., Huang, M., Gu, X., and Chen, H.-P. (2020). Nonlinear dynamic behavior of laterally loaded composite caisson-piles foundation under scour conditions. Mar. Georesources Geotechnol. 38, 1265–1280. doi:10.1080/1064119X.2020.1724217

CrossRef Full Text | Google Scholar

Wang, N., Le, Y., Hu, W., Fang, T., Zhu, B., Geng, D., et al. (2020). New interaction model for the annular zone of stepped piles with respect to their vertical dynamic characteristics. Comput. Geotech. 117, 103256. doi:10.1016/j.compgeo.2019.103256

CrossRef Full Text | Google Scholar

Wei, Q., Hao, W., Haoran, O., Yuqi, P., Ye, C., and Xudong, D. (2025). Lateral cyclic load behaviour of pile in coastal clay improved by vacuum preloading (VPM). Int. J. Phys. Model. Geotech, 1–16. doi:10.1680/jphmg.25.00010

CrossRef Full Text | Google Scholar

Wu, D., Liu, H.-L., Kong, G.-Q., Ng, C. W. W., and Cheng, X.-H. (2018a). Displacement response of an energy pile in saturated clay. Proc. Inst. Civ. Eng-Geotech Eng. 171, 285–294. doi:10.1680/jgeen.17.00152

CrossRef Full Text | Google Scholar

Wu, W., Prendergast, L., and Gavin, K. (2018b). An iterative method to infer distributed mass and stiffness profiles for use in reference dynamic beam-Winkler models of foundation piles from frequency response functions. J. Sound. Vib. 431, 1–19. doi:10.1016/j.jsv.2018.05.049

CrossRef Full Text | Google Scholar

Xuanming, D., Dingxin, Z., Abdelmalek, B., Chenglong, W., and Gang-Qiang, K. (2022). Thermo-mechanical behaviour of energy piles in overconsolidated clay under various mechanical loading levels and thermal cycles. Renewable Energy 201. doi:10.1016/j.renene.2022.10.128

CrossRef Full Text | Google Scholar

Ya, Y., Lan, Q., Qingwen, L., Miao, M., and Lu, C. (2025). A review on heat transfer enhancement for energy pile system. J. Therm. Anal. Calorim. doi:10.1007/s10973-025-14402-6

CrossRef Full Text | Google Scholar

Yang, Z., Gang-Qiang, K., and Junjie, L. (2023). Field test on cross-sectional behaviors of a retaining energy pile subjected to horizontal loads. Can. Geotech. J. 61. doi:10.1139/cgj-2023-0270

CrossRef Full Text | Google Scholar

Zhang, J., Li, X., Jing, Y., and Han, W. (2019). Bridge structure dynamic analysis under vessel impact loading considering soil-pile interaction and linear soil stiffness approximation. Adv. Civ. Eng. 2019, e5173132. doi:10.1155/2019/5173132

CrossRef Full Text | Google Scholar

Zhechen, H., Barry, L., and Phillip, W. (2025). An experimental investigation of the time dependence of shaft friction for displacement piles in lightly over-consolidated clay. Géotechnique, 1–14. doi:10.1680/jgeot.24.01043

CrossRef Full Text | Google Scholar

Zhi Yong, A., Lei, X., Jiaming, Y., and Li-Min, Z. (2025). Group effects of energy pipe piles embedded in layered transversely isotropic soils due to thermo-mechanical loading. Int. J. Numer. Anal. Methods Geomech. 49, 2294–2312. doi:10.1002/nag.3989

CrossRef Full Text | Google Scholar