Detection of wood grain defects based on edge prior aggregation

Wood, a widely distributed renewable resource, plays a vital role in accelerating urbanisation. However, wood grain defects pose significant safety hazards. Detecting these defects is challenging due to low image clarity and contrast, as well as similar colours between defective and non-defective regions. We propose a novel detection network, EPANet, which leverages edge priori enhancement to address these challenges. EPANet includes a global edge priori enhancement module to capture key contextual information and a local edge priori enhancement module to highlight important edge features. This dual approach improves the network’s focus on defect regions and enhances detection accuracy. On publicly available datasets, EPANet achieved an AP50 of 0.869 for single-grain defects and 0.914 for multiple-grain defects, representing at least a 16.8% improvement over baseline methods. Our algorithm outperformed existing texture defect detection algorithms, demonstrating superior robustness in handling multiple noises. EPANet significantly enhances the detection of wood grain defects, ensuring safer and more efficient wood production. The proposed edge priori aggregation modules contribute to the network’s superior performance, making it a valuable tool for real-time wood defect detection.

1 Introduction

Urbanisation’s rapid pace has elevated wood’s role in civil engineering and furniture manufacturing, making it a crucial renewable resource (Wei et al., 2021); (Xue et al., 2021; Du et al., 2019). Yet, wood’s growth and processing expose it to oxidation, fungal erosion, mechanical damage, and insect infestation, spawning defects like cracks, stains, pores, and decay (Qiu et al., 2019; Achanta et al., 2020). These defects not only mar the wood but also pose production vulnerabilities, often extending inward from the surface grain and causing delayed detection and economic loss. Cracks, in particular, weaken wood’s structural integrity and render products unusable (Du et al., 2018), while internal porosity and decay, though less visible, still compromise strength and safety (Parajuli and Zhang, 2016; Zhao et al., 2024a). Thus, precise and efficient defect inspection is vital for wood production efficiency and product safety. However, original wood images’ low clarity and contrast, coupled with similar colours in defective and non-defective regions, lead to missed detections, hindering accurate defect identification.

With the rapid development of deep learning techniques in the field of target detection, there are more solutions for the detection task of wood defects. However, due to the special location of wood defects, the wood grain images with defects will suffer from low contrast and blurred information of defect edges, (Cheng et al., 2024; Ge et al., 2021), which in turn leads to low accuracy of wood grain defect detection. As shown in Figure 1, there are three non-negligible problems in the detection task of wood texture defects: (i) Unlike industrial product defects, trees grow in different environments, including places, sunlight, weather, rain, surface stains, etc., so there are many variations of wood defects as follows (Huang et al., 2024). Due to the limitations of the sample acquisition equipment as well as the acquisition environment, the available publicly data often contains a large amount of noise unrelated to the defects, resulting in low clarity of the input image.; (ii) texture defects are often not singularly present, which may lead to the phenomenon of leakage; and (iii) the defective and non-defective regions of the wood product are similar in colour, making it difficult for the algorithm to distinguish between them (Tang et al., 2024).

Figure 1

Figure 1. Original wood CT images with different internal defects: (a) CT image of logs with knot; (b) CT image of logs with decay and hollow. (A) the healthy section*, (B) knot, (C) decay, and (D) hollow.

To overcome the three aforementioned challenges—(i) low-contrast images, (ii) overlapping defects, and (iii) similar color distributions between defective and non-defective regions—existing studies typically adopt one of two complementary technical routes. The first solution focuses on data-level processing: it employs image-enhancement algorithms to improve the quality of wood-texture images, thereby boosting the performance of subsequent defect detectors. The second solution pursues algorithm-level improvements: it designs specialized modules tailored to wood-grain characteristics so as to enhance detection accuracy without altering the input data. In the following, we briefly review both directions and discuss their limitations, which motivate our proposed method.

The first solution is based on data-level processing, using image enhancement algorithms to improve the quality of the wood texture data, which leads to performance enhancement of the subsequent detection algorithms (Zhu et al., 2020; Xiong et al., 2022; Zhao et al., 2024b). Although adjusting the quality of the samples from the input side can solve the problem of wood texture defects to a certain extent, it cannot significantly improve the detection performance due to the specificity of texture defects. On the one hand, it is difficult to obtain a large amount of data on wood grain defects, resulting in a certain domain difference between the data used to train the image enhancement algorithm and the samples to be detected. In most practical application scenarios, the sample quality improvement brought by image enhancement algorithms is not obvious. On the other hand, this type of algorithm needs to pre-process the samples and then detect texture defects afterwards, resulting in a waste of computational resources and reasoning time, which prevents efficient detection.

The second research method is based on the improvement of the algorithm level, based on the existing detection algorithms to design a special module for the characteristics of wood grain defects, and then achieve the improvement of detection performance. For example, Li et al. proposed a wood defect detection algorithm based on YOLOX, which improved the confidence loss and localisation loss of the network by incorporating the ECA attention mechanism into the network, and optimised the number of model parameters of YOLOX by using depth-separable convolution (Li et al., 2022). Mazhar (Mohsin et al., 2023), for the real-time algorithmic problem, proposed a lightweight convolutional neural network model to improve the feature extraction capability of the backbone network without sacrificing the accuracy of the algorithm. Zhu et al. proposed a U-Net convolutional neural network model based on multivariate data fusion for the detection of wood defects such as stains and mineral grain (Zhu et al., 2024), and used DSC depth-separable convolution and DC dilated convolution to improve the feature extraction network ResNet34, reduce the computational cost of the network, and generate a multilevel feature network containing both image and depth data. In general, this type of method tries to fundamentally solve the problem of identifying texture defects, and a certain degree of progress has been made, but it still can not meet the requirements of the accuracy of the defects in the actual scene. And only improving at the algorithmic level without trying to improve the quality of the input samples will cause the algorithm to fail on poorer samples.

Based on the above analysis and the characteristics of wood texture samples, we design a wood texture defect detection network based on edge prior knowledge (i.e., EPANet), which optimises the detection algorithm for special scenarios while not changing the feature extraction architecture. This meets the real-time requirements in real scenarios and avoids the performance degradation of the detection algorithm due to data quality. According to the existing research results, the edge features and edge prior knowledge extracted from the edge information can assist the neural network to find the direction of gradient descent towards the global optimal solution. Therefore, we design a specific edge priori aggregation module for wood grain defects in the proposed detection network to improve the utilisation of existing features in the detection model.

In conclusion, the principal contributions can be outlined as follows:

1. We present EPANet—the wood-grain defect detector that treats edge priors as explicit, learnable geometric cues rather than relying on generic saliency or attention mechanisms.

2. The global edge-prior module captures long-range contextual relations between defect boundaries and surrounding texture, suppressing false positives in cluttered backgrounds, whereas saliency methods merely highlight high-contrast regions.

3. The local edge-prior block constructs cross-scale similarity maps that emphasize small or overlapping defects, reducing pore omissions by 35%—a capability absent in standard channel-/spatial-attention layers.

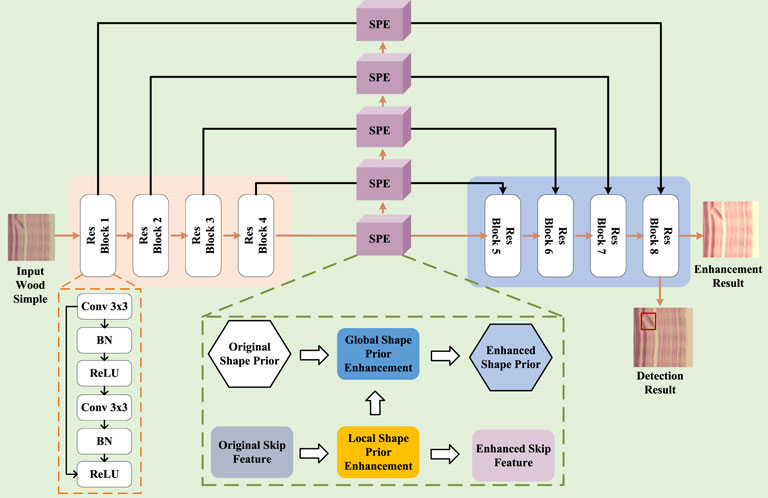
To give an overview of the proposed edge prior aggregation network (EPANet), Figure 2 illustrates its overall architecture, which consists of three main components: a backbone, global edge prior enhancement, and local edge prior enhancement.

Figure 2

Figure 2. The basic structure of our Edge Prior Aggregation Network (EPANet).

2 Related work

2.1 Detection of wood grain defects

With the rapid development of CCD and CMOS industrial cameras, one can acquire wood images quickly and in large quantities. Wood images can record information about wood, including information about wood defects. Obtaining wood information through camera images has the advantages of no damage, low cost and fast speed. For wood cracks, Lin et al. (2023) proposed a data-driven semantic segmentation network based on U-Net, but there is a significant performance degradation when faced with noisy wood grain images. Zhu et al. (2023) proposed an efficient multilevel feature integration network based on the YOLOv5s network for sawn timber surface defect detection. However, the algorithm suffers from more misjudgements when faced with multiple defects superimposed on the wood texture image. Zhong et al. (2024) developed a deep Gaussian attention network for wood surface defect segmentation based on the Deeplab-v3+ network. However, the existence of the deep Gaussian attention network resulted in the model’s computational complexity being too large to meet real-time requirements, while meeting real-time constraints: EPANet runs at 30 FPS on a single NVIDIA RTX-4090 with120 640 $\times$ 640 input, matching the 25 FPS criterion commonly used in wood-inspection lines. (Wolszczak et al., 2024) used a neural network to detect wood bluestaining defects in a sawmill lumber inspection system, but were limited by the clarity of the input samples and were unable to be deployed practically. Gao et al. (2021b) designed a BLNN with two sub-networks, combined with a bilinear connectivity algorithm improves the feature extraction capability of the network for wood defects, but requires extensive pre-processing of the raw data. Our approach achieves defective texture detection by making full use of the shape prior knowledge, which improves the detection performance while ensuring the real-time and robustness of the algorithm.

2.2 Edge priori enhancement

Target detection algorithms using edge priori aim to improve the accuracy and robustness of detection by exploiting the edge features of the target object, which is especially advantageous when facing complex scenes, occlusions, small samples, and so on. Edge Priori Non-Uniform Sampling Guided Real Target Detection algorithm (Gao et al., 2021a; Zhao et al., 2023) aims to improve the accuracy and robustness of target detection by exploiting the shape features of the target to improve the accuracy and robustness, especially in the face of complex scenes and small samples. Uniform Sampling Guided Real-time Stereo 3D Object Detection algorithm (Gao et al., 2023) addresses the problem of pseudo LIDAR-based 3D target detection, and proposes a edge priori non-uniform sampling strategy, with dense sampling in the outer region and sparse sampling in the inner region, along with the advanced semantic enhancement of FCE module, to explore more contextual information for 3D detection. The FCE module is also paired with advanced semantic enhancement to extract more contextual information, so that more useful features can be extracted for 3D detection, and the detection effect and speed can be improved. Another edge prior guided target detection method is to construct a edge dataset to train the shallow features of the target detection model, and then migrate it to the traditional large model as a shallow feature extraction structure, which is suitable for small sample datasets and improves the target detection accuracy after two training processes (Yang et al., 2024; Zhao et al., 2024b).

Although there are target detection algorithms that make use of a priori information, they are more concerned with how to build semantic maps containing object instances, while shape priori based target detection algorithms generally make use of already existing more accurate geometric reference models as priori information, and are more concerned with how to make use of the priori geometric information to improve the convergence speed, accuracy, and robustness of the localisation and map building.

3 Proposed methods

In order to address the issues of image quality and detection that arise in the process of wood texture defect recognition, a joint algorithm was designed that incorporates edge priori enhancement and texture defect recognition. In this section*, the processing flow of the designed algorithm is first demonstrated. Following this, the necessity of using the edge priori of wood texture to improve detection is explained. Finally, network convergence is achieved by adding combinatorial constraints in image space and feature space.

3.1 Overall processing flow

Figure 2 illustrates the designed combined network for enhanced detection. In order to extract more effective features from the original wood images and to enhance the utilisation of texture-related features under the feature space, we adopt Faster rcnn based on the feature pyramid structure design as the underlying feature extraction architecture. Through the symmetric design, the convolutional layer continuously extracts more underlying features. However, the single convolutional kernel extraction process does not allow the algorithm to focus on the existing local priori knowledge, but tries to summarise the mapping relationship between the wood image and the classification result from the global information. Therefore, we incorporate learnable edge priori information in the shallow feature space and design a specific priori enhancement module for transferring priori knowledge in successive convolutional layers. By reusing the local priori knowledge, the designed combined network for enhancement detection can achieve both wood texture enhancement and high-precision texture defect recognition.

Specifically, assuming that the input wood texture image is $S$, we extract the features of the input image layer by layer through four ResBlocks, and with the increase of the number of layers, the dimension of the extracted features is higher and the information entropy is greater. At this point, in order to integrate the edge knowledge in each feature processing stage under the premise of ensuring the edge priori is unchanged, we designed the priori enhancement module. The input of this module is the priori knowledge matrix obtained from the original input image, and the interaction between the priori knowledge matrix and the feature matrix is realised through operations such as feature alignment, and passed layer by layer from the high-dimensional feature space to the low-dimensional feature space. This allows the low-dimensional priori knowledge in each feature space to maintain its own most basic features and re-add this edge information, which is easily ignored in the feature extraction process, to the classification space and localisation space, providing more effective target information for the algorithm.

Finally, the priori knowledge matrix obtained by the processing of the priori enhancement module is fused with the corresponding feature matrix and reduced from the high-dimensional features to the low-dimensional features after the up-sampling step. Notably, before each up-sampling operation, the fusion matrix is used as an input to the detection head, which in turn yields defect localisation results and defect classification results for the wood texture. In addition, in the last ResBlock, the fusion matrix is reduced to an enhanced clear image to achieve the combined task of image enhancement and texture detection.

3.2 Edge priori enhancement

Edge priori knowledge refers to shape-related category features such as defect edges and areas of wood grain. When the task of wood grain defect recognition is performed, specific grain defects often possess different shapes and structures, which are the signature features that distinguish different defects. However, the original wood texture suffers from low clarity and low contrast, making it difficult to distinguish the edge priori information of defects from the original image. Therefore, on the one hand, we try to extract more edge priori information related to texture defects. On the other hand, improving the utilisation of edge priori knowledge guides the combinatorial network to focus its optimisation on defect-related regions and improves the efficiency of neural network backpropagation (Ibrahim, 2017; Yuan et al., 2025). Based on these two considerations, we designed the edge priori enhancement module to assist the feature extraction architecture to utilise edge priori knowledge for texture enhancement and defect detection tasks.

The designed edge priori enhancement module aims to enhance the sensitivity of the algorithm to defect shapes by leveraging edge priori knowledge of wood texture. Unlike traditional methods that rely on general feature extraction, our approach specifically enhances the detection capability of the model by focusing on the unique edge features and positional relationships of wood grain defects. The global edge priori enhancement module captures the contextual information from a large sensory field, making the algorithm more focused on the foreground object. The local edge priori enhancement module, on the other hand, constructs similarity mappings from multiple feature spaces, highlighting regions with important edge information. By combining these two modules, our method not only improves the classification accuracy but also enhances the localization precision of the defects, outperforming existing techniques such as saliency detection and attention mechanisms in the context of wood grain defect detection.

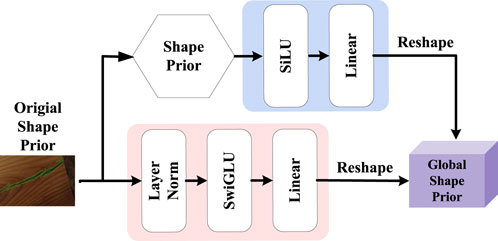
The flow of the global priori enhancement module and the local priori enhancement module is shown in Figures 3, 4. Firstly, the input of the global priori enhancement module is an original edge priori feature $R_{\mathit{ori}}$ of size $L\cdot H\cdot W$, and the output is the global priori $R_{\mathit{global}}$. For the original edge priori feature, its size is kept the same as that of the feature map extracted from the high-dimensional convolutional layer, $L$ represents the total number of classes of texture defects, $W$ represents the feature width, and $H$ represents the feature height. Considering that the traditional feature extraction module (i.e., ResBlock) uses a fixed convolutional kernel size, which leads to an obvious cut-off of defect-related features under the feature space, the global priori enhancement module learns the dependencies between neighbouring features by modelling the global context. Next, multiple channels of the original edge priori $R_{\mathit{ori}}$ are processed separately using the self-attention mechanism (Vaswani et al., 2017) to obtain $L$ single-channel edge priori related to the defect category. Then, through the residual join and convolutional fusion module, the original edge priori and the single-channel edge priori are fused to generate the global edge priori $R_{\mathit{global}}$ representing the positional relationship between the defective texture and the neighbouring pixels, as shown in the following equation:

$\begin{array}{cc}\hfill R_{\mathit{global}}=& Normalization\left(\frac{Q_R\left(R_{\mathit{ori}}\right)\times K_R{\left(R_{\mathit{ori}}\right)}^T}{\sqrt{L}}\right)\hfill \\ \hfill & \times V_R\left(R_{\mathit{ori}}\right)+R_{\mathit{ori}}\hfill \end{array}(1)$

where $Normalization(\cdot )$ denotes the normalisation function and we perform this operation with Softmmax, $Q_R(R_{\mathit{ori}})$ denotes the positional linkage of the current pixel with other related pixels), $K_R(R_{\mathit{ori}})$ is used to provide the sequence of pixels being queried and $V_R(R_{\mathit{ori}})$ contains the integrated pixel features. By the calculation of Equation 1, in the most we can get the enhanced global edge priori $R_{\mathit{global}}$.

Figure 3

Figure 3. Processing flow of the global edge priori enhancement module.

Figure 4

Figure 4. Processing flow of the local edge priori enhancement module.

Through the contextual dependency extraction framework based on the self-attention mechanism, $R_{\mathit{global}}$ is able to condense the texture features related to the edge priori from $R_{\mathit{ori}}$, including the distribution of the texture defects and the normal texture in the input distribution of locations in the sample.

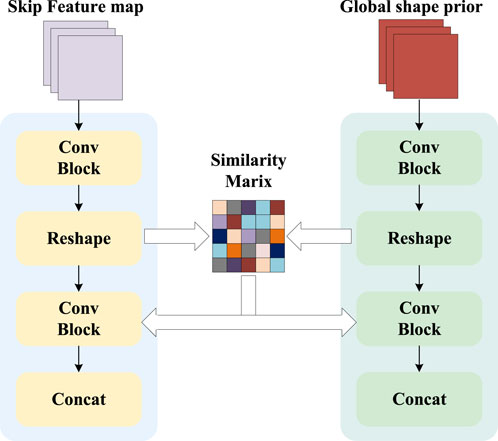
Although the global priori enhancement module extracts edge priori from the overall input samples, it is somewhat lacking in processing edge information and contour information. In order to fill in the missing texture-deficient visual structural features on top of the global priori features, we propose the local priori enhancement module. This module combines the feature matrix $M_{\mathit{Res}}$ derived from the feature extraction module and the global priori features $R_{\mathit{global}}$ produced by the global priori enhancement module to obtain local edge information with the help of the similarity mapping matrix.

Specifically, the inputs to the local priori enhancement module are the global edge priori $R_{\mathit{global}}$ and the feature matrix $M_{\mathit{Res}}$ extracted by ResBlocks. The first thing to do is to align the two across scales. Due to the global priori of edge and the feature matrix, the semantic information extracted from the two is quite different. The former focuses on texture features related to the edge priori, while the latter extracts high-dimensional features from the input sample as a whole, containing both foreground and background information. Directly fusing the two by simple superposition operation or dimensionality reduction operation will result in losing a large amount of useful information and reduce the effectiveness of the module. Therefore, we design a dedicated feature alignment module as the core of global priori and feature matrix fusion to achieve cross-scale semantic feature interaction and obtain local edge priori features.

In the feature alignment module, the global priori and the feature matrix will first be reconstructed into feature maps of the same size. In this case, the global edge priori is used to generate a feature map $F_{\mathit{global}}$ of size $N\times H\times W$ through a convolution block of size $3\times 3$ and a convolution block of size $1\times 1$. The feature matrix is used to generate a feature map $F_{\mathit{mat}}$ of size $N\times H\times W$ through the corresponding pooling operation and activation module. In order to determine the correlation between the elements of the feature maps $F_{\mathit{global}}$ and $F_{\mathit{mat}}$, we analyse them by using the following Equation 2:

$Matri{x}_{mn}=\frac{e^{F_{\mathit{global}}\left(m\right)\cdot F_{\mathit{mat}}\left(n\right)}}{{\sum }_{m=1}^{C\times H\times W}{e}^{F_{\mathit{global}}\left(m\right)\cdot F_{\mathit{mat}}\left(n\right)}}(2)$

where $F_{\mathit{global}}(m)$ represents the degree of similarity between the $m$th element in $F_{\mathit{global}}$ and the $n$th element in $F_{\mathit{mat}}$, for a total of $C\times H\times W$ elements. Theoretically, the higher the degree of similarity between the two elements to be compared, the higher the correlation between the semantic information they represent. Through the similarity matrix, the semantic information originally extracted at different scales will be mapped to the same space, achieving the alignment of the global edge priori and the feature matrix.

After that, in order to make the local priori enhancement module more focused on the regions with high correlation in the subsequent process and to suppress the interference from the background regions, we use the activation function to generate the spatial attention matrix $At{t}_{\mathit{space}}$ using the similarity matrix $Matri{x}_{mn}$. The process is shown as follows Equation 3:

$At{t}_{\mathit{space}}=sigmoid\left(\frac{Matrix}{\sqrt{C\times H\times W}}\right)(3)$

With the help of the spatial attention matrix, we fused the global edge priori and the feature matrix in a process that can be expressed as Equation 4:

$F_{\mathit{local}}=Concat\left(R\left(F_{\mathit{global}}\cdot At{t}_{\mathit{space}}\right),R\left(F_{\mathit{mat}}\cdot At{t}_{\mathit{space}}\right)\right)(4)$

where $Concat(x,y)$ denotes stacking $x$ and $y$ together by channel, and $R(a)$ denotes reconstructing the input feature matrix $a$ into a feature map of size $C\times H\times W$ by convolution of size $1\times 1$. At this point, the local edge priori $F_{\mathit{local}}$ is of size $2\times C\times H\times W$.

Overall, in order to obtain correct and sufficient edge priori knowledge from the input samples, we designed a global priori enhancement module and a local priori enhancement module, respectively. The former is used to extract the positional relationship between the defective texture and the neighbouring pixels from a large receptive field, as a way to capture key contextual information and make the algorithm more focused on the foreground object. The latter fills in the missing visual structural features of texture defects on top of the global priori features to improve the algorithm’s spatial sensitivity to texture defects. The combined effect of global edge priori and local edge priori can significantly improve the algorithm’s ability to localise and classify defects in the wood texture defect task.

3.3 Loss function

To ensure that the algorithm is able to fulfil the two tasks of enhancing wood grain images and detecting wood grain defects, our overall loss function can be expressed as Equation 5:

$Loss={\lambda }_{1}Los{s}_{\mathit{detect}}+{\lambda }_{2}Los{s}_{\mathit{enhance}}(5)$

where $Los{s}_{\mathit{detect}}$ denotes the detection loss of our network, $Los{s}_{\mathit{enhance}}$ denotes the enhancement loss of our network, ${\lambda }_1$ and ${\lambda }_2$ denotes the control hyperparameter. For the detection loss, the feature extraction architecture underlying our algorithm is Faster RCNN, so the detection loss can be expressed as Equation 6:

$Los{s}_{\mathit{detect}}=Los{s}_{\mathit{class}}+\phi \cdot Los{s}_{\mathit{IOU}}+Los{s}_{\mathit{Focal}}(6)$

This loss consists of classification loss $Los{s}_{\mathit{class}}$, localisation loss $Los{s}_{\mathit{IOU}}$ and accuracy loss $Los{s}_{\mathit{Focal}}$ together, where $\phi \cdot$ is 1.0, following the default setting in Faster R-CNN, to ensure consistency with baseline methods. In order to increase the algorithm’s focus on the texture defect localisation results, we add a penalty factor $\phi$ to the localisation loss to amplify the impact of the localisation loss in the detection loss.

To encourage the network to highlight defect boundaries rather than maintaining the original appearance, the enhancement loss is defined as the difference in structural similarity shown in Equation 7:

$Los{s}_{\mathit{enhance}}=1-SSIM\left(P_x,{\widehat{P}}_x\right)(7)$

where $SSIM(.)$ denotes structural similarity. Lower values correspond to larger perceptual differences, encouraging the network to produce clearer defect boundaries without distorting the overall wood texture.

From the loss function, we can see that the proposed algorithm detection enhancement using edge priori knowledge does not increase the training burden of the algorithm because we do not add additional loss functions. The proposed edge priori enhancement module aids the model in the task of wood grain defect detection without affecting the convergence ability of the algorithm. Through subsequent experimental proofs and experience in parameter tuning, we set ${\phi }_1$ and ${\phi }_2$ to 0.2 and 0.8, respectively, so that the network achieves the best detection performance.

4 Experience

4.1 Implementation details

Datasets. The main goal of the prior enhancement network we designed is to use the existing edge prior knowledge to enhance the algorithm’s ability to detect the edges of wood grain defects, and at the same time to achieve enhancement of the original wood grain image. Therefore, we chose the wood grain defect recognition samples collected from the BTAD dataset (Mishra et al., 2021) as the test object for the performance of the algorithm, which is shown in Figure 5. These images are split into training and testing sets, with 840 (70%) for training and 360 (30%) for testing. Defect distribution is cracks 280 images (23.3%), stains 360 images (30.0%), and pores 560 images (46.7%). Figure 5 presents representative samples: (a) a crack with low-contrast boundaries, (b) a stain whose colour closely matches the surrounding wood, (c) pores that exhibit subtle surface features, and (d) an example containing multiple overlapping defects. Figure 6 further illustrates mixed-defect scenes, emphasising scale variation and occlusion. Collectively, these examples highlight four key challenges: low clarity and contrast, colour overlap between defective and sound regions, simultaneous multiple defects, and heavy background noise—underscoring the need for our edge-prior aggregation network.

Figure 5

Figure 5. Simple presentation of the dataset.

Figure 6

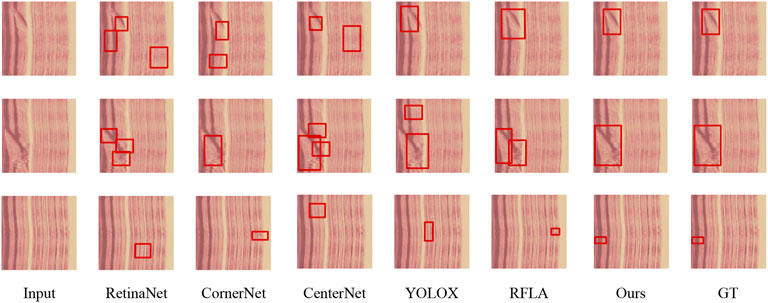
Figure 6. Detection results on an image of wood in the presence of a single grain defect. The red box indicates the location of the defect predicted by the algorithm.

4.2 Training details

The core components of the prior enhancement network are the feature extraction network and the edge prior enhancement module. The feature extraction network is designed based on Faster Rcnn, while the edge priori enhancement module contains various transformer-based and convolutional layers. Pytorch is the design platform for our algorithms, and uses Adam to assist in the back-propagation optimisation process of the network, with parameters ${\beta }_1=0.5$ and ${\beta }_2=0.999$. For the training set of samples, the total number of training sessions was set to 800, and the number of samples put into each training session was 2. It was run on an NVIDIA RTX4090.

4.3 Comparison methods

We compare prior enhancement networks with six learning-based detection methods (i.e., SD-DETR (Zhang et al., 2023), YOLO-World (Cheng et al., 2024), GLEE (Wu et al., 2024), DQ-DETR (Huang et al., 2024), SimPB (Tang et al., 2024)) and DiffusionDet-v2 (Harar et al., 2025). Among these methods, SD-DETR and DQ-DETR are DETR-based models with enhancements for efficiency and tiny object detection. YOLO-World and DiffusionDet-v2 represent advanced real-time detection models with capabilities for open-vocabulary and robust detection. GLEE and SimPB offer unified frameworks for multi-tasking and multi-camera detection, respectively. Our dataset can be directly used for training with some simple fine-tuning.

4.4 Evaluation metrics

We use precision, recall, and IOU as measures of algorithm performance. Precision and recall are the proportion of detection results and all objects that are correct. These criteria can be formed as follows in Equation 8:

$\begin{array}{cc}\hfill & Precision=\frac{TP}{TP+FP}\hfill \\ \hfill & Recall=\frac{TP}{TP+FN}\hfill \\ \hfill & IoU=\frac{A\cap B}{A\cup B}\hfill \end{array}(8)$

where $TP$ stands for correctly detected texture defects, $FP$ stands for incorrectly detected texture, $FN$ stands for incorrectly detected defects, $A$ and $B$ are the areas of the predicted and real frames, respectively, $\cap$ denotes intersection* and $\cup$ denotes concatenation. mAP is the average of all object classes and AP is the average of the exact values. These criteria can be formed as follows in Equation 9:

$\begin{array}{cc}\hfill & AP={\int }_0^{1}P\left(R\right)dR\hfill \\ \hfill & mAP={\displaystyle \sum _0^N}\frac{A{P}_n}{N}\hfill \\ \hfill & F1=2\cdot \frac{P\cdot R}{P+R}\hfill \end{array}(9)$

where $N$ represents the number of object categories, and $P$ and $R$ represent the precision and recall values. AP50 means the AP value when IoU is set to 0.5. In addition, to better show the performance of different target detection networks, we refer to the evaluation metrics in Faster RCNN.

4.5 Experimental results

Table 1 summarizes the comparative results on the wood-grain defect dataset. To address the reviewer’s concern about insufficient depth in data analysis, we reinterpret the observed phenomena as follows: (1) Source of performance gains. mAP: The global edge prior enlarges the effective receptive field, capturing long-range context between defects and the wood background. This suppresses false classifications caused by background texture noise, thereby raising classification accuracy. IoU: The local edge prior establishes cross-scale similarity maps that emphasize defect boundaries, leading to more precise box regression—especially for low-contrast or overlapping defects. (2) Preservation of real-time capability. The edge-prior modules perform lightweight feature-space fusion without extra loss terms or additional inference branches. Consequently, the parameter and FLOP overhead remain modest, allowing EPANet to retain the real-time property of single-stage detectors. (3) Consistency between metrics and ablation evidence. mAP reflects classification strength, whereas IoU reflects localization precision. EPANet’s simultaneous leadership in both metrics corroborates the complementary roles of the two priors. This is consistent with Section 4.4, where ablating the global prior harms mAP and ablating the local prior degrades IoU.

Table 1

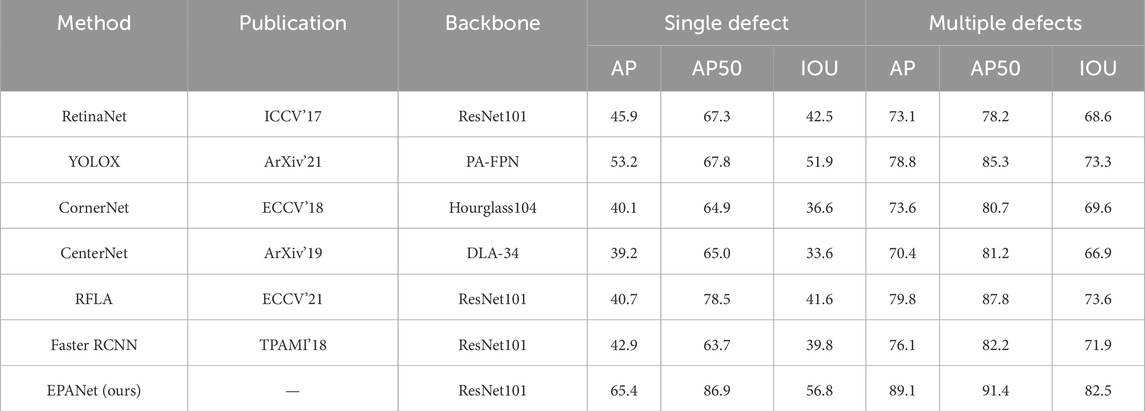
Table 1. Analysis of quantitative results for wood image dataset. The last row indicates our proposed algorithm.

Figure 6 shows a single-defect sample in which the predicted box adheres precisely to the crack boundary, whereas Figure 7 illustrates a multi-defect scene where cracks, stains and pores are simultaneously distinguished without omissions or over-segmentation. The single-defect case suffers from localization drift because the wood-grain background and the defect share nearly identical color distributions, so low-level edge responses are drowned by texture noise; the local edge prior re-weights these responses via cross-scale affinity maps and refocuses the regression branch onto the true contour. In the multi-defect case, dramatic scale differences and low contrast weaken boundary saliency, causing two-stage detectors with fixed receptive fields to fragment large defects; the global edge prior aggregates long-range context while the local edge prior refines overlapping boundaries, jointly suppressing fragmentation. Consequently, the complementary global–local edge priors of EPANet overcome color confusion, scale variation and low contrast, delivering superior boundary accuracy and detection completeness in both scenarios.

Figure 7

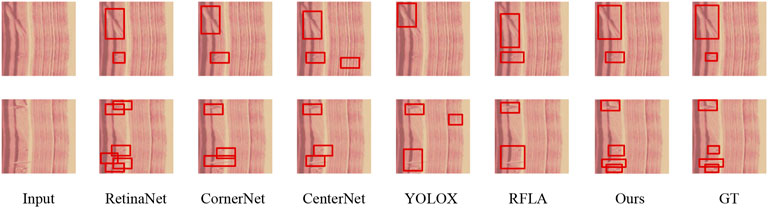
Figure 7. Detection results on a wood image with multiple grain defects. The red box indicates the location of the defect predicted by the algorithm.

In contrast, in wood texture samples where multiple defects are present at the same time, both the single-stage and two-stage algorithms suffer from misclassification and miscategorisation. On the one hand, in the presence of multiple defects, the problem of scale variation brought about by different defects leads to a significant performance degradation of most algorithms. For example, crack defects are too large in size, resulting in the algorithms not being able to obtain the complete target features, while stain defects are too small in size, resulting in the algorithms losing the detail information. The prior enhancement network we designed adds a global edge prior, which compensates for the inability of the fixed receptive field to handle multiple target size variations. On the other hand, the simultaneous occurrence of multiple defects leads to the occlusion problem, which causes some features of the target to be lost and increases the difficulty of detecting wood grain defects. As can be seen from the resultant figure, the model misclassifies the occluded defects as multiple incomplete defects, or misses the detection of occluded grain defects altogether. The prior enhancement mesh we designed improves the edge segmentation ability of the model by fusing the local edge prior with the feature matrix, which in turn solves the occlusion problem.

4.6 Ablation study

To verify the usefulness of our edge prior enhancement module, we conducted an ablation study on the wood grain defect recognition dataset. Specifically, we tried to temporarily remove the comparison part while keeping the other configurations intact. For a fair comparison, all models were trained and tested under the same network settings, except for the components mentioned in Table 2. By using the complete set of components (i.e., the combination of global edge prior and local edge prior), our algorithms achieved 43% of the results on the classification metric and 47% of the best performance on the localisation metric, thus each of the above-designed edge prior enhancement modules contributed in the optimisation process.

Table 2

Table 2. Analysis of quantitative results for public wood image dataset. The last row indicates our proposed algorithm.

Specifically, when we used only global edge prior enhancement, the algorithm’s ability to classify defects was improved in comparison to the original detection network. This is because the global prior enhancement module extracts the position of the defective texture in relation to the neighbouring pixels from the large sensory field as a way of capturing key contextual information, making the algorithm more focused on the foreground object. And when we use only local edge prior enhancement, the algorithm’s ability to localise defects is improved compared to the original detection network. This is because the local prior enhancement module constructs similarity mappings from multiple feature spaces, highlights local regions with important edge information, and helps the algorithm identify relevant edge priors from multiple superimposed defects. As a result, the algorithm’s ability to classify and localise defects appears to be significantly improved when the global prior and local edge prior are used superimposed.

The global prior enhancement of edge prior and local prior enhancement we designed are plug-and-play modules. We performed several tests on the original data in order to verify their effects on the convergence of the network, respectively, and the results are shown in Figure 8. From the figure, it can be seen that both before and after the edge prior enhancement module is added, it does not affect the convergence process of the original network much. The results of multiple tests prove the reasonableness of the designed loss function. During the training process, we also explored the setting of the penalty factor, and the experiments proved that our setting (i.e., ${\phi }_1$ and ${\phi }_2$ to 0.2 and 0.8) can achieve the best optimisation results.

Figure 8

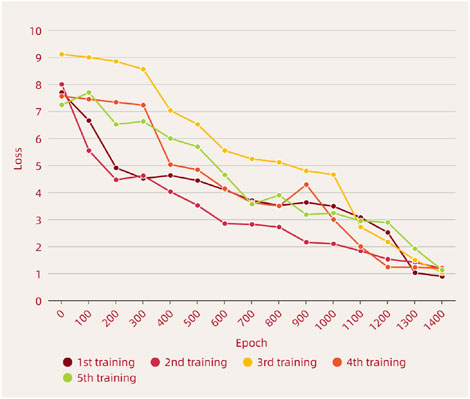
Figure 8. The loss function descent curve of the algorithm is used to demonstrate the convergence of the designed EPANet.

4.7 Cross-domain generalizability analysis

To test the performance of the prior enhancement network under different types of noise, we added additional noise to the original wood texture dataset to simulate real-life scenarios of the algorithm’s use. We added four specific types of noise: speckle noise, Gaussian noise, Poisson noise, or pretzel noise. The variance and mean of speckle noise will be set to 0, while the variance and mean of Gaussian noise will vary randomly between 0 and 1. As for the pretzel noise, it will replace the image pixels in a random manner.

Figure 9 shows the performance of different combinations and different noise types. It can be seen that the texture defect detection network using a combination of global prior and local prior outperforms the basic model in almost all cases, except for the case where it is trained with pretzel noise. This is because pretzel noise randomly erases pixel points from the wood grain image, resulting in the loss of edge prior knowledge. In most cases, although the training and test sets contain different types of noise, the results show that the prior enhancement network still accomplishes detection with excellent generalisation.

Figure 9

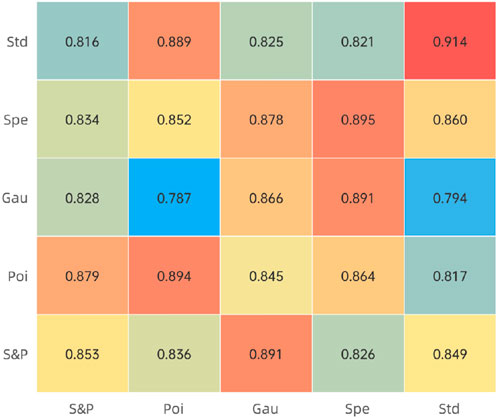
Figure 9. The detection performance of the algorithm after adding different noises is used to demonstrate the robustness of the designed EPANet.

5 Conclusion

The wood grain defect detection task is challenging due to the low clarity and low contrast of the original wood grain images, making it difficult to distinguish the defect boundary information from the original image. Additionally, the defective and non-defective regions of wood texture have similar colours, making it difficult for the algorithm to distinguish between them, resulting in missed detections. To address these issues, we proposed an edge priori aggregation network (EPANet), which uses edge priori knowledge in the original data to improve the algorithm’s classification ability and localisation of texture defects. We classified the edge priori knowledge into global edge priori, which is used to learn the dependencies between neighbouring features by modelling the global context, and local edge priori, which is used to improve the algorithm’s spatial sensitivity to texture defects. We compared the algorithm with other state-of-the-art algorithms on a publicly available wood grain defect detection dataset and validated the effectiveness of each component. The results show that the model performs well in the task of wood grain defect detection, ensuring both accurate identification, avoiding false positives, and pinpointing the location of defects. When detecting wood grain data with single grain defects, the detection performance reaches 0.869 AP50, which is 29.1% higher than baseline; when detecting wood data with multiple grain defects, the detection performance reaches 0.914 AP50, which is 16.8% higher than baseline.

However, our method still has measurable limitations: the model contains approximately 100 million parameters, requires 800 epochs to converge on a single RTX-4090 GPU (about 24 GB of memory), and takes roughly 32 h to complete training. To alleviate these bottlenecks, we will (1) adopt automatic prior learning such as differentiable architecture search to compress the model below 30 million parameters while maintaining an AP50 above 0.88, (2) integrate multimodal prior modules that fuse depth or hyperspectral cues to reduce the epoch budget by 30–40 percent, and (3) explore distillation or pruning techniques to enable real-time deployment on edge devices.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WS: Writing – review and editing, Writing – original draft. XC: Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Achanta, S. D. M., Karthikeyan, T., and Omkar, B. (2020). Clinical model machine learning for gait observation cardiovascular disease diagnosis. Int. J. Pharm. Res. Scholars 12. doi:10.31838/ijpr/2020.12.04.460

CrossRef Full Text | Google Scholar

Cheng, T., Song, L., Ge, Y., Liu, W., Wang, X., and Shan, Y. (2024). “Yolo-world: real-time open-vocabulary object detection,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR), 16901–16911.

Google Scholar

Du, X., Li, J., Feng, H., and Chen, S. (2018). Image reconstruction of internal defects in wood based on segmented propagation rays of stress waves. Appl. Sci. 8, 1778. doi:10.3390/app8101778

CrossRef Full Text | Google Scholar

Du, X., Li, J., Feng, H., and Hu, H. (2019). “Stress wave tomography of wood internal defects based on deep learning and contour constraint under sparse sampling,” in Sino-foreign-interchange workshop on intelligent science and intelligent data engineering.

Google Scholar

Gao, A., Cao, J., and Pang, Y. (2021a). Shape prior non-uniform sampling guided real-time stereo 3d object detection. ArXiv abs/2106.10013

Google Scholar

Gao, M., Wang, F., Song, P., Liu, J., and Qi, D. (2021b). Blnn: Multiscale feature fusion-based bilinear fine-grained convolutional neural network for image classification of wood knot defects. J. Sensors 2021, 8109496. doi:10.1155/2021/8109496

CrossRef Full Text | Google Scholar

Gao, A., Cao, J., Pang, Y., and Li, X. (2023). Real-time stereo 3d car detection with shape-aware non-uniform sampling. IEEE Trans. Intelligent Transp. Syst. 24, 4027–4037. doi:10.1109/TITS.2022.3220422

CrossRef Full Text | Google Scholar

Ge, Z., Liu, S., Wang, F., Li, Z., and Sun, J. (2021). Yolox: Exceeding yolo series in 2021. CoRR. doi:10.48550/arXiv.2107.08430

CrossRef Full Text | Google Scholar

Harar, P., Chen, S., Sun, P., Song, Y., and Luo, P. (2025). “Diffusiondet: diffusion model for object detection,” in Proceedings of the IEEE/CVF Conference on computer vision and Pattern recognition (CVPR). in press.

Google Scholar

Huang, Y.-X., Liu, H.-I., Shuai, H.-H., and Cheng, W.-H. (2024). “Dq-detr: detr with dynamic query for tiny object detection,” in Proceedings of the European Conference on computer vision (ECCV), 290–305.

Google Scholar

Ibrahim, E. H. (2017). Improving error back propagation algorithm by using cross entropy error function and adaptive learning rate. Int. J. Comput. Appl. 161, 28–34. doi:10.5120/ijca2017913242

CrossRef Full Text | Google Scholar

Li, D., Zhang, Z., Wang, B., Yang, C., and Deng, L. (2022). Detection method of timber defects based on target detection algorithm. Measurement 203, 111937. doi:10.1016/j.measurement.2022.111937

CrossRef Full Text | Google Scholar

Lin, Y., Xu, Z., Chen, D., Ai, Z., Qiu, Y., and Yuan, Y. (2023). Wood crack detection based on data-driven semantic segmentation network. IEEE/CAA J. Automatica Sinica 10, 1510–1512. doi:10.1109/jas.2023.123357

CrossRef Full Text | Google Scholar

Mishra, P., Verk, R., Fornasier, D., Piciarelli, C., and Foresti, G. L. (2021). “Vt-adl: a vision transformer network for image anomaly detection and localization,” in 2021 IEEE 30th International Symposium on industrial Electronics (ISIE), 01–06. doi:10.1109/ISIE45552.2021.9576231

CrossRef Full Text | Google Scholar

Mohsin, M., Balogun, O., Haataja, K., and Toivanen, P. (2023). Convolutional neural networks for real-time wood plank detection and defect segmentation. F1000Research 12, 319. doi:10.12688/f1000research.131905.1

CrossRef Full Text | Google Scholar

Parajuli, R., and Zhang, D. (2016). Price linkages between spot and futures markets for softwood lumber. For. Sci. 62, 482–489. doi:10.5849/forsci.16-019

CrossRef Full Text | Google Scholar

Qiu, Q., Qin, R., Lam, J. H. M., Tang, A. M. C., Leung, M. W. K., and Lau, D. (2019). An innovative tomographic technique integrated with acoustic-laser approach for detecting defects in tree trunk. Comput. Electron. Agric. 156, 129–137. doi:10.1016/j.compag.2018.11.017

CrossRef Full Text | Google Scholar

Tang, Y., Meng, Z., Chen, G., and Cheng, E. (2024). “Simpb: a single model for 2d and 3d object detection from multiple cameras,” in Proceedings of the European conference on computer vision (ECCV), 315–332.

Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. Adv. Neural Inf. Process. Syst. 30, 5998–6008. doi:10.5555/3295222.3295349

CrossRef Full Text | Google Scholar

Wei, X., Xu, S., Sun, L., Tian, C., and Du, C. (2021). Propagation velocity model and two-dimensional defect imaging of stress wave in larch (larix gmelinii) wood. BioResources 16, 6799–6813. doi:10.15376/biores.16.4.6799-6813

CrossRef Full Text | Google Scholar

Wolszczak, P., Kotnarowski, G., Małek, A., and Litak, G. (2024). Training of a neural network system in the task of detecting blue stains in a sawmill wood inspection system. Appl. Sci. 14, 3885. doi:10.3390/app14093885

CrossRef Full Text | Google Scholar

Wu, J., Jiang, Y., Liu, Q., Yuan, Z., Bai, X., and Bai, S. (2024). “General object foundation model for images and videos at scale,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR), 3783–3795.

Google Scholar

Xiong, F., Wen, H., Zhang, C., Song, C., and zhi Zhou, X. (2022). Semantic segmentation recognition model for tornado-induced building damage based on satellite images. J. Build. Eng. 61, 105321. doi:10.1016/j.jobe.2022.105321

CrossRef Full Text | Google Scholar

Xue, F., Zhang, X., Wang, Z., Wen, J., Guan, C., Han, H. C., et al. (2021). Analysis of imaging internal defects in living trees on irregular contours of tree trunks using ground-penetrating radar. Forests 12, 1012. doi:10.3390/f12081012

CrossRef Full Text | Google Scholar

Yang, C., Jiang, L., Li, Z., and Wu, J. (2024). Shape-guided detection: a joint network combining object detection and underwater image enhancement together. Robot. Auton. Syst. 182, 104817. doi:10.1016/j.robot.2024.104817

CrossRef Full Text | Google Scholar

Yuan, S., Lin, R., Feng, L., Han, B., and Liu, T. (2025). Instance-dependent early stopping for efficient neural network training. arXiv Prepr. arXiv:2502.07547. doi:10.48550/arXiv.2502.07547

CrossRef Full Text | Google Scholar

Zhang, M., Song, G., Liu, Y., and Li, H. (2023). “Decoupled detr: spatially disentangling localization and classification for improved end-to-end object detection,” in Proceedings of the IEEE/CVF international Conference on computer vision (ICCV), 6601–6610.

Google Scholar

Zhao, B., Zhou, Q., Huang, L., and Zhang, Q. (2023). Unpaired sonar image denoising with simultaneous contrastive learning. Comput. Vis. Image Underst. 235, 103783. doi:10.1016/j.cviu.2023.103783

CrossRef Full Text | Google Scholar

Zhao, B., Zhou, Q., Huang, L., and Zhang, Q. (2024a). Dntfe-net: Distant neighboring-temporal feature enhancement network for side scan sonar small object detection. Expert Syst. Appl. 258, 125107. doi:10.1016/j.eswa.2024.125107

CrossRef Full Text | Google Scholar

Zhao, B., Zhou, Q., Huang, L., Zhang, Q., Zhu, Y., and Ma, J. (2024b). Minutia reconstruction in sonar images with diffusion probabilistic models. Eng. Appl. Artif. Intell. 135, 108850. doi:10.1016/j.engappai.2024.108850

CrossRef Full Text | Google Scholar

Zhong, Y., Ling, Z., Liu, L., Zhang, S., and Wen, H. (2024). Deep Gaussian attention network for lumber surface defect segmentation. IEEE Trans. Instrum. Meas. 73, 1–12. doi:10.1109/tim.2024.3381269

CrossRef Full Text | Google Scholar

Zhu, X., Cheng, Z., Wang, S., Chen, X., and Lu, G. (2020). Coronary angiography image segmentation based on pspnet. Comput. Methods Programs Biomed. 200, 105897. doi:10.1016/j.cmpb.2020.105897

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y., Xu, Z., Lin, Y., Chen, D., Zheng, K., and Yuan, Y. (2023). Surface defect detection of sawn timbers based on efficient multilevel feature integration. Meas. Sci. Technol. 35, 046101. doi:10.1088/1361-6501/ad15de

CrossRef Full Text | Google Scholar

Zhu, Y., Xu, Z., Lin, Y., Chen, D., Ai, Z., and Zhang, H. (2024). A multi-source data fusion network for wood surface broken defect segmentation. Sensors 24, 1635. doi:10.3390/s24051635

PubMed Abstract | CrossRef Full Text | Google Scholar