Study on the mechanical properties of limestone materials with different moisture contents under cyclic loading and unloading

Introduction: In order to reduce the impact of secondary disasters caused by the instability of rock and soil mass (RSM) during engineering construction on the environment, and to achieve safe and efficient engineering construction. Therefore, investigating the mechanical properties (M.P.), energy evolution laws, and damage characteristics of limestone with different water saturation (w) under cyclic loading-unloading (CLU) conditions is of significant engineering significance.

Methods: This study conducted uniaxial compression (UC) and cyclic loading-unloading tests on limestone samples with different w values (i.e., 0%, 25%, 50%, 75%, 100%) to elucidate their mechanical properties and energy dissipation. The influence of w on the degradation of limestone was examined based on damage variables.

Results: The results indicated that (1) as w increases, both the compressive strength (f_c) and elastic modulus (E) of the samples gradually decrease, while the peak axial strain gradually increases. When the w exceeded 0.4%, the failure characteristics transitioned from brittleness to ductility. (2) For limestone samples with the same w, the f_c and E under CLU conditions were greater than those under uniaxial compression conditions, while the peak axial strain was smaller than that under UC conditions. Analysis using the DRA method confirmed that w did not significantly affect the deformation memory effect of limestone. (3) As the axial strain and number of cycles (N) increased, both the input energy and dissipated energy gradually increased, while the elastic energy initially increased before rapidly declining. The proportion of elastic energy first increased and then decreased, while the proportion of dissipated energy first increased, then decreased, and finally suddenly increased. Compared with UC, CLU significantly enhanced the rock’s capacity to store elastic energy. (4) For the same N, limestone with higher w exhibited greater damage than that with lower w. Moreover, samples with high w always failed earlier than those with low w under both the UC and CLU conditions.

Discussion: The research results provide a theoretical basis for understanding the dynamic response behavior and stability analysis of limestone slopes under disturbance and rainfall effects.

1 Introduction

The RSM on the open-pit mine slope is frequently subjected to cyclic disturbances resulting from long-term mining and blasting activities, which can be conceptualized as a CLU process of rocks (Liu et al., 2025). The load on the slope increases with depth, which makes it susceptible to fatigue damage and deformation (Miao et al., 2024). In addition, the infiltration of rainfall can alter the M.P. of RSM, which may lead to mining dynamic disasters and safety accidents (Li and Li, 2024; Kim et al., 2022; Liu and Wang, 2023; Wu and He, 2024; Niu et al., 2018). The RSM on the slope of an open-pit metal mine in Yunnan Province is mainly composed of limestone. It is often influenced by daily excavation and blasting activities. Additionally, the mine experiences a rainy season from July to August, characterized by heavy rainfall. This atmospheric precipitation penetrates the limestone, which gradually deteriorates its M.P. Consequently, the slope has experienced multiple local instabilities, posing a serious threat to mine safety. This instability and failure of slopes are essentially attributed to the initiation, propagation, and penetration of internal cracks under external loads. These processes are accompanied by the input, accumulation, and dissipation of energy. Therefore, investigating the M.P., energy evolution laws, and damage characteristics of water-bearing limestone under CLU conditions is crucial for the stability analysis of limestone slopes.

The stress state and loading history experienced by rocks significantly affect their deformation, strength, and damage. Under cyclic loading conditions, the strength and deformation behaviors of rocks differ markedly from those observed under monotonic loading conditions (Zhang et al., 2025; Chen et al., 2023; Zhao et al., 2024). Currently, research on the M.P. of rocks under CLU conditions represents a prominent focus in the field of rock mechanics. Yang and Xu. (2025) investigated the M.P. and deformation of granite samples under incremental CLU stress paths. They also established a stress-strain (SS) normalization theoretical model based on viscoelasticity to clarify the dynamic damage mechanism of rock samples. Zhang and Meng. (2024) calculated the elastic energy density, dissipated energy density, and input energy density of samples subjected to true triaxial CLU paths. They also analyzed the variations in these densities with increasing N and the energy distribution under CLU conditions. Ding et al. (2025) analyzed the M.P. of damaged media under CLU conditions, as well as the degradation and evolution mechanism of pores and fractures, using raw coal containing original pores and fractures as the raw materials for their studies. Zhang et al. (2023) conducted triaxial compression and CLU tests on unloaded damaged sandstone samples to explore their M.P. and energy dissipation patterns. They also analyzed the development of cracks in the rock. These investigations primarily examine the deformation, damage, and failure characteristics of rocks under CLU conditions; however, they ignore the influence of water on the M.P. of rocks.

Numerous scholars have conducted research regarding the influence of water on the M.P. of RSM. Huang et al. (2024) conducted laboratory UC, Brazilian splitting, and shear tests on loess samples to elucidate how w influences the M.P. and failure characteristics of loess. Xie et al. (2024) conducted dynamic splitting impact tests on precast concrete specimens with different w to examine their damage modes and damage evolution laws. Yuan et al. (2024) studied the effect of w on the compressive strength and energy characteristics of alkali slag ceramic aggregate concrete under UC condition. Qin et al. (2020) conducted CLU tests on sandstone with different w to study its mechanical and acoustic emission characteristics. Zhang et al. (2023) conducted CLU tests on sandstone with different w to analyze the variations in E and Poisson’s ratio.

While substantial research has investigated the M.P. of water-bearing rocks during UC and CLU processes, the differences in M.P. and energy evolution of rocks with different w remain poorly understood. Additionally, the damage evolution process under these two loading paths has received limited analysis. Therefore, this study further explored the differences in M.P., energy evolution laws, and damage evolution characteristics of limestone samples with different w under UC and CLU conditions. This investigation aims is to provide scientific support for dynamic design and disaster warning in slope engineering by quantifying the attenuation of energy distribution preferences and damage accumulation patterns through mechanical parameters. Especially in the context of intensifying climate change and frequent extreme rainfall events, the relevant findings have urgent significance for ensuring the safe extraction of mineral resources.

2 UC and CLU tests on limestone with different w

2.1 Sample preparation

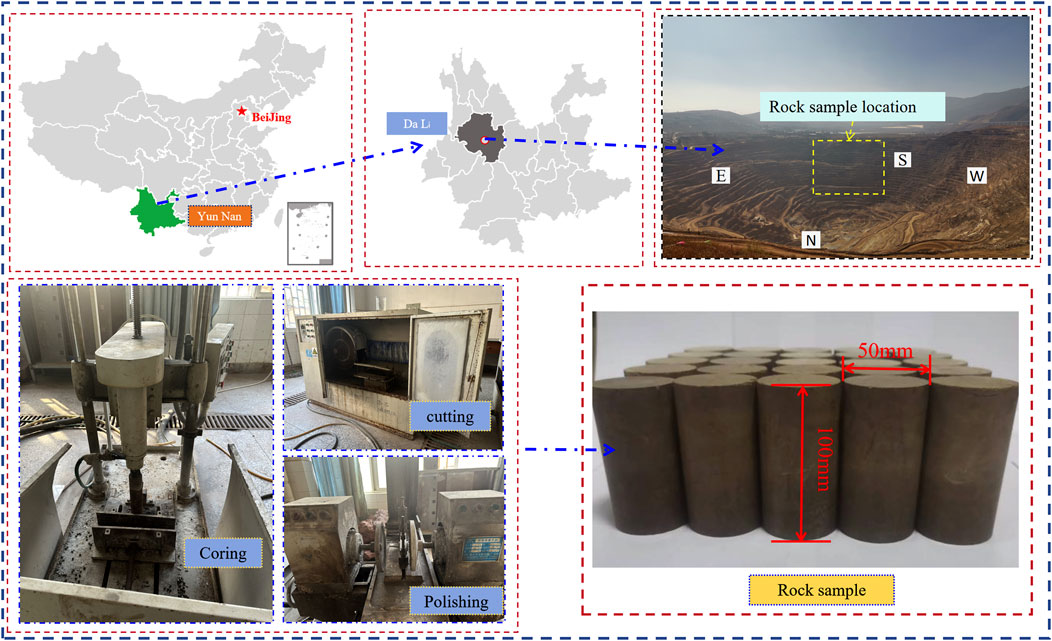
Limestone samples were collected from the 1700 m bench on the southern slope of an open-pit mine in Yunnan Province for testing. To minimize variability in the test results due to sample heterogeneity, all samples were extracted from the same location. The limestone blocks were processed into cylindrical specimens with dimensions of 50 mm in diameter and 100 mm in height in accordance with the International Society for Rock Mechanics (ISRM) standards for rock sample preparation. The ends of the cylinders were carefully polished to ensure that the non-parallelism and non-perpendicularity errors were controlled within ±0.02 mm. The samples exhibited a grayish-yellow appearance, a hard texture, high uniformity, and a low degree of weathering.

To ensure the homogeneity of rock samples, a two-step screening process was implemented prior to conducting the experiment.

(1) The dimensions and mass of the processed, dry rock samples were measured, and the initial density was calculated to be 2.737 g/cm³.

(2) The longitudinal wave velocity of the sample was tested, and samples with high wave velocity dispersion were excluded. The average velocity of the measured rock samples was determined to be 3,596 m/s.

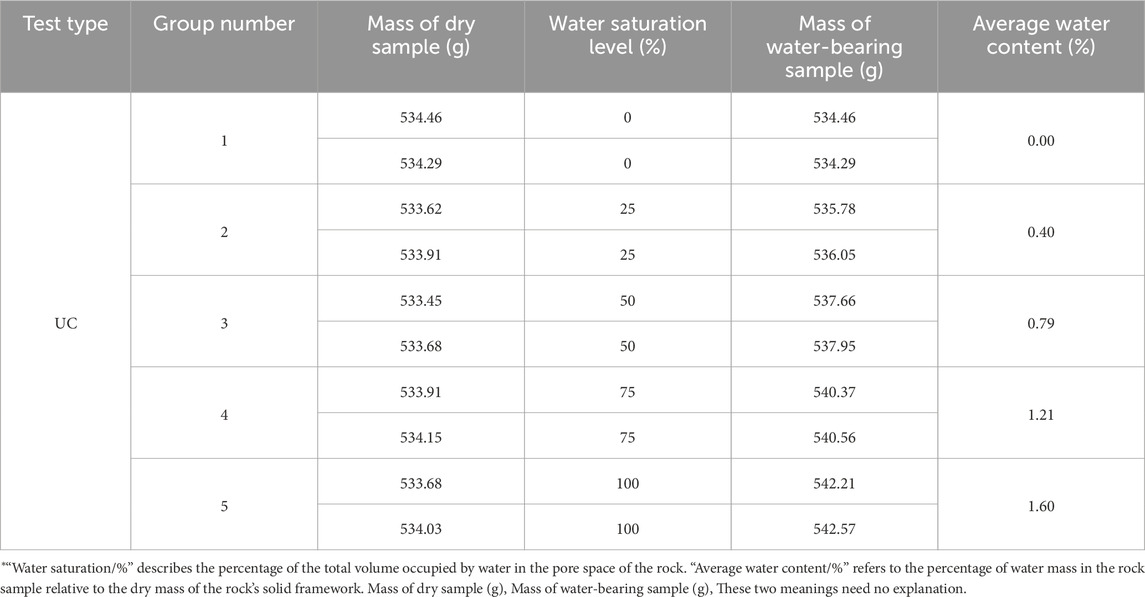
After wave velocity screening, samples containing visible joints were eliminated through visual inspection. The selected specimens met the accuracy requirements of rock mechanics testing standards. The processes for producing and screening standard rock cores are illustrated in Figures 1, 2. The 25 rock samples that met the selection criteria were divided into five equal groups (n = 5) and prepared with different w according to five gradient levels: 0%, 25%, 50%, 75%, and 100%. For each water gradient, two samples were designated for UC tests, while the remaining three samples were subjected to uniaxial CLU tests.

Figure 1

Figure 1. Preparation of standard rock samples.

Figure 2

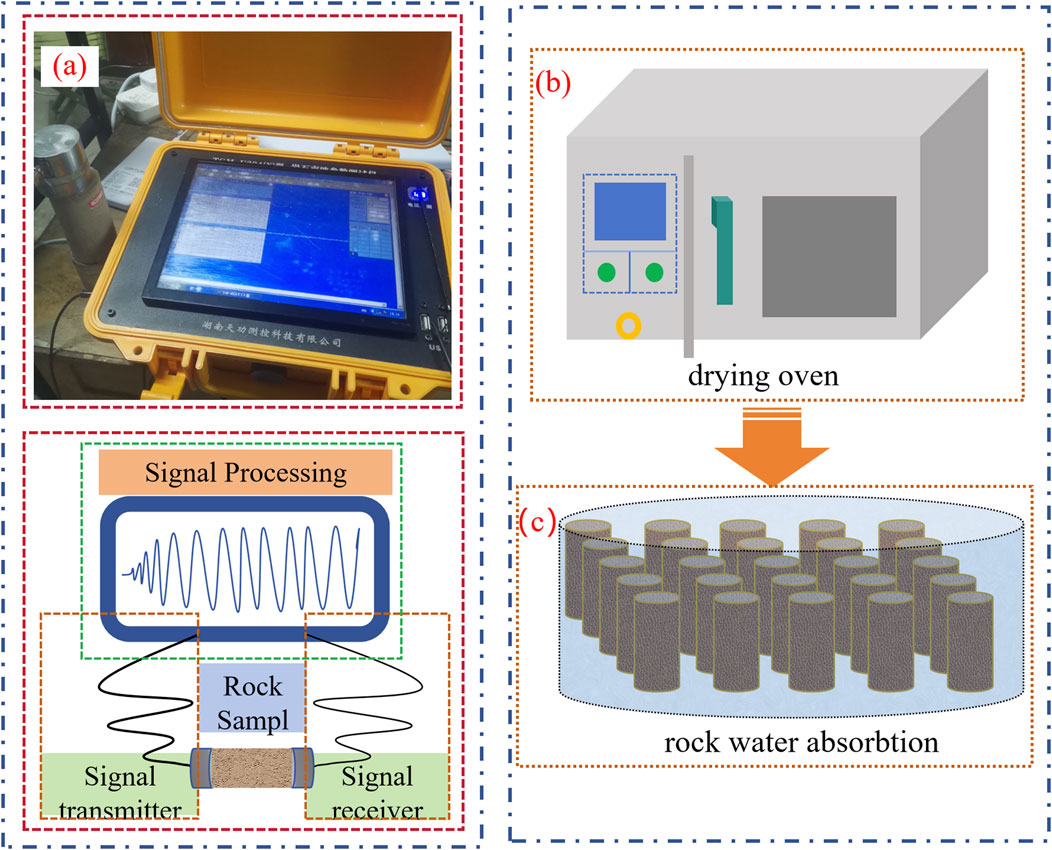
Figure 2. Preparation of limestone samples with different w. (a) Wave velocity testing; (b) Drying the rock samples; (c) Immersing the rock samples.

The preparation process for limestone samples with different w involved the following steps.

(1) The selected 25 rock samples were placed in an oven at a temperature of 105 C and dried for 24 h (Cao et al., 2024). The mass of each sample was measured consecutively twice. If the measured mass remained unchanged, the sample was deemed fully dried, and its dry mass was recorded.

(2) The dried sample were immersed in water for non-destructive, natural saturation. The samples were removed every day, their surfaces were gently wiped dry with paper, and their masses were measured. When no change in mass was observed between consecutive days, the samples was considered fully saturated.

(3) The masses corresponding to different w were calculated based on the dry and saturated masses. Limestone samples with intermediate w value were prepared by continuing the natural immersion process outlined in step 2. As the sample mass approached the targeted mass, the measurement intervals were shortened to ensure precise control. The prepared samples were sealed with plastic wrap to prevent further changes in moisture and promptly subjected to mechanical testing.

To facilitate identification, the rock samples were labeled using a marker pen. The first letters indicate the test type: D for UC test and X for CLU test. The second number represents the water saturation, and the third number refer to the number of blocks.

2.2 Experimental scheme design

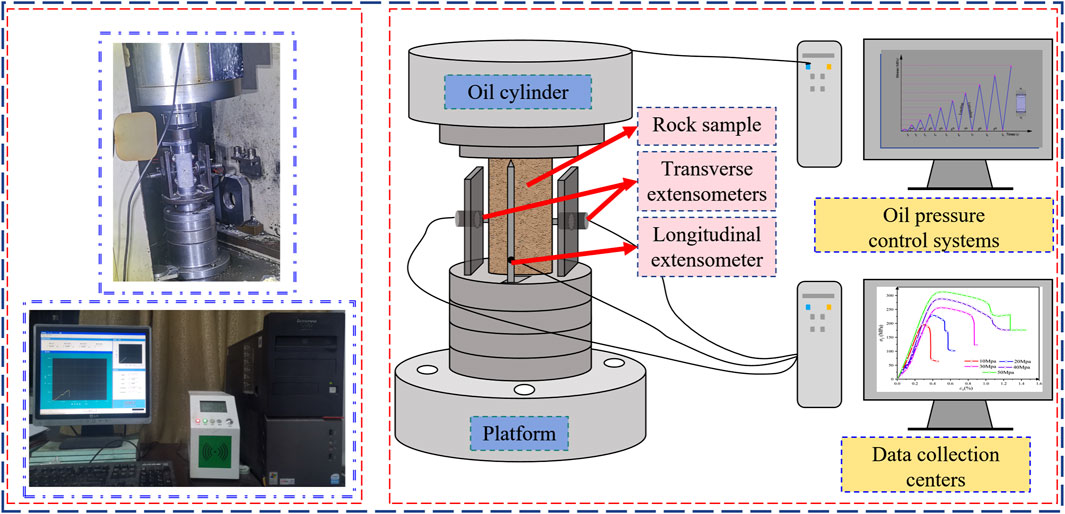
To investigate the M.P. and energy evolution laws of limestone with different w, UC and uniaxial CLU tests were conducted using the RMT 150C digital control electro-hydraulic servo testing machine, as illustrated in Figure 3.

Figure 3

Figure 3. Schematic diagram of the test process.

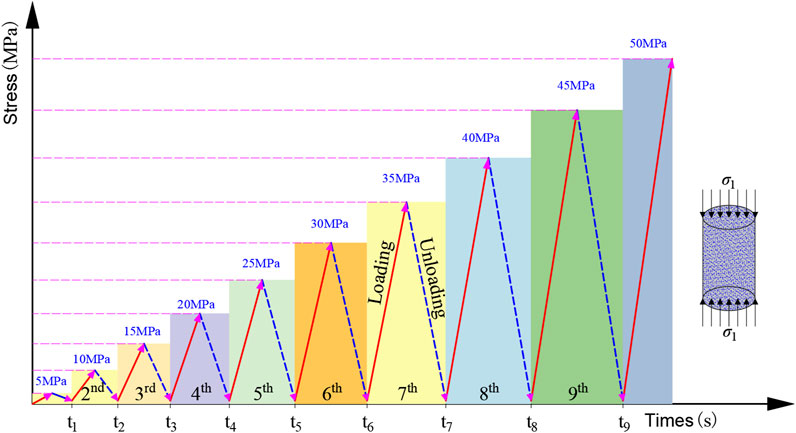
The UC tests employed a staged incremental CLU scheme. Initially, the sample was loaded from 0 MPa to 5 MPa and then unloaded to a stable level of 1.5 MPa. Subsequently, the peak load was incrementally increased by 5 MPa for each stage (10 MPa, 15 MPa, 20 MPa, etc.). The stress was decreased to the baseline value of 1.5 MPa during each unloading stage. The stress path followed a cyclic progression: 0 MPa → 5 MPa → 1.5 MPa → 10 MPa → 1.5 MPa → 15 MPa → 1.5 MPa → 20 MPa, and continued until the sample experienced macroscopic failure. The stress path is shown in Figure 4. The loading system operated under a constant rate of 0.002 mm/s throughout this process.

Figure 4

Figure 4. Stress path for CLU test.

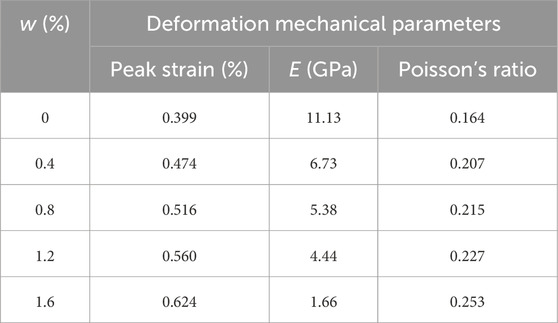
The rock samples were divided into five groups based on varying saturation levels: 0%, 25%, 50%, 75%, and 100%. Each group contains three samples, resulting in a total of 15 samples. To accurately assess the M.P. and energy evolution characteristics of limestone with different w under CLU conditions, it was essential to carefully control the N. Therefore, a series of UC tests were firstly performed. During these tests, the axial stress-strain data of the limestone samples were continuously monitored. The loading amplitude for the CLU tests was determined based on the results of the UC tests. The key parameters of the samples derived from the UC tests are summarized in Table 1.

Table 1

Table 1. Mechanical parameters of limestone at different water saturation levels.

3 Results and analysis

3.1 Characteristics of UC and CLU curves of water-bearing limestone

This study examined five groups of typical water-bearing limestone with water saturation of 0%, 25%, 50%, 75%, and 100% to analyze the axial stress-strain curves under both UC and CLU conditions, as shown in Figure 5.

Figure 5

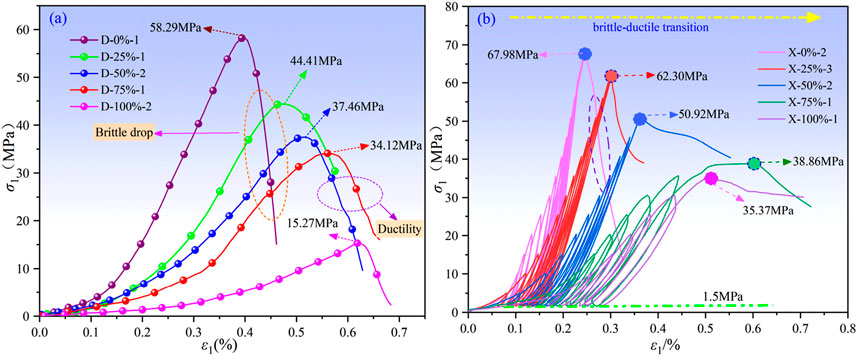
Figure 5. (a) Stress-strain curves of limestone with different w under UC conditions. (b) Stress-strain curves of limestone with different w under CLU conditions.

As depicted in Figure 5a, the axial stress of limestone increased with increasing axial strain during UC process. Upon reaching the peak stress, a decline in stress was observed as axial strain continues to increased. Notably, this stress drop was more pronounced at lower w. As the w increased, the limestone gradually transitioned to exhibit brittle-ductile characteristics. Figure 5b illustrated that limestone, as an anisotropic material, contains numerous inherent structures. The deformation of limestone samples during the CLU processes includes both elastic and plastic deformation, which is evidenced by the incomplete overlap of loading and unloading curves that creates a distinct hysteresis loop. As irreversible plastic deformation accumulated, the hysteresis loop progressively moved toward the direction of increasing strain. A higher w led to a more noticeable rightward movement of the hysteresis loop.

At lower w, the hysteresis loop appeared relatively sparse at the onset of loading. As loading progressed, the original pores within the limestone were gradually compacted, resulting in a denser hysteresis loop. Conversely, when the w reached 50%, the shape of the hysteresis loop began to reverse, and the hysteresis loop gradually became sparse as CLU continued. The irreversible plastic deformation in the sample gradually increased. Consistent with the behavior observed under UC, limestone specimens subjected to CLU exhibited pronounced ductility characteristics when w was higher than 50%, which were more significant than those observed under UC.

3.2 Strength and deformation characteristics

3.2.1 Influence of w on strength

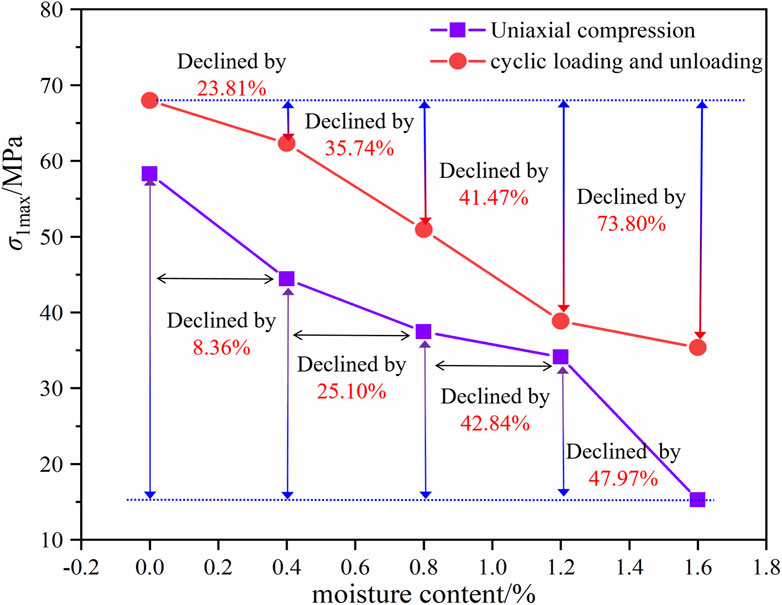
Figure 5 shows the peak strength of limestone with different w under UC and CLU conditions. Additionally, a line graph of peak stress as a function of w is presented in Figure 6.

Figure 6

Figure 6. Peak strength of limestone with different w under UC and CLU conditions.

Analysis indicated that the peak strength of limestone gradually decreases with increasing w under both UC and CLU conditions. As the w increased from 0% to 1.6%, the peak strength under UC conditions decreased by 20.42%, 30.64%, 35.55%, and 63.28%, respectively; while it decreased by 8.36%, 25.10%, 42.84%, and 47.97% under CLU conditions. This reduction in peak strength can primarily be attributed to the lubricating effect of water at lower w, which diminished the cohesion among particles within the rock and consequently reduced its strength. As the samples approached saturation, some water existed in the form of free water on the inner pore walls, leading to the development of pore water pressure. This pressure contributed to the stiffness of the rock sample under compression, which macroscopically resulted in a reduction in peak strength.

Moreover, it was observed that the peak strength of water-bearing limestone under CLU conditions is consistently higher than that under UC conditions. This disparity can be explained by the densification of original pores and microcracks within the rock during CLU process. As the loading progressed, the overall density of the rock increased, thereby reducing stress concentration in localized areas. Consequently, the uniformity of the applied load enhanced the sample’s strength, which is higher than that during UC process.

3.2.2 Influence of w on deformation

Table 2 summarizes the deformation parameters of limestone with different w obtained from UC tests.

Table 2

Table 2. Deformation M.P. of rocks under UC.

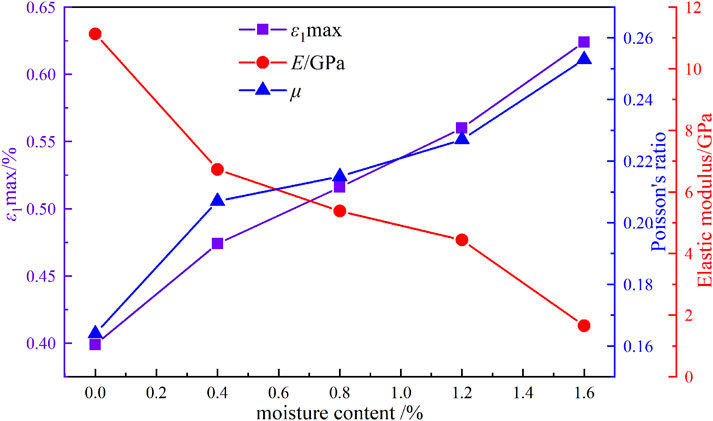
Figure 7 presents the relationship curves between mechanical parameters and w. It was demonstrated that both the peak strain and Poisson’s ratio under UC increase with rising w, while the E gradually decreases. These observations reflected a diminished ability of rock to resist deformation with higher w. The main reason lies in the fact that water significantly reduces the material’s ability to resist lateral deformation and shear deformation through two primary mechanisms: increasing pore pressure and softening the material matrix. This makes the material more prone to lateral expansion (increased strain) when subjected to axial compression. Consequently, the increase in Poisson’s ratio directly reflects how the presence of water causes significant changes in the material’s volumetric behavior under stress.

Figure 7

Figure 7. Relationship between uniaxial deformation parameters and w.

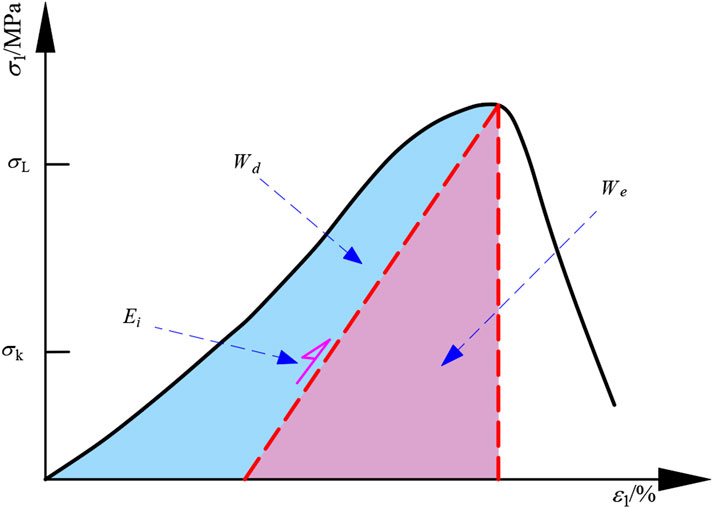
Based on the stress-strain curves from CLU tests, the E of limestone was calculated using Equations 1 and 2 (Gu et al., 2025). The calculation principle is illustrated in Figure 8, and the relationship curves between axial strain, E, and N for limestone with different w are presented in Figures 9a,b.

$E_i=\frac{\sigma }{{\epsilon }_e}(1)$

$E_j=\frac{\sigma }{\epsilon }=\frac{\sigma }{{\epsilon }_e+{\epsilon }_p}(2)$

where E_i and E_j are the elastic moduli during the loading and unloading stages, respectively; $\sigma$ is the peak stress during each loading-unloading cycle; ${\epsilon }_e$ and ${\epsilon }_p$ are the elastic and plastic strains during each loading-unloading cycle, respectively.

Figure 8

Figure 8. Calculation of E for rock samples.

Figure 9

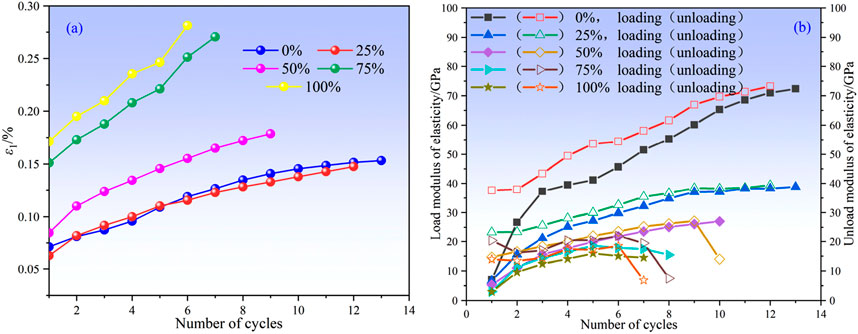
Figure 9. (a) Variation of axial strain of water-bearing limestone with N. (b) Variation of E of water-bearing limestone with N.

Figure 9a confirmed that the axial strain of the limestone gradually increases as the N increases. Notably, higher w led to greater axial strain for the same N. Figure 9b showed that at the same w, the E during the unloading stage is higher than that during the loading stage. This discrepancy arose primarily due to the compaction of existing pores and cracks within the rock during the loading stage, as well as the generation of microcracks leading to irreversible plastic deformation. During unloading, the stress decreased and the rock mainly underwent elastic recovery. Furthermore, as the w increased, the acceptable N for limestone gradually decreased, and the E for the same N gradually decreased, which is macroscopically manifested as an increase in rock deformation under identical loads.

A comparative analysis of the two loading methods revealed that, for the same w, the peak strain of limestone under UC conditions is higher than that under CLU conditions. Moreover, as CLU progressed, the compaction of microcracks and pores within the sample occurred. At the same w, the E of limestone samples under CLU conditions was significantly higher than that under UC conditions.

The characteristics exhibited by limestone in response to increasing w provide indirect insights into the reasons why mining slopes are particularly prone to instability during the rainy season.

3.3 Analysis of rock deformation memory effect

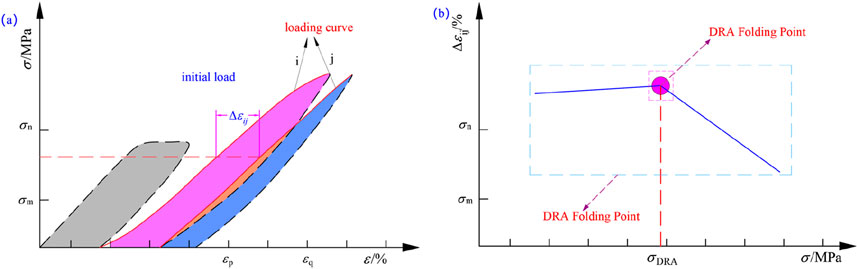
Various materials, including rocks and metals possess, can store information about external influences and display this information through specific physical quantities under certain conditions. This property is called the memory effect (Zhong et al., 2024; Huang et al., 2024; Tian et al., 2023). The memory effect of rocks is of great significance for geological engineering, geostress measurement, and rock stability analysis. The DRA method (Miao et al., 2024; Zhao et al., 2024) has been frequently employed to analyze rock deformation data during CLU processes to obtain memory information of rocks.

The principle of the DRA method is illustrated in Figure 10, where the solid lines i and j denote two successive repeated loading cycles. The strain difference function is defined as in Equation 3:

$\Delta {\epsilon }_{i,j}\left(\sigma \right)={\epsilon }_j\left(\sigma \right)-{\epsilon }_i\left(\sigma \right)\left(j>i\right)(3)$

where ${\epsilon }_j\left(\sigma \right)$ and ${\epsilon }_j\left(\sigma \right)$ are the axial strains corresponding to the same axial stress for two adjacent loading curves, as shown in Figure 10a. Assuming that the confining pressure and volumetric strain are positive, the difference in axial irreversible strain $\Delta {\epsilon }_{i,j}\left(\sigma \right)$ can be derived from Equation 1. The strain difference curve, also known as the DRA curve, is constructed with stress $\sigma$ on the horizontal axis and strain difference $\Delta {\epsilon }_{i,j}\left(\sigma \right)$ on the vertical axis, as depicted in Figure 10b. The curve exhibits a distinct inflection point, where the corresponding stress ${\sigma }_{DRA}$ represents the memory information ${\sigma }_P$. This inflection point is referred to as the DRA inflection point.

Figure 10

Figure 10. (a) Principle of strain difference calculation ${∆\mathrm{\epsilon }}_{\text{ij}}$; (b) DRA method turning curve.

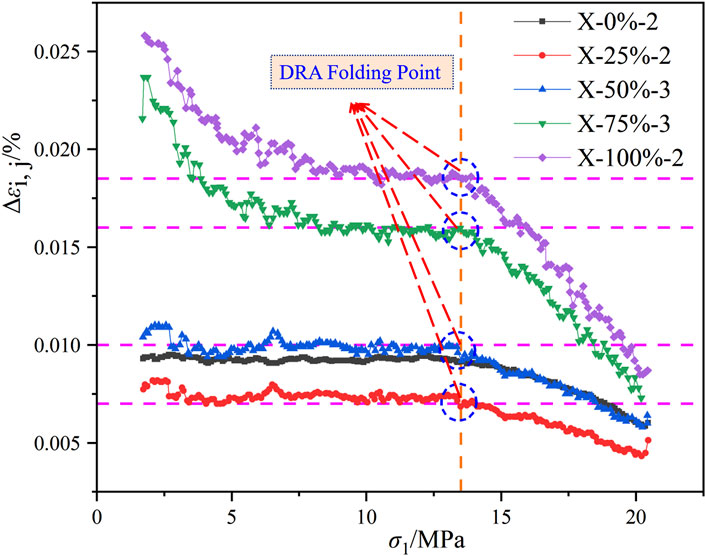
To clarify whether the w affects the memory characteristics of limestone and to provide a theoretical basis for rock stability analysis, this study analyzed the loading curves from the fourth and fifth cycles of five types of limestone with different w using the DRA method. The strain differences of limestone with identical w were averaged, and the corresponding DRA curves are presented in Figure 11.

Figure 11

Figure 11. Analysis of DRA for limestone samples with varying w.

The DRA curves illustrated that the evolution trends for limestone samples with different w remain consistent, with DRA inflection points appearing at approximately the same axial stress levels. This observation reflected a pronounced rock deformation memory effect. Therefore, it can be concluded that while hydration changes macroscopic mechanical parameters, it does not significantly interfere with the memory storage effect related to the internal stress history of the rock.

4 Analysis of energy evolution laws

The deformation and failure of rocks is a complex process involving the input, accumulation, dissipation, and release of energy. During loading and unloading processes, the testing machine exerts work on the rock sample, which in turn absorbs and releases energy. The development and propagation of internal fractures in the rocks reflect the energy dissipation (Liu et al., 2025; Chen et al., 2025). Studying these energy conversion processes can provide valuable insights into the failure mechanisms of rock samples (Yue et al., 2025).

4.1 Analysis of the energy evolution of the sample under CLU conditions

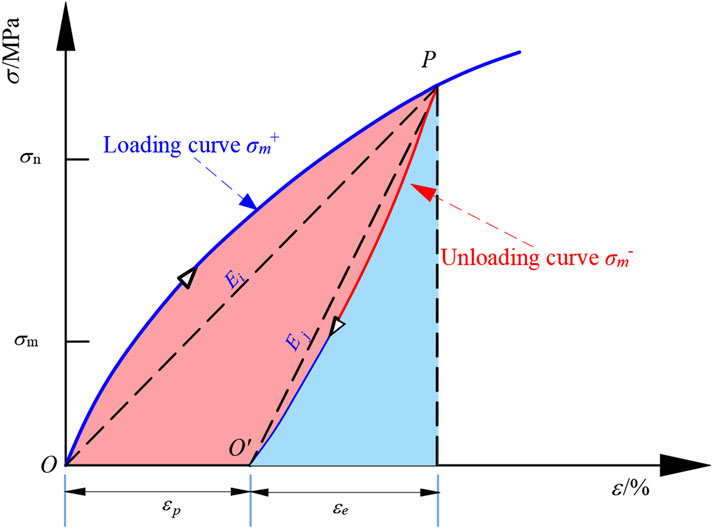
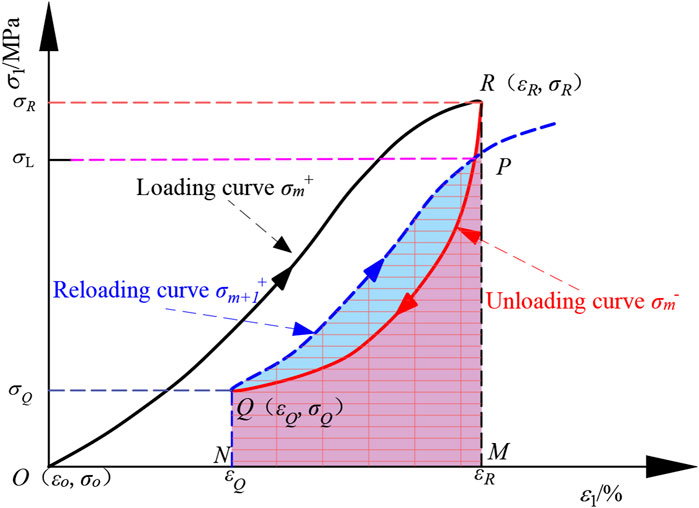
Figure 12 shows the CLU curves during the mth and (m+1)-th cycles. PQP represents the hysteresis loop formed by adjacent loading cycles, which indirectly reflects the damage process of the rock sample. The area enclosed by ORMO represents the energy input into the rock sample during the mth cycle, while the area enclosed by RMNAQ represents the stored elastic energy during the mth cycle.

Figure 12

Figure 12. Energy calculation for CLU.

During the CLU process, various energy-related parameters can be calculated according to Equations 4–7 (Wang et al., 2025; Sun et al., 2025).

$U_m={\int }_{{\epsilon }_0}^{{\epsilon }_R}{\sigma }_m^{+}d{\epsilon }_m(4)$

$U_{em}={\int }_{{\epsilon }_Q}^{{\epsilon }_R}\left({\sigma }_{\mathrm{m}}^{+}-{\sigma }_m^{-}\right)d{\epsilon }_m(5)$

$U_{dm}=U_m-U_{em}(6)$

$\mathrm{\gamma }=\raisebox{1ex}{${\mathrm{U}}_{\text{dm}}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{U}}_{\mathrm{m}}$}\right.(7)$

where $U_m$, $U_{em}$, and $U_{dm}$ are the input energy density from external loads on the rock (MJ/m³), the elastic energy density stored in the rock sample (MJ/m³), and the dissipated energy density (MJ/m³) during the mth cycle, respectively; $\mathrm{\gamma }$ represents the proportion of dissipated energy, which reflects the energy conversion relationship in limestone with different w during compression.

The values of $U_m$, $U_{em}$, and $U_{dm}$ for limestone samples with different w during each loading-unloading stage were calculated based on the stress-strain data. The relationship curves between energy density, energy proportion, and N are illustrated in Figure 13.

Figure 13

Figure 13. Energy evolution during CLU process. (a) 0%, (b) 25%, (c) 50%, (d) 75%, (e) 100%.

As illustrated in Figure 13, the energy evolution of limestone with different w during CLU processes was analyzed and compared with the axial strain versus N curve presented in Figure 9a. It was found that the U_m gradually increased with the N, while the U_em first increased and then decreased. The U_dm first remained stable and then suddenly increased.

The energy evolution trends for limestone samples with different w remained consistent. During the initial stage of loading, a significant portion of energy was first converted into dissipated energy, with the dissipated energy reaching a maximum proportion of 85%. This is primarily attributed to the presence of initial cracks and pores within the limestone. As a result, the energy input during the initial loading stage was dissipated in the form of micro-cracking and closure of pores. This phenomenon was manifested as a sharp increase in axial deformation, which corroborates the observation of a large axial strain during the first loading in Figure 9a.

As the N increased, both the U_m from the testing machine and the U_em stored in the sample increased in an orderly manner. At this point, the rock sample remained in the elastic stage, and the dissipated energy in this stage remained basically unchanged. However, as the CLU load reached the peak strength, cracks initiated and irregularly propagated due to the applied load exceeding the ultimate compressive strength of the rock sample. This results in a rapid decrease in U_em and a corresponding surge in U_dm, as a substantial amount of input energy was dissipated through the irregular crack propagation. The proportion of dissipated energy revealed a marked increase in the later CLU stage.

The differences in energy evolution of limestone with different w were comparatively studied. The integral value of the loading curve within the strain range was employed to characterize the energy input by the testing machine. It was observed that during the CLU process, lower w correlates with reduced plastic damage in rock samples for the same N, as well as reduced U_m. As the rock progressed toward failure, the cumulative integral area also decreased accordingly. As the w increased, the plastic deformation of the rock increased from the initial loading stage to rock failure. The U_m and U_dm increased significantly for the same N, while the U_em gradually decreased.

The failure processes of limestone samples with varying w derived from an energy perspective align with the conclusions drawn from the axial strain versus N curve in Figure 9a. This highlights that initial cracks and pores fundamentally contributes to the susceptibility of limestone to damage when exposed to water.

4.2 Analysis of the energy evolution of the sample under UC conditions

Assuming that there is no heat exchange between the sample and the environment during UC, the energy relationship based on Equation 6 remains valid for limestone with different w, according to the first law of thermodynamics. The relationship between U_em and U_dm is illustrated in Figure 14.

Figure 14

Figure 14. Relationship between U_em and U_dm under UC conditions.

The total energy density and U_em resulting from external loads during the compression of limestones with different w can be expressed by Equations 8 and 9 (Luo et al., 2025):

$W={\int }_0^{{\epsilon }_1}{\mathrm{\sigma }}_{1}d{\epsilon }_1+{\int }_0^{{\epsilon }_2}{\mathrm{\sigma }}_{2}d{\epsilon }_2+{\int }_0^{{\epsilon }_3}{\mathrm{\sigma }}_{3}d{\epsilon }_3(8)$

$W_e=\frac{1}{2}{\sigma }_1{\epsilon }_{1e}+\frac{1}{2}{\sigma }_2{\epsilon }_{2e}+\frac{1}{2}{\sigma }_3{\epsilon }_{3e}(9)$

By incorporating Hooke’s Law, Equation 9 can be further formulated as Equation 10:

$W_e=\frac{\left[{\sigma }_1^2+2{{\sigma }_3}^2-2\overline{\mu }\times \left(2{\sigma }_1{\sigma }_3+{\sigma }_3^2\right)\right]}{2E_i}(10)$

where $W$ represents the input energy density from uniaxial loading on the rock (MJ/m³); $W_e$ denotes the elastic energy density stored in the rock (MJ/m³); $E_i$ indicates the elastic modulus of the unloading curve (GPa), and $\mu$ represents the Poisson’s ratio.

In the case of limestones with different w under UC conditions, where they are subjected solely to axial loads with zone confining pressure (${\mathrm{\sigma }}_2={\mathrm{\sigma }}_3=0$), Equation 8 can be simplified to Equation 11. Furthermore, for computational convenience, the initial elastic modulus ${\mathrm{E}}_0$ is substituted for the elastic modulus ${\mathrm{E}}_{\mathrm{i}}$ of the unloading curve; therefore, Equation 10 can be represented as Equation 12. The damage dissipation energy density under UC conditions is determined using Equation 6.

$W={\int }_0^{{\epsilon }_1}{\mathrm{\sigma }}_{1}d{\epsilon }_1(11)$

$W_e=\frac{1}{2}\frac{{\sigma }_1^2}{E_0}(12)$

The values of $W$, $W_e$, $W_d$, and their proportions for limestones with varying w under UC conditions were computed using Equations 6, 7, 11 and 12. The relationship curves between these parameters and axial strain ${\epsilon }_1$ are presented in Figure 15.

Figure 15

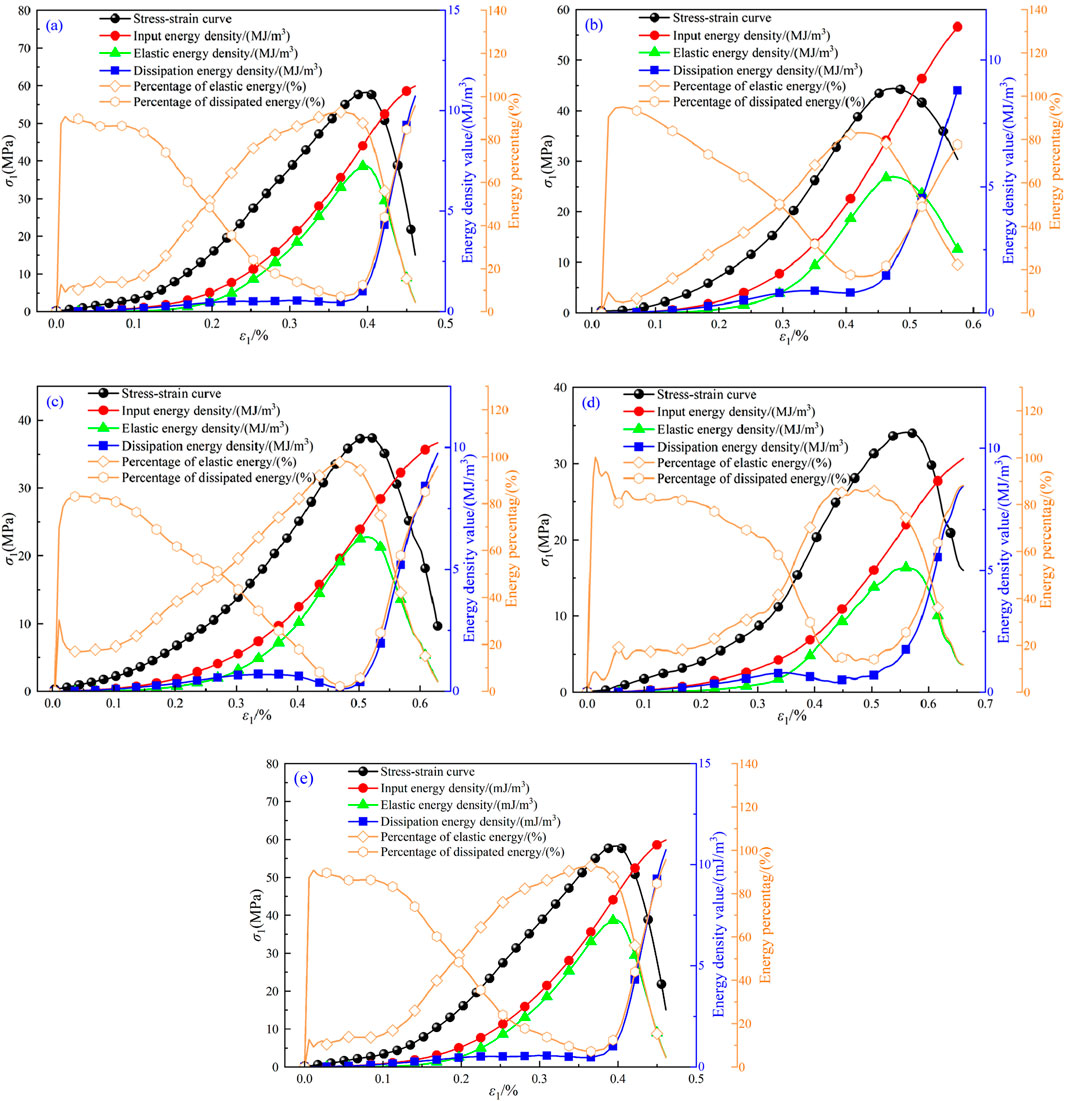
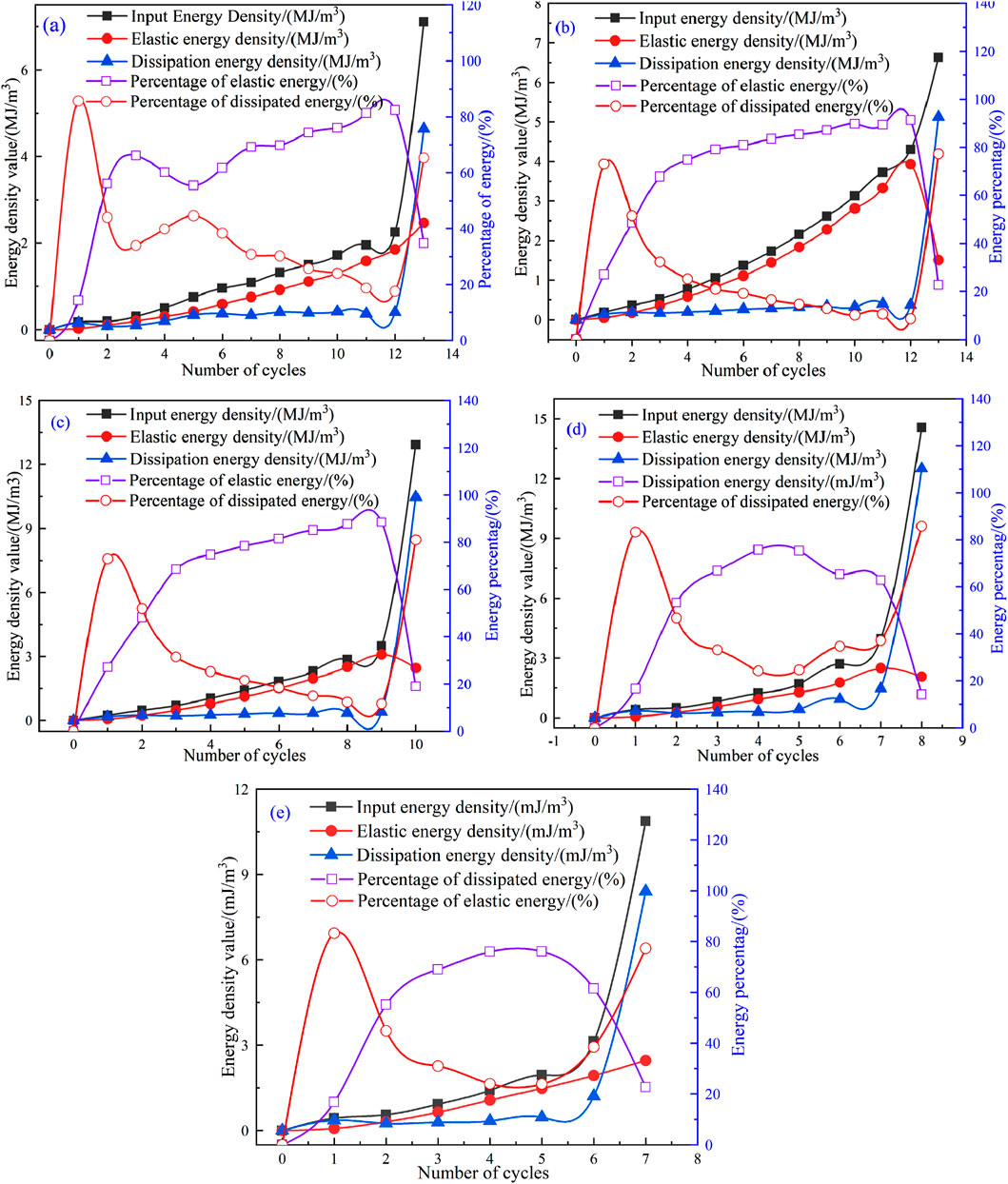
Figure 15. Energy evolution curves of the samples under UC conditions. (a) 0%, (b) 25%, (c) 50%, (d) 75%, (e) 100%.

Figure 15 revealed that under UC conditions, $W$, $W_e$, and $W_d$ gradually decrease as the w of the limestone increases.

Furthermore, the evolution trends of various energy densities under UC conditions were consistent with those under CLU conditions. In the early loading stage, the closure of initial cracks and pores in limestone consumed the majority of the energy. During the intermediate loading stage, the rock sample exhibited primarily elastic deformation behavior, and the input energy was predominantly converted into elastic potential energy and stored within the rock. The energy dissipation process was relatively smooth. As the density of stored elastic energy gradually increased, its proportion rose, while the proportion of dissipated energy decreased. In the later loading stage, when the applied load surpassed the rock’s peak strength, a significant amount of stored energy was dissipated due to crack initiation and unstable growth, resulting in rock failure. At this stage, the proportion of dissipated energy reached its maximum.

A comparative analysis of the energy evolution process of limestone under UC and CLU conditions revealed that, for the same w, the total energy density input, stored elastic energy, and dissipated energy of the rock during CLU were higher than those during UC. This finding indirectly reflected that CLU exert additional pressure on the rock, thereby facilitating increased energy absorption and storage prior to rock failure. This observation aligns with conclusions drawn from the analyses of the stress-strain curves.

4.3 Analysis of damage evolution

The damage evolution of limestone with different w is essentially a dynamic process characterized by the continuous expansion of internal micro-defects and energy dissipation. To quantitatively characterize the damage development in water-bearing limestone during the failure process, this study constructed a damage variable calculation formula for the compression process of water-saturated limestone. This is based on the strain evolution characteristics and energy conversion data obtained from CLU processes outlined in Sections 3 and 4. The formula is grounded in the principle of damage equivalence and references the definition of damage by Yang and Xu, (2025), as shown in Equations 13 and 14. The cumulative damage degree was quantitatively characterized through numerical calculation.

$D_{z\epsilon }=\frac{{\displaystyle {\sum }_1^m}{\epsilon }_1^p\left(m\right)}{{\displaystyle {\sum }_1^n}{\mathrm{\epsilon }}_1^p\left(m\right)}(13)$

$D_{zw}=\frac{{\displaystyle {\sum }_1^m}{W}_d\left(m\right)}{{\displaystyle {\sum }_1^n}{W}_d\left(m\right)}(14)$

where $D_{z\epsilon }$ represents the cumulative damage parameter based on axial strain; $D_{zw}$ denotes the cumulative damage parameter based on dissipated energy density; ${\epsilon }_1^p\left(m\right)$ indicates the plastic strain during the mth cycle; and $W_d\left(m\right)$ represents the damage dissipated energy during the mth cycle.

Figure 16a,b show the relationship curves between the damage variables and the N based on axial plastic strain and dissipated energy density, respectively. A comprehensive analysis indicated that the cumulative damage of limestone with different w increases with increasing N.

Figure 16

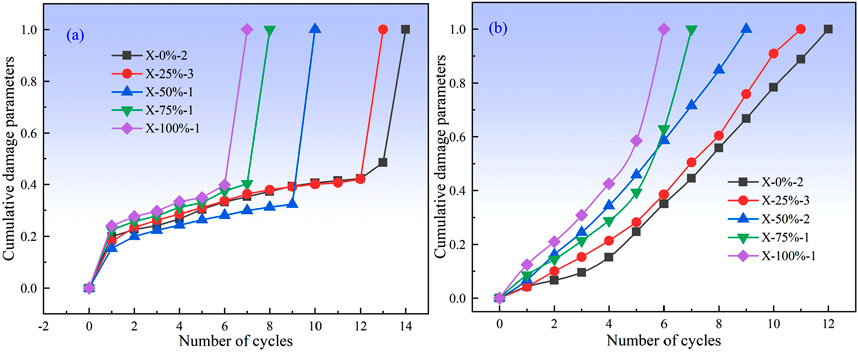
Figure 16. (a) Relationship curve between the damage variable based on axial plastic strain and the N. (b) Relationship curve between the damage variable based on the dissipated energy density and the N.

Figure 16a revealed that the relationship curve between the damage variable based on axial plastic strain and the N can be divided into four distinct stages. In the initial stage (the first cycle, from 0 to 1), there was a significant surge in cumulative damage. During the mid-cycle stage, as w decreased from high to low (corresponding cycle ranges: 1–12, 1–10, 1–8, 1-5, and 1–4), cumulative damage increased steadily. In the late cycle stage (12–13, 10–12, 8–9, 5-7, and 4–6), the rate of cumulative damage acceleration increased. In the final stage (12–14, 12–13, 9–10, 7-8, and 6–7), the cumulative damage parameter rose sharply.

Figure 16b indicates the relationship curve between the damage variable and the N based on damage dissipation energy density. It was observed that the cumulative damage increases with increasing N. When the w exceeded 0.8%, the growth rate of damage in limestone accelerated. For the same N, limestone with higher w exhibited greater damage compared to that with lower w.

Overall, limestone with higher w consistently failed earlier than that with lower w under both UC and CLU conditions. This finding underscores the significant impact of water on the mechanical behavior of limestone under load.

5 Conclusion

A series of UC and CLU tests were conducted on limestone samples with different w. An analysis was conducted on the similarities and differences in the damage evolution characteristics, M.P., and energy evolution patterns of limestone under these two loading paths. The following conclusions were drawn.

(1) The strength characteristics and failure modes of limestone exhibited significant dependence on w. As the w increased, the failure mode of limestone gradually transitioned from brittle failure to ductile failure, and its strength showed a regular decay trend. For the same w, the strength of limestone under CLU conditions was higher than that under UC conditions.

(2) The peak axial strain of limestone gradually increased with increasing w, while the E gradually decreased. When excavating slopes, sufficient consideration should be given to the influence of water on slope stability. At the same w, the E of the rock sample under CLU conditions was higher than that under UC conditions due to the gradual compaction of the original cracks caused by CLU. The DRA method analysis showed that the w has no significant effect on the deformation memory effect of limestone.

(3) Under both loading conditions, as axial strain and N increased, there was a gradual rise in both input energy and dissipated energy. The elastic energy, however, initially increased before experiencing a rapid decline after reaching peak strength. During the initial loading stage, the closure of microcracks within the rock led to significant energy dissipation, with dissipated energy comprising up to 80% of the total input. The proportion of elastic energy initially increased rose before decreasing, whereas the proportion of dissipated energy first rose, then declined, and ultimately surged. As w increased, both input and dissipated energy showed a steady increase within the same cycle, while the stored elastic energy correspondingly decreased. CLU significantly improved the rock’s capacity to store elastic energy compared to UC.

(4) For the same N, limestone with higher w exhibited greater damage than that with lower w. Moreover, limestone with w content consistently failed earlier than that with low w under both UC and CLU conditions, indicating that w significantly influences the mechanical behavior of limestone under loading conditions.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

TH: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Validation, Writing – original draft, Writing – review and editing. ZZ: Conceptualization, Project administration, Supervision, Writing – review and editing. JZ: Investigation, Methodology, Software, Validation, Writing – review and editing. YZ: Conceptualization, Methodology, Validation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by grants from the National Natural Science Foundation of China (Grant no. 51864023), the National Natural Science Foundation of China (Grant no. 52264019) and the Yunnan Major Scientific and Technological Projects (Grant no. 202202AG050014) and the Youth Project of Yunnan Province Basic Research Program(202401AU070175) is gratefully acknowledged.

Conflict of interest

Author YZ was employed by China Construction Eighth Engineering Division Corp., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, X. W., Tang, X. H., Chen, L. G., D, W., and Jiang, Y. (2024). Study on characteristics of failure and energy evolution of different moisture-containing soft rocks under cyclic disturbance loading. Mater. 17 (8), 1770. doi:10.3390/MA17081770

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, G. Q., Zhang, Y., Xu, Q., Wu, X. Z., Meng, K., and Fan, H. (2025). A novel brittle evaluation method considering the difference in energy evolution during rock failure process. Eng. Fail. Anal. 170, 170109280–109280. doi:10.1016/J.ENGFAILANAL.2025.109280

CrossRef Full Text | Google Scholar

Chen, Y. G., Chen, Y. L., Zhang, Y. F., Zhang, J. L., and Chen, T. (2023). Mechanical properties and penetration characteristics of mudstone slag-based waterproof composites under cyclic loading. Appl. Sci. 14 (1), 198. doi:10.3390/APP14010198

CrossRef Full Text | Google Scholar

Ding, Z. W., Tang, Q. B., Gong, X. W., Jia, J. D., Di, G. Q., and Chen, L. (2025). Mechanical properties and mechanism of damage and deterioration of coal under cyclic loading. Sci. Rep. 15, 4033. doi:10.1038/s41598-025-88577-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, T. T., Tao, T. J., Tian, X. C., Xie, C. J., Wang, Q., and Jia, J. (2025). A dynamic damage constitutive model considering the effect of joint inclination on the modulus of elasticity of slates. Sci. Rep. 15 (1), 10605. doi:10.1038/S41598-025-94233-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, L. M., Li, H., Wen, S. X., Xia, P. H., Zeng, F. Z., Peng, C. Y., et al. (2024). Control nucleation for strong and tough crystalline hydrogels with high water content. Nat. Commun. 15 (1), 7777. doi:10.1038/S41467-024-52264-Y

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, X. L., Xu, L., Xue, L., and Wei, X. (2024). Compression-hardening memory of the microstructure and its effect on the cyclic loading/unloading response of crystalline rock using a grain-based model. Rock Mech. Rock Eng. 57 (9), 6613–6632. doi:10.1007/S00603-024-03863-0

CrossRef Full Text | Google Scholar

Kim, Y., Rahardjo, H., Nistor, M. M., Satyanaga, A., Leong, E. C., and Sham, A. W. L. (2022). Assessment of critical rainfall scenarios for slope stability analyses based on historical rainfall records in Singapore. Environ. Earth Sci. 81 (2), 39. doi:10.1007/S12665-021-10160-4

CrossRef Full Text | Google Scholar

Li, L. Q., Li, Y. L., and Xu, Y. (2024). Instability evolution of expansive soil slope due to short duration-varying intensities of rainfall. Eng. Fail. Anal. 161, 161108313. doi:10.1016/j.engfailanal.2024.108313

CrossRef Full Text | Google Scholar

Liu, X., Wang, Y., and Leung, A. K. (2023). Numerical investigation of rainfall intensity and duration control of rainfall-induced landslide at a specific slope using slope case histories and actual rainfall records. Bull. Eng. Geol. Environ. 82 (8), 333. doi:10.1007/S10064-023-03359-1

CrossRef Full Text | Google Scholar

Liu, Y. D., Zhang, H. J., Qin, Z., Chen, X. X., and Liu, w. (2025). Energy evolution and deformation features of re-loading creep failure in yellow sandstone after cyclic water intrusion. Int. J. Rock. Mech. Min. Sci. 186, 186106019–106019. doi:10.1016/j.ijrmms.2024.106019

CrossRef Full Text | Google Scholar

Liu, Z., Si, X. F., and Wu, W. (2025). Experimental study on dynamic mechanical properties of sandstone under different damage degrees. Appl. Sci. 15 (5), 2668. doi:10.3390/APP15052668

CrossRef Full Text | Google Scholar

Luo, Y., Huang, J. C., Si, X. F., Wu, W. X., and Li, S. (2025). Failure characteristics and energy properties of red sandstone under uniaxial compression: water content effect and its application. Bull. Eng. Geol. Environ. 84 (1), 57. doi:10.1007/S10064-025-04085-6

CrossRef Full Text | Google Scholar

Miao, S. j., Liu, Z. J., Zhao, X. G., Ma, L. K., Zheng, Y. W., and Xia, D. H. (2024). Plastic and damage energy dissipation characteristics and damage evolution of Beishan granite under triaxial cyclic loading. Int. J. Rock. Mech. Min. Sci. 174, 174105644. doi:10.1016/J.IJRMMS.2024.105644

CrossRef Full Text | Google Scholar

Miao, S. J., Xia, D. H., Yang, P. J., Liu, Z. J., and Shang, X. (2024). Characteristics of stress memory and acoustic emission for siltstone under different previous stresses. Int. J. Geomechanics 24 (3). doi:10.1061/IJGNAI.GMENG-8988

CrossRef Full Text | Google Scholar

Niu, S. J., Ge, S. S., Yang, D. F., Dang, Y. H., Yu, J., and Zhang, S. (2018). Mechanical properties and energy mechanism of saturated sandstones. J. Central. South. Univ. 25 (6), 1447–1463. doi:10.1007/s11771-018-3839-z

CrossRef Full Text | Google Scholar

Qin, X. Z., Zhou, Y., and He, M. C. (2020). Experimental study on mechanical properties and acoustic emission characteristics of water bearing sandstone under stable cyclic loading and unloading. Shock. Vib. 2020, 1–15. doi:10.1155/2020/9472656

CrossRef Full Text | Google Scholar

Sun, G. W., Lu, Y., Huang, G., Liang, Q. M., and Huang, X. (2025). Mechanical and energy evolution characteristics of fractured sandstone materials: a true triaxial experimental study. Materials 18 (1), 175. doi:10.3390/MA18010175

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, Y., Yu, R. G., Chen, F. X., Meng, F. Z., and Zhang, Z. (2023). Experimental study on acoustic emission stress memory function of rock-like specimens under uniaxial compression. Int. J. Damage. Mech. 32 (8), 1008–1027. doi:10.1177/10567895231183008

CrossRef Full Text | Google Scholar

Wang, T., Zeng, G., Hu, D., and Wang, D. (2025). Numerical study on the mechanical properties, failure mode, energy dissipation, and acoustic emission of defected-rocks under uniaxial compression. Sci. Rep. 15 (1), 9595. doi:10.1038/S41598-025-88147-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, L. Z., He, B., and Peng, J. (2024). Analysis of rainfall-caused seepage into underlying bedrock slope based on seepage deformation coupling. Int. J. Geomechanics. 24 (5). doi:10.1061/IJGNAI.GMENG-9175

CrossRef Full Text | Google Scholar

Xie, F. x., Jin, Z. H., Yang, T. F., Han, X., Chen, X. D., and Zhang, Y. (2024). Dynamic splitting tensile strength of precast concrete samples with varying moisture contents. J. Mater. Civ. Eng. 36 (2). doi:10.1061/JMCEE7.MTENG-16479

CrossRef Full Text | Google Scholar

Yang, R. Z., and Xu, Y. (2025). Deformation theory and energy mechanism of cyclic dynamic mechanical damage for granite in the diversion tunnel under cyclic loading-unloading. iScience 28 (1), 111583. doi:10.1016/J.ISCI.2024.111583

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, P., Zhu, Y. S., Li, D. H., and Lu, X. (2024). Effect of freeze-thaw cycle and moisture content on compressive and energy properties of alkali slag ceramsite concrete. KSCE J. Civ. Eng. 28 (5), 1980–1991. doi:10.1007/s12205-024-1757-1

CrossRef Full Text | Google Scholar

Yue, X. P., Liu, T., Wen, T., Jia, W. J., and Wu, Y. (2025). Mechanical properties and energy evolution laws of rocks under freeze–thaw. Water 17 (3), 353. doi:10.3390/W17030353

CrossRef Full Text | Google Scholar

Zhang, H. B., Wang, L. H., Li, J. L., Deng, H., and Xu, X. (2023). Study on the mechanical properties of unloading damaged sandstone under cyclic loading and unloading. Sci. Rep. 13 (1), 7370. doi:10.1038/S41598-023-33721-Y

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q. H., Meng, X. R., and Zhao, G. (2024). Energy evolution and fractal characteristics of sandstones under true triaxial cyclic loading and unloading. Fractal. Fract. 8 (12), 714. doi:10.3390/FRACTALFRACT8120714

CrossRef Full Text | Google Scholar

Zhang, Q. H., Meng, X. R., Zhao, G. M., Li, Y. M., Xu, W. S., Liu, C. Y., et al. (2025). Damage evolution and acoustic emission characteristics of sandstone under different true triaxial cyclic loading and unloading modes. Eng. Fail. Anal. 167, 167108947–108947. doi:10.1016/j.engfailanal.2024.108947

CrossRef Full Text | Google Scholar

Zhang, Z. N., Chi, X. L., Yang, K., Lyu, X., and Wang, Y. (2023). Studies on the deformation and macro-micro-damage characteristics of water-bearing sandstone under cyclic loading and unloading tests. ACS. Omega. 8 (22), 19843–19852. doi:10.1021/acsomega.3c01750

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, K., Zhang, L., Yang, D. X., Jin, J. F., Zeng, P., Wang, X., et al. (2024). Cyclic impact damage and water saturation effects on mechanical properties and kaiser effect of red sandstone under uniaxial cyclic loading and unloading compression. Rock. Mech. Rock. Eng. 57 (1), 181–195. doi:10.1007/S00603-023-03574-Y

CrossRef Full Text | Google Scholar

Zhong, L. W., Ren, X. H., Wang, H. J., Zhao, G. C., Li, Y., and Zhu, J. (2024). Influence of the different stress paths on rock deformation memory effects using the deformation rate analysis method. Front. Earth. Sci. 12, 121459447–1459447. doi:10.3389/FEART.2024.1459447

CrossRef Full Text | Google Scholar