Influence of crosslinks and entanglements on hydrogel reinforcement: insights from molecular dynamics simulations

Entanglements and crosslinking jointly govern the mechanical performance of polyacrylamide (PAAm) hydrogels, yet their molecular roles remain poorly quantified. This study uses dissipative particle dynamics simulations to disentangle crosslinker concentration, inter-chain and intra-chain entanglement contributions to hydrogel stiffness and hardening effect. Systems were built at a uniform acrylamide (AAm) monomer concentration and identical chain length, with the crosslinker concentration varied to assess its impact. Separately, entanglement degree was modulated by varying chain length distributions under fixed crosslinking, and water content was adjusted to tune inter-chain entanglement density at constant intra-chain entanglement and crosslinker loading. Uniaxial tensile tests characterized stress-stretch responses. Our results reveal that increasing crosslinker density marginally elevates hardening effect but plateaus at higher concentrations, whereas higher inter-chain entanglement produces pronounced hardening and network resilience. Under constant crosslinking, systems with elevated entanglement exhibit significantly hardening and maintain structural integrity during large deformations. Moreover, reducing water content increases monomer concentration and inter-chain entanglements, thereby amplifying stiffness without altering intra-chain entanglement trends. These findings demonstrate that inter-chain entanglements act as dynamic “physical crosslinks,” enabling efficient load transfer and preventing network relaxation. Our study provides atomistic insight into the reinforcement mechanisms of hydrogels and offers design guidelines for tougher soft materials.

1 Introduction

Hydrogels are three-dimensional polymer networks that can imbibe large amounts of water (Fu, 2019), and their high deformability and biocompatibility make them attractive for biomedical devices, tissue engineering, flexible electronics (Jin et al., 2021) and soft robotics (Li et al., 2021). Yet conventional single-network hydrogels commonly suffer from low stiffness and limited toughness, which restricts their use in load-bearing and fatigue-sensitive applications (Fu et al., 2022; 2023; Qu et al., 2025). While increasing covalent crosslink density typically raises the elastic modulus, excessive crosslinking commonly induces network heterogeneity and stress concentration, reducing extensibility and toughness (Norioka et al., 2017; Xu et al., 2018; Zheng et al., 2018). Alternative strategies such as double-network hydrogels (Jang et al., 2007), covalently crosslinked hydrogels (Henderson et al., 2010; Sun et al., 2012), slide ring gels (Feng et al., 2020) and nanocomposites (Rafieian et al., 2019) can significantly improve toughness by introducing sacrificial or dissipative mechanisms. However, these approaches frequently entail trade-offs in manufacturability, hysteresis and recovery behavior.

Polymer chain entanglements have recently been recognized as another key reinforcement mechanism (Kim et al., 2021). Entanglements are topological interlocks between long chains that can act like effective, temporary crosslinks. In polymer physics, such entanglements underlie rubber elasticity and viscoelasticity, and in hydrogels they similarly impose topological constraints beyond the covalent network (De Gennes, 1971; Rubinstein and Panyukov, 2002). Both theory and experiment indicate that entanglements significantly influence elastic and fracture behavior (Hou et al., 2019). Kim et al. (2021) confirmed by constructing an entanglement-dominated single-network polymer system that entanglements, acting as “slip links”, can enhance stiffness without causing material embrittlement, and can improve fracture toughness through a multi-chain energy dissipation mechanism. Similarly, Zhu et al. (2024) engineered a “highly entangled” DN PAAm hydrogel where physical entanglements act like sliding crosslinks: this network achieved very high tensile strength (∼3 MPa) and fracture energy (∼8340 J/m^2) while maintaining low hysteresis. Liu et al. (2023) showed via simulation that in an entangled hydrogel, chain entanglements bear the load during the initial stretching phase; as strain increases and entanglements relax, covalent crosslinks take over the load. They observed a roughly linear correlation between entanglement density and tensile stress early in deformation. Sharma (2024) also highlights that polymer networks in dielectric elastomers contain numerous entanglements and crosslinks that jointly determine the nonlinear deformation response. These studies suggest that controlling chain entanglement is an important reinforcement strategy. Recent dynamic models of soft actuators (Nandan et al., 2023; Singh and Sharma, 2024) similarly incorporate chain entanglement along with crosslinks, indicating broad interest in these effects.

Despite this appreciation, experimentally isolating entanglement effects is very challenging. Entanglement density is not directly measurable by conventional means, and it typically correlates with polymer molecular weight and processing. Comprehending the connection between entanglement and mechanical properties remains complicated, particularly owing to constraints on length scales and the hurdles involved in directly observing them through experiments (Liu et al., 2023). The assumed crosslinked network in a hydrogel remains hypothetical, since dynamic observation at the molecular level is infeasible. These challenges mean that simulations provide a powerful alternative for probing chain-scale structure and decoupling these contributions.

Computational techniques like molecular dynamics (MD) and Monte Carlo simulations have become invaluable tools for studying the microstructural evolution of hydrogels under deformation. All-atom MD simulations capture chemistry but only for very short chains and fast timescales, so it cannot represent realistic entangled networks (An et al., 2019). Many coarse-grained MD studies have been developed to balance computational efficiency and structural fidelity (Jin et al., 2018; Lei et al., 2020; Liu et al., 2022). For example, Lei et al. (2020) built dissipative particle dynamics (DPD) bead-spring models of PAAm hydrogels and simulated large-strain deformation. This work showed that mesoscale network topology dominates stress response, but like most others it primarily characterized the crosslinked network without explicitly quantifying entanglements. In fact, many previous simulations explicitly construct polymer networks using idealized assumptions. Dissipative Particle Dynamics and related coarse-grained methods have been successfully applied to polymers and gels, but a gap remains in using them to systematically decouple the roles of entanglement versus crosslinking in determining network strength.

In this work, we address these gaps by employing a validated DPD coarse-grained PAAm model to systematically disentangle the mechanical contributions of covalent crosslinks and polymer chain entanglements. Specifically, we independently vary crosslinker concentration, chain-length distribution and water content to generate networks with controlled chemical and topological states. Uniaxial tensile simulations are carried out to obtain stress-stretch responses, and primitive-path entanglement analysis is applied to quantify inter-chain and intra-chain constraints and their evolution during deformation. Section 2 describes the methods and model details; Section 3 presents the results and discussion; and Section 4 concludes the study.

2 Simulation methodology

2.1 Coarse-grained bead-spring model of PAAm hydrogels

Currently, numerous researchers have developed multiscale molecular dynamics models for PAAm hydrogels. In this work, to further enhance computational efficiency, we adopted the DPD coarse-grained model of PAAm hydrogels developed referred by Lei et al. (2020). The model parameters were determined by matching the radial distribution function and structure factor from all-atom simulations. Uniaxial tension tests show that the model captures both hyperelastic and viscoelastic behaviors, with nominal stress-stretch curves aligning with experimental trends and demonstrating loading rate-dependent responses (Yang et al., 2019). Compared to all-atom models, the coarse-grained bead-spring model efficiently bridges mesoscale chain conformations to bulk deformation, making it suitable for studying large deformation and fracture mechanisms in single-network hydrogels.

Initially, the PAAm hydrogel structure was simplified into a bead model through coarse-grained mapping. In this scheme, two acrylamide (AAm) monomers are represented by one bead, eight water molecules are mapped to one bead, and one methylenebisacrylamide (MBAA) crosslinker is represented by one bead. This mapping method ensures that the relative molecular weights of the particles are comparable. Figure 1a illustrates the coarse-grained mapping scheme of PAAm hydrogel model, where red beads represent AAm, yellow beads denote MBAA, and blue beads correspond to water. Figure 1b shows one of the PAAm hydrogel models. The masses of the particles m, the system energy kT, and the interaction length R_C are normalized to dimensionless units, with m = kT = R_C = 1, where k is the Boltzmann constant and T is the temperature. In the normalized DPD system, a unit temperature (T = 1) corresponds to an actual temperature of 300 K. The time scale is nondimensionalized as $\tau =\sqrt{mR{\mathrm{c}}^2/kT}=1$, such that one time unit corresponds to approximately 340 ps in real time.

Figure 1

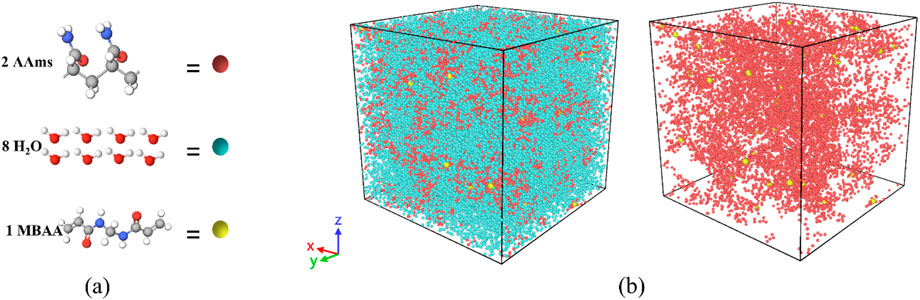
Figure 1. (a) Coarse-grained mapping scheme of PAAm hydrogel. The red bead represents two acrylamide (AAm) monomers, the blue bead represents eight water molecules, and the yellow bead represents one methylenebisacrylamide (MBAA) crosslinker. (b) Coarse-grained molecular dynamics model of PAAm hydrogel. The left diagram shows the model containing water, AAm molecules, and cross-linkers. The right diagram is a schematic of the model with water removed.

The interactions among particles consist of bond forces between connected particles ${\overrightarrow{F}}_{i-\text{bond}}$ and pairwise interactions between particle pairs ${\overrightarrow{F}}_{i-\text{pair}}$, with the latter comprising three distinct contributions:

${\overrightarrow{F}}_{i-\text{bond}}={\displaystyle \sum _j}C\left(r_{ij}-r_0\right){\widehat{r}}_{ij},(1)$

${\overrightarrow{F}}_{i-\text{pair}}={\displaystyle \sum _{i\ne j}}{{\overrightarrow{F}}_{ij}}^C+{{\overrightarrow{F}}_{ij}}^D+{{\overrightarrow{F}}_{ij}}^R,(2)$

${{\overrightarrow{F}}_{ij}}^C=a_{ij}\omega \left(r_{ij}\right),(3)$

${{\overrightarrow{F}}_{ij}}^D=-\gamma {\omega }^2\left(r_{ij}\right)\left({\widehat{r}}_{ij}·{\overrightarrow{v}}_{ij}\right),(4)$

${{\overrightarrow{F}}_{ij}}^R=\sigma \omega \left(r_{ij}\right)\alpha {\left(\Delta t\right)}^{-\frac{1}{2}},(5)$

$\omega \left(r_{ij}\right)=\left\{\begin{array}{l}1-\frac{r_{ij}}{R_{\mathrm{C}}},r_{ij}\le R_{\mathrm{C}}\\ 0,r_{ij}{R}_{\mathrm{C}}\end{array}\right..(6)$

In Equation 1, C represents the bond coefficient. In the tensile simulations, a value of C = 25 was employed to match the actual ratio between bond strength and thermal fluctuations. r₀ denotes the equilibrium bond length between two polymer beads, R_C is the cutoff radius, and the average distance between two beads is set as r₀ = R_C = 1. $r_{ij}$ denotes the distance between the ith particle and the jth particle.

In Equation 2, the pair forces consist of three components: ${\overrightarrow{F}}^C$ (a conservative force), ${\overrightarrow{F}}^D$ (a dissipative force), and ${\overrightarrow{F}}^R$ (a random force). In Equation 3, the conservative force ${\overrightarrow{F}}^C$ acts as a repulsive force within the cutoff radius $R_{\mathrm{C}}$ and varies linearly with the interparticle distance $r_{ij}$, with a repulsion coefficient $a_{ij}$. $\omega \left({}_{ij}\right)$ is a weighting factor in Equation 6 that varies between 0 and 1. In Equation 4, the dissipative force ${\overrightarrow{F}}^D$ is always directed opposite to the relative velocity $v_{ij}$ between the two particle centers, representing a viscous effect that depends on the coefficient $\gamma$ and the interparticle distance. The random force ${\overrightarrow{F}}^R$ in Equation 5 also depends on the coefficient $\sigma =\sqrt{2kT\gamma }$, the interparticle distance, and a normally distributed random variable $\alpha$. Since the dissipative and random forces serve as an energy sink and source, respectively, the study by Groot (Groot and Warren, 1997; Groot and Rabone, 2001) suggests that setting $\sigma =3$ ensures a balance between these two forces within the thermostat. Table 1 presents the specific parameters of the pair forces in the PAAm DPD coarse-grained model which were calibrated to reproduce the radial distribution function of real hydrogel networks.

Table 1

Table 1. Parameters of the pair forces in the PAAm coarse-grained model.

2.2 Uniaxial loading setups in molecular dynamics simulations

The DPD coarse-grained simulations were conducted using the parallel molecular dynamics (MD) code LAMMPS (Plimpton, 1995). Temperature control was achieved employing the Nose-Hoover thermostat (Nosé, 1984; Hoover, 1986), which is integrated within LAMMPS. The initial polymer chain configurations of PAAm molecules were generated utilizing the Monte Carlo self-avoiding random walk method (Binder, 1995). Subsequently, crosslinkers and water molecules were incorporated into the system.

This initial configuration was loaded into the MD code, where energy minimization and equilibration were performed prior to applying mechanical deformation to the amorphous polymer. We employed a molecular dynamics simulation approach similar to that described by Lei et al. (Lei et al., 2020) to simulate the crosslinking process of polymer networks. Crosslinking was implemented by periodically searching for reactive bead pairs whose separation distance fell below a chosen cutoff distance. Specifically, at fixed intervals (every 10 timesteps) we identify all reactive pairs within a cutoff $r_{cutoff}=3.0$ which avoids high-energy bonds and then form new harmonic bonds between them. Each crosslinker bead was assigned four reactive sites, allowing the formation of up to four bonds. After each bonding step, the system topology and force field were updated, and the configuration was briefly relaxed before the next reaction iteration. On average we observed that the vast majority of crosslinkers formed three to four bonds, indicating nearly full connectivity, which is consistent with saturation yields reported for thermoset curing simulations (Varshney et al., 2008).

All simulations were performed in the NVT ensemble (constant number of particles, volume, and temperature) using the standard DPD thermostat. The initial box volume was chosen to match the experimental bulk density of the PAAm hydrogel system. Initially, the system was equilibrated under the NVT ensemble for 10,000 time steps with a time step of 0.01 DPD units. Subsequently, crosslinking was initiated by forming bonds between polymer beads every 10 time steps over 400,000 steps, provided that the distance between two beads was less than the DPD cutoff radius. After crosslinking, the system was cooled to a temperature of T = 1 over 100,000 time steps and further equilibrated for an additional 100,000 time steps. This methodology aligns with standard practices in dissipative particle dynamics simulations for modeling polymer crosslinking processes. For instance, previous studies have adopted similar simulation protocols, including equilibration, crosslinking, and relaxation steps, to accurately capture the behavior of polymer networks under various conditions (Lei et al., 2020).

Subsequently, incompressible uniaxial tensile tests were simulated in the NVT ensemble at a temperature of T = 1, using a strain rate of 0.001 per DPD time unit. It is important to note that, to facilitate the implementation of incompressible uniaxial tension in LAMMPS (version of LAMMPS released on 22 December 2022), the applied strain rate corresponds to the true strain rate. Consequently, the true strain rates in the other two orthogonal directions were set to half of the applied loading rate. The time step used for the tensile tests was set to 0.01 DPD time units.

2.3 Crosslinking and entanglement

Both crosslinks and chain entanglements critically shape a polymer network’s response to deformation, encoding its topology and conformational dynamics under load. Visualizing polymer arrangements at the molecular scale remains elusive. Although raising AAm monomer concentration is known to increase entanglement density, reliably quantifying these topological constraints in experiments is still problematic. Here, molecular dynamics simulations provide a means to overcome this barrier, enabling direct analysis of network architecture and its evolution under mechanical stress.

In our study, we categorize the microscopic structure of the hydrogel system into three components: crosslinkers, inter-chain and intra-chain entanglements. As depicted in Figure 2a, when two polymer chains are connected via a crosslinker, this connection is identified as a crosslinking point. The degree of crosslinking is quantified by the ratio of crosslinker particles to the total number of particles. Inter-chain entanglements represent the network-level topological complexity between multiple chains, whereas the intra-chain entanglements capture the conformational state of single chains. The reciprocal relationship highlights the balance between intra-chain straightening and inter-chain topological interactions in polymer systems. The polymer network’s entanglements are further classified into inter-chain entanglements (network points), as shown in Figure 2b, and intra-chain entanglements shown in Figure 2c. The crosslinker content is directly determined by the amount of crosslinker added to the system, whereas the two types of entanglements are distinguished and quantified through path analysis.

Figure 2

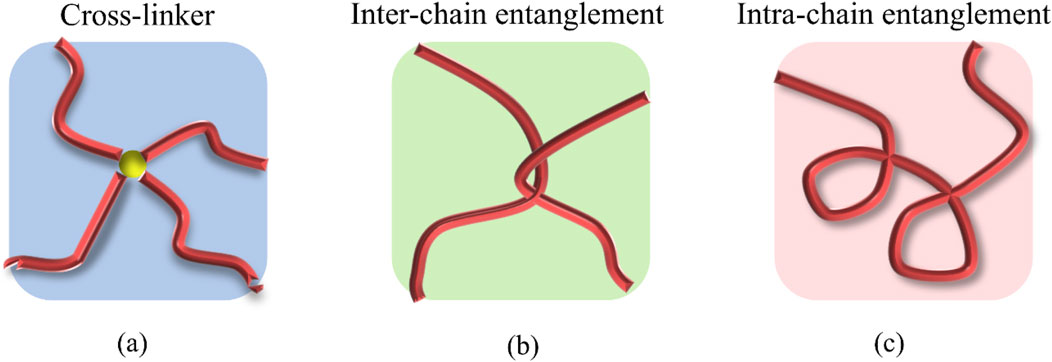
Figure 2. Schematic illustrations of (a) cross-linker, (b) inter-chain entanglements, and (c) intra-chain entanglements in PAAm hydrogels.

To calculate inter-chain and intra-chain entanglements, we employ the Z1+ algorithm to determine each chain’s original path and knot points within the system (Kröger et al., 2023). The input to Z1+ consisted of the fully periodic polymer configuration and the corresponding box dimensions. Z1+ fixes the ends of each chain at their positions and then applies a primitive-path-shrinking procedure that shortens chain contours while preventing bond crossings. The original path, or primitive path, is the shortest path after equilibration, representing the connection between the polymer chain’s two ends. The Z1+ algorithm identifies inter-chain entanglements through a geometric contraction process, which involves calculating the triangular area formed by three adjacent nodes and using adaptive neighbor lists to detect adjacent chain segments. If adjacent segments pass through this triangular area, an inter-chain entanglement is identified. These points are then used as segmentation points for the polymer network, allowing the calculation of the shortest paths for network fragments. The core of this method is to minimize the contour length while keeping chain endpoints fixed and avoiding chain crossings, thereby obtaining the shortest multiple disconnected paths. Intra-chain entanglement is calculated by determining the original path of each segment using the following equation, which yields the entanglement degree within the topological network. This methodology enables a detailed analysis of the entanglement structures within polymer networks, providing valuable insights into the factors influencing the mechanical properties of hydrogels.

The intra-chain entanglements, $N_{\mathrm{e}}$, of each chain segment can be characterized by (Everaers et al., 2004; Zhu et al., 2022).

$N_{\mathrm{e}}=\frac{a_{\text{pp}}}{b_{\text{pp}}},(7)$

where $a_{\text{pp}}$ and $b_{\text{pp}}$ are the current and initial path segment lengths of the chain, respectively (Sukumaran et al., 2005). These lengths are defined as (Foteinopoulou et al., 2006):

$a_{\text{pp}}=\frac{R^2}{L_{\text{pp}}}.(8)$

$b_{\text{pp}}=\frac{L_{\text{pp}}}{N-1},(9)$

Here, $L_{\text{pp}}$ is the length of the initial path, $R$ is the end-to-end distance of the segment, and N is the total number of atoms in the segment. In the topological analysis, the Z1+ algorithm, developed by Kröger and Foteinopoulou (Foteinopoulou et al., 2006; Kröger et al., 2023), is employed to calculate the initial paths and end-to-end distances of the chain segments.

Combining Equations 7–9, the expression for intra-chain entanglement is:

$N_e=\frac{R^2\left(N-1\right)}{L_{\text{pp}}^2}.(10)$

Here, $N-1$ serves as a correction factor relating the intra-chain entanglement to the chain length, describing the limiting value of the intra-chain entanglements. When N > 1, the shortest segment forming the chain requires at least one entanglement. As the chain is fully stretched, the initial path coincides with the end-to-end distance, resulting in an entanglement degree of $N-1$. The more pronounced the self-coiling of the chain is, the smaller the value of N_e will be.

3 Results and discussion

3.1 Stress-stretch relationships

We first constructed four PAAm hydrogel models with varying crosslinker concentrations. Each model consists of 1,000 polymer chains, with each chain containing 20 AAm monomers. By incorporating only short chains into the models, we achieved extremely low entanglement: the models exhibit negligible inter-chain entanglement, and each chain maintains a lower degree of intra-chain entanglements. Each model has a water content of 80%, corresponding to 320,000 water molecules, while the crosslinker contents of the four models are 0%, 0.25%, 0.5%, and 1% respectively. To ensure the accuracy of the results, we generated three independent network models for each case and then performed uniaxial tensile tests. All subsequent simulation tests were conducted under identical conditions, with the average derived from three independent model. Figure 3a presents the corresponding stress-stretch curves, where each curve represents the average value of three independent models in the same condition. It can be observed that as the crosslinker concentration increases, the reinforcement of the hydrogel system improves slightly, although the enhancement is not substantial. In particular, increasing the concentration from 0.5% to 1% results in almost no further hardening. The network quickly reaches a saturation regime upon the addition of crosslinks because the chains are relatively short. Moreover, our DPD simulations inherently include viscoelastic damping at the mesoscale; under the finite strain rate used, partial stress relaxation occurs during deformation. These factors collectively account for the only modest increase in the stiffness with increasing crosslink density. Figure 3b shows schematic diagrams of the model for non-crosslinked PAAm hydrogel stretched to $\lambda$ = 1, 2 and 4 in the MD simulation.

Figure 3

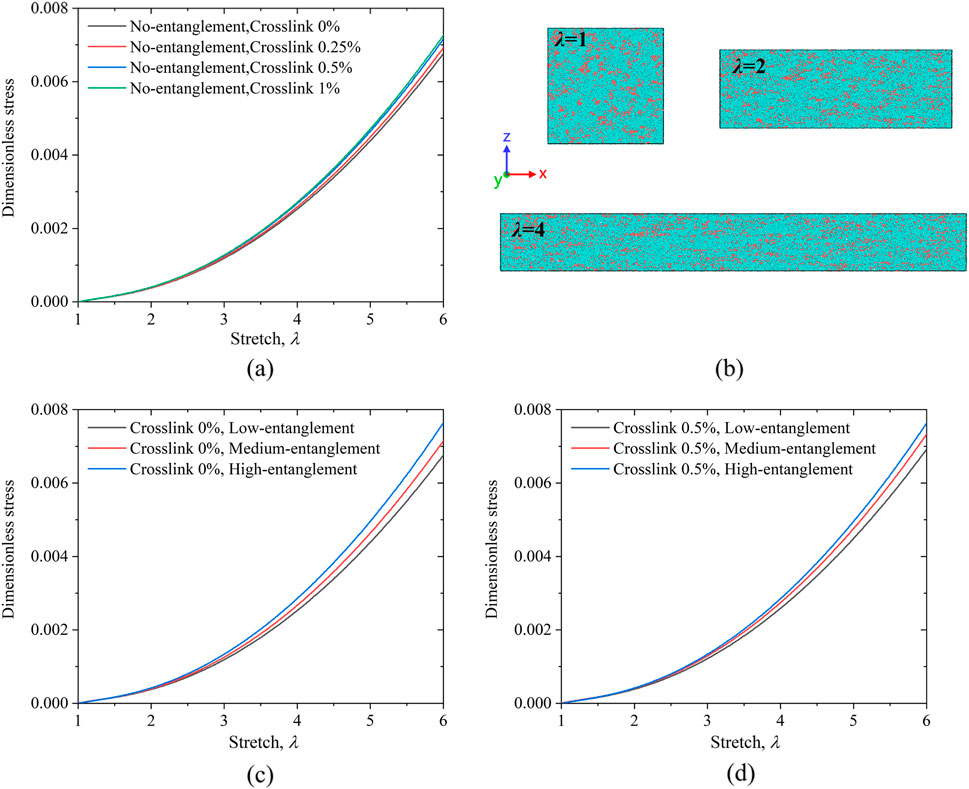
Figure 3. (a) Stress-stretch curves under uniaxial tension for models with crosslinking densities of 0%, 0.25%, 0.5%, and 1%, all without entanglements. (b) Molecular dynamics model schematics of non-crosslinked PAAm hydrogels at stretch ratios of $\lambda$ = 1, 2 and 4, respectively. (c) Stress-stretch curves under uniaxial tension for models with different degrees of entanglement in the absence of crosslinker and (d) different degrees of entanglement at a crosslinker concentration of 0.5%.

To further investigate the roles of crosslinking and entanglement in the stretching behavior of the hydrogel systems, we constructed models with identical crosslinking densities but varying entanglement levels, and subjected them to uniaxial tensile tests. In these comparative models, only the entanglement levels were altered. The model with the lowest entanglement comprises 1,000 chains, each containing 20 monomers. The moderately entangled model consists of 500 chains of 20 monomers each, along with 10 chains of 1,000 monomers. The highly entangled model contains 20 chains, each with 1,000 monomers. All models have a water content of 80%, corresponding to 320,000 water molecules. We fixed the total number of beads to maintain a constant polymer mass across all cases, ensuring that the observed mechanical differences originate from network topology rather than variations in material amount. Intuitively, as the number of long chains in the system increases, both inter-chain entanglement and the degree of intra-chain coiling are expected to increase.

Figure 3c presents the stress-stretch curves for these three PAAm hydrogel models, all with 0% crosslinking but differing entanglement levels. As the entanglement level increases, the PAAm hydrogel system exhibits a more pronounced reinforcement effect. Figure 3d shows the stress-stretch curves for the three models with a 0.5% crosslinking density and varying entanglement levels, revealing a similar trend. Since the cross-linking particles in our system form bonds randomly, the medium-entanglement system contains both short chains and long chains. Consequently, the final configuration formed includes cross-linking between short-short, long-long, and short-long chains. Crosslinks formed between long polymer chains lead to a more pronounced entangled network structure, which in turn facilitates more effective load transfer and greater mechanical reinforcement. However, the degree of improvement is less significant compared to the models with 0% crosslinking.

Based on the tensile test results in Figure 3, it is evident that in PAAm hydrogel systems, an increase in the crosslinker concentration leads to only a slight enhancement in hardening, and the incremental improvement in hardening diminishes as the crosslinker concentration continues to rise. In contrast, a higher level of entanglement produces a more pronounced increase in hardening.

3.2 Dynamic evolution analysis

From the tensile curves of the different models, it is evident that when the level of entanglement exceeds that of crosslinking, the enhancement in hydrogel hardening becomes more effective. However, the entanglement state in hydrogel systems is highly complex. To further analyze the impact of different entanglement states on hydrogel stiffness, we statistically examined the initial contents of inter-chain and intra-chain entanglements in each model, as well as their evolution during stretching.

Figures 4a,b display the variation curves of inter-chain entanglements for PAAm hydrogel models with crosslinking densities of 0% and 0.5%, respectively, with different entanglement levels. It can be observed that in the non-crosslinked models (Figure 4a), the inter-chain entanglements in both the high-entanglement and medium-entanglement systems decrease with increasing stretch. The high-entanglement system showing a more pronounced reduction in the early stages of stretching. As shown in Figure 4b, for all three models with a 0.5% crosslinking density, the inter-chain entanglement of the low- and high-entangled system remained essentially constant throughout the entire tensile deformation. In constrast, the medium-entangled system exhibited a decrease in inter-chain entanglement at higher stretch ratios. Comparative analysis of two high-entanglement PAAm hydrogel models with differing crosslinking densities indicates that crosslinking confers greater network stability, whereas the non-crosslinked system is more susceptible to kink-induced disentanglement.

Figure 4

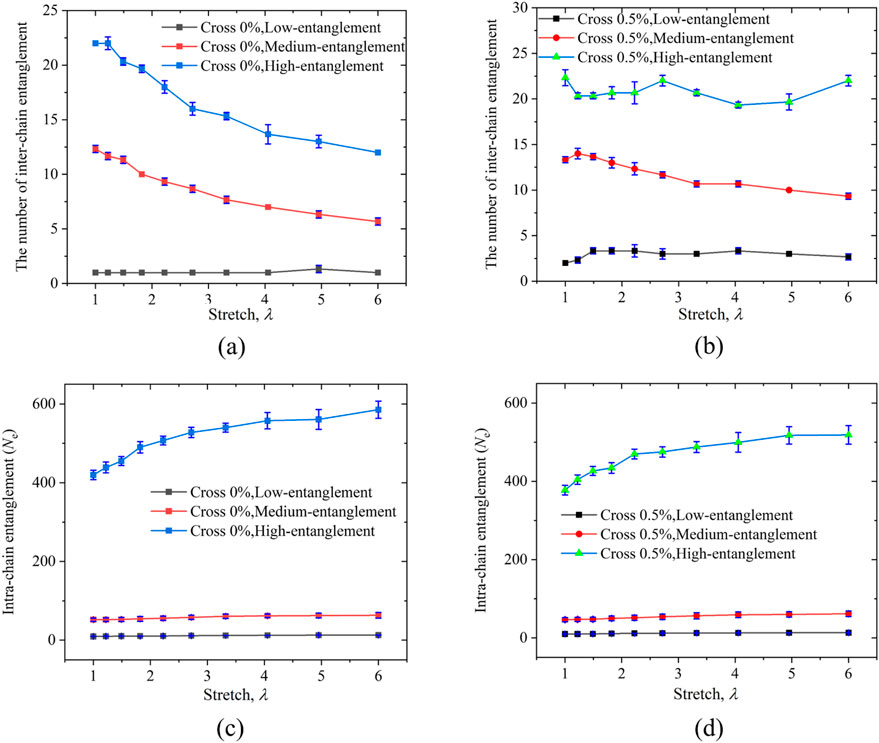
Figure 4. (a) Inter-chain entanglement statistics during uniaxial tension for three models with different entanglement degrees without crosslinkers, and (b) the corresponding statistics for models with a 0.5% crosslinker concentration. (c) Intra-chain entanglements statistics during uniaxial tension for three models with different entanglement degrees without crosslinkers, and (d) the corresponding statistics for models with a 0.5% crosslinker concentration.

Figures 4c,d respectively summarize the evolution of intra-chain entanglements, calculated using Equation 10, in PAAm hydrogel models with three different entanglement levels at crosslinking densities of 0% and 0.5%. When the PAAm hydrogel systems are stretched to 600%, the low-entanglement and medium-entanglement models exhibit no significant disentanglement. In contrast, a more noticeable disentanglement occurs in the highly entangled PAAm system. This indicates that for the PAAm system with a higher initial entanglement degree, as the stretching progresses, its chains will be gradually straightened along the stretching direction. On the other hand, for the system with almost no entanglement in the initial structure, it almost reaches the entanglement saturation state right from the start. The much lower entanglement in the medium-entangled system compared to the high-entangled system is partly because it contains only 10 long chains, and partly due to finite-size effects: with fewer long chains the probability of chain overlap decreases. This is consistent with known behavior that entanglement density depends sensitively on chain overlap fraction (Kavassalis and Noolandi, 1987; Ubertini and Rosa, 2023). Both the chain count and system-size effects contribute to the lower inter-chain entanglement in the medium entangled system. Furthermore, a comparison of hydrogel models with the same entanglement level in Figures 4c,d reveals that the crosslinker concentration has little effect on the intra-chain entanglements of the chains. Figure 5 shows schematic diagrams of inter-chain entanglement in a highly entangled PAAm hydrogel. When stretched to $\lambda$ = 2 and 3.2, the inter-chain entanglement at this region remains intact, while the intra-chain entanglements of the polymer chains increase significantly.

Figure 5

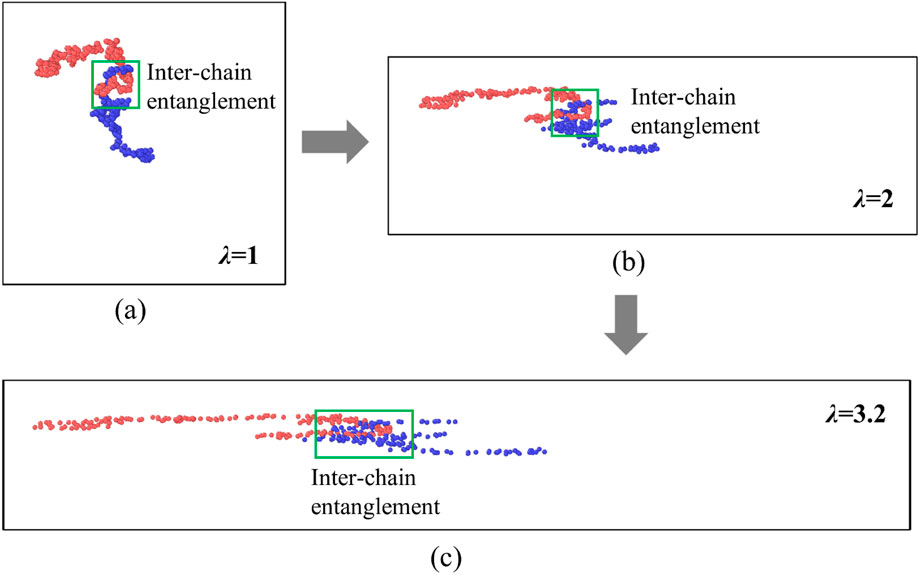
Figure 5. Schematic diagrams of model details for fragments of two different chains in a hydrogel model with 0.5% crosslinking content and high entanglement at (a) $\lambda$ = 1, (b) $\lambda$ = 2, and (c) $\lambda$ = 3.2, respectively.

3.3 The modulatory role of inter-chain and intra-chain entanglement

To further distinguish and validate the contributions of inter-chain and intra-chain entanglements during hydrogel deformation, we constructed three hydrogel systems with varying inter-chain entanglement by altering the water content while keeping the crosslinker concentration and chain length constant. These three models consist of 1,000 polymer chains, with each chain containing 20 AAm monomers. All three models contain 20 polymer chains, each consisting of 1,000 AAm monomers. The water content in the individual systems is set to 60% (120,000 water molecules), 70% (186,667 water molecules), and 80% (320,000 water molecules), respectively. The crosslinking density is fixed at 0.5% across all systems. This approach ensured that both the crosslinker concentration and intra-chain entanglements remained essentially the same across the systems. Figure 6 shows the uniaxial tensile stress-stretch curves for PAAm hydrogels with three different water contents. It is clearly observed that the tensile stress is greatly enhanced as the water content decreases. The stiffness was measured from the initial slope of the stress-stretch curve (E = 3/4×ds/dλ). With increasing water content, the entanglement of polymer chains in the PAAm hydrogel system decreases, leading to a significant reduction in stiffness (as shown in the inset of Figure 6).

Figure 6

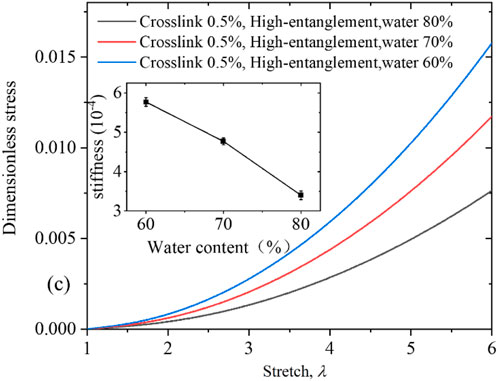
Figure 6. Uniaxial tensile stress-stretch curves and stiffness (inset) for three PAAm hydrogel models with identical crosslinker concentrations and water contents of 60%, 70%, and 80%, respectively.

In Figure 7a, we quantify the inter-chain and intra-chain entanglements of these three hydrogel systems with different water contents. The hydrogel with 60% water content exhibits the highest inter-chain entanglement. This is because, for systems of the same size, a reduction in water content leads to a significant increase in PAAm monomer concentration; with a constant chain length, the number of chains increases, resulting in more inter-chain entanglements. Moreover, during stretching, the inter-chain entanglement in all three systems remains largely unchanged, indicating that under the combined effects of crosslinking and inter-chain entanglement, the network structure is very stable. A higher initial inter-chain entanglement more readily contributes to the reinforcement of the system. Figure 7b shows the intra-chain entanglements for hydrogel models with different water contents. Prior to stretching, the initial intra-chain entanglements of the three models are essentially identical, and their trends during stretching are also similar. This indicates that during hydrogel stretching, the excessively long chains in the initial structure are not completely straightened, and thus do not contribute significantly to the system’s reinforcement. As the water content increases, the stiffness of the hydrogel decreases due to reduced entanglement. This trend can be further explained from a molecular perspective. When the hydrogel swells, water molecules infiltrate the polymer network and increase the average inter-chain spacing, effectively diluting the chain density. The decreased chain overlap probability reduces the frequency of topological constraints and weakens the inter-chain entanglement network. Consequently, the stress under deformation is mainly borne by a smaller number of load-bearing chains, leading to a pronounced softening of the macroscopic response. Similar behavior has been reported in theoretical and simulation studies, where swelling-induced dilution and reduced chain overlap directly correlate with a lower entanglement density and decreased modulus (Ubertini and Rosa, 2023).

Figure 7

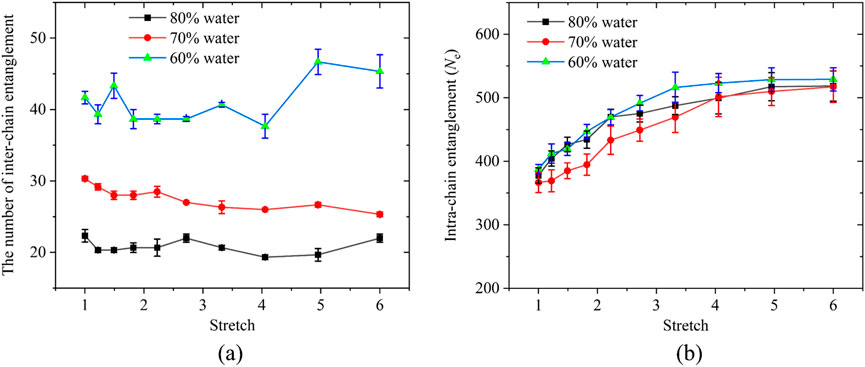
Figure 7. (a) Inter-chain entanglements and (b) intra-chain entanglements under uniaxial tension for three PAAm hydrogel models with identical crosslinker concentrations and water contents of 60%, 70%, and 80%, respectively.

Figure 8 illustrates the microscopic deformation mechanisms of high-entangled and low-entangled hydrogels during the stretching process. For high-entangled hydrogel systems composed of long chains, the initial conformations of the chains contain a large number of inter-chain entanglements, and the coiling of the chains themselves is more pronounced. During stretching, only a small number of inter-chain entanglements undergo disentanglement, and at large stretch stages, disentanglement essentially ceases, while the growth of intra-chain entanglements also decreases. In contrast, low-entanglement hydrogels with a higher proportion of short chains contain fewer inter-chain entanglements in their initial conformations. Throughout the stretching process, due to disentanglement and chain stretching, force transfer between chains is hindered, resulting in a relatively low final hardening effect.

Figure 8

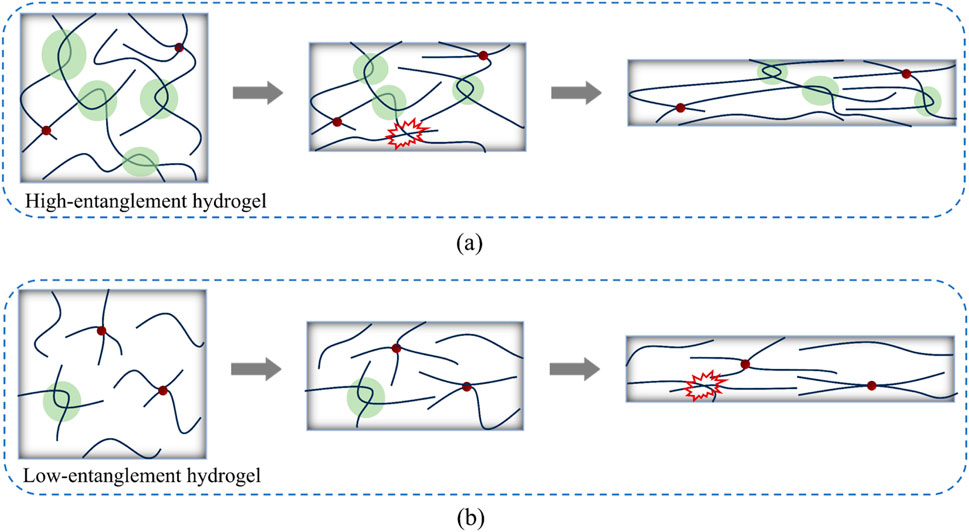
Figure 8. Schematic diagrams of chain conformation evolution in (a) high-entanglement and (b) low-entanglement hydrogels during stretching. The green shaded regions represent inter-chain entanglements, while red regions indicate disentanglement.

4 Conclusion

Molecular dynamics simulations of PAAm hydrogels have elucidated the distinct roles of chemical crosslinks and physical entanglements in governing mechanical behavior. Although increasing the crosslinker concentration marginally enhances strain hardening, the reinforcement effect plateaus once the crosslinking density exceeds 0.5%. In contrast, inter-chain entanglements markedly increase hardening and network stability, acting akin to additional crosslinks that resist deformation. Models with elevated entanglement levels display superior hardening effect and maintain entangled networks under large strains, whereas non-crosslinked systems suffer obviously kink-induced disentanglement. Furthermore, lowering water content augments monomer density and inter-chain entanglements, providing a facile route to strengthen hydrogels without altering chemical architecture. Intra-chain entanglements, by comparison, contribute minimally to bulk reinforcement under the simulated conditions. Collectively, these insights highlight that optimizing physical entanglement density—through chain length distribution or solvent tuning—is more effective than simply increasing crosslinker loading. This mechanistic understanding paves the way for the rational design of next-generation hydrogels with tailored toughness and extensibility for biomedical and soft-robotic applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

PZ: Conceptualization, Funding acquisition, Investigation, Software, Validation, Visualization, Writing – original draft, Writing – review and editing. YF: Conceptualization, Investigation, Project administration, Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by the National Natural Science Foundation of China (Nos. 12402131 and 12402203).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, M., Demir, B., Wan, X., Meng, H., Yang, N., and Walsh, T. R. (2019). Predictions of thermo mechanical properties of cross linked polyacrylamide hydrogels using molecular simulations. Advcd Theory Sims 22 (3), 1800153. doi:10.1002/adts.201800153

CrossRef Full Text | Google Scholar

Binder, K. (1995). Monte carlo and molecular dynamics simulations in polymer science. Oxford University Press.

Google Scholar

De Gennes, P.-G. (1971). Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 55, 572–579. doi:10.1063/1.1675789

CrossRef Full Text | Google Scholar

Everaers, R., Sukumaran, S. K., Grest, G. S., Svaneborg, C., Sivasubramanian, A., and Kremer, K. (2004). Rheology and microscopic topology of entangled polymeric liquids. Science 303, 823–826. doi:10.1126/science.1091215

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, L., Jia, S., Chen, Y., and Liu, Y. (2020). Highly elastic slide-ring hydrogel with good recovery as stretchable supercapacitor. Chem. Eur. J. 26, 14080–14084. doi:10.1002/chem.202001729

PubMed Abstract | CrossRef Full Text | Google Scholar

Foteinopoulou, K., Karayiannis, N. C., Mavrantzas, V. G., and Kröger, M. (2006). Primitive path identification and entanglement statistics in polymer melts: results from direct topological analysis on atomistic polyethylene models. Macromolecules 39, 4207–4216. doi:10.1021/ma060306b

CrossRef Full Text | Google Scholar

Fu, J., and in het Panhuis, M. (2019). Hydrogel properties and applications. J. Mater. Chem. B 7, 1523–1525. doi:10.1039/C9TB90023C

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, Y., Hu, X., Liu, Y., Wang, P., Chen, S., Zhou, H., et al. (2022). Impact-induced bubble interactions and coalescence in soft materials. Int. J. Solids Struct. 238, 111387. doi:10.1016/j.ijsolstr.2021.111387

CrossRef Full Text | Google Scholar

Fu, Y., Yin, T., Qu, S., and Yang, W. (2023). Cavitation/fracture transition of soft materials. J. Mech. Phys. Solids 172, 105192. doi:10.1016/j.jmps.2022.105192

CrossRef Full Text | Google Scholar

Groot, R. D., and Rabone, K. L. (2001). Mesoscopic simulation of cell membrane damage, morphology change and rupture by nonionic surfactants. Biophys. J. 81, 725–736. doi:10.1016/S0006-3495(01)75737-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Groot, R. D., and Warren, P. B. (1997). Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 107, 4423–4435. doi:10.1063/1.474784

CrossRef Full Text | Google Scholar

Henderson, K. J., Zhou, T. C., Otim, K. J., and Shull, K. R. (2010). Ionically cross-linked triblock copolymer hydrogels with high strength. Macromolecules 43, 6193–6201. doi:10.1021/ma100963m

CrossRef Full Text | Google Scholar

Hoover, W. G. (1986). Constant-pressure equations of motion. Phys. Rev. A 34, 2499–2500. doi:10.1103/PhysRevA.34.2499

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, D., Xu, J., Zhang, Y., and Sun, G. (2019). Insights into the molecular structure and reinforcement mechanism of the hydrogel-cement nanocomposite: an experimental and molecular dynamics study. Compos. Part B Eng. 177, 107421. doi:10.1016/j.compositesb.2019.107421

CrossRef Full Text | Google Scholar

Jang, S. S., Goddard, W. A., and Kalani, M. Y. S. (2007). Mechanical and transport properties of the Poly(ethylene oxide)−oly(acrylic acid) double network hydrogel from molecular dynamic simulations. J. Phys. Chem. B 111, 1729–1737. doi:10.1021/jp0656330

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, K., López Barreiro, D., Martin-Martinez, F. J., Qin, Z., Hamm, M., Paul, C. W., et al. (2018). Improving the performance of pressure sensitive adhesives by tuning the crosslinking density and locations. Polymer 154, 164–171. doi:10.1016/j.polymer.2018.08.065

CrossRef Full Text | Google Scholar

Jin, P., Fu, J., Wang, F., Zhang, Y., Wang, P., Liu, X., et al. (2021). A flexible, stretchable system for simultaneous acoustic energy transfer and communication. Sci. Adv. 7, eabg2507. doi:10.1126/sciadv.abg2507

PubMed Abstract | CrossRef Full Text | Google Scholar

Kavassalis, T. A., and Noolandi, J. (1987). New view of entanglements in dense polymer systems. Phys. Rev. Lett. 59 (23), 2674–2677. doi:10.1103/PhysRevLett.59.2674

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J., Zhang, G., Shi, M., and Suo, Z. (2021). Fracture, fatigue, and friction of polymers in which entanglements greatly outnumber cross-links. Science 374, 212–216. doi:10.1126/science.abg6320

PubMed Abstract | CrossRef Full Text | Google Scholar

Kröger, M., Dietz, J. D., Hoy, R. S., and Luap, C. (2023). The Z1+ package: shortest multiple disconnected path for the analysis of entanglements in macromolecular systems. Comput. Phys. Commun. 283, 108567. doi:10.1016/j.cpc.2022.108567

CrossRef Full Text | Google Scholar

Lei, J., Xu, S., Li, Z., and Liu, Z. (2020). Study on large deformation behavior of polyacrylamide hydrogel using dissipative particle dynamics. Front. Chem. 8, 115. doi:10.3389/fchem.2020.00115

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, G., Chen, X., Zhou, F., Liang, Y., Xiao, Y., Cao, X., et al. (2021). Self-powered soft robot in the mariana trench. Nature 591, 66–71. doi:10.1038/s41586-020-03153-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Zheng, S., Li, Z., Xu, S., Lei, J. J., and Toh, W. (2022). “Multiscale modeling of hydrogels,” in The mechanics of hydrogels (Elsevier), 187–222. doi:10.1016/B978-0-08-102862-9.00012-9

CrossRef Full Text | Google Scholar

Liu, Y., Xian, W., He, J., and Li, Y. (2023). Interplay between entanglement and crosslinking in determining mechanical behaviors of polymer networks. Int. J. Smart Nano Mater. 14, 474–495. doi:10.1080/19475411.2023.2261777

CrossRef Full Text | Google Scholar

Nandan, S., Sharma, D., and Sharma, A. K. (2023). Dynamic modeling of hard-magnetic soft actuators: unraveling the role of polymer chain entanglements, crosslinks, and finite extensibility. J. Magn. Magn. Mater. 587, 171237. doi:10.1016/j.jmmm.2023.171237

CrossRef Full Text | Google Scholar

Norioka, C., Kawamura, A., and Miyata, T. (2017). Mechanical and responsive properties of temperature-responsive gels prepared via atom transfer radical polymerization. Polym. Chem. 8, 6050–6057. doi:10.1039/C7PY01323J

CrossRef Full Text | Google Scholar

Nosé, S. (1984). A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519. doi:10.1063/1.447334

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Qu, Z., Fu, Y., Yang, Q., Wang, J., Tang, L., and Qu, S. (2025). A method for identifying the damage thresholds of porcine brain under low- and medium-strain rates. Extreme Mech. Lett. 77, 102335. doi:10.1016/j.eml.2025.102335

CrossRef Full Text | Google Scholar

Rafieian, S., Mirzadeh, H., Mahdavi, H., and Masoumi, M. E. (2019). A review on nanocomposite hydrogels and their biomedical applications. Sci. Eng. Compos. Mater. 26, 154–174. doi:10.1515/secm-2017-0161

CrossRef Full Text | Google Scholar

Rubinstein, M., and Panyukov, S. (2002). Elasticity of polymer networks. Macromolecules 35, 6670–6686. doi:10.1021/ma0203849

CrossRef Full Text | Google Scholar

Sharma, A. K. (2024). Tunable electroelastic waves in soft dielectric elastomer phononic crystals: exploring the effect of polymer chain network architecture. Int. J. Appl. Mech. 16, 2450103. doi:10.1142/S1758825124501035

CrossRef Full Text | Google Scholar

Singh, A. P., and Sharma, A. K. (2024). Dynamic modeling and analysis of soft dielectric elastomer balloon actuator with polymer chains crosslinks, entanglements and finite extensibility. Int. J. Appl. Mech. 16, 2450033. doi:10.1142/S1758825124500339

CrossRef Full Text | Google Scholar

Sukumaran, S. K., Grest, G. S., Kremer, K., and Everaers, R. (2005). Identifying the primitive path mesh in entangled polymer liquids. J. Polym. Sci. Part B Polym. Phys. 43, 917–933. doi:10.1002/polb.20384

CrossRef Full Text | Google Scholar

Sun, J.-Y., Zhao, X., Illeperuma, W. R. K., Chaudhuri, O., Oh, K. H., Mooney, D. J., et al. (2012). Highly stretchable and tough hydrogels. Nature 489, 133–136. doi:10.1038/nature11409

PubMed Abstract | CrossRef Full Text | Google Scholar

Ubertini, M. A., and Rosa, A. (2023). Topological analysis and recovery of entanglements in polymer melts. Macromolecules 56 (9), 3354–3362. doi:10.1021/acs.macromol.3c00278

PubMed Abstract | CrossRef Full Text | Google Scholar

Varshney, V., Patnaik, S. S., Roy, A. K., and Farmer, B. L. (2008). A molecular dynamics study of epoxy-based networks: cross-linking procedure and prediction of molecular and material properties. Macromolecules 41 (18), 6837–6842. doi:10.1021/ma801153e

CrossRef Full Text | Google Scholar

Xu, L., Zhao, X., Xu, C., and Kotov, N. A. (2018). Water-rich biomimetic composites with abiotic self-organizing nanofiber network. Adv. Mater. 30 (1), 1703343. doi:10.1002/adma.201703343

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C., Yin, T., and Suo, Z. (2019). Polyacrylamide hydrogels. I. Network imperfection. J. Mech. Phys. Solids 131, 43–55. doi:10.1016/j.jmps.2019.06.018

CrossRef Full Text | Google Scholar

Zheng, S., Li, Z., and Liu, Z. (2018). The fast homogeneous diffusion of hydrogel under different stimuli. Int. J. Mech. Sci. 137, 263–270. doi:10.1016/j.ijmecsci.2018.01.029

CrossRef Full Text | Google Scholar

Zhu, P., Lin, J., Xiao, R., and Zhou, H. (2022). Unravelling physical origin of the Bauschinger effect in glassy polymers. J. Mech. Phys. Solids 168, 105046. doi:10.1016/j.jmps.2022.105046

CrossRef Full Text | Google Scholar

Zhu, R., Zhu, D., Zheng, Z., and Wang, X. (2024). Tough double network hydrogels with rapid self-reinforcement and low hysteresis based on highly entangled networks. Nat. Commun. 15, 1344. doi:10.1038/s41467-024-45485-8

PubMed Abstract | CrossRef Full Text | Google Scholar