- 1Department of Mathematics, Gauhati University, Guwahati, India
- 2Department of Mathematics, Faculty of Education, Kafkas University, Kars, Turkey
- 3Department of Mathematics, Faculty of Science, University of Zakho, Zakho, Iraq
- 4Department of Mathematics, Faculty of Science, Firat University, Elazig, Turkey
The research paper aims to investigate the space-time fractional cubic-quartic non-linear Schrödinger equation in the appearance of the third, and fourth-order dispersion impacts without both group velocity dispersion, and disturbance with parabolic law media by utilizing the extended sinh-Gordon expansion method. This method is one of the strongest methods to find the exact solutions to the non-linear partial differential equations. In order to confirm the existing solutions, the constraint conditions are used. We successfully construct various exact solitary wave solutions to the governing equation, for example, singular, and dark-bright solutions. Moreover, the 2D, 3D, and contour surfaces of all obtained solutions are also plotted. The finding solutions have justified the efficiency of the proposed method.
1. Introduction and Motivation
Non-linear partial differential equations have different types of equations, one of them is the non-linear Schrödinger equation (NLSE) that relevant to the classical and quantum mechanics. The non-linear Schrödinger equation is a generalized (1 + 1)-dimensional version of the Ginzburg-Landau equation presented in 1950 in their study on supraconductivity and has been specifically reported by Chiao et al. [1] in their research of optical beams. In the past several years, various methods have been proposed to obtain the exact optical soliton solutions of the non-linear Schrödinger equation [2–12]. Dispersion and non-linearity are two of the essential components for the distribution of solitons across inter-continental regions. Usually, group velocity dispersion (GVD) level with self-phase modulation in a sensible manner allows these solitons to sustain tall range travel. In fact it might happen that the GVD is tiny and thus totally ignored, in this case the dispersion effect is determined by third and fourth order dispersion effects. Subsequently, this equation has been studied in a variety of ways, such as the Lie symmetry [13], both the -improved expansion, and the exp(−φ(ξ))−expansion methods [14], and the semi-inverse variation principle method [4]. In this study, the extended sinh-Gordon expansion method (ShGEM) is applied to the non-linear cubic-quartic Schrödinger equations with the Parabolic law of fractional order, which is given by
where u(x, t) is the complex valued wave function. The operator Dα of order α, where α ∈ (0, 1] is the fractional derivative, the parameters γ and β are real constants, a real-valued algebraic function F(|u|2) is p-times continuously differentiable, then
By using the relation of
on Equation (1), we obtain the fractional non-linear Schrödinger equations with Parabolic law as follows:
The extended sinh-Gordon expansion method is intended to a generalization of the sine-Gordon expansion equation because it is based on an auxiliary equation namely the sine-Gordon equation (see previous studies [15, 16] for details). Moreover, different computational and numerical methods have been utilized to constructed new solutions to the non-linear partial differential equations, such as the variable separated method [17], the auxiliary parameters and residual power series method [18], the Bernoulli sub-equation method [19, 20], the modified auxiliary expansion method [21], the homotopy analysis transform method [22–26], the homotopy perturbation sumudu transform method [27], the shooting method with the explicit Runge-Kutta scheme [28, 29], and the Adomian decomposition method [30]. Recently, several fractional operators have been applied to the mathematical models in order to seek their exact solutions, such as the Laplace transform [31, 32], the Nabla operator [33–35].
The outline of paper are organize the paper as follows: A short review of the conformable derivative is presented in section 2. Section 3 deals with the analysis of the ShGEM. In section 4, the method is applied to solve the non-linear Schrödinger equation involving the fractional derivatives with the parabolic law. Eventually, in section 5, we presented our conclusion of this paper.
2. Basic Definitions
The basic definitions of the conformable derivative of order α are given as follows [36–41]:
Definition 2.1. Assume the function h : (0, ∞) → ℝ then, the conformable derivative of h of order α is defined as , ∀t > 0, and 0 < α ≤ 1.
Definition 2.2. Assume that c ≥ 0 and t ≥ c, let h be a function defined on (c, t] as well as α ∈ ℝ. Then, the α-fractional integral of h is given by
if the Riemann improper integral exists.
Theorem 2.1. Let α ∈ (0, 1], and h = h(t), g = g(t) be α-conformable differentiable at a point t > 0, then:
Furthermore, if function h is differentiable, then .
Theorem 2.2. (see for details pervious research [40]): Let h be a differentiable function and α is order of the conformable derivative. Let g be a differentiable function defined in the range of h, then
here “prime” is the classical derivatives with respect to t.
3. The Extended ShGEM
In the current section, we presented the main steps of the e ShGEM (see previous study [42, 43]).
Consider the following fractional non-linear PDE:
where p = p(x, t).
Consider the wave transformation
by substitute relation Equation (8) into Equation (7), we obtain the following non-linear ODE:
Consider the trial solution of Equation (9) of the form
The parameters Aj, Bj, for (j = 1, 2, …, k) and A0 are real constants, and θ is a function of η that hold the following ODE:
The homogeneous balance principle is applied on Equation (9) to find the value of k. From the space-time fractional the sinh-Gordon equation, we have (see previous study [15, 16]).
The exact solutions of Equation (12) may be given as
and
Letting solutions of Equation (10) along with Equations (13) and (14) as the form
Finding the value of k and then inserting Equations (10) and (12) into Equation (9), we get a system of terms of:
we gather a group of over-defined non-linear algebraic equations in A0, Aj, Bj, putting the coefficients of sinhi(θ) coshj(θ) to zero, and finding the solutions of acquired system, we gain the values of A0, Aj, Bj, c1, c2, κ, and ω. Putting the values of A0, Aj, Bj, c1, c2, κ, and ω into Equations (15) and (16), we can find the solutions of Equation (7).
4. Implement of the Extended ShGEM
The implementation of the extended ShGEM to the cubic-quartic non-linear Schrödinger equation with conformable derivative is provided in this section.
Consider the wave transformation
In Equation (18), θ(x, t) represents the phase component of the soliton. The ω, κ, ν are the wave number, the soliton frequency, and the soliton velocity, respectively. Substituting wave transformation into Equation (2) and splitting the outcomes equation into real and imaginary parts, we gain
Multiply both sides of Equation (19) by U′ and integrate it, we obtain
From Equation (20), we get constraint conditions ν = 4γκ3 − 3βκ2 and β = 4γκ. Balancing the terms U‴U′ and U6 yields κ = 1. With κ = 1, Equations (10), (16), and (17) change to
and
respectively.
Inserting Equation (22) along with Equation (12) into Equation (21), and using constraint conditions provides a non-linear algebraic system. Equaling each coefficient of sinhi(θ) coshj(θ) with the same power to zero, and finding the obtained system of algebraic equations, we gain the values of the parameters. Putting the obtained values of the parameters into Equations (23) and (24), give the solutions of Equation (3).
Set 1
we get
Set 2
we get
Set 3
we get
Set 4
we get
Set 5
we obtain
Set 6
we get
Set 7
we get
5. Conclusion
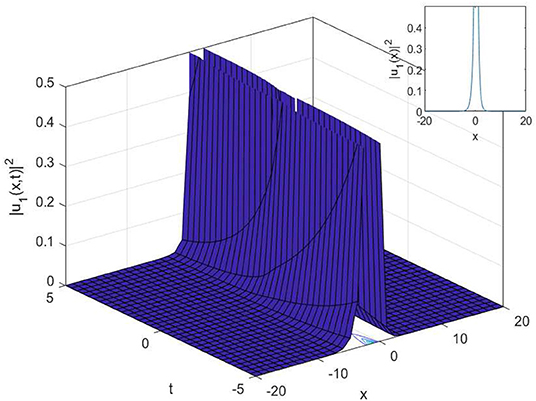
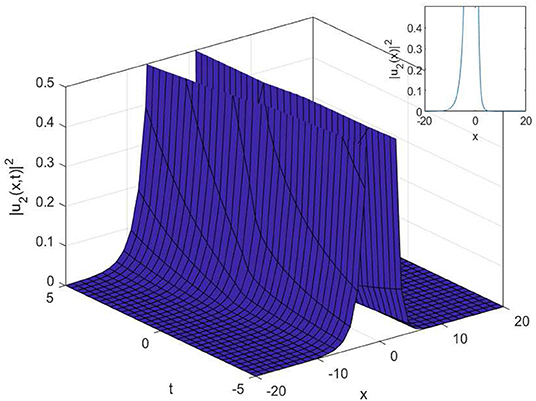
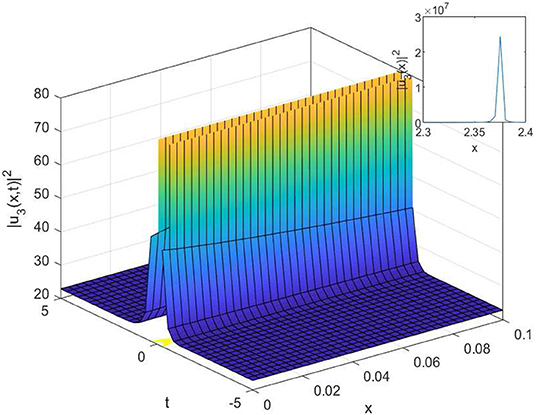
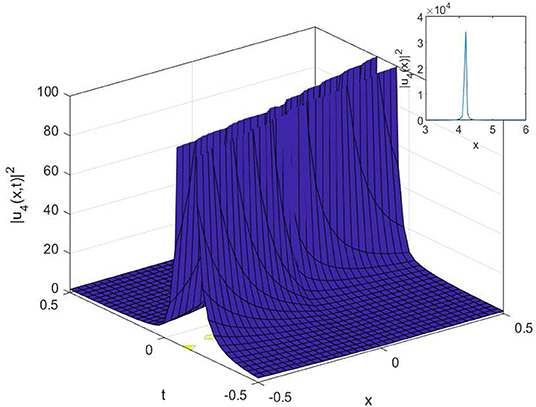
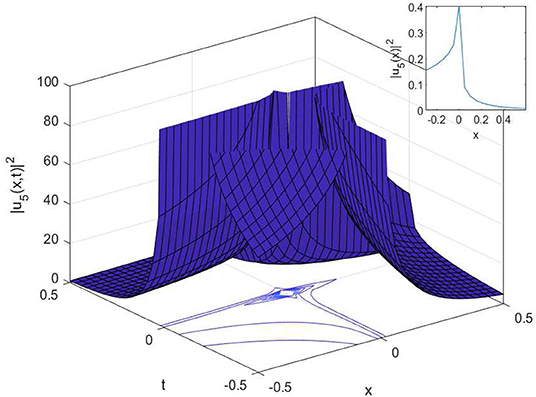
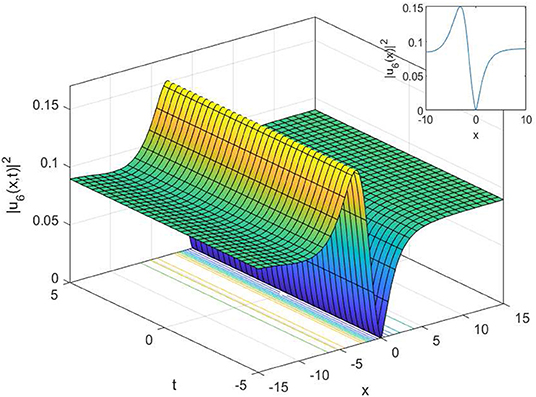
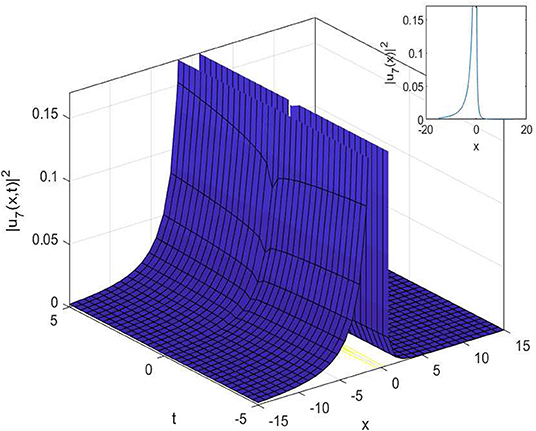
In this article, we have successfully used the extended sinh-Gordon expansion method to solve the problem for the non-linear cubic-quartic Schrödinger equations involving fractional derivatives with the Parabolic law. A traveling wave transforms in the sense of the comfortable derivative has been used to convert the governing equation into a NODE. The various optical solutions of the studied model have been constructed, for example, the singular soliton solutions as shown in Figures 1–6, and the dark-bright soliton solution as seen in Figure 7. Comparing our solutions to the results obtained in references [16–18], our findings solutions are new and different. To better analyze the dynamic attitude, and the characteristics of these solutions, the 2D, 3D and counter-surface of all obtained solutions are plotted. The study shows that this method is the effective and appropriate technique for finding the exact solution of the model considered in the paper.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
HD contributed in developing the proofs and edited the article for possible improvement. HG, KA, and RY contributed in developing the main results and proofs. All authors read the final version and approved it.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Chiao RY, Garmire E, Townes CH. Self-trapping of optical beams. Phys Rev Lett. (1964) 13:479–82. doi: 10.1103/PhysRevLett.13.479
2. Arshad M, Seadawy AR, Dianchen Lu. Exact bright–dark solitary wave solutions of the higher-order cubic–quintic nonlinear Schrödinger equation and its stability. Optik. (2017) 9:40–9. doi: 10.1016/j.ijleo.2017.03.005
3. Biswas A, Triki H, Zhou Q, Moshokoa SP, Ullah MZ, Belic M. Cubic–quartic optical solitons in Kerr and power law media. Optik. (2017) 144:357–62. doi: 10.1016/j.ijleo.2017.07.008
4. Biswas A, Arshed S. Application of semi-inverse variational principle to cubic-quartic optical solitons with kerr and power law nonlinearity. Optik. (2018) 172:847–50. doi: 10.1016/j.ijleo.2018.07.105
5. Hosseini K, Samadani F, Kumar D, Faridi M. New optical solitons of cubic-quartic nonlinear Schrödinger equation. Optik. (2018) 157:1101–5. doi: 10.1016/j.ijleo.2017.11.124
6. Houwe A, Hammouch Z, Bienvenue D, Nestor S, Betchewe G, DOKA SY. Nonlinear Schrödingers equations with cubic nonlinearity: M-derivative soliton solutions by exp(ϕ(ξ))-Expansion method. Preprints. (2019). 2019:2019030114 doi: 10.20944/preprints201903.0114.v1
7. Li HM, Xu YS, Lin J. New optical solitons in high-order dispersive cubic-quintic nonlinear Schrödinger equation. Commun Theor Phys. (2004) 41:829–32. doi: 10.1088/0253-6102/41/6/829
8. Nawaz B, Ali K, Oan Abbas S, Rizvi STR, Zhou Q. Optical solitons for non-Kerr law nonlinear Schrödinger equation with third and fourth order dispersions. Chin J Phys. (2019) 60:133–40. doi: 10.1016/j.cjph.2019.05.014
9. Seadawy AR, Kumar D, Chakrabarty AK. Dispersive optical soliton solutions for the hyperbolic and cubic-quintic nonlinear Schrödinger equations via the extended sinh-Gordon equation expansion method. Eur Phys J Plus. (2018) 133:182. doi: 10.1140/epjp/i2018-12027-9
10. Xie Y, Yang Z, Li L. New exact solutions to the high dispersive cubic–quintic nonlinear Schrödinger equation. Phys Lett A. (2018) 382:2506–14. doi: 10.1016/j.physleta.2018.06.023
11. Wang P, Shang T, Feng L, Du Y. Solitons for the cubic-quintic nonlinear Schrödinger equation with Raman effect in nonlinear optics. Opt Quant Electron. (2014) 46:1117–26. doi: 10.1007/s11082-013-9840-8
12. Srivastava HM, Gnerhan H, Ghanbari B. Exact traveling wave solutions for resonance nonlinear Schrödinger equation with intermodal dispersions and the Kerr law nonlinearity. Math Meth Appl Sci. (2019) 42:7210–21. doi: 10.1002/mma.5827
13. Bansal A, Biswas A, Zhou Q, Babatin MM. Lie symmetry analysis for cubic–quartic nonlinear Schrödinger's equation. Optik. (2018) 169:12–5. doi: 10.1016/j.ijleo.2018.05.030
14. Gao W, Ismael HF, Husien AM, Bulut H, Baskonus HB. Optical soliton solutions of the cubic-quartic nonlinear schrödinger and resonant nonlinear Schrödinger equation with the parabolic law. Appl Sci. (2020) 10:219. doi: 10.3390/app10010219
15. Baskonus HM, Bulut H, Sulaiman TA. New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method. Appl Math Nonlin Sci. (2019) 4:129–38. doi: 10.2478/AMNS.2019.1.00013
16. Ali KK, Yilmazer R, Bulut H. Analytical solutions to the coupled Boussinesq–Burgers equations via Sine-Gordon expansion method. In: 4th International Conference on Computational Mathematics and Engineering Sciences (CMES-2019). CMES 2019. Advances in Intelligent Systems and Computing, Vol. 1111. Cham: Springer. (2020). p. 233–40. doi: 10.1007/978-3-030-39112-6_17
17. Al-Ghafri KS, Rezazadeh H. Solitons and other solutions of (3 + 1)-dimensional space–time fractional modified KdV–Zakharov–Kuznetsov equation. Appl Math Nonlin Sci. (2019) 4:289–304. doi: 10.2478/AMNS.2019.2.00026
18. Kumar S, Kumar A, Momani S, Aldhaifallah M, Nisar KS. Numerical solutions of nonlinear fractional model arising in the appearance of the stripe patterns in two-dimensional systems. Adv Differ Equat. (2019) 2019:413. doi: 10.1186/s13662-019-2334-7
19. Ismael HF, Bulut H. On the Solitary Wave Solutions to the (2 + 1)-Dimensional Davey-Stewartson Equations, 4th International Conference on Computational Mathematics and Engineering Sciences (CMES-2019). CMES 2019. Advances in Intelligent Systems and Computing, vol 1111. Springer, Cham. (2020). p. 156–65. doi: 10.1007/978-3-030-39112-6_11
20. Abdulkareem HH, Ismael HF, Panakhov ES, Bulut H. Some novel solutions of the coupled Whitham-Broer-Kaup equations. In: 4th International Conference on Computational Mathematics and Engineering Sciences (CMES-2019). CMES 2019. Advances in Intelligent Systems and Computing, Vol. 1111. Cham: Springer (2020). p. 200–8. doi: 10.1007/978-3-030-39112-6_14
21. Gao W, Ismael HF, Bulut H, Baskonus HM. Instability modulation for the (2 + 1)-dimension paraxial wave equation and its new optical soliton solutions in Kerr media. Phys Scripta. (2019) 95. doi: 10.1088/1402-4896/ab4a50
22. Kumar D, Singh J, Purohit SD, Swroop R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math Modell Nat Phen. (2019) 14:304. doi: 10.1051/mmnp/2018063
23. Bhatter S, Mathur A, Kumar D, Nisar KS, Singh J. Fractional modified Kawahara equation with Mittag–Leffler law. Chaos Solit Fract. (2019) 131:109508. doi: 10.1016/j.chaos.2019.109508
24. Singh J, Kumar D, Baleanu D. New aspects of fractional Biswas–Milovic model with Mittag-Leffler law. Math Modell Nat Phen. (2019) 14:303. doi: 10.1051/mmnp/2018068
25. Kumar D, Singh J, Baleanu D. On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law. Math Methods Appl Sci. (2020) 43:443–57. doi: 10.1002/mma.5903
26. Veeresha P, Prakasha DG, Baskonus HM. New numerical surfaces to the mathematical model of cancer chemotherapy effect in caputo fractional derivatives. AIP Chaos. (2019) 29:1–14. doi: 10.1063/1.5074099
27. Goswami A, Singh J, Kumar D. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Phys A. (2019) 524:563–75. doi: 10.1016/j.physa.2019.04.058
28. Ismael HF. Carreau-Casson fluids flow and heat transfer over stretching plate with internal heat source/sink and radiation. Int J Adv Appl Sci. (2017) 4:11–5. doi: 10.21833/ijaas.2017.07.003
29. Ismael HF, Arifin NM. Flow and heat transfer in a Maxwell liquid sheet over a stretching surface with thermal radiation and viscous dissipation. JP J Heat Mass Transf. (2018) 15:847–66. doi: 10.17654/HM015040847
30. Ismael HF, Ali KK. MHD casson flow over an unsteady stretching sheet. Adv Appli Fluid Mech. (2017) 20:533–41. doi: 10.17654/FM020040533
31. Kumar D, Singh J, Al Qurashi M, Baleanu D. A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying. Adv Differ Equat. (2019) 2019:278. doi: 10.1186/s13662-019-2199-9
32. Singh J, Kumar D, Baleanu D, Rathore S. On the local fractional wave equation in fractal strings. Math Methods Appl Sci. (2019) 42:1588–95. doi: 10.1002/mma.5458
33. Ali KK, Yilmazer R. Discrete fractional solutions to the effective mass Schrödinger equation by mean of Nabla operator. AIMS Math. (2020) 5:894–903. doi: 10.3934/math.2020061
34. Ozturk O, Yilmazer R. Solutions of the radial Schrödinger equation in hypergeometric and discrete fractional forms. Commun Fac Sci Univ Ank Ser A1 Math Stat. (2019) 68:833–9. doi: 10.31801/cfsuasmas.481600
35. Yilmazer R, Discrete fractional solution of a non-homogeneous non-Fuchsian differential equations. Therm Sci. (2019) 23:S121–7. doi: 10.2298/TSCI180917336Y
36. Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Math. (2014) 264:65–70. doi: 10.1016/j.cam.2014.01.002
37. Nisar KS, Rahman G, Khan A. Some new inequalities for generalized fractional conformable integral operators. Adv Differ Equat. (2019) 2019:427. doi: 10.1186/s13662-019-2362-3
38. Nisar KS, Tassaddiq A, Rahman G, Khan A. Some inequalities via fractional conformable integral operators. J Inequal Appl. (2019) 2019:217. doi: 10.1186/s13660-019-2170-z
39. Rahman G, Ullah Z, Khan A, Set E, Nisar KS. Certain Chebyshev-type inequalities involving fractional conformable integral operators. Mathematics. (2019) 7:364. doi: 10.3390/math7040364
40. Abdeljawad T. On conformable fractional calculus. J Comput Appl Math. (2015) 279:57–66. doi: 10.1016/j.cam.2014.10.016
41. Gao W, Yel G, Haci MB, Cattani C. Complex solitons in the conformable (2 + 1)-dimensional Ablowitz-Kaup-Newell-Segur Equation. AIMS Math. (2020) 5:507–21. doi: 10.3934/math.2020034
42. Xian-Lin X, Jia-Shi T. Travelling wave solutions for Konopelchenko-Dubrovsky equation using an extended sinh-Gordon equation expansion. Commun Theor Phys. (2008) 50:1047. doi: 10.1088/0253-6102/50/5/06
Keywords: the non-linear cubic-quartic Schrödinger equation, conformable derivative, analytical solutions, the extended sinh-Gordon expansion method, solitary wave solutions
Citation: Dutta H, Günerhan H, Ali KK and Yilmazer R (2020) Exact Soliton Solutions to the Cubic-Quartic Non-linear Schrödinger Equation With Conformable Derivative. Front. Phys. 8:62. doi: 10.3389/fphy.2020.00062
Received: 29 November 2019; Accepted: 27 February 2020;
Published: 20 March 2020.
Edited by:
Devendra Kumar, University of Rajasthan, IndiaReviewed by:
Haci Mehmet Baskonus, Harran University, TurkeyK. S. Nisar, Prince Sattam Bin Abdulaziz University, Saudi Arabia
Jagdev Singh, JECRC University, India
Copyright © 2020 Dutta, Günerhan, Ali and Yilmazer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hemen Dutta, aGVtZW5fZHV0dGEwOEByZWRpZmZtYWlsLmNvbQ==
 Hemen Dutta
Hemen Dutta Hatıra Günerhan
Hatıra Günerhan Karmina K. Ali
Karmina K. Ali Resat Yilmazer
Resat Yilmazer