Abstract
The hesitant fuzzy graph (HFG) is one of the most powerful tools to find the strongest influential person in a network. Many problems of practical interest can be modeled and solved by using HFG algorithms. HFGs, belonging to the FG family, have good capabilities when faced with problems that cannot be expressed by FGs. The vague-valued hesitant fuzzy graph (VVHFG) is the generalization of the HFG. A VVHFG is a powerful and useful tool to find the influential person in various parts, such as meetings, conferences, and every group discussion. In this study, we introduce a new concept of the VVHFG. Our purpose is to develop a notion of the VVHFG and also to present some basic definitions, notations, remarks, and proofs related to VVHFGs. We propose a numerical method to find the most dominating person using our proposed work. Finally, an application of the VVHFG in decision-making has been introduced.
1 Introduction
Graphs, from ancient times to the present day, have played a very important role in various fields, including computer science and social networks, so that with the help of the vertices and edges of a graph, the relationships between objects and elements in a social group can be easily introduced. But, there are some phenomena in our lives that have a wide range of complexities that make it impossible for us to express certainty. These complexities and ambiguities were reduced with the introduction of FSs by Zadeh [1]. After introduction of fuzzy sets, FS-theory is included as part of large research fields. Since then, the theory of FSs has become a vigorous area of research in different disciplines, including life sciences, management, statistics, graph theory, and automata theory. The subject of FGs was proposed by Rosenfeld [2]. Analysis of uncertain problems by the fuzzy graph (FG) is important because it gives more integrity and flexibility to the system. An FG has good capabilities in dealing with problems that cannot be explained by weight graphs. They have been able to have wide applications even in fields such as psychology and identifying people based on cancerous behaviors. One of the advantages of the FG is its flexibility in reducing time and costs on economic issues, which has been welcomed by all managers of institutions and companies. Rashmanlou et al. [3] studied cubic fuzzy graphs. Pramanik et al. [4] presented an extension of the fuzzy competition graph and its uses in manufacturing industries. Pal [5] introduced antipodal interval-valued fuzzy graphs. Bera et al. [6] proposed certain types of m-polar, interval-valued fuzzy graphs.
Gau and Buehrer [7] proposed the concept of the vague set (VS) in 1993 by replacing the value of an element in a set with a subinterval of [0,1].
One type of the FG is the vague graph (VG). VGs have a variety of applications in other sciences, including biology, psychology, and medicine. Also, a VG could concentrate on determining the uncertainty coupled with the inconsistent and indeterminate information of any real-world problems, where FGs may not lead to adequate results. Ramakrishna [8] introduced the concept of VGs and studied some of their properties. After that, Akram et al. [9] introduced vague hypergraphs.
Cayley-VG and regularity were introduced by Akram et al. [10–12]. The concept of domination in VGs was introduced by Borzooei [13]. Rao et al. [14–16] studied certain properties of VGs and domination in vague incidence graphs. Borzooei et al. [17, 18] investigated isomorphic properties of neighborly irregular vague graphs. They also expressed new concepts of regular and highly irregular vague graphs with applications. New concepts of coloring in vague graphs with applications are presented by Krishna [19]. Kosari et al. [20, 21] expressed the notion of VG structure with application in medical diagnosis and also studied a novel description of the VG with application in transportation systems.
Torra [22, 23] developed the concept of a FS to a hesitant fuzzy set (HFS). The HFS is a powerful and effective tool to express uncertain information in multi-attribute decision-making processes as it permits the membership degree of an element to a set represented by several possible values in [0,1].
Many problems of practical interest can be modeled and solved by using HFG-algorithms. The HFG is a useful tool in modeling some problems, especially in the field of communication networks. HFGs was introduced by Pathinathan et al. [24] and extended in [25, 26]. Javaid et al. [27] studied new results of HFGs and their products. Karaaslan [28] investigated the HFGs and their applications in decision-making. Kalyan [29] defined k-regular domination in hesitancy as a fuzzy graph. Shakthivel [30] expressed domination in the hesitancy fuzzy graph. Inverse domination in HFGs and its properties was introduced by Shakthivel et al. [31]. Bai [32] investigated dual HFGs with applications to multi-attribute decision-making. The concept of isomorphic properties of m-polar fuzzy graphs is studied by Ghorai and Pal [33]. Pandey et al. [34] developed a notion of the FG in the setup of bipolar-valued hesitant fuzzy sets and so presented a new definition of a bipolar-valued hesitant fuzzy graph. Shi et al. [35] introduced the notion of homomorphism (HM) of VGs and discussed HM, isomorphism (IM), weak isomorphism (WI), and co-weak isomorphism (CWH) of VGs.
Although HFGs are better at expressing uncertain variables than FGs, they do not perform well in many real-world situations, such as IT management. Therefore, when the data come from several factors, it is necessary to use the VVHFG. VVHFGs, belonging to the FG family, have good capabilities when faced with problems that cannot be expressed by HFGs and VFGs. They are highly practical tools for the study of different computational intelligence and computer science domains. VVHFGs have several applications in real-life systems and applications where the level of the information inherited in the system varies with time and has different levels of accuracy. Homomorphisms (HMs) provide a way of simplifying the structure of objects one wishes to study, while preserving much of it that is of significance. It is not surprising that homomorphisms also appeared in graph theory and that they have proven useful in many areas. Therefore, in this study, we present a novel notion of the VVHFG and investigate HM, IM, WI, and CWI between VVHFGs and express some fundamental operations as a Cartesian product (CP), strong product (SP), and union on VVHFG. Finally, directed-VVHFGs and their application in decision-making have been given.
2 Preliminaries
In this section, we review some notions of vague graphs and their operations.
Definition 2.1A graph is an ordered pair G* = (X, E) where X is the set of vertices of G* and E ⊆ X × X is the set of edges of G*. Suppose E is the set of all 2-element subsets of X that we denoted by .(I) Let G1 = (X1, E1) and G2 = (X2, E2) be two graphs, then the CP of two graphs G1 and G2 denoted by G1 × G2 = (X1 × X2, E1 × E2) is defined as:(II) Let G1 = (X1, E1) and G2 = (X2, E2) be two graphs. Then, the SP of two graphs G1 and G2 denoted by G1 ⊗ G2 = {X1 ⊗ X2, E1 ⊗ E2} is defined as:
Definition 2.2An FG on a graph G* = (X, E) is a pair G = (ψ, θ), where ψ: X → [0, 1] is an FS on X and θ: X × X → [0, 1] is a fuzzy relation on E, such that,for all m, n ∈ X.
Definition 2.3[7]"A vague set (VS) W is a pair (tW, fW) on set X where tW and fW are taken as real-valued functions which can be defined on X → [0, 1] so that tW(m) + fW(m) ≤ 1, ∀m ∈ X.
Definition 2.4[8] Suppose G* = (X, E) is a crisp graph, a pair G = (W, Z) is named a VG on graph G* = (X, E) where W = (tW, fW) is a VS on X and Z = (tZ, fZ) is a VS on E ⊆ X × X such that,for all mn ∈ E.A VG G is named strong iffor all m, n ∈ X.
Definition 2.5[11] Suppose G = (W, Z) is a VFG on G*, the degree of vertex m is defined as deg(m) = (dt(m), df(m)) whereThe order of G is defined as
Example 2.6Consider a graph G* = (X, E), where X = {w1, w2, w3, w4, w5} and E = {w1w2, w2w3, w3w4, w1w5}. Suppose G = (W, Z) is a VFG of a graph G*, as shown in Figure 1.Graph G in Figure 1 is a VFG. Also, the degree of each vertex in the VFGG is d(w1) = (0.9, 2.1), d(w2) = (0.8, 1.3), d(w3) = (0.6, 1.5), d(w4) = (0.4, 1.5), and d(w5) = (0.3, 0.8).
FIGURE 1
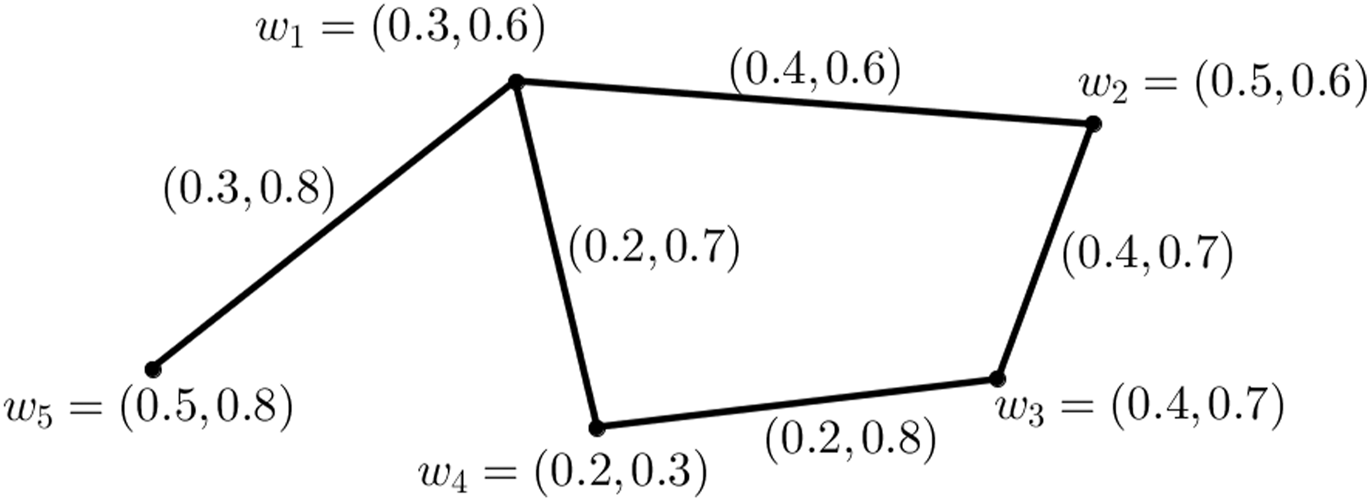
VFG.
Definition 2.7A graph G = (X, E) is called a directed graph (digraph) if it has oriented edges and the arrows on the edges show the direction of each edge. Digraph G is displayed by .
2.1. Vague-valued hesitant fuzzy set
Definition 2.8Suppose X is a set, a vague-valued hesitant fuzzy set (VVHFS) W on X is defined as:where W(a) is a subset of values in [0, 1] × [0, 1]. We name W(a) a vague-valued hesitant fuzzy element (VVHFE) defined asHere, is a vague-valued fuzzy number (VVFN) such that and .
Definition 2.9Suppose X is a non-empty universe, and for a ∈ X, suppose W(a), W1(a), and W2(a) are the VVHFEs, then,
Definition 2.10Suppose is a VVFN, then the value of score S(ma) is defined asThis means the degree of satisfaction corresponding to some characteristic features and the degree of satisfaction to some implicit contradictory features are related to a principle.
Definition 2.11Suppose W(a) is a VVHFE, then the score function S(W(a)) is defined asHere, the number of vague -values in W(a) is denoted by n(W(a)), and ma is the element in W(a), shown as the form of the VVFN.
Definition 2.12Suppose W and Z are two VVHFSs on X. Then, score-based (SB) intersection and union of two VVHFEs W(a) and Z(a) are denoted by and respectively, which is characterized byand
Definition 2.13Suppose W and Z are two VVHFSs on set X, then and .
2.2 Vague-valued hesitant fuzzy relation
Definition 2.14Suppose W and Z are two VVHFSs on set X, then the SB CP of two VVHFSs W and Z is displayed by and specified by
Definition 2.15Suppose X is a non-empty set and suppose W and Z are two VVHFSs on X, for a, b ∈ X, consider W(a, b): X × X → ([0, 1] × [0, 1]) is a VVHF relation on X, and then, we name W is SB VVHF relation on Z if,for all a, b ∈ X.All the essential notations are shown in Table 1.
TABLE 1
| Notation | Meaning |
|---|---|
| FS | Fuzzy set |
| FG | Fuzzy graph |
| VS | Vague set |
| VG | Vague graph |
| HFS | Hesitant fuzzy set |
| HFG | Hesitant fuzzy graph |
| IM | Isomorphism |
| HM | Homomorphism |
| WI | Weak isomorphism |
| CWI | Co-weak isomorphism |
| AM | Automorphism |
| CP | Cartesian product |
| SP | Strong product |
| SB | Score based |
| VVHFE | Vague-valued hesitant fuzzy element |
| VVHFN | Vague-valued hesitant fuzzy number |
| VVHFG | Vague-valued hesitant fuzzy graph |
Some essential notations.
3 Vague-valued hesitant fuzzy graph
In this part, we introduce the definition of the VVHFG with some examples.
Definition 3.1Suppose G* = (X, E) is a graph, a VVHFG on set X is an order pair G = (W, Z) where W and Z are VVHFSs in X and , respectively. If W: X → [0, 1] × [0, 1] and then, we have the following conditionsHere, Z(ab) and W(a) are VVHFEs defined asand
Example 3.2Let there be five companies in the debate competition and Congress members choose one company as the best company according to three important properties, that is, profit-making, revenue, and influence power. Congress members evaluate the communication of three properties between five companies. Suppose X is a set of five companies {m1, m2, m3, m4, m5} and E = {m1m2, m2m3, m3m4, m4m5, m5m1, m2m5, m1m4} is the communication of three properties among companies, we show the scores of vertices and edges in Table 2 and Table 3, respectively. A VVHFG is given in Figure 2.
TABLE 2
| X | Score |
|---|---|
| m1 =< (0.1, 0.8), (0.7, 0.8), (0.2, 0.5) > | −0.183 |
| m2 =< (0.3, 0.5), (0.4, 0.8) > | −0.15 |
| m3 =< (0.2, 0.4), (0.1, 0.6) > | −0.175 |
| m4 =< (0.4, 0.7), (0.6, 0.7), (0.2, 0.7) > | −0.15 |
| m5 =< (0.2, 0.3), (0.4, 0.7) > | −0.1 |
VVHF table.
TABLE 3
| E | Score |
|---|---|
| m1m2 =< (0.2, 0.9), (0.4, 0.5) > | −0.2 |
| m2m3 =< (0.1, 0.5), (0.3, 0.6) > | −0.175 |
| m3m4 =< (0.1, 0.8), (0.6, 0.9), (0.3, 0.4) > | −0.183 |
| m4m5 =< (0.4, 0.9), (0.1, 0.3), (0.5, 0.8) > | −0.167 |
| m5m1 =< (0.3, 0.9), (0.5, 0.8) > | −0.225 |
| m2m5 =< (0.4, 0.7), (0.1, 0.5) > | −0.175 |
| m1m4 =< (0.2, 0.7), (0.3, 0.9) > | −0.275 |
VVHF table.
FIGURE 2
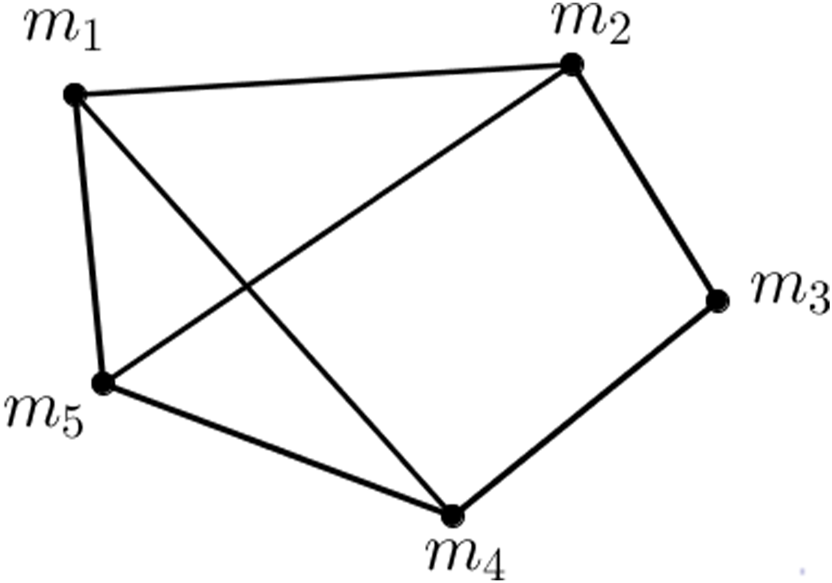
VVHFG.
Definition 3.3Suppose G = (W, Z) is a VVHFG on G* = (X, E), the SB degree of a vertex s1 ∈ X in the VVHFG is denoted by and defined as .For Example 3.2, we obtain the SB degree of every vertex in the VVHFG; therefore, we have .
Definition 3.4Suppose G1 = (W1, Z1) and G2 = (W2, Z2) are two VVHFGs on G* = (X, E), then we say that G1 is the SB VVHF-subgraph of G2, if it holds the conditions
3.1 Basic operations on VVHFGs
In this section, we express some basic operations like CP, SP, and union between VVHFGs, and also some properties in VVHFGs are established.
Definition 3.5Suppose G1 = (W1, Z1) and G2 = (W2, Z2) are two VVHFGs on the graph G* = (X, E), we give some operations and related results for VVHFGs.CP: The CP of two VVHFGs denoted by is defined as1) .2) .3) .
Proposition 3.6Suppose G1 and G2 are two VVHFGs, then is a VVHFG.
Proof.For every a ∈ X1 and a2, b2 ∈ E2, we haveFor every e ∈ X2 and a1, b1 ∈ E1, we haveSP: The SP of two VVHFGs denoted by is defined as1) .2) .3) .4) .
Proposition 3.7Suppose G1 and G2 are two VVHFGs, then is a VVHFG.
Proof.For every a ∈ X1 and a2, b2 ∈ E2, we haveFor every e ∈ X2 and a1, b1 ∈ E1, we haveFor every a1b1 ∈ E1 and a2b2 ∈ E2, we haveShown by G1 ∪ G2 = (W1 ∪ W2, Z1 ∪ Z2) s. t. S(W1(a)) = 0 if a∉X1 and S(W2(a)) = 0 if a∉X2 is defined as1) .2) .
Proposition 3.8Suppose G1 and G2 are two VVHFGs, then G1 ∪ G2 is a VVHFG.
ProofFor every ab ∈ E1 ∪ E2, we have
3.2 Isomorphism between vague-valued hesitant fuzzy graphs
In this part, we define the novel concepts of IM, HM, WI, and CWI on VVHFGs and discuss IM between VVHFGs.
Definition 3.9Suppose G1 and G2 are two VVHFGs,a HM is a mapping satisfying the following conditions:1) .2) .An IM is a bijective mapping (BM) satisfying the following conditions:1) .2) .A WI is a BM satisfying the following conditions:1) .2) .A CWI is a BM satisfying the following conditions:1) .2) .
Remark 3.10Suppose G = G1 = G2, so a HM of onto itself is called endomorphism. An IM on G* is named an automorphism (AM). Suppose is a BM, then is a BM.
Remark 3.11Suppose G = (W, Z) is a VVHFG of G* and suppose AM(G) is the set of all vague-valued hesitant AM of G is considered a map and . It is clear .
Remark 3.12Suppose G = G1 = G2, then the WI and CWI, indeed, become isomorphic.
Proposition 3.13If G1, G2 and G3 are VVHFGs, then the IM between these graphs is an equivalence relation.
Proof.For reflexivity, we use identity mapping between VVHFGs, and it is obvious. We consider a function is an IM on G1 onto G2 such that with conditionsSince is IM, we have satisfies condition (1), we haveSo, a mapping is an IM from G2 onto G1. For transitivity, we consider such that and such that are IMs between G1 onto G2 and G2 onto G3, respectively. Thus, is a composition of and such that Since the map is an IM, we haveAgain, since the map is an IM, we haveFrom expressions (2) and (4), we have..From expressions (3) and (5), we have..Hence, is an IM between G1 and G3. □
Proposition 3.14If G1, G2 and G3 are VVHFGs, then the WI between specified graphs is an equivalence relation.
Proof.Reflexivityis trivial. For anti-symmetry, we consider a function is a WI on G1 onto G2 such that with conditionsLet is a WI between G1 and G2 such that with conditionWe conclude from phrases (6) and (7) that these inequalities satisfy if and only if the VVHFGs are the same. Here, we indicate that G1 and G2 are similar because the number of edges and the corresponding edges have the same weights. Furthermore, the transitivity among graphs G1, G2 and G3 is the same as in the previous statement. □
Proposition 3.15Suppose G = (W, Z) is a VVHFG, AM(G) is the set of all AM on G. Then, (AM(G), o) forms a group.
Proof.For every θ, η ∈ AM(G) and a, b ∈ X, we haveit is clear, θoη ∈ AM(G). Also, AM(G) is associative under the mapping composition. Suppose is an identity mapping such that , for every θ ∈ Aut(G), we have θ−1 ∈ G such that , . This proof is complete. □
4 Directed-VVHFGs and their application in decision-making
Definition 4.1A directed-VVHFG of the graph G* = (X, E) with W: X → ([0, 1] × [0, 1]) and satisfies the below conditions
Definition 4.2Suppose X is a set and {Wl(a)|a ∈ X, l = 1, 2, ….., p} is a collection of VVHFEs and is the weight vector of with ωl ∈ [0, 1] and , then the vague-valued hesitant fuzzy weighted averaging (VVHFWA) operator is a mapping VVHFWA:Wp → W, whereVVHFWAthe VVHFWA operator is the vague -valued hesitant fuzzy averaging (VVHFA) operator, if we have . We can write Equation 8 as follows.VVHFA
Definition 4.3Suppose is a directed-VVHFG on G* = (X, E) and σr, r = 1, 2, …., p is adjacent VVHF-vertices of σk ∈ X, by using expression (9), we define out-degree (OD) and in-degree (ID) of a vertex σk represented by Od(σk) and Id(σk), respectively:After finding the ID and OD of each vertex, we denote its score value by S(Od(σ)) and S(Id(σ)), respectively, and determine it from definition 9. To find the D-degree of every vertex σk, we use Od(σk) − Id(σk), where Od(σk) and Id(σk) denote the score value of OD and ID of vertex σk, respectively, and shown by Ω(σk).
4.1. Application of a directed-vague-valued hesitant fuzzy graph
We cannot measure the value of influence of a person’s property, so we are always hesitant to evaluate the value of the influence of a person. On the other hand, if we do not have enough information about a person’s property, it will have a negative effect on him. In this section, we present a directed-VVHFG for such a subject. We consider the directed-VVHFG of the mental power of six people W = {x1, x2, x3, x4, x5, x6} in a scientific meeting (see Figure 3). Here, membership degrees are really valued and determine the mental power of people. Suppose W is the VVHFS on the set X as in Table 4, it indicates the mental power of people who are present in a scientific meeting. Suppose Z = {x1x4, x1x6, x2x1, x2x5, x2x6, x3x2, x4x2, x4x3, x5x6, x6x3} is the set of vague-valued directed hesitant edges as in Table 5, it determines the value of the influence of one person onto another person in a scientific meeting.
FIGURE 3
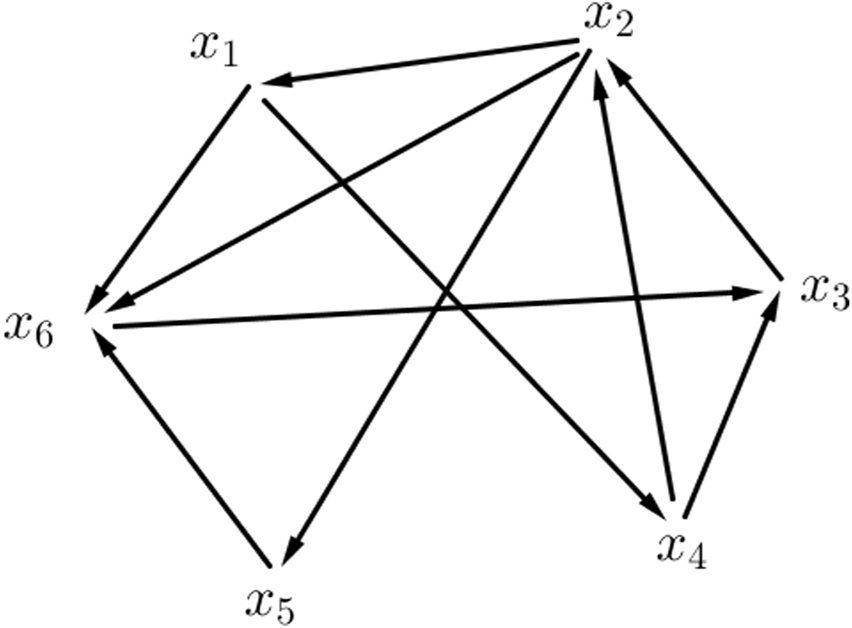
Directed-VVHFG.
TABLE 4
| W | Score |
|---|---|
| x1 =< (0.4, 0.8), (0.35, 0.5), (0.2, 0.9) > | −0.208 |
| x2 =< (0.25, 0.5), (0.6, 0.9) > | −0.137 |
| x3 =< (0.15, 0.6), (0.2, 0.4), (0.5, 0.7) > | −0.141 |
| x4 =< (0.5, 0.9), (0.25, 0.6) > | −0.189 |
| x5 =< (0.2, 0.7), (0.55, 0.8), (0.4, 0.8) > | −0.191 |
| x6 =< (0.3, 0.45), (0.2, 0.75), (0.3, 0.7) > | −0.183 |
VVHF membership of persons mental power.
TABLE 5
| Z | Score |
|---|---|
| x1x4 =< (0.15, 0.9), (0.4, 0.8) > | −0.287 |
| x1x6 =< (0.4, 0.6), (0.1, 0.9), (0.15, 0.55) > | −0.233 |
| x2x1 =< (0.45, 0.7), (0.2, 0.85) > | −0.225 |
| x2x5 =< (0.1, 0.5), (0.4, 0.8) > | −0.2 |
| x2x6 =< (0.2, 0.75), (0.15, 0.5), (0.35, 0.8) > | −0.19 |
| x3x2 =< (0.3, 0.5), (0.1, 0.5) > | −0.15 |
| x4x2 =< (0.75, 0.88), (0.25, 0.9) > | −0.195 |
| x4x3 =< (0.45, 0.7), (0.2, 0.6), (0.25, 0.9) > | −0.216 |
| x5x6 =< (0.22, 0.8), (0.5, 0.85) > | −0.232 |
| x6x3 =< (0.3, 0.75), (0.2, 0.8), (0.45, 0.9) > | −0.25 |
Value of the influence of one person on another person.
Here, we determine the OD and ID of every person as In Table 6.
TABLE 6
| OD and ID |
|---|
| Od(x1) =< (0.49, 0.98), (0.541, 0.982) > |
| Id(x1) =< (0.56, 0.955) > |
| Od(x2) =< (0.56, 0.955), (0.558, 0.975), (0.46, 0.9) > |
| Id(x2) =< (0.37, 0.75), (0.812, 0.988) > |
| Od(x3) =< (0.37, 0.75) > |
| Id(x3) =< (0.692, 0.995), (0.67, 0.988) > |
| Od(x4) =< (0.67, 0.988), (0.812, 0.988) > |
| Id(x4) =< (0.49, 0.98) > |
| Od(x5) =< (0.61, 0.97) > |
| Id(x5) =< (0.46, 0.9) > |
| Od(x6) =< (0.692, 0.995) > |
| Id(x6) =< (0.541, 0.982), (0.558, 0.975), (0.61, 0.97) > |
Out-degree and in-degree of every person.
Afterward, we obtained the score value of OD and ID of every person in the scientific meeting as in Table 7.
TABLE 7
| OD | ID |
|---|---|
| S(Od(x1)) = −0.232 | S(Id(x1)) = −0.197 |
| S(Od(x2)) = −0.208 | S(Id(x2)) = −0.139 |
| S(Od(x3)) = −0.19 | S(Id(x3)) = −0.155 |
| S(Od(x4)) = −0.123 | S(Id(x4)) = −0.245 |
| S(Od(x5)) = −0.18 | S(Id(x5)) = −0.22 |
| S(Od(x6)) = −0.151 | S(Id(x6)) = −0.203 |
Score value of out-degree and in-degree.
Finally, we determined the D-degree of every person in the scientific meeting as in Table 8.
TABLE 8
| Persons | Od − Id | D-degree |
|---|---|---|
| Ω(x1) | − 0.232 − (−0.197) | − 0.035 |
| Ω(x2) | − 0.208 − (−0.139) | − 0.069 |
| Ω(x3) | − 0.19 − (−0.155) | − 0.035 |
| Ω(x4) | − 0.123 − (−0.245) | 0.122 |
| Ω(x5) | − 0.18 − (−0.22) | 0.04 |
| Ω(x6) | − 0.151 − (−0.203) | 0.052 |
Domination degree of every person.
It is clear that the most dominating person in a scientific meeting is x4.
In HFG, all information is expressed with only one membership degree, which represents the satisfaction degree of an element corresponding to the set, and it ignores the degree of satisfaction of the element for some implicit counter property of the set. However, since the VVHFG simultaneously considers the membership and non-membership satisfaction degrees, we will use the following tables for comparative study between the VVHFG and HFG. In the HFG, the hesitant fuzzy table is composed only of the people’s satisfaction degrees corresponding to the set (in Tables 9, 10).
TABLE 9
| W | Score |
|---|---|
| x1 =< 0.8, 0.5, 0.9 > | 0.74 |
| x2 =< 0.5, 0.9 > | 0.7 |
| x3 =< 0.6, 0.4, 0.7 > | 0.57 |
| x4 =< 0.9, 0.6 > | 0.75 |
| x5 =< 0.7, 0.8, 0.8 > | 0.77 |
| 0.64 |
HF membership of persons mental power.
TABLE 10
| Z | Score |
|---|---|
| x1x4 =< 0.9, 0.8 > | 0.85 |
| x1x6 =< 0.6, 0.9, 0.55 > | 0.68 |
| x2x1 =< 0.7, 0.85 > | 0.775 |
| x2x5 =< 0.5, 0.8 > | 0.65 |
| x2x6 =< 0.75, 0.5, 0.8 > | 0.68 |
| x3x2 =< 0.5, 0.5 > | 0.5 |
| x4x2 =< 0.88, 0.9 > | 0.89 |
| x4x3 =< 0.7, 0.6, 0.9 > | 0.74 |
| x5x6 =< 0.8, 0.85 > | 0.825 |
| x6x3 =< 0.75, 0.8, 0.9 > | 0.816 |
Value of influence of one person on another person.
Here, we determine the OD and ID of every person as in Table 11.
TABLE 11
| OD and ID |
|---|
| Od(x1) =< 0.98, 0.982 > |
| Id(x1) =< 0.955 > |
| Od(x2) =< 0.9, 0.975 > |
| Id(x2) =< 0.75, 0.988 > |
| Od(x3) =< 0.75 > |
| Id(x3) =< 0.995, 0.988 > |
| Od(x4) =< 0.988, 0.988 > |
| Id(x4) =< 0.98 > |
| Od(x5) =< 0.97 > |
| Id(x5) =< 0.9 > |
| Od(x6) =< 0.995 > |
| Id(x6) =< 0.982, 0.975, 0.97 > |
Out-degree and in-degree of every person.
Afterward, we obtained the score value of OD and ID of every person in the scientific meeting as in Table 12.
TABLE 12
| OD | ID |
|---|---|
| S(Od(x1)) = 0.981 | S(Id(x1)) = 0.955 |
| S(Od(x2)) = 0.9375 | S(Id(x2)) = 0.869 |
| S(Od(x3)) = 0.75 | S(Id(x3)) = 0.9915 |
| S(Od(x4)) = 0.988 | S(Id(x4)) = 0.98 |
| S(Od(x5)) = 0.97 | S(Id(x5)) = 0.9 |
| S(Od(x6)) = 0.995 | S(Id(x6)) = 0.9756 |
Score value of out-degree and in-degree.
Finally, we determined the D-degree of every person in the scientific meeting as in Table 13.
TABLE 13
| Persons | Od − Id | D-degree |
|---|---|---|
| Ω(x1) | 0.981–0.955 | 0.026 |
| Ω(x2) | 0.9375–0.869 | 0.0685 |
| Ω(x3) | 0.75–0.9915 | − 0.2415 |
| Ω(x4) | 0.988–0.98 | 0.008 |
| Ω(x5) | 0.97–0.9 | 0.07 |
| Ω(x6) | 0.995–0.9756 | 0.0194 |
Domination degree of every person.
It is clear that the most dominating person in a scientific meeting is x5.
Through the HFG, the domination degree of each person in this scientific meeting is ranked as follows: clearly person x5 is the most dominating person in the scientific meeting. When the results of the HFG and VVHFG are examined, we realize that the domination degree and ranking of dominating people change significantly in two cases. In the VVHFG, x4 is the most dominating person in the scientific meeting, while in the HFG, person x5 is the most dominating person in the scientific meeting. Furthermore, when we examine the mental power of people in two cases a significant difference between the two results is observed. The main reason for this difference is the capability of the VVHFG, and it is simultaneously considering the membership and non-membership degrees with no restriction, while the HFG considers only one membership value.
5 Conclusion
HFGs are useful tools to determine the membership degree of an element from some possible values. This is quite common in decision-making problems. A VVHFG can accurately characterize the ambiguity of all types of networks. So, in this work, the VVHFG structure and some concepts related to VVHFGs such as HM, IM, WI, and CWI are introduced, and operations of CP, SP, and union between two VVHFGs are defined. Likewise, we defined a new notion of the VVHFG called directed-VVHFG. This concept is a useful tool to present the different decision-making processes to find the D-degree of a person in a scientific meeting through directed-VVHFG. Finally, an application of the directed-VVHFG has been presented. In our future work, we will introduce new concepts of connectivity in VVHFGs and investigate some of their properties. Also, we will study new results of global dominating sets, perfect dominating sets, connected perfect dominating sets, regular perfect dominating sets, and independent perfect dominating sets on VVHFGs.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
All the authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Natural Science Foundation of China (No. 62172116, 61972109) and the Guangzhou Academician and Expert Workstation (No. 20200115-9).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
ZadehLA. Fuzzy sets. Inf Control (1965) 8:338–53. 10.1016/s0019-9958(65)90241-x
2.
RosenfeldA. Fuzzy graphs. In: ZadehLAFuKSShimuraM, editors. Fuzzy sets and their applications. New York, NY, USA: Academic Press (1975). p. 77–95.
3.
RashmanlouHMuhiuddinGAmanathullaSKMofidnakhaeiFPalM. A study on cubic graphs with novel application. J Intell Fuzzy Syst (2021) 40(1):89–101. 10.3233/jifs-182929
4.
PramanikTMuhiuddinGAlanaziAMPalM. An extension of fuzzy competition graph and its uses in manufacturing industries. Mathematics (2020) 8:1008. 10.3390/math8061008
5.
RashmanlouHPalM. Antipodal interval-valued fuzzy graphs. Int J Appl Fuzzy Sets Artif Intelligence (2013) 3:107–30.
6.
SanchariBPalM. Certain types of m-polar interval-valued fuzzy graph. J Intell Fuzzy Syst (2020) 39(3):3137–50. 10.3233/jifs-191587
7.
GauWMLBuehrerDJ. Vague sets. IEEE Trans Syst Man Cybern (1993) 23(2):610–4. 10.1109/21.229476
8.
RamakrishnaN. Vague graphs. Int J Comput Cogn (2009) 7:51–8.
9.
AkramMGaniNSaeidAB. Vague hypergraphs. J Intell Fuzzy Syst (2014) 26:647–53. 10.3233/ifs-120756
10.
AkramMSamantaSPalM. Cayley vague graphs. J Fuzzy Maths (2017) 25(2):1–14.
11.
AkramMFengFSarwarSJunYB. Certain types of vague graphs. UPB Scientific Bull Ser A: Appl Mathematica Phys (2014) 76(1):141–54.
12.
AkramMDudekWAMurtaza YousafM. Regularity in vague intersection graphs and vague line graphs, Abstract and Applied Analysis (2014). Article ID 525389, 10 pages.
13.
BorzooeiRRashmanlouH. Domination in vague graphs and its applications. J Intell Fuzzy Syst (2015) 29(5):1933–40. 10.3233/ifs-151671
14.
RaoYKosariSShaoZ. Certain properties of vague graphs with a novel application. Mathematics (2020) 8(10):1647. 10.3390/math8101647
15.
RaoYKosariSShaoZQiangXAkhoundiMZhangX. Equitable domination in vague graphs with application in medical sciences. Front Phys9. Article ID 635-642, 2021. 10.3389/fphy.2021.635642
16.
RaoYKosariSShaoZCaiRXinyueL. A Study on Domination in vague incidence graph and its application in medical sciences. Symmetry (2020) 12(11):1885. 10.3390/sym12111885
17.
BorzooeiRARashmanlouHJunYBMathewS. Isomorphic properties of neighborly irregular vague graphs. J Intell Fuzzy Syst (2016) 30:3261–70. 10.3233/ifs-152074
18.
BorzooeiRADarabianERashmanlouHAzadiM. New concepts of regular and (highly) irregular vague graphs with applications. Fuzzy Inf Eng (2017) 9:161–79. 10.1016/j.fiae.2017.06.003
19.
Kishore KumarPKLavanyaSBroumiSRashmanlouH. New concepts of coloring in vague graphs with application. J Intell Fuzzy Syst (2017) 33:1715–21. 10.3233/jifs-17489
20.
KosariSRaoYJiangHLiuXWuPShaoZ. Vague graph Structure with Application in medical diagnosis. Symmetry (2020) 12(10):1582. 10.3390/sym12101582
21.
KouZKosariSAkhoundiM. A novel description on vague graph with application in transportation systems. J Maths2021:11. Article ID 4800499. 10.1155/2021/4800499
22.
TorraV. Hesitant fuzzy sets. Int J Intell Syst (2010) 25:529–39. 10.1002/int.20418
23.
TorraVNarukawaY. On hesitant fuzzy sets and decision. In: Proceedings of the 18th IEEE international conference on fuzzy systems. Korea: Jeju Island (2009). p. 1378–82.
24.
PathinathanTJon ArockiarajJJesintha RoslineJ. Hesitancy fuzzy graphs. Indian J Sci Technol8(35). 10.17485/ijst/2015/v8i35/86672
25.
XuZ. Hesitant fuzzy sets and theory, studies in fuzziness and sof computing. Springer-Verlag Publications (2014).
26.
ZhuBXuZXiaM. Dual hesitant fuzzy sets. Journal of Applied Mathematics. Hindawi Publishing Corporation (2012). Article ID. 879629.
27.
JavaidMKashifARashidT. Hesitant fuzzy graphs and their products. Fuzzy Inf Eng (2020) 12(2):238–52. 10.1080/16168658.2020.1817658
28.
KaraaslanF. Hesitant fuzzy graphs and their applications in decision making. J Intell Fuzzy Syst (2019) 36(3):2729–41. 10.3233/jifs-18865
29.
Sriram KalyanSK. K-regular domination in hesitancy fuzzy graph. Int J Mod Agric (2021) 10(1):195–200.
30.
ShakthivelRVikramaprasadRVinoth KumarN. Inverse domination in hesitancy fuzzy graphs. Solid State Technol (2020) 63(2):795–803.
31.
ShakthivelRVikramaprasadRVinothkumarN. Domination in hesitancy fuzzy graph. Int J Adv Sci Technol (2019) 28(16):1142–56.
32.
BaiWDingJZhangC. Dual hesitant fuzzy graphs with applications to multi-attribute decision making. Int J Cogn Comput Eng (2020) 1:18–26. 10.1016/j.ijcce.2020.09.002
33.
GhoraiGPalM. Some isomorphic properties of m-polar fuzzy graphs with applications. SpringerPlus (2016) 5(1):2104–25. 10.1186/s40064-016-3783-z
34.
PandeySDRanadiveASSamantaS. Bipolar-valued hesitant fuzzy graph and its application, social network analysis and mining. Granular Comput (2022) 4(3):559–83.
35.
ShiXKosariSMehdipoorNTalebiAAMuhiuddinG. Novel concepts in vague graphs with application in hospital’s management system. J Maths (2022) 1. Article ID 9129386. 10.1155/2022/9129386
Summary
Keywords
fuzzy graph, vague graph, vague-valued hesitant fuzzy graph, cartesian product, strong product, isomorphism
Citation
Rao Y, Chen R, Kosari S, Talebi AA and Mojahedfar M (2022) A study on vague-valued hesitant fuzzy graph with application. Front. Phys. 10:1007019. doi: 10.3389/fphy.2022.1007019
Received
29 July 2022
Accepted
12 September 2022
Published
04 October 2022
Volume
10 - 2022
Edited by
Song Zheng, Zhejiang University of Finance and Economics, China
Reviewed by
G. Muhiuddin, University of Tabuk, Saudi Arabia
Ganesh Ghorai, Vidyasagar University, India
Updates
Copyright
© 2022 Rao, Chen, Kosari, Talebi and Mojahedfar.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Saeed Kosari, Saeedkosari38@gzhu.edu.cn
This article was submitted to Statistical and Computational Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.