- 1Nuclear and Data Theory Group, Nuclear and Chemical Science Division, Lawrence Livermore National Laboratory, Livermore, CA, United States
- 2Machine Intelligence Group, Center for Applied Scientific Computing, Lawrence Livermore National Laboratory, Livermore, CA, United States
- 3Sensing and Intelligent Systems Group, Global Security Computing Applications Division, Lawrence Livermore National Laboratory, Livermore, CA, United States
- 4Centre Borelli, ENS Paris-Saclay, Université Paris-Saclay, Cachan, France
- 5Physics Department, Faculty of Science, University of Zagreb, Zagreb, Croatia
- 6Applied Statistics Group, Lawrence Livermore National Laboratory, Livermore, CA, United States
- 7Center for Complex Biological Systems, University of California Irvine, Irvine, CA, United States
- 8Université Paris-Saclay, CEA, Laboratoire Matière en Conditions Extrêmes, Bruyères-le-Châtel, France
- 9CEA, DAM, DIF, Bruyères-le-Châtel, France
From the lightest Hydrogen isotopes up to the recently synthesized Oganesson (Z = 118), it is estimated that as many as about 8,000 atomic nuclei could exist in nature. Most of these nuclei are too short-lived to be occurring on Earth, but they play an essential role in astrophysical events such as supernova explosions or neutron star mergers that are presumed to be at the origin of most heavy elements in the Universe. Understanding the structure, reactions, and decays of nuclei across the entire chart of nuclides is an enormous challenge because of the experimental difficulties in measuring properties of interest in such fleeting objects and the theoretical and computational issues of simulating strongly-interacting quantum many-body systems. Nuclear density functional theory (DFT) is a fully microscopic theoretical framework which has the potential of providing such a quantitatively accurate description of nuclear properties for every nucleus in the chart of nuclides. Thanks to high-performance computing facilities, it has already been successfully applied to predict nuclear masses, global patterns of radioactive decay like β or γ decay, and several aspects of the nuclear fission process such as, e.g., spontaneous fission half-lives. Yet, predictive simulations of nuclear spectroscopy—the low-lying excited states and transitions between them—or of nuclear fission, or the quantification of theoretical uncertainties and their propagation to basic or applied nuclear science applications, would require several orders of magnitude more calculations than currently possible. However, most of this computational effort would be spent into generating a suitable basis of DFT wavefunctions. Such a task could potentially be considerably accelerated by borrowing tools from the field of machine learning and artificial intelligence. In this paper, we review different approaches to applying supervised and unsupervised learning techniques to nuclear DFT.
1 Introduction
Predicting all the properties of every atomic nucleus in the nuclear chart, from Hydrogen all the way to superheavy elements, remains a formidable challenge. Density functional theory (DFT) offers a compelling framework to do so, since the computational cost is, in principle, nearly independent of the mass of the system Eschrig [1]. Because of our incomplete knowledge of nuclear forces and of the fact that the nucleus is a self-bound system, the implementation of DFT in nuclei is slightly different from other systems such as atoms or molecules and is often referred to as the energy density functional (EDF) formalism Schunck [2].
Simple single-reference energy density functional (SR-EDF) calculations of atomic nuclei can often be done on a laptop. However, large-scale SR-EDF computations of nuclear properties or higher-fidelity simulations based on the multi-reference (MR-EDF) framework can quickly become very expensive computationally. Examples where such computational load is needed range from microscopic fission theory Schunck and Regnier [3]; Schunck and Robledo [4] to parameter calibration and uncertainty propagation Kejzlar et al. [5]; Schunck et al. [6] to calculations at the scale of the entire chart of nuclides Erler et al. [7]; Ney et al. [8] relevant, e.g., for astrophysical simulations Mumpower et al. [9]. Many of these applications would benefit from a reliable emulator of EDF models.
It may be useful to distinguish two classes of quantities that such emulators should reproduce. What we may call “integral” quantities are quantum-mechanical observables such as, e.g., the energy, radius, or spin of the nucleus, or more complex data such as decay or capture rates. By contrast, we call “differential” quantities the basic degrees of freedom of the theoretical model. In this article, we focus on the Hartree-Fock-Bogoliubov (HFB) theory, which is both the cornerstone of the SR-EDF approach and provides the most common basis of generator states employed in MR-EDF calculations. In the HFB theory, all the degrees of freedom are encapsulated into three equivalent quantities: the quasiparticle spinors, as defined either on some spatial grid or configuration space; the full non-local density matrix ρ(rστ, r′σ′τ′) and pairing tensor κ(rστ, r′σ′τ′), where r refers to spatial coordinates, σ = ±1/2 to the spin projection and τ = ±1/2 to the isopin projection Perlińska et al. [10]; the full non-local HFB mean-field and pairing potentials, often denoted by h (rστ, r′σ′τ′) and Δ(rστ, r′σ′τ′).
Obviously, integral quantities have the clearest physical meaning and can be compared to data immediately. For this reason, they have been the focus of most of the recent efforts in applying techniques of machine learning and artificial intelligence (ML/AI) to low-energy nuclear theory, with applications ranging from mass tables Utama et al. [11]; Utama and Piekarewicz [12,13]; Niu and Liang [14]; Neufcourt et al. [15]; Lovell et al. [16]; Scamps et al. [17]; Mumpower et al. [18], β-decay rates Niu et al. [19], or fission product yields Wang et al. [20]; Lovell et al. [21]. The main limitation of this approach is that it must be repeated for every observable of interest. In addition, incorporating correlations between such observables, for example the fact that β-decay rates are strongly dependent on Qβ-values which are themselves related to nuclear masses, is not easy. This is partly because the behavior of observables such as the total energy or the total spin is often driven by underlying shell effects that can lead to very rapid variations, e.g. at a single-particle crossing. Such effects could be very hard to incorporate accurately in a statistical model of integral quantities.
This problem can in principle be solved by emulating what we called earlier differential quantities. For example, single-particle crossings might be predicted reliably with a good statistical model for the single-particle spinors themselves. In addition, since differential quantities represent, by definition, all the degrees of freedom of the SR-EDF theory, any observable of interest can be computed from them, and the correlations between these observables would be automatically reproduced. In this sense, an emulator of differential quantities is truly an emulator for the entire SR-EDF approach and can be thought of as a variant of intrusive, model-driven, model order reduction techniques discussed in Melendez et al. [22]; Giuliani et al. [23]; Bonilla et al. [24]. In the much simpler case of the Bohr collective Hamiltonian, such a strategy gave promising results Lasseri et al. [25].
The goal of this paper is precisely to explore the feasibility of training statistical models to learn the degrees of freedom of the HFB theory. We have explored two approaches: a simple one based on independent, stationary Gaussian processes and a more advanced one relying on deep neural networks with autoencoders and convolutional layers.
In Section 2, we briefly summarize the nuclear EDF formalism with Skyrme functionals with a focus on the HFB theory preserving axial symmetry. Section 3 presents the results obtained with Gaussian processes. After recalling some general notions about Gaussian processes, we analyze the results of fitting HFB potential across a two-dimensional potential energy surface in 240Pu. Section 4 is devoted to autoencoders. We discuss choices made both for the network architecture and for the training data set. We quantify the performance of autoencoders in reproducing canonical wavefunctions across a potential energy surface in 98Zr and analyze the structure of the latent space.
2 Nuclear density functional theory
In very broad terms, the main assumption of density functional theory (DFT) for quantum many-body systems is that the energy of the system of interest can be expressed as a functional of the density of particles Parr and Yang [26]; Dreizler and Gross [27]; Eschrig [1]. Atomic nuclei are a somewhat special case of DFT, since the nuclear Hamiltonian is not known exactly and the nucleus is a self-bound system Engel [28]; Barnea [29]. As a result, the form of the energy density functional (EDF) is often driven by underlying models of nuclear forces, and the EDF is expressed as a function of non-local, symmetry-breaking, intrinsic densities Schunck [2]. In the single-reference EDF (SR-EDF) approach, the many-body nuclear state is approximated by a simple product state of independent particles or quasiparticles, possibly with some constraints reflecting the physics of the problem. We notate |Φ(q)⟩ such as state, with q representing a set of constraints. The multi-reference EDF (MR-EDF) approach builds a better approximation of the exact many-body state by mixing together SR-EDF states.
2.1 Energy functional
The two most basic densities needed to build accurate nuclear EDFs are the one-body density matrix ρ and the pairing tensor κ (and its complex conjugate κ*). The total energy of the nucleus is often written as
where Enuc [ρ] represents the particle-hole, or mean-field, contribution to the total energy from nuclear forces, ECou [ρ] the same contribution from the Coulomb force, and Epair [ρ, κ, κ*] the particle-particle contribution to the energy1. In this work, we model the nuclear part of the EDF with a Skyrme-like term
which includes the kinetic energy term and reads generically
In this expression, the index t refers to the isoscalar (t = 0) or isovector (t = 1) channel and the terms
where ρc = 0.16 fm−3 is the saturation density of nuclear matter.
2.2 Hartree-Fock-Bogoliubov theory
The actual densities in (3) are obtained by solving the Hartree-Fock-Bogoliubov (HFB) equation, which derives from applying a variational principle and imposing that the energy be minimal under variations of the densities Schunck [2]. The HFB equation is most commonly solved in the form of a non-linear eigenvalue problem. The eigenfunctions define the quasiparticle (q.p.) spinors. Without proton-neutron mixing, we can treat neutrons and protons separately. Therefore, for any one type of particles, the HFB equation giving the μth eigenstate reads in coordinate space Dobaczewski et al. [35].
where h (rσ, r′σ′) is the mean field,
For the case of Skyrme energy functionals and zero-range pairing functionals, both the mean field h and pairing field
Expression 5 is written in coordinate space. In configuration space, i.e., when the q.p. spinors are expanded on a suitable basis of the single-particle (s.p.) Hilbert space, the same equation becomes a non-linear eigenvalue problem that can be written as
where h,
which is unitary:
2.3 Mean-field and pairing potentials
The mean fields are obtained by functional differentiation of the scalar-isoscalar energy functional (1) with respect to all relevant isoscalar or isovector densities, ρ0, ρ1, τ0, etc. For the case of a standard Skyrme EDF when time-reversal symmetry is conserved, the corresponding mean-field potentials in the isoscalar-isovector representation become semi-local Dobaczewski and Dudek [37,45]; Stoitsov et al. [46]; Hellemans et al. [39].
where, as before, t = 0, 1 refers to the isoscalar or isovector channel and the various contributions are.
In these expressions, μ, ν label spatial coordinates and σ is the vector of Pauli matrices in the chosen coordinate system. For example, in Cartesian coordinates, μ, ν ≡ x, y, z and σ = (σx, σy, σz). The term
Note that the full proton potential should also contain the contribution from the Coulomb potential.
The pairing field is obtained by functional differentiation of the same energy functional (1), this time with respect to the pairing density. As a result, one can show that it is simply given by
2.4 Collective space
Nuclear fission or nuclear shape coexistence are two prominent examples of large-amplitude collective motion of nuclei Schunck and Regnier [3]; Heyde and Wood [47]. Such phenomena can be accurately described within nuclear DFT by introducing a small-dimensional collective manifold, e.g., associated with the nuclear shape, where we assume the nuclear dynamics is confined Nakatsukasa et al. [48]; Schunck [2]. The generator coordinate method (GCM) and its time-dependent extension (TDGCM) provide quantum-mechanical equations of motion for such collective dynamics Griffin and Wheeler [49]; Wa Wong [50]; Reinhard and Goeke [51]; Bender et al. [32]; Verriere and Regnier [52]. In the GCM, the HFB solutions are generator states, i.e., they serve as a basis in which the nuclear many-body state is expanded. The choice of the collective manifold, that is, of the collective variables, depends on the problem at hand. For shape coexistence or fission, these variables typically correspond to the expectation value of multipole moment operators on the HFB state. A pre-calculated set of HFB states with different values for the collective variables defines a potential energy surface (PES).
In practice, PES are obtained by adding constraints to the solutions of the HFB equation. This is achieved by introducing a set of constraining operators
As is well known, the Fermi energies play in fact the role of the Lagrange parameters λa for the constraints on particle number. When performing calculations with constraints on the octupole moment, it is also important to fix the position of the center of mass. This is typically done by adding a constraint on the dipole moment
Potential energy surfaces are a very important ingredient in a very popular approximation to the GCM called the Gaussian overlap approximation (GOA) Brink and Weiguny [53]; Onishi and Une [54]; Une et al. [55]. By assuming, among other things, that the overlap between two HFB states with different collective variables q and q′ is approximately Gaussian, the GOA allows turning the integro-differential Hill-Wheeler-Griffin equation of the GCM into a much more tractable Schrödinger-like equation. The time-dependent version of this equation reads as Verriere and Regnier [52].
where the probability to be at point q of the collective space at time t is given by |g (q, t)|2, V(q) is the actual PES, typically the HFB energy as a function of the collective variables q (sometimes supplemented by some zero-point energy correction) and Bαβ(q) the collective inertia tensor. In (13), indices α and β run from 1 to the number Ncol of collective variables. While the HFB energy often varies smoothly with respect to the collective variables, the collective inertia tensor can exhibit very rapid variations near level crossings.
2.5 Canonical basis
The Bloch-Messiah-Zumino theorem states that the Bogoliubov matrix
where D and C are unitary matrices. The matrices
Starting from an arbitrary s.p. basis
In addition to simplifying the calculation of many-body observables, the canonical basis is also computationally less expensive than the full Bogoliubov basis3. As an illustration, let us take the example of the local density ρ(r). Assuming the s.p. basis
Notwithstanding the constraints imposed by the orthonormality of the q.p. spinors, the number of independent parameters in this expression approximately scales like
The number of data points now scales like 2 × Nqp × Nr + Nqp, or about
2.6 Harmonic oscillator basis
All calculations in this article were performed with the HFBTHO code Marević et al. [58]. Recall that HFBTHO works by expanding the solutions on the axially-deformed harmonic oscillator basis Stoitsov et al. [46]. Specifically, the HO basis functions are written
where n ≡ (nr, nz, Λ, Ω = Λ ±Σ) are the quantum numbers labeling basis states and.
With
All integrations are performed by Gauss quadrature, namely Gauss-Hermite for integrations along the ξ-axis of the intrinsic reference frame and Gauss-Laguerre for integrations along the perpendicular direction characterized by the variable η. In the following, we note Nz the number of Gauss-Hermite nodes and N⊥ the number of Gauss-Laguerre nodes.
3 Supervised learning with Gaussian processes
Gaussian processes (GPs) are a simple yet versatile tool for regression that has found many applications in low-energy nuclear theory over the past few years, from determining the nuclear equation of state Drischler et al. [59], quantifying the error of nuclear cross sections calculations Kravvaris et al. [60]; Acharya and Bacca [61] to modeling of neutron stars Pastore et al. [62]. In the context of nuclear DFT, they were applied to build emulators of χ2 objective functions in the UNEDF project Kortelainen et al. [63–65]; Higdon et al. [66]; McDonnell et al. [67]; Schunck et al. [6], of nuclear mass models Neufcourt et al. [15,68–70], or of potential energy surfaces in actinides Schunck et al. [34]. In this section, we test the ability of GPs to learn directly the HFB potentials across a large, two-dimensional collective space.
3.1 Gaussian processes
Gaussian processes are commonly thought of as the generalization of normally-distributed random variables (Gaussian distribution) to functions. There exists a considerable field of applications for GPs and we refer to the reference textbook by Rasmussen and Williams for a comprehensive review of the formalism and applications of GPs Rasmussen and Williams [71]. For the purpose of this work, we are only interested in the ability of GPs to be used as a regression analysis tool and we very briefly outline below some of the basic assumptions and formulas.
We assume that we have a dataset of observations
where f: x↦f(x) is the unknown function we are seeking to learn from the data. Saying that a function f is a Gaussian process means that every finite collection of function values f = (f (x1), …, f (xp)) follows a p-dimensional multivariate normal distribution. In other words, we assume that the unknown function f follows a normal distribution in ‘function space’. This is denoted by
where m: x↦m(x) is the mean function and k: (x, x′)↦k (x, x′) the covariance function, which is nothing but the generalization to functions of the standard deviation,
Thanks to the properties of Gaussian functions, the mean and covariance functions have analytical expressions as a function of the test data y and covariance k; see Eqs (2.25)-(2.26) in Rasmussen and Williams [71].
The covariance function is the central object in GP regression. It is typically parametrized both with a functional form and with a set of free parameters called hyperparameters. The hyperparameters are determined from the observed data by maximizing the likelihood function. In our tests, the covariance matrix is described by a standard Matérn 5/2 kernel,
where ℓ is the length-scale that characterizes correlations between values of the data at different locations. The length-scale is a hyper-parameter that is optimized in the training phase of the Gaussian process. In this work, we only considered stationary GPs: the correlation between data points x and x′ only depends on the distance ‖x − x′‖ between these points, not on their actual value.
3.2 Study case
3.2.1 HFB potentials
Section 2.2 showed that the HFB mean-field potential involves several differential operators. When the HFB matrix is constructed by computing expectation values of the HFB potential on basis functions, differentiation is carried over to the basis functions and computed analytically—one of the many advantages of working with the HO basis. In practice, this means that the elements of the HFB matrix are computed by multiplying spatial kernels with different objects representing either the original HO functions or their derivatives. This means that we cannot consider a single emulator for the entire HFB potential. Instead, we have to build several different ones for each of its components: the central potential U (derivative of the EDF with respect to ρ), the r- and z-derivatives of the effective mass M* (derivative with respect to the kinetic density τ), the r- and z-derivatives of the spin-orbit potential W, and the pairing field
At any given point q of the collective space, these functions are all local, scalar functions of η and ξ, fi(q) ≡ fi: (η, ξ)↦fi (η, ξ; q) where (η, ξ) are the nodes of the Gauss-Laguerre and Gauss-Hermite quadrature grid. We note generically fik(q) the value at point k of the quadrature grid (linearized) of the sample at point q of the function fi. When fitting Gaussian process to reproduce mean-field and pairing potentials, we consider a quadrature grid of Nz × N⊥ = 3,200 points. Our goal is thus to build 3,200 different emulators, one for each point k of that grid, for each of the 12 local functions characterizing the mean-field and pairing potentials. This gives a grand total of 38,400 emulators to build. While this number is large, it is still easily manageable on standard computers. It is also several orders of magnitude smaller than emulating the full set of quasiparticle spinors, as we will see in the next section.
In addition, the value of all the Lagrange parameters used to set the constraints must also be included in the list of data points. In our case, we have 5 of them: the two Fermi energies λn and λp and the three constraints on the value of the dipole, quadrupole and octupole moments, λ1, λ2 and λ3, respectively. Finally, we also fit the expectation value of the three constraints on
3.2.2 Training data and fitting procedure
We show in Figure 1 the potential energy surface that we are trying to reconstruct. This PES is for the 240Pu nucleus and was generated with the SkM* parameterization of the Skyrme energy functional Bartel et al. [72]. The pairing channel is described with the zero-range, density-dependent pairing force of Eq. 4 that has exactly the same characteristics as in Schunck et al. [73].
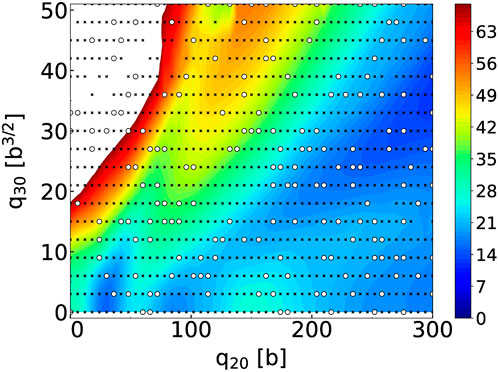
FIGURE 1. Potential energy surface of 240Pu with the SkM* EDF for the grid (q20, q30) ∈ [0 b, 300 b] × [0 b3/2, 51 b3/2] with steps δq20 = 6 b and δq30 = 3 b3/2. The black crosses are the training points, the white circles the validation points. Energies indicated by the color bar are in MeV relatively to −1820 MeV.
We imposed constraints on the axial quadrupole and octupole moments such that: 0 b ≤ q20 ≤ 300 b and 0 b3/2 ≤ q30 ≤ 51 b3/2 with steps of δq20 = 6 b and δq30 = 3 b3/2, respectively. The full PES should thus contain 918 collective points. In practice, we obtained Np = 887 fully converged solutions. Calculations were performed with the HFBTHO solver by expanding the solutions on the harmonic oscillator basis with Nmax = 28 deformed shells and a truncation in the number of states of Nbasis = 1,000. At each point of the PES, the frequency ω0 and deformation β2 of the HO basis are set according to the empirical formulas given in Schunck et al. [73]. Following standard practice, we divided the full Np = 887 dataset of points into a training (80% of the points) and validation (20% of the points) set. The selection was done randomly and resulted in Ntrain = 709 training points and Nvalid. = 178 validation points. The training points are marked as small black crosses in Figure 1 while the validation points are marked as larger white circles.
Based on the discussion in Section 3.2.1, we fit a Gaussian process to each of the 38,408 variables needed to characterize completely the HFB matrix. Since we work in a two-dimensional collective space, we have two features and the training data is represented by a two-dimensional array X of dimension (nsamples, nfeatures) with nsamples = Np and nfeatures = 2. The target values Y (= the value at point k on the quadrature grid of any of the functions fi) are contained in a one-dimensional array of size Np. Prior to the fit, the data is normalized between 0 and 1. The GP is based on a standard Matérn kernel with ν = 2.5 and length-scale ℓ. In practice, we use different length-scales for the q20 and q30 directions so that ℓ = ℓ is a vector. We initialized these values at the spacing of the grid ℓ = (δq20, δq30). We added a small amount of white noise to the Matérn kernel to account for the global noise level of the data.
3.2.3 Performance
Once the GP has been fitted on the training data, we can estimate its performance on the validation data. For each of the Nvalid. = 178 validation points, we used the GP-fitted HFB potentials to perform a single iteration of the HFB self-consistent loop and extract various observables from this single iteration. Figure 2 focuses on the total HFB energy and the zero-point energy correction ɛ0. Together, these two quantities define the collective potential energy in the collective Hamiltonian (13) of the GCM. The left panel of the figure shows the histogram of the error
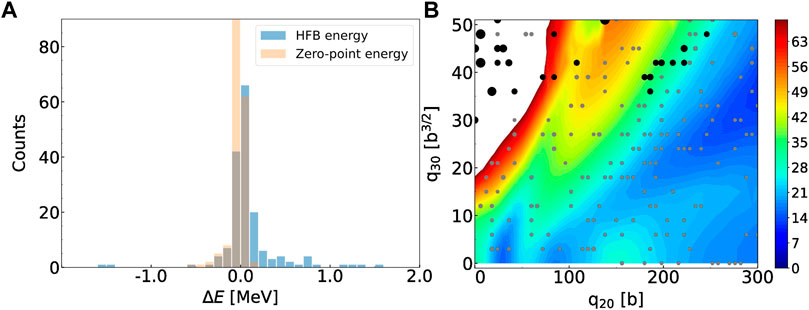
FIGURE 2. (A): Histogram of the error on the GP-predicted total HFB energy and zero-point energy correction across the validation points. Bin size is 100 keV. (B): Size of the error on the GP-predicted total HFB energy across the validation set. Gray circles have an error lower than 500 keV and the size of the markers correspond to energy bins of 100 keV. Black circles have an error greater than 500 keV and are binned by 400 keV units. Energies indicated by the color bar are in MeV relatively to −1820 MeV.
To gain additional insight, we draw in the right panel of Figure 2 each of the validation points with a marker, the size of which is proportional to the error of the prediction. To further distinguish between most points and the few outliers, we show in gray the points for which the absolute value of the error is less than 500 keV and in black the points for which it is greater than 500 keV. For the gray points, we use 5 different marker sizes corresponding to energy bins of 100 keV: the smaller grey symbol corresponds to an error smaller than 100 keV, the larger one between 400 and 500 keV. Similarly, the larger black circles have all an error greater than 500 keV and are ordered by bins of 400 keV (there are only two points for which the error is larger than 4 MeV). Interestingly, most of the larger errors are concentrated in the region of small elongation q20 < 80 b and high asymmetry q30 > 30 b3/2. This region of the collective space is very high in energy (more than 100 MeV above the ground state) and plays no role in the collective dynamics.
Note that the expectation values of the multipole moments themselves are not reproduced exactly by the GP: strictly speaking, the contour plot in the right panel of Figure 2 is drawn based on the requested values of the constraints, not their actual values as obtained by solving the HFB equation once with the reconstructed potentials. The histogram in the left panel of Figure 3 quantifies this discrepancy. It shows the absolute error
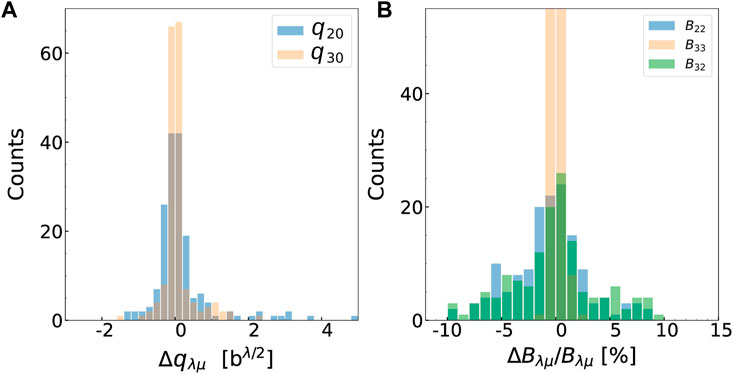
FIGURE 3. (A): Histogram of the error on the GP-predicted values of the multipole moments. The bin size is 0.2 bλ/2 with λ = 2 (quadrupole moment) or λ = 3 (octupole moment). (B): Histogram of the relative error, in percents, on the GP-predicted values of the components of the collective inertia tensor. The bin size is 1, corresponding to 1% relative errors.
The collective potential energy is only one of the two ingredients used to simulate fission dynamics. As mentioned in Section 2.4, see Eq. 13, the collective inertia tensor is another essential quantity Schunck and Robledo [4]; Schunck and Regnier [3]. In this work, we computed the collective inertia at the perturbative cranking approximation Schunck and Robledo [4]. Since we work in two-dimensional collective spaces, the collective inertia tensor
Both the total energy and the collective mass tensor are computed from the HFB solutions. However, since the GP fit is performed directly on the mean-field and pairing potentials, one can analyze the error on these quantities directly. In Figure 4, we consider two different configurations. The configuration
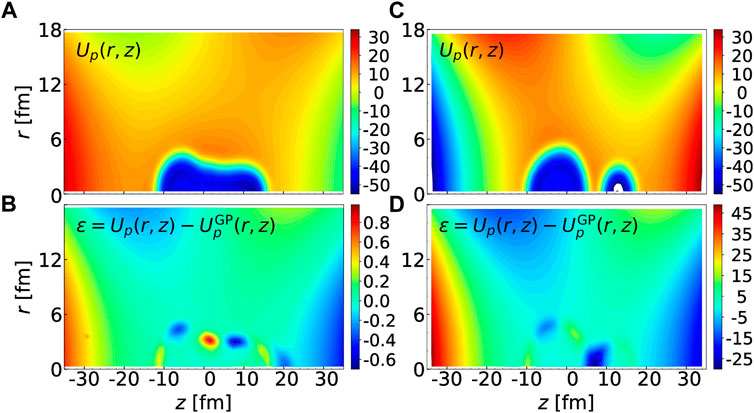
FIGURE 4. (A): Central part of the mean-field potential for protons, Up(r, z) for the configuration (q20, q30) = (198 b, 30 b3/2); (B): Error in the GP fit for that same configuration. (C): Central part of the mean-field potential for protons, Up(r, z) for the configuration (q20, q30) = (138 b, 51 b3/2); (D): Error in the GP fit for that same configuration. In all figures, the energy given by the error bar is in MeV. Note the much smaller energy scale for the bottom left panel.
We see that for the “good” configuration
Overall, Gaussian processes seem to provide an efficient way to predict HFB solutions across potential energy surfaces. Their primary advantage is that they are very simple to implement, with several popular programming environments offering ready-to-use, full GP packages, and very fast to train (a few minutes at most for a few hundreds of samples). As our examples suggest, GPs are very good at interpolating across a domain where solutions behave smoothly. In the case of PES, this implies that the training data must not contain, e.g., scissioned and non-scissioned configurations. More generally, it should not feature too many discontinuities Dubray and Regnier [75]. When these conditions are met, GPs can be used to quickly and precisely densify a PES, e.g., to obtain more precise fission paths in spontaneous fission half-live calculations Sadhukhan [76].
However, Gaussian processes are intrinsically limited. In our example, we treated the value of each potential at each point of the quadrature mesh as an independent GP. Yet, such data are in reality heavily correlated. To incorporate such correlations requires generalizing from scalar GPs to vector, or multi-output GPs Bruinsma et al. [77]. In our example of nuclear potentials, the output space would be
4 Deep learning with autoencoders
Even though self-consistent potential energy surfaces are key ingredients in the microscopic theory of nuclear fission Bender et al. [79], we must overcome two significant obstacles to generate reliable and complete PES. First, the computational cost of nuclear DFT limits the actual number of single-particle d.o.f. When solving the HFB equation with basis-expansion methods, for example, the basis must be truncated (up to a maximum of about a few thousand states, typically), making the results strongly basis-dependent Schunck [80]; even in mesh-based methods, the size of the box and lattice spacing also induce truncation effects Ryssens et al. [81]; Jin et al. [82]. Most importantly, the number of collective variables that can be included in the PES is also limited: in spontaneous fission calculations, which do not require a description of the PES up to scission, up to Ncol = 5 collective variables have been incorporated Sadhukhan [76]; when simulating the PES up to scission, only 2 collective variables are included with only rare attempts to go beyondRegnier et al. [83]; Zhao et al. [84]. As a consequence, the combination of heavily-truncated collective spaces and the adiabatic hypothesis inherent to such approaches leads to missing regions in the PES and spurious connections between distinct channels with unknown effects on physics predictions Dubray and Regnier [75]; Lau et al. [85]. The field of deep learning may offer an appealing solution to this problem by allowing the construction of low-dimensional and continuous surrogate representations of potential energy surfaces. In the following, we test the ability of autoencoders—a particular class of deep neural networks—to generate accurate low-dimensional representations of HFB solutions.
4.1 Network architecture
The term ‘deep learning’ encompasses many different types of mathematical and computational techniques that are almost always tailored to specific applications. In this section, we discuss some of the specific features of the data we seek to encode in a low-dimensional representation, which in turn help constrain the network architecture. The definition of a proper loss function adapted to quantum-mechanical datasets is especially important.
4.1.1 Canonical states
We aim at building a surrogate model for determining canonical wavefunctions as a function of a set of continuous constraints. Canonical states are denoted generically
In this work, we restrict ourselves to axially-symmetric configurations. In that case, the canonical wavefunctions are eigenstates of the projection of the total angular momentum on the symmetry axis
where
As shown by Eqs 8, Eqs 9a–9c, all mean-field and pairing potentials are functions of the Skyrme densities. The kinetic energy density τ(r, z), spin-current tensor
using Gauss-Laguerre and Gauss-Hermite quadrature. Since all the derivatives of the HO functions can be computed analytically, the expansion (25) makes it very easy to compute partial derivatives with respect to r or z, for example,
4.1.2 Structure of the predicted quantity
In the ideal case, the canonical wavefunctions evolve smoothly with the collective variables. The resulting continuity of the many-body state with respect to collective variables is a prerequisite for a rigorous description of the time evolution of fissioning systems, yet it is rarely satisfied in practical calculations. We discuss below the three possible sources of discontinuity of the canonical wavefunctions in potential energy surfaces.
First, the canonical wavefunctions are invariant through a global phase. Since the quantity we want to predict is real, the orbitals can be independently multiplied by an arbitrary sign. Even though this type of discontinuity does not impact the evolution of global observables as a function of deformation, it affects the learning of the model: since we want to obtain continuous functions, a flipping of the sign would be seen by the neural network as a discontinuity in the input data. We address this point through the choice of the loss, as discussed in Section 4.1.3, and through the determination of the training set, as detailed in Section 4.2.
Second, we work within the adiabatic approximation, which consists in building PES by selecting the q.p. vacuum that minimizes the energy at each point. When the number Ncol of collective variables of the PES is small, this approximation may lead to discontinuities Dubray and Regnier [75]. These discontinuities correspond to missing regions of the collective space and are related to the inadequate choice of collective variables. Since we want to obtain a continuous description of the fission path, we must give our neural network the ability to choose the relevant degrees of freedom. This could be achieved with autoencoders. Autoencoders are a type of neural networks analogous to the zip/unzip programs. They are widely used and greatly successful for representation learning—the field of Machine Learning that attempts to find a more meaningful representation of complex data Baldi [86]; Burda et al. [87]; Chen et al. [88]; Gong et al. [89]; Bengio et al. [90]; Zhang et al. [91]; Yu et al. [92] and can be viewed as a non-linear generalization of principal component analysis (PCA). As illustrated in Figure 5, an autoencoder Ξ typically consists of two components. The encoder E (T(φ)) encodes complex and/or high-dimensional data T(φ) to a typically lower-dimensional representation v(φ). The latent space is the set of all possible such representations. The decoder D (v(φ)) takes the low-dimensional representation of the encoder and uncompresses it into a tensor T(ϕ) as close as possible to T(φ). Such architectures are trained using a loss function that quantifies the discrepancy between the initial input and the reconstructed output,
where d (., .) defines the metric in the space of input data. We discuss the choice of a proper loss in more details in Section 4.1.3.
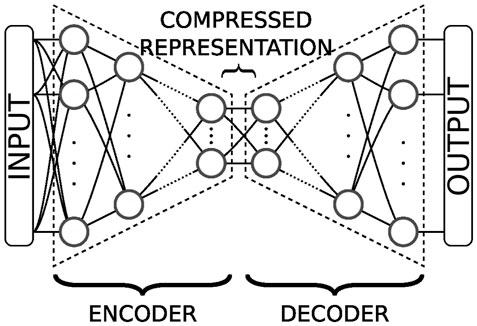
FIGURE 5. An autoencoder is the association of two blocks. The first one, on the left, compresses the input data into a lower-dimensional representation, or code, in the latent space. The second one, on the right, decompresses the code back into the original input.
Third, the evolution of the q.p. wavefunctions as a function of the collective variables q may lead to specific values qi where the q.p. solutions are degenerate. These degeneracies form a sub-manifold of dimension at most D − 2, where D is the number of collective d.o.f.s. As a consequence, they cannot appear in one-dimensional PES: q.p. solutions with the same symmetry “cannot cross” (the famous no-crossing rule von Neuman and Wigner [93]). In multi-dimensional spaces, this rule does not hold anymore: when following a closed-loop trajectory around such a degeneracy, the sign of the q.p. wavefunctions is flipped, in a similar manner that we flip side when winding around a Moebius strip Teller [94]; Longuet-Higgins et al. [95]; Longuet-Higgins [96]. In the field of quantum chemistry, such degeneracies are referred to as diabolical points or conical intersections Domcke et al. [97]; Larson et al. [98]. The practical consequence of conical intersections for deep learning is that the manifold of all the q.p. wavefunctions cannot be embedded in a D-dimensional latent space. Such singularities can be treated in two ways: (i) by using a latent space of higher dimension than needed or (ii) by implementing specific neural network layers capable of handling such cases. For now, we do not consider these situations.
4.1.3 Loss functions and metrics
As already discussed in Section 4.1.2, autoencoders are trained through the minimization of a loss function that contains a reconstruction term of the form (27). As suggested by its name, this term ensures that the autoencoder can correctly reconstruct the input tensor T(φ) from its compressed representation. It depends on a definition for the metric d (., .) used to compare the different elements of the input space. Since our canonical wavefunctions φμ are expanded on the axial harmonic oscillator basis of Section 2.6, they are discretized on the Gauss quadrature mesh without any loss of information. Therefore, both the input and output tensors of our surrogate model are a rank-3 tensor T(ϕ) ≡ T(φ) ≡ Tijk of dimensions N⊥× Nz × 2, where i is the index of the Gauss-Laguerre node along the r-axis, j the index of the Gauss-Hermite node along the z-axis, and k the index of the spin component.
A standard loss used with autoencoders is the mean-square-error (MSE). Because of the structure of our input data, see Section 4.1.1, the MSE loss reads in our case
The MSE is very general and can be thought of, quite simply, as the mean squared “distance” between the initial and reconstructed data. However, this generality implies that it does not contain any information about the properties of the data one tries to reconstruct.
Indeed, we can define a metric that is better suited to the physics we aim to describe. Let us recall that our goal is to compute potential energy surfaces that can be used, e.g., for fission simulations. These PES are nothing but generator states for the (TD)GCM mentioned in Section 2.4. The GCM relies on the norm kernel
Since the norm kernel involves the standard inner product in the many-body space, it represents the topology of that space. Therefore, it should be advantageous to use for the loss a metric induced by the same inner product that defines the norm kernel.
In our case, we want to build an AE where the encoder v(φ) = E (T(φ)) compresses the single-particle, canonical orbitals
and with the occupation amplitudes. However, it assumes that the canonical wavefunctions of each many-body state are orthogonal. This property is not guaranteed for our reconstructed canonical wavefunctions. In fact, because of this lack of orthogonality, the reconstructed wavefunctions cannot be interpreted as representing the canonical basis of the Bloch-Messiah-Zumino decomposition of the quasiparticle vacuum and the Haider and Gogny formula cannot be applied ‘as is’. However, we show in Supplementary Appendix S1 that it is possible to find a set of transformations of the reconstructed wavefunctions that allows us to define such as genuine canonical basis.
We want the loss function to depend only on the error associated with the reconstructed orbital ϕμ. Therefore, we should in principle consider the many-body state
However, computing this metric is too computationally involved to be carried out explicitly for each training data at each epoch. Instead, we keep this metric for comparing a posteriori the performance of our model.
Instead of explicitly determining
which is nothing but
where the φ(r, σ) and ϕ(r, σ) have been normalized. Since all wavefunctions are discretized on the Gauss quadrature mesh, this distance reads
where the weights W are given by
These weights, which depend on the indices n⊥ and nz in the summation, are the only difference between the squared distance loss (Eq. 35) and the MSE loss (Eq. 28). Although the distance (Eq. 35) is norm-invariant6, it still depends on the global phase of each orbital. We have explored other possible options for the loss based on norm- and phase-invariant distances; see Supplementary Appendix S2 for a list. However, we found in our tests that the distance
4.1.4 Physics-informed autoencoder
From a mathematical point of view, deep neural networks can be thought of as a series of compositions of functions. Each composition operation defines a new layer in the network. Networks are most often built with alternating linear and nonlinear layers. The linear part is a simple matrix multiplication. Typical examples of nonlinear layers include sigmoid, tanh, Rectified Linear Unit (ReLU) functions. In addition to these linear and nonlinear layers, there could be miscellaneous manipulations of the model for more specific purposes, such as adding batch normalization layers Ioffe and Szegedy [100], applying dropout Srivastava et al. [101] to some linear layers, or skip connection He et al. [102] between layers.
Our data is a smooth function defined over a N⊥× Nz = 60 × 40 grid and is analogous to a small picture. For this reason, we chose a 2D convolutional network architecture. Convolutional layers are popular for image analysis, because they incorporate the two-dimensional pixel arrangement in the construction of the weights of the network. These two-dimensional weights, or filters, capture local shapes and can model the dependent structure in nearby pixels of image data. Given a 2D m × m input array, a 2D filter F is a n × n matrix, usually with n ≪ m. If we note In the space of n × n integer-valued matrices, then the convolutional layer
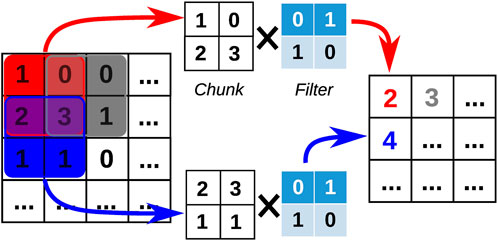
FIGURE 6. Schematic example of a convolutional layer. For any 2 × 2 chunk C of the input image on the left, this convolutional layer performs the point-wise multiplication of C with the filter F followed by the addition of all elements. This compresses the initial chunk of the image into a single integer.
In this work, we used the Resnet 18 model as our encoder and constructed the decoder from a transposed convolution architecture of the Resnet 18. The Resnet 18 model was first introduced by He et al. as a convolutional neural network for image analysis He et al. [102]. It was proposed as a solution to the degradation of performance as the network depth increases. Resnet branches an identity-function addition layer to sub-blocks (some sequential layers of composition) of a given network. While a typical neural network sub-block input and output could be represented by x and f(x), respectively, a Resnet sub-block would output f(x) + x for the same input x, as in Figure 2 of He et al. [102]. This architecture is called ‘skip connection’ and was shown to be helpful for tackling multiple challenges in training deep neural network such as vanishing gradient problem and complex loss function Li et al. [107]; He et al. [102]. Since then, the Resnet architecture has been widely successful, often being used as a baseline for exploring new architectures Zhang et al. [108]; Radosavovic et al. [109] or as the central model for many analyses Cubuk et al. [110]; Yun et al. [111]; Zhang et al. [112]. In a few cases, it was also combined with autoencoders for feature learning from high-dimensional data Wickramasinghe et al. [113].
For the decoder part, we designed a near-mirror image of the encoder using transposed convolution. Transposed convolution is essentially the opposite operation to convolution in terms of input and output dimensions. Here the meaning of transpose refers to the form of the filter matrix when the convolution layer is represented by a 1D vector input obtained from linearizing the 2D input. Note that the mirror-located filters in the decoder are independent parameters and not the actual transposed filter matrix of the encoder. Such a construction ensures symmetrical encoder and decoder models, making the decoder model close to the inverse shape of the encoder model. Figure 7 illustrates the operation: one input value is multiplied by the entire kernel (filter) and is added to the output matrix at its corresponding location. The corresponding output location for each colored input number are color-coded and show how the addition is done.
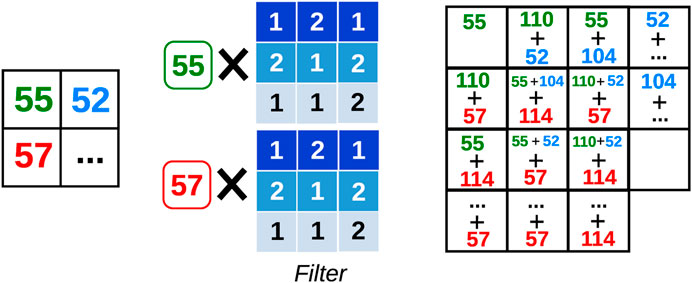
FIGURE 7. Schematic illustration of the 2D-transposed convolution. Each input value, e.g., 55, 57, etc., is multiplied by the entire kernel resulting in a 3 × 3 matrix. These matrices are then added to one another in a sliding and overlapping way.
The first and the last layer of the Resnet architecture are mostly for resizing and were minimally modified from the original Resnet 18 model since the size of our input data is significantly smaller than typical image sizes used for Resnet image classification analyses. We also modified the number of input channels of the first layer of the encoder to be 2 (for each of the spin components of the nuclear wavefunction) instead of the usual number 3 (for the RGB colors of colored images) or 1 (for black-and-white images). The spin components are closely related to each other with covariance structure, similar to how colors interact within an image. Therefore, we treat a pair of spin components as a single sample and treat each component as an input channel. The same applies to the output channel of the decoder.
The full network is represented schematically in Figure 8. Parametric Rectified Linear Unit, or PRELU, layers were added to impose nonlinearity in the model He et al. [114]. PRELU layers are controlled by a single hyperparameter that is trained with the data. Batch normalization is a standardizing layer that is applied to each batch by computing its mean and standard deviation. It is known to accelerate training by helping with optimization steps Ioffe and Szegedy [100]. The average pooling layer (bottom left) averages each local batch of the input and produces a downsized output. The upsampling layer (top right) upsamples the input using a bilinear interpolation.

FIGURE 8. Representation of our modified Resnet 18 architecture for the encoder (A) and the decoder (B). Large numbers on the left of each side label the different layers. Numbers such as 64, 128, etc. refer to the size of the filer; see text for a discussion of some of the main layers.
4.2 Training
As mentioned in Section 4.1.4, the loss is the discrepancy between the input of the encoder and the output of the decoder. The minimization of the loss with respect to all the model parameters w, such as the filter parameters, is the training process. We used the standard back-propagation algorithm to efficiently compute the gradient of the loss function with respect to the model parameters. The gradient computation is done with the chain rule, iterating from the last layer in the backward direction. We combined this with the mini-batch gradient descent algorithm: ideally, one would need the entire dataset to estimate the gradient at the current model parameter value. However, with large datasets, this becomes computationally inefficient. Instead we use a random subset of the entire data, called mini-batch, to approximate the gradient, and expedite the convergence of the optimization. For each mini-batch, we update each parameter w by taking small steps of gradient descent,
Iterating over the entire dataset once, using multiple mini-batches, is called an epoch. Typically a deep neural network needs hundreds to thousands of epochs for the algorithm to converge. Parameters such as the batch size or learning rate, the parameters of the optimizer itself (Adam’s or other), and the number of epochs are hyper-parameters that must be tuned for model fitting. For our training, we used the default initialization method in PyTorch for the model parameters. The linear layers were initialized with a random uniform distribution over [ − 1/k, 1/k], where k is the size of the weight. For example, if there are 2 input channels and 3 × 3 convolution filters are used, k = 2 × 3 × 3. PRELU layers were initialized with their default PyTorch value of 0.25. We proceeded with mini-batches of size 32 with the default β1 = 0.9, β2 = 0.999 and ϵ = 10–8: all these numbers refer to the PyTorch implementation of the Adam’s optimizer. For α, we used 0.001 as starting value and used a learning rate scheduler, which reduces the α value by a factor of 0.5 when there is no improvement in the loss for 15 epochs. After careful observation of the loss curves, we have estimated that at least 1,000 epochs are needed to achieve convergence.
To mitigate the problem of the global phase invariance of the canonical wavefunctions discussed in Section 4.1.2, we doubled the size of the dataset: at each point q of the collective space (=the sample), we added to each canonical wavefunction φμ(r, σ) the same function with the opposite sign − φμ(r, σ). The resulting dataset was then first split into three components, training, validation and test datasets, which represent 70%, 15%, and 15% of the entire data respectively. Training data is used for minimizing the loss with respect to the model parameters as explained above. Then we choose the model at the epoch that performs the best with the validation dataset as our final model. Finally, the model performance is evaluated using the test data.
4.3 Results
In this section, we summarize some of the preliminary results we have obtained after training several variants of the AE. In Section 4.3.1, we give some details about the training data and the quality of the reconstructed wavefunctions. We discuss some possible tools to analyze the structure of the latent space in Section 4.3.2. In these two sections, we only present results obtained for latent spaces of dimension D = 20. In Section 4.3.3, we use the reconstructed wavefunctions to recalculate HFB observables with the code HFBTHO. We show the results of this physics validation for both D = 20 and D = 10.
4.3.1 Performance of the network
Figure 9 shows the initial potential energy surface in 98Zr used in this work. Calculations were performed for the SkM* parametrization of the Skyrme potential with a surface-volume, density-dependent pairing force with
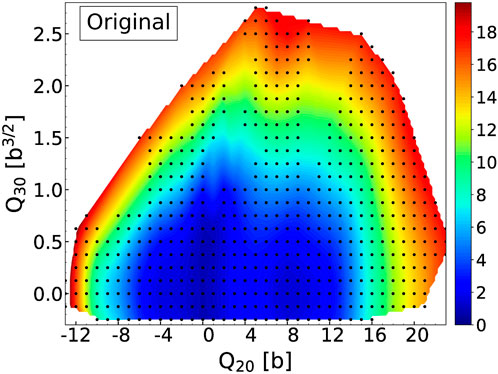
FIGURE 9. Potential energy surface of 98Zr in the (q20, q30) plane. Converged HFBTHO solutions are represented by black dots. Energies given by the color bar are in MeV relatively to the ground state.
For each of the losses discussed in Supplementary Appendix S2, we trained the AE with the slightly modified Resnet 18 architecture described in Section 4.1.4. It is important to keep in mind that the value of these losses should not be compared with one another. The only rigorous method to compare the performance of both networks would be to compute the many-body norm overlap across all the points in each case—or to perform a posteriori physics validation with the reconstructed data, as will be shown in Section 4.3.3.
To give an idea of the quality of the AE, we show in Figure 10 one example of the original and reconstructed canonical wavefunctions. Specifically, we consider the configuration (q20, q30) = ( − 7.0 b, − 0.25 b3/2) in the collective space and look at the neutron wavefunction with occupation number
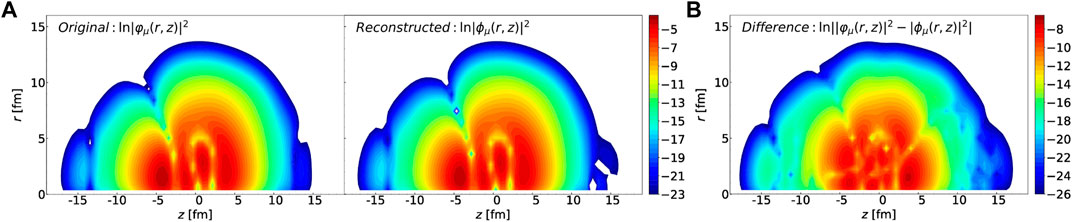
FIGURE 10. (A): Contour plot of the logarithm of the squared norm of the neutron canonical wavefunction with occupation number
4.3.2 Structure of the latent space
One of the advantages of AEs is the existence of a low-dimensional representation of the data. In principle, any visible structure in this latent space would be the signal that the network has properly learned, or encoded, some dominant features of the dataset. Here, our latent space has dimension D = 20. This means that every canonical wavefunction, which is originally a matrix of size n = N⊥× Nz, is encoded into a single vector of size D. From a mathematical point of view, the encoder is thus a function
Let us consider some (scalar) quantity P associated with the many-body state |Φ(q)⟩ at point q. Such a quantity could be an actual observable such as the total energy but it could also be an auxiliary object such as the expectation value of the multipole moment operators. In fact, P could also be a quantity associated with the individual degrees of freedom at point q, for example the q.p. energies. In general terms, we can think of P as the output value of the function
For example, if P represents the s.p. canonical energies, then the function
and it is straightforward to see that:
Since we have a total of nt = 147 wavefunctions for each of the Np = 552 points in the collective space, the encoder yields a set of nt × Np vectors of dimension D. This means that, in the latent space, every quantity P above is also represented by a cloud of nt × Np such vectors. This is obviously impossible to visualize. For this reason, we introduce the following analysis. First, we perform a linear regression in the D-dimensional latent space of a few select quantities of interest P, that is, we write
where α is a D-dimensional vector, v is the vector associated with the quantity P in the latent space and
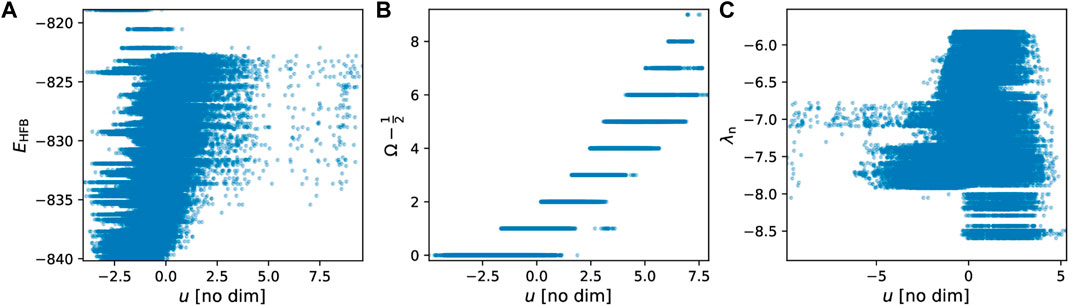
FIGURE 11. One-dimensional projections of the D-dimensional linear fit for the total energy EHFB (A), the projection Ω of the canonical state (B) and the neutron Fermi energy λn (C). Each point represents one of these quantities for a canonical wavefunction μ and a point q in the collective space.
The three cases shown in Figure 11 illustrate that the network has not always identified relevant features. The case of Ω, middle panel, is the cleanest: there is a clear slope as a function of u: if one sets u = 1, for example, then only values of 7/2 ≤ Ω ≤ 15/2 are possible. Conversely, the AE has not really discovered any feature in the neutron Fermi energy (right panel): for any given value of u, there is a large range of possible values of Fermi energies. In the case of the total energy (left panel), the situation is somewhat intermediate: there is a faint slope suggesting a linear dependency of the energy as a function of u.
4.3.3 Physics validation
The results presented in the Section 4.3.1 suggest the AE has the ability to reproduce the canonical wavefunctions with good precision. To test this hypothesis, we recalculated the HFB solution at all the training, validation and testing points by substituting in the HFBTHO binary files the original canonical wavefunctions by the ones reconstructed by the AE. Recall that only the lowest nt wavefunctions with the largest occupation were encoded in the AE (nn = 87 for neutrons and np = 60 for protons); the remaining ones were unchanged. In practice, their occupation is so small that their contribution to nuclear observables is very small (
Figure 12 shows the error on the potential energy across the (q20, q30) collective space obtained with the reconstructed canonical wavefunctions for latent spaces of dimension D = 20 (left) and D = 10 (right). In each case, we only show results obtained when using the
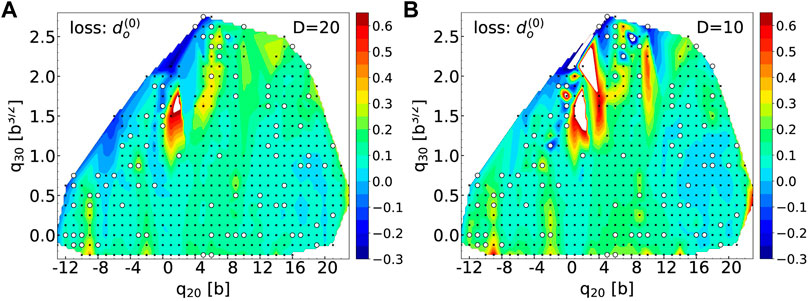
FIGURE 12. (A): Potential energy surface in the (q20, q30) plane for 98Zr obtained after replacing the first nn = 87 and np = 60 highest-occupation canonical wavefunctions by their values reconstructed by the AE for a latent space of dimension D = 20. The black dots show the location of the training points only, the white circles the location of the validation points. (B): same figure for a latent space of dimension D = 10. For both figures, energies are given in MeV.
The two histograms in Figure 13 give another measure of the quality of the AE. The histogram in the left shows the distribution of the error on the HFB energy for two sizes of the latent space, D = 20 and D = 10. For the D = 20 case, the mean error is
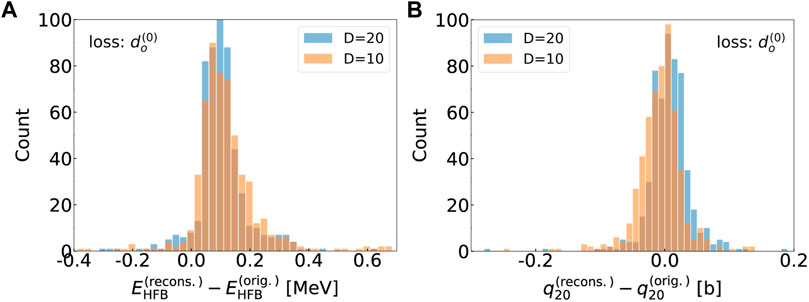
FIGURE 13. (A): Histogram of the difference in total HFB energy between the original HFBTHO calculation and the result obtained by computing the energy in the canonical basis with the reconstructed wavefunctions (see text for details). Calculations were performed both for a D = 20 and D = 10 latent space. (B): Similar histogram for the expectation value of the axial quadrupole moment.
The histogram on the right shows the distribution of the error for q20, in units of b. Here, the mean and standard deviation of the error are:
5 Conclusion
Nuclear density functional methods are amenable to large-scale calculations of nuclear properties across the entire chart of isotopes relevant for, e.g., nuclear astrophysics simulations or uncertainty quantification. However, such calculations remain computationally expensive and fraught with formal and practical issues associated with self-consistency or reduced collective spaces. In this article, we have analyzed two different techniques to build fast, efficient and accurate surrogate models, or emulators, or DFT objects.
We first showed that Gaussian processes could reproduce reasonably well the values of the mean-field and pairing-field potentials of the HFB theory across a large two-dimensional potential energy surface. The absolute error on the total energy was within ±100 keV and the relative errors on the collective inertia tensor smaller than 5%. However, GPs require the training data to be “smoothly-varying”, i.e., they should not include phenomena such as nuclear scission or, more generally, discontinuities in the PES. It is well known that GPs are not reliable for extrapolation: such a technique can thus be very practical to densify (=interpolate) an existing potential energy surface but must not be applied outside its training range.
Our implementation of standard versions of GPs is fast and simple to use, but it misses many of the correlations that exist between the values of the HFB potentials on the quadrature grid: (i) all components of the full Skyrme mean field (central, spin-orbit, etc.) are in principle related to one another through their common origin in the non-local one-body density matrix; (ii) the correlations between the value of any given potential at point (r, z) and at point (r′, z′) were not taken into account; (iii) the correlations between the variations of the mean fields at different deformations was also neglected. Incorporating all these effects may considerably increase the complexity of the emulator. In such a case, it is more natural to directly use deep-learning techniques. In this work, we reported the first application of autoencoders to emulate the canonical wavefunctions of the HFB theory. Autoencoders are a form of deep neural network that compresses the input data, here the canonical wavefunctions, into a small-dimensional space called the latent representation. The encoder is trained simultaneously with a decoder by enforcing that the training data is left invariant after compression followed by decompression. In practice, the measure of such “invariance” is set by what is called the loss of the network. We discussed possible forms of the loss that are best adapted to learning quantum-mechanical wavefunctions of many-body systems such as nuclei. We showed that such an AE could successfully reduce the data into a space of dimension D = 10 while keeping the total error on the energy lower than ΔE = 150 keV (on average). The analysis of the latent space revealed well-identified structures in a few cases, which suggests the network can learn some of the physics underlying the data. This exploratory study suggests that AE could serve as reliable canonical wavefunctions generators. The next step will involve learning a full sequence of such wavefunctions, i.e., an ordered list, in order to emulate the full HFB many-body state.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
MV led the study of autoencoders for canonical wavefunctions: design of the overall architecture of the autoencoders, development of the software stack and analysis of the results. NS led the study of Gaussian process for mean-field potentials—training and validation runs, code development and HFBTHO calculations—and supervised the whole project. IK implemented, tested and trained different architectures of autoencoders and helped with the analysis of the results. PM developed an HFBTHO module to use canonical wavefunctions in HFB calculations. KQ provided technical expertise about Gaussian processes and supervised MN, who implemented and fitted Gaussian processes to mean-field potentials. DR and RL provided technical consulting on deep neural network and the architecture of autoencoders. All authors contributed to the writing of the manuscript, and read and approved the submitted version.
Funding
This work was performed under the auspices of the United States Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. Computing support came from the Lawrence Livermore National Laboratory (LLNL) Institutional Computing Grand Challenge program.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1028370/full#supplementary-material
Footnotes
1The pairing contribution lumps together terms coming from nuclear forces, Coulomb forces and possibly rearrangement terms.
2Following Dobaczewski et al. [35,117], we employ the ‘russian’ convention where the pairing field is defined from the pairing density
3This statement is obviously not true when solving the HFB equation directly in coordinate space. In the case of the local density discussed here, the expression
4Note that B32 vanishes for axially-symmetric shapes. As a result, the relative error can be artificially large for values of q30 ≈ 0 b3/2.
5This particular scission configuration corresponds to what is called cluster radioactivity Warda and Robledo [118]; Warda et al. [119]; Matheson et al. [120]. The heavy fragment is much larger than the light one. Here, ⟨AH⟩ = 205.6, ⟨AL⟩ = 34.4.
6A distance d(u, v) is norm-invariant if for any positive real number α and β, we have d(αu, βv) = d(u, v).
7Since time-reversal symmetry is conserved, the Fermi energy is located around states with indices μp ≈ 20 and μn ≈ 29. Therefore, our choice implies that in our energy window, about 1/3 of all states are below the Fermi level and about 2/3 of them are above it.
References
2. Schunck N. IOP expanding physics. Bristol, UK: IOP Publishing (2019).Energy density functional methods for atomic nuclei.
3. Schunck N, Regnier D. Theory of nuclear fission. Prog Part Nucl Phys (2022) 125:103963. doi:10.1016/j.ppnp.2022.103963
4. Schunck N, Robledo LM. Microscopic theory of nuclear fission: A review. Rep Prog Phys (2016) 79:116301. doi:10.1088/0034-4885/79/11/116301
5. Kejzlar V, Neufcourt L, Nazarewicz W, Reinhard PG. Statistical aspects of nuclear mass models. J Phys G: Nucl Part Phys (2020) 47:094001. doi:10.1088/1361-6471/ab907c
6. Schunck N, O’Neal J, Grosskopf M, Lawrence E, Wild SM. Calibration of energy density functionals with deformed nuclei. J Phys G: Nucl Part Phys (2020) 47:074001. doi:10.1088/1361-6471/ab8745
7. Erler J, Birge N, Kortelainen M, Nazarewicz W, Olsen E, Perhac AM, et al. The limits of the nuclear landscape. Nature (2012) 486:509–12. doi:10.1038/nature11188
8. Ney EM, Engel J, Li T, Schunck N. Global description of β− decay with the axially deformed Skyrme finite-amplitude method: Extension to odd-mass and odd-odd nuclei. Phys Rev C (2020) 102:034326. doi:10.1103/PhysRevC.102.034326
9. Mumpower MR, Surman R, McLaughlin GC, Aprahamian A. The impact of individual nuclear properties onr-process nucleosynthesis. Prog Part Nucl Phys (2016) 86:86–126. doi:10.1016/j.ppnp.2015.09.001
10. Perlińska E, Rohoziński SG, Dobaczewski J, Nazarewicz W. Local density approximation for proton-neutron pairing correlations: Formalism. Phys Rev C (2004) 69:014316. doi:10.1103/PhysRevC.69.014316
11. Utama R, Piekarewicz J, Prosper HB. Nuclear mass predictions for the crustal composition of neutron stars: A bayesian neural network approach. Phys Rev C (2016) 93:014311. doi:10.1103/PhysRevC.93.014311
12. Utama R, Piekarewicz J. Refining mass formulas for astrophysical applications: A bayesian neural network approach. Phys Rev C (2017) 96:044308. doi:10.1103/PhysRevC.96.044308
13. Utama R, Piekarewicz J. Validating neural-network refinements of nuclear mass models. Phys Rev C (2018) 97:014306. doi:10.1103/PhysRevC.97.014306
14. Niu ZM, Liang HZ. Nuclear mass predictions based on Bayesian neural network approach with pairing and shell effects. Phys Lett B (2018) 778:48–53. doi:10.1016/j.physletb.2018.01.002
15. Neufcourt L, Cao Y, Nazarewicz W, Olsen E, Viens F. Neutron drip line in the Ca region from bayesian model averaging. Phys Rev Lett (2019) 122:062502. doi:10.1103/PhysRevLett.122.062502
16. Lovell AE, Mohan AT, Sprouse TM, Mumpower MR. Nuclear masses learned from a probabilistic neural network. Phys Rev C (2022) 106:014305. doi:10.1103/PhysRevC.106.014305
17. Scamps G, Goriely S, Olsen E, Bender M, Ryssens W. Skyrme-Hartree-Fock-Bogoliubov mass models on a 3D mesh: Effect of triaxial shape. Eur Phys J A (2021) 57:333. doi:10.1140/epja/s10050-021-00642-1
18. Mumpower MR, Sprouse TM, Lovell AE, Mohan AT. Physically interpretable machine learning for nuclear masses. Phys Rev C (2022) 106:L021301. doi:10.1103/PhysRevC.106.L021301
19. Niu ZM, Liang HZ, Sun BH, Long WH, Niu YF. Predictions of nuclear β-decay half-lives with machine learning and their impact on r-process nucleosynthesis. Phys Rev C (2019) 99:064307. doi:10.1103/PhysRevC.99.064307
20. Wang ZA, Pei J, Liu Y, Qiang Y. Bayesian evaluation of incomplete fission yields. Phys Rev Lett (2019) 123:122501. doi:10.1103/PhysRevLett.123.122501
21. Lovell AE, Mohan AT, Talou P. Quantifying uncertainties on fission fragment mass yields with mixture density networks. J Phys G: Nucl Part Phys (2020) 47:114001. doi:10.1088/1361-6471/ab9f58
22. Melendez JA, Drischler C, Furnstahl RJ, Garcia AJ, Zhang X. Model reduction methods for nuclear emulators. J Phys G: Nucl Part Phys (2022) 49:102001. doi:10.1088/1361-6471/ac83dd
23. Giuliani P, Godbey K, Bonilla E, Viens F, Piekarewicz J. Bayes goes fast: Uncertainty quantification for a covariant energy density functional emulated by the reduced basis method (2022). [Dataset]. doi:10.48550/ARXIV.2209.13039
24. Bonilla E, Giuliani P, Godbey K, Lee D. Training and projecting: A reduced basis method emulator for many-body physics (2022). [Dataset]. doi:10.48550/ARXIV.2203.05284
25. Lasseri RD, Regnier D, Ebran JP, Penon A. Taming nuclear complexity with a committee of multilayer neural networks. Phys Rev Lett (2020) 124:162502. doi:10.1103/PhysRevLett.124.162502
26. Parr R, Yang W. International series of monographs on chemistry. New York: Oxford University Press (1989).Density functional theory of atoms and molecules
27. Dreizler R, Gross E. Density functional theory: An approach to the quantum many-body problem. Springer-Verlag (1990). doi:10.1007/978-3-642-86105-5
28. Engel J. Intrinsic-density functionals. Phys Rev C (2007) 75:014306. doi:10.1103/PhysRevC.75.014306
29. Barnea N. Density functional theory for self-bound systems. Phys Rev C (2007) 76:067302. doi:10.1103/PhysRevC.76.067302
30. Engel YM, Brink DM, Goeke K, Krieger SJ, Vautherin D. Time-dependent Hartree-Fock theory with Skyrme’s interaction. Nucl Phys A (1975) 249:215–38. doi:10.1016/0375-9474(75)90184-0
31. Dobaczewski J, Dudek J. Time-Odd components in the rotating mean field and identical bands. Acta Phys Pol B (1996) 27:45.
32. Bender M, Heenen PH, Reinhard PG. Self-consistent mean-field models for nuclear structure. Rev Mod Phys (2003) 75:121–80. doi:10.1103/RevModPhys.75.121
33. Lesinski T, Bender M, Bennaceur K, Duguet T, Meyer J. Tensor part of the Skyrme energy density functional: Spherical nuclei. Phys Rev C (2007) 76:014312. doi:10.1103/PhysRevC.76.014312
34. Schunck N, Quinlan KR, Bernstein J. A Bayesian analysis of nuclear deformation properties with Skyrme energy functionals. J Phys G: Nucl Part Phys (2020) 47:104002. doi:10.1088/1361-6471/aba4fa
35. Dobaczewski J, Flocard H, Treiner J. Hartree-Fock-Bogolyubov description of nuclei near the neutron-drip line. Nucl Phys A (1984) 422:103–39. doi:10.1016/0375-9474(84)90433-0
36. Vautherin D, Brink DM. Hartree-Fock calculations with skyrme’s interaction. I. Spherical nuclei. Phys Rev C (1972) 5:626–47. doi:10.1103/PhysRevC.5.626
37. Dobaczewski J, Dudek J. Solution of the Skyrme-Hartree-Fock equations in the Cartesian deformed harmonic oscillator basis I. The method. Comput Phys Commun (1997) 102:166–82. doi:10.1016/S0010-4655(97)00004-0
38. Bender M, Bennaceur K, Duguet T, Heenen PH, Lesinski T, Meyer J. Tensor part of the Skyrme energy density functional. II. Deformation properties of magic and semi-magic nuclei. Phys Rev C (2009) 80:064302. doi:10.1103/PhysRevC.80.064302
39. Hellemans V, Heenen PH, Bender M. Tensor part of the Skyrme energy density functional. III. Time-odd terms at high spin. Phys Rev C (2012) 85:014326. doi:10.1103/PhysRevC.85.014326
40. Ryssens W, Hellemans V, Bender M, Heenen PH. Solution of the skyrme-hf+BCS equation on a 3D mesh, II: A new version of the Ev8 code. Comput Phys Commun (2015) 187:175–94. doi:10.1016/j.cpc.2014.10.001
41. Valatin JG. Generalized Hartree-Fock method. Phys Rev (1961) 122:1012–20. doi:10.1103/PhysRev.122.1012
42. Mang HJ. The self-consistent single-particle model in nuclear physics. Phys Rep (1975) 18:325–68. doi:10.1016/0370-1573(75)90012-5
44. Ring P, Schuck P. The nuclear many-body problem. In: Texts and monographs in physics. Springer (2004).
45. Dobaczewski J, Dudek J. Time-odd components in the mean field of rotating superdeformed nuclei. Phys Rev C (1995) 52:1827–39. doi:10.1103/PhysRevC.52.1827
46. Stoitsov MV, Dobaczewski J, Nazarewicz W, Ring P. Axially deformed solution of the Skyrme-Hartree-Fock-Bogolyubov equations using the transformed harmonic oscillator basis. The program HFBTHO (v1.66p). Comput Phys Commun (2005) 167:43–63. doi:10.1016/j.cpc.2005.01.001
47. Heyde K, Wood JL. Shape coexistence in atomic nuclei. Rev Mod Phys (2011) 83:1467–521. doi:10.1103/RevModPhys.83.1467
48. Nakatsukasa T, Matsuyanagi K, Matsuo M, Yabana K. Time-dependent density-functional description of nuclear dynamics. Rev Mod Phys (2016) 88:045004. doi:10.1103/RevModPhys.88.045004
49. Griffin JJ, Wheeler JA. Collective motions in nuclei by the method of generator coordinates. Phys Rev (1957) 108:311–27. doi:10.1103/PhysRev.108.311
50. Wa Wong C. Generator-coordinate methods in nuclear physics. Phys Rep (1975) 15:283–357. doi:10.1016/0370-1573(75)90036-8
51. Reinhard PG, Goeke K. The generator coordinate method and quantised collective motion in nuclear systems. Rep Prog Phys (1987) 50:1–64. doi:10.1088/0034-4885/50/1/001
52. Verriere M, Regnier D. The time-dependent generator coordinate method in nuclear physics. Front Phys (2020) 8:1. doi:10.3389/fphy.2020.00233
53. Brink DM, Weiguny A. The generator coordinate theory of collective motion. Nucl Phys A (1968) 120:59–93. doi:10.1016/0375-9474(68)90059-6
54. Onishi N, Une T. Local Gaussian approximation in the generator coordinate method. Prog Theor Phys (1975) 53:504–15. doi:10.1143/PTP.53.504
55. Une T, Ikeda A, Onishi N. Collective Hamiltonian in the generator coordinate method with local Gaussian approximation. Prog Theor Phys (1976) 55:498–508. doi:10.1143/PTP.55.498
56. Bloch C, Messiah A. The canonical form of an antisymmetric tensor and its application to the theory of superconductivity. Nucl Phys (1962) 39:95–106. doi:10.1016/0029-5582(62)90377-2
58. Marević P, Schunck N, Ney EM, Navarro Pérez R, Verriere M, O’Neal J. Axially-deformed solution of the Skyrme-Hartree-Fock-Bogoliubov equations using the transformed harmonic oscillator basis (iv) HFBTHO (v4.0): A new version of the program. Comput Phys Commun (2022) 276:108367. doi:10.1016/j.cpc.2022.108367
59. Drischler C, Furnstahl RJ, Melendez JA, Phillips DR. How well do we know the neutron-matter equation of state at the densities inside neutron stars? A bayesian approach with correlated uncertainties. Phys Rev Lett (2020) 125:202702. doi:10.1103/PhysRevLett.125.202702
60. Kravvaris K, Quinlan KR, Quaglioni S, Wendt KA, Navrátil P. Quantifying uncertainties in neutron-α scattering with chiral nucleon-nucleon and three-nucleon forces. Phys Rev C (2020) 102:024616. doi:10.1103/PhysRevC.102.024616
61. Acharya B, Bacca S. Gaussian process error modeling for chiral effective-field-theory calculations of np ↔ dγ at low energies. Phys Lett B (2022) 827:137011. doi:10.1016/j.physletb.2022.137011
62. Pastore A, Shelley M, Baroni S, Diget CA. A new statistical method for the structure of the inner crust of neutron stars. J Phys G: Nucl Part Phys (2017) 44:094003. doi:10.1088/1361-6471/aa8207
63. Kortelainen M, Lesinski T, Moré J, Nazarewicz W, Sarich J, Schunck N, et al. Nuclear energy density optimization. Phys Rev C (2010) 82:024313. doi:10.1103/PhysRevC.82.024313
64. Kortelainen M, McDonnell J, Nazarewicz W, Reinhard PG, Sarich J, Schunck N, et al. Nuclear energy density optimization: Large deformations. Phys Rev C (2012) 85:024304. doi:10.1103/PhysRevC.85.024304
65. Kortelainen M, McDonnell J, Nazarewicz W, Olsen E, Reinhard PG, Sarich J, et al. Nuclear energy density optimization: Shell structure. Phys Rev C (2014) 89:054314. doi:10.1103/PhysRevC.89.054314
66. Higdon D, McDonnell JD, Schunck N, Sarich J, Wild SM. A Bayesian approach for parameter estimation and prediction using a computationally intensive model. J Phys G: Nucl Part Phys (2015) 42:034009. doi:10.1088/0954-3899/42/3/034009
67. McDonnell JD, Schunck N, Higdon D, Sarich J, Wild SM, Nazarewicz W. Uncertainty quantification for nuclear density functional theory and information content of new measurements. Phys Rev Lett (2015) 114:122501. doi:10.1103/PhysRevLett.114.122501
68. Neufcourt L, Cao Y, Nazarewicz W, Viens F. Bayesian approach to model-based extrapolation of nuclear observables. Phys Rev C (2018) 98:034318. doi:10.1103/PhysRevC.98.034318
69. Neufcourt L, Cao Y, Giuliani S, Nazarewicz W, Olsen E, Tarasov OB. Beyond the proton drip line: Bayesian analysis of proton-emitting nuclei. Phys Rev C (2020) 101:014319. doi:10.1103/PhysRevC.101.014319
70. Neufcourt L, Cao Y, Giuliani SA, Nazarewicz W, Olsen E, Tarasov OB. Quantified limits of the nuclear landscape. Phys Rev C (2020) 101:044307. doi:10.1103/PhysRevC.101.044307
71. Rasmussen CE, Williams CKI. Gaussian Processes for machine learning. Adaptive computation and machine learning. Cambridge, Mass: MIT Press (2006).
72. Bartel J, Quentin P, Brack M, Guet C, Håkansson HB. Towards a better parametrisation of skyrme-like effective forces: A critical study of the SkM force. Nucl Phys A (1982) 386:79–100. doi:10.1016/0375-9474(82)90403-1
73. Schunck N, Duke D, Carr H, Knoll A. Description of induced nuclear fission with Skyrme energy functionals: Static potential energy surfaces and fission fragment properties. Phys Rev C (2014) 90:054305. doi:10.1103/PhysRevC.90.054305
74. Schunck N. Density functional theory approach to nuclear fission. Acta Phys Pol B (2013) 44:263. doi:10.5506/APhysPolB.44.263
75. Dubray N, Regnier D. Numerical search of discontinuities in self-consistent potential energy surfaces. Comput Phys Commun (2012) 183:2035. doi:10.1016/j.cpc.2012.05.001
76. Sadhukhan J. Microscopic theory for spontaneous fission. Front Phys (2020) 8:567171. doi:10.3389/fphy.2020.567171
77. Bruinsma W, Perim E, Tebbutt W, Hosking S, Solin A, Turner R. Scalable exact inference in multi-output Gaussian processes. Proceedings of the 37th international Conference on machine learning (PMLR). Proc Machine Learn Res (2020) 119:1190.
78. Álvarez MA, Rosasco L, Lawrence ND. Kernels for vector-valued functions: A review. FNT Machine Learn (2012) 4:195–266. doi:10.1561/2200000036
79. Bender M, Bernard R, Bertsch G, Chiba S, Dobaczewski J, Dubray N, et al. Future of nuclear fission theory. J Phys G: Nucl Part Phys (2020) 47:113002. doi:10.1088/1361-6471/abab4f
80. Schunck N. Microscopic description of induced fission. J Phys : Conf Ser (2013) 436:012058. doi:10.1088/1742-6596/436/1/012058
81. Ryssens W, Heenen PH, Bender M. Numerical accuracy of mean-field calculations in coordinate space. Phys Rev C (2015) 92:064318. doi:10.1103/PhysRevC.92.064318
82. Jin S, Bulgac A, Roche K, Wlazłowski G. Coordinate-space solver for superfluid many-fermion systems with the shifted conjugate-orthogonal conjugate-gradient method. Phys Rev C (2017) 95:044302. doi:10.1103/PhysRevC.95.044302
83. Regnier D, Dubray N, Schunck N, Verrière M. Microscopic description of fission dynamics: Toward a 3D computation of the time dependent GCM equation. EPJ Web Conf (2017) 146:04043. doi:10.1051/epjconf/201714604043
84. Zhao J, Nikšić T, Vretenar D. Microscopic self-consistent description of induced fission: Dynamical pairing degree of freedom. Phys Rev C (2021) 104:044612. doi:10.1103/PhysRevC.104.044612
85. Lau NWT, Bernard RN, Simenel C. Smoothing of one- and two-dimensional discontinuities in potential energy surfaces. Phys Rev C (2022) 105:034617. doi:10.1103/PhysRevC.105.034617
86. Baldi P. Autoencoders, unsupervised learning, and deep architectures. In Proceedings of ICML workshop on unsupervised and transfer learning (JMLR Workshop and Conference Proceedings) (2012), 37–49.
87. Burda Y, Grosse R, Salakhutdinov R. Importance weighted autoencoders (2015). arXiv preprint arXiv:1509.00519.
88. Chen M, Xu Z, Weinberger K, Sha F. Marginalized denoising autoencoders for domain adaptation (2012). arXiv preprint arXiv:1206.4683.
89. Gong D, Liu L, Le V, Saha B, Mansour MR, Venkatesh S, et al. Memorizing normality to detect anomaly: Memory-augmented deep autoencoder for unsupervised anomaly detection. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. October 2019 (2019). p. 1705–14.
90. Bengio Y, Courville A, Vincent P. Representation learning: A review and new perspectives. IEEE Trans Pattern Anal Mach Intell (2013) 35:1798–828. doi:10.1109/tpami.2013.50
91. Zhang F, Du B, Zhang L. Saliency-guided unsupervised feature learning for scene classification. IEEE Trans Geosci Remote Sens (2014) 53:2175–84. doi:10.1109/tgrs.2014.2357078
92. Yu J, Hong C, Rui Y, Tao D. Multitask autoencoder model for recovering human poses. IEEE Trans Ind Electron (2017) 65:5060–8. doi:10.1109/tie.2017.2739691
93. von Neuman J, Wigner E. Uber merkwürdige diskrete Eigenwerte. Uber das Verhalten von Eigenwerten bei adiabatischen Prozessen. Physikalische Z (1929) 30:467–70.
94. Teller E. The crossing of potential surfaces. J Phys Chem (1937) 41:109–16. doi:10.1021/j150379a010
95. Longuet-Higgins HC, Öpik U, Pryce MHL, Sack RA. Studies of the jahn-teller effect. II. The dynamical problem. Proc R Soc Lond A (1958) 244:1. doi:10.1098/rspa.1958.0022
96. Longuet-Higgins H. The intersection of potential energy surfaces in polyatomic molecules. Proc R Soc Lond A (1975) 344:147. doi:10.1098/rspa.1975.0095
97.W Domcke, D Yarkony, and H Köppel, editors. Conical intersections: Theory, computation and experiment. Advanced series in physical chemistry, Vol. 17. World Scientific (2011). doi:10.1142/7803
98. Larson J, Sjöqvist E, Öhberg P. Intersections in physics. An introduction to synthetic gauge theories. In Lecture notes in physics. Springer (2020). doi:10.1007/978-3-030-34882-3
99. Haider Q, Gogny D. Microscopic approach to the generator coordinate method with pairing correlations and density-dependent forces. J Phys G: Nucl Part Phys (1992) 18:993–1022. doi:10.1088/0954-3899/18/6/003
100. Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In: International conference on machine learning (PMLR) (2015). p. 448–56.
101. Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A simple way to prevent neural networks from overfitting. J machine Learn Res (2014) 15:1929–58.
102. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. June 2016 (2016). p. 770–8.
103. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Adv Neural Inf Process Syst (2012) 25.
104. Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. In: European conference on computer vision. Springer (2014). p. 818–33.
105. Sermanet P, Eigen D, Zhang X, Mathieu M, Fergus R, LeCun Y. Overfeat: Integrated recognition, localization and detection using convolutional networks (2013). arXiv preprint arXiv:1312.6229.
106. Szegedy C, Ioffe S, Vanhoucke V, Alemi AA. Inception-v4, inception-resnet and the impact of residual connections on learning. San Francisco, CA: Thirty-first AAAI conference on artificial intelligence (2017).
107. Li H, Xu Z, Taylor G, Studer C, Goldstein T. Visualizing the loss landscape of neural nets. Adv Neural Inf Process Syst (2018) 31.
108. Zhang H, Wu C, Zhang Z, Zhu Y, Lin H, Zhang Z, et al. Resnet: Split-attention networks. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition September 2022 (2022), 2736–46.
109. Radosavovic I, Kosaraju RP, Girshick R, He K, Dollár P. Designing network design spaces. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. June 2020. Seattle, WA, USA. IEEE (2020). p. 10428–36.
110. Cubuk ED, Zoph B, Shlens J, Le QV. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition workshops. June 2020. Seattle, WA, USA. IEEE (2020). p. 702–3.
111. Yun S, Han D, Oh SJ, Chun S, Choe J, Yoo Y. Cutmix: Regularization strategy to train strong classifiers with localizable features. In Proceedings of the IEEE/CVF international conference on computer vision. May 2019. IEEE (2019). p. 6023–32.
112. Zhang H, Cisse M, Dauphin YN, Lopez-Paz D. mixup: Beyond empirical risk minimization. arXiv preprint arXiv:1710.09412 (2017).
113. Wickramasinghe CS, Marino DL, Manic M. Resnet autoencoders for unsupervised feature learning from high-dimensional data: Deep models resistant to performance degradation. IEEE Access (2021) 9:40511–20. doi:10.1109/ACCESS.2021.3064819
114. He K, Zhang X, Ren S, Sun J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE international conference on computer vision February 2015 (2015), 1026–34.
115. Kingma DP, Ba J. Adam: A method for stochastic optimization (2014). arXiv preprint arXiv:1412.6980.
117. Dobaczewski J, Nazarewicz W, Werner TR, Berger JF, Chinn CR, Dechargé J. Mean-field description of ground-state properties of drip-line nuclei: Pairing and continuum effects. Phys Rev C (1996) 53:2809–40. doi:10.1103/PhysRevC.53.2809
118. Warda M, Robledo LM. Microscopic description of cluster radioactivity in actinide nuclei. Phys Rev C (2011) 84:044608. doi:10.1103/PhysRevC.84.044608
119. Warda M, Zdeb A, Robledo LM. Cluster radioactivity in superheavy nuclei. Phys Rev C (2018) 98:041602(R). doi:10.1103/PhysRevC.98.041602
Keywords: nuclear density functional theory, Gaussian process, deep learning, autoencoders, resnet
Citation: Verriere M, Schunck N, Kim I, Marević P, Quinlan K, Ngo MN, Regnier D and Lasseri RD (2022) Building surrogate models of nuclear density functional theory with Gaussian processes and autoencoders. Front. Phys. 10:1028370. doi: 10.3389/fphy.2022.1028370
Received: 25 August 2022; Accepted: 19 October 2022;
Published: 08 November 2022.
Edited by:
Christian Forssén, Chalmers University of Technology, SwedenReviewed by:
Daniel Phillips, Ohio University, United StatesMarkus Kortelainen, University of Jyväskylä, Finland
Copyright © 2022 Verriere, Schunck, Kim, Marević, Quinlan, Ngo, Regnier and Lasseri. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nicolas Schunck, c2NodW5jazFAbGxubC5nb3Y=
 Marc Verriere
Marc Verriere Nicolas Schunck
Nicolas Schunck Irene Kim
Irene Kim Petar Marević
Petar Marević Kevin Quinlan6
Kevin Quinlan6 Michelle N. Ngo
Michelle N. Ngo