Spatial and Temporal Oscillations of Surface Tension Induced by an A + B → C Traveling Front

This work describes a new mechanism for the emergence of oscillatory dynamics driven by the interaction of hydrodynamic flows and reaction-diffusion processes with no autocatalytic feedback nor prescribed hydrodynamic instability involved. To do so, we study the dynamics of an A+ B → C reaction-diffusion front in the presence of chemically-driven Marangoni flows for arbitrary initial concentrations of reactants and diffusion coefficients of all species. All the species are assumed to affect the solution surface tension thereby inducing Marangoni flows at the air-liquid interface. The system dynamics is studied by numerically integrating the incompressible Navier-Stokes equations coupled to reaction-diffusion-convection equations for the three chemical species. We report spatial and temporal oscillations of surface tension triggered by differential diffusion effects of surfactant species coupled to the chemically-induced Marangoni effect. Such oscillations are related to the discontinuous traveling of the front along the surface leading to the progressive formation of local extrema in the surface tension profiles as time evolves.

1 Introduction

Traveling fronts are recurrent examples of spatio-temporal structures observed in Nature [1–5]. In the context of chemistry, fronts are localized reactive interfaces driven by reaction-diffusion (RD) processes that may exhibit unique dynamical behaviors. For instance, for bimolecular fronts, universal time scaling behaviors of the front properties are noted [6–8] and, for autocatalytic fronts, where a reaction product (the autocatalytic species) catalyzes its own production, spatio-temporal chaos may be observed due to front instabilities [9].

Front propagation is typically influenced by spontaneous hydrodynamic motions, typically buoyancy-driven and/or surface tension-driven (Marangoni) flows, arising from composition (solutal effects) and/or temperature (thermal effects) changes across the front [10, 11]. When such flows are driven across chemical fronts in horizontally oriented-systems (e.g., in Petri dishes or thin layers), many scenarios have been shown to lead to oscillatory phenomena (see Tiani et al. [10] and references therein). In particular, in the presence of Marangoni flows driven across isothermal autocatalytic fronts, transient oscillations of concentration and fluid velocity can be seen before the long-time asymptotic dynamics is reached when the Marangoni number of the autocatalytic species, quantifying its influence on surface tension, is sufficiently large [12]. The antagonistic coupling of surface tension-driven and buoyancy-driven flows can also induce an unsteady periodic behavior of autocatalytic isothermal fronts [13]. Such oscillations, together with oscillations in the temperature field, have also been observed to emerge across exothermal autocatalytic fronts when Marangoni or buoyancy-driven flows are at play due to antagonistic contribution of thermal and solutal effects [13, 14]. The interplay of the oscillating Belousov-Zhabotinky reaction around an A+ B → oscillator configuration with buoyancy forces can also induce new chemo-hydrodynamic instabilities leading to pulsatile fingering and plumes as well as rising or sinking Turing spots [15]. When the same localized oscillating reaction is assumed to change the viscosity of the solutions involved, viscous fingering instabilities can be triggered by the reaction and can induce oscillations in situations that are stable in the absence of chemo-hydrodynamic coupling [16]. While most works on chemical oscillations focused on autocatalytic systems, Budroni et al. recently showed that a transient oscillatory dynamics can be triggered in the presence of Marangoni-driven flows across A+ B → C bimolecular fronts for equal diffusion coefficients and initial concentrations of all species, provided that the surface tension changes during the reaction are large enough [17–19]. In that case, such oscillations are explained by the competition of Marangoni convection and the vertical RD relaxation of the front. The combination of both Marangoni and buoyancy-driven flows has further been observed to lead to sustained oscillations around such bimolecular fronts [17–19]. In the absence of reaction, spontaneous oscillations can also be observed due to Marangoni instability [20–25]. A simple example is the one of a surfactant droplet dissolving under the air/water interface [22]. A solutal Marangoni instability can develop in this system either as steady convection or as oscillations.

In this work, we report an additional mechanism that may lead to transient oscillations and is a unique property of reactive systems where differential diffusion of chemical species combines with chemically-driven Marangoni convection. The mechanism we describe does not require any feedback loop nor prescribed hydrodynamic instability. As detailed below, it is also fundamentally different from the one described by Budroni et al. when the species diffuse at the same rate [17,18], since it does not involve any competition between Marangoni stresses and RD processes as described by the authors and leads to oscillations in the surface tension profiles.

The article is organized as follows. In Section 2, the model system and related governing equations are presented. In Section 3, we describe the emergence of spatio-temporal oscillations of surface tension observed by numerically integrating the governing equations for arbitrary diffusion coefficients and initial concentrations of reactants. Next, in Section 4, we illustrate the control of the oscillatory dynamics as a function of the model parameters. Eventually, conclusions and prospects are drawn in Section 5.

2 Model

The model system consists of a horizontally orientated system (see Figure 1), in which an aqueous solution containing a reactant A, of concentration a₀, is placed beside an aqueous solution containing a reactant B, of concentration b₀, along a vertical contact line at time t = 0. The species A and B diffuse at rates D_a and D_b, respectively. The two miscible reacting solutions meet at t > 0 and react according to the isothermal A+ B → C reaction to produce a third species C. The resulting localized region of space where C is produced is called the reaction front. All the species are supposed to affect the surface tension of the solution, therefore inducing gradients of surface tension leading to Marangoni flows. We assume that the air/liquid interface is not deformable and neglect the evaporation processes during the chemical reaction, so that we do not address the dynamics in the air layer. In order to focus on surface tension effects, we also consider the solution density as constant in space and time preventing any buoyancy-driven convection in solution.

FIGURE 1

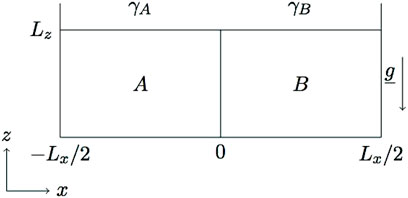
FIGURE 1. Sketch of the system. Two aqueous solutions of reactants A and B of concentrations a₀ and b₀ and of surface tension γ_A and γ_B, respectively, are initially separated in space in a 2D domain of length L_x and height L_z. The species diffuse at rates D_a and D_b.

The dimensional governing equations for the evolution of the concentrations of the reactants $\widehat{a},\widehat{b}$ and of the product $\widehat{c}$ in this system are obtained by coupling the reaction-diffusion-convection (RDC) equations for the chemical concentrations to the incompressible Navier-Stokes equations for the dimensional velocity field $\underline{\widehat{v}}=(\widehat{u},\widehat{w})$, i.e.,

$\frac{\partial \widehat{a}}{\partial \widehat{t}}+\underline{\widehat{v}}.\underline{\widehat{\nabla }}\widehat{a}=D_a{\widehat{\nabla }}^2\widehat{a}-k\widehat{a}\widehat{b},(1)$

$\frac{\partial \widehat{b}}{\partial \widehat{t}}+\underline{\widehat{v}}.\underline{\widehat{\nabla }}\widehat{b}=D_b{\widehat{\nabla }}^2\widehat{b}-k\widehat{a}\widehat{b},(2)$

$\frac{\partial \widehat{c}}{\partial \widehat{t}}+\underline{\widehat{v}}.\underline{\widehat{\nabla }}\widehat{c}=D_c{\widehat{\nabla }}^2\widehat{c}+k\widehat{a}\widehat{b},(3)$

$\frac{\partial \underline{\widehat{v}}}{\partial \widehat{t}}+\left(\underline{\widehat{v}}.\underline{\widehat{\nabla }}\right)\underline{\widehat{v}}=\nu {\widehat{\nabla }}^2\underline{\widehat{v}}-\frac{1}{{\rho }_0}\underline{\widehat{\nabla }}\widehat{p}+\underline{g},(4)$

$\widehat{\mathrm{d}\mathrm{i}\mathrm{v}}\underline{\widehat{v}}=0,(5)$

or, in dimensionless form,

$\frac{\partial a}{\partial t}+\underline{v}.\underline{\nabla }a={\nabla }^{2}a-ab,(6)$

$\frac{\partial b}{\partial t}+\underline{v}.\underline{\nabla }b={\delta }_b{\nabla }^{2}b-ab,(7)$

$\frac{\partial c}{\partial t}+\underline{v}.\underline{\nabla }c={\delta }_c{\nabla }^{2}c+ab,(8)$

$\frac{\partial \underline{v}}{\partial t}+\left(\underline{v}.\underline{\nabla }\right)\underline{v}=S_c\left({\nabla }^2\underline{v}-\underline{\nabla }p\right),(9)$

$\mathrm{d}\mathrm{i}\mathrm{v}\underline{v}=0,(10)$

where δ_b,c = D_b,c/D_a are the two diffusion coefficient ratios, D_c is the diffusion coefficient of species C, and S_c = (ν/D_a) is the Schmidt number (fixed to 10³ as typical for small species at room temperature in water), with ν = (μ/ρ₀) the kinematic viscosity, μ the dynamic viscosity and ρ₀ the solution density. To non-dimensionalize the problem, as in Tiani and Rongy [26], we have used the characteristic scales of the reaction-diffusion system: for time, τ_c = (1/ka₀) (with k the reaction rate constant), length $L_c=\sqrt{D_a{\tau }_c}$, velocity $U_c=(L_c/{\tau }_c)=\sqrt{D_a/{\tau }_c}$, concentration a₀. The pressure is scaled by p_c = (μ/τ_c) = ρ₀S_cD_a/τ_c and a new dimensionless pressure gradient incorporating the hydrostatic pressure gradient is defined as $\underline{\nabla }p=\underline{\nabla }\widehat{p}/p_c-{\rho }_0{L}_c\underline{g}/p_c$, with $\underline{g}=(0,-g)$ the gravity acceleration.

The dimensionless initial conditions are separated reactants such that, ∀z, a = 1, b = 0, c = 0, for x < 0 and a = 0, b = β, c = 0, for x ≥ 0, where β = b₀/a₀ is the ratio between the initial dimensional concentrations of B and A. The dimensionless conditions at boundaries of Figure 1 are no-flux boundary conditions (BCs) for the chemical concentrations at each boundary of the domain. The BCs for the fluid velocity field at the rigid boundaries (x = ±L_x/2 and z = 0) are no-slip conditions, u = 0 = w. At the free surface, we assume w = 0 and we use a Marangoni boundary condition for u derived from the tangential stress balance condition of the form, $\mu (\partial \widehat{u}/\partial \widehat{z})=\partial \widehat{\gamma }/\partial \widehat{x}$ at the free surface [21, 27], or in dimensionless form,

$\frac{\partial u}{\partial z}=-\sum _i{M}_i\frac{\partial c_i}{\partial x}\mathrm{a}\mathrm{t}z=L_z,(11)$

where L_x and L_z represent the dimensionless length and height of the system, respectively. In Eq. 11, the dimensionless solutal Marangoni number M_i of species i = (a, b, c) which quantifies the influence of each chemical species on the solution surface tension, is defined as,

$M_i=-\frac{1}{\mu }\sqrt{\frac{a_0}{D_{a}k}}\frac{\partial \widehat{\gamma }}{\partial {\widehat{c}}_i},(12)$

where $\widehat{\gamma }$ and ${\widehat{c}}_i$ are the dimensional solution surface tension and concentration of solute i.

For sufficiently dilute solutions, the solution surface tension is expected to vary linearly with the concentrations. Then, we can write that $\widehat{\gamma }={\widehat{\gamma }}_0+\sum _i(\partial \widehat{\gamma }/\partial {\widehat{c}}_i){\widehat{c}}_i$, with ${\widehat{\gamma }}_0$ the (dimensional) surface tension of the solvent $({\widehat{c}}_i=0,\forall i)$. Using Eq. 12, the dimensionless solution surface tension, which is defined as $\gamma =(\widehat{\gamma }-{\widehat{\gamma }}_0)/{\widehat{\gamma }}_c$ where ${\widehat{\gamma }}_c=p_c{L}_c$, therefore reads

$\gamma \left(x,t\right)=-M_{a}a\left(x,L_z,t\right)-M_{b}b\left(x,L_z,t\right)-M_{c}c\left(x,L_z,t\right).(13)$

In Eqs 12, 13, the Marangoni numbers are assumed positive, i.e., M_a,b,c ≥ 0, to describe surfactants decreasing the surface tension of the solvent with $(\partial \widehat{\gamma }/\partial {\widehat{c}}_i)<0,\forall i$. From Eq. 13, the surface tension of the initial pure A and B solutions therefore read, γ_A = −M_a and γ_B = −M_bβ, respectively.

The system dynamics is then obtained by numerically integrating the complete set of Eqs 6–10 subjected to initial conditions and BCs specified above, with the numerical procedure described in Rongy and De Wit [12]. The length L_x is chosen sufficiently large so that the results are not affected by lateral boundary effects on the time of interest, typically L_x = 350.

3 Spatio-Temporal Oscillations of Surface Tension: Mechanism

When the species diffuse at different rates, oscillations are found in the surface tension profiles for appropriate values of the model parameters (see Figure 2). Such oscillations emerge as local extrema that progressively form at different spatial positions in the surface tension profiles between γ_A and γ_B in the course of time. To explain the mechanism leading to such oscillations, we consider the simplest scenario when species A and B have the same influence on the solution surface tension, i.e. M_a = M = M_b, and we assume β > 1 so that γ_B < γ_A. However, the mechanism described below is universal and does not depend on this particular choice.

FIGURE 2

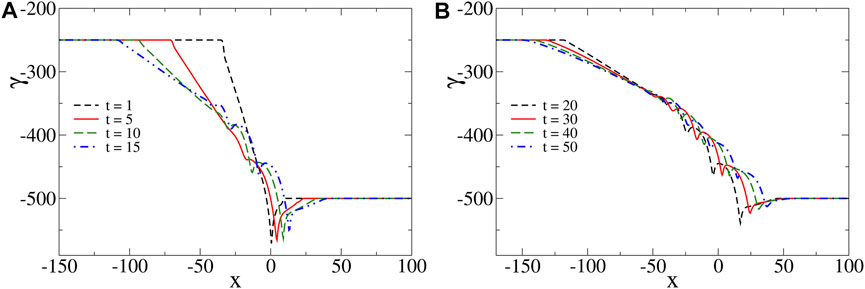
FIGURE 2. Spatial oscillations of surface tension profiles at different times for M_a = 250 = M_b, M_c = 500, β = 2, δ_b = 0.25, δ_c = 0.50 and L_z = 10. Such profiles are separated in two plots, (A,B), for clarity.

In the short-time limit, the concentration of C is negligible so that we can neglect its influence on surface tension and the related profiles are nonmonotonic with a global minimum (see Figure 2A at time t = 1). In this limit, from the pure diffusion equations, we can predict the profiles to admit two global extrema (a global maximum and a global minimum) (see reference Trevelyan et al. [28] for the analytical derivation of the corresponding RD profiles, along with the change of notation ρ ↔ − γ). We note that such a global maximum is also formed in the presence of convection but it cannot be seen on the considered scale in Figure 2A due to its negligible amplitude and thus plays no role on the system dynamics. The minimum drives two counterrotating convective rolls, a main convective roll that turns counterclockwise and is of much bigger intensity than the clockwise convective roll on the right (see Figure 3 at time t = 1). Since species A diffuses faster than species B, we note that the main convective roll and surface tension profiles are asymmetric, i.e. more elongated on the side of A than of B. Such an asymmetric convective roll deforms the reaction front across the layer and the maximum production rate of C is found at the surface. As time increases, the effect of species C becomes important. In the reaction zone which is mainly located at the surface, the concentration of C increases. Since M_c > M_a = M_b, the reactants are replaced by the more surface-active product, reducing thereby the surface tension locally and leading to the formation of the first two local extrema (a local minimum and a local maximum) in the surface tension profiles (see Figure 2A at time t = 5). The formation of such extrema locally reduces the intensity of the flow and deforms the inner structure of the main convective roll so that two counterclockwise vortices are formed in the bulk (see Figure 3 at time t = 5). Driven by the vortices, the reactants are transported from their reservoir along the surface at the spatial locations where the flow is the most intense. This generates a new intense reaction zone at the surface (around x = −10 in Figure 3 at time t = 15) while the previous one (located around x = 10 in Figure 3 at time t = 15) reduces in intensity. Inside the newly generated reaction zone, the concentration of C increases, locally reducing the surface tension and thereby inducing two additional local extrema. This RDC process repeats itself progressively forming new intense reaction zones further away towards the left (around x = −20 and x = −30 at times t = 30 and t = 50, respectively) and leading to the observed oscillations in the surface tension profiles. Since the newly generated local minima in such profiles are less pronounced than the previous ones and that the profiles stretch in the course of time, the corresponding vortices are of weaker intensities. Eventually, this process always stops generating new local extrema after some time. In the long-time limit, when all the gradients of surface tension decrease with time, the monotonic properties of the surface tension profiles as predicted by the analysis of RD profiles are recovered Trevelyan et al. [28], here corresponding to two global extrema between γ_A and γ_B (e.g., when L_z = 4 and for same values of the other parameters as in Figure 2, the RD profiles properties are recovered numerically after a time of about t = 40. This time typically increases with the intensity of convection as detailed in Section 4.)

FIGURE 3

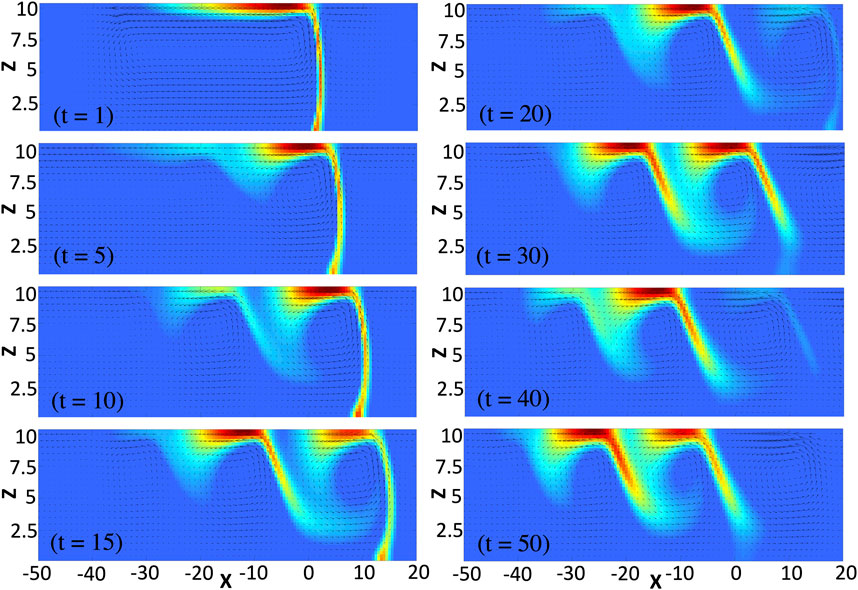
FIGURE 3. Focus on the convective rolls centered on the reaction front at different times for the same parameters values as in Figure 2. The fluid velocity field is superimposed on a 2D plot of the production rate which ranges between its maximum value, (ab)_max shown in red, and its minimum value, (ab)_min = 0, shown in blue. The front is mainly located at the surface and travels in the course of time discontinuously leading to oscillations in the surface tension profiles (cf: Figure 2). The velocity vectors are here tripled compared to their effective length to allow for a better visualization.

Thus, we deduce that oscillations in the surface tension profiles are the results of the subsequent formation of segregated reaction zones along the surface. Each one of them is a source of C production that progressively reduces the surface tension locally as the reaction zones form in the course of time. Such oscillations naturally involve complex spatial dynamics of other observables, such as the product concentration at the surface (c_S) and the horizontal component of the velocity field evaluated at the surface (u_S) (see Figure 4). We note that the profiles of c_S have wave-like tails with multiple maxima located at positions close to the ones of the local minima in the surface tension profiles. For short times, the latter are nonmonotonic with a global minimum and thus, the profiles of u_S have a negative and a positive part associated to the counterclockwise and clockwise convective rolls, respectively. As time evolves, the progressive formation of local extrema in the profiles of surface tension come along with oscillations in the profiles of u_S (u_S indeed oscillates with the gradients of surface tension according to the Marangoni boundary condition, Eq. 12), together with bulk vortices in the system as seen in Figure 3.

FIGURE 4

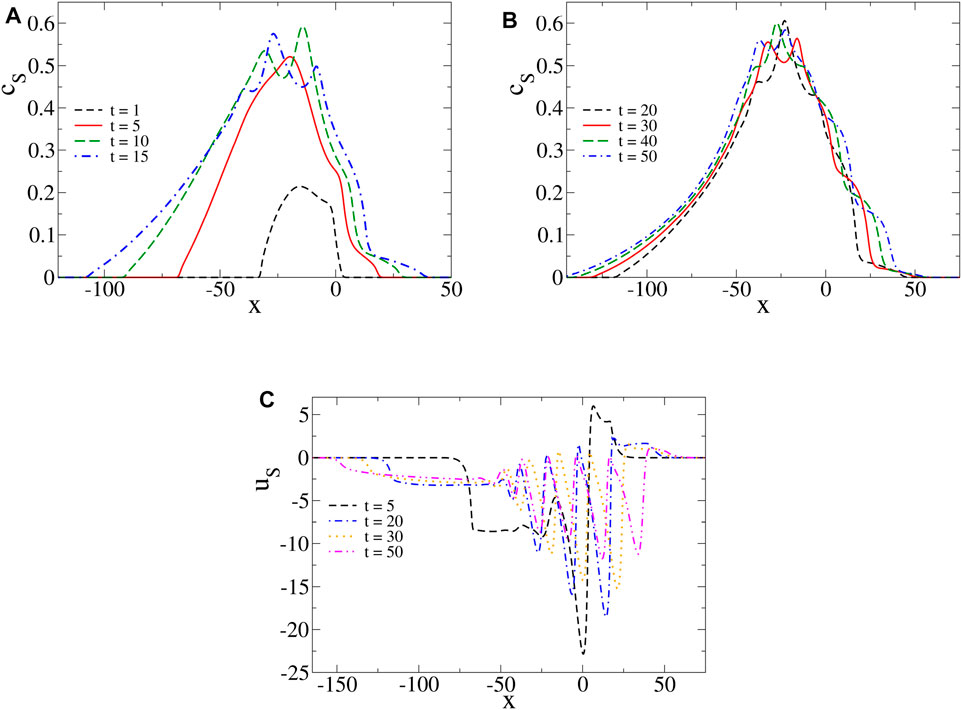
FIGURE 4. (A,B) Product concentration c_S and (C) horizontal component of the fluid velocity field u_S, at the surface, at different times and for the same parameters values as in Figure 2. We note wave-like tails in the profiles of c_S and oscillations in the profiles of u_S.

We note that the temporal oscillations of surface tension (Figure 5A) and horizontal velocity (Figure 5B) are aperiodic with irregular shapes and amplitudes. Such oscillations dampen in the course of time.

FIGURE 5

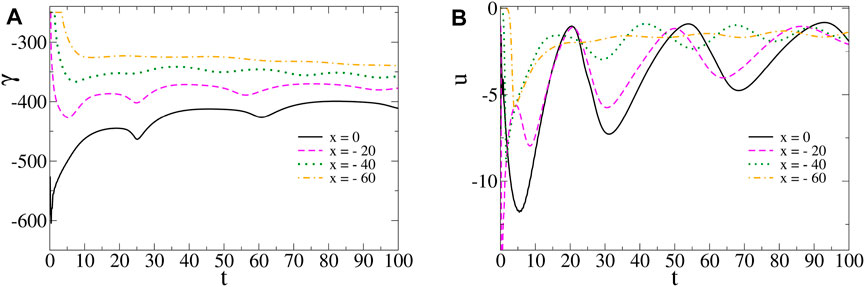
FIGURE 5. (A) Surface tension γ(x, t) and (B) horizontal component of the fluid velocity field u (x, z, t) with z = 0.90L_z, as a function of time at various spatial locations and for the same parameters values as in Figure 2. Aperiodic temporal oscillations emerge and dampen in the course of time with reducing amplitudes as we consider spatial locations further away from the center.

4 Control of the Oscillatory Dynamics

As described in Section 3, the mechanism of oscillating surface tension profiles requires the front to be (mainly) located at the free surface and to be in motion along the surface. As a result, such oscillations are prevented in the symmetric case (i.e., when β = 1 and δ_b = 1, ∀ M), where two convective rolls of identical intensity leads to a stationary front with surface tension profiles that admit either a global maximum or a global minimum (the symmetric case is described in reference Tiani and Rongy [26]). Hence, oscillations as in Figure 2 can only be triggered in an asymmetric scheme (i.e., when β ≠ 1 and/or δ_b ≠ 1).

If we arbitrary assume β > 1 (the reverse case β < 1 can be obtained straightforwardly), then γ_B < γ_A and the main (biggest) convective roll turns counterclockwise with a surface flow oriented to the left (cf: Figure 3) that brings fresh reactants B towards the side of A. In this case, we numerically find that the condition δ_b < 1, i.e. that the species A diffuses faster than B, is necessary for the oscillations to occur. Physically, this condition is expected to play the key role of bringing fresh reactants A towards the side of B to feed the reaction zone as it moves along the surface. This explanation is consistent with the variation of oscillations properties (amplitude and duration) with δ_b as explained below. When β > 1, the condition δ_b < 1 is therefore found to be essential to initiate and drive the oscillations.

The amplitude and duration of oscillations found in the profiles of surface tension critically depend on the model parameters that modulate both the intensity of convection and the diffusive fluxes of chemical species. To illustrate this, we define the maximum amplitude of the oscillations, A_max, as the maximum difference (in absolute value) of surface tension formed in the positive x-direction between a local minimum followed by a local maximum in the corresponding profiles. By following A_max in the course of time, the duration of oscillations can also be highlighted (see Figure 6).

FIGURE 6

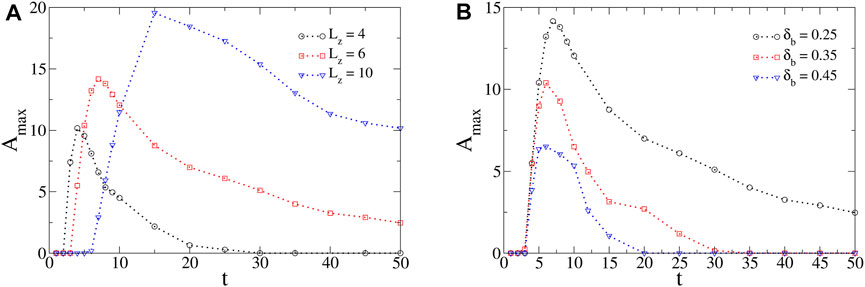
FIGURE 6. Maximum amplitude A_max of oscillations in the course of time for different values of (A) L_z and (B) δ_b. Unless varied, the values of the model parameters are M = 250, M_c = 500, δ_b = 0.25, δ_c = 0.50, β = 2 and L_z = 6. When increasing L_z or decreasing δ_b, the maximum amplitude and duration of oscillations in the profiles of surface tension are increased.

The layer thickness is a typical control parameter to modulate the intensity of Marangoni-driven flows and thus, the oscillatory dynamics. When decreasing the layer thickness, convection weakens and so does the driving force for the oscillatory process. In the limit L_z → 0, we must recover the RD surface tension profiles that cannot oscillate [28]. Hence, there exists a minimum value for the layer thickness L_z above which convection is strong enough to drive the oscillations (numerically calculated to L_z,min = 2 for our specific choice of parameters. Physically, convection is more intense by increasing L_z due to the decrease of the influence of the no-slip boundary condition at the bottom. When increasing L_z above this critical value, the maximum of A_max reached in time and the duration of the oscillatory dynamics both increase (see Figure 6A). Similarly, we find a minimum value for M (numerically calculated to M_min = 200 for the parameters chosen here) since, by increasing M, the difference of surface tension between the solutions of A and B is increased and so is the intensity of convection. Moreover, when varying δ_b, the relative importance of the diffusive fluxes towards the reaction zone are changed and so are the amplitude and duration of oscillations. In particular, when decreasing δ_b, more species A diffuse towards the side of B feeding the reaction zone as it moves along the surface. More C is therefore produced and the gradients of surface tension are enlarged. Then, the amplitude and duration of oscillations are found to be larger (see Figure 6B). Oscillations are prevented above a maximum value of δ_b (numerically evaluated to δ_b,max = 0.75 for the chosen parameters). Note that the threshold values of the model parameters are provided in this paragraph on an indicative basis only.

Thus, the onset of oscillations critically depend on the model parameters. To summarize, by varying one parameter while keeping the other ones fixed as in Figure 6, if we take β sufficiently large (more precisely, when β > β_min > 1), our numerical results indicate that oscillations emerge when δ_b < δ_b,max < 1, L_z > L_z,min, M > M_min, and for intermediate values of δ_c and M_c, where the lower and upper bounds depend on all the model parameters. We have performed the analysis up to (M, M_c) $<$ 1000, δ_b < 1 and δ_c < 15, L_z < 15, and 1 < β < 15, which defines the range of parameters values tested. We expect that the case β < 1 could be performed similarly.

5 Conclusion and Prospects

In this work, we have reported an additional mechanism for the emergence of an oscillatory dynamics unique to reactive systems where differential diffusion effects and chemically-driven Marangoni stresses are at play. Such oscillations are explained by segregated reaction zones that progressively form along the free surface in the course of time. Such segregated reaction zones increase the concentration of C at the surface reducing locally the surface tension leading to the observed oscillations in the profiles of surface tension. This mechanism of oscillations is free of chemical or prescribed hydrodynamic instability.

Next, we have shown the critical influence of the model parameters on the properties (amplitude and duration) and on the onset of oscillations. We have also provided a set of conditions on the model parameters for oscillations to occur with the restriction that M_a = M = M_b assumed for simplicity. A natural extension of this work would then be to relax those assumptions to provide a classification of the oscillatory dynamics in the full parameters space with the motivation to guide future experiments. In this context, while our results could be tested in microgravity or thin film experiments where the effects of buoyancy forces (buoyancy-driven convection) can be neglected [27], we could also include such buoyancy effects into the analysis to extend the application scope of our model to more experimental setups. We could then analyze if the presence of buoyancy forces enhances, reduces or prevents the oscillations of surface tension depending in particular on the Rayleigh number of each chemical species, which quantifies the influence of each of them on the solution density. Also, we have assumed the simplest scenario of an isothermal front traveling in adiabatic conditions (no heat loss to the surrounding). Thermal and/or heat loss effects could also be the subject of future interesting works.

As already mentioned in the introductory part, the spatio-temporal oscillations that arise from differential diffusion effects are fundamentally different from the ones described by Budroni et al. [17–19]. In that case, spatio-temporal oscillations in the velocity field and in the concentration profiles are observed when β = 1 and δ_b = 1 = δ_c, but there were no spatial oscillation of surface tension (in the sense of the formation and propagation of local extrema in such profiles). Moreover, their mechanism involves an antagonistic effect between the upward relaxation of the front driven by RD processes and the Marangoni downflow that acts to drive the product C in the opposite direction [17,18]. Here, this antagonistic effect is absent. In this sense, our results on the oscillatory dynamics are similar to those found when Marangoni flows are induced across isothermal autocatalytic fronts [12].

We hope that our results will trigger more theoretical and experimental investigations in the growing field of convective effects across traveling fronts.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

LR originally wrote the reaction-diffusion-convection code for autocatalytic fronts [12] which was adapted by RT for bimolecular fronts. The analysis of the numerical results was performed by RT under the supervision of LR. The drafts of this manuscript were written by RT and reviewed by LR. All authors have agreed with the published version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer SM declared a past collaboration with the author LR to the handling editor. The handling editor FR declared a past co-authorship with the author LR.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank the “Actions de Recherches Concertées” program and the F.R.S.-FNRS for their financial support.

References

1. Stern KH. The Liesegang Phenomenon. Chem Rev (1954) 54:79–99. doi:10.1021/cr60167a003

CrossRef Full Text | Google Scholar

2. Kapral R, Showalter K. Chemical Waves and Patterns. Dordrecht: Kluwer (1995).

Google Scholar

3. Murray JD. Mathematical Biology. Berlin: Springer-Verlag (2003).

Google Scholar

4. Volpert V, Petrovskii S. Reaction-diffusion Waves in Biology. Phys Life Rev (2009) 6:267–310. doi:10.1016/j.plrev.2009.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Stern KH. Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation. Chem Rev (2010) 329:1616.

Google Scholar

6. Gálfi L, Rácz Z. Properties of the Reaction Front in an A+B→C type Reaction-Diffusion Process. Phys Rev A (1988) 38:3151–4. doi:10.1103/physreva.38.3151

CrossRef Full Text | Google Scholar

7. Taitelbaum H, Koo Y-EL, Havlin S, Kopelman R, Weiss GH. Exotic Behavior of the Reaction Front in the A+B→C reaction-diffusion System. Phys Rev A (1992) 46:2151–4. doi:10.1103/physreva.46.2151

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Brau F, Schuszter G, De Wit A. Flow Control of A+B→C Fronts by Radial Injection. Phys Rev Lett (2017) 118:134101. doi:10.1103/physrevlett.118.134101

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Horváth D, Petrov V, Scott SK, Showalter K. Instabilities in Propagating Reaction‐diffusion Fronts. J Chem Phys (1993) 98:6332–43. doi:10.1063/1.465062

CrossRef Full Text | Google Scholar

10. Tiani R, De Wit A, Rongy L. Surface Tension- and Buoyancy-Driven Flows across Horizontally Propagating Chemical Fronts. Adv Colloid Interf Sci (2018) 255:76–83. doi:10.1016/j.cis.2017.07.020

CrossRef Full Text | Google Scholar

11. De Wit A. Chemo-Hydrodynamic Patterns and Instabilities. Annu Rev Fluid Mech (2020) 52:531–55. doi:10.1146/annurev-fluid-010719-060349

CrossRef Full Text | Google Scholar

12. Rongy L, De Wit A. Steady Marangoni Flow Traveling with Chemical Fronts. J Chem Phys (2006) 124:164705. doi:10.1063/1.2186313

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Budroni MA, Rongy L, De Wit A. Dynamics Due to Combined Buoyancy- and Marangoni-Driven Convective Flows Around Autocatalytic Fronts. Phys Chem Chem Phys (2012) 14:14619. doi:10.1039/c2cp41962a

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Rongy L, Assemat P, De Wit A. Marangoni-driven Convection Around Exothermic Autocatalytic Chemical Fronts in Free-Surface Solution Layers. Chaos (2012) 22:037106. doi:10.1063/1.4747711

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Budroni MA, De Wit A. Dissipative Structures: From Reaction-Diffusion to Chemo-Hydrodynamic Patterns. Chaos (2017) 27:104617. doi:10.1063/1.4990740

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Rana C, De Wit A. Reaction-driven Oscillating Viscous Fingering. Chaos (2019) 29:043115. doi:10.1063/1.5089028

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Budroni MA, Upadhyay V, Rongy L. Making a Simple A+B→C Reaction Oscillate by Coupling to Hydrodynamic Effect. Phys Rev Lett (2019) 122:244502. doi:10.1103/physrevlett.122.244502

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Budroni MA, Polo A, Upadhyay V, Bigaj A, Rongy L. Chemo-hydrodynamic Pulsations in Simple Batch A+B→C Systems. J Chem Phys (2021) 154:114501. doi:10.1063/5.0042560

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Budroni MA, Rossi F, Rongy L. From Transport Phenomena to Systems Chemistry: Chemohydrodynamic Oscillations in A+B→C Systems. ChemSystemsChem (2021) 3:e2100023.

Google Scholar

20. Smith MK, Davis SH. Instabilities of Dynamic Thermocapillary Liquid Layers. Part 1. Convective Instabilities. J Fluid Mech (1983) 132:119–44. doi:10.1017/s0022112083001512

CrossRef Full Text | Google Scholar

21. Nepomnyashchy AA, Velarde MG, Colinet P. Interfacial Phenomena and Convection. Boca Raton: Chapman and Hall/CRC (2002).

Google Scholar

22. Kovalchuk N. Spontaneous Oscillations Due to Solutal Marangoni Instability: Air/water Interface. Cent Eur J Chem (2012) 10:1423–41. doi:10.2478/s11532-012-0083-5

CrossRef Full Text | Google Scholar

23. Nepomnyashchy AA, Simanovskii IB. Synchronization of Marangoni Waves by Temporal Modulation of Interfacial Heat Consumption. Phys Rev Fluids (2020) 5:094007. doi:10.1103/physrevfluids.5.094007

CrossRef Full Text | Google Scholar

24. Nazareth RK, Karapetsas G, Sefiane K, Matar OK, Valluri P. Stability of Slowly Evaporating Thin Liquid Films of Binary Mixtures. Phys Rev Fluids (2020) 5:104007. doi:10.1103/physrevfluids.5.104007

CrossRef Full Text | Google Scholar

25. Nepomnyashchy AA, Simanovskii IB. Droplets on the Liquid Substrate: Thermocapillary Oscillatory Instability. Phys Rev Fluids (2021) 6:034001. doi:10.1103/physrevfluids.6.034001

CrossRef Full Text | Google Scholar

26. Tiani R, Rongy L. Influence of Marangoni Flows on the Dynamics of Isothermal A+B→C Reaction Fronts. J Chem Phys (2016) 145:124701. doi:10.1063/1.4962580

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Guyon E, Hulin J-P, Mitescu CD, Petit L. Physical Hydrodynamics. Oxford, UK: Oxford University Press (2001).

Google Scholar

28. Trevelyan PM, Almarcha C, De Wit A. Buoyancy-driven Instabilities Around Miscible A+B→C Reaction Fronts: a General Classification. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 91:023001. doi:10.1103/PhysRevE.91.023001

PubMed Abstract | CrossRef Full Text | Google Scholar