- 1Department of Physics and Astronomy “G. Galilei”, University of Padova, Padova, Italy
- 2Padua Quantum Technologies Research Center, University of Padova, Padova, Italy
- 3Department of Information Engineering, University of Padova, Padova, Italy
- 4CNR-IOM Istituto Officina dei Materiali, Trieste, Italy
The ability to encode different operations into a single miniaturized optical device is required to reduce the complexity and size of optical paths for light manipulation, which usually employs dynamic optical components, interferometric setups, and/or multiple bulky elements in cascade. A very efficient solution is provided by metalenses, which are flat optical elements able to generate and manipulate structured light beams in a compact and efficient way, offering a powerful and attractive tool in many fields, such as life science and telecommunications. In this work, we present the design and test of transmission dielectric bi-functional metalenses that exploit both the dynamic and the geometric phases, to enable the spin-controlled manipulation of different focused orbital angular momentum (OAM) beams, depending on the circularly polarized state in input. In detail, we provide numerical algorithms for the design and simulation of the meta-optics in the telecom infrared, the fabrication processes, and the optical characterization under different impinging polarized optical vortices. This solution provides new integrated flat optics for applications in imaging, optical tweezing and trapping, optical computation, and high-capacity telecommunication and encryption.
1 Introduction
Allen and co-workers’ seminal paper [1] paved the way for the research field of structured light, leading to scientific milestones and innovative applications in many areas, such as life science, information and communication technology, and quantum technologies [2–4]. In particular, wavefields carrying orbital angular momentum (OAM), so-called OAM beams or optical vortices (OVs), are endowed with peculiar ring-like intensity distributions and twisted wavefronts which revealed powerful applications in high-resolution microscopy [5], optical micro-manipulation [6–8], security [9], and light-matter interaction [10], while offering a new degree of freedom to encode information both in classical [11, 12] and single-photon regimes [13–15].
Spiral phase plates (SPPs) [16] represent one of the first stable, efficient, and compact optical elements proposed to generate structured light carrying orbital angular momentum from ordinary non-structured beams. These optics have 3D staircase profiles resembling the twisted wavefront imparted to the impinging beam [17]. It is possible to generate high-purity and multi-ring OAM beams using SPPs with both azimuthal and radial discontinuities, to enable the excitation of higher-order modes by exploiting high-resolution lithographic techniques [18–20]. Nevertheless, spiral phase plates are limited to a single functionality. The advent of metasurfaces promoted the evolution of SPPs into the so-called q-plates [21] acting on the geometric phase to impart a polarization-dependent beam shaping [21]. Rather than shaping the wavefront by changing the local thickness of an isotropic material, i.e., the dynamic phase, in q-plates the thickness is fixed while the phase is manipulated by controlling the local anisotropy of the effective material. In particular, the imparted phase is equal to twice the local orientation of the extraordinary axis, and the sign is dependent on the handedness of the circular polarization in input. The first solutions relied on controlling the inherent anisotropy of liquid crystals [21–23], then artificial anisotropy was introduced by using properly oriented digital gratings [24, 25] or dielectric resonators [26, 27], so-called metaunits, to induce an effective form of birefringence. Metasurfaces represented a revolution in optics. Moving from 3D sculptured optics to 2D flat digital meta-optics exploiting silicon manufacturing has enabled the merging of optics and silicon photonics [28, 29]. Furthermore, the metasurface paradigm has included polarization as an additional degree of freedom for light structuring, extending the optical functionalities to enable the possibility of decoupling spin from phase reshaping and building up spin-dependent optical elements [30] [31]. One solution is offered by dual-functional metasurfaces [32–35], which act locally on both the dynamic and the geometric phases. That is achieved using anisotropic nanopillars, which have different tailored shapes to act on the dynamic phase and control their local fast-axis orientation to adjust the polarization-dependent geometric phase contribution.
In this work, we present the fabrication and optical characterization of dual-functional metalenses working in the telecom infrared, specifically designed for the generation of two distinct focused OAM beams, depending on the polarization state of the impinging light. In particular, we show that by switching the input polarization handedness, it is possible to select a spin-dependent OAM shift of the desired optical vortex in input at a specific position in space. This approach improves the functionality and integration level of standard spiral phase plates and q-plates, providing new advanced optical elements for applications to high-resolution microscopy, optical micro-manipulation, and classical and quantum information.
2 Material and methods
2.1 Dual-functional metalenses design
In this work, we propose a spin-dependent dielectric metasurface made of a squared lattice (period of the lattice u = 600 nm) of birefringent metaunits (MUs), so-called metaatoms (MAs), acting both on the geometric and dynamic phases. Each metaunit is represented by a crystalline silicon (c-Si) nanofin on a c-Si substrate. The cross-section of each metaunit is chosen within a library of 13 different nanostructures with different shapes and/or orientations but the same height. In detail, as reported in our previous works [36], we find a set of rectangular-based, elliptical-based and pairs of different bevelledrectangular-based nanofins. At the same time, the height was optimized at 850 nm in order to cover the 0-2π dynamic phase range that is mandatory to satisfy the dual-functional paradigm. Since the metaunit size is below the diffraction limit, input light experiences an effective uniaxial medium with dynamic phase delays δx and δy on the two axes, referring to TM and TE linear polarizations, respectively. All the nanostructures of the library act as half-wave plates (HWP) in order to maximize the polarization conversion and, therefore, the optical efficiency [37–39]. Then, a rotation by an angle θ of the anisotropic metaunit introduces a spin-dependent geometric phase equal to ±
The objective is that two circularly polarized beams with opposite handedness (i.e., RCP and LCP) experience different phase patterns
While the dynamic phase imparts the same contribution to both the RCP and LCP input beams, the geometric phase implies the transfer of symmetrical (opposite) phase delays for the two circularly polarized states, which combine to induce the desired spin-dependent phase modulation, that is:
J is the Jones matrix of the anisotropic metaatom [40, 41].
As well known, it is possible to describe a linearly polarized beam as the linear combination of a left-handed circularly polarized state (
As we are interested in generating focused OAM beams, we need to properly design the local phase delay imparted by each metaunit in order to transfer the desired topological charge and focus the optical vortex onto two distinct points in space. To this aim, we encoded a converging lens profile
being
To impart two different topological charges in two distinct positions, we can rewrite Eq. (6) using the notations of Eqs 4, 5:
where
2.2 FEM simulations
The library of metaatoms was extrapolated by performing numerical simulations with Finite-Element Method (FEM) in the wavelength domain (COMSOL Multiphysics®). Each subunit was modelled as a silicon nanopillar (nSi = 3.5030) surrounded by air (nAir = 1) designed on the top of a silicon substrate (nSi = 3.5030), and all the materials were considered as non-absorbing [n = Re(n), Im(n) = 0]. Among all the possible configurations, a set of 13 pillars has been selected, covering the whole 2π range of dynamic phase and satisfying the conditions of half-wave plate and equal transmissions for TE and TM polarizations. Full details regarding metaunits shape and corresponding phase delays are reported in [36]. In detail, to ensure the HWP behaviour of each meta-unit, we selected metaatoms having a maximum phase difference of 0.03 rad from the HWP condition (
2.3 Fabrication
The designed metaoptics was fabricated via a two-step fabrication procedure. High-resolution electron beam lithography (EBL) was employed to transfer the optimized computational pattern onto a resist layer. In particular, a thin PMMA resist layer, deposited on a ⟨100⟩ silicon substrate, was patterned using an EBL system (Carl Zeiss Sigma 300, 30 keV beam voltage). Subsequently, a lift-off process was executed exploiting a thin mask of Al2O3. Finally, the pattern was transferred onto the underlying silicon substrate through Inductively Coupled Plasma Reactive Ion Etching (ICP-RIE). ICP-RIE was performed in a STS Multiplex ASE using a mixture of SF6:C4F8:Ar (3:6:1). The plasma conditions and etching time were optimized in order to reach the optimal thickness and, thus, reduce the zero-order contribution [47, 48].
2.4 Optical characterization setup
The beam illuminating the metasurface was produced employing a Liquid Crystal on Silicon (LCoS) spatial light modulator (SLM) (X13267-08, Hamamatsu, pixel pitch 12.5 μm) through a technique involving both phase and amplitude modulation. Collimation of the output from a DFB laser (λ = 1310 nm, 1310LD34 1-2-2-1 CCSI, AeroDiode) at the termination of a single mode fiber was achieved using an aspheric lens with a focal length of 7.5 mm (A375TM-C, Thorlabs). The beam was then linearly polarized (LPIREA100-C, Thorlabs), expanded by a first telescope (f1 = 3.5 cm, f2 = 10.0 cm), and directed towards the display of the SLM for reshaping and/or optical vortex generation (Figure 1).
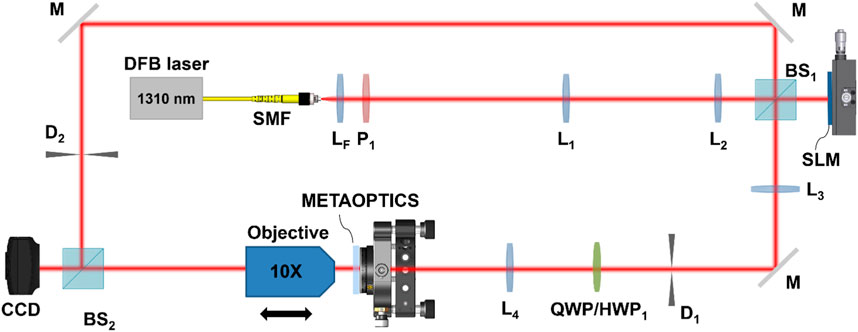
Figure 1. Scheme of the optical setup. The output of a DFB laser at 1,310 nm is collimated (LF), polarized (P1), and resized (L1, L2) before illuminating a LCoS SLM for phase manipulation and reshaping. A 50:50 beam-splitter (BS1) is used to separate the input beam and the reflected structured one, which is filtered (D1) and resized (L3, L4) before illuminating the metalens. A quarter-wave plate (QWP) or a half-wave plate (HWP) are used for polarization control. The output beam is expanded and collected on a CCD camera. A second arm can be activated (D2) and overlapped (BS2) to the output beam for interferometric analysis. M, mirrors.
A 50:50 beam-splitter was positioned before the SLM, directing the reflected structured beam into the desired optical path and enabling an additional optical path for interferometric analysis. A 4-f system (f3 = 20.0 cm, f4 = 12.5 cm) was put in cascade with an aperture in the Fourier plane to isolate the first-order encoded mode and adjust the desired illuminating beam waist. In between, a quarter-wave plate (QWP) (WPQ10M-1310, Thorlabs) or a half-wave plate (HWP1) (WPH05M-1310, Thorlabs) were used to generate circularly polarized states from the original horizontally polarized one or rotate the polarization plane of the beam exiting the SLM, respectively. The polarized beam illuminated the meta-optics, mounted on a 6-axis kinematic mount (K6XS, Thorlabs). Finally, the OAM-shifted beam was collected using a ×10 Objective (CFI E Plan Achromat ×10, Nikon) positioned on a micrometric translator stage (LX20/M, Thorlabs). The image was captured by a CCD camera (WiDy SWIR 640U-S, pixel pitch 12.5 μm). It was possible to generate an interferometric pattern using the additional optical arm, opening the iris (D2). The microscope objective was necessary to properly extract and magnify the generated beams since the focal lengths were too short to collect the beam directly on the CCD camera.
3 Results
Exploiting the dual-functional mechanism described in the previous section, we designed a spin-decoupled metalens which imparts two different topological charges
At first, we simulated the spin-decoupled behavior under the illumination of a Gaussian beam with a waist of 175 µm. To test the two different polarization-dependent responses simultaneously, we chose a linearly polarized light in input.
Figure 2 depicts, as expected, the simultaneous generation of two distinct OAM beams with the desired topological charges at 500 µm and 1000 µm. It is clear how the beam generated from the right-handed contribution has a larger waist and a lower intensity profile because it carries a higher topological charge and is focused on a plane placed at a larger distance.
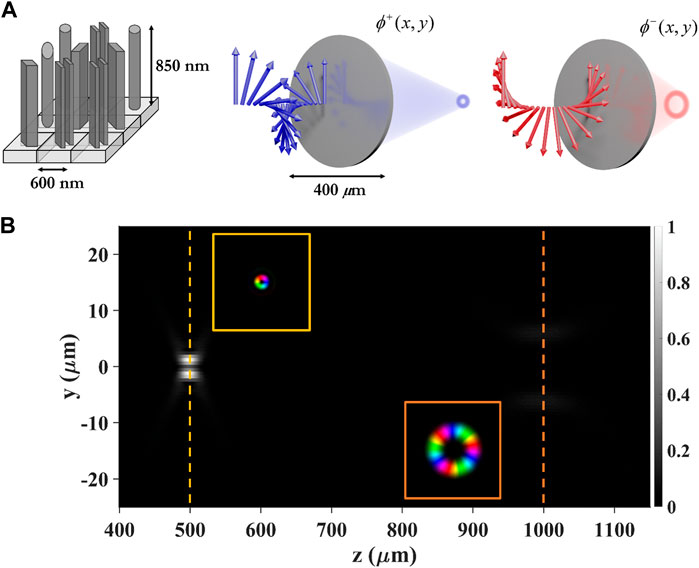
Figure 2. Metalenses schematization and bi-functionality simulation. (A) Schematization of some metaunits and whole optics features comprising the dual-functionality mechanism. (B) Numerical output under linear polarization and null topological charge (standard Gaussian beam) in input: two optical vortices with different topological charges are generated on two distinct focal planes: ℓ+ = 1 at z = 500 μm, ℓ− = 3 at z = 1000 μm.
Then, we simulated the behaviour of the metalens under the illumination of beams that already carry a topological charge (i.e., from −3 to 3). In particular, we modelled the impinging structured beam as a perfect vortex (PV) having a ring radius (
Figure 3 presents the results we have obtained. In the first row (in blue), the phase and intensity pattern of the impinging perfect vortex are reported. The second (yellow) and third (orange) rows report the generated structured beams under LCP and RCP illumination, respectively. Due to the half-wave plate behaviour, each metaatom reverses the handedness of the impinging light as reported in Eqs 4, 5, so the OAM beam focused at 500 µm is right-handed circularly polarized. Instead, the one generated at 1,000 µm is left-handed circularly polarized. As expected, we can see that the metalens acts as a dual-functional shifter of topological charge. In fact, the resulting generated beam carries a topological charge
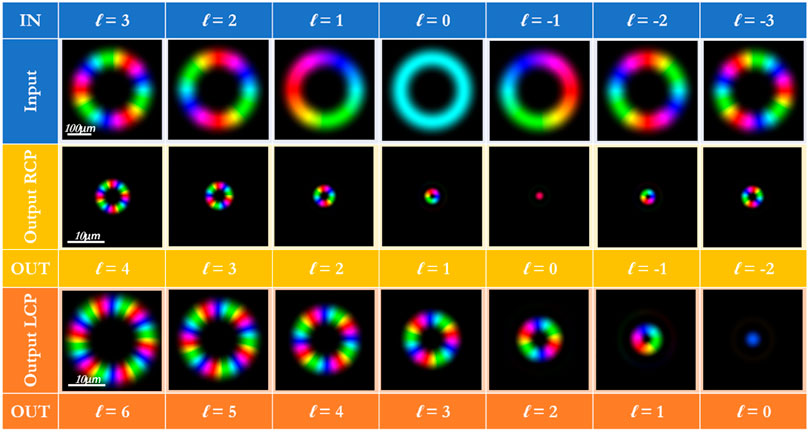
Figure 3. Numerical simulation under circularly polarized optical vortices in input. Numerical simulations of the metalens output when illuminated with circularly polarized perfect vortices of different topological charge in the range between ℓ = −3 and ℓ = +3. Depending on the handedness of the input beam, the optical vortex experiences polarization conversion and an OAM-shift equal to +1 or +3.
Subsequently, we numerically estimated the purity of the generated OAM modes by analyzing the OAM spectrum of the generated beam
where
In Figure 4, we report the OAM spectrum analysis of the output beams under the illumination conditions mentioned above. The OAM shift of the output beams with respect to the input one confirms what expected from the metalens design. The generated OAM beams show no significative presence of spurious terms for the two outgoing circularly polarized beams. The spurious contributions are lower than 0.05 for all the different impinging configurations, proving that the conversion efficiency is very high.
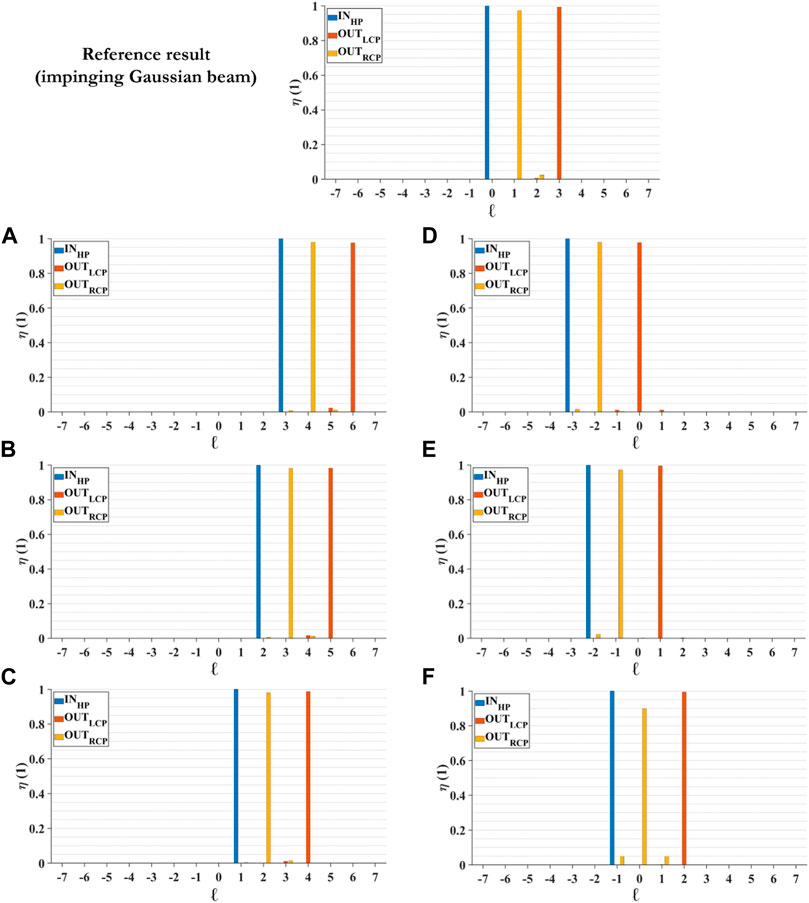
Figure 4. Purity numerical analysis. OAM-spectrum of input (blue) and output (yellow, orange) optical vortices. As expected, the output beams experience a polarization-dependent OAM shift. Input OAM equal to +3 (A), +2 (B), +1 (C), −3 (D), −2 (E), −1 (F).
Then, we fabricated the metasurface with a radius of 400 µm using the procedure described in Section 2.3.
Figure 5 displays several SEM images of the fabricated silicon metasurface.

Figure 5. Fabrication. SEM inspection of the silicon metalens at different magnifications. (A) Top view. (B) Tilted view at higher magnification.
Finally, we optically characterized the performances of the designed metalens using the optical setup reported in Section 2.4. As expected, the two output beams present an intensity pattern that varies depending on the impinging perfect vortex, suggesting an increase of the output orbital angular momentum, because of the interaction with the metalens (Figure 6B). To confirm this, we measured the interferogram pattern, which gave us information on the carried phase. It is clearly visible that the number of arms of the spiral, indicating the topological charge carried by the beam, are dictated by the sum of the impinging OAM plus the charge imparted by the metalens, which depends on the polarization state (Figure 6A).
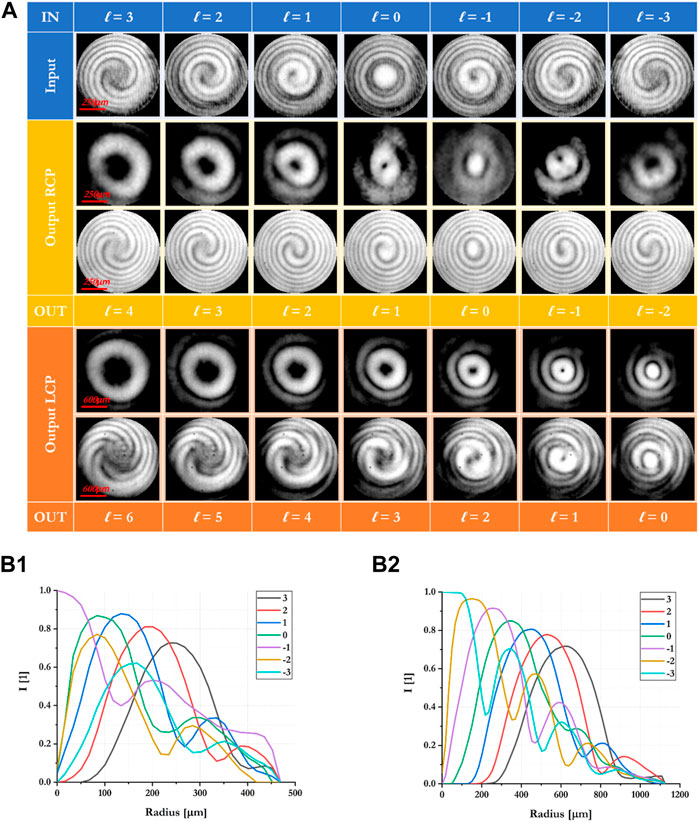
Figure 6. Experimental characterization and intensity radial profile. (A) Experimental analysis of the metalens output when illuminated with circularly-polarized perfect vortices of different topological change in the range between ℓ = −3 and ℓ = +3. Depending on the handedness of the input beam, the optical vortex experiences an OAM-shift equal to +1 or +3 and polarization conversion, as expected. Counting the number of spiral arms in the interferograms it is possible to infer the carried OAM and prove the output OAM shift with respect to the input one. (B) Intensity radial profile for right-handed (B1) and left-handed (B2) circularly polarized optical vortices as a function of the input OAM.
4 Discussion and conclusion
This work presents the design, fabrication, and test of dual-functional silicon metalenses for the polarization-controlled manipulation of OAM beams. The optical element was designed to properly generate different non-overlapping focused beams carrying orbital angular momentum depending on the polarization state of the illuminating light. This optical behaviour is achieved by exploiting the dual-functional metalens capability to act on the dynamic and geometric phases simultaneously in order to introduce spin-dependent phase delays. The metaoptics has been fabricated using a two-step process: lithography of a resist mask with EBL and subsequent pattern transfer into the silicon substrate using ICP-RIE. Finally, we have characterized the optical response of the fabricated metalens to prove the effective polarization-dependent device as a topological charge shifter. The experimental results agree with the simulations, proving the design quality and the fabrication protocols optimization. While in this paper we present the generation of OAM beam, the method can be extended to the design of any metaoptics aimed to impart given phase patterns with high dimensionality or complex symmetry [50] to the different impinging circularly polarized states of light. In particular, we generated a single wavelength library, but by selecting more complicated coupled resonant metaunits, it is possible to achieve full achromaticity [51, 52]. Dual-functionality represents a tool that boosts the optical operations of previous optical devices, such as diffractive elements or metasurfaces acting only on geometric or dynamic phases. This attractive solution can inspire advanced applications in imaging, microscopy, particle manipulation, and quantum technologies, wherever tiny and compact multi-functional optical devices, fabricated using silicon technology manufacturing, are required.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, with under reasonable request.
Author contributions
AV: Conceptualization, Methodology, Software, Writing–original draft, Writing–review and editing. DB: Methodology, Writing–original draft, Writing–review and editing. SD: Methodology, Writing–original draft, Writing–review and editing. FR: Funding acquisition, Supervision, Writing–original draft, Writing–review and editing. GR: Funding acquisition, Supervision, Writing–original draft, Writing–review and editing, Methodology, Software.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the project STRADA (Italian Presidency of the Council of Ministers) and also partially supported by the European Union under the Italian National Recovery and Resilience Plan (NRRP) of NextGenerationEU, partnership on “Telecommunications of the Future” (PE0000001–program “RESTART”).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/physreva.45.8185
2. Rubinsztein-Dunlop H, Forbes A, Berry MV, Dennis MR, Andrews DL, Mansuripur M, et al. Roadmap on structured light. J Opt (2016) 19:013001. doi:10.1088/2040-8978/19/1/013001
3. Padgett MJ. Orbital angular momentum 25 years on [Invited]. Opt Express (2017) 25(10):11265–74. doi:10.1364/oe.25.011265
4. Shen Y, Wang X, Xie Z, Min C, Fu X, Liu Q, et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light: Sci Appl (2019) 8(1):90. doi:10.1038/s41377-019-0194-2
5. Willig KI, Harke B, Medda R, Hell SW. STED microscopy with continuous wave beams. Nat Methods (2007) 4(11):915–8. doi:10.1038/nmeth1108
6. Padgett M, Bowman R. Tweezers with a twist. Nat Photon (2011) 5(6):343–8. doi:10.1038/nphoton.2011.81
7. Tian Y, Wang L, Duan G, Yu L. Multi-trap optical tweezers based on composite vortex beams. Opt Commun (2021) 485:126712. doi:10.1016/j.optcom.2020.126712
8. MacDonald MP, Paterson L, Volke-Sepulveda K, Arlt J, Sibbett W, Dholakia K. Creation and manipulation of three-dimensional optically trapped structures. Science (2002) 296(5570):1101–3. doi:10.1126/science.1069571
9. Zhang F, Guo Y, Pu M, Chen L, Xu M, Liao M, et al. Meta-optics empowered vector visual cryptography for high security and rapid decryption. Nat Commun (2023) 14(1):1946. doi:10.1038/s41467-023-37510-z
10. Lembessis VE, Babiker M. Enhanced quadrupole effects for atoms in optical vortices. Phys Rev Lett (2013) 110(8):083002. doi:10.1103/physrevlett.110.083002
11. Wang J. Twisted optical communications using orbital angular momentum. China Phys Mech Astron (2019) 62(3):34201. doi:10.1007/s11433-018-9260-8
12. Wan Z, Wang H, Liu Q, Fu X, Shen Y. Ultra-degree-of-freedom structured light for ultracapacity information carriers. ACS Photon (2023) 10(7):2149–64. doi:10.1021/acsphotonics.2c01640
13. Sit A, Bouchard F, Fickler R, Gagnon-Bischoff J, Larocque H, Heshami K, et al. High-dimensional intracity quantum cryptography with structured photons. Optica (2017) 4(9):1006–10. doi:10.1364/optica.4.001006
14. He C, Shen Y, Forbes A. Towards higher-dimensional structured light. Light: Sci Appl (2022) 11(1):205. doi:10.1038/s41377-022-00897-3
15. De Oliveira M, Nape I, Pinnell J, TabeBordbar N, Forbes A. Experimental high-dimensional quantum secret sharing with spin-orbit-structured photons. Phys Rev A (2020) 380 101(4):042303. doi:10.1103/physreva.101.042303
16. Khonina SN, Kotlyar VV, Shinkaryev MV, Soifer VA, Uspleniev GV. The phase rotor filter. J Mod Opt (1992) 39:1147–54. doi:10.1080/09500349214551151
17. Turnbull GA, Robertson DA, Smith GM, Allen L, Padgett MJ. The generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phase plate. Opt Commun (1996) 127:183–8. doi:10.1016/0030-4018(96)00070-3
18. Massari M, Ruffato G, Gintoli M, Ricci F, Romanato F. Fabrication and characterization of high-quality spiral phase plates for optical applications. Appl Opt (2015) 54(13):409 4077–83. doi:10.1364/ao.54.004077
19. Ruffato G, Massari M, Romanato F. Generation of high-order Laguerre–Gaussian modes by means of spiral phase plates. Opt Lett (2014) 39(17):5094–7. doi:10.1364/ol.39.005094
20. Ruffato G, Massari M, Carli M, Romanato F. Spiral phase plates with radial discontinuities for the generation of multiring orbital angular momentum beams: fabrication, characterization, and application. Opt Eng (2015) 54(11):111307. doi:10.1117/1.oe.54.11.111307
21. Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys Rev Lett (2006) 96:163905. doi:10.1103/physrevlett.96.163905
22. Brasselet E. Tunable high-resolution macroscopic self-engineered geometric phase optical elements. Phys Rev Lett (2018) 121(3):033901. doi:10.1103/physrevlett.121.033901
23. Ruffato G, Brasselet E, Massari M, Romanato F. Electrically activated spin-controlled orbital angular momentum multiplexer. Appl Phys Lett (2018) 113(1):011109. doi:10.1063/1.5030844
24. Desiatov B, Mazurski N, Fainman Y, Levy U. Polarization selective beam shaping using nanoscale dielectric metasurfaces. Opt Express (2015) 23(17):22611–8. doi:10.1364/oe.23.022611
25. Ruffato G, Romanato F. Design of continuously variant metasurfaces for conformal transformation optics. Opt Express (2020) 28(23):34201–18. doi:10.1364/oe.400627
26. Devlin RC, Ambrosio A, Wintz D, Oscurato SL, Zhu AY, Khorasaninejad M, et al. Spin-to-orbital angular momentum conversion in dielectric metasurfaces. Opt Express (2017) 25(1):377–93. doi:10.1364/oe.25.000377
27. Chen MH, Liu YL, Su VC. Gallium nitride-based geometric and propagation metasurfaces for vortex beam emissions. Heliyon (2024) 10(3):e25436. doi:10.1016/j.heliyon.2024.e25436
28. Genevet P, Capasso F, Aieta F, Khorasaninejad M, Devlin R. Recent advances in planar optics: from plasmonic to dielectric metasurfaces. Optica (2017) 4:139–52. doi:10.1364/optica.4.000139
29. Capasso F. The future and promise of flat optics: a personal perspective. Nanophotonics (2018) 7(6):953–7. doi:10.1515/nanoph-2018-0004
30. Devlin RC, Ambrosio A, Rubin NA, Mueller JPB, Capasso F. Arbitrary spin-to–orbital angular momentum conversion of light. Science (2017) 358(6365):896–901. doi:10.1126/science.aao5392
31. Huo P, Zhang C, Zhu W, Liu M, Zhang S, Zhang S, et al. Photonic spin-multiplexing metasurface for switchable spiral phase contrast imaging. Nano Lett (2020) 20(4):2791–8. doi:10.1021/acs.nanolett.0c00471
32. Li S, Li X, Zhang L, Wang G, Zhang L, Liu M, et al. Efficient optical angular momentum manipulation for compact multiplexing and demultiplexing using a dielectric metasurface. Adv Opt Mater (2020) 8(8), 1901666. doi:10.1002/adom.201901666
33. Guo Y, Zhang S, Pu M, He Q, Jin J, Xu M, et al. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation. Light: Sci Appl (2021) 10(1):63–1. doi:10.1038/s41377-021-00497-7
34. Su VC, Chiang CH, Chen MH, Xu KL, Huang SY. Metasurface-based perfect vortex beam for optical eraser. Commun Phys (2024) 7(1):36. doi:10.1038/s42005-024-01525-9
35. Zhao H, Wang X, Liu S, Zhang Y. Highly efficient vectorial field manipulation using a transmitted tri-layer metasurface in the terahertz band. Opto-Electronic Adv (2023) 6(2):220012–1. doi:10.29026/oea.2023.220012
36. Vogliardi A, Ruffato G, Dal Zilio S, Bonaldo D, Romanato F. Dual-functional metalenses for the polarization-controlled generation of focalized vector beams in the telecom infrared. Sci Rep (2023) 13(1):10327. doi:10.1038/s41598-023-36865-z
37. Lin D, Fan P, Hasman E, Brongersma ML. Dielectric gradient metasurface optical elements. Science (2014) 345(6194):298–302. doi:10.1126/science.1253213
38. Khorasaninejad M, Crozier KB. Silicon nanofin grating as a miniature chirality-distinguishing beam-splitter. Nat Comm. (2014) 5(1):5386–6. doi:10.1038/ncomms6386
39. Zheng G, Mühlenbernd H, Kenney M, Li G, Zentgraf T, Zhang S. Metasurface holograms reaching 80% efficiency. Nat Nanotech (2015) 10(4):308–12. doi:10.1038/nnano.2015.2
40. Vogliardi A, Romanato F, Ruffato G. Design of dual-functional metaoptics for the spin-controlled generation of orbital angular momentum beams. Front Phys (2022) 10:586. doi:10.3389/fphy.2022.870770
41. Zhang K, Yuan Y, Ding X, Ratni B, Burokur SN, Wu Q. High-efficiency metalenses with switchable functionalities in microwave region. ACS Appl Mater Inter (2019) 11(31):28423–30. doi:10.1021/acsami.9b07102
43. Su VC, Huang SY, Chen MH, Chiang CH, Xu KL. Optical metasurfaces for tunable vortex beams. Adv Opt Mater (2023) 11(24):2301841. doi:10.1002/adom.202301841
44. Aieta F, Genevet P, Kats M, Capasso F. Aberrations of flat lenses and aplanatic metasurfaces. Opt Express (2013) 21(25):31530–9. doi:10.1364/oe.21.031530
45. Aieta F, Genevet P, Kats MA, Yu N, Blanchard R, Gaburro Z, et al. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett (2012) 12(9):4932–6. doi:10.1021/nl302516v
47. Vogliardi A, Ruffato G, Bonaldo D, Dal Zilio S, Romanato F. Silicon metaoptics for the compact generation of perfect vector beams in the telecom infrared. Opt Lett (2023) 48(18):4925–8. doi:10.1364/ol.501239
48. Vogliardi A, Ruffato G, Bonaldo D, Dal Zilio S, Romanato F. All-dielectric metaoptics for the compact generation of double-ring perfect vector beams. Nanophotonics (2023) 12(22):4215–28. doi:10.1515/nanoph-2023-0555
49. Ruffato G, Massari M, Romanato F. Multiplication and division of the orbital angular momentum of light with diffractive transformation optics. Light: Sci Appl (2019) 8(1):113. doi:10.1038/s41377-019-0222-2
50. Shen Y. Rays, waves, SU (2) symmetry and geometry: toolkits for structured light. J Opt (2021) 23(12):124004. doi:10.1088/2040-8986/ac3676
51. Chen WT, Zhu AY, Capasso F. Flat optics with dispersion-engineered metasurfaces. Nat Rev Mater (2020) 5:604–20. doi:10.1038/s41578-020-0203-3
Keywords: metalens, meta-optics, flat optics, orbital angular momentum, structured light
Citation: Vogliardi A, Bonaldo D, Dal Zilio S, Romanato F and Ruffato G (2024) Design, fabrication, and test of bi-functional metalenses for the spin-dependent OAM shift of optical vortices. Front. Phys. 12:1381156. doi: 10.3389/fphy.2024.1381156
Received: 02 February 2024; Accepted: 04 April 2024;
Published: 07 May 2024.
Edited by:
Bertrand Kibler, UMR6303 Laboratoire Interdisciplinaire Carnot de Bourgogne (ICB), FranceReviewed by:
Vin-Cent Su, National United University, TaiwanYijie Shen, Nanyang Technological University, Singapore
Copyright © 2024 Vogliardi, Bonaldo, Dal Zilio, Romanato and Ruffato. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gianluca Ruffato, Z2lhbmx1Y2EucnVmZmF0b0B1bmlwZC5pdA==
 Andrea Vogliardi
Andrea Vogliardi Daniele Bonaldo2,3
Daniele Bonaldo2,3 Simone Dal Zilio
Simone Dal Zilio Filippo Romanato
Filippo Romanato Gianluca Ruffato
Gianluca Ruffato