Abstract
This paper provides a comprehensive overview of the development of flux-driven Josephson Parametric Amplifiers (JPAs) as Quantum Noise Limited Amplifier for axion search experiments conducted at the Center for Axion and Precision Physics Research (CAPP) of the Institute for Basic Science. It focuses on the characterization, and optimization of JPAs, which are crucial for achieving the highest sensitivity in axion particle detection. We discuss various characterization techniques, methods for improving bandwidth, and the attainment of ultra-low noise temperatures. JPAs have emerged as indispensable tools in CAPP’s axion search endeavors, playing a significant role in advancing our understanding of fundamental physics and unraveling the mysteries of the Universe.
1 Introduction
CAPP was established in October 2013, entering the realm of axion physics following the notable contributions of experiments like the Axion Dark Matter Experiment (ADMX), Haloscope At Yale Sensitive To Axion Cold dark matter (HAYSTAC), etc. [1–4]. These experiments paved the way for axion research, and CAPP aimed to build on these achievements. It focused on establishing itself as a significant player in the field by pushing the boundaries in all relevant parameters and expanding the detection sensitivity.
It is extremely difficult to observe axions because of their weak interactions with Standard Model (SM) fields. In the presence of a magnetic field, an axion with a mass of and momentum generates an electric field described by the Lagrangian (Eq. 1),where is axion to two-photon coupling constant [5]; is the axion dark matter field [6, 7] and are external magnetic and generated electrical field, respectively. Alternatively, it can be said that in the presence of a magnetic field, the axion field mixes with the electromagnetic field of same frequency. The resulting field has frequency defined by the simple equation (Eq. 2):Here, and represent the Planck constant and the speed of light in vacuum, respectively. The kinetic energy of virialized axions is small, however, this kinetic energy broadens the line following a Maxwellian distribution with an equivalent quality factor of [8]. To enhance the signal, we can adopt the haloscope concept introduced by Sikivie in 1983 [9] and first applied in 1987 by the authors of [10]. Sikivie’s proposed experimental setup involves a detector consisting of a microwave cavity resonator immersed in a strong magnetic field and cooled to cryogenic temperatures. The cavity plays a crucial role in resonantly accumulating the produced photons from the converted axion dark-matter field. When the frequency of the axion signal aligns with the resonance of the cavity, it may be observed using specialized low-noise readout equipment.
2 Haloscope
The axion haloscope employs a cavity with a high-quality factor, positioned within a strong magnetic field for the detection of signals arising when the axion frequency aligns with the cavity’s resonance. For the output signal power in haloscope experiments a larger magnetic field and cavity volume result in a greater conversion of axions into microwave photons (Eq. 3) [11]:where is the coupling constant of the axion-photon interaction with values of and 0.36 for the Kim-Shifman-Vainshtein-Zakharov (KSVZ) [12, 13] and Dine-Fischler-Srednicki-Zhitnitskii (DFSZ) [14, 15] models, respectively; is the fine structure constant; , and are the decay constant, local halo density and mass of the axion dark matter, respectively. is the coupling constant between the cavity and the readout system, with the term defining the fraction of the output power. is the cavity resonance frequency; is the magnetic permeability of free space; symbolizes the external magnetic field; , and are the cavity volume, form factor for a particular mode, in our case , and the cavity loaded quality factor, . The form factor characterizes the degree of overlap between the cavity mode and the external magnetic field (Eq. 4) [16]:where is the relative permittivity within the cavity. A higher quality factor ensures that converted microwave photons persist within the cavity for extended durations, thereby amplifying the signal. Reducing the physical temperature of the cavity and minimizing noise from the receiver chain, further enhance the efficiency of axion detection.
In haloscope experiments, the typical cavity shape is cylindrical, fitting efficiently into the design of a regular solenoid superconducting magnet, making optimal use of the magnet’s bore volume. The cavity commonly utilizes the mode, where the electric field aligns with the cylinder’s axis and results in the maximum form factor. The central frequency of the cavity is primarily determined by its inner diameter. To precisely set the resonance frequency, one or more tuning rods, movable inside the cavity, are employed. Dielectric materials or highlyconductive metals are chosen for the tuning rod based on the desired frequency.
To access the cavity signal, a movable antenna is employed to optimize the coupling . As indicated in Eq. 3, the output power strongly depends on cavity parameters , , and . This necessitates optimization of the cavity design, considering the impact of tuning rods on and aiming to avoid mode cross-coupling. The axion conversion power in the experiments performed at CAPP typically lays in a range between to W. Such minuscule power levels impose stringent demands on the initial stage of our readout system.
The signal frequency is linked to the axion’s mass , an attribute that is currently unknown. Therefore, it is necessary to scan across an extensive frequency spectrum to maximize the probability of capturing this signal. The speed at which this frequency scan can be executed [8]: denotes the chosen signal-to-noise ratio (for the average of 5 and the threshold of 3.7 for a confidense level of 90%); represents the data acquisition (DAQ) efficiency; is the system noise temperature.
Consequently, the scanning frequency rate is inversely proportional to the square of the total system noise. Hence, one of our primary goals is to minimize it, thereby augmenting of our scanning speed. System noise emanates from multiple sources within our setup, encompassing noise generated by the cavity, other passive components and the amplifiers. To achieve the lowest noise levels, it is imperative to cool down all readout components to temperatures lower than, , where are the Boltzmann constants, respectively, and denotes the minimum scanning frequency of the cavity.
The most advanced amplifiers are capable of approaching noise levels close to the quantum limit. This article is dedicated to the adaptation and application of such amplifiers. In the following sections, we will elaborate on our measurement techniques for the JPAs, present their key parameters, and showcase both single JPA and multiple JPA readouts, including their respective noise characteristics.
3 Flux-driven JPA
In the earlier stages of CAPP axion search experiments, such as CAPP-9 T and CAPP-PACE [17, 18], we utilized state-of-the-art semiconductor amplifiers. The InP high-electron-mobility transistor (HEMT) is renowned for its ability to provide the lowest noise temperature in cryogenic low noise amplifier (LNA) applications. We employed the amplifiers LNF-LNC06_2A, manufactured by Low Noise Factory, which is specifically designed for cryogenic use [19]. These devices exhibit exceptionally low noise temperatures, reaching about 1.2 K when operated at temperatures below 10 K for frequencies around 1 GHz [20]. These experiments demonstrated CAPP’s capability to create a high-quality radio-frequency (RF) tunable cavity, maintain low temperatures, and operate a strong superconducting magnet in persistent mode [17, 18]. It also provided invaluable experience in data collection and processing. However, readouts chain based on cryogenic HEMT amplifiers have noise levels several tens of times higher than the quantum noise limit. For this case it would take several decades to scan the range between 1 and 2 GHz with DFSZ sensitivity.
3.1 JPA design
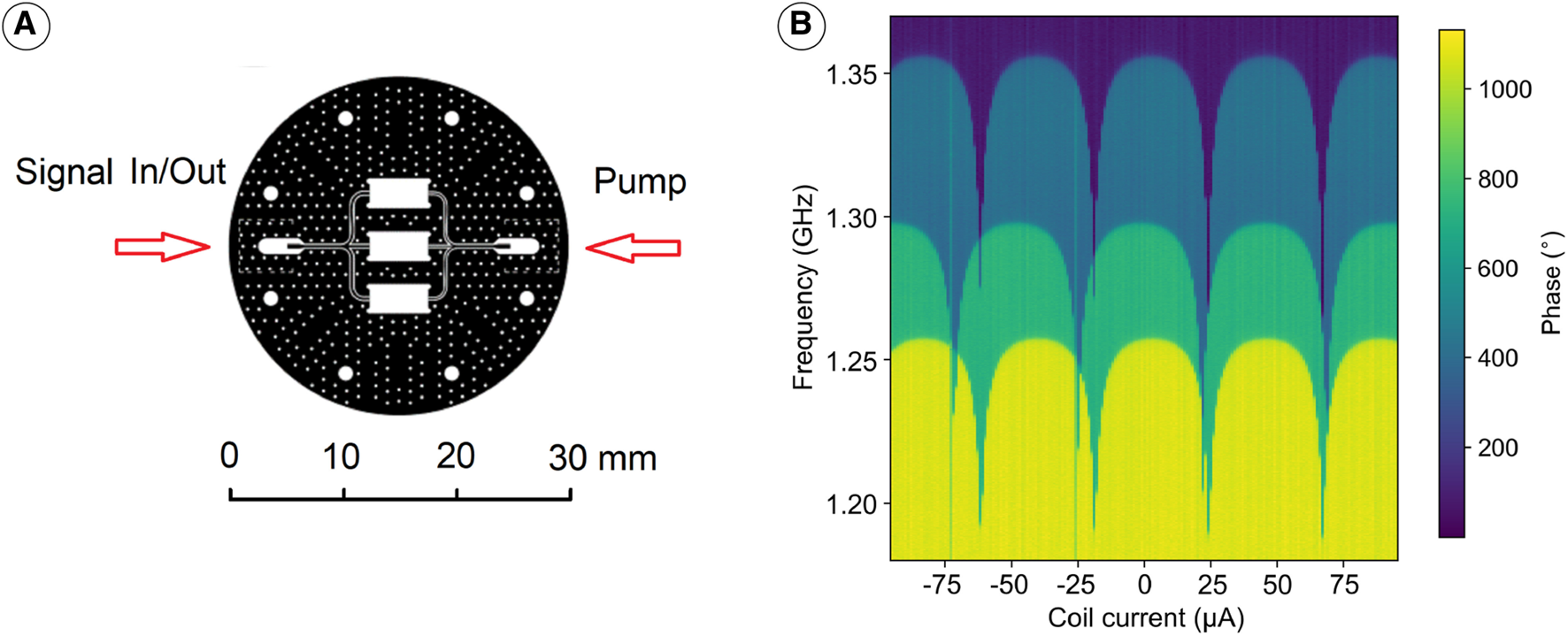
Despite significant advancements in the simulation and development of wideband Josephson amplifiers, such as traveling wave JPAs and impedance-transformed parametric amplifiers (see, for instance [21–32]), we have not identified one that operates within our required frequency range and maintains consistent 10 kHz frequency increments for gain and noise characterization across the entire range from 1 to 2 GHz. To achieve near-quantum-noise-limited amplification, we use a flux-driven JPA designed and fabricated for these experiments in RIKEN and the University of Tokyo [33]. This JPA design consists of a resonator terminated by a superconducting quantum interference device (SQUID), as depicted in Figure 1. The main features of the devices are defined by using photolithography techniques on Nb film deposited on a 0.3-mm-thick silicon substrate. The SQUID, using Dolan-bridge type junctions [34], is fabricated using electron-beam lithography followed by shadow evaporation of aluminium. Its inner loop has a diameter of roughly 16 m, and the junctions are designed to have identical critical currents of approximately 2 A. The SQUID connects the resonator to ground. A pump line couples inductively to the SQUID, delivering a modulated flux at twice the resonance frequency. This pump signal is rejected by the resonator as it only permits odd harmonics, and therefore does not couple into the signal input-output line. The pump line is shunted to ground close to the SQUID location, improving the inductive coupling. A static magnetic field generated by a superconducting coil is used to tune the frequency of the JPA.
FIGURE 1
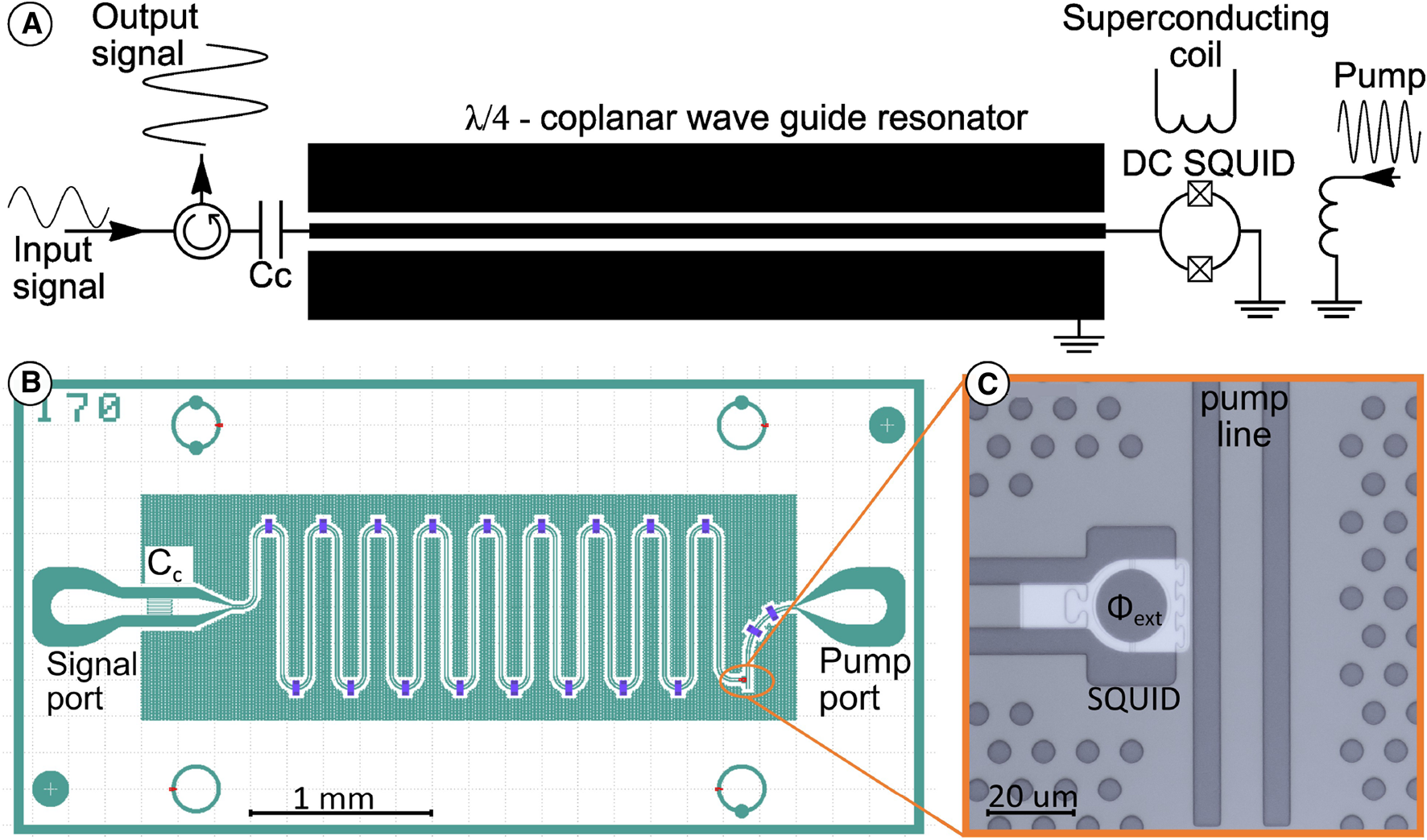
Flux-driven JPA. (A) Equivalent circuit diagram of the JPA. A flux bias defines the average inductance of the SQUID loop (the Josephson junctions are denoted as in the loop), while the pump is modulating this flux at twice the frequency of the signal to be amplified. Since the signal’s input and output utilize the same port, a cryogenic circulator is required to operate the amplifier. (B) JPA layout, where is the interdigitated capacitor. The resonator is implemented as a meander line, whose length determining the maximum JPA frequency. (C) Image of the SQUID (light structure in the center). The pump line is inductively coupled to the SQUID.
Different JPAs were designed for amplifying different signal frequencies by changing the length of the line. The instantaneous bandwidth of the device is designed by choosing the coupling capacitor size. A larger instantaneous bandwidth, when keeping the design otherwise constant, necessities in an increased pump strength for a certain gain and will have a reduced saturation power. The tunable bandwidth of these devices was limited by the small ratio of the SQUID inductance to the geometric inductance of the coplanar waveguide (CPW), which has been addressed in more recent JPA designs to be used in future experiments. The devices were designed using COMSOL simulations to obtain the capacitance value of the interdigitated capacitor and the resonance frequency of the CPW resonator. Numerical simulations using the negative resistance model [35] were employed to predict the needed pump power, achievable gain, tunable range and instantaneous bandwidth.
The JPA is operated in the three-wave mixing mode [36], where the frequencies of the pump , signal , and idler are related by:
The JPA chips have dimensions of 0.3 , see Fig. 1b), and are fixed on top of a copper block. A printed pircuit board (PCB) to connect microwave lines to the input and pump lines is fixed on the same copper block and wirebonded to the chip. This copper block is encased within a copper base for the DC bias coil and thermally bonded to it. When not in use, this assembly is stored in an antistatic plastic box at room temperature within an evacuated desiccator. The detailed sample holder design is described elsewhere [37].
4 JPA measurement setup
4.1 RF setup
In Figure 2, one can observe the basic setup for testing and for the axion search experiment, featuring various temperature stages, including 300 K, 4 K, still, cold plate (CP), and mixing chamber plate (MXC) of the dilution refrigerator (DR). This design is adaptable to different types of DRs and the nature of the experiment. It offers inputs for measuring various parameters such as tuning frequency range, gain, instantaneous bandwidth, and noise temperature of the JPAs. All RF connections from the 300 K flange to the 4K plate are made with CuNi coaxial 0.047-inch-diameter cables, provided either by BlueFors (BF) [38] or made in-house. Below 4K, some of the RF lines are done with the same cable, while the signal lines are constructed using KEYCOM [39] superconducting NbTi 0.047-inch-diameter cables to minimize heat load and reduce losses. Each input line is equipped with a series of attenuators, thermally anchored to each temperature stage of the fridge, to reduce Johnson noise originating from higher temperature stages. The attenuator values are chosen by considering the equation below Eq. (7):where is the output noise temperature of the attenuator, is the output noise temperature of the attenuator on the previous temperature stage, is the physical temperature of the attenuator, and is the attenuation coefficient. Here, we assumed that the physical temperature of the attenuator equals the temperature of the corresponding stage of the fridge. This assumption is appropriate since the dissipation and self-heating are negligible when small power signals are involved. The RF chain was installed on the MXC plate and consists of a range of cryogenic microwave components, including couplers, circulators, and isolators. Prior to their use at mK temperatures, each component was preliminary characterized on a cold testing bench. To control the bias current we use a Yokogawa GS200 current source [40].
FIGURE 2
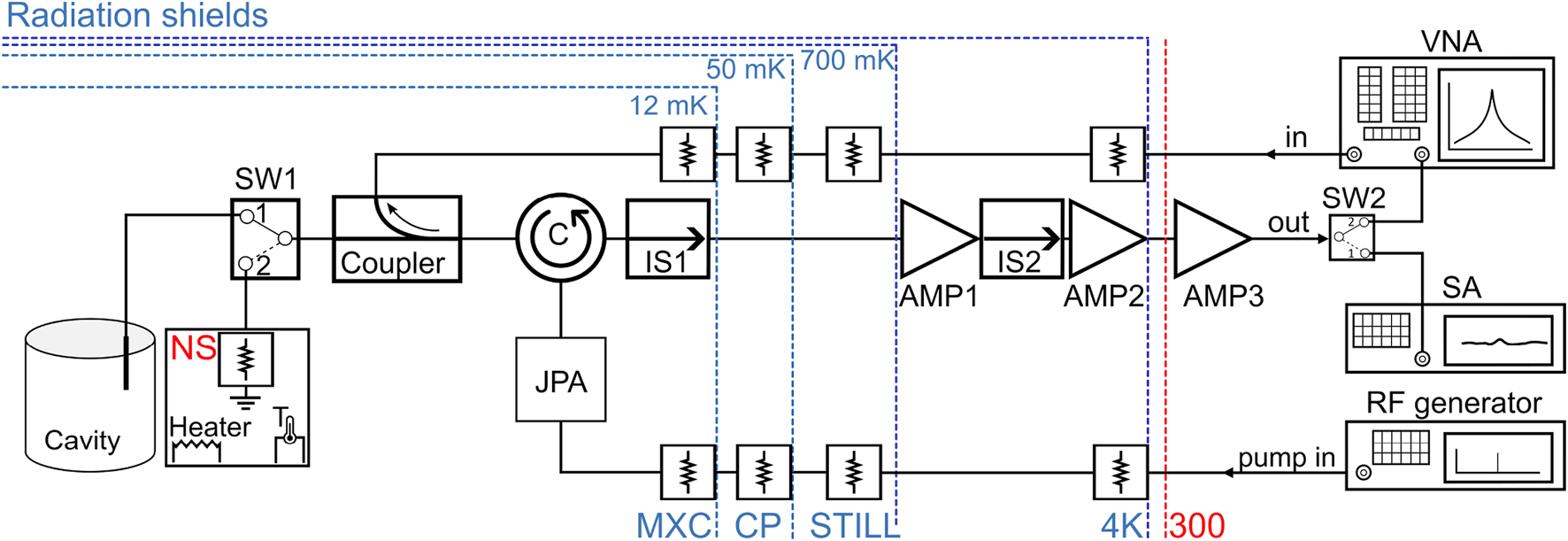
JPA readout diagram with either a cavity or a noise source at the input. Components arranged from left to right: noise source for tests or cavity for experiment run, SW1: RF switch to toggle between JPA-test and axion-experiment modes; the Coupler: “cold” directional coupler for injecting test signals into the JPA; components C and IS1 are a cryogenic RF-circulator and an RF isolator; AMP1 and AMP2: cryogenic HEMT amplifiers; IS2: RF isolator between HEMTs; AMP3: room temperature amplifier; SW2: RF switch between VNA and SA; VNA, SA, and RF generator.
4.2 DC wiring, cold DC filters and switch boxes
To test our JPAs and other RF and DC components, we set up a dedicated test system using a BF LD400 dry fridge [41]. To enhance our testing capabilities, we implemented a set of 32 differential lines, each individually shielded, into the fridge. These lines are constructed using twisted pairs, each placed within a Teflon matrix and equipped with its own CuNi braided shield. For pairs connecting the room temperature (RT) flange to the 4 K stage, we utilized cables with 0.1 mm diameter brass wires. For connections between the 4 K stage and the MXC, twisted pairs were made from copper nickel coated 0.1 mm NbTi wires. The cables were thermally connected to each temperature stage through their CuNi shields. On the 4 K stage, they were thermally connected via a specialized interconnection box, providing a transition between brass and superconducting wires. At a base temperature of approximately 11 mK on the MXC, the estimated maximum heat load from wires connected to the upper stage does not exceed 0.8 W.
In the fridge DC lines, we incorporated DC filter assemblies at the 4 K stage. Each of our filter assemblies contained 12 differential T-type RC filters. In the lines used to provide power for the HEMT amplifiers, the RC filters are replaced with LC filters in order to reduce resistive losses. These filters are constructed on a two-layer PCB, utilizing both sides as ground planes to minimize interference and enhance thermalization, see (Figures 3A,B).
FIGURE 3

DC and RF wiring. (A) Top and (B) bottom views of the cryogenic filter block for the BF fridge. The block contains 12 differential T-type RC filters designed for standard BF DC lines and is mounted on the 4 K stage of the fridge. (C) DC and (D) RF boxes of the test fridge BF4 located at room temperature.
To safeguard the connectors on the top of the BF fridge from potential damage due to frequent connection and disconnection during testing, we have designed two specialized boxes for DC and RF connections (Figures 3C, D). These boxes are permanently connected to the fridge, and all connections for setup, testing, and experiments are made within these boxes. The RF box also houses an RF amplifier, while the DC box features switches controlled by a 40-411-001 PXI 64 Channel Relay Driver Module [42] based on a PXES-2590 chassis [43], enabling flexible configurations for testing purposes.
4.3 Noise source
Our setup incorporates a noise source (NS), facilitating the measurement of noise parameters for the JPAs and cryogenic HEMT amplifiers. The NS is a separate assembly comprising a wideband matched 50 terminator, fixed on a bulkhead, labelled as “2” in Figure 4A, a heater “3”, and a thermometer “4”. These components have been integrated onto a copper fixture (1). To enhance thermal connections, the enclosure was plated with gold of 6 m thick. The NS equivalent circuit is shown in Figure 4B.
FIGURE 4
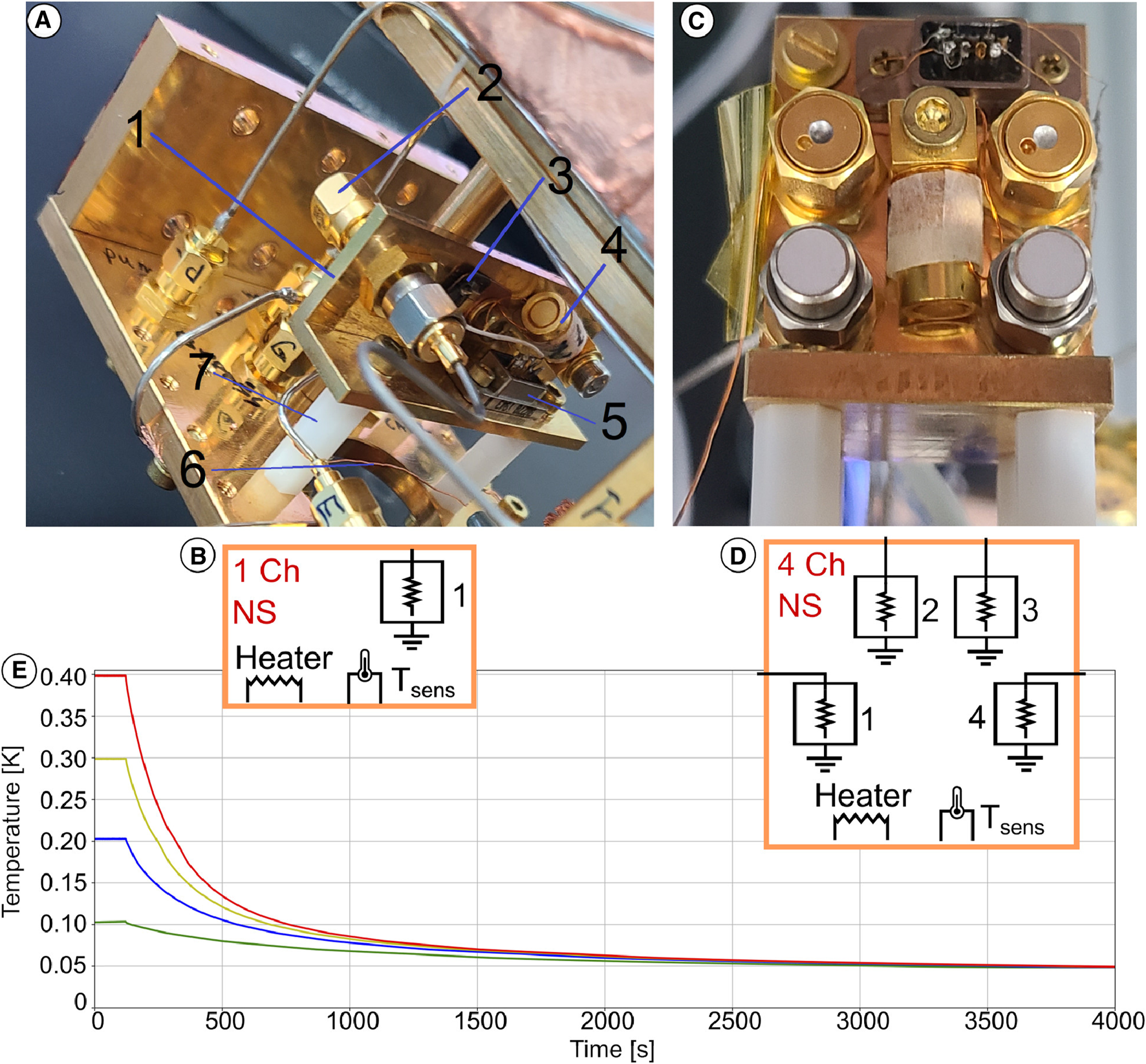
Cryogenic NS. (A) One-channel NS components on the MXC assembly: 1 - enclosure, 2 - 50 terminator, 3 - heater, 4 - thermometer, 5 - connector, 6 - thermalization wire, 7 - isolating plastic stand. (B) Equivalent circuit of the one channel NS. (C) Four-channel NS and (D) its equivalent circuit [44]. (E) Cooling of a single-channel NS heated up to 100, 200, 300 and 400 mK [44]. The NS is thermally connected to the MXC with the temperature stabilized at 50 mK. (E) adapted with permission from ref. [44] licensed under Creative Commons Attribution 4.0 License.
This NS has been designed for placement on the MXC plate of dry BF or wet Leiden dilution refrigerators. Our design prioritizes compact dimensions, minimizing the footprint on the MXC plate while ensuring adequate heat capacity for thermal stabilization. Bulkhead SMA adapters were employed to establish connections between the 50 cryogenic wideband matched loads (2) and the measurement chain. These adapters, in conjunction with the wideband XMA cryogenic 50 terminations boasting a maximum voltage standing wave ratio (VSWR) of 1.15, guarantee 50 matched connections across the frequency range up to 18 GHz. At temperature , the source generates Johnson-Nyquist noise with the noise temperature in accordance with the Nyquist theorem:
For the interconnections between the NS and the rest of the measurement chain, we utilized 0.047-inch-diameter NbTi microwave coaxial cables. Three superconducting NbTi twisted-pair cables within braided CuNi shields were employed to connect the temperature sensor (4) and heater (3) to the micro-Sub-D-9 connector (5) of the NS. The four-point temperature measurements were conducted using a calibrated ruthenium-oxide temperature sensor. The heater was crafted using a 100 precision resistor, with its housing carefully removed. It was then securely attached to the NS assembly using epoxy glue. The Lake Shore Cryotronics 372 AC resistance bridge and temperature controller enabled precise temperature measurements and control. NbTi superconducting twisted pairs and RF cables were utilized to minimize losses and thermal conductance between the MXC and the NS connectors. Additionally, the NS assembly was securely attached to the MXC plate using two 20-mm-long plastic spacers (7). Since both DC and RF connections to the NS were made using superconducting cables, thermal anchoring to the MXC plate primarily relied on a weak link created with copper wire (6).
Through a proportional-integral-derivative (PID) controller, the NS temperature could be adjusted from 50 mK to 1 K without affecting the MCX plate temperature. Initially, we employed a single-channel NS in our setup. However, as our testing requirements evolved and the demand for increased testing speed became apparent, we transitioned to a four-channel NS configuration [44], all housed within a single enclosure as shown in Figure 4C. The four channel NS equivalent circuit is shown in Figure 4D. This allowed us to significantly accelerate our testing processes.
The time it takes for the temperature of the NS to stabilize depends on the heat capacitance of the NS itself, along with all the components mounted on it, and its thermal coupling to the MXC. This thermal conductance of the coupling is determined by the length and diameter of the copper magnet wire, the annealing of the wire, and the quality of the contacts between the wire, the NS enclosure on one side, and the MXC plate on the other. To ensure efficient thermal transfer, we took careful steps to establish good contacts. We removed the insulation clad from the wire and pressed the wire against the enclosure and plate using brass screws. We attempted to enhance contact reliability by introducing clamp contacts on both sides of the wires, but this approach led to a significant reduction in thermal conductivity, preventing us from lowering the temperature of our NS below about 180 mK. We attribute this to the introduction of substantial mechanical defects in the crimped connections, resulting in a significant increase in thermal resistance. A similar effect has been observed in other experiments [45]. After returning to our initial connection method, the thermal connection was restored.
In Figure 4E, the relaxation of the NS temperature after it was set to target temperatures is shown. The relaxation curve deviates from an exponential shape due to the strong non-linearity of thermal conductance and heat capacities at millikelvin temperatures.
4.4 Shielding of JPAs and RF components from magnetic fields
According to Eq. 5, the scanning speed of axion haloscope searches is strongly determined by the magnet’s strength and size, making it one of the pivotal factors in these experiments. The presence of such a magnet also generates a large magnetic field in its vicinity. Contemporary magnets incorporate compensation coils to establish a reduced magnetic field zone near the magnet. Nevertheless, the available space for this purpose is constrained by the size of the fridge. Consequently, it may not be sufficient to accommodate all sensitive components. Our superconducting magnets, which generate a magnetic field ranging from 8 to 18 T, with an aperture up to 320 mm, produces in a magnetic field strength of below 20 mT around the RF-readout components. As such, magnetic shielding is necessary.
4.4.1 RF switch shielding
Within our experimental setup, we face the challenge of potential magnetic field interference affecting a range of critical components, including circulators, isolators, HEMT amplifiers, and notably, the JPA. To surmount this challenge, we have used shielded components, like circulators and isolators. For the unshielded components that can only function in low magnetic field environments, such as RF switches (Figures 5A, B), special shields made from carbon steel S45C were implemented. The results of the shield simulation are shown in Figures 5C, D.
FIGURE 5

Two types of RF switches used at CAPP, with and without magnetic shields made from carbon steel S45C. (A) Three-position RF switch. (B) Five-position RF switch. (C) and (D) 3D simulation of the magnetic field strength in ANSYS [46] under an external vertical magnetic field of 100 mT for the three-position and five-position RF switches, respectively, are shown in the cross-sectional view.
4.4.2 Onion shield
JPAs contain the most sensitive component to magnetic fields, i.e., the SQUID. In order to safeguard them against the influence of magnetic fields, we have developed a three-layer shielding system [47], referred to as the Onion Shield (OS) due to its nested design, see Figure 6A. The performance of the OS results from its design and the properties of the materials used.
FIGURE 6
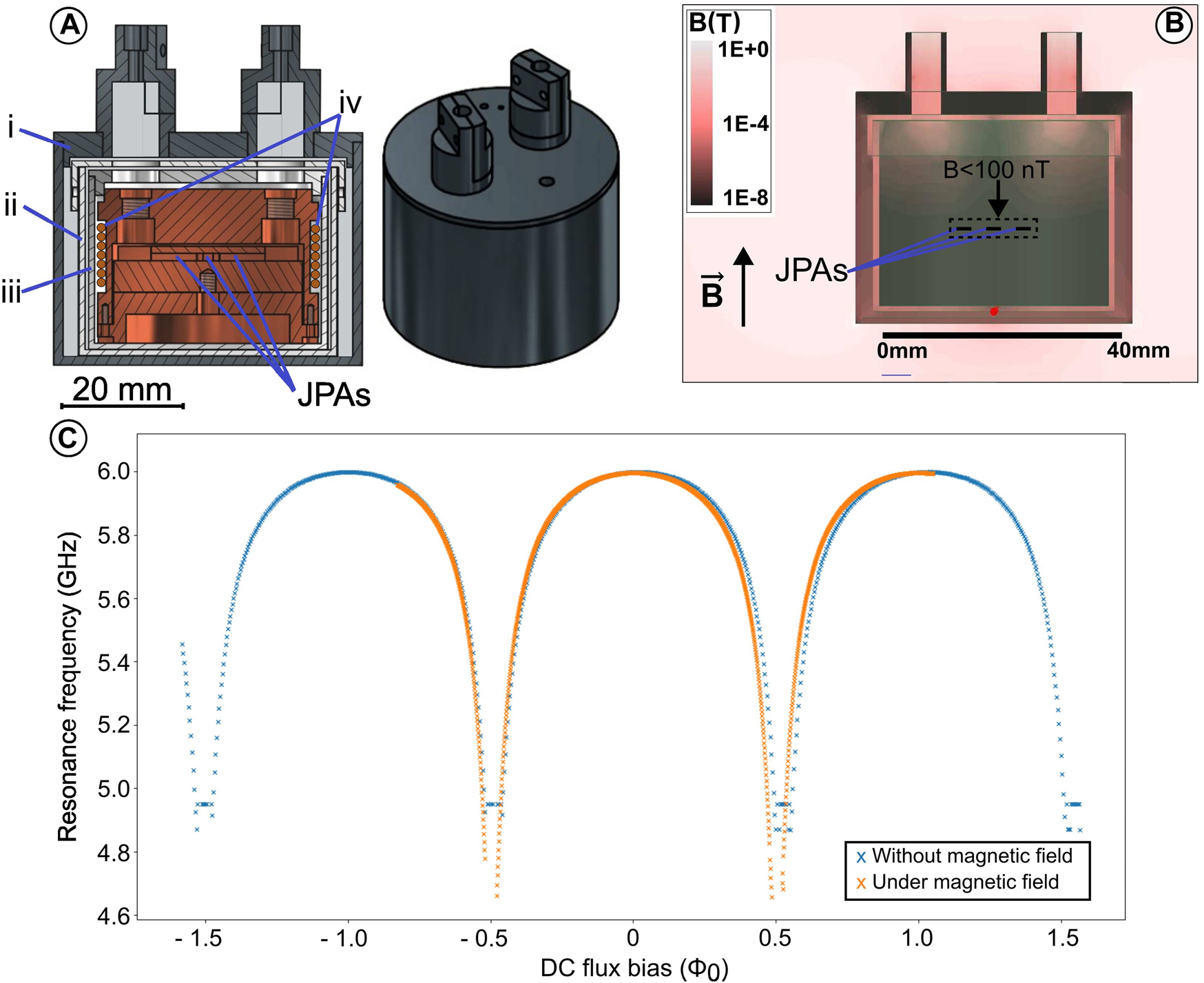
Onion shield. (A) Three-layer design of the shield. (I) Niobium or NbTi superconducting shield, (ii) CRYOPHY shield, (iii) inner superconducting Al shield, (iv) cross section view of the DC bias coil. The JPA locations are indicated by the arrows. (B) 3D simulation of the magnetic field in ANSYS [46], including only the two outer layers of the OS, under an external field of 50 mT and at a temperature of 100 mK. (C) Resonance frequency of the JPA in the passive mode depending on the applied DC flux bias, both in the presence and absence of an applyed vertical residual magnetic field of the superconducting magnet [47]. The external field strength at the components location is about 50 mT and measured field 50–100 nT, which corresponds to 3D ANSYS simulation. The corresponded shielding factor ranges between and . (C) adapted with permission from ref. [47] licensed under Creative Commons Attribution 4.0 License.
The shield has three layers, each with its own function to block and control magnetic fields (Table 1). The outermost layer (1) in Figure 6A), constructed with Nb or Nb alloy superconducting materials, has a high critical magnetic field value, and the external magnetic field is shielded by it only at cryogenic temperatures. The second layer 2), consisting of a ferromagnetic material with high magnetic permeability [48, 49], shields magnetic fields penetrating the outer shield through the structural openings. Finally, the innermost layer (3) is also made of superconducting aluminum with a critical temperature of about 1.2 K.
TABLE 1
| Layer | Outer | Middle | Inner |
|---|---|---|---|
| Material | Nb or NbTi | CRYOPHY | Al |
| Superconducting transition, K | 9.2-11 | N/A | 1.2 |
| Maximum magnetic field, T | >0.1 | (saturation) | <0.01 |
Onion shield layer properties.
At non-cryogenic temperatures, the OS acts like a regular magnetic shield due to its second layer made of ferromagnetic material. In fields with a magnitude close to the Earth’s field, the calculated field inside the OS is a few tens of nT. During the initial cooling, the outermost layer undergoes a superconducting transition at the critical temperature (for our material choice it is between 9.2 and 11 K). During the transition from the normal to the superconducting state, the outer layer of the OS “freezes” the Earth’s magnetic field inside the shield. Throughout this process, the magnetic field inside the second shield, composed of a ferromagnetic material, remains predominantly unaffected.
As the cooling process continues and the temperature approaches the critical point for the innermost layer 3) of the shield, its phase transition occurs. This innermost layer of the shield, made of superconducting aluminum, freezes the residual magnetic field that penetrated through the previous layers, i.e., a few tens of nT.
Since the first layer of the OS is in a superconducting state, while the field strength of the magnet increases, a persistent current appears on the surface of the first layer of the OS due to Meissner effect. This current freezes the magnetic field within this layer. However, some magnetic field penetration is inevitable through the openings required for cable routing and thermalization.
The second shielding layer plays a pivotal role in substantially reducing the penetration of the magnetic field into the first layer of the OS. However, again due to cable holes, there is a small penetration through it. This change in the residual field of the ferromagnetic shield is further shielded by the aluminum layer. Persistent currents induced on the surface of the third shield counteract minor field fluctuations within the second layer, ensuring that these fluctuations do not impact the magnetic field within the OS internal volume. Consequently, this configuration effectively shields the internal volume from the influence of external magnet field variations. The magnetic field at the location of the JPAs is approximately 50 mT when the magnet is running at 12 T. The magnetic field within the shield at this position experiences only marginal changes, even when the magnet is on, remaining within a range of 50–100 nT. This is confirmed by both simulation and experiments. Simulations in Figure 6B and measurement, in Figure 6C, showed consistent results. The measurements were done with JPA #18 (see Table 2). A more detailed investigation of the OS in fields greater than 0.1 T will be presented in a future publication.
TABLE 2
| JPA | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 |
|---|---|---|---|---|---|---|---|---|---|
| Min Frequency , GHz | 1.006 | 1.118 | 1.141 | 1.2 | 1.32 | 1.35 | 1.4 | 1.48 | 1.56 |
| Max Frequency , GHz | 1.071 | 1.185 | 1.171 | 1.251 | 1.401 | 1.40 | 1.45 | 1.55 | 1.64 |
| Tunable range, MHz | 65 | 67 | 30 | 51 | 81 | 50 | 50 | 70 | 80 |
| , mK | <90 | <90 | <60 | <95 | <80 | <80 | <85 | <75 | <85 |
| 3.5 | 3.2 | 2.13 | 3.2 | 2.38 | 2.38 | 2.44 | 2.01 | 2.15 | |
| Bandwidth at 20 dB gain (kHz) | >150 | >150 | >100 | >200 | >150 | >150 | >150 | >200 | >200 |
| JPA | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 |
|---|---|---|---|---|---|---|---|---|---|
| Min Frequency, GHz | 1.63 | 1.64 | 2.27 | 2.30 | 2.35 | 2.35 | 3.7 | 5.1 | 5.5 |
| Max Frequency , GHz | 1.73 | 1.74 | 2.31 | 2.45 | 2.5 | 2.5 | 3.85 | 5.4 | 6.0 |
| Tunable range, MHz | 100 | 100 | 40 | 150 | 150 | 150 | 120 | 300 | 500 |
| , mK | <80 | <80 | <120 | <130 | <100 | <110 | <120 | <145 | <150 |
| 1.93 | 1.92 | 2.16 | 2.32 | 1.67 | 1.83 | 1.3 | 1.12 | 1.04 | |
| Bandwidth at 20 dB gain (kHz) | >200 | >150 | >100 | >200 | >200 | >100 | >300 | >1000 | >1000 |
Characteristics of some of the JPAs measured at physical temperature of 30 mK.
5 JPA characterization
For all of our devices, we conduct thorough testing procedures. Since the JPA functions as a resonant amplifier, our objectives are to determine the tunable range, explore the relationships between gain, instantaneous bandwidth, and noise as a function of pump power and detuning frequency, and establish the input signal range within which the amplifier does notsaturate. The key steps in our characterization process include.
1. Passive resonance identification by measuring the resonance frequency as a function of the DC flux.
2. Gain parametric map (paramap) construction (gain vs pump power and detuning per bias current ), illustrating the gain concerning both pump power and detuning frequency.
3. The 1 dB gain compression point measurement in order to determine the input saturation power of the amplifier.
4. Noise paramap generation by measuring the noise temperature vs pump power and detuning.
5.1 Resonance frequency vs. DC flux bias current
In the passive regime, where no pump signal is applied, the JPA operates as a weakly coupled quarter-wave resonator, shorted to ground through a non-hysteretic SQUID, and coupled to the outside circuit via a capacitor (see Figure 1A). When subjected to a small input signal, the SQUID remains in a superconducting state, effectively acting as a flux-dependent inductor. Consequently, we can treat the JPA as a quarter-wavelength resonator, with its effective inductance tunable by adjusting the flux going through the SQUID loop (Eq. 9),where Wb represents the flux quantum, and signifies the critical currents of junction 1 and junction 2, respectively.
The operating frequency of the JPA is determined by both the physical dimensions of the transmission line and the inductance of the SQUID. To adjust this frequency within a specific range, we utilize an inductively coupled DC flux bias coil. This coil is constructed as a single-layer coil wound with 0.05 mm copper-coated NbTi wire on a copper core, featuring an inner diameter of 32.5 mm and a length of 11.5 mm. It comprises 200 windings and has an approximate resistance of 200 at room temperature.
The impedance of a quarter-wavelength resonator becomes finite and real at resonance, ideally zero. As a result, the reflection coefficient exhibits a dip at resonance. However, in the low loaded quality factor regime, it results in a small and broad dip spread over a wide frequency range (approximately 100–200 MHz). When measuring the JPA through various components, each with its own characteristics, distinguishing this dip becomes challenging. On the other hand, phase measurement is comparatively easier because the resonance induces a 360-degree phase shift, whereas the phase shifts of other components do not exhibit such a strong frequency dependence. For this reason, we utilize phase-frequency measurements. We examine the JPA by sending a tiny signal towards it and recording the reflected signal. To separate the incoming and outgoing waves, a circulator is employed. The signal from the JPA is then amplified using two low-noise cryogenic HEMT amplifiers, AMP1 and AMP2, and RT amplifier AMP3, see Figure 2. The output signal recorded at the VNA input is influenced by several frequency-dependent components within the chain, resulting in the observed signal profile depicted in Figure 7A. The reflection signal of the JPA is obtained through measurements using a VNA in the configuration shown in Figure 2. Subsequently, the phase information of this spectrum is employed to extract the resonance frequency, utilizing a parameter fit based on Ref. [50]. The resonance frequency is measured as a function of the coil current, as shown in Figure 7B. The measurement reveals that the minimum observable resonance frequency was below 1.25 GHz, while the maximum reached 1.33 GHz. However, at lower frequencies, the JPA exhibits large sensitivity to flux noise, attributed to the higher , and therefore this device was only used above 1.26 GHz.
FIGURE 7
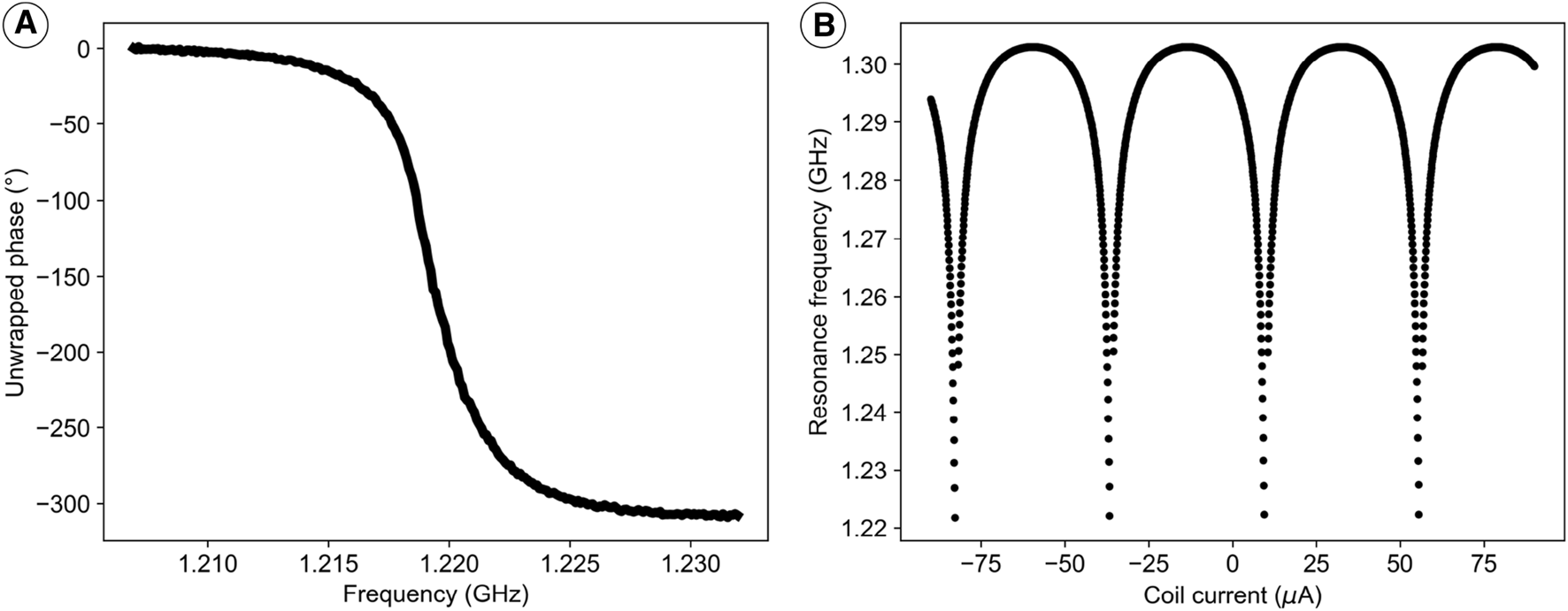
The passive resonance of the JPA. (A) Dependence of phase vs frequency for a JPA measurement in the circuit in Figure 2 for a fixed current when the pump signal is switched off. (B) Relationship between the resonance frequency and the DC flux bias for a JPA.
The phase of reflected signal is given by Eq. 10:Here, indicates the frequency deviation from the resonance frequency . signifies the half-width of the resonance curve, determined by the internal quality factor . It signifies the bandwidth of the resonator attributed to its internal losses. Similarly, denotes the half-width of the resonance curve, determined by the external quality factor . It denotes the bandwidth of the resonator, accounting for both intrinsic and coupling losses.
5.2 JPA gain measurement
Upon applying a pump signal with frequency , the three-wave mixing mode obeys Eq. 6. Using the JPA in three-wave mixing mode causes an amplified signal and an idler mode to appear symmetrically around . In the circuit shown in Figure 2, we estimate the JPA gain through the change in amplification in the output by comparing transmission measurements with the JPA in both on and off states. This establishes the baseline measurement, denoted as . A separate measurement is performed with a microwave short circuit connector replacing the JPA to assess the accuracy of this baseline. The comparison indicates that the baseline obtained from this off-resonance measurement is at most less efficient than if an ideal reflection was achieved.
Next, the JPA is tuned to the desired working point, and a subsequent transmission measurement is taken. From these two measurements, the power gain is determined via equation:To find the optimal working point, we measure a “paramap”, which represents the dependence of measured at on the pump frequency and pump power . The offset is enough to avoid the degenerate mode of the JPA. This measurement is repeated for all tuning frequencies of the JPA by varying .
To determine the operational points across the entire frequency range, we devised a two-step procedure. Optimization included finding values of and for minimum noise and acceptable gain across the entire operational frequency range controlled by the value. Our desired gain falls within the range of 15–20 dB, which minimizes the noise contribution of the subsequent HEMT amplifiers.
During paramap measurements, after each adjustment of , the resonance frequency is established through phase measurements and subsequent parameter fitting. With the detuning defined as , iso-gain contours exhibit a minimum in required pump power near , as depicted in Figure 8A. Initially, this minimum is observed at specific frequencies; however, it gradually shifts towards lower detunings, a phenomenon attributed to pump-induced shifts in the resonance frequency [50]. As illustrated in Figure 8A, amplification can reach up to 40 dB.
FIGURE 8
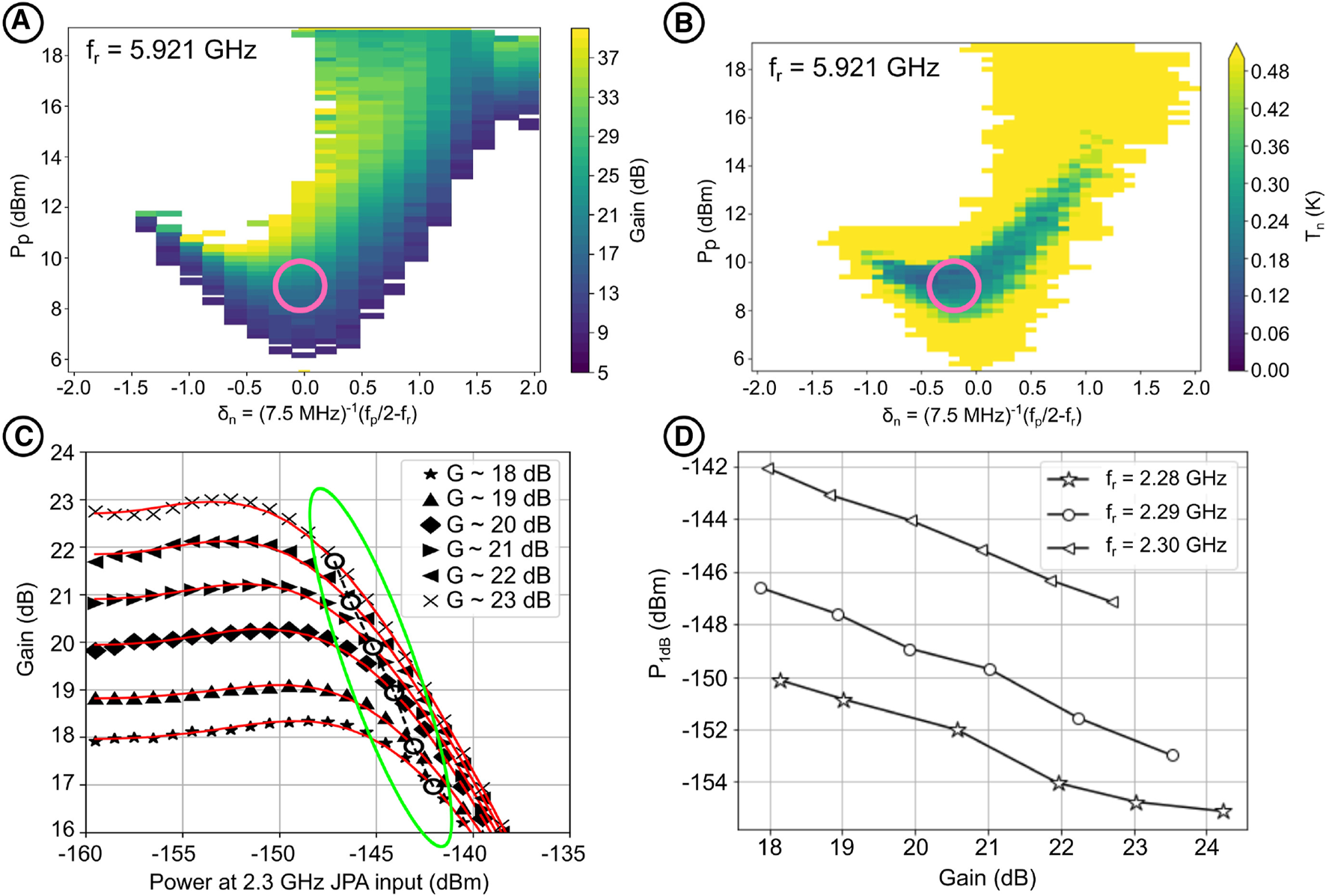
Characterization of the JPAs. (A) and (B) Gain and noise parameter maps of the JPA #18 for GHz. The area of optimal working points for GHz is shown with pink circles. is the normalized detunning, refers to the JPA bandwidth. (C,D) Gain dependence on input power for a resonance frequency of 2.3 GHz and P1dB compression point for three resonance frequencies measured for JPA #12 [52]. (D) adapted with permission from ref. [52] licensed under CC BY 4.0.
Based on the data acquired from the gain paramap, we outlined an area of interest and measured a noise paramap (Figure 8B) within that region. The displayed gain and noise paramap are for a JPA #18. As evident, we recorded an added noise level of around 150 mK for this amplifier, slightly exceeding the quantum limit for a phase insensitive amplifier at this frequency 141 mK [51].
For each JPA, we conducted numerous measurements at different frequencies of interest to pinpoint the optimal configuration. The results presented in Figures 8C, D showcase the outcomes of noise measurements for the JPA #18 using different settings at two distinct frequencies. The red vertical lines correspond to the quantum limits for each of these frequencies. As illustrated, for each frequency, we achieved parameters that align with very low noise levels, approaching the quantum limit.
5.3 P1dB measurement
Due to the nonlinear nature of the JPA, its gain will saturate beyond certain signal and pump amplitudes. A common method for assessing amplifier saturation involves determining the output power at which the gain decreases by 1 dB. This process involves driving the amplifier with a continuous tone at the desired signal frequency and progressively raising the input power level while tracking the output power. is an indicator that the system deviates from the desired small-signal behavior.
Our measurement of was conducted at 1 kHz across the entire JPA tunable range and various pump powers, each corresponding to different gains. The results are illustrated in Figures 8C, D. The power due to the axion signal, which is expected to be around , is significantly below the saturation power of the JPA. However, for a few JPAs it was observed that thermal noise at the input can also induce saturation, altering the device behavior. As an example, when we considered a device with operating frequencies around at gains exceeding , we observed saturation due to thermal noise when the NS temperature exceeded . While this may not render the device unusable at these frequencies, we need to careful during direct noise temperature measurements using a NS in these frequency and gain ranges [52].
5.4 Idler mode and added noise
In the three-wave mixing non-degenerative mode, an idler tone appears with frequency (see Figure 9). The amplification of the signal at the idler frequency is equal to (Eq. 12) [53].When the input signal of the frequency is applied to the JPA, the output of the amplifier will have two power terms, corresponding to and frequencies (Eq. 13):At , the added noise equals half a photon [54, 55].
FIGURE 9
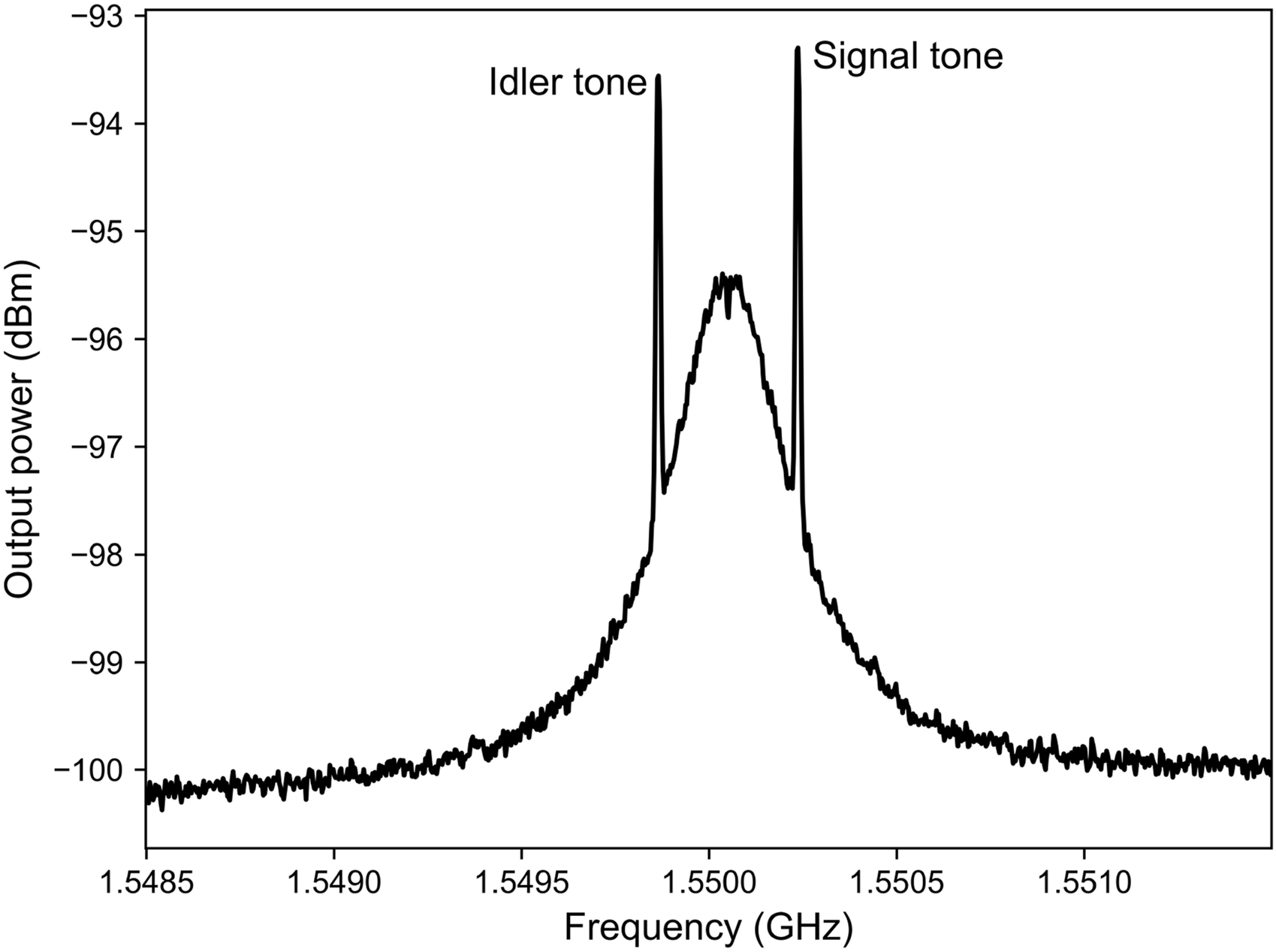
JPA output power measured by the spectrum analyzer including the amplified signal and its idler. A single signal tone is applied to the input of the JPA.
5.5 Noise measurement
To ascertain the noise temperature of the JPA, we utilize two steps. The first is based on the Y-factor method [56], while the second involves measuring the noise spectrum both with the JPA on and off, a technique known as the spectrum comparison method [57, 58].
5.5.1 Modified Y-factor
To measure the noise temperature, we utilized a methodology akin to the well-established Y-factor method [56], employing the NS discussed earlier in Section 4.3. The Y-factor technique is commonly applied in the field of RF and microwave measurements, particularly for evaluating the noise figure of amplifiers or receivers. It involves calculating the ratio of output noise power observed when a system is connected to a calibrated hot source (high temperature) to that observed when connected to a calibrated cold source (low temperature) . Mathematically, it is expressed as:The right part of Eq. 14 reflects the fact that the system noise temperatures and are proportional to the corresponding noise powers. The noise temperature of a system in both cases contains the amplifier-added noise :
From Eqs 14, 15, knowing , we obtain Eq. 16:where is the bandwidth. The advantage of this method is that it does not affect the precision of gain measurement . So, the original Y-factor method measures the noise temperature at two points. To mitigate the influence of quantum effects on Johnson noise given by Eq. 8 and ensure control linearity, which can be compromised by JPA saturation, we have modified the standard method by measuring at multiple temperature points.
For illustration we considered the measurement of noise with a 2.3 GHz JPA (see Figure 10A). The noise power emerging from the system was measured with the SA with a 1 kHz resolution bandwidth. The power spectra were recorded at NS temperatures of 60, 120, and 180 mK. The power values were converted into power spectral densities (PSD) by dividing them by the resolution bandwidth of the SA. The pump power and resonance frequency were adjusted to achieve a JPA gain of approximately 20 dB.
FIGURE 10
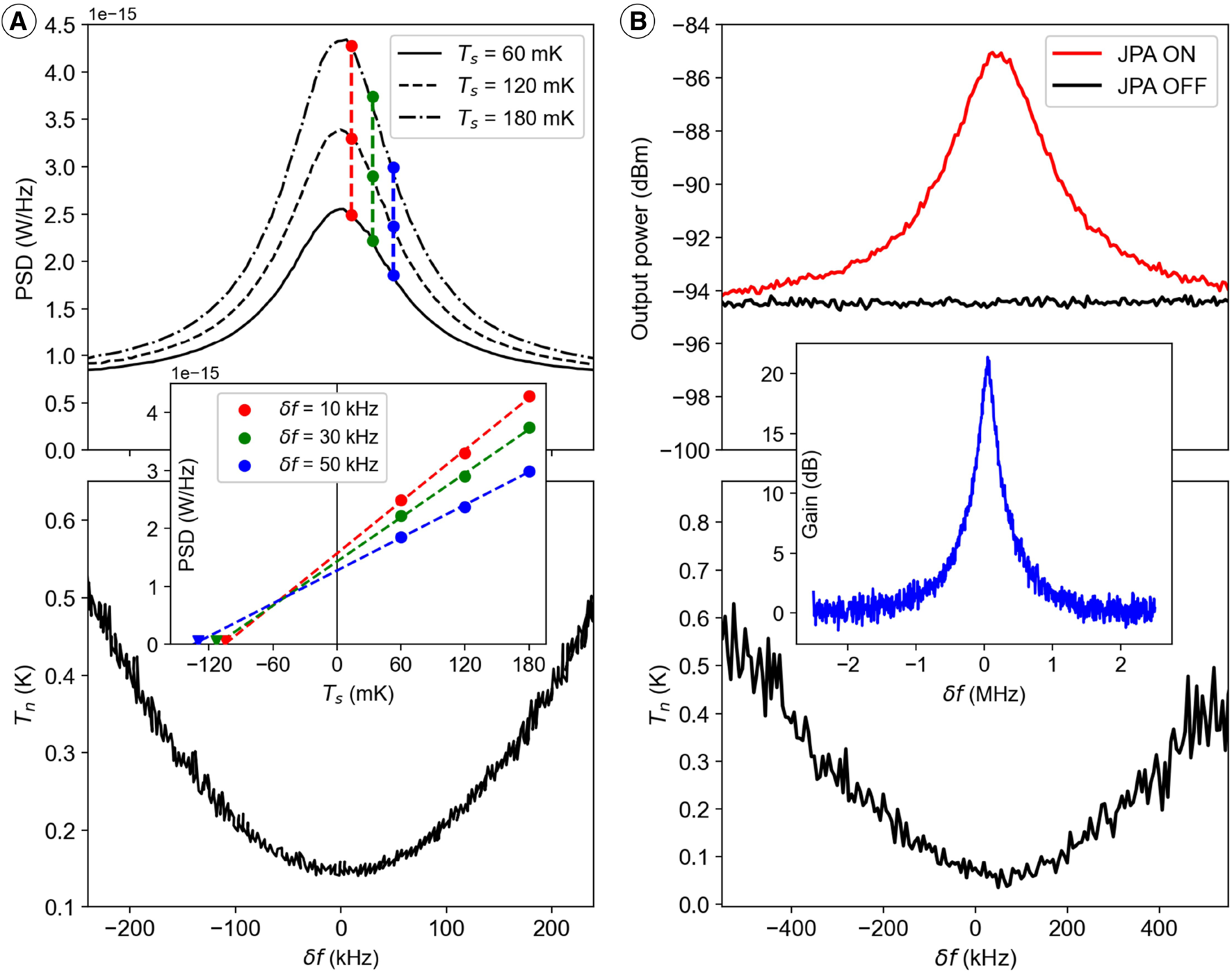
Noise measurements from two different JPAs: (A) JPA #12 noise measured using the Y-factor method. The upper plot shows the power spectral densities measured for 2.305 GHz for three noise source temperatures at the optimal working point [52]. The inset displays the PSD dependence on the NS temperature for three frequencies deviation , which were used to demonstrate a calculation the noise temperature of the JPA. The noise temperatures at different are determined at the points where the lines intersect the PSD axis at 0. The minimum added noise temperature of the JPA is defined as the minimum of by interpolation of the vs curve shown in the bottom plot. (B) JPA #9 noise measured using the spectrum comparison method. The upper plot shows the output power spectra for the JPA ON and JPA OFF. The inset displays the JPA gain curve. The noise temperature depending on the offset frequency is shown in the bottom plot. (A) adapted with permission from ref [52] licensed under CC BY 4.0.
The lower limit on noise temperature for linear, phase-insensitive amplifiers is described by Eq. 17 [59]:which results in approximately 55.2 mK at 2.3 GHz. From the measurement in Figure 10A we obtained a total added noise temperature of mK, at the cavity physical temperature of 50 mK. This cavity temperature at 2.3 GHz frequency, according to E.g., 8, corresponds to a noise temperature of 70 mK. Therefore, the total system noise temperature is estimated to be mK. The lower bound for is determined by the standard quantum limit (SQL) [60], which is approximately 110 mK at 2.3 GHz. Therefore, for the 2.3 GHz haloscope experiment, we obtain a total system noise of 1.7 SQL.
5.5.2 Spectrum comparison
The second method we use in the noise measurement is the spectrum comparison method. An advantage of this method is that it does not require the continuous usage of a NS, resulting in faster measurements as there is no need for changing the temperature. This technique is applicable because the JPA can be switched on and off, allowing noise measurements in both states. The off state of the JPA corresponds to a condition where (absence of the pumping signal of the JPA and changing the bias current to move the JPA passive resonance away from the measured frequency range). The noise calculation consists of comparing the power spectra of the JPA in the “on” and “off” states and deducing and from the results obtained with the JPA in the off state.
Initially, we characterized the HEMT noise by performing the Y-factor method with the JPA turned off. For our experiments around 1 GHz the best noise we have measured with the RF-chain including HEMTs corresponds to 1 K, which is approximately 40 times the half-quanta limit. and are measured using a VNA. After that the JPA is turned on, and is measured. The JPA gain is calculated using Eq. 11. The VNA emits a signal of ample strength, rendering the noise negligible. By sweeping the frequency of the narrow-band signal, we can obtain the dependence of .
The noise power spectrum on the output of AMP3 (see Figure 2), , is recorded by a SA when the JPA is on. Upon determining , can be estimated. Consequently, the total added noise of the JPA chain measured with the spectrum comparison method, , is computed as Eq. 18:
As confirmed by our measurements, both methods yield results that are consistent within the measurement error. However, the spectrum comparison method allows achieving the same precision much faster. In recent experiments, we have only utilized the modified Y-factor method to measure the frequency dependence of the noise temperature of the HEMT amplifier chain. We have employed spectrum comparison methods to measure the noise of the JPA (Figure 10B).
5.6 Optimization of working point
5.6.1 Paramap optimization
Based on the JPA tests described in this section, we obtain an optimal working point (OWP) for each signal frequency and JPA gain of choice (usually close to 20 dB by three parameters: , , and . To determine the OWP, we used mainly two approaches. Historically the first method is based on the observation that the minimum noise at otherwise equal conditions coincides with the lowest .
The JPA gain is a function of frequency, typically with a peak occurring at
. Using
to denote the peak gain value, the tuning is done by following the steps below.
1. Tune such that is equal to the desired .
2. Set to .
3. Increase until the desired gain is obtained.
4. Repeat steps 2 and 3 for small deviations from by changing .
5. Pick a set of , , that has the lowest for the desired gain at .
Before running the experiment, we conduct a series of preliminary measurements to determine the optimal values of the JPA parameters , which include , , and . Further details are described in [61].
We have also devised a method to heuristically find an optimized working point using the Nelder-Mead algorithm [62]. This approach allowed us to identify a working point with a low noise temperature near a given initial seed [63].
5.7 CAPP JPA collection
Since 2019, we have designed and tested over 40 JPAs for CAPP’s axion search experiments. Parameters for some of these JPAs are presented in Table 2. The minimum operation frequency is defined as the frequency at which the operating point starts to jump between different branches of the DC bias current-frequency characteristics, making gain and noise measurements impossible.
6 Extension of amplification bandwidth
Our primary challenge stemmed from the constrained tunable range imposed by the necessity to cool down our substantial 1.2-ton magnet using liquid helium. Consequently, we opted for a wet dilution refrigerator as a key component in our experimental setup to ensure safe superconducting magnet operations. Each cooldown of the dilution refrigerator consumes several hundred liters of liquid helium, and replacing the JPA requires several weeks of effort. Therefore, it is practical to match the amplifier’s bandwidth with the cavity’s, which is approximately 300 MHz. This can be achieved by employing a split-band technique, wherein each amplifier operates within its designated frequency band.
6.1 Cold multiplexer
Initially we considered a measurement setup with a microwave RF switch as the simplest means for extending the scanning frequency range of the RF chain. The multiplexing design of the multiple JPA readout scheme was based on the five-position RF switch, shown as SW2 in Figure 5A. This way, we designed the setup, such that each channel of the RF switch is connected to the one of five JPAs, utilizing a common output, see Figure 11A. The axion signal detection chain starts from the cavity, connecting to the RF switch SW1, which is used to switch between the cavity (scanning for axions) and the noise source (noise measurements). The first directional coupler DC1 connects to the BYPASS line, which is used for the characterizing of the passive resonances of each JPA. Similar to the circuit diagram shown in Figure 2 the cryogenic circulator C1 is connected to the JPA. The five-position RF switch SW2 switches between JPAs according to the operating frequency range in axion search experiment. The pump line for each JPA utilizes a power divider PD, and the pump frequency and power are set according to the active JPA. The output of multiplexed JPA circuit is connected to the microwave isolator I and an additional directional coupler DC2. DC2 is needed to perform additional measurements of the HEMT chain, see HEMT bypass line in Figure 11A, to measure the losses in the output chain of the JPA, and to precisely characterise the noise temperature. In order to characterize the differences in transmission for each channel of the RF switch, we performed additional measurements with the circuit diagram shown in Figure 11B. We used a four channel noise source [44], shown as 4 CH NS, with 4 identical cryogenic wideband terminators connected to the five-position RF switch. The common port of the RF switch is connected to the cryogenic circulator and to the JPA. We performed measurements of the JPA noise temperature for each of the channels and did not observe any differences.
FIGURE 11
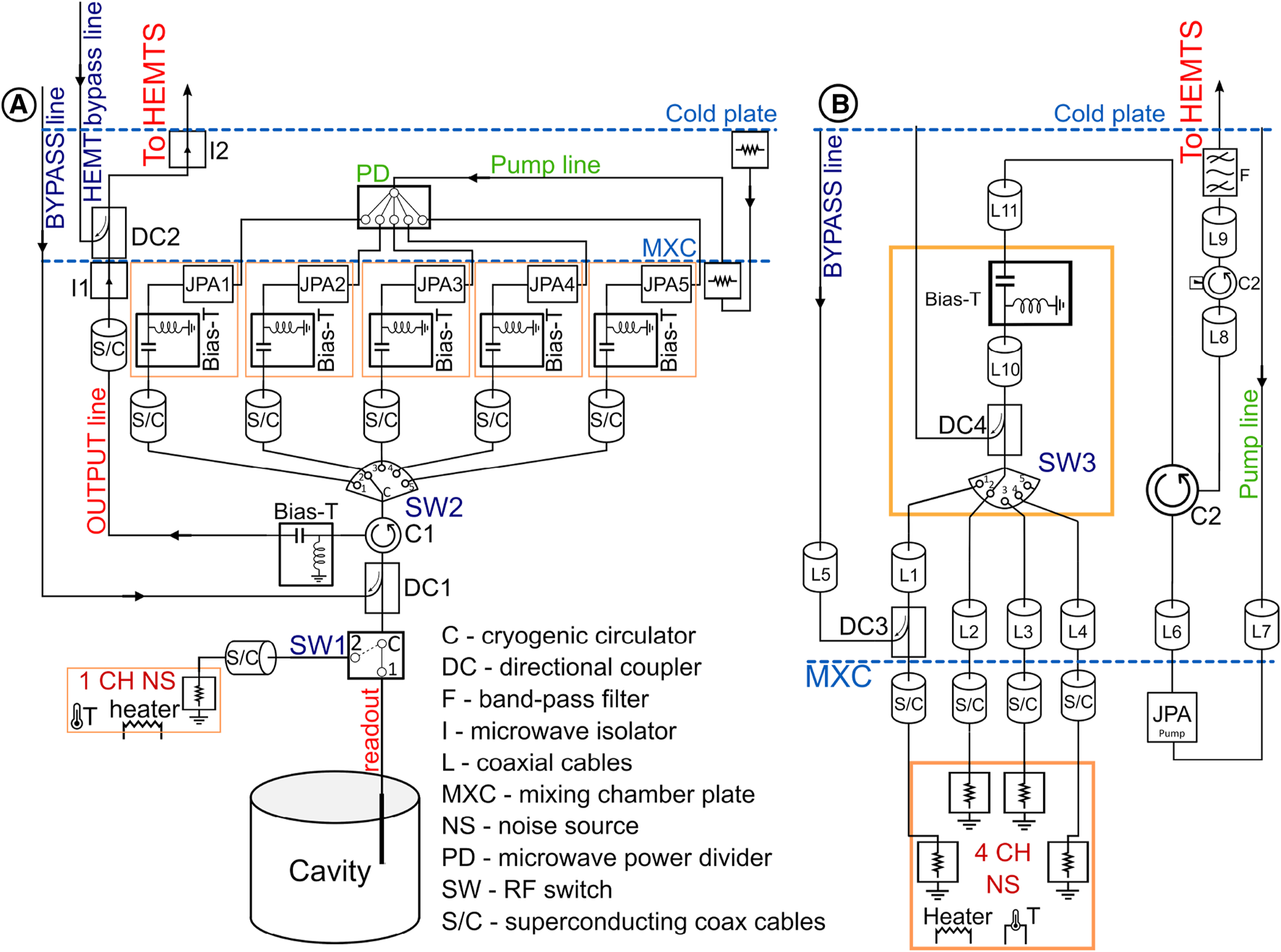
JPA multiplexing setup at the MXC: (A) The diagram of the detection chain in the axion search experiment. The setup consists of the cavity readout line and five JPAs measuring line. The switching is provided by the RF switch SW1. Compared with the JPA readout 2, a 5-position RF switch SW2 is added, which connects five JPAs through superconducting cables and protective bias-tees. The setup utilizes one channel noise source 1 CH NS. The pump signal is split using the power divider PD. The output is followed by an additional bias-tee, cryogenic microwave isolator I1, directional coupler DC2, and cryogenic isolator I2. (B) Setup for characterizing the transmission of each channel of the 5-position RF switch.
In our early tests, we encountered an issue where a JPA was damaged. Further investigation revealed the potential for charge accumulation on the switch electrodes during mechanical movement. This accumulated charge could discharge at the moment of switching, generating current and voltage pulses that posed a threat to the amplifiers. At mK temperatures, leakage current can be exceptionally low due to charge carriers freezing in insulating materials, resulting in prolonged charge retention on the electrodes. Once we recognized this issue, we implemented bias tees, shown as Bias-T in Figure 11A, to safely discharge the switch, enabling us to use this method for switching between several JPAs without causing damage. Another challenge associated with this method is the necessity to supply a substantial current (250 mA) inside the fridge to facilitate channel switching and reset the RF switch. To achieve this, we would need to modify the fridge by adding more low-resistance cables. As of now, this modification has been deferred. After addressing these issues, the proposed circuit scheme, which utilizes a 5-position multiplexer combined with the parallel-series connection design described in the next chapter, will allow for the expansion of the operating frequency range beyond 1 GHz.
6.2 Series connection of JPAs
In order to increase the bandwidth of our readout, we introduced a series connection involving an additional (see it simplified in Figure 12A) JPA alongside the first JPA (JPA1 and JPA2, see Figure 12B). During measurements, only one JPA operates at a given time, while the other JPA remains detuned from its operational frequency using a DC flux bias. This configuration seamlessly integrates into the readout chain via the second circulator, resulting in additional losses of approximately 0.4 dB at frequencies around 1 GHz. These losses, corresponding to less than 10% of the signal, lead to a minor acceptable increase in noise temperature.
FIGURE 12
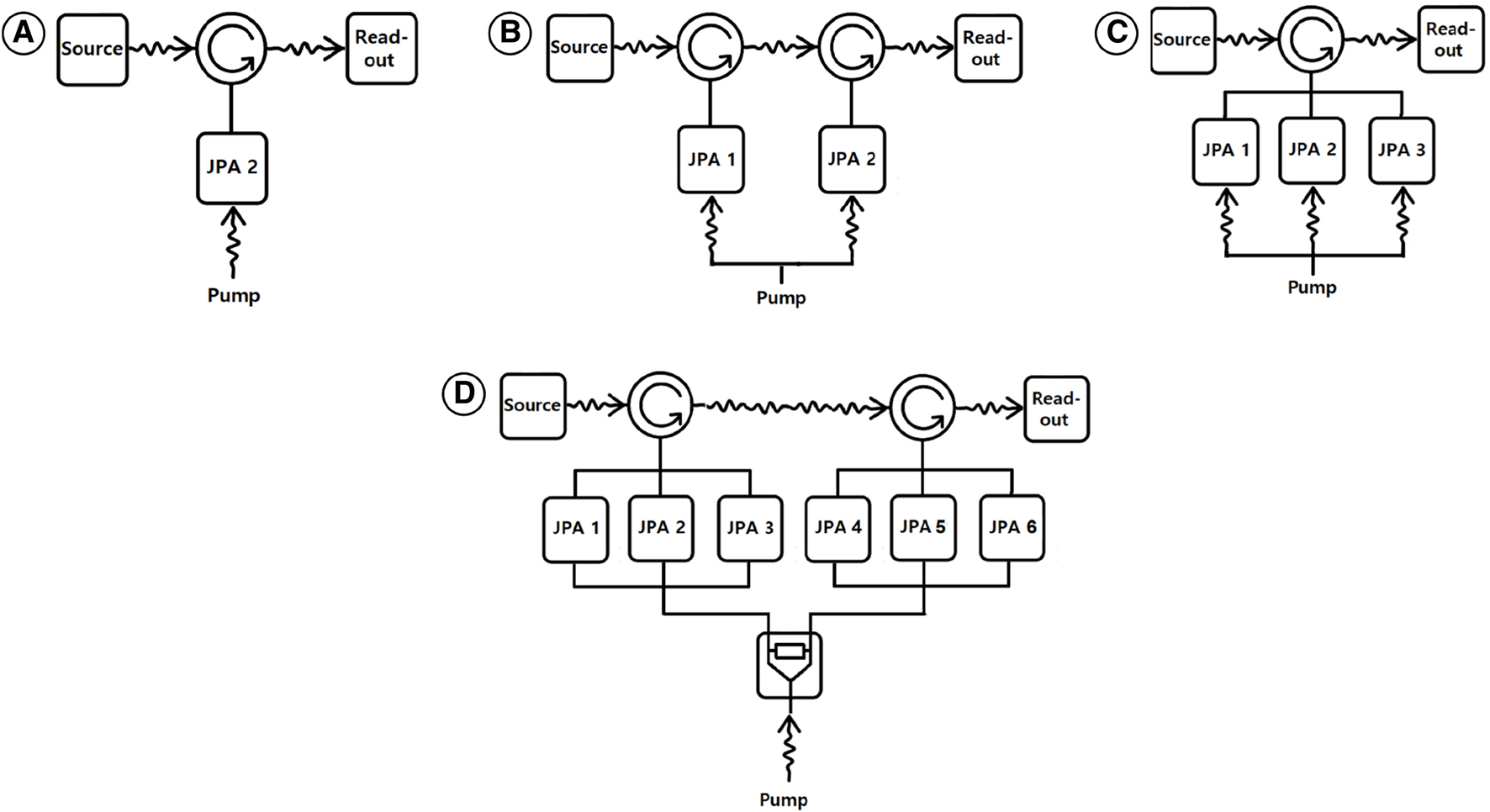
Simplified amplifier schematics. (A) single JPA connection, (B) serial connection, (C) parallel and (D) parallel-serial connections.
The series connection has enabled us to simultaneously use two JPAs within the same cooldown cycle, a setup we have employed in our test fridges since 2021.
6.3 Parallel connection of JPAs
The second idea for the bandwidth extension is to connect multiple JPAs with different frequencies on a single PCB, which appeared feasible given that the wavelength of the signal at 1–2 GHz significantly exceeds the length of the PCB traces of a few mm (Figure 12C). The dimensions of the PCB we use comfortably accommodate three chips, as depicted in Figure 13A.
FIGURE 13
Parallel connection of three JPAs [37, 64, 69]. (A) PCB for the parallel connection of 3 JPAs. The DC flux bias is common for all of the JPAs and is created by a 200-turn coil wound with superconducting wire around the PCB holder (not shown). (B) Dependence of the resonance frequency on bias current for three JPAs connected in parallel, with the JPA pump switched off. Adapted with permission from ref [64] licensed under Creative Commons Attribution 4.0 International License.
The initial measurements using this parallel configuration demonstrated that the JPAs can operate independently, exhibiting noise and gain characteristics similar to those in a single-JPA operation configuration [64]. However, certain challenges may arise because the two JPAs on opposite sides of the PCB (see Figure 13A) share the same sensitivity to DC bias, causing their flux-to-frequency characteristics to change similarly. In Figure 13A, we can see three JPAs mounted on a PCB in order of their highest passive resonance frequency (HPRF): 1.28, 1.295, and 1.36 GHz. In Figure 13B, one can see the dependence of the resonance frequency on bias current for the three JPAs connected in parallel, with the JPA pump power switched off. As we can observe, there is similarity in the DC flux bias sensitivity of the JPAs with maximum resonance frequencies of 1.28 and 1.36 GHz. This similarity can potentially lead to interference in the most sensitive low-frequency range, a matter which is discussed further in Section 6.5.
6.4 Parallel-serial connection
Combining the two ideas and developing a parallel-serial JPA readout, where two parallel configurations are linked in series was the next logical step [65]. This configuration was initially evaluated in an RF assembly named “Leo-I”, which contained all RF components intended to be placed at MXC. The goal was to test the entire assembly in a dry fridge first, before moving it to the wet CAPP-MAX fridge without any modifications.
In assembly we use a magnetically shielded triple junction circulator 3CCFC11-1-MS-Sfffff custom manufactured by Ferrit-Quasar company [66]. Its first and second circulators connected to the two Orion shields and the third circulator used as an output isolator. The signal connection between NS and
In our dry testing fridge the further signal amplification is done with two LNF-LNC062A amplifiers [19]. Between amplifiers we placed a shielded 3CCC11-2-MS isolator [67] to prevent back action of reflected signal. The amplifiers and isolators are mounted on the 4 K stage of the dry fridge. In CAPP-MAX experiment we use a wet fridge manufactured by Leiden Cryogenics [68], where space on 4 K stage is limited and isolator is mounted and thermalized on the cold plate with a temperature of 120–150 mK.
Before the dry fridge test, we arranged three JPAs in parallel with HPRFs of 1.07, 1.12, and 1.13 GHz in the first holder based on the Onion shield, while the second holder accommodated a single JPA of 1.185 GHz. Unfortunately, the middle JPA of 1.12 GHz, which was initially mounted and characterized on a single-JPA PCB version, was damaged during the transfer to the three-JPA PCB setup. Subsequent tests on the remaining three JPAs confirmed that all of them exhibited low noise levels while maintaining a required gain of 20 dB.
The complexity introduced into the readout chain led to some uneven frequency response and variations in HEMT noise temperature measured with the JPA off, ranging from 1.09 to 1.7 K (see Figures 14A, B). This cannot be entirely eliminated due to inherent phase delays in cables and the theoretical impossibility of achieving a perfect match for three-port non-reciprocal components within the chain. However, we accepted this limitation because at a JPA gain of 20 dB, the effect of the next HEMT amplification stage on noise is reduced by a factor of 100, resulting in only a small impact on the system noise temperature (Figures 14C, F).
FIGURE 14
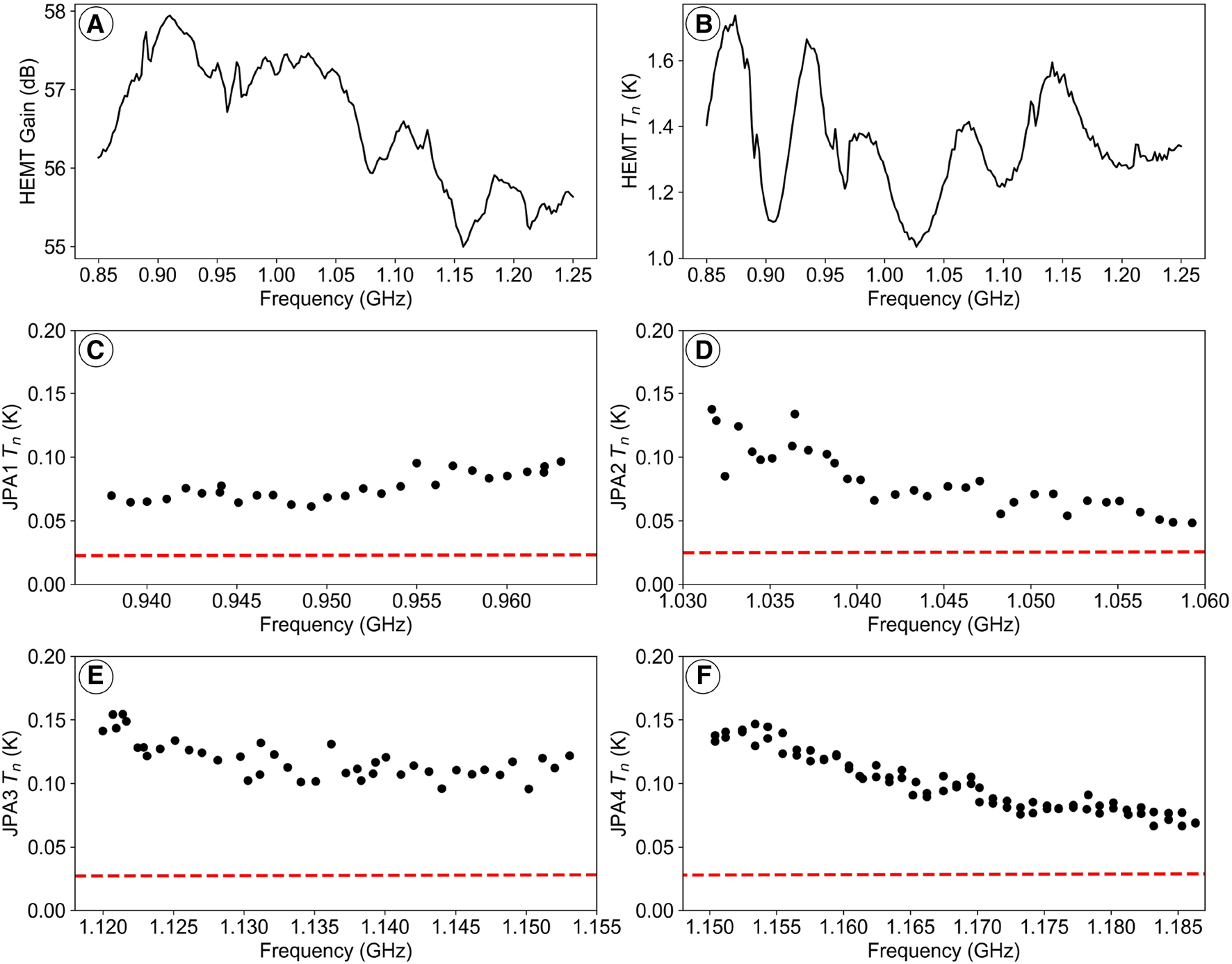
Characteristics of multi-JPA amplifier based on Leo I assembly. (A) HEMT amplifier gain, (B) HEMT amplifier noise. (A) and (B) were measured with all JPAs OFF. (C–F) Noise temperatures of JPAs 1–4, respectively. The red dashed line corresponds to the quantum limit for the amplifier added noise.
In Run 6 of the CAPP-MAX experiment, as mentioned earlier, three JPAs were in operation. Two of them were situated within one holder, while the third was mounted in a separate holder. The DC flux bias was shared by connecting the DC flux coils of both holders in series. Further details of the measurements conducted during Run 6 of the CAPP-MAX experiment utilizing this amplifier can be found in [37, 69].
6.5 JPA interference in split band amplifier
For Run 7 of the CAPP-MAX experiment, we prepared a new “Leo II” assembly, comprising a full set of 6 JPAs with HPRFs of 1.25, 1.30, 1.36, 1.40, 1.45, and 1.50 GHz in a parallel-serial connection as shown in Figure 12D. To minimize possible interference, we ordered the JPAs to avoid close operating frequencies among neighbors. In the first holder, we positioned JPAs starting with the lowest HPRF (1.25 GHz), followed by 1.36 GHz, and finally 1.45 GHz. The second holder followed a sequencing of 1.30 GHz, 1.40 GHz, and 1.50 GHz.
Tests of this assembly (Figure 15) in the dry fridge revealed characteristics similar to those of Leo I. These JPAs allowed us to cover a frequency range of about 300 MHz, spanning from 1.2 to 1.5 GHz. However, interference between some of the JPAs at their lowest operating frequencies emerged during testing.
FIGURE 15
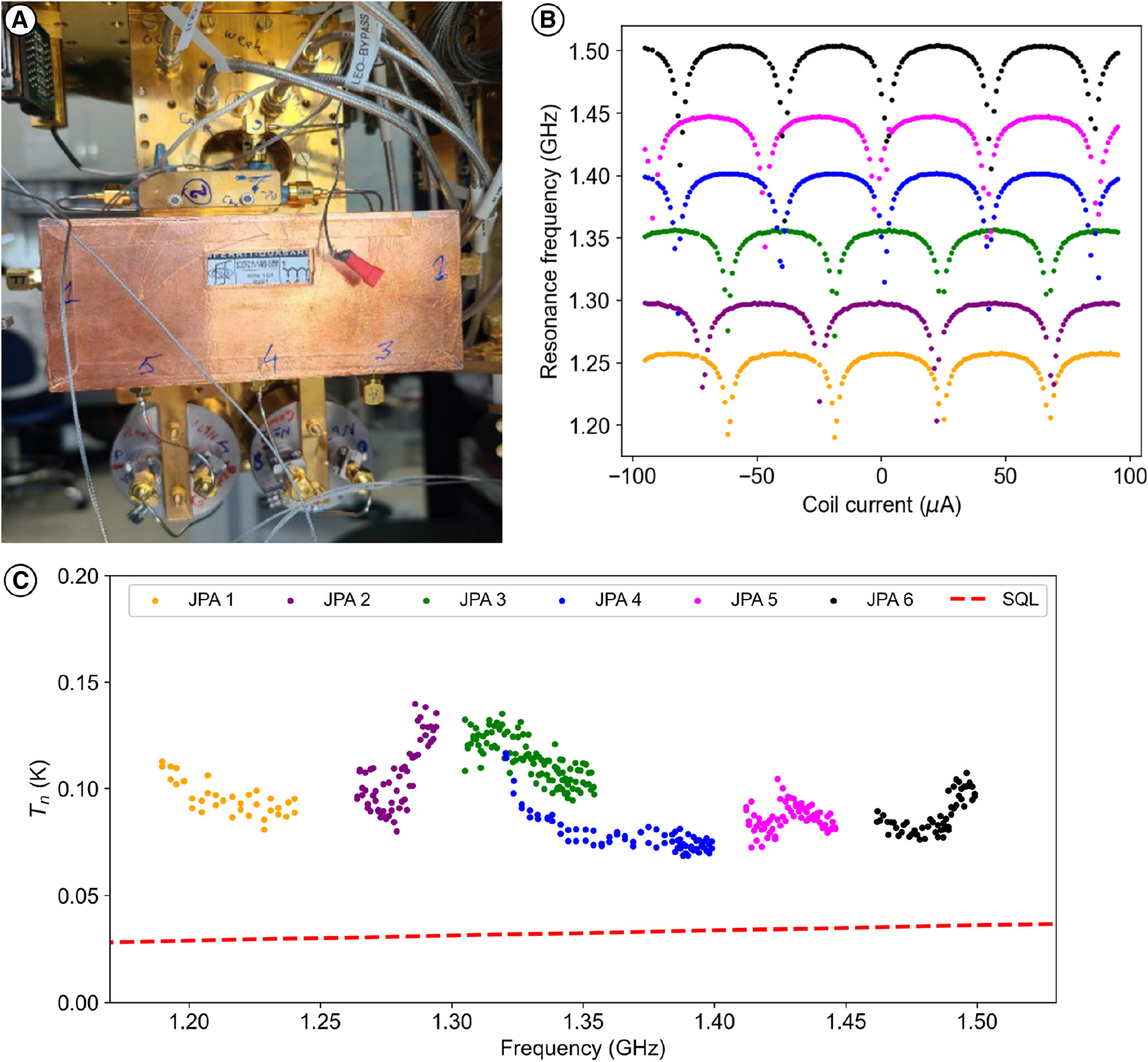
Six-JPA assembly (Leo II). (A) Assembly installed at the mixing chamber plate of the dry dilution refrigerator. (B) Flux-sweep curves of the six JPAs. (C) Added noise temperature depending on the frequency for the six JPAs. Each color on (B) and (C) corresponds to a JPA. The red dashed line corresponds to the quantum limit for the amplifier added noise.
This setup was tested with a series connection of DC bias lines for the two JPA holders. This configuration posed challenges, particularly in achieving detuning of the JPA resonance frequencies from each other, especially within the narrow range of the lowest operating frequencies where the sensitivity of JPAs to interference is most pronounced. Due to the use of dc bias coils with the same design and almost identical JPA flux sensitivities, leveraging the periodicity of SQUID characteristics was not feasible. Utilizing another branch of the flux-to-frequency characteristic would have resulted in the same interference problem. We decided not to modify the design due to the risk of damage.
While it would have been feasible to utilize different twisted pairs to supply DC flux bias current for the second holder, we deliberated several ideas to tackle this issue, with the objective of minimizing the interval between runs without requiring time-consuming fridge modifications.
Another approach involved connecting the DC-flux coils in parallel, with small resistors of different values in series with the coils in each branch. In this configuration, the coils will have different sensitivity to input current, but there is still a probability of interference for JPAs in different holders due to overlap at lower frequencies.
Furthermore, we developed and implemented a new circuit design using Schottky diodes. This circuit allowed us to independently apply two DC flux biases to two JPA holders using the same twisted pair of wires. It achieved this by separating the flux biases using currents of different directions to bias one or the other JPA holder. The circuit featured a diode rectifier operating at the 4 K stage of the fridge to address heat dissipation in the diodes [70].
A potential issue arose during the operation of GaAs diodes in proximity to a strong magnetic field due to the field’s effect on the diode’s performance. This effect could lead to changes in properties depending on the orientation of the diode in the magnetic field [71]. To mitigate this concern, we replaced each of the two diodes with three diodes, each oriented along different orthogonal Cartesian axes [70].
After Run 6 of our axion experiment, we re-accessed the fridge design. We decided to upgrade our DC lines and implement a twisted pair to control the second JPA holde independently. As a result, for Run 7, we were able to forego the use of this diode circuit, postponing its installation.
Before Run 7, we conducted a 6-JPA assembly (Leo-II) measurements and confirmed their noise characteristics (see Figure 15C) in the experiment fridge.
7 Conclusion
In this paper, we have presented an overview of the characterization and implementation of JPAs at CAPP, detailing the processes involved in achieving high sensitivity in axion detection. Drawing from the established flux-driven JPA technology developed by RIKEN and the University of Tokyo, we successfully adapted these amplifiers for the CAPP haloscope search experiments through several key developments.
1. We investigated and devised methods to operate flux-driven JPAs across a continuous frequency range. This involved introducing the paramap method to determine the operating points aimed at achieving specific gains and minimal noise. We established a test setup based on a dilution fridge, complemented by a computer-controlled system for JPA testing and experiment execution.
2. We introduced two methods for extending the effective amplifier frequency range, utilizing series and parallel connections. Our experiments with multiple JPA configurations, including the 6-JPA assembly, have demonstrated the efficacy of our approaches in achieving a broad frequency range. By selecting JPA sequences and employing different techniques, we successfully minimized interference and maximized sensitivity without compromising noise characteristics. By connecting 6 JPAs, each with an operating frequency band of 48–52 MHz and different central frequencies, we expanded our coverage to approximately 300 MHz, which is almost six times the range of a single JPA. It enhances our scanning capabilities by minimizing downtime and helium loss during cooldowns for the CAPP-MAX system [37].
3. We introduced a nested shield based on superconductors and CRYOPHY, enabling operation in high magnetic fields up to 0.1 T without saturating the CRYOPHY and achieving a shielding factor of – with residual fields below 100 nT for stable JPA operation. A patent application for this innovation is currently underway.
4. Our JPA development has facilitated the implementation of JPA-based amplifiers in various CAPP experiments, as described in [37, 72–76], and has allowed the CAPP to contribute to the global axion search effort.
These developments pave the way for further breakthroughs in future CAPP experiments. We also hope that our split-band amplifier technique will be a valuable tool for potential applications in other fields of study, such as basic science experiments and quantum computer readouts, extending its utility beyond its initial scope.
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
SU: Conceptualization, Formal Analysis, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. JK: Data curation, Formal Analysis, Investigation, Software, Visualization, Writing–review and editing. CK: Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–review and editing. BI: Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–review and editing. JK: Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–review and editing. AvL: Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–review and editing. YN: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Resources, Supervision, Validation, Visualization, Writing–review and editing. SA: Data curation, Formal Analysis, Investigation, Validation, Visualization, Writing–review and editing. SO: Data curation, Investigation, Validation, Visualization, Writing–review and editing. MK: Data curation, Formal Analysis, Investigation, Visualization, Writing–review and editing. YS: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Institute for Basic Science (IBS-R017-D1) and JSPS KAKENHI (Grant No. JP22H04937). AV was supported by a JSPS postdoctoral fellowship.
Acknowledgments
The authors thank Dr. Seongtae Park for his assistance with the PCB development.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Glossary
| ADMX | Axion Dark Matter Experiment |
| BF | BlueFors |
| CAPP | Center for Axion and Precision Physics Research |
| CP | Cold plate |
| CPW | Coplanar waveguide |
| DAQ | Data acquisition |
| DR | Dilution refrigerator |
| DFSZ | Dine-Fischler-Srednicki-Zhitnitskii |
| HAYSTAC | Haloscope At Yale Sensitive To Axion Cold dark matter |
| HEMT | High-electron-mobility transistor |
| HPRF | Highest passive resonance frequency |
| IBS | Institute for Basic Science |
| JPAs | Josephson Parametric Amplifiers |
| KAIST | Korea Advanced Institute of Science and Technology |
| KSVZ | Kim-Shifman-Vainshtein-Zakharov |
| LNA | Low noise amplifier |
| MXC | Mixing chamber plate |
| NS | Noise source |
| OS | Onion Shield |
| OWP | Optimal working point |
| PCB | Printed pircuit board |
| PID | Proportional-integral-derivative |
| PSD | Power spectral densities |
| RF | Radio-frequency |
| RQC | RIKEN Center for Quantum Computing |
| RT | Room temperature |
| SA | Spectrum analyzer |
| SM | Standard Model |
| SQL | Standard quantum limit |
| SQUID | Superconducting quantum interference device |
| VNA | Vector network analyzer |
| VSWR | Voltage standing wave ratio |
References
1.
Du N Force N Khatiwada R Lentz E Ottens R Rosenberg LJ et al Search for invisible axion dark matter with the axion dark matter experiment. Phys Rev Lett (2018) 120:151301. 10.1103/physrevlett.120.151301
2.
Braine T Cervantes R Crisosto N Du N Kimes S Rosenberg LJ et al Extended search for the invisible axion with the axion dark matter experiment. Phys Rev Lett (2020) 124:101303. 10.1103/physrevlett.124.101303
3.
Brubaker BM Zhong L Gurevich YV Cahn SB Lamoreaux SK Simanovskaia M et al First results from a microwave cavity axion search at 24 μeV. Phys Rev Lett (2017) 118:061302. 10.1103/physrevlett.118.061302
4.
Backes KM Palken DA Al Kenany S Brubaker BM Cahn SB Droster A et al A quantum enhanced search for dark matter axions. Nature (2021) 590:238–42. 10.1038/s41586-021-03226-7
5.
Grilli di Cortona G Hardy E Vega JP Villadoro G . The QCD axion, precisely. High Energ Phys. (2016) 2016(34):34–6. 10.1007/jhep01(2016)034
6.
Wilczek F . Problem of strong p and t invariance in the presence of instantons. Phys Rev Lett (1978) 40:279–82. 10.1103/physrevlett.40.279
7.
Weinberg S . A new light boson?Phys Rev Lett (1978) 40:223–6. 10.1103/physrevlett.40.223
8.
Kim D Jeong J Youn SW Kim Y Semertzidis YK . Revisiting the detection rate for axion haloscopes. J Cosmol Astropart Phys (2020) 2020(03):066. 066, mar 2020. 10.1088/1475-7516/2020/03/066
9.
Sikivie P . Experimental tests of the invisible axion. Phys Rev Lett (1983) 51:1415–7. 10.1103/physrevlett.51.1415
10.
DePanfilis S Melissinos AC Moskowitz BE Rogers JT Semertzidis YK Wuensch WU et al Limits on the abundance and coupling of cosmic axions at 4.5 < ma < 5.0 μeV. Phys Rev Lett (1987) 59:839–42. 10.1103/PhysRevLett.59.839
11.
Brubaker BM . First results from the HAYSTAC axion search. PhD thesis (2018).
12.
Kim JE . Weak-interaction singlet and strong \mathrm{CP} invariance. Phys Rev Lett (1979) 43:103–7. 10.1103/physrevlett.43.103
13.
Shifman MA Vainshtein AI Zakharov VI . Can confinement ensure natural CP invariance of strong interactions?Nucl Phys B (1980) 166:493–506. 10.1016/0550-3213(80)90209-6
14.
Zhitnitsky AP . Possible suppression of axion-hadron interactions. Sov J Nucl Phys (Engl Transl.) (1980) 31(2):260.
15.
Dine M Fischler W Srednicki M . A simple solution to the strong CP problem with a harmless axion. Phys Lett B (1981) 104:199–202. 10.1016/0370-2693(81)90590-6
16.
Jeong J Youn SW Bae S Kim D Kim Y Semertzidis YK . Analytical considerations for optimal axion haloscope design. J Phys G (2022) 49(5):055201. 10.1088/1361-6471/ac58b4
17.
Jeong J Youn SW Bae S Kim J Seong T Kim JE et al Search for invisible axion dark matter with a multiple-cell haloscope. Phys Rev Lett (2020) 125(22):221302. 10.1103/physrevlett.125.221302
18.
Kwon O Lee D Chung W Ahn D Byun HS Caspers F et al First results from an axion haloscope at capp around 10.7 μeV. Phys Rev Lett (2021) 126:191802. 10.1103/physrevlett.126.191802
19.
Lownoisefactory. LNF-LNC0.6_2A (2024). Available from: https://lownoisefactory.com/product/lnf-lnc0-6_2a/ (Accessed July 16 2024).
20.
Schleeh J Alestig G Halonen J Malmros A Nilsson B Nilsson PÅ et al Ultralow-power cryogenic InP HEMT with minimum noise temperature of 1 K at 6 GHz. IEEE Electron Device Lett (2012) 33(5):664–6. 10.1109/led.2012.2187422
21.
Castellanos-Beltran MA Lehnert KW . Widely tunable parametric amplifier based on a superconducting quantum interference device array resonator. Appl Phys Lett (2007) 91(8):083509. 10.1063/1.2773988
22.
Eom H Day PK LeDuc HG Zmuidzinas J . A wideband, low-noise superconducting amplifier with high dynamic range. Nat Phys (2012) 8(8):623–7. 10.1038/nphys2356
23.
Yaakobi O Friedland L Macklin C Siddiqi I . Parametric amplification in josephson junction embedded transmission lines. Phys Rev B (2013) 87:144301. 10.1103/physrevb.87.144301
24.
Mutus JY White TC Barends R Chen Y Chen Z Chiaro B et al Strong environmental coupling in a Josephson parametric amplifier. Appl Phys Lett (2014) 104(26):263513. 07. 10.1063/1.4886408
25.
White TC Mutus JY Hoi I-C Barends R Campbell B Chen Y et al Traveling wave parametric amplifier with Josephson junctions using minimal resonator phase matching. Appl Phys Lett (2015) 106(24):242601. 06. 10.1063/1.4922348
26.
Macklin C O’Brien K Hover D Schwartz ME Bolkhovsky V Zhang X et al A near–quantum-limited josephson traveling-wave parametric amplifier. Sci (2015) 350(6258):307–10. 10.1126/science.aaa8525
27.
Adamyan AA de Graaf SE Kubatkin SE Danilov AV . Superconducting microwave parametric amplifier based on a quasi-fractal slow propagation line. J Appl Phys (2016) 119(8):083901. 10.1063/1.4942362
28.
Miano A Mukhanov OA . Symmetric traveling wave parametric amplifier. IEEE Trans Appl Supercond (2019) 29(5):1–6. 10.1109/tasc.2019.2904699
29.
Urade Y Zuo K Baba S Sandbo Chang CW Nittoh K-I Inomata K et al Flux-driven impedance-matched Josephson parametric amplifier with improved pump efficiency. In: APS march meeting abstracts, volume 2021 of APS meeting abstracts (2021). A28.010.
30.
Lu Y-P Zuo Q Pan J-Z Jiang J-L Wei X-Y Li Z-S et al An easily-prepared impedance matched josephson parametric amplifier. Chin Phys B (2021) 30(6):068504. 10.1088/1674-1056/ac0420
31.
Giachero A Barone C Borghesi M Carapella G Caricato AP Carusotto I et al Detector array readout with traveling wave amplifiers. J Appl Phys (2021) 209:658–66. 10.1007/s10909-022-02809-6
32.
Gaydamachenko V Kissling C Dolata R Zorin AB . Numerical analysis of a three-wave-mixing Josephson traveling-wave parametric amplifier with engineered dispersion loadings. J Appl Phys (2022) 132(15):154401–10. 10.1063/5.0111111
33.
Yamamoto T Inomata K Watanabe M Matsuba K Miyazaki T Oliver WD et al Flux-driven Josephson parametric amplifier. Appl Phys Lett (2008) 93(4):042510. 10.1063/1.2964182
34.
Dolan GJ . Offset masks for lift-off photoprocessing. Appl Phys Lett (1977) 31(5):337–9. 10.1063/1.89690
35.
Kyle M . Sundqvist and Per Delsing. Negative-resistance models for parametrically flux-pumped superconducting quantum interference devices. EPJ Quan Technol (2014) 1(1):1–21. 10.1140/epjqt6
36.
Roy A Devoret M . Introduction to parametric amplification of quantum signals with Josephson circuits. Comptes Rendus Physique (2016) 17(7):740–55. 10.1016/j.crhy.2016.07.012
37.
Ahn S Kim JM Ivanov BI Kwon O Byun HS van Loo AF et al Extensive search for axion dark matter over 1 GHz with CAPP’s Main Axion eXperiment. Phys Rev X (2024). arXiv:2402.12892, accepted in. 10.48550/arXiv.2402.12892
38.
Bluefors. Enabling the future of quantum technology (2024). Available from: https://bluefors.com (Accessed July 16 2024).
39.
KEYCOM. Superconducting coaxial cable assemblies (0.085"/0.047"/0.034" type NbTi-NbTi superconducting coaxial cables) (2024). Available from: https://keycom.co.jp/eproducts/upj/upj7/page.htm (Accessed July 16 2024).
40.
Yokogawa. Site map (2023). Available from: https://tmi.yokogawa.com/kr/solutions/products/generators-sources/source-measure-units/gs200/ (Accessed July 16 2024).
41.
Bluefors. Dilution refrigerator measurement systems (2022). Available from: https://bluefors.com/products/dilution-refrigerator-measurement-systems/ (Accessed July 16 2024).
42.
Pickeringtest. 64 channel relay driver module (2024). Available from: https://www.pickeringtest.com/en-us/product/64-channel-relay-driver-module (Accessed July 16 2024).
43.
Adlinktech. Products PXI PXIe platform PXIChassis PXES-2590 (2024). Available from: https://www.adlinktech.com/Products/PXI_PXIe_platform/PXIChassis/PXES-2590 (Accessed July 16 2024).
44.
Ivanov BI Kim J Kutlu Ç van Loo AF Nakamura Y Uchaikin SV et al Four-channel system for characterization of Josephson parametric amplifiers. In: Proc. Of the 29th international Conference on low temperature physics (LT29), pages 0112001–0112006. JPS conProc (2023). 10.7566/jpscp.38.011200
45.
Rybka G . Private communication (2023).
46.
Ansys. Ansys simulation software (2024). Available from: https://www.ansys.com/ (Accessed July 16 2024).
47.
Uchaikin SV Ivanov BI Kim J Kutlu Ç van Loo AF Nakamura Y et al CAPP axion search experiments with quantum noise limited amplifiers. In: Proc. Of the 29th international conference on low temperature physics (LT29). JPS ConProc (2023). p. 0112011–6. 10.7566/JPSCP.38.011201
48.
Aperam. Product cryophy (2024). Available from: https://www.aperam.com/product/CRYOPHY/ (Accessed July 16 2024).
49.
Arpaia P Buzio M Capatina O Eiler K Langeslag SAE Parrella A et al Effects of temperature and mechanical strain on ni-fe alloy cryophy for magnetic shields. J Magn Magn Mater (2019) 475:514–23. 10.1016/j.jmmm.2018.08.055
50.
Krantz P Reshitnyk Y Wustmann W Bylander J Simon G Oliver WD et al Investigation of nonlinear effects in Josephson parametric oscillators used in circuit quantum electrodynamics. New J Phys (2013) 15(10):105002. 10.1088/1367-2630/15/10/105002
51.
Haus HA Mullen JA . Quantum noise in linear amplifiers. Phys Rev (1962) 128:2407–13. 10.1103/physrev.128.2407
52.
Kutlu Ç van Loo AF Uchaikin SV Matlashov A Lee D Oh S et al Characterization of a flux-driven Josephson parametric amplifier with near quantum-limited added noise for axion search experiments. Supercond Sci Technol (2021) 34:085013. 10.1088/1361-6668/abf23b
53.
Yurke B Corruccini LR Kaminsky PG Rupp LW Smith AD Silver AH et al Observation of parametric amplification and deamplification in a josephson parametric amplifier. Phys Rev A (1989) 39:2519–33. 10.1103/physreva.39.2519
54.
Kuzmin L Likharev K Migulin V Zorin A . Quantum noise in josephson-junction parametric amplifiers. IEEE Trans Magn (1983) 19(3):618–21. 10.1109/tmag.1983.1062472
55.
Babourina-Brooks E Doherty A Milburn GJ . Quantum noise in a nanomechanical duffing resonator. New J Phys (2008) 10(10):105020. 10.1088/1367-2630/10/10/105020
56.
Engen GF . A new method of characterizing amplifier noise performance. IEEE Trans Instrum Meas (1970) 19(4):344–9. 10.1109/tim.1970.4313925
57.
Friis HT . Noise figures of radio receivers. Proc IRE (1944) 32(7):419–22. 10.1109/jrproc.1944.232049
58.
Sliwa KM Hatridge M Narla A Shankar S Frunzio L Schoelkopf RJ et al Reconfigurable josephson circulator/directional amplifier. Phys Rev X (2015) 5:041020. 10.1103/physrevx.5.041020
59.
Clerk AA Devoret MH Girvin SM Marquardt F Schoelkopf RJ . Introduction to quantum noise, measurement, and amplification. Rev Mod Phys (2010) 82:1155–208. 10.1103/revmodphys.82.1155
60.
Caves CM . Quantum limits on noise in linear amplifiers. Phys Rev D (1982) 26:1817–39. 10.1103/physrevd.26.1817
61.
Kutlu Ç Ahn S Uchaikin SV Lee S van Loo AF Nakamura Y et al Systematic approach for tuning flux-driven Josephson parametric amplifiers for stochastic small signals. In: Proc. Of the 29th international Conference on low temperature physics (LT29), pages 0112021–0112027. JPS con. Proc. (2023). 10.7566/JPSCP.38.011202
62.
Nelder JA Mead R A simplex method for function minimization. Comput J (1965) 7(4):308–13. 10.1093/comjnl/7.4.308
63.
Kim Y Jeong J Youn SW Bae S van Loo AF Nakamura Y et al Parameter Optimization of Josephson Parametric Amplifiers Using a Heuristic Search Algorithm for Axion Haloscope Search. Electronics (2024) 13: 2127. 10.3390/electronics13112127
64.
Uchaikin SV Kim J Ivanov BI van Loo AF Nakamura Y Ahn S et al Improving amplification bandwidth by combining Josephson parametric amplifiers for active axion search experiments at IBS/CAPP. J Low Temp Phys (2024). 10.1007/s10909-024-03090-5
65.
Kim J Ko M Uchaikin SV Ivanov BI van Loo AF Nakamura Y et al Wideband amplification for IBS-CAPP’s axion search experiments. J Low Temp Phys (2023). 10.21203/rs.3.rs-3550142/v1
66.
Ferrite Quasar. Available from: http://ferrite-quasar.ru/index.html.
67.
Ferrite Quasar. Available from: http://ferrite-quasar.ru/products/cci/cci7e.html (Accessed July 16 2024).
68.
Leiden Cryogenics BV . High end custom dilution refrigerators (2022). Available from: https://leidencryogenics.nl/ (Accessed July 16 2024).
69.
Kim J Ivanov BI Kutlu Ç Park S van Loo AF Nakamura Y et al Josephson parametric amplifier in axion experiments. In: Proc. Of the 29th international Conference on low temperature physics (LT29), pages 0111991–0111996. JPS con. Proc. (2023). 10.7566/JPSCP.38.011199
70.
Ko MS Uchaikin SV Ivanov BI Kim JM Oh S Gkika V . Expanding scanning frequency range of Josephson parametric amplifier axion haloscope readout with Schottky diode bias circuit. In: Proc. IEEE 24th international conference of young professionals in electron devices and materials (EDM) (2023). p. 810–3. 10.1109/EDM58354.2023.10225136
71.
Sun ZG Mizuguchi M Manago T Akinaga H . Magnetic-field-controllable avalanche breakdown and giant magnetoresistive effects in Goldsemi-insulating-GaAs Schottky diode. Appl Phys Lett (2004) 85(23):5643–5. 10.1063/1.1834733
72.
Kim J Kwon O Kutlu Ç Chung W Matlashov A Uchaikin S et al Near-quantum-noise axion dark matter search at CAPP around 9.5 μeV. Phys Rev Lett (2023) 130:091602. 10.1103/physrevlett.130.091602
73.
Yi AK Ahn S Kutlu Ç Kim JM Ko BR Ivanov BI et al Axion dark matter search around 4.55 μeV with Dine-Fischler-Srednicki-Zhitnitskii sensitivity. Phys Rev Lett (2023) 130:071002. 10.1103/physrevlett.130.071002
74.
Yi AK Ahn S Kutlu Ç Kim JM Ko BR Ivanov BI et al Search for the Sagittarius tidal stream of axion dark matter around 4.55 μeV. Phys Rev D (2023) 108:L021304. 10.1103/physrevd.108.l021304
75.
Kutlu Ç Lee S Uchaikin SV Ahn S Bae S Jeong J et al Search for qcd axion dark matter around 24.5 μeV using an 8-cell microwave resonant cavity haloscope and a flux-driven Josephson parametric amplifier. In: Proc. Of science,- 41st international conference on high energy physics (ICHEP2022) - astroparticle physics and cosmology, 414 (2023). 10.22323/1.414.0092
76.
Kim Y Jeong J Youn SW Bae S Lee K van Loo AF et al Experimental search for invisible axions as a test of axion cosmology around 22 μeV (2023). arXiv:2312.11003 [hep-ex].
Summary
Keywords
axion dark matter, cavity haloscope, Josephson parametric amplifier, quantum noise limited amplifier, low temperature thermalization
Citation
Uchaikin SV, Kim J, Kutlu C, Ivanov BI, Kim J, van Loo AF, Nakamura Y, Ahn S, Oh S, Ko M and Semertzidis YK (2024) Josephson parametric amplifier based quantum noise limited amplifier development for axion search experiments in CAPP. Front. Phys. 12:1437680. doi: 10.3389/fphy.2024.1437680
Received
24 May 2024
Accepted
25 June 2024
Published
23 July 2024
Volume
12 - 2024
Edited by
Frank Franz Deppisch, University College London, United Kingdom
Reviewed by
Toshiaki Inada, International Center for Elementary Particle Physics, The University of Tokyo, Japan
Tatsumi Nitta, International Center for Elementary Particle Physics, The University of Tokyo, Japan
Updates
Copyright
© 2024 Uchaikin, Kim, Kutlu, Ivanov, Kim, van Loo, Nakamura, Ahn, Oh, Ko and Semertzidis.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sergey V. Uchaikin, uchaikin@ibs.re.kr
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.