Slant spacelike ruled surfaces and their Bertrand offsets

In this work, we investigate the synthesis problem of slant spacelike ruled surfaces and associated Bertrand offsets $(\mathcal{B}\mathcal{O})$ in ${\mathcal{E}}_1^3$ (Minkowsk 3-space). We provide the parametric equation for a non-developable spacelike ruled surface $(\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S})$ by using the Blaschke frame $(\mathcal{B}\mathcal{F})$. This results in the amplitude to control a family of curvature functions defining the domestic form of this $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$. Therefore, we found the appropriate $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ criteria to be slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$. Thus, several new Bertrand offsets $(\mathcal{B}\mathcal{O})$ for slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ are investigated and constructed.

1 Introduction

The fundamental principle of a directed line’s motion in connection with a solid body is referred to as the $\mathcal{R}\mathcal{S}$ concept in spatial kinematics. This notion holds great importance in conventional differential geometry and has been the subject of extensive research by numerous scholars, as demonstrated by [1–7]. From a geometric perspective, the properties of $\mathcal{R}\mathcal{S}$ and their offset surfaces have been analyzed in both Euclidean and non-Euclidean spaces. Bertrand curves were examined in the field of line-geometry by Ravani and Ku, revealing that $\mathcal{R}\mathcal{S}$ can possess an infinite number of $\mathcal{B}\mathcal{O}$, similar to how a plane curve can possess an infinite number of $\mathcal{B}$ mates [8]. Küçük and Gürsoy provided certain characterizations of $\mathcal{B}\mathcal{O}$ related to the trajectory of $\mathcal{R}\mathcal{S}$ by studying the relationships between the projection areas for the spherical curves of $\mathcal{B}\mathcal{O}$ and their integral invariants [9]. Kasap and Kuruoğlu conducted an analysis of the integral invariants of the couple of $\mathcal{R}\mathcal{S}$ in the Euclidean 3-space ${\mathcal{E}}^3$, as documented in [10]. By considering the orthonormal frame along striction curve of a ruled surface, Önder has defined slant ruled surfaces in the Euclidean 3-space [11]. Moreover, Kaya and Önder have studied the position vectors and some differential equation characterizations for slant ruled surfaces in the Euclidean 3-space ${\mathcal{E}}^3$ [12–14]. They have also defined a new type of slant ruled surface as the Darboux slant ruled surface and characterized for this type of slant surfaces [15]. In [16], Önder introduced some characterizations for a non-null ruled surface to be a slant ruled surface in Minkowski 3-space ${\mathcal{E}}_1^3$. In their study, Kasap and Kuruoğlu investigated $\mathcal{B}\mathcal{O}$ of $\mathcal{R}\mathcal{S}$ in Minkowski 3-space ${\mathcal{E}}_1^3$, as documented in [17]. [18] demonstrated the involute–evolute offsets of $\mathcal{R}\mathcal{S}$. Orbay et al. began studying the Mannheim offsets of $\mathcal{R}\mathcal{S}$ in [19]. Önder and Uğurlu conducted a study on the relationships between invariants of Mannheim offsets of $\mathcal{T}\mathcal{L}\mathcal{R}\mathcal{S}$. They also formulated many considerations for the development of these surface offsets [20, 21]. In view of the involute–evolute offsets of the ruled surface in [7], Şentürk and Yüce described the integral invariants of the involute–evolute offsets of $\mathcal{R}\mathcal{S}$s using the geodesic Frenet frame [22].

In recent times, Yoon has investigated the evolute offsets of $\mathcal{R}\mathcal{S}$ in $\mathcal{E}\text{\_}{1}^3$ with a stationary Gaussian curvature and mean curvature [23]. A plethora of comprehensive treatises has been published on this subject, as demonstrated by the numerous written works, such as [24–27]. However, to the best of our knowledge, no prior work has focused on constructing $\mathcal{B}\mathcal{O}$ of slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$, utilizing the geometric attributes of the striction curve $(\mathcal{S}\mathcal{C})$. Here, we intend to fill the gap in the existing literature.

In this paper, with the identification of slant curves, we treat the structure issue of the $\mathcal{B}\mathcal{O}$ of a slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ family in Minkowski 3-space ${\mathcal{E}}_1^3$. Therefore, we extend the parametrization of $\mathcal{B}\mathcal{O}$ for any slant non-developable $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$. Furthermore, we inquire into the ownerships of these $\mathcal{S}\mathcal{L}\mathcal{R}$ surfaces and grant their distribution. Meanwhile, we extend some interpretative paradigms to display $\mathcal{S}\mathcal{L}\mathcal{R}$ surfaces with their $\mathcal{B}\mathcal{O}$ along mutual geodesic, line of curvature, and asymptotic curve. Our ramifications in this paper may be beneficial in any area that demands documentation around surfaces due to the descriptions supplying insights into surfaces theory.

2 Basic concepts

Let ${\mathcal{E}}_1^3$ indicate the Minkowski 3-space [28, 29]. For vectors $\mathfrak{a}=\left(a_1,a_2,a_3\right)$ and $\mathfrak{b}=(b_1,b_2,b_3)$ in ${\mathcal{E}}_1^3,$

$⟨\mathfrak{a},\mathfrak{b}⟩=a_1{b}_1-a_2{b}_2+a_3{b}_3$

is named the Lorentzian inner product. We also explain a vector

$\mathfrak{a}\times \mathfrak{v}=\left(a_2{b}_3-a_3{b}_2,a_1{b}_3-a_3{b}_1,a_1{b}_2-a_2{b}_1\right).$

Since $<,>$ is an indefinite metric, recall that a vector $\mathfrak{a}\in {\mathcal{E}}_1^3$ can have one of three causal natures; it can be $\mathcal{S}\mathcal{L}$ if $⟨\mathfrak{a},\mathfrak{a}⟩>0$ or $\mathfrak{a}=\mathbf{0}$, timelike $(\mathcal{T}\mathcal{L})$ if $⟨\mathfrak{a},\mathfrak{a}⟩<0$, and null or lightlike if $⟨\mathfrak{a},\mathfrak{a}⟩=0$ and $\mathfrak{a}\ne \mathbf{0}$. The norm of $\mathfrak{a}\in {\mathcal{E}}_1^3$ is explained by $‖\mathfrak{a}‖=\sqrt{\left|⟨\mathfrak{a},\mathfrak{a}⟩\right|}$; then, the hyperbolic and Lorentzian (de Sitter space) unit spheres are

${\mathcal{H}}_{+}^2=\left\{\mathfrak{a}\in {\mathcal{E}}_1^3\mid {‖\mathfrak{a}‖}^2≔a_1^2-a_2^2+a_3^2=-1\right\}(1)$

and

${\mathcal{S}}_1^2=\left\{\mathfrak{a}\in {\mathcal{E}}_1^3\mid {‖\mathfrak{a}‖}^2≔a_1^2-a_2^2+a_3^2=1\right\}.(2)$

2.1 Ruled surface

$\mathcal{R}\mathcal{S}$ is a surface produced by a line $\mathcal{L}$ mobile on a curve $\mathbf{c}(v)$. The several locations of the line coined the producers or rulings of the surface. Such a surface, thus, has the ruled form [1–6]

$\mathfrak{R}:\mathfrak{y}\left(v,t\right)=\mathfrak{c}\left(v\right)+v\mathfrak{b}\left(v\right),v\in I\text{,\hspace{0.17em}}t\in \mathbb{R},(3)$

such that ${‖\mathfrak{b}‖}^2=\sigma (\pm 1),{‖{\mathfrak{b}}^{\prime }‖}^2=\eta (\pm 1),<{\mathfrak{c}}^{\prime },{\mathfrak{b}}^{\prime }>=0$; $\prime =\frac{d}{dv}$. In this circumstance, the curve $\mathfrak{c}(v)$ is the striction curve $(\mathcal{S}\mathcal{C})$ and $v$ is the arc length of the spherical non-null curve $\mathfrak{b}(v)$. If $\mathfrak{b}$ is not stationary or not null or ${\mathfrak{b}}^{\prime }$ null, then the Blaschke Frame $\mathcal{B}\mathcal{F}$ for $\mathfrak{b}(v)$ will be registered as

$\left.\begin{array}{c}\mathfrak{b}=\mathfrak{b}\left(v\right),\mathfrak{z}\left(v\right)={\mathfrak{b}}^{\prime },\mathfrak{g}\left(v\right)=\mathfrak{b}\times \mathfrak{z},\hfill \\ \mathfrak{b}\times \mathfrak{z}=\mathfrak{g},\mathfrak{b}\times \mathfrak{g}=\sigma \mathfrak{z},\mathfrak{z}\times \mathfrak{g}=-\eta \mathfrak{b},{‖\mathfrak{g}‖}^2=-\sigma \eta ,\hfill \end{array}\right\}(4)$

where $\mathfrak{b},\mathfrak{z},\mathfrak{g}$ are named the ruling, the central normal, and the central tangent, respectively. The Blaschke formula is from Equation 4

$\left(\begin{array}{c}\hfill {\mathfrak{b}}^{\prime }\hfill \\ \hfill {\mathfrak{z}}^{\prime }\hfill \\ \hfill {\mathfrak{g}}^{\prime }\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill -\sigma \eta \hfill & \hfill 0\hfill & \hfill \gamma \hfill \\ \hfill 0\hfill & \hfill \sigma \gamma \hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathfrak{b}\hfill \\ \hfill \mathfrak{z}\hfill \\ \hfill \mathfrak{g}\hfill \end{array}\right),(5)$

where $\gamma (v)=\det ({\mathfrak{b}}^{\prime \prime },{\mathfrak{b}}^{\prime },\mathfrak{b})$ is the spherical curvature of $\mathfrak{b}(v)$. In view of $\mathcal{B}\mathcal{F}$ with signs $\sigma$, $\eta$, and $-\sigma \eta$, $\mathcal{S}\mathcal{C}$ is

${\mathfrak{c}}^{\prime }\left(v\right)=\stackrel{v}{\underset{0}{\int }}\left(\sigma \mathrm{\Delta }\left(v\right)\mathfrak{b}\left(v\right)-\sigma \eta \delta \left(v\right)\mathfrak{g}\left(v\right)\right)dv.(6)$

$\gamma (v)$, $\mathrm{\Delta }(v)$, and $\delta (v)$ are titled the curvature parameters of $\mathfrak{R}$. The geometrical view of these parameters is proved as follows:$\chi$ is the spherical curvature of the spherical image curve $\mathfrak{b}(v)$; $\mathrm{\Delta }$ depicts the angle through the tangent of $\mathcal{S}\mathcal{C}$ and the ruling of $\mathfrak{R}$; and $\delta$ is the distribution parameter of $\mathfrak{R}$, from Equation 3 at the ruling $\mathfrak{b}$.

In this study, we will meditate a non-developable $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ nominated by $(\sigma ,\eta )=(1,-1)$. Then,

$\left.\begin{array}{c}\left(\begin{array}{c}\hfill {\mathfrak{b}}^{\prime }\hfill \\ \hfill {\mathfrak{z}}^{\prime }\hfill \\ \hfill {\mathfrak{g}}^{\prime }\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill \gamma \hfill \\ \hfill 0\hfill & \hfill \gamma \hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathfrak{b}\hfill \\ \hfill \mathfrak{z}\hfill \\ \hfill \mathfrak{g}\hfill \end{array}\right)=\varpi \times \left(\begin{array}{c}\hfill \mathfrak{b}\hfill \\ \hfill \mathfrak{z}\hfill \\ \hfill \mathfrak{g}\hfill \end{array}\right),\hfill \\ \hfill \\ \mathfrak{b}\times \mathfrak{z}=\mathfrak{g},\mathfrak{b}\times \mathfrak{g}=\mathfrak{z},\mathfrak{z}\times \mathfrak{g}=\mathfrak{b},{‖\mathfrak{b}‖}^2=-{‖\mathfrak{z}‖}^2={‖\mathfrak{g}‖}^2=1,\hfill \end{array}\right\}(7)$

where $\varpi (\mathfrak{v})=\gamma \mathfrak{b}-\mathfrak{g}$ is the Darboux vector from Equation 6, and

${\mathfrak{c}}^{\prime }\left(v\right)=\stackrel{v}{\underset{0}{\int }}\left(\mathrm{\Delta }\left(v\right)\mathfrak{b}\left(v\right)+\delta \left(v\right)\mathfrak{g}\left(v\right)\right)dv.(8)$

Therefore, a non-developable $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ can be perceived as follows:

$\mathfrak{R}:\mathfrak{y}\left(v,t\right)=\mathfrak{c}\left(v\right)+t\mathfrak{b}\left(v\right),t\in I,v\in \mathbb{R}.(9)$

The unit normal vector is

$\mathfrak{u}\left(v,t\right)=\frac{{\mathfrak{y}}_t\times {\mathfrak{y}}_v}{‖{\mathfrak{y}}_t\times {\mathfrak{y}}_v‖}=\frac{t\mathfrak{g}+\delta \mathfrak{z}}{\sqrt{-t^2+{\delta }^2}},\left|t\right|>\left|\delta \right|.(10)$

Note that $\mathfrak{u}(v,0)$ is identical with $\mathfrak{z}$, which is the central normal at the striction point. The curvature axis of $\mathfrak{b}(v)\in {\mathcal{S}}_1^2$ is from Equations 1, 2

$\mathfrak{e}\left(v\right)=\frac{\varpi }{‖\varpi ‖}=\frac{\gamma }{\sqrt{{\gamma }^2+1}}\mathfrak{b}-\frac{1}{\sqrt{{\gamma }^2+1}}\mathfrak{g}.(11)$

Let $\psi$ be the radii of curvature through $\mathfrak{b}$ and $\mathfrak{e}$. Then, from Equation 11

$\mathfrak{e}\left(v\right)=\cos \psi \mathfrak{b}-\sin \psi \mathfrak{g}\text{,\hspace{0.17em}with\hspace{0.17em}}\cot \psi =\gamma \left(v\right).(12)$

Definition 1. [16] In ${\mathcal{E}}_1^3$, a surface can be determined by the induced metric on it. Hence, a surface is called

$•$ $\mathcal{T}\mathcal{L}$ surface iff the metric is Lorentzian metric.

$•$ $\mathcal{S}\mathcal{L}$ surface iff the metric is a positive definite Riemannian metric.

$•$ Null surface iff the metric is null.

Corollary 1. The curvature $\kappa (v)$, the torsion $\tau (v)$, and the geodesic curvature $\gamma (v)$ of $\mathfrak{b}(v)\in {\mathcal{S}}_1^2$ fulfill that

$\kappa \left(v\right)=\sqrt{{\gamma }^2+1}=\frac{1}{\sin \psi }=\frac{1}{\rho \left(v\right)},\tau \left(v\right)≔\pm {\psi }^{\prime }=\pm \frac{{\gamma }^{\prime }}{{\gamma }^2+1}.(13)$

Corollary 2. If $\gamma (v)$ is a specified, then $\mathfrak{b}(v)\in {\mathcal{S}}_1^2$ is a Lorentzian circle.

Proof. Through Equation 13, we can see that $\gamma$, which is stationary, yields $\tau (v)=0$, and $\kappa (v)$ is stationary, which reveals $\mathfrak{b}(v)\in {\mathcal{S}}_1^2$ is a Lorentzian circle (If $\gamma (v)\ne 0$) or a Lorentzian great circle (when $\gamma (v)=0$).

Let’s state the Darboux frame $\{\mathfrak{c}(v);{\mathfrak{j}}_1,{\mathfrak{j}}_2,{\mathfrak{j}}_3\}$; let ${\mathfrak{c}}^{\prime }(v){‖{\mathfrak{c}}^{\prime }(v)‖}^{-1}={\mathfrak{f}}_1(v)$ be the tangent unit to $\mathfrak{c}(v)$, ${\mathfrak{j}}_3=-\mathfrak{z}(v)$ is the surface unit normal along $\mathfrak{c}(v)$, and ${\mathfrak{j}}_2(v)={\mathfrak{j}}_1\times {\mathfrak{j}}_3$ be the tangent unit to $\mathfrak{R}$. Therefore, we can write

$\left.\begin{array}{c}\left(\begin{array}{c}\hfill {\mathfrak{j}}_1\hfill \\ \hfill {\mathfrak{j}}_2\hfill \\ \hfill {\mathfrak{j}}_3\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill \cos \varphi \hfill & \hfill 0\hfill & \hfill \sin \varphi \hfill \\ \hfill -\sin \varphi \hfill & \hfill 0\hfill & \hfill \cos \varphi \hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathfrak{b}\hfill \\ \hfill \mathfrak{z}\hfill \\ \hfill \mathfrak{g}\hfill \end{array}\right),\hfill \\ \hfill \\ {‖{\mathfrak{j}}_1‖}^2={‖{\mathfrak{j}}_2‖}^2=-{‖{\mathfrak{j}}_3‖}^2=1,\hfill \end{array}\right\}(14)$

and

$\frac{\mathrm{\Delta }}{\sqrt{{\delta }^2+{\mathrm{\Delta }}^2}}=\cos \varphi \text{,\hspace{0.17em}}\frac{\delta }{\sqrt{{\delta }^2+{\mathrm{\Delta }}^2}}=\sin \varphi .(15)$

Let $u$ be the arc length of $\mathbf{c}(v)$, that is, $du=\sqrt{{\delta }^2+{\mathrm{\Delta }}^2}dv$. Then, from Equations 14, 15 the Darboux formula is expressed as

$\frac{d}{du}\left(\begin{array}{c}\hfill {\mathfrak{j}}_1\hfill \\ \hfill {\mathfrak{j}}_2\hfill \\ \hfill {\mathfrak{j}}_3\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill {\gamma }_g\hfill & \hfill -{\gamma }_n\hfill \\ \hfill -{\gamma }_g\hfill & \hfill 0\hfill & \hfill {\tau }_g\hfill \\ \hfill {\gamma }_n\hfill & \hfill -{\tau }_g\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathfrak{j}}_1\hfill \\ \hfill {\mathfrak{j}}_2\hfill \\ \hfill {\mathfrak{j}}_3\hfill \end{array}\right),(16)$

where

${\gamma }_g\left(v\right)=\frac{1}{{\delta }^2+{\mathrm{\Delta }}^2}\frac{d}{du}\left(\delta \frac{d\mathrm{\Delta }}{du}-\mathrm{\Delta }\frac{d\delta }{du}\right),{\gamma }_n\left(v\right)=\frac{\mathrm{\Delta }+\gamma \delta }{{\delta }^2+{\mathrm{\Delta }}^2}\text{,\hspace{0.17em}}{\tau }_g\left(v\right)=\frac{\delta -\gamma \mathrm{\Delta }}{{\delta }^2+{\mathrm{\Delta }}^2}.(17)$

${\gamma }_g(v)$, ${\gamma }_n(v)$, and ${\tau }_g(v)$ are the geodesic curvature, the normal curvature, and the geodesic torsion of $\mathbf{c}(\varkappa )$, respectively. Therefore, using Equations 16, 17

1) $\mathbf{c}(v)$ is a $\mathcal{S}\mathcal{L}$ geodesic curve iff ${\gamma }_g(v)=0\iff \delta \frac{d\mathrm{\Delta }}{du}-\mathrm{\Delta }\frac{d\delta }{du}=0$;

2) $\mathbf{c}(v)$ is a $\mathcal{S}\mathcal{L}$ asymptotic curve iff ${\gamma }_n(v)=0\iff \mathrm{\Delta }+\gamma \delta =0$;

3) $\mathbf{c}(v)$ is a $\mathcal{S}\mathcal{L}$ curvature line iff ${\tau }_g(v)=0\iff \delta -\gamma \mathrm{\Delta }=0$.

Remark 1. From Equation 8 and the above notations, we state that

(a) if $\delta (v)=0$, then $\mathfrak{R}$ is a $\mathcal{S}\mathcal{L}$ tangential developable, and

${\gamma }_g\left(v\right)=0\text{,\hspace{0.17em}}{\gamma }_n\left(v\right)=\frac{1}{\mathrm{\Delta }},{\tau }_g\left(v\right)=-\frac{\gamma }{\mathrm{\Delta }}.$

(b) if $\mathrm{\Delta }(v)=0$, then $\mathfrak{R}$ is a $\mathcal{S}\mathcal{L}$ binormal surface, and

${\gamma }_g\left(v\right)=0\text{,\hspace{0.17em}}{\gamma }_n\left(v\right)=\frac{\gamma }{\delta },{\tau }_g\left(v\right)=\frac{1}{\delta }.$

(c) if $\delta (v)=\mathrm{\Delta }(v)=0$, then $\mathfrak{R}$ is a $\mathcal{S}\mathcal{L}$ cone, and

${\gamma }_g\left(v\right)={\gamma }_n\left(v\right)={\tau }_g\left(v\right)=0.$

Definition 2. [14] A ruled surface is named a slant ruled surface if all its rulings have a stationary angle with a definite line.

3 Bertrand offsets for slant $\mathcal{S}\mathcal{L}\mathcal{R}$ surfaces

In this section, we contemplate and analyze the $\mathcal{B}\mathcal{O}$ for slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$. Then, a theory hassling to the theory of the Bertrand curves can be broadened for such surfaces.

In comparable with [30], a point ${\mathfrak{e}}_0(v)\in {\mathcal{S}}_1^2$ will be heading an ${\mathfrak{e}}_k$ curvature axis of the curve$\mathfrak{b}(v)\in {\mathcal{S}}_1^2$; for all $v$ such that $<{\mathfrak{e}}_0,\mathfrak{b}(v)>=0$, but $<{\mathfrak{e}}_0,{\mathfrak{b}}_1^{t+1}(v)>\ne 0$. Here, ${\mathfrak{b}}_1^{t+1}$ signalizes the tth derivative of $\mathfrak{b}(v)$ with regard to $v$. For the first curvature axis $\mathfrak{e}$ of$\mathfrak{b}(v)$, we find $<\mathfrak{e},{\mathfrak{b}}^{\prime }>=\pm <\mathfrak{e},\mathfrak{z}>=0$, and $<\mathfrak{e},{\mathfrak{b}}^{\prime \prime }>=\pm <\mathfrak{e},\mathfrak{b}+\gamma \mathfrak{g}>\ne 0$. So, $\mathfrak{e}$ is at least an ${\mathfrak{e}}_2$ curvature axis of $\mathfrak{b}(v)\in {\mathcal{S}}_1^2$. We now sign a height function $d:I\times {\mathcal{S}}_1^2\to \mathbb{R}$, by $d(v,{\mathfrak{e}}_0)=<{\mathfrak{e}}_0,\mathfrak{b}>$. We set the notation $d(v)=d(v,{\mathfrak{e}}_0)$ for any specified point ${\mathfrak{e}}_0\in {\mathcal{S}}_1^2$.

Proposition 1. Under the overhead presumptions, we capture the following:

i) $d$ will be specified in the first evaluation iff ${\mathfrak{e}}_0\in Sp\{\mathfrak{b},\mathfrak{g}\}$, that is,

$d^{\prime }=0\iff <{\mathfrak{b}}^{\prime },{\mathfrak{e}}_0>=0\iff <\mathfrak{z},{\mathfrak{e}}_0>=0\iff {\mathfrak{e}}_0=c_1\mathfrak{b}+c_2\mathfrak{g};$

for real numbers $c_1,c_2\in \mathbb{R}$, and $c_1^2+c_2^2=1$.

ii) $d$ will be specified in the second evaluation iff ${\mathfrak{e}}_0$ is the ${\mathfrak{e}}_2$ curvature axis of ${\mathfrak{e}}_0\in {\mathcal{S}}_1^2$, that is,

$d^{\prime }=d^{\prime \prime }=0\iff {\mathfrak{b}}_0=\pm \mathfrak{b}.$

iii) $d$ will be specified in the third evaluation iff ${\mathfrak{e}}_0$ is the ${\mathfrak{e}}_3$ curvature axis of ${\mathfrak{e}}_0\in {\mathcal{S}}_1^2$, that is,

$d^{\prime }=d^{\prime \prime }=d^{\prime \prime \prime }=0\iff {\mathfrak{e}}_0=\pm \mathfrak{e}\text{,\hspace{0.17em}and\hspace{0.17em}}{\gamma }^{\prime }\ne 0.$

iv) $d$ will be specified in the fourth evaluation iff ${\mathfrak{e}}_0$ is the ${\mathfrak{e}}_4$ curvature axis of ${\mathfrak{e}}_0\in {\mathcal{S}}_1^2$, that is,

$d^{\prime }=d^{\prime \prime }=d^{\prime \prime \prime }=d^{iv}=0\iff {\mathfrak{e}}_0=\pm \mathfrak{e}\text{,\hspace{0.17em}}{\gamma }^{\prime }=0\text{,\hspace{0.17em}and\hspace{0.17em}}{\gamma }^{\prime \prime }\ne 0.$

Proof. For $d^{\prime }$, we determine

$d^{\prime }=<{\mathfrak{b}}^{\prime },{\mathfrak{e}}_0>.(18)$

So, we realize

$d^{\prime }=0\iff <\mathfrak{z},{\mathfrak{e}}_0>=0\iff {\mathfrak{e}}_0=c_1\mathfrak{b}+c_3\mathfrak{g};(19)$

for real numbers $c_1$, $c_2\in \mathbb{R}$, and $c_1^2+c_2^2=1$, the consequence is evident.2- Derivation of Equation 18 displays that

$d^{\prime \prime }=<{\mathfrak{b}}^{\prime \prime },{\mathfrak{e}}_0>=<\mathfrak{b}+\gamma \mathfrak{g},{\mathfrak{e}}_0>.(20)$

By Equations 18–20, we determine

$d^{\prime }=d^{\prime \prime }=0\iff <{\mathfrak{b}}^{\prime },{\mathfrak{e}}_0>=<{\mathfrak{b}}^{\prime \prime },{\mathfrak{e}}_0>=0\iff {\mathfrak{e}}_0=\pm \frac{{\mathfrak{b}}^{\prime }\times {\mathfrak{b}}^{\prime \prime }}{‖{\mathfrak{b}}^{\prime }\times {\mathfrak{b}}^{\prime \prime }‖}=\pm \mathfrak{e}.$

3- Differentiation of Equation 20 displays that

$d^{\prime \prime \prime }=<{\mathfrak{b}}^{\prime \prime \prime },{\mathfrak{e}}_0>=\left(1+{\gamma }^2\right)<\mathfrak{z},{\mathfrak{e}}_0>+{\gamma }^{\prime }<\mathfrak{g},{\mathfrak{e}}_0>.$

Thus, we gain

$d^{\prime }=d^{\prime \prime }=d^{\prime \prime \prime }=0\iff {\mathfrak{b}}_0=\pm \mathfrak{b}\text{,\hspace{0.17em}and\hspace{0.17em}}{\gamma }^{\prime }\ne 0.$

4- By corresponding debates, we can also determine

$d^{\prime }=d^{\prime \prime }=d^{\prime \prime \prime }=d^{iv}=0\iff {\mathfrak{b}}_0=\pm \mathfrak{b}\text{,\hspace{0.17em}}{\gamma }^{\prime }=0\text{,\hspace{0.17em}and\hspace{0.17em}}{\gamma }^{\prime \prime }\ne 0.$

The proof is finished.

In view of Proposition 1, we determine

(a) The osculating circle $\mathcal{S}(\rho ,{\mathfrak{e}}_0)$ of $\mathfrak{b}(v)\in {\mathcal{S}}_1^2$ is displayed by

$<{\mathfrak{e}}_0,\mathfrak{b}>=\sqrt{1+{\rho }^2},<{\mathfrak{b}}^{\prime },{\mathfrak{e}}_0>=0,<{\mathfrak{b}}^{\prime \prime },{\mathfrak{e}}_0>=0,$

which are pointed via the situation that the osculating circle must have touch of at least third order at $\mathfrak{b}(v_0)$ iff ${\gamma }^{\prime }\ne 0$.

(b) The curve $\mathfrak{b}(v)\in {\mathcal{S}}_1^2$ and the osculating circle $\mathcal{S}(\rho ,{\mathfrak{e}}_0)$ have touched at least fourth order at $\mathfrak{b}(v_0)$ iff ${\gamma }^{\prime }=0$ and ${\gamma }^{\prime \prime }\ne 0$.

Through this method, by catching into meditation the curvature axes of $\mathfrak{b}(v)\in {\mathcal{S}}_1^2$, we can attain a concatenation of curvature axes ${\mathfrak{e}}_2$, ${\mathfrak{e}}_3$,…, ${\mathfrak{e}}_n$. The ownerships and the joint links via these curvature axes are much pleasant troubles. For example, it is facile to catch that if ${\mathfrak{e}}_0=\pm \mathfrak{e}$ and ${\gamma }^{\prime }=0$, $\mathfrak{b}(v)$ located at $\psi$ is specified relative to ${\mathfrak{e}}_0$. At this position, the curvature axis is fixed up to second order and $\mathfrak{R}$ is a slant $\mathcal{T}\mathcal{L}\mathcal{R}\mathcal{S}$.

Theorem 1. A non-developable $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ is a slant $\mathcal{SLRS}$ iff its geodesic curvature $\gamma (v)$ is fixed.

Definition 3. Let $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$ be two non-developable ruled $\mathcal{S}\mathcal{L}$ surfaces in ${\mathcal{E}}_1^3$. $\mathfrak{R}$ is entitled a $\mathcal{B}\mathcal{O}$ of ${\mathfrak{R}}^{*}$ if there exists a bijection via their rulings such that $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$ possess a reciprocal central normal at the conformable striction points.

Let ${\mathfrak{R}}^{*}$ be a $\mathcal{B}\mathcal{O}$ of $\mathfrak{R}$ and $\left\{{\mathfrak{c}}^{*}(v^{*}){\mathfrak{b}}^{*}(v^{*}),{\mathfrak{z}}^{*}(v^{*}),{\mathfrak{g}}^{*}(v^{*})\right\}$ is the $\mathcal{B}\mathcal{F}$ of ${\mathfrak{R}}^{*}$, as shown in Equations 7–9. Then, the surface ${\mathfrak{R}}^{*}$ can be allocated by

${\mathfrak{R}}^{*}:{\mathfrak{y}}^{*}\left(v^{*},t\right)={\mathfrak{c}}^{*}\left(v^{*}\right)+t{\mathfrak{b}}^{*}\left(v^{*}\right),t\in \mathbb{R},(21)$

where

${\mathfrak{c}}^{*}\left(v^{*}\right)=\mathfrak{c}\left(v\right)+{\mathrm{\Gamma }}^{*}\left(v\right)\mathfrak{z}\left(v\right).(22)$

Here, ${\mathrm{\Gamma }}^{*}(v)$ is the distance through the proportional striction points of $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$. Through the differentiation of Equation 21 via $v$ and considering Equation 22, we assign

${\mathfrak{z}}^{*}{v}^{{*}^{\prime }}=\left(\mathrm{\Delta }+{\mathrm{\Gamma }}^{*}\right)\mathfrak{b}+{\mathrm{\Gamma }}^{{*}^{\prime }}\mathfrak{z}+\left(\delta +\gamma {\mathrm{\Gamma }}^{*}\right)\mathfrak{g}.(23)$

Since ${\mathfrak{z}}^{*}=\mathfrak{z}$ at the congruent striction points of $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$, we gain ${\mathrm{\Gamma }}^{{*}^{\prime }}=0\Rightarrow {\mathrm{\Gamma }}^{*}$ is fixed. Furthermore, given that $\mathrm{\Gamma }$ is the angle among the rulings of $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$, that is,

$<{\mathfrak{b}}^{*},\mathfrak{b}>=\cos \mathrm{\Gamma }.(24)$

By differentiation of Equation 23, we gain

$<{\mathfrak{z}}^{*},\mathfrak{b}>v^{{*}^{\prime }}+<{\mathfrak{b}}^{*},\mathfrak{z}>\hspace{0.17em}=-{\mathrm{\Gamma }}^{\prime }\sin \mathrm{\Gamma }.(25)$

Since ${\mathfrak{z}}^{*}=\mathfrak{z}$, then we realize ${\mathrm{\Gamma }}^{\prime }=0\Rightarrow \mathrm{\Gamma }$ is fixed. Moreover, at the congruent striction points of $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$, we observe that $<{\mathfrak{g}}^{*},\mathfrak{g}>=\cos \mathrm{\Gamma }$. Then, by Equation 24

$\left(\begin{array}{c}\hfill {\mathfrak{b}}^{*}\hfill \\ \hfill {\mathfrak{z}}^{*}\hfill \\ \hfill {\mathfrak{g}}^{*}\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill \cos \mathrm{\Gamma }\hfill & \hfill 0\hfill & \hfill \sin \mathrm{\Gamma }\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill -\sin \mathrm{\Gamma }\hfill & \hfill 0\hfill & \hfill \cos \mathrm{\Gamma }\hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathfrak{b}\hfill \\ \hfill \mathfrak{z}\hfill \\ \hfill \mathfrak{g}\hfill \end{array}\right).(26)$

If $\mathrm{\Gamma }=0$(resp. $\frac{\pi }{2}$), then $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$ are parallel (resp. oriented) offsets.

Theorem 2. The couple $(\mathrm{\Gamma },{\mathrm{\Gamma }}^{*})$ is fixed at the corresponding striction points of $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$.

It is apparent from Theorem 2 that a non-developable $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$, frequently, has a binary infinity of $\mathcal{B}\mathcal{O}$. Every $\mathcal{B}\mathcal{O}$ can be displayed by a fixed linear offset ${\mathrm{\Gamma }}^{*}\in \mathbb{R}$ and a fixed-angle offset $\mathrm{\Gamma }\ge 0$. Therefore, if ${\mathfrak{R}}^{*}$ is a $\mathcal{B}\mathcal{O}$ of $\mathfrak{R}$, then $\mathfrak{R}$ is also a $\mathcal{B}\mathcal{O}$ of ${\mathfrak{R}}^{*}$.

Let ${\mathfrak{u}}^{*}(v^{*},t)$ be the $\mathcal{S}\mathcal{L}$ unit normal of ${\mathfrak{R}}^{*}$. Then, as shown in Equation 10, we locate

${\mathfrak{u}}^{*}\left(v^{*},t\right)=\frac{{\mathfrak{y}}_v^{*}\times {\mathfrak{y}}_t^{*}}{‖{\mathfrak{y}}_v^{*}\times {\mathfrak{y}}_t^{*}‖}=\frac{t{\mathfrak{g}}^{*}+{\delta }^{*}{\mathfrak{z}}^{*}}{\sqrt{-t^2+{\delta }^{*2}}},\left|t\right|>\left|{\delta }^{*}\right|,(27)$

where ${\delta }^{*}$ is the distribution parameter of ${\mathfrak{R}}^{*}$.

The dissimilarity between the normal to a $\mathcal{R}\mathcal{S}$ and its $\mathcal{B}\mathcal{O}$ is apparent from Equations 10, 26. This demonstrates that the $\mathcal{B}\mathcal{O}$ of a $\mathcal{R}\mathcal{S}$ is often not a parallel offset. Therefore, the parallel circumstances through ${\mathfrak{R}}^{*}$ in view of $\mathfrak{R}$ can be exhibited by the following:

Theorem 3. $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$ are parallel offsets iff $(a)\delta ={\delta }^{*}$, with $(b)$, their Blaschke frames, being conformable.

Proof. Let ${\mathfrak{u}}^{*}(v^{*},t)\times \mathfrak{u}(v,t)=0$, that is, $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$ are parallel offsets. Then, by Equations 10, 26, we acquire

$t\left({\delta }^{*}-\delta \cos \mathrm{\Gamma }\right)\mathfrak{b}-t^2\sin \mathrm{\Gamma }\mathfrak{z}-t\delta \sin \mathrm{\Gamma }\mathfrak{g}=0,$

which is assumed true for any value $t\ne 0$, that is, $\delta ={\delta }^{*}$, and $\mathrm{\Gamma }=0$.

Let the two events hold true, that is, $\delta ={\delta }^{*}$ and $\mathrm{\Gamma }=0$. Then, substituting them into ${\mathfrak{u}}^{*}(v^{*},t)\times \mathfrak{u}(v,t)$ using Equation 27, we acquire

${\mathfrak{u}}^{*}\left(v^{*},t\right)\times \mathfrak{u}\left(v,t\right)=\frac{t{\mathfrak{g}}^{*}+{\delta }^{*}{\mathfrak{z}}^{*}}{\sqrt{-t^2+{\delta }^{*2}}}\times \frac{t\mathfrak{g}+\delta \mathfrak{z}}{\sqrt{-t^2+{\delta }^2}},$

which indicates that $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$ are parallel offsets since the previous ${\mathfrak{u}}^{*}(v^{*},t)\times \mathfrak{u}(v,t)$ is a zero vector.

Using the same approach, but with a developable surface $\delta =0$, we encounter the following:

Corollary 3. A developable $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ and its developable $\mathcal{B}\mathcal{O}$ are parallel offsets iff their Blaschke frames are identical.

Corollary 4. A developable $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ and its non-developable $\mathcal{B}\mathcal{O}$ cannot be parallel offsets.

Furthermore, we also detect

$\frac{d}{d{v}^{*}}\left(\begin{array}{c}\hfill {\mathfrak{b}}^{*}\hfill \\ \hfill {\mathfrak{z}}^{*}\hfill \\ \hfill {\mathfrak{g}}^{*}\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill {\gamma }^{*}\hfill \\ \hfill 0\hfill & \hfill {\gamma }^{*}\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathfrak{b}}^{*}\hfill \\ \hfill {\mathfrak{z}}^{*}\hfill \\ \hfill {\mathfrak{g}}^{*}\hfill \end{array}\right),(28)$

where

$d{v}^{*}=\left(\cos \mathrm{\Gamma }+\gamma \sin \mathrm{\Gamma }\right)dv,{\gamma }^{*}d{v}^{*}=\left(\gamma \cos \mathrm{\Gamma }-\sin \mathrm{\Gamma }\right)dv.(29)$

By takeoff $d{v}^{*}/dv$, we locate using Equations 28, 29

$\left(\gamma -{\gamma }^{*}\right)\cos \mathrm{\Gamma }+\left({\gamma }^{*}\gamma -1\right)\sin \mathrm{\Gamma }=0.(30)$

This presents a new perspective of $\mathcal{B}\mathcal{O}$ of $\mathcal{S}\mathcal{L}\mathcal{R}$ surfaces, specifically focusing on their geodesic curvatures.

Theorem 4. $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$ are $\mathcal{BOSLR}$ surfaces iff Equation 30 is fulfilled.

Corollary 5. $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$ are parallel offsets iff ${\gamma }^{*}-\gamma =0$.

Corollary 6. $\mathfrak{R}$ and ${\mathfrak{R}}^{*}$ are oriented offsets iff ${\gamma }^{*}\gamma -1=0$.

For $\gamma (v)$ being fixed, from Equations 7, 12, we have the ODE, ${\mathfrak{b}}^{\prime \prime \prime }-{\kappa }^2{\mathfrak{b}}^{\prime }=\mathbf{0}$. In accordance with several algebraic manipulations, the solution is

$\mathfrak{b}\left(\varkappa \right)=\left(\cos \psi ,\sin \psi \sinh \varkappa ,\sin \psi \cosh \varkappa \right)\text{,}(31)$

where $\psi$ is fixed and $\varkappa =\sqrt{1+{\gamma }^2}v$. Then,

$\left.\begin{array}{c}\mathfrak{z}\left(\varkappa \right)=\frac{d\mathfrak{b}}{d\varkappa }{‖\frac{d\mathfrak{b}}{d\varkappa }‖}^{-1}=\left(0,\cosh \varkappa ,\sinh \varkappa \right),\hfill \\ \mathfrak{g}\left(\varkappa \right)=\mathfrak{b}\times \mathfrak{z}=\left(-\sin \psi ,\cos \psi \sinh \varkappa ,\cos \psi \cosh \varkappa \right).\hfill \end{array}\right\}(32)$

Therefore, from Equations 8, 30, 31, $\mathcal{S}\mathcal{C}\mathfrak{c}(\varkappa )$ is expressed as

$\mathfrak{c}\left(\varkappa \right)≔\left(\begin{array}{c}\hfill {\mathfrak{c}}_1\hfill \\ \hfill {\mathfrak{c}}_2\hfill \\ \hfill {\mathfrak{c}}_3\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \left(\stackrel{\varkappa }{\underset{0}{\int }}\mathrm{\Delta }d\varkappa \right)\cos \psi -\left(\stackrel{\varkappa }{\underset{0}{\int }}\delta d\varkappa \right)\sin \psi \hfill \\ \hfill \left(\stackrel{\varkappa }{\underset{0}{\int }}\mathrm{\Delta }\sinh \varkappa d\varkappa \right)\sin \psi +\left(\stackrel{\varkappa }{\underset{0}{\int }}\delta \sinh \varkappa d\varkappa \right)\cos \psi \hfill \\ \hfill \left(\stackrel{\varkappa }{\underset{0}{\int }}\mathrm{\Delta }\cosh \varkappa d\varkappa \right)\sin \psi +\left(\stackrel{\varkappa }{\underset{0}{\int }}\delta \cosh \varkappa d\varkappa \right)\cos \psi \hfill \end{array}\right).(33)$

Hence, from Equations 9, 30–33, the slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ is expressed as

$\mathfrak{R}:\mathfrak{r}\left(\varkappa ,t\right)=\left(c_1,c_2,c_3\right)+t\left(\cos \psi ,\sin \psi \sinh \varkappa ,\sin \psi \cosh \varkappa \right).(34)$

Furthermore, by Equations 20, 25, 33, $\mathcal{B}\mathcal{O}{\mathfrak{R}}^{*}$ is expressed as

${\mathfrak{R}}^{*}{:\mathfrak{r}}^{*}\left(\varkappa ,t\right)=\left(\begin{array}{c}\hfill c_1+{\mathrm{\Gamma }}^{*}\sinh \varkappa +t\cos \varpi \hfill \\ \hfill c_2+{\mathrm{\Gamma }}^{*}\cosh \varkappa +t\sin \varpi \sinh \varkappa \hfill \\ \hfill c_3+t\sin \varpi \cosh \varkappa \hfill \end{array}\right),t\in \mathbb{R},(35)$

where $\varpi =\psi +\mathrm{\Gamma }$ and ${\mathrm{\Gamma }}^{*}$ can control the shape of ${\mathfrak{R}}^{*}$; here, we will set ${\mathrm{\Gamma }}^{*}=-0.5$, $\psi =\frac{\pi }{4}$, $-4\le t\le 4$, and $-3\le \varkappa \le 3$.

3.1 Classifications of the slant $\mathcal{S}\mathcal{L}\mathcal{R}$ and its $\mathcal{B}\mathcal{O}$

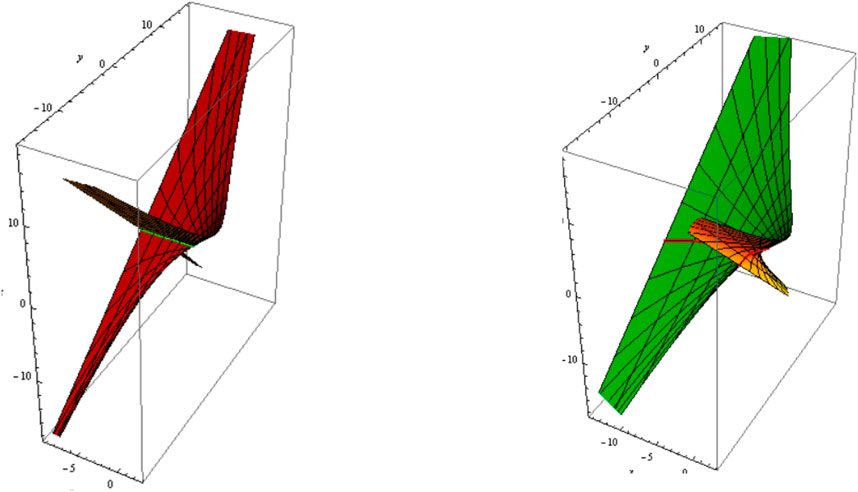
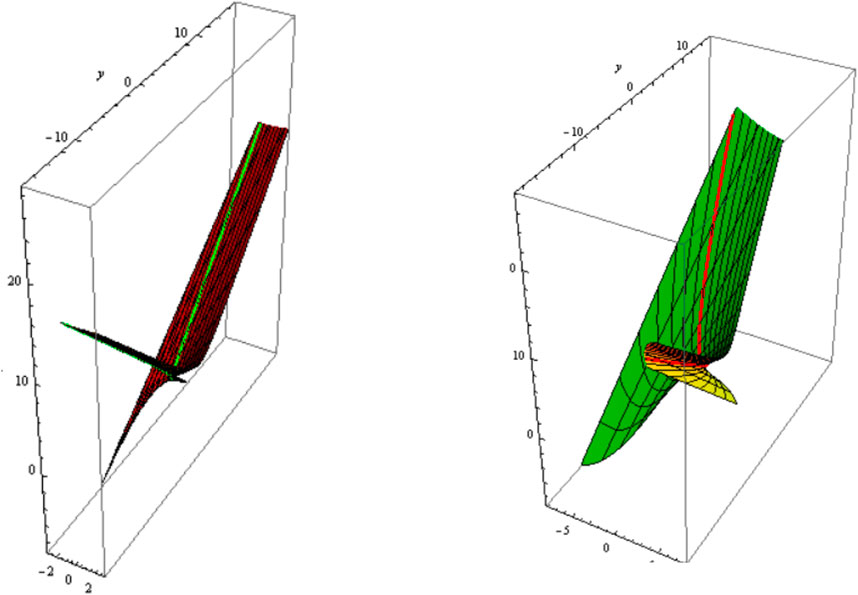
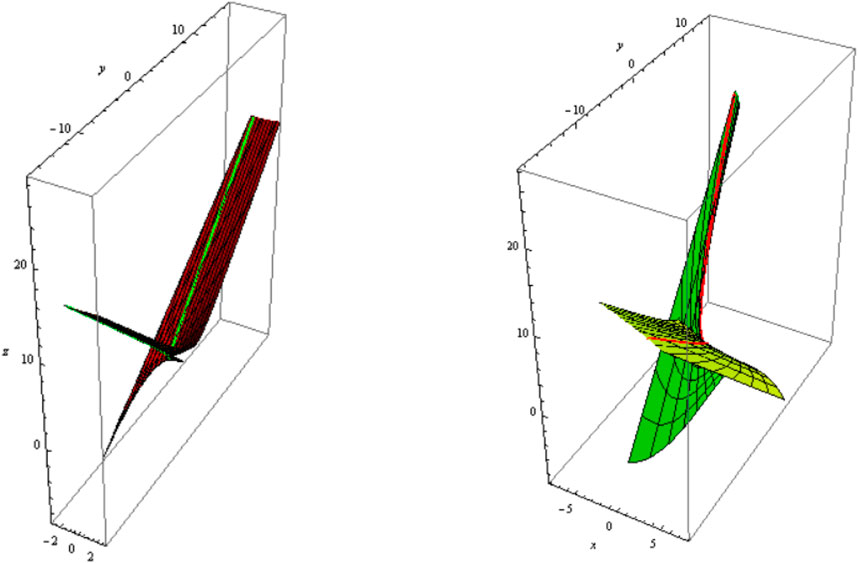
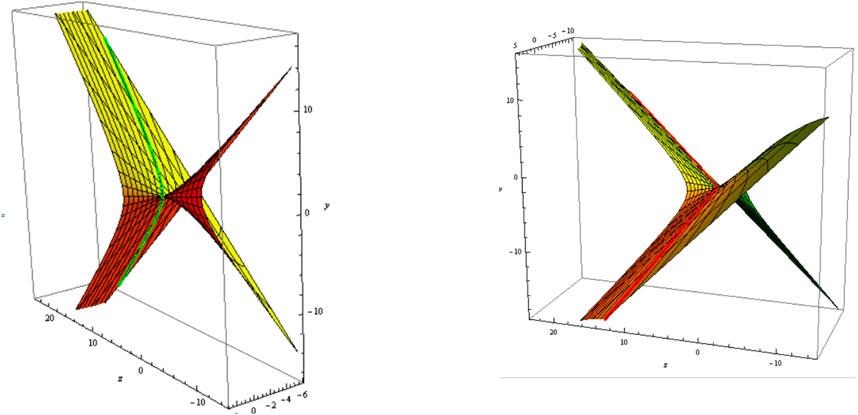
From Equations 34, 35, the slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ and its $\mathcal{B}\mathcal{O}$ can be distributed as follows:1) Let $\mathcal{S}\mathcal{C}$ be a $\mathcal{S}\mathcal{L}$ asymptotic curve, i.e., ${\gamma }_n=0\Rightarrow \mathrm{\Delta }+\gamma \delta =0$. The slant $\mathcal{S}\mathcal{L}\mathcal{R}$ and its parallel (oriented) $\mathcal{B}\mathcal{O}$ are shown in Figure 1 ;Figure 2; $\mathrm{\Delta }=\varkappa$.

Figure 1

Figure 1. Slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ (left) and its parallel $\mathcal{BO}$ (right).

Figure 2

Figure 2. Slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ (left) and its oriented $\mathcal{BO}$ (right).

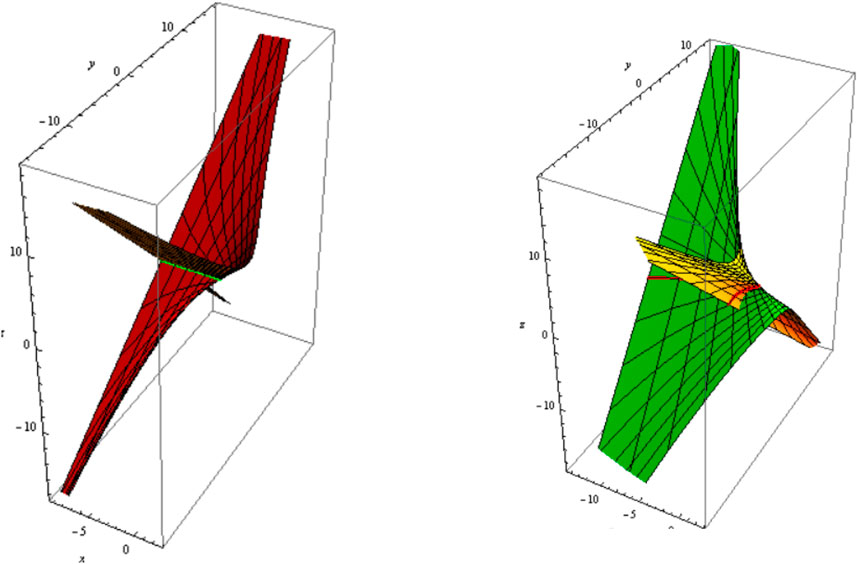
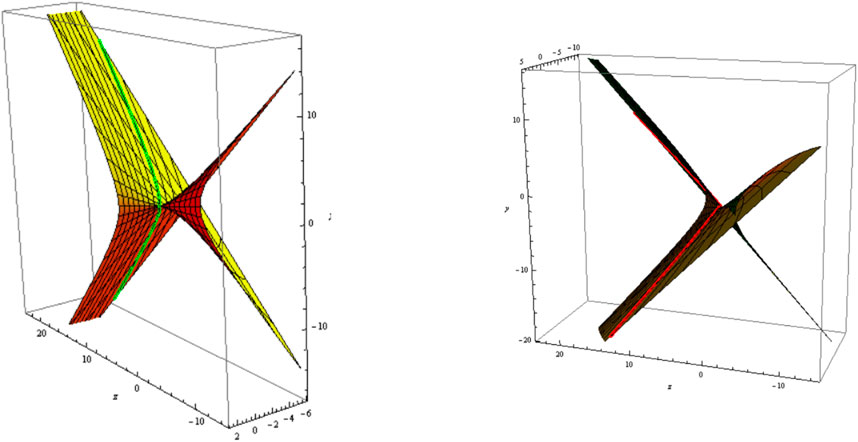
2) Let $\mathcal{S}\mathcal{C}$ be a $\mathcal{S}\mathcal{L}$ geodesic curve, i.e.,

${\gamma }_g\left(v\right)=0\iff \delta \frac{d\mathrm{\Delta }}{du}-\mathrm{\Delta }\frac{d\delta }{du}=0\Rightarrow \delta /\mathrm{\Delta }=c,$

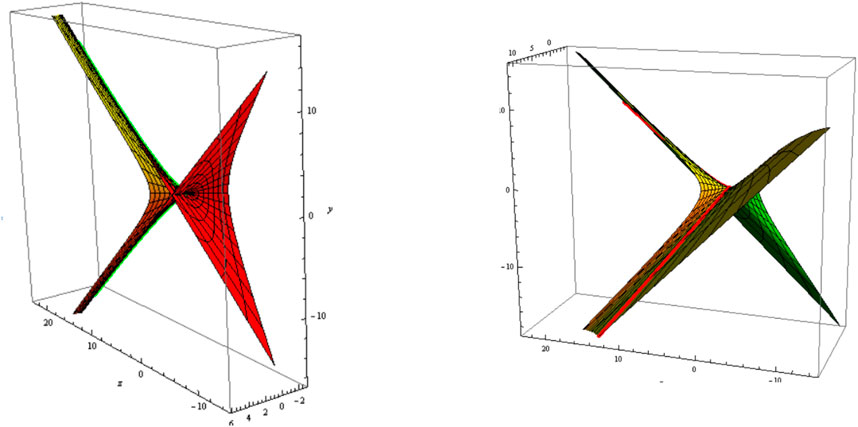
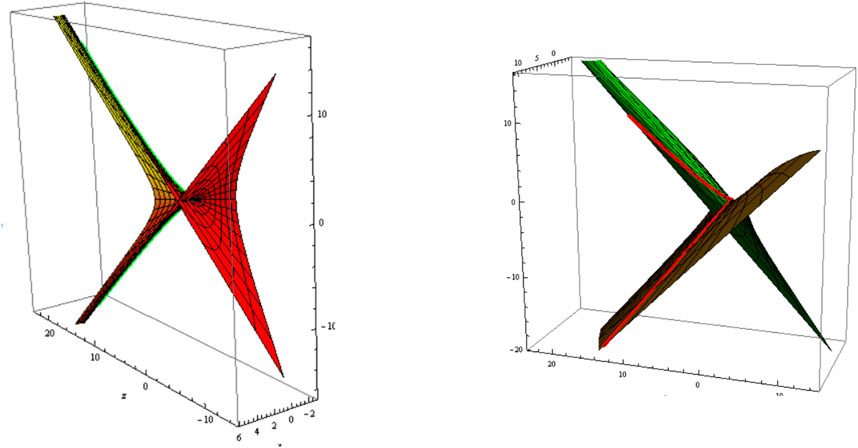
where $c$ is a real constant. The slant $\mathcal{S}\mathcal{L}\mathcal{R}$ and its parallel (oriented) $\mathcal{B}\mathcal{O}$ are shown in Figure 3 (Figure 4); $c=-2$ and $\mathrm{\Delta }(\varkappa )=\varkappa$.

Figure 3

Figure 3. Slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ (left) and its parallel $\mathcal{BO}$ (right).

Figure 4

Figure 4. Slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ (left) and its oriented $\mathcal{BO}$ (right).

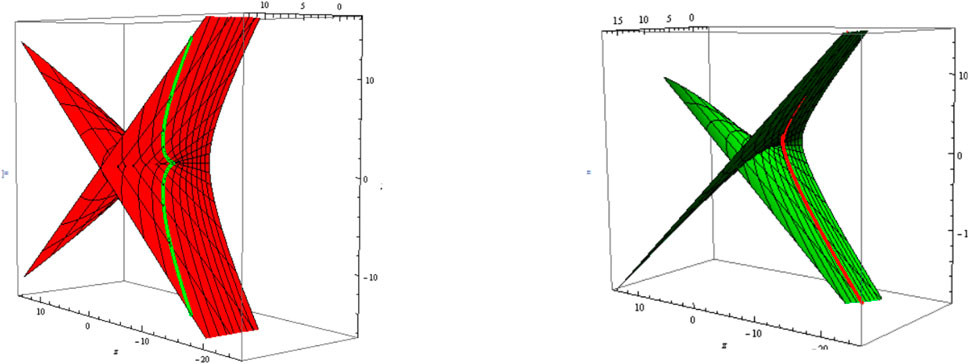
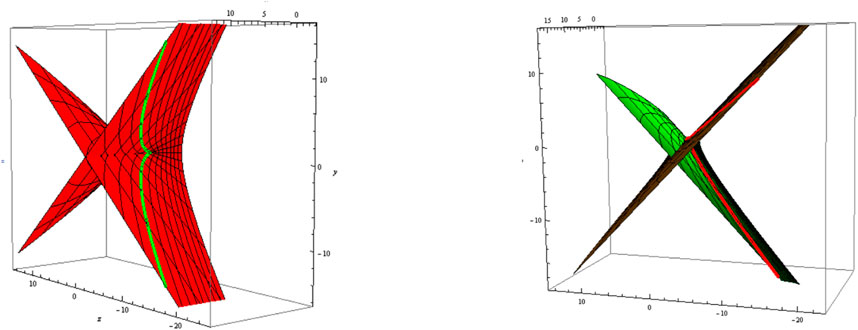
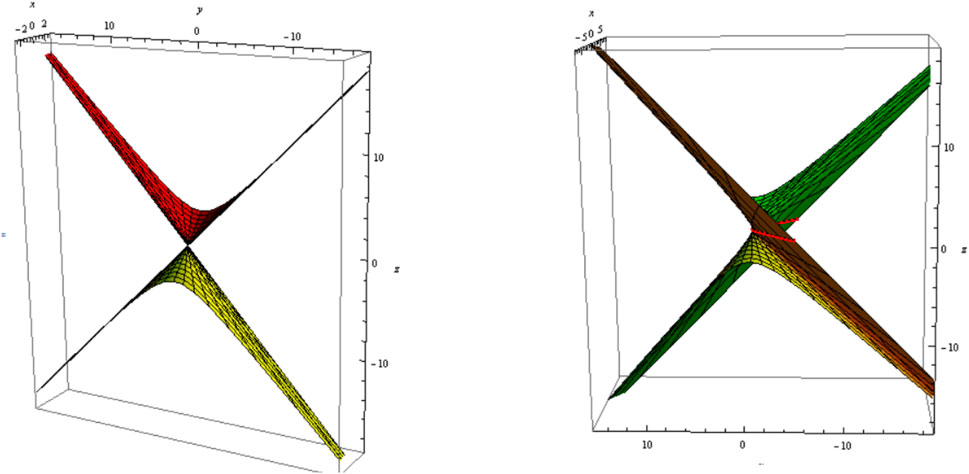
3) Let $\mathcal{S}\mathcal{C}$ be a $\mathcal{S}\mathcal{L}$ curvature line, i.e., ${\tau }_g(v)=0\iff \delta -\gamma \mathrm{\Delta }=0$. The slant $\mathcal{S}\mathcal{L}\mathcal{R}$ and its parallel (oriented) $\mathcal{B}\mathcal{O}$ are shown in Figure 5 (Figure 6); $\mathrm{\Delta }(\varkappa )=\varkappa$.

Figure 5

Figure 5. Slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ (left) and its parallel $\mathcal{BO}$ (right).

Figure 6

Figure 6. Slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ (left) and its oriented $\mathcal{BO}$ (right).

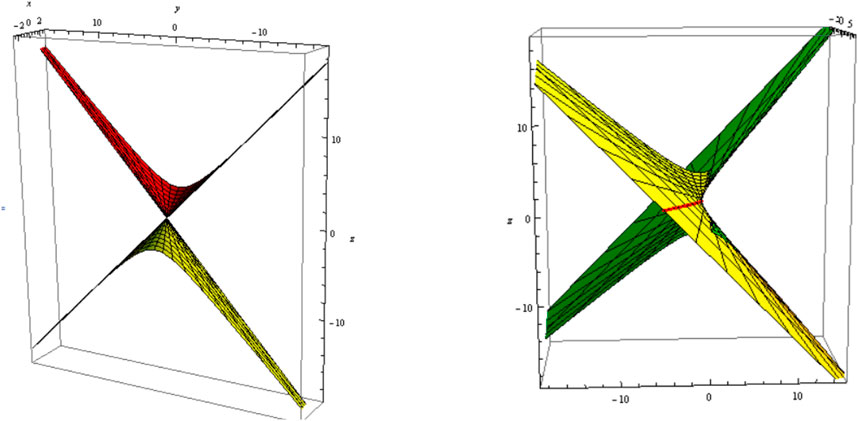
4) Let $\delta =0$, i.e., $\mathfrak{R}$ be a $\mathcal{S}\mathcal{L}$ tangential developable. The slant $\mathcal{S}\mathcal{L}\mathcal{R}$ and its parallel (oriented) $\mathcal{BO}$ are shown in Figure 7 (Figure 8); $\mathrm{\Delta }(\varkappa )=\varkappa$.

Figure 7

Figure 7. Slant $\mathcal{S}\mathcal{L}$ tangential (left) and its parallel $\mathcal{BO}$ (right).

Figure 8

Figure 8. Slant $\mathcal{S}\mathcal{L}$ tangential (left) and its oriented $\mathcal{BO}$ (right).

5) Let $\mathrm{\Delta }=0$, that is, $\mathfrak{R}$ be a $\mathcal{S}\mathcal{L}$ binormal. The slant $\mathcal{S}\mathcal{L}$ binormal and its parallel (oriented) $\mathcal{B}\mathcal{O}$ are shown in Figure 9 (Figure 10); $\delta (\varkappa )=\varkappa$.

Figure 9

Figure 9. Slant $\mathcal{S}\mathcal{L}$ binormal (left) and its parallel $\mathcal{BO}$ (right).

Figure 10

Figure 10. Slant $\mathcal{S}\mathcal{L}$ binormal (left) and its oriented $\mathcal{BO}$ (right).

6) Let $\mathrm{\Delta }=\delta =0$, that is, $\mathfrak{R}$ be a $\mathcal{S}\mathcal{L}$ cone. The slant $\mathcal{S}\mathcal{L}$ cone and its parallel (oriented) $\mathcal{B}\mathcal{O}$ are shown in Figure 11 (Figure 12); $\delta (\varkappa )=\varkappa$.

Figure 11

Figure 11. Slant $\mathcal{S}\mathcal{L}$ cone (left) and its parallel $\mathcal{BO}$ (right).

Figure 12

Figure 12. Slant $\mathcal{S}\mathcal{L}$ cone (left) and its oriented $\mathcal{BO}$ (right).

4 Conclusion

This work explores the features of slant curves and develops and classifies slant $\mathcal{S}\mathcal{L}\mathcal{R}$ surfaces and their $\mathcal{B}\mathcal{O}$ in Minkowski 3-space ${\mathcal{E}}_1^3$ using the Blaschke domain. Next, we construct contemporary $\mathcal{S}\mathcal{L}\mathcal{R}$ surfaces in Lorentzian line space and determine their $\mathcal{B}\mathcal{O}$. In addition, we also obtain various groupings by a slant $\mathcal{S}\mathcal{L}\mathcal{R}\mathcal{S}$ and its striction curve. These advancements are expected to enhance the usefulness of model-based manufacturing in mechanical outputs and geometric patterning. The authors intend to correlate this study across several domains and examine the classification of singularities, as identified in [31, 32].

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

AA: conceptualization, data curation, formal analysis, funding acquisition, methodology, resources, writing–original draft, and writing–review and editing. RA-B: conceptualization, data curation, formal analysis, investigation, methodology, resources, supervision, validation, visualization, and writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article: Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R337).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Gugenheimer HW. Differential geometry. New York: Graw-Hill (1956). 162–9.

Google Scholar

2. Bottema O, Roth B. Theoretical kinematics. New York: North-Holland Press (1979).

Google Scholar

3. Karger A, Novak J. Space kinematics and lie groups. New York: Gordon and Breach Science Publishers (1985).

Google Scholar

4. Papaionnou SG, Kiritsis D. An application of Bertrand curves and surfaces to CAD/CAM. Computer Aided Des (1985) 17(8):348–52. doi:10.1016/0010-4485(85)90025-9

CrossRef Full Text | Google Scholar

5. Schaaf JA, Ravani B. Geometric continuity of ruled surfaces. Computer Aided Geometric Des (1998) 15:289–310. doi:10.1016/s0167-8396(97)00032-0

CrossRef Full Text | Google Scholar

6. Peternell M, Pottmann H, Ravani B. On the computational geometry of ruled surfaces. Comput.-Aided Des (1999) 31:17–32. doi:10.1016/s0010-4485(98)00077-3

CrossRef Full Text | Google Scholar

7. Pottman H, Wallner J. Computational line geometry. Berlin, Heidelberg: Springer-Verlag (2001).

Google Scholar

8. Ravani B, Ku TS. Bertrand offsets of ruled and developable surfaces. Computer Aided Des (1991) 23(2):145–52. doi:10.1016/0010-4485(91)90005-h

CrossRef Full Text | Google Scholar

9. Küçük A, Gürsoy O. On the invariants of Bertrand trajectory surface offsets. AMC (2004) 151(3):763–773. Available at: https://www.sciencedirect.com/science/article/pii/S0096300303005344. doi:10.1016/S0096-3003(03)00534-4

CrossRef Full Text | Google Scholar

10. Kasap E, Kuruoglu N. Integral invariants of the pairs of the Bertrand ruled surface. Bull Pure Appl Sci Sect E Math (2002) 21:37–44.

Google Scholar

11. Önder M. Slant ruled surfaces. Transnational J Pure Appl Mathematics (2018) 1(1):63–82.

Google Scholar

12. Kaya O, Önder M. Position vector of a developable h-slant ruled surfaces. TWMS J App Eng Math (2017) 7(2):322–31.

Google Scholar

13. Kaya O, Önder M. Position vector of a developable q-slant ruled surfaces. Korean J Math (2018) 26(4):545–59. doi:10.11568/kjm.2018.26.4.545

CrossRef Full Text | Google Scholar

14. Önder M. Onur Kaya, characterizations of slant ruled surfaces in the euclidean 3-space. Caspian J Math Sci (2017) 6(1):82–9. doi:10.22080/cjms.2017.1637

CrossRef Full Text | Google Scholar

15. Önder M. Onur Kaya, Darboux slant ruled surfaces. Azerbaijan J Mathematics (2015) 5(1):64–72.

Google Scholar

16. Önder M. Non-null slant ruled surfaces. AIMS Mathematics (2019) 4(3):384–96. doi:10.3934/math.2019.3.384

CrossRef Full Text | Google Scholar

17. Kasap E, Kuruoglu N. The Bertrand offsets of ruled surfaces in R¹₃. Acta Math Vietnam (2006) 31:39–48.

Google Scholar

18. Kasap E, Yuce S, Kuruoglu N. The involute-evolute offsets of ruled surfaces. Iranian J Sci Tech Transaction A (2009) 33:195–201.

Google Scholar

19. Orbay K, Kasap E, Aydemir I. Mannheim offsets of ruled surfaces. Math Probl Eng (2009) 2009. doi:10.1155/2009/160917

CrossRef Full Text | Google Scholar

20. Önder M, Uğurlu HH. Frenet frames and invariants of timelike ruled surfaces. Ain Shams Eng J (2013) 4:507–13. doi:10.1016/j.asej.2012.10.003

CrossRef Full Text | Google Scholar

21. Önder M, Uğurlu HH. Spacelike regle yüzeylerin Frenet çatıları ve Frenet i̇nvaryantları. Dokuz Eylul University-Faculty Eng J Sci Eng (2017) 19(57):712–22. doi:10.21205/deufmd.2017195764

CrossRef Full Text | Google Scholar

22. Şentürk GY, Yüce S. Properties of integral invariants of the involute-evolute offsets of ruled surfaces. Int J Pure Appl Math (2015) 102:757–68. doi:10.12732/ijpam.v102i4.13

CrossRef Full Text | Google Scholar

23. Yoon DW. On the evolute offsets of ruled surfaces in Minkowski 3-space. Turk J Math (2016) 40(40):594–604. doi:10.3906/mat-1502-11

CrossRef Full Text | Google Scholar

24. Yıldırım H. Slant ruled surfaces and slant developable surfaces of spacelike curves in Lorentz-Minkowski 3-space. Filomat (2018) 32(14):4875–95. doi:10.2298/fil1814875y

CrossRef Full Text | Google Scholar

25. Alluhaibi N, Abdel-Baky RA, Naghi M. On the Bertrand offsets of timelike ruled surfaces in Minkowski 3-space. Symmetry (2022) 14(4):673. doi:10.3390/sym14040673

CrossRef Full Text | Google Scholar

26. Nazra S, Abdel-Baky RA. Bertrand offsets of ruled surfaces with Blaschke frame in Euclidean 3-space. Axioms (2023) 12:649. doi:10.3390/axioms12070649

CrossRef Full Text | Google Scholar

27. Mofarreh F, Abdel-Baky RA. Surface pencil pair interpolating Bertrand pair as common asymptotic curves in Euclidean 3-space. Mathematics (2023) 11(16):3495. doi:10.3390/math11163495

CrossRef Full Text | Google Scholar

28. Walrave J, Leuven KU. Curves and surfaces in Minkowski space. Leuven, Belgium: Faculty of Science (1995). Ph.D. Thesis.

Google Scholar

29. O’Neil B. Semi-riemannian geometry geometry, with applications to relativity. New York, NY, USA: Academic Press (1983).

Google Scholar

30. W Bruce J, Giblin PJ. Curves and singularities. 2nd ed. Cambridge: Cambridge University Press (1992).

Google Scholar

31. Almoneef A, Abdel-Baky RA. Singularity properties of spacelike circular surfaces. Symmetry (2023) 15:842. doi:10.3390/sym15040842

CrossRef Full Text | Google Scholar

32. Nazra S, Abdel-Baky RA. Singularities of non-lightlike developable surfaces in Minkowski 3-space. Mediterr J Math (2023) 20:45. doi:10.1007/s00009-022-02252-7

CrossRef Full Text | Google Scholar