Broadband continuous absorber based on dual-mode coupling resonance

The continuous detection of visible to near-infrared light is a critical focus in optics due to its broad application value. To address this challenge, we present a graphene-based gradient groove metasurface (GGM) that enables efficient broadband absorption by simultaneously exciting surface plasmon polariton (SPP) resonance and Fabry-Pérot (FP)-like cavity resonance within multiple grooves. This dual-mode coupling effectively mitigates SPP losses and overcomes the size constraints of FP cavities, allowing for broadband, angle-insensitive absorption from 600 to 1,100 nm with an average absorption rate of 87.5%. Finite element simulations further show that variations in groove fillet radius variations from 5 nm to 20 nm and sidewall inclination variations from 0.02 to 0.22, result in absorption deviations of less than 2% and 6%, respectively, demonstrating the structure’s robustness against industrial processing errors. These findings suggest that the proposed GGM structure can significantly expand the application range of photodetectors in the visible to near-infrared wavelength bands, offering a promising solution for optical sensing applications.

1 Introduction

Optoelectronic devices capable of detecting wavelengths from visible to near-infrared hold significant application value [1–3]. Graphene, a two-dimensional material with unique optoelectronic properties, has garnered substantial attention from researchers due to its ultrafast carrier mobility and broad absorption spectrum [4–9]. However, its intrinsic absorptivity of only 2.3% significantly hinders its application in optoelectronic devices [10–13]. Consequently, research on enhancing graphene absorption has been ongoing, with current studies focusing on mechanisms such as surface plasmon resonance [14, 15], Fabry-Pérot resonance [16–19], guided-mode resonance [20, 21], and optical Tamm states [22, 23]. Notably, some researchers have proposed using a combination of metasurface and plasmonic nanostructures to construct broadband continuum absorbers with high absorption rates [24, 25]. This absorber type is achieved by integrating multiple graphene resonators of similar sizes, enabling broadband light absorption through the fusion of resonance responses with subtle frequency differences [26–28]. Additionally, graphene resonator units with gradient size variations can induce a continuous plasmon excitation response [29–31]. By precisely designing the physical dimensions of graphene resonators, effective light absorption over a more comprehensive frequency range can be realized.

Broadband continuous detection has always been a research hotspot in optics [32–35]. Several approaches have been explored to achieve efficient light absorption, including photonic structures, thin-film materials, and metasurface. Photonic crystal structures, for instance, are effective at trapping light via the bandgap effect, but their narrow bandwidth and fabrication complexity often limit their practical applications [36]. Thin-film absorbers, while popular for their simple structure and high transmittance, are constrained by issues such as material stability and scalability, which restrict their range of applications [37, 38]. Besides, Huang et al. [39] designed a broadband tunable absorber based on graphene, employing a complementary cross-crossed ellipsoidal graphene (CCOSG) metasurface structure. This design achieves broadband absorption with an absorption rate exceeding 90% in the range of 1.2 THz to 1.8 THz, with the high absorption bandwidth reaching over 40%. The tunability of the absorption operating band is realized by adjusting the Fermi energy level of graphene through an applied voltage. The absorber unit structure designed by Dang et al. [40] is in a single-layer metal truncated pyramid resonator-dielectric-metal configuration, with an absorption of 98% at normal incidence in the wavelength range of 417–1,091 nm and greater than 99% in the range of 822–1,054 nm. The absorbance is maintained in the transverse electric (TE) and transverse magnetic (TM) modes with slight variations in the incident angle. Meanwhile, its unique structure also leads to difficulties in industrial processing. Sang et al. [41] developed an angle-insensitive graphene broadband absorber covering the visible spectrum by integrating graphene sheets with a multi-groove structure separated by a polymethyl methacrylate (PMMA) spacer layer. This design achieved an average absorption efficiency of 71.1% in the 450–800 nm spectral range. However, its performance in the near-infrared wavelength range is suboptimal, indicating significant potential for improvement in overall absorption efficiency. These research findings offer significant theoretical and practical references for developing novel broadband-absorbing materials. Most research in graphene broadband continuous detection is concentrated on the terahertz band, with substantial potential for improvement in the visible and near-infrared bands. Detection within visible and near-infrared wavelengths is essential in biomedical, military, and other applications. Therefore, advancing research on broadband detection within this range is of considerable prospective significance.

In this paper, we design a gradient groove metasurface structure (GGM) based on graphene and analyze the absorption spectra of a single groove structure to study the absorption principle from visible light to near-infrared band and the influence of structural parameter changes on the absorption of the target band. We realized that increasing the width of the groove can increase the absorption rate while making the absorption peak blue-shifted. Increasing the depth of the groove can increase the absorption rate while making the absorption peak red-shifted. Therefore, we gradient the multiple-groove structure from wide to narrow and from shallow to deep to achieve broadband continuous absorption, effectively solving the problem of low absorption rate of traditional absorber structures in the visible to near-infrared wavelength range. The structure achieves an overall average absorption of 87.5% in the wavelength range of 600 nm–1,100 nm and 60.3% in the wavelength range of 600 nm–1,200 nm for the graphene layer, truly realizing a broad-spectrum continuum of absorption from the visible to the near-infrared wavelength bands. Finally, we use the finite element method to simulate the effect of common industrial processing errors on the designed structure’s spectral absorption, demonstrating the structure’s engineering utility. The findings reveal that the structure tolerates groove right-angle errors and vertical sidewall errors to a significant extent; this dramatically extends the range of applications for detectors in the visible to near-infrared wavelength bands. Compared to photonic structures and thin films, GGM structure brings broader continuum absorption in the visible to near-infrared wavelength bands with higher reliability and scalability.

2 Structure, numerical and theoretical model

As shown in Figure 1, a GGM structure is constructed. The primary operating band of the structure is 600–1,100 nm, which is particularly significant in fields such as military applications, agriculture, and biomedical imaging [42, 43]. However, within this band, graphene exhibits quasi-semiconducting electromagnetic properties, with limited absorption and insufficient excitation of SPP resonance. To address these limitations, we have precisely tuned the electromagnetic response of graphene using a metasurface, successfully exciting dual-mode Fabry-Pérot (FP) and SPP resonances within the operating range, thereby enhancing graphene’s absorption. Additionally, we incorporated a dielectric material SiO₂ into the structure to facilitate SPP resonance while mitigating the issue of high losses. This combination ultimately enables the designed structure to achieve efficient broadband absorption across the 600–1,100 nm range. The GGM structure consists of a series of structural units cascaded with multiple metal grooves varying in depths (denoted as $d$) and widths (denoted as $w$). The upper material is a ten-layer monolayer graphene overlay. The substrate material is SiO₂, and a layer of Ag metal grating is positioned on top of the substrate. The grating grooves are also filled with SiO₂, and a spacer layer of thickness $t$ is formed above them. SiO₂ exhibits low optical loss in the visible and near-infrared wavelength bands, effectively allowing it to conduct light signals without significant absorption. Additionally, it possesses excellent high-temperature resistance and mechanical strength, which considerably broadens the application scenarios for optoelectronic devices.

Figure 1

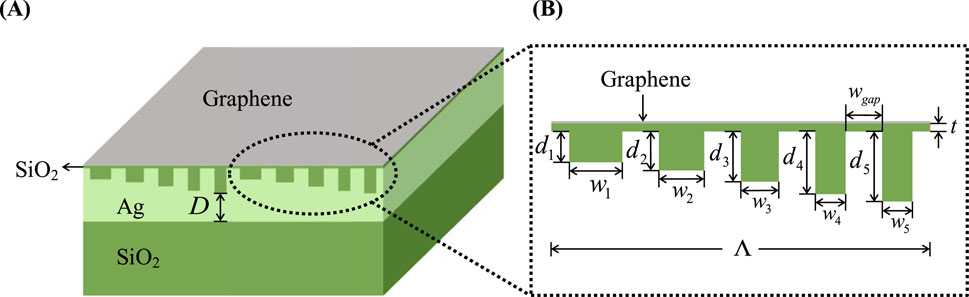
Figure 1. Structural diagram (A) Schematic structure of graphene-based GGM and cross-section of periodic structural units in three dimensions. (B) Structural parameters of grooves.

In the experimental setup, a transverse magnetic (TM) wave is incident from one end of the air medium at an angle ${\theta }_c$. The period of the metal grating is $\mathrm{\Lambda }$, and the thickness of the film layer at the bottom of the metal grating is $D$. The structure utilizes a sub-wavelength metal Ag grating where the period $\mathrm{\Lambda }$ satisfies $\mathrm{\Lambda }<\frac{\lambda }{\left(1+\sin {\theta }_c\right)}$, ensuring sufficient optical thickness $D$ (here set as $D=100\text{nm}$) to minimize transmission losses within the targeted research band, considering the skin depth of Ag. The absorption rate is defined as $A=1-R$ where $R$ represents reflectivity.

In the field of electromagnetic wave simulation, the two most commonly used research methods are the finite element method (FEM) and the finite-difference time-domain (FDTD) method. This article mainly uses the finite element method to numerically simulate and analyze the absorption spectrum and local electromagnetic field of the target structure in the frequency domain. In the FEM simulation, we combined periodic boundary conditions and perfectly matched layers to enhance the accuracy of the results. Periodic boundary conditions were applied to the left and right sides of the structure to simulate the optical behavior of the GGM structure under infinite repetition. The top boundary serves as the excitation port for the wave source, and absorption coefficients of the structure are calculated using area partitioning to assess the absorption contributions of different active layers. A perfectly matched layer is applied to the lower boundary to prevent electromagnetic wave reflections, approximating an infinite space condition. To optimize computational efficiency, a non-uniform mesh with a minimum grid size of 0.1 nm is used for the graphene layer. The structure is irradiated by TE-polarized plane waves (parallel to the y-axis) at an incidence angle. This configuration not only improves simulation accuracy but also allows for an efficient evaluation of the structure’s light absorption properties in practical applications.

To rigorously simulate the optical properties of graphene across a broad spectral range, this study employs the Kubo formula, incorporating both interband and intraband electronic transitions. This approach is extensively utilized in the electromagnetic modeling of graphene [44, 45]. In the visible to near-infrared wavelength band, the refractive index of SiO₂ is 1.46, while the complex refractive index of Ag is referenced to Palik’s data [46]. The dielectric constant of graphene is ${\epsilon }_g=\frac{1+i{\sigma }_g}{\left(\omega {\epsilon }_0{t}_0\right)}$, the thickness of the graphene layer is $t_0$, and the conductivity of graphene ${\sigma }_g\left(\omega \right)={\sigma }_{\mathrm{int}ra}\left(\omega \right)+{\sigma }_{\mathrm{int}er}\left(\omega \right)$, which consists of both the in-band and inter-band conductivities, is denoted by Equations 1, 2 [47]:

${\sigma }_{\mathrm{int}ra}\left(\omega \right)=-i\frac{e^2{k}_{B}T}{\pi {\mathrm{\hslash }}^2\left(\omega -2i\mathrm{\Gamma }\right)}\left[\frac{{\mu }_c}{k_{B}T}+2\ln \left(e^{-\frac{{\mu }_c}{k_{B}T}}+1\right)\right](1)$

${\sigma }_{\mathrm{int}er}\left(\omega \right)=-i\frac{e^2}{4\pi \mathrm{\hslash }}\ln \left[\frac{2\left|{\mu }_c\right|-\left(\omega -i2\mathrm{\Gamma }\right)\mathrm{\hslash }}{2\left|{\mu }_c\right|+\left(\omega -i2\mathrm{\Gamma }\right)\mathrm{\hslash }}\right](2)$

Where $e$ and $\mathrm{\hslash }$ are the elementary charge and reduced Planck’s constant, respectively. $k_B$ is the Boltzmann constant, ${\mu }_c$ is the chemical potential, $T$ is set to 300 K, $\mathrm{\Gamma }=\frac{1}{\left(2\tau \right)}$ is the scattering rate of the carriers, the momentum relaxation time $\tau$ is set to $0.5ps$, and the chemical potential of graphene ${\mu }_c=0.15\text{eV}$.

The material dielectric constant of the Ag layer can be described by the Drude model, as shown in Equation 3 [48]:

${\epsilon }_{Ag}\left(\omega \right)=1-\frac{{\omega }_p^2}{{\omega }^2+i\gamma \omega }(3)$

Where ${\omega }_p$ is the plasma frequency and $\gamma$ is the damping coefficient, for the study band in this paper, the ${\omega }_p=9.1\text{eV}=1.37\times {10}^{16}\text{rad}/\mathrm{s}$, $\gamma =0.018\text{eV}=0.27\times {10}^{14}\text{rad}/\mathrm{s}$, TM waves of Ag are incident at an angle of incidence ${\theta }_c$ from the air side, which excites the surface plasmon polariton (SPP) resonance on the surface of the metallic Ag layer, at which time the wavevector conditions are satisfied Equation 4:

$k_{SPP}=\frac{\omega }{c}\sin {\theta }_c-m\frac{2\pi }{\mathrm{\Lambda }}(4)$

Where $c$ is the vacuum speed of light, $k_{SPP}=\omega \sqrt{\frac{\frac{{\epsilon }_{Ag}}{\left(1+{\epsilon }_{Ag}\right)}}{c}}$ is the SPP wavevector, $m$ is the grating diffraction level taken $\pm 1$, and the corresponding resonance wavelength is denoted by Equation 5:

${\lambda }_{SPP}=\mathrm{\Lambda }\sqrt{\frac{{\epsilon }_{Ag}}{\left(1+{\epsilon }_{Ag}\right)}}(5)$

Furthermore, in order to be able to visually explore the absorptivity of graphene and the absorptive contribution of the graphene layer in this structure, the light absorption of the graphene layer is distinguished from the total light absorption of the overall structure, and the corresponding absorptivity is expressed by Equation 6 [48]:

${\mathrm{A}}_{graphene}=\frac{\left[P_{up}\left(\lambda \right)-{\mathrm{P}}_{down}\left(\lambda \right)\right]}{{\mathrm{P}}_{in}\left(\lambda \right)}(6)$

Where $P_{in}$ denotes the incident optical power, $P_{up}\left(\lambda \right)$ and $P_{down}\left(\lambda \right)$ denote the optical power of the incident light with wavelength $\lambda$ passing through the interface between the top and bottom of the graphene layer, respectively. All these values can be extracted from the total physical field simulated in the finite element software simulation.

3 Results and discussion

3.1 Research on the absorption of the single groove structure

The single groove structure is analyzed first. Figures 2A, B show the enhanced absorption spectra and the magnetic field distribution at the peak position of the single groove structure, with the structural parameter $\mathrm{\Lambda }=500\text{nm}$, $D=100\text{nm}$, $w=50\text{nm}$, $d=50\text{nm}$, $t=10\text{nm}$. When TM-polarized light is incident perpendicular to the surface, as shown in Figure 2A, the absorbance of the entire structure reaches peaks at two wavelengths, ${\lambda }_1=508\text{nm}$ and ${\lambda }_2=779\text{nm}$, corresponding to 24.7% and 56.6% absorption by the graphene layer, respectively. These values represent a significant improvement over the intrinsic light absorption of graphene.

Figure 2

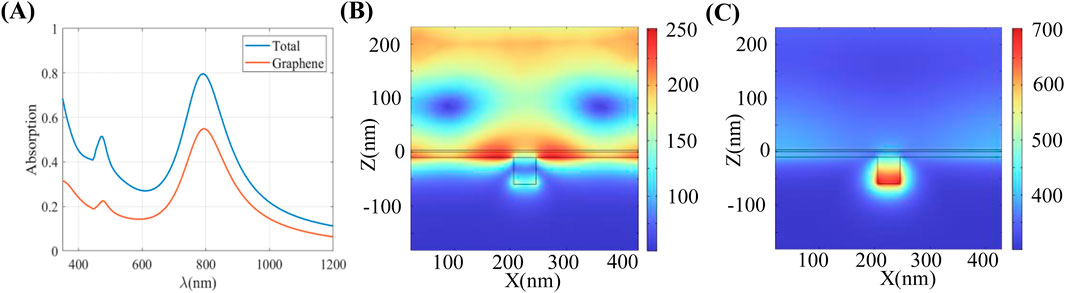
Figure 2. (A) Total absorption spectrum of metal single groove graphene structure and absorption spectrum of graphene layer, two consistent absorption peaks appeared. (B) Magnetic field distribution of the structure at absorption peak wavelength $\lambda =508\text{nm}$. (C) Magnetic field distribution of the structure at absorption peak wavelength $\lambda =779\text{nm}$.

As shown in Figure 2B, at the first absorption peak in the short-wavelength band, the light field energy is primarily concentrated on the surface of the metal grating, indicating the excitation of SPP resonance. The SPP resonance wavelength ${\lambda }_{SPP}=519\text{nm}$, calculated according to Equation 5, coincides with the short-wavelength band absorption peak position ${\lambda }_1=508\text{nm}$. This strong correlation confirms that the first resonance absorption enhancement in the short-wavelength band originates from the SPP resonance excited by the metal surface. When the SPP is successfully excited, electromagnetic coupling occurs in the metal groove, causing the light field energy to be strongly localized and gradually released. The graphene layer on top absorbs part of this energy, leading to an increased absorption rate. However, the SPP also determines that the light field energy is perpendicular to the interface direction between the metal and the medium and decays rapidly. This rapid decay results in a small full width at half maximum (FWHM) for the first enhancement, leading to a narrow absorption spectral width.

From Figure 2C, it is evident that the field enhancement mainly occurs in the metal groove for the second absorption peak, displaying typical cavity resonance characteristics. Based on the Fabry-Pérot (FP) cavity resonance model, the resonance position is primarily influenced by the metal groove’s depth $d$ and the groove’s effective refractive index $n_{eff}$. This relationship can be expressed by Equation 7:

$2n_{eff}d+\frac{1}{2}\lambda =M\lambda (7)$

Where $n_{eff}$ is the effective refractive index of the metal groove, $M$ is a positive integer representing the resonance mode, and $n_{eff}$ is a parameter related to the width of the groove $w$. The resonance is also influenced by the permittivity of the spacer layer (SiO₂) and the dielectric constant of the metal Ag layer. This effective refractive index can be equated to the mode refractive index of the metal/insulator/metal (MIM) waveguide structure. The variation of the effective refractive index can be determined by Equation 7.

With the structural parameters shown in Figure 1, the estimated Fabry-Pérot resonance wavelength is located at ${\lambda }_{FP}=667\text{nm}$, which deviates from ${\lambda }_2=779\text{nm}$ in Figure 2A. This deviation occurs because the presence of the spacer layer effectively extends the cavity length. When the thickness of the spacer layer is included in the calculations, the corrected resonance position aligns well with the actual measured value.

Figure 3A illustrates the effect of varying the groove widths $d$ on the absorption spectra of graphene while keeping the depth of the metal groove constant. The other structural parameters are consistent with those in Figure 1. In the short-wavelength region, the resonance absorption properties are not significantly affected by the groove width when it is varied within the range of 20–70 nm. The absorptance of the graphene layer is slightly affected by the groove width, but the position of the absorption peak remains almost unchanged, which can be explained by Equation 5.

Figure 3

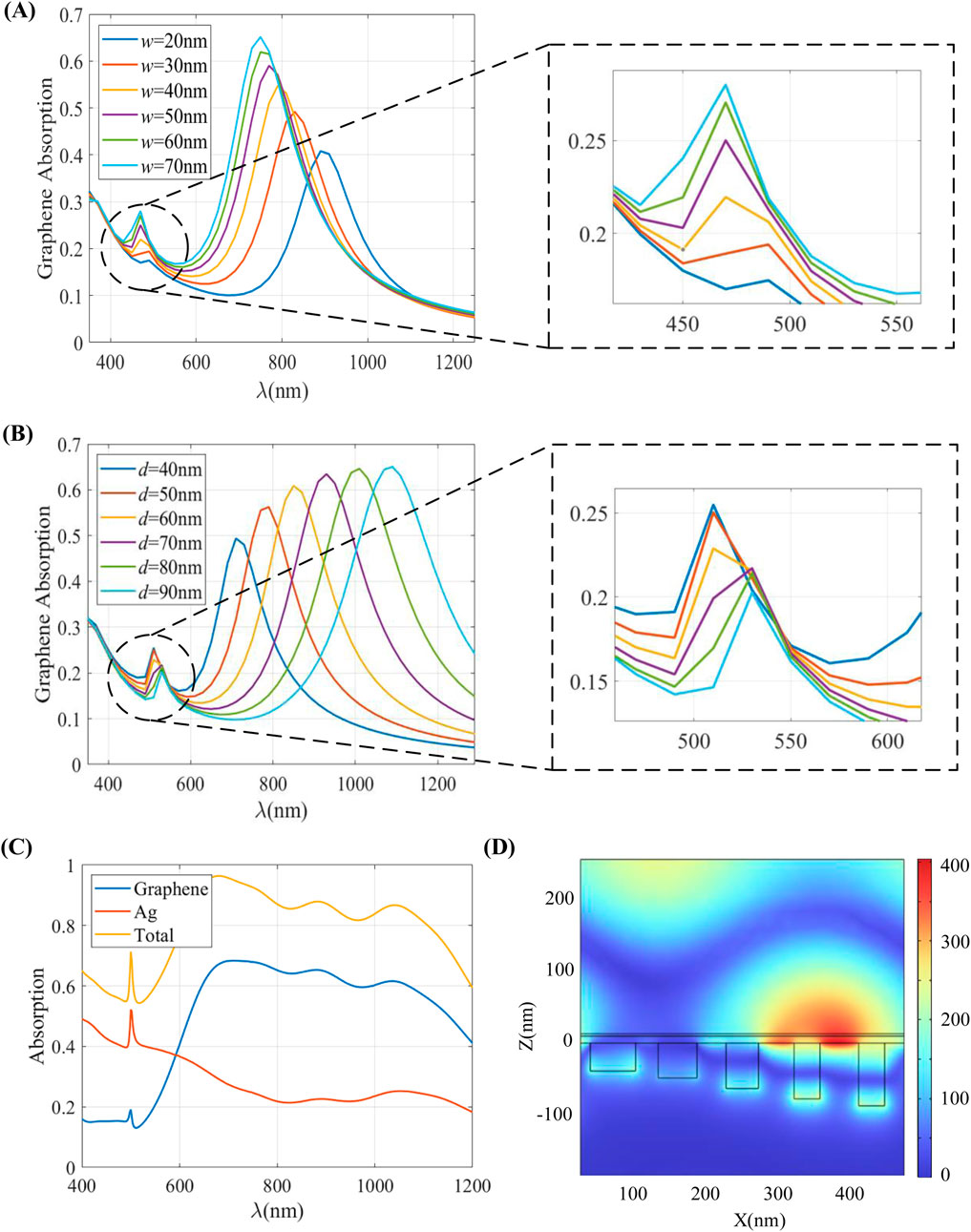
Figure 3. (A) Absorption spectrum of graphene layer with changes in metal groove width $w$, as $w$ increases, the absorption peak appears to be significantly blue-shifted. Magnification: magnified view of the first absorption peak. (B) Absorption spectrum of graphene layer with changes in metal groove depth $d$, as $d$ increases, the absorption peak appears to be significantly red-shifted. Magnification: magnified view of the first absorption peak. (C) Absorption spectra of the total structure, graphene layer, and Ag layer of GGM structure. (D) Magnetic field distribution of the structure at absorption peak wavelength $\lambda =498\text{nm}$.

However, for the second absorption peak in the long wavelength band, the position, size, and absorption bandwidth of the peak are indeed influenced by the width of the metal groove. When the width of the metal groove increases, there is a decrease in the effective refractive index $n_{eff}$, resulting in a blueshift of the absorption peak position. Moreover, there is a notable enhancement in absorption as the groove width increases.

As shown in Figure 3B, the absorption spectra of graphene layers with different depths $d$ of the metal groove are depicted when the width of the groove is fixed at 50 nm, with other parameters consistent with Figure 1. Increasing the depth $d$ of the metal groove from 40 nm to 90 nm primarily affects the resonant wavelength of the SPP resonance. This resonance wavelength is influenced by the angle of incidence ${\theta }_c$ and the grating period $\mathrm{\Lambda }$, as the optical field energy corresponding to the SPP resonance concentrates mainly at the junction between the metal surface and the medium. The change in metal groove depth $d$ has minimal impact on the absorption of the graphene layers in the short-wavelength region. However, in the long-wavelength region, variations in groove depth $d$ significantly affect the position, size, and absorption bandwidth of the absorption peaks. In this scenario, absorption enhancement primarily originates from the Fabry-Pérot resonance of the metal groove. They are increasing the cavity length by increasing $d$ results in a decrease in resonance frequency for each cavity, leading to a significant redshift in the position of the absorption peaks. This flexibility allows for precisely regulating graphene layer absorption properties by selecting different groove widths $w$ and depths $d$.

Furthermore, cascading multiple metal grooves within the same unit structure, each with individually designed depths and widths tailored to different wavelength bands, enables the superposition of absorption properties across different metal grooves. This approach provides a viable solution for achieving continuous broadband absorption from the visible to near-infrared wavelength bands. Optimizing the unit structure design also holds promise for further expanding the absorption spectrum.

In summary, for a consistent groove depth, increasing the groove width decreases the effective refractive index and increases the absorption rate, resulting in a blue shift of the absorption peak. Conversely, increasing the groove depth lowers the resonant frequency and enhances the absorption rate for a consistent groove width, causing a red shift of the absorption peak. However, it is essential to note that micro-nanostructure dimensions impose limitations on infinitely varying the groove width and depth to achieve optimal absorption. Additionally, by cascading multiple metal grooves within the same unit structure and individually designing the depth and width of each groove to target different wavelength bands, the absorption characteristics of different metal grooves can be superimposed, thereby achieving continuous absorption across the visible to near-infrared wavelength range.

3.2 Research on the absorption of multi-groove metasurface structures

Based on the above study, multiple metal grooves with different widths can be incorporated into a single periodic structural unit to achieve multiple resonance enhancements within the same structure. This approach does not consider the mutual influence of the actual absorption between the grooves. The structure is a cascade of multiple gratings with the same period but different duty cycles. By designing the depths of the grooves accordingly, the absorption spectra of the final overall structure can be regarded as a superposition of the absorption spectra of these multiple cascade structures.

As shown in Figure 1, the schematic diagram of the GGM structured cell integrates several metal grooves with different depths and widths. The widths of the grooves are $w_1=70\text{nm}$, $w_2=60\text{nm}$, $w_3=50\text{nm}$, $w_4=40\text{nm}$, $w_5=40\text{nm}$ and the depths are $d_1=40\text{nm}$, $d_2=50\text{nm}$, $d_3=65\text{nm}$, $d_4=80\text{nm}$, $d_5=90\text{nm}$, respectively, from left to right, and $w_{gap}=48\text{nm}$. Figure 3C illustrates the absorption spectrum for TM waves incident perpendicularly. The absorption enhancement at short wavelengths originates from the SPP resonance excited on the metal surface. The incidence angle ${\theta }_c$ and the grating period $\mathrm{\Lambda }$ determine the resonance wavelength ${\lambda }_{SPP}$.

Consequently, even after superposing the absorption spectra of multiple metal grooves, a pronounced absorption spike remains, and the overall absorption rate in the 400–600 nm wavelength range exceeds 55%. Figure 3D displays the magnetic field distribution at the peak wavelength $\lambda =498\text{nm}$. The light field localization on the metal surface indicates clear SPP resonance. The absorption enhancement is due to the Fabry-Pérot resonance of multiple cavities for the long wavelength range. The positions and magnitudes of the absorption peaks vary with the widths and depths of the metal grooves, resulting in different absorption peaks. This superposition of absorption peaks achieves a continuous broad spectrum, with an overall average absorbance of 87.5% in the 600–1,100 nm wavelength range.

Additionally, it is observed that the absorption contribution at short wavelengths primarily comes from the Ag layer, while at long wavelengths, it predominantly comes from the graphene layer. In the long wavelength range, the energy of the incident light is mainly dissipated in the graphene layer rather than in the Ag layer, resulting in an average absorption rate of 60.3% for the graphene layer in the 600–1,200 nm wavelength range. Figures 4A–C show the magnetic field distribution at wavelengths of 680 nm, 880 nm, and 1,050 nm, respectively. Clear cavity resonance is evident, with the light field confined within the metal grooves. Different grooves correspond to different resonance modes. Specifically, for shorter wavelengths, the field enhancement is concentrated in the shallower grooves, and as the wavelength increases, the field enhancement position shifts to the deeper grooves.

Figure 4

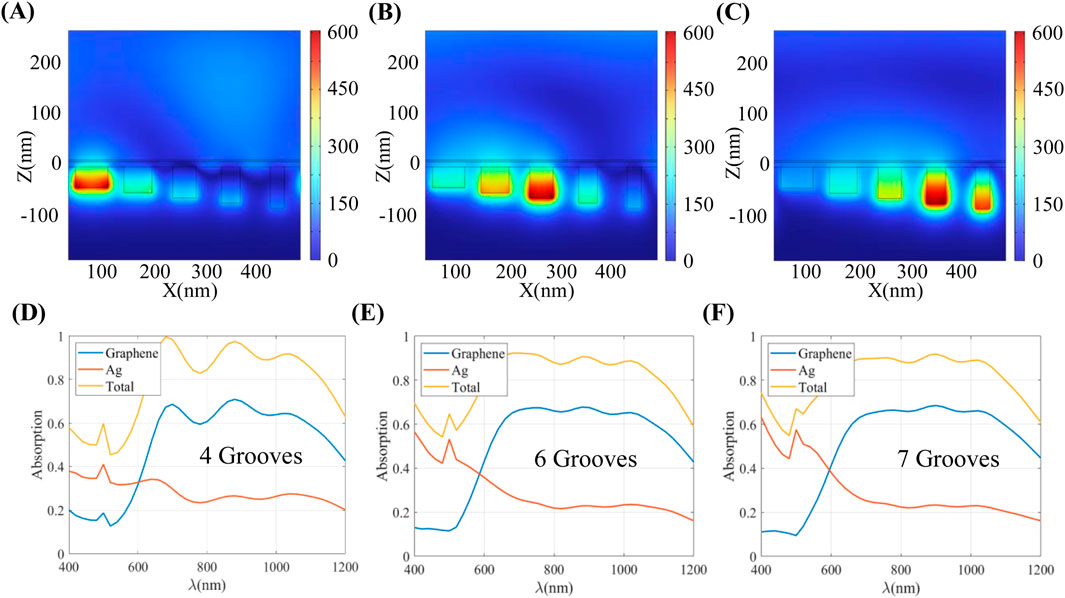
Figure 4. Magnetic field distribution of structures at wavelengths (A) $\lambda =680\text{nm}$ (B) $\lambda =880\text{nm}$ (C) $\lambda =1050\text{nm}$. Absorption spectrum of graphene metasurface with different number of grooves (D) 4 grooves. (E) 6 grooves. (F) 7 grooves.

This approach realizes the cascading of multiple metal grooves within the same structural unit to enhance both the graphene layer’s absorbance and the structure’s overall absorbance. This enhancement is achieved through the excitation of SPP resonance and Fabry-Pérot resonance, further validating the physical mechanism behind the continuous broadband absorption of graphene based on the GGM. However, the number of metal grooves that can be integrated into the metasurface structural unit is limited for a fixed period. As the number of grooves increases and the spacing between them decreases, the electromagnetic interaction between different grooves has a more significant impact on the absorption performance of the graphene layer and the overall absorption performance of the structure. Therefore, achieving an infinite expansion of the absorption spectral width is not feasible through simple superposition of grooves.

To flexibly control the absorption performance of graphene and the overall structure, it is essential to adjust the number, width, and depth of grooves in the structural unit. This adjustment allows for optimization of the absorption properties to meet specific requirements and enhance the overall efficiency of the structure.

The absorption spectra of the GGM structural unit cascaded with four, six, and seven metal grooves are presented in Figures 4D–F, respectively. Compared with the absorption shown in Figure 3C, which integrates five grooves, it is evident that fewer metal grooves result in more significant fluctuations in the absorption spectra and more uneven absorption bands. This phenomenon is attributed to the dispersion of the single-groove absorption spectra, where the absorption peaks of each single groove are widely spaced at different wavelengths, preventing them from superimposing to form broad and flat absorption bands. As the number of metal grooves increases, individual grooves’ absorption spectra become closer. Consequently, the features of single grooves are less pronounced in the combined absorption spectrum of multiple grooves, leading to a more uniform and flat overall absorption line with no significant difference in the average absorption rate.

Additionally, increasing the number of grooves does not significantly broaden the absorption spectra. Beyond a wavelength of 1,100 nm, the absorption rates begin to show a decreasing trend, and the absorption peaks no longer exhibit the characteristics of single-groove absorption. This phenomenon suggests that the structural units have a fixed period, which limits the local enhancement of the light field in the deeper grooves.

Based on the structure of the 7 grooves, Figure 5A illustrates the influence of the spacing between each metal groove $w_{gap}$ on the total and the graphene layer absorption rate, respectively. The figure shows that as the spacing between the metal grooves decreases, the absorption of the graphene layer also decreases. This reduction in absorption is attributed to the proximity of the metal grooves, which leads to electromagnetic solid coupling between neighboring grooves. This coupling results in mixing, which consequently lowers the absorption rate.

Figure 5

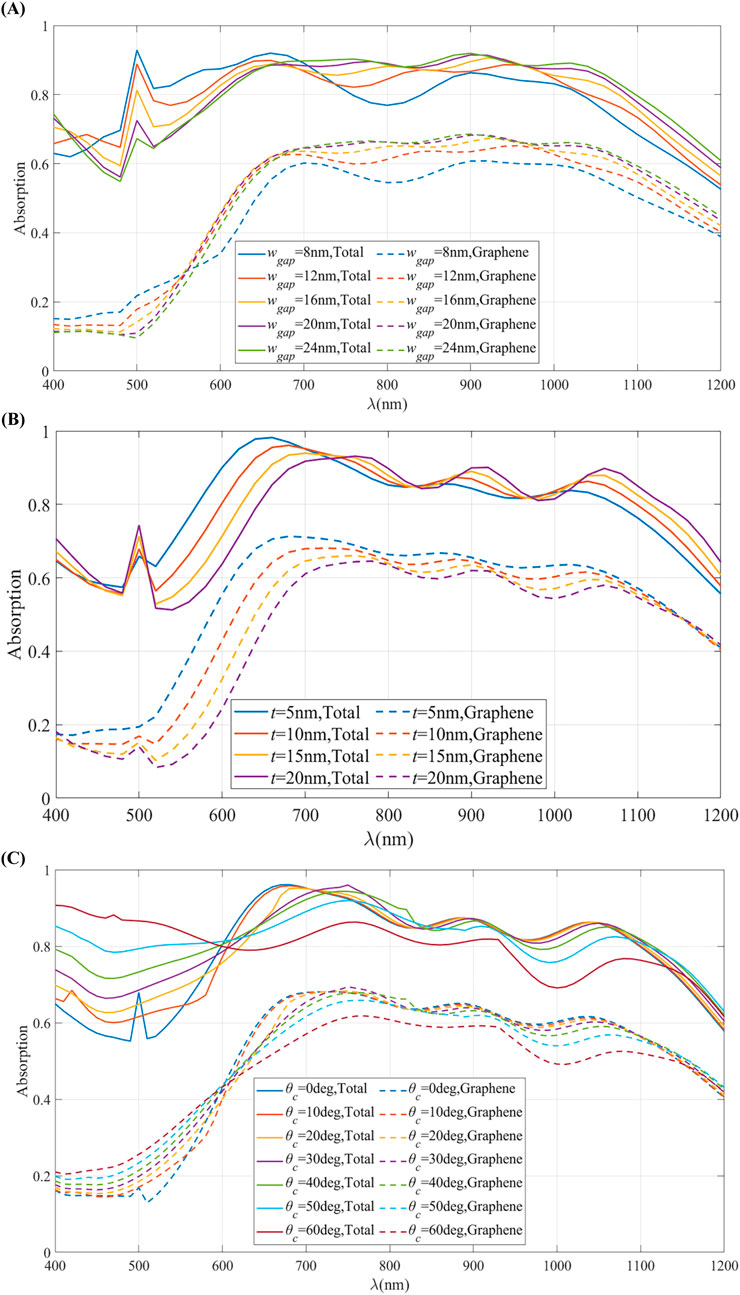
Figure 5. (A) Absorption spectra of the total structure and graphene layer with changes in the spacing of metal grooves $w_{gap}$. (B) Absorption spectra of the total structure and graphene layer with changes in interlayer thickness $t$. (C) Absorption spectra of the total structure and graphene layer with changes in incident angle ${\theta }_c$.

To further evaluate the absorption performance of the graphene layer in the GGM-integrated structure, Figure 5B shows the effect of the spacer layer thickness $t$ on the absorption properties of the graphene layer. The other structural parameters are the same as those in Figure 1. As the thickness of the spacer layer $t$ increases from 5 nm to 20 nm, the broad absorption band is maintained, but there is a noticeable decrease in absorption. This reduction occurs because as the thickness of the spacer layer increases, the top graphene layer gradually moves away from the light field. The spacer layer also acts as a buffer, attenuating the electromagnetic coupling between the metal and the graphene to some extent, which leads to a decrease in the absorption rate. Moreover, the increase in the spacer layer thickness extends the length of the Fabry-Pérot-like cavity, causing a redshift in the absorption band. For optimal overall absorption rate of the structure, a spacer layer thickness of $t=10\text{nm}$ is selected.

Figure 5C shows the absorption spectra of the overall structure and the graphene layer for different incident angles ${\theta }_c$. The other structural parameters are consistent with those in Figure 1. The structure demonstrates insensitivity to changes in the incident light angle. Even when the incident angle is increased to 60°, the overall structure maintains a high absorption level and stable broadband performance. In the long-wavelength range, field enhancement primarily occurs within the metal grooves, and changes in the incident angle ${\theta }_c$ have minimal impact on the Fabry-Pérot resonance, which remains robust against angle variations. However, the SPP resonance is more affected by changes in the incident angle. When the incident light is oblique, the simplicity of the SPP resonance, which corresponds to the $\pm 1$ diffraction order, is disrupted. They are causing the two corresponding absorption peaks to shift in opposite directions, flattening the superimposed absorption spectrum. Unlike many previous graphene-based absorbers, this structure achieves continuous broadband absorption that is insensitive to the angle of light incidence. This feature is highly significant for applications in various fields, such as broadband detection and omnidirectional absorbers.

3.3 The influence of machining accuracy on absorption

The preparation and processing accuracy of micro-nano structures is crucial in the application of optoelectronic devices. This precision not only influences the optical performance, operational stability, and reliability of the device but also impacts the degree of integration, which in turn affects the device’s operational performance and efficiency. Therefore, to achieve high-performance light-absorbing structures, it is essential to employ high-precision preparation and processing technologies. These technologies ensure the accuracy, consistency, and stability of the micro-nano structures. Additionally, a deep understanding of the optical properties of these micro-nano structures is necessary to optimize the performance and efficiency of the devices. These properties involve comprehensive studies and analyses to fine-tune the structural parameters, ensuring the devices meet the desired specifications and performance criteria in various applications.

In practical applications, the minimum number of unit cells in the metasurface array structure must not only satisfy electromagnetic performance requirements but also account for the precision of the MEMS machining process and manufacturing costs. According to related research, the local electromagnetic response is generally considered to stabilize after the array reaches a scale of 11 × 11 [49, 50]. Furthermore, from a MEMS processing perspective, this metasurface array is achievable with current processing precision. To more directly understand the impact of processing accuracy on the overall structure and the absorption properties of the graphene layer, we simulate actual processing errors by artificially introducing geometrical inaccuracies into the model. For the GGM structure proposed in this paper, the preparation of gradient groove metallic gratings is the most complex. Considering the machining errors of the micro-nano deep grooves, factors such as right-angle machining accuracy, the vertical accuracy of the sidewall of the deep groove, positional accuracy of the groove, and surface roughness may affect the absorption of the structure. Here, we have specifically simulated and analyzed the grooves’ right-angle machining accuracy and the sidewalls’ vertical accuracy. Rounded corners are added at the bottom of the metal grooves to simulate the actual right-angle machining errors. The specific changes are illustrated in Figures 6A, B, with the radius of the rounded corners set to $r$. As shown in Figure 6C, we present the absorption properties of the overall structure and the graphene layer for variations in $r$ from 5 nm to 20 nm. When the deep grooves have no right-angle machining errors, the average absorption of the overall structure is 78.96% in the 400–1,200 nm range and 87.68% in the 600–1,200 nm range. The average absorption of the graphene layer is 50.04% in the 400–1,200 nm range and 62.48% in the 600–1,200 nm range. When the radius of the fillet changes from 5 nm to 20 nm, the corresponding absorption rate changes are detailed in Tables 1, 2, showing deviations of no more than 2%. Therefore, it can be concluded that without changing the depth of the metal grooves, the right-angle machining accuracy has minimal effect on the absorption performance. The structure can maintain a broad absorption band and achieve continuous broadband absorption.

Figure 6

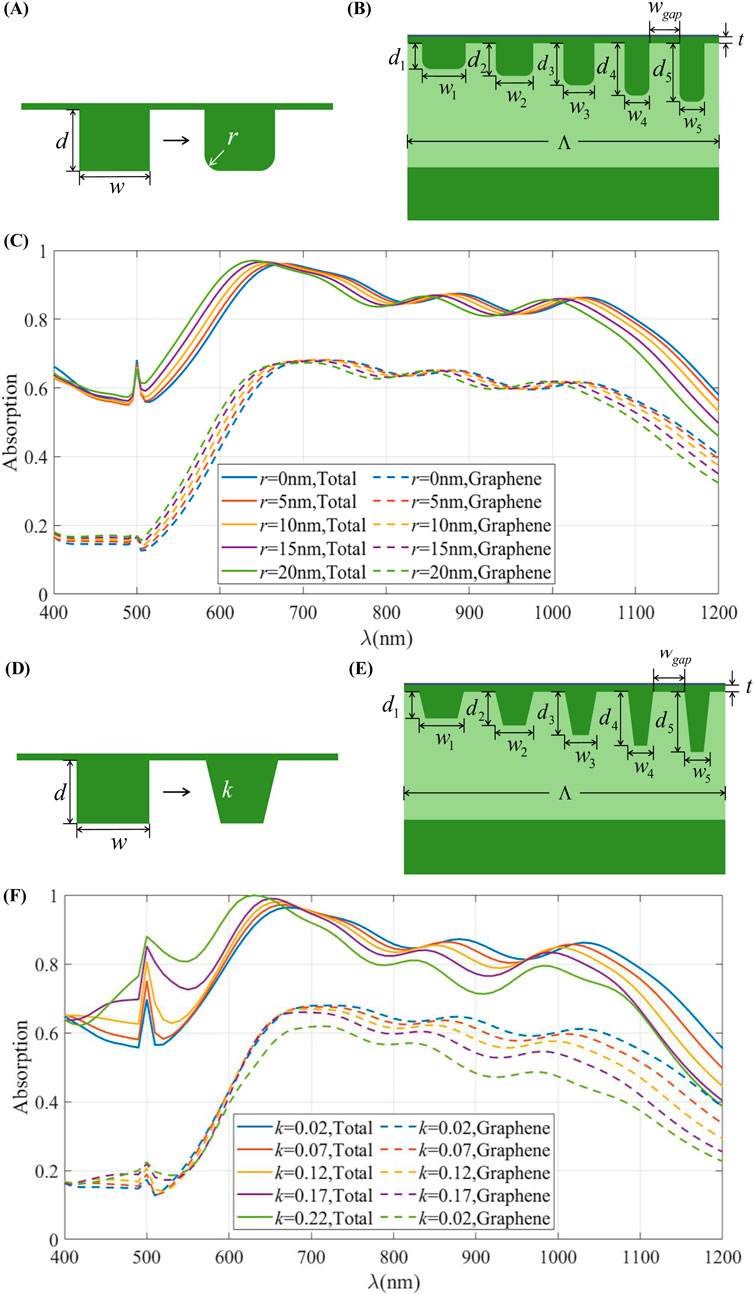
Figure 6. (A) Schematic diagram of metal groove fillet error (B) Schematic diagram of structural unit cross-section with added fillet error. (C) Absorption spectra of the overall structure and graphene layer of metal grooves with different sizes of right-angle machining errors at the bottom (D) Schematic diagram of verticality error of metal groove sidewall. (E) Schematic diagram of structural unit cross-section with added sidewall verticality error. (F) The overall structure and absorption spectrum of the graphene layer of the metal groove sidewall with different processing errors in perpendicularity.

Table 1

Table 1. The influence of right-angle machining error on absorption in the range of 400–1200 nm.

Table 2

Table 2. Effect of right-angle machining error on absorption in the range of 600–1100 nm.

Additionally, in the machining process, the deep straight groove may maintain a different width at the top and bottom, resulting in inclined sidewalls. This inclination affects the absorption of the structure. To simulate the perpendicularity error in actual processing, an inclination angle is added to the model’s sidewall of the metal groove. The specific structural changes are shown in Figures 6D, E, where the slope of the sidewall is set to $k$. As shown in Figure 6F, the influence of the sidewall inclination on the overall absorption performance and the absorption properties of the graphene layer is displayed. It can be observed that, with the gradual increase of $k$, i.e., the increase of the perpendicularity error of the sidewall, the absorption rate of the graphene layer significantly decreases. This phenomenon occurs because the size of the groove opening remains unchanged, and the perpendicularity error results in a decrease in the adequate width of the groove. As illustrated in Figure 3A, decreasing the groove width reduces the absorption rate. When the groove sidewall’s tilt changes from 0.02 to 0.22, the corresponding change in absorption rate is provided in Tables 3, 4; when the tilt is less than 0.2, the deviation can be controlled within 10%. This data indicates that when the vertical error is kept within a specific range, the decrease in absorption rate remains within an acceptable range. Overall, as long as the adequate depth and width of each metal groove are maintained, the specific shape characteristics of each groove have minimal impact on the absorption properties of the overall structure and the graphene layer. This property significantly reduces the requirements for fine processing of micro- and nanostructures, greatly enhancing the manufacturability and practicability of the devices.

Table 3

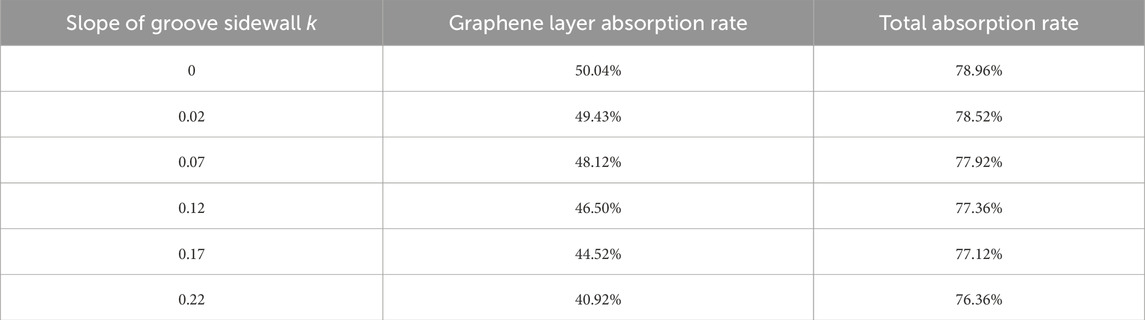
Table 3. Effect of machining error on absorption of groove sidewall verticality within the range of 400–1200 nm.

Table 4

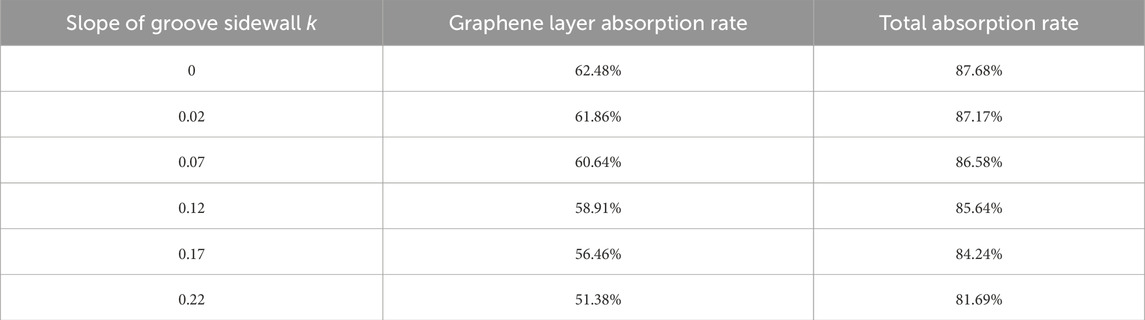
Table 4. The influence of machining errors in the perpendicularity of groove sidewalls within the range of 600–1100 nm on absorption.

4 Discussion

In this paper, we design a structure that integrates a graphene layer with a gradient groove metasurface (GGM). Firstly, we investigate the absorption spectrum of a single groove structure, demonstrating its capability for dual-band absorption across visible to near-infrared wavelengths. Building on this, we explore the impact of varying structure parameters on absorption characteristics. Subsequent expansion to gradient groove structure and achieve continuous absorption across the visible to near-infrared wavelength bands through systematic parameter design for each groove. In the wavelength range of 600 nm–1,100 nm, the overall average absorption of the structure reaches 87.5%, and in the range of 600 nm–1,200 nm, the average absorption of the graphene layer reaches 60.3%. This structure also exhibits insensitivity to incident angle variations. Finally, we investigate the fabrication process of the metasurface and the influence of groove processing accuracy on absorption. Our findings reveal that the structure can tolerate deviations such as groove right-angle errors and sidewall vertical errors to a significant extent. This tolerance effectively mitigates the complexity and cost of device applications and provides a theoretical basis for large-scale preparation. The GGM structure demonstrates high scalability due to its compatibility with industrial processing tolerances and its inherent modular, periodic design. Nevertheless, material constraints represent a primary challenge in advancing GGM structures toward practical application. Although CVD enables precise graphene deposition, it encounters substantial difficulties when scaled for large-area fabrication. Specifically, the deposition and transfer processes of large-area graphene are susceptible to issues such as wrinkling and cracking, which can negatively impact absorption properties. Furthermore, the high costs associated with producing high-quality graphene and silver continue to pose significant barriers to the practical implementation and commercialization of GGM structures.

In general, most current metasurface designs still rely on a single resonance mode to enhance absorption, which typically results in a narrow operating band and limits broadband absorption [51–53]. In contrast, this study introduces an innovative approach to achieve broadband absorption by coupling dual-mode resonance with a metasurface. This design significantly broadens the absorption bandwidth while reducing fabrication complexity and cost, without introducing additional structural complexity. The concept of multi-mode coupled metasurface offers new insights and potential for the future design of broadband absorbers.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HL: Conceptualization, Supervision, Writing–review and editing. YL: Data curation, Visualization, Writing–original draft. WL: Data curation, Methodology, Writing–review and editing. TL: Data curation, Validation, Writing–review and editing. SZ: Funding acquisition, Software, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is financially supported by the Basic Frontier Science and Technology Innovation Research Project of Army Engineering University of PLA. (No. KYZXJQZL2204).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tsai J, Chien Al., Kang Ju., Leung S, Kang S, Garza LA. Hyperspectral measurement of skin reflectance detects differences in the visible and near-infrared regions according to race, gender and body site. J Eur Acad Dermatol Venereol (2021) 35:e330–e333. doi:10.1111/jdv.17076

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Shao Y, Li Y, Jiang L, Pan J, He Y, Dou X. Identification of pesticide varieties by detecting characteristics of Chlorella pyrenoidosa using Visible/Near infrared hyperspectral imaging and Raman microspectroscopy technology. Water Res (2016) 104:432–40. doi:10.1016/j.watres.2016.08.042

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Dong J, Dong X, Li Y, Peng Y, Chao K, Gao C, et al. Identification of unfertilized duck eggs before hatching using visible/near infrared transmittance spectroscopy. Comput Elect Agric (2019) 157:471–8. doi:10.1016/j.compag.2019.01.021

CrossRef Full Text | Google Scholar

4. Sun Y, Zhang J. Strategies for scalable gas-phase preparation of free-standing graphene. CCS Chem (2021) 3:1058–77. doi:10.31635/ccschem.020.202000289

CrossRef Full Text | Google Scholar

5. Zhang S, Liu H, Zhang J, Li W, Wang H, Tian C, et al. Dynamically switchable triple-band absorption enhancement of graphene by a subwavelength grating coupled hybrid structure. Results Phys (2022) 43:106057. doi:10.1016/j.rinp.2022.106057

CrossRef Full Text | Google Scholar

6. Koppens FHL, Mueller T, Avouris PH, Ferrari AC, Vitiello MS, Polini M. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat Nanotech (2014) 9:780–93. doi:10.1038/nnano.2014.215

CrossRef Full Text | Google Scholar

7. Long M, Wang P, Fang H, Hu W. Progress, challenges, and opportunities for 2D material based photodetectors. Adv Funct Mater (2019) 29:1803807. doi:10.1002/adfm.201803807

CrossRef Full Text | Google Scholar

8. Asif M, Munir RM, Wang Q, Ouyang Z. Graphene-based polarization insensitive structure of ultra-wideband terahertz wave absorber. Opt Mater (2024) 154:115759. doi:10.1016/j.optmat.2024.115759

CrossRef Full Text | Google Scholar

9. Yang S, Wang G, Zhang X, Liu J, Li M, Jia Y A switchable and adjustable terahertz absorber using vanadium dioxide and graphene. Opt Mater (2024) 154:115704. doi:10.1016/j.optmat.2024.115704

CrossRef Full Text | Google Scholar

10. Rezaei I, Ali Mohammad Khani A, Biabanifard S, Soltani-Zanjani M. A reconfigurable narrow and wide band multi bias graphene based THz absorber. Opt and Laser Tech (2022) 151:107996. doi:10.1016/j.optlastec.2022.107996

CrossRef Full Text | Google Scholar

11. Miroshnichenko AE, Flach S, Kivshar YS. Fano resonances in nanoscale structures. Rev Mod Phys (2010) 82:2257–98. doi:10.1103/RevModPhys.82.2257

CrossRef Full Text | Google Scholar

12. Vy ND, Chinh ND, Dat LT, Pham VNT. Significant enhancement of optical absorption of graphene inside a metallic optical microcavity. Opt Commun (2024) 566:130658. doi:10.1016/j.optcom.2024.130658

CrossRef Full Text | Google Scholar

13. Zhang H, Zheng G, Xian F, Zou X, Wang J. Near-unity absorption of graphene monolayer with a triple-layer waveguide coupled grating. Opt Mater (2017) 72:476–81. doi:10.1016/j.optmat.2017.06.053

CrossRef Full Text | Google Scholar

14. Ruan JF, Tu JY, Wang DL, Tao Z, Yuan Y, Ji SW. Perfect absorption based on Ti3C2Tx surface plasmon resonance. Opt Mater (2023) 137:113604. doi:10.1016/j.optmat.2023.113604

CrossRef Full Text | Google Scholar

15. Min BK, Nguyen V-T, Kim SJ, Yi Y, Choi C-G. Surface plasmon resonance-enhanced near-infrared absorption in single-layer MoS2 with vertically aligned nanoflakes. ACS Appl Mater Inter (2020) 12:14476–83. doi:10.1021/acsami.9b18148

CrossRef Full Text | Google Scholar

16. Cordaro A, van de Groep J, Raza S, Pecora EF, Priolo F, Brongersma ML. Antireflection high-index metasurfaces combining mie and fabry-pérot resonances. ACS Photon (2019) 6:453–9. doi:10.1021/acsphotonics.8b01406

CrossRef Full Text | Google Scholar

17. He J, Zhang M, Liang Y, Shu S, Li B, Li B, et al. Ultra-narrow band absorber in visible region based on the couple of Fabry-Pérot and guide mode resonance. Opt Commun (2023) 547:129851. doi:10.1016/j.optcom.2023.129851

CrossRef Full Text | Google Scholar

18. Cho W, Hwang J, Lee SY, Park J, Han N, Lee CH, et al. Highly sensitive and cost-effective polymeric-sulfur-based mid-wavelength infrared linear polarizers with tailored fabry–pérot resonance. Adv Mater (2023) 35:2209377. doi:10.1002/adma.202209377

CrossRef Full Text | Google Scholar

19. Janfaza M, Mansouri-Birjandi MA, Tavousi A. Tunable plasmon-induced reflection based on graphene nanoribbon Fabry-Perot resonator and nanodisks. Opt Mater (2018) 84:675–80. doi:10.1016/j.optmat.2018.07.055

CrossRef Full Text | Google Scholar

20. Elsehrawy F, Niemi T, Cappelluti F. Guided-mode resonance gratings for enhanced mid-infrared absorption in quantum dot intermediate-band solar cells. Opt Express, OE (2018) 26:A352–A359. doi:10.1364/OE.26.00A352

CrossRef Full Text | Google Scholar

21. Park GC, Park K. Tunable dual-wavelength absorption switch with graphene based on an asymmetric guided-mode resonance structure. Opt Express, OE (2021) 29:7307–20. doi:10.1364/OE.416394

CrossRef Full Text | Google Scholar

22. Li Z, Li H, Hu Z-D, Zhou J, Wang J, Khakhomov S. Lithography-free high sensitivity perfect absorption based on Graphene/α-MoO3/SiC and Tamm plasmonic structure. Opt and Laser Tech (2024) 169:110125. doi:10.1016/j.optlastec.2023.110125

CrossRef Full Text | Google Scholar

23. Li Y, Lu H, Zheng J, Li S, Xuan X, Zhao J. Perfect light absorption in monolayer MoS2 empowered by optical Tamm states. col (2021) 19:103801. doi:10.3788/COL202119.103801

CrossRef Full Text | Google Scholar

24. Bin-Alam MS, Reshef O, Mamchur Y, Alam MZ, Carlow G, Upham J, et al. Ultra-high-Q resonances in plasmonic metasurfaces. Nat Commun (2021) 12:974. doi:10.1038/s41467-021-21196-2

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Cheng Y, Chen F, Luo H. Plasmonic chiral metasurface absorber based on bilayer fourfold twisted semicircle nanostructure at optical frequency. Nanoscale Res Lett (2021) 16:12. doi:10.1186/s11671-021-03474-6

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chen Z, Cai P, Wen Q, Chen H, Tang Y, Yi Z, et al. Graphene multi-frequency broadband and ultra-broadband terahertz absorber based on surface plasmon resonance. Electronics (2023) 12:2655. doi:10.3390/electronics12122655

CrossRef Full Text | Google Scholar

27. Zhu J, Wu C, Ren Y. Broadband terahertz metamaterial absorber based on graphene resonators with perfect absorption. Results Phys (2021) 26:104466. doi:10.1016/j.rinp.2021.104466

CrossRef Full Text | Google Scholar

28. Tang C, Nie Q, Cai P, Liu F, Gu P, Yan Z, et al. Ultra-broadband near-infrared absorption enhancement of monolayer graphene by multiple-resonator approach. Diamond Relat Mater (2024) 141:110607. doi:10.1016/j.diamond.2023.110607

CrossRef Full Text | Google Scholar

29. Rahad R, Mohsin ASM, Belal Hossain Bhuian M, Rahman MM. Graphene-Metamaterial based tunable broadband polarization insensitive absorber for terahertz antenna design. In: IEEE journals and magazine | IEEE xplore (2024). Available from: https://ieeexplore.ieee.org/document/10483070 (Accessed July 3, 2024).

CrossRef Full Text | Google Scholar

30. Liu PQ, Luxmoore IJ, Mikhailov SA, Savostianova NA, Valmorra F, Faist J, et al. Highly tunable hybrid metamaterials employing split-ring resonators strongly coupled to graphene surface plasmons. Nat Commun (2015) 6:8969. doi:10.1038/ncomms9969

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Chen R, Peng F, Yan Z, Yang Z, Chen S, Chang Z Plasmon-enhanced infrared absorption in graphene nanodot array. Plasmonics (2023) 18:2205–12. doi:10.1007/s11468-023-01939-1

CrossRef Full Text | Google Scholar

32. Dong Y, Yu D, Li G, Li G, Ma H. Tunable ultrathin ultrabroadband metamaterial absorber with graphene-stack-based structure at lower terahertz frequency. Physica E: Low-dimensional Syst Nanostructures (2021) 128:114608. doi:10.1016/j.physe.2020.114608

CrossRef Full Text | Google Scholar

33. Lin H, Sturmberg BCP, Lin K-T, Yang Y, Zheng X, Chong TK A 90-nm-thick graphene metamaterial for strong and extremely broadband absorption of unpolarized light. Nat Photon (2019) 13:270–6. doi:10.1038/s41566-019-0389-3

CrossRef Full Text | Google Scholar

34. Liu D, Cui Z. Broadband terahertz absorber based on patterned slotted vanadium dioxide. Opt Mater (2024) 152:115478. doi:10.1016/j.optmat.2024.115478

CrossRef Full Text | Google Scholar

35. Zhu Y, Niu H, Li Y, Lv T, Li H, Fan X, et al. Tunable metamaterial broadband perfect absorber based on double-layer graphene nanofilm. Opt Mater (2024) 149:115085. doi:10.1016/j.optmat.2024.115085

CrossRef Full Text | Google Scholar

36. Hossain T, Mamun AA, Islam F, Hassan MM. Efficient broadband light absorption in a bioinspired silicon photonic structure. J Phys Chem C (2024) 128:8522–30. doi:10.1021/acs.jpcc.4c01827

CrossRef Full Text | Google Scholar

37. Li Z, Palacios E, Butun S, Kocer H, Aydin K. Omnidirectional, broadband light absorption using large-area, ultrathin lossy metallic film coatings. Sci Rep (2015) 5:15137. doi:10.1038/srep15137

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Luca DD, Kortge D, Gennaro ED, Russo R, Bermel P. Ultra-thin sputter-deposited infrared rugate mirror for enhancing solar-to-thermal energy conversion. Opt Lett OL (2022) 47:230–3. doi:10.1364/OL.442839

CrossRef Full Text | Google Scholar

39. Huang ML, Cheng YZ, Cheng ZZ, Chen HR, Mao XS, Gong RZ. Design of a broadband tunable terahertz metamaterial absorber based on complementary structural graphene. Materials (2018) 11:540. doi:10.3390/ma11040540

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Dang PT, Vu TV, Kim J, Park J, Nguyen V-C, Vo DD, et al. Efficient broadband truncated-pyramid-based metamaterial absorber in the visible and near-infrared regions. Crystals (2020) 10:784. doi:10.3390/cryst10090784

CrossRef Full Text | Google Scholar

41. Sang T, Gao J, Yin X, Qi H, Wang L, Jiao H. Angle-insensitive broadband absorption enhancement of graphene using a multi-grooved metasurface. Nanoscale Res Lett (2019) 14:105. doi:10.1186/s11671-019-2937-7

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Chimene D, Alge DL, Gaharwar AK. Two-dimensional nanomaterials for biomedical applications: emerging trends and future prospects. Adv Mater (2015) 27:7261–84. doi:10.1002/adma.201502422

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Kostarelos K. Translating graphene and 2D materials into medicine. Nat Rev Mater (2016) 1:16084–2. doi:10.1038/natrevmats.2016.84

CrossRef Full Text | Google Scholar

44. Zangeneh-Nejad F, AbdollahRamezani S, Arik K, Khavasi A. Beam focusing using two-dimensional graphene-based meta-reflect-array. 24th Iranian Conference on Electrical Engineering (ICEE). Shiraz, Iran: ICEE (2016). p. 613–6. doi:10.1109/IranianCEE.2016.7585595

CrossRef Full Text | Google Scholar

45. Brunetti G, Conteduca D, Dell’Olio F, Ciminelli C, Armenise MN. Design of an ultra-compact graphene-based integrated microphotonic tunable delay line. Opt Express (2018) 26:4593. doi:10.1364/OE.26.004593

PubMed Abstract | CrossRef Full Text | Google Scholar

46. ED Palik, editor List of contributors for volume II. In: Handbook of optical constants of solids. Burlington: Academic Press (2023) xv–xviii. doi:10.1016/B978-012544415-6.50001-7

CrossRef Full Text | Google Scholar

47. Prokopeva LJ, Wang D, Kudyshev ZA, Kildishev AV. Computationally efficient surface conductivity graphene model for active metadevices. In: IEEE journals and magazine | IEEE xplore (2024). Available from: https://ieeexplore.ieee.org/document/8966620 (Accessed July 3, 2024).

Google Scholar

48. Lu H, Cumming BP, Gu M. Highly efficient plasmonic enhancement of graphene absorption at telecommunication wavelengths. Opt Lett OL (2015) 40:3647–50. doi:10.1364/OL.40.003647

CrossRef Full Text | Google Scholar

49. Thrane PCV, Meng C, Ding F, Bozhevolnyi SI. MEMS tunable metasurfaces based on gap plasmon or fabry–pérot resonances. Nano Lett (2022) 22:6951–7. doi:10.1021/acs.nanolett.2c01692

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Shen S, Ruan Z, Li S, Yuan Y, Tan H. The influence of periodicity on the optical response of cube silicon metasurfaces. Results Phys (2021) 23:104057. doi:10.1016/j.rinp.2021.104057

CrossRef Full Text | Google Scholar

51. Wang L, Yi Y, Yi Z, Bian L, Zhang J, Yang H A perfect absorber of multi-band, tunable monolayer patterned graphene based on surface plasmon resonance. Diamond Relat Mater (2022) 130:109498. doi:10.1016/j.diamond.2022.109498

CrossRef Full Text | Google Scholar

52. Jarahizadeh Y, Shirkani H, Sadeghi Z, Mehrabi M. Designing a perfect surface plasmon resonance absorber based on graphene and hexagonal boron nitride photonic crystal nanorods. J Phys Chem Sol (2023) 183:111634. doi:10.1016/j.jpcs.2023.111634

CrossRef Full Text | Google Scholar

53. Chen X-Y, Yu K, Zheng S-W, Qian M-D, Liu Y-F. Dual-band, high sensitivity, angle-insensitive graphene—perfect absorber based on surface plasmon resonance. Diamond Relat Mater (2024) 142:110728. doi:10.1016/j.diamond.2023.110728

CrossRef Full Text | Google Scholar