Reflection of P1-wave incident obliquely at the free surface of a fluid-saturated half-space: a comprehensive study via the model of soil mechanics

Introduction: Elastic wave propagation in fluid-saturated porous media is of great significance in various fields. Based on the soil mechanics model of a two-phase medium, the reflection problem of an obliquely incident plane P₁-wave at the free surface is systematically explored, which aims to reveal the physical mechanism of wave propagation in saturated semi-infinite space.

Methods: The dispersion characteristic equations of body waves are obtained by using the Helmholtz decomposition method. The theoretical formulas of reflection coefficients and surface displacements are derived and verified for correctness by simplifying. Finally, numerical investigations are carried out on the variations of the displacement reflection coefficients and surface displacements with the incident angle for different boundary conditions, wave frequencies f, porosities n, Poisson’s ratios ν, and modulus ratios E_w/μ.

Results: It is shown that the surface response of half-space is somewhat affected by the boundary conditions while little influenced by the wave frequency. It is also found that the effects of material properties on the surface response cannot be ignored.

Discussion: These conclusions provide a theoretical basis for wave survey technology of seismic engineering and site seismic response analysis.

1 Introduction

Elastic wave propagation in fluid-saturated porous media has been studied for many years. It is of theoretical and practical significance in various fields such as soil dynamics, geotechnical engineering, earthquake engineering, geophysics, acoustics, petroleum engineering, etc. The reflection of elastic waves in saturated two-phase media is one of the important branches. Due to the existence of pore water in the soil skeleton, the mechanical properties of two-phase media become very complex, which results in the problem of wave propagation being much more complicated than that of a single-phase medium [1, 2]. Therefore, when the seismic wave propagates to the free surface of two-phase media, it will show complex reflection characteristics.

It is well known that Biot first predicted the existence of three body waves in a two-phase medium, namely, the fast P₁-wave, the slow P₂-wave, and the S-wave. The three body waves are dispersed and attenuated, the speed and attenuation of which are related to the frequency and the properties of saturated soil materials [3, 4]. All these laid the foundation for the theoretical study of wave propagation in a fluid-saturated porous medium. After that, many scholars studied the various aspects of wave propagation in such medium. The P₂-wave with strong dispersion and high attenuation characteristics was successively confirmed through experiments by Plona and Berryman in 1980 [5, 6]. Following the Biot model, different two-phase medium models, including the Zienkiewicz model [7, 8], the Men Fu-lu model [9–11], the model of soil mechanics [12], and the theory of mixture [13], were proposed by different researchers. Chen and Liao [14] compared the first four models in detail and pointed out the essential differences between them. They also theoretically explained that the soil mechanics model is a special case of the Biot model, which has the advantage of a clear physical meaning of modeling parameters. At the same time, more and more scholars used the Biot model to study the reflection of elastic waves at the boundary of the fluid-saturated medium. For example, Deresiewicz [15] deduced theoretical formulas for the reflection coefficient of plane waves incident on a free interface of a non-dissipative liquid-filled porous solid. Deresiewicz and Rice [16] derived analytical formulas for the reflection coefficients and reflection angles of body waves (P₁-, P₂-, and SV-waves) incident upon a free interface because of the dissipation. Xu et al. [17] presented analytical expressions of reflection coefficients when P₁-wave incident obliquely at four kinds of plane interfaces of saturated soil (i.e., free drainable/undrainable boundary, fixed drainable/undrainable boundary) and analyzed the effect of incident frequency, incident angle, and interface conditions on reflection coefficients. Lin et al. [18–20] investigated the dynamic response (e.g., surface displacement, surface strain, rocking strains, and energy partitions) of a half-space saturated with inviscid fluid subjected to obliquely incident P₁- or SV-wave in the case of free draining boundary, and he also adopted the linear porosity-modulus relation. Unlike Lin et al. [20], Rjoub [21, 22] presented the dynamic response (same as Lin et al., but without surface displacement) of a half-space saturated with viscous fluid, considering the oblique incidence of P₁- and SV-waves. Tajuddin and Hussaini [23] studied the reflection of body waves at free permeable and impermeable boundaries and rigid permeable and impermeable boundaries. Xia et al. [24] developed the secular equation of the Rayleigh surface wave and discussed its dispersion characteristic in a poroelastic half-space. You [25] discussed the free-surface motion caused by incident P₁- or SV- wave in drained or undrained boundary conditions based on the exact dynamic-stiffness matrix of half-space. Nie and Xu [26] deduced the wave field solutions by using the Wave Based Method and the boundary conditions (i.e., permeable and impermeable conditions) of saturated half-space when incident P- and SV-waves, and they also showed the effects of permeability coefficient, angle, and frequency on them. Yang [27] introduced the concept of homogeneous pore fluid into Biot’s theory to analyze the saturation effects of subsoil on ground motions when an inclined SV-wave incident on the free surface of a partially saturated half-space. Later, based on governing equations of a three-phase medium, Chen [28] explained that a special wave mode conversion occurred when the fast P₁-wave incident at a certain angle on the nearly saturated soil. Zhou [29] investigated the dynamic response of P₁- and SV- waves incident at the interface of partially saturated soil and discussed the effects of boundary conditions, water saturation, frequency, Poisson’s ratio, and modulus ratio (i.e., shear modulus of soil frame to bulk modulus of fluid) on it. Xue et al. [30] explored the phenomenon of wave mode conversion for a P₁-wave incident on the surface of a partially saturated half-space, and the critical saturation degree and angle of wave mode conversion were found for a specific nearly saturated soil. Afterward, wave propagation in the semi-infinite space was further enriched to the reflection and refraction of waves at different interfaces [31–37] and extended to wave propagation in the distinct media [38–43].

Since Chinese scholar Men proposed the soil mechanics model, quite a few researchers have also used it to study the wave propagation characteristics in a two-phase medium from theoretical [44–50] and practical views [51–54]. Among them, it is worth mentioning that Chen and Men [52] and Cui [51] presented a new method to understand the mechanism of soil liquefaction. Chen [44] and Chen et al. [45] analyzed the near-field wave motions combing the transmitting boundary. Recently, Xiao et al. [49] investigated the propagation and attenuation characteristics of Rayleigh waves in ocean sites. A preliminary analysis of the wave propagation characteristics in the infinite saturated medium based on the model of soil mechanics has been conducted by Zhang et al. [50]. The results showed that the frequency and soil properties may have a significant influence on the velocity and attenuation coefficient of the three body waves. For this reason, these parameters are bound to affect the reflection of each wave incident upon a free plane boundary.

Among the existing literature, the velocity of plane P₁-wave is the fastest, and the attenuation of it is slow in the saturated infinite space. Therefore, it is of great interest to study the propagation characteristic of P₁-wave under different boundary conditions in a fluid-saturated half-space. However, it is rare to use the model of soil mechanics to study the propagation of elastic waves in the semi-infinite field. As mentioned above, the model of soil mechanics is introduced to discuss the reflection of P₁-wave on the free surface of saturated two-phase media in this paper. By Fortran software, numerical analysis is conducted to study the effects of boundary drainage, wave frequency, porosity, Poisson’s ratio, and modulus ratio on the displacement reflection coefficients and surface displacements.

2 The propagation theory of elastic wave based on the model of soil mechanics

2.1 The equations of motion

The model of soil mechanics for a fluid-saturated medium in which the liquid phase is assumed to be ideal, the solid phase is isotropic elastic, and the compression modulus of solid particles in point contact tends to infinity, can be expressed as [12, 44, 49, 50].

$\left\{\begin{array}{l}\mu \Delta \mathit{u}+\left(\lambda +\mu \right)\nabla \left(\nabla ·\mathit{u}\right)+\left(1-n\right)\nabla p_f+\left[B\right]\left(\dot{\mathit{U}}-\dot{\mathit{u}}\right)={\rho }_1\ddot{\mathit{u}}\\ n\nabla p_f-\left[B\right]\left(\dot{\mathit{U}}-\dot{\mathit{u}}\right)={\rho }_2\ddot{\mathit{U}}\\ \left(1-n\right)\nabla ·\mathit{u}+n\nabla ·\mathit{U}-\frac{n}{E_{\mathrm{w}}}{p}_f=0\end{array}\right.(1)$

Where, $\Delta$ (=${\nabla }^2$) is the Laplace operator in the Cartesian Coordinate, $\nabla$ is the Hamiltonian operator. $\mathit{u}$, $\dot{\mathit{u}}$, and $\ddot{\mathit{u}}$ denote the solid phase’s displacement, velocity, and acceleration vector, respectively. $\mathit{U}$, $\dot{\mathit{U}}$ and $\ddot{\mathit{U}}$ represent the absolute displacement, velocity, and acceleration vector of the liquid phase separately. $\lambda$ and $\mu$ are the classical Lame constants, which are functions of the Poisson’s ratio υ and the elastic modulus of the solid phase E, $\lambda$ = $E\upsilon /\left(\left(1+\upsilon \right)\left(1-2\upsilon \right)\right)$ and $\mu$ = $E/2\left(1+\upsilon \right)$. n is the porosity. ${\rho }_1$ and ${\rho }_2$ are defined to describe the solid and liquid density per unit volume, in which ${\rho }_1$ = $\left(1-n\right){\rho }_{\mathrm{s}}$ and ${\rho }_2$ = $n{\rho }_{\mathrm{w}}$, ${\rho }_{\mathrm{s}}$ and ${\rho }_{\mathrm{w}}$ are the solid and fluid mass densities separately. $p_f$ is the true pore pressure. $E_{\mathrm{w}}$ refers to the bulk modulus of liquid. k (=$K/{\rho }_{\mathrm{w}}g$) is the dynamic permeability coefficient of the solid skeleton, in which K (m/s) is the permeability coefficient that satisfies Darcy’s law, and g is the gravitation acceleration. $\left[B\right]$ represents the dissipation coefficient, which is a third-order diagonal matrix. $\left[B\right]$ = $diag\left(b_x,b_y,b_z\right)$, and $b_x$ = $b_y$ = $b_z$ = $n^2/k$ in the isotropic medium.

2.2 Solutions of the equations

Considering Helmholtz’s resolution, we introduce scalar potential functions (${\varphi }_{\mathrm{s}}$, ${\varphi }_{\mathrm{w}}$) and vector potential functions (${\mathit{\psi }}_{\mathbf{s}}$, ${\mathit{\psi }}_{\mathbf{w}}$) to describe the displacements of solid- and liquid-phase, which can be written as follows [11, 50, 55].

$\left\{\begin{array}{l}\mathit{u}=\nabla {\varphi }_{\mathrm{s}}+\nabla \times {\mathit{\psi }}_{\mathrm{s}}\\ \mathit{U}=\nabla {\varphi }_{\mathrm{w}}+\nabla \times {\mathit{\psi }}_{\mathrm{w}}\end{array}\right.(2)$

Insertion of Equation 2 in Equation 1 yields the wave equation expressed by potential function, as can be shown in the following form [50].

$\left\{\begin{array}{l}{\rho }_1{\ddot{\varphi }}_{\mathrm{s}}-\left(\lambda +2\mu \right)\Delta {\varphi }_{\mathrm{s}}=p_f-{\rho }_2{\ddot{\varphi }}_{\mathrm{w}}\\ {\rho }_1{\ddot{\mathit{\psi }}}_{\mathrm{s}}-\mu \Delta {\mathit{\psi }}_{\mathrm{s}}=-{\rho }_2{\ddot{\mathit{\psi }}}_{\mathrm{w}}\\ n{p}_f-\left[B\right]\left({\dot{\varphi }}_{\mathrm{w}}-{\dot{\varphi }}_{\mathrm{s}}\right)-{\rho }_2{\ddot{\varphi }}_{\mathrm{w}}=0\\ {\rho }_2{\ddot{\mathit{\psi }}}_{\mathrm{w}}+\left[B\right]\left({\dot{\mathit{\psi }}}_{\mathrm{w}}-{\dot{\mathit{\psi }}}_{\mathrm{s}}\right)=0\\ \left(1-n\right)\Delta {\varphi }_{\mathrm{s}}+n\Delta {\varphi }_{\mathrm{w}}-\frac{n}{E_{\mathrm{w}}}{p}_f=0\end{array}\right.(3)$

The in-plane wave problem in a fluid-saturated medium is a P-SV wave problem in the xoz plane. Assuming the displacements $\mathit{u}$ and $\mathit{U}$ are independent of the coordinate y. The scalar potential functions ${\varphi }_{\mathrm{s}}$ = ${\varphi }_{\mathrm{s}}\left(x,z,t\right)$, and ${\varphi }_{\mathrm{w}}$ = ${\varphi }_{\mathrm{w}}\left(x,z,t\right)$ in the xoz plane. The vector potential functions ${\mathit{\psi }}_{\mathbf{s}}$ =(0, ${\psi }_{\mathrm{s}}\left(x,z,t\right)$,0), and ${\mathit{\psi }}_{\mathbf{w}}$ =(0, ${\psi }_{\mathrm{w}}\left(x,z,t\right)$,0). The components of solid-phase displacement ($u_x$, $u_z$) and the components of liquid-phase displacement ($U_x$, $U_z$) can be written in the form of potential functions, as shown in Equations 4a, 4b; [1, 20]. The potential function expressions of normal stress (${\sigma }_{zz}$) and shear stress (${\sigma }_{xz}$) are written in Equation 4c by the plane strain character. From the fifth of Equation 3, the potential function expression of pore fluid pressure ($p_f$) can be given by the third of Equation 4c.

$\left\{\begin{array}{l}{u}_x=\frac{\mathrm{\partial }{\varphi }_{\mathrm{s}}}{\mathrm{\partial }x}-\frac{\mathrm{\partial }{\psi }_{\mathrm{s}}}{\mathrm{\partial }z}\\ u_z=\frac{\mathrm{\partial }{\varphi }_{\mathrm{s}}}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{\psi }_{\mathrm{s}}}{\mathrm{\partial }x}\end{array}\right.(\mathrm{4a})$

$\left\{\begin{array}{l}{U}_x=\frac{\mathrm{\partial }{\varphi }_{\mathrm{w}}}{\mathrm{\partial }x}-\frac{\mathrm{\partial }{\psi }_{\mathrm{w}}}{\mathrm{\partial }z}\\ U_z=\frac{\mathrm{\partial }{\varphi }_{\mathrm{w}}}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{\psi }_{\mathrm{w}}}{\mathrm{\partial }x}\end{array}\right.(\mathrm{4b})$

$\left\{\begin{array}{l}{\sigma }_{zz}=\left(\lambda +\frac{1-n}{n}{E}_{\mathrm{w}}\right){\nabla }^2{\varphi }_{\mathrm{s}}+2\mu \left(\frac{{\mathrm{\partial }}^2{\varphi }_{\mathrm{s}}}{\mathrm{\partial }{z}^2}+\frac{{\mathrm{\partial }}^2{\psi }_{\mathrm{s}}}{\mathrm{\partial }x\mathrm{\partial }z}\right)+E_{\mathrm{w}}{\nabla }^2{\varphi }_{\mathrm{w}}\\ {\sigma }_{xz}=2\mu \frac{{\mathrm{\partial }}^2{\varphi }_{\mathrm{s}}}{\mathrm{\partial }x\mathrm{\partial }z}+\mu \left(\frac{{\mathrm{\partial }}^2{\psi }_{\mathrm{s}}}{\mathrm{\partial }{x}^2}-\frac{{\mathrm{\partial }}^2{\psi }_{\mathrm{s}}}{\mathrm{\partial }{z}^2}\right)\\ p_f=\frac{1-n}{n}{E}_{\mathrm{w}}{\nabla }^2{\varphi }_{\mathrm{s}}+E_{\mathrm{w}}{\nabla }^2{\varphi }_{\mathrm{w}}\end{array}\right.(\mathrm{4c})$

Assuming the plane harmonic wave solutions of the potential functions in the following forms [11].

$\left\{\begin{array}{l}{\varphi }_{\mathrm{s}}=A_{\mathrm{s}}{e}^{i\left(\omega t-{\mathit{k}}_{\mathbf{P}}·\mathit{r}\right)}\\ {\varphi }_{\mathrm{w}}=A_{\mathrm{w}}{e}^{i\left(\omega t-{\mathit{k}}_{\mathbf{P}}·\mathit{r}\right)}\\ {\psi }_{\mathrm{s}}=B_{\mathrm{s}}{e}^{i\left(\omega t-{\mathit{k}}_{\mathbf{S}}·\mathit{r}\right)}\\ {\psi }_{\mathrm{w}}=B_{\mathrm{w}}{e}^{i\left(\omega t-{\mathit{k}}_{\mathbf{S}}·\mathit{r}\right)}\end{array}\right.(5)$

Where, $A_{\mathrm{s}}$ and $A_{\mathrm{w}}$ are the potential function amplitudes of solid- and liquid-phases for P-wave, respectively. $B_{\mathrm{s}}$ and $B_{\mathrm{w}}$ represent the potential function amplitudes of solid- and liquid-phases for S-wave separately. ${\mathit{k}}_{\mathbf{P}}$ and ${\mathit{k}}_{\mathbf{S}}$ denote the propagation directions of P- and S-waves (wave vector). $k_{\mathrm{P}}$ and $k_{\mathrm{S}}$ are the values of vectors (${\mathit{k}}_{\mathbf{P}}$ and ${\mathit{k}}_{\mathbf{S}}$), with $k_{\mathrm{P}}$ and $k_{\mathrm{S}}$ representing the wave numbers of P- and S-waves, respectively. $\mathit{r}$ denotes the position vector. $i$ = $\sqrt{-1}$. ω is the circular frequency of a wave.

Substituting Equation 5 into Equation 3, we can obtain the dispersion equations of P- and S-waves.

$\begin{array}{ll}\hfill & \frac{\left(\lambda +2\mu \right)n{E}_{\mathrm{w}}}{{\rho }_1{\rho }_2}{\left(\frac{k_{\mathrm{P}}}{\omega }\right)}^4-\left\{\left(\frac{\lambda +2\mu }{{\rho }_1}+\frac{n{E}_{\mathrm{w}}}{{\rho }_2}+\frac{{\left(1-n\right)}^2{E}_{\mathrm{w}}}{n{\rho }_1}\right)\right.\hfill \\ \hfill & \left.-\frac{ib}{\omega {\rho }_1{\rho }_2}\left(\lambda +2\mu +\frac{E_{\mathrm{w}}}{n}\right)\right\}{\left(\frac{k_{\mathrm{P}}}{\omega }\right)}^2+1-\frac{ib}{\omega }\left(\frac{1}{{\rho }_1}+\frac{1}{{\rho }_2}\right)=0\hfill \end{array}(\mathrm{6a})$

$\left(\frac{ib\mu }{\omega {\rho }_1{\rho }_2}-\frac{\mu }{{\rho }_1}\right){\left(\frac{k_{\mathrm{S}}}{\omega }\right)}^2+1-\frac{ib}{\omega }\left(\frac{1}{{\rho }_1}+\frac{1}{{\rho }_2}\right)=0(\mathrm{6b})$

It can be seen from Equations 6a, 6b that the velocities and attenuation coefficients for two kinds of compressional waves (P₁- and P₂- waves) and one shear wave (S- wave) in an unbounded saturated medium are calculated. All three body waves are dispersed and attenuated, which are related to the properties of medium and wave frequency.

3 Reflection of P₁-wave in a semi-infinite saturated medium

The obliquely incident P₁-wave at the free surface of a semi-infinite saturated medium is a free field problem and also an important part of the site response analysis. In this case, the stresses on the free surface are zero. The upper medium is air without density, and the lower medium is saturated soil. We now introduce a rectangular coordinate system, with x as the horizontal axis and z as the vertical axis. The z-axis points downward vertically, which is directed into the interior of the two-phase medium. The half-space is bounded by a horizontal plane (z = 0). The plane P₁-wave with angular frequency ω is incident from the bottom to the free surface at an angle θ_IP. Then the reflected P₁-, P₂-, and SV-waves are generated in the saturated medium (i.e., z > 0), whose angles of reflection are θ_R1, θ_R2, and θ_RS. All the reflected waves travel at the incident wave frequency (ω). The geometry considered in this paper is shown in Figure 1.

Figure 1

Figure 1. Fluid-saturated half-space subjected to an incident P₁-wave.

According to Snell’s law, the relations between the angles of the reflected and incident waves are given by [55, 56].

$\frac{V_{\mathrm{P}1}}{\sin {\theta }_{\text{IP}}}=\frac{V_{\mathrm{P}1}}{\sin {\theta }_{\mathrm{R}1}}=\frac{V_{\mathrm{P}2}}{\sin {\theta }_{\mathrm{R}2}}=\frac{V_{\mathrm{S}}}{\sin {\theta }_{\text{RS}}}(7)$

Where, V_P1, V_P2, and V_S are the wave velocities. As is shown in Equation 7, the reflection angles of each reflected wave can be determined when the wave velocity and incident angle are known. Moreover, the reflection angle (θ_R1) of the P₁ wave is the same as its incident angle (θ_IP).

3.1 Potential functions of elastic wave

In the two-phase medium (i.e., the half-space z > 0), the incident P₁-wave gives rise to reflected waves of all three types, i.e., P₁-, P₂-, and SV- waves. The expressions for solid- and liquid-phases potential functions of P-wave (${\varphi }_{\mathrm{s}}$, ${\varphi }_{\mathrm{w}}$) and SV-wave (${\psi }_{\mathrm{s}}$, ${\psi }_{\mathrm{w}}$) are shown in Equation 8; [27]. The plane harmonic solutions of potential functions for different waves are shown in Equations 9a-9d; [27].

$\left\{\begin{array}{l}{\varphi }_{\mathrm{s}}={\varphi }_{\mathrm{s}1}^{\mathrm{I}}+{\varphi }_{\mathrm{s}1}^{\mathrm{R}}+{\varphi }_{\mathrm{s}2}^{\mathrm{R}}\\ {\varphi }_{\mathrm{w}}={\varphi }_{\mathrm{w}1}^{\mathrm{I}}+{\varphi }_{\mathrm{w}1}^{\mathrm{R}}+{\varphi }_{\mathrm{w}2}^{\mathrm{R}}\\ {\psi }_{\mathrm{s}}={\psi }_{\mathrm{s}}^{\mathrm{R}}\\ {\psi }_{\mathrm{w}}={\psi }_{\mathrm{w}}^{\mathrm{R}}\end{array}\right.(8)$

$\left\{\begin{array}{l}{\varphi }_{\mathrm{s}1}^{\mathrm{I}}=A_{\mathrm{s}1}^{\mathrm{I}}\exp \left[i\left(\omega t-k_{1x}^{\mathrm{I}}x+k_{1z}^{\mathrm{I}}z\right)\right]\\ {\varphi }_{\mathrm{w}1}^{\mathrm{I}}=A_{\mathrm{w}1}^{\mathrm{I}}\exp \left[i\left(\omega t-k_{1x}^{\mathrm{I}}x+k_{1z}^{\mathrm{I}}z\right)\right]\end{array}\right.(\mathrm{9a})$

$\left\{\begin{array}{l}{\varphi }_{\mathrm{s}1}^{\mathrm{R}}=A_{\mathrm{s}1}^{\mathrm{R}}\exp \left[i\left(\omega t-k_{1x}^{\mathrm{R}}x-k_{1z}^{\mathrm{R}}z\right)\right]\\ {\varphi }_{\mathrm{w}1}^{\mathrm{R}}=A_{\mathrm{w}1}^{\mathrm{R}}\exp \left[i\left(\omega t-k_{1x}^{\mathrm{R}}x-k_{1z}^{\mathrm{R}}z\right)\right]\end{array}\right.(\mathrm{9b})$

$\left\{\begin{array}{l}{\varphi }_{\mathrm{s}2}^{\mathrm{R}}=A_{\mathrm{s}2}^{\mathrm{R}}\exp \left[i\left(\omega t-k_{2x}^{\mathrm{R}}x-k_{2z}^{\mathrm{R}}z\right)\right]\\ {\varphi }_{\mathrm{w}2}^{\mathrm{R}}=A_{\mathrm{w}2}^{\mathrm{R}}\exp \left[i\left(\omega t-k_{2x}^{\mathrm{R}}x-k_{2z}^{\mathrm{R}}z\right)\right]\end{array}\right.(\mathrm{9c})$

$\left\{\begin{array}{l}{\psi }_{\mathrm{s}}^{\mathrm{R}}=B_{\mathrm{s}}^{\mathrm{R}}\exp \left[i\left(\omega t-k_{\mathrm{s}x}^{\mathrm{R}}x-k_{\mathrm{s}z}^{\mathrm{R}}z\right)\right]\\ {\psi }_{\mathrm{w}}^{\mathrm{R}}=B_{\mathrm{w}}^{\mathrm{R}}\exp \left[i\left(\omega t-k_{\mathrm{s}x}^{\mathrm{R}}x-k_{\mathrm{s}x}^{\mathrm{R}}z\right)\right]\end{array}\right.(\mathrm{9d})$

Where, ${\varphi }_{\mathrm{s}1}^{\mathrm{I}}$ (${\varphi }_{\mathrm{w}1}^{\mathrm{I}}$) is a potential function in the solid (liquid) of incident P₁-wave. $A_{\mathrm{s}1}^{\mathrm{I}}$ and $A_{\mathrm{w}1}^{\mathrm{I}}$ are the amplitudes of the corresponding potential functions. Similarly, ${\varphi }_{\mathrm{s}1}^{\mathrm{R}}$, ${\varphi }_{\mathrm{s}2}^{\mathrm{R}}$, and ${\psi }_{\mathrm{s}}^{\mathrm{R}}$ are the solid-phase potential functions of the reflected P₁-, P₂-, and SV-waves, respectively. $A_{\mathrm{s}1}^{\mathrm{R}}$, $A_{\mathrm{s}2}^{\mathrm{R}}$ and $B_{\mathrm{s}}^{\mathrm{R}}$ correspond to the solid-phase potential amplitudes. ${\varphi }_{\mathrm{w}1}^{\mathrm{R}}$, ${\varphi }_{\mathrm{w}2}^{\mathrm{R}}$ and ${\psi }_{\mathrm{w}}^{\mathrm{R}}$ denote the liquid-phase potential functions of the reflected P₁-, P₂-, and SV-waves, separately. $A_{\mathrm{w}1}^{\mathrm{R}}$, $A_{\mathrm{w}2}^{\mathrm{R}}$ and $B_{\mathrm{w}}^{\mathrm{R}}$ are the liquid-phase potential amplitudes. $k_{1x}^{\mathrm{I}}$ and $k_{1z}^{\mathrm{I}}$ represent the components of the incident P₁-wave vector in the x and z directions. $k_{1x}^{\mathrm{R}}$ and $k_{1z}^{\mathrm{R}}$ are the components of the reflected P₁-wave vector in the x and z directions. Similarly, $k_{2x}^{\mathrm{R}}$, $k_{2z}^{\mathrm{R}}$, $k_{\mathrm{s}x}^{\mathrm{R}}$ and $k_{\mathrm{s}z}^{\mathrm{R}}$ are the components of the reflected P₂- and SV- wave vectors of the corresponding directions.

Following the geometric relationship of wave vectors, it can be seen that the wave vectors and their components of all waves satisfy the equalities Equation 10. Moreover, by Snell’s law, the x-components of the wave numbers for the incident and reflected waves are the same, as shown in Equation 11; [55, 56].

$\left\{\begin{array}{l}{\left(k_{1x}^{\mathrm{I}}\right)}^2+{\left(k_{1z}^{\mathrm{I}}\right)}^2={\left(k_1^{\mathrm{I}}\right)}^2\\ {\left(k_{1x}^{\mathrm{R}}\right)}^2+{\left(k_{1z}^{\mathrm{R}}\right)}^2={\left(k_1^{\mathrm{R}}\right)}^2\\ {\left(k_{2x}^{\mathrm{R}}\right)}^2+{\left(k_{2z}^{\mathrm{R}}\right)}^2={\left(k_2^{\mathrm{R}}\right)}^2\\ {\left(k_{\mathrm{s}x}^{\mathrm{R}}\right)}^2+{\left(k_{\mathrm{s}z}^{\mathrm{R}}\right)}^2={\left(k_{\mathrm{s}}^{\mathrm{R}}\right)}^2\end{array}\right.(10)$

$k_{1x}^{\mathrm{I}}=k_{1x}^{\mathrm{R}}=k_{2x}^{\mathrm{R}}=k_{\mathrm{s}x}^{\mathrm{R}}(11)$

From Equations 6a, 6b, the relations between the various amplitudes in Equations 9 can be obtained as follows.

${\delta }_1=\frac{A_{\mathrm{w}1}^{\beta }}{A_{\mathrm{s}1}^{\beta }}=\frac{\left(\lambda +2\mu +\frac{1-n}{n}{E}_{\mathrm{w}}\right){\left(k_1^{\beta }\right)}^2-{\rho }_1{\omega }^2}{{\rho }_2{\omega }^2-E_{\mathrm{w}}{\left(k_1^{\beta }\right)}^2},\beta =\mathrm{I},\mathrm{R}(\mathrm{12a})$

${\delta }_2=\frac{A_{\mathrm{w}2}^{\mathrm{R}}}{A_{\mathrm{s}2}^{\mathrm{R}}}=\frac{\left(\lambda +2\mu +\frac{1-n}{n}{E}_{\mathrm{w}}\right){\left(k_2^{\mathrm{R}}\right)}^2-{\rho }_1{\omega }^2}{{\rho }_2{\omega }^2-E_{\mathrm{w}}{\left(k_2^{\mathrm{R}}\right)}^2}(\mathrm{12b})$

${\delta }_{\mathrm{s}}=\frac{B_{\mathrm{w}}^{\mathrm{R}}}{B_{\mathrm{s}}^{\mathrm{R}}}=\frac{\mu {\left(k_{\mathrm{s}}^{\mathrm{R}}\right)}^2-{\rho }_1{\omega }^2}{{\rho }_2{\omega }^2}(\mathrm{12c})$

Where, δ₁, δ₂, and δ_s are the amplitude ratios of potentials related to liquid and solid phases for P₁-, P₂-, and SV-waves, respectively.

3.2 Boundary conditions and solutions

3.2.1 Boundary conditions of the free surface

When P₁-wave is obliquely incident on the free surface of the saturated medium, the boundary conditions can be completely permeable or impermeable, i.e., (a) Open-pore boundary and (b) Sealed-pore boundary [15, 57]. In case (a), the pore fluid can flow freely, so the normal and shear stresses of the soil skeleton and the pore pressure are zeros. Under condition (b), the pore fluid is enclosed in a porous medium, so the normal and shear stresses of the soil skeleton and the displacement of solid related to liquid are zeros. Then, the drained and undrained conditions can be expressed as [17].

$\left\{\begin{array}{l}{\sigma }_{ij\left|z=0^{+}\right.}=0\\ p_{f\left|z=0^{+}\right.}=0\end{array}\right.(\mathrm{13a})$

$\left\{\begin{array}{l}{\sigma }_{ij\left|z=0^{+}\right.}=0\\ u_{z\left|z=0^{+}\right.}-U_{z\left|z=0^{+}\right.}=0\end{array}\right.(\mathrm{13b})$

In which the subscripts (i, j = x, z) represent the components in both x and z directions. ${\sigma }_{ij\left|z=0^{+}\right.}$ denotes the total stress of a saturated two-phase medium. $p_{f\left|z=0^{+}\right.}$ is the pore pressure of the boundary.

On inserting Equations 4a–4c, together with Equation 12a, 12b, 12c, into Equations 13a, 13b, and taking account of Equation 10 and Equation 11, we find the analytical formulas of amplitude ratios under permeable and impermeable boundaries, i.e., $A_{\mathrm{s}1}^{\mathrm{R}}/A_{\mathrm{s}1}^{\mathrm{I}}$, $A_{\mathrm{s}2}^{\mathrm{R}}/A_{\mathrm{s}1}^{\mathrm{I}}$, and $B_{\mathrm{s}}^{\mathrm{R}}/A_{\mathrm{s}1}^{\mathrm{I}}$. The formulas in the form of the matrix are through

${\left[S_{\mathrm{P}-\text{SV}}\right]}_f{\left\{A_{\mathrm{s}1}^{\mathrm{R}},A_{\mathrm{s}2}^{\mathrm{R}},B_{\mathrm{s}}^{\mathrm{R}}\right\}}^{\mathrm{T}}={\left\{F\right\}}^{\mathrm{T}}{A}_{\mathrm{s}1}^{\mathrm{I}}(\mathrm{14a})$

${\left[{\overline{S}}_{\mathrm{P}-\text{SV}}\right]}_f{\left\{A_{\mathrm{s}1}^{\mathrm{R}},A_{\mathrm{s}2}^{\mathrm{R}},B_{\mathrm{s}}^{\mathrm{R}}\right\}}^{\mathrm{T}}={\left\{\overline{F}\right\}}^{\mathrm{T}}{A}_{\mathrm{s}1}^{\mathrm{I}}(\mathrm{14b})$

Where, the superscript $\overline{}$ denotes the impermeable boundary. $\left\{F\right\}$ and $\left\{\overline{F}\right\}$ are the matrixes related to the incident P₁-wave. ${\left[S_{\mathrm{P}-\text{SV}}\right]}_f$ and ${\left[{\overline{S}}_{\mathrm{P}-\text{SV}}\right]}_f$ are the 3-order matrixes corresponding to the reflected waves. The elements of $\left\{F\right\}$, $\left\{\overline{F}\right\}$, ${\left[S_{\mathrm{P}-\text{SV}}\right]}_f$, and ${\left[{\overline{S}}_{\mathrm{P}-\text{SV}}\right]}_f$ are given in the Appendix.

3.2.2 Surface response of saturated half-space

Without loss of generality, we assume the potential function amplitude of the incident wave equals unity, i.e., $A_{\mathrm{s}1}^{\mathrm{I}}$ = 1 [1]. Substituting Equations 11, 12a–c into Equations 14a, b, we can obtain the potential function amplitudes of the reflected waves $A_{\mathrm{s}1}^{\mathrm{R}}$, $A_{\mathrm{s}2}^{\mathrm{R}}$, and $B_{\mathrm{s}}^{\mathrm{R}}$ (i.e., the amplitude reflection coefficients of P₁-, P₂-, and SV-waves). Then inserting $A_{\mathrm{s}1}^{\mathrm{R}}$, $A_{\mathrm{s}2}^{\mathrm{R}}$, and $B_{\mathrm{s}}^{\mathrm{R}}$ into Equation 4a, the solid-phase displacement reflection coefficients of each reflected wave are given through the expressions

$\left\{\begin{array}{l}{R}_{\mathrm{s}1}^{\mathrm{R}}=A_{\mathrm{s}1}^{\mathrm{R}}\\ R_{\mathrm{s}2}^{\mathrm{R}}=\frac{k_2^{\mathrm{R}}}{k_1^{\mathrm{I}}}{A}_{\mathrm{s}2}^{\mathrm{R}}\\ R_{\text{ss}}^{\mathrm{R}}=\frac{k_{\mathrm{s}}^{\mathrm{R}}}{k_1^{\mathrm{I}}}{B}_{\mathrm{s}}^{\mathrm{R}}\end{array}\right.(15)$

Where, $R_{\mathrm{s}1}^{\mathrm{R}}$, $R_{\mathrm{s}2}^{\mathrm{R}}$, and $R_{\text{ss}}^{\mathrm{R}}$ are employed to denote the displacement reflection coefficients of P₁-, P₂-, and SV-waves in the solid phase, respectively.

Insertion of Equations 8, 9 in Equation 4a yields the surface displacement components (e.g., the horizontal and vertical displacements u_x and u_z) of the solid phase corresponding to the sum of one incident and three reflected waves may be written

$\left\{\begin{array}{l}{u}_x=k_{1x}^{\mathrm{I}}{A}_{\mathrm{s}1}^{\mathrm{I}}+k_{1x}^{\mathrm{R}}{A}_{\mathrm{s}1}^{\mathrm{R}}+k_{2x}^{\mathrm{R}}{A}_{\mathrm{s}2}^{\mathrm{R}}-k_{\mathrm{s}z}^{\mathrm{R}}{B}_{\mathrm{s}}^{\mathrm{R}}\\ u_z=-k_{1z}^{\mathrm{I}}{A}_{\mathrm{s}1}^{\mathrm{I}}+k_{1z}^{\mathrm{R}}{A}_{\mathrm{s}1}^{\mathrm{R}}+k_{2z}^{\mathrm{R}}{A}_{\mathrm{s}2}^{\mathrm{R}}+k_{\mathrm{s}x}^{\mathrm{R}}{B}_{\mathrm{s}}^{\mathrm{R}}\end{array}\right.(16)$

4 Degenerate validation of solutions

4.1 Validation of degenerate formulas

Let the liquid density ${\rho }_{\mathrm{w}}$ = 0, and the bulk modulus of liquid $E_{\mathrm{w}}$ = 0. Then, the solution in this paper can degenerate into the case of a P-wave incident on the free interface of a single-phase medium. Now, the potential amplitude ratios of the liquid-solid phase in the two-phase medium ${\delta }_1$ = 0, ${\delta }_2$ = 0, and ${\delta }_{\mathrm{s}}$ = 0. And the wave vector of the reflected P₁-wave is the same as that of the P₂-wave, i.e., $k_1^{\mathrm{R}}$ = $k_2^{\mathrm{R}}$, $k_{1z}^{\mathrm{R}}$ = $k_{2z}^{\mathrm{R}}$. When the two-phase medium is reduced to a single-phase medium, the velocity of P-wave $V_{\mathrm{P}}$ = $\sqrt{\left(\lambda +2\mu \right)/{\rho }_{\mathrm{s}}}$, the velocity of SV-wave $V_{\mathrm{S}}$ = $\sqrt{\mu /{\rho }_{\mathrm{s}}}$, which can be derived from the dispersion Equations 6a, 6b. The potential amplitude of the reflected P-wave $A_{\mathrm{s}}^{\mathrm{R}}$ = $A_{\mathrm{s}1}^{\mathrm{R}}$ + $A_{\mathrm{s}2}^{\mathrm{R}}$. Accordingly, Equation 14a, 14b can be simplified as

$\left\{\begin{array}{l}\mu \left(\frac{V_{\mathrm{P}}^2}{V_{\mathrm{S}}^2}{\left(k_1^{\mathrm{I}}\right)}^2-2{\left(k_{1x}^{\mathrm{I}}\right)}^2\right)\left(A_{\mathrm{s}}^{\mathrm{I}}+A_{\mathrm{s}}^{\mathrm{R}}\right)+2\mu k_{\mathrm{s}x}^{\mathrm{R}}{k}_{\mathrm{s}z}^{\mathrm{R}}{B}_{\mathrm{s}}^{\mathrm{R}}=0\\ 2\mu k_{1x}^{\mathrm{I}}{k}_{1z}^{\mathrm{I}}\left(A_{\mathrm{s}}^{\mathrm{R}}-A_{\mathrm{s}}^{\mathrm{I}}\right)+\mu \left({\left(k_{\mathrm{s}x}^{\mathrm{R}}\right)}^2-{\left(k_{\mathrm{s}z}^{\mathrm{R}}\right)}^2\right)B_{\mathrm{s}}^{\mathrm{R}}=0\end{array}\right.(17)$

Equation 17 is further simplified to obtain a new expression, which is the same as the Equations of a single-phase medium in Stein and Wysession [56]. It can be seen that the reflection of the P-wave on the free surface of a single-phase medium is a special case in this paper.

4.2 Validation of numerical analysis

To further verify the correctness of the formulas for reflection coefficient and surface displacement, Equation 17 is compared with the curve of P-wave incident on the free surface of a single-phase medium in Pujol [55]. The parameters for single-phase media are taken from Pujol [55], namely, $V_{\mathrm{P}}/V_{\mathrm{S}}$ = 1.732 and υ = 0.25. The variations of amplitude ratios and surface displacements with the incident angle are shown in Figure 2 when the P-wave is incident on the interface. It is noted that the displacement components u_x and u_z in Figure 2b are normalized by a factor $k_1^{\mathrm{I}}$, which represents the displacement intensity of the incident P-wave. If not specified, the surface displacements in the following figures are all normalized.

Figure 2

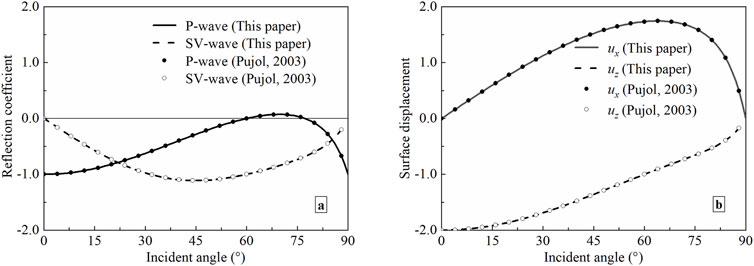
Figure 2. Surface response versus P-wave incident angle for an elastic half-space. (a) Amplitude reflection coefficient; (b) Surface displacement.

It can be seen from Figure 2 that the calculated results of Equation 17 are consistent with those of Pujol [55]. This is sufficient to demonstrate the correctness of the formula derived in this paper.

5 Numerical analysis

In this section, we use the formulas derived above to compute the displacement reflection coefficients and surface displacements when the plane P₁-wave is incident obliquely on the free boundary of a fluid-saturated half-space. Numerical examples are conducted in Fortran to explore the influence of boundary conditions, wave frequency, and characteristics of saturated soil materials (the porosity n, the Poisson’s ratio υ, the fluid bulk modulus to the stiffness of soil E_w/μ) on the surface response of saturated half-space. Some soil parameters of the two-phase medium used in the calculation are taken from Ref. [21] and listed as follows: ρ_s = 2650 kg.m^-3, ρ_w = 1000 kg.m^-3, E_w = 2.0 × 10⁹Pa, and k = 1.0 × 10^-7 m³.s/kg. The other soil parameters, i.e., the porosity n, the Poisson’s ratio υ, and the modulus ratio E_w/μ, will be given in the analysis of each section below.

Figure 3 through Figure 7 present the variations of the displacement reflection coefficients and surface displacements as described in Equations 15, 16 with incident angles under different conditions, i.e., boundary conditions, wave frequencies, porosities, Poisson’s, and modulus ratios. It can be seen that the displacement reflection coefficients and surface displacements vary smoothly with the incident angle of the P₁-wave. The displacement reflection coefficient of the P₂-wave is one order of magnitude smaller than those of the other reflected waves (P₁- and SV-waves). When the P₁-wave is at normal or grazing incidence, i.e., the incident angle equals zero or 90°, only the incident wave is reflected, and the reflected P₂- and SV-waves vanish. At this time, the displacement reflection coefficient of the reflected P₁-wave is −1.0, of which the phase is opposite to that of the incident P₁-wave. This is consistent with the reflection characteristics of compressive P-wave on the surface of an elastic medium [56]. Furthermore, when the incident P₁-wave strikes the interface perpendicularly, the surface displacements u_x = 0, u_z = −2.0. When the incident angle is 90°, the surface displacements u_x = 0.0, u_z = 0.0, which implies that the reflected P₁-wave annihilates the incident P₁-wave at the free surface. And the phase difference between u_x and u_z is 180° [51]. This holds for a single-phase medium as well [55]. In addition, with increasing incident angle, the vertical displacement u_z decreases, while the horizontal displacement u_x increases before reaching its peak value (near θ_IP = 60°) and has a reverse tendency thereafter.

Figure 3

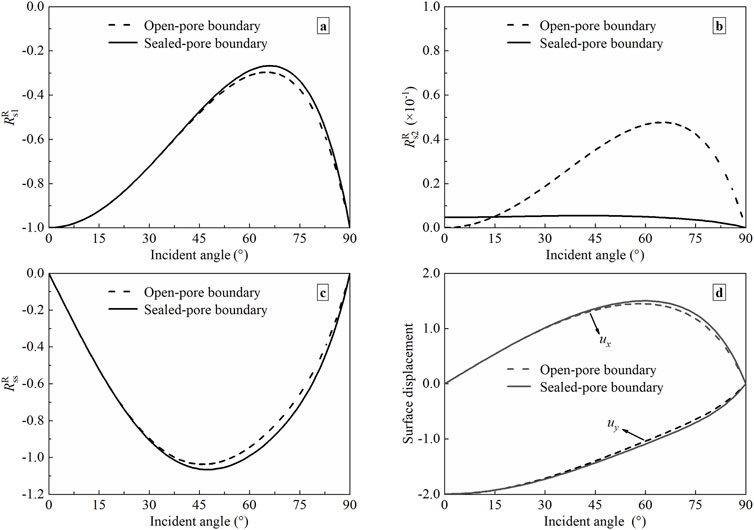
Figure 3. The displacement reflection coefficients and surface displacements versus incident angle with different permeable boundaries. (a) P₁-wave; (b) P₂-wave; (c) SV-wave; (d) Surface displacement.

5.1 Influence of boundary conditions

When P₁-wave propagates in a saturated half-space, specific solutions can be obtained using appropriate boundary conditions. The single control variable method is introduced to analyze the influence of boundary drainage on the surface response of half space. The values of the physical parameters of the saturated poroelastic half-space are selected from Section 5, and the other parameters are as follows: n = 0.1, υ = 0.2, and E_w/μ = 0.1. The frequency of incident wave f = 100 Hz. The curves in Figure 3 represent the displacement reflection coefficients and surface displacements with distinct boundaries.

It can be seen from Figure 3a that the displacement reflection coefficient of P₁-wave decreases with an increase in the incident angle before reaching its minimum value near 65ºunder different conditions. Moreover, when the incident angle θ_IP is greater than 36°, the displacement reflection coefficient under the impermeable interface is more than that of the permeable interface. Figure 3b shows that the displacement reflection coefficient of the P₂-wave is much less than those of other reflected P₁- and SV-waves, and the coefficient under a permeable interface is greater than that under an impermeable boundary. From Figure 3c, for the reflected SV-wave, the displacement reflection coefficient increases with a rise in the incident angle before attaining its maximum value near 45°. Also, the displacement reflection coefficient at an impermeable interface is more than that at a permeable interface if the θ_IP is within the range of 16º-90°. Given Figure 3d, u_x reaches its peak value at approximately 60°, while u_z reaches its peak value at 0°, and the peak value of u_z is larger than that of u_x. If θ_IP < 30°, the vertical and horizontal displacements (e.g., u_x and u_z) under two boundary conditions are the same. However, if θ_IP > 30°, both displacements u_x and u_z (absolute values) increase slightly under the impervious interface. Accordingly, the boundary conditions have a certain effect on the surface response of half-space, and this effect manifests a considerable dependence on the incident angle.

5.2 Influence of wave frequency

As analyzed in Refs. [2, 50], all three body waves are dispersive and attenuated, and the velocities and attenuation are frequency-dependent. To illustrate the effects of wave frequency on the reflection, four different values of wave frequency are considered in this paper, i.e., f = 1, 10, 100, and 1000 Hz. The four typical frequencies are within the common frequency range used in engineering and experimental testing [58]. The soil parameters remain invariable, as described in Section 5.1. The boundary is completely permeable. Figure 4 shows the variations of displacement coefficients and surface displacements with the incident angle for different frequencies.

Figure 4

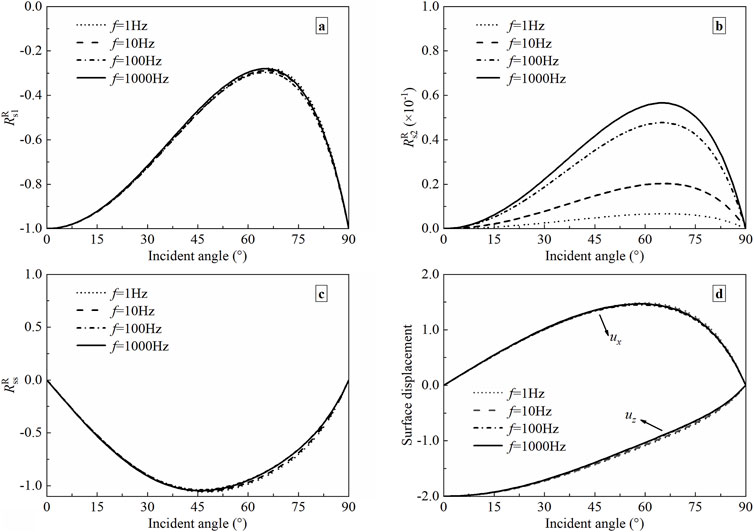
Figure 4. The displacement reflection coefficients and surface displacements versus incident angle with different frequencies. (a) P₁-wave; (b) P₂-wave; (c) SV-wave; (d) Surface displacement.

It is clear from Figure 4 that the surface response is not sensitive to wave frequency. However, the displacement reflection coefficient of P₂-wave decreases as the frequency is reduced. This result matches the case of Rjoub [21]. So, the frequency is assumed to be 100 Hz when analyzing the effect of soil parameters on surface response next.

5.3 Influence of porosity

Since porosity mainly affects the loose degree of soil, it is instructive to investigate the effect of porosity on the displacement reflection coefficients and surface displacements. Except for the porosity, the soil parameters remain invariable, as described in Section 5.1. The frequency of the incident plane P₁-wave is also taken to be 100 Hz. The boundary is completely permeable. The variations with the incident angle of displacement coefficients and surface displacements are shown in Figure 5 in the case that the porosity n = 0.1, 0.2, 0.3, and 0.4, respectively.

Figure 5

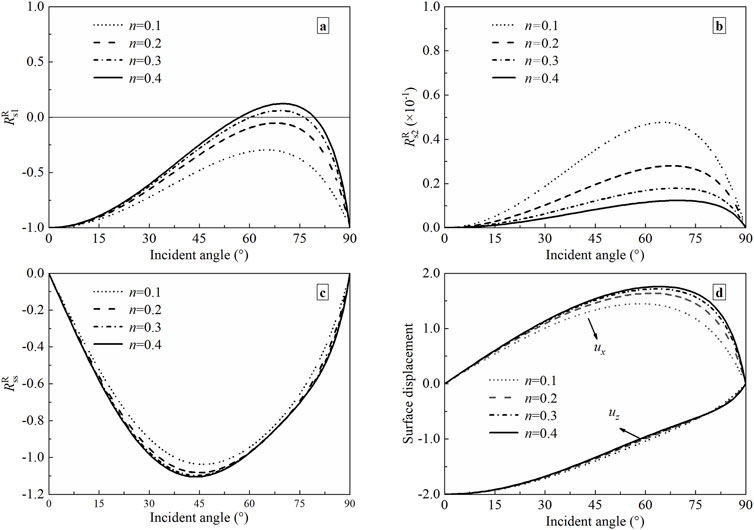
Figure 5. The displacement reflection coefficients and surface displacements versus incident angle with different porosities. (a) P₁-wave; (b) P₂-wave; (c) SV-wave; (d) Surface displacement.

It is shown in Figure 5a that the variations of displacement reflection coefficient for reflected P₁-wave with porosity are very complex. When the porosity n = 0.3 and 0.4, a special wave mode conversion occurs, namely, only P₂-and SV- waves are reflected, and the reflected P₁-wave is not generated. Under the case that n = 0.3, the displacement reflection coefficient of P₁-wave exhibits zero values at incident angles of 60° and 77°. The angles for incidence corresponding to wave mode conversion are 57ºand 79° with the instance that n = 0.4. If the porosity n = 0.1 and 0.2, this phenomenon disappears. Moreover, the displacement reflection coefficient for P₁-wave decreases with the increase of porosity when the incident angles θ_IP < 57ºor θ_IP > 79°. From Figures 5b, c, the displacement reflection coefficient for SV-wave (P₂-wave) increases (decreases) with the increase in porosity, and that for P₂-wave is the smallest of all three reflected waves as described in Section 5.1. It is noticed from Figure 5d that the horizontal displacement u_x increases with a rise in porosity. However, the porosity considered in this study has little impact on vertical displacement u_z. The effect of porosity on the surface response depends on the incident angle to a large extent.

5.4 Influence of Poisson’s ratio

The Poisson’s ratio mainly affects Lame constants (λ and μ), which reflect the consolidation status of the soil. To investigate the effects of Poisson’s ratio on the displacement reflection coefficients and surface displacements, the soil parameters remain constants as described in Section 5.1, except for Poisson’s ratio. The frequency of the incident plane P₁-wave f = 100 Hz. The boundary is completely permeable. Figure 6 shows the effects of Poisson’s ratio on the displacement reflection coefficients and surface displacements. In calculations, the Poisson’s ratio (υ) is taken to be 0.1, 0.2, 0.3, and 0.4.

Figure 6

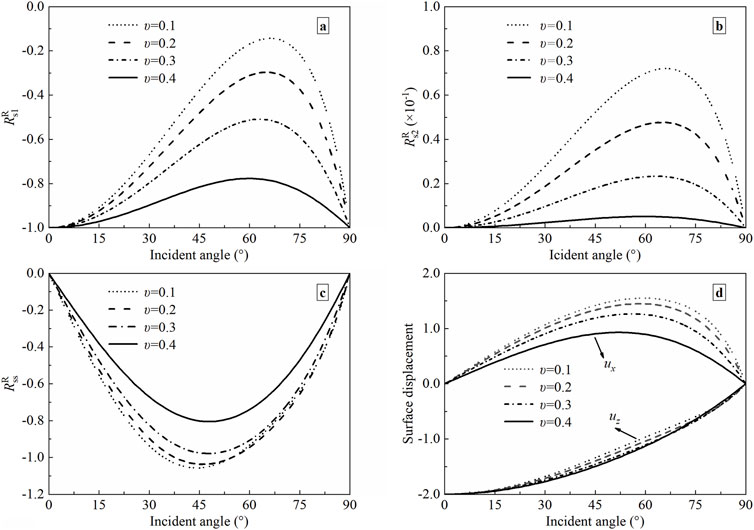
Figure 6. The displacement reflection coefficients and surface displacements versus incident angle with different Poisson’s ratios (a) P₁-wave; (b) P₂-wave; (c) SV-wave; (d) Surface displacement.

It can be found from Figures 6a–c that the displacement reflection coefficient of P₁-wave increases with the increasing Poisson’s ratio at the same incident angle, while those of P₂- and SV-waves diminish with a rise of Poisson’s ratio. For all three reflected waves, the amplitude of variation is related to the incident angle. As observed in Figure 6d, the horizontal displacement u_x (the vertical displacement u_z) decreases (increases) with the rise of Poisson’s ratio. When the Poisson’s ratio increases, the variation range of horizontal displacement is larger than that of vertical displacement, and the variation range depends on the incident angle.

5.5 Influence of modulus ratio

The modulus ratio mainly affects the stiffness of the soil layer in the saturated half-space. The larger the modulus ratio is, the softer the soil layer is. For this reason, there is a need to study the effects of the modulus ratio on the displacement reflection coefficients and surface displacements. Except for the modulus ratio, the soil parameters are taken according to Section 5.1. The frequency f of the incident plane P₁-wave is taken as 100 Hz. The boundary is completely permeable. The modulus ratio E_w/μ = 0.1, 1.0, 10, and 100. Figure 7 depicts the displacement reflection coefficients and surface displacements as a function of incident angle for the above four values of modulus ratio.

Figure 7

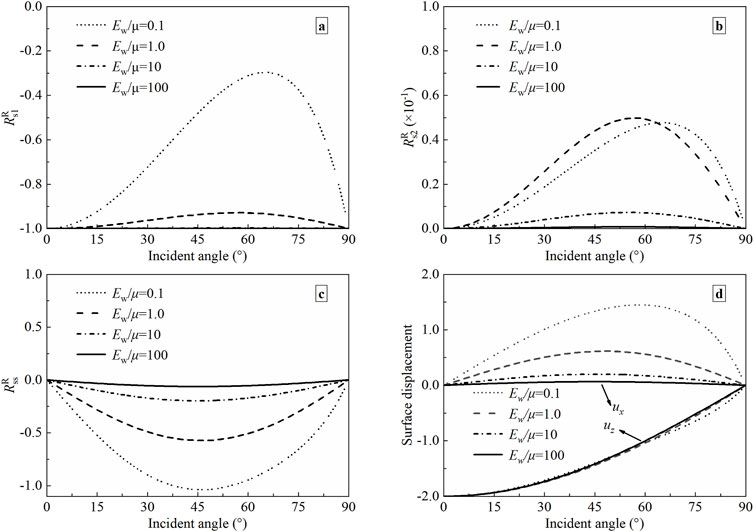
Figure 7. The displacement reflection coefficients and surface displacements versus incident angles with different modulus ratios (a) P₁-wave; (b) P₂-wave; (c) SV-wave; (d) Surface displacement.

It can be revealed from Figure 7 that the displacement reflection coefficients and surface displacements vary with the modulus ratio. As can be seen from Figures 7a–c, the displacement reflection coefficient of P₁-wave (P₂- or SV-wave) increases (decreases) with the increasing modulus ratio at the same incident angle. The variation amplitude is related to the incident angle. Moreover, when the modulus ratio E_w/μ = 100, the displacement reflection coefficient of P₁-wave increases towards −1.0, and that of SV-wave reduces to nearly 0, indicating that soft soil mainly transmits compression waves. All in all, the effect of incident angle on the reflection coefficients of P₂ and SV waves diminishes with the increase of the modulus ratio. Figure 7d shows us that the horizontal displacement u_x decreases with a rise in modulus ratio, while the vertical displacement u_z is less affected. For E_w/μ = 100, the peak displacement u_x decreases to 0.063. The extent of influence is decided by the incident angle.

6 Conclusion

Based on the soil mechanics model in a fluid-saturated medium, the dispersion equation of elastic waves is established. When the P₁-wave travels toward the free ground of a two-phase medium, the theoretical formulas of displacement reflection coefficient and surface displacement for all reflected waves are also obtained by combining the boundary conditions. Thereafter, the analytical expressions mentioned above degenerate to the reflection problem of a single-phase half-space to verify correctness. At last, when the boundary conditions, wave frequency, porosity, Poisson’s ratio, and modulus ratio are taken to be different values, the variation of the surface response of saturated half-space with the incident angle of P₁-wave is numerically analyzed. In light of the previous discussion, some main conclusions can be summarized as follows.

(1) The displacement reflection coefficient and surface displacement are angle-dependent. When the incident angle θ_IP equals 0ºor 90°, only reflected P₁-wave occurs.

(2) The boundary conditions have a certain effect on the surface response of half-space. The surface displacements in the impermeable interface are slightly larger than those in the permeable interface, and the magnitude of the increase is related to the incident angle.

(3) For all frequencies being considered, its influence on surface response is insignificant.

(4) The effect of material properties (i.e., porosity, Poisson’s ratio, and modulus ratio) on the surface response is discussed in detail. The wave mode conversion will occur when the porosity n = 0.3, 0.4. The displacement component u_x (u_z) decreases (increases) with a rise in Poisson’s ratio. The effect of the modulus ratio can not be ignored. The impacts of all soil parameters strongly depend on the incident angle.

In addition, the conclusions drawn in this paper not only theoretically reveal that more attention should be paid to the influence exerted by the incident angle of elastic waves in soil dynamics research but also have practical engineering significance for the commonly used seismic reflection wave method and well-logging data processing in the field of engineering seismic exploration.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BZ: Funding acquisition, Investigation, Methodology, Writing–original draft, Writing–review and editing. LQ: Project administration, Software, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research work was funded by the Science Research Project of Hebei Education Department, QN2025419, BZ.

Acknowledgments

The authors would like to thank the Science Research Project of Hebei Education Department (Grant No. QN2025419) for funding the work presented in this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wu S. Wave propagation in soils. Beijing: Science Press (1997). p. 62–89.

Google Scholar

2. Yang J, Wu S, Cai Y. Characteristics of propagation of elastic waves in saturated soils. J Vib Eng (1996)(02) 128–37.doi:10.16385/j.cnki.issn.1004-4523.1996.02.011

CrossRef Full Text | Google Scholar

3. Biot MA. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J Acoust Soc Am (1956) 28(2):168–78. doi:10.1121/1.1908239

CrossRef Full Text | Google Scholar

4. Biot MA. Theory of propagation of elastic waves in a fluid-saturated porous solid: II. Higher frequency range. J Acoust Soc Am (1956) 28(2):179–91. doi:10.1121/1.1908241

CrossRef Full Text | Google Scholar

5. Plona TJ. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies. Appl Phys Lett (1980) 36:259–61. doi:10.1063/1.91445

CrossRef Full Text | Google Scholar

6. Berryman JG. Confirmation of Biot’s theory. Appl Phys Lett (1980) 37:382–4. doi:10.1063/1.91951

CrossRef Full Text | Google Scholar

7. Zienkiewicz OC, Chang CT, Bettess P. Drained, undrained, consolidating and dynamic behaviour assumptions in soils. Geotechnique (1980) 30(4):385–95. doi:10.1680/geot.1980.30.4.385

CrossRef Full Text | Google Scholar

8. Zienkiewicz OC, Shiomi T. Dynamic behaviour of saturated porous media; the generalized Biot formulation and its numerical solution. Int J Numer Anal Met (1984) 8(1):71–96. doi:10.1002/nag.1610080106

CrossRef Full Text | Google Scholar

9. Men F. Wave propagation in a porous, saturated elastic medium. Acta Geophys Sinica (1965) 14(02):107–14. (in Chinese).

Google Scholar

10. Men F. Problems of wave propagation in porous fluid-saturated media. Acta Geophys Sinica (1981) 24(01):65–76. (in Chinese).

Google Scholar

11. Men F. Dissipation and dispersion of seismic waves in water-saturated strata. Acta Geophys Sinica (1984) 27(1):64–73. (in Chinese).

Google Scholar

12. Men F. On wave propagation in fluid-saturated porous media. Conf Soil Dyn Earthquake Eng (1982)(1) 225–38.

Google Scholar

13. Bowen RM, Reinicke KM. Plane progressive waves in a binary mixture of linear elastic materials. J Appl Mech (1978) 45(3):493–9. doi:10.1115/1.3424351

CrossRef Full Text | Google Scholar

14. Chen S, Liao Z. Study on mechanic models of two-phase media. Earthquake Eng Eng Vibration (2002) 22(04):1–8. doi:10.13197/j.eeev.2002.04.001

CrossRef Full Text | Google Scholar

15. Deresiewicz H. The effect of boundaries on wave propagation in a liquid-filled porous solid: I. Reflection of plane waves at a free plane boundary (non-dissipative case). B Seismol Soc Am (1960) 50(4):599–607. doi:10.1785/BSSA0500040599

CrossRef Full Text | Google Scholar

16. Deresiewicz H, Rice JT. The effect of boundaries on wave propagation in a liquid-filled porous solid: III. Reflection of plane waves at a free plane boundary (general case). B Seismol Soc Am (1962) 52(3):595–625. doi:10.1785/BSSA0520030595

CrossRef Full Text | Google Scholar

17. Xu C, Wu S, Cai Y, Chen Y. Wave reflection at the plane interface of saturated soil. Explo Shock Waves (1998)(01) 9–15. (in Chinese).

Google Scholar

18. Lin CH, Lee VW, Trifunac MD. On the reflection of elastic waves in a poroelastic half-space saturated with non-viscous fluid. In: Department of civil engineering. Los Angeles, CA: University of Southern California (2001). Report No. CE01-04.

Google Scholar

19. Lin CH. Wave propagation in a poroelastic half-space saturated with inviscid fluid [dissertation thesis]. Los Angeles: University of Southern California (2002).

Google Scholar

20. Lin CH, Lee VW, Trifunac MD. The reflection of plane waves in a poroelastic half-space saturated with inviscid fluid. Soil Dyn Earthq Eng (2005) 25(3):205–23. doi:10.1016/j.soildyn.2004.10.009

CrossRef Full Text | Google Scholar

21. Al Rjoub YS. The reflection of P-waves in a poroelastic half-space saturated with viscous fluid. Soil Dyn Earthq Eng (2013) 49:218–30. doi:10.1016/j.soildyn.2013.02.016

CrossRef Full Text | Google Scholar

22. Al Rjoub YS. The Reflection of SV-waves in a poroelastic half-space saturated with viscous fluid. In: 13th international conference. Italy, Pisa (2013). doi:10.1016/j.soildyn.2013.07.001

CrossRef Full Text | Google Scholar

23. Tajuddin M, Hussaini S. Reflection of plane waves at boundaries of a liquid filled poroelastic half-space. J Appl Geophys (2005) 58(1):59–86. doi:10.1016/j.jappgeo.2005.04.003

CrossRef Full Text | Google Scholar

24. Xia T, Chen L, Wu S. Characteristics of Rayleigh waves in a saturated half-space soil. J Hydraul Eng (1998)(02) 48–54. (in Chinese).

Google Scholar

25. You H. Elastic wave scattering by a canyon or tunnel in layered saturated half space [dissertation thesis]. Tianjin: Tianjin University (2005).

Google Scholar

26. Nie W, Xu X. The wave fields solution of half space saturated porous medium when incident P, SV waves. Site Invest Sci Tech (2007)(02) 18–20+53. doi:10.3969/j.issn.1001-3946.2007.02.005

CrossRef Full Text | Google Scholar

27. Yang J. Saturation effects of soils on ground motion at free surface due to incident SV waves. J Eng Mech (2002) 128(12):1295–303. doi:10.1061/(ASCE)0733-9399(2002)128:12(1295)

CrossRef Full Text | Google Scholar

28. Chen J. Wave propagation in unsaturated and partially saturated soils [dissertation thesis]. Shanghai: Tongji University (2000).

Google Scholar

29. Zhou X. Study on wave characteristic and dynamic response of partially saturated soils [dissertation thesis]. Hangzhou: Zhejiang University (2006).

Google Scholar

30. Xue S, Chen S, Chen R, Sun X, Wang Y. Analysis on wave mode conversion of incident P₁ wave in nearly saturated soil. Chin Quart Mech. (2005)(01) 128–33. doi:10.3969/j.issn.0254-0053.2005.01.019

CrossRef Full Text | Google Scholar

31. Kumar R, Kumar S, Miglani A. Reflection and transmission of plane waves between two different fluid-saturated porous half-spaces. J Appl Mech Tech Ph (2011) 52:773–82. doi:10.1134/S0021894411050129

CrossRef Full Text | Google Scholar

32. Singh P, Chattopadhyay A, Srivastava A, Singh AK. Reflection and transmission of P-waves in an intermediate layer lying between two semi-infinite media. Pure Appl Geophys (2018) 75(12):4305–19. doi:10.1007/s00024-018-1896-8

CrossRef Full Text | Google Scholar

33. Zhou D, Yin X, Zong Z. The characteristics of reflection and transmission coefficients of porous medium saturated with an ideal fluid. Ann Geophys-italy (2019) 62(5). doi:10.4401/ag-7815

CrossRef Full Text | Google Scholar

34. Wang E, Carcione José M, Ba J, Liu Y. Reflection and transmission of plane elastic waves at an interface between two double-porosity media: effect of local fluid flow. Surv Geophys (2020) 41(2):283–322. doi:10.1007/s10712-019-09572-6

CrossRef Full Text | Google Scholar

35. Kumar M, Singh A, Kumari M, Barak MS. Reflection and refraction of elastic waves at the interface of an elastic solid and partially saturated soils. Acta Mech (2020) 232:33–55. doi:10.1007/s00707-020-02819-z

CrossRef Full Text | Google Scholar

36. Kumari M, Barak M, Singh A, Kumar M. Effect of various physical properties on the reflection coefficients of inhomogeneous waves at the stress-free surface of partially saturated soils induced by obliquely incident fast P-wave. J Ocean Eng Sci (2022) 7(3):225–36. doi:10.1016/j.joes.2021.08.003

CrossRef Full Text | Google Scholar

37. Zhang J, Ma Q, Jiang H. Study on the transmission and reflection of P₁ wave at the interface between saturated soil and saturated frozen soil medium. Rock Soil Mech (2024) 45(10):3139–52. doi:10.16285/j.rsm.2023.1801

CrossRef Full Text | Google Scholar

38. Kumar R, Deswal S. Wave propagation in micropolar liquid-saturated porous solid. Indian J Pure Ap Mat (2000) 31(10):1317–38.

Google Scholar

39. Dai Z. Research on wave propagation in double porosity media [dissertation thesis]. Shanghai: Shanghai Jiaotong University (2006).

Google Scholar

40. Chen W, Xia T, Huang R, Zhou X. Reflection characteristics of P₁ waves at the free boundary of unsaturated soil. Eng Mech (2013) 30(9):56–62. doi:10.6052/j.issn.1000-4750.2012.04.0269

CrossRef Full Text | Google Scholar

41. Qiu H. Research on propagation characteristics of elastic waves in Biot-type three-phase medium [dissertation thesis]. Hangzhou: Zhejiang University (2019).

Google Scholar

42. Awad E, Dai W, Sobolev S. Thermal oscillations and resonance in electron-phonon interaction process. Z Angew Math Phys (2024) 75(4):143. doi:10.1007/s00033-024-02277-w

CrossRef Full Text | Google Scholar

43. Awad E. Modeling of anomalous thermal conduction in thermoelectric magnetohydrodynamics: Couette formulation with a multiphase pressure gradient. Phys Fluids (2024) 36(3). doi:10.1063/5.0190970

CrossRef Full Text | Google Scholar

44. Chen S. Numerical simulation for near-field wave motion in two-phase media [dissertation thesis]. Harbin: China Earthquake Administration, Institute of Engineering Mechanics (2002).

Google Scholar

45. Chen S, Liao Z, Chen J. A decoupling FEM for simulating near-field wave motions in two-phase media. Chin J Geophys. (2005) 48(4):909–17. doi:10.3321/j.issn:0001-5733.2005.04.025

CrossRef Full Text | Google Scholar

46. Jing L, Zhuo X, Wang X. Effect of complex site on seismic wave propagation. Earthq Eng Eng Vib (2005) 25(6):16–23. doi:10.13197/j.eeev.2005.06.004

CrossRef Full Text | Google Scholar

47. Jing L, Zhuo X, Wang X. The effect of complex media on seismic wave propagation. Chin J Geotech Eng. (2005) 27(4):393–7. doi:10.3321/j.issn:1000-4548.2005.04.006

CrossRef Full Text | Google Scholar

48. Wang X. Analysis on wave propagation in two-dimensional saturated media [master's thesis]. Harbin: China Earthquake Administration. Institute of Engineering Mechanics (2003).

Google Scholar

49. Xiao M, Cui J, Li Y, Jiang J, Shan Y, Duhee P. Propagation characteristics of Rayleigh waves and their influence on seabed dynamics in ocean sites. J Hunan Univ (Natural Sciences) (2023) 50(05):191–203. doi:10.16339/j.cnki.hdxbzkb.2023069

CrossRef Full Text | Google Scholar

50. Zhang B, Chen X, Qiu L, Dong J, Zhou Z, Ji Z, et al. (2023). Characteristic of elastic wave propagation in fluid-saturated porous media based on the model of soil mechanics. Pure Appl Geophys. 180(6): 2309–26. doi:10.1007/s00024-023-03269-z

CrossRef Full Text | Google Scholar

51. Cui J. The wave propagation in saturated soil layer and sand liquefaction [dissertation thesis]. Harbin: China Earthquake Administration. Institute of Engineering Mechanics (2002).

Google Scholar

52. Chen W, Men F. Study on FEM to simulate slip and seismic liquefaction of slope-field by theory of two-phased dynamics. Earthq Eng Eng Vib (2002) 22(01):132–40. doi:10.13197/j.eeev.2002.01.023

CrossRef Full Text | Google Scholar

53. Chen W. A direct differential method for nonlinear dynamic response of sand layer under water. Rock Soil Mech (2007) 28(s1):698–702. doi:10.16285/j.rsm.2007.s1.152

CrossRef Full Text | Google Scholar

54. Li Y. Analysis on nonlinear ground response in one dimension based on the theory of wave propagation in two-phase media [master’s thesis]. Harbin: China Earthquake Administration. Institute of Engineering Mechanics (2008).

Google Scholar

55. Pujol J. Elastic wave propagation and generation in seismology. New York: Cambridge University Press. (2003).

CrossRef Full Text | Google Scholar

56. Stein S, Wysession M. An introduction to seismology, earthquakes, and earth structure. Oxford: Blackwell Publishing (2003).

Google Scholar

57. Deresiewicz H, Skalak R. On uniqueness in dynamic poroelasticity. B Seismol Soc Am (1963) 53(4):783–8. doi:10.1785/BSSA0530040783

CrossRef Full Text | Google Scholar

58. Chen W, Xia T, Chen W, Zhai C. Propagation of plane P-waves at interface between elastic solid and unsaturated poroelastic medium. Appl Math Mech (2012) 33(7):829–44. doi:10.1007/s10483-012-1589-6

CrossRef Full Text | Google Scholar

Appendix

Let $q_1=\frac{1-n}{n}+{\delta }_1$ and $q_2=\frac{1-n}{n}+{\delta }_2$, then the elements of $\left\{F\right\}$, $\left\{\overline{F}\right\}$, ${\left[S_{\mathrm{P}-\text{SV}}\right]}_f$, and ${\left[{\overline{S}}_{\mathrm{P}-\text{SV}}\right]}_f$ are shown as follows.

1. The amplitude coefficients of the incident P₁-wave

$\left\{F\right\}=\left\{-\left(\lambda +q_1{E}_{\mathrm{w}}\right){\left(k_1^{\mathrm{I}}\right)}^2-2\mu {\left(k_{1z}^{\mathrm{I}}\right)}^2,2\mu k_{1x}^{\mathrm{I}}{k}_{1z}^{\mathrm{I}},-q_1{E}_{\mathrm{w}}{\left(k_1^{\mathrm{I}}\right)}^2\right\}$

$\left\{\overline{F}\right\}=\left\{-\left(\lambda +q_1{E}_{\mathrm{w}}\right){\left(k_1^{\mathrm{I}}\right)}^2-2\mu {\left(k_{1z}^{\mathrm{I}}\right)}^2,2\mu k_{1x}^{\mathrm{I}}{k}_{1z}^{\mathrm{I}},\left(1-{\delta }_1\right)k_{1z}^{\mathrm{I}}\right\}$

2. The amplitude coefficients of all the reflected waves

${\left[S_{\mathrm{P}-\text{SV}}\right]}_f=\left[\begin{array}{ccc}{d}_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ d_{31}& d_{32}& d_{33}\end{array}\right],{\left[{\overline{S}}_{\mathrm{P}-\text{SV}}\right]}_f=\left[\begin{array}{ccc}{d}_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ {\overline{d}}_{31}& {\overline{d}}_{32}& {\overline{d}}_{33}\end{array}\right];$

$\begin{array}{ll}\hfill & d_{11}=\left(\lambda +q_1{E}_w\right){\left(k_1^{\mathrm{I}}\right)}^2+2\mu {\left(k_{1z}^{\mathrm{I}}\right)}^2,d_{12}=\left(\lambda +q_2{E}_w\right){\left(k_2^{\mathrm{R}}\right)}^2+2\mu {\left(k_{2z}^{\mathrm{R}}\right)}^2,\hfill \\ \hfill & d_{13}=2\mu k_{\mathrm{s}x}^{\mathrm{R}}{k}_{\mathrm{s}z}^{\mathrm{R}};\hfill \end{array}$

$d_{21}=2\mu k_{1x}^{\mathrm{I}}{k}_{1z}^{\mathrm{I}},d_{22}=2\mu k_{2x}^{\mathrm{R}}{k}_{2z}^{\mathrm{R}},d_{23}=\mu \left({\left(k_{\mathrm{s}x}^{\mathrm{R}}\right)}^2-{\left(k_{\mathrm{s}z}^{\mathrm{R}}\right)}^2\right);$

$d_{31}=q_1{E}_w{\left(k_1^{\mathrm{I}}\right)}^2,d_{32}=q_2{E}_w{\left(k_2^{\mathrm{R}}\right)}^2,d_{33}=0;$

${\overline{d}}_{31}=\left(1-{\delta }_1\right)k_{1z}^{\mathrm{I}},{\overline{d}}_{32}=\left(1-{\delta }_2\right)k_{2z}^{\mathrm{R}},{\overline{d}}_{33}=\left(1-{\delta }_{\mathrm{s}}\right)k_{\mathrm{s}x}^{\mathrm{R}}.$

Nomenclature

Symbols:

E_w bulk modulus of pore water (unit: Pa)

K permeability coefficient (unit: m/s)

k dynamic permeability coefficient (unit: m³.s/kg)

n porosity

υ Poisson’s ratio

λ, μ Lame’s constants of solid phase (unit: Pa)

E elastic modulus of the solid phase (unit: Pa)

ρ_w pore fluid mass density (unit: Kg/m³)

ρ_s solid mass density (unit: Kg/m³)

ρ total density (unit: Kg/m³)

p_f true pore pressure (unit: Pa)

ω angular frequency

u,$\dot{\mathbf{u}}$,$\ddot{\mathbf{u}}$ displacement, velocity, and acceleration vectors of the solid phase (unit: m, m/s, m/s²)

U, $\dot{\mathbf{U}}$, $\ddot{\mathbf{U}}$ displacement, velocity, and acceleration vectors of fluid phase (unit: m, m/s, m/s²)

${\varphi }_{\mathrm{s}}$, ${\mathit{\psi }}_{\mathbf{s}}$ potential functions associated with solid phase

${\varphi }_{\mathrm{w}}$, ${\mathit{\psi }}_{\mathbf{w}}$ potential functions associated with pore fluid.