Transformer network enhanced by dual convolutional neural network and cross-attention for wheelset bearing fault diagnosis

Advances in deep learning methods have demonstrated remarkable progress in wheelset fault diagnosis. However, current deep neural networks suffer from design flaws, including low accuracy, high computational complexity, limitations in frequency-domain analysis, and inefficient long time-series feature encoding. To address these challenges, this study proposes a Transformer network model based on dual convolutional neural networks and cross-attention enhancement (Trans-DCC) for wheelset bearing fault diagnosis. The model incorporates a dual feature fusion mechanism in the first layer of the Transformer encoder, utilizing dual CNNs to extract low-level time-frequency features while reducing subsequent attention computation complexity. Additionally, a cross-attention mechanism is integrated into the last encoder layer, combining multi-head attention with time- and frequency-domain features from a feedforward connection layer. Attention weights are computed to prioritize critical features before enhancement fusion. Finally, fully connected layers and a softmax classifier are employed for fault classification. Experimental evaluation on a train wheelset bearing dataset confirms the model’s effectiveness, demonstrating high diagnostic accuracy. The proposed Trans-DCC model overcomes key limitations of existing methods by enhancing feature extraction and fusion, offering a robust solution for wheelset bearing fault diagnosis.

1 Introduction

Wheelset bearings mainly undertake functions such as support, transmission, and motion conversion. Their service condition directly determines the security and stability of train operation. Therefore, it is greatly significant for monitoring the health status and diagnosing the faults of wheelset bearings.

Nowadays, the vibration signal processing is mainly used in the wheel bearing faults diagnosis [1]. Ding J [2] et al. used an automatic detection system for wheel bearing faults, AFDMLEWT, which is based on multilevel empirical wavelet transform. Xin G [3] et al. used logarithmic short-time Fourier transform and improved calibration convolution. Although this type of fault diagnosis method can determine the type or location of damage to the train wheelset bearings, it overly relies on expert knowledge, resulting in maintenance personnel being unable to independently support the overall operation in many scenarios [4–6].

Subsequently, machine learning methods emerged in practical applications due to their advantages of automatically fitting sample features and classification [7]. The traditional machine learning methods mainly include statistical decision. They utilize different concepts to classify extracted features [8, 9]. Euldji R [10] et al. used a decision system by vibration analysis and decision tree to detect the state of wheelset bearings. However, traditional machine learning still requires varying degrees of manual feature extraction, and in order to apply the extracted features to machine learning, relevant algorithms need to be used to compress the features [11].

Recently, deep learning algorithms have been mainly utilized in mechanical fault diagnosis due to their superior automatic feature-learning capabilities. Jovanovic Let al. [12] explored the potential of convolutional neural networks (CNNs) for patient gain freezing associated with Parkinson’s disease. Purkovic S et al. [13] explored the potential of using CNNs in conjunction with audio analysis for the identification of respiratory problems. Peng D et al. [14] used a multibranch multi-scale CNN in wheelset bearing fault diagnosis. DENG F et al. [15] used a lightweight neural network model called ShuffleNet. In order to further improve the accuracy and robustness of fault diagnosis, research workers began to introduce attention mechanisms into deep learning models. Salb M et al. [16] explored the potential of multiheaded recurrent architectures to forecast cloud instance prices based on historical and instance data. Petrovic A et al. [17] explored the potential of using CNNs in conjunction with audio analysis for the identification of respiratory problems. Cui X et al. [18] presented a novel load prediction model, which integrates the whale optimization algorithm (WOA) to refine the hyperparameters of an LSTM model bolstered by an attention (ATT) mechanism and a CNN. Yuan Z et al. [19] proposed a graph attention-based multichannel transfer learning network in wheelset bearing fault diagnosis. Fault features of multiple working conditions are transferred by combining a recurrence graph attention residual network (ResGANet) with multiple distribution adaptations and a multichannel diagnosis decision strategy. Liao J X [20] proposed an attention-embedded quadratic network, and it can facilitate effective and interpretable bearing fault diagnosis. However, the receptive field range in CNNs and the attention mechanism is often limited by the size of the convolutional kernel, which can only consider local information of the features. To avoid the shortcomings, a transformer architecture that can enhance the global features to the wheelset bearing fault diagnosis is applied [21, 22]. Ding Y et al. [23] used a new time–frequency transformer (TFT) model that addresses the shortcomings of CNNs in terms of computational efficiency and feature representation. Hou Y et al. [24] used an improved transformer, which is based on the multifeature parallel fusion model diagnosis method. With the widespread application of transformer models, their drawbacks are gradually becoming apparent. Traditional transformer models often adopt a hierarchical framework, which makes it difficult to integrate feature information and weakens the learning ability of local features. To overcome this shortcoming, some research workers combined the transformer and CNNs to extract features from both the global and local perspectives, achieving the extraction of all features. Xinyu Gu et al. [25] suggested a novel SOH estimation based on data preprocessing methods and a CNN-transformer framework. Zhao J et al. [26] developed a predictive pretrained transformer (PPT) model that enhanced the identification of both short-term and long-term patterns in time-series data. Therefore, a new network that combines a dual-channel CNN and transformer is proposed in this paper. The main contributions of this article are as follows:

(1) The dual feature fusion model is proposed, in which two CNNs extract fault features by both the time domain and frequency domain simultaneously. FFT is used to achieve global correlation encoding in the frequency domain, mining hidden the fault features.

(2) A cross-feature fusion attention model, cross-attention (CA), is added at the last layer of the transformer to achieve deep fusion of temporal and spatial dual scale features and comprehensively extract the feature of vibration signal.

(3) A new framework called Trans-DCC has been proposed, which includes the local feature extraction in CNNs and the global and temporal feature extraction in the transformer network, achieving comprehensive encoding and extraction of global information.

The rest of this paper is as follows: Section 2 describes basic principles of CNNs and transformer encoders. Section 3 provides a detailed introduction to the proposed Trans-DCC model and its training process. The fourth section presents the effectiveness of fault classification for wheelset bearings through experiments. Section 5 is the conclusion.

2 Related work

2.1 Local feature extraction with CNNs

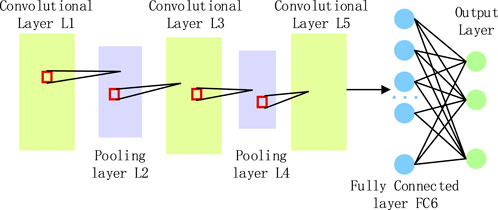
A CNN extracts local features of input vibration signals through convolution operations [27]. Convolutional kernels (also known as filters) slide over the signal and perform dot product operations with the signal to capture local patterns or structures in the signal. Each convolution kernel generates a feature map that represents the presence and strength of specific types of local features in the signal [28]. Convolutional kernels use the same weight parameters when sliding across the entire signal, greatly reducing the model parameters and improving the efficiency of feature extraction. By using convolution kernels of different sizes or constructing multi-scale CNN structures, signal features at different time scales can be captured, as shown in Figure 1.

Figure 1

Figure 1. Architecture of CNN.

2.2 Global feature extraction with transformer

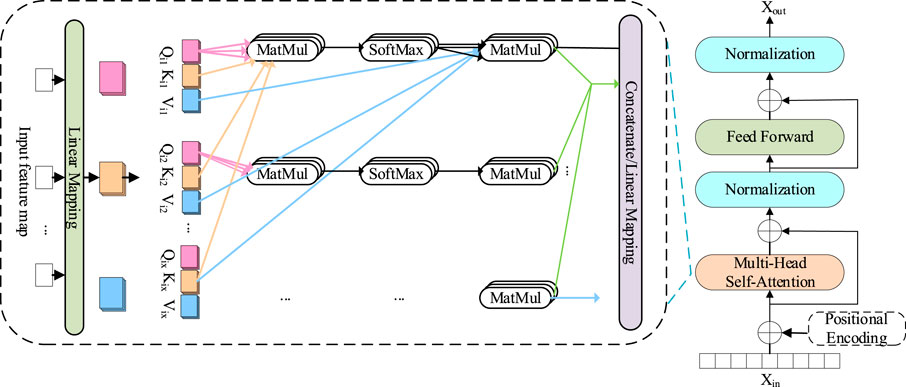
Multi-head attention (MHA) is the critical component of the transformer, as shown in Figure 2. Based on the self-attention mechanism, MHA is an improved method [29]. The advantage of multi-head attention is that it can handle problems with multiple focus points and effectively handle complex semantic relationships. The multi-head attention mechanism splits the input tensor into $h$ sub-tensor when calculating the attention matrix, and each sub-tensor learns attention information in a different way [30]. Then, for each sub-tensor, a self-attention calculation is performed to obtain an output tensor ${MultiHead\left(Q,K,V\right)}_i$. At last, the final output, $MultiHead\left(Q,K,V\right)$, is obtained by merging all the output tensors together.

Figure 2

Figure 2. Architecture of transformer encoder.

$Q\in R^{d\times d},K\in R^{d\times d},V\in R^{d\times d}$ are the learned dimensional query, key, and value vectors. $h$ represents the number of heads. Specifically, the calculation of multi-head attention is as follows Equation 1:

$MultiHead\left(Q,K,V\right)=Concat\left({head}_1,\cdots ,{head}_h\right)W^O,(1)$

where head_i represents the $i$-th attention head of the input sequence, $W^O$ is the weight parameter for linear projection, and $Concat\left(·\right)$ is the splicing operation.

${head}_i=Attention\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right),i=1,\cdots ,h.(2)$

In the above Equation 2, $W^Q\in R^{d\times hq},W^K\in R^{d\times hk},W^V\in R^{d\times hv}$ 和$W^O\in R^{hd\times d}$ are the learned projection matrices. So, each attention head is obtained through $Q,K,V$ self-attention calculation as follows Equation 3:

$Attention\left(Q,K,V\right)=Softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V,(3)$

where $d_k$ is the dimension size, which is used to scale the size of attention. Softmax (•) normalizes the last dimension data in the matrix.

In order to better capture the characteristics between different frequency components and the health status of bearings, we introduced learnable filters. These filters can learn and capture useful features in vibration signals, thereby better reflecting the condition of bearings. The Trans-DCC framework utilizes frequency domain data for multi-scale global information fusion, revealing fault characteristics. The introduction of transformer architecture helps to encode global contextual features of input signals, further improving the accuracy of the health status prediction. This transformer framework accurately simulates the complex relationship between input vibration signals and bearing health status.

For the feature extraction task of one-dimensional vibration signals, a dense connection mechanism based on element-level addition is used between CNN layers, thus alleviating gradient vanishing and model degradation. This network design can reduce the calculation and parameter complexity of the model while ensuring performance, thereby accelerating the speed of feature extraction.

Convolutional operations have been widely applied to many tasks [31, 32]. Usually, convolution operation is as follows Equation 4:

$O_c\left(i\right)=b\left(i\right)+{\displaystyle \sum _{\sigma \in \mathrm{\Omega }}}W\left(i,\sigma \right)·X\left(i+\sigma \right),(4)$

where b is the bias, Ω represents the size of the CNN kernel, and $i$ is the time index of the input. When the function W (•) is exponent independent, the convolution operation is equivalent to the traditional CNN layer [33–35]. When W (•) is a function including $i$ and σ, this convolution operation has some complex types of layers, such as variable row convolution [36] or dynamic convolution [37]. When b is 0, the above equation becomes Equation 5:

$O_c\left(i\right)={\displaystyle \sum _{\sigma \in \mathrm{\Omega }}}W\left(i,\sigma \right)·X\left(i+\sigma \right).(5)$

The self-attention module is represented as follows Equation 6:

$Atten=F\left(Q,K,V\right)=softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V,(6)$

where $\mathrm{Q}\in R^{d_{in}\times d_q},\mathrm{R}\in R^{d_{in}\times d_k},andV\in R^{d_{in}\times d_v}$ represent three matrices, which are calculated by $Q=W_q\left(X\right),K=W_k\left(X\right),andV=W_v\left(X\right)$, respectively.

Due to $d_k$ being a constant, the self-attention mechanism of point generation can be expressed as follows Equation 7:

$Atten\left(\mathit{i}\right)={\displaystyle {\sum }_{\mathit{\sigma }\in \mathit{\psi }}}{\overline{\mathit{w}}}_q\left(\mathit{i}\right)·{\overline{\mathit{w}}}_{\mathit{q}}\left(\mathit{i}+\mathit{\sigma }\right)·{\mathit{W}}_{\mathit{}}\left(\mathit{i}+\mathit{\sigma }\right).(7)$

$\overline{W_q}$ and $\overline{W_k}$ represent the normalization function of softmax and $\sqrt{d_k}$, respectively, and ψ represents the size of the input. Therefore, $\text{Atten}\left(i\right)$ is as follows Equation 8:

$Atten\left(i\right)={\displaystyle \sum _{\sigma \in \mathrm{\psi }}}{W}_a\left(i,\sigma \right)·W_v\left(i+\sigma \right),(8)$

where ${\mathrm{W}}_{\mathrm{q}}\left(\mathrm{i},\mathrm{\sigma }\right)={\overline{\mathrm{W}}}_{\mathrm{q}}\left(\mathrm{i}\right)·{\overline{\mathrm{W}}}_{\mathrm{k}}\left(\mathrm{i}+\mathrm{\sigma }\right)$.

On comparing Equations 5, 8, two differences between convolution and self-attention can be found. In Equation 5, Ω represents the kernel size, including a portion of the input. In Equation 8, ψ is the entire size of the input. The self-attention is defined in Equation 8.

3 Proposed method

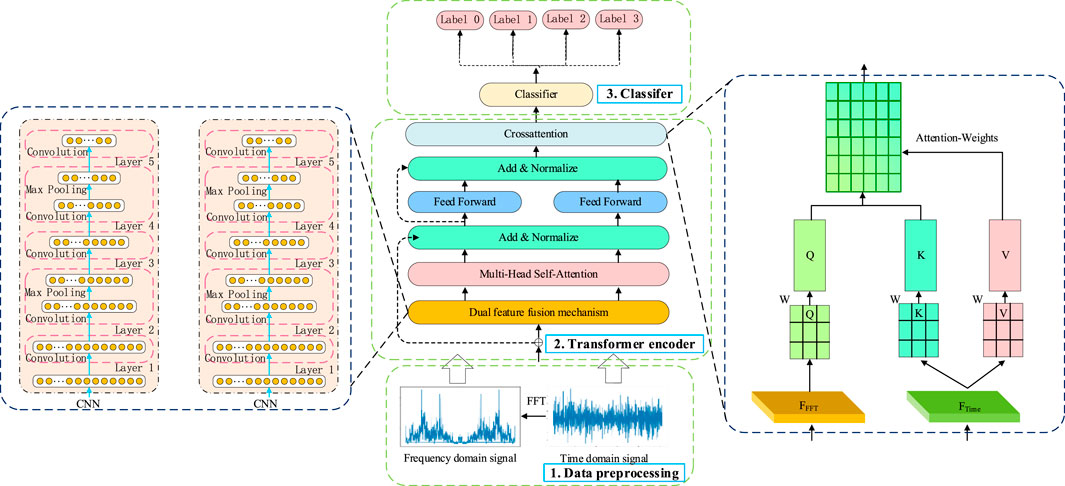
When analyzing one-dimensional vibration signals of faulty wheelset bearings, using either time-domain or frequency-domain analysis methods alone has certain limitations. Time-domain analysis mainly focuses on the characteristics of signal changes over time, which can capture the transient response and waveform features of the signal. However, it is not intuitive enough for analyzing the frequency signals and frequency response. Frequency-domain analysis converts signals and can intuitively analyze the frequency components of the signal and the frequency response of system. Therefore, this paper adds a dual feature fusion in the transformer encoder, using dual CNNs to separately extract the time-domain and frequency-domain features, achieving comprehensive feature extraction. This framework consists of three parts: data preprocessing, transformer encoder composed of the dual feature fusion mechanism and cross-attention mechanism, and classifier, as shown in Figure 3.

Figure 3

Figure 3. Structure of the proposed Trans-DCC.

3.1 Dual feature fusion mechanism

The dual feature fusion mechanism is a key component of Trans-DCC and the first step in achieving valuable feature fusion and related encoding. First, Trans-DCC uses two convolutional neural network branches to process the input time-domain and frequency-domain signals. Convolution operations can extract valuable features from complex signals. The convolution operation in each convolutional neural network uses multiple convolution kernels, each with different extraction functions, which can extract different levels of features from the input signal while discarding irrelevant features. M different convolution kernels are represented by µ₁, µ₂, … , µ_m. When the one-dimensional vibration signal δ[n] is input, the output θ_i [n] of the i-th convolution kernel can be expressed as follows Equation 9:

${\theta }_i\left[n\right]=\left(\delta ⨂{\mu }_i\right)\left[n\right]={\displaystyle \sum _{k=-\infty }^{\infty }}\delta \left[k\right]\times {\mu }_i\left[n-k\right],(9)$

where ⊗ represents the convolution. By using different convolutions, multiple distinct features can be extracted from a signal.

Trans-DCC uses a dual branch convolution model to extract time-domain and frequency-domain features, where the time-domain convolution branch processes time-domain features and the frequency-domain convolution branch processes frequency-domain features. Using j to represent the branch number of a convolutional network (j = 0 is the time domain and j = 1 represents the frequency domain), each branch of the convolutional network contains multiple convolution kernels, µ_j,i. Therefore, output θ_j,i [n] of the i-th convolution kernel of the j-th convolutional branch model can be expressed as follows Equation 10:

${\theta }_{j,i}\left[n\right]=\left({\delta }_j⨂{\mu }_{j,i}\right)\left[n\right]={\displaystyle \sum _{k=-\infty }^{\infty }}{\delta }_j\left[k\right]\times {\mu }_{j,i}\left[n-k\right].(10)$

The above process achieves the extraction of multiple time-domain and frequency-domain features. The frequency-domain signals have characteristic of parameter sharing, where different positions can share the same weight. This weight-sharing mechanism helps capture global features, thus handling remote dependencies. For the input time series signal X∈R^C×L, $C$ represents the number of input feature vectors and L represents the length of the input feature vectors. The frequency-domain signal is as follows Equation 11:

$\sigma =F\left[X\right]\in R^{C\times L},(11)$

where F[·] represents the fast Fourier transform and σ represents the complex output signals containing amplitude and phase at different frequencies. For Fourier transformed data σ, the amplitude and phase in the vibration signal can be obtained.

A frequency-domain convolutional branch network consisting of two different learnable weights, represented by W_{amp_weight} and W_{pha_weight}, is designed. These two sets of weights are multiplied by the amplitude and phase, respectively, and processed as convolution kernels Equations 12, 13:

${\eta }_{amplitude}=\sqrt{Re{\left(\sigma \right)}^2+Im{\left(\sigma \right)}^2}(12)$

${\eta }_{phase}=\mathit{arctan}\left(\frac{Im\left(\sigma \right)}{Re\left(\sigma \right)}\right).(13)$

The size of the learnable filter is γ∈R^C×L. The frequency-domain output obtained by element-wise multiplication (also known as the Hadamard product) between the converted frequency-domain signal and γ as follows Equations 14–16:

$\beta =\gamma ·\sigma \in R^{C\times L}(14)$

${\eta }_{amplitude}={\eta }_{amplitude}\times W_{amp\_weight},(15)$

${\eta }_{phase}={\eta }_{phase}\times W_{pha\_weight}.(16)$

According to the task requirements, adjusting W_{amp_weight}, W_{pha_weigh}, and γ can achieve global frequency adjustment of the signal. By enhancing frequencies of greater concern and reducing less relevant frequencies, the network can design filters in the frequency domain of specific tasks, thereby enhancing the flexibility and adaptability of data processing.

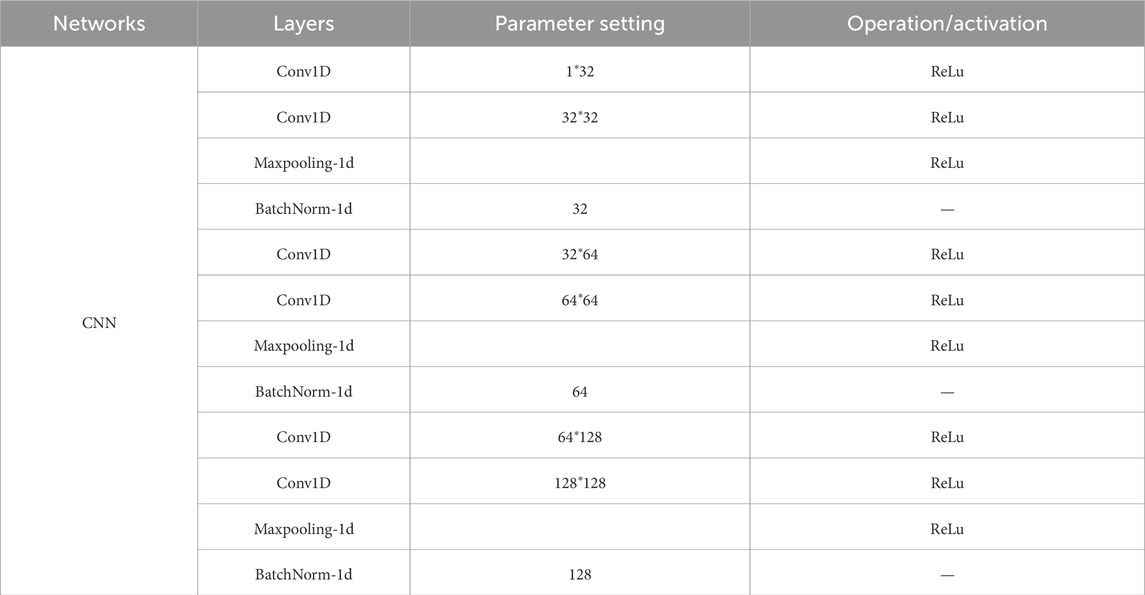
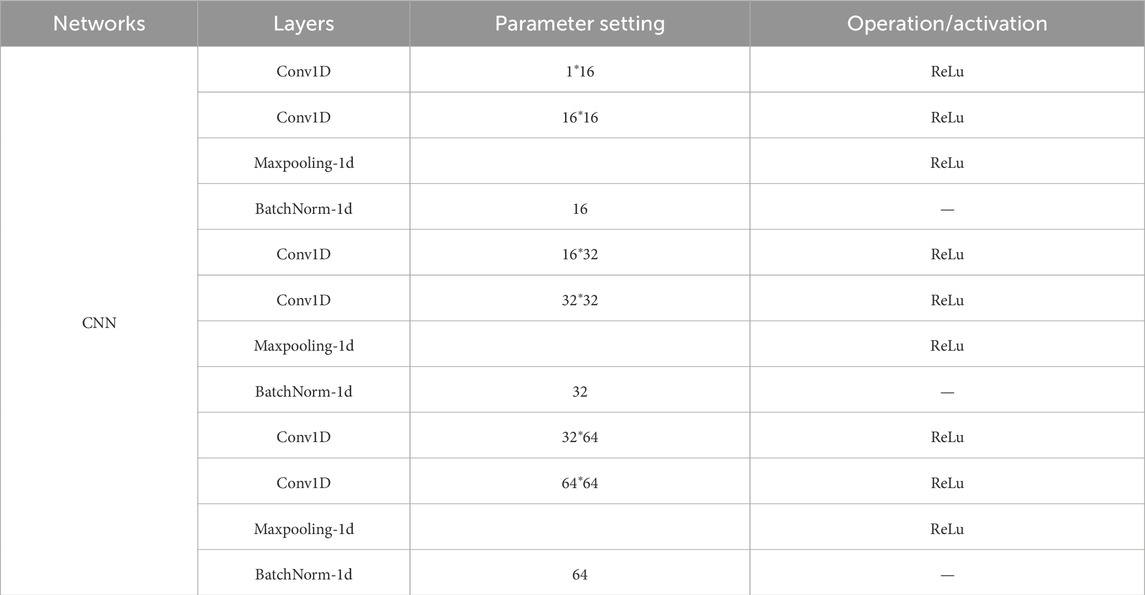
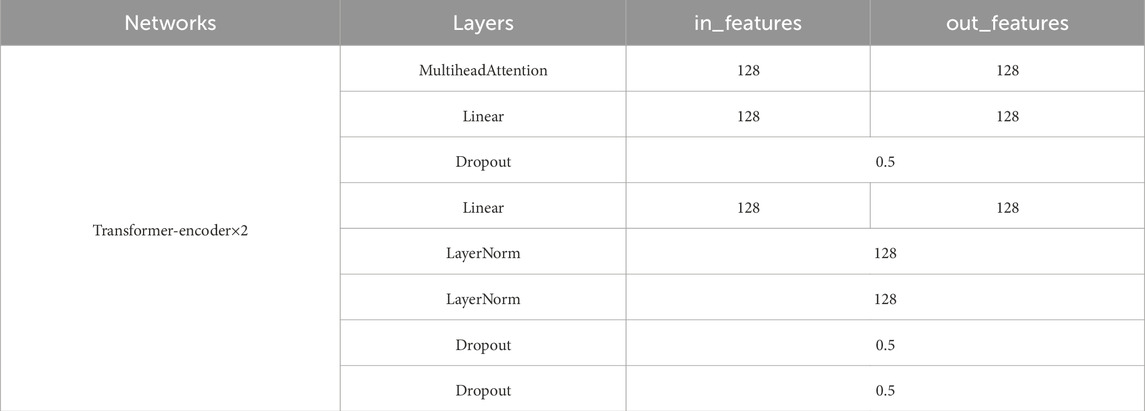
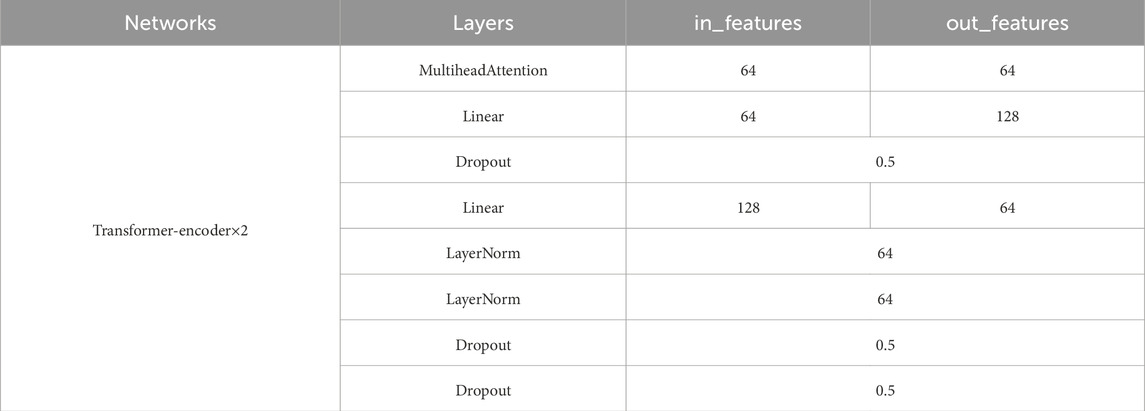
The grid search method was adopted to systematically traverse a variety of hyperparameter combinations, and the optimal hyperparameters were determined through cross-validation. Specifically, a series of candidate values were set for key hyperparameters such as the learning rate, batch size, convolutional kernel size, and the number of heads in the attention mechanism, and the optimal combination was found through grid search. In Tables 1–4, the training process and hyperparameters of the time-domain and frequency-domain CNNs are shown.

Table 1

Table 1. CNN structure and hyperparameters for extracting the time-domain features.

Table 2

Table 2. CNN structure and hyperparameters for extracting the space-domain features.

Table 3

Table 3. Transformer-encoder network structure and hyperparameters for the time-domain features.

Table 4

Table 4. Transformer-encoder network structure and hyperparameters for the space-domain features.

3.2 Cross-attention layer of the transformer

Traditional transformer models tend to focus on local context, which may not be sufficient for tasks that require broader information exchange and capture global feature correlations [38]. To solve this problem, a cross-attention mechanism is added after the feedforward fully connected layer.

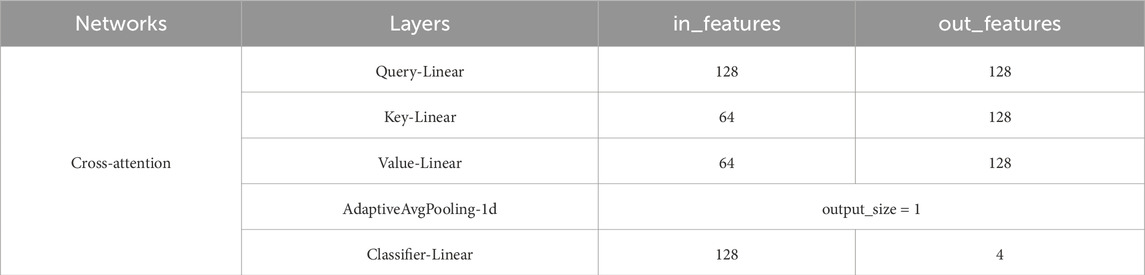
Cross-attention can calculate attention on two different sequences. In the framework proposed in this article, the inputs of cross-attention are time-domain features $X_1\in R^{n\times d_1}$ extracted comprehensively by the transformer network from the time-domain CNN. Frequency-domain features $X_2\in R^{n\times d_2}$ are extracted comprehensively by the transformer network from the frequency-domain CNN. One part is query set $Q$, and the other part is the key value set, K. First, similarity in time-domain and frequency-domain features is calculated by dot product to generate attention weights, namely, the query set $Q=X_1{W}^Q$ and key value set $K=V=X_2{W}^K$. Based on attention weights, time-domain and frequency-domain features are weighted and fused to generate a fused feature representation. These features contain both time-domain and frequency-domain information of the original signal, which helps to more comprehensively describe the characteristic state of the faulty wheel bearing. The calculation is as follows Equation 17:

$CrossAttention\left(X_1,X_2\right)=Softmax\left(\frac{Q{K}^T}{\sqrt{d_2}}\right)V.(17)$

where $W^Q\in R^{d_1\times d_k}$ and $W^K\in R^{d_2\times d_k}$ are the learned projection matrices, where $d_k$ is dimensions of the key value set. The output of the cross-attention is a tensor of size $n\times d_2$, and for each row vector, its attention weight for all row vectors is given. The training process and hyperparameters of cross-attention to extract time and frequency fusion feature network Trans-DCC are shown in Table 5.

Table 5

Table 5. Network structure and hyperparameters of cross-attention.

The paper aims to establish the relationship between bearing vibration signals and bearing fault categories. Model parameters are updated through backpropagation. Here, by cross-entropy loss (CE), differences in actual and estimated values are calculated. CE represents the following Equation 18:

$CELoss=-\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{c=1}^C}{y}_{i,c}·\log \left(p_{i,c}\right),(18)$

where N is the number of samples in each batch and C represents the number of types of faults. When the sample is a fault sample, y_i,c is 1; otherwise, it is 0. p_i,c is the probability that the predicted sample i belongs to class C.

4 Experimental verification

4.1 Dataset description

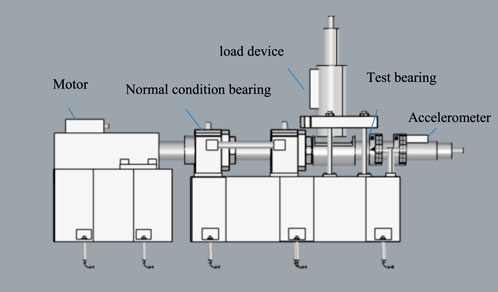
Datasets of high-speed train wheelset bearings are usually collected from the comprehensive test bench of high-speed train wheelset bearings, as shown in Figure 4. The test bench consists of a driving motor, an axial loading device, a radial loading device, supporting bearings, and test bearings, among others. Data collected in the test are the vibration signals of the faulty wheelset bearing. The accelerometer and its location are shown in Figure 5. Photographs of test bearing are shown in Figure 6. The sensitivity of the acceleration sensor is 2.505 mv/m/s², which is installed above the test wheelset bearing.

Figure 4

Figure 4. Photograph of the wheelset bearing test platform.

Figure 5

Figure 5. Details of the test platform.

Figure 6

Figure 6. Photograph of the test bearing: (a) normal condition, (b) inner ring fault, (c) outer ring fault, and (d) rolling element fault.

In the test, the sampling frequency was 12.8 kHz. The bearing mainly includes four healthy states: outer ring fault ($\mathrm{O}$), inner ring fault ($\mathrm{I}$), rolling element fault (B), and normal state ($\mathrm{N}$), as shown in Figure 6. Detailed information of the test bearings is shown in Table 6.

Table 6

Table 6. Detail of the test wheelset bearings.

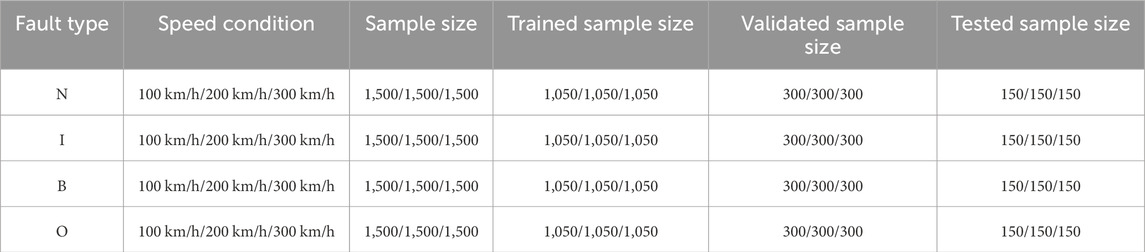
Fault samples are collected using the above test bearings at different speeds. The load during operation is set to 5 t. So, 12 experimental data points were collected for validation, as shown in Figure 7. A sliding window was used to perform nonoverlapping segmentation on the collected vibration signals. A total of 1,024 data points are present in each sample, and 1,500 samples are obtained for each experimental data. Therefore, a total of 18,000 samples were obtained from 12 test data. All samples from different operating conditions were placed in one dataset, and their order was disrupted. The ratio of training, validation, and testing data is 7:2:1. The differences in datasets often help test the generalization performance of a network, as shown in Table 7.

Figure 7

Figure 7. Data of wheelset fault bearings.

Table 7

Table 7. Detail of the test dataset.

To improve the quality of the data, the following preprocessing steps are taken:

(1) Random noise is often present in the data, so a low-pass was used to denoise it. By filtering out the high-frequency noise components, the impact of noise on model performance was effectively reduced.

(2) To eliminate the dimensional differences between features, the min–max normalization method is used to scale the data to the range [0,1]. Then, the datasets are divided into training, validation, and test sets, with proportions of 70%, 15%, and 15%, respectively. This division method helps to evaluate the generalization ability of the model.

(3) Fourier transform is used to extract frequency domain features to capture the periodic changes in the data.

4.2 Comparison and analysis of sample generation effect

In this section, the fault diagnosis results, based on our proposed Trans-DCC, are analyzed. Comparing with other methods, estimating Trans-DCC model, the model used for experimental verification in this article was written in Python 3.8. The deep learning framework uses PyTorch 1.3, with experiments and training conducted on the Windows 11 operating system and NVIDIA GeForce RTX 4060, Intel Xeon Gold 6530 CPU, 32 GB RAM, and 16 GB memory.

4.2.1 Comparison and analysis of sample generation effect

The convergence behavior of the Trans-DCC model is shown in Figure 8. Accuracy of the training and validation datasets are stabilized, which proves the fast convergence speed of the Trans-DCC model. In the initial training stage, the generalization ability of the Trans-DCC model is enhanced by dropout, which results in the slight fluctuations in the loss of the validation dataset. However, these fluctuations will gradually decrease, and the model will achieve stable performance.

Figure 8

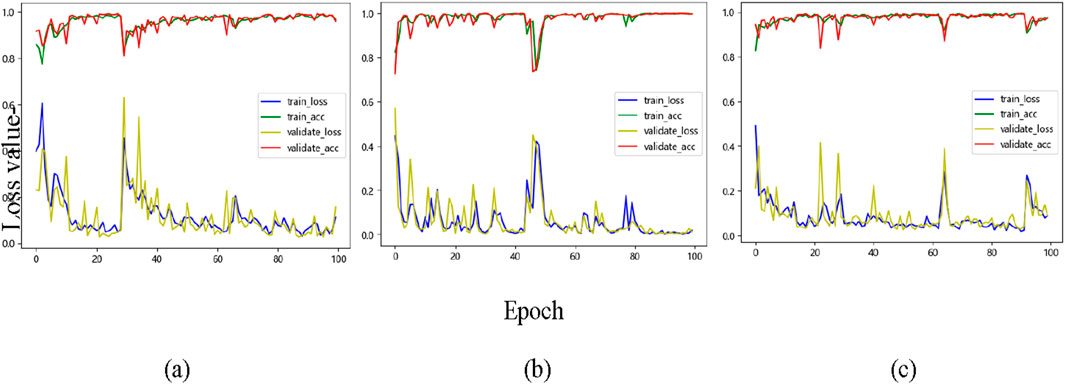
Figure 8. Loss and accuracy curves of the proposed Trans-DCC on the wheelset bearing dataset for (a) 100 km/h, (b) 200 km/h, and (c) 300 km/h.

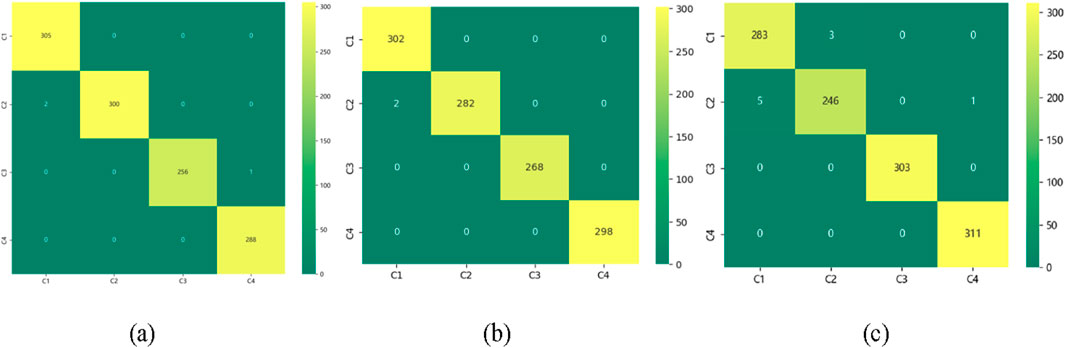
T-distributed random neighbor embedding (t-SNE) [24] was used to simplify the high-dimensional features of the final hidden layer into a 2-D vector distribution, as shown in Figure 9. Visualization results indicate that the Trans-DCC model can effectively obtain unique feature fault patterns using short-term signal sequences and accurately distinguish various fault types even under complex and diverse working conditions. In addition, the confusion matrix of the test results is shown in Figure 10. Rows represent the actual fault types input, whereas lists represent estimated fault types. In the mixed dataset, as shown in Figure 10, the accuracy has been consistently high, with only sporadic misclassifications observed in wheel bearing failures. These results emphasize the robustness and efficiency of the proposed Trans-DCC in fault diagnosis tasks.

Figure 9

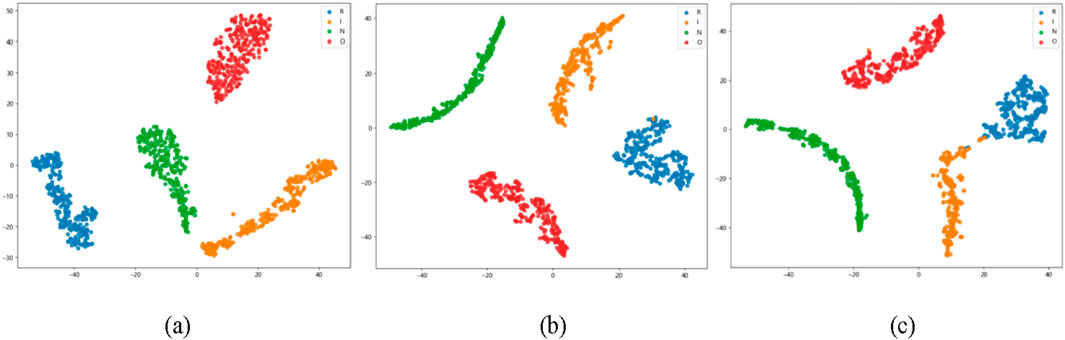
Figure 9. 2-D visualization results of extracted features from (a) 100 km/h, (b) 200 km/h, and (c) 300 km/h.

Figure 10

Figure 10. Confusion matrixes of (a) 100 km/h, (b) 200 km/h, and (c) 300 km/h.

4.2.2 Diagnostic results of ablation

In this experiment, we considered two channels, namely, the time-domain CNN transformer and the frequency-domain CNN transformer. In order to further analyze the impact of the time-domain and frequency-domain models on the performance of the Trans-DCC model, in this paper, we conducted two different ablation experiments to verify and analyze, and the evaluation indicators were taken as the average of three speed conditions. In the two ablation experiments, the input signals were time-domain vibration signals and frequency-domain vibration signals, which were, respectively, passed through CNN transformer. The results are shown in Table 8.

Table 8

Table 8. Result of the ablation experiment.

After visualizing the features extracted from the two ablation experiments (see Figure 11), it can be observed that there is actually some overlap between their departmental regions, indicating that the single channel fault diagnosis method has classification coupling; that is, the diagnostic effect is insufficient. This further validates the accuracy and robustness of the proposed dual channel approach from a lateral perspective.

Figure 11

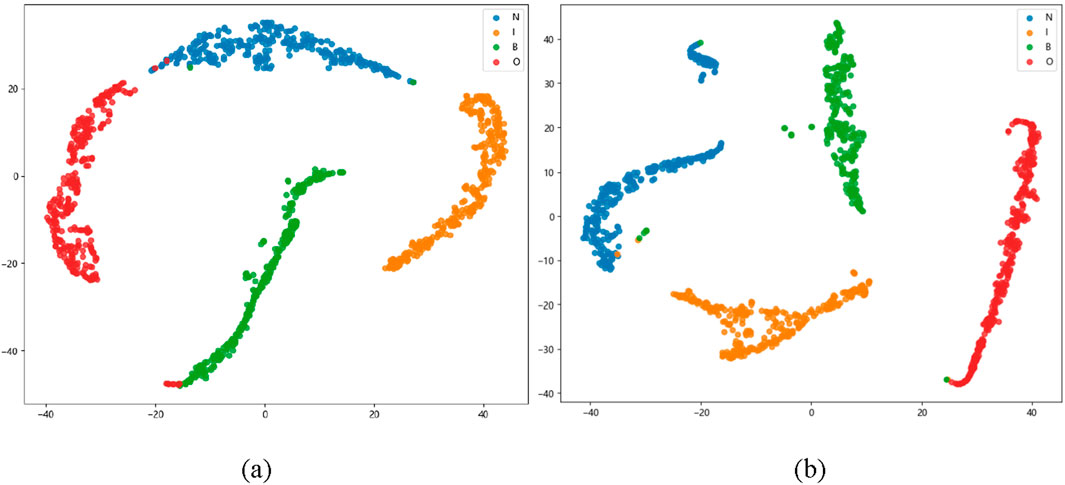
Figure 11. Ablation experiment of Trans-DCC. (a) CNN-transformer. (b) CNN extracting the frequency domain signal.

4.2.3 Comparison of different methods

In order to analyze the performance of the Trans-DCC model, comparative experiments are conducted using different methods. Five models, namely, 1DCNN [39], 2DCNN [40], transformer [23], CNN transformer [41], and TCFormer CA, are applied for the diagnosis and classification of wheel bearing faults. Experiments were conducted on wheelset bearing datasets to investigate the performance of five models, that is, 1DCNN, 2DCNN, transformer, CNN transformer, and TCFormer CA, under different operating conditions. As shown in Table 9, 1DCNN and 2DCNN perform well under low-speed conditions, with accuracies of 94.24% and 95.76%, respectively. When the speed increases from 100 km/h to 300 km/h, both transformer and CNN transformer decrease to below 94%, making it difficult to perform well under high-speed conditions, which indicates that the speed is significant for the feature extraction process. Under high-speed conditions, the performance of each model generally decreases, indicating difficulty in extracting useful feature information from high-speed signals. TCFormer CA maintains excellent performance under all operating conditions, with an accuracy rate consistently above 98%, demonstrating strong fault diagnosis capabilities. The comparison results of all networks are shown in Figure 12.

Table 9

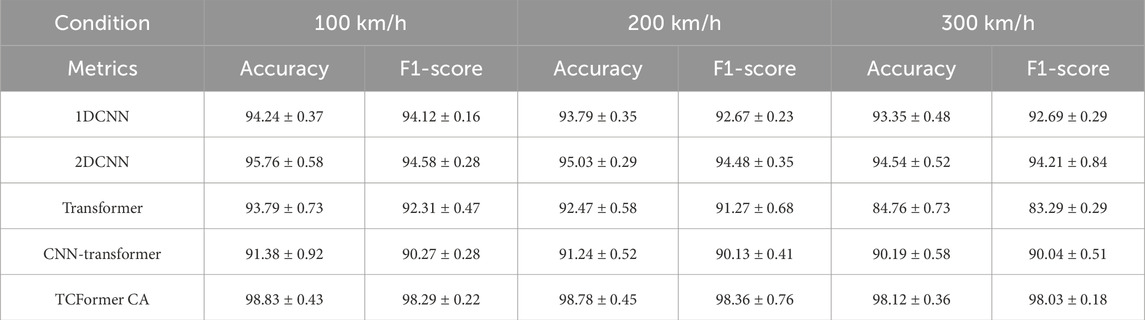
Table 9. Experiment results of 1DCNN, 2DCNN, transformer, CNN-transformer, and TCFormer CA in multiple conditions of wheelset bearing dataset.

Figure 12

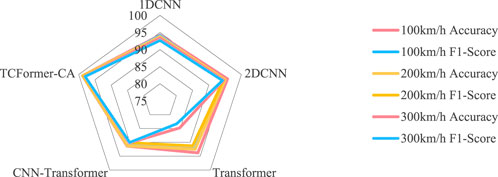
Figure 12. Radar plot of Trans-DCC and other comparative methods at 100 km/h, 200 km/h, and 300 km/h prediction results.

5 Conclusion

A Trans-DCC framework with dual domain feature extraction capability is proposed to avoid the issue of accuracy in high-speed train wheelset bearings fault diagnosis. The conclusions are summarized as follows: 1) the designed CNN transformers (CFormers) dual domain feature extraction network fully extracts the time-domain feature and the frequency-domain feature of vibration signals, and the ability of distinguishing are enhanced between various fault signals. 2) Complexity of attention computation in the transformer model is reduced by dual CNN transformers (TCFormers) network channel using the few data requirements of the original transformer. 3) The cross-attention mechanism of the Trans-DCC framework can deeply mine long-term faults and effectively adapt to bearing fault diagnosis problems under various working conditions.

The experiments and analysis conducted on the train wheelset bearing dataset demonstrate that the proposed model Trans-DCC surpasses the other four models in terms of stability and exhibits a high degree of accuracy in fault diagnosis at different speeds. The double convolutional neural network and cross-attention weight in the MSTF model reveal its diagnostic capability. Although the model proposed in this paper has excellent performance, there is still potential for further development. Future work should focus on enhancing the model’s ability in interpretability learning to adapt to a broader range of scenarios.

Data availability statement

The datasets presented in this article are not readily available because they belong to the internal confidential data of Shijiazhuang Tiedao University and cannot be made public. Requests to access the datasets should be directed to cnh6aGFvamluZ0AxMjYuY29t.

Author contributions

JZ: Conceptualization, Formal Analysis, Software, Visualization, Writing – original draft. JL: Investigation, Methodology, Resources, Supervision, Writing – review and editing. ZL: Resources, Writing – review and editing. ZM: Data curation, Project administration, Validation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was supported by the National Natural Science Foundation of China (No. 12393783), the National Natural Science Foundation of China (No.12072207), the National Natural Science Foundation of China under Grant (No. 52205571) Guangdong Provincial Department of Education (No: 2019KTSCX240), and Hebei Province Higher Education Scientific and Technological Research Project (No: ZD2020401).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yang S, Gu X, Liu Y, Hao R, Li S. A general multi-objective optimized wavelet filter and its applications in fault diagnosis of wheelset bearings. Mech Syst Signal Process (2020) 145:106914. doi:10.1016/j.ymssp.2020.106914

CrossRef Full Text | Google Scholar

2. Ding J, Ding C. Automatic detection of a wheelset bearing fault using a multi-level empirical wavelet transform. Measurement (2019) 134:179–92. doi:10.1016/j.measurement.2018.10.064

CrossRef Full Text | Google Scholar

3. Xin G, Li Z, Jia L, Zhong Q, Dong H, Hamzaoui N, et al. Fault diagnosis of wheelset bearings in high-speed trains using logarithmic short-time Fourier transform and modified self-calibrated residual network. IEEE Trans Ind Inform (2021) 18(10):7285–95. doi:10.1109/tii.2021.3136144

CrossRef Full Text | Google Scholar

4. Xu M, Yao H. Fault diagnosis method of wheelset based on EEMD-MPE and support vector machine optimized by quantum-behaved particle swarm algorithm. Measurement (2023) 216:112923. doi:10.1016/j.measurement.2023.112923

CrossRef Full Text | Google Scholar

5. Liu Z, Wang H, Liu J, Qin Y, Peng D. Multitask learning based on lightweight 1DCNN for fault diagnosis of wheelset bearings. IEEE Trans Instrumentation Meas (2020) 70:1–11. doi:10.1109/tim.2020.3017900

CrossRef Full Text | Google Scholar

6. Yuan H, Wu N, Chen X, Wang Y. Fault diagnosis of rolling bearing based on shift invariant sparse feature and optimized support vector machine. Machines (2021) 9(5):98. doi:10.3390/machines9050098

CrossRef Full Text | Google Scholar

7. Zhang J, Hu X, Zhong X, Zhou H. Fault diagnosis of axle box bearing with acoustic signal based on chirplet transform and support vector machine. Shock and Vibration (2022) 2022(1):1–12. doi:10.1155/2022/9868999

CrossRef Full Text | Google Scholar

8. Ismail M, Vardhan VH, Mounika VA, Padmini KS. An effective heart disease prediction method using artificial neural network. Int J Innovative Technology Exploring Eng (2019) 8(8):1529–32.

Google Scholar

9. Zhang H, Sun J, Hou K, Li Q, Liu H. Improved information entropy weighted vague support vector machine method for Transformer fault diagnosis. High Voltage (2022) 7(3):510–22. doi:10.1049/hve2.12095

CrossRef Full Text | Google Scholar

10. Euldji R, Boumahdi M, Bachene M. Decision-making based on decision tree for ball bearing monitoring[C]//2020 2nd international workshop on human-centric smart environments for health and well-being (IHSH). IEEE (2021) 171–5.

Google Scholar

11. Ye Y, Zhu B, Huang P, Peng B. OORNet: a deep learning model for on-board condition monitoring and fault diagnosis of out-of-round wheels of high-speed trains. Measurement (2022) 199:111268. doi:10.1016/j.measurement.2022.111268

CrossRef Full Text | Google Scholar

12. Jovanovic L, Damaševičius R, Matic R, Kabiljo M, Simic V, Kunjadic G, et al. Detecting Parkinson’s disease from shoe-mounted accelerometer sensors using convolutional neural networks optimized with modified metaheuristics. PeerJ Computer Sci (2024) 10:e2031. doi:10.7717/peerj-cs.2031

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Purkovic S, Jovanovic L, Zivkovic M, Antonijevic M, Dolicanin E, Tuba E, et al. Audio analysis with convolutional neural networks and boosting algorithms tuned by metaheuristics for respiratory condition classification. J King Saud University-Computer Inf Sci (2024) 36(10):102261. doi:10.1016/j.jksuci.2024.102261

CrossRef Full Text | Google Scholar

14. Peng D, Wang H, Liu Z, Zhang W, Zuo MJ, Chen J. Multibranch and multiscale CNN for fault diagnosis of wheelset bearings under strong noise and variable load condition. IEEE Trans Ind Inform (2020) 16(7):4949–60. doi:10.1109/tii.2020.2967557

CrossRef Full Text | Google Scholar

15. Deng F, Ding H, Lü H. Fault diagnosis of high-speed train wheelset bearing based on a lightweight neural network. Chin J Eng (2021) 43(11):1482–90.

Google Scholar

16. Salb M, Jovanovic L, Elsadai A, Bacanin N, Simic V, Pamucar D, et al. Cloud spot instance price forecasting multi-headed models tuned using modified PSO. J King Saud University-Science (2024) 36(11):103473. doi:10.1016/j.jksus.2024.103473

CrossRef Full Text | Google Scholar

17. Petrovic A, Jovanovic L, Venkatachalam K, Zivkovic M, Bacanin N, Budimirovic N. Anomaly detection in electrocardiogram signals using metaheuristic optimized time-series classification with attention incorporated models. Int J Hybrid Intell Syst (2024) 20(2):159–83. doi:10.3233/his-240004

CrossRef Full Text | Google Scholar

18. Cui X, Zhu J, Jia L, Wang J, Wu Y. A novel heat load prediction model of district heating system based on hybrid whale optimization algorithm (WOA) and CNN-LSTM with attention mechanism. Energy (2024) 312:133536. doi:10.1016/j.energy.2024.133536

CrossRef Full Text | Google Scholar

19. Yuan Z, Ma Z, Li X, Liu S, Mu T, Chen Y. A graph attention based multichannel transfer learning network for wheelset bearing fault diagnosis with nonshared fault classes. IEEE Sensors J (2023) 24(2):1929–40. doi:10.1109/jsen.2023.3337853

CrossRef Full Text | Google Scholar

20. Liao JX, Dong HC, Sun ZQ, Sun J, Zhang S, Fan FL. Attention-embedded quadratic network (qttention) for effective and interpretable bearing fault diagnosis. IEEE Trans Instrumentation Meas (2023) 72:1–13. doi:10.1109/tim.2023.3259031

CrossRef Full Text | Google Scholar

21. Yang Z, Cen J, Liu X, Xiong J, Chen H. Research on bearing fault diagnosis method based on Transformer neural network. Meas Sci Technology (2022) 33(8):085111. doi:10.1088/1361-6501/ac66c4

CrossRef Full Text | Google Scholar

22. Luo X, Wang H, Han T, Zhang Y. FFT-trans: enhancing robustness in mechanical fault diagnosis with fourier transform-based transformer under noisy conditions. IEEE Trans Instrumentation Meas (2024) 73:1–12. doi:10.1109/tim.2024.3381688

CrossRef Full Text | Google Scholar

23. Ding Y, Jia M, Miao Q, Cao Y. A novel time–frequency Transformer based on self–attention mechanism and its application in fault diagnosis of rolling bearings. Mech Syst Signal Process (2022) 168:108616. doi:10.1016/j.ymssp.2021.108616

CrossRef Full Text | Google Scholar

24. Hou Y, Wang J, Chen Z, Ma J. Diagnosisformer: an efficient rolling bearing fault diagnosis method based on improved Transformer. Eng Appl Artif Intelligence (2023) 124:106507. doi:10.1016/j.engappai.2023.106507

CrossRef Full Text | Google Scholar

25. Gu X, See KW, Li P, Shan K, Wang Y, Zhao L, et al. A novel state-of-health estimation for the lithium-ion battery using a convolutional neural network and Transformer model. Energy (2023) 262:125501. doi:10.1016/j.energy.2022.125501

CrossRef Full Text | Google Scholar

26. Zhao J, Wang Z, Wu Y, Burke AF. Predictive pretrained Transformer (PPT) for real-time battery health diagnostics. Appl Energy (2025) 377:124746. doi:10.1016/j.apenergy.2024.124746

CrossRef Full Text | Google Scholar

27. Kou L, Qin Y, Zhao X, Chen X. A multi-dimension end-to-end CNN model for rotating devices fault diagnosis on high-speed train bogie. IEEE Trans Vehicular Technology (2019) 69(3):2513–24. doi:10.1109/tvt.2019.2955221

CrossRef Full Text | Google Scholar

28. Wang H, Liu Z, Peng D, Yang M, Qin Y. Feature-level attention-guided multitask CNN for fault diagnosis and working conditions identification of rolling bearing. IEEE Trans Neural networks Learn Syst (2021) 33(9):4757–69. doi:10.1109/tnnls.2021.3060494

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Zhao Z, Jiao Y. A fault diagnosis method for rotating machinery based on CNN with mixed information. IEEE Trans Ind Inform (2022) 19:9091–101. doi:10.1109/tii.2022.3224979

CrossRef Full Text | Google Scholar

30. Vaswani A, Shazeer N, Parmar N. Attention is all you need. Adv Neural Inf Process Syst (2017) 30.

Google Scholar

31. Liang P, Yu Z, Wang B, Xu X, Tian J. Fault transfer diagnosis of rolling bearings across multiple working conditions via subdomain adaptation and improved vision Transformer network. Adv Eng Inform (2023) 57:102075. doi:10.1016/j.aei.2023.102075

CrossRef Full Text | Google Scholar

32. Yuan Z, Li X, Liu S, Ma Z. A recursive multi-head graph attention residual network for high-speed train wheelset bearing fault diagnosis. Meas Sci Technology (2023) 34(6):065108. doi:10.1088/1361-6501/acb609

CrossRef Full Text | Google Scholar

33. Li S, Xu Y, Jiang W, Zhao K, Liu W. A modular fault diagnosis method for rolling bearing based on mask kernel and multi-head self-attention mechanism. Trans Inst Meas Control (2024) 46(5):899–912. doi:10.1177/01423312231188777

CrossRef Full Text | Google Scholar

34. Peng D, Wang H, Desmet W, Gryllias K. RMA-CNN: a residual mixed-domain attention CNN for bearings fault diagnosis and its time-frequency domain interpretability. J Dyn Monit Diagn (2023). doi:10.37965/jdmd.2023.156

CrossRef Full Text | Google Scholar

35. Athisayam A, Kondal M. A smart CEEMDAN, bessel transform and CNN-based scheme for compound gear-bearing fault diagnosis. J Vibration Eng and Tech (2024) 12:393–412. doi:10.1007/s42417-024-01422-z

CrossRef Full Text | Google Scholar

36. Hou J, Lu X, Zhong Y, He W, Zhao D, Zhou F. Rolling bearing fault diagnosis method by using feature extraction of convolutional time-frequency image. Proc Inst Mech Eng C: J Mech Eng Sci (2024) 238(9):4212–28. doi:10.1177/09544062231203541

CrossRef Full Text | Google Scholar

37. Ozcan IH, Devecioglu OC, Ince T, Eren L, Askar M. Enhanced bearing fault detection using multichannel, multilevel 1D CNN classifier. Electr Eng (2022) 104(2):435–47. doi:10.1007/s00202-021-01309-2

CrossRef Full Text | Google Scholar

38. Wang J, Wang D, Wang S, Li W, Song K. Fault diagnosis of bearings based on multi-sensor information fusion and 2D convolutional neural network. IEEE Access (2021) 9:23717–25. doi:10.1109/access.2021.3056767

CrossRef Full Text | Google Scholar

39. Wang X, Mao D, Li X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement (2021) 173:108518. doi:10.1016/j.measurement.2020.108518

CrossRef Full Text | Google Scholar

40. Yang J, Liu J, Xie J, Wang C, Ding T. Conditional GAN and 2-D CNN for bearing fault diagnosis with small samples. IEEE Trans Instrumentation Meas (2021) 70:1–12. doi:10.1109/tim.2021.3119135

CrossRef Full Text | Google Scholar

41. Chen H, Wei J, Huang H, Wen L, Yuan Y, Wu J. Novel imbalanced fault diagnosis method based on generative adversarial networks with balancing serial CNN and Transformer (BCTGAN). Expert Syst Appl (2024) 258:125171. doi:10.1016/j.eswa.2024.125171

CrossRef Full Text | Google Scholar