Fisheye omnidirectional stereo depth estimation assisted with edge-awareness

The wide field of view of fisheye cameras introduces significant image distortion, making accurate depth estimation more challenging compared to pinhole camera models. This paper proposes a fisheye camera panoramic depth estimation network based on edge awareness, aimed at improving depth estimation accuracy for fisheye images. We design an Edge-Aware Module (EAM) that dynamically weights features extracted by a Residual Convolutional Neural Network (Residual CNN) using the extracted edge information. Subsequently, a spherical alignment method is used to map image features from different cameras to a unified spherical coordinate system. A cost volume is built for different depth hypotheses, which is then regularized using a 3D convolutional network. To address the issue of depth value discretization, we employ a hybrid classification and regression strategy: the classification branch predicts the probability distribution of depth categories, while the regression branch uses weighted linear interpolation to compute the final depth values based on these probabilities. Experimental results demonstrate that our method outperforms existing approaches in terms of depth estimation accuracy and object structure representation on the OmniThings, OmniHouse, and Urban Dataset (sunny). Therefore, our method provides a more accurate depth estimation solution for fisheye cameras, effectively handling the strong distortion inherent in fisheye images, with improved performance in both depth estimation and detail preservation.

1 Introduction

Depth estimation is a fundamental task in computer vision, crucial for applications such as autonomous driving, robotic navigation, and virtual reality. It involves reconstructing the 3D structure of a scene from one or more images, enabling spatial awareness and environmental perception. Traditional depth estimation methods, however, rely on cameras with a limited field of view (FoV), which may not capture sufficient environmental details in certain scenarios [1, 2].

Fisheye cameras, with an ultra-wide FoV of up to 180°, offer significant advantages in large-scale monitoring and robotic vision, allowing for comprehensive environmental coverage. Despite this, their non-linear imaging characteristics pose challenges for traditional depth estimation techniques, which often fail to handle the distortions in fisheye images, particularly at the image edges [3, 4]. The image edges are compressed, causing barrel distortion, where straight lines appear curved, especially in peripheral regions, leading to depth estimation errors [5]. (Radial Distortion) Misalignments between the lens and sensor introduce shifts that impact stereo matching and depth accuracy [6]. (Tangential Distortion) These distortions lead to errors that vary across the image. While the center remains relatively undistorted, the edges suffer substantial deviations, making traditional geometric correction methods like rectification ineffective, as they cause information loss at the periphery [7]. Classical methods like stereo vision and geometric correction approaches, such as those by Kannala et al. [8], attempt to address these distortions, but they remain limited in performance for fisheye images, especially in dynamic or complex environments where distortions are more pronounced.

Another approach involves using depth sensors, such as LiDAR or structured-light cameras, to directly measure depth. While these methods provide high accuracy and precision, they often require additional hardware, which increases costs and complexity. Furthermore, these sensors can be sensitive to environmental factors such as lighting conditions, reflections, or obstructions, which can degrade their performance in certain scenarios, particularly in indoor or dynamic environments [9, 10]. Moreover, sensor-based methods are less effective in featureless or unstructured environments, where depth information may be sparse or unreliable.

In recent years, deep learning methods have revolutionized depth estimation, achieving impressive results across a variety of image processing tasks. Notable approaches like Eigen et al.’s multi-scale network [11] and Laina et al.’s residual network [12] have demonstrated high accuracy for depth prediction from single images. For fisheye images, deep learning has also been applied to overcome lens distortion challenges [13]. These methods utilize convolutional neural networks (CNNs) to learn spatial features and effectively handle distortion. Despite these advances, the non-linear distortions inherent in fisheye lenses continue to present significant challenges. Therefore, developing specialized deep learning models tailored for fisheye camera images remains essential for improving depth estimation accuracy and robustness in real-world applications, especially in complex or dynamic environments.

Up to now, many methods for omnidirectional depth estimation based on fisheye cameras have been proposed. Deep learning-based methods include Omnidet [14], which introduces a multi-task visual perception network that jointly trains six tasks-depth estimation, visual odometry, semantic segmentation, motion segmentation, object detection, and lens distortion detection-to support 360°near-field perception. Omnimvs [15] presents a novel end-to-end deep neural network model for panoramic depth estimation from a wide-baseline multi-view stereo setup. This method can build panoramic images from four fisheye images and perform depth estimation. Furthermore, Omnimvs also proposes a large-scale synthetic dataset [15]. CasOmniMVS [16] builds on this by introducing a cascaded architecture that uses a dynamic spherical scanning approach to progressively refine 360° depth estimation over multiple stages. Non-deep learning methods, such as Sphere Stereo [17], propose an efficient spherical stereo vision method that operates directly on multi-view fisheye images without requiring additional spherical calibration.

These methods represent innovative approaches to fisheye-based depth estimation, but each has its limitations. The multi-task approach in Omnidet [14], for example, appears somewhat redundant for the single task of depth estimation, potentially impacting its accuracy. The end-to-end deep network in Omnimvs [15] does not effectively integrate information beyond RGB images for depth estimation. Sphere Stereo [17] is prone to estimation errors in low-texture regions and on smooth surfaces with strong reflections.

We believe that for applications such as autonomous driving, 3D reconstruction, and augmented reality, accurate depth estimation of the overall structure of objects is crucial. Inspired by Omnidet’s multi-task approach [14], we introduce edge information as guidance for depth estimation. Edge information reflects the structural features of objects and subtle textures, while not overly complicating the task of depth estimation, thereby enhancing accuracy without sacrificing performance.

Among methods that incorporate edge information, StereoNet [18] first proposed an end-to-end deep learning architecture for real-time stereo matching, generating high-quality, edge-preserving, and quantization-free disparity maps. The method [19] presents an approach for single-image depth estimation based on edge extraction networks and dark channel priors (DCP). A Generative Adversarial Network (GAN) is used to construct an edge extraction network to select effective depth edges from multiple edges in the image. SPDET [20] introduces a self-supervised panoramic depth estimation network, which designs an edge-aware loss function to optimize depth estimation performance on panoramic images.

In this paper, we propose an edge-aware fisheye camera omnidirectional depth estimation network. To enhance the network’s sensitivity to edges, we construct an Edge-Aware Module (EAM) in the feature extraction stage, which dynamically weights features extracted by the Residual CNN using both spatial and channel attention mechanisms. Afterward, spherical alignment projects the image features from different cameras into a unified spherical coordinate system. By aligning the features, we calculate the cost volume over multiple depth hypotheses. To improve the stability of the cost volume, we use a 3D convolutional network for cost volume regularization. Since the depth values in the cost volume are discretized into multiple depth categories, we employ a mixed classification and regression strategy to predict the final depth map. The classification branch predicts the probability distribution of each pixel belonging to a specific depth category, while the regression branch uses weighted linear interpolation based on the probability distribution to compute the final depth value for each pixel. This approach ensures depth accuracy while maintaining smoothness. Experimental results on the OmniThings, OmniHouse, and Urban Dataset (sunny) [15, 21] demonstrate that our method outperforms existing methods in terms of both depth estimation accuracy and the representation of object structure.

The main contributions of this paper compared to existing methods are as follows.

• We propose a novel feature extraction method that combines Residual CNN and the Edge-Aware Module (EAM), effectively capturing structural features and edge details from images to enhance depth estimation accuracy, especially in object edges and detailed regions.

•We employ a spherical alignment approach to unify the image features from different cameras into a single spherical coordinate system, addressing the consistency issue in depth estimation across different viewpoints. Additionally, we optimize the construction of the cost volume and use a 3D convolutional network for cost volume regularization, capturing spatial correlations between the depth, horizontal, and vertical dimensions, which effectively reduces noise and enhances depth estimation robustness.

•We design a hybrid classification and regression strategy to predict the final depth map. Moreover, by introducing edge information, particularly in object boundary regions, we further enhance the accuracy of depth estimation and reduce blur and errors in transitional areas. We also propose a dual loss function that combines depth estimation loss and edge matching loss, further aligning the structural information in edge features with the depth estimation task.

The remainder of this paper is organized as follows: Section 2 introduces the proposed method and network architecture, Section 3 presents the experimental results and provides a comprehensive analysis, and Section 4 concludes the paper.

2 Methods

2.1 Network architecture

As shown in Figure 1, the proposed network is composed of several sequential stages: input, feature extraction, spherical alignment, cost volume regularization and depth regression. The proposed network introduces innovations in feature extraction and loss function design to achieve accurate depth estimation from grayscale fisheye images. The feature extraction module integrates a Residual Convolutional Neural Network (Residual CNN) and an Edge-Aware Module (EAM). The Residual CNN captures structural features while maintaining efficient gradient flow, and the EAM enhances edge-specific details using Sobel convolution and attention mechanisms. These components work together to extract both structural and boundary features, crucial for accurate depth estimation. To optimize depth prediction, we design a novel loss function combining depth estimation loss and edge matching loss. The depth estimation loss minimizes pixel-wise errors, while the edge matching loss aligns the edges of the predicted depth map with those of the input image. This dual-loss strategy ensures precise depth estimation, particularly around object boundaries, improving the overall robustness and accuracy of the network.

Figure 1

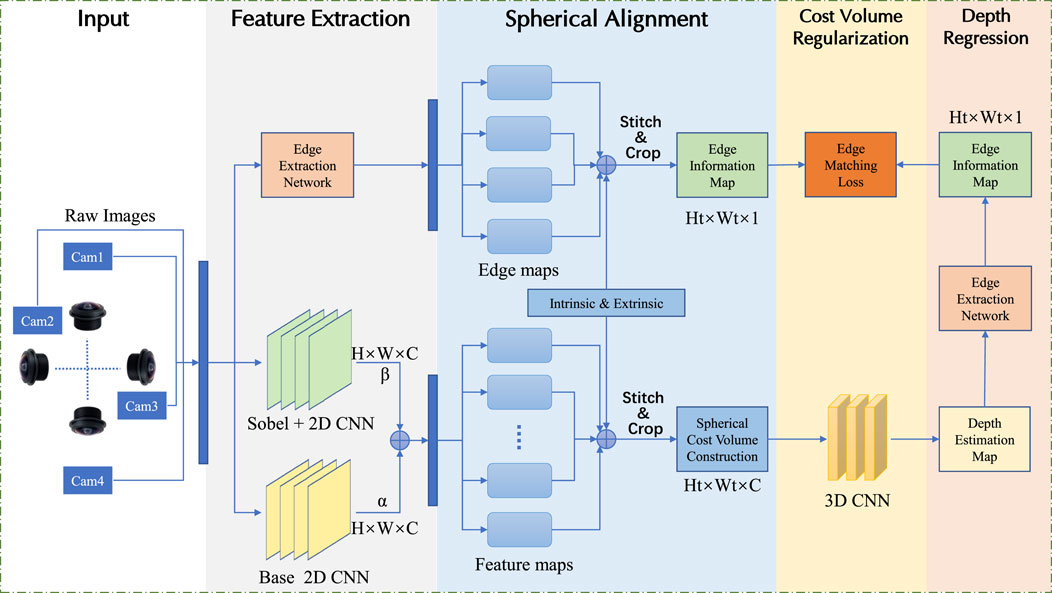
Figure 1. Overview of the network: four input images are fed into the feature extraction stage to get conventional and edge features.These feature maps are converted into sphere feature maps in the feature alignment stage to built cost volume.The edge information of the depth map generated in the depth regression stage compares with the edge information generated from raw image inputs to guide the generation of the final depth map.

2.2 Network input overview

The input to the network consists of grayscale fisheye images captured from $N_{\mathit{cam}}$cameras at different viewpoints. Each input image has a resolution of $H\times W$.The objective of this stage is to preprocess the input data and generate feature maps for subsequent processing. These feature maps serve as the basis for depth estimation tasks in later stages.

2.3 Feature extraction

We designed an feature extraction module with two blocks: Residual Convolutional Neural Network(Residual CNN) and Edge-Aware Module(EAM). This module is designed to process input images into meaningful representations, focusing on both structural and edge-specific features to achieves more accurate depth estimation for edge structures and object texture details.

2.3.1 Residual convolutional neural network (residual CNN)

The input images are processed through a convolutional network with residual connections, which improves gradient flow during training and mitigates the vanishing gradient problem. These residual connections allow for efficient learning of base features essential for depth estimation. The resulting feature maps are then downsampled to a resolution of $\frac{1}{2}H\times \frac{1}{2}W\times C$, balancing computational efficiency with the retention of key structural information.

2.3.2 Edge-aware module (EAM)

To enhance the network’s ability to capture object boundaries and fine details, the Edge-Aware Module (EAM) is applied to the feature maps produced by the residual CNN. The EAM performs two key functions: extracting edge-specific features and dynamically refining feature importance through attention mechanisms.

The first function involves edge feature extraction, where Sobel convolution is employed to generate edge-specific feature maps. The Sobel convolution is a discrete differentiation operator that computes spatial gradient approximations to identify regions of high intensity variation in digital images, corresponding to edge features. This technique employs two orthogonal $\mathbf{3}\times \mathbf{3}$ convolution kernels designed to measure horizontal $({\mathbf{G}}_{\mathbf{x}})$ and vertical $({\mathbf{G}}_{\mathbf{y}})$ directional gradients:

${\mathbf{G}}_{\mathbf{x}}=\left[\begin{array}{ccc}\hfill -1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill -2\hfill & \hfill 0\hfill & \hfill 2\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],{\mathbf{G}}_{\mathbf{y}}=\left[\begin{array}{ccc}\hfill -1\hfill & \hfill -2\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 2\hfill & \hfill 1\hfill \end{array}\right].$

For each pixel at coordinates $(i,j)$, the horizontal and vertical gradients are computed through discrete convolution between the respective kernel and local image neighborhood. The gradient magnitude $\mathbf{M}(\mathbf{i},\mathbf{j})$ and orientation $\theta (i,j)$ are then calculated as:

$\begin{array}{ll}\hfill M\left(i,j\right)& =\sqrt{G_x{\left(i,j\right)}^2+G_y{\left(i,j\right)}^2},\hfill \\ \hfill \theta \left(i,j\right)& =\arctan \left(\frac{G_y\left(i,j\right)}{G_x\left(i,j\right)}\right).\hfill \end{array}$

High gradient magnitudes indicate rapid intensity changes characteristic of edges. A threshold $\mathbf{T}$ is applied to $\mathbf{M}(\mathbf{i},\mathbf{j})$ to distinguish significant edges from noise:

$E\left(i,j\right)=\left\{\begin{array}{cc}1,\hfill & \text{if\hspace{0.17em}}M\left(i,j\right)>T,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\right.$

The directional nature of the kernels enhances vertical and horizontal edge sensitivity while providing inherent noise suppression through weighted neighborhood averaging. This makes Sobel convolution particularly effective for extracting geometrically salient boundaries in images while maintaining computational efficiency.

Within our network pipeline, raw input images are first subjected to Gaussian blur denoising, followed by gradient computation through horizontal and vertical Sobel convolutions using convolution kernel ${\mathbf{G}}_{\mathbf{x}}$ and ${\mathbf{G}}_{\mathbf{y}}$. The resulting gradient magnitudes are normalized to the $[\mathrm{0,255}]$ intensity range, after which a fixed threshold $(T=130)$ is applied to distinguish edge features (gradient values $>130$) from background regions (gradient values $\le 130$).These features capture critical boundary details and object textures, complementing the base features extracted by the residual CNN.

The second function introduces attention mechanisms to refine the extracted features further. The channel attention mechanism computes the importance of each feature channel by applying global pooling, assigning higher weights to channels most relevant to the task. In parallel, the spatial attention mechanism generates an attention map through convolution operations, emphasizing key spatial regions such as edges and fine textures. Together, these mechanisms adaptively enhance the representation of the most critical features for depth estimation. The block extracts features with shape $\frac{1}{2}H\times \frac{1}{2}W\times C$,where $H$ and $W$ represent input height and width.

2.3.3 Feature fusion

The base features and edge features are combined using a weighted summation:

$F_{\mathit{out}}=\alpha \cdot F_{\mathit{struct}}+\beta \cdot F_{\mathit{edge}}(1)$

Here, $\alpha$ and $\beta$ are trainable parameters dynamically updated during training and both initialized with a value of 0.5. This adaptive fusion enhances the network’s ability to capture both low-level edge details and high-level contextual features. $F_{\mathit{out}}$ is a tensor with a shape of $\frac{1}{2}H\times \frac{1}{2}W\times C$ as well.

2.4 Spherical alignment

2.4.1 Unified projection to a common spherical coordinate system

The input fisheye images are first projected from their respective camera coordinate systems to a unified spherical coordinate system as shown in Figure 2. For each fisheye camera, the transformation from image coordinates $(u,v)$ to spherical coordinates $(d,\theta ,\varphi )$ is defined as follows:

Figure 2

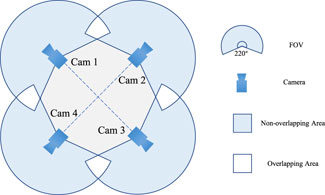
Figure 2. The structure of the multi-camera rig system.In feature alignment stage, we convert feature points from the camera coordinate system to sphere coordinate system using instrinsic and extrinsic camera parameters.

A pixel $(u,v)$ n the fisheye image is transformed into the 3D camera coordinate system using the intrinsic camera matrix $K_i$ and a depth hypothesis:

$d:X_c=d\cdot K_i^{-1}\left[\begin{array}{c}\hfill u\hfill \\ \hfill v\hfill \\ \hfill 1\hfill \end{array}\right](2)$

The 3D point in the camera coordinate system $X_c$ is then mapped to the world coordinate system using the extrinsic camera parameters $R_i$(rotation) and $t_i$:

$X_w=R_i{X}_c+t_i(3)$

Finally, the world coordinates $(x,y,z)$ are converted to spherical coordinates $(d,\theta ,\varphi )$, where:

$d=\Vert {\mathbf{X}}_w\Vert ,\theta =\arctan 2\left(y,x\right),\varphi =\arcsin \left(\frac{z}{d}\right).(4)$

where $d$ is the radial distance, $\theta$ is the horizontal angle$([-\pi ,\pi ])$, and $\varphi$ is the vertical angle$([-\frac{\pi }{2},\frac{\pi }{2}])$.

This projection ensures that features from all cameras are geometrically aligned in the spherical coordinate system, facilitating the subsequent cost volume construction.

2.4.2 Cost volume construction

The spherical cost volume is constructed to represent the feature consistency across multiple views at varying depth hypotheses $d_k$. For each depth hypothesis, the features from all cameras are projected onto a unified spherical coordinate grid $(\theta ,\varphi )$ using the projection process described earlier. This step ensures that the features from different cameras are spatially aligned on the spherical coordinate system, facilitating consistency evaluation. But in our network, the inverse of the depth $d_k^{\prime }=\frac{1}{d_k}$ is used, which is motivated by the non-linear distribution of depth variations in 3D scenes. Depth changes are more significant for objects closer to the camera and become less noticeable as the distance increases. By representing depth as its inverse, the distribution of depth differences is normalized, ensuring more uniform spacing between the hypothetical spherical surfaces in the cost volume. This approach enhances the accuracy of depth estimation, particularly in scenes with a wide range of depth values. Furthermore, to reduce the computational overhead associated with estimating continuous values, the inverse depth $d_k^{\prime }$ is discretized into a finite number of spherical surface indices $idx$. This discretization enables the efficient representation of depth hypotheses while maintaining sufficient resolution for accurate depth estimation. The discretization process is as follows:

The range of the inverse depth, $[d_{\text{min}}^{\prime },d_{\text{max}}^{\prime }]$, is divided into $N$ equally spaced intervals, where the spacing for each interval is defined as:

$\mathrm{\Delta }{d}^{\prime }=\frac{d_{\text{max}}^{\prime }-d_{\text{min}}^{\prime }}{N-1},(5)$

For a given inverse depth value $d^{\prime }$, we use the function in [17] for computing the corresponding index $\text{idx}$ of the hypothetical spherical surface:

$idx=\frac{d_k^{\prime }-d_{\text{min}}^{\prime }}{\mathrm{\Delta }{d}^{\prime }}=\frac{N-1}{d_{\text{max}}^{\prime }-d_{\text{min}}^{\prime }}\cdot \left(d_k^{\prime }-d_{\text{min}}^{\prime }\right).(6)$

This discretization reduces the computational complexity by converting the continuous depth estimation problem into a discrete search over a finite number of hypothetical spherical surfaces. It also ensures efficient representation and computation of depth hypotheses while maintaining sufficient accuracy for depth reconstruction.

To quantify the consistency of features across views, the cost volume $C(idx,\theta ,\varphi )$ is defined as the aggregation of feature differences between each camera and the mean feature across all cameras at a given depth hypothesis. Mathematically, this is expressed as:

$C\left(idx,\theta ,\varphi \right)={\displaystyle \sum _{i=1}^{N_{\text{cam}}}}{‖F_i\left(idx,\theta ,\varphi \right)-\bar{F}\left(d_k,\theta ,\varphi \right)‖}^2,(7)$

where $F_i(idx,\theta ,\varphi )$ represents the feature value from the $i$-th camera at the given depth index $idx$ and angular position $(\theta ,\varphi )$, and $\bar{F}(idx,\theta ,\varphi )$ is the mean feature value across all cameras, calculated as:

$\bar{F}\left(idx,\theta ,\varphi \right)=\frac{1}{N_{\text{cam}}}{\displaystyle \sum _{i=1}^{N_{\text{cam}}}}{F}_i\left(idx,\theta ,\varphi \right).(8)$

To enhance robustness in cost volume construction, alternative fusion strategies can be employed. One common approach is variance-based fusion, where the cost is computed as:

$C\left(idx,\theta ,\varphi \right)=\frac{1}{N_{\text{cam}}}{\displaystyle \sum _{i=1}^{N_{\text{cam}}}}{\left(F_i\left(idx,\theta ,\varphi \right)-\bar{F}\left(idx,\theta ,\varphi \right)\right)}^2.(9)$

The cost volume thus encodes the multi-view feature consistency for all depth hypotheses and spherical coordinates, serving as the foundation for subsequent depth estimation.

Through spherical alignment and cost volume construction, followed by stitching and cropping, the feature maps generated from four images are combined into a single feature map with dimensions $H_t\times W_t\times C$, here, $H_t=160,W_t=640$, which is subsequently utilized for cost volume regularization. Simultaneously, boundary information extracted from the original images using an edge detection network undergoes an identical stitching and cropping process, resulting in a boundary map of dimensions $H_t\times W_t\times 1$. This boundary map serves as auxiliary information to refine and optimize the depth estimation process.

2.5 Cost volume regularization

Our method employs 3D convolutional networks for cost volume regularization to capture spatial and depth-wise correlations, improving consistency and reducing noise. The raw cost volume$C_{\mathit{raw}}(idx,\theta ,\varphi )$ is processed using a series of 3D convolutional layers to extract local and global dependencies. Formally, the regularized cost volume is expressed as:

$C_{\mathit{reg}}\left(idx,\theta ,\varphi \right)=\mathbf{C}\mathbf{o}\mathbf{n}\mathbf{v}\mathbf{3}\mathbf{D}\left(C_{\mathit{raw}}\left(idx,\theta ,\varphi \right)\right)(10)$

where Conv3D represents the 3D convolution operation applied across the depth, horizontal, and vertical dimensions.

By leveraging the hierarchical feature extraction capability of the 3D convolutional network, our method smooths inconsistencies in the cost volume and enhances the discriminative power of depth hypotheses. This regularization step ensures robust depth estimation, even in challenging scenarios with noisy or incomplete data.

2.6 Depth regression

The final depth map is estimated using a hybrid classification and regression strategy. The depth values in the cost volume are discretized into $N$ depth categories, allowing the classification branch to predict the probability distribution $P(i,j,n)$ for each pixel $(i,j)$ belonging to depth $d_n$ using a cross-entropy loss function. Based on the probability distribution, the regression branch computes the final depth value using a weighted linear interpolation:

$D_{\text{pred}}\left(i,j\right)={\displaystyle \sum _{n=0}^{N-1}}P\left(i,j,n\right)\cdot d_n,(11)$

where $P(i,j,n)$ represents the probability that pixel $(i,j)$ belongs to depth $d_n$. This hybrid approach combines the robustness of classification with the precision of regression, ensuring smooth and accurate depth estimation. The output is expected to be a depth map with a shape of $H_t\times W_t\times 3$.

2.7 Edge-based depth estimation optimization

To make the generated depth map more accurate, particularly around object boundaries, we designed an edge-based optimization strategy. The edge detection branch extracts edge information from the RGB image and guides the depth estimation branch to refine the depth map. The introduction of edge information significantly improves the boundary quality of the depth map, reduces blur in transition regions, and minimizes errors in depth discontinuity areas. We extract a binary edge maps of input images using an edge extraction network proposed in Li et al. [22], then the maps are stitched and cropped into a full binary edge map with a shape of $H_t\times W_t\times 1$.Simultaneously, we utilized this network to extract a binary edge map from the depth map we get in the stage of depth regression. Two binary edge maps has the same shape.

We use an additionally designed loss function to simultaneously account for the differences in depth estimation and edge information, optimizing our task of end-to-end depth estimation.

2.8 Loss function

Our loss function consists of two components: the depth estimation loss(Loss 1) and the edge matching loss(Loss 2). In the depth estimation loss, we use the SmoothL1 loss to measure the pixel-level error between the generated depth map $D_{\mathit{pred}}$ and the ground truth depth map $D_{gt}$:

$\mathbf{L}\mathbf{o}\mathbf{s}\mathbf{s}\mathbf{1}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\mathbf{S}\mathbf{m}\mathbf{o}\mathbf{o}\mathbf{t}\mathbf{h}\mathbf{L}\mathbf{1}\left(D_{\text{pred}}\left(i\right),D_{\text{gt}}\left(i\right)\right)(12)$

In the edge matching loss, we employ the $\mathbf{S}\mathbf{m}\mathbf{o}\mathbf{o}\mathbf{t}\mathbf{h}\mathbf{L}\mathbf{1}$ loss to measure the discrepancy between the edges of the generated depth map $\mathcal{E}(D_{\text{pred}})$ and the edges of the input RGB image $\mathcal{E}(I_{\text{rgb}})$:

$\mathbf{L}\mathbf{o}\mathbf{s}\mathbf{s}\mathbf{2}=\frac{1}{N}{\displaystyle \sum _{j=1}^N}\mathbf{S}\mathbf{m}\mathbf{o}\mathbf{o}\mathbf{t}\mathbf{h}\mathbf{L}\mathbf{1}\left(\mathcal{E}\left(D_{\text{pred}}\right)\left(j\right),\mathcal{E}\left(I_{\text{rgb}}\right)\left(j\right)\right)(13)$

Here,$\mathcal{E}(\cdot )$ represents the edge extraction network, and $N$ is the total number of pixels in the edge map.The definition of SmoothL1 is as follows:

$\mathbf{S}\mathbf{m}\mathbf{o}\mathbf{o}\mathbf{t}\mathbf{h}\mathbf{L}\mathbf{1}\left(x,y\right)=\left\{\begin{array}{cc}0.5\cdot {\left(x-y\right)}^2,\hfill & \text{if\hspace{0.17em}}|x-y|<1,\hfill \\ |x-y|-0.5,\hfill & \text{otherwise}.\hfill \end{array}\right.(14)$

The total loss function $(\mathbf{L}\mathbf{o}\mathbf{s}\mathbf{s})$ is defined as

$\mathbf{L}\mathbf{o}\mathbf{s}\mathbf{s}=\alpha \cdot \mathbf{L}\mathbf{o}\mathbf{s}\mathbf{s}\mathbf{1}+\beta \cdot \mathbf{L}\mathbf{o}\mathbf{s}\mathbf{s}\mathbf{2},(15)$

where $\alpha$ and $\beta$ are weighting hyper-parameters used to balance the depth estimation loss and the edge matching loss.

3 Experiment

3.1 Setup details

This study utilizes the Omnidirectional Stereo Dataset, specifically designed for multi-view omnidirectional stereo depth estimation tasks. The dataset contains pairs of fisheye images captured under various environmental conditions, along with corresponding ground truth depth maps. It includes several subsets: Sunny, containing cityscape scenes under sunny conditions; Cloudy, with scenes captured under cloudy weather conditions; Sunset, featuring synthetic scenes with low light due to sunset conditions; OmniHouse, comprising indoor environments with diverse lighting and layout conditions; and OmniThings, used for evaluating depth estimation on various object types, including scenes with complex occlusions and geometries. Each image has a resolution of 768 × 800 pixels and includes four fisheye images covering a 220° field of view, along with 360° omnidirectional depth maps at 640-pixel resolution, providing a comprehensive basis for training and evaluating depth estimation methods. Experiments were conducted on a machine with an NVIDIA V100 GPU, running Ubuntu 18.04 and PyTorch 1.1.0. In all our experiments, the output and the GT depth maps are cropped to $H_t=160$ and $W_t=640$. The number of sweep spheres is set to $N=192$. To optimize our network, we trained our network on the OmniHouse, OmniThings and Sunny datasets for 30 epochs. The three datasets we utilized in this study were devided with 70 percent of the data allocated for training and the remaining 30 percent reserved for testing. This split ensures that the model is trained on a majority of the data while maintaining a separate subset for evaluating its performance objectively. We choose the AdamW optimizer, and the start learning rate $\lambda$ is set to be 0.0025 for the first 20 epochs and 0.00025 for the rest 10 epochs.

3.2 Experiments

3.2.1 Quantitative evaluation

Table 1 presents a quantitative comparison of our proposed method with three baseline models (Model 1, OmniMVS-ft, and CasOmniMVS-ft) on the panoramic stereo dataset. The evaluation metrics include Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and the percentage of pixels where the depth error exceeds 1 meter, 3 meters, and 5 meters. The results demonstrate that our method outperforms all baseline models across these metrics, particularly in handling fisheye images with strong wide-angle distortion. Specifically, our method shows lower MAE and RMSE values, and the percentage of pixels with errors greater than a threshold (denoted as ”>n”) is smaller, indicating that our method maintains high accuracy across various depth ranges.

Table 1

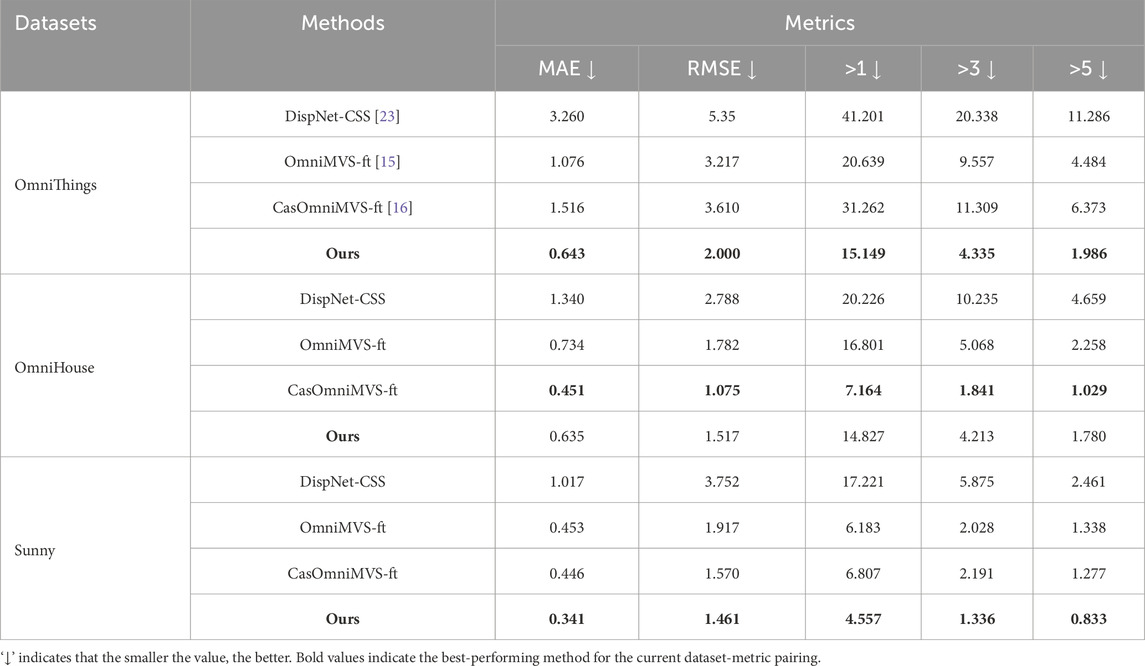
Table 1. Quantitative comparisons of depth estimation models on the Omnidirectional Stereo Dataset. The metrics include MAE (Mean Absolute Error), RMSE (Root Mean Squared Error), and the percentage of pixels with depth errors greater than 1 m, 3 m, and 5 m.

Our improvements stem from the introduction of an Edge-Aware Module (EAM), which effectively enhances the network’s sensitivity to edge information. This is especially crucial for fisheye camera images, where strong wide-angle distortion often causes the geometric structure of objects to be severely warped. Traditional depth estimation methods struggle to accurately capture the true shape of these objects, resulting in large depth estimation errors. The Edge-Aware Module improves depth estimation accuracy in object edges and detailed regions by emphasizing edge features, significantly reducing MAE and RMSE. After multiple rounds of model training and convergence, the weights in the Base 2D CNN for feature fusion consistently demonstrated higher values than the weights in the Sobel+2D CNN (average ratio 1.8:1). Under low-light conditions, values increased significantly, showing a 37.2% improvement compared to baseline measurements. This optimized weighting ratio enables the model to better learn edge information, thereby establishing a solid foundation for accurate depth estimation.

Furthermore, our method incorporates an enhanced cost volume regularization strategy, which stabilizes estimates across different depth hypotheses, further improving the overall depth estimation accuracy. Compared to baseline methods, our approach exhibits more balanced performance across different depth error distributions, demonstrating its advantages in estimating large-scale depth variations and fine-depth differences.

3.2.2 Qualitative evaluation

Figure 3 illustrates the qualitative analysis results of our proposed method compared to other methods on the same dataset. As shown in the image, our method performs better in areas such as object edge regions (highlighted by the yellow dashed boxes in the figure), low-texture regions(highlighted by the white boxes in the figure) compared to other methods.

Figure 3

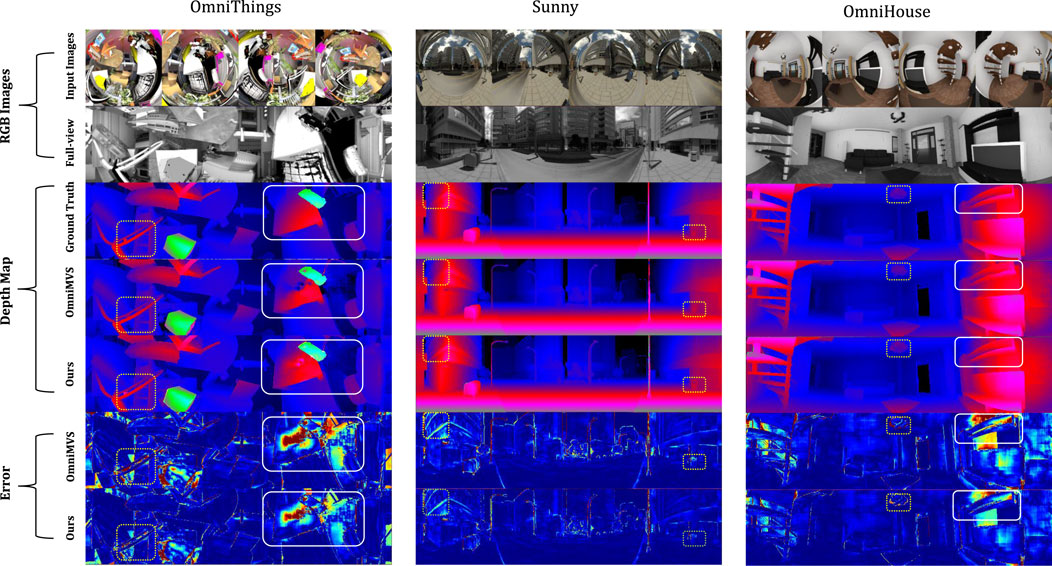
Figure 3. A detailed comparison with the sunny dataset from OmniThings, OmniHouse, and Urban Dataset demonstrates the performance of our method compared to OmniMVS, especially in terms of edge and object structure details. The results show that our method handles details better and achieves smaller overall errors.

Moreover, from the predicted depth maps, it is evident that our method excels in restoring object structures. The introduction of the Edge-Aware Module enables better capture of geometric features, especially in complex scenes where object edges and structures are more accurately reconstructed. For instance, under occlusion or complex lighting conditions, the depth estimates with edge information not only maintain smoothness but also enhance the clarity of object contours, thereby improving the overall structural perception of the scene.

Additionally, through spherical alignment and the hybrid classification-regression strategy, we are able to align multi-view data and process different depth categories using a weighted averaging method. This further enhances the smoothness and consistency of the depth maps, particularly in complex environments, such as outdoor urban landscapes. In the qualitative analysis, our method demonstrates excellent adaptability and robustness in these dynamic scenarios.

3.3 Disccusion

The experimental results, as presented in both quantitative and qualitative evaluations, demonstrate the effectiveness of our proposed depth estimation method compared to traditional approaches. Quantitatively, our method outperforms baseline models such as OmniMVS-ft and CasOmniMVS-ft across all key metrics, including MAE, RMSE, and the percentage of pixels with depth errors exceeding thresholds of 1m, 3m, and 5 m. Specifically, we observe significant reductions in MAE and RMSE, with a notable improvement in the percentage of accurate depth estimates in challenging areas, such as the image boundaries where fisheye distortion is most pronounced. Qualitatively, our method excels in regions with pronounced distortion, such as object edges and low-texture areas, as highlighted by the yellow dashed boxes and white boxes in Figure 3. In contrast, baseline models struggle to maintain accuracy in these regions. These results confirm that incorporating edge detection into our approach is key to improving depth estimation, particularly in fisheye images with significant distortion.

As shown in Figure 3, we achieve a better error than that OmniMVS can do. Despite good results at the edges of the object and an improvement in error performance in low-texture areas, the error value still does not fall to a reasonable level. This is really the next issue that we are committed to solving. Our next goal was to modify the network architecture and refine the feature extraction part to enhance the network’s perception of low-texture areas.

4 Conclusion

In this study, we present a depth estimation method specifically designed for fisheye cameras, incorporating edge detection to address the challenges posed by lens distortions. Using the Omnidirectional Stereo Dataset, we show that traditional methods struggle with fisheye distortions, especially at the image edges. By integrating edge detection, our approach enhances depth estimation accuracy, particularly in areas with significant distortion.Experimental results on datasets demonstrate that our method outperforms baseline models in key metrics. These results highlight the effectiveness of edge detection in improving depth estimation in complex, wide-angle environments.

Beyond foundational autonomous driving applications (e.g., automated parking, curb detection), our wide-field-of-view framework with edge-aware refinement shows potential for 3D reconstruction and VR systems by leveraging structural cues from distortion-prone regions. Future work will prioritize real-time processing of fisheye video streams and enhanced structural representation via edge-guided optimization. Additionally, integrating multi-modal sensor fusion (e.g., sparse LiDAR) could address occlusion limitations in complex scenes. These directions aim to bridge the gap between computational efficiency and precision in wide-angle depth estimation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JS: Conceptualization, Funding acquisition, Methodology, Resources, Supervision, Visualization, Writing – original draft, Writing – review and editing. HX: Investigation, Visualization, Writing – original draft, Writing – review and editing. SG: Conceptualization, Software, Validation, Visualization, Writing – review and editing. Xunqi Zheng: Supervision, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported in part by the Basic Science Center Program of the National Natural Science Foundation of China (no. 62388101) and the Fundamental Research Funds for the Central Universities (2023ZKPYJD06). It was also funded by the Student Innovation Training Program of China University of Mining and Technology (Beijing) (202414022).

Acknowledgments

The authors would like to thank the editors and reviewers for their efforts in supporting the publication of this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhang Z. A flexible new technique for camera calibration. IEEE Transactions on Pattern Analysis and Machine Intelligence (2000) 22 (11):1330–1334. doi:10.1109/34.888718

CrossRef Full Text | Google Scholar

2. Hirschmüller H. Stereo processing by semiglobal matching and mutual information. IEEE Transactions on Pattern Analysis and Machine Intelligence (2008) 30 (2):328–341. doi:10.1109/TPAMI.2007.1166

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Son E, Lee J, Lee JY, Jeon HG. Monocular depth estimation from a fisheye camera based on knowledge distillation. Sensors (2023) 23 (24):9866. doi:10.3390/s23249866

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Zhang X, Li Y, Chen M. A fisheye distortion correction method based on deep learning. Proceedings of the 2022 6th International Conference on Electronic Information Technology and Computer Engineering (EITCE '22) (2022):1999–2004. doi:10.1145/3573428.3573692

CrossRef Full Text | Google Scholar

5. Hartley R, Zisserman A. Multiple view geometry in computer vision. Cambridge University Press (2004).

Google Scholar

6. Jiang H, Lou Z, Ding L, Xu R, Tan M, Jiang W, et al. Defom-stereo: depth foundation model based stereo matching. arXiv preprint arXiv:2501.09466 (2025).

Google Scholar

7. Yao Y, Ishikawa R, Ando S, Kurata K, Ito N, Shimamura J, et al. Non-learning stereo-aided depth completion under mis-projection via selective stereo matching. IEEE Access (2021) 9: 136674–136686. doi:10.1109/ACCESS.2021.3117710

CrossRef Full Text | Google Scholar

8. Kannala J, Brandt SS. A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses. IEEE Transactions on Pattern Analysis and Machine Intelligence (2006) 28 (8):1335–1340. doi:10.1109/TPAMI.2006.153

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhang J, Singh S. LOAM: lidar odometry and mapping in real-time. Robotics: Science and Systems (2014). doi:10.15607/RSS.2014.X.007

CrossRef Full Text | Google Scholar

10. Salvi J, Pages J, Batlle J. Pattern codification strategies in structured light systems. Pattern Recognition (2004) 37 (4):827–849. doi:10.1016/j.patcog.2003.10.002

CrossRef Full Text | Google Scholar

11. Eigen D, Puhrsch C, Palm L. Depth map prediction from a single image using a multi-scale deep network. Adv Neural Inf Process Syst (Neurips) (2014).

Google Scholar

12. Laina I, Rupprecht C, Gaidon A. Deeper depth prediction with fully convolutional residual networks. In: European conference on computer vision (ECCV) (2016). p. 203–20.

Google Scholar

13. Liao Z, Zhou W. DaFIR: distortion-aware representation learning for fisheye image rectification. IEEE Transactions on Circuits and Systems for Video Technology (2024) 34 (5):3606–3618. doi:10.1109/TCSVT.2023.3315967

CrossRef Full Text | Google Scholar

14. Kumar VR, Yogamani SK, Rashed H, Sistu G, Witt C, Leang I, et al. Omnidet: surround view cameras based multi-task visual perception network for autonomous driving. CoRR abs/2102 (2021) 6(07448):2830–7. doi:10.1109/lra.2021.3062324

CrossRef Full Text | Google Scholar

15. Won C, Ryu J, Lim J. Omnimvs: end-to-end learning for omnidirectional stereo matching. In: 2019 IEEE/CVF international conference on computer vision (ICCV) (2019). p. 8986–95. doi:10.1109/ICCV.2019.00908

CrossRef Full Text | Google Scholar

16. Wang P, Li M, Cao J, Du S, Li Y. Casomnimvs: cascade omnidirectional depth estimation with dynamic spherical sweeping. Appl Sci (2024) 14:517. doi:10.3390/app14020517

CrossRef Full Text | Google Scholar

17. Meuleman A, Jang H, Jeon DS, Kim MH. Real-time sphere sweeping stereo from multiview fisheye images. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR) (2021). p. 11423–32.

Google Scholar

18. Khamis S, Fanello S, Rhemann C, Kowdle A, Valentin J, Izadi S. Stereonet: guided hierarchical refinement for real-time edge-aware depth prediction. In: Proceedings of the European conference on computer vision (ECCV) (2018). p. 573–90.

Google Scholar

19. Li Y, Jung C, Kim J. Single image depth estimation using edge extraction network and dark channel prior. IEEE Access (2021) 9:112454–65. doi:10.1109/ACCESS.2021.3100037

CrossRef Full Text | Google Scholar

20. Zhuang C, Lu Z, Wang Y, Xiao J, Wang Y. Spdet: edge-aware self-supervised panoramic depth estimation transformer with spherical geometry. IEEE Trans Pattern Anal Machine Intelligence (2023) 45:12474–89. doi:10.1109/TPAMI.2023.3272949

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Won C, Ryu J, Lim J. Sweepnet: wide-baseline omnidirectional depth estimation. In: IEEE international conference on robotics and automation (ICRA) (2019). p. 6073–9.

Google Scholar

22. Li Y, Jung C, Kim J. Single image depth estimation using edge extraction network and dark channel prior. IEEE Access (2021b) 9:112454–65. doi:10.1109/ACCESS.2021.3100037

CrossRef Full Text | Google Scholar

23. Ilg E, Saikia T, Keuper M, Brox T. Occlusions, motion and depth boundaries with a generic network for disparity, optical flow or scene flow estimation. CoRR abs/1808 (2018):01838.

Google Scholar