- 1Dipartimento di Fisica e Astronomia, Universitá di Bologna, Bologna, Italy
- 2Istituto di Radio Astronomia, Istituto Nazione di Astro Fisica (INAF), Bologna, Italy
Introduction: The “simulation hypothesis” is a radical idea which posits that our reality is a computer simulation. We wish to assess how physically realistic this is, based on physical constraints from the link between information and energy, and based on known astrophysical constraints of the Universe.
Methods: We investigate three cases: the simulation of the entire visible Universe, the simulation of Earth only, or a low-resolution simulation of Earth compatible with high-energy neutrino observations.
Results: In all cases, the amounts of energy or power required by any version of the simulation hypothesis are entirely incompatible with physics or (literally) astronomically large, even in the lowest resolution case. Only universes with very different physical properties can produce some version of this Universe as a simulation.
Discussion: It is simply impossible for this Universe to be simulated by a universe sharing the same properties, regardless of technological advancements in the far future.
1 Introduction
The “simulation hypothesis” (SH) is a radical and thought-provoking idea with ancient and noble philosophical roots (for example, works by Descartes [1] and Berkeley [2]) and frequent echoes in the modern literature, which postulates that the reality we perceive is the creation of a computer program.
The modern version of the debate usually refers to an influential article by Bostrom [3], although several coeval science fiction movies contributed to popularizing this theme1.
Despite its immense popularity, this topic has rarely been investigated scientifically because, at first sight, it might seem to be entirely out of the boundaries of falsifiability and hence relegated to social media buzz and noise.
A remarkable exception is the work by Beane et al. [4], who investigated the potentially observable consequences of the SH by exploring the particular case of a cubic spacetime lattice. They found that the most stringent bound on the inverse lattice spacing of the universe is
Our starting point is that “ information is physical” [5, 6], and hence, any numerical computation requires a certain amount of power, energy, and computing time, and the laws of physics can clearly tell us what is possible to simulate and under which conditions. We can use these simple concepts to assess the physical plausibility—or impossibility—of a simulation reproducing the Universe2 we live within, and even of some lower resolution version of it.
Moreover, the powerful physical nature of information processing allows us to even sketch the properties that any other universe simulating us must have in order for the simulation to be feasible.
This paper is organized as follows: Section 2 presents the quantitative framework we will use to estimate the information and energy budget of simulations; Section 3 will present our results for different cases of the SH; and Section 4 will critically assess some of the open issues in our treatment. Our conclusions are summarized in Section 4.6.
2 Methods: the holographic principle and information-energy equivalence
In order to assess which resources are needed to simulate a given system, we need to quantify how much information can be encoded in a given portion of the Universe (or in its totality). The holographic principle (HP) arguably represents the most powerful tool for establishing this connection. It was inspired by the modeling of black hole thermodynamics through the Bekenstein bound (see below), according to which the maximum entropy of a system scales within its encompassing surface rather than its enclosing volume. The HP is at the core of the powerful anti-de Sitter/conformal field theory correspondence (AdS/CFT), which links string theory with gravity in five dimensions with the quantum field theory of particles with no gravity on a four-dimensional space [7].
According to the HP, a stable and asymptotically flat spacetime region with the boundary of area
where obviously
In Equation 2,
Next, we can use the classical information-entropy equivalence [11], which states that the minimum entropy production connected with any 1-bit measurement is given by Equation 3:
where the log(2) reflects the binary decision. The amount of entropy for a single 1-bit measurement (or for any single 1-bit flip, i.e., a computing operation) can be greater than this fundamental amount but not smaller; otherwise, the second law of thermodynamics would be violated.
Therefore, the total information (in [bits]) that can possibly be encoded within the holographic surface
How much energy is required to encode an arbitrary amount of information
where
It is interesting to compute the ratio between the enclosed energy within the holographic surface,
This physically means even at the low temperature of
The exact bounds derived from Equation 4 depend on what systems are considered and on how
3 Results: information requirements and energy bounds
3.1 Full simulation of the visible Universe
Based on the above formulas, we can first estimate the total information contained within the holographic surface with radius equal to the observable radius of the Universe,
Based on Equation 4, Equation 9 results in a maximum information of
which results into an ecoding energy given by Equation 10:
Assuming a computing temperature equal to the microwave background temperature nowadays

Table 1. Summary of the size, resolution, memory, and energy requirements of the tested simulation hypotheses.
As anticipated, because
As noted above, slightly different estimates for the total information content of the Universe can be obtained by replacing the Bekenstein bound with the Hawking–Bekenstein formula, which computes the entropy of the Universe if that would be converted into a black hole, as in Equation 11:
which is in line with similar estimates in the recent literature (Egan and Lineweaver [15], once we rescaled the previous formula for the volume within the cosmic event horizon rather than from the volume within the observable Universe; see also Profumo et al. [16] for a more recent estimate) and obviously incredibly larger than the amount of information that is generated even by the most challenging “cosmological” simulations produced to-date in astrophysics (e.g.,
This leads to the FIRST CONCLUSION: simulating the entirety of our visible Universe at full resolution (i.e., down to the Planck scale) is physically impossible.
3.2 Full simulation of planet Earth
Next, we can apply the same logic to compute the total memory information needed to describe our planet (
Again, based on Equation 4, we get Equation 12:
and for the total energy needed to code this information, Equation 13:
assuming, very optimistically (as it will be discussed later), that
Therefore, the initialization of a complete simulation of “just” a planet like Earth requires either converting the entire stellar mass of a typical globular cluster into energy or using the equivalent energy necessary to unbind all stars and matter components in the Milky Way.
Elaborating on the implausibility of such a simulation, based on its energy cost, is straightforward: while this is indeed the requirement simply to begin the simulation, roughly the same amount of energy needs to be dissipated for each timestep of the simulation. This means that already after
Moreover, while the minimum mass required to contain this information corresponds to a black hole mass prescribed by Equation 11, which gives
which is 70% of the radius of Jupiter
Interestingly, such planetary-sized computers were theoretically explored by Sandberg [12], who presented a thorough study of all practical limitations connected to heat dissipation, computing power, connectivity, and bandwidth, arriving at a typical estimate of
If a black hole actively accretes matter, the kinetic temperature acquired by accreted matter is very large, and is given by Equation 15:
That is, regardless of the actual mass and radius of the black hole into consideration, the temperature acquired by accreted particles is in the
This leads to a SECOND CONCLUSION: simulating planet Earth at full resolution (i.e., down to the Planck scale) is practically impossible, as it requires access to a galactic amount of energy.
3.3 Low-resolution simulations of Planet Earth
Next, we shall explore the possibility of “partial” or “low-resolution” simulations of planet Earth, in which the simulation must only resolve scales that are routinely probed by human experiments or observations while using some sort of “subgrid” physics for any smaller scale.
The Planck scale
What is the smallest scale,
High-energy physics, through the De Broglie relation,
A much larger energy scale is probed by the detection of ultra-high-energy cosmic rays (UHECRs) as they cross our atmosphere and trigger the formation of observable Cherenkov radiation and fluorescent light [21, 22]. Observed UHECRs are characterized by a power-law distribution of events, and the largest energy ever recorded for an UHECR is
Luckily, high-energy astrophysics still comes to the rescue due to the detection of very high-energy extragalactic neutrinos crossing the inside of our planet. Since the first discovery of energetic neutrinos by the IceCube observatory [27, 28], the existence of a background radiation of neutrinos, likely of extragalactic origin, in the
Equation 17 gives a minimum encoding energy:
if we very conservatively use
At face value, this energy requirement is far less astronomical than the previous one: it corresponds to the conversion into the energy of
Equation 11 gives the size of the minimum black hole capable of storing
We largely used here the seminal work by Lloyd [13] for the computing capabilities of black holes. The ultimate compression limit of a black hole can provide in principle the most performing computing configuration for any simulation. Thus, by showing that not even in this case can the simulation be performed, we can argue about its physical impossibility. Based on the classical picture of black holes, no information is allowed to escape from within the event horizon. However, the quantum mechanical view is different as it allows, through the emission of Hawking radiation as black holes evaporate, to transfer some information on the outside. Following Lloyd [13], even black holes may theoretically be programmed to encode the information to be processed within their horizon. Then, an external observer, by examining the correlations in the Hawking radiation emitted as they evaporate, might be retrieving the result of the simulation outside. Even such a tiny black hole has a very long evaporation timescale:
The temperature relative to the Hawking radiation for such a black hole is given by Equation 18:
Quantum mechanics constrains the maximum rate at which a system can move from one distinguishable quantum state to another. A quantum state with average energy
In Equation 19,
Estimating the working temperature of such a device is not obvious. As an upper bound, we can use the temperature of accreted material at the event horizon of an astrophysical black hole from Equation 15
By multiplying for the total number of bits encoded in such a black hole, Equation 21 gives its total maximum computing power:
On the other hand, if the black hole does not accrete matter, the lowest temperature at the event horizon is the temperature relative to the Hawking radiation:
In this case, we get the total computing power:
This computing power may seem immense, yet it is not enough to advance the low-resolution simulation of planet Earth in a reasonable wall-clock time. We notice that the minimum timestep that the simulation must resolve in order to consistently propagate the highest energy neutrinos we observe on Earth is
which are in both cases absurdly long wall-clock times. Therefore, an additional speed-up of order
which means converting into energy many more than all stars in all galaxies within the visible Universe (and using a black hole with mass
This leads us to the THIRD CONCLUSION: even the lowest possible resolution simulation of Earth (at a scale compatible with experimental data) requires geologically long timescales, making it entirely implausible for any purpose.
4 Discussion
Needless to say, in such a murky physical investigation, several assumptions can be questioned, and a few alternative models can be explored. Here, we review a few that appear to be relevant, even if it is anticipated that the enthusiasts of the SH will probably find other escape routes.
4.1 Can highly parallel computing make the simulation of the low-resolution Earth possible?
A reasonable question would be whether performing highly parallel computing could significantly reduce the computing time estimated at the end of Section 3.3. In general, if the required computation is serial, the energy can be concentrated in particular parts of the computer, while if it is parallelizable, the energy can be spread out evenly among the different parts of the computer.
The communication time across the black hole horizon
4.2 What if the time stepping is not determined by neutrino observations?
What if (for reasons beyond what our physics can explain) high-energy neutrinos can be accurately propagated in the simulation with a time stepping much coarser than the one prescribed by
4.3 What about quantum computing?
By exploiting the fundamental quantum properties of superposition and entanglement, quantum computers perform better than classical computers for a large variety of mathematical operations [38]. In principle, quantum algorithms are more efficient in using memory, and they may reduce time and energy requirements [39] by implementing exponentially fewer steps than classical programs. However, these important advantages compared to classical computers do not change the problems connected with the SH analyzed in this work, which solely arise from the relationship between spacetime, information density, and energy. According to the HP, the information bound used here is the maximum allowed within a given holographic surface with radius
4.4 What if the holographic principle does not apply?
One possibility is that the HP, for whatever reason, does not apply as a reliable proxy for the information content of a given physical system. It is worth reminding that the HP prescribes the maximum information content to scale with the surface, and not the volume, of a system; hence, it generally already provides a very low information budget estimate compared to all other proxies in which information scales with the volume instead. In this sense, the estimates used in this paper (including in the low-resolution simulation of Earth in Section 3.3) already appear as conservatively low quantities. If the HP is not valid, then a larger amount of bits can be encoded within a given surface with radius
4.5 Plot twist: a simulated Universe simulates how the real universe might be
Our results suggest that no technological advancement will make the SH possible in any universe that works like ours.
However, the limitations outlined above might be circumvented if the values of some of the fundamental constants involved in our formalisms are radically different than the canonic values they have in this Universe. Saying anything remotely consistent about the different physics operating in any other universe is an impossible task, let alone guessing which combinations of constants would still allow the development of any form of intelligent life. Nevertheless, for the sake of argument, we make the very bold assumption that in each of the explored variations, some sort of intelligent form of life can form and that it will be interested in computing and simulations. Under this assumption, we can then explore numerical changes to the values of fundamental constants involved in the previous modeling to see whether combinations exist that make at least a low-resolution simulation of our planet doable with limited time and energy.
So, in a final plot twist whose irony should not be missed, now this Universe (which might be a simulation) attempts to Monte Carlo simulate how the “real universe” out there could be for the simulation of this Universe to be possible. We assume that all known physical laws involved in our formalisms are valid in all universes, but we allow each of the key fundamental constants to vary randomly across realizations. For the sake of the exercise, we shall fix the total amount of information required for the low-resolution simulation of our planet discussed in Section 3.3
The simulation consists of a Monte Carlo exploration of the six-dimensional parameter space of the fundamental constants that entered our previous derivation:
In Figure 1, we give the results of the Monte Carlo simulation, in which we show samplings of the distribution of allowed combinations of constants, normalized to the value each of them has in this Universe. Although the exploration of the full 6-dimensional parameters space is complex, a few things can be noticed already. First, two well-correlated parameters here are
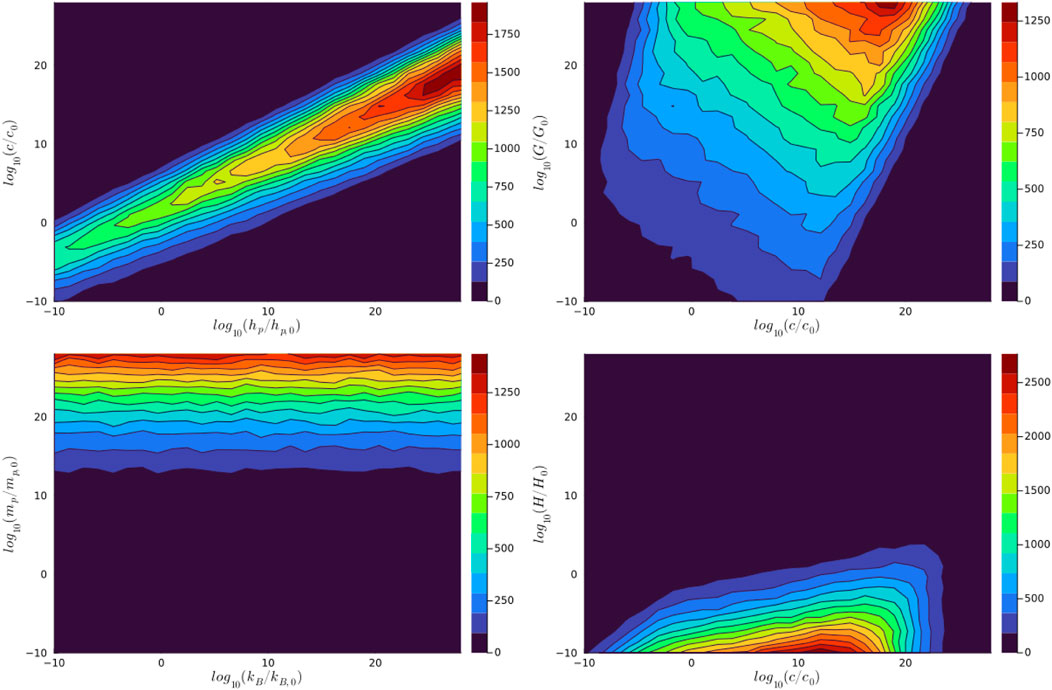
Figure 1. Examples of the distribution of allowed values of the fundamental constants (rescaled to their value in this Universe) necessary to perform a low-resolution simulation of Earth in other universes, as predicted with Monte Carlo simulations. Each axis gives the allowed value for each constant, normalized to its value in this Universe.
In general, this simulation shows that combinations of parameters exist to make the SH for a low-resolution version of planet Earth possible (and similarly, also for higher-resolution versions of the SH), although they require orders of magnitudes differences compared to the physical constants of this Universe. It is beyond the goal of this work to further elaborate whether any of the many possible combinations make sense, based on known physics, if they can support life, and whether those hypothetical forms of life will be interested in numerics and physics, as we are9.
4.6 What if the universe performing the simulation is entirely different from our Universe?
Guessing how conservation laws for energy and information apply in a universe with entirely different laws, or whether they should even apply in the first place, appears impossible, and this entirely prevents us from guessing whether the SH is possible in such a case. For example, hypothetical conscious creatures in the famous Pac-Man video game in the 1980s will simply be incapable of figuring out the constraints on the universe in which their reality is being simulated, even based on all the information they can gather around them. They would not guess the existence of gravity, for example; they would probably measure energy costs in “Power Pellets,” and they would not conceive the existence of a third dimension, or of an expanding spacetime, and so on. Even if they could ever realize the level of graininess of their reality and make the correct hypothesis of living in a simulation, they would never guess how the real universe (“our” Universe, if it is real indeed) functions in a physical sense. In this respect, our modeling shows that the SH can be reasonably well tested only with respect to universes that are at least playing according to the physics playbook—while everything else10 appears beyond the bounds of falsifiability and even theoretical speculation.
5 Conclusion
We used standard physical laws to test whether this Universe or some low-resolution version of it can be the product of a numerical simulation, as in the popular simulation hypothesis [3].
One first key result is that the simulation hypothesis has plenty of physical constraints to fulfil because any computation is bound to obey physics. We report that such constraints are so demanding that all plausible approaches tested in this work (in order to reproduce at least a fraction of the reality we humans experience) require access to impossibly large amounts of energy or computing power. We are confident that this conclusively shows the impossibility of a “Matrix” scenario for the SH, in which our reality is a simulation produced by future descendants, machines, or any other intelligent being in a Universe that is exactly the one we (think we) live in—a scenario famously featured in the “The Matrix” movie in 1999, among many others. We showed that this hypothesis is simply incompatible with all we know about physics, down to scales that have already been robustly explored by telescopes, high-energy particle colliders, and other direct experiments on Earth.
What if our reality is instead the product of a simulation, in which physical laws (e.g., fundamental constants) different from our reality are used? A second result of this work is that, even in this alienating scenario, we can still robustly constrain the range of physical constants allowed in the reality simulating us. In this sense, the strong physical link between computing and energy also offers a fascinating way to connect hypothetical different levels of reality, each one playing according to the same physical rules. In our extremely simplistic Monte Carlo scan of models with different fundamental constants, a plethora of combinations seems to exist, although we do not dare to guess which ones could be compatible with stable universes, the formation of planets, and the further emergence of intelligent life. The important point is that each of such solutions implies universes entirely different from this one. Finally, the question of whether universes with entirely different sets of physical laws or dimensionalities could produce our Universe as a simulation seems to be entirely outside of what is scientifically testable, even in theory.
At this point, we shall notice that a possible “simulation hypothesis,” which does not pose obvious constraints on computing, might be the solipsistic scenario in which the simulation simulates “just” the single activity of the reader’s brain (yes: you), while all the rest is a sophisticated and very detailed hallucination. In this sense, nothing is new from Renee Descartes’ “evil genius” or “Deus deceptor”—that is, for some reason, an entire universe is produced in a sort of simulation, only to constantly fool us—from its more modern version of “Boltzmann brains” [45]. Conversely, a more contrived scenario in which the simulation simulates only the brain activity of single individuals appears to quickly run into the limitations of the SH exposed in this work: a shared and consistent experience of reality requires a consistent simulated model of the world, which quickly escalates into a too-demanding model of planet Earth down to very small scales as soon as physical experiments are involved.
At this fascinating crossroad between physics, computing, and philosophy, it is interesting to notice that the last egotistic version of the SH appears particularly hard to test or debunk with physics, as the latter indeed appears to be entirely relying on the concept of a reality external to the observing subject—be it a real or a simulated one. However, the possibility of a quantitative exercise like the one attempted here also shows that the power of physics is otherwise immense, as even the most outlandish and extreme proposal about our reality must fall within the range of what physics can investigate, test, and debunk.
Luckily, even in the most probable scenario of all (the Universe is not a simulation), the number of mysteries for physics to investigate is still so immense that even dropping this fascinating topic cannot make science any less interesting.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
FV: Writing – original draft and writing – review and editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Acknowledgments
I have used the Astrophysics Data Service (ADS) and arXiv preprint repository extensively during this project and for writing this article, the precious online Cosmological Calculator by E. Wright, and the Julia language for the simulations of Section 4.5. This peculiar investigation was prompted by a public conference given for the 40th anniversary of the foundation of Associazione Astrofili Vittorio Veneto, where the author took his first steps into astronomy. I wish to thank Maksym Tsizh and Chiara Capirini for their useful comments on the draft of the paper, and Maurizio Bonafede for useful suggestions on the geophysical analysis of the core-mantle boundary used in Section 3.3.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1For example, it was the central topic of the 2016 Isaac Asimov Memorial Debate, featuring several astrophysicists and physicists: https://www.youtube.com/watch?v=wgSZA3NPpBs. This theme still periodically surges and generates a lot of “noise” on the web, indicating both the fascination it rightfully produces in the public and the difficulty of debunking it.
2As a sign of respect for what this astrophysicist honestly thinks is the only “real” Universe, which is the one we observe through a telescope, I will use the capital letter for this Universe—even if, for the sake of argument, is at times assumed to be only a simulation, being run in another universe.
3It must be noted that also reversible computation, with no deletion of bits or dissipation of energy, is possible. However, irreversible computation is unavoidable both for several many-to-one logical operations (AND or ERASE) as well as for error correction, in which several erroneous states are mapped into a single correct state [12, 13].
4For the sake of argument, because we surmise here the existence of a skilled simulator that somehow can use computing centers as large as a planet-sized black hole, we can concede with no difficulty that it can also create a consistent simulation of the experience of
5As a matter of fact, in almost any conceivable numerical simulation that is run in physics, the Planck constant and its associated length scale
6Especially because we focus here on the simulation of Earth, a reasonable question would be whether such low-resolution simulation would still be capable of reproducing the observed biological process on the planet. A
7It should also be considered that the time dilatation effect of general relativity will also introduce an additional delay factor between what is computed by the black hole and what is received outside, although the amount of the delay depends on where exactly the computation happens.
8Very likely to be named differently in any other universe.
9The full direct simulation of such cases, possibly down to the resolution at which conscious entities will emerge out of the simulation and start questioning whether their universe is real or simulated, is left as a trivial exercise to the reader.
10A possibility for such a model to work may be that all scientists are similar to “non playable characters” in video games, that is, roughly sketched and unconscious parts of the simulation, playing a pre-scripted role (in this case, reporting fake measurements).
References
2. Berkeley GA. Treatise concerning the principles of human knowledge, 1734. Menston: Scolar Press (1734).
3. Bostrom BN. Are we living in a computer simulation?. Philos Q (2003) 53:243–55. doi:10.1111/1467-9213.00309
4. Beane SR, Davoudi Z, J Savage M. Constraints on the universe as a numerical simulation. Eur Phys J A (2014) 50:148. doi:10.1140/epja/i2014-14148-0
5. Landauer R. Information is a physical entity. Physica A Stat Mech its Appl (1999) 263:63–7. doi:10.1016/S0378-4371(98)00513-5
6. Landauer R. The physical nature of information. Phys Lett A (1996) 217:188–93. doi:10.1016/0375-9601(96)00453-7
7. Maldacena JM. The large $N$ limit of superconformal field theories and supergravity. Adv Theor Math Phys (1998) 2:231–52. doi:10.4310/ATMP.1998.v2.n2.a1
8. Bousso R. The holographic principle. Rev Mod Phys (2002) 74:825–74. doi:10.1103/RevModPhys.74.825
9. Bekenstein JD. Black holes and information theory. Contemp Phys (2004) 45:31–43. doi:10.1080/00107510310001632523
10. Suskind L, Lindesay J. An introduction to black holes, information and the string theory revolution: the holographic universe (2005).
11. Szilard L. über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Z Physik (1929) 53:840–56. doi:10.1007/BF01341281
12. Sandberg A. The physics of information processing superobjects: daily life among the jupiter brains. J Evol Technology (1999) 5.
13. Lloyd S. Ultimate physical limits to computation. Nature (2000) 406:1047–54. doi:10.1038/35023282
14. Page DN. Comment on a universal upper bound on the entropy-to-energy ratio for bounded systems. Phys Rev D (1982) 26:947–9. doi:10.1103/PhysRevD.26.947
15. Egan CA, Lineweaver CH. A larger estimate of the entropy of the universe. Astrophysical J (2010) 710:1825–34. doi:10.1088/0004-637X/710/2/1825
16. Profumo S, Colombo-Murphy L, Huckabee G, Diaz Svensson M, Garg S, Kollipara I, et al. A new census of the universe’s entropy (2024). arXiv e-prints arXiv:2412.11282. doi:10.48550/arXiv.2412.11282
17. Vogelsberger M, Genel S, Springel V, Torrey P, Sijacki D, Xu D, et al. Properties of galaxies reproduced by a hydrodynamic simulation. Nature (2014) 509:177–82. doi:10.1038/nature13316
18. Baumgardt H, Hilker M. A catalogue of masses, structural parameters, and velocity dispersion profiles of 112 Milky Way globular clusters. Mon Not R Astron Soc (2018) 478:1520–57. doi:10.1093/mnras/sty1057
19. Posti L, Helmi A. Mass and shape of the Milky Way’s dark matter halo with globular clusters from Gaia and Hubble. Astron Astrophys (2019) 621:A56. doi:10.1051/0004-6361/201833355
20. Soldin D. The forward physics facility at the HL-LHC and its synergies with astroparticle physics (2024). arXiv e-prints arXiv:2501.04714. doi:10.48550/arXiv.2501.04714
21. Aloisio R, Berezinsky V, Blasi P. Ultra high energy cosmic rays: implications of Auger data for source spectra and chemical composition. J Cosmol Astropart Phys (2014) 2014:020. doi:10.1088/1475-7516/2014/10/020
22. Abbasi RU, Abe M, Abu-Zayyad T, Allen M, Anderson R, Azuma R, et al. Study of ultra-high energy cosmic ray composition using telescope array’s middle drum detector and surface array in hybrid mode. Astroparticle Phys (2015) 64:49–62. doi:10.1016/j.astropartphys.2014.11.004
23. Bird DJ, Corbato SC, Dai HY, Elbert JW, Green KD, Huang MA, et al. Detection of a cosmic ray with measured energy well beyond the expected spectral cutoff due to cosmic Microwave radiation. Astrophys J (1995) 441:144. doi:10.1086/175344
24. Unger M, Farrar GR. Where did the amaterasu particle come from? The Astrophysical J Lett (2024) 962:L5. doi:10.3847/2041-8213/ad1ced
25. Jenkins J, Mousavi S, Li Z, Cottaar S. A high-resolution map of Hawaiian ulvz morphology from scs phases. Earth Planet Sci Lett (2021) 563:116885. doi:10.1016/j.epsl.2021.116885
26. Li Z, Leng K, Jenkins J, Cottaar S. Kilometer-scale structure on the core–mantle boundary near Hawaii. Nat Commun (2024) 13:2787. doi:10.1038/s41467-022-30502-5
27. IceCube Collaboration. Evidence for high-energy extraterrestrial neutrinos at the IceCube detector. Science (2013) 342:1242856. doi:10.1126/science.1242856
28. Aartsen MG, Abbasi R, Abdou Y, Ackermann M, Adams J, Aguilar JA, et al. First observation of PeV-energy neutrinos with IceCube. Phys Rev Lett (2013) 111:021103. doi:10.1103/PhysRevLett.111.021103
29. Buson S, Tramacere A, Oswald L, Barbano E, Fichet de Clairfontaine G, Pfeiffer L, et al. Extragalactic neutrino factories (2023). arXiv e-prints arXiv:2305.11263. doi:10.48550/arXiv.2305.11263
30. Neronov A, Savchenko D, Semikoz DV. Neutrino signal from a population of seyfert galaxies. Galaxies (2024) 132:101002. doi:10.1103/PhysRevLett.132.101002
31. Padovani P, Gilli R, Resconi E, Bellenghi C, Henningsen F. The neutrino background from non-jetted active galactic nuclei. Astron Astrophys (2024) 684:L21. doi:10.1051/0004-6361/202450025
32. KM3NeT Collaboration. Observation of an ultra-high-energy cosmic neutrino with KM3NeT. Nature (2025) 638:376–82. doi:10.1038/s41586-024-08543-1
33. Ossiander M, F S, V S, R P, A S, T L, et al. Attosecond correlation dynamics. Nat Phys (2017) 13:280–5. doi:10.1038/nphys3941
34. Markevitch M, Vikhlinin A. Shocks and cold fronts in galaxy clusters. Phys Rep (2007) 443:1–53. doi:10.1016/j.physrep.2007.01.001
35. Vayner A, Zakamska NL, Ishikawa Y, Sankar S, Wylezalek D, Rupke DSN, et al. First results from the JWST early release science program Q3D: powerful quasar-driven galactic scale outflow at z = 3. Astrophys J (2024) 960:126. doi:10.3847/1538-4357/ad0be9
36. Mazzali PA, McFadyen AI, Woosley SE, Pian E, Tanaka M. An upper limit to the energy of gamma-ray bursts indicates that GRBs/SNe are powered by magnetars. Mon Not R Astron Soc (2014) 443:67–71. doi:10.1093/mnras/stu1124
37. Abbott BP, Abbott R, Abbott TD, Abernathy MR, Acernese F, Ackley K, et al. Properties of the binary black hole merger gw150914. Phys Rev Lett (2016) 116:241102. doi:10.1103/PhysRevLett.116.241102
38. Simon D. On the power of quantum computation. In: Proceedings 35th Annual Symposium on Foundations of Computer Science; Nov 20-22, 1994; Santa Fe, NM, USA (1994). p. 116–23. doi:10.1109/SFCS.1994.365701
39. Chen S. Are quantum computers really energy efficient? Nat Comput Sci (2023) 3:457–60. doi:10.1038/s43588-023-00459-6
40. Vazza F. On the complexity and the information content of cosmic structures. Mon Not R Astron Soc (2017) 465:4942–55. doi:10.1093/mnras/stw3089
41. Vazza F. How complex is the cosmic web? Mon Not R Astron Soc (2020) 491:5447–63. doi:10.1093/mnras/stz3317
43. Prokopenko M, Boschetti F, Ryan AJ. An information-theoretic primer on complexity, self-organization, and emergence. Complexity (2009) 15:11–28. doi:10.1002/cplx.20249
44. Shalizi CR. Causal architecture, complexity and self-organization in the time series and cellular automata. Madison: University of Wisconsin (2001). Ph.D. thesis.
Keywords: cosmology, information, simulations, black holes, computing
Citation: Vazza F (2025) Astrophysical constraints on the simulation hypothesis for this Universe: why it is (nearly) impossible that we live in a simulation. Front. Phys. 13:1561873. doi: 10.3389/fphy.2025.1561873
Received: 16 January 2025; Accepted: 07 March 2025;
Published: 17 April 2025.
Edited by:
Jan Sladkowski, University of Silesia in Katowice, PolandReviewed by:
Filiberto Hueyotl-Zahuantitla, Cátedra CONACYT-UNACH, MexicoElmo Benedetto, University of Salerno, Italy
Copyright © 2025 Vazza. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: F. Vazza, ZnJhbmNvLnZhenphMkB1bmliby5pdA==
 F. Vazza
F. Vazza