- School of Mathematics, Shanghai University of Finance and Economics, Shanghai, China
This paper studies first- and second-order coherence problems for
1 Introduction
Over the past few years, technological development in communication networks has greatly increased interest in distributed coordination for networks of dynamical agents. As one of the fundamental problems in cooperative control, the consensus problem for multi-agent systems has been investigated from various perspectives [1–5]. In the context of networks (graphs) of agents, consensus means that agents represented by nodes (vertices) reach an agreement on a certain issue, such as pace, load, or direction and velocity.
In realistic applications, communication between agents is often degraded due to environmental uncertainty or communication uncertainty, for example, thermal, fading channel, and quantization noises during encoding and decoding. Without uncertainties, it is well known that when the graph is connected, the states of autonomous systems converge exponentially to the average of the initial state values. In the presence of stochastic disturbances, however, the state evolution becomes a stochastic process and fluctuates around the average of the current node states. Thus, it is of great interest to consider how robust distributed consensus algorithms are to external disturbances [6–16]. Network coherence [8–16] quantifies the steady-state variance of these fluctuations and can be considered a measure of the robustness of the consensus process to the additive noise. Networks with small steady-state variance have high network coherence and can be considered to be more robust to noise than networks with low coherence [13–16]. For both first- and second-order systems, network coherence can be measured by the
Because massive networks often consist of small pieces, for example, communities [17] and motifs [18], graph products, by which one can build a large network out of two or more smaller ones, are widely used as an effective method for generating large-scale networks. Analysis of product networks offers critical insights into understanding the dynamics of real-world large-scale networks. Specifically, graph products have been explored to construct and reveal structural and functional relationships between factor systems and the associated composite system [19–22].
Common graph products include direct products and strong products [23], Cartesian products [24], Kronecker products [25], and corona products [26]. Among them, corona product graphs have attracted a great deal of attention due to their complex but unique structures and wide range of applications in coding theory, DNA sampling, UAV formation, and some special chemical and biological structures or communities [27–34]. The concept of the corona product of graphs was first introduced by Frucht and Harary [27]. In [28], the authors introduced the edge corona of graphs and calculated the corresponding spectrum. The properties of spectra and Laplacian spectra of corona products have been extensively studied in spectral graph theory [35–38]. Some recently widely concerned indices, such as the Sombor index and the Kirchhoff index, have been derived from corona product graphs [39, 40]. Notably, some related advancements in graph theory have been reported in [41–45]. In the literature, based on the spectral analysis of the Laplacian and normalized Laplacian matrices, Kemeny’s constant, global mean-first-passage time of random walks, and the number of spanning trees were studied in various network structures. Specifically, Kemeny’s constant represents the cumulative sum of relaxation time scales and has specific applications in computing a graph’s Kirchhoff index. These research achievements and methods are enlightening for further studies on corona networks.
The first-order coherence of weighted corona networks was examined from the weighted Laplacian spectra perspective in [46]. It is noteworthy that, in addition to the basic corona product investigated in [46], multiple variants of corona operation have been introduced and studied, including edge corona [35], neighborhood corona [36], subdivision double corona, Q-graph double corona, R-graph double corona [37], and iterative corona [38], etc. Therefore, further research on consensus algorithms of various kinds of corona networks is necessary. Moreover, little research has clearly addressed the relationship between the coherence of the corona network and that of its factor networks, and research results on the second-order or higher-order coherence of corona networks are still rare.
The multilayer network is a frontier research branch of network science. The multilayered structure has many examples in reality, for instance, the interactions between the power grid and the Internet, friendship and family relations, or transportation and aviation networks [47, 48]. Lately, a multilayered graph based on the duplication of corona products was introduced in [49, 50]. Varghese and Susha [49] determined the Laplacian spectrum and discussed the number of spanning trees, the Kirchhoff index, and the incidence energy of the graph. The controllability of the
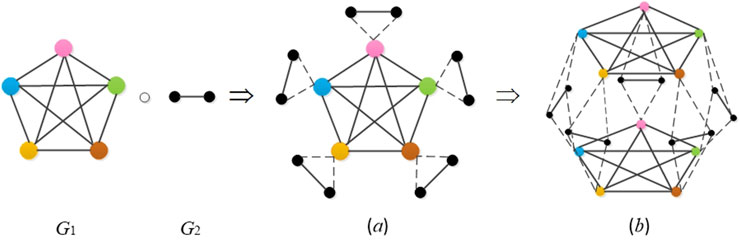
Figure 1. Illustration of
With the introduction of duplication, the classic corona graph is generalized from a single-layer structure to a multilayered structure. It is necessary and significant to extend the consensus theory to the
Inspired by these questions, this study explores the robustness of consensus algorithms for
The rest of this paper is organized as follows. Section 2 reviews the definition of
2 Notations and preliminaries
This section briefly reviews the definition of the first- and second-order network coherence and the formation of
2.1 Notations
Some available notations used in this study are given in the abbreviations.
2.2 Coherence in networks with first-order dynamics
Consider a network with underlying undirected graph
where
It has been shown [6–9] that
where
2.3 Coherence in networks with second-order dynamics
In the second-order system, such as the vehicle formation problem, the node states consist of a position vector
where
The network coherence of the second-order system in Equation 3 is defined in terms of
This value is also completely determined by the eigenvalues of the Laplacian matrix [8, 9, 15],
where
Note that networks with smaller steady-state variance
The following lemma gives the well-known Vieta’s formulas, which will be leveraged in the following coherence analysis.
Lemma 1. [52] Let
and
where
2.4
As an extension of the classic corona network, an
Definition 1. [49, 50] Let
Let
The join operation of two disjoint graphs is also an effective method for generating large-scale networks [51]. As an extension, [46] presented the weighted join operation as below.
Definition 2. [46, 51] The join of two disjoint graphs
In [49, 50], the characteristic polynomial of the
Lemma 2. [49, 50] Let
3 Main results
This section studies the first- and second-order coherence problems for
3.1 First-order coherence of the
Theorem 1. Let
Proof. By Def. 1, the
(i) 0;
(ii)
(iii)
(iv)
(v) Two roots of the equation
From Equation 2, the first-order network coherence of
Let
and
Combining the Laplacian spectrum of
The proof is completed.
Remark 1. From Equation 7, Theorem 1 implies that
It is worth noting that the phenomenon of high coherence of the corona network
In Equation 7,
Lemma 3. Let
Proof. For the Laplacian matrix
Theorem 2. Let
Proof. Let
where
Suppose that
From Lemma 3, the characteristic polynomial of
Therefore, the Laplacian eigenvalues of
Similarly, the Laplacian eigenvalues of
Moreover, we have
and
Remark 2. Setting
which is consistent with the result of [46] (see Theorem 3 of [46] for details).
In the proof of Theorem 2, the first-order coherence of the join graphs
Remark 3. From Equation 11, Theorem 2 shows, for fixed values of
3.2 Second-order coherence of the
This subsection investigates the second-order coherence of the
Theorem 3. Let
Proof. Based on Equation 4, to evaluate the second-order network coherence of
and
The result of the theorem is then deduced by combining the analysis of the Laplacian spectrum of
From Equation 17, a conclusion similar to Remark 1 can be drawn for the second-order network coherence in
Remark 4. Theorem 3 implies that
From Remark 4, the notable topological property of high coherence of corona networks
Theorem 4. Let
Proof. The Laplacian eigenvalues of
and
The theorem is then proved by combining the analysis of the Laplacian spectrum of
Remark 5. Setting
In the proof of Theorem 4, the second-order coherence for the join graphs
Remark 6. Similar to the first-order noisy consensus algorithms, for fixed values of
4 Examples and simulations
This section verifies the theoretical results of Section 3 with numerical examples.
Example 1: Consider the network coherence of the
The Laplacian eigenvalues of
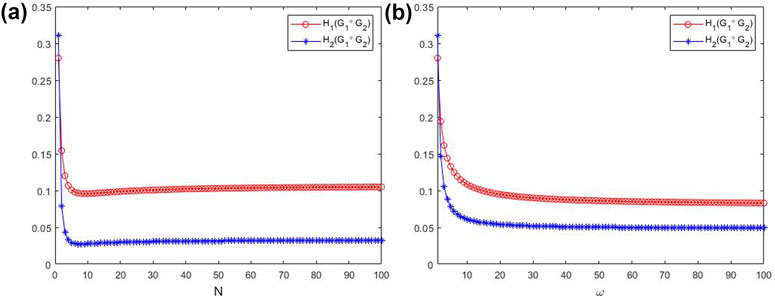
Figure 2 shows the asymptotic trend of
The dependence of
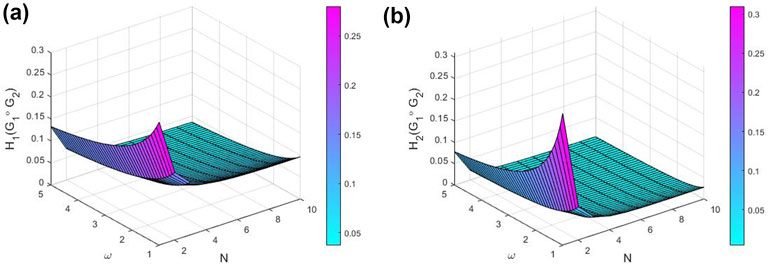
Figure 3. (a)
Example 2: In this example, the relationship between the coherence of the
In case (I), the
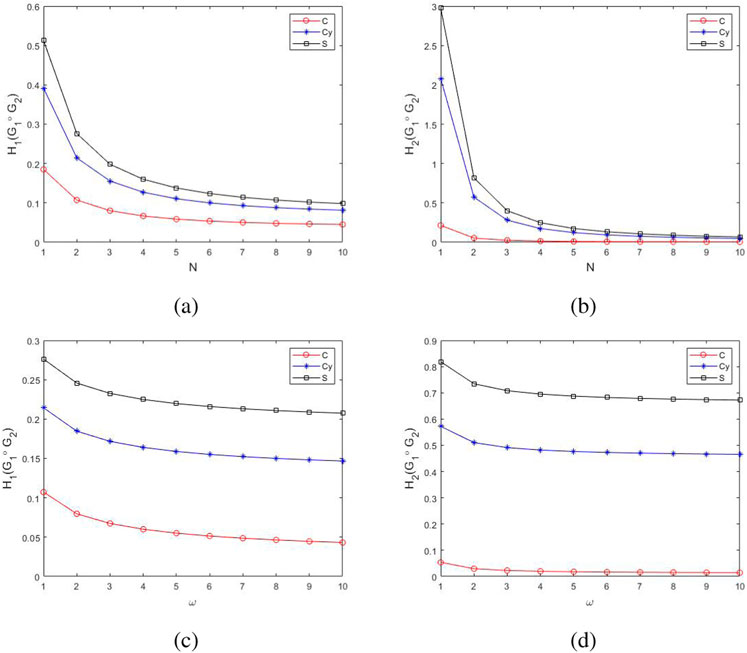
Figure 4.
In case (II), the
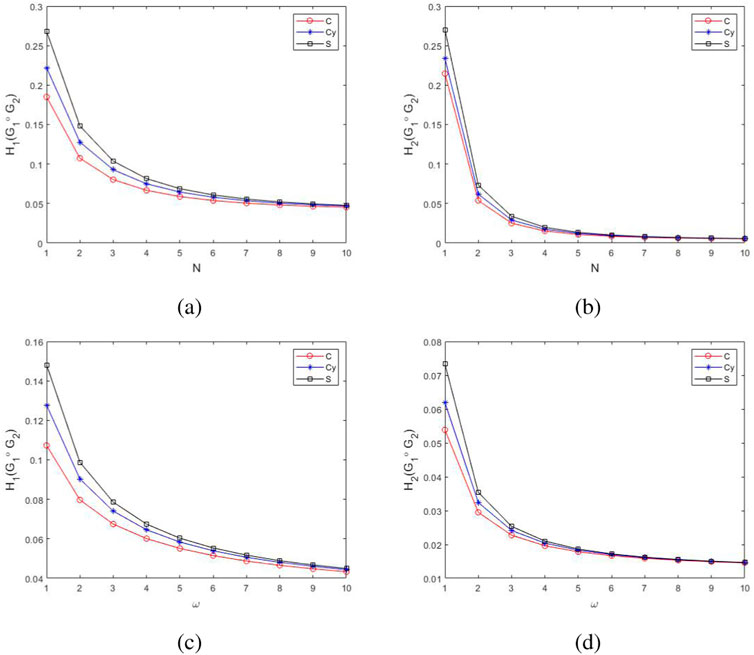
Figure 5.
The influence of the factor networks
5 Conclusion
In this paper, coherence problems in
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
CL: Writing – original draft and Writing – review and editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
References
1. Ren W, Beard R, Atkins E. A survey of consensus problems in multi-agent coordination. In: Proc. Amer. Control conf. (2005). p. 1859–64.
2. Blondel V, Hendrickx J, Olshevsky A, Tsitsiklis J. Convergence in multiagent coordination, consensus, and flocking. In: Proc. CDC-ECC (2005). p. 2996–3000.
3. Olfati-Saber R, Fax JA, Murray RM. Consensus and cooperation in networked multi-agent systems. Proc IEEE (2007) 95(1):215–33. doi:10.1109/jproc.2006.887293
4. Li Z, Duan Z, Chen G, Huang L. Consenus of multiagent systems and synchronization of complex networks: a unified viewpoint. IEEE Trans Circuits Syst (2010) 57(1):213–24. doi:10.1109/TCSI.2009.2023937
5. Kim BY, Ahn HS. Consensus-based coordination and control for building automation systems. IEEE Trans Control Syst Technol (2015) 23(1):364–71. doi:10.1109/TCST.2014.2325896
6. Xiao L, Boyd S, Kim SJ. Distributed average consensus with least-mean-square deviation. J Parallel Distrib Comput (2007) 67:33–46. doi:10.1016/j.jpdc.2006.08.010
7. Young GF, Scardovi L, Leonard NE. Robustness of noisy consensus dynamics with directed communication. In: Proc. Amer. Control conf. (2010). p. 6312–7.
8. Bamieh B, Jovanović M, Mitra P, Patterson S. Coherence in large-scale networks: dimension dependent limitations of local feedback. IEEE Trans Automat Control (2012) 57(9):2235–49. doi:10.1109/TAC.2012.2195839
9. Patterson S, Bamieh B. Consensus and coherence in fractal networks. IEEE Trans Control Netw Syst (2014) 1(4):338–48. doi:10.1109/tcns.2014.2357552
10. Yi Y, Zhang Z, Lin Y, Chen G. Small-world topology can significantly improve the performance of noisy consensus in a complex network. Comput J (2015) 58(12):3242–54. doi:10.1093/comjnl/bxv014
11. Wang X, Xu H, Ma C. Consensus problems in weighted hierarchical graphs. Fractals (2019) 27(6):1950086. doi:10.1142/s0218348x19500865
12. Qi Y, Zhang Z, Yi Y, Li H. Consensus in self-similar hierarchical graphs and sierpiński graphs: convergence speed, delay robustness, and coherence. IEEE Trans Cybern (2019) 49(2):592–603. doi:10.1109/tcyb.2017.2781714
13. Tyler S, Iman S, John L, Florian D. Topology design for optimal network coherence. Eur Control Conf (2015) 575–80. doi:10.1109/ECC.2015.7330566
14. Wang X, Xu H, Dai M. First-order network coherence in 5-rose graphs. Physica A (2019) 527:121129. doi:10.1016/j.physa.2019.121129
15. Yi Y, Zhang Z, Shan L, Chen G. Robustness of first- and second-order consensus algorithms for a noisy scale-free small-world Koch network. IEEE Trans Control Syst Technol (2017) 25:342–50. doi:10.1109/tcst.2016.2550582
16. Sun W, Ding Q, Zhang J, Chen F. Coherence in a family of tree networks with an application of Laplacian spectrum. Chaos: Interdiscip J Nonlinear Sci (2014) 24:043112. doi:10.1063/1.4897568
17. Girvan M, Newman ME. Community structure in social and biological networks. Proc Natl Acad Sci USA (2002) 99:7821–6. doi:10.1073/pnas.122653799
18. Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U. Network motifs: simple building blocks of complex networks. Science (2002) 298:824–7. doi:10.1126/science.298.5594.824
19. Chapman A, Nabi-Abdolyousefi M, Mesbahi M. Controllability and observability of network-of-networks via Cartesian products. IEEE Trans Autom Control (2014) 59(10):2668–79. doi:10.1109/tac.2014.2328757
20. Iqbal M, Leth J, Ngo TD. Cartesian product-based hierarchical scheme for multi-agent systems. Automatica (2018) 88:70–5. doi:10.1016/j.automatica.2017.11.009
21. Tran TN, Chapman A. Generalized graph product: spectrum, trajectories and controllability. In: Proc. IEEE conf. Decis. Control (2018). p. 5358–63.
22. Hao Y, Wang Q, Duan Z, Chen G. Controllability of Kronecker product networks. Automatica (2019) 110:108597. doi:10.1016/j.automatica.2019.108597
23. Hammack R, Imrich W, Klavžar S. Handbook of product graphs. New York, NY, USA: Taylor and Francis (2011).
24. Liu B, Hu M, Huang J, Su H. Controllability of Cartesian product signed networks. IEEE Trans Syst Man Cybern., Syst (2023) 53(11):7125–37. doi:10.1109/tsmc.2023.3292838
25. Doostmohammadian M, Khan UA. Minimal sufficient conditions for structural observability/controllability of composite networks via Kronecker product. IEEE Trans Signal Inf Process Netw (2020) 6:78–87. doi:10.1109/tsipn.2019.2960002
26. Wang X, Hao Y, Wang Q. On the controllability of corona product network. J Franklin Inst (2020) 357(10):6228–40. doi:10.1016/j.jfranklin.2020.03.037
27. Frucht R, Harary F. On the corona of two graphs. Aequationes Math (1970) 4(3):264–325. doi:10.1007/bf01817769
28. Hou Y, Shiu W-chee. The spectrum of the edge corona of two graphs. Elec J Lin Alg (2010) 20:586–94. doi:10.13001/1081-3810.1395
29. Bonchev D, Balaban AT, Liu X, Klein DJ. Molecular cyclicity and centricity of polycyclic graphs. I. Cyclicity based on resistance distances or reciprocal distances. Int J Quan Chem. (1994) 50(1):1–20. doi:10.1002/qua.560500102
30. Singh GP, Borah A, Ray S. A review paper on corona product of graphs. Adv Appl Math Sci (2020) 19(10):1047–54. doi:10.37418/aams.19.10.1
31. Feng M, Wang K. Identifying codes of corona product graphs. Disc Appl Math (2014) 169:88–96. doi:10.1016/j.dam.2013.12.017
32. Winder L, Phillips C, Richards N, Ochoa-Corona F, Hardwick S, Vink CJ, et al. Evaluation of DNA melting analysis as a tool for species identification. Methods Ecol Evol (2011) 2(3):312–20. doi:10.1111/j.2041-210x.2010.00079.x
33. De N. Application of corona product of graphs in computing topological indices of some special chemical graphs. In: S Saha, editor. Handbook of research on applied cybernetics and systems science. The United States of America: IGI Global (2017).
34. Huilgol MI, Divya B, Balasubramanian K. Distance degree vector and scalar sequences of corona and lexicographic products of graphs with applications to dynamic NMR and dynamics of nonrigid molecules and proteins. Theor Chem Acc (2021) 140(3):25–6. doi:10.1007/s00214-021-02719-y
35. Barik S, Pati S, Sarma BK. The spectrum of the corona of two graphs. SIAM J Disc Math (2007) 21(1):47–56. doi:10.1137/050624029
36. Gopalapillai I. The spectrum of neighborhood corona of graphs. Kra J Math (2011) 35:493–500. doi:10.5666/KMJ.2011.35.2.493
37. Barik S, Sahoo G. On the laplacian spectra of some variants of corona. Lin Alg Appl (2017) 512(1):32–47. doi:10.1016/j.laa.2016.09.030
39. Shang Y. Sombor index and degree-related properties of simplicial networks. Appl Math Comput (2022) 419:126881. doi:10.1016/j.amc.2021.126881
40. Liu J, Zhao J, Cai Z. On the generalized adjacency, Laplacian and signless Laplacian spectra of the weighted edge corona networks. Physica A (2019) 540:123073. doi:10.1016/j.physa.2019.123073
41. Zaman S, Ullah A. Kemeny’s constant and global mean first passage time of random walks on octagonal cell network. Math Meth Appl Sci (2023) 46:9177–86. doi:10.1002/mma.9046
42. Yu X, Zaman S, Ullah A, Saeedi G, Zhang X. Matrix analysis of hexagonal model and its applications in global mean-first-passage time of random walks. IEEE Access (2023) 11:10045–52. doi:10.1109/access.2023.3240468
43. Yan T, Kosar Z, Aslam A, Zaman S, Ullah A. Spectral techniques and mathematical aspects of K4 chain graph. Phys Scr (2023) 98:045222. doi:10.1088/1402-4896/acc4f0
44. Zaman S, Mustafa M, Ullah A, Siddiqui MK. Study of mean-first-passage time and Kemenys constant of a random walk by normalized Laplacian matrices of a penta-chain network. Eur Phys J Plus (2023) 138:770. doi:10.1140/epjp/s13360-023-04390-7
45. Kosar Z, Zaman S, Ali W, Ullah A. The number of spanning trees in a K5 chain graph. Phys Scr (2023) 98:125239. doi:10.1088/1402-4896/ad07b9
46. Du W, Zhu J, Gao H, Li X. Consensus analysis of the weighted corona networks. Front Phys (2022) 10:948247. doi:10.3389/fphy.2022.948247
47. Kivela M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer networks. J Compl Net (2014) 2:203–71. doi:10.1093/comnet/cnu016
48. Boccaletti S, Bianconi G, Criado R, del Genio C, Gómez-Gardeñes J, Romance M, et al. The structure and dynamics of multilayer networks. Phys Rep (2014) 544(1):1–122. doi:10.1016/j.physrep.2014.07.001
49. Varghese RP, Susha D. On the spectra of a new duplication based corona of graphs. Notes Num Theor Disc Math (2021) 27(1):208–20. doi:10.7546/nntdm.2021.27.1.208-220
50. Liu B, Li X, Huang J, Su H. Controllability of N-duplication corona product networks with laplacian dynamics. IEEE Trans Neural Netw Learn Syst (2023):3336948. doi:10.1109/TNNLS.2023.3336948
Keywords: robustness, network coherence, N-duplication weighted corona network, Laplacian spectrum, join operation
Citation: Liu C (2025) First- and second-order network coherence in N-duplication weighted corona networks. Front. Phys. 13:1562805. doi: 10.3389/fphy.2025.1562805
Received: 18 January 2025; Accepted: 13 May 2025;
Published: 20 June 2025.
Edited by:
Adriano Tiribocchi, National Research Council (CNR), ItalyReviewed by:
Asad Ullah, Karakoram International University, PakistanJian Zhu, China University of Mining and Technology, China
Copyright © 2025 Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chao Liu, bGl1LmNoYW9Ac2h1ZmUuZWR1LmNu
 Chao Liu
Chao Liu