Deep plug-and-play denoising prior with total variation regularization for low-dose CT

X-ray computed tomography (CT) is widely used in clinical practice for screening and diagnosing patients, as it enables the acquisition of high-resolution images of internal tissues and organs in a non-invasive manner. However, this has led to growing concerns about the cumulative radiation risks associated with X-ray exposure. Low-dose CT (LDCT) reduces radiation doses but results in increased noise and artifacts, significantly affecting diagnostic accuracy. LDCT image denoising remains a challenging task in medical image processing. To enhance LDCT image quality and leverage the flexibility and effectiveness of plug-and-play denoising methods, this paper proposes a novel deep plug-and-play denoising method. Specifically, we first introduce a deep residual block convolutional neural network (DRBNet) with residual noise learning. We then train the DRBNet using a hybrid loss function combining L1 and multi-scale structural similarity (M-SSIM) losses, while regularizing the training with total variation (TV). After training, the DRBNet is integrated as a deep denoiser prior into a half-quadratic splitting-based method to solve the LDCT image denoising problem. Experimental results demonstrate that the proposed plug-and-play method, using the DRBNet prior, outperforms state-of-the-art methods in terms of noise reduction, artifact suppression, and preservation of textural and edge information when compared to standard normal-dose CT (NDCT) scans. A blind reader study with two experienced radiologists further confirms that our method surpasses other denoising approaches in terms of clinical image quality.

1 Introduction

Currently, X-ray computed tomography (CT), known for its versatile imaging capabilities and high resolution, is one of the most widely used medical imaging modalities for clinical diagnosis [1]. CT is employed in various medical fields, including dental CT, whole-body diagnostic CT, and C-arm CT. However, medical CT involves the exposure of patients to ionizing radiation, which poses potential risks such as immune function decline, metabolic abnormalities, and harm to reproductive organs [2, 3]. In light of the hazards associated with excessive X-ray radiation, researchers have made considerable efforts to reduce radiation doses during CT scans. Generally, reducing the radiation dose can be achieved by shortening the X-ray exposure time or lowering the current of the X-ray tube [4]. However, decreasing X-ray radiation levels often leads to an increase in noise and artifacts in the reconstructed CT images [5]. Figure 1 illustrates CT scans obtained using normal-dose CT (NDCT) and low-dose CT (LDCT), with the LDCT image demonstrating noticeable noise and artifacts that compromise the accuracy of clinical diagnoses. In LDCT, image quality is often degraded by noise and artifacts, which significantly affect the confidence of radiologists’ assessments. Various approaches have been developed to improve the image quality of LDCT scans.

Figure 1

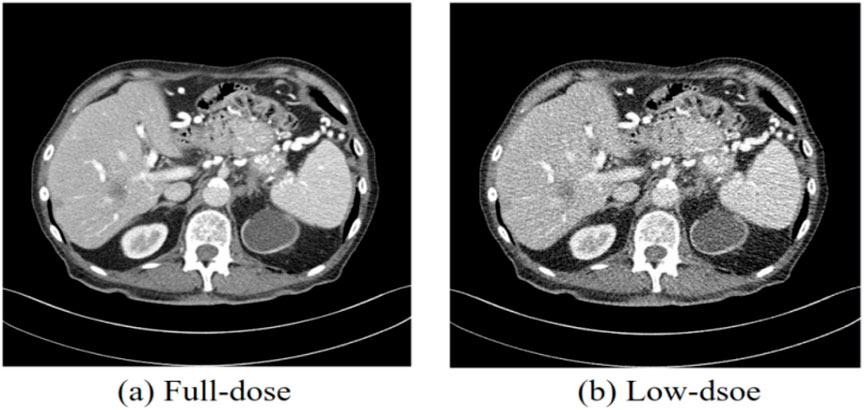
Figure 1. CT images obtained from normal-dose CT and low-dose CT. (a) Normal-dose CT image, (b) Low-dose CT image. The display window ranges: 160 to 240 HU.

In general, there are three primary methods for denoising LDCT images: (a) sinogram filtering in raw projection data, (b) iterative reconstruction (IR) techniques, and (c) post-image processing in reconstructed LDCT images.

Sinogram filtering techniques involve directly suppressing noise and smoothing the projection data before the image reconstruction process. Manduca et al. proposed a bilateral filtering method for noise reduction in LDCT projection data, which demonstrated superior denoising performance compared to the reconstruction kernels provided by vendors [6]. Balda et al. introduced a structure-adaptive filter to reduce noise while preserving structural integrity in projection data [7]. Other classical approaches include the multiscale penalized weighted least-squares algorithm for restoring low-dose sinogram data and the penalized likelihood method to smooth projection data [8]. Despite their effectiveness, sinogram filtering methods are challenging to implement in practice due to difficulties in accessing raw CT projection data from various CT scanners produced by different vendors. Iterative reconstruction (IR) techniques leverage prior information about the target image domain to resolve LDCT issues iteratively. These techniques estimate denoised CT images incrementally. Several image priors for LDCT have been proposed, including total variation (TV) [9, 10], dictionary learning [11–13], non-local means [14], and low-rank matrix decomposition [15]. Although IR techniques enhance the quality of denoised LDCT images, they come with a high computational cost due to the iterative projection and back-projection stages, which significantly increase the time required for CT image reconstruction.

Unlike raw sinogram filtering and IR techniques, post-image processing directly addresses reconstructed LDCT images, rather than the raw projection data. Moreover, post-image processing methods can be seamlessly integrated into the workflow of current CT scanners. Recently, a significant amount of research has focused on denoising LDCT images through post-image processing techniques. By leveraging redundant information from previous normal-dose CT (NDCT) scans, Ma et al. adapted non-local means (NLM) for noise reduction in LDCT images [16]. Similarly, Li et al. modified the NLM filter by incorporating a local noise level map to improve noise reduction in CT images [17]. Inspired by sparse representation theory, Chen et al. proposed a patch-based dictionary learning approach to suppress both noise and streak artifacts, thereby improving the quality of abdominal tumor LDCT images [18]. Additionally, the block-matching 3D (BM3D) algorithm [19], which has been successfully applied to denoise CT images in various studies [20, 21], was also explored. However, the noise and artifacts in reconstructed LDCT images are complex, often exhibiting a non-uniform distribution, making them difficult to handle using these traditional post-processing techniques.

The significant progress made in deep neural networks has sparked new approaches and holds great potential in fields such as computer vision (CV), natural language processing (NLP), and speech recognition [22]. This advancement in deep learning has also inspired researchers to apply these techniques for image denoising, including noise reduction and artifact suppression in LDCT. Convolutional neural networks (CNNs), which are hierarchical multi-layer deep neural networks, have demonstrated efficacy in several image processing applications, including image classification [23], super-resolution [24], and noise reduction [25]. Early deep learning-based approaches for LDCT denoising enhanced feature extraction and mapping within network models by increasing the depth of convolutional layers, such as residual encoder-decoder [26], 2D CNN [27], 3D CNN [28], and cascaded CNN [29]. However, these methods often result in over-smoothed denoised images. To address this issue, generative adversarial networks (GANs) [30] have been introduced to LDCT denoising. In GAN-based methods, a generative network (G) is trained to produce realistic images, while a discriminator network (D) is trained to distinguish between real and fake images. Yang et al. integrated perceptual loss with the Wasserstein GAN (WGAN) loss function to enhance the effectiveness of LDCT image denoising [31]. Ma et al. proposed a residual-CNN-block GAN with least squares (LSGAN) for this task [32]. Although these methods have improved denoising to some extent, the stability of the GAN training process still requires refinement.

Given the challenges outlined above, this paper focuses on plug-and-play image denoising [33] for LDCT image enhancement. Due to the flexibility and effectiveness of plug-and-play-based algorithms in solving a wide range of inverse problems, this approach has attracted significant attention from researchers. The core principle of plug-and-play image denoising involves using the variable splitting technique to unroll the energy function and substituting any off-the-shelf models for the prior term of the associated sub-problem in image denoising [34]. Unlike conventional image denoising methods that rely on hand-crafted prior terms, plug-and-play image denoising approaches implicitly design the prior term through a plug-and-play denoiser [35]. Notably, deep neural networks, with their large capacity for feature extraction, can be employed to learn the LDCT denoiser, thereby yielding promising results in noise reduction. In this paper, we present DRBNet, a deep residual block convolutional neural network (CNN) with residual noise learning for LDCT denoising. The DRBNet is trained with a constraint of total variation (TV) regularization. The deep denoiser prior we propose aims to extract the residual noise from the LDCT image, which is then fed into the model. Our presented plug-and-play denoising prior, DRBNet, is a learning deep model, which is different from existing plug-and-play prior. Our plug-and-play method with learning prior integrates flexibility that the model-based methods owns and effectiveness that the learning-based approaches possesses. The denoised CT image is derived by subtracting the learned residual noise map from the input LDCT image. The contributions of this work are summarized as follows.

(1) Novel deep plug-and-play denoising method: We introduce a new approach for LDCT image denoising by employing a deep residual block CNN (DRBNet) with residual noise learning as the denoising prior.

(2) Hybrid loss function: The DRBNet prior is trained using a hybrid loss function, combining L1 loss with multi-scale structural similarity (MS-SSIM) loss. Additionally, the training procedure is regularized with total variation (TV) to enhance denoising performance.

(3) Integration with a plug-and-play method: The trained DRBNet is incorporated into a half quadratic splitting-based method to solve the LDCT image denoising problem. This approach effectively combines the strengths of learning-based methods and model-based methods, offering both flexibility and performance.

(4) Superior performance: Extensive experiments demonstrate that our proposed plug-and-play method with DRBNet significantly outperforms existing state-of-the-art methods in suppressing noise and artifacts while preserving textural and edge information, when compared with standard NDCT scans.

The remainder of this article is structured as follows: Section 2 presents the plug-and-play image denoising method and the architecture of the deep CNN plug-and-play prior (DRBNet). Section 3 details the experimental setup and results. The concluding remarks are provided in the final section.

2 Methods

2.1 Degradation of LDCT images

Access to raw projection data from CT scans is typically restricted due to encryption by CT scanner vendors, making post-image processing techniques a viable alternative for LDCT image denoising. The LDCT denoising problem can be framed as an image denoising task once the corresponding NDCT image is available. The primary difference between natural image denoising and LDCT denoising lies in the statistical properties of LDCT, which are challenging to model accurately in the image domain. These statistical properties, characterized by high correlation and variation, substantially impact the performance of noise-dependent methods. The quantum noise inherent in X-ray projection data results in complex noise and artifacts in reconstructed LDCT images, further complicating noise reduction. Deep neural networks (DNNs), as learning-based methods, are well-suited to address these challenges, as they leverage large training datasets that are less dependent on noise type. We now formulate the denoising model for LDCT images as follows.

2.2 Deep plug-and-play noise reduction for LDCT

In the image spatial domain, the degradation process of LDCT images can be modeled by Equation 1. An LDCT image is typically viewed as a degraded NDCT image corrupted by noise.

$\mathit{x}={\mathit{y}\downarrow }_{\mathrm{s}}+\mathit{n}(1)$

where $x\in {\mathrm{R}}^{m\times n}$ denotes the LDCT image, ${\downarrow }_s$ and $n$ are the degradation and extra noise (for example, Poisson noise) respectively. $y\in {\mathrm{R}}^{m\times n}$ represents the corresponding NDCT image. In short, Equation 1 conveys that the LDCT image $x$ is a deteriorated, blurred, and noised version of a clean NDCT image $y$.

Using the degradation model described in Equation 1, we can proceed to formulate its energy function in the next step. The formal energy function can be derived from the Maximum A Posteriori (MAP) probability in Equation 2, as follows:

${\min }_y\frac{1}{2{\sigma }^2}|\left|x-{y\downarrow }_s\right|{|}^2+\lambda \varphi \left(y\right)(2)$

where $\frac{1}{2{\sigma }^2}|\left|x-{y\downarrow }_s\right|{|}^2$ represents the data fidelity term (or likelihood term) which determined by LDCT corrupting processing of Equation 1, $\varphi \left(y\right)$ denotes the regularization term and $\lambda$ is the regularized factor. The learning-based inference models correspond to this energy function, where the deterioration of the LDCT image is represented by the LDCT and NDCT images.

To solve Equation 2, we employ variable splitting with an auxiliary variable z, which allows us to reformulate the problem as an equivalent constrained optimization, as described below.

$\widehat{y}=\mathit{arg}{\min }_y\frac{1}{2{\sigma }^2}|\left|x-z\right|{|}^2+\lambda \varphi \left(y\right),\text{subject\hspace{0.17em}to\hspace{0.17em}}z=y{\downarrow }_s(3)$

For simplicity, Equation 3 can be solved using the half quadratic splitting (HQS) algorithm. Typically, we approach Equation 3 with HQS by minimizing the problem presented in Equation 4, which introduces an additional quadratic penalty term.

$L_{\mu }\left(y,z\right)=\frac{1}{{2\sigma }^2}\left|\left|x-z\right|\right.{|}^2+\lambda \varphi \left(y\right)+\frac{\mu }{2}\left.‖\left||\right||z\right|-y{\downarrow }_s|{|}^2(4)$

where $\mathrm{\mu }$ represents the penalty term parameter. Increasing μ will cause $z$ to approach $y{\downarrow }_s$ more closely. We observe that when iteratively solving Equation 4 with Equation (5) and Equation 6, the parameter μ increases in a non-decreasing manner.

$z_{k+1}=\arg \text{mi}{\mathrm{n}}_z‖\left.\left||\right||x-z\right|{|}^2+\mu {\sigma }^2\left.‖\left||\right||z-\right|y_k{\downarrow }_s|{|}^2(5)$

$y_{k+1}=\arg \text{mi}{\mathrm{n}}_y‖\left|\right|{\mathrm{z}}_{k+1}-{y\downarrow }_s|{|}^2+\lambda \varphi \left(y\right)(6)$

Equation 7 pertains to the variable z, while Equation 8 concerns y, representing two alternating minimization problems. In particular, we assume that the convolutional operation with kernel K is conducted under circular boundary conditions. This assumption allows for the formulation of a fast closed-form solution for $z_{k+1}$, as shown below:

$z_{k+1}={\mathcal{F}}^{-1}\left(\frac{\overline{\mathcal{F}\left(K\right)}\mathcal{F}\left(x\right)+\mu {\sigma }^2\mathcal{F}\left(y_k{\downarrow }_s\right)}{\overline{\mathcal{F}\left(K\right)}\mathcal{F}\left(K\right)+\mu {\sigma }^2}\right)(7)$

where $\mathcal{F}\left(·\right)$ is the fast Fourier transform (FFT) and ${\mathcal{F}}^{-1}\left(·\right)$ represents the inverse FFT (IFFT), respectively. $\overline{\mathcal{F}\left(·\right)}$ is the complex conjugate with respect to $\mathcal{F}\left(·\right)$. K is the kernel of convolutional operation.

We analyze Equation 6 on the view of Bayesian perspective and re-formulate it as follows:

$y_{k+1}=\mathit{arg}{\min }_y\frac{1}{2{\left(1/\mu \right)}^2}|\left|z_{k+1}-y{\downarrow }_s\right|{|}^2+\lambda \varphi \left(y\right)(8)$

Equation 8 addresses the denoising of $z_{k+1}$ with a corruption factor s, assuming that $z_{k+1}$ is a degraded version of a clear NDCT image y, corrupted by Poisson noise with a noise level of ${\left(1/\mathrm{\mu }\right)}^{1/2}$. From another perspective, Equation 8 tackles noise reduction using a simplified degradation model as follows (as Equation 9 described):

$x=y{\downarrow }_s+n(9)$

Consequently, we replace Equation 8 with a DNN-based LDCT image denoiser, which is trained on corrupted images at low-dose noise levels. For simplicity, Equation 6 and Equation 8 can be further consolidated as Equation 10.

$y_{k+1}=Denoiser\left(z_{k+1},s,{\left(1/\mu \right)}^{1/2}\right)(10)$

Because the prior term is implicitly defined in $Denoiser\left(·\right)$, as represented in Equation 10, it is referred to as a denoiser prior. Equations 5, 6 represent two sub-problems that are relatively easy to solve. On the one hand, the degradation procedure, Equation 9 with ${\downarrow }_s$ derived from a full-dose clean CT image, corresponds to a closed-form solution, and Equation 5 handles this. On the other hand, Equation 6 maps the blurred and noisy LDCT image to a clean NDCT image. After several iterations, the denoised LDCT image is reconstructed, approximating the corresponding full-dose image.

In summary, the detailed algorithm for our proposed deep plug-and-play DRBNet prior for LDCT denoising is outlined in Algorithm 1.

2.3 Deep denoiser prior for LDCT denoising

It is noteworthy that residual learning deep convolutional neural networks (CNNs) are both effective and efficient for image processing and computer vision tasks. Residual deep CNNs can alleviate challenges related to gradient vanishing and diffusion during training. By using skip connections, residual CNNs can learn both local and global features simultaneously. Unlike typical deep CNN-based image denoisers, which directly predict the latent clean denoised image, we propose a deep residual block CNN (DRBNet) with residual noise learning. Specifically, our deep denoiser prior extracts residual noise from the LDCT image, which is then input into the model. The latent denoised CT image is obtained by subtracting the learned residual noise map from the input LDCT image. The overall architecture of our DRBNet is illustrated in Figure 2.

Figure 2

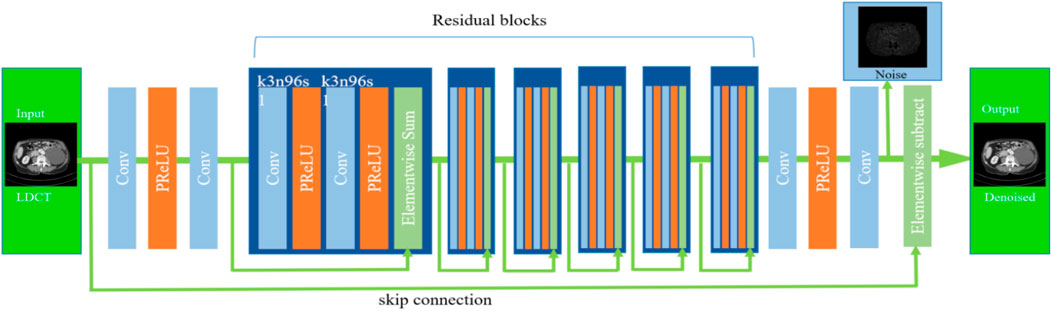
Figure 2. Architecture of deep residual blocks CNN (DRBNet) prior. It contains a shallow feature extractor and residual learning blocks.

Our proposed DRBNet differs from traditional deep neural networks (DNNs) in several key aspects. First, DRBNet learns the noise map from the LDCT image and then derives the latent denoised CT image by subtracting the noise map from the input LDCT image. In contrast, classic deep CNNs directly output the latent denoised CT image. Second, in this paper, we exclude batch normalization layers, as these can introduce extra artifacts and weaken the generalization power of the model during training. Third, we increase the number of feature channels in each convolutional layer, setting the feature channels to 96 in each residual block of the DRBNet.

Specifically, the first two convolutional layers of DRBNet are designed to extract shallow feature maps from the input LDCT image. These feature maps are then passed into the residual learning blocks. Each convolutional layer is configured with 3 × 3 filters, 96 feature maps, and a stride of 1. For simplicity, each convolutional layer in the residual learning blocks is set up similarly.

2.4 Hybrid objective loss regularized through total variation

Once the architecture of the deep CNN denoiser is established, it must be trained to learn the features of LDCT images. To capture the characteristics of noise, we use a hybrid loss function that combines the multiscale structural similarity index (MS-SSIM) and L1 loss. L1 loss helps suppress noise and improves the signal-to-noise ratio, while MS-SSIM loss preserves high-frequency details in CT images. Additionally, we regularize the optimization with a total variation (TV) term to better preserve texture and edge information during training. TV regularization sharpens the denoised LDCT image while maintaining edges and gradient information, which is crucial for medical imaging. In summary, the loss function used to train our proposed DRBNet is formulated as follows (Equation 11):

$L_{total}={\gamma }_1\times L_{MS-SSIM}+{\gamma }_2\times L_1+{\gamma }_3\times L_{TV}(11)$

where ${\gamma }_1$, ${\gamma }_2$, and ${\gamma }_3$ are the weights for the MS-SSIM loss, L1 loss, and L_TV loss respectively. $L_{total}$ is the overall loss function training our DRBNet denoiser prior, $L_{MS-SSIM}$ denotes the part of MS-SSIM loss, and $L_{TV}$ represents the penalty term of the TV regularization.

The introduction of the total variation (TV) regularization term during the training of DRBNet serves to differentiate among the potentially infinite solutions for the deep CNN denoiser prior and select the one with optimal characteristics as the denoised low-dose CT (LDCT) image. Specifically, the TV regularization term is defined as follows (Equation 12):

$L_{TV}={‖\widehat{y}‖}_{TV}=\int {‖\nabla \widehat{y}\left(i\right)‖}_{1}di(12)$

where $\nabla \widehat{y}\left(i\right)$ denotes the gradient of the denoised low-dose CT image $\widehat{y}$ at a pixel $i$. The penalty term of the TV regularization has been demonstrated to be robust for removing noise and artifacts in the denoised image $\widehat{y}$.

3 Experiments and results

3.1 Datasets for experiments

In this study, we used a public clinical CT dataset from the Mayo Clinic, released for the 2016 NIH-AAPM-Mayo Clinic Low Dose CT Grand Challenge, to train and test the proposed DRBNet prior. The Mayo CT dataset includes 2,378 pairs of normal-dose CT (NDCT) images and their corresponding simulated LDCT images from 10 anonymized patients. The slice thickness in the dataset is 3.0 mm, and each CT image is of size 512 × 512 pixels. For training and testing the proposed DRBNet denoiser prior, we selected pairs of normal-dose and quarter-dose CT images from this dataset. To ensure fairness, we employed cross-validation in the training and validation of the model. Specifically, while the model was trained using CT image pairs from nine patients, the data from the 10th patient was used for validation.

The performance of deep learning-based noise reduction methods heavily depends on the availability of a large training sample size. A substantial volume of valid training data can significantly enhance the denoising performance of the deep learning model. To extend the size of the CT dataset and improve the denoising performance of DRBNet, we applied an overlapping patch strategy in our experiments. This approach not only captures spatial interconnections across patches but also expands the training data by augmenting the patch scale. From the dataset, we randomly extracted 89,520 image patches of size 64 × 64 pixels for training.

3.2 Training details

The DRBNet denoiser prior was optimized using the Adam algorithm. We set the mini-batch size to 16 and used the following hyperparameters for Adam $\mathrm{\alpha }=10^{-5}$, ${\mathrm{\beta }}_1=0.9$, ${\mathrm{\beta }}_2=0.99$. Based on our experimental observations, the weighting parameters governing the trade-off among the components of the loss function (11) were set to ${\gamma }_1=0.7$, ${\gamma }_2=0.2$, and ${\gamma }_3=0.1$. The convolutional kernels were initialized with a random Gaussian distribution. The initial learning rate was set to $1e^{-5}$, gradually decreasing to $1e^{-7}$. The total number of epochs for training DRBNet was set to 100. The DRBNet model was implemented using PyTorch, and training was accelerated using an NVIDIA GPU RTX2080TI, with a total training time of approximately 12 h.

The denoised LDCT images were evaluated using three common metrics: peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and root mean square error (RMSE). Specifically, PSNR is crucial for assessing the performance of LDCT denoising, with higher PSNR values indicating greater similarity to the original clean image. SSIM measures the structural similarity between the denoised image and its ground truth. A higher SSIM value, closer to 1, indicates a better approximation to the original image. RMSE quantifies the difference between the denoised LDCT image and the ground truth clean full-dose image, with smaller RMSE values indicating better denoising performance.

3.3 Compared methods

We compared the proposed DRBNet denoiser prior for LDCT with six other state-of-the-art approaches: NLM, BM3D, K-SVD, RED-CNN, WGAN, and SMGAN. NLM, BM3D, and K-SVD are the three most popular conventional noise reduction methods, which have been commonly employed for LDCT denoising. RED-CNN, WGAN, and SMGAN are deep learning-based methods that represent some of the most prominent approaches for LDCT denoising. The parameters for all the compared methods were set based on the recommendations from the original studies. Additionally, the three deep learning-based methods were trained using the same source data as our proposed DRBNet denoiser prior.

3.4 Convergence

The theoretical convergence of the plug-and-play framework for noise reduction was examined in [36, 37]. Since our proposed DRBNet prior represents a specific case of this framework, we present empirical evidence to demonstrate its convergence in this study. Figure 3 illustrates the convergence curves of DRBNet on the training set from the Mayo CT dataset. It is evident that DRBNet converges rapidly to a fixed solution. While training with the overall loss that includes TV regularization leads to a slightly slower convergence compared to training without TV regularization, the inclusion of TV constraints results in higher output image quality. Given that our DRBNet denoiser prior has been trained end-to-end on a substantial set of LDCT images, it does not require iterative noise reduction solutions, which marks a distinct advantage over traditional plug-and-play denoising methods. In practice, we balance performance and processing speed by adjusting the total number of epochs during training.

Figure 3

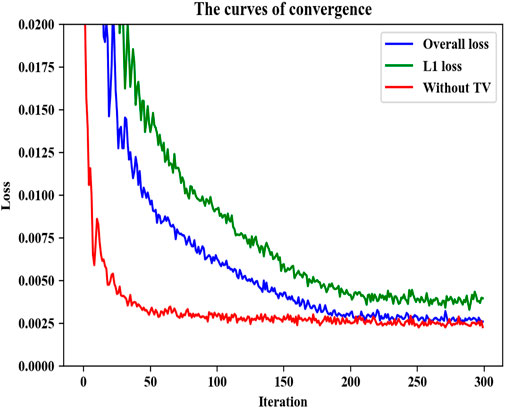
Figure 3. Convergence curves of our proposed DRBNet prior on the training set in the Mayo CT dataset.

3.5 Visual results

To evaluate the noise reduction performance of our proposed plug-and-play prior for LDCT image denoising, two denoised results of the representative LDCT images are analyzed.

Figures 4–7 show results from proposed DRBNet prior and the compared denoising methods. Figures 4, 5 show the entire CT scans, while Figures 6, 7 focus on the regions of interest (ROIs), marked by red rectangles in Figures 4, 5. The display window for all figures is set to the range of [-160, 240] HU. CT images inherently contain rich textures representing organ and tissue structures. However, as depicted in the figures, the LDCT images are heavily contaminated with noise and artifacts, which can hinder clinicians’ ability to accurately assess lesions, diseases, or tissue morphology. All compared denoising algorithms succeed to some degree in removing noise and artifacts. However, NLM and BM3D provide minimal improvement in noise removal, with noticeable residual noise and artifacts still evident in the enlarged ROI images (see Figure 6b c; Figure 7b,c). The denoising effect of K-SVD is marginally better than that of NLM and BM3D. The results from RED-CNN suffer from over-smoothing, resulting in the loss of fine texture details in the tissue and anatomical structures due to its use of the mean squared error (MSE) loss during training. The denoised CT image from LSGAN reduces noise while maintaining texture information. However, the results obtained using our proposed DRBNet prior, as shown in Figure 4g; Figure 7g, effectively remove noise and suppress artifacts while preserving crucial texture details that are vital for clinical diagnosis.

Figure 4

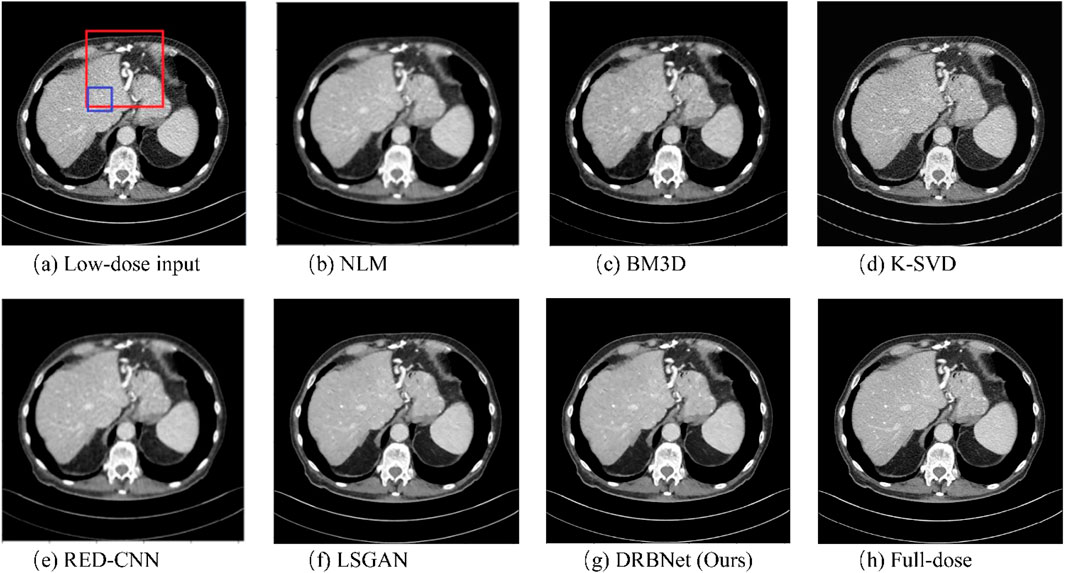
Figure 4. Results of a low-dose CT scan produced by compared algorithms from the testing set. (a) Low-dose, (b) NLM, (c) BM3D, (d) K-SVD, (e) RED-CNN (f) LSGAN, (g) DRBNet (Ours), (h) Full-dose. The display window ranges: 160 to 240 HU.

Figure 5

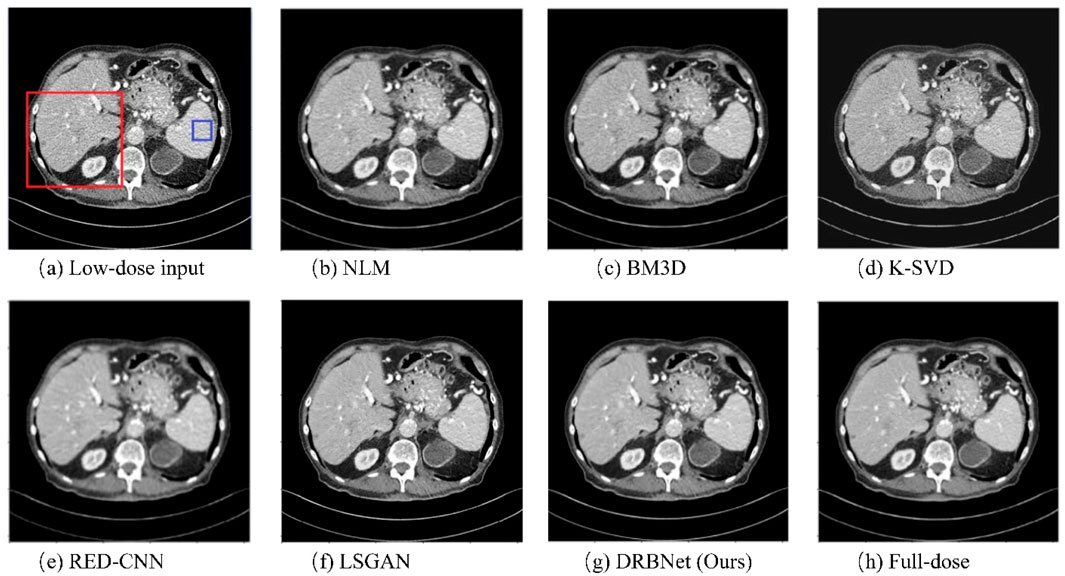
Figure 5. Results of a low-dose CT scan produced by comparing algorithms from the testing set. (a) Low-dose, (b) NLM, (c) BM3D, (d) K-SVD, (e) RED-CNN (f) LSGAN, (g) DRBNet (Ours), (h) Full-dose. The display window ranges: 160 to 240 HU.

Figure 6

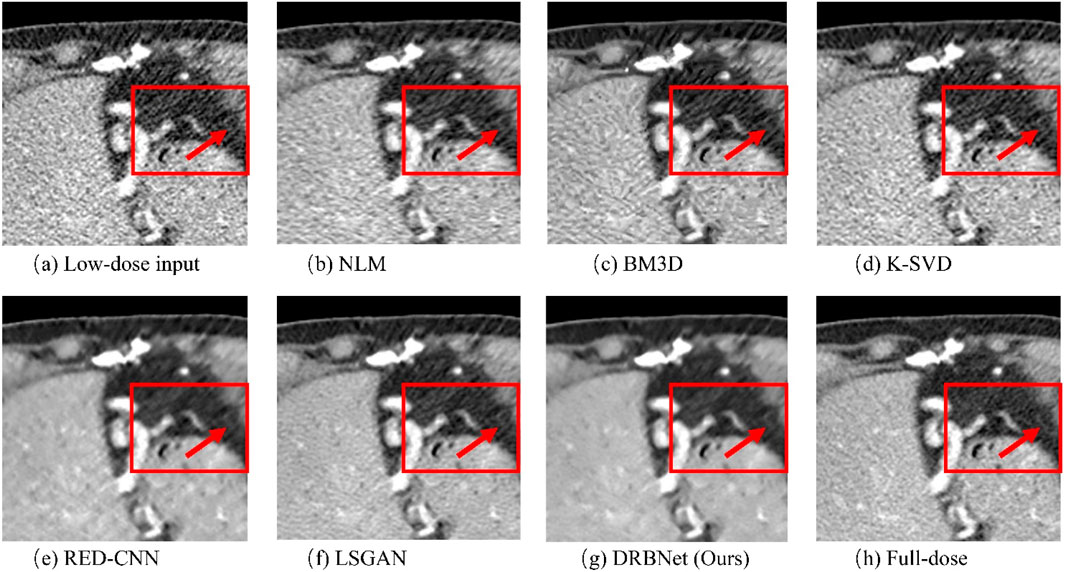
Figure 6. Zoomed ROI (region of interest) parts of labeled by the rectangle in Figure 3. (a) Low-dose, (b) NLM, (c) BM3D, (d) K-SVD, (e) RED-CNN (f) LSGAN, (g) DRBNet (Ours), (h) Full-dose. The display window ranges: 160 to 240 HU.

Figure 7

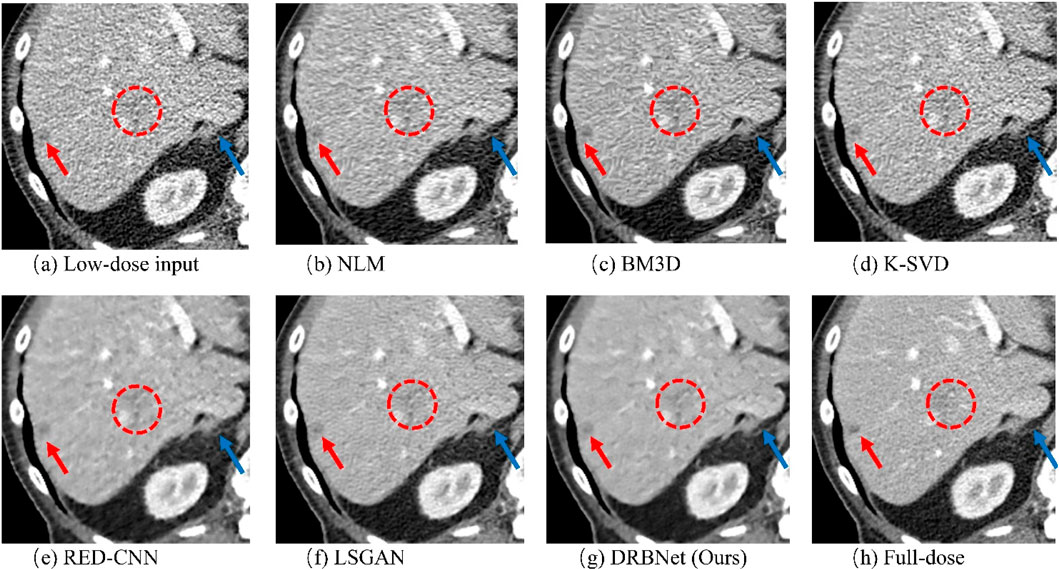
Figure 7. Zoomed ROI (region of interest) parts of labeled by the rectangle in Figure 4. (a) Low-dose, (b) NLM, (c) BM3D, (d) K-SVD, (e) RED-CNN (f) LSGAN, (g) DRBNet (Ours), (h) Full-dose. The display window ranges: 160 to 240 HU.

In Figure 6, the zoomed-in ROI, marked in Figure 4 with a red rectangle, contains rich tissue texture information. This ROI section includes intricate tissue details that are nearly obscured by significant noise and artifacts. Notably, the textures indicated by the red arrow in Figure 6a are blurred and unclear in the original LDCT input. The NLM, BM3D, and K-SVD methods struggle to restore these fine textures. RED-CNN causes excessive smoothing, resulting in further blurring, while LSGAN still leaves some residual noise that could affect clinical diagnosis. However, in Figure 6g, the result from our proposed DRBNet prior clearly restores the fine texture and removes the noise. In Figure 7g, the low attenuation lesions, highlighted by the red circle and red arrow, along with the subtle details indicated by the blue arrow, are restored by our approach and closely resemble the full-dose target. Overall, the observations from Figures 4–7 demonstrate that the visual results produced by our DRBNet prior are highly promising.

For visualizing and understanding the internal working mechanism of our proposed DRBNet, Figure 8 shows feature maps from our model once the training is finished. Modules in DRBNet performing CT image feature extraction is significant for tasks of LDCT image denoising. The Feature maps shown in Figure 8 are organized into an array with size of 8 × 16. Each small sub-image emphasizes the features of the original CT images, i. e., whole structures, edges, and boundaries. Thus, we believe that the proposed DRBNet can fully learn the features of CT images and can fully demonstrate its capabilities in the tasks of low-dose CT image denoising.

Figure 8

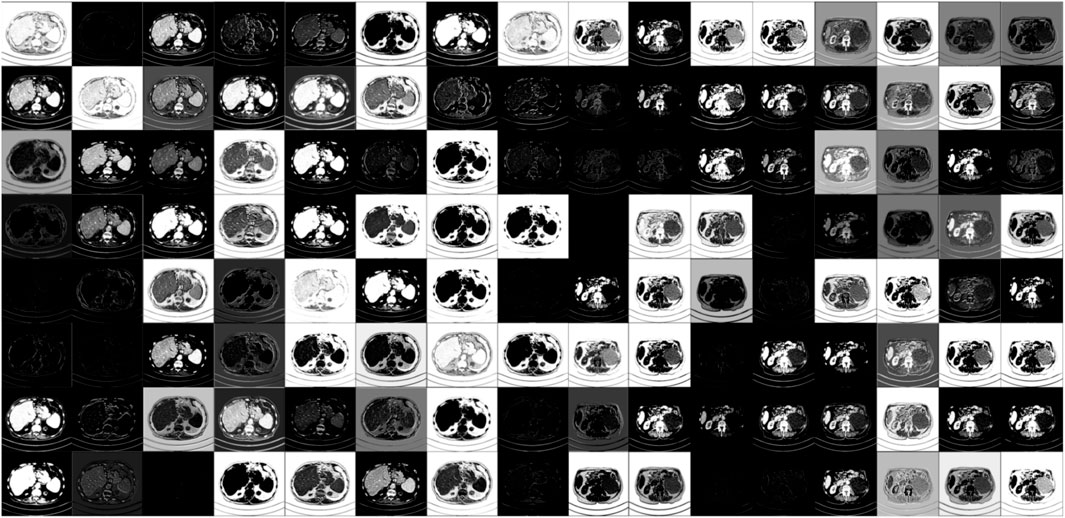
Figure 8. Visualization of feature maps of CT images extracted from different layers in our proposed trained DRBNet.

We applied a group of LDCT image containing a sum of 200 LDCT images from a local hospital to further validate our proposed DRBNet. Figure 9 provide three typical cases resulted from DRBNet prior. The residual noise is gained from the normal-dose CT images minus the denoised CT images. From Figure 9, the visual effect and quantitative metrics (PSNR/SSIM/RMSE) of the denoised CT images further demonstrate the effectiveness of DRBNet.

Figure 9

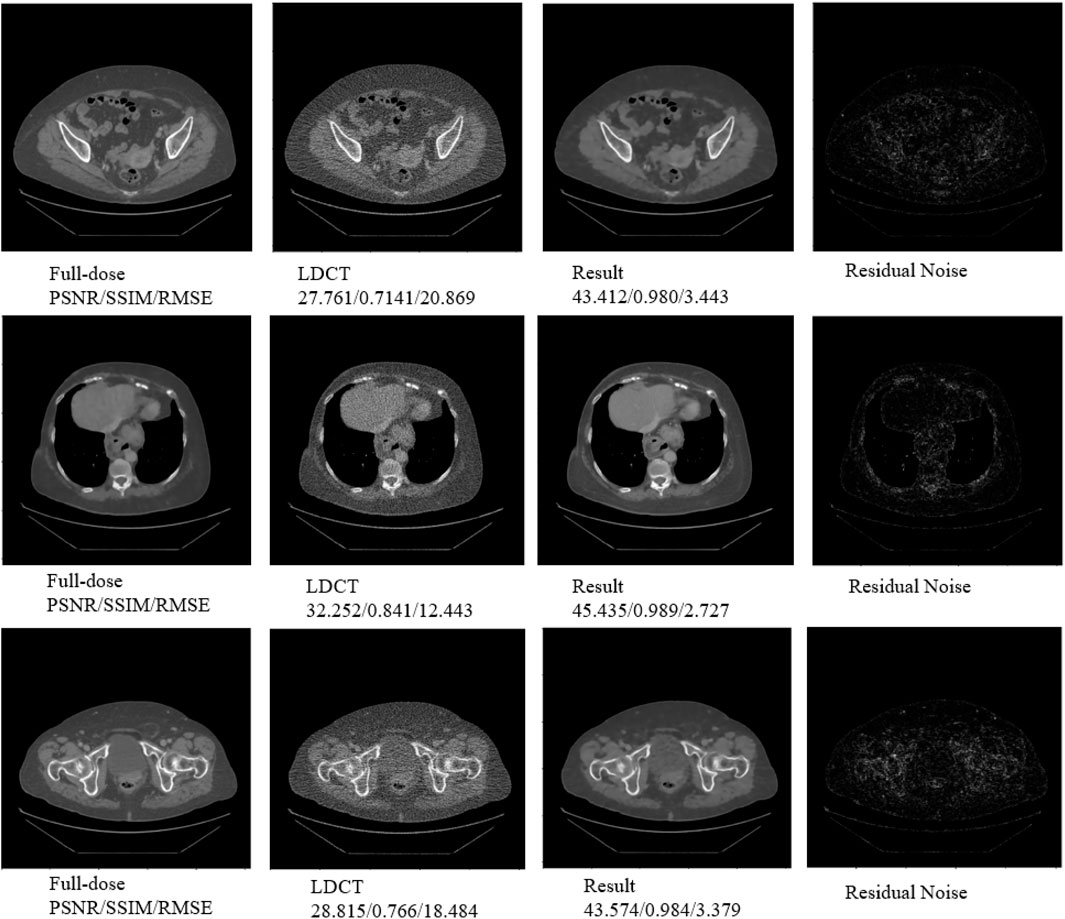
Figure 9. Three typical cases resulted from DRBNet prior for LDCT denoising. The raw CT images are provided by a local hospital. The residual noise is gained from the full-dose CT images minus the denoised CT images.

3.6 Quantitative analysis

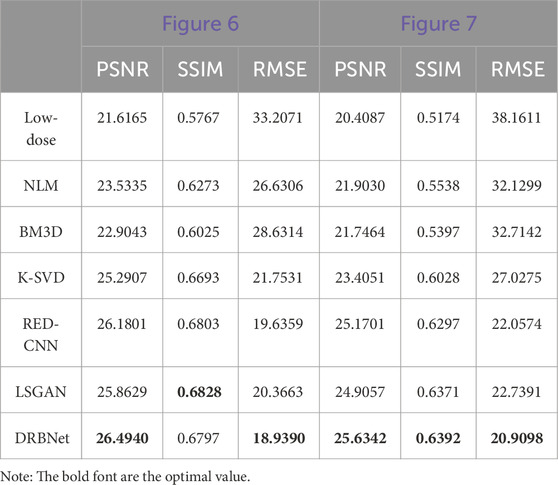
In this section, we present three key evaluation metrics—PSNR, SSIM, and RMSE—to quantitatively assess the performance of our proposed DRBNet prior and compare it with other state-of-the-art approaches. Table 1 provides the quantitative results for the images shown in Figures 4, 5, while Table 2 summarizes the results for the zoomed-in ROIs from Figures 6, 7.

Table 1

Table 1. Quantitative results for whole-CT images shown in Figures 4, 5 using different methods.

Table 2

Table 2. Quantitative measurements for zoomed ROIs shown in Figures 6, 7 using different methods.

As shown in Table 1, our proposed DRBNet prior outperforms the state-of-the-art methods in terms of PSNR, SSIM, and RMSE. These results align with the visual improvements observed in Figures 4, 5. In Table 2, the quantitative measurements of our DRBNet prior for the zoomed ROIs from Figures 4, 5 also demonstrate superior performance, with the exception of SSIM in Figure 6. This deviation may be due to the fact that the abdomen CT scan, which contains rich soft tissue textures, benefits from LSGAN’s noise reduction in this particular case. Furthermore, Table 3 presents the average quantitative performance of our DRBNet prior on a testing set comprising over two hundred LDCT scans. From Table 3, we observe that the DRBNet outperforms the compared state-of-the-art methods in terms of PSNR, SSIM, and RMSE.

Table 3

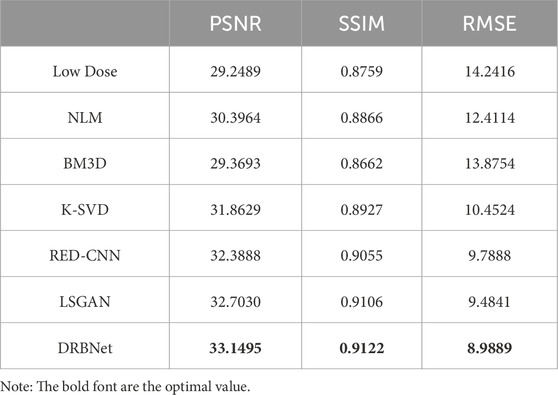
Table 3. Average values of quantitative performance for the testing set with other state-of-the-art methods.

3.7 Blind reader study

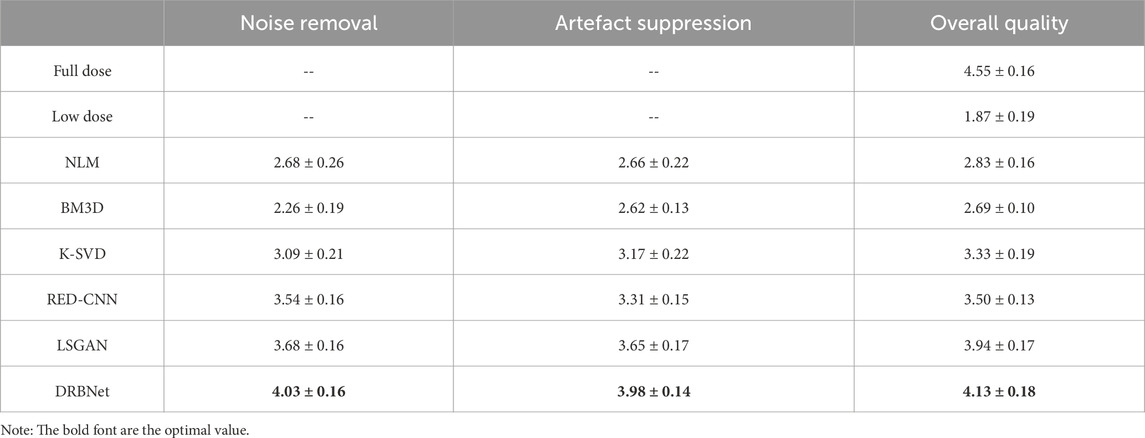
To assess the clinical image quality of the denoised LDCT scans, we conducted a blind reader study using 10 groups of CT scans. Each group consists of an LDCT image, its corresponding full-dose version, and denoised LDCT images generated using the competing methods. In the blind reader study, the low-dose and full-dose images were used as baseline and gold-standard references, respectively. Two radiologists, each with over 5 years of clinical experience, independently rated each denoised LDCT image on a five-point scale (1 representing poor quality and five representing excellent quality), focusing on noise reduction, artefact suppression, and overall image quality. Table 4 provides the mean and standard deviation (SD) of the final assessments from both radiologists.

Table 4

Table 4. Statistical analysis of image quality scores of other state-of-the-art methods.

From Table 4, it is evident that the LDCT images received the lowest scores due to their degraded quality. All noise reduction algorithms improved the scores to varying degrees. However, compared to the other denoising methods, our proposed DRBNet prior achieved the highest scores for noise reduction, artifact suppression, and overall image quality. In summary, the blind reader study demonstrates the superior capabilities of DRBNet in reducing noise, suppressing artifacts, and enhancing image quality. More importantly, the images produced by DRBNet meet the perceptual requirements of the human visual system (HVS), as shown in Figure 4; Figure 7.

We also conducted the experiments to compare the denoising performance of DRBNet alone and plug-and-play + DRBNet prior (called DRBNet in this study) with mean quantitative metrics of PSNR, SSIM and RMSE on the test set. The compared results are 32.9399/0.9092/9.2030 and 33.1495/0.9122/8.9889 (PSNR/SSIM/RMSE) respectively. This demonstrates the merits of plug-and-play + denoiser prior.

3.8 Ablation with/with TV regularization

To validate the instrument of the TV regularization, we conduct ablation experiments to demonstrate its effectiveness for improving the quality of denoised LDCT images. We trained the DRBNet with/without TV regularization included in the hybrid loss function. Quantitative measurements of the experimental results are shown in Table 5. One can see that our presented DRBNet is improved by training with TV regularization.

Table 5

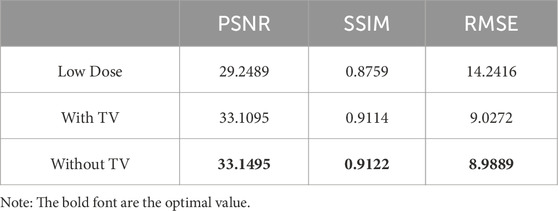
Table 5. Quantitative measurements of the experimental results with/without TV regularization included in the hybrid loss function.

3.9 Model efficiency

The complexity of the denoising model is determined by the architecture of network model, to further explore the efficiency, complexity, and inference speed of different denoising models, we compare parameter sizes, memory usage, and inference speed of the methods in this study. The results are shown in Table 6. From Table 6, it shows that our proposed DRBNet gets the least running time, although it has the most parameters and memory usage compared other deep learning-based methods. NLM, BM3D and K-SVD are traditional methods for image denoising which requires more running time. Once training process is finished, deep learning-based methods only require fewer running time for inference. In total, according to denoising performance and model efficiency, DRBNet is competitive algorithm with noise reduction and artefacts removal for LDCT.

Table 6

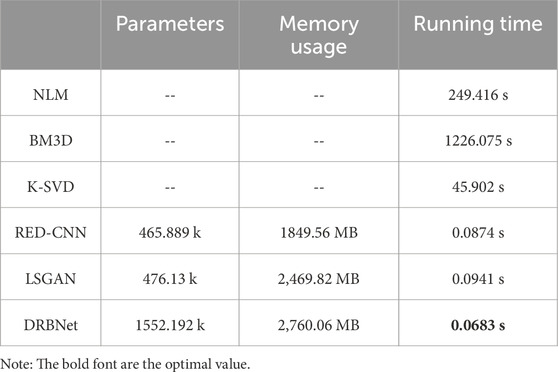
Table 6. Comparisons of parameter size, memory usage, and running time under different denoising methods (k: kilo, MB: mega bytes, fps: frame per second).

3.10 Model deployment

After training and fine-tuning deep learning model, it can be deployed to a running environment as a necessary part of the workflow for CT imaging and medical analysis. Our proposed DRBNet prior can be encapsulated into an application programming interface (API) using an appropriate tool such Flask or Djano, so that it can be called by other applications. Also, DRBNet prior can be converted into a deployable format utilizing Torchscript so that it is able to execute in other program language such as C++.

Algorithm 1

Algorithm 1.Deep Plug-and-play Prior Image Restoration with TV Regularization for Low-dose CT.

4 Conclusion

This paper introduces a residual deep plug-and-play denoising method for LDCT image denoising. We first explain the principles of plug-and-play noise reduction for LDCT, followed by solving the corresponding energy function using the half-quadratic splitting algorithm, which leverages the strengths of the plug-and-play framework. This modular approach is particularly effective for LDCT image denoising, making the proposed DRBNet prior well-suited for this task. Additionally, the denoiser prior can be integrated into a plug-and-play framework for LDCT denoising. Our extensive experimental results validate the effectiveness and feasibility of the deep denoiser-based plug-and-play method for LDCT. It is worth noting that there are opportunities for further enhancement, such as integrating other types of deep learning-based image priors, such as deep generative priors or discriminative priors, to improve LDCT denoising performance.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YM: Conceptualization, Funding acquisition, Methodology, Project administration, Writing – original draft, Writing – review and editing. YZ: Formal Analysis, Software, Writing – review and editing. LC: Formal Analysis, Visualization, Writing – review and editing. QJ: Data curation, Validation, Writing – review and editing. FS: Formal Analysis, Data curation, Writing – review and editing. BW: Conceptualization, Investigation, Methodology, Project administration, Resources, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported in part by the Doctoral Research Foundation Project of Tongren University under Grant trxyDH2222 and in part by the Scientific Research Project of Tongren City under Grant [2023] No. 40 in part by the College Students’ Innovation and Entrepreneurship Training Program of Guizhou Province under Grant S2024106651893.

Acknowledgments

The authors also thank the reviewers and associate editor for their constructive comments and suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rubin GD. Computed tomography: revolutionizing the practice of medicine for 40 years. Radiology (2014) 273:S45–S74. doi:10.1148/radiol.14141356

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Brenner DJ, Hall EJ. Risk of cancer from diagnostic X-rays. Lancet (2004) 363:2192. doi:10.1016/s0140-6736(04)16519-7

PubMed Abstract | CrossRef Full Text | Google Scholar

3. De González AB, Mahesh M, Kim K-P. Projected cancer risks from computed tomographic scans performed in the United States in 2007. Arch Intern Med (2009) 169:2071–7. doi:10.1001/archinternmed.2009.440

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Naidich DP, Marshall CH, Gribbin C, Arams RS, McCauley DI. Low-dose CT of the lungs: preliminary observations. Radiology (1990) 175:729–31. doi:10.1148/radiology.175.3.2343122

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhang J, Gong W, Ye L, Wang F, Shangguan Z, Cheng Y. A review of deep learning methods for denoising of medical low-dose CT images. Comput Biol Med (2024) 171:108112. doi:10.1016/j.compbiomed.2024.108112

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Manduca A, Yu L, Trzasko JD, Khaylova N, Kofler JM, McCollough CM, et al. Projection space denoising with bilateral filtering and CT noise modeling for dose reduction in CT. Med Phys (2009) 36:4911–9. doi:10.1118/1.3232004

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Balda M, Hornegger J, Heismann B. Ray contribution masks for structure adaptive sinogram filtering. IEEE Trans Med Imaging (2012) 31:1228–39. doi:10.1109/tmi.2012.2187213

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Li T, Li X, Wang J. Nonlinear sinogram smoothing for low-dose X-ray CT. IEEE Trans Nucl Sci (2004) 51:2505–13. doi:10.1109/TNS.2004.834824

CrossRef Full Text | Google Scholar

9. Sidky EY, Pan X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys Med Biol (2008) 53:4777–807. doi:10.1088/0031-9155/53/17/021

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhang Y, Zhang W, Chen H, Yang M, Li T, Zhou J. Few-view image reconstruction combining total variation and a high-order norm. Int J Imag Syst Tech (2013) 23:249–55. doi:10.1002/ima.22058

CrossRef Full Text | Google Scholar

11. Xu Q, Yu H, Mou X, Zhang L, Hsieh J, Wang G. Low-dose X-ray CT reconstruction via dictionary learning. IEEE Trans Med Imag (2012) 31:1682–97. doi:10.1109/TMI.2012.2195669

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zhang Y, Mou X, Wang G, Yu H. Tensor-based dictionary learning for spectral CT reconstruction. IEEE Trans Med Imaging (2016) 36:142–54. doi:10.1109/tmi.2016.2600249

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Aharon M, Elad M, Bruckstein A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans Signal Process (2006) 54:4311–22. doi:10.1109/tsp.2006.881199

CrossRef Full Text | Google Scholar

14. Chen Y, Yang Z, Hu Y, Yang G, Zhu Y, Li Y, et al. Thoracic low-dose CT image processing using an artifact suppressed large-scale nonlocal means. Phys Med Biol (2012) 57:2667–88. doi:10.1088/0031-9155/57/9/2667

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Cai J-F, Jia X, Gao H, Jiang SB, Shen Z, Zhao H. Cine cone beam CT reconstruction using low-rank matrix factorization: algorithm and a proof-of-principle study. IEEE Trans Med Imaging (2014) 33:1581–91. doi:10.1109/tmi.2014.2319055

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ma J, Huang J, Feng Q, Zhang H, Lu H, Liang Z, et al. Low-dose computed tomography image restoration using previous normal-dose scan. Med Phys (2011) 38:5713–31. doi:10.1118/1.3638125

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Li Z, Yu L, Trzasko JD, Lake DS, Blezek DJ, Fletcher JG, et al. Adaptive nonlocal means filtering based on local noise level for CT denoising. Med Phys (2014) 41:011908. doi:10.1118/1.4851635

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Chen Y, Yin X, Shi L, Shu H, Luo L, Coatrieux J-L, et al. Improving abdomen tumor low-dose CT images using a fast dictionary learning based processing. Phys Med Biol (2013) 58:5803–20. doi:10.1088/0031-9155/58/16/5803

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Dabov K, Foi A, Katkovnik V, Egiazarian K. Image denoising with block-matching and 3D filtering. In: SPIE proceedings (SPIE) (2013). p. 1–12. doi:10.1117/12.643267

CrossRef Full Text | Google Scholar

20. Fumene Feruglio P, Vinegoni C, Gros J, Sbarbati A, Weissleder R. Block matching 3D random noise filtering for absorption optical projection tomography. Phys Med Biol (2010) 55:5401–15. doi:10.1088/0031-9155/55/18/009

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kang D, Slomka P, Nakazato R, Woo J, Berman DS, Kuo C-CJ, et al. Image denoising of low-radiation dose coronary CT angiography by an adaptive block-matching 3D algorithm. In: SPIE proceedings (SPIE) (8669). doi:10.1117/12.2006907

CrossRef Full Text | Google Scholar

22. Liu W, Wang Z, Liu X, Zeng N, Liu Y, Alsaadi FE. A survey of deep neural network architectures and their applications. Neurocomputing (2017) 234:11–26. doi:10.1016/j.neucom.2016.12.038

CrossRef Full Text | Google Scholar

23. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: 2016 IEEE Conference on computer Vision and pattern recognition (CVPR) (IEEE) (2015). p. 770–8. doi:10.1109/cvpr.2016.90

CrossRef Full Text | Google Scholar

24. Dong C, Loy CC, He K, Tang X. Image super-resolution using deep convolutional networks. IEEE Trans Pattern Anal Mach Intell (2015) 38:295–307. doi:10.1109/tpami.2015.2439281

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Chen H, Zhang Y, Zhang W, Liao P, Li K, Zhou J, et al. aLow-dose CT via convolutional neural network. Biomed Opt Express (2017) 8:679. doi:10.1364/boe.8.000679

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chen H, Zhang Y, Kalra MK, Lin F, Chen Y, Liao P, et al. Low-Dose CT with a residual encoder-decoder convolutional neural network. IEEE Trans Med Imaging (2017) 36:2524–35. doi:10.1109/tmi.2017.2715284

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ma Y, Feng P, He P, Long Z, Wei B. Low-dose CT with a deep convolutional neural network blocks model using mean squared error loss and structural similar loss. In: Eleventh international Conference on information Optics and photonics (CIOP 2019) (SPIE) (2016). p. 26. doi:10.1117/12.2542662

CrossRef Full Text | Google Scholar

28. Shan H, Zhang Y, Yang Q, Kruger U, Kalra MK, Sun L, et al. Correction for “3D convolutional encoder-decoder network for low-dose CT via transfer learning from a 2D trained network.”. IEEE Trans Med Imaging (2018) 37:1522–34. doi:10.1109/tmi.2018.2878429

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wu D, Kim K, Fakhri GE. A cascaded convolutional neural network for x-ray low-dose CT image denoising. In: International joint conference on neural networks (2017). doi:10.48550/arXiv.1705.04267

CrossRef Full Text | Google Scholar

30. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial networks. Commun ACM (2020) 63:139–44. doi:10.1145/3422622

CrossRef Full Text | Google Scholar

31. Yang Q, Yan P, Zhang Y, Yu H, Shi Y, Mou X, et al. Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss. IEEE Trans Med Imaging (2018) 37:1348–57. doi:10.1109/tmi.2018.2827462

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Ma Y, Wei B, Feng P, He P, Guo X, Wang G. Low-dose CT image denoising using a generative adversarial network with a hybrid loss function for noise learning. IEEE Access (2020) 8:67519–29. doi:10.1109/access.2020.2986388

CrossRef Full Text | Google Scholar

33. Chan SH, Wang X, Elgendy OA. Plug-and-play ADMM for image restoration: fixed-point convergence and applications. IEEE Trans Comput Imaging (2016) 3:84–98. doi:10.1109/tci.2016.2629286

CrossRef Full Text | Google Scholar

34. Lai Z, Wei K, Fu Y. Deep plug-and-play prior for hyperspectral image restoration. Neurocomputing (2022) 481:281–93. doi:10.1016/j.neucom.2022.01.057

CrossRef Full Text | Google Scholar

35. Zhang K, Li Y, Zuo W, Zhang L, Van Gool L, Timofte R. Plug-and-play image restoration with deep denoiser prior. IEEE Trans Pattern Anal Mach Intell (2021) 44:6360–76. doi:10.1109/tpami.2021.3088914

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Buzzard GT, Chan SH, Sreehari S, Bouman CA. Plug-and-play unplugged: optimization-free reconstruction using consensus equilibrium. SIAM J Imaging Sci (2018) 11:2001–20. doi:10.1137/17m1122451

CrossRef Full Text | Google Scholar

37. Reehorst ET, Schniter P. Regularization by denoising: clarifications and new interpretations. IEEE Trans Comput Imaging (2018) 5:52–67. doi:10.1109/tci.2018.2880326

PubMed Abstract | CrossRef Full Text | Google Scholar