Stochastic bifurcation phenomenon and multistable behaviors in a fractional Rayleigh–Duffing oscillator under recycling noise

This study examines the stochastic bifurcation phenomenon in a fractional and multistable Rayleigh–Duffing oscillator subjected to recycling noise excitation. First, using the harmonic balance method and minimizing the mean-square error, an approximate integerorder equivalent system was derived for the original fractional-order system. Subsequently, the steady-state probability density function (sPDF) of the system amplitude was obtained via stochastic averaging. The critical conditions for stochastic P-bifurcation (SPB) were then determined using the singularity theory. The stationary PDF curves of the system amplitude were qualitatively analyzed across regions delineated by transition set curves. Finally, Monte Carlo simulations confirmed the analytical findings, validating the theoretical framework. These results provide insights for improving system response control through fractional-order controller design.

1 Introduction

Fractional calculus extends classical calculus to non-integer orders, enabling the characterization of memory effects in viscoelastic materials more effectively than integer-order derivatives. The fractional derivative, expressed as a convolution, inherently represents memory and cumulative effects over time. Consequently, it has proven to be a superior mathematical tool for modeling memory properties [1–4] and has found applications in various fields, including anomalous diffusion, non-Newtonian fluid mechanics, soft matter physics, and viscoelastic mechanics. Compared to integer-order calculus, fractional derivatives provide a more precise description of diverse reaction processes [5–9]. Given the prevalence of ambient noise in engineering, it is crucial to investigate the dynamic properties of stochastic systems and the influence of fractional-order parameters and noise excitations.

Recent studies have extensively examined the dynamics of nonlinear multistable systems under various noise excitations, yielding significant results [10–14]. For integer-order systems, research on Duffing–Van der Pol oscillators under Lévy noise [12], colored noise [13], and combined harmonic and random excitations [10, 11, 14] has garnered considerable attention. Wu and Hao [15] analyzed the tri-stable stochastic P-bifurcation (SPB) in a generalized Duffing–Van der Pol oscillator subjected to multiplicative colored noise, deriving an analytical expression for the system’s steady-state probability density function (sPDF) and evaluating the effects of noise intensity and system parameters. Qian and Chen [16] investigated the random vibration of a modified single-degree-of-freedom vibro-impact oscillator with a recovery factor under broadband noise and determined the sPDF of the system’s energy and amplitude envelope using the Markov approximation. This approach was validated through numerical examples. He [17] proposed an improved amplitude–frequency formulation for nonlinear oscillators and verified the reliability by considering the solution of a Duffing oscillation. Fan [18] utilized He’s frequency–amplitude formulation to solve the Duffing harmonic oscillator problem. The results indicated that not only is the solution procedure simple, but also, the result obtained is valid for the whole solution domain with high accuracy.

For fractional-order systems, Huang and Jin [19] examined the response and sPDF of a strongly nonlinear single-degree-of-freedom system under Gaussian white noise. Sun and Yang [20] employed the random averaging method and the generalized harmonic function method to assess the stability of a fractional-order energy acquisition system under Gaussian white noise, focusing on the effects of noise intensity, fractional derivative order, and coefficients on the system’s stochastic response. Li et al. [21] explored bistable SPB in a Duffing–Van der Pol system with fractional derivatives under concurrent multiplicative and additive colored noise, demonstrating that variations in linear damping, fractional derivative order, and noise intensity induce SPB.

Nonlinear oscillations [22] have been widely studied because of their relevance in energy harvesting [23], nonlinear controller design [24], and multi-degree-of-freedom systems, including three-degree-of-freedom auto-parametric systems [25] and six-degrees-of-freedom rigid body systems [26]. Li and He [27, 28] proposed a fractional complex transform to convert fractional differential equations into ordinary differential equations so that all analytical methods devoted to advanced calculus can be easily applied to fractional calculus, and some examples were given to verify the effectiveness of the proposed method. He [29, 30] proposed a new perturbation method that does not require a small parameter in an equation to analyze the nonlinear oscillators, and the effectiveness of the proposed method was verified through examples. Wang and He [31] used the variational iteration method to give an extremely simple and elementary derivation of the temperature distribution of a reaction-diffusion process. It was shown that the method is very effective and convenient compared with the exact solution. He [32] proposed an improved fractional variational iteration method to solve the space and time fractional telegraph equations more effectively. He and his colleagues utilized the fractal variational principle to explore the solutions of numerous fractional equations [33–36].

Owing to the complexity of fractional derivatives, it is generally only possible to qualitatively analyze their parametric effects on the vibration characteristics of fractional-order systems, making it difficult to determine critical parameter values [37–39]. However, identifying critical parameter conditions is essential for the analysis and design of fractional-order systems. Fractals are self-similar structures with repeating patterns across scales, and the fractal oscillators always show that the oscillator components exhibit fractal geometry and multi-band resonance or hierarchical frequency responses due to self-similar structures, such as the fractal micro-electromechanical systems (MEMS). He et al. [40] mainly study the vibration system in a fractal space. Unlike fractals, fractional calculus introduces memory effects and power-law dynamics, often modeling complex materials or non-local interactions. Furthermore, fractional oscillators always indicate the dynamical systems governed by fractional-order differential equations that contain the fractional-order derivative element $\frac{d^{\alpha }x\left(t\right)}{d{t}^{\alpha }},$ where $\alpha$ is a non-integer, and display power-law relaxation, non-exponential decay, and frequency responses that diverge from classical harmonic oscillators.

In this study, we have mainly investigated the nonlinear vibration of fractional-order stochastic systems by examining the effects of fractional derivatives and noise excitations. A generalized multistable Rayleigh–Duffing system with a fractional element excited by additive recycling noise is used as the dynamic model. Using singularity theory and stochastic averaging, critical parametric conditions for SPB are derived, followed by an analysis of sPDF across different regions in the parametric plane.

2 Derivation for the isovalent system

There are many definitions of fractional derivatives. The following definitions are introduced:

The Caputo derivative of the function $x\left(t\right)$ defined on the interval $\left[a,b\right]$ is formulated as

${}_a{}^{C}D^p\left[x\left(t\right)\right]=\frac{1}{\mathrm{\Gamma }\left(m-p\right)}{\int }_a^t\frac{x^{\left(m\right)}\left(u\right)}{{\left(t-u\right)}^{1+p-m}}du,(1)$

where $p$ represents the order of the fractional derivative ${}_a{}^{C}D^p\left[x\left(t\right)\right]$, $m-1<p\le m,m\in N$, $t\in \left[a,b\right]$, $\mathrm{\Gamma }\left(m\right)$ is the Euler Gamma function, and $x^{\left(m\right)}\left(t\right)$ is the m order derivative of $x\left(t\right)$.

The Riemann–Liouville derivative of the function $x\left(t\right)$ defined on the interval $\left[a,b\right]$ is formulated as

${}_{a}D^p\left[x\left(t\right)\right]=\frac{1}{\mathrm{\Gamma }\left(m-p\right)}\frac{d^m}{d{t}^m}{\int }_a^t\frac{x\left(u\right)}{{\left(t-u\right)}^{1+p-m}}du,(2)$

where $p$ represents the order of the fractional derivative ${}_{a}D^p\left[x\left(t\right)\right]$, and $m-1<p\le m,m\in N$, $t\in \left[a,b\right]$, $\mathrm{\Gamma }\left(m\right)$ is the Euler Gamma function.

The two-scale fractal derivatives with respect to $t$ and $x$ are defined respectively as [41]

$\begin{array}{l}{u}_{t^{\alpha }}=\frac{\mathrm{\partial }u}{\mathrm{\partial }{t}^{\alpha }}\left(t_0,x\right)\\ =\mathrm{\Gamma }\left(1+\alpha \right)\underset{\begin{array}{l}t-t_0\to \Delta t\\ \Delta t\ne 0\end{array}}{\lim }\frac{u\left(t,x\right)-u\left(t_0,x\right)}{{\left(t-t_0\right)}^{\alpha }},\\ =\mathrm{\Gamma }\left(1+\alpha \right)\underset{\begin{array}{l}t-t_0\to \Delta t\\ \Delta t\ne 0\end{array}}{\lim }\frac{u\left(t,x\right)-u\left(t_0,x\right)}{\Delta t^{\alpha }}\end{array}(3)$

$\begin{array}{l}{u}_{x^{\beta }}=\frac{\mathrm{\partial }u}{\mathrm{\partial }{x}^{\beta }}\left(t,x_0\right)\\ =\mathrm{\Gamma }\left(1+\beta \right)\underset{\begin{array}{l}x-x_0\to \Delta x\\ \Delta x\ne 0\end{array}}{\lim }\frac{u\left(t,x\right)-u\left(t,x_0\right)}{{\left(x-x_0\right)}^{\beta }},\\ =\mathrm{\Gamma }\left(1+\beta \right)\underset{\begin{array}{l}x-x_0\to \Delta x\\ \Delta x\ne 0\end{array}}{\lim }\frac{u\left(t,x\right)-u\left(t,x_0\right)}{\Delta x^{\beta }}\end{array}(4)$

where $p$ represents the fractal in time and the order of the fractal derivative.

He’s fractal derivative of the function $x\left(t\right)$ is formulated as [42–44]

$\frac{dx\left(t\right)}{d{t}^p}=\underset{t^{、}-t}{\lim }\frac{x\left(t\right)-x\left(t^{、}\right)}{t^p-{t^{、}}^p},(5)$

where $p$ represents the fractal in time and the order of the fractal derivative.

Comparing with the fractional derivatives mentioned in Equations 1–5, the initial conditions of the Caputo fractional derivative have a clear physical interpretation and align with those of integer-order differential equations. Therefore, it is employed in this study and expressed as

$\left\{\begin{array}{l}{}_a{}^{C}D^p\left[x\left(t\right)\right]=\frac{1}{\mathrm{\Gamma }\left(m-p\right)}{\int }_a^t\frac{x^{\left(m\right)}\left(u\right)}{{\left(t-u\right)}^{1+p-m}}du,m<p<m+1,\\ {}_a{}^{C}D^p\left[x\left(t\right)\right]=x^{\left(m\right)}\left(t\right),p=m\end{array}\right.(6)$

where $p$ represents the order of the fractional derivative ${}_a{}^{C}D^p\left[x\left(t\right)\right]$, $m-1<p\le m,m\in N$, $x^{\left(m\right)}\left(t\right)$ is the $m\text{th}$ integer-order derivative for $x\left(t\right)$, and $\mathrm{\Gamma }\left(m\right)$ is the Gamma function.

Slightly differing from the fractional derivative’s definition in Equation 6 and for a deterministic physical system, the initial motion time of the oscillators is $t=0$, and the Caputo fractional derivative is commonly adopted as

${}_0{}^{C}D^p\left[x\left(t\right)\right]=\frac{1}{\mathrm{\Gamma }\left(m-p\right)}{\int }_0^t\frac{x^{\left(m\right)}\left(u\right)}{{\left(t-u\right)}^{1+p-m}}du,(7)$

where $m-1<p\le m,m\in N$.

This study explores the generalized Rayleigh-Duffing oscillator system with the fractional-order damping element described in Equation 7 and driven by recycling noise as

$\ddot{x}-\left(-\epsilon +{\alpha }_1{\dot{x}}^2-{\alpha }_2{\dot{x}}^4\right)\dot{x}+w^{2}x+{\alpha }_0{x}^3+\beta {}_0{}^{C}D^{p}x=\eta \left(t\right),(8)$

where $\epsilon$ denotes the coefficient of linear damping, while ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, and ${\alpha }_4$ denote the coefficients for nonlinear damping in the system. The term ${}_0{}^{C}D^p\left[x\left(t\right)\right]$ refers to the Caputo derivative with order $p$ ($0\le p\le 1$). The recycling noise is represented by $\eta \left(t\right)$, which can be indicated as $\eta \left(t\right)=\xi \left(t\right)+k\xi \left(t-\tau \right)$, where $\xi \left(t\right)$ denotes the Gaussian white noise with intensity $D$. $\tau$ is the time delay, and $\left|k\right|\le 1$ is the fraction of the secondary noise. The autocorrelation function of $\eta \left(t\right)$ is indicated as

$〈\zeta \left(t\right)\zeta \left(0\right)〉=2D\left[\left(1+k^2\right)\delta \left(t\right)+k\delta \left(t-\tau \right)+k\delta \left(t+\tau \right)\right](9)$

and the power spectral density for $\eta \left(t\right)$ can be obtained as

$S\left(w\right)=2D\left[1+k^2+2k\cos \left(w\tau \right)\right].(10)$

The recycling noise is strongly correlated at time $t$ and $t\pm \tau$.

The fractional derivative incorporates both damping and stiffness forces [45–47]. He and Liu [48] further emphasized that the fractal–fractional derivative combines damping and inertial forces. Based on this, the isovalent system in this study can be denoted as

$\ddot{x}\left(t\right)-\left(-\epsilon +{\alpha }_1{\dot{x}}^2-{\alpha }_2{\dot{x}}^4+C\left(p,w\right)\right)\dot{x}+\left(K\left(p,w\right)+w^2\right)x+{\alpha }_0{x}^3=\eta \left(t\right),(11)$

where $C\left(p,w\right)$ and $K\left(p,w\right)$ represent the undetermined coefficients of the isovalent restoring and damping forces of ${}_0{}^{C}D^p\left[x\left(t\right)\right]$, respectively.

The discrepancy between the systems (Equation 8) and (Equation 11) is

$e=C\left(p,w\right)\dot{x}+\beta {}_0{}^{C}D^{p}x-K\left(p,w\right)x.(12)$

By following the isovalent principle [49] and minimizing the mean-square error given in Equation 12, the undetermined coefficients $C\left(p,w\right)$ and $K\left(p,w\right)$ can be indicatedd as follows:

$\left\{\begin{array}{l}\mathrm{\partial }E\left[e^2\right]/\mathrm{\partial }\left(C\left(p,w\right)\right)=0\\ \mathrm{\partial }E\left[e^2\right]/\mathrm{\partial }\left(K\left(p,w\right)\right)=0.\end{array}\right.(13)$

The substitution of Equation 12 into Equation 13 yields

$\left\{\begin{array}{l}E\left[-c\left(a\right){\dot{x}}^2+w^2\left(a\right)x\dot{x}-\dot{x}{}_0{}^{C}D^{p}x\right]=\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_0^T\left(-c\left(a\right){\dot{x}}^2+w^2\left(a\right)x\dot{x}-\dot{x}{}_0{}^{C}D^{p}x\right)\\ dt=0\\ E\left[-c\left(a\right)\dot{x}x+w^2\left(a\right)x^2-x{}_0{}^{C}D^{p}x\right]=\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_0^T\left(-c\left(a\right)\dot{x}x+w^2\left(a\right)x^2-x{}_0{}^{C}D^{p}x\right)\\ dt=0\end{array}\right..(14)$

Assuming that the original system (Equation 8) exhibits a stationary solution in the periodic form, as described below

$x\left(t\right)=a\left(t\right)\cos \phi \left(t\right),(15)$

where $\phi \left(t\right)=wt+\theta$, then

$\left\{\begin{array}{l}\dot{x}\left(t\right)=-wa\left(t\right)\sin \phi \left(t\right)\\ \ddot{x}\left(t\right)=-w^{2}a\left(t\right)\cos \phi \left(t\right).\end{array}\right.(16)$

The substitution of Equations 15, 16 into Equation 14 yields

$\begin{array}{l}\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_0^T\left(-c\left(a\right){\dot{x}}^2+w^2\left(a\right)x\dot{x}-\dot{x}{}_0{}^{C}D^{p}x\right)dt\\ =\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_0^T\left(-c\left(a\right)a^2{w}^2{\sin }^2\phi -a^{2}w{w}^2\left(a\right)\sin \phi \cos \phi +aw\sin \phi {}_0{}^{C}D^{p}x\right)dt\\ =-\frac{-c\left(a\right)a^2{w}^2}{2}+\frac{1}{\mathrm{\Gamma }\left(1-p\right)}\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_o^T\left[\left(aw\sin \phi \right){\int }_0^t\frac{\dot{x}\left(t-\tau \right)}{{\tau }^{\alpha }}d\tau \right]dt\\ =-\frac{-c\left(a\right)a^2{w}^2}{2}-\frac{1}{\mathrm{\Gamma }\left(1-p\right)}\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_o^T\\ \left(a^2{w}^2\sin \phi {\int }_0^t\frac{\sin \phi \cos \left(w\tau \right)-\cos \phi \sin \left(w\tau \right)}{{\tau }^{\alpha }}\right)dt=0\end{array}.(17)$

$\begin{array}{l}\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_0^T\left(-c\left(a\right)\dot{x}x+w^2\left(a\right)xx-x{}_0{}^{C}D^{p}x\right)dt\\ =\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_0^T\left(c\left(a\right)a^{2}w\sin \phi \cos \phi +a^2{w}^2\left(a\right){\cos }^2\phi -a\cos \phi {}_0{}^{C}D^{p}x\right)dt\\ =\frac{a^2{w}^2\left(a\right)}{2}-\frac{1}{\mathrm{\Gamma }\left(1-p\right)}\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_o^T\left[\left(a\cos \phi \right){\int }_0^t\frac{\dot{x}\left(t-\tau \right)}{{\tau }^{\alpha }}d\tau \right]dt\\ =\frac{a^2{w}^2\left(a\right)}{2}+\frac{1}{\mathrm{\Gamma }\left(1-p\right)}\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_o^T\\ \left(a^{2}w\cos \phi {\int }_0^t\frac{\sin \phi \cos \left(w\tau \right)-\cos \phi \sin \left(w\tau \right)}{{\tau }^{\alpha }}\right)dt=0\end{array}.(18)$

To further simplify Equations 17, 18 , asymptotic integrals are introduced as follows:

$\left\{\begin{array}{l}{\int }_0^t\frac{\cos \left(w\tau \right)}{{\tau }^p}d\tau =w^{p-1}\left(\mathrm{\Gamma }\left(1-p\right)\sin \left(\frac{p\pi }{2}\right)+\frac{\sin \left(wt\right)}{{\left(wt\right)}^p}+o\left({\left(wt\right)}^{-p-1}\right)\right)\\ {\int }_0^t\frac{\sin \left(w\tau \right)}{{\tau }^p}d\tau =w^{p-1}\left(\mathrm{\Gamma }\left(1-p\right)\cos \left(\frac{p\pi }{2}\right)-\frac{\cos \left(wt\right)}{{\left(wt\right)}^p}+o\left({\left(wt\right)}^{-p-1}\right)\right)\end{array}\right..(19)$

By inserting Equations 15, 16, and 19 into Equations 17, 18 and executing the integral averaging of $\phi$, the final expressions of $C\left(p,w\right)$ and $K\left(p,w\right)$ can be obtained as

$\left\{\begin{array}{l}C\left(p,\tau \right)=-\beta w^{p-1}\sin \left(\frac{p\pi }{2}\right)\\ K\left(p,\tau \right)=\beta w^p\cos \left(\frac{p\pi }{2}\right)\end{array}\right..(20)$

Combining the detailed expression of Equation 20 and thus, the equivalent oscillator corresponding to the system (Equation 11) could be rewritten as

$\ddot{x}\left(t\right)-\gamma \dot{x}+w_0^{2}x+{\alpha }_0{x}^3=\xi \left(t\right),(21)$

where

$\left\{\begin{array}{l}\gamma =-\epsilon +{\alpha }_1{\dot{x}}^2-{\alpha }_2{\dot{x}}^4-\beta w^{p-1}\sin \left(\frac{p\pi }{2}\right).\\ w_0^2=w^2+\beta w^p\cos \left(\frac{p\pi }{2}\right)\end{array}\right.(22)$

3 Stationary PDF for the system amplitude

To derive the sPDF of the system amplitude, we assume that the system (Equation 21) possesses the solution with periodic form, and following the methodology outlined in [50], we implement the transformation as follows:

$\left\{\begin{array}{l}X=x\left(t\right)=a\left(t\right)\cos \mathrm{\Phi }\left(t\right)\\ Y=\dot{x}=-a\left(t\right)w_0\sin \mathrm{\Phi }\left(t\right),\\ \mathrm{\Phi }\left(t\right)=w_{0}t+\theta \left(t\right)\end{array}\right.(23)$

where $w_0$ denotes the intrinsic frequency of the isovalent system (Equation 21) and is described as in Equation 22, $a\left(t\right)$ and $\theta \left(t\right)$ denote the magnitude and temporal alignment characteristics of the system response, respectively, and in that order, both are random processes.

By inserting Equation 23 into Equation 21 and utilizing the deterministic averaging approach, we can obtain

$\left\{\begin{array}{l}\frac{\mathrm{d}a}{\mathrm{d}t}=F_{11}\left(a,\theta \right)+{\mathrm{G}}_{11}\left(a,\theta \right)\eta \left(t\right)\\ \frac{\mathrm{d}\theta }{\mathrm{d}t}=F_{21}\left(a,\theta \right)+G_{21}\left(a,\theta \right)\eta \left(t\right)\end{array}\right.(24)$

in which

$\left\{\begin{array}{l}{F}_{11}\left(a,\theta \right)=\frac{\sin \mathrm{\Phi }}{w_0}[a{w}_0\sin \mathrm{\Phi }(-\epsilon +{\alpha }_1{a}^2{w}_0^2{\sin }^2\mathrm{\Phi }-{\alpha }_2{a}^4{w}_0^4{\sin }^2\mathrm{\Phi }\\ \left.-\beta w^{p-1}\sin \left(\frac{p\pi }{2}\right))+{\alpha }_0{a}^3{\cos }^3\mathrm{\Phi }\right]\\ F_{21}\left(a,\theta \right)=\frac{\cos \mathrm{\Phi }}{a{w}_0}[a{w}_0\sin \mathrm{\Phi }(-\epsilon +{\alpha }_1{a}^2{w}_0^2{\sin }^2\mathrm{\Phi }-{\alpha }_2{a}^4{w}_0^4{\sin }^2\mathrm{\Phi }\\ \left.-\beta w^{p-1}\sin \left(\frac{p\pi }{2}\right))+{\alpha }_0{a}^3{\cos }^3\mathrm{\Phi }\right]\\ G_{11}=-\frac{\sin \mathrm{\Phi }}{w_0}\\ G_{21}=-\frac{\cos \mathrm{\Phi }}{a{w}_0}\end{array}\right..(25)$

The stochastic differential equation in Equation 24 is interpreted within the Stratonovich framework [51]. By incorporating the requisite Wong–Zakai correction [52], the resulting Itô representation can be formulated as follows:

$\left\{\begin{array}{l}\mathrm{d}a=\left[F_{11}\left(a,\theta \right)+F_{12}\left(a,\theta \right)\right]\mathrm{d}t+{\sigma }_{11}\left(a,\theta \right)\mathrm{d}B\left(t\right)\\ \mathrm{d}\theta =\left[F_{21}\left(a,\theta \right)+F_{22}\left(a,\theta \right)\right]\mathrm{d}t+{\sigma }_{21}\left(a,\theta \right)\mathrm{d}B\left(t\right)\end{array}\right.,(26)$

where $B\left(t\right)$ denotes the unit Wiener process and we can obtain

$\left\{\begin{array}{l}{F}_{12}\left(a,\theta \right)=S\left(w\right)\frac{\mathrm{\partial }{G}_{11}}{\mathrm{\partial }a}{G}_{11}+S\left(w\right)\frac{\mathrm{\partial }{G}_{11}}{\mathrm{\partial }\theta }{G}_{21}=\frac{{\cos }^2\left(\mathrm{\Phi }\right)}{2a{w}_0^2}S\left(w\right)\\ F_{22}\left(a,\theta \right)=S\left(w\right)\frac{\mathrm{\partial }{G}_{21}}{\mathrm{\partial }a}{G}_{11}+S\left(w\right)\frac{\mathrm{\partial }{G}_{21}}{\mathrm{\partial }\theta }{G}_{21}=-\frac{\sin \left(2\mathrm{\Phi }\right)}{2a^2{w}_0^2}S\left(w\right)\\ {{\sigma }_{11}}^2\left(a,\theta \right)={\int }_{-\infty }^{\infty }{G}_{11}\left(a,\theta \right)G_{11}\left(a,\theta ,t+h\right)R\left(h\right)dh\\ =\frac{2{\sin }^2\left(\mathrm{\Phi }\right)}{w_0^2}S\left(w\right)\\ {{\sigma }_{22}}^2\left(a,\theta \right)={\int }_{-\infty }^{\infty }{G}_{21}\left(a,\theta \right)G_{21}\left(a,\theta ,t+h\right)R\left(h\right)dh\\ =\frac{2{\cos }^2\left(\mathrm{\Phi }\right)}{a^2{w}_0^2}S\left(w\right)\end{array}\right..(27)$

Combining the expression of Equations 9, 10 and employing the stochastic averaging approach [53], and further applying the period averaging to Equation 26 over $\mathrm{\Phi }$, we can derive the relevant Itô stochastic differential formula as follows:

$\left\{\begin{array}{l}\mathrm{d}a=m_1\left(a\right)\mathrm{d}t+{\sigma }_1\left(a\right)\mathrm{d}B\left(t\right)\\ \mathrm{d}\theta =m_2\left(a\right)\mathrm{d}t+{\sigma }_2\left(a\right)\mathrm{d}B\left(t\right)\end{array}\right..(28)$

The accurate expression for the averaged diffusion and drift coefficients can be determined as:

$\left\{\begin{array}{l}{m}_1\left(a\right)=-\frac{1}{2}\left(\beta w^{p-1}\sin \left(\frac{p\pi }{2}\right)+\epsilon \right)a+\frac{3}{8}{\alpha }_1{w}_0^2{a}^3\\ -\frac{5}{16}{\alpha }_2{a}^5+\frac{{\sigma }^2}{2a{w}_0^2}\\ {{\sigma }_1}^2\left(a\right)=\frac{1}{2\pi }{\int }_0^{2\pi }\frac{2{\sin }^2\left(\mathrm{\Phi }\right)}{w_0^2}S\left(w\right)\mathrm{d}\mathrm{\Phi }=\frac{2{\sigma }^2}{w_0^2}\\ m_2\left(a\right)=\frac{3{\alpha }_0{a}^2}{8w_0}\\ {{\sigma }_2}^2\left(a\right)=\frac{1}{2\pi }{\int }_0^{2\pi }\frac{2{\cos }^2\left(\mathrm{\Phi }\right)}{a^2{w}_0^2}S\left(w\right)\mathrm{d}\mathrm{\Phi }=\frac{2{\sigma }^2}{a^2{w}_0^2}\end{array}\right.,(29)$

where $w_0^2=w^2+\beta w^p\cos \left(\frac{p\pi }{2}\right),{\sigma }^2=D\left[1+k^2+2k\cos \left(w\tau \right)\right]$.

Equations 28, 29 show that the averaged Itô equation for the amplitude $a\left(t\right)$ does not depend on $\theta \left(t\right)$; therefore, the random process $a\left(t\right)$ represents a one-dimensional diffusion process. Thus, the corresponding Fokker–Planck–Kolmogorov (FPK) formula for $a\left(t\right)$ can be written as:

$\frac{\mathrm{\partial }\mathrm{\rho }\left(a,t\right)}{\mathrm{\partial }t}=-\frac{\mathrm{\partial }}{\mathrm{\partial }a}\left[m_1\left(a\right)\mathrm{\rho }\left(a\right)\right]+\frac{1}{2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{a}^2}\left[\left({{\sigma }_1}^2\left(a\right)\right)\mathrm{\rho }\left(a\right)\right].(30)$

The conditions for boundary fulfillment of ρ(a) in Equation 30 are

$\left\{\begin{array}{l}\mathrm{\rho }\left(a\right)=c,c\in \left(-\infty ,+\infty \right)asa=0\\ \mathrm{\rho }\left(a\right)\to 0,\frac{\mathrm{\partial }\overline{p}}{\mathrm{\partial }a}\to 0asa\to \infty \end{array}\right..(31)$

According to the boundary conditions (Equation 31), the system amplitude’s sPDF is expressed as:

$\mathrm{\rho }\left(a\right)=\frac{C}{{{\sigma }_1}^2\left(a\right)}\exp \left[{\int }_0^a\frac{2m_1\left(u\right)}{{{\sigma }_1}^2\left(u\right)}\mathrm{d}u\right],(32)$

where C is the constant after normalization.

By inserting Equation 29 into Equation 32, the detailed equation for the system amplitude’s sPDF is expressed as:

$\mathrm{\rho }\left(a\right)=\frac{Ca{w}_0^2}{{\sigma }^2}\exp \left[-\frac{a^2{w}_0^2\Delta }{7680{\sigma }^2}\right]$

in which

$\Delta =3840\left(\epsilon +\beta w^{p-1}\sin \left(\frac{p\pi }{2}\right)\right)-1440{\alpha }_1{w}_0^2{a}^2+800{\alpha }_2{w}_0^4{a}^4(33)$

4 SPB for the system amplitude

The SPB phenomenon refers to the variation in the number of peaks observed in the sPDF curves. In this section, we utilize the singularity theory to discuss the parametric impacts on the SPB behaviors of the system and to determine the crucial parametric conditions.

For simplicity, $\mathrm{\rho }\left(a\right)$ is presented by

$\mathrm{\rho }\left(a\right)=CR\left(a,k,\tau ,\epsilon ,w,p,{\alpha }_1,{\alpha }_2\right)·\exp \left[Q\left(a,k,\tau ,\epsilon ,w,p,{\alpha }_1,{\alpha }_2\right)\right],(34)$

where

$\left\{\begin{array}{l}R\left(a,\sigma ,\epsilon ,w,p,{\alpha }_1,{\alpha }_2\right)=\frac{a{w}_0^2}{{\sigma }^2}\\ Q\left(a,\sigma ,\epsilon ,w,p,{\alpha }_1,{\alpha }_2\right)=-\frac{a^2{w}_0^2}{7680{\sigma }^2}(3840\left(\epsilon +\beta w^{p-1}\sin \left(\frac{p\pi }{2}\right)\right)\\ -1440{\alpha }_1{w}_0^2{a}^2+800{\alpha }_2{w}_0^4{a}^4)\\ w_0^2=w^2+\beta w^p\cos \left(\frac{p\pi }{2}\right)\\ {\sigma }^2=D\left[1+k^2+2k\cos \left(w\tau \right)\right]\end{array}\right..(35)$

Based on the singularity theory [54], the system amplitude’s sPDF must fulfill the requirements

$\left\{\begin{array}{l}\frac{\mathrm{\partial }\mathrm{\rho }\left(a\right)}{\mathrm{\partial }a}=0\\ \frac{{\mathrm{\partial }}^2\mathrm{\rho }\left(a\right)}{\mathrm{\partial }{a}^2}=0\end{array}\right..(36)$

Inserting Equations 33, 34 into Equation 36, we can derive the conditions as follows [15, 21]:

$H=\left\{R^{\prime }+R{Q}^{\prime }=0,R^{″}+2R^{\prime }{Q}^{\prime }+R{Q}^{″}+R{Q^{\prime }}^2=0\right\},(37)$

where $H$ denotes the crucial condition for the variations of the number of peaks in the sPDF curve.

Equations 34, 35, and 37 show that the fractional derivative’s order $p$, the correlation time $\tau$ in the noise, and the noise intensity $D$ can all induce the SPB behaviors of the system. The impacts of the three-dimensional parametric surface are difficult to display and describe; therefore, we only show the two-dimensional cross-section for the transition set to reveal the influences of the noise delay $\tau$ and noise intensity $D$ below.

4.1 Taking ($p,D$) as unfolding parameters

Taking the parameters as $\epsilon =-0.2$, ${\alpha }_1=2.45$, ${\alpha }_2=4.6$, $w=1$, $\beta =1$, $k=1$, $\tau =0.1$, based on Equation 37, the boundary set for SPB of the system (Equation 21) with parameters $p$ and $D$ are obtained (Figure 1).

Figure 1

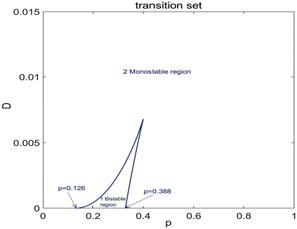
Figure 1. Transition set curves under additive recycling noise (taking $p$ and $D$ as the unfolding parameters).

As shown in Figure 1, the transition set curve’s intercepts at $D=0$ represent the bifurcation values $p_1=0.126$ and $p_2=0.388$, respectively. Under the influence of additive recycling noise, the boundary set curve of the system (Equation 21) takes on a triangular shape. Moreover, the unfolding parametric plane is assigned to two sub-regions by the boundary set curve. Based on the theory of singularity analysis , the topological structure of the sPDF curve at various points ($p,D$) within the same region is qualitatively similar.

Initially, we investigated the sPDF $\mathrm{\rho }\left(a\right)$ of the system amplitude with the joint PDF $p\left(x,\dot{x}\right)$ for a point ($p,D$) in the two sub-regions shown in Figure 1 separately. Subsequently, we contrasted the theoretical solution with the numerical result obtained through Monte Carlo simulation (MCS) of the initial system (3) utilizing the numerical simulation method of fractional derivative [45]. Figures 2, 3 show the respective outcomes.

Figure 2

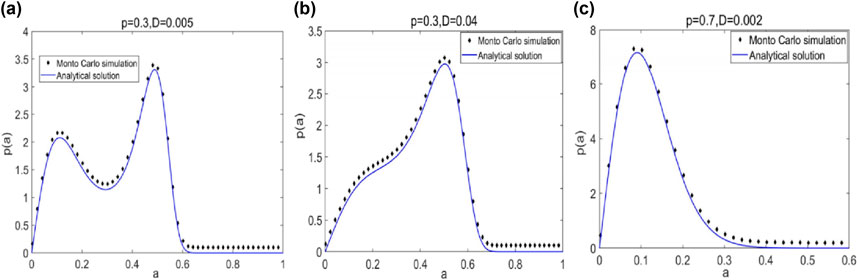
Figure 2. PDF $\mathrm{\rho }\left(a\right)$ of amplitude in different sub-regions of Figure 1 (taking $p$ and $D$ as unfolding parameters). (a) Parameters ($p,D$) in Region 1 of Figure 1, (b) Parameters ($p,D$) in Region 2 of Figure 1, and (c) Parameters ($p,D$) in Region 3 of Figure 1.

Figure 3

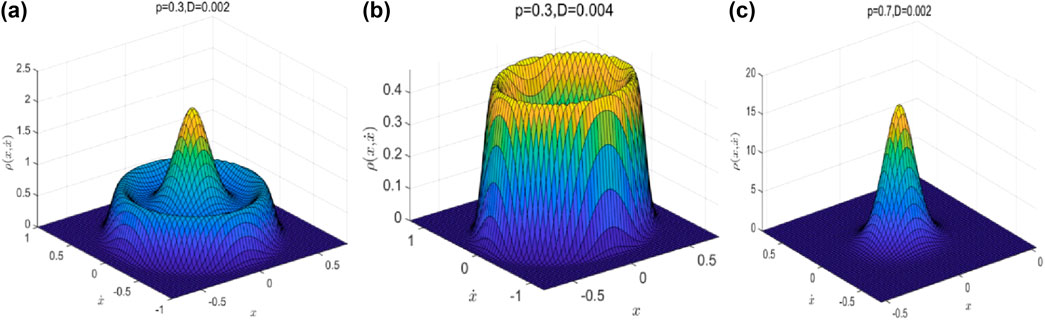
Figure 3. Joint PDF $\mathrm{\rho }\left(x,\dot{x}\right)$ in different sub-regions of Figure 1 (taking $p$ and $D$ as the unfolding parameters). (a) Parameters ($p,D$) in Region 1 of Figure 1, (b) Parameters ($p,D$) in Region 2 of Figure 1, and (c) Parameters ($p,D$) in Region 3 of Figure 1.

As shown in Figure 2, the parametric region ($p,D$), where the sPDF curves are multi-modal, is enclosed by the nearly triangular region in Figure 1, and Region 1 can form a bi-modal region of the sPDF curve for the system amplitude.

Considering ($p,D$) as $p=0.3$ and $D=0.005$ in Region 1, the sPDF $\mathrm{\rho }\left(a\right)$ of the system has two peaks, and a stable limit cycle emerges with a corresponding amplitude $a$ distant from the original position. Notably, the probability around the origin is nonzero, indicating the concurrent coexistence of the equilibrium point and the limit cycle within the system (Figures 2A, 3A). Conversely, when the folding parameters (p,D) set asg $p=0.3,D=0.004$ in Region 2, the peak of the sPDF $\mathrm{\rho }\left(a\right)$ is distant from the origin, and a stable limit cycle persists within the system (Figures 2B, 3B); thus, the system is in a monostable state at this moment. When the folding parameters ($p,D$) are considered $p=0.7$ and $D=0.002$ in Region 3, the peak of the sPDF $\mathrm{\rho }\left(a\right)$ is near the origin, and the system has an equilibrium point (Figures 2C, 3C); thus, the system is also in a monostable state at this moment.

4.2 Taking ($\tau ,D$) as unfolding parameters

Taking the folding parameters as $\epsilon =-0.2$, ${\alpha }_1=2.45$, ${\alpha }_2=4.6$, $w=1$, $\beta =1$, $k=1$, $p=0.35$, based on Equation 37, the critical parametric curve (transition set) of SPB for system (21) about unfolding parameters $\tau$ and $D$ can also be obtained (Figure 4).

Figure 4

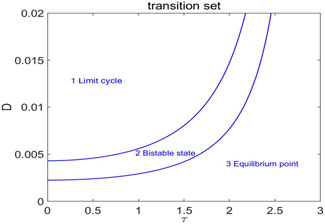
Figure 4. Transition set curves under additive recycling noise (taking $\tau$ and $D$ as the unfolding parameters).

As shown in Figure 4, the unfolding parametric plane is segmented into three geometrically separated zones by the transition set curve. Based on the singularity analysis theory discussed above, the sPDF curves $\mathrm{\rho }\left(a\right)$ for different parameters ($\tau ,D$) in the same region exhibit qualitatively similar topological structures.

Here, we discuss the steady-state PDF $\mathrm{\rho }\left(a\right)$ of the amplitude with the joint PDF $\mathrm{\rho }\left(x,\dot{x}\right)$ for a given point ($\tau ,D$) in each sub-region (Figure 4). Subsequently, we contrast the theoretical outcomes with the numerical result obtained by the MCS of the initial system (3) utilizing the numerical simulation technique of fractional derivative [45]. Figures 5, 6, respectively, show the corresponding outcomes.

Figure 5

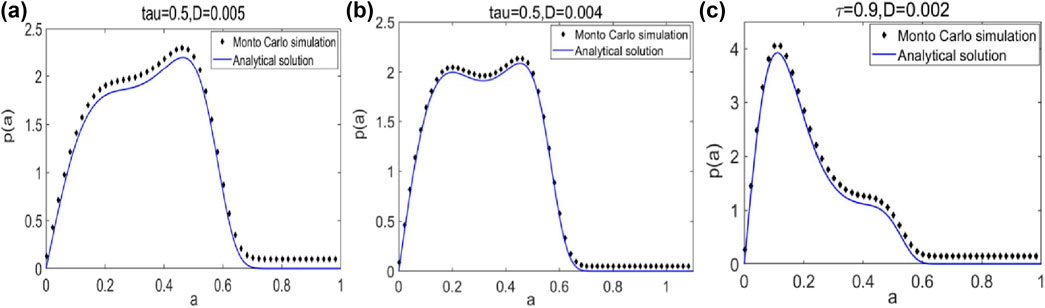
Figure 5. PDF $\mathrm{\rho }\left(a\right)$ of system amplitude in different sub-regions of Figure 4 (taking $\tau$ and $D$ as the unfolding parameters). (a) Parameters ($\tau ,D$) in Region 1 of Figure 4, (b) Parameters ($\tau ,D$) in Region 2 of Figure 4, and (c) Parameters ($\tau ,D$) in Region 3 of Figure 4.

Figure 6

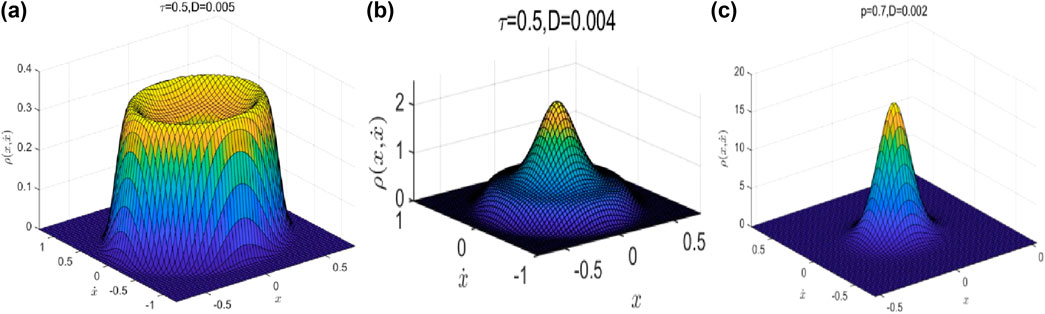
Figure 6. Joint PDF $\mathrm{\rho }\left(x,\dot{x}\right)$ in the different sub-regions of Figure 4 (taking $\tau$ and $D$ as the unfolding parameters). (a) Parameters ($\tau ,D$) in Region 1 of Figure 4, (b) Parameters ($\tau ,D$) in Region 2 of Figure 4, and (c) Parameters ($\tau ,D$) in Region 3 of Figure 4.

In Figure 4, when the folding parameters ($\tau ,D$) are adopted in Region 1, the sPDF curve $\mathrm{\rho }\left(a\right)$ of the system amplitude exhibits a prominent peak located at a significant distance from the origin, and $\mathrm{\rho }\left(x,\dot{x}\right)$ has a circular basin, as shown in Figures 5A, 6A. Thus, the system only has a limit cycle (large amplitude motion) at this time. In Region 2, the sPDF curve $\mathrm{\rho }\left(a\right)$ also has a remarkable peak near the original point, and the probability far away from the origin point is nonzero. $\mathrm{\rho }\left(x,\dot{x}\right)$ also has a circular basin and a peak (Figures 5B, 6B). A limit cycle and an equilibrium point exist in the given system (3) simultaneously. Further in Region 3, the PDFs $\mathrm{\rho }\left(a\right)$ and $\mathrm{\rho }\left(x,\dot{x}\right)$ both have an apparent peak close to the origin (Figures 5C, 6C); therefore, the system has only one equilibrium point at this time.

The results obtained above indicate that the sPDF curve of the system amplitude can arise in various types depending on the values of the order $p$ for the fractional derivative, the correlation time $\tau$ in the noise, and the noise intensity $D$. The findings imply that the sPDF $\mathrm{\rho }\left(a\right)$ could be modulated by the system parameters $p$, $D$, and $\tau$, respectively. Additionally, comparing the numerical data derived from MCS and the analytical solutions derived from the stochastic averaging technique demonstrates good alignment, validating the conceptual analysis process.

5 Conclusion

This study investigated the SPB behavior of a fractional bistable Rayleigh–Duffing system subjected to additive recycling noise. Using the isovalent principle, the original fractional-order system was transformed into an equivalent integer-order system of comparable significance. The sPDF of the system amplitude was derived by applying the stochastic averaging method. Furthermore, employing the singularity theory, critical parametric conditions for SPB were established. The results indicate that the fractional derivative order $p$, correlation time $\tau$, and recycling noise intensity $D$ can each induce SPB, leading to a transition from a single- to a dual-peak sPDF curve, depending on the unfolding parameters. By selecting appropriate unfolding parameters according to the critical parametric conditions acquired, the system response can be confined to minor vibrations near equilibrium, thereby mitigating instability and potential damage caused by nonlinear jumps or large amplitude oscillations. These findings provide valuable theoretical insights for system design in engineering fields such as mechanical engineering and electrical engineering. The agreement between numerical results obtained via MCS and analytical solutions further validates our theoretical analysis.

However, the system studied in the article is the single-degree-of-freedom system, and the complexity and the abstraction of the state space increase the difficulty of analyzing the high-dimensional dynamic system. The investigation of two-degrees-of-freedom systems or even higher dimensional and coupled systems driven by other noises, such as Lévy noise or Poisson noise, should be the next focus of research .

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Y-JL: formal analysis and writing – original draft. Z-QW: formal analysis, methodology, and writing – original draft. Y-TS: writing – review and editing. X-YZ: data curation and writing – review and editing. S-LC: data curation and writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work in this paper was funded by the National Natural Science Foundation of China (Grant Nos. 12002120, 12072222, 11672349, and 11902287), the Natural Science Foundation of Henan Province (Grant No. 252300420315), the Youth Backbone Teacher Training Project, and the Academic and Technical Leader of Henan University of Urban Construction (Grant Nos. YCJQNGGJS202-111 and YCJXSJSDTR202308).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Xu MY, Tan WC. Theoretical analysis of the velocity field, stress field and vortex sheet of generalized second order fluid with fractional anomalous diffusion. Sci China Ser A-mat (2001) 44:1387–99. doi:10.1007/BF02877067

CrossRef Full Text | Google Scholar

2. Sabatier J, Agrawal OP, Machado JAT. Advances in fractional calculus. Dordrecht: Springer (2007).

Google Scholar

3. Podlubny I. Fractional-order systems and P controllers. IEEE Trans Autom Contol (1999) 44:208–14. doi:10.1109/9.739144

CrossRef Full Text | Google Scholar

4. Monje CA, Chen YQ, Vinagre BM, Xue DY, Batlleet VF. Fractional-order systems and controls: fundamentals and applications. London: Springer-Verlag (2010).

Google Scholar

5. He JH, Qian MY. A fractal approach to the diffusion process of red ink in a saline water. Therm Sci (2022) 26:2447–51. doi:10.2298/TSCI2203447H

CrossRef Full Text | Google Scholar

6. Zuo YT. Effect of SiC particles on viscosity of 3-D print paste: a fractal rheological model and experimental verification. Therm Sci (2021) 25:2405–9. doi:10.2298/TSCI200710131Z

CrossRef Full Text | Google Scholar

7. Liang YH, Wang KJ. A new fractal viscoelastic element: promise and applications to Maxwell-rheological model. Therm Sci (2021) 25:1221–7. doi:10.2298/TSCI200301015L

CrossRef Full Text | Google Scholar

8. Chen W. An intuitive study of fractional derivative modeling and fractional quantum in soft matter. J Vib Control (2008) 14:1651–7. doi:10.1177/1077546307087398

CrossRef Full Text | Google Scholar

9. Dai DD, Ban TT, Wang YL, Zhang W. The piecewise reproducing kernel method for the time variable fractional order advection-reaction-diffusion equations. Therm Sci (2021) 25:1261–8. doi:10.2298/TSCI200302021D

CrossRef Full Text | Google Scholar

10. Rong HW, Wang XD, Xu W, Meng G, Fang T. On double-peak probability density functions of a Duffing oscillator under narrow-band random excitations. Acta Phys Sin (2005) 54:2557–61. doi:10.7498/aps.54.2557

CrossRef Full Text | Google Scholar

11. Rong HW, Wang XD, Meng G, Xu W, Fang T. On double peak probability density functions of duffing oscillator to combined deterministic and random excitations. Appl Math Mech-engl (2006) Ed(27):1569–76. doi:10.1007/s10483-006-1115-z

CrossRef Full Text | Google Scholar

12. Xu Y, Gu R, Zhang H, Xu W, Duan J. Stochastic bifurcations in a bistable Duffing-Van der Pol oscillator with colored noise. Phys Rev E (2011) 83:056215. doi:10.1103/PhysRevE.83.056215

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Gu RC, Xu Y, Hao ML, Yang ZQ. Stochastic bifurcations in Duffing-van der Pol oscillator with Lévy stable noise. Acta Phys Sin (2011) 60:1466–7. doi:10.7498/aps.60.060513

CrossRef Full Text | Google Scholar

14. Zakharova A, Vadivasova T, Anishchenko V, Koseska A, Kurths J. Stochastic bifurcations and coherencelike resonance in a self-sustained bistable noisy oscillator. Phys Rev E (2010) 81:011106. doi:10.1103/PhysRevE.81.011106

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wu ZQ, Hao Y. Stochastic P-bifurcations in tri-stable van der Pol-Duffing oscillator with multiplicative colored noise. Acta Phys Sin (2015) 64:060501. doi:10.7498/aps.64.060501

CrossRef Full Text | Google Scholar

16. Qian JM, Chen LC. Random vibration of SDOF vibro-impact oscillators with restitution factor related to velocity under wide-band noise excitations. Mech Syst Signal Pr (2021) 147:107082. doi:10.1016/j.ymssp.2020.107082

CrossRef Full Text | Google Scholar

17. He JH. An improved amplitude-frequency formulation for nonlinear oscillators. Int J Nonlin Sci Num (2008) 9:211–2. doi:10.1515/IJNSNS.2008.9.2.211

CrossRef Full Text | Google Scholar

18. Fan J. He’s frequency–amplitude formulation for the Duffing harmonic oscillator. Comput Math Appl (2009) 58:2473–6. doi:10.1016/j.camwa.2009.03.049

CrossRef Full Text | Google Scholar

19. Huang ZL, Jin XL. Response and stability of a SDOF strongly nonlinear stochastic system with light damping modeled by a fractional derivative. J Sound Vib (2009) 319:1121–35. doi:10.1016/j.jsv.2008.06.026

CrossRef Full Text | Google Scholar

20. Sun YH, Yang YG. Stochastic averaging for the piezoelectric energy harvesting system with fractional derivative element. IEEE Access (2020) 8:59883–90. doi:10.1109/ACCESS.2020.2983540

CrossRef Full Text | Google Scholar

21. Li W, Zhang MT, Zhao JF. Stochastic bifurcations of generalized Duffing-van der Pol system with fractional derivative under colored noise. Chin Phys B (2017) 26:090501–69. doi:10.1088/1674-1056/26/9/090501

CrossRef Full Text | Google Scholar

22. He CH, El-Dib YO. A heuristic review on the homotopy perturbation method for non-conservative oscillators. J Low Freq Noise V A (2022) 41:572–603. doi:10.1177/14613484211059264

CrossRef Full Text | Google Scholar

23. He CH, Amer TS, Tian D, Abolila AF, Galal AA. Controlling the kinematics of a spring-pendulum system using an energy harvesting device. J Low Freq Noise (2022) 41:1234–57. doi:10.1177/146-13484221077474

CrossRef Full Text | Google Scholar

24. He CH, Tian D, Moatimid GM, Salman HF, Zekry MH. Hybrid rayleigh-van der pol-duffing oscillator: Stability analysis and controller. J Low Freq Noise V A (2022) 41:244–68. doi:10.1177/14613484211026407

CrossRef Full Text | Google Scholar

25. He JH, Amer TS, Abolila AF, Galal AA. Stability of three degrees-of-freedom auto-parametric system. Alex Eng J (2022) 61:8393–415. doi:10.1016/j.aej.2022.01.064

CrossRef Full Text | Google Scholar

26. He JH, Amer TS, El-Kafly HF, Galal AA. Modelling of the rotational motion of 6-DOF rigid body according to the Bobylev-Steklov conditions. Results Phys (2022) 35:105391. doi:10.1016/j.rinp.2022.105391

CrossRef Full Text | Google Scholar

27. Li ZB, He JH. Fractional complex transform for fractional differential equations. Math Comput Appl (2010) 15:970–3. doi:10.3390/mca15050970

CrossRef Full Text | Google Scholar

28. Li ZB. An extended fractional complex transform. Int J Nonlin Sci Num (2010) 11:335–8. doi:10.1515/IJNSNS.2010.11.S1.335

CrossRef Full Text | Google Scholar

29. He JH. Homotopy perturbation method: a new nonlinear analytical technique. Appl Math Comput (2003) 135:73–9. doi:10.1016/S0096-3003(01)00312-5

CrossRef Full Text | Google Scholar

30. He JH. The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl Math Comput (2004) 151:287–92. doi:10.1016/S0096-3003(03)00341-2

CrossRef Full Text | Google Scholar

31. Wang SQ, He JH. Variational iteration method for a nonlinear reaction-diffusion process. Int J Chem React Eng (2008) 6:1–8. doi:10.2202/1542-6580.1630

CrossRef Full Text | Google Scholar

32. He JH. An approximation to solution of space and time fractional telegraph equations by the variational iteration method. Math Probl Eng (2012) 2012:394212. doi:10.1155/2012/394212

CrossRef Full Text | Google Scholar

33. He JH. On the fractal variational principle for the Telegraph equation. Fractals (2021) 29:2150022. doi:10.1142/S0218348X21500225

CrossRef Full Text | Google Scholar

34. He JH. Variational principle for the generalized KdV-burgers equation with fractal derivatives for shallow water waves. J Appl Comput Mech (2020) 6:735–40. doi:10.22055/JACM.2019.14813

CrossRef Full Text | Google Scholar

35. He JH, Hou WF, He CH, Saeed T, Hayat T. Variational approach to fractal solitary waves. Fractals (2021) 29:2150199. doi:10.1142/S0218348X21501991

CrossRef Full Text | Google Scholar

36. He JH, He CH, Saeed T. A fractal modification of Chen-Lee-Liu equation and its fractal variational principle. Int J Mod Phys (2021) 35:2150214. doi:10.1142/S0217979221502143

CrossRef Full Text | Google Scholar

37. Li Y, Wu Z, Lan Q, Cai Y, Xu H, Sun Y. Stochastic transition behaviors in a tri-stable van der Pol oscillator with fractional delayed element subject to Gaussian white noise. Therm Sci (2022) 26:2713–25. doi:10.2298/TSCI2203713L

CrossRef Full Text | Google Scholar

38. Li Y, Wu Z, Lan Q, Cai Y, Xu H, Sun Y. Transition behaviors of system energy in a bi-stable van Ver Pol oscillator with fractional derivative element driven by multiplicative Gaussian white noise. Therm Sci (2022) 26:2727–36. doi:10.2298/TSCI2203727L

CrossRef Full Text | Google Scholar

39. Shen Y, El-Dib Y. A periodic solution of the fractional Sine-Gordon equation arising in architectural engineering. J Low Freq Noise V A (2021) 40:683–91. doi:10.1177/1461348420917565

CrossRef Full Text | Google Scholar

40. He JH, Moatimid GM, Zekry MH. Forced nonlinear oscillator in a fractal space. Facta Uiv-ser Mech (2022) 20:001–20. doi:10.22190/FUME220118004H

CrossRef Full Text | Google Scholar

41. He JH. Fractal calculus and its geometrical explanation. Results Phys (2018) 10:272–6. doi:10.1016/j.rinp.2018.06.011

CrossRef Full Text | Google Scholar

42. He JH, El-Dib YO. A tutorial introduction to the two-scale fractal calculus and its application to the fractal zhiber-shabat oscillator. Fractals (2021) 29:2150268. doi:10.1142/S0218348X21502686

CrossRef Full Text | Google Scholar

43. Wang QLX, Shi XY, He JH, Li ZB. Fractal calculus and its application to explanation of biomechanism of polar bear hairs. Fractals (2018) 26:1850086. doi:10.1142/S0218348X1850086X

CrossRef Full Text | Google Scholar

44. He JH. A new fractal derivation. Therm Sci (2011) 15:145–7. doi:10.2298/TSCI11S1145H

CrossRef Full Text | Google Scholar

45. Chen LC, Wang WH, Li ZS, Zhu W. Stationary response of Duffing oscillator with hardening stiffness and fractional derivative. Int J Nonlin Mech (2013) 48:44–50. doi:10.1016/j.ijnonlinmec.2012.08.001

CrossRef Full Text | Google Scholar

46. Chen LC, Li ZS, Zhuang QQ, Zhu W. First-passage failure of single-degree-of-freedom nonlinear oscillators with fractional derivative. J Vib Control (2013) 19:2154–63. doi:10.1177/1077546312456057

CrossRef Full Text | Google Scholar

47. Shen YJ, Yang SP, Xing HJ, Ma H. Primary resonance of Duffing oscillator with two kinds of fractional-order derivatives. Int J Nonlin Mech (2012) 47:975–83. doi:10.10-16/j.ijnonlinmec.2012.06.012

CrossRef Full Text | Google Scholar

48. He CH, Liu C. A modified frequency-amplitude formulation for fractal vibration systems. Fractals (2022) 30:2250046. doi:10.1142/S0218348X22500463

CrossRef Full Text | Google Scholar

49. Yang YG, Xu W, Sun YH, Gu XD. Stochastic response of van der Pol oscillator with two kinds of fractional derivatives under Gaussian white noise excitation. Chin Phys B (2016) 25:020201–21. doi:10.1088/1674-1056/25/2/020201

CrossRef Full Text | Google Scholar

50. Chen LC, Zhu WQ. Stochastic response of fractional-order van der Pol oscillator. Theor Appl Mech Lett (2014) 4:013010–72. doi:10.1063/2.1401310

CrossRef Full Text | Google Scholar

51. Xu C, Roberts AJ. On the low-dimensional modelling of Stratonovich stochastic differential equations. Physica A (1996) 225:62–80. doi:10.1016/0378-4371(95)00387-8

CrossRef Full Text | Google Scholar

52. Wu ZQ, Hao Y. Three-peak P-bifurcations in stochastically excited van der Pol-Duffing oscillator. Sci Sin Phys Mech Astron (2013) 43:524–9. doi:10.1360/132012-692

CrossRef Full Text | Google Scholar

53. Zhu WQ. Random vibration. Beijing, China: Science Press (1992).

Google Scholar

54. Ling FH. Catastrophe theory and its applications. In: Shang hai jiao tong. Shanghai, China: University Press (1987).

Google Scholar