Analytical solutions for the forced KdV equation with variable coefficients

This paper focuses on obtaining the exact solutions to the variable-coefficient forced Korteweg-de Vries (KdV) equation for modeling spatial inhomogeneity in fluids. By combining the direct similarity reduction-based CK method with the (G'/G) expansion method, three new similarity solutions are obtained for this variable-coefficient forced KdV equation.

1 Introduction

The forced KdV equation with variable coefficients plays a crucial role in researching the waves motion and nonlinear phenonmeno [1], and it attracts more and more research attentions [2]. In this paper, we examine the forced KdV equation with variable coefficients:

$u_t+a\left(t\right)u{u}_x+b\left(t\right)u_{\mathit{xxx}}+c\left(t\right)u+d\left(t\right)u_x=f\left(x,t\right),(1.1)$

where $u=u(x,t)$ is the wave function and $x$ and $t$ are scaled spatial and temporal coordinates, respectively. $a(t)$ is a nonlinearity coefficient, $b(t)$ is a dispersive coefficient, $c(t)$ is a line-damping coefficient, $d(t)$ is a dissipative coefficient, and $f(x,t)$ represents the external force effect function. Under suitable selections of the coefficient functions, Equation 1.1 reduces to a sequence of integrable systems or describe the nonlinear waves in a fluid-filled tube [3], weakly nonlinear waves in the water of variable depth [4], and it models the spatial inhomogeneity in fluids [5]. The classical KdV equation was first derived from shallow water wave theory to describe the propagation of water waves in the long wave limit (surface gravity waves) [6]. The coefficients of variation in Equation 1.1 are due to geometric and physical inhomogeneities [3, 7].

In this context, we suppose that the external force effect function has the following form according to [5]:

$f\left(x,t\right)=f_1\left(t\right)x+f_2\left(t\right).(1.2)$

In particular, when $a(t)={\mu }_1$, $b(t)={\mu }_2$, $c(t)=0$, $d(t)={\mu }_3(t)-{\mu }_1\mu (t)$, and $f(x,t)=0$, H.L. Demiray [8] obtained the solitary wave solution via coordinate transformation. When $a(t)=\frac{3c^3}{2}$, $b(t)=\frac{1}{6c}$, $c(t)=-\frac{1}{2c}$, $d(t)=0$, and $f(x,t)=0$, H.L. Demiray [9] obtained a progressive wave-type solution through the reductive perturbation method. When $f_1(t)=0$, Zhang et al. [10] utilized the Wronskian technique and Hirota method to obtain a bilinear form and an analytic N-soliton-like solution. On the basis of symbolic computation, Tian et al. [11] obtained solutions for the Airy, Hermit and Jacobian elliptic functions [12]. Utilizing the Hirota bilinear method, Yu et al. [13] obtained an N-soliton solution and a type of analytic solution.

Various methods have been applied to search for exact solutions to nonlinear evolution equations (see [14–23]), including the $(G/G)$ expansion method [22, 24], the Hirota bilinear method [18], the inverse scattering transform method [16], the CK direct method [15], and the nonclassic Lie group method [14], among others.

In general, solving ordinary differential equations is easier than directly constructing partial differential equations. However, owing to variable coefficients, it remains difficult to solve an ordinary differential equation with variable coefficients. In the present work, first, by applying the direct similarity reduction-based CK method, we transform the partial differential equation shown in (1.1) into an ordinary differential equation. Then, solutions are obtained for the above ordinary differential equation via the $(G/G)$ expansion method. Finally, we can obtain three new similarity solutions to the variable-coefficient forced KdV equation in (1.1) and express the graphics of these similarity solutions. This equation may represent the main profile of these solutions for Equation 1.1.

2 Direct similarity reduction-based CK method

We hypothesize that the solution to Equation 1.1 takes the following form:

$u\left(x,t\right)=U\left(x,t,w\left(z\left(x,t\right)\right)\right).(2.1)$

Indeed, Equation 2.1 may represent the general form of the similarity solutions for Equation 1.1 (see [25]), and it is sufficient to consider the solutions for Equation 1.1 in the form of Equation 2.1. By substituting Equations 1.2, 2.1 into (1.1), we obtain

$\begin{array}{cc}\hfill & \left[U_t+U_{w}w{z}_t\right]+a\left(t\right)U\left[U_x+U_{w}w{z}_x\right]+c\left(t\right)U+d\left(t\right)\left[U_x+U_{w}w{z}_x\right]\hfill \\ \hfill & +b\left(t\right)\left\{U_{\mathit{xxx}}+3U_{\mathit{xxw}}w{z}_x\right.+U_{\mathit{www}}{\left(w\right)}^3{z}_x^3+U_{xw}\left[3w{z}_x^2+3w{z}_{xx}\right]\hfill \\ \hfill & +U_{ww}\left[3ww{z}_x^3+3w^2{z}_{xx}{z}_x\right]+3U_{\mathit{xww}}{w}^2{\left(z_x\right)}^2\hfill \\ \hfill & +\left.U_w\left[w{z}_x^3+3w{z}_{xx}{z}_x+w{z}_{\mathit{xxx}}\right]\right\}=f_1\left(t\right)x+f_2\left(t\right),\hfill \end{array}(2.2)$

where $w=dw/dz$, $w=d^{2}w/d{z}^2$, and $w=d^{3}w/d{z}^3$. To reduce Equation 2.2 to an ordinary differential equation with respect to $w(z)$, the derivatives of $w(z)$ should be only functions of $z$ and $w$. Moreover, when conducting normalization with a coefficient of $w$, namely, $U_w{z}_x^{3}b(t)$, the coefficients of $ww$ must satisfy

$U_w{z}_x^{3}b\left(t\right){\mathrm{\Gamma }}_1\left(w,z\right)=b\left(t\right)U_{ww}{z}_x^3,(2.3)$

where ${\mathrm{\Gamma }}_1(w,z)$ is a function and can be determined as follows. From Equation 2.3, we have

${\mathrm{\Gamma }}_1\left(w,z\right)=\frac{U_{ww}}{U_w}.$

After an integration step, we obtain

$\int {\mathrm{\Gamma }}_1\left(w,z\right)dw=\ln U_w-\ln {\beta }_0\left(x,t\right),$

where $\ln {\beta }_0(x,t)$ is the integral function. Letting $\ln {\mathrm{\Gamma }}_2(w,z)=\int {\mathrm{\Gamma }}_1(w,z)dw$, we have

${\mathrm{\Gamma }}_2\left(w,z\right)=\frac{U_w}{{\beta }_0\left(x,t\right)}.$

After an integration process, we obtain

$\int {\mathrm{\Gamma }}_2\left(w,z\right)=\frac{1}{{\beta }_0\left(x,t\right)}\left[U-{\alpha }_0\left(x,t\right)\right],(2.4)$

where ${\alpha }_0(x,t)$ is the function generated via integration. Let ${\mathrm{\Gamma }}_3(w,z)=\int {\mathrm{\Gamma }}_2(w,z)dw$; from Equation 2.4, we have that

$U={\beta }_0\left(x,t\right){\mathrm{\Gamma }}_3\left(w,z\right)+{\alpha }_0\left(x,t\right).$

Letting ${\mathrm{\Gamma }}_3(w,z)=w(z)$, ${\alpha }_0(x,t)=\alpha (x,t)$, and ${\beta }_0(x,t)=\beta (x,t)$, we have

$u\left(x,t\right)=\alpha \left(x,t\right)+\beta \left(x,t\right)w\left[z\left(x,t\right)\right].(2.5)$

Next, we compute $\alpha (x,t)$, $\beta (x,t)$, and $z(x,t)$. By substituting Equation 2.5 into Equation 2.2, we deduce that

$\begin{array}{cc}\hfill & b\left(t\right)\beta z_x^{3}w+wb\left(t\right)\left[3{\beta }_x{z}_x^2+3\beta z_x{z}_{xx}\right]+w\left[\beta z_t+a\left(t\right)\alpha \beta z_x+d\left(t\right)\beta z_x\right.\hfill \\ \hfill & +b\left(t\right)\left(3{\beta }_{xx}{z}_x+3{\beta }_x{z}_{xx}\right.\left.\left.+\beta z_{\mathit{xxx}}\right)\right]+wwa\left(t\right){\beta }^2{z}_x+w^{2}a\left(t\right)\beta {\beta }_x\hfill \\ \hfill & +w\left[{\beta }_t+a\left(t\right)\left(\alpha {\beta }_x+{\alpha }_x\beta \right)+c\left(t\right)\beta +d\left(t\right){\beta }_x+b\left(t\right){\beta }_{\mathit{xxx}}\right]\hfill \\ \hfill & +{\alpha }_t+a\left(t\right)\alpha {\alpha }_x+\alpha c\left(t\right)+d\left(t\right){\alpha }_x+b\left(t\right){\alpha }_{\mathit{xxx}}-\left[f_1\left(t\right)x+f_2\left(t\right)\right]=0.\hfill \end{array}(2.6)$

For the above equation to reduce to a solvable equation with respect to $w(z)$, the ratios of the coefficients $w(z)$ and the derivatives of the equation must be dependent on $z$ alone. This condition provides the relationships for $\alpha (x,t)$, $\beta (x,t)$, and $z(x,t)$, ensuring that any solution is a similarity reduction solution. Then, we introduce the following three footnotes (see [15]).

Remark 1. We adopt the coefficient of $w$ (i.e., $b(t)\beta z_x^3$) as the normalizing factor and thus impose the condition that the other coefficients must take the form $b(t)\beta z_x^3\mathrm{\Gamma }(z)$, where $\mathrm{\Gamma }(z)$ is a function of $z$ that needs to be determined.

Remark 2. Uppercase Greek letters are reserved for undetermined functions of $z$, ensuring that after performing operations (such as differentiation, integration, exponentiation, and rescaling), the result can still be denoted by the same letter. For example, the derivative of $\mathrm{\Gamma }(z)$ is denoted as $\mathrm{\Gamma }(z)$.

Remark 3. Three degrees of freedoms exist in the determination of $\alpha$, $\beta$, $z$ and $w$ and can be exploited (without loss of generality) to keep the proposed method manageable:

(i) if $\alpha (x,t)$ is expressed as $\alpha ={\alpha }_0(x,t)+\beta (x,t)\mathrm{\Omega }(z)$, we can simplify it by setting $\mathrm{\Omega }(z)=0$, which is equivalent to performing the substitution $w(z)\to w(z)-\mathrm{\Omega }(z)$;

(ii) if $\beta (x,t)$ is expressed as $\beta ={\beta }_0(x,t)\mathrm{\Omega }(z)$, we can simplify it by setting $\mathrm{\Omega }(z)=1$, which is equivalent to performing the substitution $w(z)\to w(z)/\mathrm{\Omega }(z)$];

(iii) if $z(x,t)$ is determined by an equation with the form $\mathrm{\Omega }(z)=z_0(x,t)$, where $\mathrm{\Omega }(z)$ is any invertible function, then we can take $\mathrm{\Omega }(z)=z$ [by substituting $z\to {\mathrm{\Omega }}^{-1}(z)$].

The general similarity reduction of Equation 1.1 can be determined via this method.

For Equation 2.2 to be reduced to an ordinary differential equation in terms of $w(z)$, the ratios of the various derivatives of $w(z)$ must depend on the functions of $w$ and $z$. When implementing normalization with the coefficient of $w$, namely, $b(t)\beta z_x^3$, the coefficients of $ww$ must satisfy certain conditions.

$b\left(t\right)\beta z_x^3{\mathrm{\Gamma }}_4\left(z\right)=a\left(t\right){\beta }^2{z}_x,$

where ${\mathrm{\Gamma }}_4(z)$ is a function to be determined. From Remark 3 (ii), we have

$\beta =\frac{b\left(t\right)}{a\left(t\right)}{z}_x^2.(2.7)$

The coefficient of $w^2$ requires that

$b\left(t\right)\beta z_x^3{\mathrm{\Gamma }}_5\left(z\right)=a\left(t\right)\beta {\beta }_x,(2.8)$

where ${\mathrm{\Gamma }}_5(z)$ is a function to be determined. By substituting Equation 2.8 into Equation 2.7, we obtain

$z_x^2{\mathrm{\Gamma }}_5\left(z\right)=2z_{xx}.$

From Remark 2, after applying a scale transformation, we have

$z_x{\mathrm{\Gamma }}_5\left(z\right)+\frac{z_{xx}}{z_x}=0.$

An integration step yields the following:

${\mathrm{\Gamma }}_5\left(z\right)+ln{z}_x=\mathrm{\Theta }\left(t\right),$

where $\mathrm{\Theta }(t)$ is the integration function. From Remark 2, this can be exponentiated:

$z_x{\mathrm{\Gamma }}_5=\mathrm{\Theta }\left(t\right).$

Integrating again gives

${\mathrm{\Gamma }}_5=x\mathrm{\Theta }\left(t\right)+\mathrm{\Sigma }\left(t\right),$

where $\mathrm{\Sigma }(t)$ is another integration function. We obtain the following equation through Remark 3 (iii).

$z=x\theta \left(t\right)+\sigma \left(t\right),(2.9)$

where $\theta (t)$ and $\sigma (t)$ are functions to be determined.

By substituting Equation 2.9 into Equation 2.7, we have that

$\beta =\frac{b\left(t\right)}{a\left(t\right)}\theta {\left(t\right)}^2.(2.10)$

With the coefficient of $w$, we have

$b\left(t\right)\beta z_x^3{\mathrm{\Gamma }}_6\left(z\right)=\beta z_t+a\left(t\right)\alpha \beta z_x+d\left(t\right)\beta z_x+b\left(t\right)\left(3{\beta }_{xx}{z}_x+3{\beta }_x{z}_{xx}+\beta z_{\mathit{xxx}}\right).$

where ${\mathrm{\Gamma }}_6(z)$ is a function to be determined. From Equations 2.9, 2.10, we have

$b\left(t\right){\theta }^3{\mathrm{\Gamma }}_6\left(z\right)=x\frac{d\theta }{dt}+\frac{d\sigma }{dt}+a\left(t\right)\alpha \theta +d\left(t\right)\theta ,$

From Remark 3(i), we obtain

$\alpha =-\frac{1}{a\left(t\right)\theta }\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)-\frac{d\left(t\right)}{a\left(t\right)}.(2.11)$

Substituting Equations 2.9–2.11 into (Equation 2.2), we have

$\begin{array}{cc}\hfill & {\theta }^5\frac{b^2\left(t\right)}{a\left(t\right)}\left(w+ww\right)+w\left\{\frac{a\left(t\right)\left[b\left(t\right){\theta }^2+2b\left(t\right)\theta \frac{d\theta }{dt}\right]-a\left(t\right)b\left(t\right){\theta }^2}{a{\left(t\right)}^2}\right.\hfill \\ \hfill & \left.-\frac{b\left(t\right)\theta }{a\left(t\right)}\frac{d\theta }{dt}+\frac{b\left(t\right)c\left(t\right){\theta }^2}{a\left(t\right)}\right\}\hfill \\ \hfill & +\left[\frac{1}{\theta }\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)+d\left(t\right)\right]\frac{1}{a\left(t\right)\theta }\frac{d\theta }{dt}\hfill \\ \hfill & -c\left(t\right)\left[\frac{1}{a\left(t\right)\theta }\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)+\frac{d\left(t\right)}{a\left(t\right)}\right]-\frac{x\frac{d^2\theta }{d{t}^2}+\frac{d^2\sigma }{d{t}^2}}{a\left(t\right)\theta }\hfill \\ \hfill & \hfill \\ \hfill & +\frac{\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)\left[\frac{d\theta }{dt}a\left(t\right)+a\left(t\right)\theta \right]}{{\theta }^2{a}^2\left(t\right)}-\frac{d\left(t\right)a\left(t\right)-d\left(t\right)a\left(t\right)}{a^2\left(t\right)}\hfill \\ \hfill & -\left[f_1\left(t\right)x+f_2\left(t\right)\right]=0.\hfill \end{array}(2.12)$

We proceed to transform Equation 2.12 into an ordinary differential equation for $w(z)$. By using the coefficients of $w$ and $ww$ (i.e., ${\theta }^5\frac{b^2(t)}{a(t)}$), we deduce that the coefficients of $w$ and $w^0$ must satisfy

${\theta }^5\frac{b^2\left(t\right)}{a\left(t\right)}{\gamma }_1\left(z\right)=\frac{a\left(t\right)\left[b\left(t\right){\theta }^2+2b\left(t\right)\theta \frac{d\theta }{dt}\right]-a\left(t\right)b\left(t\right){\theta }^2}{a^2\left(t\right)}-\frac{b\left(t\right)\theta }{a\left(t\right)}\frac{d\theta }{dt}+\frac{b\left(t\right)c\left(t\right){\theta }^2}{a\left(t\right)},(2.13)$

$\begin{array}{cc}\hfill {\theta }^5\frac{b^2\left(t\right)}{a\left(t\right)}{\gamma }_2\left(z\right)=& \left[\frac{1}{\theta }\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)+d\left(t\right)\right]\frac{1}{a\left(t\right)\theta }\frac{d\theta }{dt}\hfill \\ \hfill & -c\left(t\right)\left[\frac{1}{a\left(t\right)\theta }\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)+\frac{d\left(t\right)}{a\left(t\right)}\right]-\frac{x\frac{d^2\theta }{d{t}^2}+\frac{d^2\sigma }{d{t}^2}}{a\left(t\right)\theta }\hfill \\ \hfill & +\frac{\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)\left[\frac{d\theta }{dt}a\left(t\right)+a\left(t\right)\theta \right]}{{\theta }^2{a}^2\left(t\right)}\hfill \\ \hfill & -\frac{d\left(t\right)a\left(t\right)-d\left(t\right)a\left(t\right)}{a^2\left(t\right)}-\left[f_1\left(t\right)x+f_2\left(t\right)\right],\hfill \end{array}(2.14)$

where ${\gamma }_1(z)$ and ${\gamma }_2(z)$ are functions to be determined. Since $z=x\theta (t)+\sigma (t)$ and the right-hand side of Equation 2.14 is linear in terms of $x$, we can assume that ${\gamma }_2(z)=Az+B$, where $A$ and $B$ are constants. From Equation 2.14, we have that

$\begin{array}{cc}\hfill {\theta }^5\frac{b^2\left(t\right)}{a\left(t\right)}\left[A\left(x\theta +\sigma \right)+B\right]=& \left[\frac{1}{\theta }\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)+d\left(t\right)\right]\frac{1}{a\left(t\right)\theta }\frac{d\theta }{dt}\hfill \\ \hfill & -c\left(t\right)\left[\frac{1}{a\left(t\right)\theta }\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)+\frac{d\left(t\right)}{a\left(t\right)}\right]\hfill \\ \hfill & -\frac{x\frac{d^2\theta }{d{t}^2}+\frac{d^2\sigma }{d{t}^2}}{a\left(t\right)\theta }+\frac{\left(x\frac{d\theta }{dt}+\frac{d\sigma }{dt}\right)\left[\frac{d\theta }{dt}a\left(t\right)+a\left(t\right)\theta \right]}{{\theta }^2{a}^2\left(t\right)}\hfill \\ \hfill & -\frac{d\left(t\right)a\left(t\right)-d\left(t\right)a\left(t\right)}{a^2\left(t\right)}\hfill \\ \hfill & -\left[f_1\left(t\right)x+f_2\left(t\right)\right].\hfill \end{array}(2.15)$

By comparing the coefficients of $x$, we obtain

$A{\theta }^6\frac{b^2\left(t\right)}{a\left(t\right)}=-\frac{1}{a\left(t\right)\theta }\frac{d^2\theta }{d{t}^2}+\frac{1}{a^2\left(t\right){\theta }^2}\frac{d\theta }{dt}\left[\frac{d\theta }{dt}a\left(t\right)+a\left(t\right)\theta \right]+\frac{1}{a\left(t\right){\theta }^2}{\left[\frac{d\theta }{dt}\right]}^2-\frac{c\left(t\right)}{a\left(t\right)\theta }\frac{d\theta }{dt}-f_1\left(t\right),(2.16)$

$\begin{array}{cc}\hfill {\theta }^5\frac{b^2\left(t\right)}{a\left(t\right)}\left(A\sigma +B\right)=& -\frac{1}{a\left(t\right)\theta }\frac{d^2\sigma }{d{t}^2}+\frac{1}{a^2\left(t\right){\theta }^2}\frac{d\sigma }{dt}\left[\frac{d\theta }{dt}a\left(t\right)+a\left(t\right)\theta \right]\hfill \\ \hfill & \hfill -\frac{1}{a^2\left(t\right){\theta }^2}\left[d\left(t\right)a\left(t\right)-d\left(t\right)a\left(t\right)\right]\\ \hfill & +\left[\frac{1}{\theta }\frac{d\theta }{dt}+d\left(t\right)\right]\frac{1}{a\left(t\right)\theta }\frac{d\theta }{dt}\hfill \\ \hfill & \hfill +c\left(t\right)\left[-\frac{1}{a\left(t\right)\theta }\frac{d\sigma }{dt}-\frac{d\left(t\right)}{a\left(t\right)}\right]-f_2\left(t\right).\end{array}(2.17)$

Let

$f_1\left(t\right)=\frac{1}{a\left(t\right){\theta }^2}{A}^2+\frac{Aa\left(t\right)\theta +2A^{2}a\left(t\right)}{a^2\left(t\right){\theta }^2}-A\frac{c\left(t\right)}{a\left(t\right)\theta }-A{\theta }^6\frac{b^2\left(t\right)}{a\left(t\right)},(2.18)$

and

$\begin{array}{cc}\hfill f_2\left(t\right)=& -{\theta }^5\frac{b^2\left(t\right)}{a\left(t\right)}\left(A\sigma +B\right)+\frac{1}{a^2\left(t\right){\theta }^2}B\left[Aa\left(t\right)+a\left(t\right)\theta \right]\hfill \\ \hfill & \hfill -\frac{1}{a^2\left(t\right){\theta }^2}\left[d\left(t\right)a\left(t\right)-d\left(t\right)a\left(t\right)\right]\\ \hfill & +\left[\frac{1}{\theta }A+d\left(t\right)\right]\frac{1}{a\left(t\right)\theta }A+c\left(t\right)\left[-\frac{1}{a\left(t\right)\theta }B-\frac{d\left(t\right)}{a\left(t\right)}\right].\hfill \end{array}(2.19)$

It follows from Equations 2.18, 2.19, 2.16, 2.17 that

$\left\{\begin{array}{cc}\hfill \theta =& At+A_0,\hfill \\ \hfill \sigma =& Bt+B_0,\hfill \end{array}\right.(2.20)$

where $A_0$ and $B_0$ are integral constants. For the convenience of the calculation process, we assume that

$\frac{a\left(t\right)}{a\left(t\right)}-\frac{b\left(t\right)}{b\left(t\right)}\theta =A+c\left(t\right)\theta -A{\theta }^{4}b\left(t\right).(2.21)$

By substituting Equations 2.20–2.21 into Equation 2.13, we obtain ${\gamma }_1(z)=A$. Then, substituting ${\gamma }_1(z)=A$ and ${\gamma }_2(z)=Az+B$ into Equation 2.12 yields

$w+ww+Aw+Az+B=0,(2.22)$

where $A$ and $B$ are arbitrary constants. Upon substituting Equations 2.9–2.11 and (Equation 2.20) into Equation 2.5, we can deduce that

$\begin{array}{cc}\hfill u=& \frac{b\left(t\right)}{a\left(t\right)}{\left(At+A_0\right)}^{2}w\left(z\right)-\frac{1}{a\left(t\right)\left(At+A_0\right)}\left(xA+B\right)-\frac{d\left(t\right)}{a\left(t\right)},\hfill \\ \hfill z=& x\left(At+A_0\right)+Bt+B_0,\hfill \end{array}(2.23)$

where $w(z)$ satisfies Equation 2.22.

Next, we try to compute the exact solutions for Equation 2.22 based on the $(G/G)$ expansion method. More precisely, we suppose that Equation 2.22 has solutions in the following form:

$w\left(z\right)={\displaystyle \sum _{i=1}^m}{a}_i\left(z\right)\left(G/G\right),$

where $m\in N$. To balance $w$ and $ww$, we can take $m=2$, and then we have

$w\left(z\right)=a_0\left(Z\right)+a_1\left(z\right)\left(G/G\right)+a_2\left(z\right){\left(G/G\right)}^2,(2.24)$

where $G$ satisfies the following ordinary differential equation:

$G+\lambda G+\mu G=0,(2.25)$

where $\lambda$ and $\mu$ are constants. By substituting Equation 2.24 and Equation 2.25 into Equation 2.22 and comparing their coefficients, we deduce that

$\left\{\begin{array}{cc}\hfill & -24a_2-2a_2^2=0,\hfill \\ \hfill & -3\left(-4a_2+a_1+10a_2\lambda \right)+6a_2-24a_2\lambda \hfill \\ \hfill & +\left[a_2\left(a_1-a_1\lambda -2\mu a_2\right)-2a_1{a}_2\right]=0,\hfill \\ \hfill & -2\left(a_2-2a_1-4\lambda a_2+3\lambda a_1+8a_2\mu +4a_2{\lambda }^2\right)-4a_2+2a_1+10a_2\lambda \hfill \\ \hfill & -3\lambda \left(-4a_2+2a_1+10a_2\lambda \right)\hfill \\ \hfill & -24a_2\mu -2a_0{a}_2+a_1\left(a_1-a_1\lambda -2a_2\mu \right)+a_2\left(a_1-\lambda a_1-2a_2\mu \right)=0,\hfill \\ \hfill & -\left(a_1-2a_1\lambda -4a_2\mu +a_1{\lambda }^2+6a_2\lambda \mu +2a_1\mu \right)+a_2-2a_1-4a_2\lambda \hfill \\ \hfill & +3a_1\lambda +8a_2\mu +4a_2{\lambda }^2\hfill \\ \hfill & -2\lambda \left(a_2-2a_1-4a_2\lambda +8a_2\mu +4a_2{\lambda }^2\right)-3\mu \left(-4a_2+2a_1+10a_2\right)a_0\hfill \\ \hfill & \left(a_1-a_1\lambda -2a_2\mu \right)\hfill \\ \hfill & +a_1\left(a_1-a_1\lambda -2a_2\mu \right)+a_2\left(a_0-a_1\mu \right)+A{a}_2=0,\hfill \\ \hfill & a_1-2a_1\lambda -4a_2\mu +a_1{\lambda }^2+6a_2\lambda \mu +2a_1\mu -\lambda \hfill \\ \hfill & \left(a_1-2a_1\lambda -4a_2\mu +a_1\lambda +6a_2\lambda \mu \right.\hfill \\ \hfill & \left.+2a_1\mu \right)-2\mu \left(a_2-2a_1-4a_2\lambda +3a_1\lambda +8a_2\mu +4a_2{\lambda }^2\right)\hfill \\ \hfill & +a_1\left(a_0-a_1\mu \right)\hfill \\ \hfill & a_0\left(a_1-a_1\lambda -2a_2\mu \right)+A{a}_1=0,\hfill \\ \hfill & a_0-a_1\mu -\mu \left(a_1-a_1\lambda -2a_2\mu \right)-\mu \left(a_1-2a_1\lambda -4a_2\mu +a_1{\lambda }^2+6a_2\lambda \mu +2a_1\mu \right)\hfill \\ \hfill & +A{a}_0+Az+B=0.\hfill \end{array}\right.$

Then, we obtain

$\left\{\begin{array}{cc}\hfill & a_0\left(z\right)=11{\lambda }^2-8\mu +\left[3\lambda -12\mu -\frac{2\mu \left(6\lambda -24\mu \right)}{2\lambda +3}\right]e^{\left(2\lambda +3\right)z}\hfill \\ \hfill & +\frac{1+2{\lambda }^2+3\lambda }{24\left(2\lambda +3\right)}{\left(12\lambda -48\mu \right)}^2{e}^{2\left(2\lambda +3\right)z},\hfill \\ \hfill & a_1\left(z\right)=\left(6\lambda -24\mu \right)\frac{2}{2\lambda +3}{e}^{\left(2\lambda +3\right)z},\hfill \\ \hfill & a_2\left(z\right)=-12.\hfill \end{array}\right.(2.26)$

The following exact solution forms exist for Equation 2.22, and they can be acquired by substituting Equation 2.26 into Equation 2.24.

Case 1.If ${\lambda }^2-4\mu >0$, then

$\begin{array}{cc}\hfill w_1\left(z\right)=& 11{\lambda }^2-8\mu +\left[3\lambda -12\mu -\frac{2\mu \left(6\lambda -24\mu \right)}{2\lambda +3}\right]e^{\left(2\lambda +3\right)z}\hfill \\ \hfill & +\frac{1+2{\lambda }^2+3\lambda }{24\left(2\lambda +3\right)}{\left(12\lambda -48\mu \right)}^2{e}^{2\left(2\lambda +3\right)z}\hfill \\ \hfill & +\left(6\lambda -24\mu \right)\frac{2}{2\lambda +3}{e}^{\left(2\lambda +3\right)z}\hfill \\ \hfill & \left[\frac{\sqrt{{\lambda }^2-4\mu }}{2}\frac{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)}{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)}-\frac{\lambda }{2}\right]\hfill \\ \hfill & -12{\left[\frac{\sqrt{{\lambda }^2-4\mu }}{2}\frac{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)}{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)}-\frac{\lambda }{2}\right]}^2.\hfill \end{array}(2.27)$

Case 2.If ${\lambda }^2-4\mu <0$, then

$\begin{array}{cc}\hfill w_2\left(z\right)=& 11{\lambda }^2-8\mu +\left[3\lambda -12\mu -\frac{2\mu \left(6\lambda -24\mu \right)}{2\lambda +3}\right]e^{\left(2\lambda +3\right)z}\hfill \\ \hfill & +\frac{1+2{\lambda }^2+3\lambda }{24\left(2\lambda +3\right)}{\left(12\lambda -48\mu \right)}^2{e}^{2\left(2\lambda +3\right)z}\hfill \\ \hfill & +\left(6\lambda -24\mu \right)\frac{2}{2\lambda +3}{e}^{\left(2\lambda +3\right)z}\hfill \\ \hfill & \left[\frac{\sqrt{4\mu -{\lambda }^2}}{2}\frac{A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)}-\frac{\lambda }{2}\right]\hfill \\ \hfill & -12{\left[\frac{\sqrt{4\mu -{\lambda }^2}}{2}\frac{A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)}-\frac{\lambda }{2}\right]}^2.\hfill \end{array}(2.28)$

Case 3. If ${\lambda }^2-4\mu =0$, then

$\begin{array}{cc}\hfill w_3\left(z\right)=& 11{\lambda }^2-8\mu +\left[3\lambda -12\mu -\frac{2\mu \left(6\lambda -24\mu \right)}{2\lambda +3}\right]e^{\left(2\lambda +3\right)z}\hfill \\ \hfill & +\frac{1+2{\lambda }^2+3\lambda }{24\left(2\lambda +3\right)}{\left(12\lambda -48\mu \right)}^2{e}^{2\left(2\lambda +3\right)z}\hfill \\ \hfill & +\left(6\lambda -24\mu \right)\frac{2}{2\lambda +3}{e}^{\left(2\lambda +3\right)z}\left[\frac{A_2}{A_1+A_{2}z}-\frac{\lambda }{2}\right]\hfill \\ \hfill & -12{\left[\frac{A_2}{A_1+A_{2}z}-\frac{\lambda }{2}\right]}^2.\hfill \end{array}(2.29)$

3 Conclusion

Substitute Equation 2.27–2.29 into Equation 2.23 and the following forms of similarity solutions exist for Equation 1.1.

Case 1. If ${\lambda }^2-4\mu >0$, then

$\begin{array}{cc}\hfill u_1\left(x,t\right)=& \left\{11{\lambda }^2-8\mu +\left[3\lambda -12\mu -\frac{2\mu \left(6\lambda -24\mu \right)}{2\lambda +3}\right]e^{\left(2\lambda +3\right)z}\right.\hfill \\ \hfill & +\frac{1+2{\lambda }^2+3\lambda }{24\left(2\lambda +3\right)}{\left(12\lambda -48\mu \right)}^2{e}^{2\left(2\lambda +3\right)z}\hfill \\ \hfill & +\left(6\lambda -24\mu \right)\frac{2}{2\lambda +3}{e}^{\left(2\lambda +3\right)z}\hfill \\ \hfill & \left[\frac{\sqrt{{\lambda }^2-4\mu }}{2}\frac{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)}{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)}-\frac{\lambda }{2}\right]\hfill \\ \hfill & -\left.12{\left[\frac{\sqrt{{\lambda }^2-4\mu }}{2}\frac{A_{1}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)+A_{2}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)}{A_{1}sinh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)+A_{2}cosh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}z\right)}-\frac{\lambda }{2}\right]}^2\right\}\hfill \\ \hfill & \frac{b\left(t\right)}{a\left(t\right)}{\left(At+A_0\right)}^2-\frac{1}{a\left(t\right)\left(At+A_0\right)}\left(xA+B\right)-\frac{d\left(t\right)}{a\left(t\right)}.\hfill \end{array}(3.1)$

The similar solution corresponding to Case 1 is expressed in Figure 1.

The values determined for $u_1(x,t)$ when $\lambda =1,\mu =-1,A_1=100,A_2=A=B=A_0=B_0=a(t)=b(t)=d(t)=1$.

Case 2. If ${\lambda }^2-4\mu <0$, then

$\begin{array}{cc}\hfill u_2\left(x,t\right)=& \left\{11{\lambda }^2-8\mu +\left[3\lambda -12\mu -\frac{2\mu \left(6\lambda -24\mu \right)}{2\lambda +3}\right]e^{\left(2\lambda +3\right)z}\right.\hfill \\ \hfill & +\frac{1+2{\lambda }^2+3\lambda }{24\left(2\lambda +3\right)}{\left(12\lambda -48\mu \right)}^2{e}^{2\left(2\lambda +3\right)z}\hfill \\ \hfill & +\left(6\lambda -24\mu \right)\frac{2}{2\lambda +3}{e}^{\left(2\lambda +3\right)z}\hfill \\ \hfill & \left[\frac{\sqrt{4\mu -{\lambda }^2}}{2}\frac{A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)}-\frac{\lambda }{2}\right]\hfill \\ \hfill & \left.-,12{\left[\frac{\sqrt{4\mu -{\lambda }^2}}{2}\frac{A_{1}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)+A_{2}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)}{A_{1}cos\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)+A_{2}sin\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}z\right)}-\frac{\lambda }{2}\right]}^2\right\}\hfill \\ \hfill & \frac{b\left(t\right)}{a\left(t\right)}{\left(At+A_0\right)}^2-\frac{1}{a\left(t\right)\left(At+A_0\right)}\left(xA+B\right)-\frac{d\left(t\right)}{a\left(t\right)}.\hfill \end{array}(3.2)$

Figure 1

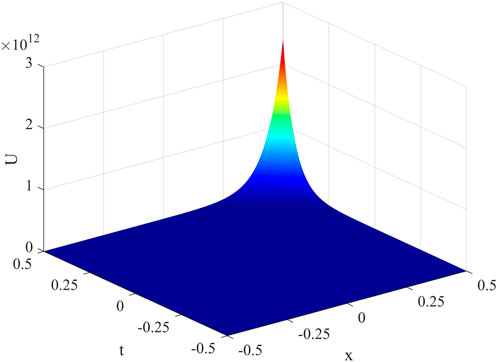
Figure 1. The values determined for u₁(x, t) when λ = 1, μ = −1, A₁ = 100, A₂ = A = B = A₀ = B₀ = a(t) = b(t) = d(t) = 1.

The similar solution corresponding to Case 2 is expressed in Figure 2.

Figure 2

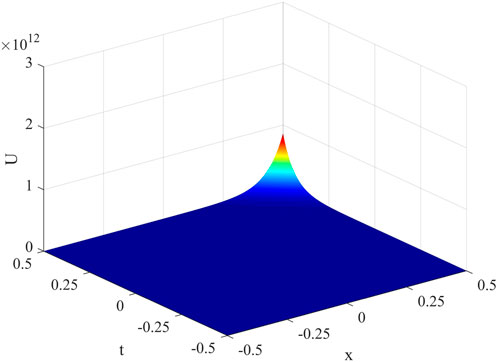
Figure 2. The values determined for u₂(x, t) when λ = 1, μ = 1, A₁ = 100, A₂ = A = B = A₀ = B₀ = a(t) = b(t) = d(t) = 1.

The values determined for $u_2(x,t)$ when $\lambda =1,\mu =1,A_1=100,A_2=A=B=A_0=B_0=a(t)=b(t)=d(t)=1$.

Case 3. If ${\lambda }^2-4\mu =0$, then

$\begin{array}{cc}\hfill u_3\left(x,t\right)=& \left\{11{\lambda }^2-8\mu +\left[3\lambda -12\mu -\frac{2\mu \left(6\lambda -24\mu \right)}{2\lambda +3}\right]e^{\left(2\lambda +3\right)z}\right.\hfill \\ \hfill & +\frac{1+2{\lambda }^2+3\lambda }{24\left(2\lambda +3\right)}{\left(12\lambda -48\mu \right)}^2{e}^{2\left(2\lambda +3\right)z}\hfill \\ \hfill & +\left(6\lambda -24\mu \right)\frac{2}{2\lambda +3}{e}^{\left(2\lambda +3\right)z}\left[\frac{A_2}{A_1+A_{2}z}-\frac{\lambda }{2}\right]\hfill \\ \hfill & \left.-,12{\left[\frac{A_2}{A_1+A_{2}z}-\frac{\lambda }{2}\right]}^2\right\}\frac{b\left(t\right)}{a\left(t\right)}{\left(At+A_0\right)}^2\hfill \\ \hfill & -\frac{1}{a\left(t\right)\left(At+A_0\right)}\left(xA+B\right)-\frac{d\left(t\right)}{a\left(t\right)}.\hfill \end{array}(3.3)$

The similar solution corresponding to Case 3 is expressed in Figure 3.

Figure 3

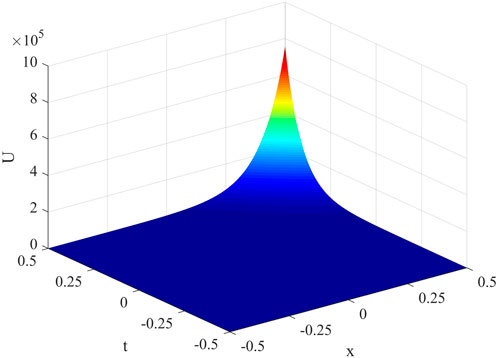
Figure 3. The values determined for u₃(x, t) when λ = 2, A₁ = 100, μ = A₂ = A = B = A₀ = B₀ = a(t) = b(t) = d(t) = 1.

The values determined for $u_3(x,t)$ when $\lambda =2,A_1=100,\mu =A_2=A=B=A_0=B_0=a(t)=b(t)=d(t)=1$.

According to the above discussion, the shape of the graphic is sensitive to the values of $x$ and $t$. Indeed, we can clearly see the change trends exhibited by these three graphs, which are in exponential form. The constraints on the solution of the variable coefficient equation obtained by Method 1 are simple and less categorical than those of the previous article [26].

In the present work, we investigate the variable-coefficient forced KdV equation. As a result, this paper not only reduces the equation to an ordinary differential equation via the direct similarity reduction-based CK method but also obtains similarity solutions from the solutions of the above ordinary differential equation. This provides a simpler method for studying the variable-coefficient forced KdV equation. It simplifies the mathematical solution process and facilitates fluctuation control and application design in engineering practice. Many other variable-coefficient nonlinear partial differential equations can also be investigated via this method.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JW: Conceptualization, Writing – original draft, Writing – review and editing. JF: Writing – review and editing, Visualization. JD: Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tian SF, Zhang HQ. On the integrability of a generalized variable-coefficient forced Korteweg-de Vries equation in fluids. Stud Appl Math (2014) 132(3):212–46. doi:10.1111/sapm.12026

CrossRef Full Text | Google Scholar

2. Mohammed WW, Al-Askar FM. New stochastic solitary solutions for the modified Korteweg-de Vries equation with stochastic term/random variable coefficients. AIMS Math (2024) 9(8):20467–81. doi:10.3934/math.2024995

CrossRef Full Text | Google Scholar

3. Demiray H. The effect of a bump on wave propagation in a fluid-filled elastic tube. Int J Eng Sci (2004) 42(2):203–15. doi:10.1016/s0020-7225(03)00284-2

CrossRef Full Text | Google Scholar

4. Holloway PE, Pelinovsky E, Talipova T. A generalized Korteweg-de Vries model of internal tide transformation in the coastal zone. J Geophys Res C (1999) 104:18333–50. doi:10.1029/1999jc900144

CrossRef Full Text | Google Scholar

5. Yu X, Sun ZY, Zhou KW, Shen YJ. Spacial inhomogeneity and nonlinear tunneling for the forced KdV equation. Appl Math Lett (2018) 75:30–6. doi:10.1016/j.aml.2017.05.015

CrossRef Full Text | Google Scholar

6. Korteweg DJ, de Vries G. On the change of form of long waves advancing in a rectangular canal and on a new tipe of long stationary waves. Phil Mag 39(1895):422–43. doi:10.1080/14786449508620739

CrossRef Full Text | Google Scholar

7. Xu F. Application of exp-function method to symmetric regularized long wave (SRLW) equation. Phys Lett A (2008) 372:252–7. doi:10.1016/j.physleta.2007.07.035

CrossRef Full Text | Google Scholar

8. Demiray HL. Forced KdV equation in a fluid-filled elastic tube with variable initial stretches. Chaos Solitons Fractals (2009) 42(3):1388–95. doi:10.1016/j.chaos.2009.03.067

CrossRef Full Text | Google Scholar

9. Demiray HL. Weakly nonlinear waves in water of variable depth: variable-coefficient Korteweg-de Vries equation. Comput Math Appl (2010) 60(6):1747–55. doi:10.1016/j.camwa.2010.07.005

CrossRef Full Text | Google Scholar

10. Zhang CY, Yao ZZ, Zhu HW, Xu T, Li J, Meng XH, et al. Exact AnalyticN-soliton-like solution in wronskian form for a generalized variable-coefficient Korteweg-de Vries model from plasmas and fluid dynamics. Chin Phys Lett (2007) 24:1173–6. doi:10.1088/0256-307x/24/5/013

CrossRef Full Text | Google Scholar

11. Tian B, Wei GM, Zhang CY, Shan WR, Gao YT. Transformations for a generalized variable-coefficient Korteweg-de Vries model from blood vessels, Bose-Einstein condensates, rods and positons with symbolic computation. Phys Lett A (2006) 356(1):8–16. doi:10.1016/j.physleta.2006.03.080

CrossRef Full Text | Google Scholar

12. Khalique CM, Adeyemo OD, Monashane MS. Exact solutions, wave dynamics and conservation laws of a generalized geophysical Korteweg de Vries equation in ocean physics using Lie symmetry analysis. Adv Math Models Appl (2024) 9:147–72. doi:10.62476/amma9147

CrossRef Full Text | Google Scholar

13. Yu X, Gao YT, Sun ZY, Liu Y. Solitonic propagation and interaction for a generalized variable-coefficient forced Korteweg-de Vries equation in fluids. Phys Rev E (2011) 83:056601. doi:10.1103/physreve.83.056601

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bluman GW, Cole JD. The general similarity solution of the heat equation. J Math Fluid Mech (1969) 18:1025–42. doi:10.1512/iumj.1969.18.18074

CrossRef Full Text | Google Scholar

15. Clarkson PA, Kruskal MD. New similarity reductions of the Boussinesq equation. J Math Phys (1989) 30(10):2201–13. doi:10.1063/1.528613

CrossRef Full Text | Google Scholar

16. Gardner CS, Greene JM, Kruskal MD, Martin DK, Robert MM. Method for solving the Korteweg-de Vries equation. Phys Rev Lett (1967) 19(19):1095–7. doi:10.1103/physrevlett.19.1095

CrossRef Full Text | Google Scholar

17. Guo Q, Liu J. New exact solutions to the nonlinear Schrödinger equation with variable coefficients. Results Phys (2020) 16:102857. doi:10.1016/j.rinp.2019.102857

CrossRef Full Text | Google Scholar

18. Hirota R. Exact solution of the kortewegde Vries equation for multiple collisions of solitons. Phys Rev Lett (1971) 27(18):1192–4. doi:10.1103/physrevlett.27.1192

CrossRef Full Text | Google Scholar

19. Wu GC, Xia TC. A new method for constructing soliton solutions and periodic solutions of nonlinear evolution equations. Phys Lett A (2008) 372(5):604–9. doi:10.1016/j.physleta.2007.07.064

CrossRef Full Text | Google Scholar

20. Wu GC, Xia TC. Uniformly constructing exact discrete soliton solutions and periodic solutions to differential-difference equations. Comput Math Appl (2009) 58:2351–4. doi:10.1016/j.camwa.2009.03.022

CrossRef Full Text | Google Scholar

21. Wu GC. Uniformly constructing soliton solutions and periodic solutions to Burgers-Fisher equation. Comput Math Appl (2009) 58:2355–7. doi:10.1016/j.camwa.2009.03.023

CrossRef Full Text | Google Scholar

22. Wang ML, Li XZ, Zhang JL. The (G/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys Lett A (2008) 372(4):417–23. doi:10.1016/j.physleta.2007.07.051

CrossRef Full Text | Google Scholar

23. Adeyemo OD, Khalique CM, Gasimov YS, Villecco F. Variational and non-variational approaches with Lie algebra of a generalized (3+ 1)-dimensional nonlinear potential Yu-Toda-Sasa-Fukuyama equation in Engineering and Physics. Alexandria Eng J (2023) 63:17–43. doi:10.1016/j.aej.2022.07.024

CrossRef Full Text | Google Scholar

24. Koç DA, Gasimov YS, Bulut H. A study on the investigation of the traveling wave solutions of the mathematical models in physics via (m + (1/G))-expansion method. Adv Math Models Appl (2024) 9(1):5–13. doi:10.62476/amma9105

CrossRef Full Text | Google Scholar

25. Bluman GW, Cole JD. Similarity methods for differential equations. Berlin: Springer (1974).

Google Scholar

26. Lu DC, Hong BJ, Tian LX. Explicit and exact solutions to the variable coefficient combined KdV equation with forced term (2006). p. 5617–22.

Google Scholar