Symmetries and topological phase transitions in modified Haldane models with long-range hoppings and gain-loss effects

We investigate a non-Hermitian modified Haldane model on a honeycomb lattice incorporating third nearest neighbor hopping $t_3$. The results indicate that the system satisfies the pseudo-Hermitian and anti-$\mathcal{PT}$ symmetries, ensuring the reality and orthogonality of the eigenstates. We present the phase diagrams in the $m/t_2$-$\varphi$ and $m/t_2$-$t_3$ planes to elucidate the topological phases of the system. For specific values of $t_3$, the system reveals Chern insulating phases characterized by Chern numbers $\pm 2$ and $\pm 1$, alongside trivial insulating phases. Upon introducing gain and loss $\gamma$ in the on-site energy, additional phases with Chern number $\pm 1$ emerge between the two Chern insulating phases. The edge states possess topological properties and their number corresponds to the value of the Chern number by calculating and analyzing the edge states of a semi-infinite honeycomb lattice. Due to symmetry breaking caused by the truncation of the real-space lattice, the edge states acquire a significant amount of imaginary energy, while most of the bulk state energies remain almost real. Our work enhances understanding of the influence of long-range hoppings and gain-loss effects on the topological phases of non-Hermitian modified Haldane models.

1 Introduction

Since the discovery of the quantum Hall effect and topological insulators [1–7], substantial research has concentrated on the topological properties of the two-dimensional honeycomb lattice. A series of novel topological phases beyond the classical Landau phase transition theory have been discovered, making the exploration of novel topological phases and phase transitions [8–19] a rapidly emerging hotspot in the field of condensed matter physics. The Haldane model [20], a seminal contribution to the field of topological materials, offers a theoretical framework for understanding the band structure, topological invariants, and edge states associated with a honeycomb lattice. This model describes a honeycomb lattice with nearest-neighbor (N1) and next-nearest-neighbor (N2) hoppings terms, along with staggered on-site energy that breaks inversion symmetry. Moreover, the Haldane model exemplifies a distinctive system in which quantum Hall effect [20, 21] is inherently linked to the properties of the lattice band structure through the introduction of a magnetic phase ${\varphi }_{ij}$, rather than depending on an external strong magnetic field. This magnetic phase is reflected in the complex hopping terms $t_2{e}^{i{\varphi }_{ij}}$, which break time-reversal symmetry without generating a net magnetic flux within the plaquettes. By varying the Haldane flux and the on-site energy, the system can undergo a topological phase transition from a normal insulator to a Chern insulator.

Over the past few decades, research on topological phases and topological phase transitions in two-dimensional materials has primarily been based on the assumption of Hermitian Hamiltonians. However, real physical systems are typically open and interact with the environment, making it inevitable to search for novel topological phases in non-Hermitian systems. In recent years, significant advances have been achieved in investigating topological phases and properties associated with the Haldane model in non-Hermitian systems incorporating gain and loss mechanisms [22–26]. Unlike their Hermitian counterparts, non-Hermitian systems not only provide accurate simulations of the open system behaviors in practical environments [27, 28], but they also exhibit unique features, including complex-valued energy spectra [29–31], nonorthogonal eigenvectors [32], parity-time $(\mathcal{P}\mathcal{T})$ symmetry [33–35], and skin effects [36–38]. The existence of these non-Hermitian properties significantly enriches the topological phases associated with topological invariants extending beyond the existing Hermitian framework, which is crucial for exploring exotic physical phenomena. Long-range hopping and non-Hermiticity are particularly noteworthy. Theoretically, certain systems, such as the decorated honeycomb lattice [39], the multiorbital triangular lattice [40], and ultracold atomic gas on a triangular lattice [8, 9], have been predicted to exhibit non-trivial topological phases with higher Chern numbers by adding long-range hopping. Experimentally, the study of non-Hermitian two-dimensional lattices has been conducted in photonic lattices [41–46], cold atom systems [47–49], and electronic circuits [50–53]. Notably, previous studies have shown that topological phase transitions in both Hermitian [10, 11, 14–16, 19] and non-Hermitian systems [23–26] can be induced by variations in the staggered on-site energy and the hopping terms, including long-range hopping terms that may lead to novel topological phases and large Chern numbers. Such changes can significantly affect the band behavior of the system, particularly regarding the opening and closing of energy gaps and the inversion of bands, which serve as vital indicators of topological phase transitions. Given that most studies have concentrated on two-band systems, it is natural to question whether long-range hopping terms will yield a richer topological phase and induce topologically nontrivial states in the multi-band non-Hermitian modified Haldane model with gain and loss.

Inspired by the aforementioned inquiries, we explore the topological properties of the non-Hermitian modified Haldane model, which incorporates the third nearest neighbor (N3) hopping $t_3$. Our findings reveal that the model exhibits pseudo-Hermitian and anti-$\mathcal{P}\mathcal{T}$ symmetry, ensuring the presence of purely real eigenvalues and pairwise orthogonality of eigenstates. To further elucidate our observations regarding the topological phases, we present the phase diagrams in the $m/t_2$-$\varphi$ and $m/t_2$-$t_3$ planes, respectively. The introduction of $t_3$ results in exhibiting higher Chern numbers $C=\pm 2$. Notably, when we incorporate gain and loss in the on-site energy, the system reveals additional phases characterized by Chern numbers $\pm 1$ located between the two Chern insulating phases. To substantiate the existence of topological phases, we utilize a semi-infinite honeycomb lattice geometry to investigate the properties of edge states. Due to the truncation of the lattice in real space, the reality and orthogonality of the eigenstates are affected. Consequently, the energies of the edge states display significant imaginary components, whereas the energies of the majority of bulk states remain nearly real.

2 Model and Hamiltonian

We consider a non-Hermitian Haldane model on the honeycomb lattice, as illustrated in Figure 1. This model features distinct complex on-site mass terms, with the real parts $\pm m$ denoted by thick and thin outlines, while the imaginary parts $\pm \gamma$, representing on-site gain or loss, are illustrated using red and blue colors. The lattice vectors are defined as ${\mathbf{a}}_1=(\mathrm{1,0})$ and ${\mathbf{a}}_2=(0,\sqrt{3})$, respectively. The coupling strength for N1 is represented by $t_1$, whereas the coupling strength for N2 is associated with an amplitude $t_2$ and a complex phase denoted by ${\varphi }_{ij}$. The phase ${\varphi }_{ij}$ is defined along the electron hops, being positive for clockwise and negative for anticlockwise directions. Additionally, coupling N3 is considered with a strength of $t_3$. In momentum space, the Hamiltonian of the system can be written as

$H\left(k\right)=\left(\begin{array}{cccc}\hfill {\xi }_1\hfill & \hfill {\xi }_2\hfill & \hfill {\xi }_4\hfill & \hfill {\xi }_5\hfill \\ \hfill {\xi }_2^{*}\hfill & \hfill {\xi }_3\hfill & \hfill {\xi }_5^{*}\hfill & \hfill {\xi }_6\hfill \\ \hfill {\xi }_4\hfill & \hfill {\xi }_5\hfill & \hfill {\xi }_1^{*}\hfill & \hfill {\xi }_2\hfill \\ \hfill {\xi }_5^{*}\hfill & \hfill {\xi }_6\hfill & \hfill {\xi }_2^{*}\hfill & \hfill {\xi }_3^{*}\hfill \end{array}\right),(1)$

where

$\begin{array}{ll}\hfill {\xi }_1& =-m-i\gamma +2t_2\cos \varphi \cos k_x-2t_2\sin \varphi \sin k_x,\hfill \\ \hfill {\xi }_2& =2t_1\cos \left(k_x/2\right)e^{-i\sqrt{3}{k}_y/6},\hfill \\ \hfill {\xi }_3& =m-i\gamma +2t_2\cos \varphi \cos k_x+2t_2\sin \varphi \sin k_x,\hfill \\ \hfill {\xi }_4& =4t_2\cos \left(\varphi -k_x/2\right)\cos \left(\sqrt{3}{k}_y/2\right),\hfill \\ \hfill {\xi }_5& =\left(t_1+2t_3\cos k_x\right)e^{i\sqrt{3}{k}_y/3}+t_3{e}^{-i2\sqrt{3}{k}_y/3},\hfill \\ \hfill {\xi }_6& =4t_2\cos \left(\varphi +k_x/2\right)\cos \left(\sqrt{3}{k}_y/2\right),\hfill \end{array}(2)$

where $\mathbf{k}=(k_x,k_y)$ denotes the wave vector. For $\gamma =0$ and $t_3=0$, the terms associated with gain-loss and long-range hopping in Equations 1, 2 vanish, and the current system reduces to the well-known Haldane model [20]. It undergoes a topological phase transition between a quantum anomalous Hall insulator (QAHI) and a trivial insulator occurs when $m=\pm 3\sqrt{3}{t}_2\sin \varphi$, and holds the point group symmetry of ${\mathcal{C}}_3$ $(m\ne 0)$.

Figure 1

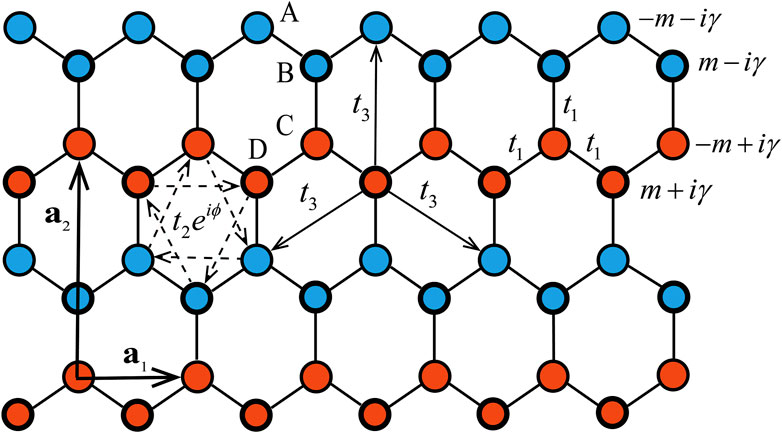
Figure 1. Schematic of a modified non-Hermitian Haldane lattice with complex on-site mass terms, where the real parts $\pm m$ are represented by thick and thin outlines, and the imaginary parts $\pm \gamma$ corresponding to on-site gain or loss are depicted using red and blue colors. $t_1$ and $t_3$ represent the N1 and N3 hopping strengths, respectively. N2 hopping strength is associated with an amplitude $t_2$ and a complex phase represented by ${\varphi }_{ij}$. ${\mathbf{a}}_{\mathbf{1}}$ and ${\mathbf{a}}_{\mathbf{2}}$ denote the lattice vectors.

3 Results and discussion

3.1 Pseudo-Hermitian and anti-$\mathcal{P}\mathcal{T}$ symmetries

We turn to discuss the symmetries of the current system with $\gamma \ne 0$ and $t_3\ne 0$. Now, we choose the Haldane flux $\varphi =-\pi /2$ and define $4\times 4$ matrices expressed as follows

${\mathrm{\Gamma }}_u=\left(\begin{array}{cc}\hfill 0\hfill & \hfill {\sigma }_u\hfill \\ \hfill {\sigma }_u\hfill & \hfill 0\hfill \end{array}\right),(3)$

where ${\sigma }_{u=0}$ is the identity matrix and ${\sigma }_{u=\mathrm{1,2,3}}$ are the $2\times 2$ Pauli matrices. It can be shown that the $\mathrm{\Gamma }$ matrices defined in Equation 3 satisfy the following properties: ${\mathrm{\Gamma }}_0{\mathrm{\Gamma }}_0$ = $I$, ${\mathrm{\Gamma }}_0$ = ${\mathrm{\Gamma }}_0^{†}$, and $\left\{{\mathrm{\Gamma }}_i,{\mathrm{\Gamma }}_j\right\}=2{\delta }_{ij}$ for $i,j=\mathrm{1,2,3}$. We find that the current non-Hermitian Hamiltonian satisfies the pseudo-Hermiticity condition symmetry [30, 54–56], and a relation can be proved by

${\mathrm{\Gamma }}_{0}H\left(k\right){\mathrm{\Gamma }}_0=H{\left(k\right)}^{†},(4)$

We introduce a complete set of biorthonormal eigenvectors $\{\langle {\psi }_m|,|{\psi }_n\rangle \}$ that satisfy the biorthogonality condition $⟨{\psi }_m|{\psi }_n⟩={\delta }_{mn}$. Considering the eigenvalue equation $\langle {\psi }_m|H(k)=\langle {\psi }_m|E_m$ and $H{(k)}^{†}|{\psi }_m\rangle =E_m^{*}|{\psi }_m\rangle$, we derive ${\mathrm{\Gamma }}_0{\mathrm{\Gamma }}_{0}H(k)({\mathrm{\Gamma }}_0|{\psi }_m\rangle )={\mathrm{\Gamma }}_{0}H{(k)}^{†}|{\psi }_m\rangle$ = $E_m^{*}({\mathrm{\Gamma }}_0|{\psi }_m\rangle )$. This implies that the energy eigenvalues of $H(k)$ are purely real or occur in complex conjugate pairs. Additionally, the current non-Hermitian Hamiltonian also satisfies the anti-$\mathcal{P}\mathcal{T}$ symmetry condition [35, 57–59].

$\left\{H\left(k\right),{\mathrm{\Gamma }}_3{\mathrm{\Gamma }}_{1}T\right\}=0,(5)$

where $T$ denotes the complex conjugation operator. By combining the anti-commutation relation $\left\{{\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_3\right\}$ = 0 and the eigenvalue equation $H(k)|{\psi }_n\rangle$ = $E_n|{\psi }_n\rangle$, we can derive the following equation $H(k){\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_{3}T|{\psi }_n\rangle ={\mathrm{\Gamma }}_3{\mathrm{\Gamma }}_{1}T(H(k)|{\psi }_n\rangle )=-E_n^{*}{\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_{3}T|{\psi }_n\rangle$. By defining $|{\psi }_{n^{\prime }}\rangle$ = ${\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_{3}T|{\psi }_n\rangle$, we conclude that $|{\psi }_{n^{\prime }}\rangle$ is an eigenstate of $H(k)$ with eigenvalue $-E_n^{*}$. Furthermore, the orthogonality of the eigenstates $|{\psi }_{n^{\prime }}\rangle$ = ${\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_{3}T|{\psi }_n\rangle$ and $|{\psi }_n\rangle$ can be further proved; specifically, the inner product $⟨{\psi }_n|{\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_{3}T|{\psi }_n⟩=0$. It is important to note that if the phases of the N2 couplings deviate from $\pm \pi /2,H(k)$ would not satisfy the symmetries discussed above. In Figures 2a, b, we illustrate the real and imaginary parts of the energy spectrum in momentum space with parameters $t_1=1$, $m/t_2=3$, $\gamma =0.5$, $t_3=0.5$, and $\varphi =-\pi /2$. It has been observed that specific real components of the energy spectrum correspond to imaginary components with non-zero values, which are attributed to on-site gain and loss. Furthermore, there are regions where the imaginary component is zero, signifying the presence of purely real energy eigenvalues. This observation is consistent with the previously discussed symmetries.

Figure 2

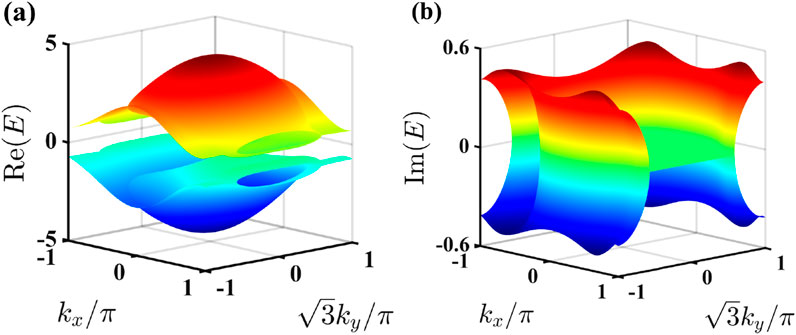
Figure 2. (a) Real and (b) imaginary parts of the energy spectrum of modified non-Hermitian Haldane model in momentum space. The parameters of the system are set to $t_1=1$, $m/t_2=3$, $\gamma =0.5$, $t_3=0.5$, and $\varphi =-\pi /2$.

3.2 Chern numbers and phase diagram

To compute the Berry phase of multi-band systems in $k$-space using a discretized approximation, we select a mesh of closely spaced $k$-points $\{{\mathbf{k}}_i\}$ that covers the relevant region of the Brillouin zone. We begin with the states $|{\psi }_{n,{\mathbf{k}}_0}\rangle ,|{\psi }_{n,{\mathbf{k}}_1}\rangle ,\dots ,|{\psi }_{n,{\mathbf{k}}_{N-1}}\rangle$ in an arbitrary gauge. For each neighboring pair of points, we compute the overlap $M_{mn}^{({\mathbf{k}}_i,{\mathbf{k}}_{i+1})}=⟨{\psi }_{m,{\mathbf{k}}_i}|{\psi }_{n,{\mathbf{k}}_{i+1}}⟩$, where $m,n\in \{\mathrm{1,2,3,4}\}$ label the energy bands. Utilizing these overlaps, we can obtain the total Berry phase ${\phi }_{\text{tot}}$ for the two valence bands within the first Brillouin zone via Equation 6:

$\phi =-\mathrm{Im}\ln \left(\prod _{i=0}^{N-1}\det M^{({\mathbf{k}}_i,{\mathbf{k}}_{i+1})}\right),(6)$

which can then be used to calculate the Chern number as $C={\phi }_{\text{tot}}/2\pi$. This process further facilitates the construction of phase diagrams. In Figure 3, we present the phase diagrams of the two valence bands within the parameter space defined by $\varphi$ and $m/t_2$. Specifically, for (a) $\gamma =0.5$ and $t_3=0$; (b) $\gamma =0$ and $t_3=2$; and (c) $\gamma =0.5$ and $t_3=2$. The remaining parameter is fixed at $t_1=1$. In the absence of N3 hopping, Figure 3a reveals three distinct regions of Chern insulators: a pink region with a Chern number of $C=+1$, a blue region with Chern number $C=-1$, and a white region representing a trivial topological state with $C=0$. In this scenario, the system reduces to the case described in Ref. [24], exhibiting a phase diagram analogous to the well-known Haldane model [20]. However, upon introducing N3 hopping with $t_3=2$ and the on-site energy $\gamma =0$, significant changes in the Chern insulating regions are observed in Figure 3b. These regions now exhibit distinct Chern numbers: $C=+2$ (cyan region), $C=-2$ (red region), $C=+1$ (pink region), $C=-1$ (blue region), and $C=0$ (white region), respectively. It is evident that N3 hopping considerably alters the Chern numbers, but no additional topological phases emerge. When both N3 hopping and the on-site energy are included with $\gamma =0.5$ and $t_3=2$, we observe the emergence of higher Chern numbers and an additional region of topological phases. As illustrated in Figure 3c, this additional topological phase region is characterized by a Chern number of $C=+1$ and $C=-1$. It is situated between the two Chern insulating regions, specifically between the blue and cyan regions and between the pink and red regions. Thus, the introduction of N3 hopping facilitates the attainment of a large Chern number in our system, while the on-site energy $\gamma$ induces additional phase regions when $t_3$ is present.

Figure 3

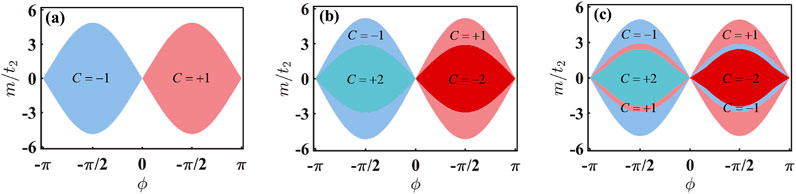
Figure 3. Phase diagrams of the two valence bands in the non-Hermitian modified Haldane model are depicted on the $m/t_2$-$\varphi$ planes for (a) $\gamma =0.5$, $t_3=0$; (b) $\gamma =0$, $t_3=2$; and (c) $\gamma =0.5$, $t_3=2$, with $t_1$ fixed at 1. The cyan and red regions represent the Chern insulating phases with $C=+2$ and $C=-2$, respectively. The pink and blue regions denote Chern insulating phases with $C=+1$ and $C=-1$, respectively. The white region signifies the conventional insulator phase with a zero Chern number.

To demonstrate the impact of N3 hopping on the topological properties of the system, we present a phase diagram of the two valence bands as a function of $m/t_2$ and $t_3$. For Figure 4a, we set $\gamma =0$; and for Figure 4b, $\gamma =0.5$. The remaining parameters are fixed at $t_1=1$ and $\varphi =-\pi /2$. In Figure 4, it is observed that in the absence of N3 hopping, a topological phase is characterized by a non-zero Chern number of $C=-1$, which persists even for the minimal value of $t_3$. With an increase in $t_3$, additional topological phases can be obtained. In Figure 4a, where the on-site energy term $\gamma$ is set to 0, three distinct regions corresponding to different Chern numbers are identified. The cyan region indicates a Chern number of $C=+2$, while the blue region corresponds to $C=-1$. These two regions represent nontrivial topological phases with non-zero Chern numbers. Conversely, the white region signifies a Chern number value of $C=0$, indicating a topologically trivial insulating phase. When the on-site energy $\gamma$ is introduced, an additional phase region emerges between the two distinct Chern insulating phases, as illustrated in Figure 4b. This new phase is characterized by a Chern number of $C=+1$, which contrasts with the phase diagram presented in Figure 4a. Notably, the introduction of non-Hermiticity leads to a transformation of the non-trivial phase characterized by a Chern number of $C=+2$ to $C=+1$. This transformation is significant as it plays a crucial role in the emergence of new regions of topological phases and in facilitating topological phase transitions that are attributed to changes in the eigenvalue spectrum. Setting the Haldane flux to $\varphi$ to $\varphi =\pi /2$ keeps the phase diagram consistent; however, the Chern numbers will experience a sign reversal. Then, we show the Chern numbers of the system as a function of $m/t_2$ for fixing the value of $t_3=2$. As depicted in Figures 4c, d, we observe a series of phase transitions. Specifically, in Figure 4c, the Chern number varies successively as $C=0$, $C=-1$, $C=2$, again $C=-1$, and ultimately returns to $C=0$. In contrast, Figure 4d reveals a different trend: the Chern number changes from $C=0$ to $C=-1$, remains at $C=+1$, progresses to $C=+2$, returns to $C=+1$, stays at $C=-1$, and finally reverts to $C=0$. In both figures, the variations in the Chern number indicate the occurrence of topological phase transitions.

Figure 4

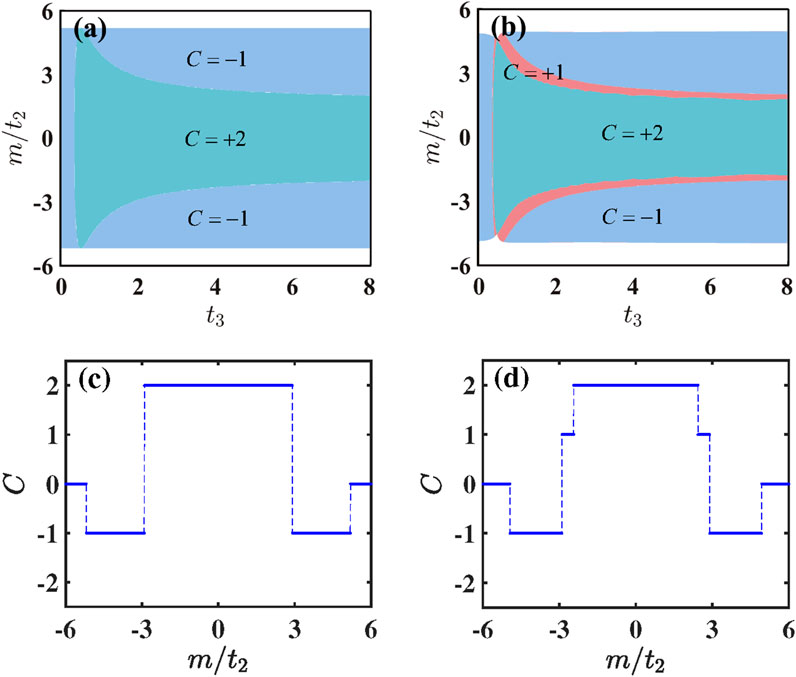
Figure 4. Phase diagrams of the two valence bands are depicted on the $m/t_2$-$t_3$ planes for (a) $\gamma =0$ and (b) $\gamma =0.5$. The cyan and blue regions represent the Chern insulating phases with $C=+2$ and $C=-1$, and while the white region signifies the conventional insulator phase with a zero Chern number. The Chern number as a function of $m/t_2$ is shown for (c) $\gamma =0$ and (d) $\gamma =0.5$. Other parameters are choosen by $t_1=1$, $t_3=2$, and $\varphi =-\pi /2$.

3.3 Topological edge states in semi-infinite honeycomb lattice

According to the bulk-boundary correspondence, edge states are expected to emerge in systems characterized by a non-zero Chern number. Previous studies, including those involving the Haldane model [20], have corroborated this behavior by demonstrating that the number of edge states corresponds to the associated Chern number. To clarify the bulk-edge correspondence and determine whether the edge states in the current system exhibit topological or trivial properties, we will analyze the characteristics of edge states in a semi-infinite honeycomb lattice ribbon geometry [16, 60–62]. This geometry is infinite in the $x$-direction and finite in the $y$-direction. The presence of edges disrupts translational symmetry in the $y$-direction while maintaining it in the $x$-direction. The sites along the y-direction are designated as $A_1,B_1,C_1,D_1,\dots ,A_N,B_N,C_N,D_N$, as illustrated in Figure 5. By applying the Fourier transform exclusively in the $x$-direction, we can readily derive the following four sets of coupled eigenvalue equations of the wave functions

$\begin{array}{ll}\hfill E_{k_x}{A}_{k_x,n}& =t_1\left[\left\{1+e^{-i{k}_x}\right\}{B}_{k,n}+D_{k,n-1}\right]\hfill \\ \hfill & +\left[-m-i\gamma +2t_2\cos \left(\varphi \right)\cos \left(k_x\right)-2t_2\sin \left(\varphi \right)\sin \left(k_x\right)\right]A_{k,n}\hfill \\ \hfill & +\left(t_2{e}^{-i\varphi }+t_2{e}^{i\varphi }{e}^{-i{k}_x}\right)\left(C_{k,n}+C_{k,n-1}\right)+t_3\left[D_{k,n}+2\cos k_x{D}_{k,n-1}\right],\hfill \\ \hfill E_{k_x}{B}_{k_x,n}& =t_1\left[\left\{1+e^{i{k}_x}\right\}{A}_{k,n}+C_{k,n}\right]\hfill \\ \hfill & +\left[m-i\gamma +2t_2\cos \left(\varphi \right)\cos \left(k_x\right)+2t_2\sin \left(\varphi \right)\sin \left(k_x\right)\right]B_{k,n}\hfill \\ \hfill & +\left(t_2{e}^{-i\varphi }+t_2{e}^{i\varphi }{e}^{i{k}_x}\right)\left(D_{k,n}+D_{k,n-1}\right)+t_3\left[C_{k,n-1}+2\cos k_x{C}_{k,n}\right],\hfill \\ \hfill E_{k_x}{C}_{k_x,n}& =t_1\left[\left\{1+e^{i{k}_x}\right\}{D}_{k,n}+B_{k,n}\right]\hfill \\ \hfill & +\left[-m+i\gamma +2t_2\cos \left(\varphi \right)\cos \left(k_x\right)-2t_2\sin \left(\varphi \right)\sin \left(k_x\right)\right]C_{k,n}\hfill \\ \hfill & +\left(t_2{e}^{i\varphi }+t_2{e}^{-i\varphi }{e}^{i{k}_x}\right)\left(A_{k,n}+A_{k,n+1}\right)+t_3\left[B_{k,n+1}+2\cos k_x{B}_{k,n}\right],\hfill \\ \hfill E_{k_x}{D}_{k_x,n}& =t_1\left[\left\{1+e^{-i{k}_x}\right\}{B}_{k,n}+A_{k,n+1}\right]\hfill \\ \hfill & +\left[m+i\gamma +2t_2\cos \left(\varphi \right)\cos \left(k_x\right)+2t_2\sin \left(\varphi \right)\sin \left(k_x\right)\right]D_{k,n}\hfill \\ \hfill & +\left(t_2{e}^{i\varphi }+t_2{e}^{-i\varphi }{e}^{-i{k}_x}\right)\left(B_{k,n}+B_{k,n+1}\right)+t_3\left[A_{k,n}+2\cos k_x{A}_{k,n+1}\right].\hfill \end{array}(7)$

Figure 5

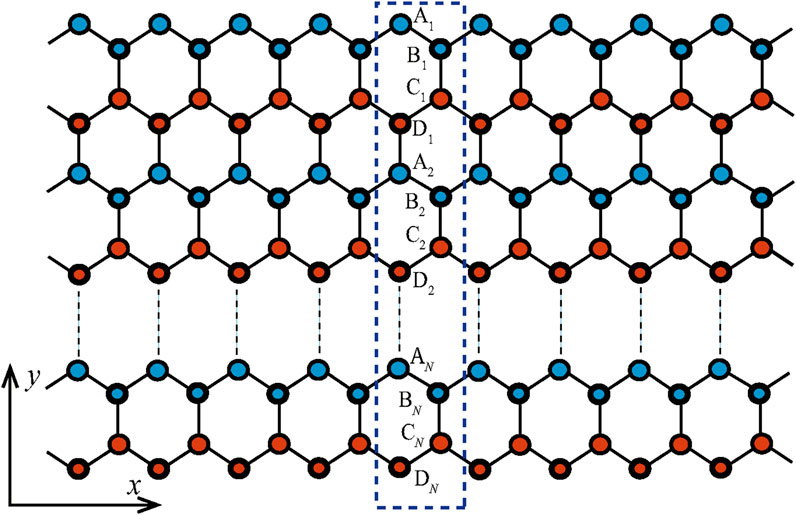
Figure 5. Schematic of a semi-infinite ribbon with zigzag edges to be finite along the $y$ direction and infinite along the $x$ direction. The dashed-lined rectangle containing $N=160$ unit cells along the $y$-direction.

where $n$ is an integer ranging from 1 to $N$ and $N$ represents the total number of unit cells along the $y$-direction with $N=160$. The coefficients $A_{k,n}$, $B_{k,n}$, $C_{k,n}$, and $D_{k,n}$ correspond to the respective wave functions. By solving Equation 7, we can obtain the energy eigenvalue spectra of a semi-infinite ribbon as a function of momentum $k_x$, as illustrated in Figures 6a–d. We set the value of the N3 hopping parameter for (a) $t_3=0.1$, (b) $t_3=0.6$, (c) $t_3=1.4$, and (d) $t_3=2$. The other parameters are fixed at $t_1=1$, $\gamma =0.5$, and $\varphi =-\pi /2$. In Figure 6a, there are two edge states along the zigzag edges ($x$ axis) of the ribbon. These two edge states continuously connect the bulk bands as $k_x$ changes, propagating along opposite edges of the ribbon. This indicates that the system is in a topological state, characterized by gapped bulk states and gapless edge states that traverse the energy gap. This observation is consistent with the Chern number phase diagram, where the Chern number is $C=-1$. As $t_3$ increases, the band gap closes and subsequently reopens. We observe the presence of two pairs of topologically protected gapless edge states in the energy gap, with each zigzag edge of the ribbon hosting two independently propagating edge states, as shown in Figure 6b. This result aligns with the phase diagram, where $t_3=0.6$ corresponds to a phase with a Chern number of $C=2$. With the further increase of $t_3$, the number of edge states changes again. In both Figures 6c, d, there are two edge states traversing the energy gap, each propagating along a zigzag edge and corresponding to Chern numbers $C=1$ and $C=-1$, respectively. Additionally, we conduct a finite-size effect analysis on the edge states of the semi-infinite band. Our findings indicate that as the number of lattice sites along the $y$-direction increases, the spectrum of the edge states becomes increasingly dense. However, this densification does not compromise the robustness of the edge states nor does it induce skin effects. We present the imaginary part of the energy eigenvalues, represented by the color bar. Due to the truncation of the lattice in real space, the symmetry of Equations 4, 5 is broken, disrupting the reality and orthogonality of the system’s eigenstates. Consequently, the edge state energies exhibit significant imaginary components, whereas the energies of most bulk states remain nearly real.

Figure 6

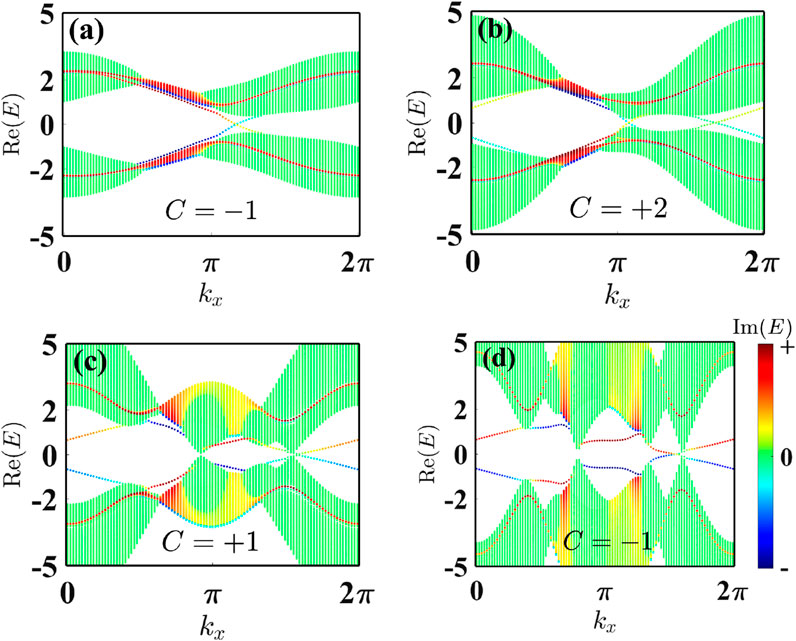
Figure 6. Energy spectra of a semi-infinite ribbon as a function of dimensionless momentum $k$ with $k_x$ are shown for (a) $t_3=0.1$, (b) $t_3=0.6$, (c) $t_3=1.4$, and (d) $t_3=2$. The other parameters are chosen by $t_1=1$, $m/t_2=3$, $\gamma =0.5$, and $\varphi =-\pi /2$. The colorbar represents the imaginary part of the energy eigenvalues.

4 Conclusion

We have constructed a non-Hermitian modified Haldane model and analyzed its symmetries, demonstrating that the system satisfies both the pseudo-Hermitian and anti-$\mathcal{P}\mathcal{T}$ symmetries. This finding indicates the presence of pure real regions within the energy spectrum. Furthermore, we have obtained two distinct phase diagrams in the $m/t_2$-$\varphi$ plane and the $m/t_2$-$t_3$ plane by computing the Chern numbers. Our results indicate that the system can support higher Chern numbers of $\pm 2$ when $t_3$ is present. More importantly, by introducing gain and loss to the on-site energy, the system reveals additional phases between the two Chern insulating phases, characterized by Chern numbers of $\pm 1$. To substantiate the existence of these topological phases, we employed a semi-infinite honeycomb lattice geometry to investigate the characteristics of topological edge states. We found that the edge states span the energy gap and continuously connect the bulk bands, exhibiting topological properties consistent with the Chern number. Additionally, the truncation of the lattice in real space disrupts the reality and orthogonality of the eigenstates, resulting in significant imaginary components in the edge state energies. In contrast, the energies of most bulk states remain nearly real. Our work provides a deeper understanding of the impact of long-range hopping on the topological phases of non-Hermitian modified Haldane models.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

X-CC: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review and editing. X-FN: Formal Analysis, Software, Writing – original draft. Y-W-YL: Formal Analysis, Software, Writing – original draft. W-XC: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by National Natural Science Foundation of China (Grant No. 62301472) and Jilin Provincial Natural Science Foundation of China (Grant No. YDZJ202201ZYTS298).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. von Klitzing K. The quantized Hall effect. Rev Mod Phys (1986) 58:519–31. doi:10.1103/RevModPhys.58.519

CrossRef Full Text | Google Scholar

2. Hasan MZ, Kane CL. Colloquium: topological insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/RevModPhys.82.3045

CrossRef Full Text | Google Scholar

3. Qi XL, Zhang SC. Topological insulators and superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

4. Zhang Y, Kartashov YV, Ferrando A. Interface states in polariton topological insulators. Phys Rev A (2019) 99:053836. doi:10.1103/PhysRevA.99.053836

CrossRef Full Text | Google Scholar

5. Dey B, Kapri P, Pal O, Ghosh TK. Unconventional phases in a Haldane model of dice lattice. Phys Rev B (2020) 101:235406. doi:10.1103/PhysRevB.101.235406

CrossRef Full Text | Google Scholar

6. Denner MM, Skurativska A, Schindler F, Fischer MH, Thomale R, Bzdušek T, et al. Exceptional topological insulators. Nat Commun (2021) 12:5681. doi:10.1038/s41467-021-25947-z

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Mai P, Feldman BE, Phillips PW. Topological Mott insulator at quarter filling in the interacting Haldane model. Phys Rev Res (2023) 5:013162. doi:10.1103/PhysRevResearch.5.013162

CrossRef Full Text | Google Scholar

8. Alase A, Feder DL. Generating and detecting topological phases with higher Chern number. Phys Rev A (2021) 103:053305. doi:10.1103/PhysRevA.103.053305

CrossRef Full Text | Google Scholar

9. Łącki M, Zakrzewski J, Goldman N. A dark state of Chern bands: designing flat bands with higher Chern number. SciPost Phys (2021) 10:112. doi:10.21468/SciPostPhys.10.5.112

CrossRef Full Text | Google Scholar

10. Wang B, Zhou X, Lin H, Bansil A. Higher-order topological insulator phase in a modified Haldane model. Phys Rev B (2021) 104:L121108. doi:10.1103/PhysRevB.104.L121108

CrossRef Full Text | Google Scholar

11. Chang ZW, Hao WC, Liu X. Topological defects in Haldane model and higher Chern numbers in monolayer graphene. J Phys Condens Matter (2022) 34:485502. doi:10.1088/1361-648X/ac98fc

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Mondal S, Basu S. Topological phases of a semi-Dirac Chern insulator in the presence of extended range hopping. Phys Rev B (2022) 105:235441. doi:10.1103/PhysRevB.105.235441

CrossRef Full Text | Google Scholar

13. Li Q, Wu YJ, Yu J, He J. Phase driven topological states in correlated Haldane model on a honeycomb lattice. J Phys Condens Matter (2022) 34:275602. doi:10.1088/1361-648X/ac6851

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Geng WJ, Wang YJ, Zhang ZX, Cao J, Cui WX, Wang HF. Separable zero energy topological edge states and nonzero energy gap states in the nonreciprocal Su-Schrieffer-Heeger model. Phys Rev B (2023) 108:144109. doi:10.1103/PhysRevB.108.144109

CrossRef Full Text | Google Scholar

15. Jia W, Zhou XC, Zhang L, Zhang L, Liu XJ. Unified characterization for higher-order topological phase transitions. Phys Rev Res (2023) 5:L022032. doi:10.1103/PhysRevResearch.5.L022032

CrossRef Full Text | Google Scholar

16. He WX, Mondaini R, Luo HG, Wang X, Hu S. Phase transitions in the Haldane-Hubbard model. Phys Rev B (2024) 109:035126. doi:10.1103/PhysRevB.109.035126

CrossRef Full Text | Google Scholar

17. Yang F, Ling YX, Yan XH, Qi L, Zhang X, Han Y, et al. Porous Haldane model: topological phase transitions and flat bands. J Phys Condens Matter (2024) 37:075501. doi:10.1088/1361-648X/ad9723

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Guan JH, Lou WK, Chang K. Topological hidden phase transition in honeycomb bilayers with a high Chern number. Phys Rev B (2024) 110:165303. doi:10.1103/PhysRevB.110.165303

CrossRef Full Text | Google Scholar

19. Cheng S, Jiang Y, Xianlong G. Bulk-edge correspondence for the nonlinear eigenvalues problem of the Haldane model. Phys Rev B (2024) 109:134201. doi:10.1103/PhysRevB.109.134201

CrossRef Full Text | Google Scholar

20. Haldane FDM. Model for a Quantum Hall Effect without Landau Levels: condensed-matter realization of the “parity anomaly”. Phys Rev Lett (1988) 61:2015–8. doi:10.1103/PhysRevLett.61.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Chang CZ, Zhang J, Feng X, Shen J, Zhang Z, Guo M, et al. Experimental observation of the Quantum Anomalous Hall Effect in a magnetic topological insulator. Science (2013) 340:167–70. doi:10.1126/science.1234414

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Gong Z, Ashida Y, Kawabata K, Takasan K, Higashikawa S, Ueda M. Topological phases of non-Hermitian systems. Phys Rev X (2018) 8:031079. doi:10.1103/PhysRevX.8.031079

CrossRef Full Text | Google Scholar

23. Xue H, Wang Q, Zhang B, Chong YD. Non-Hermitian Dirac Cones. Phys Rev Lett (2020) 124:236403. doi:10.1103/PhysRevLett.124.236403

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Teo HT, Xue H, Zhang B. Topological phase transition induced by gain and loss in a photonic Chern insulator. Phys Rev A (2022) 105:053510. doi:10.1103/PhysRevA.105.053510

CrossRef Full Text | Google Scholar

25. Li Y, Liang C, Wang C, Lu C, Liu YC. Gain-loss-induced hybrid skin-topological effect. Phys Rev Lett (2022) 128:223903. doi:10.1103/PhysRevLett.128.223903

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sun J, Li CA, Feng S, Guo H. Hybrid higher-order skin-topological effect in hyperbolic lattices. Phys Rev B (2023) 108:075122. doi:10.1103/PhysRevB.108.075122

CrossRef Full Text | Google Scholar

27. Eleuch H, Rotter I. Open quantum systems with loss and gain. Int J Theor Phys (2015) 54:3877–88. doi:10.1007/s10773-014-2375-3

CrossRef Full Text | Google Scholar

28. Ashida Y, Gong Z, Ueda M. Non-Hermitian physics. Adv Phys (2020) 69:249–435. doi:10.1080/00018732.2021.1876991

CrossRef Full Text | Google Scholar

29. Leykam D, Bliokh KY, Huang C, Chong YD, Nori F. Edge modes, degeneracies, and topological numbers in non-Hermitian systems. Phys Rev Lett (2017) 118:040401. doi:10.1103/PhysRevLett.118.040401

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kawabata K, Shiozaki K, Ueda M, Sato M. Symmetry and topology in non-Hermitian physics. Phys Rev X (2019) 9:041015. doi:10.1103/PhysRevX.9.041015

CrossRef Full Text | Google Scholar

31. Fan A, Liang SD. Complex energy plane and topological invariant in non-Hermitian systems. Front Phys (2022) 17:33501. doi:10.1007/s11467-021-1122-5

CrossRef Full Text | Google Scholar

32. Brody DC. Biorthogonal quantum mechanics. J Phys A: Math Theor (2013) 47:035305. doi:10.1088/1751-8113/47/3/035305

CrossRef Full Text | Google Scholar

33. Bender CM, Boettcher S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys Rev Lett (1998) 80:5243–6. doi:10.1103/PhysRevLett.80.5243

CrossRef Full Text | Google Scholar

34. Bender CM, Brody DC, Jones HF. Complex extension of quantum mechanics. Phys Rev Lett (2002) 89:270401. doi:10.1103/PhysRevLett.89.270401

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Guo A, Salamo GJ, Duchesne D, Morandotti R, Volatier-Ravat M, Aimez V, et al. Observation of PT-symmetry breaking in complex optical potentials. Phys Rev Lett (2009) 103:093902. doi:10.1103/PhysRevLett.103.093902

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Song F, Yao S, Wang Z. Non-Hermitian skin effect and chiral damping in open quantum systems. Phys Rev Lett (2019) 123:170401. doi:10.1103/PhysRevLett.123.170401

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Okugawa R, Takahashi R, Yokomizo K. Second-order topological non-Hermitian skin effects. Phys Rev B (2020) 102:241202. doi:10.1103/PhysRevB.102.241202

CrossRef Full Text | Google Scholar

38. Yi Y, Yang Z. Non-Hermitian skin modes induced by on-site dissipations and chiral tunneling effect. Phys Rev Lett (2020) 125:186802. doi:10.1103/PhysRevLett.125.186802

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Chen WC, Liu R, Wang YF, Gong CD. Topological quantum phase transitions and topological flat bands on the star lattice. Phys Rev B (2012) 86:085311. doi:10.1103/PhysRevB.86.085311

CrossRef Full Text | Google Scholar

40. Yang S, Gu ZC, Sun K, Das Sarma S. Topological flat band models with arbitrary Chern numbers. Phys Rev B (2012) 86:241112. doi:10.1103/PhysRevB.86.241112

CrossRef Full Text | Google Scholar

41. Harari G, Bandres MA, Lumer Y, Rechtsman MC, Chong YD, Khajavikhan M, et al. Topological insulator laser: theory. Science (2018) 359:eaar4003. doi:10.1126/science.aar4003

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Luo XW, Zhang C. Higher-Order topological corner states induced by gain and loss. Phys Rev Lett (2019) 123:073601. doi:10.1103/PhysRevLett.123.073601

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Ozawa T, Price HM, Amo A, Goldman N, Hafezi M, Lu L, et al. Topological photonics. Rev Mod Phys (2019) 91:015006. doi:10.1103/RevModPhys.91.015006

CrossRef Full Text | Google Scholar

44. Kremer M, Biesenthal T, Maczewsky LJ, Heinrich M, Thomale R, Szameit A. Demonstration of a two-dimensional $\mathcal{P}\mathcal{T}$-symmetric crystal. Nat Commun (2019) 10:435. doi:10.1038/s41467-018-08104-x

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Song AY, Sun XQ, Dutt A, Minkov M, Wojcik C, Wang H, et al. PT-symmetric topological edge-gain effect. Phys Rev Lett (2020) 125:033603. doi:10.1103/PhysRevLett.125.033603

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Yan Q, Zhao B, Zhou R, Ma R, Lyu Q, Chu S, et al. Advances and applications on non-Hermitian topological photonics. Nanophotonics (2023) 12:2247–71. doi:10.1515/nanoph-2022-0775

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Zhang DW, Zhu YQ, Zhao Y, Yan H, Zhu SL. Topological quantum matter with cold atoms. Adv Phys (2018) 67:253–402. doi:10.1080/00018732.2019.1594094

CrossRef Full Text | Google Scholar

48. Li L, Lee CH, Gong J. Topological switch for non-Hermitian skin effect in cold-atom systems with loss. Phys Rev Lett (2020) 124:250402. doi:10.1103/PhysRevLett.124.250402

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Xu ZC, Zhou Z, Cheng E, Lang LJ, Zhu SL. Gain/loss effects on spin-orbit coupled ultracold atoms in two-dimensional optical lattices. Sci China Phys Mech Astron (2022) 65:283011. doi:10.1007/s11433-022-1898-7

CrossRef Full Text | Google Scholar

50. Luo K, Feng J, Zhao YX, Yu R. Nodal manifolds bounded by exceptional points on non-Hermitian honeycomb lattices and electrical-circuit realizations arXiv: mesoscale and nanoscale physics (2018) arXiv:1810.09231. doi:10.48550/arXiv.1810.09231

CrossRef Full Text | Google Scholar

51. Ezawa M. Electric circuits for non-Hermitian Chern insulators. Phys Rev B (2019) 100:081401. doi:10.1103/PhysRevB.100.081401

CrossRef Full Text | Google Scholar

52. Wu J, Huang X, Yang Y, Deng W, Lu J, Deng W, et al. Non-Hermitian second-order topology induced by resistances in electric circuits. Phys Rev B (2022) 105:195127. doi:10.1103/PhysRevB.105.195127

CrossRef Full Text | Google Scholar

53. Zhang X, Wu C, Yan M, Liu N, Wang Z, Chen G. Observation of continuum Landau modes in non-Hermitian electric circuits. Nat Commun (2024) 15:1798. doi:10.1038/s41467-024-46122-0

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Mostafazadeh A. Pseudo-Hermitian representation of quantum mechanics. Int J Geom Meth Mod Phys (2010) 7:1191–306. doi:10.1142/S0219887810004816

CrossRef Full Text | Google Scholar

55. He P, Zhu YQ, Wang JT, Zhu SL. Quantum quenches in a pseudo-Hermitian Chern insulator. Phys Rev A (2023) 107:012219. doi:10.1103/PhysRevA.107.012219

CrossRef Full Text | Google Scholar

56. Starkov GA, Fistul MV, Eremin IM. Formation of exceptional points in pseudo-Hermitian systems. Phys Rev A (2023) 108:022206. doi:10.1103/PhysRevA.108.022206

CrossRef Full Text | Google Scholar

57. El-Ganainy R, Makris KG, Khajavikhan M, Musslimani ZH, Rotter S, Christodoulides DN. Non-Hermitian physics and PT symmetry. Nat Phys (2018) 14:11–9. doi:10.1038/nphys4323

CrossRef Full Text | Google Scholar

58. Ni X, Smirnova D, Poddubny A, Leykam D, Chong Y, Khanikaev AB. PT phase transitions of edge states at PT symmetric interfaces in non-Hermitian topological insulators. Phys Rev B (2018) 98:165129. doi:10.1103/PhysRevB.98.165129

CrossRef Full Text | Google Scholar

59. Cen J, Saxena A. Anti-PT symmetric qubit: decoherence and entanglement entropy. Phys Rev A (2022) 105:022404. doi:10.1103/PhysRevA.105.022404

CrossRef Full Text | Google Scholar

60. Ablowitz MJ, Curtis CW, Ma YP. Linear and nonlinear traveling edge waves in optical honeycomb lattices. Phys Rev A (2014) 90:023813. doi:10.1103/PhysRevA.90.023813

CrossRef Full Text | Google Scholar

61. Ling HY, Kain B. Topological study of a Bogoliubov–de Gennes system of pseudo-spin-1/2 bosons with conserved magnetization in a honeycomb lattice. Phys Rev A (2022) 105:023319. doi:10.1103/PhysRevA.105.023319

CrossRef Full Text | Google Scholar

62. Ren B, Wang H, Belić MR, Li Y, Zhu X, Zhang Y. Zero-energy edge states and solitons in strained photonic graphene. Phys Rev A (2023) 107:043504. doi:10.1103/PhysRevA.107.043504

CrossRef Full Text | Google Scholar