Dynamic analysis of the fractal nonlinear oscillators with coordinate-dependent mass

The dynamic behavior of nonlinear oscillators can be researched more accurately in the micro-scale. In this paper, a modified nonlinear oscillator with coordinate-dependent mass by He’s fractal derivative is first given. Then, the energy balance method and modified harmonic balance method are utilized to constructed the first-order and second-order approximate solutions of the fractal model. Next, two sets of parameters are choosen, the obtained numerical solution are compared with the Runge-kuta (RK) solution, and the results demonstrate that the second-order approximate solution is more accurate. In addition, by comparing the solutions under the different fractal dimensions, one can be found that the fractal dimension does not change global properties of the oscillators, but the vibration behaviors gradually accelerates with the increase of the fractal dimension, which means that we can study the oscillation behavior more clearly in the micro-scale.

1 Introduction

Nonlinear oscillations have significant applications in physics, mechanics, and other engineering problems. Typically, differential equations involved in these engineering and physical phenomena are nonlinear. However, methods for solving linear differential equations are easy to construct and have been thoroughly studied. Conversely, computational methods of nonlinear differential equations (NDEs) are relatively less available, and it is difficult to obtain exact solutions, numerical approximations are frequently achieved. Currently, many mathematicians and physicists have proposed a variety of analytical methods for nonlinear problems, such as Homotopy Perturbation Method [1, 2], Adomian decomposition method [3, 4], Variational iteration method [5–7], Hamiltonian-based method [8, 9], Energy Balance Method [10, 11], Harmonic Balance Method [12, 13], Amplitude Frequency Formulation [14, 15] and so on for computing NDEs.

Recently, Lev et al investigate the properties of nonlinear oscillator withcoordinate-dependent mass, and discussed the order parameter-space-space-time duality and phase trajectories [16], which has the folowing form

$\left(1+\epsilon x^2\right)D_{tt}x+\epsilon x{\left(D_{t}x\right)}^2-x\left(1-x^2\right)=0,(1.1)$

with subject to the initial conditions

$x\left(0\right)=A,D_{t}x\left(0\right)=0,(1.2)$

where $D_{t}x$ and $D_{tt}x$ are denote the first and second derivative of $x$ with respect to time $t$, respectively.

Research has shown that such nonlinear oscillators can describe phase transitions in physics and play an important role in quark confinement, cosmos-logical model, and spinodal decomposition [16]. Subsequently, many scholars have systematically studied the numerical solution of the model. Wu et al. applied the Homotopy perturbation method to solve the nonlinear oscillator with nolinear or negative linear term, which the negative coefficient is expanded by adopting the parameter expansion method, and obtained the existence condition for the periodic solutions [17]. The frequency-amplitude formulation with ${\omega }^4$ is used to this nonlinear oscillator, the results are identical with those obtained by Homotopy perturbation method, which proves the validity of the frequency-amplitude formulation with ${\omega }^4$ [18]. Wang et al combined He’s frequency–amplitude formulation and average residuals to solve the nonlinear oscillation model with negative term [19]. Very recently, based on fractional complex transform and global residue harmonic balance method, Lu et al researched the fractional order form of the nonlinear oscillators with coordinate-dependent mass, numerical results show that this method is robust and effective [20].

Theoretically, it is necessary to investigate the physical phenomena of the nonlinear oscillators from different time scales, because the exact nonlinear vibrational behavior can be captured at the microscopic scale. Reviewing the two-scale theory proposed by He [21, 22], it can describe the relation of nonlinear systems between different scales. Moreover, He proposed a simple fractal derivative by variational iteration method and clarified its application to the interpretation of polar bear hair in [23]. Subsequently, inspired by the two-scale and He’s fractal derivatives, researches of nonlinear oscillators for the fractal corrections can be found in many literatures [24–27].

In this paper, we make fractal corrections to Equation 1.1 based on two-scale theory and fractal derivatives to study the microscopic scale behavior. The fractal version of Equation 1.1 can be written in the following form

$\left(1+\epsilon x^2\right)D_{tt}^{\alpha }x+\epsilon x{\left(D_t^{\alpha }x\right)}^2-x\left(1-x^2\right)=0,(1.3)$

with subject to the initial conditions

$x\left(0\right)=A,D_t^{\alpha }x\left(0\right)=0,(1.4)$

in whihch $D_t^{\alpha }x$ and $D_{tt}^{\alpha }x$ are He’s fractal derivatives of $x$ with respect to time $t$ that is given by

$D_t^{\alpha }x=\mathrm{\Gamma }\left(1+\alpha \right)\underset{\genfrac{}{}{0pt}{}{t-t_0=\mathrm{\Delta }t}{\mathrm{\Delta }t\ne 0}}{\lim }\frac{u\left(t\right)-u\left(t_0\right)}{{\left(t-t_0\right)}^{\alpha }},$

and the second-order fractal derivative $D_{tt}^{\alpha }x$ satisfies the chain rule $D_{tt}^{\alpha }x=D_t^{\alpha }{D}_t^{\alpha }x$.

The fractal two-scale transform is an effective tool for studying fractal models [27]. Typically, for a given fractal problem, fractal two-scale transformation can transform the fractal model into a continuous problem. Since it was proposed, it attracted the attention of many scholars. Based on the transform $T=t^{\alpha }$, Equations 1.3–1.4 can be converted to

$\left(1+\epsilon x^2\right)D_{TT}x+\epsilon x{\left(D_{T}x\right)}^2-x\left(1-x^2\right)=0,(1.5)$

and the initial conditions are

$x\left(0\right)=A,D_{T}x\left(0\right)=0.(1.6)$

The layout of this paper is given as follows: In Section 2, the energy balance method is adopted to solve the fractal problem (1.3). In Section 3, we succesfully construct first- and second-order approximation solution of the fractal model by using the Modified Harmonic Balance Method. In Section 4, we present numerical experiments and analyze the dynamic behavior of this fractal nonlinear oscillator. In addition, some conclusive remarks are placed in the last section.

2 The energy balance method

The energy balance method is usually based on the variational principle and is an effective way for solving nonlinear oscillation problems. In order to employ the energy balance method, the variational principle of Equation 1.5 should be established at the first time. By using the semi-inverse method, Equation 1.5 has the following variational principle

$\begin{array}{cc}\hfill J\left(u\right)& ={\int }_0^{\frac{T}{4}}\left\{\frac{1}{2}{\left(D_{T}x\right)}^2\left(1+\epsilon x^2\right)-\left(\frac{1}{4}{x}^4-\frac{1}{2}{x}^2\right)\right\}dT\hfill \\ \hfill & ={\int }_0^{\frac{T}{4}}\left(D-S\right)dT,\hfill \end{array}(2.1)$

in which $D$ and $S$ indicate the kinetic energy and potential energy, respectively. Their specific forms are as follows

$\begin{array}{cc}\hfill D& =\frac{1}{2}{\left(D_{T}x\right)}^2\left(1+\epsilon x^2\right),\hfill \\ \hfill S& =\frac{1}{4}{x}^4-\frac{1}{2}{x}^2.\hfill \end{array}(2.2)$

Thus, the Hamiltonian invariant can be written as

$\hslash =D+S=\frac{1}{2}{\left(D_{T}x\right)}^2\left(1+\epsilon x^2\right)-\frac{1}{2}{x}^2+\frac{1}{4}{x}^4.(2.3)$

In view of the energy conservation theory, the Hamiltonian invariant remains constant throughout the vibration process, which obtains

$\hslash =D+S=\frac{1}{2}{\left(D_{T}x\right)}^2\left(1+\epsilon x^2\right)-\frac{1}{2}{x}^2+\frac{1}{4}{x}^4={\hslash }_0.(2.4)$

Supposing that the solution of Equation 1.1 has the following form

$x_1=Acos\left({\omega }_{0}T\right).(2.5)$

According to the initial condition Equation 1.2, substituting it into Equation 2.4, we have

${\hslash }_0=-\frac{1}{2}{A}^2+\frac{1}{4}{A}^4.(2.6)$

Then Equation 2.4 can be rewritten as

$\hslash -{\hslash }_0=\frac{1}{2}{\left(D_{T}x\right)}^2\left(1+\epsilon x^2\right)-\frac{1}{2}{x}^2+\frac{1}{4}{x}^4-\left(\frac{1}{4}{A}^4-\frac{1}{2}{A}^2\right)=0.(2.7)$

Substituting Equation 2.5 into Equation 2.7 and setting ${\omega }_{0}T=\frac{\pi }{4}$, one has

$\frac{1}{4}{A}^2{\varpi }^2\left(1+\frac{\epsilon }{2}{A}^2\right)-\frac{1}{4}{A}^2+\frac{1}{16}{A}^4-\left(\frac{1}{4}{A}^4-\frac{1}{2}{A}^2\right)=0.(2.8)$

By simplifying the above equation yields

${\varpi }^2\left(1+\frac{\epsilon }{2}{A}^2\right)=-1+\frac{3}{4}{A}^2,(2.9)$

and the frequency can be easily obtained from Equation 2.9

$\varpi =\sqrt{\frac{\frac{3}{4}{A}^2-1}{1+\frac{\epsilon }{2}{A}^2}}=\sqrt{\frac{3A^2-4}{2A^2\epsilon +4}}>0.(2.10)$

Therefore, the solution of Equation 1.1 is

$x\left(T\right)=A\cos \left(\sqrt{\frac{3A^2-4}{2A^2\epsilon +4}}T\right),(2.11)$

which is in complete agreement with the references [17–19]. On account of Equation 1.1, we can acquire the solution of Equation 1.3 as

$x\left(T\right)=A\cos \left(\sqrt{\frac{3A^2-4}{2A^2\epsilon +4}}{t}^{\alpha }\right).(2.12)$

3 The modified harmonic balance method

Here, we assume that the first order approximate solution has the following form

$x_1=Acos\left({\omega }_{1}T\right).(3.1)$

Substituting Equation 3.1 into Equation 1.1 and taking the coefficient of term $cos({\omega }_{1}T)$ as zero, the algebraic equation is given by

$-\frac{1}{2}{A}^3{\omega }_1^2\epsilon -A{\omega }_1^2+\frac{3}{4}{A}^3-A=0.(3.2)$

From Equation 3.2, we acquire the first-order approximate frequency

${\omega }_1=\sqrt{\frac{3A^2-4}{2A^2\epsilon +4}}.(3.3)$

Thus the first-order approximation analytical solution of Equation 1.1 is

$x_1=Acos\left(\sqrt{\frac{3A^2-4}{2A^2\epsilon +4}}T\right),(3.4)$

and this result is fully consistent with Equation 2.12.

Then we investigate the second-order approximation solution and the corresponding form can be written as

$x_2=A\cos \left({\omega }_{2}T\right)+A\lambda \left(\cos \left(3{\omega }_{2}T\right)-\cos \left({\omega }_{2}T\right)\right).(3.5)$

Substituting Equation 3.5 into Equation 1.1 and collectiong the coefficients of $cos({\omega }_{2}T)$ and $cos(3{\omega }_{2}T)$, one has.

$\left(4A^2{\omega }_2^2\epsilon -\frac{3}{2}{A}^2\right){\lambda }^3+\left(-\frac{7}{2}{A}^2{\omega }_2^2\epsilon +\frac{9}{4}{A}^2\right){\lambda }^2+\left({\omega }_2^2+1-\frac{3A^2}{2}\right)\lambda (3.6)$

$\begin{array}{ll}\hfill & -\frac{A^2{\omega }_2^2\epsilon }{2}-{\omega }_2^2-1+\frac{3A^2}{4}=0,\hfill \\ \hfill & \times \hspace{0.17em}\left(-9A^2{\omega }_2^2\epsilon +2A^2\right){\lambda }^3+\left(\frac{17}{2}{A}^2{\omega }_2^2\epsilon -\frac{9}{4}{A}^2\right){\lambda }^2\hfill \\ \hfill & +\left(-\frac{7}{2}{A}^2{\omega }_2^2\epsilon +\frac{3}{4}{A}^2-9{\omega }_2^2-1\right)\lambda \hfill \end{array}(3.7)$

$-\frac{A^2{\omega }_2^2\epsilon }{2}+\frac{A^2}{4}=0.$

By simplification Equation 3.6, we have

${\omega }_2=\sqrt{\frac{6A^2{\lambda }^3-9A^2{\lambda }^2+6A^2\lambda -3A^2-4\lambda +4}{16A^2\epsilon {\lambda }^3-14A^2\epsilon {\lambda }^2-2A^2\epsilon +4\lambda -4}}.(3.8)$

Replacing Equation 3.8 with ${\omega }_2^2$ in Equation 3.7, the followig nonlinear algebraic equation in terms of $\lambda$ can be derived

$\begin{array}{cc}\hfill & -88A^4\epsilon {\lambda }^6+272A^4\epsilon {\lambda }^5+\left(-432A^4\epsilon +80A^2\epsilon -184A^2\right){\lambda }^4\hfill \\ \hfill & +\left(384A^4\epsilon -224A^2\epsilon +256A^2\right){\lambda }^3+\left(-164A^4\epsilon +192A^2\epsilon -168A^2+128\right){\lambda }^2\lambda \hfill \\ \hfill & +\left(24A^4\epsilon -40A^2\epsilon +100A^2-128\right)+4A^4\epsilon -8A^2\epsilon -4A^2=0.\hfill \end{array}(3.9)$

The higher order terms of $\lambda$ more than second order has almost no effect on $\lambda$. Thus, more than second order of $\lambda$ can be ignored, one has

$v\left(8A^2\epsilon +4A^2-4A^4\epsilon -\left(-164A^4\epsilon +192A^2\epsilon -168A^2+128\right){\lambda }^2\right)=\lambda ,(3.10)$

in which

$v=\frac{1}{24A^4\epsilon -40A^2\epsilon +100A^2-128}.(3.11)$

The power series solution of Equation 3.10 with respect to $v$ is

$\lambda =a_{1}v+a_2{v}^3+\cdots ,(3.12)$

where

$\begin{array}{cc}\hfill a_1& =-4A^4\epsilon +8A^2\epsilon +4A^2,\hfill \\ \hfill a_2& =64\left(41A^4\epsilon -48A^2\epsilon +42A^2-32\right)A^4{\left(A^2\epsilon -2\epsilon -1\right)}^2.\hfill \end{array}$

Next, inserting Equation 3.12 into the $\lambda$ of Equation 3.8, a second-order approximate frequency can be easily ontained.

Thus, the second-order approximation solution of Equation 1.5 is $x_2=A\cos ({\omega }_{2}T)+A\lambda (\cos (3{\omega }_{2}T)-\cos ({\omega }_{2}T))$ where $\lambda$ and ${\omega }_2$ are provided by the equations above.

4 Numerical simulation

In this section, we take the following parameters to verify the effectiveness of these two methods for the nonlinear oscillations with fractal correction.

For the parameters $A=2$ and $\epsilon =0.0001$, we calculate the numerical solutions for the first-order, second-order, and Runge-Kutta methods at different $t$ with $\alpha =1$, and provided their relative errors compared to the Runge-Kutta (RK) solution. From the last two columns of Table.1, it can be seen that although the first-order approximate solution seems to be sufficiently accurate, the relative error of the second-order approximate solution compared to the RK solution is almost one-fifth of the relative error of the first-order approximate solution to the RK solution. This indicates that the second-order solution constructed by the modified harmonic balance method has higher accuracy.

Table 1

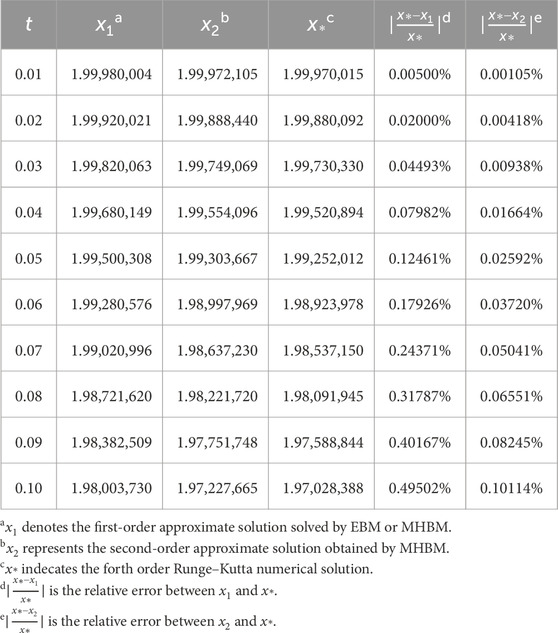
Table 1. First- and second-order approximate solutions of Equation 1.3 compared with numerical solution ($\alpha =1$, $A=2$ and $\epsilon =0.0001$).

Figure 1 further validates this viewpoint. Figure 1A presents the solution curves for three methods, showing that the second-order approximate solution almost coincides with the RK curve, whereas the first-order approximate solution, represented by the blue curve, has noticeable differences compared to the red and green curves. Figure 1B displays the corresponding phase plane trajectories for the three methods within one period, revealing that the phase plane trajectories of the second-order approximate solution and the RK solution nearly identical.

Figure 1

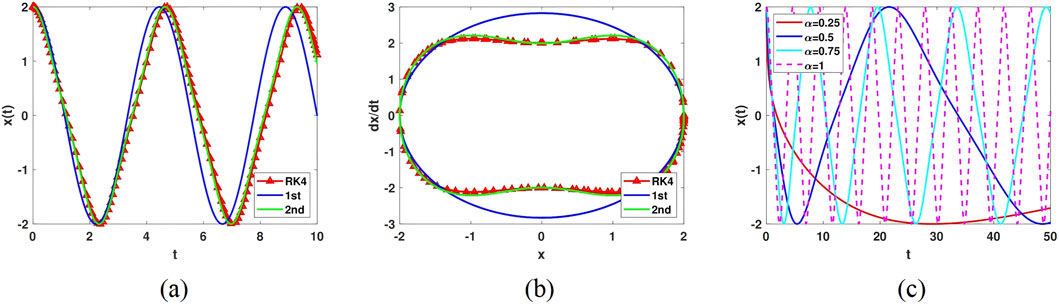
Figure 1. The dynamic behaviours of Equation 1.3 for $\alpha =1$, $A=2$ and $\epsilon =0.0001$. (A) Solution plots of the three methods. (B) Phase plane trajectories of the three methods. (C) Solution plots for different fractal dimensions.

Furthermore, Figure 1C shows the image curves of the second-order approximate solutions for Equation 1.3 when $\alpha$ takes the values of 0.25, 0.5, 0.75, and 1, respectively. It is easy to find that the fractal dimension $\alpha$ has a significant influence on the nonlinear vibration behavior. The vibration is singular periodic when $\alpha =0.25$. As $\alpha$ gradually increases, the frequency of the vibration behavior accelerates. Until $\alpha =1$, the vibration exhibits a clear periodicity. It also can be seen that although the frequency of the graphic changes significantly with the change of $\alpha$, the amplitude remains unchanged, indicating that the fractal dimension does not alter the macroscopic behavior of the nonlinear oscillator. Therefore, in low dimensional situations, that is, micro scale, it is more beneficial to research the vibration behavior of nonlinear oscillator.

5 Conclusion

In this article, based on the fractal modified nonlinear oscillators with coordinate-dependent mass, the accurate approximate solutions are successfully constructed by the impactful techniques, which are the energy balance method and the modified harmonic balance method under fractal case. The numerical results indicate that the second-order approximate solution can achieve good accuracy. In addition, in the case of low fractal dimension, the change of vibration behavior is slower, and gradually accelerates as the dimension increases, which is more helpful for us to investigate nonlinear oscillations from the perspective of microscale. Therefore, the method presented of our paper can be considered as an effective alternative to existing methods.

Author contributions

WL: Formal Analysis, Funding acquisition, Writing – original draft, Writing – review and editing. FL: Data curation, Software, Writing – original draft. PW: Funding acquisition, Methodology, Supervision, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Pinxia Wu was supported by the Scientific Research Fund of Hunan Provincial Education Department (Grant No. 23B0639); WL was supported by the Jiangxi Vocational College of Applied Technology high skill and high-level talents special project (JXYY-G2023001). This work was supported in part by the Scientific Research Fund of Hunan Provincial Education Department (Grant No. 23B0639); in part by the Jiangxi Vocational College of Applied Technology high skill and high-level talents special project (JXYY-G2023001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. He J. Homotopy perturbation method: a new nonlinear analytical technique. Appl Math Comput (2003) 135(1):73–9. doi:10.1016/s0096-3003(01)00312-5

CrossRef Full Text | Google Scholar

2. He J. Addendum: new interpretation of homotopy perturbation method. Int J Mod Phys B (2006) 20(18):2561–8. doi:10.1142/s0217979206034819

CrossRef Full Text | Google Scholar

3. Wang Q. Numerical solutions for fractional KdV-Burgers equation by Adomian decomposition method. Appl Math Comput (2006) 182(2):1048–55. doi:10.1016/j.amc.2006.05.004

CrossRef Full Text | Google Scholar

4. Hosseini MM, Nasabzadeh H. On the convergence of Adomian decomposition method. Appl Math Comput (2006) 182(1):536–43. doi:10.1016/j.amc.2006.04.015

CrossRef Full Text | Google Scholar

5. He J. Variational iteration method-a kind of non-linear analytical technique: some examples. Int J non-linear Mech (1999) 34(4):699–708. doi:10.1016/s0020-7462(98)00048-1

CrossRef Full Text | Google Scholar

6. He J, Wu X. Variational iteration method: new development and applications. Comput and Math Appl (2007) 54(7-8):881–94. doi:10.1016/j.camwa.2006.12.083

CrossRef Full Text | Google Scholar

7. Tatari M, Dehghan M. On the convergence of He’s variational iteration method. J Comput Appl Math (2007) 207(1):121–8. doi:10.1016/j.cam.2006.07.017

CrossRef Full Text | Google Scholar

8. He J, Hou W, Qie N, Gepreel KA, Shirazi AH, Sedighi HM. Hamiltonian-based frequency-amplitude formulation for nonlinear oscillators. Facta Universitatis, Ser Mech Eng (2021) 19(2):199–208. doi:10.22190/fume201205002h

CrossRef Full Text | Google Scholar

9. Wang K, Zhu H. Periodic wave solution of the Kundu-Mukherjee-Naskar equation in birefringent fibers via the Hamiltonian-based algorithm. Europhysics Lett (2022) 139(3):35002. doi:10.1209/0295-5075/ac3d6b

CrossRef Full Text | Google Scholar

10. He JH. Preliminary report on the energy balance for nonlinear oscillations. Mech Res Commun (2002) 29(2-3):107–11. doi:10.1016/s0093-6413(02)00237-9

CrossRef Full Text | Google Scholar

11. Mehdipour I, Ganji D, Mozaffari M. Application of the energy balance method to nonlinear vibrating equations. Curr Appl Phys (2010) 10(1):104–12. doi:10.1016/j.cap.2009.05.016

CrossRef Full Text | Google Scholar

12. Yan Z, Dai H, Wang Q, N. Atluri S. Harmonic BalanceMethods: a review and recent developments. Comput Model Eng Sci (2023) 137:1419–59. doi:10.32604/cmes.2023.028198

CrossRef Full Text | Google Scholar

13. Wu P, He J, Jiao M. Couple of the harmonic balance method and gamma function for the helmholtz-duffing oscillator with small amplitude. J Vibration Eng and Tech (2023) 11(5):2193–8. doi:10.1007/s42417-022-00697-4

CrossRef Full Text | Google Scholar

14. He J, Yang Q, He C, Khan Y. A simple frequency formulation for the tangent oscillator. Axioms (2021) 10(4):320. doi:10.3390/axioms10040320

CrossRef Full Text | Google Scholar

15. Wu P, Ling W, Li X, He X, Xie L. Dynamics research of Fangzhu’s nanoscale surface. J Low Frequency Noise, Vibration Active Control (2022) 41(2):479–87. doi:10.1177/14613484211052753

CrossRef Full Text | Google Scholar

16. Lev B, Tymchyshyn V, Zagorodny A. On certain properties of nonlinear oscillator with coordinate-dependent mass. Phys Lett A (2017) 381(39):3417–23. doi:10.1016/j.physleta.2017.08.049

CrossRef Full Text | Google Scholar

17. Wu Y, He J. Homotopy perturbation method for nonlinear oscillators with coordinate dependent mass. Results Phys (2018) 10:270–1. doi:10.1016/j.rinp.2018.06.015

CrossRef Full Text | Google Scholar

18. Ren Z. The frequency-amplitude formulation with ω⁴ for fast insight into a nonlinear oscillator. Results Phys (2018) 11:1052–3. doi:10.1016/j.rinp.2018.10.062

CrossRef Full Text | Google Scholar

19. Wang K, Liu J. A fast insight into the nonlinear oscillators with coordinate-dependent mass. Results Phys (2022) 39:105759. doi:10.1016/j.rinp.2022.105759

CrossRef Full Text | Google Scholar

20. Lu J, Ma L. Numerical analysis of a fractional nonlinear oscillator with coordinate-dependent mass. Results Phys (2022) 43:106108. doi:10.1016/j.rinp.2022.106108

CrossRef Full Text | Google Scholar

21. He J. A tutorial review on fractal spacetime and fractional calculus. Int J Theor Phys (2014) 53(11):3698–718. doi:10.1007/s10773-014-2123-8

CrossRef Full Text | Google Scholar

22. He J, Ain Q. New promises and future challenges of fractal calculus: from two-scale thermodynamics to fractal variational principle. Therm Sci (2020) 24(2 Part A):659–81. doi:10.2298/tsci200127065h

CrossRef Full Text | Google Scholar

23. He J, Li Z, Wang Q. A new fractional derivative and its application to explanation of polar bear hairs. J King Saud University-Science (2016) 28(2):190–2. doi:10.1016/j.jksus.2015.03.004

CrossRef Full Text | Google Scholar

24. He J, El-Dib Y, Mady AA (2021). Homotopy perturbation method for the fractal toda oscillator. Fractal and Fractional, 5(3): 93. doi:10.3390/fractalfract5030093

CrossRef Full Text | Google Scholar

25. Chen B, Lu J, Xia Z. Numerical investigation of the fractal capillary oscillator. J Low Frequency Noise, Vibration Active Control (2023) 42(2):579–88. doi:10.1177/14613484221131245

CrossRef Full Text | Google Scholar

26. El-Dib Y. Stability analysis of a time-delayed Van der Pol–Helmholtz–Duffing oscillator in fractal space with a non-perturbative approach. Commun Theor Phys (2024) 76(4):045003. doi:10.1088/1572-9494/ad2501

CrossRef Full Text | Google Scholar

27. He J, El-Dib Y. A tutorial introduction to the two-scale fractal calculus and its application to the fractal Zhiber–Shabat oscillator. Fractals (2021) 29(08):2150268. doi:10.1142/s0218348x21502686

CrossRef Full Text | Google Scholar