Nuclear radii from first principles

With the combination of nuclear interactions from chiral effective field theory and various many-body techniques, one can perform systematically improvable ab initio calculations. As the improvable framework enables us to quantify the uncertainty, it is particularly useful to make a prediction for which performing experiments is difficult or even impossible. Neutron skin thickness, the difference between neutron and proton distribution radii, is a key quantity related to the properties of infinite nuclear matter. Since neutrons do not have a net electric charge, the neutron-distribution radius is difficult to measure, preventing precise measurement of neutron skin thickness. On the other hand, recent developments in laser spectroscopy techniques can provide detailed information on the charge distribution and opportunities for detailed comparisons to theoretical results. Testing the theoretical frameworks with the measurable charge radii should be a step toward predicting other quantities, such as neutron skin thickness. This contribution reviews recent advances in nuclear radii and neutron skin from ab initio calculations.

1 Introduction

The size of a nucleus is the fundamental observable of the nucleus, similar to the energies. The size can be quantified by mean-square (ms) radius $⟨R^2⟩$ or root-mean-square (rms) radius $\sqrt{⟨R^2⟩}$. Nuclear radii provide additional insights into nuclear structure. For example, a large radius signifies halo nuclei, whose nucleon density distributions are widely spread out compared to those of stable nuclei [1, 2]. Also, the behavior of charge radii over the isotopic chain can tell us about the nuclear structure, such as magic numbers and deformation [3–6].

The radii provide stringent tests of our theoretical understanding of nuclear systems. As the current nuclear theory is not directly connected with quantum chromodynamics (QCD), the fundamental theory of strong force governing a nucleus, disagreements between measured and theoretical radii indicate insufficiencies in our understanding of not only quantum many-body problems but nuclear interactions. Addressing these disagreements sheds light on how the theoretical models could be improved [7–10].

Moreover, a precise understanding of nuclear radii can impact astrophysics. The neutron skin thickness $R_{\text{skin}}$, defined as $R_{\text{skin}}=\sqrt{⟨R_n^2⟩}-\sqrt{⟨R_p^2⟩}$, with the ms neutron radius $⟨R_n^2⟩$ and proton radius $⟨R_p^2⟩$, strongly correlates with infinite nuclear matter properties [11, 12]. Although infinite nuclear matter does not exist on Earth, it is realized as a neutron star in the universe. The mass and radius of a neutron star are typical observables. Theoretically, neutron star mass and radius can be calculated by solving the Tolman–Oppenheimer–Volkoff equation with the nuclear equation of state (EoS). The EoS is characterized by energy per particle $e$ as a function of density $\rho$ and proton-neutron asymmetry $\beta =\frac{{\rho }_n-{\rho }_p}{\rho }$. Note that ${\rho }_p$, ${\rho }_n$, and $\rho ={\rho }_p+{\rho }_n$ are proton, neutron, and nucleon densities, respectively. Then, one expands $e(\rho ,\beta )$ around $\beta =0$:

$e\left(\rho ,\beta \right)=e\left(\rho ,0\right)+S\left(\rho \right){\beta }^2+\cdots .$

Here, $e(\rho ,0)$ is the energy of symmetric nuclear matter, and $S(\rho )$ is the symmetry energy. Around the symmetric nuclear matter saturation density ${\rho }_0$, $e(\rho ,0)$ and $S(\rho )$ can be expanded as

$e\left(\rho ,0\right)=e_0+\frac{1}{2}K{\left(\frac{\rho -{\rho }_0}{3{\rho }_0}\right)}^2+\cdots ,S\left(\rho \right)=S_0+L\left(\frac{\rho -{\rho }_0}{3{\rho }_0}\right)+\cdots ,$

with saturation energy $e_0$, incompressibility $K$, symmetry energy $S_0$ at $\rho ={\rho }_0$, and slope of the symmetry energy $L$. As seen in many studies, $L$ is strongly correlated with the radius and maximum mass of neutron stars (see Ref. [13] for example). From available mean-field theory calculations, unfortunately, $L$ is not sufficiently constrained. At the same time, one can find a strong correlation between $R_{\text{skin}}$ of ²⁰⁸Pb and $L$. The correlation indicates that a precise knowledge of $R_{\text{skin}}$ illuminates physics in neutron stars.

Furthermore, $R_{\text{skin}}$ is relevant for the coherent elastic neutrino-nucleus scattering (CE$\nu$NS). Neutrinos interact with a nucleus via the neutral current, and thus, the nuclear weak form factor is essential in CE$\nu$NS cross section calculations. Since the weak charges of neutron and proton are almost −1 and 0, respectively, CE$\nu$NS cross sections are sensitive to neutron density distribution. Precise measurements of CE$\nu$NS cross sections will allow us to extract $R_{\text{skin}}$ [14]. Conversely, precise $R_{\text{skin}}$ calculations may impact investigations of neutrino properties.

In the above two examples, precise knowledge of $R_{\text{skin}}$ is crucial. However, the experimental determination is unfortunately limited as the neutron density distribution is difficult to measure. Therefore, reliable theoretical calculations are strongly needed. A nuclear ab initio calculation framework is a possible approach to predict $R_{\text{skin}}$ quantified uncertainty. In this contribution, we discuss the current status of ab initio calculations for nuclear charge radii and neutron skin thickness. This article is organized as follows. In Section 2, the framework of nuclear ab initio calculations is briefly introduced. In Section 3, recent results of charge radii are presented to demonstrate the quality of the ab initio calculations. Recent progress in neutron skin from ab initio calculations is summarized in Section 4. The conclusions is presented in Section 5.

2 Ab initio nuclear theory

Here, we briefly discuss an ab initio nuclear theory. All the properties of nuclei are expected to be explained if one begins with QCD. The ab initio nuclear theory should be defined in terms of quarks and gluons degrees of freedom. Of course, it is currently impossible to compute the properties of nuclei starting from QCD, except for very light nuclei, though the recent progress in QCD simulation on a lattice is remarkable [15, 16]. A possible way is to rely on the nucleon degrees of freedom. However, it makes the definition of ab initio calculations ambiguous. Actually, it seems the definitions of nuclear ab initio calculations have been evolving. Up to the 2000s, nuclear ab initio calculation was regarded as a framework to solve exactly nuclear many-body problems. In the calculation, one begins with a nuclear Hamiltonian, which precisely reproduces, for example, the nucleon-nucleon scattering phase shifts. Nowadays, one of the interpretations of nuclear ab initio calculation is a systematically improvable framework both for obtaining operators expressed in terms of nucleon degrees of freedom and for solving nuclear many-body problems [17, 18]. The systematically improvable framework, in principle, enables us to quantify the propagated theoretical uncertainty, and thus, a probabilistically meaningful prediction can be made. There are two key points to build the framework, i.e., constructing nuclear operators and solving the nuclear many-body problem. In the following, these aspects will be discussed.

2.1 Nuclear Hamiltonian and radius operator

Interactions between nucleons are the essential ingredient for understanding the nuclear structure. The history of nuclear interactions began with the pion-exchange theory proposed by Yukawa in 1935 [19], and many efforts have been made since then. Although our understanding of nuclear interactions remains incomplete, chiral effective field theory (ChEFT) provides a systematically improvable way to derive them.

The chiral effective Lagrangian is described using the pion and nucleon (and delta isobar as an option) degrees of freedom. The terms entering the Lagrangian are constrained by the chiral symmetry. While the symmetry restricts the number of allowed terms, one still has an infinite number of terms. To organize a controllable framework, Weinberg introduced a power counting scheme defined by the ratio of two energy scales [20–22]. The first energy scale $p$ corresponds to the pion mass or Fermi momentum of the system of interest. The second scale $\mathrm{\Lambda }$ is the breakdown scale and roughly corresponds to the $\rho$ meson mass, $\sim 700$ MeV, which has already been integrated out from the theory. Then, the Lagrangian is expanded according to the power of the small parameter $Q=p/\mathrm{\Lambda }$. In the same manner, an expansion for nuclear interactions can be defined [23–25], and the diagrams are shown in Figure 1.

Figure 1

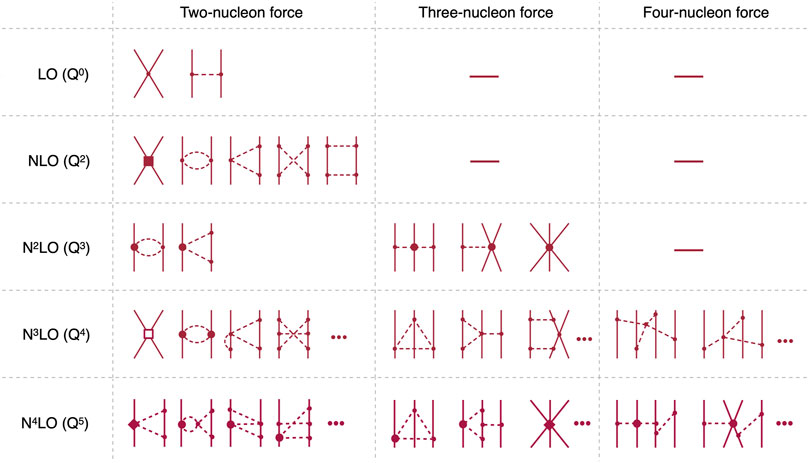
Figure 1. Expansion of nuclear forces. The diagrams are organized according to the power of $Q$. Solid dots, filled circles, filled squares, filled diamonds, and open squares represent the contributions from different orders in the effective chiral Lagrangian. The figure is reprinted from Ref. [23] under the CC BY 4.0 license.

There are several points worth emphasizing. In the expansion, not only nucleon-nucleon (NN) interaction terms $V_{\text{NN}}$, but also many-nucleon interactions, such as three-nucleon interaction $V_{3\text{N}}$ and four-nucleon interaction $V_{4\text{N}}$ can be derived systematically. The expansion in Figure 1 naturally explains the hierarchy of the many-body interactions, e.g., $V_{\text{NN}}>V_{3\text{N}}>V_{4\text{N}}$. The unknown parameters, referred to as low-energy constants (LECs), appear in the expansion and are illustrated by solid dots, filled circles, filled squares, filled diamonds, and open squares in the figure. The LECs are constrained by the existing experimental data, for example, nucleon-nucleon scattering data. The power counting scheme suggests the possibility of performing an uncertainty quantification. Some uncertainty quantification methods can be found in Refs. [26–29]. Finally, ChEFT can provide us with systematic expansions for couplings to the electroweak sector [30–36]. Owing to the systematic expansion, one can derive higher-order two-body current operators, which solve the long-standing quenching problem in the Gamow-Teller transition [37]. The importance of the two-body current operators for the magnetic observables was also reported [31, 32, 38–40].

From ChEFT, up to the 3N term, one can find nuclear Hamiltonian

$H=T+V^{\text{NN}}+V^{3\text{N}},(1)$

with the kinetic energy term $T$, NN interaction $V^{\text{NN}}$, and 3N interaction $V^{3\text{N}}$. The second quantization form of the operator is given as

$\begin{array}{cc}\hfill T& ={\displaystyle \sum _{p{p}^{\prime }}}{t}_{p{p}^{\prime }}{a}_p^{†}{a}_{p^{\prime }},\hfill \\ \hfill V^{\text{NN}}& =\frac{1}{4}{\displaystyle \sum _{pq{p}^{\prime }{q}^{\prime }}}{V}_{pq{p}^{\prime }{q}^{\prime }}^{\text{NN}}{a}_p^{†}{a}_q^{†}{a}_{q^{\prime }}{a}_{p^{\prime }},\hfill \\ \hfill V^{3\text{N}}& =\frac{1}{36}{\displaystyle \sum _{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}}{V}_{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}^{3\text{N}}{a}_p^{†}{a}_q^{†}{a}_r^{†}{a}_{r^{\prime }}{a}_{q^{\prime }}{a}_{p^{\prime }},\hfill \end{array}$

with the creation (annihilation) operator $a_p^{†}$ $(a_p)$ of a single-particle state $p$. Assuming a widely used harmonics oscillator single-particle state, $p$ represents a set of quantum numbers $p=(n_p,l_p,j_p,m_p,t_{z,p})$, where $n_p$ is the radial quantum number, $l_p$ is the orbital angular momentum, $j_p$ is the total angular momentum, $m_p$ is the $z$-component of $j_p$, and $t_{z,p}$ is the $z$-component of the isospin. The $t_{p{p}^{\prime }}$, $V_{pq{p}^{\prime }{q}^{\prime }}^{\text{NN}}$, $V_{pqr{p}^{\prime }{q}^{\prime }r}^{3\text{N}}$ are the matrix elements of the one-body kinetic term, NN and 3N interactions, respectively. Note that $V_{pq{p}^{\prime }{q}^{\prime }}^{\text{NN}}$ includes a correction due to the translational invariance of the system as well as the Coulomb interaction between protons.

2.1.1 Radius operators

In addition to Hamiltonian, we briefly discuss the radius operators. Classically, an ms radius $R^2$ can be computed with the corresponding density $\rho (\mathit{r})$ as

$R^2=\frac{1}{\mathcal{N}}\int d\mathit{r}{r}^2\rho \left(\mathit{r}\right),$

with the normalization factor $\mathcal{N}=\int d\mathit{r}\rho (\mathit{r})$. However, the coordinate-space density might not always be useful. Actually, for charge density distribution, it is not straightforward to include the contributions of the nucleon charge density. In the momentum space, such contribution is already built in by definition, and we begin with the momentum-space density $\tilde{\rho }(\mathit{q})=\int d\mathit{r}{e}^{i\mathit{q}\cdot \mathit{r}}\rho (\mathit{r})$. With $\tilde{\rho }(\mathit{q})$, one can define the angle-averaged form factor $F(q)$

$F\left(q\right)=\frac{1}{4\pi }\int d\widehat{\mathit{q}}\tilde{\rho }\left(\mathit{q}\right).(2)$

Now, we can use the well-known partial wave decomposition formula for the plane wave function: $e^{i\mathit{q}\cdot \mathit{r}}=4\pi {\sum }_{\lambda \mu }{i}^{\lambda }{j}_{\lambda }(qr)Y_{\lambda \mu }^{*}(\widehat{\mathit{q}})$$Y_{\lambda \mu }(\widehat{\mathit{r}})$. Here, $j_{\lambda }(x)$ is the order $\lambda$ spherical Bessel function of the first kind, and $Y_{\lambda \mu }(\widehat{\mathit{x}})$ is the spherical harmonics with the usual notation. Note that $\widehat{\mathit{x}}$ indicates the unit vector, i.e., $\widehat{\mathit{x}}=\mathit{x}/|\mathit{x}|$. Owing to the orthonormality of the spherical harmonics, one finds $F(q)=\int d\mathit{r}{j}_0(qr)\rho (\mathit{r})$. Since the small $x$ limit of the $j_0(x)$ is known as

$j_0\left(x\right)\approx 1-\frac{x^2}{6}+\frac{x^4}{120}\left(x\ll 1\right),(3)$

the ms radius is obtained as

$R^2=-\frac{6}{F\left(0\right)}\underset{q\to 0}{\lim }\frac{d}{d{q}^2}F\left(q\right).(4)$

We can apply Equation 4 to find, for example, the ms point-proton radius using the intrinsic point-proton density:

${\tilde{\rho }}_p\left(\mathit{q}\right)={\displaystyle \sum _{i=1}^A}\left(\frac{1+{\tau }_i}{2}\right)e^{i\mathit{q}\cdot \left({\mathit{r}}_i-{\mathit{R}}_{\text{cm}}\right)}.$

Here, ${\tau }_i=1(-1)$ indicates that $i$-th nucleon is proton (neutron), ${\mathit{r}}_i$ is the coordinate vector of the $i$-th nucleon, and ${\mathit{R}}_{\text{cm}}$ is the center-of-mass vector, ${\mathit{R}}_{\text{cm}}=\frac{1}{A}{\sum }_{i=1}^A{\mathit{r}}_i$. Plugging this into (Equation 2) and performing the angular integral, one finds the point-proton form factor $F_p(q)$ as $F_p(q)={\sum }_{i=1}^A\left(\frac{1+{\tau }_i}{2}\right)j_0(x_i)$ with $x_i=q|{\mathit{r}}_i-{\mathit{R}}_{\text{cm}}|$. Thus the point-proton ms radius $R_p^2$ is given as

$R_p^2=\frac{1}{Z}{\displaystyle \sum _{i=1}^A}\left(\frac{1+{\tau }_i}{2}\right)|{\mathit{r}}_i-{\mathit{R}}_{\text{cm}}{|}^2,(5)$

with the proton number $Z$, the normalization of the form factor: $F_p(0)=\int d\mathit{r}{\rho }_p(\mathit{r})=Z$. In the same manner, with the neutron number $N$, the ms point-neutron radius $R_n^2$ can be found as

$R_n^2=\frac{1}{N}{\displaystyle \sum _{i=1}^A}\left(\frac{1-{\tau }_i}{2}\right)|{\mathit{r}}_i-{\mathit{R}}_{\text{cm}}{|}^2.(6)$

So far, the radii are classically defined. However, one can obtain the ms point-proton and point-neutron radius operators by applying the usual quantization procedure to Equations 5, 6, respectively. Writing the expectation value of $R_p^2$ and $R_n^2$ operators as $⟨R_p^2⟩$ and $⟨R_n^2⟩$, respectively, the neutron skin thickness $R_{\text{skin}}$ is defined as

$R_{\text{skin}}=\sqrt{\langle R_n^2\rangle }-\sqrt{\langle R_p^2\rangle }.$

In nuclear physics, the most frequently measured is the charge radius, as it can be precisely measured by electromagnetic probes. To this end, one can begin with the intrinsic charge density ${\tilde{\rho }}_{\text{ch}}(\mathit{q})$:

$\begin{array}{cc}\hfill {\rho }_{\text{ch}}\left(\mathit{q}\right)& \approx {\displaystyle \sum _{i=1}^A}\left\{e{G}_i^E\left(q^2\right)\left[1-\frac{q^2}{8m^2}\right]\right.\hfill \\ \hfill & +\left.\frac{ie}{4m^2}\left[2G_i^M\left(q^2\right)-G_i^E\left(q^2\right)\right]\mathit{q}\cdot \left[\left({\mathit{p}}_i-\frac{{\mathit{P}}_{\text{cm}}}{A}\right)\times {\mathit{\sigma }}_i\right]\right\}{e}^{i\mathit{q}\cdot \left({\mathit{r}}_i-{\mathit{R}}_{\text{cm}}\right)},\hfill \end{array}(7)$

with nucleon mass $m$, momentum of $i$-th nucleon ${\mathit{p}}_i$, center-of-mass momentum ${\mathit{P}}_{\text{cm}}={\sum }_{i=1}^A{\mathit{p}}_i$, and Sachs form factors $G_i^E(q^2)$ and $G_i^M(q^2)$. Here, $G_i^E(q^2)$ and $G_i^M(q^2)$ are given as.

$G_i^E\left(q^2\right)=\left(\frac{1+{\tau }_i}{2}\right)G_p^E\left(q^2\right)+\left(\frac{1-{\tau }_i}{2}\right)G_n^E\left(q^2\right),$

$G_i^M\left(q^2\right)=\left(\frac{1+{\tau }_i}{2}\right)G_p^M\left(q^2\right)+\left(\frac{1-{\tau }_i}{2}\right)G_n^M\left(q^2\right),$

with proton/neutron Sachs form factors $G_{p/n}^E(q^2)$ and $G_{p/n}^M(q^2)$. Note that the higher order terms in $1/m$ are omitted. Again, owing to the orthogonality of the spherical harmonics, the charge form factor is obtained as

$F_{\text{ch}}\left(q\right)=e{\displaystyle \sum _{i=1}^A}\left\{G_i^E\left(q^2\right)\left[1-\frac{q^2}{8m^2}\right]j_0\left(x_i\right)-\frac{q^2}{2m^2}\left[G_i^M\left(q^2\right)-\frac{1}{2}{G}_i^E\left(q^2\right)\right]\left({\mathit{\ell }}_i\cdot {\mathit{\sigma }}_i\right)\frac{j_1\left(x_i\right)}{x_i}\right\},$

with the $i$-th nucleon’s orbital angular momentum ${\mathit{\ell }}_i=({\mathit{r}}_i-{\mathit{R}}_{\text{cm}})\times ({\mathit{p}}_i-{\mathit{P}}_{\text{cm}}/A)$, which is often approximated as ${\mathit{\ell }}_i\approx {\mathit{r}}_i\times {\mathit{p}}_i$. From Equation 4, the ms charge radius is obtained as

$R_{\text{ch}}^2\left(q\right)=R_p^2+r_p^2+\frac{N}{Z}{r}_n^2+R_{\text{DF}}^2+R_{\text{SO}}^2,(8)$

with

$\begin{array}{cc}\hfill r_{p/n}^2& =-6\underset{q\to 0}{\lim }\frac{d{G}_{p/n}^E\left(q^2\right)}{d{q}^2},{\mu }_{p/n}=G_{p/n}^M\left(0\right),\hfill \\ \hfill R_{\text{DF}}^2& =\frac{3}{4m^2},R_{\text{SO}}^2=\frac{1}{m^{2}Z}{\displaystyle \sum _{i=1}^A}\left[\left(\frac{1+{\tau }_i}{2}\right)\left({\mu }_p-\frac{1}{2}\right)+\left(\frac{1-{\tau }_i}{2}\right){\mu }_n\right]\left({\mathit{\ell }}_i\cdot {\mathit{\sigma }}_i\right).\hfill \end{array}$

Here, $r_{p/n}^2$ is the proton/neutron charge radius, and ${\mu }_{p/n}$ is the proton/neutron magnetic moment. Note that $G_p^E(0)=1$ and $G_n^E(0)=0$ are used. From Equation 8, the ms charge radius is interpreted as the sum of the ms point-proton radius and corrections. The $r_p^2$ and $r_n^2$ are the nucleon finite-size corrections. The $R_{\text{DF}}^2$ and $R_{\text{SO}}^2$ are known as Darwin-Foldy and spin-orbit terms, respectively. Note that $R_{\text{SO}}^2$ depends on the nuclear wave function, while the other corrections are not. The charge density given in Equation 7 is a standard starting point. At higher orders in ChEFT, however, additional contributions to the charge density can be found [33, 34, 36, 41, 42]. So far, investigating the effects of the two-body charge density is limited to the light nuclei [43]. Therefore, further studies are needed to clarify the effects of such terms on the charge radii.

Finally, we note the 4th moment of charge density $R_{\text{ch}}^4$. Very recently, it was shown that a sequence of isotope shifts of $R_{\text{ch}}^4$ are measurable [44]. In Ref. [44], $R_{\text{ch}}^4$ was approximately computed as the 4th moment of the point-proton density $R_p^4$. For future work, we note the operator expression. With the expansion in Equation 3, $R_{\text{ch}}^4$ can be obtained from the second derivative of the charge form factor:

$R_{\text{ch}}^4=\frac{60}{F_{\text{ch}}\left(0\right)}\underset{q\to 0}{\lim }\frac{d}{d{q}^2}\frac{d}{d{q}^2}{F}_{\text{ch}}\left(q\right).$

Similar to the derivation of $R_{\text{ch}}^2$, one can find the expression of $R_{\text{ch}}^4$ as

$R_{\text{ch}}^4=R_p^4+\frac{10}{3}\left(r_p^2{R}_p^2+\frac{N}{Z}{r}_n^2{R}_n^2\right)+\frac{5}{2m^2}\left(R_p^2+r_p^2+\frac{N}{Z}{r}_n^2\right)+r_p^4+\frac{N}{Z}{r}_n^4+R_{\text{SO}}^4,$

with the 4th moment of proton/neutron charge density $r_{p/n}^4$, defined as $r_{p/n}^4=60\frac{d^2{G}_{p/n}^E(q^2)}{d^2{q}^2}{|}_{q^2=0}$. Also, the 4th moment of the point-proton density $R_p^4$ and spin-orbit correction $R_{\text{SO}}^4$ are

$\begin{array}{cc}\hfill R_p^4& =\frac{1}{Z}{\displaystyle \sum _{i=1}^A}\left(\frac{1+{\tau }_i}{2}\right)|{\mathit{r}}_i-{\mathit{R}}_{\text{cm}}{|}^4,\hfill \\ \hfill R_{\text{SO}}^4& =\frac{2}{m^{2}Z}{\displaystyle \sum _{i=1}^A}\left[\left(\frac{1+{\tau }_i}{2}\right)\left({\mu }_p-\frac{1}{2}\right)+\left(\frac{1-{\tau }_i}{2}\right){\mu }_n\right]\left({\mathit{\ell }}_i\cdot {\mathit{\sigma }}_i\right)|{\mathit{r}}_i-{\mathit{R}}_{\text{cm}}{|}^2\hfill \\ \hfill & +\frac{10}{3m^{2}Z}{\displaystyle \sum _{i=1}^A}\left[\left(\frac{1+{\tau }_i}{2}\right)\left(r_{M,p}^2-\frac{r_p^2}{2}\right)+\left(\frac{1-{\tau }_i}{2}\right)\left(r_{M,n}^2-\frac{r_n^2}{2}\right)\right]\left({\mathit{\ell }}_i\cdot {\mathit{\sigma }}_i\right),\hfill \end{array}$

with the ms proton/neutron magnetic radius $r_{M,p/n}^2$, defined as $r_{M,p/n}^2=-6\frac{d{G}_{p/n}^M(q^2)}{d{q}^2}{|}_{q^2=0}$. We note that $R_{\text{ch}}^4$ depends on $R_n^2$, as discussed in Ref. [45].

2.2 Many-body problem

The problem now is to solve the non-relativistic many-body Schrödinger equation

$H|\mathrm{\Psi }\rangle =E|\mathrm{\Psi }\rangle ,$

where $|\mathrm{\Psi }\rangle$ and $E$ are the eigenstate and corresponding energy, respectively. The range of the applicability of ab initio many-body methods has been expanding rapidly over the past decades [17]. In the 2000s, researchers in the nuclear physics community started to use numerical methods, whose computational cost scales polynomially as a function of $A$. This development has been essential for enabling numerous ab initio nuclear structure studies, and the achievements in the quarter century are highlighted in Figure 2.

Figure 2

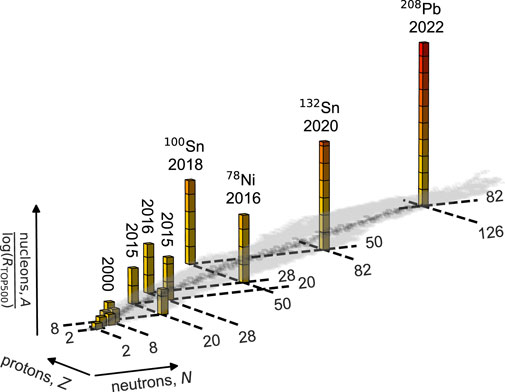
Figure 2. Progress of nuclear ab initio calculations over the last quarter century. The bars highlight years of the first realistic computations of doubly magic nuclei. The height of each bar corresponds to the mass number $A$ divided by the logarithm of the total compute power $R_{\text{TOP}500}$ (in flop/second) of the pertinent TOP500 list. The figure is adapted from Ref. [46] under the CC BY 4.0 license.

A straightforward way to solve the equation would be to insert the completeness relation ${\sum }_{i=1}^{\infty }|{\mathrm{\Phi }}_i\rangle \langle {\mathrm{\Phi }}_i|=1$ with the known orthonormal basis set $\{|{\mathrm{\Phi }}_1\rangle ,|{\mathrm{\Phi }}_2\rangle ,\dots \}$. Then, the problem is equivalent to diagonalize the Hamiltonian matrix:

$\left(\begin{array}{ccc}\hfill \langle {\mathrm{\Phi }}_1|H|{\mathrm{\Phi }}_1\rangle \hfill & \hfill \langle {\mathrm{\Phi }}_1|H|{\mathrm{\Phi }}_2\rangle \hfill & \hfill \cdots \hfill \\ \hfill \langle {\mathrm{\Phi }}_2|H|{\mathrm{\Phi }}_1\rangle \hfill & \hfill \langle {\mathrm{\Phi }}_2|H|{\mathrm{\Phi }}_2\rangle \hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right)\left(\begin{array}{c}\hfill c_1\hfill \\ \hfill c_2\hfill \\ \hfill ⋮\hfill \end{array}\right)=E\left(\begin{array}{c}\hfill c_1\hfill \\ \hfill c_2\hfill \\ \hfill ⋮\hfill \end{array}\right).$

The component of the vector $c_i$ is given by $⟨{\mathrm{\Phi }}_i|\mathrm{\Psi }⟩$. To solve the eigenvalue problem numerically, one needs to introduce the truncation to a finite number of bases $N_{\text{SD}}$, and $N_{\text{SD}}$ needs to be increased until the results converge. On a supercomputer, a typical limit of $N_{\text{SD}}$ is $\sim 10^{11}$. Due to this limitation, applications of the exact diagonalization method are usually limited up to $A\sim 20$ systems [17, 47, 48, 49, 50]. Another option is the quantum Monte Carlo (QMC) method (see Ref. [51–53] for applications in nuclear physics). Similarly to the exact diagonalization method, a typical QMC application limit is also $A\sim 20$. An alternative method is solving the problem on the lattice, known as nuclear lattice EFT [54, 55]. Remarkably, recent efforts have made the calculations up to $A\sim 40$ possible [56]. Despite the limitations, the results from the above mentioned exact methods are valuable to benchmark those from the approximate many-body methods discussed below.

2.2.1 Normal ordering

To compute the medium and heavy-mass nuclei, one can use expansion methods based on a reference state $|\mathrm{\Phi }\rangle$. The first step is to take normal order for all the creation and annihilation operator strings with respect to $|\mathrm{\Phi }\rangle$. Then, Hamiltonian (Equation 1) can be rewritten as

$H=E^{\left[0\right]}+F^{\left[1\right]}+{\mathrm{\Gamma }}^{\left[2\right]}+W^{\left[3\right]}.$

Here, $E^{[0]}$, $F^{[1]}$, ${\mathrm{\Gamma }}^{[2]}$, and $W^{[3]}$ are the zero-, one-, two-, and three-body parts of the Hamiltonian after the rearrangement, and the superscript ^[n] indicates that the term is $n$-body. Each term is given as

$\begin{array}{cc}\hfill F^{\left[1\right]}& ={\displaystyle \sum _{p{p}^{\prime }}}{f}_{p{p}^{\prime }}\left\{a_p^{†}{a}_{p^{\prime }}\right\}\hfill \\ \hfill {\mathrm{\Gamma }}^{\left[2\right]}& =\frac{1}{4}{\displaystyle \sum _{pq{p}^{\prime }{q}^{\prime }}}{\mathrm{\Gamma }}_{pq{p}^{\prime }{q}^{\prime }}\left\{a_p^{†}{a}_q^{†}{a}_{q^{\prime }}{a}_{p^{\prime }}\right\}\hfill \\ \hfill W^{\left[3\right]}& =\frac{1}{36}{\displaystyle \sum _{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}}{W}_{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}\left\{a_p^{†}{a}_q^{†}{a}_r^{†}{a}_{r^{\prime }}{a}_{q^{\prime }}{a}_{p^{\prime }}\right\}.\hfill \end{array}$

The brace indicates that the creation and annihilation operators are normal ordered with respect to $|\mathrm{\Phi }\rangle$, i.e., $⟨\mathrm{\Phi }|\{a_p^{†}{a}_q^{†}\dots a_{q^{\prime }}{a}_{p^{\prime }}\}|\mathrm{\Phi }⟩=0$. If $|\mathrm{\Phi }\rangle$ is uncorrelated, for example, the Hartree–Fock solution, $E_0$, $f_{p{p}^{\prime }}$, ${\mathrm{\Gamma }}_{pq{p}^{\prime }{q}^{\prime }}$, and $W_{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}$ can be written as

$\begin{array}{c}{E}_0={\displaystyle \sum _{p{p}^{\prime }}}{t}_{p{p}^{\prime }}{\rho }_{p{p}^{\prime }}+\frac{1}{2}{\displaystyle \sum _{pq{p}^{\prime }{q}^{\prime }}}{V}_{pq{p}^{\prime }{q}^{\prime }}^{\text{NN}}{\rho }_{p{p}^{\prime }}{\rho }_{q{q}^{\prime }}\hfill \\ +\frac{1}{6}{\displaystyle \sum _{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}}{V}_{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}^{3\text{N}}{\rho }_{p{p}^{\prime }}{\rho }_{q{q}^{\prime }}{\rho }_{r{r}^{\prime }},\hfill \\ f_{p{p}^{\prime }}=t_{p{p}^{\prime }}+{\displaystyle \sum _{q{q}^{\prime }}}{V}_{pq{p}^{\prime }{q}^{\prime }}^{\text{NN}}{\rho }_{q{q}^{\prime }}+\frac{1}{2}{\displaystyle \sum _{qr{q}^{\prime }{r}^{\prime }}}{V}_{qrp{q}^{\prime }{r}^{\prime }{p}^{\prime }}^{3\text{N}}{\rho }_{q{q}^{\prime }}{\rho }_{r{r}^{\prime }},\hfill \\ {\mathrm{\Gamma }}_{pq{p}^{\prime }{q}^{\prime }}=V_{pq{p}^{\prime }{q}^{\prime }}^{\text{NN}}+{\displaystyle \sum _{r{r}^{\prime }}}{V}_{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}^{3\text{N}}{\rho }_{r{r}^{\prime }},\hfill \\ W_{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}=V_{pqr{p}^{\prime }{q}^{\prime }{r}^{\prime }}^{3\text{N}},\hfill \end{array}$

with the one-body density ${\rho }_{p{p}^{\prime }}=⟨\mathrm{\Phi }|a_p^{†}{a}_{p^{\prime }}|\mathrm{\Phi }⟩$. Since the effect of $W^{[3]}$ term is usually small [57–60], we omit the term, known as the normal-ordered two-body (NO2B) approximation:

$H\approx H_{\text{NO}2\text{B}}=E^{\left[0\right]}+F^{\left[1\right]}+{\mathrm{\Gamma }}^{\left[2\right]}.(9)$

2.2.2 Similarity transformation method

Beginning with Hamiltonian (Equation 9), one needs to evaluate the effects of the many-body correlations on top of the reference state. To incorporate the many-body correlations, the diagrammatic expansion or similarity transformation methods can be applied. As diagrammatic expansion methods, one can find many-body perturbation theory [61] and self-consistent Green’s function method [62, 63]. In this review, we quickly introduce the similarity transformation methods. The many-body Schrödinger equation is equivalent to

$\tilde{H}|\mathrm{\Phi }\rangle =E|\mathrm{\Phi }\rangle ,$

with

$\tilde{H}=e^{\mathrm{\Omega }}{H}_{\text{NO}2\text{B}}{e}^{-\mathrm{\Omega }},|\mathrm{\Phi }\rangle =e^{\mathrm{\Omega }}|\mathrm{\Psi }\rangle .(10)$

In general, $\mathrm{\Omega }$ operator includes up to $A$-body terms:

$\mathrm{\Omega }={\mathrm{\Omega }}^{\left[1\right]}+{\mathrm{\Omega }}^{\left[2\right]}+\cdots +{\mathrm{\Omega }}^{\left[A\right]}.$

The transformation $e^{\mathrm{\Omega }}$ makes the reference state the eigenstate of $\tilde{H}$, without changing the energy eigenvalue of the original Hamiltonian. In other words, the transformation suppresses the off-diagonal matrix elements between $|\mathrm{\Phi }\rangle$ and the other states, which is known as the decoupling.

In the coupled-cluster method [64] (CCM), $\mathrm{\Omega }$ is known as the cluster operator, which includes only the particle-hole excitation operators. As a consequence, the transformed Hamiltonian $\tilde{H}$ becomes non-Hermitian. While, in the in-medium similarity renormalization group [65, 66] (IMSRG), $\mathrm{\Omega }$ is chosen as the anti-Hermitian and includes not only the particle-hole excitation operators but also the de-excitation counterparts, and $\tilde{H}$ becomes Hermitian.

During the transformation (Equation 10), the many-body terms are induced. This can be seen by rewriting the transformation with the Baker–Campbell–Hausdorff (BCH) formula:

$\tilde{H}=H_{\text{NO}2\text{B}}+\left[\mathrm{\Omega },H_{\text{NO}2\text{B}}\right]+\frac{1}{2!}\left[\mathrm{\Omega },\left[\mathrm{\Omega },H_{\text{NO}2\text{B}}\right]\right]+\frac{1}{3!}\left[\mathrm{\Omega },\left[\mathrm{\Omega },\left[\mathrm{\Omega },H_{\text{NO}2\text{B}}\right]\right]\right]+\cdots .$

Assuming that the $\mathrm{\Omega }$ operator has one- and two-body parts, the commutator is classified as

$\begin{array}{cc}\hfill \left[\mathrm{\Omega },H_{\text{NO}2\text{B}}\right]& ={\left[{\mathrm{\Omega }}^{\left[1\right]},F^{\left[1\right]}\right]}^{\left[0\right]}+{\left[{\mathrm{\Omega }}^{\left[2\right]},{\mathrm{\Gamma }}^{\left[2\right]}\right]}^{\left[0\right]}+{\left[{\mathrm{\Omega }}^{\left[1\right]},F^{\left[1\right]}\right]}^{\left[1\right]}\hfill \\ \hfill & +{\left[{\mathrm{\Omega }}^{\left[1\right]},{\mathrm{\Gamma }}^{\left[2\right]}\right]}^{\left[1\right]}+{\left[{\mathrm{\Omega }}^{\left[2\right]},F^{\left[1\right]}\right]}^{\left[1\right]}+{\left[{\mathrm{\Omega }}^{\left[2\right]},{\mathrm{\Gamma }}^{\left[2\right]}\right]}^{\left[1\right]}\hfill \\ \hfill & +{\left[{\mathrm{\Omega }}^{\left[1\right]},{\mathrm{\Gamma }}^{\left[2\right]}\right]}^{\left[2\right]}+{\left[{\mathrm{\Omega }}^{\left[2\right]},F^{\left[1\right]}\right]}^{\left[2\right]}+{\left[{\mathrm{\Omega }}^{\left[2\right]},{\mathrm{\Gamma }}^{\left[2\right]}\right]}^{\left[2\right]}\hfill \\ \hfill & +{\left[{\mathrm{\Omega }}^{\left[2\right]},{\mathrm{\Gamma }}^{\left[2\right]}\right]}^{\left[3\right]}.\hfill \end{array}$

The commutator of ${\mathrm{\Omega }}^{[2]}$ and ${\mathrm{\Gamma }}^{[2]}$ operators induces the three-body term. In the end, nested commutators will induce up to $A$-body term. To make numerical calculations feasible, making an approximation is unavoidable. A typical approximation is to keep up to the two-body part for $\mathrm{\Omega }$, $\tilde{H}$, and all the commutators:

$\begin{array}{cc}\hfill \mathrm{\Omega }& \approx {\mathrm{\Omega }}^{\left[1\right]}+{\mathrm{\Omega }}^{\left[2\right]},\hfill \\ \hfill \tilde{H}& \approx {\tilde{E}}^{\left[0\right]}+{\tilde{F}}^{\left[1\right]}+{\tilde{\mathrm{\Gamma }}}^{\left[2\right]}.\hfill \end{array}$

This approximation is very efficient and usually accurate enough. Discussions on extensions beyond the two-body approximation in CCM and IMSRG can be found in Refs. [57, 59, 67–75].

In the IMSRG, $\mathrm{\Omega }$ is obtained by solving the following ordinary differential equation [76]:

$\frac{d\mathrm{\Omega }}{ds}={\displaystyle \sum _{n=0}^{\infty }}\frac{B_n}{n!}{\left[\mathrm{\Omega }\left(s\right),\eta \left(s\right)\right]}^{\left(n\right)}$

with

${\left[\mathrm{\Omega }\left(s\right),\eta \left(s\right)\right]}^{\left(0\right)}=\eta \left(s\right),{\left[\mathrm{\Omega }\left(s\right),\eta \left(s\right)\right]}^{\left(n\right)}=\left[\mathrm{\Omega }\left(s\right),{\left[\mathrm{\Omega }\left(s\right),\eta \left(s\right)\right]}^{\left(n-1\right)}\right],$

and the $n$-th Bernoulli number $B_n$. The $s$ and $\eta (s)$ are the flow parameter and anti-Hermitian generator of the differential equation, respectively. The equation is solved from $s=0$ to $\infty$ with the initial condition $\mathrm{\Omega }(0)=0$. Note that $\eta (s)$ is also truncated at the two-body level. In usual applications, the white generator (and its variants) is used, where the matrix element is expressed as

$\langle i|\eta \left(s\right)|j\rangle =\frac{\langle i|\tilde{H}\left(s\right)|j\rangle }{\langle i|\tilde{H}\left(s\right)|i\rangle -\langle j|\tilde{H}\left(s\right)|j\rangle }$

with the s-dependent transformed Hamiltonian $\tilde{H}(s)=e^{\mathrm{\Omega }(s)}{H}_{\text{NO}2\text{B}}{e}^{-\mathrm{\Omega }(s)}$, the off-diagonal matrix element to be suppressed $⟨i|\tilde{H}(s)|j⟩$, and the energy difference $⟨i|\tilde{H}(s)|i⟩-⟨j|\tilde{H}(s)|j⟩$. Once $\mathrm{\Omega }(s)$ is obtained, the radius operators can also be transformed with the BCH transformation. One of the advantages of the IMSRG is that one can choose $|i\rangle$ and $|j\rangle$ as desired, and it enables us to decouple a small valence space with the other space, known as valence-space IMSRG (VS-IMSRG) [77]. With well-established shell-model calculation codes such as ANTOINE [78], NuShell [79], BIGSTICK [80], KSHELL [81], etc., one can access open-shell systems and excited states starting from the underlying Hamiltonian and without any phenomenological adjustments.

2.3 Parameter optimization strategy

As discussed in Section 2.1, unknown LECs appear in ChEFT. Here, we summarize how the LECs of the frequently used interactions in this review were determined.

• ${\mathbf{\lambda }}_{\text{NN}}/{\mathbf{\Lambda }}_{3\text{N}}$ [82]: Combinations of next-to-next-to-next-to-leading order (${\text{N}}^3$LO) NN and next-to-next-to-leading order (${\text{N}}^2$LO) 3N interactions. The LECs of the NN part are optimized with the NN scattering phase-shift and deuteron data by Entem and Machleidt [83]. Further, the NN part was softened by free-space SRG [84] with the momentum scale ${\lambda }_{\text{NN}}$. The LECs of the 3N part non-locally regulated with the momentum scale ${\mathrm{\Lambda }}_{3\text{N}}$ were determined with the triton binding energy and ⁴He radius. Depending on the pion-nucleon couplings $c_i$s from Entem and Machleidt (EM) [83], NN partial wave analysis (PWA) [85], and Epelbaum, Glöckle, and Meißner (EGM) [86], some choices are available. A widely used combination is ${\lambda }_{\text{NN}}=1.8$ ${\text{fm}}^{-1}$ and ${\mathrm{\Lambda }}_{3\text{N}}=2.0$ ${\text{fm}}^{-1}$ with $c_i$s from Ref. [83], i.e., 1.8/2.0 (EM) interaction. The 1.8/2.0 (EM) interaction reproduces the ground-state energies up to heavy systems [87–89], while it significantly underestimates the radii [87].

•N²LO$\text{s}\text{a}\text{t}$ [7]: ${\text{N}}^2$LO NN and 3N interactions, which are non-locally regulated with the momentum scale 450 MeV. All the LECs were optimized simultaneously with the few-body data and some selected properties up to $A=25$ systems with the POUNDerS algorithm [90]. It reproduces the ground-state energies and charge radii simultaneously roughly up to $A\sim 100$ systems.

•$\mathbf{\Delta }$N²LO_GO(394) [9]: ${\text{N}}^2$LO NN and 3N interactions from ChEFT with delta isobar excitation effects [91] ($\mathrm{\Delta }$-full ChEFT). The NN and 3N interactions are non-locally regulated with the momentum scale 394 MeV, which is approximately 2 ${\text{fm}}^{-1}$. NN and 3N LECs are simultaneously optimized with the few-body data and nuclear matter properties with the POUNDerS algorithm [90]. It reproduces the ground-state energies and radii of the $A=16$ to 132 systems [9].

•$\mathbf{\Delta }$N²LO non-implausible interactions [46, 92, 93]: A set of ${\text{N}}^2$LO NN and 3N interactions obtained with $\mathrm{\Delta }$-full ChEFT. The NN and 3N interactions are non-locally regulated. With an implausibility measure, one can iteratively exclude a region of the initial parameter space. The procedure is known as history matching [94, 95]. Typical observables defining the implausibility measure are few-body data, including the NN scattering phase-shift data. In Ref. [46], the 34 non-implausible parameter sets were found.

3 Charge radius

The nuclear charge radius is the most precisely measurable nuclear radius via electron scattering, laser spectroscopy, and muonic atom spectroscopy techniques. Here, we briefly discuss the recent progress in the charge radius studies from ab initio calculations. For simplicity, we omit angle brackets when writing expectation values. For example, $⟨R_{\text{ch}}^2⟩$ is simply written as $R_{\text{ch}}^2$. Similarly, rms radii are denoted by $R_p$, $R_n$, $R_{\text{ch}}$, etc.

3.1 Light nuclei

Radius data are valuable for optimizing nuclear interactions. For example, the deuteron radius was used to check the quality of high-precision nucleon-nucleon (NN) potentials such as AV18 [96] and CD-Bonn [97]. Furthermore, the data of few-body systems are important to constrain the three-nucleon (3N) interaction. The inclusion of few-body data to optimize nuclear Hamiltonians has become feasible due to the developments in exact many-body techniques such as Faddeev [98], Faddeev-Yakubovsky [99], hyperspherical harmonics [100], no-core shell-model [101], and QMC [52, 53]. In ChEFT, two additional parameters $c_D$ and $c_E$ appear in the 3N one-pion and contact diagrams at the leading order. Since it is known that the binding energies of 3N systems are strongly correlated, additional data are needed to constrain $c_D$ and $c_E$. Thus, the radii of the few-body systems are the potential candidates to further constrain the 3N LECs. For example, $c_D$ and $c_E$ in the widely used 1.8/2.0 (EM) interaction are determined to reproduce the triton binding energy and ⁴He matter radius. Also, the radii data were used to define the implausibility measure and to exclude the parameter space domains [46, 92, 93].

Moreover, the radii of few-body systems will be used to test the effect of the higher-order terms in the charge density operator. Deriving the analytical form of the charge radius operators is expected to be non-trivial for higher-order terms, especially the two-body contributions. In that case, computing the charge form factor and resorting to Equation 4 would be the most straightforward way. Indeed, in Table 1, within the numerical precision, one can see the equivalence between the two approaches, i.e., computing charge radii from the radius operator and the derivative of the form factor. All the radii are computed with the 1.8/2.0 (EM) interaction. The significant disagreement with the experimental ⁴He radius seems to be due to the updated proton radius [104].

Table 1

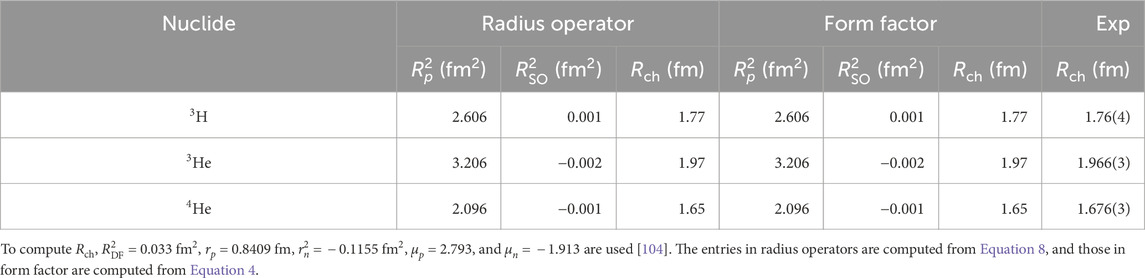
Table 1. Radii of three-body systems and ⁴He, computed with the Jacobi-coordinate no-sore shell model [102,103] using the 1.8/2.0 (EM) [82, 83] interaction.

3.2 Medium-mass and heavy nuclei

In the late 2000s to early 2010s, applications of the many-body methods whose computational costs scale polynomially with the system size began, such as the coupled-cluster method (CCM) [64], self-consistent Green’s function approach [62, 63], and in-medium similarity renormalization group (IMSRG) [65, 66, 77] enabling us to access medium-mass nuclei [17]. Initially, the numerical calculations were mostly done for the ground-state energies; soon after, the calculations of radii began. Owing to the advancement, it became possible to optimize the nuclear interactions using both few-body data and, for example, ¹⁶O radius [7–9]. The inclusion of beyond-few-body data enables us to extrapolate our knowledge from well-known to less-known systems.

Numerical calculations for heavy nuclei $A\gtrsim 100$ have been a challenge. As found in Refs. [105, 106], the calculations did not fully converge with respect to the 3N interaction space. Although the authors of Ref. [106] claimed that the extraction of radii is possible due to the convergence pattern of the computed radii, the fully converged results still need to be pursued. By leveraging the NO2B approximation (Equation 9), commonly used in standard calculations, one can overcome the limitation. In Ref. [89], a new technique to store the 3N matrix elements entering the NO2B Hamiltonian was introduced, which allows the reduction of memory size by two orders of magnitude. Due to this technical development, it is currently possible to obtain numerically converged results for $A\sim 200$ systems.

The study of charge radii provides insights into both nuclear interactions and the employed many-body approximations. Since the global behavior of charge radii appears to be well approximated by Hartree-Fock calculations, the deviations from experimental data indicate the insufficiency of the employed nuclear interaction. For example, the frequently used 1.8/2.0 (EM) interaction tends to predict too small radii [87]. Intuitively, smaller radii correspond to a higher density near the center of nuclei, which, in turn, is expected to lead to a higher saturation density in infinite nuclear matter calculations. Indeed, it was shown that the 1.8/2.0 (EM) interaction shows saturation at a higher density than empirical estimates [107]. Recently, based on a similar idea of the 1.8/2.0 (EM) interaction and optimizing with respect to the ¹⁶O data in addition to the few-body data, some nuclear interactions were developed. These interactions can accurately reproduce the ground-state energies and radii across the nuclear chart, including the neutron-rich region [10].

Recent advancements in experimental techniques, in particular laser spectroscopy, have significantly improved the precision of charge radii measurements, especially for exotic nuclei [4], providing stringent tests of employed nuclear Hamiltonian and many-body methods. Figure 3 shows the charge radii of nickel isotopes [108]. Panels (a) and (b) in the figure compare the results with the CC, SCGF, and IMSRG methods using the ${\text{N}}^2{\text{LO}}_{\text{sat}}$ interaction in absolute and relative scales, respectively, as well as those from the experiments. Here, the CC and SCGF uncertainties were estimated including the many-body uncertainty, while the IMSRG error bars were obtained from only the model-space variations (see [108] for more details). The theory results are consistent with each other, with only a few exceptions in the neutron deficient side, where the SCGF and IMSRG results do not overlap. From the figure, it is expected that the many-body method uncertainty for the absolute radii near spherical nuclei is about a few percent. Also, ab initio results reproduce the isotope shifts in the nickel isotopes.

Figure 3

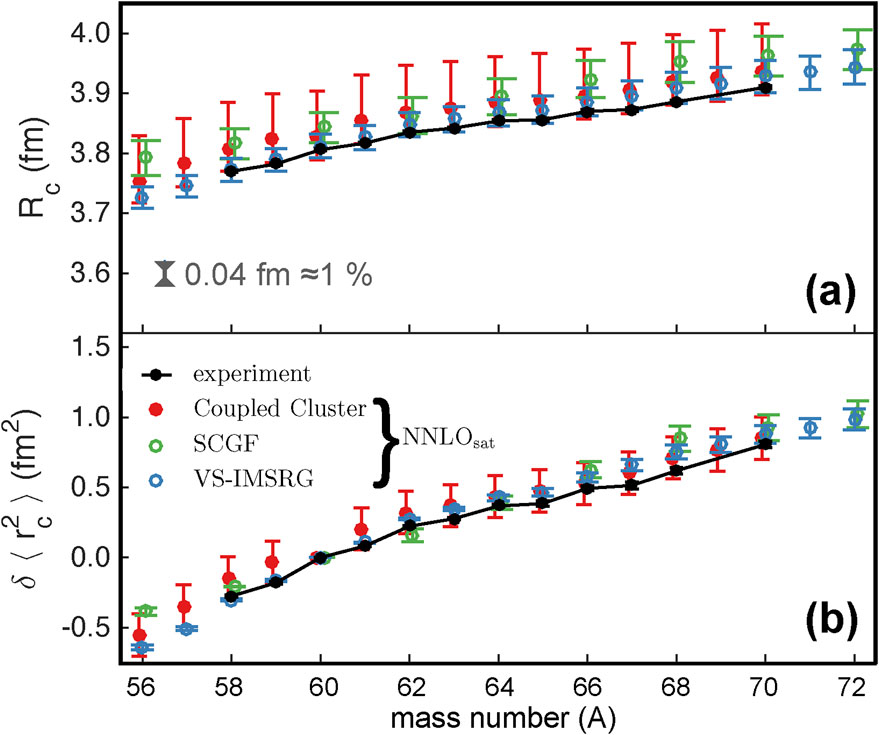
Figure 3. Charge radii for nickel isotopes. The experimental data [108] are illustrated with the points connected by the line. The absolute radii (a) and isotope shifts relative to ⁶⁰Ni (b) are shown. All the theory results are computed with the ${\text{N}}^2{\text{LO}}_{\text{sat}}$ interaction [7]. The figure is adapted from Ref. [108] under the CC BY 4.0 license.

In Figure 4, the odd-even staggering (OES) of binding energy and charge radius of the copper isotopes are shown. The OES is defined as

${\mathrm{\Delta }}_X^{\left[3\right]}=\frac{1}{2}\left[X\left(N+1\right)-2X\left(N\right)+X\left(N-1\right)\right].$

Here, $X$ is either binding energy or charge radius. In the figure, it is observed that the OES of the binding energy is reasonably reproduced both in density functional theory (DFT) and VS-IMSRG calculations. On the other hand, in the OES of the charge radius, the difference between DFT and VS-IMSRG results can be seen. In the DFT, it looks neither Fy(std) [109] nor Fy$(\mathrm{\Delta }r)$ [110, 111] can reproduce the reduction towards $N=50$. The VS-IMSRG results by 2.0/2.0 (PWA) and 1.8/2.0 (EM) interactions [82] reproduce the trend, while the size of the OES is imperfect around $N=40$, which is likely due to the missing proton excitations from $\pi f_{7/2}$ orbital. We note that the two interactions shown here do not reproduce the absolute charge radii as expected from the failure to reproduce the nuclear saturation density. The figure demonstrates that the radii OES is sensitive to the nuclear structure and that ab initio calculations sometimes could reproduce the detailed behavior of the radii as well as (or even better than) the DFT. A similar reproduction of the detailed behavior in the VS-ISMRG was also observed in a heavier region [113].

Figure 4

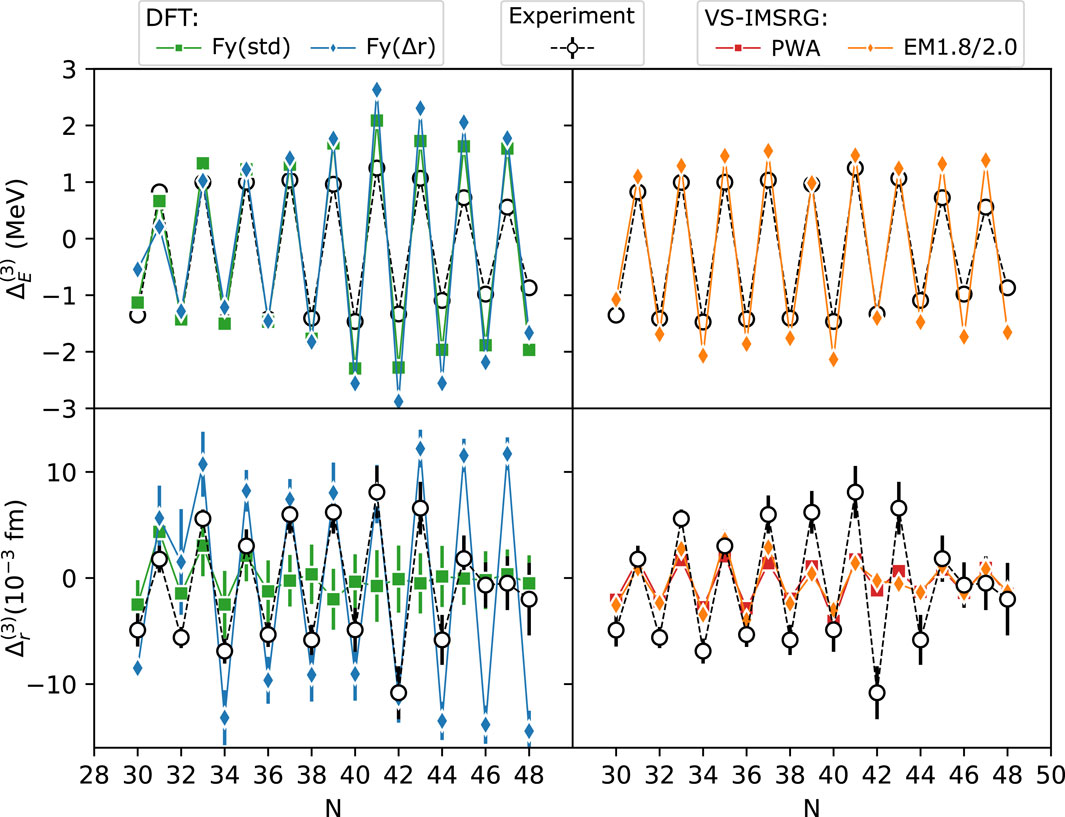
Figure 4. The OES of binding energies and charge radii in copper isotopes as a function of neutron number $N$. For the VS-IMSRG calculations, 2.0/2.0 (PWA) and 1.8/2.0 (EM) interaction [82] results are given by red squares and orange diamonds, respectively. For the DFT calculations, green squares are used for the Fy(std) [109] functional and blue diamonds for the Fy$(\mathrm{\Delta }r)$ [110, 111] functional. Error bars on the DFT calculations represent the statistical contribution. The calculations in the left panels were performed with DFT, while the right panels show the VS-IMSRG results. The figure is reprinted from Ref. [112] under the CC BY 4.0 license.

Despite the success discussed above, we should not forget that many challenges remain in ab initio radius calculations [114–119]. A typical example would be the behavior in the calcium charge radii in ^40–48Ca [109, 120]. The earlier shell-model calculation [120] demonstrated that the excitation across $Z=20$ is essential to explain the behavior from ⁴⁰Ca to ⁴⁸Ca. However, even if one explicitly includes such excitations in the VS-IMSRG [121], the parabolic isotope shift behavior could not be reproduced, although it was found that activating the ⁴⁰Ca core is needed to reproduce the magnetic dipole moment [39]. Note that the recent work with IMSRG showed that the inclusion of triple correlation effects does not resolve this issue [75]. These issues must be addressed in future studies.

4 Neutron skin thickness

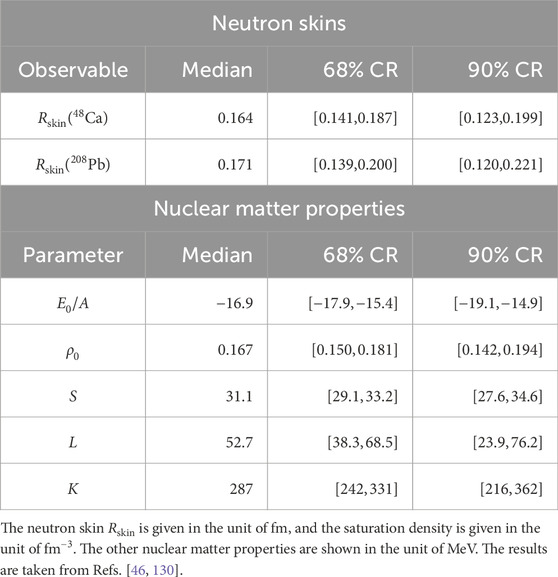
The neutron skin thickness is a key quantity to connect our understanding of finite nuclei and infinite nuclear matter. A pioneering work with the ab initio framework was done by Hagen et al. [122], where they computed point-proton and neutron radii of ⁴⁸Ca based on ${\lambda }_{\text{NN}}/{\mathrm{\Lambda }}_{3\text{N}}$ [82] and ${\text{N}}^2{\text{LO}}_{\text{sat}}$ [7] interactions. They found a strong correlation between them, and a smaller neutron skin range compared to the DFT results. Their findings are strengthened by the measurement of electric dipole polarizability of ⁴⁸Ca [123]. Also, the recent CREX [124] experiment result, $R_{\text{skin}}$(⁴⁸Ca)$=0.121\pm 0.026(\mathrm{e}\mathrm{x}\mathrm{p}.)\pm 0.024(\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l})$ fm, is consistent with the result in Ref. [122], which is $0.12\lesssim R_{\text{skin}}$(⁴⁸Ca) $\lesssim 0.15$ fm.

²⁰⁸Pb is the most appealing nucleus in terms of neutron skin calculations as it shows a strong correlation with the nuclear matter properties. In Ref. [46], a first prediction for the neutron skin of ²⁰⁸Pb was made after incorporating the uncertainties due to both nuclear Hamiltonians and many-body approaches. The results are illustrated in Figure 5. In the work, starting from the 34 non-implausible interactions after the history-matching technique (green distribution), the interactions are weighted according to the reproduction of the selected data of ⁴⁸Ca, to approximately obtain the posterior predictive distribution under the ⁴⁸Ca data (blue distribution). The procedure was validated with the existing data, and the predicted $68\%$ credible range of the ²⁰⁸Pb neutron skin is $0.14\le R_{\text{skin}}$(²⁰⁸Pb)$\le 0.20$ fm (pink distributions). Also, nuclear matter properties are summarized in Table 2 with a minor correction [130]. Remarkably, the predicted range excludes a thicker neutron skin predicted in mean-field type studies. It was found that the reproduction of the phase shift data in an intermediate energy prevents to have a thicker neutron skin.

Figure 5

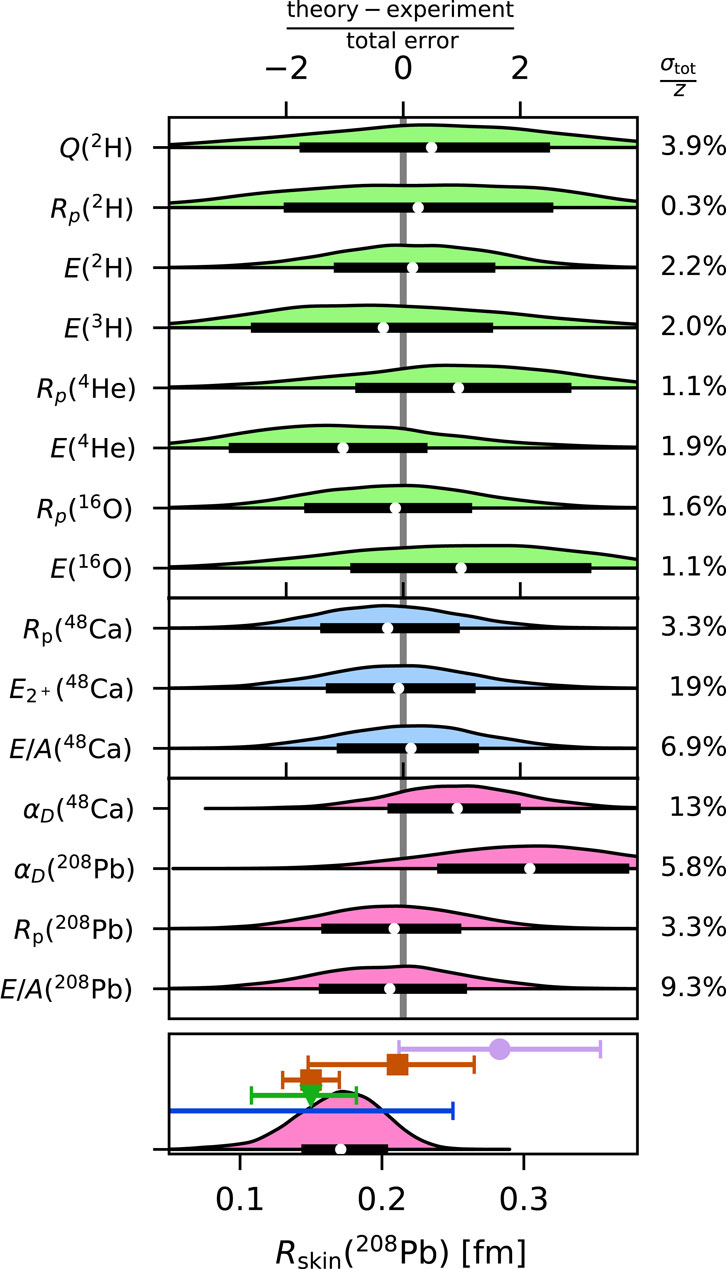
Figure 5. Probability distributions of selected observables for light to heavy nuclei. The green and blue distributions are for the observables used in the history-matching and likelihood calibration procedures, respectively. The posterior predictive distributions are indicated by the pink distributions. The nuclear observables shown are ²H quadrupole moment Q(²H), ²H point-proton radius R_p(²H), ²H ground-state energy E(²H), ³H ground-state energy E(³H), ⁴He point-proton radius R_p(⁴He), ⁴He ground-state energy E(⁴He), ¹⁶O point-proton radius R_p(¹⁶O), ¹⁶O ground-state energy E(¹⁶O), ⁴⁸Ca point-proton radius R_p(⁴⁸Ca), ⁴⁸Ca $2_1^{+}$ excitation energy E₂(⁴⁸Ca), ⁴⁸Ca ground-state energy per particle E/A(⁴⁸Ca), ⁴⁸Ca electric dipole polarizability ${\alpha }_D$(⁴⁸Ca), ²⁰⁸Pb electric dipole polarizability ${\alpha }_D$(²⁰⁸Pb), ²⁰⁸Pb point-proton radius $R_p$(²⁰⁸Pb), ²⁰⁸Pb ground-state energy per particle $E/A$(²⁰⁸Pb), and ²⁰⁸Pb neutron skin $R_{\text{skin}}$(²⁰⁸Pb). In the $R_{\text{skin}}$(²⁰⁸Pb) panel, the results are compared to the experimental (or observational) ones with electroweak [125] (purple), hadronic [126, 127] (red), electromagnetic [128] (green), and gravitational-wave [129] (blue) probes. The figure is reprinted from Ref. [46] under the CC BY 4.0 license.

Table 2

Table 2. Median, 68% and 90% credible regions of neutron skins and nuclear matter properties.

An experimentally clean extraction of neutron distribution is challenging as the neutron’s net electric charge vanishes. Parity-violating electron scattering (PVES) offers a model-independent way to access the neutron distribution because the process detects the contribution from the weak $Z$ boson. Since the exchanged $Z$ boson couples with the weak charge, which is almost $-1$ for the neutron and 0 for the proton, the neutron distribution can be deduced. In CREX and PREX experiments, the neutron skin thicknesses of ⁴⁸Ca [124] and ²⁰⁸Pb [125] were measured through the PVES process, respectively. In Figure 6, the situation is summarized. In the figure, the correlated uncertainty of the ab initio result is estimated by assuming that the distribution can be expressed by a multivariate normal distribution. For the covariance matrix, we use the 68% credible ranges found in Ref. [46] and the correlation coefficient. The correlation coefficient is obtained with the 19 non-implausible interaction results that are consistent with both credible ranges of ⁴⁸Ca and ²⁰⁸Pb. This procedure would approximately account for the correlation due to the LEC variations. A way to quantify the correlated uncertainty, including other sources such as the EFT and many-body methods, is being pursued and will be addressed in future work. As shown in the figure, none of the currently available theoretical models fall within (or overlap with) the $1\sigma$ region of the combined CREX and PREX results. We should, however, note that the comparison in terms of neutron skins might not be ideal, as the experimentally measured quantities were PVES asymmetry. For the ab initio calculations, to access the PVES asymmetries in a consistent way, similar to the recent work for the $\mu \to e$ conversion process [145], one would need to consistently compute nuclear densities and electron wave function. Additionally, the currently neglected contributions, such as the electromagnetic and weak two-body currents, may play a role. Therefore, further investigation would be needed to draw a conclusion.

Figure 6

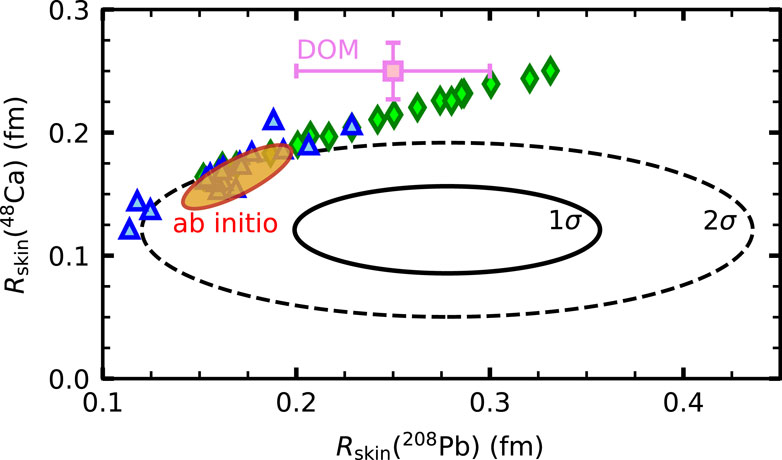
Figure 6. Neutron skin thickness of ⁴⁸Ca and ²⁰⁸Pb. The CREX [124] and PREX [125] experimental results are shown by the ellipses. The green diamonds (blue triangles) represent the relativistic [131–136] (non-relativistic [137–142], [90], [143], [13]) mean-field theory results. The ab initio results [46] and dispersive optical model (DOM) results [144] are also shown. For the ab initio result, the correlated uncertainty is obtained based on the correlation observed in the 19 non-implausible interaction results, which are consistent with the estimated 68% credible ranges [46]. The figure is adapted from Ref. [124].

Finally, it is worth noting that there could be another observable that correlates with $R_{\text{skin}}$ and the properties of nuclear matter. Recently, a strong correlation between the charge radii difference in mirror nuclei $\mathrm{\Delta }{R}_{\text{ch}}^{\text{mirr}}$ and the relevant quantities has been suggested, mainly in the mean-field studies [146–150]. Since $\mathrm{\Delta }{R}_{\text{ch}}^{\text{mirr}}$ is probed purely by the electromagnetic processes, experimental measurements of $\mathrm{\Delta }{R}_{\text{ch}}^{\text{mirr}}$ are expected to be easier than those of $R_{\text{skin}}$, where weak or strong interaction would be involved. Testing the suggested correlations is currently in progress within the ab initio framework [151, 152].

5 Conclusion

This review focuses on the recent progress in ab initio studies for nuclear radii. The current nuclear ab initio framework consists of deriving the nuclear Hamiltonian and relevant operators from ChEFT and solving the quantum many-body problem with a controllable approximation. The advantage of the framework is that one can quantify the uncertainties at each step and propagate them to the final results. It is particularly useful to make a prediction for which performing experiments is difficult or even impossible.

The range of applicability of the ab initio calculations is rapidly expanding, which is primarily driven by developments in the many-body methods whose computational costs scale polynomially with the system size. Currently, ²⁰⁸Pb is accessible starting from ChEFT. However, it does not mean that one can accurately compute the properties of all the nuclei up to ²⁰⁸Pb. The emergence of collective phenomena, such as deformation and clustering, based on the underlying interactions is still an open question. The related recent efforts focusing on the deformation can be found in Refs. [153–163].

Recent developments in experimental techniques have significantly improved the precision of charge radii measurements, providing stringent tests of the theoretical models. We observed that the results from different ab initio many-body methods starting with the same nuclear Hamiltonian basically agree with each other. Through the comparison, we find a few percent uncertainty due to the many-body approximation for the near spherical systems. Although the reproduction of the absolute charge radii strongly depends on the employed interaction, the local trends seem to be well reproduced by the ab initio calculations. For example, the performance of the ab initio results looks better than that of DFT for the odd-even staggering of the charge radii in the copper isotopes.

As suggested in many earlier mean-field theory studies, precise knowledge of $R_{\text{skin}}$ can be a key to shedding light on neutron star physics. Since the experimental determination is difficult as $R_{\text{skin}}$ involves the neutron density distribution, a reliable theoretical prediction is strongly required. After quantifying the uncertainties from the nuclear Hamiltonian and many-body methods, in Ref. [46], the predicted $68\%$ credible ranges are given as $0.141\le R_{\text{skin}}$(⁴⁸Ca) $\le 0.187$ fm and $0.139\le R_{\text{skin}}$(²⁰⁸Pb) $\le 0.20$ fm. While the predicted range of ⁴⁸Ca is consistent with the CREX experimental result, there is a mild tension between theory and PREX experimental results in ²⁰⁸Pb (see Figure 6). The reason for the tension is still unclear, and further efforts are needed.

Author contributions

TM: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is in part supported by JST ERATO Grant No. JPMJER2304, Japan.

Acknowledgments

The author would like to thank all his collaborators for fruitful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tanihata I. Neutron halo nuclei. J. Phys. G Nucl. Part. Phys. (1996) 22:157–98. doi:10.1088/0954-3899/22/2/004

CrossRef Full Text | Google Scholar

2. Tanihata I, Savajols H, Kanungo R. Recent experimental progress in nuclear halo structure studies. Prog. Part. Nucl. Phys. (2013) 68:215–313. doi:10.1016/j.ppnp.2012.07.001

CrossRef Full Text | Google Scholar

3. Ruiz RFG, Vernon AR. Emergence of simple patterns in many-body systems: from macroscopic objects to the atomic nucleus. Eur. Phys. J. A (2020) 56:136. doi:10.1140/epja/s10050-020-00134-8

CrossRef Full Text | Google Scholar

4. Yang X, Wang S, Wilkins S, Ruiz RG. Laser spectroscopy for the study of exotic nuclei. Prog. Part. Nucl. Phys. (2023) 129:104005. doi:10.1016/j.ppnp.2022.104005

CrossRef Full Text | Google Scholar

5. Reinhard PG, Nazarewicz W. Statistical correlations of nuclear quadrupole deformations and charge radii. Phys. Rev. C (2022) 106:014303. doi:10.1103/PhysRevC.106.014303

CrossRef Full Text | Google Scholar

6. Naito T, Oishi T, Sagawa H, Wang Z. Comparative study on charge radii and their kinks at magic numbers. Phys. Rev. C (2023) 107:054307. doi:10.1103/PhysRevC.107.054307

CrossRef Full Text | Google Scholar

7. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys. Rev. C (2015) 91:051301. doi:10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

8. Hüther T, Vobig K, Hebeler K, Machleidt R, Roth R. Family of chiral two-plus three-nucleon interactions for accurate nuclear structure studies. Phys. Lett. B (2020) 808:135651. doi:10.1016/j.physletb.2020.135651

CrossRef Full Text | Google Scholar

9. Jiang WG, Ekström A, Forssén C, Hagen G, Jansen GR, Papenbrock T. Accurate bulk properties of nuclei from A = 2 to ∞ from potentials with Δ isobars. Phys. Rev. C (2020) 102:054301. doi:10.1103/PhysRevC.102.054301

CrossRef Full Text | Google Scholar

10. Arthuis P, Hebeler K, Schwenk A. Neutron-rich nuclei and neutron skins from chiral low-resolution interactions. arXiv (2024). doi:10.48550/arXiv.2401.06675

CrossRef Full Text | Google Scholar

11. Alex BB. Neutron radii in nuclei and the neutron equation of state. Phys. Rev. Lett. (2000) 85:5296–9. doi:10.1103/PhysRevLett.85.5296

CrossRef Full Text | Google Scholar

12. Roca-Maza X, Centelles M, Viñas X, Warda M. Neutron skin of ²⁰⁸Pb, nuclear symmetry energy, and the parity radius experiment. Phys. Rev. Lett. (2011) 106:252501. doi:10.1103/PhysRevLett.106.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Erler J, Horowitz CJ, Nazarewicz W, Rafalski M, Reinhard PG. Energy density functional for nuclei and neutron stars. Phys. Rev. C (2013) 87:044320. doi:10.1103/PhysRevC.87.044320

CrossRef Full Text | Google Scholar

14. Cadeddu M, Giunti C, Li YF, Zhang YY. Average CsI neutron density distribution from COHERENT data. Phys. Rev. Lett. (2018) 120:072501. doi:10.1103/PhysRevLett.120.072501

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ishii N, Aoki S, Hatsuda T. Nuclear force from lattice QCD. Phys. Rev. Lett. (2007) 99:022001. doi:10.1103/PhysRevLett.99.022001

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Beane SR, Chang E, Cohen SD, Detmold W, Lin HW, Luu TC, et al. Light nuclei and hypernuclei from quantum chromodynamics in the limit of SU(3) flavor symmetry. Phys. Rev. D (2013) 87:034506. doi:10.1103/PhysRevD.87.034506

CrossRef Full Text | Google Scholar

17. Hergert H. A guided tour of ab initio nuclear many-body theory. Front. Phys. (2020) 8:1. doi:10.3389/fphy.2020.00379

CrossRef Full Text | Google Scholar

18. Ekström A, Forssén C, Hagen G, Jansen GR, Jiang W, Papenbrock T. What is ab initio in nuclear theory? Front. Phys. (2023) 11. doi:10.3389/fphy.2023.1129094

CrossRef Full Text | Google Scholar

19. Yukawa H. On the interaction of elementary particles. I. Proc. Phys. Math. Soc. Japan (1935) 17:48–57. doi:10.11429/ppmsj1919.17.0_48

CrossRef Full Text | Google Scholar

20. Weinberg S. Nuclear forces from chiral Lagrangians. Phys. Lett. B (1990) 251:288–92. doi:10.1016/0370-2693(90)90938-3

CrossRef Full Text | Google Scholar

21. Weinberg S. Effective chiral Lagrangians for nucleon-pion interactions and nuclear forces. Nucl. Phys. B (1991) 363:3–18. doi:10.1016/0550-3213(91)90231-L

CrossRef Full Text | Google Scholar

22. Weinberg S. Three-body interactions among nucleons and pions. Phys. Lett. B (1992) 295:114–21. doi:10.1016/0370-2693(92)90099-P

CrossRef Full Text | Google Scholar

23. Epelbaum E, Krebs H, Reinert P. High-precision nuclear forces from chiral EFT: state-of-the-art, challenges, and outlook. Front. Phys. (2020) 8:1–30. doi:10.3389/fphy.2020.00098

CrossRef Full Text | Google Scholar

24. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev. Mod. Phys. (2009) 81:1773–825. doi:10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

25. Machleidt R, Entem D. Chiral effective field theory and nuclear forces. Phys. Rep. (2011) 503:1–75. doi:10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

26. Epelbaum E, Krebs H, Meißner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur. Phys. J. A (2015) 51:53. doi:10.1140/epja/i2015-15053-8

CrossRef Full Text | Google Scholar

27. Furnstahl RJ, Phillips DR, Wesolowski S. A recipe for EFT uncertainty quantification in nuclear physics. J. Phys. G Nucl. Part. Phys. (2015) 42:034028. doi:10.1088/0954-3899/42/3/034028

CrossRef Full Text | Google Scholar

28. Melendez JA, Wesolowski S, Furnstahl RJ. Bayesian truncation errors in chiral effective field theory: nucleon-nucleon observables. Phys. Rev. C (2017) 96:024003. doi:10.1103/PhysRevC.96.024003

CrossRef Full Text | Google Scholar

29. Melendez JA, Furnstahl RJ, Phillips DR, Pratola MT, Wesolowski S. Quantifying correlated truncation errors in effective field theory. Phys. Rev. C (2019) 100:044001. doi:10.1103/PhysRevC.100.044001

CrossRef Full Text | Google Scholar

30. Park TS, Marcucci LE, Schiavilla R, Viviani M, Kievsky A, Rosati S, et al. Parameter-free effective field theory calculation for the solar proton-fusion and hep processes. Phys. Rev. C (2003) 67:055206. doi:10.1103/PhysRevC.67.055206

CrossRef Full Text | Google Scholar

31. Pastore S, Girlanda L, Schiavilla R, Viviani M, Wiringa RB. Electromagnetic currents and magnetic moments in chiral effective field theory (χeft). Phys. Rev. C (2009) 80:034004. doi:10.1103/PhysRevC.80.034004

CrossRef Full Text | Google Scholar

32. Pastore S, Pieper SC, Schiavilla R, Wiringa RB. Quantum Monte Carlo calculations of electromagnetic moments and transitions in A ≤ 9 nuclei with meson-exchange currents derived from chiral effective field theory. Phys. Rev. C (2013) 87:035503. doi:10.1103/PhysRevC.87.035503

CrossRef Full Text | Google Scholar

33. Kölling S, Epelbaum E, Krebs H, Meißner UG. Two-pion exchange electromagnetic current in chiral effective field theory using the method of unitary transformation. Phys. Rev. C (2009) 80:045502. doi:10.1103/PhysRevC.80.045502

CrossRef Full Text | Google Scholar

34. Kölling S, Epelbaum E, Krebs H, Meißner UG. Two-nucleon electromagnetic current in chiral effective field theory: one-pion exchange and short-range contributions. Phys. Rev. C (2011) 84:054008. doi:10.1103/PhysRevC.84.054008

CrossRef Full Text | Google Scholar

35. Krebs H, Epelbaum E, Meißner UG. Nuclear axial current operators to fourth order in chiral effective field theory. Ann. Phys. (N. Y). (2017) 378:317–95. doi:10.1016/j.aop.2017.01.021

CrossRef Full Text | Google Scholar

36. Krebs H, Epelbaum E, Meißner UG. Nuclear electromagnetic currents to fourth order in chiral effective field theory. Few-body Syst. (2019) 60:31. doi:10.1007/s00601-019-1500-5

CrossRef Full Text | Google Scholar

37. Gysbers P, Hagen G, Holt JD, Jansen GR, Morris TD, Navrátil P, et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat. Phys. (2019) 15:428–31. doi:10.1038/s41567-019-0450-7

CrossRef Full Text | Google Scholar

38. Friman-Gayer U, Romig C, Hüther T, Albe K, Bacca S, Beck T, et al. Role of chiral two-body currents in ⁶Li magnetic properties in light of a new precision measurement wit. Phys. Rev. Lett. (2021) 126:102501. doi:10.1103/PhysRevLett.126.102501

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Miyagi T, Cao X, Seutin R, Bacca S, Ruiz RFG, Hebeler K, et al. Impact of two-body currents on magnetic dipole moments of nuclei. Phys. Rev. Lett. (2024) 132:232503. doi:10.1103/PhysRevLett.132.232503

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Chambers-Wall G, Gnech A, King GB, Pastore S, Piarulli M, Schiavilla R, et al. Quantum Monte Carlo calculations of magnetic form factors in light nuclei. Phys. Rev. Lett. (2024) 133:212501. doi:10.1103/PhysRevLett.133.212501

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Pastore S, Girlanda L, Schiavilla R, Viviani M. Two-nucleon electromagnetic charge operator in chiral effective field theory χEFT up to one loop. Phys. Rev. C (2011) 84:024001. doi:10.1103/PhysRevC.84.024001

CrossRef Full Text | Google Scholar

42. Krebs H. Nuclear currents in chiral effective field theory. Eur. Phys. J. A (2020) 56:234. doi:10.1140/epja/s10050-020-00230-9

CrossRef Full Text | Google Scholar

43. King GB, Chambers-Wall G, Gnech A, Pastore S, Piarulli M, Wiringa RB. Longitudinal form factors of A ≤ 10 nuclei in a chiral effective field theory approach. Phys. Rev. C (2024) 110:054325. doi:10.1103/PhysRevC.110.054325

CrossRef Full Text | Google Scholar

44. Door M, Yeh CH, Heinz M, Kirk F, Lyu C, Miyagi T, et al. Search for new bosons with ytterbium isotope shifts. arXiv:2403 (2024) 07792. doi:10.1103/PhysRevLett.134.063002

CrossRef Full Text | Google Scholar

45. Kurasawa H, Suzuki T. The nth-order moment of the nuclear charge density and contribution from the neutrons. Prog. Theor. Exp. Phys. (2019) 2019. doi:10.1093/ptep/ptz121

CrossRef Full Text | Google Scholar

46. Hu B, Jiang W, Miyagi T, Sun Z, Ekström A, Forssén C, et al. Ab initio predictions link the neutron skin of 208Pb to nuclear forces. Nat. Phys. (2022) 18:1196–200. doi:10.1038/s41567-022-01715-8

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Hergert H, Binder S, Calci A, Langhammer J, Roth R. Ab initio calculations of even oxygen isotopes with chiral two- plus three-nucleon interactions. Phys. Rev. Lett. (2013) 110:242501. doi:10.1103/PhysRevLett.110.242501

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Roth R, Calci A, Langhammer J, Binder S. Evolved chiral NN + 3N Hamiltonians for ab initio nuclear structure calculations. Phys. Rev. C (2014) 90:024325. doi:10.1103/PhysRevC.90.024325

CrossRef Full Text | Google Scholar

49. Hao Y, Navrátil P, Norrgard EB, Iliaš M, Eliav E, Timmermans RGE, et al. Nuclear spin-dependent parity-violating effects in light polyatomic molecules. Phys. Rev. A (2020) 102:052828. doi:10.1103/PhysRevA.102.052828

CrossRef Full Text | Google Scholar

50. Froese P, Navrátil P. Ab initio calculations of electric dipole moments of light nuclei. Phys. Rev. C (2021) 104:025502. doi:10.1103/PhysRevC.104.025502

CrossRef Full Text | Google Scholar

51. Pieper SC, Wiringa RB. Quantum monte carlo calculations of light nuclei. Annu. Rev. Nucl. Part. Sci. (2001) 51:53–90. doi:10.1146/annurev.nucl.51.101701.132506

CrossRef Full Text | Google Scholar

52. Carlson J, Gandolfi S, Pederiva F, Pieper SC, Schiavilla R, Schmidt KE, et al. Quantum Monte Carlo methods for nuclear physics. Rev. Mod. Phys. (2015) 87:1067–118. doi:10.1103/RevModPhys.87.1067

CrossRef Full Text | Google Scholar

53. Gandolfi S, Lonardoni D, Lovato A, Piarulli M. Atomic nuclei from quantum Monte Carlo calculations with chiral EFT interactions. Front. Phys. (2020) 8. doi:10.3389/fphy.2020.00117

CrossRef Full Text | Google Scholar

54. Lee D. Lattice simulations for few- and many-body systems. Prog. Part. Nucl. Phys. (2009) 63:117–54. doi:10.1016/j.ppnp.2008.12.001

CrossRef Full Text | Google Scholar

55. Lähde TA, Meißner UG. Nuclear lattice effective field theory. In: Lecture notes in physics, 957. Cham: Springer International Publishing (2019). doi:10.1007/978-3-030-14189-9

CrossRef Full Text | Google Scholar

56. Elhatisari S, Bovermann L, Ma YZ, Epelbaum E, Frame D, Hildenbrand F, et al. Wavefunction matching for solving quantum many-body problems. Nature (2024) 630:59–63. doi:10.1038/s41586-024-07422-z

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Hagen G, Papenbrock T, Dean DJ, Schwenk A, Nogga A, Włoch M, et al. Coupled-cluster theory for three-body Hamiltonians. Phys. Rev. C (2007) 76:034302. doi:10.1103/PhysRevC.76.034302

CrossRef Full Text | Google Scholar

58. Roth R, Binder S, Vobig K, Calci A, Langhammer J, Navrátil P. Medium-mass nuclei with normal-ordered chiral NN + 3N interactions. Phys. Rev. Lett. (2012) 109:052501. doi:10.1103/PhysRevLett.109.052501

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Binder S, Langhammer J, Calci A, Navrátil P, Roth R. Ab initio calculations of medium-mass nuclei with explicit chiral 3N interactions. Phys. Rev. C (2013) 87:021303. doi:10.1103/PhysRevC.87.021303

CrossRef Full Text | Google Scholar

60. Djärv T, Ekström A, Forssén C, Jansen GR. Normal-ordering approximations and translational (non)invariance. Phys. Rev. C (2021) 104:024324. doi:10.1103/PhysRevC.104.024324

CrossRef Full Text | Google Scholar

61. Tichai A, Roth R, Duguet T. Many-body perturbation theories for finite nuclei. Front. Phys. (2020) 8:1–29. doi:10.3389/fphy.2020.00164

CrossRef Full Text | Google Scholar

62. Dickhoff W, Barbieri C. Self-consistent Green’s function method for nuclei and nuclear matter. Prog. Part. Nucl. Phys. (2004) 52:377–496. doi:10.1016/j.ppnp.2004.02.038

CrossRef Full Text | Google Scholar

63. Somà V. Self-consistent Green’s function theory for atomic nuclei. Front. Phys. (2020) 8:1–31. doi:10.3389/fphy.2020.00340

CrossRef Full Text | Google Scholar

64. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean DJ. Coupled-cluster computations of atomic nuclei. Rep Prog. Phys. (2014) 77:096302. doi:10.1088/0034-4885/77/9/096302

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Hergert H, Bogner S, Morris T, Schwenk A, Tsukiyama K. The In-Medium Similarity Renormalization Group: a novel ab initio method for nuclei. Phys. Rep. (2016) 621:165–222. doi:10.1016/j.physrep.2015.12.007

CrossRef Full Text | Google Scholar

66. Hergert H. In-medium similarity renormalization group for closed and open-shell nuclei. Phys. Scr. (2017) 92:023002. doi:10.1088/1402-4896/92/2/023002

CrossRef Full Text | Google Scholar

67. Roth R, Gour JR, Piecuch P. Ab initio coupled-cluster and configuration interaction calculations for O 16 using the V UCOM interaction. Phys. Rev. C (2009) 79:054325. doi:10.1103/PhysRevC.79.054325

CrossRef Full Text | Google Scholar

68. Morris TD, Simonis J, Stroberg SR, Stumpf C, Hagen G, Holt JD, et al. Structure of the lightest tin isotopes. Phys. Rev. Lett. (2018) 120:152503. doi:10.1103/PhysRevLett.120.152503

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Miorelli M, Bacca S, Hagen G, Papenbrock T. Computing the dipole polarizability of 48Ca with increased precision. Phys. Rev. C (2018) 98:014324. doi:10.1103/PhysRevC.98.014324

CrossRef Full Text | Google Scholar

70. Heinz M, Tichai A, Hoppe J, Hebeler K, Schwenk A. In-medium similarity renormalization group with three-body operators. Phys. Rev. C (2021) 103:044318. doi:10.1103/PhysRevC.103.044318

CrossRef Full Text | Google Scholar

71. Bonaiti F, Bacca S, Hagen G. Ab initio coupled-cluster calculations of ground and dipole excited states in He 8. Phys. Rev. C (2022) 105:034313. doi:10.1103/PhysRevC.105.034313

CrossRef Full Text | Google Scholar

72. Bonaiti F, Bacca S, Hagen G, Jansen GR. Electromagnetic observables of open-shell nuclei from coupled-cluster theory. Phys. Rev. C (2024) 110:044306. doi:10.1103/PhysRevC.110.044306

CrossRef Full Text | Google Scholar

73. He BC, Stroberg SR. Factorized approximation to the in-medium similarity renormalization group IMSRG(3). Phys. Rev. C (2024) 110:044317. doi:10.1103/PhysRevC.110.044317

CrossRef Full Text | Google Scholar

74. Stroberg SR, Morris TD, He BC. In-medium similarity renormalization group with flowing 3-body operators, and approximations thereof. Phys. Rev. C (2024) 110:044316. doi:10.1103/PhysRevC.110.044316

CrossRef Full Text | Google Scholar

75. Heinz M, Miyagi T, Stroberg SR, Tichai A, Hebeler K, Schwenk A. Improved structure of calcium isotopes from ab initio calculations. Phys. Rev. C (2024) 111:034311. doi:10.1103/PhysRevC.111.034311

CrossRef Full Text | Google Scholar

76. Morris TD, Parzuchowski NM, Bogner SK. Magnus expansion and in-medium similarity renormalization group. Phys. Rev. C (2015) 92:034331. doi:10.1103/PhysRevC.92.034331

CrossRef Full Text | Google Scholar

77. Stroberg SR, Hergert H, Bogner SK, Holt JD. Nonempirical interactions for the nuclear shell model: an update. Annu. Rev. Nucl. Part. Sci. (2019) 69:307–62. doi:10.1146/annurev-nucl-101917-021120

CrossRef Full Text | Google Scholar

78. Caurier E, Nowacki F. Present status of shell model techniques. Acta Phys. Pol. B (1999) 30:705.

Google Scholar

79. Brown B, Rae W. The shell-model code NuShellX@MSU. Nucl. Data Sheets (2014) 120:115–8. doi:10.1016/j.nds.2014.07.022

CrossRef Full Text | Google Scholar

80. Johnson CW, Ormand WE, McElvain KS, Shan H. BIGSTICK: a flexible configuration-interaction shell-model code. arXiv:1801 (2018) 08432. doi:10.48550/arXiv.1801.08432

CrossRef Full Text | Google Scholar

81. Shimizu N, Mizusaki T, Utsuno Y, Tsunoda Y. Thick-restart block Lanczos method for large-scale shell-model calculations. Comput. Phys. Commun. (2019) 244:372–84. doi:10.1016/j.cpc.2019.06.011

CrossRef Full Text | Google Scholar

82. Hebeler K, Bogner SK, Furnstahl RJ, Nogga A, Schwenk A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys. Rev. C (2011) 83:031301. doi:10.1103/PhysRevC.83.031301

CrossRef Full Text | Google Scholar

83. Entem DR, Machleidt R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys. Rev. C (2003) 68:041001. doi:10.1103/PhysRevC.68.041001

CrossRef Full Text | Google Scholar

84. Bogner SK, Furnstahl RJ, Perry RJ. Similarity renormalization group for nucleon-nucleon interactions. Phys. Rev. C (2007) 75:061001. doi:10.1103/PhysRevC.75.061001

CrossRef Full Text | Google Scholar

85. Rentmeester MCM, Timmermans RGE, de Swart JJ. Determination of the chiral coupling constants c₃ and c₄ in new pp and np partial-wave analyses. Phys. Rev. C (2003) 67:044001. doi:10.1103/PhysRevC.67.044001

CrossRef Full Text | Google Scholar

86. Epelbaum E, Glöckle W, Meißner UG. The two-nucleon system at next-to-next-to-next-to-leading order. Nucl. Phys. A (2005) 747:362–424. doi:10.1016/j.nuclphysa.2004.09.107

CrossRef Full Text | Google Scholar

87. Simonis J, Stroberg SR, Hebeler K, Holt JD, Schwenk A. Saturation with chiral interactions and consequences for finite nuclei. Phys. Rev. C (2017) 96:014303. doi:10.1103/PhysRevC.96.014303

CrossRef Full Text | Google Scholar

88. Stroberg SR, Holt JD, Schwenk A, Simonis J. Ab initio limits of atomic nuclei. Phys. Rev. Lett. (2021) 126:022501. doi:10.1103/PhysRevLett.126.022501

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Miyagi T, Stroberg SR, Navrátil P, Hebeler K, Holt JD. Converged ab initio calculations of heavy nuclei. Phys. Rev. C (2022) 105:014302. doi:10.1103/PhysRevC.105.014302

CrossRef Full Text | Google Scholar

90. Kortelainen M, Lesinski T, Moré J, Nazarewicz W, Sarich J, Schunck N, et al. Nuclear energy density optimization. Phys. Rev. C (2010) 82:024313. doi:10.1103/PhysRevC.82.024313

CrossRef Full Text | Google Scholar

91. Ekström A, Hagen G, Morris TD, Papenbrock T, Schwartz PD. Δ isobars and nuclear saturation. Phys. Rev. C (2018) 97:024332. doi:10.1103/PhysRevC.97.024332

CrossRef Full Text | Google Scholar

92. Kondo Y, Achouri NL, Falou HA, Atar L, Aumann T, Baba H, et al. First observation of 28O. Nature (2023) 620:965–70. doi:10.1038/s41586-023-06352-6

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Jiang WG, Forssén C, Djärv T, Hagen G. Nuclear-matter saturation and symmetry energy within Δ -full chiral effective field theory. Phys. Rev. C (2024) 109:L061302. doi:10.1103/PhysRevC.109.L061302

CrossRef Full Text | Google Scholar

94. Bower RG, Goldstein M, Vernon I. Galaxy formation: a Bayesian uncertainty analysis. Bayesian Anal (2010) 5. doi:10.1214/10-BA524

CrossRef Full Text | Google Scholar

95. Vernon I, Goldstein M, Bower R. Galaxy Formation: bayesian history matching for the observable universe. Stat. Sci. (2014) 29. doi:10.1214/12-STS412

CrossRef Full Text | Google Scholar

96. Wiringa RB, Stoks VGJ, Schiavilla R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys. Rev. C (1995) 51:38–51. doi:10.1103/PhysRevC.51.38

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Machleidt R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys. Rev. C (2001) 63:024001. doi:10.1103/PhysRevC.63.024001

CrossRef Full Text | Google Scholar

98. Faddeev LD. Scattering theory for a three particle system. Zh. Eksp. Teor. Fiz. (1960) 39:1459.

Google Scholar

99. Yakubovsky O. On the Integral equations in the theory of N particle scattering. Sov.J.Nucl.Phys. (1967) 5:937.

Google Scholar

100. Marcucci LE, Dohet-Eraly J, Girlanda L, Gnech A, Kievsky A, Viviani M. The hyperspherical harmonics method: a tool for testing and improving nuclear interaction models. Front. Phys. (2020) 8. doi:10.3389/fphy.2020.00069

CrossRef Full Text | Google Scholar

101. Barrett BR, Navrátil P, Vary JP. Ab initio no core shell model. Prog. Part. Nucl. Phys. (2013) 69:131–81. doi:10.1016/j.ppnp.2012.10.003

CrossRef Full Text | Google Scholar

102. Navrátil P, Barrett BR. Four-nucleon shell-model calculations in a Faddeev-like approach. Phys. Rev. C (1999) 59:1906–18. doi:10.1103/PhysRevC.59.1906

CrossRef Full Text | Google Scholar

103. Navrátil P, Vary JP, Barrett BR. Large-basis ab initio no-core shell model and its application to 12 C. Phys. Rev. C (2000) 62:054311. doi:10.1103/PhysRevC.62.054311

CrossRef Full Text | Google Scholar

104. Navas S, Amsler C, Gutsche T, Hanhart C, Hernández-Rey JJ, Lourenço C, et al. Review of particle physics. Phys. Rev. D (2024) 110:030001. doi:10.1103/PhysRevD.110.030001

CrossRef Full Text | Google Scholar

105. Binder S, Langhammer J, Calci A, Roth R. Ab initio path to heavy nuclei. Phys. Lett. B (2014) 736:119–23. doi:10.1016/j.physletb.2014.07.010

CrossRef Full Text | Google Scholar

106. Arthuis P, Barbieri C, Vorabbi M, Finelli P. Ab initio computation of charge densities for Sn and Xe isotopes. Phys. Rev. Lett. (2020) 125:182501. doi:10.1103/PhysRevLett.125.182501

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Drischler C, Hebeler K, Schwenk A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys. Rev. Lett. (2019) 122:042501. doi:10.1103/PhysRevLett.122.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Malbrunot-Ettenauer S, Kaufmann S, Bacca S, Barbieri C, Billowes J, Bissell ML, et al. Nuclear charge radii of the nickel isotopes ^58–68,70Ni. Phys. Rev. Lett. (2022) 128:022502. doi:10.1103/PhysRevLett.128.022502

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Reinhard PG, Nazarewicz W. Toward a global description of nuclear charge radii: exploring the Fayans energy density functional. Phys. Rev. C (2017) 95:064328. doi:10.1103/PhysRevC.95.064328

CrossRef Full Text | Google Scholar

110. Gorges C, Rodríguez LV, Balabanski DL, Bissell ML, Blaum K, Cheal B, et al. Laser spectroscopy of neutron-rich tin isotopes: a discontinuity in charge radii across the N=82 shell closure. Phys. Rev. Lett. (2019) 122:192502. doi:10.1103/PhysRevLett.122.192502

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Miller AJ, Minamisono K, Klose A, Garand D, Kujawa C, Lantis JD, et al. Proton superfluidity and charge radii in proton-rich calcium isotopes. Nat. Phys. (2019) 15:432–6. doi:10.1038/s41567-019-0416-9

CrossRef Full Text | Google Scholar

112. de Groote RP, Billowes J, Binnersley CL, Bissell ML, Cocolios TE, Day Goodacre T, et al. Measurement and microscopic description of oddˆˆe2ˆˆ80ˆˆ93even staggering of charge radii of exotic copper isotopes. Nat. Phys. (2020) 16:620–4. doi:10.1038/s41567-020-0868-y

CrossRef Full Text | Google Scholar

113. Karthein J, Ricketts CM, Garcia Ruiz RF, Billowes J, Binnersley CL, Cocolios TE, et al. Electromagnetic properties of indium isotopes illuminate the doubly magic character of 100Sn. Nat. Phys. (2024) 20:1719–25. doi:10.1038/s41567-024-02612-y

CrossRef Full Text | Google Scholar

114. Garcia Ruiz RF, Bissell ML, Blaum K, Ekström A, Frömmgen N, Hagen G, et al. Unexpectedly large charge radii of neutron-rich calcium isotopes. Nat. Phys. (2016) 12:594–8. doi:10.1038/nphys3645

CrossRef Full Text | Google Scholar

115. Novario SJ, Hagen G, Jansen GR, Papenbrock T. Charge radii of exotic neon and magnesium isotopes. Phys. Rev. C (2020) 102:051303. doi:10.1103/PhysRevC.102.051303

CrossRef Full Text | Google Scholar

116. Heylen H, Devlin CS, Gins W, Bissell ML, Blaum K, Cheal B, et al. High-resolution laser spectroscopy of ^27–32Al. Phys. Rev. C (2021) 103:014318. doi:10.1103/PhysRevC.103.014318

CrossRef Full Text | Google Scholar

117. Koszorús Á, Vormawah L, Beerwerth R, Bissell M, Campbell P, Cheal B, et al. Proton-neutron pairing correlations in the self-conjugate nucleus 42Sc. Phys. Lett. B (2021) 819:136439. doi:10.1016/j.physletb.2021.136439

CrossRef Full Text | Google Scholar

118. Koszorús Á, Yang XF, Jiang WG, Novario SJ, Bai SW, Billowes J, et al. Publisher Correction: charge radii of exotic potassium isotopes challenge nuclear theory and the magic character of N = 32. Nat. Phys. (2021) 17:539. doi:10.1038/s41567-021-01192-5

CrossRef Full Text | Google Scholar

119. König K, Fritzsche S, Hagen G, Holt JD, Klose A, Lantis J, et al. Surprising charge-radius kink in the Sc isotopes at N = 20. Phys. Rev. Lett. (2023) 131:102501. doi:10.1103/PhysRevLett.131.102501

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Caurier E, Langanke K, Martínez-Pinedo G, Nowacki F, Vogel P. Shell model description of isotope shifts in calcium. Phys. Lett. B (2001) 522:240–4. doi:10.1016/S0370-2693(01)01246-1

CrossRef Full Text | Google Scholar

121. Miyagi T, Stroberg SR, Holt JD, Shimizu N. Ab initio multishell valence-space Hamiltonians and the island of inversion. Phys. Rev. C (2020) 102:034320. doi:10.1103/PhysRevC.102.034320

CrossRef Full Text | Google Scholar

122. Hagen G, Ekström A, Forssén C, Jansen GR, Nazarewicz W, Papenbrock T, et al. Neutron and weak-charge distributions of the 48 Ca nucleus. Nat. Phys. (2016) 12:186–90. doi:10.1038/nphys3529

CrossRef Full Text | Google Scholar

123. Birkhan J, Miorelli M, Bacca S, Bassauer S, Bertulani CA, Hagen G, et al. Electric dipole polarizability of ⁴⁸Ca and implications for the neutron skin. Phys. Rev. Lett. (2017) 118:252501. doi:10.1103/PhysRevLett.118.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Adhikari D, Albataineh H, Androic D, Aniol KA, Armstrong DS, Averett T, et al. Precision determination of the neutral weak form factor of ⁴⁸Ca. Phys. Rev. Lett. (2022) 129:042501. doi:10.1103/PhysRevLett.129.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Adhikari D, Albataineh H, Androic D, Aniol K, Armstrong DS, Averett T, et al. Accurate determination of the neutron skin thickness of ²⁰⁸Pb through parity-violation in electron scat. Phys. Rev. Lett. (2021) 126:172502. doi:10.1103/PhysRevLett.126.172502

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Trzcińska A, Jastrzȩbski J, Lubiński P, Hartmann FJ, Schmidt R, von Egidy T, et al. Neutron density distributions deduced from antiprotonic atoms. Phys. Rev. Lett. (2001) 87:082501. doi:10.1103/PhysRevLett.87.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

127. Zenihiro J, Sakaguchi H, Murakami T, Yosoi M, Yasuda Y, Terashima S, et al. Neutron density distributions of ^204,206,208Pb deduced via proton elastic scattering at E_p=295 MeV. Phys. Rev. C (2010) 82:044611. doi:10.1103/PhysRevC.82.044611

CrossRef Full Text | Google Scholar

128. Tarbert CM, Watts DP, Glazier DI, Aguar P, Ahrens J, Annand JRM, et al. Neutron skin of ²⁰⁸Pb from coherent pion photoproduction. Phys. Rev. Lett. (2014) 112:242502. doi:10.1103/PhysRevLett.112.242502

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Fattoyev FJ, Piekarewicz J, Horowitz CJ. Neutron skins and neutron stars in the multimessenger era. Phys. Rev. Lett. (2018) 120:172702. doi:10.1103/PhysRevLett.120.172702

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Hu B, Jiang W, Miyagi T, Sun Z, Ekström A, Forssén C, et al. Author Correction: ab initio predictions link the neutron skin of 208Pb to nuclear forces. Nat. Phys. (2024) 20:169. doi:10.1038/s41567-023-02324-9

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Todd-Rutel BG, Piekarewicz J. Neutron-rich nuclei and neutron stars: a new accurately calibrated interaction for the study of neutron-rich matter. Phys. Rev. Lett. (2005) 95:122501. doi:10.1103/PhysRevLett.95.122501

PubMed Abstract | CrossRef Full Text | Google Scholar

132. Fattoyev FJ, Horowitz CJ, Piekarewicz J, Shen G. Relativistic effective interaction for nuclei, giant resonances, and neutron stars. Phys. Rev. C (2010) 82:055803. doi:10.1103/PhysRevC.82.055803

CrossRef Full Text | Google Scholar

133. Fattoyev FJ, Piekarewicz J. Has a thick neutron skin in 208Pb been ruled out? Phys. Rev. Lett. (2013) 111:162501. doi:10.1103/PhysRevLett.111.162501

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Chen WC, Piekarewicz J. Building relativistic mean field models for finite nuclei and neutron stars. Phys. Rev. C (2014) 90:044305. doi:10.1103/PhysRevC.90.044305

CrossRef Full Text | Google Scholar

135. Chen WC, Piekarewicz J. Searching for isovector signatures in the neutron-rich oxygen and calcium isotopes. Phys. Lett. B (2015) 748:284–8. doi:10.1016/j.physletb.2015.07.020

CrossRef Full Text | Google Scholar

136. Reed BT, Fattoyev FJ, Horowitz CJ, Piekarewicz J. Implications of PREX-2 on the equation of state of neutron-rich matter. Phys. Rev. Lett. (2021) 126:172503. doi:10.1103/PhysRevLett.126.172503

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Skyrme T. The effective nuclear potential. Nucl. Phys. (1958) 9:615–34. doi:10.1016/0029-5582(58)90345-6

CrossRef Full Text | Google Scholar

138. Vautherin D, Brink DM. Hartree-Fock calculations with skyrme’s interaction. I. Spherical nuclei. Phys. Rev. C (1972) 5:626–47. doi:10.1103/PhysRevC.5.626

CrossRef Full Text | Google Scholar

139. Bartel J, Quentin P, Brack M, Guet C, Håkansson HB. Towards a better parametrisation of Skyrme-like effective forces: a critical study of the SkM force. Nucl. Phys. A (1982) 386:79–100. doi:10.1016/0375-9474(82)90403-1

CrossRef Full Text | Google Scholar

140. Chabanat E, Bonche P, Haensel P, Meyer J, Schaeffer R. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nucl. Phys. A (1998) 635:231–56. doi:10.1016/S0375-9474(98)00180-8

CrossRef Full Text | Google Scholar

141. Horowitz CJ, Piekarewicz J. Neutron radii of 208Pb and neutron stars. Phys. Rev. C (2001) 64:062802. doi:10.1103/PhysRevC.64.062802

CrossRef Full Text | Google Scholar

142. Klüpfel P, Reinhard PG, Bürvenich TJ, Maruhn JA. Variations on a theme by Skyrme: a systematic study of adjustments of model parameters. Phys. Rev. C (2009) 79:034310. doi:10.1103/PhysRevC.79.034310

CrossRef Full Text | Google Scholar

143. Kortelainen M, McDonnell J, Nazarewicz W, Reinhard PG, Sarich J, Schunck N, et al. Nuclear energy density optimization: large deformations. Phys. Rev. C (2012) 85:024304. doi:10.1103/PhysRevC.85.024304

CrossRef Full Text | Google Scholar

144. Atkinson MC, Mahzoon MH, Keim MA, Bordelon BA, Pruitt CD, Charity RJ, et al. Dispersive optical model analysis of 208Pb generating a neutron-skin prediction beyond the mean field. Phys. Rev. C (2020) 101:044303. doi:10.1103/PhysRevC.101.044303

CrossRef Full Text | Google Scholar

145. Heinz M, Hoferichter M, Miyagi T, Noël F, Schwenk A. Ab initio calculations of overlap integrals for μ → e conversion in nuclei. arXiv:2412 04545 (2024). doi:10.48550/arXiv.2412.04545

CrossRef Full Text | Google Scholar

146. Brown BA. Mirror charge radii and the neutron equation of state. Phys. Rev. Lett. (2017) 119:122502–5. doi:10.1103/PhysRevLett.119.122502

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Yang J, Piekarewicz J. Difference in proton radii of mirror nuclei as a possible surrogate for the neutron skin. Phys. Rev. C (2018) 97:014314. doi:10.1103/PhysRevC.97.014314

CrossRef Full Text | Google Scholar

148. Brown BA, Minamisono K, Piekarewicz J, Hergert H, Garand D, Klose A, et al. Implications of the 36Ca-36S and 38Ca-38Ar difference in mirror charge radii on the neutron matter equation of state. Phys. Rev. Res. (2020) 2:022035. doi:10.1103/PhysRevResearch.2.022035

CrossRef Full Text | Google Scholar

149. Pineda SV, König K, Rossi DM, Brown BA, Incorvati A, Lantis J, et al. Charge radius of neutron-deficient ^{54}Ni and symmetry energy constraints using the difference in mirror pair charge radii. Phys. Rev. Lett. (2021) 127:182503. doi:10.1103/PhysRevLett.127.182503

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Bano P, Pattnaik SP, Centelles M, Viñas X, Routray TR. Correlations between charge radii differences of mirror nuclei and stellar observables. Phys. Rev. C (2023) 108:015802. doi:10.1103/PhysRevC.108.015802

CrossRef Full Text | Google Scholar

151. Novario SJ, Lonardoni D, Gandolfi S, Hagen G. Trends of neutron skins and radii of mirror nuclei from first principles. Phys. Rev. Lett. (2023) 130:032501. doi:10.1103/PhysRevLett.130.032501

PubMed Abstract | CrossRef Full Text | Google Scholar

152. Hu BS. How do mirror charge radii constrain density dependence of the symmetry energy? Phys. Lett. B (2024) 857:138969. doi:10.1016/j.physletb.2024.138969

CrossRef Full Text | Google Scholar

153. Yao JM, Bally B, Engel J, Wirth R, Rodríguez TR, Hergert H. Ab initio treatment of collective correlations and the neutrinoless double beta decay of Ca 48. Phys. Rev. Lett. (2020) 124:232501. doi:10.1103/PhysRevLett.124.232501

PubMed Abstract | CrossRef Full Text | Google Scholar

154. Frosini M, Duguet T, Ebran JP, Bally B, Hergert H, Rodríguez TR, et al. Multi-reference many-body perturbation theory for nuclei. Eur. Phys. J. A (2022) 58:64. doi:10.1140/epja/s10050-022-00694-x

CrossRef Full Text | Google Scholar

155. Frosini M, Duguet T, Ebran JP, Bally B, Mongelli T, Rodríguez TR, et al. Multi-reference many-body perturbation theory for nuclei. Eur. Phys. J. A (2022) 58:63. doi:10.1140/epja/s10050-022-00693-y

CrossRef Full Text | Google Scholar

156. Frosini M, Duguet T, Ebran JP, Somà V. Multi-reference many-body perturbation theory for nuclei. Eur. Phys. J. A (2022) 58:62. doi:10.1140/epja/s10050-022-00692-z

CrossRef Full Text | Google Scholar

157. Hagen G, Novario SJ, Sun ZH, Papenbrock T, Jansen GR, Lietz JG, et al. Angular-momentum projection in coupled-cluster theory: structure of ³⁴Mg. Phys. Rev. C (2022) 105:064311. doi:10.1103/PhysRevC.105.064311

CrossRef Full Text | Google Scholar

158. Ekström A, Forssén C, Hagen G, Jansen GR, Papenbrock T, Sun ZH. How chiral forces shape neutron-rich Ne and Mg nuclei. arXiv:2305 (2023) 06955. doi:10.48550/arXiv.2305.06955

CrossRef Full Text | Google Scholar

159. Sun ZH, Djärv TR, Hagen G, Jansen GR, Papenbrock T. Structure of odd-mass Ne, Na, and Mg nuclei. arXiv:2409 (2024) 02279. doi:10.1103/PhysRevC.111.044304

CrossRef Full Text | Google Scholar

160. Sun ZH, Ekström A, Forssén C, Hagen G, Jansen GR, Papenbrock T. Multiscale physics of atomic nuclei from first principles. arXiv:2404 (2024) 00058. doi:10.1103/PhysRevX.15.011028

CrossRef Full Text | Google Scholar

161. Hu B, Sun Z, Hagen G, Jansen G, Papenbrock T. Ab initio computations from 78Ni towards 70Ca along neutron number N = 50. Phys. Lett. B (2024) 858:139010. doi:10.1016/j.physletb.2024.139010

CrossRef Full Text | Google Scholar

162. Hu BS, Sun ZH, Hagen G, Papenbrock T. Ab initio computations of strongly deformed nuclei near Zr 80. Phys. Rev. C (2024) 110:L011302. doi:10.1103/PhysRevC.110.L011302

CrossRef Full Text | Google Scholar

163. Belley A, Yao JM, Bally B, Pitcher J, Engel J, Hergert H, et al. Ab initio uncertainty quantification of neutrinoless double-beta decay in Ge 76. Phys. Rev. Lett. (2024) 132:182502. doi:10.1103/PhysRevLett.132.182502

PubMed Abstract | CrossRef Full Text | Google Scholar