- 1State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, China
- 2School of Cyberspace Security, Beijing University of Posts and Telecommunications, Beijing, China
- 3College of Computer and Cyber Security, Fujian Normal University, Fuzhou, China
- 4National Engineering Research Center of Disaster Backup and Recovery, Beijing University of Posts and Telecommunications, Beijing, China
An efficient quantum implementation of the advanced encryption standard (AES) is crucial for reducing the complexity of implementing an exhaustive key search through Grover’s algorithm. In this paper, we study how to construct resource-efficient quantum circuits for AES. We consider the product of T-gates depth and width (TDW) and the product of full depth and width (FDW) as optimization targets. We propose a generic method, called the controlled control qubit cascade (CCQC) technique, to construct quantum circuits for nonlinear components with reduced TDW and FDW. Using this, we construct a quantum circuit for the AES S-box. Compared with recent work presented at ASIACRYPT 2023, our S-box quantum circuit achieves reductions of 2.3% in TDW and 45.2% in FDW. Additionally, we propose a new key schedule strategy to reduce the full depth of the AES quantum circuit. Finally, the trade-offs between T-gates depth and width and the parallel numbers of S-box and TDW are analyzed.
1 Introduction
Quantum technology, including cryptography Shor and Preskill [1]; Qin et al. [2], quantum computing Grover [3]; Shor [4], and quantum precision measurement Braginsky and Khalili [5]; Childs et al. [6], is the frontier of a new round of scientific and technological revolution. Quantum computing has been widely applied in fields including quantum cryptography Zhou et al. [7]; Gong et al. [8], quantum simulation Buluta and Nori [9], machine learning Song et al. [10, 11]; Li et al. [12, 13], solving equations Childs et al. [14]; Wan et al. [15, 16], and cryptanalysis Kaplan et al. [17]; Cai et al. [18]. The threats that quantum computing poses to existing cryptographic systems are well-known. Once large-scale quantum computers become operational, Shor’s algorithm will be capable of breaking asymmetric cryptographic schemes that rely on the discrete logarithm and factoring problems, such as RSA, ECDH, and ECC Shor [4]; Shor [19]. For symmetric cryptography, the primary challenges posed by quantum computation arise from Simon’s algorithm and Grover’s algorithm. When a quantum oracle that implements the target cryptographic quantum circuit can be accessed, Simon’s algorithm can undermine various symmetric cryptographic schemes by finding hidden periods Kaplan et al. [17]; Bonnetain et al. [20], while Grover’s algorithm can provide quadratic acceleration for exhaustive key searches that attack block ciphers Grover [3].
Due to the extremely high cost of quantum resources, estimating the quantum resources needed to attack block ciphers using Grover’s algorithm is crucial for reducing the implementation difficulty of such attacks and accurately predicting their actual implementation time. The advanced encryption standard (AES) Daemen [21] is one of the most widely used block ciphers today; thus, evaluating the quantum resources needed to attack it is highly significant. Moreover, the National Institute of Standards and Technology (NIST) has proposed the standardization of post-quantum cryptography by defining security categories 1, 3, and 5 based on the computational resources needed for exhaustive key searches on AES-128, AES-192, and AES-256, respectively. The key to applying Grover’s algorithm to AES lies in implementing the Grover oracle, which utilizes the AES quantum circuit to mark the correct key during the search process. Consequently, the precise estimation and careful optimization of the quantum circuit implementing AES have attracted significant attention in recent years.
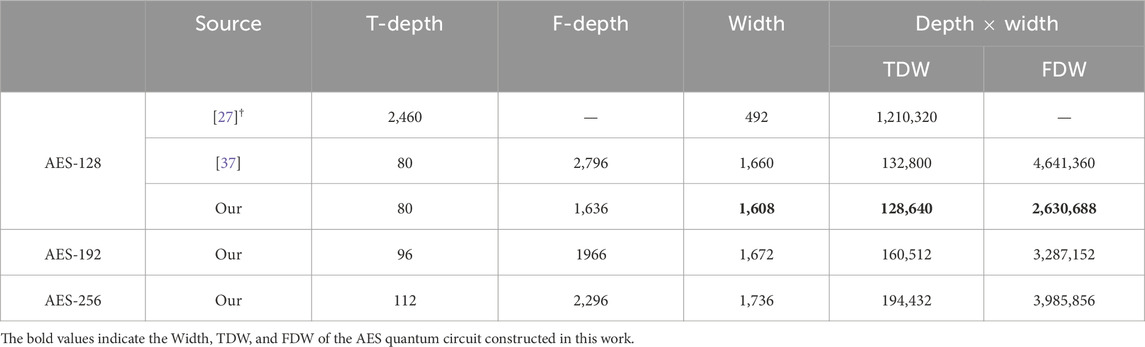
Computational resources are often measured by quantum circuit size. Metrics commonly used to measure quantum circuits include width, depth, and the number of quantum gates Specifically, width refers to the number of logical qubits needed in a quantum circuit. Meanwhile, the minimum stages of quantum gates that can be executed in parallel in a circuit is called depth. We can measure the depth of all elementary gates within the circuit or focus specifically on the depth of a particular quantum gate, depending on the requirements of our demand. From a physical implementation perspective, realizing quantum circuits with a large width or deep depth is quite difficult Sun et al. [22]. Therefore, prior works have often focused on ways to reduce either the width Grassl et al. [23]; Zou et al. [24]; Li et al. [25] or depth Jaques et al. [26]; Huang and Sun [27] required for Grover’s attack on AES. However, there is often a trade-off between these two metrics. For example, optimizing the width of a quantum circuit may lead to a very large depth, which in turn makes Grover’s attack difficult to implement. Hence, it is also very feasible to consider the product of width and depth as a metric for measuring the size of a quantum circuit. Specifically, because the running time of fault-tolerant quantum computers is proportional to the T-gates depth Fowler [28]; Amy et al. [29, 30], the T-gates depth is also commonly used as an optimization target. For distinction, this paper refers to the depth of all elementary gates as the F-depth and to the T-gates depth as the T-depth. Considering the significance of F-depth and T-depth, we introduce the definitions of FDW as the product of F-depth and width and TDW as the product of T-depth and width, respectively.
1.1 Related works
One of the key challenges in implementing the AES quantum circuit is constructing the quantum circuit for the nonlinear component S-box. Previous works can generally be categorized into three types based on optimization goals for S-box quantum circuits: reducing width, depth, or the product of width and depth. We introduce related works from these three perspectives.
1.1.1 Reducing width
This field was initiated by Grassl et al., who utilized the Itoh–Tsujii algorithm to find the multiplicative inverse in a finite field
1.1.2 Reducing depth
Jang et al. [35] constructed the first S-box quantum circuit aimed at reducing depth. However, the focus was usually on T-depth. Huang and Sun [27] formulated a technique that transforms a classical circuit with a multiplicative depth of
1.1.3 Reducing the product of width and depth
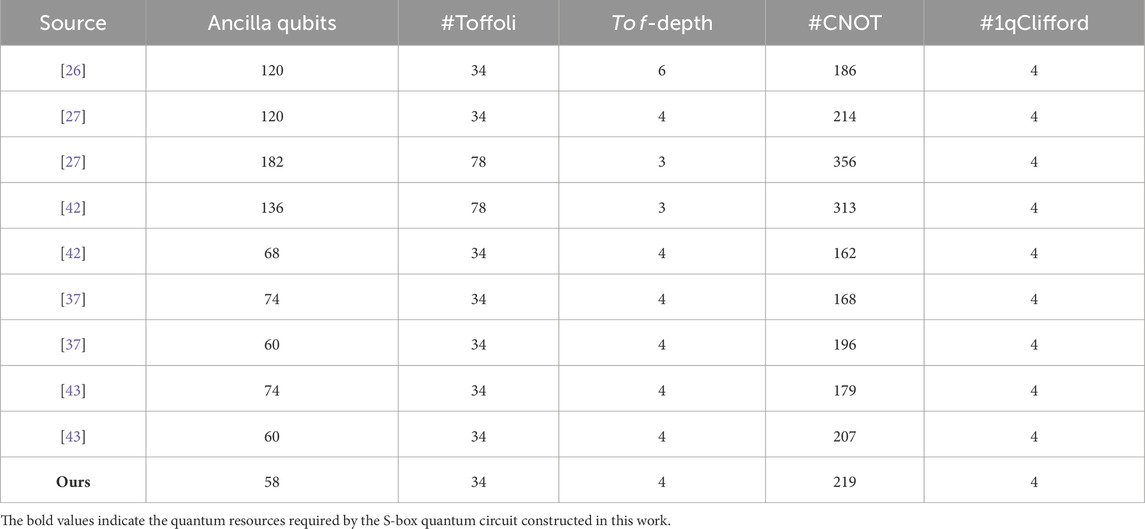
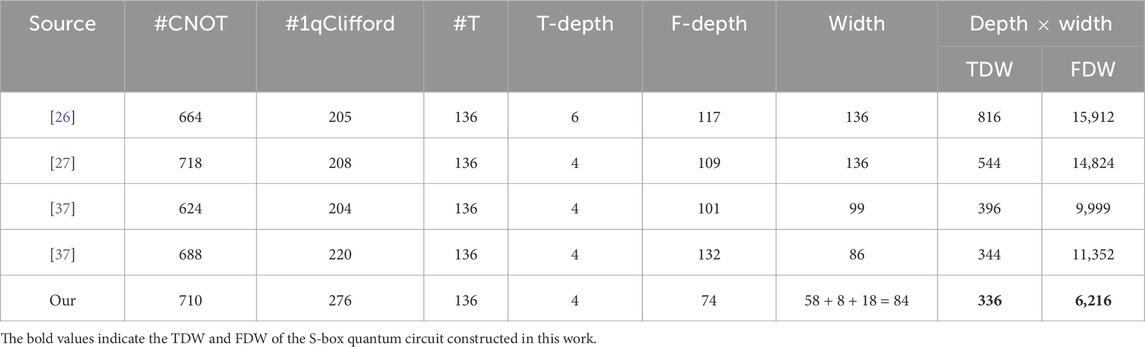
This metric was first presented and optimized by Jaques et al. Jang et al. [35], but fewer studies focused on it. Most recently, the product of width and depth has begun to receive attention. Liu et al. proposed a technique called m-XOR at ASIACRYPT 2023 Liu et al. [37] that can identify reusable qubits. They also designed a compact circuit structure for the S-box and constructed an S-box quantum circuit with a product of T-depth and width equal to 344.
1.2 Our contributions
We analyze the algebraic structures of S-box classical circuits, uncovering the intrinsic connections between multiplicative nodes. This inspires our controlled control qubit cascade (CCQC) technique for constructing quantum circuits with optimized TDW and FDW. Applying CCQC, our S-box quantum circuit reduces TDW by 2.3% and FDW by 45.2% compared to ASIACRYPT 2023 work Liu et al. [37]. We develop a key schedule strategy to reduce AES circuit F-depth. With this and our S-box circuit, we estimate the quantum resources required to implement iterative AES-128. Finally, we analyze the trade-offs of T-depth and width, as well as S-box parallelism versus TDW. Finally, we analyze T-depth vs. width and S-box parallelism vs. TDW trade-offs.
2 Preliminaries
2.1 Synthesis of quantum circuits
A qubit is typically denoted as
and a non-Clifford gate
2.2 Classical circuits and directed acyclic graphs (DAG)
This paper utilizes concepts related to classical circuits and directed acyclic graphs (DAGs) to explain the circuit construction method Cong and Ding [39]. Therefore, this section will introduce these relevant concepts. A classical circuit can be represented by a DAG
where
2.3 The advanced encryption standard
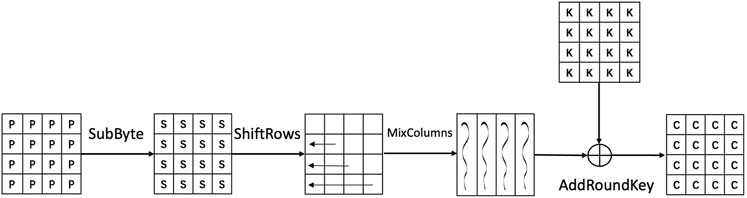
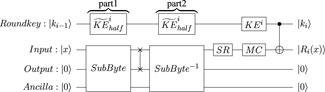
The advanced encryption standard (AES) is a block cipher standardized by the NIST Daemen [21]. Three variants, AES-128, AES-192, and AES-256, correspond to three different original key lengths. The detailed process of the AES algorithm is that the input 128-bit data block is initially XOR with the first 128 bits of the original key. Then, a specific number of round function iterations constitute the encryption process of AES: 10 rounds, 12 rounds, and 14 rounds for AES-128, AES-192, and AES-256, respectively. There are four operations during a round function in Figure 2: SubByte, ShiftRow, MixColumn, and AddRoundKey. MixColumn is omitted in the final round iteration.
Each block in a
where the elements in matrix
3 Constructing a circuit for an S-box with a low TDW and FDW
The universal method for constructing an S-box quantum circuit can be summarized in two steps. First, identify a classical circuit that implements the S-box. Then, implement this classical circuit in a quantum circuit. We chose the S-box classical circuit proposed by Boyar and Peralta [36], whose circuit depth had been optimized by heuristic algorithms. This section introduces the construction method: the controlled control qubit cascade (CCQC) technique for the S-box quantum circuit.
3.1 Constructing a quantum circuit with a low TDW and FDW
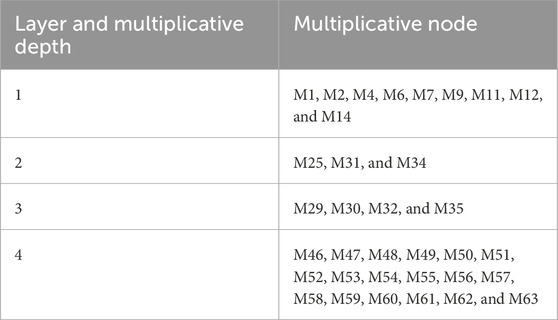
We introduce constructing an S-box quantum circuit by studying the S-box classical circuit Boyar and Peralta [36]. Based on the relevant knowledge presented in Equations 1, 2, we compute the multiplicative depth of all multiplicative nodes within this classical circuit and stratify all multiplicative nodes according to their multiplicative depth, as shown in Table 1, where we assign nodes with greater multiplicative depth to the higher layers.
The variables
Observation 1. The eight outputs of the S-box can be derived by linear combinations of all multiplicative nodes with a multiplicative depth of 4.
Example 1.
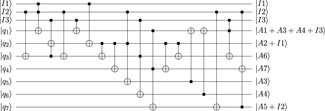
We illustrate this method through a classical circuit in Example 1. We calculate the multiplicative depth of all multiplicative nodes in Example 1 and stratify them hierarchically. During the stratifying of multiplicative nodes in Example 1, we further observe that there usually exist additive nodes among different layers. These additive nodes merge nodes with smaller multiplicative depth to become the input for multiplicative nodes in a higher layer.
Theorem 1. In a given classical circuit, any multiplicative node can be expressed as the product of a linear combination of its lower layer multiplicative nodes and the primary inputs.
Theorem 1 shows that the highest-level multiplicative nodes can be obtained from lower-level multiplicative nodes and the primary inputs. The proof of Theorem 1 can be found in Supplementary Material. Table 2 lists the algebraic relationships between the multiplicative nodes from different layers of Example 1. Algorithm 1 can ascertain the algebraic relationships between multiplicative nodes in any classical circuit.
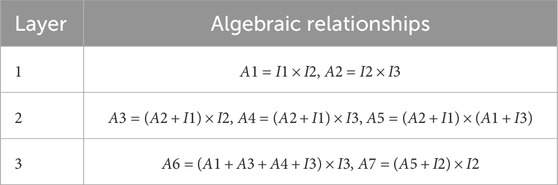
Table 2. Algebraic relationships between the multiplicative nodes from Example 1.
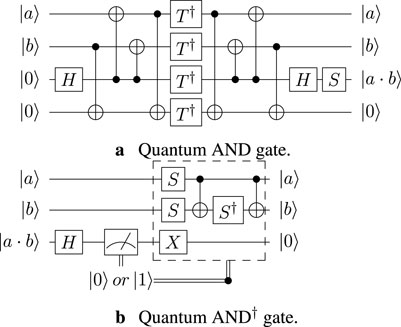
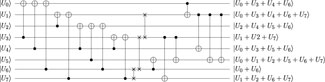
The CCQC technique prepares multiplicative nodes in the quantum circuit hierarchically, and multiplicative nodes at the same layer are prepared in parallel. Because a qubit cannot be used in different quantum gates at the same time, to support the parallelism of quantum AND gates, ancilla qubits are needed to copy variables that are used as inputs to different multiplicative nodes. We can liken the inputs of multiplicative nodes to the control qubits of Toffoli gates and the outputs of the multiplicative nodes to controlled qubits. We use Toffoli gates due to the compactness of its visualization and the convenience of explanation. Then, the core concept of the CCQC technique is to use the controlled qubits of lower-layer multiplicative nodes as the control qubits for higher-layer multiplicative nodes. To elaborate, we take advantage of the qubits occupied by lower-layer multiplicative nodes as controlled qubits within the CNOT network, transforming these lower-layer controlled qubits into inputs for higher-layer multiplicative nodes. Figure 3 implements the highest-layer multiplicative nodes from Table 2 by our CCQC technique.
Constructing an S-box quantum circuit using the CCQC technique is more complex. We preprocess the S-box classical circuit followed by Theorem 1 and list the algebraic relationships among multiplicative nodes in Supplementary Material. Upon analyzing the classical circuit for the S-box, we obtain Observation 2.
Observation 2. All inputs of the lowest layer multiplicative nodes are also the inputs of the highest layer multiplicative nodes.
We find that it is beneficial to save qubits if primary inputs can be the inputs of multiplicative nodes directly. If not, extra qubits are needed to prepare inputs for multiplicative nodes. Therefore, we select eight linearly independent inputs
Algorithm 2 interprets how to construct a quantum circuit with the CCQC technique. List Prepared includes the prepared multiplicative nodes, and Anc includes ancilla qubits that are introduced to ensure quantum AND gates can be executed in parallel. Operation CNOT
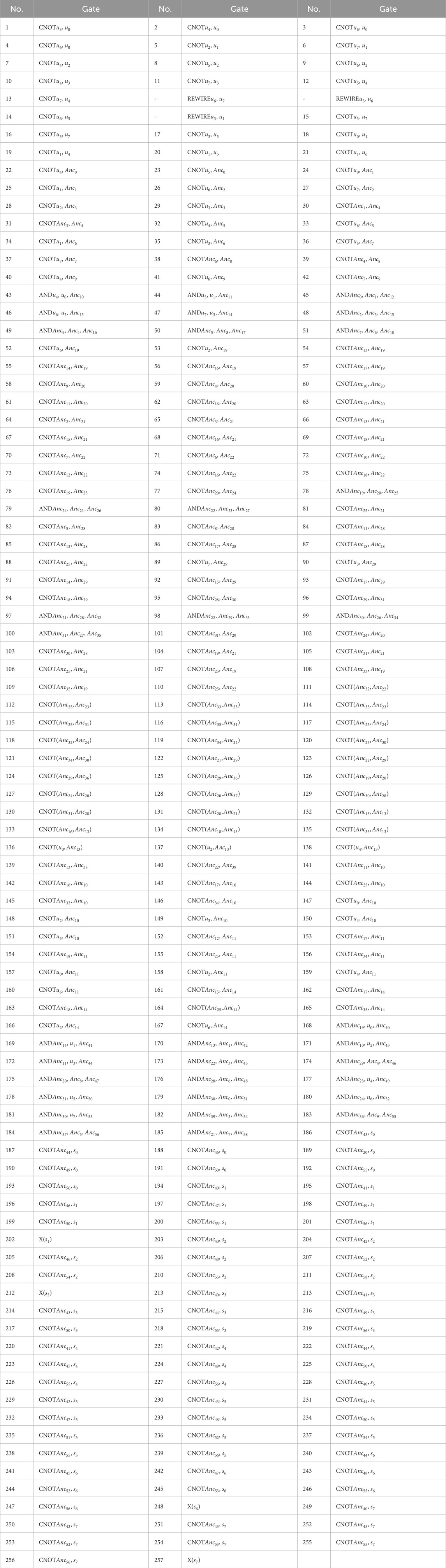
Various implementations of S-box quantum circuits have been proposed, with some utilizing Toffoli gates and others employing AND gates. We present a comparison of the quantum resource costs in S-box quantum circuits based on the Toffoli gate in Table 4, focusing on previous works that study low Toffoli depth S-boxes. Additionally, Jang et al. [35] and Liu et al. [37] conducted a comprehensive comparison by decomposing Toffoli gates in different manners. However, this paper adopts AND gates to achieve lower circuit depth. Therefore, we need an additional 18 ancilla qubits to support the preparation of the fourth layer multiplicative nodes. After executing the fourth layer of AND gates, those 18 ancilla bits are reset to
Two types of S-boxes are required to construct the AES quantum circuit in the next section. The first S-box implements
4 Optimized quantum circuits for AES
This section discusses the implementation of the quantum circuit of AES. We begin by explaining how each component can be implemented in a quantum circuit, followed by how to implement the iterative encryption circuits for AES under a pipeline structure and a round-in-place structure. We address estimating the quantum resources required to implement AES. It is important to emphasize that all the circuits mentioned in this section are implemented with the maximum parallelism numbers of an S-box.
4.1 Components of AES and their implementations
4.1.1 SubByte and SubWord
The S-box is the core cryptographic component used to implement SubByte and SubWord. Its quantum circuit implementation is detailed in previous sections. SubByte needs 16 S-boxes, and SubWord needs four S-boxes.
4.1.2 ShiftRow and RotWord
ShiftRow and RotWord only perform cyclical leftward shifts but do not change the state of bytes. Both can be implemented in a quantum circuit entirely through rewiring. Following Grassl et al. [23], we considered rewiring as a free operation, thus excluding it from cost estimates.
4.1.3 MixColumn and Rcon
MixColumn can be implemented with an in-place quantum circuit due to the invertibility of its
4.1.4 AddRoundKey
AddRoundKey is executed in a quantum circuit through a CNOT network, where the round key qubits act as control bits and the 128 qubits for the AES data block act as controlled bits in the CNOT network.
4.1.5 Keyexpansion
As mentioned before, the key used in the AddRoundKey comes from the round key generated by the Keyexpansion. Hence, Keyexpansion is also an iterative process that uses ten rounds, eight rounds, and seven rounds for AES-128, AES-192, and AES-256, respectively. In this paper, we adopt the in-place circuit structure proposed by Jaques et al. [26] to realize the Keyexpansion iteration by combining it with the SubByte subcircuit implemented by S-boxes. For detailed circuit structure, please refer to Jaques et al. [26]. Each round of Keyexpansion process generates four, six, and eight words that correspond to AES-128, AES-192, and AES-256, respectively.
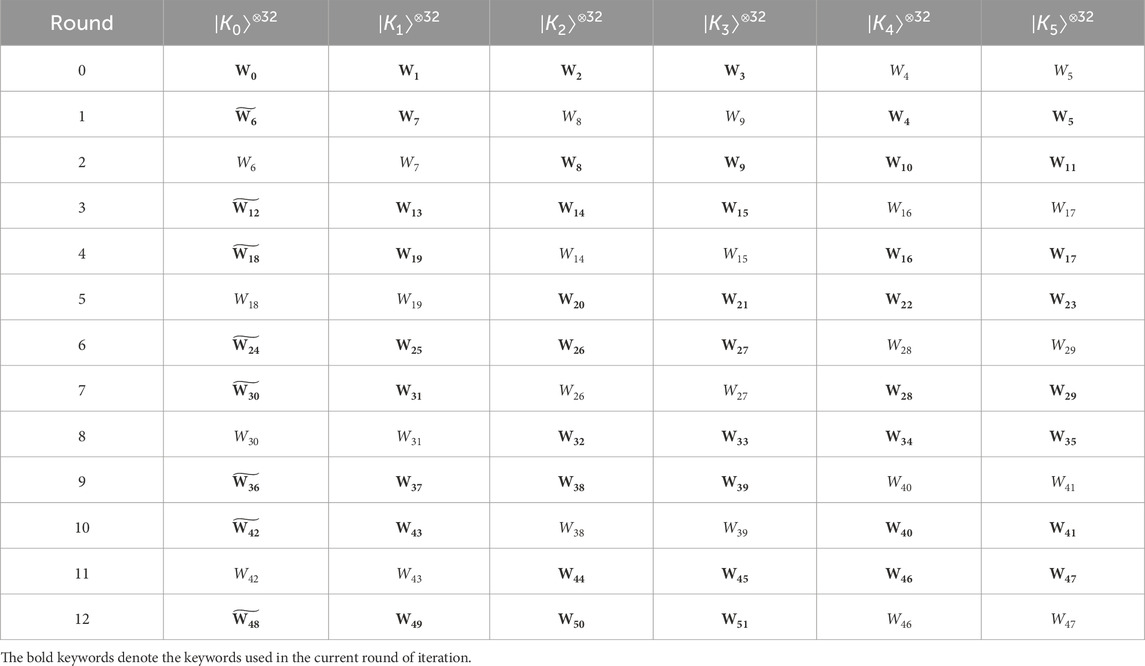
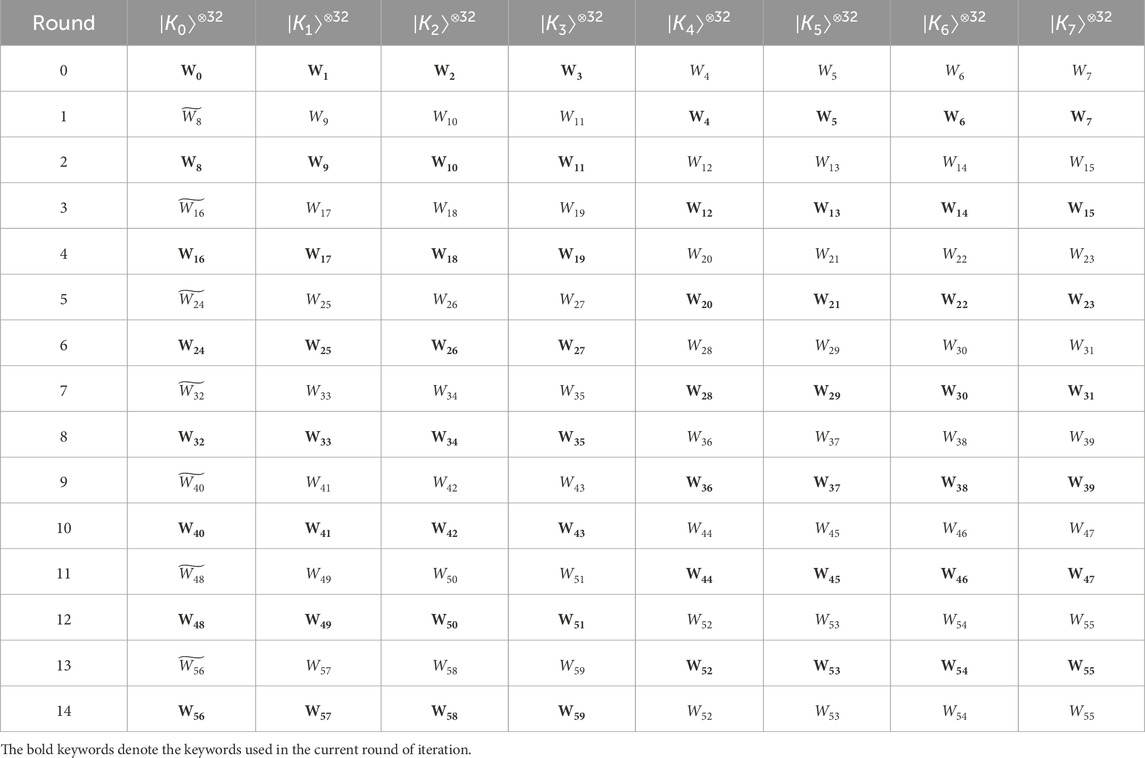
The key schedule strategy controls the iterative progress of Keyexpansion, and a reasonable key schedule strategy can make the circuit more compact. We designed a new key schedule strategy that reduces the F-depth. The criterion of our key schedule strategy is to ensure that the SubWord subcircuit must be executed in parallel with the SubByte subcircuit. For AES-128, the Keyexpansion’s iteration is synchronized with the round function’s iteration. However, it should be noted that subcircuits of Rcon and SubWord must be executed in parallel with the SubByte subcircuit, and the remainder subcircuit of Keyexpansion executes in parallel with the MixColumn subcircuit. Due to the iterative rounds of Keyexpansion, it is slightly more complex to arrange the circuit layout of AES-192 and AES-256 in a reasonable way to make the circuit more compact. We summarize the key schedule process corresponding to each iteration of the round function for AES-192 and AES-256 in Tables 6, 7. The leftmost column in the tables indicates the round function’s iterative round, while the remaining columns show which key word is stored in the 32 qubit registers during the key schedule process.
4.2 AES quantum circuit with a pipeline structure
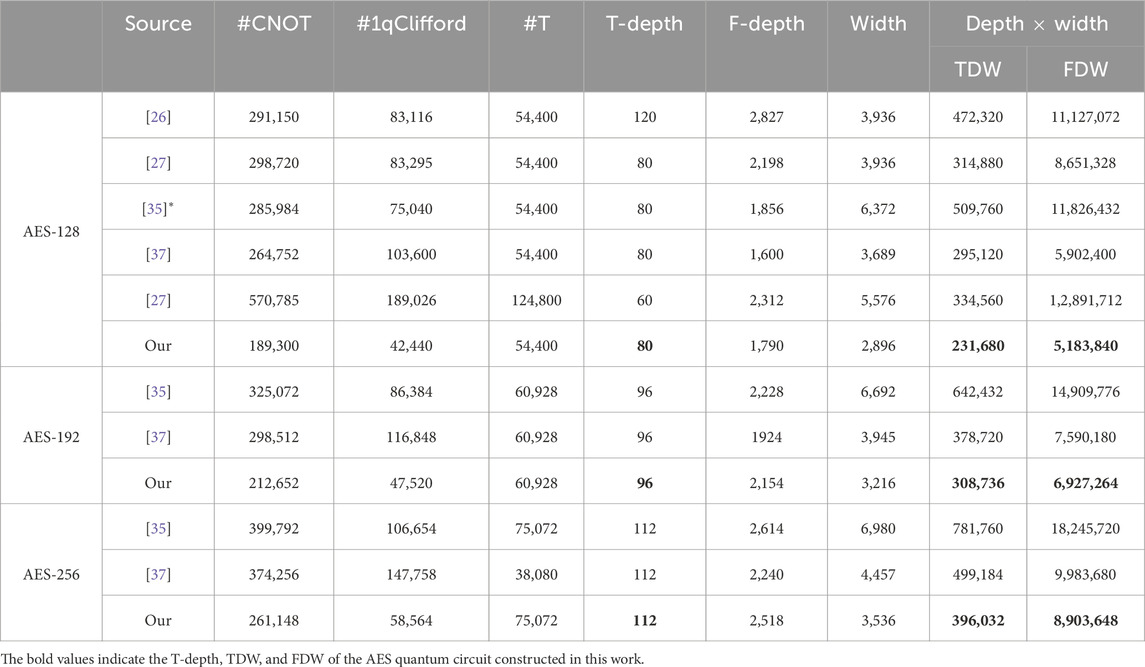
The pipeline structure Jaques et al. [26] was proposed by Jaques et al. to reduce the depth of the circuit. The characteristic of the pipeline structure is that after completing one round iterative round function, it directly allocates new qubits to implement the next round iterative round function. Jang et al. [42] further refined the pipeline structure into a regular version and a shallow version. We adopted the regular version because the regular version has high parallelism while considering the depth-qubit trade-off. We integrated our S-box quantum circuit into the regular-version pipeline structure and estimated the quantum resources required to implement the AES forward circuit and its adjoint circuit. Table 8 compares our work with previous works under the same structure. It is worth noting that Liu et al. [37] and Jang et al. [35] only provide the resources for a forward circuit. Therefore, we have multiplied the metrics other than width by 2 in Table 8.
For the implementation of AES-128, the quantum circuit that applies our S-box quantum circuit with pipeline structure has a T-depth of 80. Compared to the state-of-the-art work with the same T-depth, our approach achieves a 21.5% reduction in TDW and a 12.2% reduction in FDW. In the case of AES-192, the quantum circuit that applies our S-box quantum circuit with a pipeline structure has a T-depth of 96. Compared to the state-of-the-art work with the same T-depth, our approach achieves an 18.5% reduction in TDW and an 8.7% reduction in FDW. Regarding AES-256, the quantum circuit that applies our S-box quantum circuit with a pipeline structure has a T-depth of 112. Compared to the state-of-the-art work with the same T-depth, our approach achieves a 20.7% reduction in TDW and a 10.9% reduction in FDW.
4.3 AES quantum circuit with a round-in-place structure
The round-in-place structure Huang and Sun [27] was proposed by Huang et al. to maximize the reuse of qubits and greatly reduce circuit width. They showed the method to construct the inverse S-box quantum circuit based on an S-box quantum circuit, an additional 42 CNOT gates, and four X gates. For more details, please refer to Huang and Sun [27]. With the inverse S-box quantum circuit, they constructed the iterative encryption in an in-place manner; see Figure 5. Because the T-depth of one round iteration with the round-in-place structure is twice that of the pipeline structure, we divide
We also apply our S-box quantum circuit to the round-in-place structure and estimate quantum resources for implementing the AES forward circuit without its adjoint circuit. Table 9 compares our work with previous works under the round-in-place structure. Because Liu et al. [37] did not provide the F-depth of AES-128, we calculate the F-depth of their circuit based on the F-depth of the S-box they applied to an R structure. Apart from the F-depth, all other metrics are directly derived from Liu et al. The quantum circuit that applies our S-box quantum circuit with a round-in-place structure had a T-depth of 80. Compared with the circuit of Liu et al. with the same T-depth, we achieved a modest reduction of 3.1% in TDW and a substantial reduction of 43.3% in FDW.
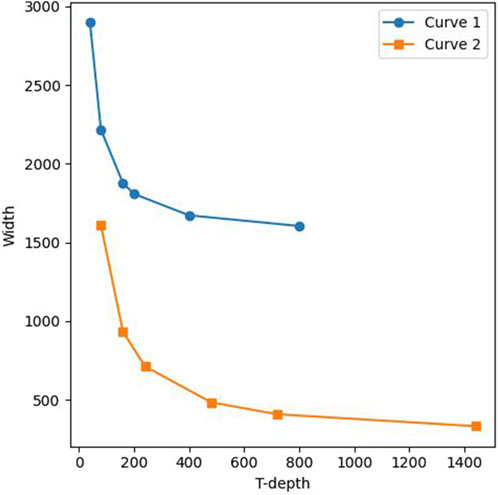
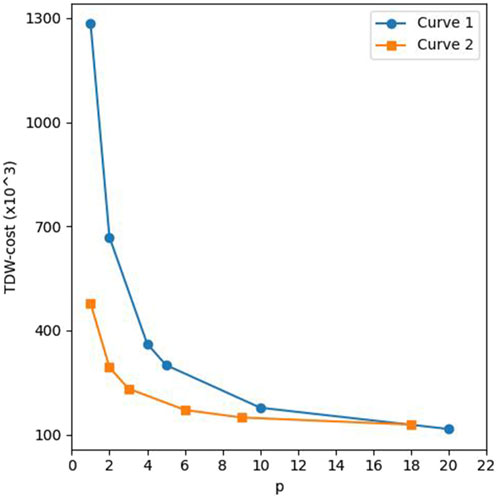
5 Trade-offs of circuit metrics
This section shows the trade-offs between T-depth and width, the parallel numbers
6 Conclusion
We propose the CCQC technique for constructing quantum circuits for nonlinear components, providing a general method to reduce both TDW and FDW. Additionally, we design a new key schedule strategy to reduce the F-depth of the AES quantum circuit. This paper introduces significantly optimized AES quantum circuits, achieving improvements in TDW and FDW. Our research provides a new idea for constructing quantum circuits for nonlinear components of other block ciphers with low TDW and FDW. However, the CCQC technique is more suitable for constructing quantum circuits with low TDW and FDW for classical circuits that have a lower multiplicative depth. On the other hand, solely focusing on reducing the multiplicative depth of a circuit implies the need for more intermediate values, which in turn costs more qubits when constructing the quantum circuit. Therefore, the impact of multiplicative depth on TDW and FDW is worth further exploration. Finally, we find that for the S-box quantum circuit designed in this article, implementing the iterative AES quantum circuit by regular-version pipeline structure is more advantageous for FDW and TDW.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
L-LJ: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing – original draft, and writing – review and editing. B-BC: writing – original draft and writing – review and editing. FG: writing – original draft, writing – review and editing, conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, and visualization. S-JQ: writing – original draft and writing – review and editing. Z-PJ: writing – original draft and writing – review and editing. Q-YW: writing – original draft and writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by the National Natural Science Foundation of China (Grant Nos. 62272056, 62372048, and 62371069).
Acknowledgments
I would like to express my sincere gratitude to the Tianyan Quantum Computing Program for providing valuable resources and support. Your platform has greatly facilitated my learning and deepened my understanding of quantum computing.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1582819/full#supplementary-material
References
1. Shor PW, Preskill J. Simple proof of security of the bb84 quantum key distribution protocol. Phys Rev Lett (2000) 85:441–4. doi:10.1103/physrevlett.85.441
2. Qin L, Liu B, Gao F, Huang W, Xu B, Li Y. Decoy-state quantum private query protocol with two-way communication. Physica A: Stat Mech its Appl (2024) 633:129427. doi:10.1016/j.physa.2023.129427
3. Grover LK. A fast quantum mechanical algorithm for database search. In: Proceedings of the twenty-eighth annual ACM symposium on Theory of computing (1996). p. 212–9.
4. Shor PW. Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings 35th annual symposium on foundations of computer science (Ieee) (1994). p. 124–34.
6. Childs AM, Preskill J, Renes J. Quantum information and precision measurement. J Mod Opt (2000) 47:155–76. doi:10.1080/095003400148123
7. Zhou N-R, Chen Z-Y, Liu Y-Y, Gong L-H. Multi-party semi-quantum private comparison protocol of size relation with d-level ghz states. Adv Quan Tech (2024):2400530. doi:10.1002/qute.202400530
8. Gong L-H, Li M-L, Cao H, Wang B. Novel semi-quantum private comparison protocol with bell states. Laser Phys Lett (2024) 21:055209. doi:10.1088/1612-202x/ad3a54
10. Song Y, Wu Y, Wu S, Li D, Wen Q, Qin S A quantum federated learning framework for classical clients. Sci China Phys Mech and Astron (2024) 67:250311. doi:10.1007/s11433-023-2337-2
11. Song Y, Li J, Wu Y, Qin S, Wen Q, Gao F. A resource-efficient quantum convolutional neural network. Front Phys (2024) 12:1362690. doi:10.3389/fphy.2024.1362690
12. Li J, Gao F, Lin S, Guo M, Li Y, Liu H, et al. Quantum k-fold cross-validation for nearest neighbor classification algorithm. Physica A: Stat Mech its Appl (2023) 611:128435. doi:10.1016/j.physa.2022.128435
13. Li L, Li J, Song Y, Qin S, Wen Q, Gao F. An efficient quantum proactive incremental learning algorithm. Sci China Phys Mech and Astron (2025) 68:210313–9. doi:10.1007/s11433-024-2501-4
14. Childs AM, Kothari R, Somma RD. Quantum algorithm for systems of linear equations with exponentially improved dependence on precision. SIAM J Comput (2017) 46:1920–50. doi:10.1137/16m1087072
15. Wan L-C, Yu C-H, Pan S-J, Gao F, Wen Q-Y, Qin S-J. Asymptotic quantum algorithm for the toeplitz systems. Phys Rev A (2018) 97:062322. doi:10.1103/physreva.97.062322
16. Wan L-C, Yu C-H, Pan S-J, Qin S-J, Gao F, Wen Q-Y. Block-encoding-based quantum algorithm for linear systems with displacement structures. Phys Rev A (2021) 104:062414. doi:10.1103/physreva.104.062414
17. Kaplan M, Leurent G, Leverrier A, Naya-Plasencia M. Breaking symmetric cryptosystems using quantum period finding. In: Advances in Cryptology–CRYPTO 2016: 36th Annual International Cryptology Conference; August 14-18, 2016; Santa Barbara, CA, USA. Proceedings, Part II 36 Springer (2016). p. 207–37.
18. Cai B-B, Wu Y, Dong J, Qin S-J, Gao F, Wen Q-Y. Quantum attacks on 1k-aes and prince. Computer J (2023) 66:1102–10. doi:10.1093/comjnl/bxab216
19. Shor PW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev (1999) 41:303–32. doi:10.1137/s0036144598347011
20. Bonnetain X, Leurent G, Naya-Plasencia M, Schrottenloher A. Quantum linearization attacks. In: Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the Theory and Application of Cryptology and Information Security; December 6–10, 2021; Singapore. Proceedings, Part I 27 Springer (2021). p. 422–52.
22. Sun X, Tian G, Yang S, Yuan P, Zhang S. Asymptotically optimal circuit depth for quantum state preparation and general unitary synthesis. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2023) 42:3301–14. doi:10.1109/tcad.2023.3244885
23. Grassl M, Langenberg B, Roetteler M, Steinwandt R. Applying grover’s algorithm to aes: quantum resource estimates. In: International workshop on post-quantum cryptography. Springer (2016). p. 29–43.
24. Zou J, Wei Z, Sun S, Liu X, Wu W. Quantum circuit implementations of aes with fewer qubits. In: Advances in cryptology–ASIACRYPT 2020: 26th international conference on the theory and application of cryptology and information security, daejeon, South Korea, december 7–11, 2020, proceedings, Part II 26. Springer (2020). p. 697–726.
25. Li Z, Cai B, Sun H, Liu H, Wan L, Qin S, et al. Novel quantum circuit implementation of advanced encryption standard with low costs. Sci China Phys Mech and Astron (2022) 65:290311. doi:10.1007/s11433-022-1921-y
26. Jaques S, Naehrig M, Roetteler M, Virdia F. Implementing grover oracles for quantum key search on aes and lowmc. In: Advances in Cryptology–EUROCRYPT 2020: 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques; May 10–14, 2020; Zagreb, Croatia. Proceedings, Part II 30 Springer (2020). p. 280–310.
27. Huang Z, Sun S. Synthesizing quantum circuits of aes with lower t-depth and less qubits. In: International conference on the theory and application of cryptology and information security. Springer (2022). p. 614–44.
29. Amy M, Maslov D, Mosca M, Roetteler M. A meet-in-the-middle algorithm for fast synthesis of depth-optimal quantum circuits. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2013) 32:818–30. doi:10.1109/tcad.2013.2244643
30. Amy M, Maslov D, Mosca M. Polynomial-time t-depth optimization of clifford+ t circuits via matroid partitioning. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2014) 33:1476–89. doi:10.1109/tcad.2014.2341953
31. Chung D, Lee S, Choi D, Lee J. Alternative tower field construction for quantum implementation of the aes s-box. IEEE Trans Comput (2021) 71:2553–64. doi:10.1109/tc.2021.3135759
32. Wang Z-G, Wei S-J, Long G-L. A quantum circuit design of aes requiring fewer quantum qubits and gate operations. Front Phys (2022) 17:41501. doi:10.1007/s11467-021-1141-2
33. Boyar J, Peralta R. A new combinational logic minimization technique with applications to cryptology. In: Experimental Algorithms: 9th International Symposium, SEA 2010; May 20-22, 2010; Ischia Island, Naples, Italy. Proceedings 9 Springer (2010). p. 178–89.
34. Li Z, Gao F, Qin S, Wen Q. New record in the number of qubits for a quantum implementation of aes. Front Phys (2023) 11:1171753. doi:10.3389/fphy.2023.1171753
35. Jang K, Baksi A, Kim H, Seo H, Chattopadhyay A. Improved quantum analysis of speck and lowmc (full version). Cryptology ePrint Archive (2022). doi:10.1007/978-3-031-22912-1_23
36. Boyar J, Peralta R. A small depth-16 circuit for the aes s-box. In: IFIP international information security conference. Cambridge: Springer (2012). p. 287–98.
37. Liu Q, Preneel B, Zhao Z, Wang M. Improved quantum circuits for aes: reducing the depth and the number of qubits. In: International conference on the theory and application of cryptology and information security. Springer (2023). p. 67–98.
38. Nielsen MA, Chuang IL. Quantum computation and quantum information. Cambridge University Press (2010).
39. Cong J, Ding Y. Combinational logic synthesis for lut based field programmable gate arrays. ACM Trans Des Automation Electron Syst (Todaes) (1996) 1:145–204. doi:10.1145/233539.233540
40. Markov K, Patel I, Hayes J. Optimal synthesis of linear reversible circuits. Quan Inf Comput (2008) 8:0282–94. doi:10.26421/qic8.3-4-4
41. Xiang Z, Zeng X, Lin D, Bao Z, Zhang S. Optimizing implementations of linear layers. IACR Trans Symmetric Cryptology (2020) 120–45. doi:10.46586/tosc.v2020.i2.120-145
42. Jang K, Baksi A, Kim H, Song G, Seo H, Chattopadhyay A. Quantum analysis of aes. Cryptology ePrint Archive (2022). doi:10.62056/ay11zo-3y
43. Shi H, Feng X. Quantum circuits of aes with a low-depth linear layer and a new structure. In: International conference on the theory and application of cryptology and information security. Springer (2024). p. 358–95.
Keywords: Grover algorithm, AES, S-box, quantum circuit, quantum resource optimization
Citation: Jiang L-L, Cai B-B, Gao F, Qin S-J, Jin Z-P and Wen Q-Y (2025) Constructing resource-efficient quantum circuits for AES. Front. Phys. 13:1582819. doi: 10.3389/fphy.2025.1582819
Received: 25 February 2025; Accepted: 07 March 2025;
Published: 22 April 2025.
Edited by:
Nanrun Zhou, Shanghai University of Engineering Sciences, ChinaReviewed by:
Lihua Gong, Shanghai University of Engineering Sciences, ChinaYefeng He, Xi’an University of Post and Telecommunications, China
Copyright © 2025 Jiang, Cai, Gao, Qin, Jin and Wen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fei Gao, Z2FvZkBidXB0LmVkdS5jbg==
 Liao-Liang Jiang1,2
Liao-Liang Jiang1,2 Fei Gao
Fei Gao Su-Juan Qin
Su-Juan Qin