Abstract
An efficient quantum implementation of the advanced encryption standard (AES) is crucial for reducing the complexity of implementing an exhaustive key search through Grover’s algorithm. In this paper, we study how to construct resource-efficient quantum circuits for AES. We consider the product of T-gates depth and width (TDW) and the product of full depth and width (FDW) as optimization targets. We propose a generic method, called the controlled control qubit cascade (CCQC) technique, to construct quantum circuits for nonlinear components with reduced TDW and FDW. Using this, we construct a quantum circuit for the AES S-box. Compared with recent work presented at ASIACRYPT 2023, our S-box quantum circuit achieves reductions of 2.3% in TDW and 45.2% in FDW. Additionally, we propose a new key schedule strategy to reduce the full depth of the AES quantum circuit. Finally, the trade-offs between T-gates depth and width and the parallel numbers of S-box and TDW are analyzed.
1 Introduction
Quantum technology, including cryptography Shor and Preskill [1]; Qin et al. [2], quantum computing Grover [3]; Shor [4], and quantum precision measurement Braginsky and Khalili [5]; Childs et al. [6], is the frontier of a new round of scientific and technological revolution. Quantum computing has been widely applied in fields including quantum cryptography Zhou et al. [7]; Gong et al. [8], quantum simulation Buluta and Nori [9], machine learning Song et al. [10, 11]; Li et al. [12, 13], solving equations Childs et al. [14]; Wan et al. [15, 16], and cryptanalysis Kaplan et al. [17]; Cai et al. [18]. The threats that quantum computing poses to existing cryptographic systems are well-known. Once large-scale quantum computers become operational, Shor’s algorithm will be capable of breaking asymmetric cryptographic schemes that rely on the discrete logarithm and factoring problems, such as RSA, ECDH, and ECC Shor [4]; Shor [19]. For symmetric cryptography, the primary challenges posed by quantum computation arise from Simon’s algorithm and Grover’s algorithm. When a quantum oracle that implements the target cryptographic quantum circuit can be accessed, Simon’s algorithm can undermine various symmetric cryptographic schemes by finding hidden periods Kaplan et al. [17]; Bonnetain et al. [20], while Grover’s algorithm can provide quadratic acceleration for exhaustive key searches that attack block ciphers Grover [3].
Due to the extremely high cost of quantum resources, estimating the quantum resources needed to attack block ciphers using Grover’s algorithm is crucial for reducing the implementation difficulty of such attacks and accurately predicting their actual implementation time. The advanced encryption standard (AES) Daemen [21] is one of the most widely used block ciphers today; thus, evaluating the quantum resources needed to attack it is highly significant. Moreover, the National Institute of Standards and Technology (NIST) has proposed the standardization of post-quantum cryptography by defining security categories 1, 3, and 5 based on the computational resources needed for exhaustive key searches on AES-128, AES-192, and AES-256, respectively. The key to applying Grover’s algorithm to AES lies in implementing the Grover oracle, which utilizes the AES quantum circuit to mark the correct key during the search process. Consequently, the precise estimation and careful optimization of the quantum circuit implementing AES have attracted significant attention in recent years.
Computational resources are often measured by quantum circuit size. Metrics commonly used to measure quantum circuits include width, depth, and the number of quantum gates Specifically, width refers to the number of logical qubits needed in a quantum circuit. Meanwhile, the minimum stages of quantum gates that can be executed in parallel in a circuit is called depth. We can measure the depth of all elementary gates within the circuit or focus specifically on the depth of a particular quantum gate, depending on the requirements of our demand. From a physical implementation perspective, realizing quantum circuits with a large width or deep depth is quite difficult Sun et al. [22]. Therefore, prior works have often focused on ways to reduce either the width Grassl et al. [23]; Zou et al. [24]; Li et al. [25] or depth Jaques et al. [26]; Huang and Sun [27] required for Grover’s attack on AES. However, there is often a trade-off between these two metrics. For example, optimizing the width of a quantum circuit may lead to a very large depth, which in turn makes Grover’s attack difficult to implement. Hence, it is also very feasible to consider the product of width and depth as a metric for measuring the size of a quantum circuit. Specifically, because the running time of fault-tolerant quantum computers is proportional to the T-gates depth Fowler [28]; Amy et al. [29, 30], the T-gates depth is also commonly used as an optimization target. For distinction, this paper refers to the depth of all elementary gates as the F-depth and to the T-gates depth as the T-depth. Considering the significance of F-depth and T-depth, we introduce the definitions of FDW as the product of F-depth and width and TDW as the product of T-depth and width, respectively.
1.1 Related works
One of the key challenges in implementing the AES quantum circuit is constructing the quantum circuit for the nonlinear component S-box. Previous works can generally be categorized into three types based on optimization goals for S-box quantum circuits: reducing width, depth, or the product of width and depth. We introduce related works from these three perspectives.
1.1.1 Reducing width
This field was initiated by Grassl et al., who utilized the Itoh–Tsujii algorithm to find the multiplicative inverse in a finite field for an S-box Grassl et al. [23]. Consequently, extensive subsequent works Chung et al. [31]; Wang et al. [32]; Li et al. [25] focused on efficiently solving the multiplicative inverse in . These works leveraged the properties of tower fields to map elements from an extension field to a subfield, thereby leading to the design of S-box circuits with low widths. Alternatively, Zou et al. [24] and Huang and Sun [27] employed the classical S-box circuit proposed by Boyar and Peralta [33] to construct S-box quantum circuits with low width, leveraging the fact that this classical S-box circuit’s multiplicative complexity was optimized by a heuristic algorithm. Huang and Sun [27] developed an in-place circuit structure for an S-box, and Li et al. [34] utilized this circuit to construct an S-box quantum circuit with five ancilla qubits.
1.1.2 Reducing depth
Jang et al. [35] constructed the first S-box quantum circuit aimed at reducing depth. However, the focus was usually on T-depth. Huang and Sun [27] formulated a technique that transforms a classical circuit with a multiplicative depth of into a quantum circuit with a T-depth of . They utilized the S-box classical circuit Boyar and Peralta [36] to construct an S-box quantum circuit aimed at optimizing T-depth. Furthermore, Huang et al. optimized the classical S-box circuit Boyar and Peralta [36] and constructed an S-box quantum circuit with the theoretically lowest T-depth of 3 using this optimized classical circuit. Additionally, Huang et al. provided theoretical proof that the T-depth equals 3.
1.1.3 Reducing the product of width and depth
This metric was first presented and optimized by Jaques et al. Jang et al. [35], but fewer studies focused on it. Most recently, the product of width and depth has begun to receive attention. Liu et al. proposed a technique called m-XOR at ASIACRYPT 2023 Liu et al. [37] that can identify reusable qubits. They also designed a compact circuit structure for the S-box and constructed an S-box quantum circuit with a product of T-depth and width equal to 344.
1.2 Our contributions
We analyze the algebraic structures of S-box classical circuits, uncovering the intrinsic connections between multiplicative nodes. This inspires our controlled control qubit cascade (CCQC) technique for constructing quantum circuits with optimized TDW and FDW. Applying CCQC, our S-box quantum circuit reduces TDW by 2.3% and FDW by 45.2% compared to ASIACRYPT 2023 work Liu et al. [37]. We develop a key schedule strategy to reduce AES circuit F-depth. With this and our S-box circuit, we estimate the quantum resources required to implement iterative AES-128. Finally, we analyze the trade-offs of T-depth and width, as well as S-box parallelism versus TDW. Finally, we analyze T-depth vs. width and S-box parallelism vs. TDW trade-offs.
2 Preliminaries
2.1 Synthesis of quantum circuits
A qubit is typically denoted as , and refers to a -qubit quantum system that can also be represented by unit vectors in Nielsen and Chuang [38]. A quantum circuit transforms the initial input state into the final output state through a series of unitary operations, where the unitary transformation is a linear map and satisfies , and is the adjoint of . Any unitary transformation can be constructed by a composition and a tensor product of a universal gate set. A universal gate set consists of a finite number of single-qubit gates and two-qubit gates. And can be obtained by reversing the order of adjoint gates in . Quantum circuits require that ancilla qubits should be ultimately returned to ; thus, is typically used for uncompute operations. We adopt the Clifford + T set as this gate set that can be implemented fault-tolerantly on a large set of surface codes. The Clifford + T set includesand a non-Clifford gate , where . We also apply the Pauli- gate , which can implement . Here, “” implies XOR. The CNOT gate implements , and the Toffoli gate implements . In quantum circuits, X gates, CNOT gates, and Toffoli gates, respectively, perform the corresponding classical NOT, XOR, and operations. The quantum AND gate is similar with the Toffoli gate to . The difference is that the quantum AND gate requires the input state of the target qubit as . In this paper, the quantum circuit we constructed perfectly meets this condition. Hence, we adopt a quantum AND gate because the T-depth of the quantum AND gate is 1 Huang and Sun [27]. The quantum AND gate, together with its adjoint, are illustrated in Figure 1.
FIGURE 1
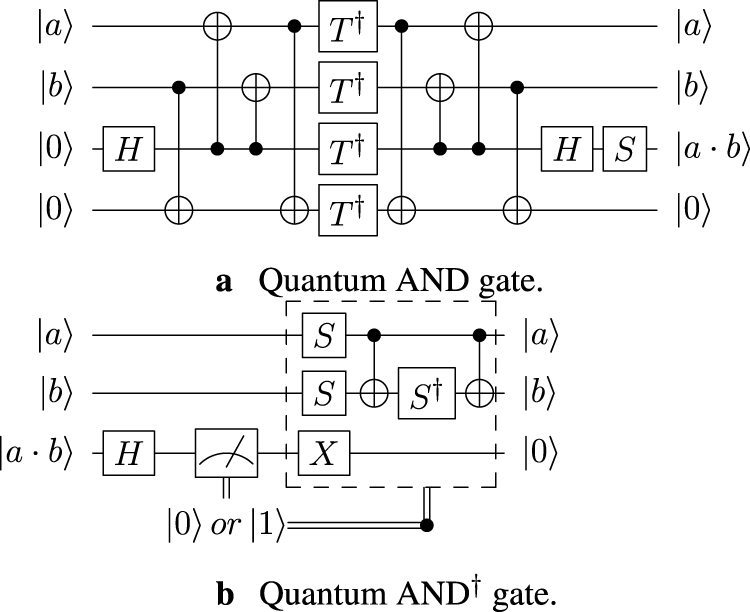
The quantum AND gate and its adjoint (a) quantum AND gate and (b) quantum gate.
2.2 Classical circuits and directed acyclic graphs (DAG)
This paper utilizes concepts related to classical circuits and directed acyclic graphs (DAGs) to explain the circuit construction method Cong and Ding [39]. Therefore, this section will introduce these relevant concepts. A classical circuit can be represented by a DAG with a set of nodes and a set of edges . Nodes represent basic gates in classical circuits, and edges denote the direction of bit-flow in the classical circuit. The inputs of a classical circuit are often called the primary inputs. If there is a path from node to node , is a predecessor of , and is a successor of . Let us define the function , which returns 1 if is a multiplicative node and 0 otherwise. The multiplicative depth of node is the maximum number of multiplicative gates on any path that begin with a primary input and end with a node . The function of multiplicative depth iswhere denotes the set of all predecessor nodes of . The multiplicative depth of a circuit is the maximal multiplicative depth of its nodes
2.3 The advanced encryption standard
The advanced encryption standard (AES) is a block cipher standardized by the NIST Daemen [21]. Three variants, AES-128, AES-192, and AES-256, correspond to three different original key lengths. The detailed process of the AES algorithm is that the input 128-bit data block is initially XOR with the first 128 bits of the original key. Then, a specific number of round function iterations constitute the encryption process of AES: 10 rounds, 12 rounds, and 14 rounds for AES-128, AES-192, and AES-256, respectively. There are four operations during a round function in Figure 2: SubByte, ShiftRow, MixColumn, and AddRoundKey. MixColumn is omitted in the final round iteration.
FIGURE 2
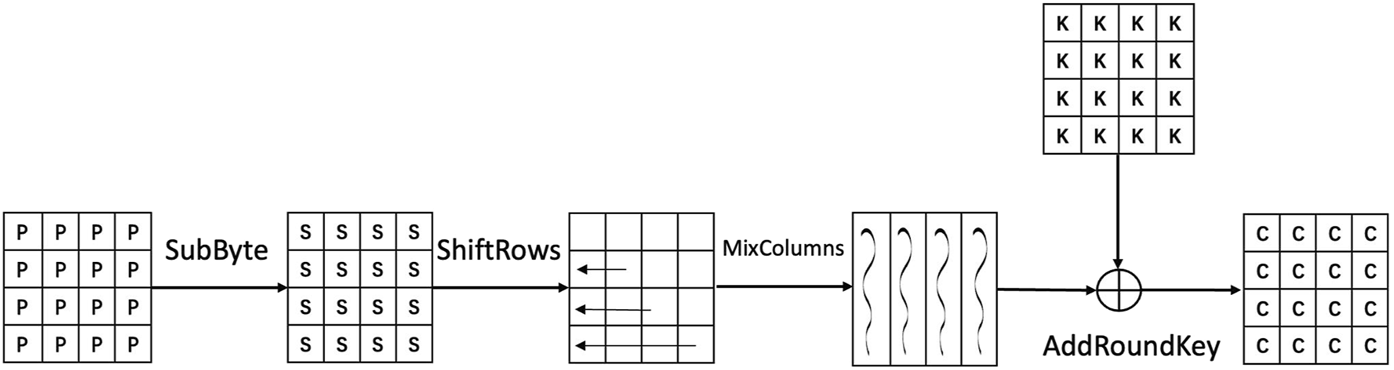
Round function process of the AES.
Each block in a matrix represents a byte. AddRoundKey applies the XOR operations to the round key and the 16 bytes. SubByte transforms the 16-byte state using the S-box. ShiftRow performs a cyclical leftward shift of the blocks in the -th row by positions, where . MixColumn treats each column as a polynomial over the finite field and multiplies these polynomials by a fixed polynomial. It is a linear transformation that can be modeled as a matrix in where the elements in matrix are represented in hexadecimal. The current round key is generated from the preceding round key by Keyexpansion. Four bytes in a column of the matrix represent a word . Three operations are involved in the Keyexpansion: RotWord, Rcon, and SubWord. RotWord performs a cyclical leftward shift of words from the round key by one position. Rcon applies the XOR operations to the round key and a constant vector. SubWord transforms the state of one word from a round key by an S-box.
3 Constructing a circuit for an S-box with a low TDW and FDW
The universal method for constructing an S-box quantum circuit can be summarized in two steps. First, identify a classical circuit that implements the S-box. Then, implement this classical circuit in a quantum circuit. We chose the S-box classical circuit proposed by Boyar and Peralta [36], whose circuit depth had been optimized by heuristic algorithms. This section introduces the construction method: the controlled control qubit cascade (CCQC) technique for the S-box quantum circuit.
3.1 Constructing a quantum circuit with a low TDW and FDW
We introduce constructing an S-box quantum circuit by studying the S-box classical circuit Boyar and Peralta [36]. Based on the relevant knowledge presented in Equations 1, 2, we compute the multiplicative depth of all multiplicative nodes within this classical circuit and stratify all multiplicative nodes according to their multiplicative depth, as shown in Table 1, where we assign nodes with greater multiplicative depth to the higher layers.
TABLE 1
| Layer and multiplicative depth | Multiplicative node |
|---|---|
| 1 | M1, M2, M4, M6, M7, M9, M11, M12, and M14 |
| 2 | M25, M31, and M34 |
| 3 | M29, M30, M32, and M35 |
| 4 | M46, M47, M48, M49, M50, M51, M52, M53, M54, M55, M56, M57, M58, M59, M60, M61, M62, and M63 |
Hierarchical multiplicative nodes from an S-box classical circuit.
The variables in the classical circuit Boyar and Peralta [36] represent the primary inputs of the S-box, while denote the outputs of the S-box. Analyzing these eight outputs leads to Observation 1. Based on our previous experience, the linear combinations of existing quantum states can be prepared easily by several CNOT gates in a quantum circuit. Therefore, our CCQC technique focuses on how to prepare multiplicative nodes with maximum multiplicative depth in classical circuits.
Observation 1The eight outputs of the S-box can be derived by linear combinations of all multiplicative nodes with a multiplicative depth of 4.
Example 1,,,,,,,,,,,.
We illustrate this method through a classical circuit in Example 1. We calculate the multiplicative depth of all multiplicative nodes in Example 1 and stratify them hierarchically. During the stratifying of multiplicative nodes in Example 1, we further observe that there usually exist additive nodes among different layers. These additive nodes merge nodes with smaller multiplicative depth to become the input for multiplicative nodes in a higher layer.
In a given classical circuit, any multiplicative node can be expressed as the product of a linear combination of its lower layer multiplicative nodes and the primary inputs.
Theorem 1 shows that the highest-level multiplicative nodes can be obtained from lower-level multiplicative nodes and the primary inputs. The proof of Theorem 1 can be found in Supplementary Material. Table 2 lists the algebraic relationships between the multiplicative nodes from different layers of Example 1. Algorithm 1 can ascertain the algebraic relationships between multiplicative nodes in any classical circuit.
TABLE 2
| Layer | Algebraic relationships |
|---|---|
| 1 | , |
| 2 | , , |
| 3 | , |
Algebraic relationships between the multiplicative nodes from Example 1.
Algorithm 1
1:Input: Any classical circuit
2:Output: A novel classical circuit that derived the algebraic relationships between multiplicative nodes
3:Function EXPAND
4: //is the start node
5:
6:fordo
7: //
8: if is addictive node then
9: //is the input of
10: EXPAND
11: else
12: Update with the production of in
13: endif
14:
15: endfor
16: End Function
17: for each node do
18: if is multiplicative node then
19: EXPAND
20: else
21: Continue
22: endif
23: endfor
24: Return
The CCQC technique prepares multiplicative nodes in the quantum circuit hierarchically, and multiplicative nodes at the same layer are prepared in parallel. Because a qubit cannot be used in different quantum gates at the same time, to support the parallelism of quantum AND gates, ancilla qubits are needed to copy variables that are used as inputs to different multiplicative nodes. We can liken the inputs of multiplicative nodes to the control qubits of Toffoli gates and the outputs of the multiplicative nodes to controlled qubits. We use Toffoli gates due to the compactness of its visualization and the convenience of explanation. Then, the core concept of the CCQC technique is to use the controlled qubits of lower-layer multiplicative nodes as the control qubits for higher-layer multiplicative nodes. To elaborate, we take advantage of the qubits occupied by lower-layer multiplicative nodes as controlled qubits within the CNOT network, transforming these lower-layer controlled qubits into inputs for higher-layer multiplicative nodes. Figure 3 implements the highest-layer multiplicative nodes from Table 2 by our CCQC technique.
FIGURE 3
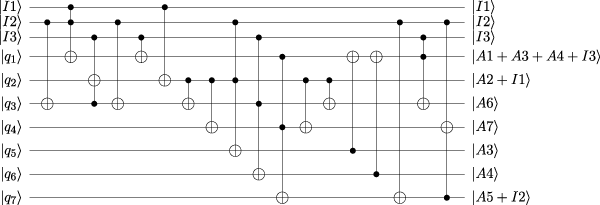
Constructing a quantum circuit with the CCQC technique.
Constructing an S-box quantum circuit using the CCQC technique is more complex. We preprocess the S-box classical circuit followed by Theorem 1 and list the algebraic relationships among multiplicative nodes in Supplementary Material. Upon analyzing the classical circuit for the S-box, we obtain Observation 2.
Observation 2All inputs of the lowest layer multiplicative nodes are also the inputs of the highest layer multiplicative nodes.
We find that it is beneficial to save qubits if primary inputs can be the inputs of multiplicative nodes directly. If not, extra qubits are needed to prepare inputs for multiplicative nodes. Therefore, we select eight linearly independent inputs from the first layer as a new set of basis. We adopt the method proposed by Patel et al. Markov et al. [40] to construct an in-place circuit that needs 17 CNOT gates to implement the transformation; see Figure 4. This new basis is used as the primary input when constructing an S-box quantum circuit with the help of Algorithm 2.
FIGURE 4
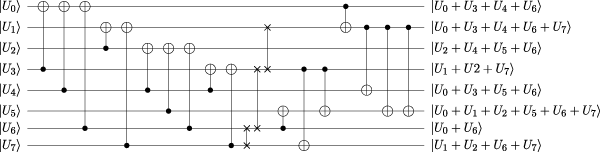
The quantum circuit to change the basis for the S-box.
Algorithm 2 interprets how to construct a quantum circuit with the CCQC technique. List Prepared includes the prepared multiplicative nodes, and Anc includes ancilla qubits that are introduced to ensure quantum AND gates can be executed in parallel. Operation CNOT means qubit is a controlled qubit in the CNOT network, and Uncompute means do an uncompute operation to release qubit . Note that after preparing multiplicative nodes from the fourth layer, we still need to construct the outputs , ,…, through CNOT gates and X gates. We list all allocated qubits and gates of the S-box quantum circuit constructed by Algorithm 2 in Table 3. Among them, the definitions of a CNOT gate, AND gate, X gate, and REWIRE operation are as follows: CNOT, , , AND, , , , , X, REWIRE, , . We implemented our S-box quantum circuit on Microsoft Q# to verify its correctness. The details can be viewed in the online code at https://github.com/kyolxs/Constructing-Resource-Efficient-Quantum-Circuits-for-AES.
TABLE 3
| No. | Gate | No. | Gate | No. | Gate |
|---|---|---|---|---|---|
| 1 | CNOT, | 2 | CNOT, | 3 | CNOT, |
| 4 | CNOT, | 5 | CNOT, | 6 | CNOT, |
| 7 | CNOT, | 8 | CNOT, | 9 | CNOT, |
| 10 | CNOT, | 11 | CNOT, | 12 | CNOT, |
| 13 | CNOT, | - | REWIRE, | - | REWIRE, |
| 14 | CNOT, | - | REWIRE, | 15 | CNOT, |
| 16 | CNOT, | 17 | CNOT, | 18 | CNOT, |
| 19 | CNOT, | 20 | CNOT, | 21 | CNOT, |
| 22 | CNOT, | 23 | CNOT, | 24 | CNOT, |
| 25 | CNOT, | 26 | CNOT, | 27 | CNOT, |
| 28 | CNOT, | 29 | CNOT, | 30 | CNOT, |
| 31 | CNOT, | 32 | CNOT, | 33 | CNOT, |
| 34 | CNOT, | 35 | CNOT, | 36 | CNOT, |
| 37 | CNOT, | 38 | CNOT, | 39 | CNOT, |
| 40 | CNOT, | 41 | CNOT, | 42 | CNOT, |
| 43 | AND, , | 44 | AND, , | 45 | AND, , |
| 46 | AND, , | 47 | AND, , | 48 | AND, , |
| 49 | AND, , | 50 | AND, , | 51 | AND, , |
| 52 | CNOT, | 53 | CNOT, | 54 | CNOT, |
| 55 | CNOT, | 56 | CNOT, | 57 | CNOT, |
| 58 | CNOT, | 59 | CNOT, | 60 | CNOT, |
| 61 | CNOT, | 62 | CNOT, | 63 | CNOT, |
| 64 | CNOT, | 65 | CNOT, | 66 | CNOT, |
| 67 | CNOT, | 68 | CNOT, | 69 | CNOT, |
| 70 | CNOT, | 71 | CNOT, | 72 | CNOT, |
| 73 | CNOT, | 74 | CNOT, | 75 | CNOT, |
| 76 | CNOT, | 77 | CNOT, | 78 | AND, , |
| 79 | AND, , | 80 | AND, , | 81 | CNOT, |
| 82 | CNOT, | 83 | CNOT, | 84 | CNOT, |
| 85 | CNOT, | 86 | CNOT, | 87 | CNOT, |
| 88 | CNOT, | 89 | CNOT, | 90 | CNOT, |
| 91 | CNOT, | 92 | CNOT, | 93 | CNOT, |
| 94 | CNOT, | 95 | CNOT, | 96 | CNOT, |
| 97 | AND, , | 98 | AND, , | 99 | AND, , |
| 100 | AND, , | 101 | CNOT, | 102 | CNOT, |
| 103 | CNOT, | 104 | CNOT, | 105 | CNOT, |
| 106 | CNOT, | 107 | CNOT, | 108 | CNOT, |
| 109 | CNOT, | 110 | CNOT, | 111 | CNOT |
| 112 | CNOT | 113 | CNOT | 114 | CNOT |
| 115 | CNOT | 116 | CNOT | 117 | CNOT |
| 118 | CNOT | 119 | CNOT | 120 | CNOT |
| 121 | CNOT | 122 | CNOT | 123 | CNOT |
| 124 | CNOT | 125 | CNOT | 126 | CNOT |
| 127 | CNOT | 128 | CNOT | 129 | CNOT |
| 130 | CNOT | 131 | CNOT | 132 | CNOT |
| 133 | CNOT | 134 | CNOT | 135 | CNOT |
| 136 | CNOT | 137 | CNOT | 138 | CNOT |
| 139 | CNOT, | 140 | CNOT, | 141 | CNOT, |
| 142 | CNOT, | 143 | CNOT, | 144 | CNOT, |
| 145 | CNOT, | 146 | CNOT, | 147 | CNOT, |
| 148 | CNOT, | 149 | CNOT, | 150 | CNOT, |
| 151 | CNOT, | 152 | CNOT, | 153 | CNOT, |
| 154 | CNOT, | 155 | CNOT, | 156 | CNOT, |
| 157 | CNOT, | 158 | CNOT, | 159 | CNOT, |
| 160 | CNOT, | 161 | CNOT, | 162 | CNOT, |
| 163 | CNOT, | 164 | CNOT | 165 | CNOT, |
| 166 | CNOT, | 167 | CNOT, | 168 | AND, , |
| 169 | AND, , | 170 | AND, , | 171 | AND, , |
| 172 | AND, , | 173 | AND, , | 174 | AND, , |
| 175 | AND, , | 176 | AND, , | 177 | AND, , |
| 178 | AND, , | 179 | AND, , | 180 | AND, , |
| 181 | AND, , | 182 | AND, , | 183 | AND, , |
| 184 | AND, , | 185 | AND, , | 186 | CNOT, |
| 187 | CNOT, | 188 | CNOT, | 189 | CNOT, |
| 190 | CNOT, | 191 | CNOT, | 192 | CNOT, |
| 193 | CNOT, | 194 | CNOT, | 195 | CNOT, |
| 196 | CNOT, | 197 | CNOT, | 198 | CNOT, |
| 199 | CNOT, | 200 | CNOT, | 201 | CNOT, |
| 202 | X | 203 | CNOT, | 204 | CNOT, |
| 205 | CNOT, | 206 | CNOT, | 207 | CNOT, |
| 208 | CNOT, | 210 | CNOT, | 211 | CNOT, |
| 212 | X | 213 | CNOT, | 213 | CNOT, |
| 214 | CNOT, | 215 | CNOT, | 216 | CNOT, |
| 217 | CNOT, | 218 | CNOT, | 219 | CNOT, |
| 220 | CNOT, | 221 | CNOT, | 222 | CNOT, |
| 223 | CNOT, | 224 | CNOT, | 225 | CNOT, |
| 226 | CNOT, | 227 | CNOT, | 228 | CNOT, |
| 229 | CNOT, | 230 | CNOT, | 231 | CNOT, |
| 232 | CNOT, | 233 | CNOT, | 234 | CNOT, |
| 235 | CNOT, | 236 | CNOT, | 237 | CNOT, |
| 238 | CNOT, | 239 | CNOT, | 240 | CNOT, |
| 241 | CNOT, | 242 | CNOT, | 243 | CNOT, |
| 244 | CNOT, | 245 | CNOT, | 246 | CNOT, |
| 247 | CNOT, | 248 | X | 249 | CNOT, |
| 250 | CNOT, | 251 | CNOT, | 252 | CNOT, |
| 253 | CNOT, | 254 | CNOT, | 255 | CNOT, |
| 256 | CNOT, | 257 | X |
Quantum circuit for the S-box implementation.
Algorithm 2
Input: Algebraic relationships between multiplicative nodes of a given classical circuit
2: Output: A quantum circuit to implement the highest layer
Initialize empty lists Prepared and Anc
4:
//denotes maximum layer of
6: whiledo
ifAnc is not empty then
8: forAncdo
if is not required by -th layer then
10: Uncompute
remove from Anc
12: endif
endfor
14: endif
for-th layer do
16: ifPrepared is required by only required by then
CNOT
18: else
Introduce new ancilla qubit and add to Anc
20: CNOT
endif
22: endfor
prepare multiplicative nodes in -th layer by quantum AND gates
24: for-th layer do
add to Prepared
26: endfor
28: endwhile
Various implementations of S-box quantum circuits have been proposed, with some utilizing Toffoli gates and others employing AND gates. We present a comparison of the quantum resource costs in S-box quantum circuits based on the Toffoli gate in Table 4, focusing on previous works that study low Toffoli depth S-boxes. Additionally, Jang et al. [35] and Liu et al. [37] conducted a comprehensive comparison by decomposing Toffoli gates in different manners. However, this paper adopts AND gates to achieve lower circuit depth. Therefore, we need an additional 18 ancilla qubits to support the preparation of the fourth layer multiplicative nodes. After executing the fourth layer of AND gates, those 18 ancilla bits are reset to , and eight of them can be used directly to prepare , ,…, . After the execution of the S-box, an S- is necessary to uncompute ancilla qubits. We list a comparison of the quantum resources costs in the S-box and the S- based on the AND gate in Table 5. Among those works, the S-box quantum circuit proposed by Liu et al. at ASIACRYPT 2023 Liu et al. [37] has the same T-depth and a similar width as our work. Because their proposed m-XOR technique can identify reusable qubits, it is very effective in reducing width. Therefore, their work is similar to our work in terms of the TDW. In fact, during our preprocessing to obtain an S-box classical circuit, we frequently find that variables or appear even times within the same formulation , . Due to the properties of the XOR operation, these variables can be directly eliminated, avoiding unnecessary CNOT gates targeting the same qubit and thereby reducing the F-depth.
TABLE 4
| Source | Ancilla qubits | #Toffoli | -depth | #CNOT | #1qClifford |
|---|---|---|---|---|---|
| [26] | 120 | 34 | 6 | 186 | 4 |
| [27] | 120 | 34 | 4 | 214 | 4 |
| [27] | 182 | 78 | 3 | 356 | 4 |
| [42] | 136 | 78 | 3 | 313 | 4 |
| [42] | 68 | 34 | 4 | 162 | 4 |
| [37] | 74 | 34 | 4 | 168 | 4 |
| [37] | 60 | 34 | 4 | 196 | 4 |
| [43] | 74 | 34 | 4 | 179 | 4 |
| [43] | 60 | 34 | 4 | 207 | 4 |
| Ours | 58 | 34 | 4 | 219 | 4 |
Comparison of quantum resources for low Toffoli depth S-boxes based on a Toffoli gate.
The bold values indicate the quantum resources required by the S-box quantum circuit constructed in this work.
TABLE 5
| Source | #CNOT | #1qClifford | #T | T-depth | F-depth | Width | Depth width | |
|---|---|---|---|---|---|---|---|---|
| TDW | FDW | |||||||
| [26] | 664 | 205 | 136 | 6 | 117 | 136 | 816 | 15,912 |
| [27] | 718 | 208 | 136 | 4 | 109 | 136 | 544 | 14,824 |
| [37] | 624 | 204 | 136 | 4 | 101 | 99 | 396 | 9,999 |
| [37] | 688 | 220 | 136 | 4 | 132 | 86 | 344 | 11,352 |
| Our | 710 | 276 | 136 | 4 | 74 | 58 + 8 + 18 = 84 | 336 | 6,216 |
Comparison of quantum resources for an S-box and an S- based on an AND gate.
The bold values indicate the TDW and FDW of the S-box quantum circuit constructed in this work.
Two types of S-boxes are required to construct the AES quantum circuit in the next section. The first S-box implements in SubByte. The second S-box implements in SubWord. Our S-box quantum circuit can directly accommodate both situations. We do not differentiate between these two types of S-boxes in our subsequent discussions.
4 Optimized quantum circuits for AES
This section discusses the implementation of the quantum circuit of AES. We begin by explaining how each component can be implemented in a quantum circuit, followed by how to implement the iterative encryption circuits for AES under a pipeline structure and a round-in-place structure. We address estimating the quantum resources required to implement AES. It is important to emphasize that all the circuits mentioned in this section are implemented with the maximum parallelism numbers of an S-box.
4.1 Components of AES and their implementations
4.1.1 SubByte and SubWord
The S-box is the core cryptographic component used to implement SubByte and SubWord. Its quantum circuit implementation is detailed in previous sections. SubByte needs 16 S-boxes, and SubWord needs four S-boxes.
4.1.2 ShiftRow and RotWord
ShiftRow and RotWord only perform cyclical leftward shifts but do not change the state of bytes. Both can be implemented in a quantum circuit entirely through rewiring. Following Grassl et al. [23], we considered rewiring as a free operation, thus excluding it from cost estimates.
4.1.3 MixColumn and Rcon
MixColumn can be implemented with an in-place quantum circuit due to the invertibility of its binary matrix A number of studies by Jang et al. [35]; Liu et al. [37]; Xiang et al. [41] have been conducted on the implementation of MixColumn. We use an in-place circuit Liu et al. [37] that requires only 98 CNOT gates to implement MixColumn with an F-depth of 16. It can easily be realized for the Rcon operation by applying X gates in the first word of the round key as necessary.
4.1.4 AddRoundKey
AddRoundKey is executed in a quantum circuit through a CNOT network, where the round key qubits act as control bits and the 128 qubits for the AES data block act as controlled bits in the CNOT network.
4.1.5 Keyexpansion
As mentioned before, the key used in the AddRoundKey comes from the round key generated by the Keyexpansion. Hence, Keyexpansion is also an iterative process that uses ten rounds, eight rounds, and seven rounds for AES-128, AES-192, and AES-256, respectively. In this paper, we adopt the in-place circuit structure proposed by Jaques et al. [26] to realize the Keyexpansion iteration by combining it with the SubByte subcircuit implemented by S-boxes. For detailed circuit structure, please refer to Jaques et al. [26]. Each round of Keyexpansion process generates four, six, and eight words that correspond to AES-128, AES-192, and AES-256, respectively.
The key schedule strategy controls the iterative progress of Keyexpansion, and a reasonable key schedule strategy can make the circuit more compact. We designed a new key schedule strategy that reduces the F-depth. The criterion of our key schedule strategy is to ensure that the SubWord subcircuit must be executed in parallel with the SubByte subcircuit. For AES-128, the Keyexpansion’s iteration is synchronized with the round function’s iteration. However, it should be noted that subcircuits of Rcon and SubWord must be executed in parallel with the SubByte subcircuit, and the remainder subcircuit of Keyexpansion executes in parallel with the MixColumn subcircuit. Due to the iterative rounds of Keyexpansion, it is slightly more complex to arrange the circuit layout of AES-192 and AES-256 in a reasonable way to make the circuit more compact. We summarize the key schedule process corresponding to each iteration of the round function for AES-192 and AES-256 in Tables 6, 7. The leftmost column in the tables indicates the round function’s iterative round, while the remaining columns show which key word is stored in the 32 qubit registers during the key schedule process. are original key of AES-192, and are original key of AES-256. The key words with a wavy line on top indicate the key words generated by SubWord and need to be executed in parallel with the SubByte subcircuit. The bold keywords denote the key words used in the current round of iteration.
TABLE 6
| Round | ||||||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 | ||||||
| 11 | ||||||
| 12 |
The key schedule process of AES-192.
The bold keywords denote the keywords used in the current round of iteration.
TABLE 7
| Round | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
| 6 | ||||||||
| 7 | ||||||||
| 8 | ||||||||
| 9 | ||||||||
| 10 | ||||||||
| 11 | ||||||||
| 12 | ||||||||
| 13 | ||||||||
| 14 |
The key schedule process of AES-256.
The bold keywords denote the keywords used in the current round of iteration.
4.2 AES quantum circuit with a pipeline structure
The pipeline structure Jaques et al. [26] was proposed by Jaques et al. to reduce the depth of the circuit. The characteristic of the pipeline structure is that after completing one round iterative round function, it directly allocates new qubits to implement the next round iterative round function. Jang et al. [42] further refined the pipeline structure into a regular version and a shallow version. We adopted the regular version because the regular version has high parallelism while considering the depth-qubit trade-off. We integrated our S-box quantum circuit into the regular-version pipeline structure and estimated the quantum resources required to implement the AES forward circuit and its adjoint circuit. Table 8 compares our work with previous works under the same structure. It is worth noting that Liu et al. [37] and Jang et al. [35] only provide the resources for a forward circuit. Therefore, we have multiplied the metrics other than width by 2 in Table 8.
TABLE 8
| Source | #CNOT | #1qClifford | #T | T-depth | F-depth | Width | Depth width | ||
|---|---|---|---|---|---|---|---|---|---|
| TDW | FDW | ||||||||
| AES-128 | [26] | 291,150 | 83,116 | 54,400 | 120 | 2,827 | 3,936 | 472,320 | 11,127,072 |
| [27] | 298,720 | 83,295 | 54,400 | 80 | 2,198 | 3,936 | 314,880 | 8,651,328 | |
| [35]∗ | 285,984 | 75,040 | 54,400 | 80 | 1,856 | 6,372 | 509,760 | 11,826,432 | |
| [37] | 264,752 | 103,600 | 54,400 | 80 | 1,600 | 3,689 | 295,120 | 5,902,400 | |
| [27] | 570,785 | 189,026 | 124,800 | 60 | 2,312 | 5,576 | 334,560 | 1,2,891,712 | |
| Our | 189,300 | 42,440 | 54,400 | 80 | 1,790 | 2,896 | 231,680 | 5,183,840 | |
| AES-192 | [35] | 325,072 | 86,384 | 60,928 | 96 | 2,228 | 6,692 | 642,432 | 14,909,776 |
| [37] | 298,512 | 116,848 | 60,928 | 96 | 1924 | 3,945 | 378,720 | 7,590,180 | |
| Our | 212,652 | 47,520 | 60,928 | 96 | 2,154 | 3,216 | 308,736 | 6,927,264 | |
| AES-256 | [35] | 399,792 | 106,654 | 75,072 | 112 | 2,614 | 6,980 | 781,760 | 18,245,720 |
| [37] | 374,256 | 147,758 | 38,080 | 112 | 2,240 | 4,457 | 499,184 | 9,983,680 | |
| Our | 261,148 | 58,564 | 75,072 | 112 | 2,518 | 3,536 | 396,032 | 8,903,648 | |
Quantum resources for implementing AES and its adjoint circuit with a pipeline structure.
The bold values indicate the T-depth, TDW, and FDW of the AES quantum circuit constructed in this work.
For the implementation of AES-128, the quantum circuit that applies our S-box quantum circuit with pipeline structure has a T-depth of 80. Compared to the state-of-the-art work with the same T-depth, our approach achieves a 21.5% reduction in TDW and a 12.2% reduction in FDW. In the case of AES-192, the quantum circuit that applies our S-box quantum circuit with a pipeline structure has a T-depth of 96. Compared to the state-of-the-art work with the same T-depth, our approach achieves an 18.5% reduction in TDW and an 8.7% reduction in FDW. Regarding AES-256, the quantum circuit that applies our S-box quantum circuit with a pipeline structure has a T-depth of 112. Compared to the state-of-the-art work with the same T-depth, our approach achieves a 20.7% reduction in TDW and a 10.9% reduction in FDW.
4.3 AES quantum circuit with a round-in-place structure
The round-in-place structure Huang and Sun [27] was proposed by Huang et al. to maximize the reuse of qubits and greatly reduce circuit width. They showed the method to construct the inverse S-box quantum circuit based on an S-box quantum circuit, an additional 42 CNOT gates, and four X gates. For more details, please refer to Huang and Sun [27]. With the inverse S-box quantum circuit, they constructed the iterative encryption in an in-place manner; see Figure 5. Because the T-depth of one round iteration with the round-in-place structure is twice that of the pipeline structure, we divide into two halves to save ancilla qubits. After dividing into two-halves, there needs an accumulative total of 18 S-boxes in each part, two S-boxes in and 16 S-boxes or inverse S-boxes in or .
FIGURE 5
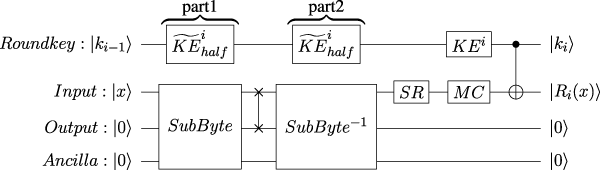
The iterative encryption circuit with a round-in-place structure.
We also apply our S-box quantum circuit to the round-in-place structure and estimate quantum resources for implementing the AES forward circuit without its adjoint circuit. Table 9 compares our work with previous works under the round-in-place structure. Because Liu et al. [37] did not provide the F-depth of AES-128, we calculate the F-depth of their circuit based on the F-depth of the S-box they applied to an R structure. Apart from the F-depth, all other metrics are directly derived from Liu et al. The quantum circuit that applies our S-box quantum circuit with a round-in-place structure had a T-depth of 80. Compared with the circuit of Liu et al. with the same T-depth, we achieved a modest reduction of 3.1% in TDW and a substantial reduction of 43.3% in FDW.
TABLE 9
| Source | T-depth | F-depth | Width | Depth width | ||
|---|---|---|---|---|---|---|
| TDW | FDW | |||||
| AES-128 | [27]† | 2,460 | — | 492 | 1,210,320 | — |
| [37] | 80 | 2,796 | 1,660 | 132,800 | 4,641,360 | |
| Our | 80 | 1,636 | 1,608 | 128,640 | 2,630,688 | |
| AES-192 | Our | 96 | 1966 | 1,672 | 160,512 | 3,287,152 |
| AES-256 | Our | 112 | 2,296 | 1,736 | 194,432 | 3,985,856 |
Quantum resources for implementing forward AES with a round-in-place structure.
The bold values indicate the Width, TDW, and FDW of the AES quantum circuit constructed in this work.
5 Trade-offs of circuit metrics
This section shows the trade-offs between T-depth and width, the parallel numbers of the S-box and TDW. We construct four AES-128 circuits by combining the pipeline structure and round-in-place structure with our S-box quantum circuit. We set different values for in these four circuits and estimate their width, T-depth, and TDW. We define the pipeline structure using our S-box quantum circuit as Circuit 1, and the round-in-place structure using our S-box quantum circuit is represented by Circuit 2. It should be noted that due to the different structural characteristics of these two circuit structures, we set for the pipeline structure to be a factor of 20 and for the round-in-place structure to be a factor of 18. Figure 6 shows the trade-off curves for the T-depth and width of the different circuits. Figure 7 reflects the influence of on TDW. The points on the curves correspond to different values of . In the same curve, the points on the right correspond to smaller values of . From left to right, the points on Circuit 1 correspond to , respectively. From left to right, points on Circuit 2 correspond to , respectively.
FIGURE 6
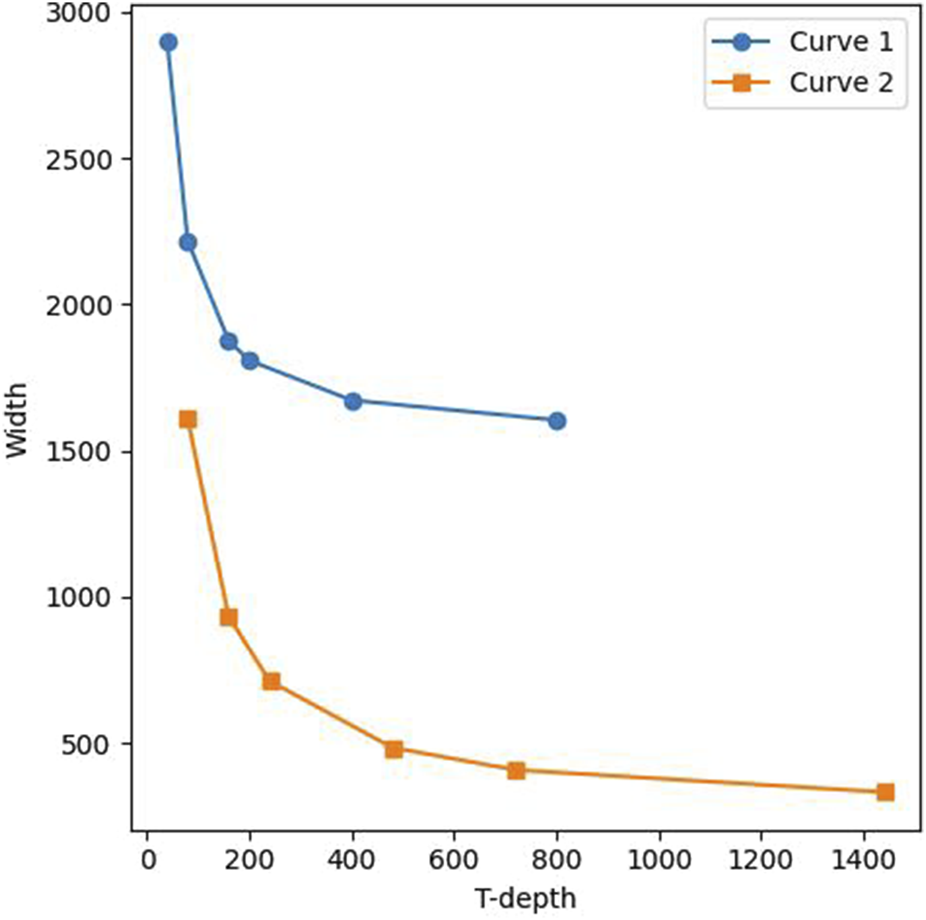
The trade-off between T-depth and width for AES-128.
FIGURE 7
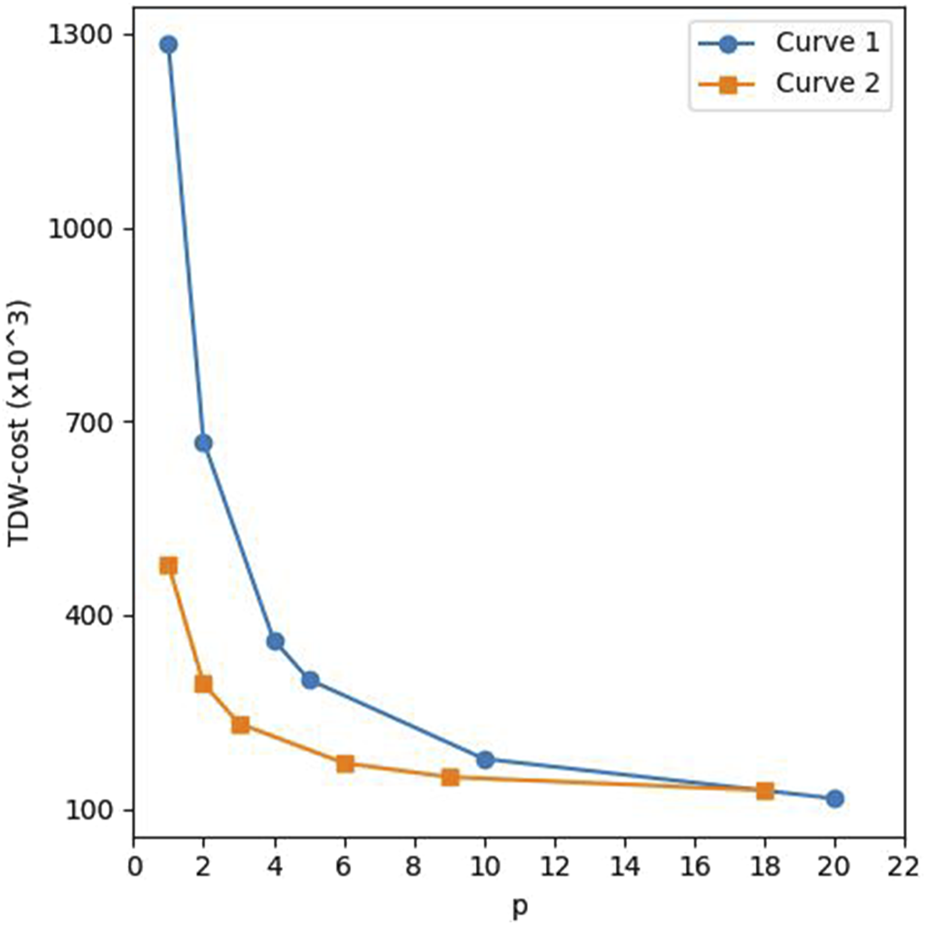
The influence of on TDW.
6 Conclusion
We propose the CCQC technique for constructing quantum circuits for nonlinear components, providing a general method to reduce both TDW and FDW. Additionally, we design a new key schedule strategy to reduce the F-depth of the AES quantum circuit. This paper introduces significantly optimized AES quantum circuits, achieving improvements in TDW and FDW. Our research provides a new idea for constructing quantum circuits for nonlinear components of other block ciphers with low TDW and FDW. However, the CCQC technique is more suitable for constructing quantum circuits with low TDW and FDW for classical circuits that have a lower multiplicative depth. On the other hand, solely focusing on reducing the multiplicative depth of a circuit implies the need for more intermediate values, which in turn costs more qubits when constructing the quantum circuit. Therefore, the impact of multiplicative depth on TDW and FDW is worth further exploration. Finally, we find that for the S-box quantum circuit designed in this article, implementing the iterative AES quantum circuit by regular-version pipeline structure is more advantageous for FDW and TDW.
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
L-LJ: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing – original draft, and writing – review and editing. B-BC: writing – original draft and writing – review and editing. FG: writing – original draft, writing – review and editing, conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, and visualization. S-JQ: writing – original draft and writing – review and editing. Z-PJ: writing – original draft and writing – review and editing. Q-YW: writing – original draft and writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by the National Natural Science Foundation of China (Grant Nos. 62272056, 62372048, and 62371069).
Acknowledgments
I would like to express my sincere gratitude to the Tianyan Quantum Computing Program for providing valuable resources and support. Your platform has greatly facilitated my learning and deepened my understanding of quantum computing.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1582819/full#supplementary-material
References
1.
ShorPWPreskillJ. Simple proof of security of the bb84 quantum key distribution protocol. Phys Rev Lett (2000) 85:441–4. 10.1103/physrevlett.85.441
2.
QinLLiuBGaoFHuangWXuBLiY. Decoy-state quantum private query protocol with two-way communication. Physica A: Stat Mech its Appl (2024) 633:129427. 10.1016/j.physa.2023.129427
3.
GroverLK. A fast quantum mechanical algorithm for database search. In: Proceedings of the twenty-eighth annual ACM symposium on Theory of computing (1996). p. 212–9.
4.
ShorPW. Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings 35th annual symposium on foundations of computer science (Ieee) (1994). p. 124–34.
5.
BraginskyVBKhaliliFY. Quantum measurement. Cambridge University Press (1995).
6.
ChildsAMPreskillJRenesJ. Quantum information and precision measurement. J Mod Opt (2000) 47:155–76. 10.1080/095003400148123
7.
ZhouN-RChenZ-YLiuY-YGongL-H. Multi-party semi-quantum private comparison protocol of size relation with d-level ghz states. Adv Quan Tech (2024):2400530. 10.1002/qute.202400530
8.
GongL-HLiM-LCaoHWangB. Novel semi-quantum private comparison protocol with bell states. Laser Phys Lett (2024) 21:055209. 10.1088/1612-202x/ad3a54
9.
BulutaINoriF. Quantum simulators. Science (2009) 326:108–11. 10.1126/science.1177838
10.
SongYWuYWuSLiDWenQQinSA quantum federated learning framework for classical clients. Sci China Phys Mech and Astron (2024) 67:250311. 10.1007/s11433-023-2337-2
11.
SongYLiJWuYQinSWenQGaoF. A resource-efficient quantum convolutional neural network. Front Phys (2024) 12:1362690. 10.3389/fphy.2024.1362690
12.
LiJGaoFLinSGuoMLiYLiuHet alQuantum k-fold cross-validation for nearest neighbor classification algorithm. Physica A: Stat Mech its Appl (2023) 611:128435. 10.1016/j.physa.2022.128435
13.
LiLLiJSongYQinSWenQGaoF. An efficient quantum proactive incremental learning algorithm. Sci China Phys Mech and Astron (2025) 68:210313–9. 10.1007/s11433-024-2501-4
14.
ChildsAMKothariRSommaRD. Quantum algorithm for systems of linear equations with exponentially improved dependence on precision. SIAM J Comput (2017) 46:1920–50. 10.1137/16m1087072
15.
WanL-CYuC-HPanS-JGaoFWenQ-YQinS-J. Asymptotic quantum algorithm for the toeplitz systems. Phys Rev A (2018) 97:062322. 10.1103/physreva.97.062322
16.
WanL-CYuC-HPanS-JQinS-JGaoFWenQ-Y. Block-encoding-based quantum algorithm for linear systems with displacement structures. Phys Rev A (2021) 104:062414. 10.1103/physreva.104.062414
17.
KaplanMLeurentGLeverrierANaya-PlasenciaM. Breaking symmetric cryptosystems using quantum period finding. In: Advances in Cryptology–CRYPTO 2016: 36th Annual International Cryptology Conference; August 14-18, 2016; Santa Barbara, CA, USA. Proceedings, Part II 36 Springer (2016). p. 207–37.
18.
CaiB-BWuYDongJQinS-JGaoFWenQ-Y. Quantum attacks on 1k-aes and prince. Computer J (2023) 66:1102–10. 10.1093/comjnl/bxab216
19.
ShorPW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev (1999) 41:303–32. 10.1137/s0036144598347011
20.
BonnetainXLeurentGNaya-PlasenciaMSchrottenloherA. Quantum linearization attacks. In: Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the Theory and Application of Cryptology and Information Security; December 6–10, 2021; Singapore. Proceedings, Part I 27 Springer (2021). p. 422–52.
21.
DaemenJ (1999). Aes proposal: rijndael
22.
SunXTianGYangSYuanPZhangS. Asymptotically optimal circuit depth for quantum state preparation and general unitary synthesis. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2023) 42:3301–14. 10.1109/tcad.2023.3244885
23.
GrasslMLangenbergBRoettelerMSteinwandtR. Applying grover’s algorithm to aes: quantum resource estimates. In: International workshop on post-quantum cryptography. Springer (2016). p. 29–43.
24.
ZouJWeiZSunSLiuXWuW. Quantum circuit implementations of aes with fewer qubits. In: Advances in cryptology–ASIACRYPT 2020: 26th international conference on the theory and application of cryptology and information security, daejeon, South Korea, december 7–11, 2020, proceedings, Part II 26. Springer (2020). p. 697–726.
25.
LiZCaiBSunHLiuHWanLQinSet alNovel quantum circuit implementation of advanced encryption standard with low costs. Sci China Phys Mech and Astron (2022) 65:290311. 10.1007/s11433-022-1921-y
26.
JaquesSNaehrigMRoettelerMVirdiaF. Implementing grover oracles for quantum key search on aes and lowmc. In: Advances in Cryptology–EUROCRYPT 2020: 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques; May 10–14, 2020; Zagreb, Croatia. Proceedings, Part II 30 Springer (2020). p. 280–310.
27.
HuangZSunS. Synthesizing quantum circuits of aes with lower t-depth and less qubits. In: International conference on the theory and application of cryptology and information security. Springer (2022). p. 614–44.
28.
FowlerAG. Time-optimal quantum computation (2012). arXiv preprint arXiv:1210.4626.
29.
AmyMMaslovDMoscaMRoettelerM. A meet-in-the-middle algorithm for fast synthesis of depth-optimal quantum circuits. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2013) 32:818–30. 10.1109/tcad.2013.2244643
30.
AmyMMaslovDMoscaM. Polynomial-time t-depth optimization of clifford+ t circuits via matroid partitioning. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2014) 33:1476–89. 10.1109/tcad.2014.2341953
31.
ChungDLeeSChoiDLeeJ. Alternative tower field construction for quantum implementation of the aes s-box. IEEE Trans Comput (2021) 71:2553–64. 10.1109/tc.2021.3135759
32.
WangZ-GWeiS-JLongG-L. A quantum circuit design of aes requiring fewer quantum qubits and gate operations. Front Phys (2022) 17:41501. 10.1007/s11467-021-1141-2
33.
BoyarJPeraltaR. A new combinational logic minimization technique with applications to cryptology. In: Experimental Algorithms: 9th International Symposium, SEA 2010; May 20-22, 2010; Ischia Island, Naples, Italy. Proceedings 9 Springer (2010). p. 178–89.
34.
LiZGaoFQinSWenQ. New record in the number of qubits for a quantum implementation of aes. Front Phys (2023) 11:1171753. 10.3389/fphy.2023.1171753
35.
JangKBaksiAKimHSeoHChattopadhyayA. Improved quantum analysis of speck and lowmc (full version). Cryptology ePrint Archive (2022). 10.1007/978-3-031-22912-1_23
36.
BoyarJPeraltaR. A small depth-16 circuit for the aes s-box. In: IFIP international information security conference. Cambridge: Springer (2012). p. 287–98.
37.
LiuQPreneelBZhaoZWangM. Improved quantum circuits for aes: reducing the depth and the number of qubits. In: International conference on the theory and application of cryptology and information security. Springer (2023). p. 67–98.
38.
NielsenMAChuangIL. Quantum computation and quantum information. Cambridge University Press (2010).
39.
CongJDingY. Combinational logic synthesis for lut based field programmable gate arrays. ACM Trans Des Automation Electron Syst (Todaes) (1996) 1:145–204. 10.1145/233539.233540
40.
MarkovKPatelIHayesJ. Optimal synthesis of linear reversible circuits. Quan Inf Comput (2008) 8:0282–94. 10.26421/qic8.3-4-4
41.
XiangZZengXLinDBaoZZhangS. Optimizing implementations of linear layers. IACR Trans Symmetric Cryptology (2020) 120–45. 10.46586/tosc.v2020.i2.120-145
42.
JangKBaksiAKimHSongGSeoHChattopadhyayA. Quantum analysis of aes. Cryptology ePrint Archive (2022). 10.62056/ay11zo-3y
43.
ShiHFengX. Quantum circuits of aes with a low-depth linear layer and a new structure. In: International conference on the theory and application of cryptology and information security. Springer (2024). p. 358–95.
44.
SelingerP. Quantum circuits of t-depth one. Phys Rev A—Atomic, Mol Opt Phys (2013) 87:042302. 10.1103/physreva.87.042302
Summary
Keywords
Grover algorithm, AES, S-box, quantum circuit, quantum resource optimization
Citation
Jiang L-L, Cai B-B, Gao F, Qin S-J, Jin Z-P and Wen Q-Y (2025) Constructing resource-efficient quantum circuits for AES. Front. Phys. 13:1582819. doi: 10.3389/fphy.2025.1582819
Received
25 February 2025
Accepted
07 March 2025
Published
22 April 2025
Volume
13 - 2025
Edited by
Nanrun Zhou, Shanghai University of Engineering Sciences, China
Reviewed by
Lihua Gong, Shanghai University of Engineering Sciences, China
Yefeng He, Xi’an University of Post and Telecommunications, China
Updates
Copyright
© 2025 Jiang, Cai, Gao, Qin, Jin and Wen.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fei Gao, gaof@bupt.edu.cn
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.