An efficient and privacy protection group authentication scheme in the industrial internet of things

Industrial Internet of Things (IIoT) integrates the latest information and communication technology with the industrial economy, driving the intelligent transformation of the industry. However, with the rapid development of IIoT, its security challenges are increasingly severe. Therefore, this paper focuses on the security protection of industrial Internet, especially the application and challenges of group schemes. By analyzing the security requirements of IIoT, this paper proposes a secure and effective group authentication scheme for IIoT. Based on the Chinese remainder theorem, this scheme supports authorizing users to remotely access a set of industrial sensor devices and uses a three factor authentication method to verify the legitimacy of user identity. At the same time, through Chebyshev chaotic mapping, symmetric encryption, secret sharing technique and the Chinese remainder theorem, this scheme constructs a secure group session key to ensure encrypted transmission and integrity verification of data. The experimental results show that this scheme performs well in both security and computational efficiency, especially in large-scale group communication scenarios, which can significantly reduce communication latency and overhead.

Highlights

• This paper proposes a secure and effective authentication scheme for IIoT based on the Chinese Remainder

• The experimental results show that this scheme performs well in both security and computational efficiency.

1 Introduction

Industrial Internet of Things (IIoT) represents the fusion of new information technology and the industrial economy, emerging as a pivotal driver for industrial transformation and upgrading [1]. By enabling seamless connectivity, IIoT has forged a novel manufacturing and service framework, offering robust underpinning for the intelligent evolution of traditional industries, providing strong support for the intelligent transformation of traditional industries. However, with the rapid development of IIoT, its security and privacy issues are also increasingly prominent [2–4]. Especially in the context of the widespread deployment for industrial equipment and the generation of massive industrial data, how to ensure the safe communication, data integrity and availability of IIoT has become the focus and hotspot of current research [5].

In IIoT, the number of industrial devices is huge. The data generated by these devices is not only huge, but also often involves the privacy of users and enterprises [6]. For example, industrial production data, control instructions, identity privacy information, etc., are all important resources in the industrial Internet. However, because IIoT usually uses open channels for communication, attackers have the opportunity to obtain industrial privacy data through tampering, forgery, replay and other attacks, and undermine the security communication and data integrity of IIoT [7]. These attacks not only cause economic losses to users and businesses, but may also have immeasurable impacts on the entire industrial ecosystem [8]. Therefore, how to build a safe and reliable IIoT system to guarantee the security has become an important topic of IIoT security protection [9]. Among them, authentication schemes have received widespread attention as key means to solve this problem [6]. In IIoT, this can verify the identity of users and intelligent devices participating in communication. Meanwhile, by negotiating session keys, the requirements for data encryption can be met, ensuring the security of communication and the integrity of data. At present, authentication schemes have been widely applied in multiple fields. For example, in smart grid, it can ensure the stable operation and data security of the power grid system. In cloud computing, it can protect the security of cloud storage and cloud computing resources. In smart cities, it can ensure the intelligence and safety of urban infrastructure. In wireless sensor networks, it can ensure secure communication and data transmission between sensor nodes [10–12].

In recent years, IIoT based on group schemes has been widely applied in industrial manufacturing [13]. Group scheme allows a group of users or devices to jointly negotiate a key on an insecure channel, thereby achieving secure communication within the group. This protocol has a broad application prospect in IIoT, especially in the production, transportation and use processes that require the joint participation of multiple industrial entities. However, the application of group scheme in IIoT also faces many challenges [14–16]. Firstly, the large number and widespread distribution of industrial entities significantly increase the complexity and cost of group key negotiation. Secondly, industrial data frequently encompasses sensitive information, necessitating data security and privacy protection measures during group key negotiation. In addition, the attack means in IIoT system are diverse and complex. How to build a group key agreement scheme that can resist various attacks is also an urgent problem to be solved. Aiming at the challenge in IIoT, this paper proposes a secure and efficient group authentication scheme.

1.1 Contribution

The main contribution of this article are as follows:

(1) This paper proposes a secure and effective authentication scheme for IIoT based on the Chinese Remainder Theorem, which supports authorized users to remotely access a set of industrial sensor devices and ensures communication security and data integrity. By using passwords, biometric recognition and smart card, this scheme effectively verifies the legitimacy of user identity in the IIoT. At the same time, using Chebyshev chaotic mapping, symmetric encryption, secret sharing technology and Chinese remainder theorem, this scheme constructs a secure session key between a legitimate group of industrial sensor devices and achieves encrypted transmission and integrity verification of data through this session key.

(2) In order to verify the effectiveness and performance of the group authentication scheme proposed, we conducted extensive experimental verification and performance evaluation. The experimental results show that this scheme performs well in both security and computational efficiency. Especially in large-scale group communication scenarios, this scheme can significantly reduce communication latency and overhead.

1.2 Roadmap of this article

The organizational structure of the subsequent content is summarized as follows: Section 2 discusses related field work. In section 3, we elaborated on the relevant models and core technologies in detail. Section 4 focuses on a detailed description of the group authentication scheme. To comprehensively verify the effectiveness and practicality, we conducted security and performance evaluations in Sections 5, 6, respectively. In Section 7, we summarized the entire paper.

2 Related work

The authentication scheme is the first line of defense to ensure the security of user data and privacy in IIoT. Numerous scholars have conducted extensive research on authentication schemes.

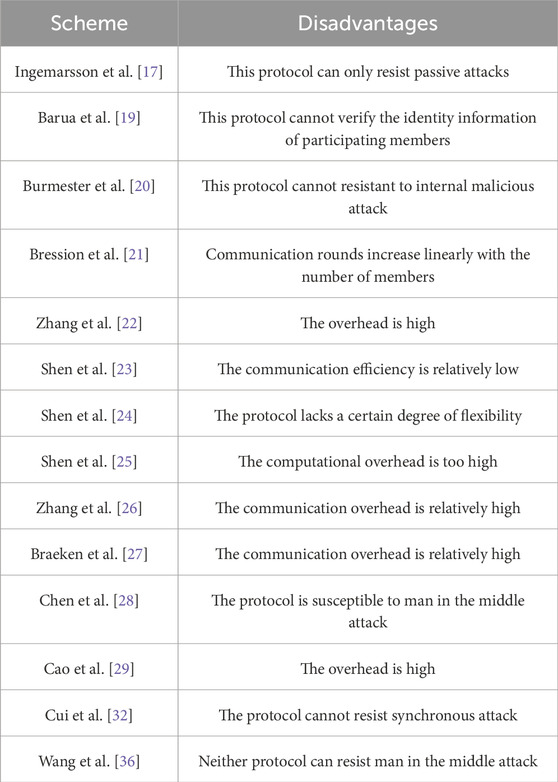
Ingemarsson et al. [17] designed a circular interaction model that supports key negotiation and extended the number of negotiators to multiple parties. But this protocol can only resist passive attack. In order to meet the dynamic changes of group users, Kim et al. [18] introduced a binary tree-based group key negotiation protocol and provided an inspiring security proof. Subsequently, Barua et al. [19] designed a group key agreement protocol based on a ternary tree. But it still cannot verify the identity information of participating members. Burmester et al. [20] developed a group protocol that can achieve information sharing between groups with only two rounds of communication, and can also resist impersonation attack initiated by external nodes. Its disadvantage was that it cannot resist malicious attacks launched from within. Therefore, Bression et al. [21] presented a password-authenticated group protocol. Although this protocol can verify the user’s identity, communication rounds would increase linearly as the number of participating communication members increases. Zhang et al. [22] introduced a novel group protocol, in which users cannot deny the information sent, but overhead was high. Shen et al. [23] constructed a group protocol. This scheme introduced a combination structure into group key negotiation, which to some extent reduces communication overhead. However, due to the high number of communication rounds, the communication efficiency was relatively low. Shen et al. [24] proposed an identity based key agreement protocol, which introduced a mathematical structure of block design to achieve group key agreement supporting entity authentication. But the protocol lacked a certain degree of flexibility. Shen et al. [25] designed a group protocol based on block design by optimizing the data structure of the block design. However, due to the introduction of Weil pairing operation in the protocol, the computation overhead was too high. Zhang et al. [26] designed a vehicle authentication and key negotiation scheme. In addition, to address the issue of short-term key leakage, this solution can ensure the security of session keys without leaking long-term keys. However, its communication overhead was relatively high. Braeken et al. [27] introduced a public key group protocol that can significantly reduce the computational overhead caused by pairing operations. Due to the use of broadcast communication in this protocol, it would also increase communication overhead. Chen et al. [28] presented a group authentication protocol. However, this protocol was susceptible to man in the middle attack. Cao et al. [29] presented a group authentication protocol based on [28]. This protocol utilized aggregate signatures to aggregate a set of signatures into one signature, improving the computational efficiency in authentication and key negotiation processes. However, Lai et al. [30] pointed out that this method had too much overhead and designed a group authentication protocol to reduce computational costs. Li et al. [31] designed a protocol. This protocol enabled dynamic updates of group members and reduced communication overhead during group authentication and key negotiation processes. Cui et al. [32] presented a scalable authentication scheme based on ECC and hash functions. However, their scheme cannot resist temporary secret leak attack. Vinoth et al. [33] presented a group protocol in IIoT. This protocol was based on the Chinese remainder theorem and symmetric encryption technology to negotiate group key. However, this protocol cannot resist synchronous attack. Ming et al. [34] presented a one-to-many authentication protocol for industrial Internet based on ECC and Chinese remainder theorem. However, it could not resist synchronous attack. Li et al. [35] presented a scheme that supported dynamic updates of group members, which can reduce the communication overhead of signature transmission during the authentication process. Wang et al. [36] proposed two protocols. In the two proposed protocols, the generation of group session keys can ensure the security of communication between devices, but neither protocol can resist man in the middle attack. Wang et al. [37] proposed a key negotiation protocol with one round of communication. In this protocol, once the user responsible for generating system parameters was compromised, the privacy information would be tracked. Li et al. [38] proposed a lightweight anonymous authentication protocol to protect the privacy of IIoT and achieve secure IIoT communication. The protocol had been validated, demonstrating its comprehensive ability to overcome various vulnerabilities and prevent malicious attacks. Table 1 shows a summary of the schemes.

Table 1

Table 1. Summary of the schemes.

In summary, it can be found that various authentication and key negotiation schemes have their own concerns. In most schemes, on the one hand, the authentication and key negotiation processes are not lightweight enough to meet the needs of resource constrained devices. On the other hand, it cannot meet sufficient security requirements in IIoT, such as internal attacks, key leak, man in the middle attacks, etc. In order to better address these issues and adapt to the need for lighter authentication schemes, this paper is dedicated to researching lightweight authentication scheme suitable for IIoT.

3 Preliminaries

3.1 Network model

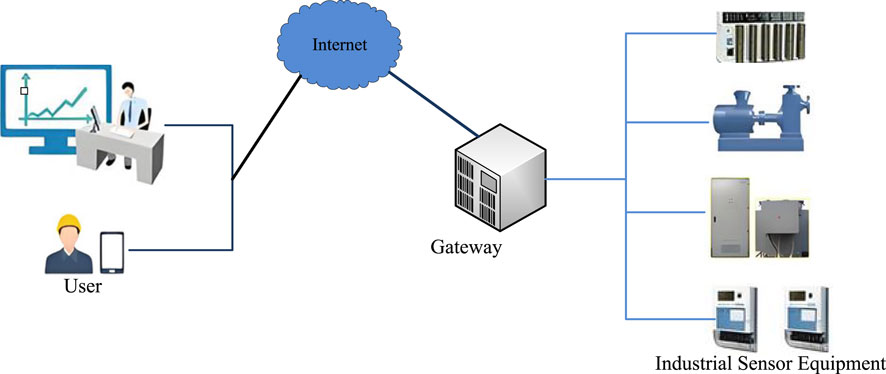
In Figure 1, the network architecture built in this paper includes three protocol participating entities: User, Gateway (GW) and Industrial Sensor Equipment (ISE) [31–37]. In industrial application scenarios, ISE serves as data acquisition terminals, responsible for real-time monitoring of industrial environmental parameters and providing users with accurate working condition information services. These equipments have heterogeneous characteristics and may include various types of sensor nodes such as temperature, pressure, vibration, etc. Due to their inherent hardware limitations, these devices typically have limited computing power and storage space, and are susceptible to physical attacks when deployed in open environments. Therefore, they are defined as semi trusted entities in the security model. As the core control node in network architecture, GW plays an important role in cluster management. It is not only responsible for coordinating the registration and authentication process between users and equipments, but also participates in the key negotiation process. It is a key entity to ensure the secure operation of the system. As the main operator of IIoT, users need to complete identity registration and securely store authentication credentials in smart cards and gateways. After completing registration and authentication, authorized users can communicate securely with the sensor device cluster through GW. The authentication mechanism of the network model mainly includes the following steps. Firstly, the user’s identity is verified during the login phase, followed by initiating authentication and key negotiation requests. GW acts as a relay node to broadcast the requests to the ISE cluster. After receiving the request, a session key will be generated through a secure protocol. Ultimately, encrypted communication is achieved between users and ISE cluster through negotiated temporary session keys.

Figure 1

Figure 1. System model.

3.2 Threat model

This article uses the Dolev Yao threat model [39] to formally verify the security of the designed authentication scheme. Communication participants exchange data on a fully open and unprotected transmission channel. The characteristics of this model are as follows:

(1) Hash functions satisfy one-way property and collision resistance, ensuring their computational security.

(2) Potential attackers have the ability to fully control communication channels and can carry out malicious operations including eavesdropping, interception, replay, and tampering.

3.3 Chebyshev chaotic mapping

The definition of the Chebyshev polynomial is as follows [40]: for variables n and x, where $n\in Z^{*}$, $x\in \left[-1,1\right]$, the n-th order Chebyshev polynomial $T_n\left(x\right)$ is a function from [-1,1] to [-1,1], defined as follows: $T_n\left(x\right)=\cos \left(\text{narccos}\left(\mathrm{x}\right)\right)$. When $n\ge 2$, recursive iteration definition can be used to calculate: $T_n\left(x\right)=\left(2\mathrm{x}{T}_{n-1}\left(\mathrm{x}\right)-T_{n-2}\left(\mathrm{x}\right)\right)$, where $T_0\left(x\right)=1,T_1\left(x\right)=x$.

Chebyshev polynomials have semigroup properties, which means that for any $m,n\in Z^{*}$, there is $T_m\left(T_n\left(x\right)\right)=T_m\left(T_n\left(x\right)\right)=T_{mn}\left(x\right)\mathit{mod}p$.

Zhang et al. proved that in Chebyshev polynomial, extending the range of variable $x$ to the real field ($-\infty$, $+\infty$), $T_n\left(x\right)$ still maintains the semigroup property.

The definition of the extended Chebyshev polynomial is as follows: for variables n and x, where $\in Z^{*}$ , $x\in (-\infty$, $+\infty$), the definition of an n-order extended Chebyshev polynomial is as follows: $T_n\left(x\right)=\cos \left(\text{narccos}\left(\mathrm{x}\right)\right)$ (mod $p$),where p is a large prime number. When $n\ge 2$, recursive iteration definition can be used to calculate: $T_n\left(x\right)=\left(2\mathrm{x}{T}_{n-1}\left(\mathrm{x}\right)-T_{n-2}\left(\mathrm{x}\right)\right)\left(\mathrm{mod}p\right)$,where $T_0\left(x\right)=1,T_1\left(x\right)=x$. Extended Chebyshev polynomials also possess semigroup properties.

Definition 1. Chebyshev Discrete Logarithm Problem (CDLP): If the value of $T_n\left(x\right)$ and $x$ are known, solving a problem of order n is called CDLP. This is a computational problem that cannot calculate the order n.

Definition 2. Chebyshev Diffie Hellman Problem (CDHP): If the values of $T_m\left(x\right)$, $T_n\left(x\right)$ and $x$ are known, solving the problem of Tmn is called CDHP. This is also a computational challenge that cannot be effectively solved.

3.4 Chinese remainder theorem

Assuming there are k coprime positive integers $m_1,m_2,\cdots ,m_k$, and corresponding k integers $a_1,a_2,\cdots ,a_k$. The goal of the Chinese remainder theorem is to find an integer X that satisfies the following system of congruence equations [41]:

$\left\{\begin{array}{c}X\equiv a_1\left(\mathit{mod}{m}_1\right)\\ X\equiv a_2\left(\mathit{mod}{m}_2\right)\\ ⋮\\ X\equiv a_k\left(\mathit{mod}{m}_k\right)\end{array}\right.$

The specific steps for solving the Chinese remainder theorem are as follows:

The product of modulus $M\equiv m_1*m_2*\cdots *m_k$ is calculated. This product M will be used as the modulus of the final solution.

For each $i\left(1\le i\le k\right)$, $M_i=M/m_i$ is calculated by dividing M by each modulus to obtain the quotient.

For each i, $M_i{M}_i^{\prime }\equiv 1\left(\mathit{mod}{m}_i\right)$ is calculated.

The solution $X\equiv a_1{M}_1{M}_1^{\prime }+a_2{M}_2{M}_2^{\prime }+\cdots +a_k{M}_k{M}_k^{\prime }\left(\mathit{mod}M\right)$ is calculated.

X is the unique solution of the congruence equation system.

3.5 Secret sharing technique

Secret sharing technology employs algorithms to divide a secret value, denoted as s, into n distinct secret shares and distributes these shares among n users [42]. Each user possesses one unique secret share. To recover the original secret value s, a minimum of t or more users must provide their respective secret shares, enabling the reconstruction of the secret value s. That is, n users will all receive the reconstructed secret value s, thus achieving the goal of sharing the secret value s.

4 Proposed scheme

4.1 Initialization stage

Gateway (GW) selects a prime number p, a random number x and a secret value s, and calculates the public key ${\mathrm{T}}_{Pub}={\mathrm{T}}_s\left(x\right)$. GW selects dynamic encryption/decryption for ${\text{Enc}}_k\left(·\right)/{\mathrm{D}}_k\left(·\right)$ and secure hash function $\mathrm{H}\left(·\right)$. Finally, GW stores the secret value s and publicly discloses {$x,{\mathrm{T}}_s\left(x\right)$, ${\text{Enc}}_k\left(·\right)/{\mathrm{D}}_k\left(·\right)$, $\mathrm{H}\left(·\right)$}. Figure 2 is login and mutual authentication.

Figure 2

Figure 2. Login and mutual authentication.

4.2 Registration

User $U_j$ selects a unique user identity ${ID}_j$, user password ${PW}_j$ and user biometric information $B_j$. $U_j$ calculates (${\omega }_j,{\phi }_j$) = Gen($B_j$) to obtain the biometric key ${\omega }_j$. $U_j$ randomly selects a number $r_j$, calculates $P_j={\mathrm{T}}_{r_j}\left(x\right)$ and $R_j=H\left({ID}_j,{PW}_j,{\omega }_j\right)\oplus r_j$. Finally, $U_j$ securely sends the message {${ID}_j,R_j$, $P_j$} to GW. After receiving {${ID}_j,R_j$, $P_j$}, GW randomly selects $u_j$, calculates the corresponding public key $U_{\mathrm{j}}={\mathrm{T}}_{u_j}\left(x\right)$, ${UP}_{\mathrm{j}}={\mathrm{T}}_{u_j}\left(P_j\right)={\mathrm{T}}_{u_j{r}_j}\left(x\right)$, hash value $K_j=H\left({ID}_j,{UP}_{\mathrm{j}}\right)$, and then calculates the value ${\mathrm{A}R}_j=K_j\oplus R_j\oplus {UP}_{\mathrm{j}},{\mathrm{S}R}_j=H\left(s,R_j,u_j\right)$, ${\mathrm{C}R}_j={\mathrm{S}R}_j\oplus R_j$. At the same time, it generates ${TID}_j$ for the user and stores the data $\left({\text{TID}}_{\mathrm{j}},{\mathrm{S}R}_j,K_j\right.$). Finally, GW generates a smart card (SC) and stores the data {${TID}_j,{\mathrm{A}R}_j$, $U_{\mathrm{j}}$, ${\mathrm{C}R}_j$} in the smart card before sending it to $U_{\mathrm{j}}$. After receiving the message, $U_j$ calculates ${\text{UP}}_j^{*}={\mathrm{T}}_{r_j}\left(U_{\mathrm{j}}\right)={\mathrm{T}}_{u_j{r}_j}\left(x\right),{RPR}_j=H\left({ID}_j,{PW}_j,{\omega }_j\right)$, ${\mathrm{K}}_{\mathrm{j}}^{\prime }={\mathrm{A}R}_j\oplus {\text{UP}}_j^{*}\oplus R_j$, ${DR}_j=H\left({ID}_j,{\omega }_j\right)\oplus r_j$, ${\text{CR}}_{\mathrm{j}}^{\prime }={\mathrm{C}R}_j\oplus R_j\oplus H\left({ID}_j,{\omega }_j,r_j\right),{\text{AR}}_j^{\prime }={\mathrm{K}}_{\mathrm{j}}^{\prime }\oplus H\left({ID}_j,{PW}_j,{\omega }_j,r_j\right)$, ${VR}_j=H\left({RPR}_j,{\mathrm{K}}_{\mathrm{j}}^{\prime },r_j,H\left({ID}_j,{\omega }_j\right)\right)$. Finally, $U_j$ stores {${TID}_j,{\text{AR}}_j^{\prime },{\text{CR}}_j^{\prime },{DR}_j,{VR}_j,{\phi }_j$} into ${SC}_{\mathrm{j}}$.

Industrial Sensor Equipment (ISE) is registered with GW. GW assigns unique identity information ${ID}_i$ (i = 1,2, … ,n) to each ${ISE}_i$, selects a secret value $\gamma \in Z_q^{*}$, and $a$ polynomial $f\left(x\right)=a_0+a_{1}x+\cdots +a_{n-1}{x}^{n-1}\mathit{mod}p$, where $a_0=H\left(\gamma \right)$. GW assigns a different positive integer $d_i$ to each ${ISE}_i$ and calculates $s_i=f\left(d_i\right)$. GW assigns a coprime positive integer $y_i$ to each ${ISE}_i$ and calculates ${\mathrm{Y}={\prod }_{i=1}^n{y}_i,\mathrm{Y}}_i=Y/y_i,Y_i{t}_i\equiv 1\left(\mathit{mod}{y}_i\right)$ , $S={\sum }_{i=1}^n{t}_i{Y}_i\mathit{mod}Y$. GW stores the value S and then sends the message {${ID}_i,s_i,y_{\mathrm{i}}$} to each ${ISE}_i$.

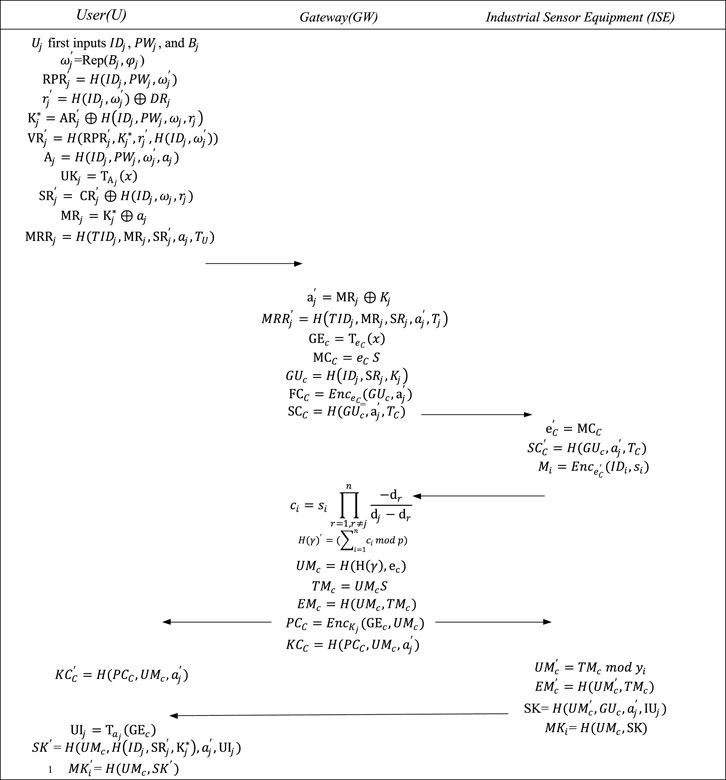
4.3 Login and mutual authentication

(1) $U_j$ first inputs ${ID}_j$, ${PW}_j$ and $B_j$, and the smart card reconstructs and calculates ${\omega }_j^{\prime }$ = Rep($B_j,{\phi }_j$), ${\text{RPR}}_j^{\prime }=H\left({ID}_j,{PW}_j,{\omega }_j^{\prime }\right)$, $r_j^{\prime }=H\left({ID}_j,{\omega }_j^{\prime }\right)\oplus {DR}_j$, ${\mathrm{K}}_j^{*}={\text{AR}}_j^{\prime }\oplus H\left({ID}_j,{PW}_j,{\omega }_j^{\prime },r_j\right)$, ${\text{VR}}_j^{\prime }=H\left({\text{RPR}}_j^{\prime },K_j^{*},r_j^{\prime },H\left({ID}_j,{\omega }_j^{\prime }\right)\right)$. Then ${SC}_j$ checks whether ${\text{VR}}_j^{\prime }$ and ${VR}_j$ are equal to verify the identity of $U_j$. If they are equal, then the identity of $U_j$ has been verified. $U_j$ generates $a_j$ and the current timestamp $T_j$. ${SC}_j$ calculates ${\mathrm{A}}_j=H\left({ID}_j,{PW}_j,{\omega }_j^{\prime },a_j\right)$, ${{\text{UK}}_j=\mathrm{T}}_{{\mathrm{A}}_j}\left(x\right)$, ${\text{SR}}_j^{\prime }={\text{CR}}_j^{\prime }\oplus H\left({ID}_j,{\omega }_j,r_j\right)$, ${\text{MR}}_j={\mathrm{K}}_j^{*}\oplus a_j$, ${\text{MRR}}_j=H\left(T{ID}_j,{\text{MR}}_j,{\text{SR}}_j^{\prime },a_j,T_U\right)$, and then sends the message { $T{ID}_j,{\text{UK}}_j,{\text{MR}}_j,{\text{MRR}}_j,T_j$} to GW.

(2) After receiving the sent message, GW first verifies whether $T_j$ is valid. If it is valid, authentication continues. Otherwise, GW refuses authentication. GW retrieves the ${\mathrm{S}R}_j\text{\hspace{0.17em}and\hspace{0.17em}}{K}_j$ of $U_j$ from the database using $T{ID}_j$. GW calculates $a_j^{\prime }={\text{MR}}_j\oplus K_j$, ${MRR}_j^{\prime }=H\left(T{ID}_j,{\text{MR}}_j,{\mathrm{S}R}_j,a_j^{\prime },T_j\right).$ Then GW checks whether ${MRR}_j^{\prime }$ and ${\text{MRR}}_j$ are equal. If they are equal, authentication continues, otherwise authentication ends. GW randomly generates $e_C$ and $T_C$, and calculates ${{\text{GE}}_c=\mathrm{T}}_{e_C}\left(x\right)$, ${\text{MC}}_C=e_{C}S$, ${GU}_c=H\left({ID}_j,{\mathrm{S}R}_j,K_j\right).$ GW generates encrypted messages ${\text{FC}}_C={Enc}_{e_C}\left({GU}_c,a_j^{\prime }\right)$, ${\text{SC}}_C=H\left({GU}_c,a_j^{\prime },T_C\right)$. Finally, GW broadcasts the message {${\text{MC}}_C,{\text{UK}}_j,{\text{FC}}_C,{\text{SC}}_C,T_C$} to ${ISE}_{\mathrm{i}}$.

(3) When each ${ISE}_{\mathrm{i}}$ receives {${\text{MC}}_C,{\text{UK}}_j,{\text{FC}}_C,{\text{SC}}_C,T_C$}, it checks whether $T_C$ is legal. If it is within the legal range, ${ISE}_{\mathrm{i}}$ calculates ${\mathrm{e}}_C^{\prime }={\text{MC}}_C\mathit{mod}{y}_i$. ${ISE}_{\mathrm{i}}$ decrypts the value ${\text{FC}}_C$ using ${\mathrm{e}}_C^{\prime }$ to obtain message ${GU}_c,a_j^{\prime }$. Then ${ISE}_{\mathrm{i}}$ calculates ${SC}_C^{\prime }=H\left({GU}_c,a_j^{\prime },T_C\right)$ and verifies GW by comparing whether ${SC}_C^{\prime }$ and ${\text{SC}}_C$ values are equal. ${ISE}_{\mathrm{i}}$ encrypts the message $M_i={Enc}_{e_C^{\prime }}\left({ID}_i,s_i\right)$ using ${\mathrm{e}}_C^{\prime }$ and generates the current timestamp $T_i$. It then sends the message {$M_i,T_i$} to GW.

(4) After receiving n ${ISE}_{\mathrm{i}}$ messages, GW first checks whether $T_i$ is legal. If it is within the legal range, GW decrypts the message ${\mathrm{M}}_i$ through ${\mathrm{e}}_{\mathrm{C}}$ to obtain ${ID}_{\mathrm{i}},{\mathrm{s}}_i$. Then, GW calculates $c_i=s_i{\displaystyle {\prod }_{r=1,r\ne j}^n}\frac{-{\mathrm{d}}_r}{{\mathrm{d}}_j-{\mathrm{d}}_r}$, $H{\left(\gamma \right)}^{\prime }=\left({\sum }_{i=1}^n{c}_i\mathit{mod}p\right)$ through secret sharing algorithm, verifying whether $H{\left(\gamma \right)}^{\prime }$ = ? H (γ). If it is true, then the identities of n ${ISE}_{\mathrm{i}}$ have been verified. GW generates the current timestamp $T_{CS}$, calculates ${UM}_c=H\left(\mathrm{H}\left(\gamma \right),{\mathrm{e}}_{\mathrm{c}}\right),{TM}_c={UM}_{c}S,{EM}_c=H\left({UM}_c,{TM}_c\right)$ ${PC}_C={Enc}_{K_j}\left({\text{GE}}_c,{UM}_c\right)$, ${KC}_C=H\left({PC}_C,{UM}_c,a_j^{\prime }\right)$ Finally, GW broadcasts messages {${TM}_C,{EM}_C$} to n ${ISE}_{\mathrm{i}}$ and sends messages {${PC}_C,{KC}_C,T_{CS}$} to $U_j$.

(5) When ${ISE}_{\mathrm{i}}$ receives the sent message, it calculates ${UM}_c^{\prime }={TM}_c\mathit{mod}{y}_i$, ${EM}_c^{\prime }=H\left({UM}_c^{\prime },{TM}_c\right)$, and verifies whether ${EM}_c^{\prime }$ = ? ${EM}_c$. If it is true, GW is verified. At this time, ${\text{IU}}_j={\mathrm{T}}_{{\mathrm{e}}_C^{\prime }}\left({\text{UK}}_j\right)$ and session key SK = $H\left({UM}_c^{\prime },{GU}_c,a_j^{\prime },{\text{IU}}_j\right)$ are calculated. Finally, ${ISE}_{\mathrm{i}}$ calculates ${MK}_i$ = $H\left({UM}_c^{\prime },\text{SK}\right)$ and sends {${MK}_i$} to $U_j$ to verify that the session keys are equal.

(6) When $U_j$ receives n messages, it checks whether $T_{CS}$ is legal. If it is within the legal range, $U_j$ decrypts ${PC}_C$ using ${\mathrm{K}}_j^{*}$ to obtain ${\text{GE}}_c,{UM}_c$. Then $U_j$ calculates ${KC}_C^{\prime }=H\left({PC}_C,{UM}_c,a_j^{\prime }\right)$ and verifies whether ${KC}_C^{\prime }$ = ? ${KC}_C$. If it is true, then GW is verified. And $U_j$ calculates ${\text{UI}}_j={\mathrm{T}}_{a_j}\left({\text{GE}}_c\right)$, session key ${SK}^{\prime }$ = $H\left({UM}_c,H\left({ID}_j,{\text{SR}}_j^{\prime },{\mathrm{K}}_j^{*}\right),a_j^{\prime },{\text{UI}}_j\right)$, ${MK}_i^{\prime }$ = $H\left({UM}_c,{SK}^{\prime }\right)$ and verifies whether ${MK}_i$ = ? ${MK}_i^{\prime }$. If it is true, then $U_j$ and ${ISE}_{\mathrm{i}}$ generate the same session key.

5 Security analysis

5.1 Heuristic analysis

According to the security requirements of the plan, we will conduct the following security analysis.

(1) Anonymity: In this article, the user’s identity ${ID}_j$ is not transmitted in plaintext over the channel, but is transmitted through a temporary identity $T{ID}_j$. Attackers in the channel could not obtain the user’s true identity, thus achieving user identity anonymity and protecting the user’s identity privacy. In addition, in each session, users will select different random values and timestamps to calculate communication information. After intercepting the two sessions, attackers cannot connect the information values of the two sessions to obtain the secret parameters. Therefore, this scheme achieves anonymous and the disconnection of session information.

(2) Message authentication and integrity: In this scheme, communication entities verify each other’s legitimacy by validating messages, thus providing message authentication. Since messages are generated through secret values, no adversary can generate valid messages, ensuring authentication between communicating entities and message integrity.

(3) Mutual authentication: In this article, gateway verifies the identity of the user by checking whether ${MRR}_j^{\prime }$ and ${\text{MRR}}_j$ are equal. Each device within the group calculates ${\mathrm{e}}_C^{\prime }={\text{MC}}_C\mathit{mod}{y}_i$ using the Chinese remainder theorem. Then, by decrypting the ${\text{FC}}_C$ value using ${\mathrm{e}}_C^{\prime }$, the message ${GU}_c,a_j^{\prime }$ is obtained. Then, ${SC}_C^{\prime }=H\left({GU}_c,a_j^{\prime },T_C\right)$ is calculated, and the identity of the gateway is verified by comparing whether ${SC}_C^{\prime }$ and ${\text{SC}}_C$ are equal. Then each device in the group sends its own secret share to the gateway, which uses a secret sharing algorithm to calculate $c_i=s_i{\displaystyle {\prod }_{r=1,r\ne j}^n}\frac{-{\mathrm{d}}_r}{{\mathrm{d}}_j-{\mathrm{d}}_r}$, $H{\left(\gamma \right)}^{\prime }=\left({\sum }_{i=1}^n{c}_i\mathit{mod}p\right)$, verifying whether $H{\left(\gamma \right)}^{\prime }$ is equal to the stored H (γ). Finally, $U_i$ calculates ${KC}_C^{\prime }=H\left({PC}_C,{UM}_c,a_j^{\prime }\right)$ and checkes whether ${KC}_C^{\prime }$ and ${KC}_C$ are equal to verify device information. $U_j$ verifies the identity information of the gateway by calculating ${MK}_i^{\prime }$ = $H\left({UM}_c,{SK}^{\prime }\right)$ and checking whether ${MK}_i$ and ${MK}_i^{\prime }$ are equal.

(4) Resist replay attack: In the scheme, each message is accompanied by a timestamp. By checking the validity of the timestamp, the entities can determine whether the message is replayed. If the timestamp of the received message differs too much from the current time, that is, the timestamp exceeds a predetermined time window and the entity can reject the message. This mechanism ensures the timeliness of messages and prevents adversaries from deceiving by replaying previously legitimate messages.

(5) Resistance to modification attack: The message used to verify entity integrity is calculated based on the secret value. It is dynamically updated, which means that the entity generates new secret values during each communication process. When an entity receives a message, it can use the corresponding secret value to calculate the verification value of the message and compare it with the authentication value in the message. If there is a mismatch, the entity can determine that the message has been modified and reject the message. Therefore, this scheme can resist modification attack.

(6) Resistance to man in the middle attack: Through the analysis of message verification and modification attacks, it can be found that when the attacker modifies a message, the entity will be unable to pass the verification of the message. The entity will detect that the integrity of the message has been compromised and immediately realize that the transmitted content has been tampered with. This mechanism makes the attack more difficult, as attackers cannot intercept and modify messages in the communication link without being detected by entities.

(7) To resist impersonation attack: In order to disguise request messages sent by legitimate users, adversaries need to send the correct { $T{ID}_j,{\text{UK}}_j,{\text{MR}}_j,{\text{MRR}}_j,T_j$}. As mentioned above, due to the secret values ${\text{SR}}_j^{\prime }$ and $a_j$ contained in the ${\text{MRR}}_j$, the adversary cannot obtain valid information through intercepted messages, and therefore cannot successfully impersonate legitimate users for impersonation attack.

(8) Smart card loss attack: When a user loses their smart card or is stolen, the adversary can use power analysis to obtain user information stored on the smart card, including {${TID}_j,{\text{AR}}_j^{\prime },{\text{CR}}_j^{\prime },{DR}_j,{VR}_j,{\phi }_j$}. To impersonate a legitimate user, the adversary must pass the ${VR}_j$ verification step. Due to the lack of the information {${ID}_j,{PW}_j,{\omega }_j^{\prime }$}, direct simulation of a legitimate user for login via the smart card is infeasible.

(9) Session key security: The final key SK = $H\left({UM}_c^{\prime },{GU}_c,a_j^{\prime },{\text{IU}}_j\right)$ can be calculated separately. The response message does not contain the complete form of SK. If the attacker intercepts the message, they need to obtain temporary secret values ${UM}_c^{\prime },{GU}_c,a_j^{\prime }$ and ${\text{IU}}_j$. However, attackers are unable to know these critical information. Hence, they cannot ascertain the key information from the message and are unable to generate SK.

(10) Forward security: In each session, new timestamps and secret values are used to calculate SK = $H\left({UM}_c^{\prime },{GU}_c,a_j^{\prime },{\text{IU}}_j\right)$ using the Chebyshev chaotic mapping. Therefore, SK leakage in any session will not affect other session keys. Even if attackers can obtain long-term secret values from GW, they cannot calculate a valid group key SK. This is because the parameters required for calculating SK include temporary secret values, which are dynamically generated and unique in each session. The attacker is unable to derive the value required to calculate SK from known long-term secret values. Therefore, even if attackers know the current SK and/or long-term secrets stored in the GW, they still cannot calculate the keys for other sessions. This enhances the security of the scheme, protecting the confidentiality and integrity of the session.

5.2 Scyther analysis

Scyther is a formal verification tool widely used for verifying security protocols [43]. It effectively analyzes and verifies these protocols, detecting potential attacks and vulnerabilities, and provide clear termination results for protocols with infinite sessions and infinite state sets by characterizing the protocol and generating limited representations of all possible protocol behaviors. And according to the opponent’s ability, it is convenient to choose a security model, including the standard Dolev Yao model, as well as other models, supporting parallel analysis of the protocol. The Scyther tool requires the use of Security Policy Definition Language (SPDL) to model the protocol and propose security statements to analyze security functionality.

In this article, we employ Scyther to conduct security simulation analysis on our proposed scheme. Using SPDL, we delineate the protocol model. For analytical simplicity, we focus on three primary roles: U, GW, and ISE. We adopt the Dolev-Yao model to verify the security, assuming attackers have full network control and can execute various attacks. Subsequently, we model our scheme in SPDL and specify its security properties through Scyther declarations. Figure 3 demonstrates that our scheme successfully recognizes all Scyther declarations and remains attack-free under Scyther’s scrutiny.

Figure 3

Figure 3. Scyther result.

6 Performance analysis

6.1 Computation overhead

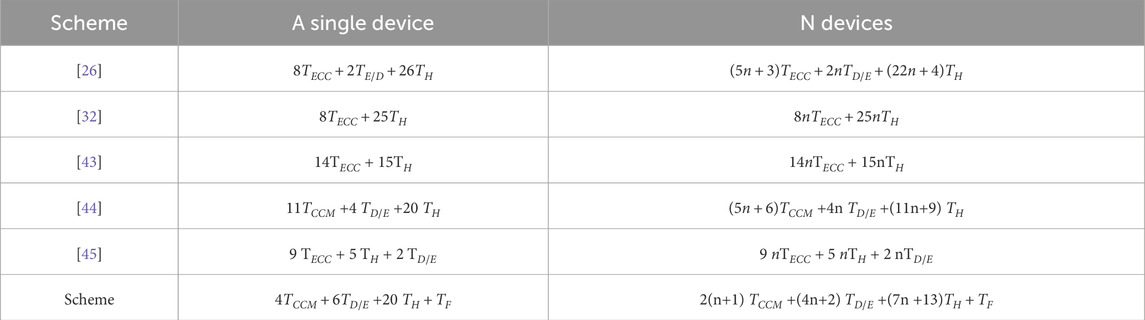
In this section, we mainly analyzed the performance of our proposed scheme from the perspective of computation overhead. We mainly compare the scheme with [26, 32, 43, 44]. According to the experimental results, a laptop equipped with Intel(R)Core(TM) i5-8250U CPU @ 1.60 GHz, 8.0 GB memory and Windows 10 operating system was selected for the experiment [46]. In terms of computation cost, we only consider the scalar multiplication of elliptic curve cryptography ($T_{ECC}$), hash operation ($T_H$), chaotic mapping operation ($T_{CCM}$), biometric fuzzy extractor ($T_F$), and symmetric encryption/decryption ($T_{D/E}$), while ignoring other operations. The computational cost of these encryption operations is $T_{ECC}\approx T_F\approx$ 2.324 ms, $T_{D/E}$ $\approx$ 0.0068, $T_{CCM}$ $\approx$ 0.242 ms and $T_H$ $\approx$ 0.0423 ms. The main computation costs are the authentication phase. Therefore, here we verify the performance of the protocol by comparing the authentication cost of a single device and N devices. In our protocol, the authentication costs are $4T_{CCM}+6T_{D/E}$ +20 $T_H+T_F$ and 2(n+1) $T_{CCM}+$ (4n+2) ${\mathrm{T}}_{\mathrm{D}/\mathrm{E}}+$ (7n $+13)T_H+T_F$, respectively. In [26], the authentication costs are $8T_{ECC}+{2T}_{E/D}+26T_H$ and $\left(5n+3\right)T_{ECC}+{2nT}_{D/E}+\left(22n+4\right)T_H$, respectively. In [32], the authentication costs are $8T_{ECC}+{25T}_H$ and $8n{T}_{ECC}+{25nT}_H$, respectively. In [44], the authentication costs are $14{\mathrm{T}}_{ECC}$ + $15{\mathrm{T}}_H$ and $14n{\mathrm{T}}_{ECC}$ + $15\mathrm{n}{\mathrm{T}}_H$, respectively. In [45], the authentication costs are $11T_{CCM}$ +4 $T_{D/E}$ +20 $T_H$ and $\left(5n+6\right)T_{CCM}$ +4n $T_{D/E}$ +(11n+9) $T_H$. In [38], the authentication costs are 9 ${\mathrm{T}}_{ECC}$ + 5 ${\mathrm{T}}_H$ + 2 ${\mathrm{T}}_{D/E}$ and 9 $n{\mathrm{T}}_{ECC}$ + 5 $n{\mathrm{T}}_H$ + 2 ${\text{nT}}_{D/E}$. Table 2 presents the computation overhead. Notably, our scheme exhibits the lowest computational overhead in comparison to the others. And as the number of users increases, the advantages will become increasingly apparent.

Table 2

Table 2. Computational overhead.

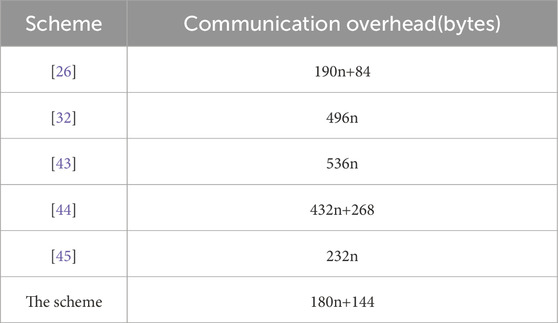
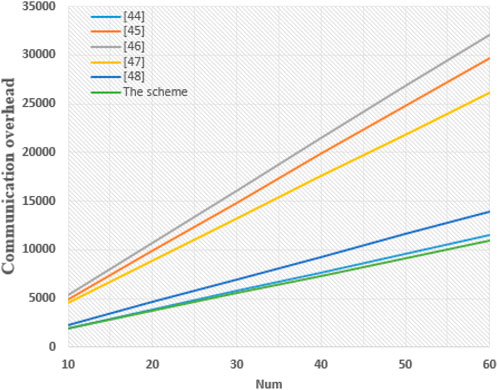
6.2 Communication overhead

Here, we will compare the communication overhead. Assuming the output sizes of elliptic curve algorithm, Chebyshev chaotic mapping, identity information, hash function, random number, symmetric encryption/decryption, and timestamp are 40 bytes, 40 bytes, 20 bytes, 20 bytes, 20 bytes, 16 bytes, and 4 bytes, respectively. In our scheme, during the U authentication phase, the communication overhead is { $T{ID}_j,{\text{UK}}_j,{\text{MR}}_j,{\text{MRR}}_j,T_j$} sent by U. GW forwards its authentication messages{${\text{MC}}_C,{\text{UK}}_j,{\text{FC}}_C,{\text{SC}}_C,T_C$}. ISE verifies its identity message and generates corresponding response information $\left\{M_i,T_i\right\}$. GW verifies its identity message and generates corresponding response information {${TM}_C,{EM}_C$} and {${PC}_C,{KC}_C,T_{CS}$}, and then forwards it to U and ISE. ISE verifies its response message and generates corresponding confirmation information {${MK}_i$}, and then forwards it to U. Therefore, the total cost of our plan is 180n+144. Through similar schemes, we can obtain the communication overhead of other schemes as shown in Table 3. From Figure 4, our scheme has significant advantages compared to other schemes.

Table 3

Table 3. The comparison of the communication overhead.

Figure 4

Figure 4. Communication overhead.

7 Conclusion

In this article, we propose a secure and efficient group authentication scheme based on the Chinese Remainder Theorem, aiming at the challenge of group key agreement in IIoT. This scheme achieves the legitimacy verification of user identity and constructs a secure session key using Chebyshev chaotic mapping, symmetric encryption, secret sharing technology and China Remainder Theorem to achieve encrypted transmission and integrity verification of data. The experimental results show that this scheme performs well in both security and computational efficiency, especially in large-scale group communication scenarios, which can significantly reduce communication latency and overhead. Therefore, the group authentication scheme provides an effective solution for the security protection of IIoT, which has important theoretical significance. In the future, we will continue to study the performance of this scheme in more application scenarios, and continue to optimize and improve its performance to better serve the security protection of IIoT.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

TW: Investigation, Resources, Software, Validation, Writing – original draft. BS: Data curation, Resources, Software, Validation, Writing – review and editing. JX: Conceptualization, Methodology, Project administration, Supervision, Visualization, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sisinni E, Saifullah A, Han S, Jennehag U, Gidlund M. Industrial internet of things: challenges, opportunities, and directions. IEEE Trans Ind Inform (2018) 14(11):4724–34. doi:10.1109/tii.2018.2852491

CrossRef Full Text | Google Scholar

2. Hu Y, Jia Q, Yao Y, Lee Y, Lee M, Wang C Industrial internet of things intelligence empowering smart manufacturing: a literature review. IEEE Internet Things J (2024) 11:19143–67. doi:10.1109/jiot.2024.3367692

CrossRef Full Text | Google Scholar

3. Naouri A, Nouri NA, Khelloufi A, Sada AB, Ning H, Dhelim S. Efficient fog node placement using nature-inspired metaheuristic for IoT applications. Cluster Comput (2024) 27(6):8225–41. doi:10.1007/s10586-024-04409-3

CrossRef Full Text | Google Scholar

4. Miao J, Wang Z, Wang M, Garg S, Hossain MS, Rodrigues JJ. Secure and efficient communication approaches for industry 5.0 in edge computing. Computer Networks (2024) 242:110244. doi:10.1016/j.comnet.2024.110244

CrossRef Full Text | Google Scholar

5. Sasikumar A, Ravi L, Devarajan M, Selvalakshmi A, Almaktoom AT, Almazyad AS Blockchain-assisted hierarchical attribute-based encryption scheme for secure information sharing in industrial internet of things. IEEE Access (2024) 12:12586–601. doi:10.1109/access.2024.3354846

CrossRef Full Text | Google Scholar

6. Zou S, Cao Q, Lu R, Wang C, Xu G, Ma H A robust and effective 3-factor authentication protocol for smart factory in IIoT. Computer Commun (2024) 220:81–93. doi:10.1016/j.comcom.2024.04.011

CrossRef Full Text | Google Scholar

7. Guo Y, Guo Y, Xiong P, Yang F, Zhang C. A provably secure and practical end-to-end authentication scheme for tactile Industrial Internet of Things. Pervasive Mobile Comput (2024) 98:101877. doi:10.1016/j.pmcj.2024.101877

CrossRef Full Text | Google Scholar

8. Xiao N, Wang Z, Sun X, Miao J. A novel blockchain-based digital forensics framework for preserving evidence and enabling investigation in industrial Internet of Things. Alexandria Eng J (2024) 86:631–43. doi:10.1016/j.aej.2023.12.021

CrossRef Full Text | Google Scholar

9. Zhang Q, Wu J, Zhong H, He D, Cui J. Efficient anonymous authentication based on physically unclonable function in industrial internet of things. IEEE Trans Inf Forensics Security (2023) 18(18):233–47. doi:10.1109/tifs.2022.3218432

CrossRef Full Text | Google Scholar

10. Wei H, Miao J, Lv J, Chen C -M, Kumari S, Amoon M. Secure and trustworthy data management mechanism for dance-consumer electronics in AIoT. IEEE Trans Consumer Electronics (2024) 1. doi:10.1109/tce.2024.3471573

CrossRef Full Text | Google Scholar

11. Khelloufi A, Ning H, Naouri A, Sada AB, Qammar A, Khalil A A multimodal latent-features-based service recommendation system for the social internet of things. IEEE Trans Comput Social Syst (2024) 11(4):5388–403. doi:10.1109/tcss.2024.3360518

CrossRef Full Text | Google Scholar

12. Cui J, Yu J, Zhong H, Wei L, Liu L. Chaotic map-based authentication scheme using physical unclonable function for internet of autonomous vehicle. IEEE Trans Intell Transportation Syst (2022) 24(3):3167–81. doi:10.1109/tits.2022.3227949

CrossRef Full Text | Google Scholar

13. Xu Z, Liang W, Li K -C, Xu J, Zomaya AY, Zhang J. A time-sensitive token-based anonymous authentication and dynamic group key agreement scheme for industry 5.0. IEEE Trans Ind Inform (2022) 18(10):7118–27. doi:10.1109/tii.2021.3129631

CrossRef Full Text | Google Scholar

14. Zhang S, Lee J-H. A group signature and authentication scheme for blockchain-based mobile-edge computing. IEEE Internet Things J (2020) 7(5):4557–65. doi:10.1109/jiot.2019.2960027

CrossRef Full Text | Google Scholar

15. Wei D, Shi F, Dhelim S. A self-supervised learning model for unknown internet traffic identification based on surge period. Future Internet (2022) 14(10):289. doi:10.3390/fi14100289

CrossRef Full Text | Google Scholar

16. Islam SKH, Obaidat MS, Vijayakumar P, Abdulhay E, Li F, Reddy MKC. A robust and efficient password-based conditional privacy preserving authentication and group-key agreement protocol for VANETs. Future Generation Computer Syst (2018) 84:216–27. doi:10.1016/j.future.2017.07.002

CrossRef Full Text | Google Scholar

17. Ingemarsson I, Tang D, Wong C. A conference key distribution system. IEEE Trans Inf Theor (1982) 28(5):714–20. doi:10.1109/tit.1982.1056542

CrossRef Full Text | Google Scholar

18. Kim Y, Perrig A, Tsudik G. Tree-based group key agreement. ACM Trans Inf Syst Security (Tissec) (2004) 7(1):60–96. doi:10.1145/984334.984337

CrossRef Full Text | Google Scholar

19. Barua R, Dutta R, Sarkar P. Extending Joux’s protocol to multi party key agreement. In: Progress in Cryptology-INDOCRYPT 2003: 4th International Conference on Cryptology in India; December 8-10, 2003; New Delhi, India. Springer Berlin Heidelberg (2003). p. 205–17.

CrossRef Full Text | Google Scholar

20. Burmester M, Desmedt Y. A secure and efficient conference key distribution system. In: Advances in Cryptology—EUROCRYPT'94: Workshop on the Theory and Application of Cryptographic Techniques; May 9–12, 1994; Perugia, Italy. Springer Berlin Heidelberg (1995). p. 275–86.

CrossRef Full Text | Google Scholar

21. Bresson E, Chevassut O, Pointcheval D. Group Diffie-Hellman key exchange secure against dictionary attacks. In: International Conference on the Theory and Application of Cryptology and Information Security; Berlin, Heidelberg. Springer Berlin Heidelberg (2002). p. 497–514.

CrossRef Full Text | Google Scholar

22. Zhang R, Zhang L, Choo KKR, Chen T. Dynamic authenticated asymmetric group key agreement with sender non-repudiation and privacy for group-oriented applications. IEEE Trans Dependable Secure Comput (2021) 20(1):492–505. doi:10.1109/tdsc.2021.3138445

CrossRef Full Text | Google Scholar

23. Shen J, Zhou T, Liu X, Chang YC. A novel Latin-square-based secret sharing for M2M communications. IEEE Trans Ind Inform (2018) 14(8):3659–68. doi:10.1109/tii.2018.2810840

CrossRef Full Text | Google Scholar

24. Shen J, Moh S, Chung I. Identity-based key agreement protocol employing a symmetric balanced incomplete block design. J Commun networks (2012) 14(6):682–91. doi:10.1109/jcn.2012.00034

CrossRef Full Text | Google Scholar

25. Shen J, Zhou T, He D, Zhang Y, Sun X, Xiang Y. Block design-based key agreement for group data sharing in cloud computing. IEEE Trans dependable secure Comput (2017) 16(6):996–1010. doi:10.1109/tdsc.2017.2725953

CrossRef Full Text | Google Scholar

26. Zhang J, Zhong H, Cui J, Xu Y, Liu L. SMAKA: secure many-to-many authentication and key agreement scheme for vehicular networks. IEEE Trans Inf Forensics Security (2020) 16:1810–24. doi:10.1109/tifs.2020.3044855

CrossRef Full Text | Google Scholar

27. Braeken A. Pairing free asymmetric group key agreement protocol. Computer Commun (2022) 181:267–73. doi:10.1016/j.comcom.2021.10.011

CrossRef Full Text | Google Scholar

28. Chen YW, Wang JT, Chi KH, Tseng CC. Group-based authentication and key agreement. Wireless Personal Commun (2012) 62(4):965–79. doi:10.1007/s11277-010-0104-7

CrossRef Full Text | Google Scholar

29. Cao J, Ma M, Li H. A group-based authentication and key agreement for mtc in lte networks. In: 2012 IEEE Global Communications Conference (GLOBECOM). IEEE (2012). p. 1017–22.

Google Scholar

30. Lai C, Li H, Lu R, Shen XS. Se-aka: a secure and efficient group authentication and key agreement protocol for lte networks. Computer Networks (2013) 57(17):3492–510. doi:10.1016/j.comnet.2013.08.003

CrossRef Full Text | Google Scholar

31. Li J, Wen M, Zhang T. Group-based authentication and key agreement with dynamic policy updating for mtc in lte-a networks. IEEE Internet Things J (2015) 3(3):408–17. doi:10.1109/jiot.2015.2495321

CrossRef Full Text | Google Scholar

32. Cui J, Zhang X, Zhong H, Liu L. Extensible conditional privacy protection authentication scheme for secure vehicular networks in a multi-cloud environment. IEEE Trans Inf Forensics Security (2019) 15:1654–67. doi:10.1109/tifs.2019.2946933

CrossRef Full Text | Google Scholar

33. Vinoth R, Deborah LJ, Vijayakumar P, Kumar N. Secure multifactor authenticated key agree ment scheme for industrial iot. IEEE Internet Things J (2020) 8(5):3801–11. doi:10.1109/jiot.2020.3024703

CrossRef Full Text | Google Scholar

34. Ming Y, Yang P, Mahdikhani H, Lu R. A secure one-to-many authentication and key agreement scheme for industrial iot. IEEE Syst J (2022) 17:2225–36. doi:10.1109/jsyst.2022.3209868

CrossRef Full Text | Google Scholar

35. Li J, Wen M, Zhang T. Group-based authentication and key agreement with dynamic policy updating for MTC in LTE-A networks. IEEE Internet Things J (2015) 3(3):408–17. doi:10.1109/jiot.2015.2495321

CrossRef Full Text | Google Scholar

36. Wang M, Yan Z. Privacy-Preserving authentication and key agreement protocols for D2D group communications. IEEE Trans Ind Inform (2018) 14(8):3637–47. doi:10.1109/tii.2017.2778090

CrossRef Full Text | Google Scholar

37. Wang L, Tian Y, Zhang D, Lu Y. Constant-round authenticated and dynamic group key agreement protocol for D2D group communications. Inf Sci (2019) 503:61–71. doi:10.1016/j.ins.2019.06.067

CrossRef Full Text | Google Scholar

38. Li N, Ma M, Wang H. ASAP-IIOT: an anonymous secure authentication protocol for industrial internet of things. Sensors (2024) 24(4):1243. doi:10.3390/s24041243

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Miao J, Wang Z, Wu Z, Ning X, Tiwari P. A blockchain-enabled privacy-preserving authentication management protocol for Internet of Medical Things. Expert Syst Appl (2024) 237:121329. doi:10.1016/j.eswa.2023.121329

CrossRef Full Text | Google Scholar

40. Long Y, Peng C, Tan W, Chen Y. Blockchain-based anonymous authentication and key management for internet of things with Chebyshev chaotic maps. IEEE Trans Ind Inform (2024) 20:7883–93. doi:10.1109/tii.2024.3366975

CrossRef Full Text | Google Scholar

41. Zhang J, Cui J, Zhong H, Chen Z, Liu L. PA-CRT: Chinese remainder theorem based conditional privacy-preserving authentication scheme in vehicular ad-hoc networks. IEEE Trans Dependable Secure Comput (2019) 18(2):722–35. doi:10.1109/tdsc.2019.2904274

CrossRef Full Text | Google Scholar

42. Shree S, Zhou C, Barati M. Data protection in internet of medical things using blockchain and secret sharing method. The J Supercomputing (2024) 80(4):5108–35. doi:10.1007/s11227-023-05657-7

CrossRef Full Text | Google Scholar

43. Belfaik Y, Lotfi Y, Sadqi Y, Safi S . A comparative study of protocols’ security verification tools: avispa, scyther, ProVerif, and tamarin. In: International Conference on Digital Technologies and Applications. Cham: Springer Nature Switzerland (2024). p. 118–28.

CrossRef Full Text | Google Scholar

44. Yadav KA, Vijayakumar P. LPPSA: an efficient Lightweight Privacy-Preserving Signature-based Authentication protocol for a vehicular ad hoc network. Ann telecommunications (2022) 77:473–89. doi:10.1007/s12243-021-00897-1

CrossRef Full Text | Google Scholar

45. Miao J, Wang Z, Xue X, Wang M, Lv J, Li M. Lightweight and secure D2D group communication for wireless IoT. Front Phys (2023) 11:1210777. doi:10.3389/fphy.2023.1210777

CrossRef Full Text | Google Scholar

46. Wang W, Han Z, Alazab M, Gadekallu TR, Zhou X, Su C. Ultra super fast authentication protocol for electric vehicle charging using extended chaotic maps. IEEE Trans Industry Appl (2022) 58(5):5616–23. doi:10.1109/tia.2022.3184668

CrossRef Full Text | Google Scholar