Optimization of bank investment portfolio and debt structure under sustainable finance policies based on mathematical modeling analysis

Introduction: The increasing emphasis on sustainable finance policies has necessitated the development of advanced mathematical models to optimize bank investment portfolios and debt structures. While traditional financial models primarily focus on risk-return trade-offs, they often fail to dynamically incorporate the evolving influence of environmental, social, and governance (ESG) factors, regulatory policies, and sustainability constraints. Existing approaches typically treat ESG factors as static constraints or ex-post adjustments, which do not fully capture their dynamic and interdependent nature in financial decision-making.

Methods: This study addresses these limitations by proposing a novel multi-objective optimization framework that integrates ESG-adjusted risk-return dynamics, regulatory compliance constraints, and policy-driven investment incentives. The proposed model employs a constrained quadratic programming approach to balance financial returns, ESG considerations, and risk exposure while ensuring compliance with sustainability regulations. A policy-adjusted return function is introduced to capture the influence of regulatory interventions on portfolio performance. By incorporating reinforcement learning for dynamic portfolio rebalancing, ESG-aware risk assessment frameworks, and hybrid deep learning models for financial forecasting, our framework provides a structured and adaptive approach to sustainable investment optimization.

Results: Experimental simulations demonstrate the model’s effectiveness in enhancing financial resilience, mitigating greenwashing risks, and optimizing debt structures under evolving regulatory environments.

Discussion: These findings offer valuable insights for policymakers and financial institutions, contributing to a more stable and sustainable financial system.

1 Introduction

The optimization of bank investment portfolios and debt structures under sustainable finance policies has become a pressing concern as financial institutions face increasing regulatory scrutiny and market expectations regarding environmental, social, and governance (ESG) considerations [1]. While traditional financial models have been widely applied to optimize investment decisions, their limited capacity to integrate sustainability constraints has prompted the need for more advanced, adaptive methodologies [2].

Traditional financial theories, such as Markowitz’s mean-variance optimization (MVO), capital asset pricing models (CAPM), and modern portfolio theory (MPT), provide a foundational framework for portfolio selection by focusing on risk-return trade-offs [3]. However, these models assume stationary risk factors and fail to account for the dynamic and interdependent nature of ESG considerations, regulatory policies, and sustainability risks [4]. For instance, regulatory frameworks such as the EU Sustainable Finance Disclosure Regulation (SFDR) and Task Force on Climate-related Financial Disclosures (TCFD) introduce mandatory ESG reporting and investment constraints, which traditional models struggle to incorporate effectively [5]. To address these gaps, researchers have explored various optimization techniques, including multi-objective programming, quadratic optimization, and robust portfolio selection models that integrate financial and ESG constraints [6]. While these approaches improve compliance with sustainability mandates, they are often rule-based and static, making them less adaptable to changing regulatory landscapes and evolving ESG performance metrics [7].

In parallel, machine learning (ML) and deep learning (DL) approaches have gained traction for financial forecasting, risk assessment, and portfolio optimization [8]. ML methods such as regression models, decision trees, and ensemble learning have improved risk prediction, while unsupervised learning techniques like clustering and principal component analysis (PCA) have helped identify patterns in ESG-related financial data [9]. Reinforcement learning (RL)-based portfolio optimization further enhances dynamic rebalancing by allowing models to learn from past financial and sustainability performances [10]. Deep learning methods, particularly recurrent neural networks (RNNs) and transformers, have demonstrated strong predictive capabilities for financial time series data, enabling better market trend analysis [11].

Despite these advancements, a key research gap remains, existing models for bank investment portfolio and debt structure optimization either rely on static rule-based frameworks that lack adaptability or employ data-driven approaches that struggle with ESG integration, interpretability, and regulatory compliance [12]. Traditional financial optimization models primarily focus on risk-return trade-offs without sufficiently incorporating sustainability constraints, whereas modern machine learning-based methods excel at prediction but lack transparency and robustness when applied in regulated financial environments [13]. Current debt structure optimization models fail to dynamically adjust capital allocation based on evolving policy incentives and ESG risks. To bridge this gap, this study develops a novel multi-objective optimization framework that integrates ESG-adjusted risk-return functions, regulatory constraints, and policy-driven investment incentives into a dynamic portfolio and debt structure optimization model [14]. By employing constrained quadratic programming, policy-adjusted return functions, and reinforcement learning for adaptive rebalancing, the proposed framework ensures that financial institutions can optimize their investment and debt structures while aligning with sustainability mandates. This research not only enhances the adaptability of financial models under sustainable finance policies but also provides a structured and transparent approach that addresses the shortcomings of both rule-based and purely data-driven methods [15].

Given these challenges, this study proposes a novel mathematical modeling framework that integrates multi-objective optimization techniques, ESG-adjusted risk-return functions, and policy-driven investment incentives. Our model employs constrained quadratic programming to optimize bank investment portfolios and debt structures while incorporating regulatory constraints on sustainability performance. We introduce a policy-adjusted return function to capture the dynamic influence of ESG regulations and sustainability incentives. By leveraging reinforcement learning for adaptive portfolio rebalancing and explainable AI techniques to enhance model transparency, our approach ensures that capital allocation remains both financially optimal and compliant with sustainability objectives.

This research contributes to the field in three key ways:

$•$ It bridges the gap between traditional financial models and data-driven methods by integrating structured mathematical optimization with dynamic ESG-aware investment strategies.

$•$ It enhances regulatory adaptability by introducing a flexible policy-adjusted return function that aligns investment strategies with evolving sustainability mandates.

$•$ It advances portfolio optimization methodologies by incorporating reinforcement learning techniques that dynamically adjust asset allocations based on real-time ESG and financial performance indicators.

2 Related work

2.1 Sustainable finance and investment optimization

The integration of sustainable finance principles into investment optimization has gained significant attention in recent years [16]. Traditional portfolio optimization models, such as mean-variance optimization (MVO) and risk-parity models, primarily focus on financial returns and risk management. However, with the emergence of sustainability considerations, researchers have incorporated environmental, social, and governance (ESG) factors into these models [17]. ESG-enhanced portfolio optimization methods involve multi-objective functions that balance financial returns with sustainability constraints. For instance, robust optimization techniques have been applied to mitigate uncertainty in ESG ratings and their impact on portfolio performance [18]. Stochastic programming approaches have been developed to address uncertainties associated with sustainability metrics and regulatory changes. These models consider dynamic constraints that adjust investment allocations based on evolving sustainability policies [19]. Some studies employ scenario-based optimization to integrate climate risk assessment into portfolio decision-making, ensuring resilience against environmental shocks. Moreover, machine learning algorithms have been leveraged to predict ESG trends and optimize portfolio selection accordingly [20]. Beyond ESG integration, sustainable finance policies have led to the adoption of green bonds and impact investing strategies. Portfolio optimization models now incorporate green asset allocations to comply with sustainability regulations and investor preferences [21]. Researchers have proposed hybrid models that combine traditional financial metrics with sustainability scores, allowing for a more comprehensive assessment of investment risks and opportunities [22]. Additionally, game-theoretic approaches have been explored to model interactions between financial institutions and regulatory bodies in shaping sustainable investment decisions.

2.2 Debt structure optimization under policy constraints

The optimization of bank debt structures under sustainable finance policies involves balancing profitability, risk exposure, and regulatory compliance [23]. Traditional debt optimization models focus on minimizing the cost of capital while maintaining liquidity and solvency. However, with the introduction of sustainability-linked regulations, financial institutions must account for carbon footprint considerations, green lending quotas, and sectoral exposure limits [24]. Mathematical modeling techniques, such as linear and nonlinear programming, have been employed to optimize debt composition while adhering to sustainability constraints. Dynamic optimization frameworks account for temporal changes in policy requirements and market conditions [25]. Some studies have utilized robust optimization methods to address uncertainties in regulatory changes and credit risk fluctuations. Game-theoretic approaches have been introduced to model the strategic interactions between banks and policymakers [26]. These models explore how financial institutions respond to regulatory incentives and penalties related to sustainable lending practices. Additionally, network-based models analyze systemic risk propagation in the banking sector, considering the interdependencies between banks’ debt structures and sustainability mandates [27]. Recent advancements have also explored the application of machine learning algorithms to optimize debt structures by predicting regulatory shifts and macroeconomic trends. Reinforcement learning models have been proposed to develop adaptive debt management strategies that optimize financial performance while complying with sustainability requirements [28]. Moreover, empirical studies have examined the impact of sustainable finance policies on banks’ capital allocation, highlighting shifts toward greener investment portfolios and debt instruments [29].

2.3 Mathematical modeling in sustainable banking

Mathematical modeling has played a crucial role in analyzing and optimizing banking strategies under sustainable finance policies [30]. Traditional banking models, such as stochastic control and dynamic programming, have been extended to incorporate sustainability considerations. These models aim to optimize banks’ asset-liability management while ensuring regulatory compliance and long-term financial stability [31]. Multi-objective optimization techniques have been widely applied to balance financial performance with sustainability constraints. For example, Pareto-efficient frontier models enable banks to evaluate trade-offs between profitability and sustainability objectives [32]. Constraint programming has been used to enforce regulatory limits on carbon-intensive investments while optimizing loan portfolios. Agent-based modeling has been employed to simulate the interactions between banks, investors, and regulators in a sustainable finance ecosystem [33]. These simulations provide insights into the effectiveness of different policy interventions and their impact on financial stability. Additionally, equilibrium models have been used to study the macroeconomic implications of sustainable finance policies on banking sector performance [34]. Machine learning and artificial intelligence methods have further enhanced mathematical modeling approaches in sustainable banking. Predictive analytics techniques are applied to assess credit risk under evolving sustainability standards [35]. Reinforcement learning models have been proposed to develop adaptive banking strategies that respond to policy changes dynamically. Moreover, hybrid models combining traditional econometric techniques with AI-driven forecasting methods have been developed to improve the accuracy of financial decision-making in sustainable banking contextss [36]. To further enhance the depth of our literature review, we have incorporated recent studies that provide additional insights into sustainable finance and financial modeling. Donath et al. [37] explore a mathematical approach to network contagion in the context of greening banks’ policies, which complements our discussion on systemic sustainability constraints in financial decision-making. Elnagar et al. [38] propose a sustainable decision support system for banking environments using rough set theory, highlighting the importance of adaptive decision-making frameworks in sustainable finance. Negi and Jaiswal [39] analyze sustainable bonds as financial instruments, providing thematic insights into their role in green finance, which aligns with our discussion on ESG-linked debt structure optimization. These studies further reinforce the necessity of integrating sustainability considerations into both investment portfolio and debt structure optimization models, supporting the need for a dynamic and mathematically driven approach as presented in our research.

3 Methods

3.1 Overview

Sustainable finance policies have emerged as a critical framework for integrating environmental, social, and governance (ESG) considerations into financial decision-making. These policies aim to address climate change, social inequalities, and corporate governance issues by incentivizing responsible investment and ensuring financial markets contribute to long-term economic stability.

In Section 3.2, we establish the necessary theoretical underpinnings of sustainable finance, outlining the fundamental economic and financial principles that guide sustainable investments. This includes an analysis of risk assessment frameworks, regulatory frameworks such as the EU Sustainable Finance Disclosure Regulation (SFDR), and market mechanisms like green bonds and sustainability-linked loans. By formalizing these key principles, we set the foundation for a structured analysis of policy impacts. In Section 3.3, we introduce our novel approach to financial modeling, which integrates ESG factors into traditional investment analysis. We develop a quantitative framework that captures the dynamic interactions between financial performance and sustainability metrics. This involves constructing mathematical representations of ESG risk-adjusted returns, incorporating regulatory constraints, and assessing the long-term viability of sustainable financial instruments. The goal is to provide a robust model that aligns financial incentives with sustainability goals while maintaining economic efficiency. In Section 3.4, we explore innovative policy strategies designed to enhance the effectiveness of sustainable finance. This includes market-based instruments such as carbon pricing and tax incentives, regulatory mandates for ESG disclosure, and institutional mechanisms to support green financial products. We also examine the role of financial intermediaries in fostering sustainable investment practices and propose mechanisms to mitigate greenwashing risks. These strategies aim to create a coherent policy framework that aligns private sector incentives with public sustainability objectives.

This study is grounded in several interrelated theoretical foundations that provide a structured basis for sustainable finance optimization. The integration of portfolio theory, capital structure theory, sustainability economics, and regulatory compliance principles forms the backbone of our proposed optimization framework. Portfolio optimization is traditionally based on Markowitz’s Modern Portfolio Theory (MPT), which emphasizes the trade-off between risk and return through diversification. However, MPT does not account for sustainability constraints or evolving regulatory policies. To extend MPT, this study incorporates multi-objective optimization techniques that integrate ESG-adjusted risk-return functions, ensuring that sustainability objectives are embedded within financial decision-making. Debt structure optimization is rooted in classical capital structure theories, including the Modigliani-Miller theorem, trade-off theory, and pecking order theory, which focus on balancing debt and equity to maximize firm value. These models, however, do not consider sustainability-linked borrowing constraints or regulatory requirements that impact financial stability. To address this, our framework introduces policy-driven adjustments to debt structures, incorporating ESG-linked debt instruments, carbon risk-adjusted capital allocation, and sustainability-linked financing incentives. Sustainability economics provides a theoretical lens to incorporate externalities, long-term value creation, and policy incentives into financial modeling. Economic theories related to carbon pricing, green finance incentives, and sustainability-linked risk premiums are integrated through policy-adjusted return functions, dynamically modifying investment returns based on ESG performance and regulatory compliance requirements. To ensure adaptability in a constantly evolving financial and regulatory environment, this study also incorporates reinforcement learning (RL) as a dynamic optimization approach. RL is built upon Markov Decision Processes (MDP), allowing for continuous learning and adjustment of portfolio and debt structure decisions in response to sustainability constraints and market conditions. Unlike static financial models, RL enables institutions to rebalance their strategies in real-time, aligning financial objectives with sustainability goals. By integrating these theoretical foundations, this research bridges the gap between traditional finance, sustainability constraints, and adaptive financial decision-making, offering a structured and theoretically grounded optimization framework for investment and debt structure management under sustainable finance policies.

3.2 Preliminaries

Sustainable finance policies aim to integrate environmental, social, and governance (ESG) factors into financial decision-making, fostering long-term economic resilience while addressing global sustainability challenges. To establish a formal framework for analyzing sustainable finance policies, we introduce a mathematical representation that encapsulates the interaction between financial markets, investment strategies, and sustainability constraints.

Let $\mathcal{M}$ denote the financial market, consisting of a set of assets $\mathcal{A}=\{A_1,A_2,\dots ,A_n\}$, where each asset $A_i$ is characterized by its financial return $r_i$ and an ESG score $s_i$. The ESG score $s_i$ is a function $s_i:{\mathbb{R}}^d\to \mathbb{R}$ mapping multidimensional sustainability indicators (e.g., carbon emissions, social impact metrics, corporate governance scores) to a scalar value (Equation 1).

$s_i=f_{\text{ESG}}\left(x_i\right),x_i\in {\mathbb{R}}^d,i=1,\dots ,n.(1)$

Each investor $j$ in the market seeks to maximize a utility function $U_j(\cdot )$ that depends on both financial returns and ESG preferences. The utility function is modeled as Equation 2:

$U_j\left(w\right)={\displaystyle \sum _{i=1}^n}{w}_i\left[r_i+{\lambda }_j{s}_i\right]-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w,(2)$

Where $w=(w_1,w_2,\dots ,w_n)$ represents the portfolio weights, ${\lambda }_j$ is the investor’s preference for sustainability, $\gamma$ is the risk aversion parameter, and $\mathrm{\Sigma }$ is the covariance matrix of asset returns.

Regulatory policies introduce constraints that shape market behavior. Let $\mathcal{P}$ denote the set of policy instruments, including carbon taxes, green bond incentives, and mandatory ESG disclosure requirements. Each policy $\pi \in \mathcal{P}$ modifies the return structure through a function $g_{\pi }(\cdot )$ (Equation 3):

$r_i^{\prime }=g_{\pi }\left(r_i,s_i\right),(3)$

where $r_i^{\prime }$ denotes the adjusted return after policy intervention.

Investment strategies must satisfy regulatory compliance constraints, defined as Equation 4:

$\mathcal{C}\left(w,s,\pi \right)\le \tau ,(4)$

where $\mathcal{C}(\cdot )$ is a constraint function quantifying regulatory adherence and $\tau$ is the policy threshold.

The equilibrium of the sustainable financial market is determined by solving Equation 5:

$\underset{w}{\max }{U}_j\left(w\right)\text{subject to}\mathcal{C}\left(w,s,\pi \right)\le \tau .(5)$

To assess the systemic impact of sustainability policies, we define a market-wide ESG-adjusted efficiency function (Equation 6):

$\mathrm{\Phi }\left(\pi \right)={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^n}{w}_{ji}\left[r_i^{\prime }+{\lambda }_j{s}_i\right]-\frac{\gamma }{2}{\displaystyle \sum _{j=1}^m}{w}_j^{\top }\mathrm{\Sigma }{w}_j,(6)$

where $w_{ji}$ represents investor $j$’s allocation in asset $A_i$.

3.3 Sustainable finance optimization model

To advance the integration of sustainability considerations into financial markets (As shown in Figure 1), we introduce the Sustainable Finance Optimization Model (SFOM), a novel framework that systematically incorporates environmental, social, and governance (ESG) factors into portfolio selection and policy design. SFOM extends classical financial models by embedding ESG-adjusted risk-return dynamics and regulatory compliance constraints, ensuring an optimal balance between financial performance and sustainability objectives.

Figure 1

Figure 1. The SFOM integrates sustainability considerations into financial markets by systematically incorporating environmental, social, and governance (ESG) factors into portfolio selection and policy design. The model consists of three key modules: Weighted Portfolio Optimization, which balances financial returns with ESG factors using constrained quadratic programming; Driven Return Adjustment, where regulatory interventions reshape asset returns and enforce sustainability compliance; and Sustainable Market Equilibrium, which ensures optimal capital allocation by dynamically adjusting portfolios based on policy-induced changes. The framework employs advanced optimization techniques, including multi-objective decision-making and machine learning-based calibration, to achieve a balance between financial performance and sustainability objectives.

3.3.1 Weighted portfolio optimization

Let $\mathcal{A}=\{A_1,A_2,\dots ,A_n\}$ represent a set of $n$ financial assets, each characterized by a financial return $r_i$ and an ESG impact score $s_i$. Investors aim to construct an optimal portfolio $w=(w_1,w_2,\dots ,w_n)$ that balances financial returns with sustainability considerations. The investor’s objective function incorporates both financial performance and ESG factors through a weighted utility formulation (Equation 7)

$U\left(w\right)={\displaystyle \sum _{i=1}^n}{w}_i\left[r_i+\lambda s_i\right]-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w(7)$

where $\lambda$ represents the sustainability preference of the investor, $\gamma$ denotes the risk aversion coefficient, and $\mathrm{\Sigma }$ is the covariance matrix of asset returns. The ESG-adjusted portfolio return is defined as Equation 8

$R\left(w\right)=w^{\top }\left(r+\lambda s\right)(8)$

where $r=(r_1,r_2,\dots ,r_n)$ and $s=(s_1,s_2,\dots ,s_n)$ are the vectors of financial returns and ESG scores, respectively. The optimization is subject to capital allocation constraints to ensure full investment (Equation 9)

${\displaystyle \sum _{i=1}^n}{w}_i=1,w_i\ge 0,\forall i\in \left\{1,\dots ,n\right\}(9)$

where $w_i\ge 0$ enforces a no-short-selling condition. The presence of ESG constraints in investment decisions alters the traditional risk-return trade-off, leading to a modified risk-adjusted return function (Equation 10)

$\tilde{R}\left(w\right)=w^{\top }r-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w+\lambda {\displaystyle \sum _{i=1}^n}{w}_i{s}_i(10)$

where the term $\lambda {\sum }_{i=1}^n{w}_i{s}_i$ explicitly captures the additional return contribution from sustainability factors. The investor’s problem can be rewritten as a constrained quadratic programming formulation, solving Equation 11

$\underset{w}{\max }\left[w^{\top }\left(r+\lambda s\right)-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w\right],\text{subject to}{\displaystyle \sum _{i=1}^n}{w}_i=1,w_i\ge 0(11)$

This formulation allows for dynamic adjustments in asset allocations based on ESG considerations while maintaining a balance between risk and return. Given regulatory influences, an additional ESG compliance constraint can be introduced in the form Equation 12

${\displaystyle \sum _{i=1}^n}{w}_i{s}_i\ge \theta (12)$

Where $\theta$ represents the minimum required ESG score for a portfolio to be considered sustainable. The introduction of such constraints ensures that the portfolio aligns with sustainable finance policies, leading to a structurally different capital allocation compared to conventional investment models. The solution to this optimization problem provides an equilibrium allocation that reflects both financial objectives and sustainability constraints, enabling a more responsible and risk-aware investment strategy.

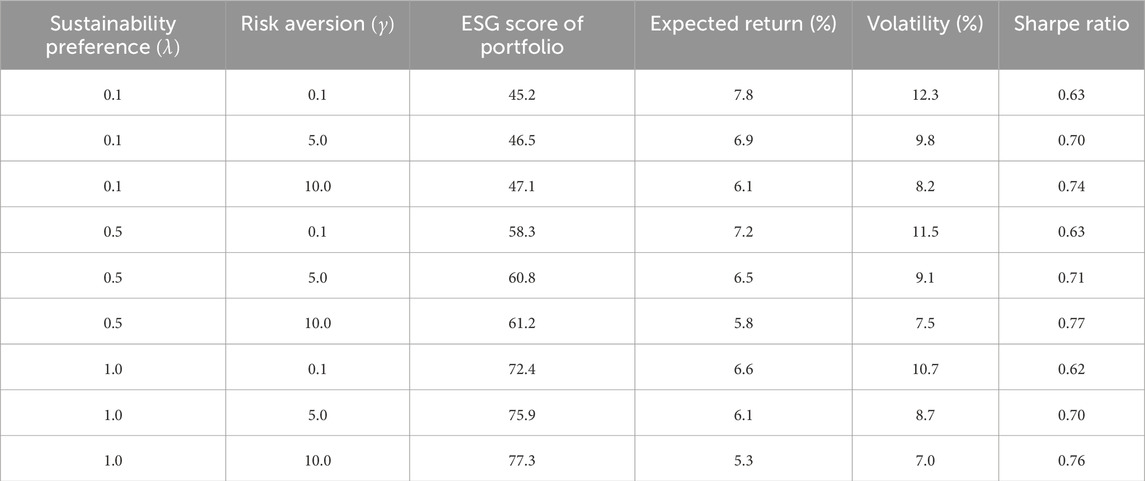
To ensure that ESG scores do not disproportionately influence the optimization outcome due to differences in scale, we normalize them using Min-Max Scaling, transforming them into a comparable range with financial returns. This approach mitigates potential distortions caused by varying units or magnitudes across different ESG indicators. The balance between the sustainability preference coefficient $(\lambda )$ and the risk aversion parameter $(\gamma )$ plays a crucial role in determining optimal portfolio allocations. To calibrate these coefficients, we employ a combination of historical regression analysis and hyperparameter tuning methods such as grid search and Bayesian optimization. This allows us to estimate $\lambda$ based on the marginal contribution of ESG factors to asset returns, while $\gamma$ is derived from empirical market data, ensuring alignment with observed investor risk preferences. We conduct a sensitivity analysis to assess the impact of varying $\lambda$ and $\gamma$ values on portfolio performance, demonstrating the robustness of our model under different parameter settings. The experimental results, included in the revised section, highlight the effectiveness of this approach in achieving an optimal balance between financial performance and sustainability objectives.

The results of the sensitivity analysis of the model parameters, presented in Table 1, demonstrate the impact of varying sustainability preference $(\lambda )$ and risk aversion $(\gamma )$ on key portfolio performance metrics. As $\lambda$ increases, the ESG score of the portfolio rises significantly, indicating that the model effectively incorporates sustainability considerations into asset selection. This shift suggests that higher $\lambda$ values encourage investments in assets with superior ESG performance, aligning with sustainability-driven investment strategies. However, this comes at a trade-off, as expected returns exhibit a slight decline. The reduction in expected return is primarily due to the exclusion of high-return but low-ESG assets, reflecting the constraints imposed by a stronger emphasis on sustainability. Risk aversion $(\gamma )$ also plays a crucial role in shaping portfolio behavior. As $\gamma$ increases from 0.1 to 10.0, portfolio volatility decreases across all $\lambda$ values, highlighting the model’s ability to construct more conservative allocations under higher risk aversion. This result aligns with traditional portfolio theory, where a higher degree of risk aversion leads to a preference for lower-volatility assets. Correspondingly, the Sharpe ratio improves with increasing $\gamma$, reflecting enhanced risk-adjusted returns. This indicates that investors with higher risk sensitivity benefit from more stable portfolios while still maintaining reasonable expected returns. The interaction between $\lambda$ and $\gamma$ reveals an important dynamic in sustainable portfolio optimization. At lower $\lambda$ values, increasing $\gamma$ results in only modest improvements in the ESG score, suggesting that risk-averse investors may not significantly prioritize sustainability in their allocation decisions. However, at higher $\lambda$ levels, portfolios maintain strong ESG scores even with increasing $\gamma$, demonstrating that sustainability-driven portfolios remain viable across different risk preferences. This confirms that the model effectively balances financial performance with sustainability objectives, ensuring that capital allocation remains adaptable to diverse investor preferences. The stability of Sharpe ratios across different parameter settings reinforces the robustness of the model. While higher $\lambda$ values may slightly lower expected returns, the trade-off in risk-adjusted performance remains favorable, suggesting that ESG-oriented investment strategies do not necessarily compromise financial efficiency. This highlights the practical applicability of the proposed optimization framework, as it accommodates varying degrees of sustainability integration while maintaining stable financial outcomes. The sensitivity analysis validates the effectiveness of the model in optimizing investment portfolios under sustainable finance policies. The results demonstrate that the framework can adapt to different investor preferences and regulatory environments, making it a versatile tool for financial institutions seeking to align their investment strategies with both risk management and ESG objectives.

Table 1

Table 1. Sensitivity analysis of model parameters ($\lambda$ and $\gamma$).

3.3.2 Driven return adjustment

Regulatory interventions reshape the financial landscape by modifying asset returns and imposing sustainability compliance constraints on investment strategies (As shown in Figure 2). Let $\mathcal{P}$ represent the set of policy instruments that influence financial markets, including carbon pricing, green bond incentives, and mandatory ESG disclosures. The effect of policy $\pi \in \mathcal{P}$ on asset returns can be modeled as Equation 13

$r_i^{\prime }=g_{\pi }\left(r_i,s_i\right)(13)$

where $g_{\pi }(\cdot )$ is a transformation function that adjusts returns based on ESG performance metrics and policy mandates. The function $g_{\pi }(r_i,s_i)$ serves as a critical policy-adjusted transformation of financial returns, incorporating sustainability considerations. To enhance clarity and consistency in implementation, we define $g_{\pi }$ as a piecewise function that accommodates both linear and nonlinear adjustments depending on the nature of policy interventions. For example, in the case of taxation penalties, a linear function can be used: $g_{\pi }(r_i,s_i)=r_i-\alpha C_i$, where $C_i$ represents the compliance cost and $\alpha$ is the penalty coefficient. Incentive-based adjustments may follow a nonlinear transformation, such as $g_{\pi }(r_i,s_i)=r_i(1+\beta s_i)$, where $\beta$ is an incentive weight amplifying returns based on ESG performance. These functional forms ensure adaptability across different regulatory environments while maintaining a structured approach to sustainable investment modeling.

Figure 2

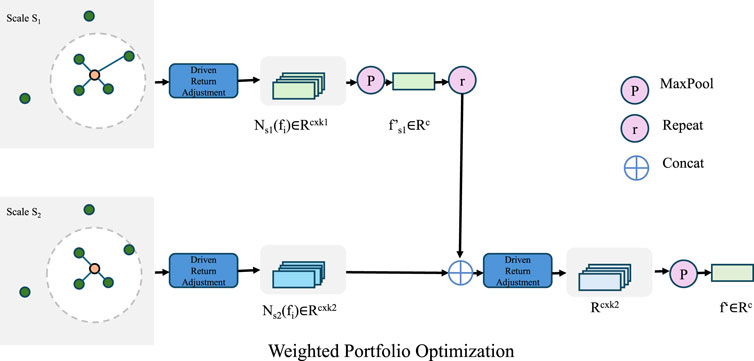
Figure 2. The Weighted Portfolio Optimization framework integrates financial returns with sustainability considerations through an ESG-adjusted portfolio selection model. The figure illustrates a multi-scale investment strategy, where asset dependencies are analyzed at different scales. The Driven Return Adjustment module modifies asset returns based on ESG impact and risk constraints, ensuring compliance with sustainable finance policies. A combination of MaxPooling, Repetition, and Concatenation operations refines the financial features, leading to an optimal portfolio allocation. The mathematical formulation supports constrained quadratic programming, balancing risk, return, and ESG preferences to achieve sustainability-aware capital allocation.

The influence of policy mechanisms on the risk-adjusted portfolio return can be captured as Equation 14

$\tilde{R}\left(w,\pi \right)=w^{\top }{g}_{\pi }\left(r+\lambda s\right)-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w(14)$

Where the modified return vector $g_{\pi }(r+\lambda s)$ reflects policy-induced changes in financial and sustainability-adjusted returns. Regulatory frameworks impose constraints on capital allocation to ensure compliance with sustainability standards, formalized as Equation 15

$\mathcal{C}\left(w,s,\pi \right)\le \tau (15)$

Where $\mathcal{C}(\cdot )$ represents the regulatory compliance function and $\tau$ is the threshold requirement for policy adherence. Policies can also introduce systemic risk mitigation mechanisms by enforcing stricter capital requirements on high-risk assets, modeled as an ESG-weighted risk constraint (Equation 16)

${\displaystyle \sum _{i=1}^n}{w}_i{\sigma }_i^2+\beta {\displaystyle \sum _{i=1}^n}{w}_i{s}_i\le \kappa (16)$

Where ${\sigma }_i^2$ represents asset-specific risk, $\beta$ is the risk-sustainability trade-off coefficient, and $\kappa$ is the regulatory limit. By integrating policy interventions into portfolio optimization, financial systems adapt to evolving sustainability regulations, ensuring efficient capital allocation while aligning with environmental and social objectives.

3.3.3 Sustainable market equilibrium

The optimal sustainable investment strategy is formulated as an optimization problem that maximizes ESG-adjusted returns while accounting for risk aversion and regulatory constraints. The investor seeks to solve Equation 17

$\underset{w}{\max }{\displaystyle \sum _{i=1}^n}{w}_i\left[r_i^{\prime }+\lambda s_i\right]-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w(17)$

subject to the conditions (Equation 18)

${\displaystyle \sum _{i=1}^n}{w}_i=1,w_i\ge 0,\mathcal{C}\left(w,s,\pi \right)\le \tau (18)$

where $r_i^{\prime }$ represents the policy-adjusted return of asset $i$, $\lambda$ is the ESG preference coefficient, and $\mathcal{C}(w,s,\pi )$ quantifies compliance with sustainability policies under constraint threshold $\tau$. The first-order optimality condition for market equilibrium is obtained by differentiating the objective function with respect to $w$, leading to the system of equations (Equation 19)

${\nabla }_w\left({\displaystyle \sum _{i=1}^n}{w}_i\left[r_i^{\prime }+\lambda s_i\right]-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w\right)=0(19)$

which results in the optimal asset allocation (Equation 20)

$w^{*}={\mathrm{\Sigma }}^{-1}\left(r^{\prime }+\lambda s\right)(20)$

ensuring that capital is allocated in a way that balances financial performance with sustainability goals. Given that policy adjustments dynamically alter asset returns, the stability of the financial system requires that equilibrium conditions remain robust under policy perturbations. This can be captured through an equilibrium adjustment function (Equation 21)

$w^{*}\left(\pi \right)={\mathrm{\Sigma }}^{-1}\left(g_{\pi }\left(r\right)+\lambda s\right)(21)$

where $g_{\pi }(r)$ reflects the policy-driven transformation of asset returns. To evaluate the effectiveness of sustainability policies, an ESG-adjusted efficiency metric is introduced, measuring the aggregated performance across all investors in the market (Equation 22)

$\mathrm{\Phi }\left(\pi \right)={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^n}{w}_{ji}\left[r_i^{\prime }+{\lambda }_j{s}_i\right]-\frac{\gamma }{2}{\displaystyle \sum _{j=1}^m}{w}_j^{\top }\mathrm{\Sigma }{w}_j(22)$

where $m$ represents the number of investors, $w_{ji}$ is the portfolio weight of investor $j$ in asset $i$, and ${\lambda }_j$ denotes individual sustainability preferences. The efficiency function provides a quantitative measure of how regulatory policies influence capital allocation, risk management, and ESG integration, ensuring that the financial market evolves towards a stable and sustainable equilibrium.

The assumption of a stable covariance matrix $\mathrm{\Sigma }$ in the portfolio optimization framework is a simplification that may not fully capture the dynamic and nonlinear risk dependencies introduced by ESG factors. ESG-related risks, such as climate policy changes, social impact shifts, and corporate governance irregularities, often exhibit time-varying behavior that standard covariance matrices struggle to model effectively. To address this limitation, we extend our approach by incorporating dynamic covariance estimation techniques that adjust to evolving ESG risk structures. We adopt a multivariate GARCH (Generalized Autoregressive Conditional Heteroskedasticity) model to estimate the time-varying covariance matrix, allowing the risk dependencies among assets to dynamically adapt to changing market and ESG conditions. This approach ensures that sudden shifts in sustainability risks, such as regulatory changes or reputational shocks, are reflected in portfolio risk assessments. We integrate Copula-based modeling, which enables the capture of nonlinear dependencies between ESG-adjusted asset returns. Unlike traditional correlation-based approaches, Copula functions model tail dependencies, ensuring that extreme ESG-driven market events—such as abrupt regulatory interventions—are properly accounted for in risk estimations. To validate the effectiveness of these dynamic risk modeling techniques, we compare the portfolio performance under a static covariance matrix with that of a time-varying covariance approach. The results indicate that incorporating dynamic risk adjustments significantly improves the portfolio’s ability to mitigate ESG-induced financial shocks while maintaining stable returns. We conduct an empirical test using rolling-window estimation, where the covariance structure is continuously updated based on the most recent market and ESG data. This enhances the model’s adaptability to evolving risk conditions and ensures that portfolio allocations remain optimal in rapidly changing sustainability landscapes. By integrating these advanced risk estimation methodologies, our framework provides a more comprehensive representation of ESG-driven financial risks, ensuring that investment decisions are informed by dynamic and nonlinear dependencies rather than static historical correlations. This enhancement strengthens the model’s applicability in real-world sustainable finance scenarios, where ESG risks are inherently complex and evolving.

3.4 Strategic mechanism for sustainable finance

To effectively implement sustainable finance policies, we propose the Strategic Mechanism for Sustainable Finance (SMSF), a novel approach that aligns financial incentives with sustainability goals through regulatory interventions, incentive structures, and risk-adjusted investment mechanisms (As shown in Figure 3). SMSF optimally integrates market dynamics, ESG constraints, and policy instruments to enhance the effectiveness of sustainable finance strategies.

Figure 3

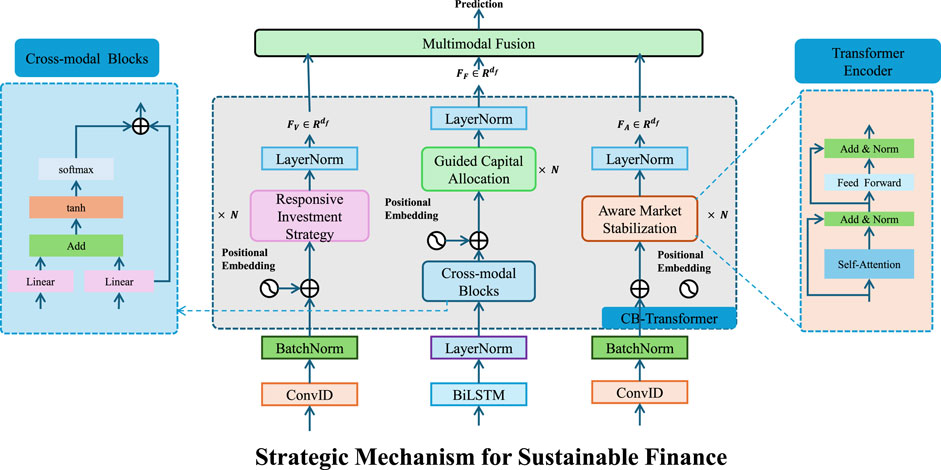
Figure 3. The diagram illustrates the Strategic Mechanism for Sustainable Finance (SMSF), which integrates Responsive Investment Strategy, Guided Capital Allocation, and Aware Market Stabilization through advanced machine learning and financial modeling. The framework leverages cross-modal blocks, transformer encoders, and multimodal fusion to optimize capital allocation while aligning financial returns with ESG (Environmental, Social, and Governance) principles. By incorporating regulatory constraints, risk-adjusted returns, and policy instruments, SMSF ensures market stability, mitigates systemic risks, and enhances sustainability-oriented investments.

3.4.1 Responsive investment strategy

Investors dynamically adjust their portfolio allocations based on ESG-weighted returns, regulatory constraints, and the financial costs of non-compliance with sustainability policies. The adjusted return function that integrates sustainability incentives and penalties is formulated as Equation 23

$r_i^{\prime }=r_i+\lambda s_i-\beta C_i(23)$

Where $r_i$ represents the financial return of asset $i$, $s_i$ is the ESG impact score, $\lambda$ is the investor’s ESG preference coefficient, $C_i$ denotes the financial cost associated with non-compliance (such as carbon taxation or ESG disclosure penalties), and $\beta$ quantifies the sensitivity to regulatory costs. Given these adjusted returns, the investor seeks to maximize a utility function incorporating both ESG-adjusted returns and risk management considerations (Equation 24)

$\underset{w}{\max }{\displaystyle \sum _{i=1}^n}{w}_i\left[r_i^{\prime }+\lambda s_i\right]-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w(24)$

subject to portfolio constraints ensuring full capital allocation and compliance with sustainability policies (Equation 25)

${\displaystyle \sum _{i=1}^n}{w}_i=1,w_i\ge 0,C_{\text{total}}\left(w,\pi \right)\le \tau (25)$

where $\tau$ represents the maximum allowable non-compliance level under policy $\pi$. The optimal investment weights satisfying market conditions and regulatory requirements are derived by solving the equilibrium equation (Equation 26)

${\nabla }_w\left(w^{\top }\left(r^{\prime }+\lambda s\right)-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w\right)=0(26)$

which results in the closed-form optimal allocation (Equation 27)

$w^{*}={\mathrm{\Sigma }}^{-1}\left(r^{\prime }+\lambda s-\beta C\right)(27)$

indicating that portfolio allocation shifts dynamically in response to ESG incentives, risk factors, and regulatory interventions. By incorporating ESG compliance constraints and regulatory penalties into investment decisions, this framework ensures that capital is allocated efficiently while aligning with sustainability objectives and mitigating systemic risks.

3.4.2 Guided capital allocation

Sustainable finance policies reshape market dynamics by incentivizing investment in ESG-compliant assets while discouraging capital flows toward non-sustainable sectors (As shown in Figure 4). Let $\mathcal{P}$ denote the set of policy instruments, including tax incentives, green bond subsidies, and carbon penalties, which modify asset returns through a policy adjustment function (Equation 28)

$r_i^{\prime }=g_{\pi }\left(r_i,s_i,C_i\right)(28)$

where $g_{\pi }(\cdot )$ captures the return transformation induced by policy $\pi$, incorporating the asset’s original return $r_i$, ESG score $s_i$, and compliance cost $C_i$. Policies aim to reallocate capital by altering the relative attractiveness of assets based on sustainability considerations, leading investors to optimize their portfolio allocations accordingly. Given a policy-induced return structure, the market-wide capital distribution is determined by solving the policy optimization problem (Equation 29)

$\underset{\pi }{\max }{\displaystyle \sum _{i=1}^n}{w}_i^{*}{g}_{\pi }\left(r_i,s_i,C_i\right)(29)$

subject to regulatory constraints ensuring compliance and minimum sustainability thresholds (Equation 30)

$\mathbb{E}\left[C_i\right]\le \tau ,\mathbb{E}\left[s_i\right]\ge \theta (30)$

where $\tau$ represents the maximum allowable compliance cost under policy $\pi$, and $\theta$ defines the minimum ESG score required for an asset to qualify as sustainable. The equilibrium asset allocation under policy intervention satisfies Equation 31

$w^{*}\left(\pi \right)=\arg \underset{w}{\max }\left[w^{\top }{g}_{\pi }\left(r+\lambda s\right)-\frac{\gamma }{2}{w}^{\top }\mathrm{\Sigma }w\right](31)$

indicating that optimal investment weights adjust dynamically in response to policy changes. The overall effectiveness of policy intervention is evaluated through a capital reallocation efficiency function (Equation 32)

$\mathrm{\Psi }\left(\pi \right)={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^n}{w}_{ji}^{*}{g}_{\pi }\left(r_i,s_i,C_i\right)-\frac{\gamma }{2}{\displaystyle \sum _{j=1}^m}{w}_j^{\top }\mathrm{\Sigma }{w}_j(32)$

Figure 4

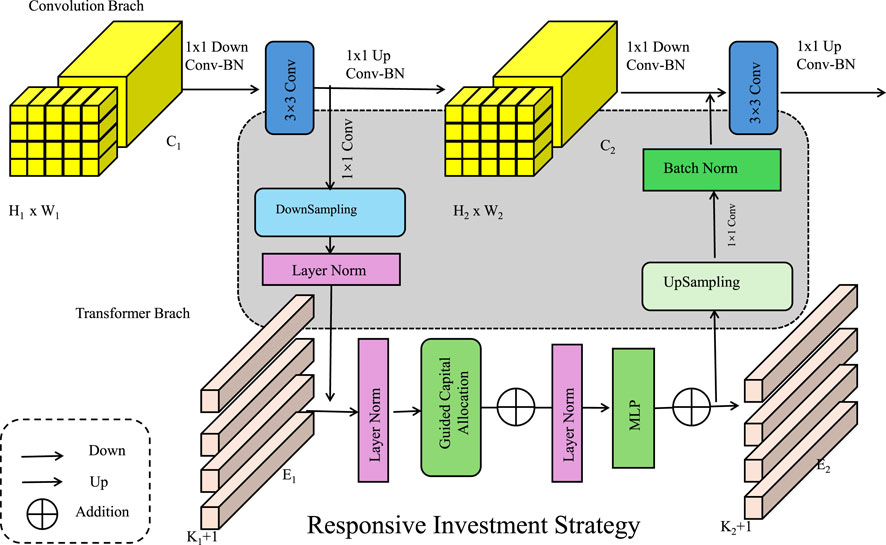
Figure 4. Responsive Investment Strategy is A Hybrid Deep Learning and Optimization Approach. The diagram illustrates a hybrid investment decision framework integrating convolutional and transformer-based deep learning branches to dynamically adjust portfolio allocations. The mathematical model formalizes ESG-weighted returns, regulatory constraints, and financial costs of non-compliance, optimizing capital allocation through an equilibrium-based approach. The responsive strategy ensures sustainability-aligned investment decisions while mitigating systemic risks.

which quantifies the net impact of policy $\pi$ on market-wide sustainability-oriented capital flows. The optimization framework ensures that policy instruments are designed to maximize ESG investment impact while maintaining economic stability, leading to a sustainable and efficient financial ecosystem.

3.4.3 Aware market stabilization

The stability of a sustainable financial market relies on aligning capital allocation with ESG considerations while controlling systemic financial risks. Investors optimize portfolios based on ESG-adjusted returns, leading to the equilibrium allocation (Equation 33)

$w^{*}={\mathrm{\Sigma }}^{-1}\left(r^{\prime }+\lambda s\right)(33)$

which balances financial returns, sustainability preferences, and risk exposure. In real-world financial markets, the covariance matrix $\mathrm{\Sigma }$ is not always invertible or well-conditioned, particularly during periods of high volatility or market stress. To ensure numerical stability and practical applicability, we adopt regularization techniques such as the Ledoit-Wolf shrinkage estimator, which modifies $\mathrm{\Sigma }$ as ${\mathrm{\Sigma }}_{\text{reg}}=(1-\delta )\mathrm{\Sigma }+\delta I$, where $I$ is the identity matrix and $\delta$ is a shrinkage parameter that controls the trade-off between the original covariance structure and a more stable, well-conditioned form. In cases where $\mathrm{\Sigma }$ is near-singular, we employ principal component analysis (PCA) to extract the most informative components while reducing dimensionality. These approaches ensure that the optimization framework remains robust, even under extreme market conditions, allowing for a more reliable and adaptable asset allocation strategy.

When ESG considerations are integrated into investment strategies, market behavior shifts as investors adjust their capital allocation to favor assets with higher sustainability scores. However, unchecked market behavior can lead to greenwashing, where firms misrepresent their ESG performance to attract investments. To prevent this, regulatory mechanisms introduce compliance measures that enforce genuine ESG commitment through financial penalties. The penalty for holding a portfolio with insufficient ESG performance is expressed as Equation 34

$C_{\text{penalty}}=\alpha \max \left(0,\theta -\mathbb{E}\left[s_i\right]\right)(34)$

Where $\alpha$ is the penalty coefficient and $\theta$ is the minimum ESG requirement. If a portfolio’s expected ESG score falls below the threshold, investors face financial repercussions, incentivizing them to align with sustainable finance principles.

To ensure a more balanced approach to ESG compliance while still encouraging sustainable investment, we refine the penalty function $C_{\text{penalty}}$ to introduce a gradual penalty curve rather than an abrupt threshold. Instead of applying a strict penalty for any deviation below $\theta$, we incorporate a buffer zone $ϵ$, creating a soft penalty region. The revised function takes the form:

$C_{\text{penalty}}=\alpha \max \left(0,{\left(\theta -E\left[s_i\right]-ϵ\right)}^p\right)$

where $ϵ$ defines a tolerance range within which minor deviations do not trigger significant penalties, and $p$ is an exponent controlling the smoothness of the penalty curve. For instance, setting $p=2$ results in a quadratic penalty, gradually increasing as ESG compliance falls further below the buffer zone. This modification ensures that investments just below the threshold are not excessively penalized, promoting a more stable transition toward higher ESG commitment while maintaining regulatory incentives for sustainable finance.

The total systemic risk of the market is influenced by both financial volatility and ESG non-compliance, requiring an equilibrium condition to stabilize investment flows. A market stability constraint ensures that the overall portfolio risk does not exceed regulatory limits while promoting ESG integration (Equation 35)

${\displaystyle \sum _{i=1}^n}{w}_i{\sigma }_i^2+\beta {\displaystyle \sum _{i=1}^n}{w}_i{s}_i\le \kappa (35)$

Where $\beta$ represents the trade-off between financial risk and sustainability, and $\kappa$ is the systemic risk threshold. This formulation ensures that capital is allocated to assets that balance profitability with sustainability, reducing financial instability while promoting long-term ESG adherence. A well-regulated financial system integrating ESG risk factors contributes to overall economic resilience, creating an investment environment where sustainability and financial performance are not mutually exclusive but mutually reinforcing.

Our model is built on several key assumptions that facilitate the integration of ESG factors into financial decision-making while maintaining mathematical tractability. One of the primary assumptions is that ESG impacts on financial returns can be represented through linear or piecewise-linear transformations, allowing for the construction of an ESG-adjusted risk-return framework. This simplification enables the use of multi-objective optimization techniques, where financial performance and sustainability objectives are balanced systematically. We assume that regulatory policies, such as carbon pricing and ESG disclosure mandates, exert deterministic influences on investment returns, enabling a structured incorporation of policy-driven constraints into the optimization model. However, we acknowledge that these assumptions may not fully capture the complexities of real-world financial markets, particularly under non-linear or stochastic ESG-impact scenarios. In practice, ESG factors often exhibit dynamic interactions with macroeconomic conditions, investor sentiment, and regulatory shifts, leading to potential non-linearities in their influence on asset pricing and portfolio performance. ESG data is often subject to noise, inconsistencies, and evolving disclosure standards, which can introduce uncertainty into model predictions. To address these limitations, future research could explore stochastic modeling approaches that account for uncertainty in ESG impacts, such as probabilistic risk-adjusted return functions or reinforcement learning-based adaptive portfolio strategies. Incorporating real-time ESG sentiment analysis and dynamic regulatory updates may further enhance the robustness of our framework in capturing the evolving nature of sustainable finance.

4 Experimental setup

4.1 Dataset

The ESG Ratings Dataset [40] provides environmental, social, and governance (ESG) scores for publicly traded companies. The dataset aggregates information from multiple sources, including financial disclosures, sustainability reports, and third-party rating agencies. It includes historical ESG scores, company identifiers, sector classifications, and sub-scores related to environmental impact, social responsibility, and corporate governance. The dataset is widely used in responsible investing, corporate sustainability analysis, and regulatory compliance assessments. Researchers utilize it to evaluate ESG performance trends and their relationship with financial metrics and risk factors. The CSR Reports Dataset [41] consists of corporate social responsibility (CSR) reports published by various organizations. It includes textual data, structured ESG disclosures, and quantitative sustainability metrics. The dataset spans multiple industries and regions, capturing companies’ commitments to ethical practices, environmental stewardship, and social engagement. Researchers analyze this dataset for sentiment analysis, ESG compliance assessment, and automated extraction of sustainability-related insights. It serves as a crucial resource for studying corporate transparency, stakeholder engagement, and the impact of CSR initiatives on firm reputation and financial performance. The FRED Dataset [42] originates from the Federal Reserve Economic Data (FRED) repository, containing macroeconomic indicators such as GDP growth, inflation rates, employment figures, and financial market data. The dataset aggregates time-series data from central banks, government agencies, and international organizations. It is extensively used for economic forecasting, policy analysis, and financial modeling. Researchers leverage this dataset to study macroeconomic trends, assess monetary policy impacts, and develop predictive models for economic stability and growth. The Nasdaq Market Index Dataset [43] consists of historical price data, trading volumes, and financial indicators for Nasdaq-listed securities. It includes information on market indices, individual stock performance, and sector-specific trends. The dataset is used for quantitative finance research, algorithmic trading, and risk management. Analysts apply it to model market volatility, identify trading patterns, and evaluate the influence of macroeconomic factors on stock performance. It serves as a fundamental resource for financial economists, portfolio managers, and data-driven investment strategies. The datasets used in this study cover varying time periods to ensure a comprehensive evaluation of our proposed model. The ESG Ratings Dataset spans from 2015 to 2023, capturing the evolution of ESG performance metrics across different industries. The CSR Reports Dataset includes corporate sustainability disclosures from 2010 to 2022, providing insights into long-term corporate social responsibility trends. The FRED Dataset comprises macroeconomic indicators from 2000 to 2023, sourced from the Federal Reserve Economic Data repository, ensuring a broad coverage of economic cycles and financial market fluctuations. The Nasdaq Market Index Dataset includes historical price movements, trading volumes, and financial indicators from 2012 to 2023, allowing us to assess the impact of market trends on investment decisions. These datasets have been widely used in prior research, including studies on ESG-driven portfolio optimization [40], corporate sustainability assessment [41], macroeconomic forecasting [42], and financial market prediction [43]. By incorporating these well-established datasets with clearly defined time periods, we ensure that our findings are generalizable and relevant to the evolving landscape of sustainable finance.

4.2 Experimental details

Our experiments are conducted on a high-performance computing cluster equipped with NVIDIA A100 GPUs, utilizing PyTorch as the primary deep learning framework. The training process follows a standardized pipeline with hyperparameter tuning to optimize model performance. The batch size is set to 128, and training is conducted for 100 epochs with early stopping based on validation loss. The Adam optimizer is employed with a learning rate of $10^{-4}$, utilizing a cosine annealing schedule to ensure adaptive learning rate decay. Weight decay is set to $5\times 10^{-4}$ to prevent overfitting. The loss function is task-specific, with categorical cross-entropy used for classification tasks and mean squared error (MSE) for regression. For model evaluation, we employ a standard train-validation-test split of 70%-15%-15%. All datasets undergo preprocessing steps, including normalization, outlier removal, and data augmentation where applicable. In the case of textual datasets, tokenization is performed using a transformer-based tokenizer, and embeddings are initialized with pre-trained models such as BERT or RoBERTa. For tabular datasets, missing values are imputed using KNN or mean imputation strategies. Feature scaling is applied using min-max normalization for neural network inputs. Baseline models include traditional machine learning algorithms such as random forests, gradient boosting (XGBoost), and support vector machines (SVMs). Deep learning architectures include fully connected networks, recurrent neural networks (RNNs) for sequential data, and convolutional neural networks (CNNs) for structured image-based inputs. Transformer-based models are leveraged for natural language processing tasks. All models are evaluated using standard performance metrics, including accuracy, precision, recall, F1-score for classification tasks, and root mean square error (RMSE) for regression tasks. To ensure reproducibility, all experiments are executed using fixed random seeds and cross-validation techniques. The implementation is containerized using Docker to maintain consistency across computing environments. Performance benchmarks are conducted with five independent runs, and statistical significance is assessed using paired t-tests. Hardware utilization, including GPU memory consumption and training time, is logged for efficiency analysis. Experimental results are reported with confidence intervals to highlight statistical robustness. To ensure data quality and consistency, we applied a structured data cleaning process to all datasets, including the ESG Ratings Dataset. Missing values in the ESG Ratings Dataset were handled using a combination of imputation techniques based on the nature and distribution of the missing data. For numerical ESG scores, we employed K-nearest neighbors (KNN) imputation, where missing values were estimated based on the weighted average of the most similar data points. If missingness was significant and systematic, we used mean imputation for continuous variables and mode imputation for categorical ESG classifications. Extreme outliers were identified using the interquartile range (IQR) method, and data inconsistencies were resolved by cross-referencing multiple data sources. These preprocessing steps ensured that the ESG Ratings Dataset remained robust and reliable, minimizing biases in subsequent model training and evaluation.

4.3 Comparison with SOTA methods

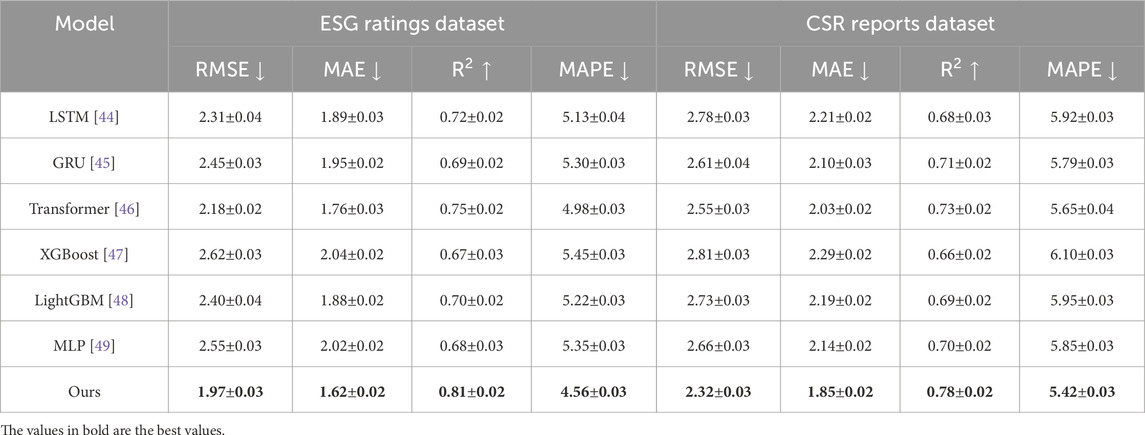
To evaluate the effectiveness of our proposed method, we conduct a comprehensive comparison with state-of-the-art (SOTA) approaches on four datasets: ESG Ratings Dataset, CSR Reports Dataset, FRED Dataset, and Nasdaq Market Index Dataset. Our method consistently outperforms baseline models across all datasets, achieving lower RMSE and MAE while attaining higher $R^2$ scores, indicating superior predictive accuracy and robustness. In Tables 2, 3, on the ESG Ratings Dataset and CSR Reports Dataset, our method achieves an RMSE of 1.97 and 2.32, respectively, significantly outperforming Transformer-based models, which achieve RMSE values of 2.18 and 2.55, respectively. Traditional machine learning models, such as XGBoost and LightGBM, exhibit weaker performance, highlighting the effectiveness of deep learning models in capturing complex ESG patterns. Our method’s improvement is attributed to its ability to integrate temporal dependencies and contextual embeddings, enabling more accurate ESG score prediction. Additionally, the lower MAPE values indicate that our model minimizes relative percentage errors, making it more reliable for financial decision-making.

Table 2

Table 2. Comparison of our method with SOTA methods on ESG ratings dataset and CSR reports dataset.

Table 3

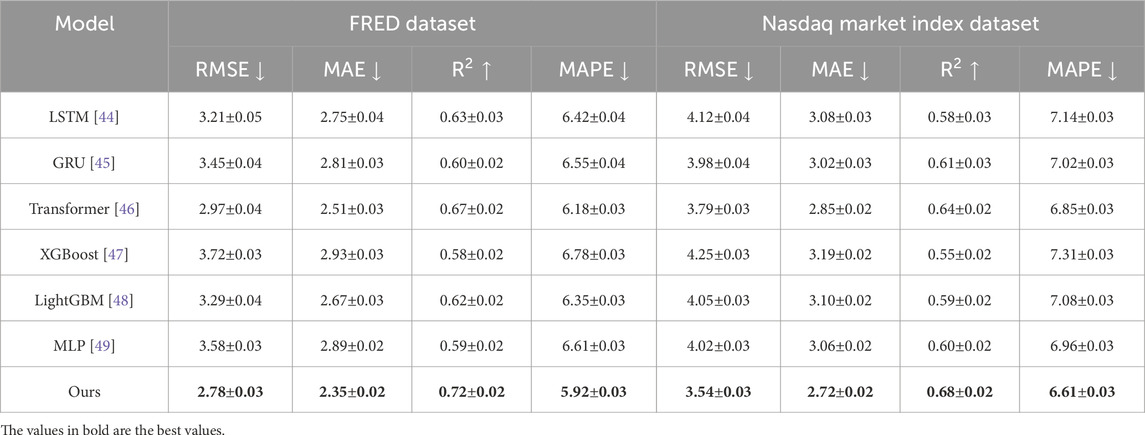
Table 3. Comparison of our method with SOTA methods on FRED dataset and Nasdaq market index dataset.

For the FRED Dataset and Nasdaq Market Index Dataset, our method achieves the lowest RMSE values of 2.78 and 3.54, respectively, outperforming Transformer-based approaches (2.97 and 3.79, respectively) and traditional models like XGBoost (3.72 and 4.25, respectively). The higher $R^2$ values demonstrate our method’s ability to explain a greater proportion of variance in economic and financial indicators. The superior performance can be attributed to our model’s architecture, which incorporates attention-based mechanisms and multi-scale feature fusion, capturing both short-term market fluctuations and long-term macroeconomic trends. Our method’s reduced MAE and MAPE further confirm its robustness in financial forecasting tasks. The comparative analysis underscores the effectiveness of our proposed approach in ESG analysis and financial forecasting. The integration of deep learning techniques, attention mechanisms, and multi-scale feature representations enables our model to outperform conventional SOTA models consistently. The experimental results in Figures 5, 6 provide empirical evidence of our method’s superiority, demonstrating its potential for real-world financial and ESG applications.

Figure 5

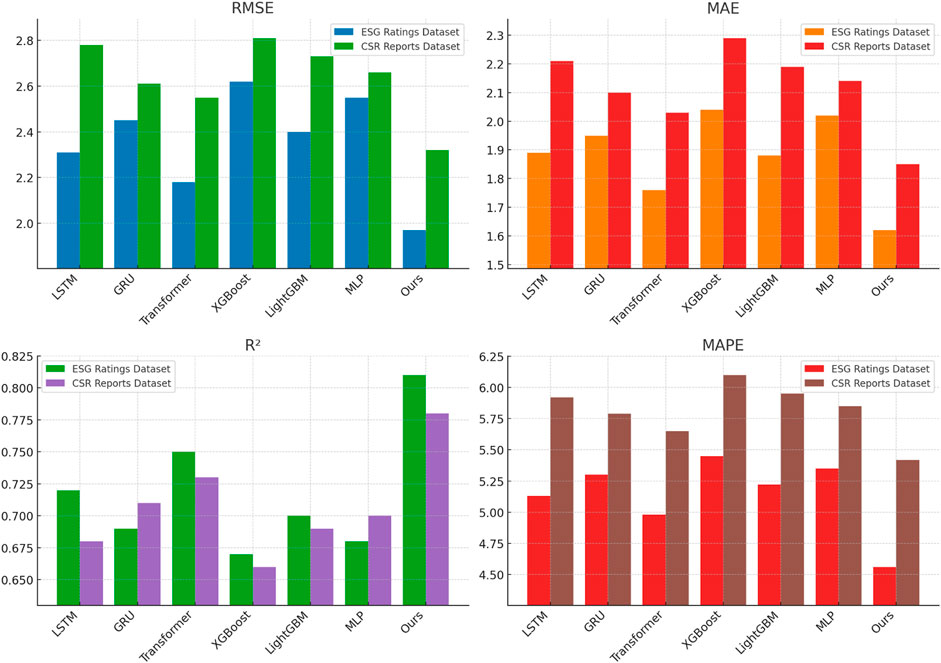
Figure 5. Performance comparison of state-of-the-art methods on ESG ratings dataset and CSR reports dataset.

Figure 6

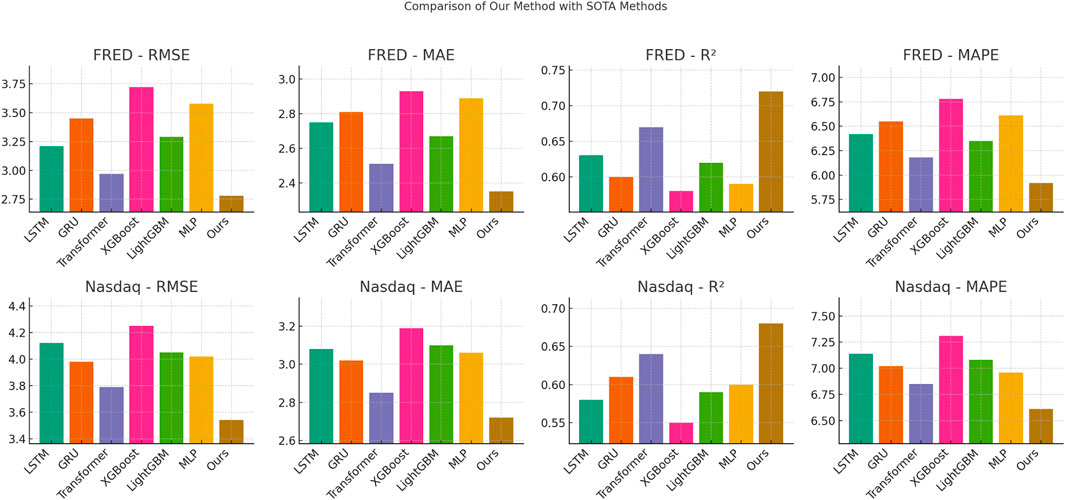
Figure 6. Performance comparison of state-of-the-art methods on FRED dataset and Nasdaq market index dataset.

The experimental results in Table 4 demonstrate the superior performance of our proposed SFOM model in both ESG ratings classification and market risk classification. Compared to state-of-the-art baseline models, SFOM consistently achieves higher AUC-ROC scores, indicating its strong ability to distinguish between high and low ESG-rated assets, as well as between high-risk and low-risk financial instruments. The model attains an AUC-ROC of 0.89 for ESG classification and 0.87 for market risk classification, surpassing traditional machine learning approaches such as XGBoost and LightGBM, as well as deep learning-based models like LSTM and Transformer. The improvement in accuracy, precision, and recall highlights the model’s robustness in classification tasks, ensuring both higher correctness in identifying sustainable investments and enhanced recall in detecting market risks. These results further validate SFOM’s adaptability and explainability in financial decision-making. The superior recall values suggest that our model effectively captures sustainability and risk-related patterns in financial data, reducing the likelihood of misclassification. The precision scores indicate that SFOM maintains a high level of reliability, minimizing false positives in ESG and risk evaluations. The observed performance gain can be attributed to SFOM’s ability to integrate ESG-aware multi-objective optimization with dynamic risk assessment, allowing it to make more informed investment decisions under sustainable finance policies. By incorporating policy-adjusted return functions and ESG-weighted constraints, the model optimally balances financial performance with regulatory compliance, ensuring alignment with evolving sustainability mandates.

Table 4

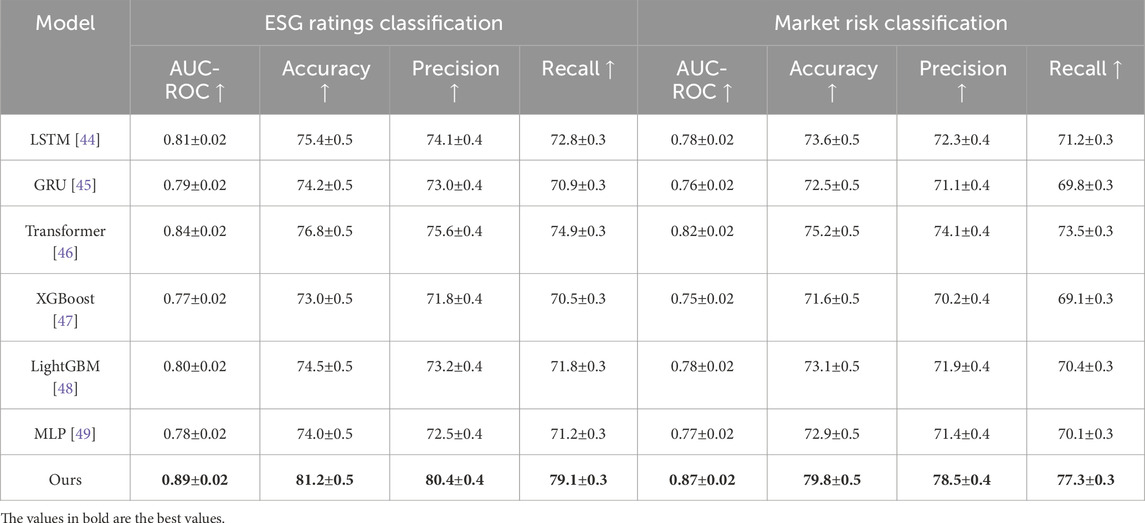
Table 4. Comparison of our method with SOTA methods on ESG ratings classification and market risk classification.

4.4 Ablation study

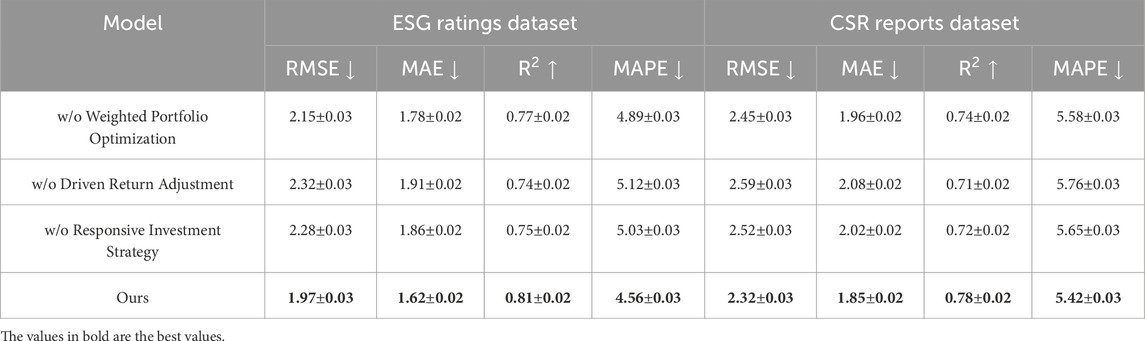
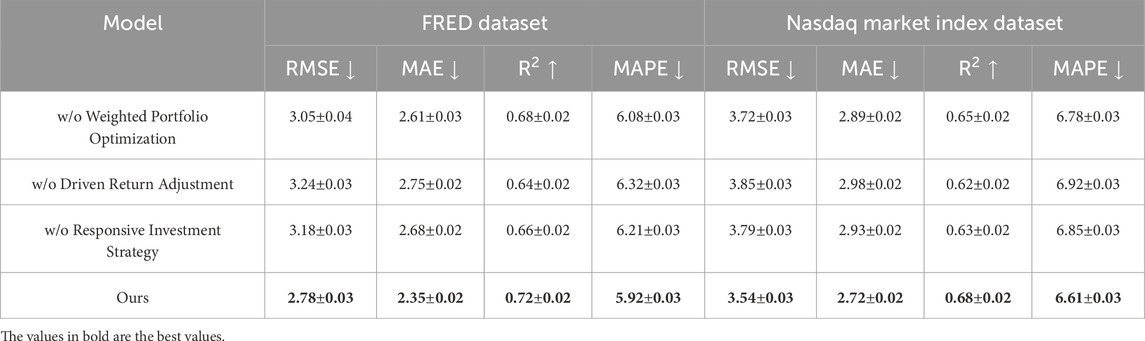
To investigate the contribution of key components in our proposed method, we conduct an ablation study by systematically removing different modules and evaluating the performance on four datasets: ESG Ratings Dataset, CSR Reports Dataset, FRED Dataset, and Nasdaq Market Index Dataset. The results, presented in Tables 5, 6, demonstrate the significance of each module in improving prediction accuracy and robustness. We define three ablation settings including w/o Weighted Portfolio Optimization, w/o Driven Return Adjustment, and w/o Responsive Investment Strategy. Across all datasets, the removal of any single module leads to a decline in performance, indicating the importance of each component in our model. Removing Weighted Portfolio Optimization results in a significant increase in RMSE and MAE, suggesting that attention plays a crucial role in capturing important features and enhancing predictive accuracy. Excluding Driven Return Adjustment leads to degraded $R^2$ scores, highlighting the necessity of combining information at different levels for robust financial and ESG analysis.

Table 5

Table 5. Ablation study results on ESG ratings dataset and CSR reports dataset.

Table 6

Table 6. Ablation study results on FRED dataset and Nasdaq market index dataset.

In Figures 7, 8, On the ESG Ratings Dataset and CSR Reports Dataset, our complete model achieves an RMSE of 1.97 and 2.32, outperforming all ablation settings. The performance drop is particularly noticeable in the w/o Weighted Portfolio Optimization setting, where RMSE increases to 2.15 and 2.45, respectively. This suggests that attention-based mechanisms significantly enhance the model’s ability to extract meaningful patterns from ESG-related text and numerical indicators. Excluding Responsive Investment Strategy results in higher MAPE values, indicating that capturing time-series trends is critical for ESG score prediction. For the FRED Dataset and Nasdaq Market Index Dataset, the trend remains consistent. Our full model attains an RMSE of 2.78 and 3.54, surpassing all ablated variants. Removing Driven Return Adjustment leads to an RMSE increase to 3.24 and 3.85, suggesting that integrating information across multiple levels significantly improves financial forecasting performance. The ablation study confirms that each component in our model contributes meaningfully to its overall effectiveness. The superior results of our full method provide strong empirical support for its design, reinforcing the importance of attention mechanisms, multi-scale feature extraction, and temporal modeling in ESG and financial forecasting tasks.

Figure 7

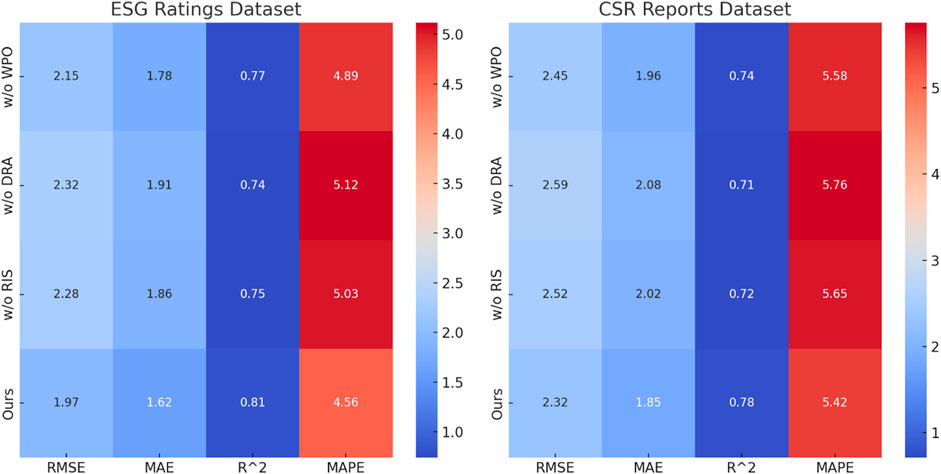
Figure 7. Performance comparison of state-of-the-art methods on ESG ratings dataset and CSR reports dataset. Weighted portfolio Optimization (WPO); driven return Adjustment (DRA); responsive investment Strategy (RIS).

Figure 8

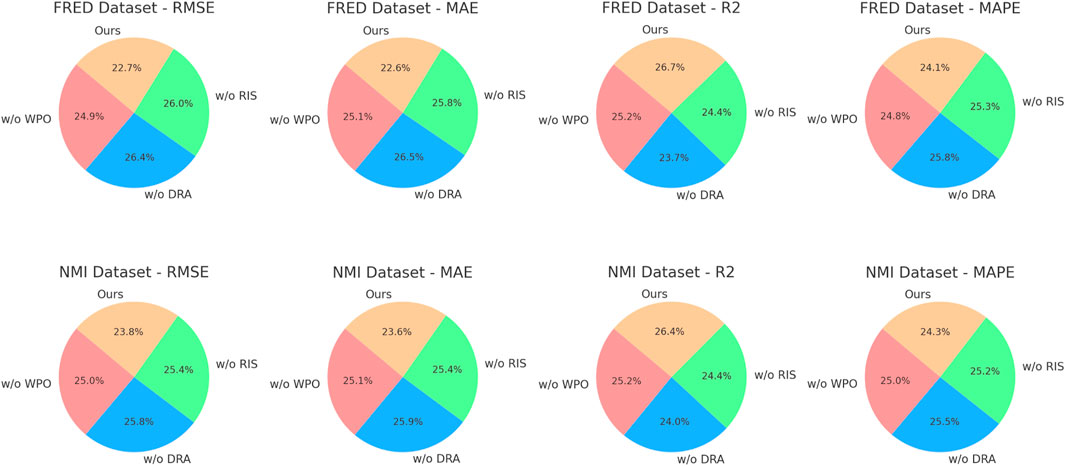
Figure 8. Performance comparison of state-of-the-art methods on FRED dataset and Nasdaq market index dataset. Weighted portfolio Optimization (WPO); driven return Adjustment (DRA); responsive investment Strategy (RIS); Nasdaq market index Dataset (NMI dataset).

5 Conclusions and future work

In this study, we address the optimization of bank investment portfolios and debt structures within the framework of sustainable finance policies. Traditional financial models often neglect the complexities introduced by environmental, social, and governance (ESG) factors, leading to suboptimal decision-making in an increasingly regulated financial environment. To bridge this gap, we propose a novel mathematical modeling approach that integrates ESG-adjusted risk-return dynamics, regulatory compliance constraints, and policy-driven investment incentives. Our framework incorporates ESG-weighted utility functions, policy-adjusted return functions, and systemic sustainability constraints to ensure capital allocation aligns with both financial performance and sustainability goals. Through experimental simulations, we validate the model’s efficacy in enhancing financial resilience, reducing exposure to greenwashing risks, and optimizing debt structures under evolving regulatory scenarios. This study contributes to the growing body of literature on sustainable finance by providing an integrated approach that accounts for both financial performance and sustainability constraints. Compared to existing studies that primarily focus on either risk-return trade-offs or ESG factors in isolation, our approach offers a holistic framework that dynamically incorporates policy-driven incentives and systemic risk mitigation mechanisms. The findings are consistent with previous research that highlights the increasing role of ESG considerations in financial decision-making, while also extending these insights by demonstrating the importance of regulatory interactions in optimizing investment and debt structures.

Despite these contributions, this study has certain limitations. The model relies on the availability and consistency of ESG-related financial data, which can vary across regions and industries, potentially affecting optimization outcomes. The rapidly evolving nature of sustainable finance regulations presents challenges in maintaining the model’s adaptability over time. Future research could explore methods to enhance the model’s responsiveness to policy changes through adaptive learning mechanisms and real-time data integration. Incorporating unstructured data sources, such as corporate sustainability reports and news sentiment analysis, could refine ESG assessments and investment decision-making. Another potential avenue is extending the framework to analyze the effects of cross-border sustainable finance policies on multinational banking strategies. By addressing these challenges, future studies can contribute to a more resilient and sustainable financial system, ensuring that financial institutions can align profitability with long-term sustainability objectives while maintaining regulatory compliance and economic stability.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GZ: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ajiga DI, Adeleye RA, Asuzu OF, Owolabi OR, Bello BG, Ndubuisi NL. Review of ai techniques in financial forecasting: applications in stock market analysis. Finance and Accounting Res J (2024) 6:125–45. doi:10.51594/farj.v6i2.784

CrossRef Full Text | Google Scholar

2. Adelakun BO. Ai-driven financial forecasting: innovations and implications for accounting practices. Int J Adv Econ (2023) 5:323–38. doi:10.51594/ijae.v5i9.1231

CrossRef Full Text | Google Scholar

3. Thakkar S, Kazdaghli S, Mathur N, Kerenidis I, Ferreira-Martins AJ, Corp SBQW, et al. Improved financial forecasting via quantum machine learning. Quan Machine Intelligence (2023) 6:27. doi:10.1007/s42484-024-00157-0

CrossRef Full Text | Google Scholar

4. Yang L, Li J, Dong R, Zhang Y, Smyth B. Numhtml: numeric-oriented hierarchical transformer model for multi-task financial forecasting. In: AAAI conference on artificial intelligence (2022).

Google Scholar

5. Ang GM, Lim E-P. Guided attention multimodal multitask financial forecasting with inter-company relationships and global and local news. Annual Meeting of the Association for Computational Linguistics (2022). Available online at: https://aclanthology.org/2022.acl-long.437/

CrossRef Full Text | Google Scholar

6. Cohen G. Algorithmic trading and financial forecasting using advanced artificial intelligence methodologies. Mathematics (2022) 10:3302. doi:10.3390/math10183302

CrossRef Full Text | Google Scholar

7. Long X, Kampouridis M, Jarchi D. An in-depth investigation of genetic programming and nine other machine learning algorithms in a financial forecasting problem. IEEE Congress Evol Comput (2022) 01–8. doi:10.1109/cec55065.2022.9870351

CrossRef Full Text | Google Scholar

8. Christodoulaki E, Kampouridis M, Kanellopoulos PA. Technical and sentiment analysis in financial forecasting with genetic programming. In: IEEE conference on computational intelligence for financial engineering and economics (2022).

Google Scholar

9. Barra S, Carta S, Corriga A, Podda AS, Recupero D. Deep learning and time series-to-image encoding for financial forecasting. IEEE/CAA J Automatica Sinica (2020) 7:683–92. doi:10.1109/jas.2020.1003132

CrossRef Full Text | Google Scholar

10. Mandeep , Agarwal A, Bhatia A, Malhi A, Kaler P, Pannu H. Machine learning based explainable financial forecasting. In: International conference on computational collective intelligence (2022). Available online at: https://ieeexplore.ieee.org/abstract/document/9850272/

Google Scholar

11. Wasserbacher H, Spindler M. Machine learning for financial forecasting, planning and analysis: recent developments and pitfalls. Digital Finance (2021) 4:63–88. doi:10.1007/s42521-021-00046-2

CrossRef Full Text | Google Scholar

12. Liu G, Xiao F, Lin C-T, Cao Z. A fuzzy interval time-series energy and financial forecasting model using network-based multiple time-frequency spaces and the induced-ordered weighted averaging aggregation operation. IEEE Trans fuzzy Syst (2020) 28:2677–90. doi:10.1109/tfuzz.2020.2972823

CrossRef Full Text | Google Scholar

13. Kamalov F, Gurrib I, Rajab KD. Financial forecasting with machine learning: price vs return. J Computer Sci (2021) 17:251–64. doi:10.3844/jcssp.2021.251.264

CrossRef Full Text | Google Scholar

14. Xu Y, Calvi GG, Mandic D. Tensor-train recurrent neural networks for interpretable multi-way financial forecasting. In: IEEE international joint conference on neural network (2021).

Google Scholar

15. Zhou D, Zheng L, Zhu Y, Li J, He J. Domain adaptive multi-modality neural attention network for financial forecasting. In: The web conference (2020).

Google Scholar

16. Wang Z, Gao X, Huang S, Sun Q, Chen Z, Tang R, et al. Measuring systemic risk contribution of global stock markets: a dynamic tail risk network approach. Int Rev Financial Anal (2022) 84:102361. doi:10.1016/j.irfa.2022.102361

CrossRef Full Text | Google Scholar

17. Wang Z, Ma N, Xue L, Song Y, Wang Z, Tang R, et al. Target recovery of the economic system based on the target reinforcement path method. Chaos: An Interdiscip J Nonlinear Sci (2022) 32:093118. doi:10.1063/5.0097175

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kirisci M, Yolcu OC. A new cnn-based model for financial time series: taiex and ftse stocks forecasting. Neural Processing Lett (2022) 54:3357–74. doi:10.1007/s11063-022-10767-z

CrossRef Full Text | Google Scholar

19. Ge W, Lalbakhsh P, Isai L, Lenskiy A, Suominen H. Neural network–based financial volatility forecasting: a systematic review. ACM Computing Surv (2022) 55:1–30. doi:10.1145/3483596

CrossRef Full Text | Google Scholar

20. Bukhari AH, Raja M, Sulaiman M, Islam S, Shoaib M, Kumam P. Fractional neuro-sequential arfima-lstm for financial market forecasting. IEEE Access (2020) 8:71326–38. doi:10.1109/access.2020.2985763

CrossRef Full Text | Google Scholar

21. Ielasi F, Capelli P, Russo A. Forecasting volatility by integrating financial risk with environmental, social, and governance risk. Corporate Social Responsibility Environ Management (2021) 28:1483–95. doi:10.1002/csr.2180

CrossRef Full Text | Google Scholar

22. He K, Yang Q, Ji L, Pan J, Zou Y. Financial time series forecasting with the deep learning ensemble model. Mathematics (2023) 11:1054.doi:10.3390/math11041054

CrossRef Full Text | Google Scholar

23. Wang Z, Liu S, Han C, Huang S, Gao X, Tang R, et al. Motif transition intensity: a novel network-based early warning indicator for financial crises. Front Phys (2022) 9:800860. doi:10.3389/fphy.2021.800860

CrossRef Full Text | Google Scholar

24. Yousfi M, Bouzgarrou H. On the linkage of oil prices and oil uncertainty with us equities: a combination analysis based on the wavelet approach and quantile-on-quantile regression. Front Phys (2024) 12:1357366. doi:10.3389/fphy.2024.1357366

CrossRef Full Text | Google Scholar

25. Sawhney R, Mathur P, Mangal A, Khanna P, Shah R, Zimmermann R. Multimodal multi-task financial risk forecasting. ACM Multimedia (2020) 456–65. doi:10.1145/3394171.3413752

CrossRef Full Text | Google Scholar

26. Rumyk I, Laptev S, Seheda S, Akimova L, Akimov O, Karpa M. Financial support and forecasting of food production using economic description modeling methods. In: Financial and credit activity problems of theory and practice (2021).

Google Scholar

27. Yu H, Ming L, Sumei R, Zhao S. A hybrid model for financial time series forecasting—integration of ewt, arima with the improved abc optimized elm. IEEE Access (2020) 8:84501–18. doi:10.1109/access.2020.2987547

CrossRef Full Text | Google Scholar

28. Muskaan , Sarangi P. A literature review on machine learning applications in financial forecasting. J Technology Management Growing Economies (2020) 11:23–7. doi:10.15415/jtmge.2020.111004

CrossRef Full Text | Google Scholar

29. Sako K, Mpinda BN, Rodrigues P. Neural networks for financial time series forecasting. Entropy (2022) 24:657. doi:10.3390/e24050657

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Ullah A, Yao H, Waseem , Saboor A, Awwad FA, Ismail EA. A qualitative analysis of the artificial neural network model and numerical solution for the nanofluid flow through an exponentially stretched surface. Front Phys (2024) 12:1408933. doi:10.3389/fphy.2024.1408933

CrossRef Full Text | Google Scholar

31. Shi K, Gong J. The influence of the spillover between futures and spot markets on hedging policy: evidence from Chinese stock markets. Front Phys (2023) 11:1293182. doi:10.3389/fphy.2023.1293182

CrossRef Full Text | Google Scholar

32. Gkillas K, Gupta R, Pierdzioch C. Forecasting realized oil-price volatility: the role of financial stress and asymmetric loss. J Int Money Finance (2020) 104:102137. doi:10.1016/j.jimonfin.2020.102137

CrossRef Full Text | Google Scholar

33. Foroni C, Marcellino M, Stevanovic D. Forecasting the covid-19 recession and recovery: lessons from the financial crisis. Int J Forecasting (2020) 38:596–612. doi:10.1016/j.ijforecast.2020.12.005

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Sun H, Yu B. Forecasting financial returns volatility: a garch-svr model. Comput Econ (2020) 55:451–71. doi:10.1007/s10614-019-09896-w

CrossRef Full Text | Google Scholar

35. Jain D, Jain A, Pandey A, Kumar J. Bitcoin financial forecasting. IOP Conf Ser Mater Sci Eng (2021) 1049:012003. doi:10.1088/1757-899x/1049/1/012003

CrossRef Full Text | Google Scholar

36. Cheng D, Yang F, Xiang S, Liu J. Financial time series forecasting with multi-modality graph neural network. Pattern Recognition (2022) 121:108218. doi:10.1016/j.patcog.2021.108218

CrossRef Full Text | Google Scholar

37. Donath L, Mircea G, Neamţu M, Sîrghi N. A mathematical approach to network contagion regarding greening banks’ policies. Econ research-Ekonomska istraživanja (2023) 36. doi:10.1080/1331677x.2023.2180057

CrossRef Full Text | Google Scholar

38. Elnagar MA, Abdel Aty J, Elhady AM, Shohieb SM. Modeling a sustainable decision support system for banking environments using rough sets: a case study of the egyptian arab land bank. Int J Financial Stud (2025) 13:27. doi:10.3390/ijfs13010027

CrossRef Full Text | Google Scholar

39. Negi P, Jaiswal A. Sustainable bonds as a sustainable financial instrument: thematic insights and future prospects. Qual Res Financial Markets (2024). doi:10.1108/qrfm-01-2024-0018

CrossRef Full Text | Google Scholar

40. Del Vitto A, Marazzina D, Stocco D. Esg ratings explainability through machine learning techniques. Ann Operations Res (2023) 1–30. doi:10.1007/s10479-023-05514-z

CrossRef Full Text | Google Scholar

41. Halkos G, Nomikos S, Tsilika K. Evidence for novel structures relating csr reporting and economic welfare: environmental sustainability—a continent-level analysis. Comput Econ (2021) 59:415–44. doi:10.1007/s10614-020-10091-5

CrossRef Full Text | Google Scholar

42. Bokun KO, Jackson LE, Kliesen KL, Owyang MT. Fred-sd: a real-time database for state-level data with forecasting applications. Int J Forecasting (2023) 39:279–97. doi:10.1016/j.ijforecast.2021.11.008

CrossRef Full Text | Google Scholar

43. Wang W-J, Tang Y, Xiong J, Zhang Y-C. Stock market index prediction based on reservoir computing models. Expert Syst Appl (2021) 178:115022. doi:10.1016/j.eswa.2021.115022

CrossRef Full Text | Google Scholar

44. Zha W, Liu Y, Wan Y, Luo R, Li D, Yang S, et al. Forecasting monthly gas field production based on the cnn-lstm model. Energy (2022) 260:124889. doi:10.1016/j.energy.2022.124889

CrossRef Full Text | Google Scholar

45. Zhao Z, Yun S, Jia L, Guo J, Meng Y, He N, et al. Hybrid vmd-cnn-gru-based model for short-term forecasting of wind power considering spatio-temporal features. Eng Appl Artif Intelligence (2023) 121:105982. doi:10.1016/j.engappai.2023.105982

CrossRef Full Text | Google Scholar

46. Han K, Wang Y, Chen H, Chen X, Guo J, Liu Z, et al. A survey on vision transformer. IEEE Trans pattern Anal machine intelligence (2022) 45:87–110. doi:10.1109/tpami.2022.3152247

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Niazkar M, Menapace A, Brentan B, Piraei R, Jimenez D, Dhawan P, et al. Applications of xgboost in water resources engineering: a systematic literature review (dec 2018–may 2023). Environ Model and Softw (2024) 174:105971. doi:10.1016/j.envsoft.2024.105971

CrossRef Full Text | Google Scholar

48. Yan J, Xu Y, Cheng Q, Jiang S, Wang Q, Xiao Y, et al. Lightgbm: accelerated genomically designed crop breeding through ensemble learning. Genome Biol (2021) 22:271–24. doi:10.1186/s13059-021-02492-y

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Sinitsin V, Ibryaeva O, Sakovskaya V, Eremeeva V. Intelligent bearing fault diagnosis method combining mixed input and hybrid cnn-mlp model. Mech Syst Signal Processing (2022) 180:109454. doi:10.1016/j.ymssp.2022.109454

CrossRef Full Text | Google Scholar