Assessing carbon footprint and performance of the Kalman filter track fitter in the CBM experiment

The CBM experiment at FAIR (GSI, Germany) is among the most significant upcoming projects in heavy-ion physics. It is designed to investigate the properties of dense baryonic matter under extreme conditions. A key feature of the experiment is the high interaction rate, reaching up to $10^7$ collisions per second, resulting in the production of substantial volumes of experimental data that must be processed and analyzed in real time. To meet this computational challenge, the CBM experiment employs a high-performance tracking algorithm based on the Cellular Automaton for track finding and the Kalman Filter for track fitting. The algorithm is designed for efficient parallel execution on modern multicore and GPU architectures. We evaluate the performance and energy efficiency of the Kalman Filter-based fitting algorithm on both CPUs and GPUs. The GPU implementation demonstrates up to a threefold improvement in energy efficiency, resulting in a proportional reduction in power consumption and associated CO₂ emissions during data processing. These results highlight the significance of energy-efficient computing in high-rate heavy-ion experiments. The analysis provides a quantitative estimate of the carbon footprint associated with track reconstruction and demonstrates how hardware choices influence overall emissions in large-scale data processing workflows.

1 Introduction

Heavy-ion physics central a pivotal role in advancing our understanding of the fundamental properties of matter under extreme conditions. By studying collisions of heavy ions at high energies, researchers probe the behavior of quark-gluon plasma, a state of matter believed to have existed just moments after the Big Bang. These experiments help uncover the forces and interactions between the most basic constituents of matter, providing insight into the early evolution of the universe and guiding our understanding of phase transitions in nuclear matter at unprecedented energy densities.

Experimental facilities, such as particle accelerators and complex detector systems, provide unique opportunities to study the properties of elementary particles and their interactions at extreme energies, conditions that cannot be replicated in low-energy laboratory environments.

Research on particle collisions began with relatively simple tasks that could be handled manually, such as reconstructing particle trajectories in bubble chambers. However, as knowledge and understanding of the complex aspects of matter and interactions grew, the need for more in-depth analysis and investigation of increasingly intricate systems arose. As the volume of experimental data expanded and the complexity of the questions to be addressed increased, the demands on data processing and analysis methods grew significantly.

Modern research in heavy-ion physics is associated with the need to process vast volumes of data generated from high-energy nuclear collisions. This requires not only high-performance computing systems but also advanced analysis methods and algorithms capable of efficiently processing data and extracting meaningful information. As the complexity of the tasks and the volume of data increase, the demands for speed and quality of computational processing become critically important for the successful execution of research and the achievement of new scientific discoveries.

The results of modern experiments in heavy-ion physics can no longer be efficiently processed on individual computers and require the resources of large computational centers. Data analysis necessitates dozens or even hundreds of high-performance processors (CPUs) and graphics accelerators (GPUs), integrated into computing clusters and equipped with powerful cooling systems. These computational systems are major consumers of electrical energy.

On the other hand, the issue of global warming presents the scientific community and industry with the significant challenge of conserving energy and reducing greenhouse gas emissions. The growing energy demands associated with large-scale computing systems are in conflict with the need to reduce the carbon footprint. In the context of global efforts to minimize climate impact, it is essential to explore and implement innovative approaches to improving the energy efficiency of computational infrastructures. In addition, attention must be paid to the efficient use of computational resources, both in terms of task distribution and optimization of the programs and algorithms themselves.

One of the key experiments in heavy-ion physics is the CBM (Compressed Baryonic Matter) [1] experiment, planned to take place at the FAIR accelerator (Facility for Antiproton and Ion Research). Its primary objective is to study the properties of strongly interacting matter at high net-baryon densities, aiming to explore the QCD phase diagram and the possible existence of a first-order phase transition and a critical point.

New experiments at FAIR are being developed with the latest trends in energy efficiency in mind. As part of this initiative, the Green IT Cube [2], an innovative computing infrastructure, was built specifically to minimize energy consumption and reduce the carbon footprint. Furthermore, the Goethe HLR (now upgraded to Goethe NHR) [3], a high-performance computing cluster, is available to support research projects. In the latest Green500 ranking from June 2024 [4], Goethe NHR holds the 17th position globally in terms of energy efficiency.

This work is dedicated to the study of the energy efficiency of an algorithm that plays a crucial role in particle collision reconstruction, the Kalman filter-based trajectory fitting algorithm [5]. It is interesting to note that this optimized algorithm has reduced the runtime of the original scalar algorithm by a significant factor of 120.000. Currently, this algorithm is actively used in large-scale heavy-ion physics experiments, such as ALICE at CERN and STAR at BNL, as well as in the track searching and analysis procedures of the future CBM experiment. The high efficiency of the algorithm for track fitting has previously been studied in Kisel and for CBM Collaboration [6], also investigating the scaling of the number of tracks fitted per time for different computing architectures.

2 Research

2.1 Algorithm

Charged particle trajectories reconstruction is one of the most important and complex stages of experimental data processing in heavy-ion physics. The reconstruction result is a set of measurements (hits) that form a curve line that corresponds to the track. At the same time, the physical analysis is based not on a set of hits, but on the trajectory parameters within the accepted track model (Figure 1a).

Figure 1

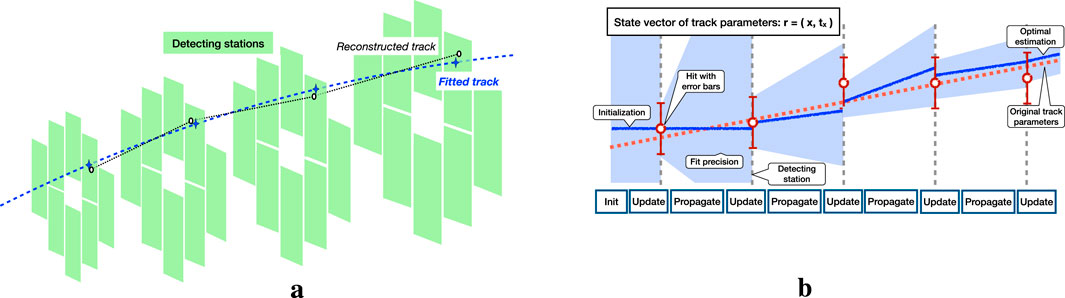
Figure 1. Illustration of the concept of track fitting (a) and an example of a straight track fitting (b). (a) Illustration of the concept of track fitting in a detector with forward geometry. (b) An example of a sequential workflow for fitting a simple straight [7].

The process of parameterizing the particle’s trajectory over a set of discrete measurements is called fitting. Depending on the specific task and the track model used, various algorithms can carry fitting from the simplest (approximation by a line, parabola, circle) to complex multistage algorithms, such as the Kalman Filter (KF). At present, KF is the most popular and frequently used recursive algorithm for estimating track parameters which makes it possible to efficiently calculate the track state vector even in the case of a small number of erroneously attached hits, as well as to make a decision about the correctness of finding the tracks as a whole.

The basic element of the algorithm is the state vector, which includes the track parameters determined by the selected track model. The covariance matrix corresponds to uncertainties and correlations related to the state vector.

After initialization of the parameters and elements of the covariance matrix, the further operation of the algorithm consists of subsequent extrapolation and filtering of the state vector. The extrapolation process is the transport of the state vector to the point of the next measurement, i.e., to the next detector station. Filtering or updating allows us to correct the state vector taking into account the added measurement and recalculate the covariance matrix, considering the predicted and real parameters of the trajectory at the current point (Figure 1b).

The KF track fitter under consideration makes it possible to fit three-dimensional tracks, taking into account additional physical effects that determine the trajectory of a charged particle, such as multiple scattering and a magnetic field. Thus, the algorithm allows one to parameterize a smooth line, which corresponds to the measured particle trajectory.

The KF offers a wide range of possibilities for the parallelization of computations, both on the data level and on the task level. The set of operations performed is the same for each track, but does not depend on third-party cross conditions or the results of processing other tracks. Computing scalability is limited only by the capabilities of the hardware.

One of the key requirements of the CBM experiment is the real-time data processing. This step is essential due to the vast volumes of raw data, which cannot be stored, and the filtering of interesting events requires their full reconstruction. The expected heavy-ion collision rate reaches 10 MHz, with preliminary estimates indicating up to 1,000 particles per event [8]. Therefore, to successfully carry out the experiment, the speed of the algorithms and the available computational power must be sufficient to reconstruct and fit up to $10^{10}$ particle trajectories per second.

Kalman Filter plays an important role in the process of track reconstruction and parameterization. Therefore, the speed of the fit has a significant impact on the overall event processing time, while its energy efficiency directly affects the overall energy consumption of the computations.

2.2 Setup and input data

The SIMD KF Track Fitter package was developed as a benchmark for evaluating the speed of the upgraded KF when using various computing equipment. While the standard KF requires double-precision calculations, the optimized algorithm [9] shows stable and correct results when working in the single-precision mode. This allows us to take full advantage of the built-in SIMD capabilities of modern CPUs. At the same time, the mutual independence of individual tasks provides almost unlimited scaling of calculations, effectively using the maximum available CPU or GPU threads.

SIMD intrinsics utilization is provided by using special header files or the Vector classes (Vc) [10] package. Any of the options allows one to quickly switch between different versions of instructions and perform calculations on registers of any length available on the device. Parallelization on the CPU is organized using the OpenMP API and Pthread to provide CPU affinity. Finally, GPU computing is done by using the OpenCL framework.

The test configuration corresponds to the STS detector [8] of the CBM experiment. The setup includes 7 planes of detecting stations installed one after another to operate in the fixed target mode. The test data is a set of individual tracks selected from central Au+Au collisions simulated with CbmRoot at the energy of 25 GeV per nucleon. A suitable track must be reconstructable and have one hit on each of the detecting stations.

The benchmark evaluates only the time of calculations related directly to the track fitting procedure. Time and overhead costs in preparing input data and saving results are not taken into account. Measuring the speed of computing on the CPU using OpenMP is carried out using the standard ROOT class TStopwatch, which makes it possible to get the difference in time between the start and end of calculations. The total execution time of the task is measured, which corresponds to the completion of the slowest thread. It is worth noting that the test data is prepared in such a way that each thread receives a full and equal load. When computing on the GPU, the OpenCL framework profiling methods are used, which allow us to get the start and end times of kernel calculations.

2.3 Computational resources

The study was conducted on the hybrid computing cluster Goethe NHR at Goethe University in Frankfurt, which is involved in the preparation work for the CBM experiment. Goethe NHR boasts a very good data center energy efficiency ratio, with a Power Usage Effectiveness ($PUE$, the ratio of total energy consumption to the energy consumption of the computational resources) of 1.076 at the time of the research, compared to traditional values for similarly sized data centers, which are typically around ∼1.56 [11]. Later, Goethe-NHR computing equipment was transferred to the GSI Green IT Cube with even higher energy efficiency PUE<1.07. Additionally, when calculating energy efficiency, the carbon intensity factor $CI$ was considered, which for Germany is approximately 380 $gC{O}_2/kWh$ according to data from Statista.com [12].

As part of the study, benchmarking was performed on both CPUs and GPUs. The CPU benchmarks were conducted on paired AMD EPYC 7742 processors, built on the Zen 2 architecture, each with 64 cores (128 threads) and a TDP (Thermal Design Power) of approximately 3.52 W per core. The GPU benchmarks were run on AMD MI210 graphics accelerators, which have a TDP of 300 W.

2.4 Methodology

As the foundation for our study, we selected the methodology for assessing the carbon footprint and energy efficiency of computational tasks presented in the article Green Algorithms: Quantifying the Carbon Emissions of Computation [13]. This methodology enables the calculation of the carbon footprint of computational operations based on parameters such as task execution time, the number of computational cores used (CPU or GPU), the amount of memory involved, and the energy efficiency of the data center where the computations are performed. The method offers a simple and universal approach to estimating the carbon emissions caused by computations, making it applicable to a wide range of tasks and hardware architectures.

For the calculation of energy consumption, the following formula is used:

$E=t\times \left(n_c\times P_c\times u_c+n_m\times P_m\right)\times PUE\times 0.001(1)$

where:

$•$ $E$ — energy consumption (kWh),

$•$ $t$ — task execution time (hours),

$•$ $n_c$ — number of computational cores,

$•$ $P_c$ — power consumed by one computational core (W),

$•$ $u_c$ — core utilization factor (from 0 to 1),

$•$ $n_m$ — amount of memory used (GB),

$•$ $P_m$ — power consumed by 1 gigabyte of memory (W),

$•$ $PUE$ — Power Usage Effectiveness of the data center.

After calculating the energy consumption, the carbon footprint of the task is determined. For this, the carbon intensity factor $CI$, which depends on the location and the methods of energy production, is used. The total carbon footprint $C$ (in grams of $C{O}_2$-equivalent) is calculated using the following formula:

$C=E\times CI(2)$

This methodology has several strengths. First, it is universal and applicable to many types of computations, from local servers to cloud solutions, making it useful for a wide range of users. Second, it accounts for important parameters, such as the energy efficiency of data centers and the carbon intensity of energy sources, allowing accurate and context-specific calculations.

When using this method for energy efficiency analysis, it is important to keep in mind certain assumptions. Energy consumption during CPU computations is calculated as the product of the number of cores used and the TDP of each core, in other words, $P_c$ from Equation 1 is taken as $TD{P}_{\mathit{core}}=TDP/N_{\mathit{cores}}$. This approach does not account for modern processor technologies that optimize core performance based on overall device load, which can lead to a slight underestimation of energy consumption when many cores are idle. Additionally, hyper-threading is not considered, and its energy impact can vary significantly depending on the task. On the other hand, if we assume that the processor is already using all available cores and has reached its maximum TDP, adding virtual threads should not affect energy consumption.

As for GPUs, the method assumes that the full TDP is used in the calculations, regardless of the device’s actual load. Consequently, the total energy consumption may be overestimated, except in cases where the GPU is operating under maximum load.

In Figure 2, the graphs illustrate the dependence of energy consumption on the utilization levels of both the AMD EPYC 7742 CPU and AMD MI210 GPU, used in this study. To evaluate the CPU power consumption characteristics (Figure 2a), we used both a theoretical estimate based on the number of cores (blue) used and real-world power consumption measurements (red) taken using a 1-phase power analyzer ZES Zimmer LMG95, which collects server power consumption information in real time. The results considered were obtained as the difference between the power consumption under load and the power consumption in idle mode.

Figure 2

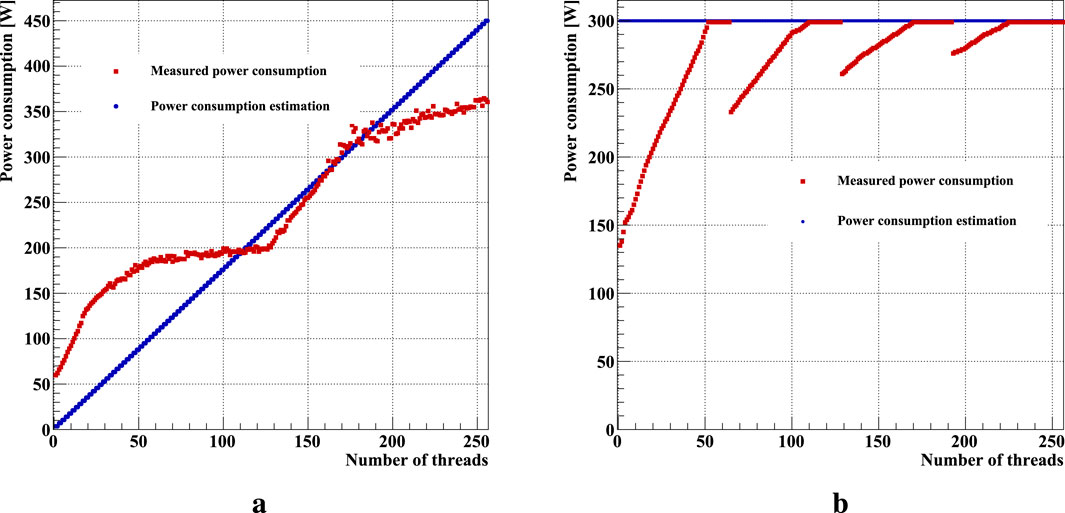
Figure 2. Power consumption of the (a) CPUs (2x AMD EPYC 7742) and (b) GPU (AMD MI210) depending on the model of the device utilization.

The actual power consumption of the CPU increases non-linearly with higher workloads. The observed behavior is largely determined by the specific characteristics of the processor and the server configuration. In the hardware setup under consideration, the power consumption curve for each CPU exhibits a distinctly convex structure, with a noticeable decline in the incremental power increase after utilizing half of the available cores (Figure 2). At the same time, performance gains remain at a high level, as shown in Figure 3a.

Figure 3

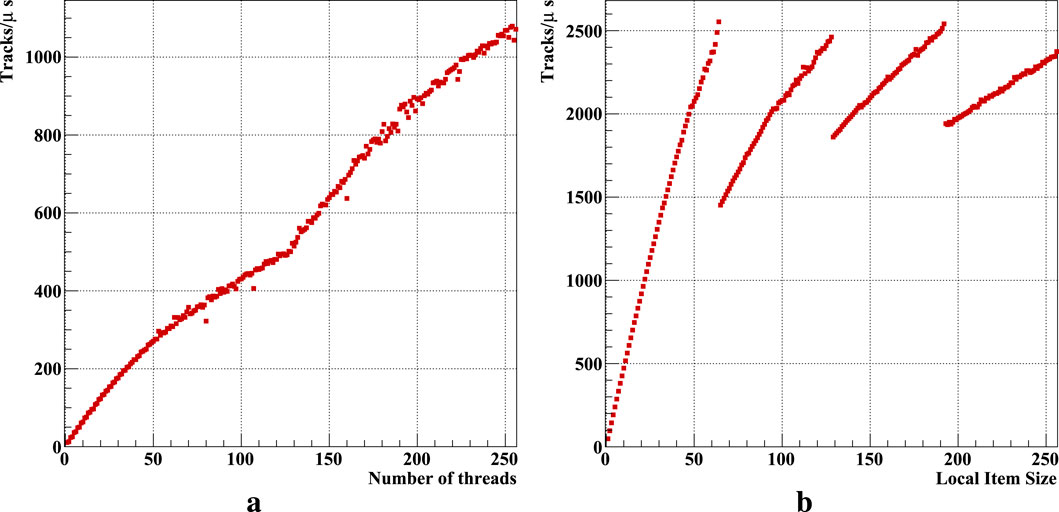
Figure 3. KF Track Fitter scalability measured on the (a) CPUs (2x AMD EPYC 7742) and (b) GPU (AMD MI210).

Since the measurements are conducted with CPU affinity enabled, the observed power consumption is not influenced by the use of virtual threads but is instead a characteristic of the CPU itself. The maximum power consumption of each processor does not reach the specified TDP value. Furthermore, it is worth mentioning that power consumption under low workloads is approximately 50 W higher than expected. This discrepancy is likely attributable to server settings that configure the CPUs and cooling system to maintain minimal energy usage during idle states.

GPU energy consumption was monitored directly during algorithm execution using the rocm-smi utility, part of the AMD ROCm software platform. The graph shown in Figure 2b illustrates the dependence of GPU energy consumption during computations on the selected local item size, which corresponds to the device’s load level. Even when using only one thread per block on the GPU, the device’s power consumption approaches almost half of its full TDP, amounting to 136 W. Idle unused threads still consume energy despite the absence of actual computations. Peak power consumption is reached at an incomplete but sufficiently high level of device utilization and eventually plateaus.

The authors of Green Algorithm offer an energy efficiency assessment of algorithms through either a dedicated website or a console application, which runs on a server and directly interacts with the task scheduler. This approach is primarily aimed at analyzing large-scale tasks with execution times measured in hours. In contrast, the KF Track Fitter is an ultra-fast algorithm, where its speed is defined not by the execution time of a single task, but by the number of tasks completed per unit of time. For this reason, modifications were made to the measurement methodology to evaluate the energy consumption for fitting a specific number of tracks. Additionally, due to the algorithm’s wide range of parallelization settings, the effect of these configurations on the final performance metrics was assessed. To account for this, a new factor, $k/N$, is introduced into Equation 1, where $k$ is the number of tracks for energy consumption evaluation, and $N$ is the total number of tracks processed per unit of time.

3 Results and discussion

The Kalman Filter Track Fitter benchmark provides numerous options for launching parallel computations, allowing researchers to explore the algorithm’s performance on various hardware configurations. Vectorized computations are available using all major instruction sets of modern Intel processors: scalar (32-bit, 1 floating point variable), SSE (128-bit, 4 floating point variables), AVX2 (256-bit, 8 floating point variables), and AVX512 (512-bit, 16 floating point variables). Each instruction set has its own characteristics in terms of its impact on CPU energy consumption. However, in our study the testing was primarily conducted using the AVX2 instruction set, as it is the most advanced in terms of vectorization efficiency available on the AMD EPYC CPUs.

Parallel computations are implemented using the OpenMP standard. The program is executed sequentially with varying numbers of threads, ranging from 1 up to 2 CPUs $\times$ 64 cores $\times$ 2 threads = 256 threads. Computational threads are pinned to cores according to the CPU topology, ensuring that the primary and hyper-threading threads of each core are utilized sequentially. Task distribution is done statically with a step size of 1,000 tracks, while the total number of tracks is a multiple of 1,000. This eliminates overhead associated with task distribution in the given context. As a result, we obtain the algorithm’s performance, expressed as the number of tracks fitted per unit of time.

The computations on the GPU are implemented using the OpenCL framework, with optimization for local memory utilization for the most frequently accessed variables. The program is executed with various local item size values, ranging from 1 to 256. Using more threads per block is considered impractical, as the optimal block size for AMD GPUs is 64 elements, and the chosen configurations will allow a full assessment of the relevant patterns. Additionally, an excessive number of threads would lead to local memory overflow and a corresponding decrease in computational speed.

The scalability of the fitting algorithm’s computation speed is shown in Figure 3. The graph of computation speed growth depending on the number of threads used on the CPU (Figure 3a) exhibits a nearly linear shape with some deviations and changes in slope. The independence of threads and the equivalence of computations in each thread result in a proportional increase in overall performance. The slightly convex shape of the histogram segments reflects the characteristics of the processor’s power supply depending on the load.

At low loads, with up to 64 threads in use, we can clearly see the effect of hyperthreading in Figure 3a. This is reflected in the ladder-like structure of the graph, in which the performance gain for every second thread that uses a virtual core is no more than 20%–30%. At higher loads, some artifacts caused by CPU power optimization are noticeable, which also affects the efficiency of hyperthreading, making the results difficult to interpret.

The utilization of AVX2 instructions for data-level parallelization ensures high performance of the algorithm by fully populating SIMD vectors with 8 single-precision floating-point elements. The resulting track fitting speed in the context of this study varies from 10.5 $\text{tracks}/\mu \text{s}$ when using a single core, to 1071.3 $\text{tracks}/\mu \text{s}$ at maximum CPU load.

The AMD MI210 graphics card features 104 compute units (CUs), each supporting 64 threads. This GPU structure defines the scalability characteristics of parallel computations (Figure 3b). The histogram clearly shows a stepwise pattern with increments of 64 elements. Using an incomplete set of threads within a CU results in idle computations and a proportional decrease in the overall performance of the algorithm.

The minimum computation speed is 48.4 $\text{tracks}/\mu \text{s}$ with an energy consumption of approximately 135 Wh, which significantly surpasses the CPU’s performance under similar load conditions due to the structural differences between the devices. As the number of active threads increases, performance grows at a rate of about 48 $\text{tracks}/\mu \text{s}$ per thread. Peak performance reaches 2553.5 $\text{tracks}/\mu \text{s}$ when utilizing all 64 threads. With further increases in the local item size, the algorithm’s performance decreases in proportion to the ratio of active to idle threads. Subsequent performance peaks show similar, though slightly lower, results. As the number of tasks per CU increases, the amount of both global and local memory used grows, leading to minor additional overhead costs.

The final energy consumption values (Figure 4) were calculated for each pair of total energy consumption per unit of time (Figure 2) and computation speed (Figure 3) using Equation 1, with an estimation for fitting $k=10^{10}$ tracks. In addition to the energy spent directly on the calculations, the equation takes into account the memory energy consumption at the rate of $P_m$ = 0.3725 W/GB.

Figure 4

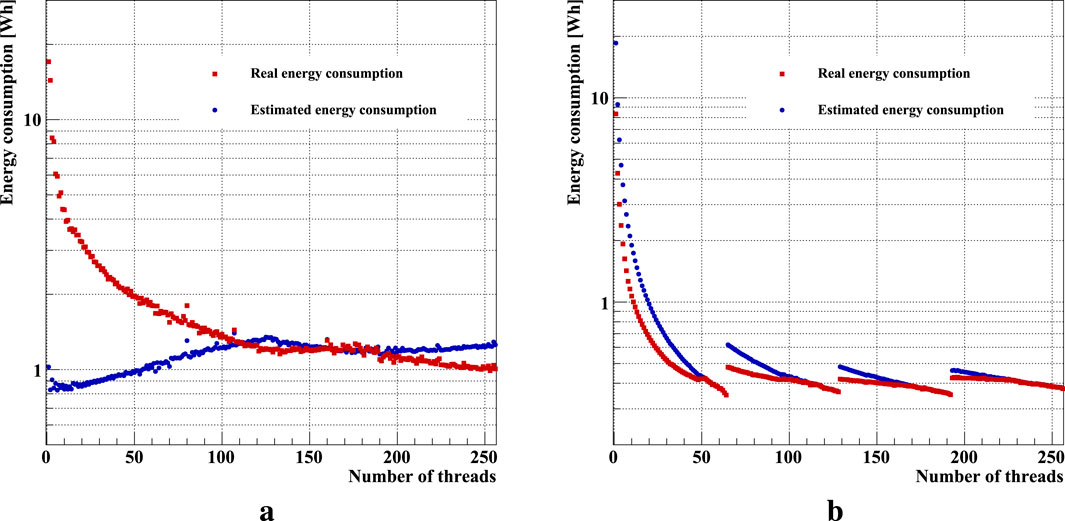
Figure 4. Energy consumption of the Kalman Filter Track Fitter for processing $10^{10}$ tracks, measured on (a) CPUs (2x AMD EPYC 7742) and (b) GPU (AMD MI210).

The Kalman Filter track fitter does not require significant amounts of additional memory for calculations and storing intermediate results. The main memory consumption is for storing information about the detector geometry, as well as directly processed data: tracks and hits they consist of.

In the benchmark under consideration, information about each of the 7 detector stations takes up 156 bytes. In real-world applications, this value can increase to several tens of KB, mainly due to a more detailed map of the station material. This amount of memory use has almost no effect on overall energy consumption.

The main memory consumption is for tracks that are being fitted, primarily due to their number. In the benchmark, this value is 240 bytes per track. Since the fitting process occurs in batches, the amount of memory used $n_m$ was determined based on the simultaneous storage of up to $10^6$ tracks. If this parameter is significantly increased, energy costs for temporary data storage start to outweigh the computation costs, which does not align with the algorithm’s usage model. Thus, the results provide insight into the approximate energy cost of track fitting that can be expected in the CBM experiment over the course of 1 s, under conditions of maximum particle interaction rates with high collision centrality, when the largest number of fragments is produced.

It should be noted that many of the conditions considered for the upcoming CBM experiment are estimates based on theoretical models and tend to result in inflated numbers. For this reason, the results of the study cannot be regarded as precise values but rather as approximate estimates of the algorithm’s energy consumption. These estimates, however, provide valuable insights into the main trends and allow for a rough assessment of the algorithm’s energy efficiency.

According to theoretical estimates (Figure 2a, blue markers), fitting $10^{10}$ particle trajectories using the Kalman filter on modern CPUs required between 0.83 and 1.25 Wh of electricity (Figure 4a, blue markers). The wavelike structure of the histogram is caused by the uneven growth in computation speed with linear increases in energy consumption.

Actual power consumption measurements (Figure 4a, red markers) show clear differences from the estimates in areas of high or low CPU utilization, whereas they are rather close to the estimates for medium CPU utilization. Computations on a small number of threads lead to relatively low power efficiency, which is an obvious effect of the jump and a sharp further growth of power consumption with a more uniform increase in the speed of calculations. At the same time, the power efficiency at maximum CPU load looks better than theoretical. Fitting $10^{10}$ tracks in this case requires about 1.00 Wh of electricity.

Now, knowing the energy cost for fitting $10^{10}$ tracks—representing the hypothetical peak track output per second—we can calculate the carbon footprint for 1 day of algorithm operation using Equation 2, as outlined in the Green Algorithms methodology. The choice of a 24-h time interval is made for clarity and ease of further extrapolation, as the experiment and data processing will be conducted continuously around the clock.

$C=E\times CI=24\text{h}\times 60\text{min}\times 60\text{sec}\times 0.0010\text{kWh}\times 380{\text{gCO}}_2/\text{kWh}=\mathrm{32,832}{\text{gCO}}_2$

Thus, particle trajectory fitting in the CBM experiment using CPUs at maximum load could result in up to 32.8 kg of ${\text{CO}}_2$ emissions per day. To make this more relatable, these emissions can be expressed in terms of driving distance and carbon sequestration (Table 1).

Table 1

Table 1. Comparison of energy consumption across different computing setups under optimal resource utilization.

According to open data from the European Environment Agency [14], the average ${\text{CO}}_2$ emissions for new cars in Europe are $102.2{\text{gCO}}_2/\text{km}$. Therefore, the ${\text{CO}}_2$ emissions in the scenario considered would correspond to:

$\frac{\mathrm{32,832}{\text{gCO}}_2}{102.2{\text{gCO}}_2/\text{km}}\approx 321\text{km}$

Consistent with studies [15], a tree absorbs 10—12 ${\text{kgCO}}_2$ per year, depending on growth conditions, or approximately $1\text{kg/month}$. Thus, the daily ${\text{CO}}_2$ emissions from the fitting of the experimental data would be equivalent to about 3 tree-year. These comparisons give a clearer sense of the environmental impact of the computational tasks involved in the CBM experiment.

By comparison, processing $10^{10}$ tracks at minimum CPU load requires approximately 17 times more electricity, resulting in a corresponding increase in carbon dioxide production.

As a means of self-validation, we also compared the calculated results with the output data from the online calculator Green Algorithms (Figure 5), whose operation served as the foundation for developing the research methodology. The calculations performed by the online calculator were based on the use of 1,195 CPU cores over 24 h. This setup is expected to enable the fitting of $10^{10}$ tracks per second, according to previously obtained estimates of the algorithm’s performance (Figure 3a). It should also be noted that the measured peak energy consumption of the system under consideration was 20% lower than the maximum values used by the authors of Green Algorithms by default.

Figure 5

Figure 5. The estimated results for electricity consumption and carbon footprint of fitting $10^{10}$ tracks per second in real time over 24 h, determined using the Green Algorithms online calculator.

Daily electricity consumption, according to our calculations, amounted to 86.4 kWh, which is approximately 20% lower than the result provided by the online calculator and therefore fully aligns with the expected values. The difference in the mass of the emitted $C{O}_2$ is only about 10%. This discrepancy arises from the use of different values for the carbon intensity factor in the calculations. Specifically, Green Algorithms uses data from 2020 (338.66 $gC{O}_2/kWh$), while our research is based on more recent figures from 2023 (380 $gC{O}_2/kWh$). Accounting for this difference reconciles the results. An even more pronounced discrepancy in the driving distance metric reflects not only the influence of prior carbon emission calculations, but also a significant difference in the average $C{O}_2$ emissions per 100 km for vehicles: 175 $gC{O}_2/km$ (2019) in Green Algorithms compared to 102.2 $gC{O}_2/km$ (2024) in our study.

Thus, it can be concluded that the results of our study align with the stated methodology and correlate well with the estimates provided by the Green Algorithms online calculator. However, it is equally important to note that indirect estimations are highly dependent on the coefficients used, which may vary over time or differ depending on the source. Such estimates can be utilized to enhance the interpretability of the results, but they are not sufficiently precise on their own.

The dependence of GPU energy consumption on the device load is much more pronounced (Figure 4b). We will examine two extreme cases in terms of carbon footprint and compare the obtained results with the data from the CPU.

The worst energy efficiency occurs when only one thread per compute unit is used. Low computational performance combined with high energy consumption results in a requirement of approximately 8.34 Wh to process $10^{10}$ tracks. These computations result in up to 273.8 ${\text{kgCO}}_2$ per day. This is equivalent to driving a car for a distance of 2,679 km. Compensation for such emissions would require around 274 tree-months of ${\text{CO}}_2$ sequestration.

Optimal GPU energy efficiency is largely determined by the proper utilization of computational resources to achieve maximum fitting speed. This corresponds to configurations where all threads are utilized, that is, when the local item size is a multiple of 64. The peak efficiency is similar across settings, but the best value is achieved with a local item size of 64, resulting in an energy consumption of 0.35 Wh per $10^{10}$ tracks.

Converting this result similarly to the previously obtained data, we arrive at the following values. Daily ${\text{CO}}_2$ emissions amount to approximately 11.5 kg, which is 3 times less than in the case of CPU usage. This is equivalent to a trip by car of 112.4 km. Such environmental impact would be compensated for by approximately 12.6 tree-months of ${\text{CO}}_2$ sequestration.

4 Conclusion

In this work, an analysis of the efficiency of the Kalman Filter-based fitting algorithm, which plays a key role in particle trajectory reconstruction in heavy-ion physics experiments such as the CBM experiment at FAIR, was conducted. The study included an assessment of computational resources, energy consumption, and carbon footprint when executing the algorithm on modern processors and graphics accelerators. The results show that the algorithm, optimized for SIMD instructions and multithreading, provides high performance and efficiency in the reconstruction and analysis of particle trajectories.

Further analysis reveals that CPU energy efficiency improves with increasing thread count, but power management mechanisms lead to nonuniform efficiency gains. At low CPU loads, baseline power consumption reduces efficiency, whereas at peak loads, real energy usage remains below theoretical estimates. GPU efficiency depends on optimal resource utilization—under low occupancy, energy costs rise sharply, while full utilization achieves up to three times lower energy consumption per fitted track compared to the CPU.

This reduction in energy consumption leads to a threefold decrease in ${\text{CO}}_2$ emissions and, consequently, in the amount of carbon sequestration needed. Therefore, optimizing the algorithm for GPU execution not only enhances computational efficiency but also significantly reduces the carbon footprint of experimental data processing in heavy-ion physics.

The data obtained highlight the importance of further optimizing algorithms and computational systems to achieve a balance between performance and energy efficiency, especially in the context of increasing data volumes and heightened demands for computational power. In the face of global efforts to reduce carbon footprints, the development of “green” computing algorithms and infrastructures is becoming an integral part of the modern scientific process, particularly in the field of heavy-ion physics.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://drive.google.com/file/d/1fhft9Idc-ixYgQoIcoGlsJa5uuDbxJtm/view?usp&equals;sharinghttps://drive.google.com/file/d/1AM582g4on6AuH6JVJKK1QVhYNvJ6Lyvj/view?usp&equals;sharing.

Author contributions

GK: Conceptualization, Investigation, Writing – review and editing, Validation, Data curation, Writing – original draft, Project administration, Formal Analysis, Methodology, Resources, Software, Visualization. IK: Writing – review and editing, Formal Analysis, Project administration, Data curation, Conceptualization, Validation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was partly funded by the German Federal Ministry of Education and Research [grant numbers 05H21VKRC2, 01IS21092, 05P24RF3, 05P24RF7], Germany, and Helmholtz Research Academy Hesse for FAIR (project ID 2.1.4.2.5), Germany.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. Generative AI (ChatGPT 4o) was used to check grammar and make minor stylistic adjustments to some parts of the main text and conclusion. AI was not used to generate descriptions of significant parts of the study.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Senger P, Friese V. CBM progress report 2021. Progress report GSI-2022-00599. Darmstadt, Germany: GSI Darmstadt (2022). doi:10.15120/GSI-2022-00599

CrossRef Full Text | Google Scholar

2. GSI Helmholtzzentrum für Schwerionenforschung. Green IT Cube: supercomputing center for GSI and FAIR. (2023). Available online at: https://www.gsi.de/en/researchaccelerators/research_an_overview/green-it-cube. (Accessed June 12, 2025).

Google Scholar

3. Center for Scientific Computing Goethe University Frankfurt. Goethe–NHR: performance and hardware details. (2024). Available online at: https://csc.unifrankfurt.de/wiki/doku.phpid=public:service:goethe-hlr. (Accessed June 12, 2025).

Google Scholar

4. TOP500. Green 500 list, 2024. (2024). Available online at: https://top500.org/lists/green500/2024/06/. (Accessed June 12, 2025).

Google Scholar

5. Gorbunov S, Kebschull U, Kisel I, Lindenstruth V, Müller W. Fast SIMDized Kalman filter based track fit. Computer Phys Commun (2008) 178:374–83. doi:10.1016/j.cpc.2007.10.001

CrossRef Full Text | Google Scholar

6. Kisel Ifor CBM Collaboration. Event topology reconstruction in the CBM experiment. J Phys Conf Ser (2018) 1070:012015. doi:10.1088/1742-6596/1070/1/012015

CrossRef Full Text | Google Scholar

7. Kozlov G. Cellular automaton based track finder in the STAR experiment (BNL, USA). Doctoralthesis. Frankfurt am Main, Germany: Universitätsbibliothek Johann Christian Senckenberg (2022).

Google Scholar

8. J Heuser, W Müller, V Pugatch, P Senger, CJ Schmidt, C Sturm, and et al. editors [GSI report 2013-4] technical Design report for the CBM silicon tracking system (STS). Darmstadt: GSI (2013).

Google Scholar

9. Zyzak M. Online selection of short-lived particles on many-core computer architectures in the CBM experiment at FAIR. Doctoralthesis. Frankfurt am Main, Germany: Universitätsbibliothek Johann Christian Senckenberg (2016).

Google Scholar

10. Kretz M. Extending C++ for explicit data-parallel programming via SIMD vector types. doctoralthesis. Universitätsbibliothek Johann Christian Senckenberg (2015).

Google Scholar

11. Uptime Institute Research Team. Uptime Institute Global Data Center Survey 2024. (2024). Available online at: https://datacenter.uptimeinstitute.com/rs/711-RIA-145/images/2024.GlobalDataCenterSurvey.Report.pdf.

Google Scholar

12. Statista. Development of the CO2 emissions factor in theelectricity mix in Germany from 1990 to 2023. (2023). Available online at: https://www.statista.com/statistics/1386327/co2-emissions-factor-electricity-mix-germany/ (Accessed June 12, 2025).

Google Scholar

13. Lannelongue L, Grealey J, Inouye M. Green algorithms: quantifying the carbon footprint of computation. Adv Sci (2021) 8:2100707. doi:10.1002/advs.202100707

PubMed Abstract | CrossRef Full Text | Google Scholar

14. European Environment Agency. Average CO₂ emissions of pools of car manufacturers. (2024). Available online at: https://www.eea.europa.eu/en/analysis/maps-and-charts/data-visualization-55. (Accessed June 12, 2025).

Google Scholar

15. Akbari H. Shade trees reduce building energy use and CO₂ emissions from power plants. Environ Pollut (2002) 116:S119–26. doi:10.1016/S0269-7491(01)00264-0

PubMed Abstract | CrossRef Full Text | Google Scholar