New discrete memristive hyperchaotic map: modeling, dynamic analysis, and application in image encryption

With the rapid development of information technology, the demand for ensuring data security and privacy protection has become increasingly urgent. The purpose of this study is to address the limitations of existing image encryption methods and develop a more secure and efficient image encryption scheme. To achieve this, we adopt a research method that involves constructing a new type of discrete memristor hyperchaotic map by coupling an upgraded cosine discrete memristor with the Cubic map, and then conducting in-depth analysis of the system’s dynamic characteristics using phase diagrams, Lyapunov exponential spectra, and bifurcation diagrams to confirm its ability to reach a hyperchaotic state. Based on this hyperchaotic map, we propose a new image encryption scheme, generating high-quality chaotic sequences through its excellent chaotic characteristics to effectively scramble and diffuse image data, and also introducing a novel forward and reverse diffusion strategy in the diffusion process to enhance encryption efficiency. Through experiments on various images, we verify the algorithm’s effectiveness in improving encryption strength, reducing information leakage risks, and ensuring data security. Finally, the results of keyspace analysis, histogram analysis, correlation analysis, and information entropy demonstrate that the scheme has high security and practicability, along with good application prospects and practical value.

1 Introduction

Chaos is a non-linear kinematic system widely used in the biological and social sciences of nature [1–5]. The application of chaotic systems due to their randomness, unpredictability, and initial state sensitivity brings many advantages [6–10], and hyperchaotic systems further extend this complexity [11–14]. Hyperchaotic systems are oscillators with two positive Lyapunov exponents, but chaotic systems have only one, so hyperchaotic systems have more complex dynamical behaviors than general chaotic systems [15–18]. In a continuous system, at least four dimensions or more are required to produce hyperchaos, while in discrete systems, it is possible to produce a hyperchaotic state in two dimensions and have abundant dynamic behaviors [19, 20]. Mostafaee et al. proposed a novel exponential hyperchaotic system with complex dynamics and analyzed the dynamic behaviors of chaotic attractors, bifurcation graphs, and equilibrium points [21].

Based on the principle of symmetry and completeness of circuit variables, Chua proposed a mathematical model to describe the relationship between charge and magnetic flux, namely, a memristor [22]. As a non-linear resistive element, memristor can adjust the resistance or conductance value through charge or magnetic flux due to its small size and low power consumption [23, 24], and its unique non-linear electrical transport characteristics similar to neural synapses have attracted much attention in many fields [25–28]. In addition, memristors are widely used in chaotic systems to improve nonlinear dynamic behavior [4, 29–31]. It should be noted that most of the research on memristive chaotic systems is limited to the continuous-time domain [32–36], but the common application of continuous memristors will lead to problems such as high computational cost and poor controllability, so the concept of discrete memristors is introduced. In addition, discrete maps have simpler iterative equations and higher computational efficiency than continuous systems [37–41].

Discrete memristor-fusion chaos mapping can generate rich dynamic behaviors such as hyperhybrid and coexisting attractors [42–45], and can also enhance sequence complexity and chaos range [46–48]. Pan et al. [49] proposed a discrete memristor model based on difference theory, describing in detail the process of constructing a discrete memristor by difference theory. Peng et al. [50] established a Simulink model of discrete memristor chaos mapping and verified the feasibility of discrete memristors. Liu et al. [38] reported a discrete two-dimensional memristive map and observed the coexistence of its hidden attractors. Bao et al. [51] reported a new two-dimensional discrete memristive hyperchaotic map.

With the continuous advancement of image encryption technology, researchers have found that it is difficult to improve image encryption with a single chaotic system [52, 53]. In order to ensure people’s privacy, Banu S et al. studied traditional encryption algorithms such as AES, RSA, and DES [54], but this algorithm is more suitable for text message encryption. Therefore, it is necessary to develop an efficient encryption scheme to solve the security problem of image encryption [55]. Researchers have investigated a variety of image encryption schemes, such as the application of chaos theory [56], optical methods [57], and compressive sensing [58] to image encryption algorithms. Among them, the characteristics of chaos theory are extremely consistent with the requirements of image encryption schemes, which also promotes the development of chaotic digital image encryption. An image encryption scheme based on double chaotic cyclic shift and Joseph’s problem uses the complexity and unpredictability of chaotic systems to enhance the encryption effect. Xu et al. proposed a fast image encryption algorithm based on compressed sensing and hyperchaotic map [59], which uses the sparse representation of compressed sensing and the randomness of chaotic map to realize image encryption and decryption. Chen et al. proposed an optical multiimage encryption method based on multiplane phase retrieval and interference [60], which significantly enhances encryption security and robustness of encryption through the complexity and unpredictability of optical components. However, when applied to image encryption, the image encryption algorithm is inefficient due to weaknesses such as discontinuous chaotic regions and narrow chaotic ranges of the chaotic map [61, 62]. In short, the structural defects of the image encryption algorithms and the low performance of chaos theory will lead to the inefficiency of the encryption algorithms, and it is difficult to resist ordinary security attacks.

With the rapid development of information technology, data security and privacy protection are confronted with unprecedented challenges. Traditional image encryption technologies are gradually showing their limitations when dealing with complex and changeable security threats, and there is an urgent need to explore more efficient and secure encryption solutions. In this context, this paper conducts in-depth research and achieves a series of innovative results. Firstly, a new two-dimensional hyperchaotic map is proposed. By skillfully combining the classical cubic map with the improved cosine discrete memristor, a new discrete memristive map is constructed, which provides new ideas for the research of chaotic systems. Secondly, the encryption method is innovated. The chaotic sequence generated by the new chaotic map is integrated into the encryption algorithm. Through operations such as index scrambling and forward and reverse diffusion of images, the image encryption process is optimized. Thirdly, the characteristics of the system are analyzed in multiple dimensions. By studying the parameter-dependent phase diagram, Lyapunov exponential spectrum, bifurcation diagram, and coexisting attractors, and verifying the pseudo-randomness, the chaotic characteristics of the system suitable for image encryption are revealed. Through simulation and analysis of the dynamic characteristics of the chaotic system, it is verified that the system is highly sensitive to parameters, thus providing a new approach for image encryption. Moreover, the chaotic sequence is incorporated into the encryption algorithm. Through operations like index scrambling and diffusion on images and security analysis, it is confirmed that the proposed scheme has extremely high security and anti-interference capabilities, indicating that the chaotic characteristics of the system possess great application value in the field of image encryption.

The general structure of this paper is as follows. Section 2 mainly introduces the Cubic map and the proposed discrete memristor, and then constructs the proposed discrete memristor hyperchaotic map and analyzes its performance; Section 3 shows the rich dynamics of a new discrete memristive hyperchaotic map; Section 4 details the image encryption algorithm; Section 5 summarizes the work of this paper and illustrates the prospects for future research directions.

2 Design of a new discrete hyperchaotic map model

2.1 Mathematical model of discrete hyperchaotic map

Discrete hyperchaotic map is a unique dynamic system, and the key point is to improve the complexity and security of the system with the help of high-dimensional chaos characteristics. Based on the Cubic map, a new discrete hyperchaotic map model can be constructed. Memristors, as the fourth fundamental circuit element, relate charge to magnetic flux and possess unique memory characteristics. In this paper, a cosine-type discrete memristor is proposed, in which the relationship between current and voltage and the relationship between internal charge variables is described as Equation 1:

$\left\{\begin{array}{cc}\hfill & V\left(n\right)=M\left(q\left(n\right)\right)\cdot I\left(n\right)\hfill \\ \hfill & q\left(n+1\right)=q\left(n\right)+I\left(n\right)\hfill \end{array}\right.(1)$

where $M(q(n))=cos(q(n))$ is the periodically varying discrete memory resistance, $q$ is the internal charge variable of the memristor, $V$ and $I$ are the voltage and current of the memristor respectively, and an improved class of discrete memristors can be obtained by increasing the parameters $g$ and constant $k$ of the coupling strength of the cosine discrete memristor, the memristor model is shown in Equation 2:

$\left\{\begin{array}{cc}\hfill & V\left(n\right)=M\left(q\left(n\right)\right)\cdot I\left(n\right)=\left[k+g\cdot cos\left(q\left(n\right)\right)\right]\cdot I\left(n\right)\hfill \\ \hfill & q\left(n+1\right)=q\left(n\right)+I\left(n\right)\hfill \end{array}\right.(2)$

Adding the power supply $I(n)=Asin(\omega n)$ ($\omega$ is the radian frequency) as input to the discrete memristor produces a characteristic volt-ampere graph as shown in Figure 1. The fixed parameters $A=0.1$, $g=1$, $k=1$ and $q0=0.1$, it can be seen from the figure that the volt-ampere characteristic curve of the discrete memristor is a diasteretic loop diagram in the shape of “8” through the origin point, when $A=0.1$ and $\omega =0.3$, 0.4, 0.7 are taken, Figure 1a is the volt-ampere characteristic curve of the frequency-dependent tight hysteresis loop shape, from which it can be seen that with the increase of radian frequency, the area of the hysteresis loop gradually decreases, and finally tends to a straight line. When $\omega =0.7$ and $A=0.1$, 0.15, 0.2, the characteristic curve of the volt-ampere of the discrete memristor is shown in Figure 1b. As the amplitude A decreases, the area of the tight hysteresis loop gradually decreases and finally tends to a straight line. Therefore, its volt-ampere characteristics fully meet the requirements of generalized memristor characteristics.

Figure 1

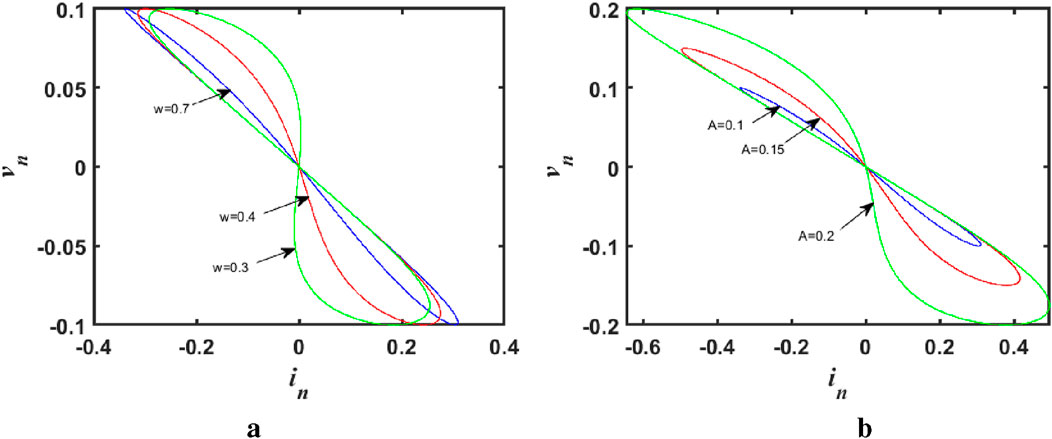
Figure 1. Properties of discrete memristors when $I(n)=Asin(\omega n)$. (a) Hysteresis loop at A = 0.1, ω = 0.3, 0.4, 0.7. (b) Hysteresis loop at ω = 0.7, A = 0.1, 0.15, 0.2.

Through the analysis of numerical simulation, the trajectory distribution and dynamic behavior characteristics of the model can be clearly observed under different initial conditions. It can be seen that the discrete hyperchaotic map not only opens up a new perspective for the research of chaos theory, but also lays a solid theoretical foundation for practical application in related fields.

2.2 Application of discrete memristor in hyperchaotic map

Compared with traditional chaotic maps, discrete hyperchaotic maps exhibit richer dynamic characteristics in parameter space, including irregular periodicity and extreme sensitivity to initial conditions [46]. In the hyperchaotic mapping system, the memristor interacts with other maps. The nonlinear characteristics of the memristor will be coupled with the characteristics of other components, thus generating more complex nonlinear dynamic behaviors, so as to improve the complexity and robustness of their chaotic behavior.

The cubic map is a discrete chaotic map with a simple structure. Its iterative equation is shown in Equation 3:

$x\left(n+1\right)=ax{\left(n\right)}^3-bx\left(n\right)(3)$

By introducing the memristor model (Equation 2) into the Cubic map, a new two-dimensional discrete memristive chaotic system can be obtained:

$\left\{\begin{array}{cc}\hfill & x\left(n+1\right)=ax{\left(n\right)}^3-b\left(1+gcos\left(y\left(n\right)\right)\right)x\left(n\right)\hfill \\ \hfill & y\left(n+1\right)=y\left(n\right)+x\left(n\right)\hfill \end{array}\right.(4)$

When the parameters are $a=0.30,g=0.6,b=1.50$, the two indices are $LE1=0.506156$ and $LE2=0.0820328$, respectively, the system (Equation 4) has two positive Lyapunov exponents, and the system is in a hyperchaotic state at this time. The phase diagram of its hyperchaotic attractor is shown in Figure 2. As can be seen in Figure 2, the structure of the map is simple, but the dynamic behavior is complex.

where $a$, $b$, and $g$ are the control parameters, and in practical applications, the discrete memristor realizes the real-time adjustment of the dynamic behavior in the hyperchaotic map model through its variable resistance characteristics. This mechanism not only improves the adaptability of the system, but also expands the application range of the hyperchaotic map in the field of information encryption.

Figure 2

Figure 2. Hyperchaotic phase diagram.

3 Construction and dynamic analysis of a new discrete hyperchaotic map

3.1 Fixed point

In the study of chaotic systems, an immobile point is one of the important features of a dynamical system, denoting a state that remains unchanged during the evolution of the system. For a new type of discrete hyperchaotic map, it is of great theoretical and practical significance to determine the location and properties of its fixed points. The fixed point of 2D-DMC is the solution to Equation 5.

$\left\{\begin{array}{cc}\hfill & x\ast =a{\left(x\ast \right)}^3-b\left(1+g\cos \left(y\ast \right)\right)x\ast \hfill \\ \hfill & y\ast =y\ast +x\ast \hfill \end{array}\right.(5)$

From Equation 5, it follows that 2D-DMC has infinite fixed points, which can be expressed as $F=(x\ast ,y\ast )=(0,Q)$, where $Q$ is an arbitrary constant. The characteristic equation of the system can be obtained using the Jacobian matrix of fixed points F as shown in Equation 6.

$P\left(\lambda \right)=\left(\lambda -1\right)\left[\lambda +b\left(1+g\cos Q\right)\right](6)$

It can be seen that the eigenvalue ${\lambda }_1=1$ always lies in the unit circle, and whether ${\lambda }_2$ lies inside or outside the unit circle depends on the parameters $b,g$ and the internal initial condition Q of the memristor. Therefore, by adjusting the parameters $b,g$ and $Q$, the fixed point of the 2D-DMC can be placed in an unstable or critical stable state.

The properties of these fixed points determine the complexity of hyperchaotic maps and their potential applications in image encryption. Further studies show that appropriate initial values and parameters can make fixed points exhibit rich dynamic behaviors, thus enhancing the security of chaotic systems.

In general, the study of fixed points provides an important theoretical basis for the application of new discrete hyperchaotic maps. Through in-depth analysis of the properties of fixed points, we can understand the behavior characteristics of chaotic systems and provide valuable guidance for the design and implementation of image encryption algorithms.

3.2 Parametric bifurcation graphs and lyapunov exponents

In the dynamic analysis, the chaotic characteristics of the model can be evaluated by using tools such as the Lyapunov exponent and the bifurcation diagram. In order to explore the sensitivity of the system to different parameters, the dynamic behavior of the system is analyzed in detail by a bifurcation diagram and the Lyapunov exponential spectrum.

(1) The influence of the parameter $b$ on the system: set the parameter $a=0.3,g=0.6$ to explore the influence of the system parameter $b$ on the discrete memristor system. The initial state is $x1=0.1$ and $y1=0.1$. In the range of $b\in$[1.1, 1.5], $LEs$ and their bifurcation plots of the discrete memristor chaos map are shown in Figures 3a, b.

Figure 3

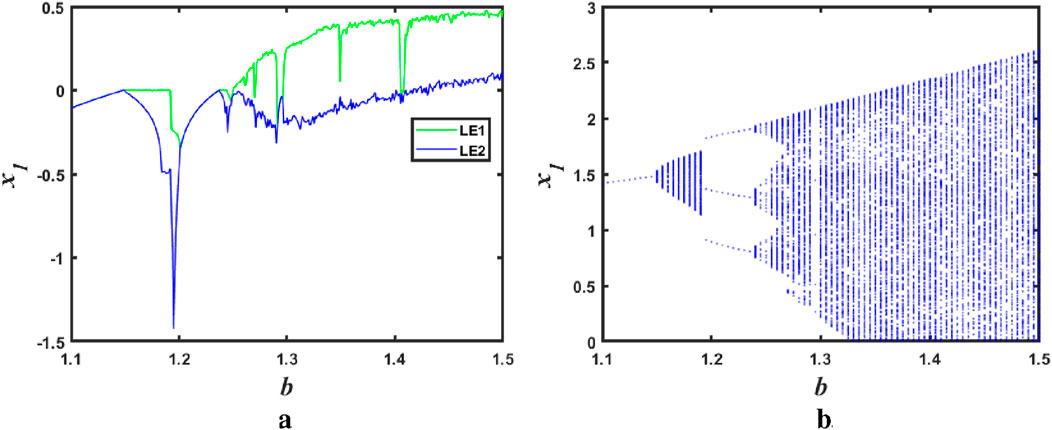
Figure 3. The Lyapunov exponent spectrum and bifurcation diagram of $b\in$[1.1,1.5]. (a) Lyapunov exponent spectrum. (b) Bifurcation Graph.

As can be seen in the figure, when the parameter $b\in$[1.43, 1.54] range, the system has two positive Lyapunov exponents, indicating that the system is in a hyperchaotic state in this range. For example, when b = 1.48, the phase diagram of the hyperchaotic attractor is shown in Figure 4a. In the range of parameters $b\in$ (1.25,1.27), $b\in$[1.28,1.29) and $b\in$[1.3,1.41), the system has a positive Lyapunov index, indicating that the system is in a chaotic state in this range. For example, when $b=1.26$, 1.29, and 1.35, the chaotic attractor of the system is shown in Figures 4b–d. When the parameters are in the range of $b\in$[1.1, 1.25], the system is in a periodic state. For example, when $b=1.15$ and $b=1.20$, the chaotic attractor of the system is shown in Figures 4e, f. Through numerical simulation of the model, the rich trajectory behavior and dynamic behavior of the discrete memristor system can be observed under different initial conditions.

Figure 4

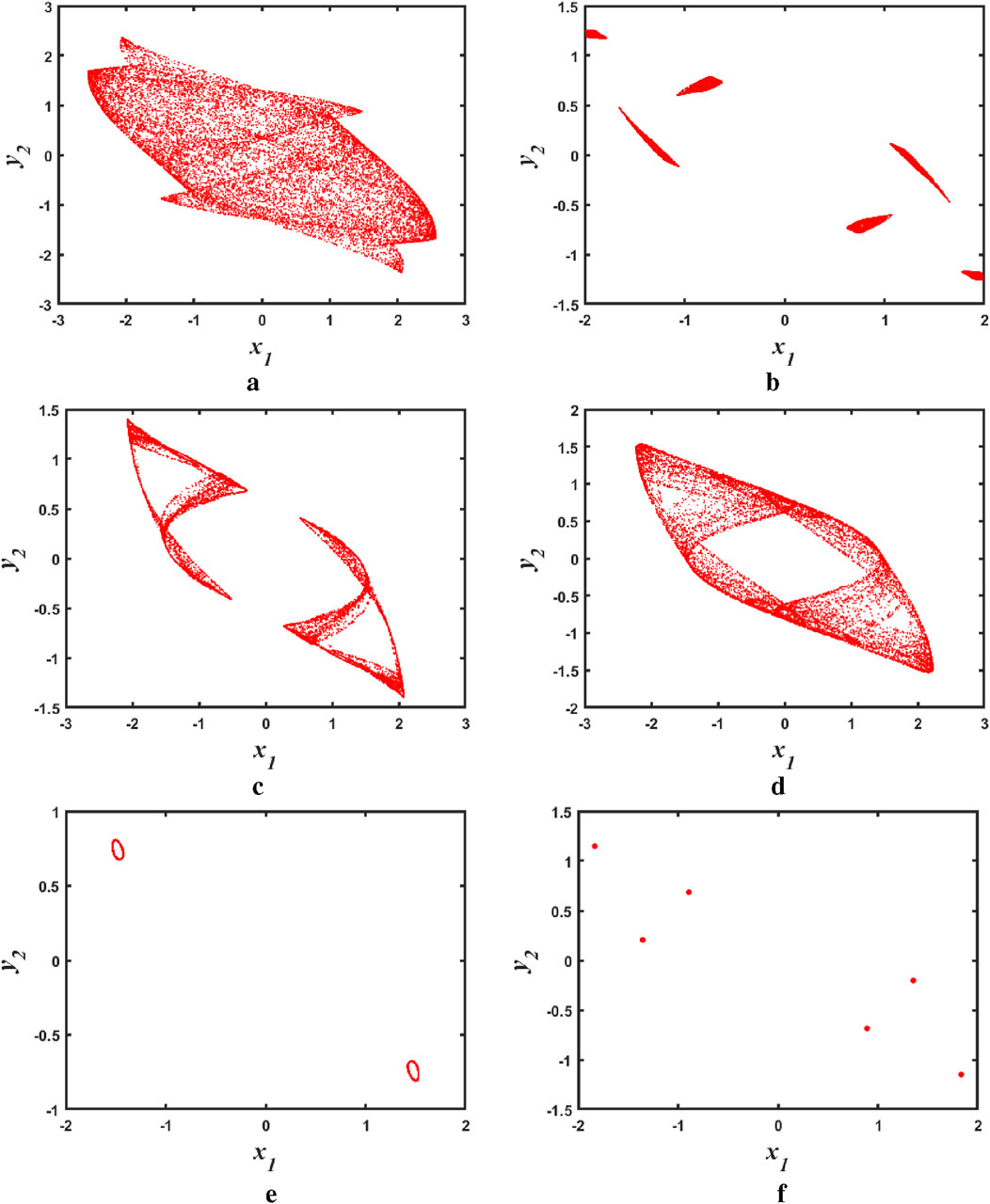
Figure 4. Phase diagram of a discrete memristive chaotic system as a function of parameter $b$. (a) b = 1.48. (b) b = 1.26. (c) b = 1.29. (d) b = 1.35. (e) b = 1.15. (f) b = 1.20.

(2) Impact of the parameter $a$ on the system: Similarly, to explore the impact of parameter $a$ on the system, parameter $b$ is set to 1.5, $g$ to 0.6, and parameter $a$ varies within the range [2, 5]. The $LEs$ of the discrete memristor chaotic map and its bifurcation diagram are shown in Figure 5.

Figure 5

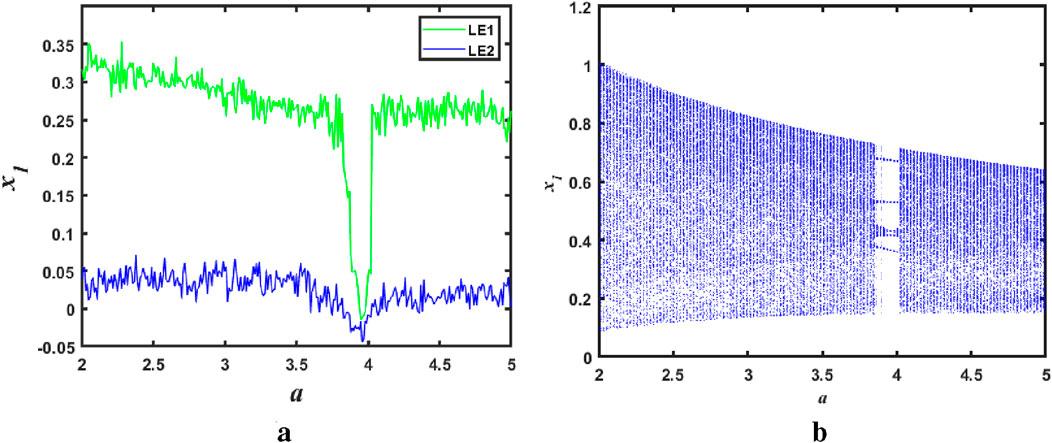
Figure 5. The Lyapunov exponent spectrum and bifurcation diagram of $a\in$[2,5]. (a) Lyapunov exponential spectrum. (b) Bifurcation diagram.

As can be seen in Figure 5, when $a\in$[2, 3.95) and $a\in$(4.08, 5), the discrete memristor chaotic system exhibits hyperchaotic behavior. For example, when $a=2.5$ and 4.5, it can be seen that the system has two positive Lyapunov exponents, and the chaotic attractors of the system are shown in Figures 6a, b. When $a\in$[3.95, 3.98], the system has a periodic attractor. For example, when $a=3.96$, the chaotic attractor of the system is shown in Figure 6c. When $a\in$[4.06, 4.08], the system has a positive Lyapunov exponent and is in a chaotic state. For example, when $a=4.07$, the chaotic attractor of the system is shown in Figure 6d. The analysis of the comprehensive parameter bifurcation diagram and the Lyapunov exponent can provide a solid theoretical basis for the application of new discrete hyperchaotic maps.

Figure 6

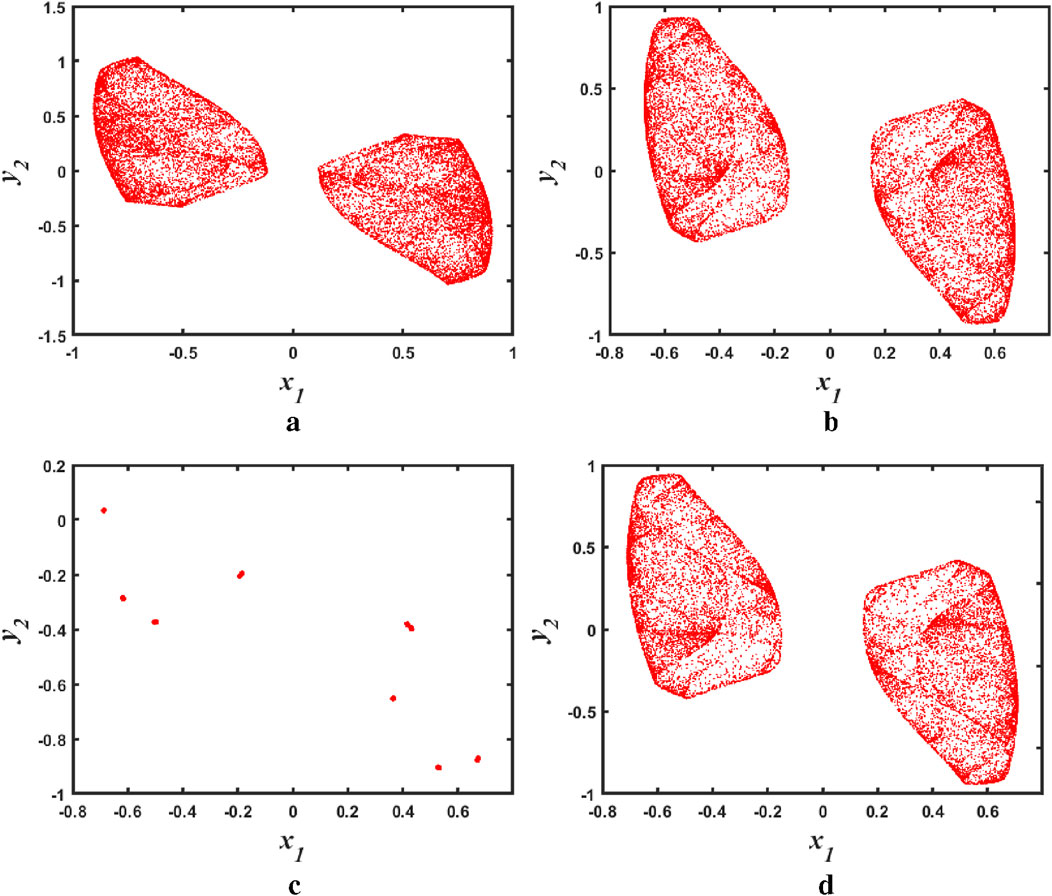
Figure 6. Phase diagram of a discrete memristive chaotic system as a function of parameter $a$. (a) a = 2.5. (b) a = 4.5. (c) a = 3.96. (d) a = 4.07.

(3) The influence of the parameter $g$ on the system: In addition, to explore the influence of parameter $g$ on the discrete memristor system, parameters $a=2.5$ and $b=1.5$ are set to make the parameter $g$ change in the range of $[\mathrm{0,0.61}]$, and the $LEs$ and their bifurcation diagrams of the chaotic map of the discrete memristor are shown in Figure 7.

Figure 7

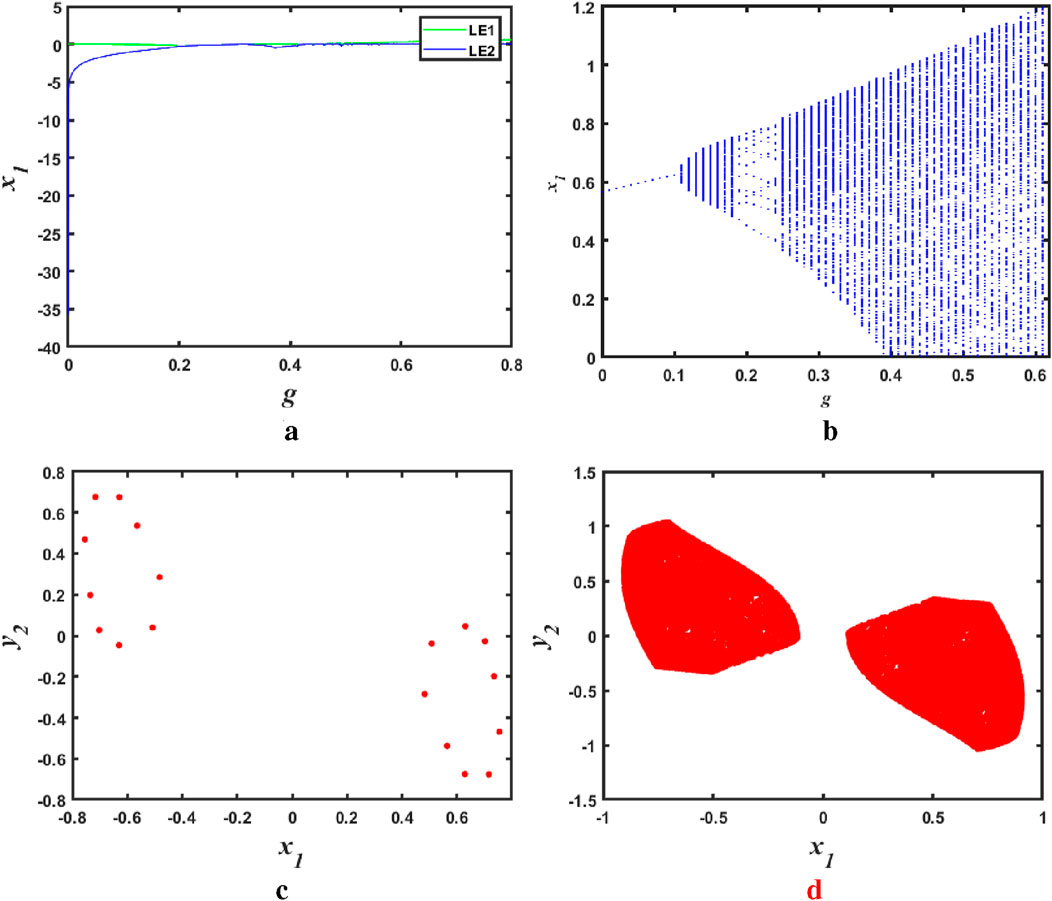
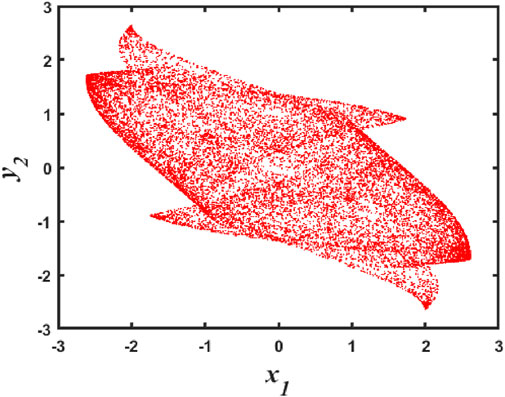
Figure 7. The Lyapunov exponent spectrum, bifurcation diagram and phase diagram of $g\in$[0,0.6]. (a) Lyapunov exponential spectrum. (b) Bifurcation diagram. (c) g = 0.42. (d) g = 0.6.

When parameters $a=2.5,b=1.5$ and initial values $(x1,y1)=(0.1,0.1)$ are selected, the bifurcation plot and LE exponential spectra for parameter $g$ are shown in Figures 7a, b. As can be seen in Figure 7, with the change of parameter $g$, the discrete memristive chaotic system enters the chaotic state from the typical periodic bifurcation, and a complex window period appears in the chaotic region. When $g\in$[0.31, 0.32], the system has a positive LE exponent and presents a chaotic state, and at $g\in$[0, 0.31) and $g\in$(0.32, 0.32], the discrete memristic chaotic system behaves periodically. For example, when $g=0.42$, the periodic attractor of the system is shown in Figure 7c. When $g\in$[0.57, 0.6], there are two positive LE exponents, and the discrete memristic chaotic system exhibits hyperchaotic behavior. For example, when $g=0.6$, the discrete memristive chaotic attractor of the system is shown in Figure 7d.

The discrete memristive chaotic attractors corresponding to the different parameter values $g$ are shown in Figure 8. It can be observed that the chaotic attractor has a complex fractal structure and with increasing parameter $g$, the originally separated chaotic attractor, as shown in Figure 8a, gradually merges with the adjustment of system parameters to form a more complex and unique global attractor, as shown in Figure 8d. The synthesis process of chaotic attractors increases the dimension and complexity of the state space of the system, so that the discrete memristive chaotic system can be flexibly applied to the field of information security. In addition, in the discrete memristive chaotic system, the chaotic sequence generated by the composite attractor has better randomness and non-repeatability, and this complex dynamic behavior makes the output sequence of the system difficult to predict, which provides a high degree of nonlinear characteristics for the encryption process and increases the difficulty of cracking.

Figure 8

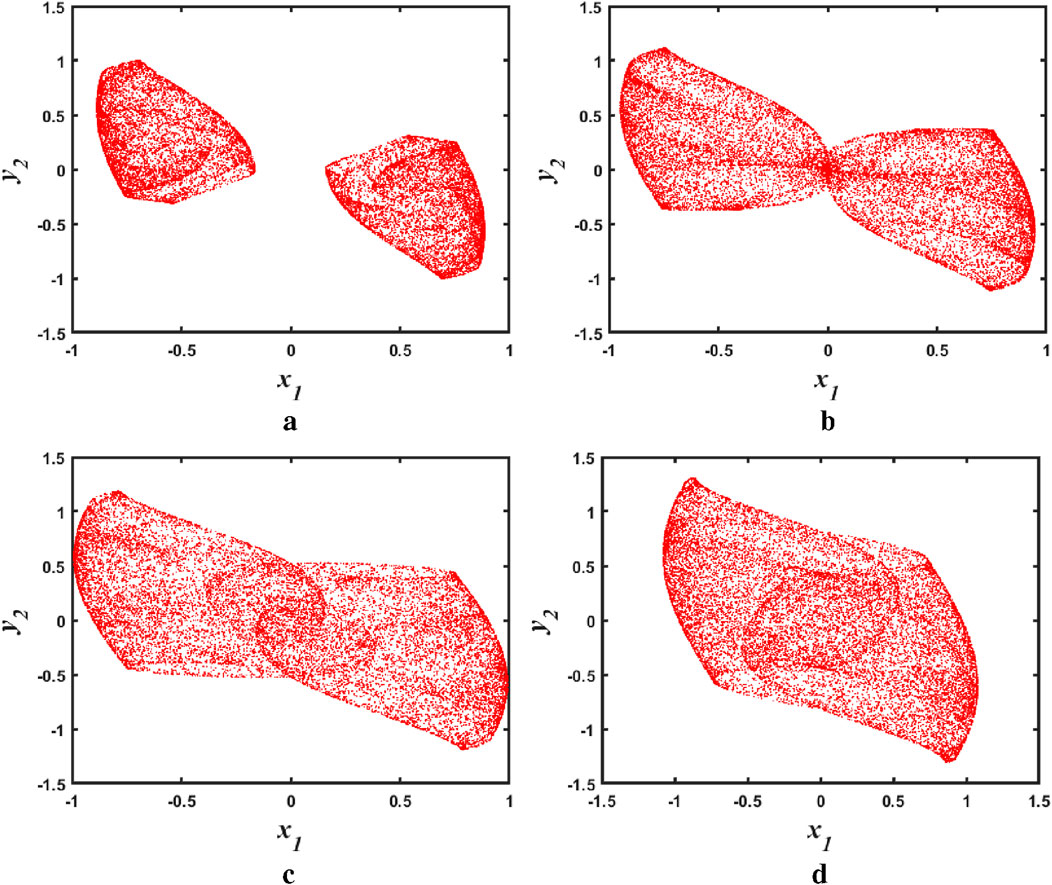
Figure 8. Phase diagram of $g\in$[0.57,0.8] discrete memristive hyperchaotic map. (a) g = 0.58. (b) g = 0.65. (c) g = 0.70. (d) g = 0.80.

3.3 Random analysis

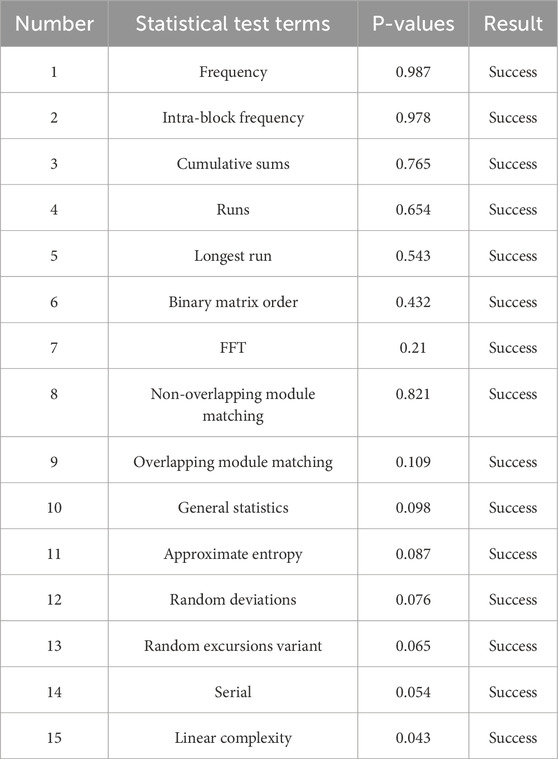
Discrete memristive hyperchaoticmap has been widely used to improve the credibility of data analysis, random number generation, and encrypted communication. In these areas, randomness is a critical requirement, as the resulting chaotic sequences that do not have sufficient randomness can easily be cracked or predicted, compromising the security of the application. Through the randomness test, the randomness and safety of chaotic sequences generated by the discrete memristive hyperchaotic map can be evaluated. To test the randomness of chaotic sequences, we performed two statistical tests, NIST and 0-1. NIST tests are a series of standardized tests that are used to evaluate and verify the security of random number generators and cryptographic algorithms to check whether the generated data are random. The test results are shown in Table 1, from which it can be found that all P values are greater than 0.01, indicating that the key system has successfully passed the test and the generated data have sufficient security and randomness.

Table 1

Table 1. The NIST test results.

The “0-1 test” generally refers to a statistical test performed on a random number or chaotic sequence, mainly to evaluate whether the resulting sequence is sufficiently random to meet specific statistical requirements and application needs. Firstly, a chaotic sequence with a duration of more than 2000 was randomly selected, and the values were selected at a certain step interval for testing, and the test results are shown in Table 2. As you can see from the results in the table, the test result value is close to 1. This indicates that the discrete memristive hyperchaotic map exhibits a high degree of randomness.

Table 2

Table 2. The 0-1 test results.

Based on the results shown in Tables 1, 2, it can be concluded that the key system derived from the discrete memristive hyperchaos map has excellent randomness. Chaotic randomness testing is of great significance in application security, data analysis, and simulation, which can ensure the security of the application and meet the security and reliability requirements required for image encryption.

4 Design and implementation of image encryption algorithm

4.1 An image encryption scheme based on hyperchaotic map

In this section, a novel image encryption scheme based on a two-dimensional hyperchaotic map based on cyclic shift, forward and reverse diffusion, and global displacement is introduced. By combining key steps such as pixel diffusion and displacement, hyperchaotic sequences are used to reorder the pixel positions of the original image and disrupt the overall structure of the image. On the one hand, the displacement process ensures randomness, while diffusion further enhances the complexity of image encryption. The processed chaotic sequence and pixel value are used to perform XOR operations to further improve the encryption strength and reduce the risk of information leakage. The steps are as follows:

1. Select the original image and perform channel separation, and select a grayscale image of $m\times n$ as the original image. $m\times n$ chaotic sequences $X(m),Y(n)$ are generated from the state variables $x0,y0$, and two chaotic sequences $X(m)$ and $Y(n)$ are generated using a Gaussian chaotic neural network, which is used for row and column shifts, respectively.

2. Generate m$\times$n chaotic sequences from the state variables $x0,y0$ The chaotic sequences $Z(m,n)$ and the scrambled image are added pixel by pixel to achieve positive diffusion. Regenerate $m\times n$ chaotic sequences $W(m,n)$ from state variables $x0,y0$. The chaotic sequence $W(m,n)$ and the image after forward diffusion are subtracted pixel by pixel to achieve reverse diffusion.

3. Based on the chaotic characteristics of the hyperchaotic sequences $X(m)$ and $Y(n)$, a permutation index matrix is generated. According to the permutation index matrix, the position of the image is rearranged after forward and reverse diffusion processing. For each pixel position $(i,j)$ in the image, determine its corresponding displacement position $(i^{\prime },j^{\prime })$ in the permutation index matrix and move the pixel value from position $(i,j)$ to position $(i^{\prime },j^{\prime })$. In this way, all pixels of the image are rearranged in the order determined by the chaotic sequence, which completely changes the pixel distribution of the image and hides the structure and information of the original image.

The image encryption algorithm of the new discrete memristive chaotic system provides a secure and powerful encryption scheme for grayscale image encryption. In the encryption stage, the plaintext image undergoes cyclic shift, forward and reverse diffusion, and global substitution operations, combined with the dynamic key generated by the chaotic system, and finally generates an irreversible ciphertext image,as shown in Figure 9a. During decryption, global substitution, forward and reverse diffusion, and cyclic shift are performed in reverse, and the original pixel value and position are restored by the same chaos key to achieve lossless decryption,as shown in Figure 9b.

Figure 9

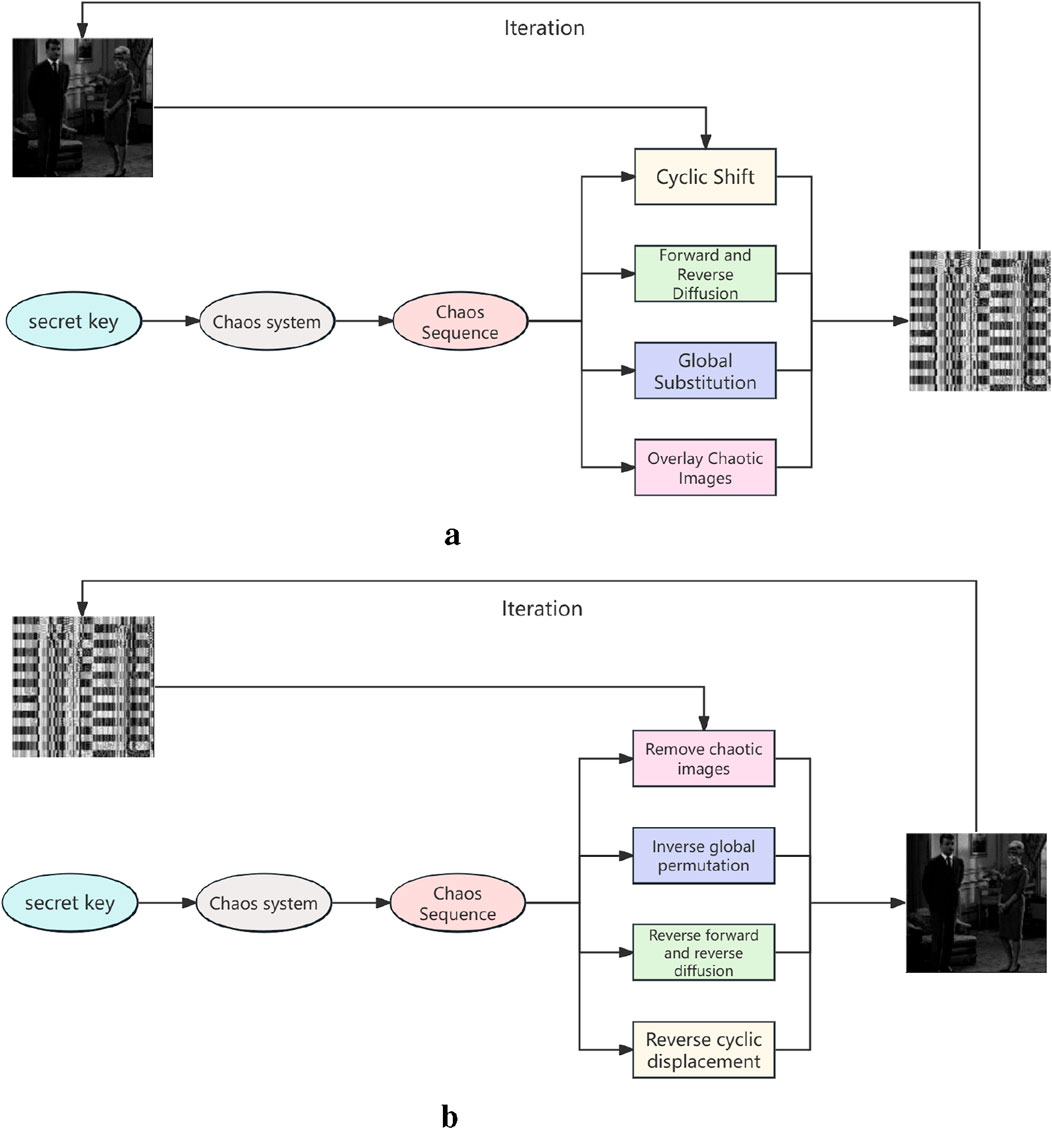
Figure 9. Encryption and decryption process diagram. (a) Encryption Flow Diagram. (b) Decryption Process Diagram.

4.2 Performance analysis of encryption algorithms

In image encryption algorithms, the size of the key space directly determines the security of the encryption. To verify the feasibility and effectiveness of the proposed algorithm, simulation tests were performed using Matlab 2023b, with the key set as $g=0.6,a=3,b=1.8$ and $(x0,y0)=(0.1,0.1)$. A chaotic sequence required for encryption was generated using a discrete memristive chaotic system, and then the image was encrypted through the encryption algorithm. When establishing a new discrete hyperchaotic map, the selection of the key depends on multiple parameters, such as initial conditions and the dynamic characteristics of the system. As shown in Figures 10a, d, g is the original image before the above-mentioned algorithm is encrypted, Figures 10b, e, h are the encrypted image after using the above-mentioned encryption algorithm, and Figures 10c, f, i are the decryption image after using the above-mentioned algorithm. In order to verify the security of the encryption effect of the system, this paper conducted performance analysis, mainly including key space analysis, histogram analysis, correlation analysis, and information entropy analysis.

Figure 10

Figure 10. Encryption and decryption effects of images. (a) Plaintext image. (b) Encryption-image. (c) Decryption-image. (d) Plaintext image. (e) Encryption-image. (f) Decryption-image. (g) Plaintext image. (h) Encryption-image. (i) Decryption-image.

4.2.1 Key space analysis

In image encryption algorithms, the size of the key space directly determines the security of the encryption. Studies have shown that the larger the key space, the more difficult it is for attackers to crack. It is generally accepted that the size of the key space should be greater than 2,128 [45] to ensure security. The keys of IES-CTG are $a,b,g,x0$ and $y0$, and the parameter intervals $a\in$[2,3], $b\in$[1.6,1.8], $g\in$[0.5, 0.6] and the initial value range $x0\in$[0.1, 0.3], $y0\in$ [0.1, 0.3], and the results of image encryption and decryption are shown in Figure 10. Therefore, the key space S of the IES-CTG is shown in Equation 7:

$S=S_1\times S_2\times S_3\times S_4\times S_5=8\times 10^{71}\approx 2^{238}(7)$

where $S_1=(3-2)\times 10^{15},S_2=(1.8-1.6)\times 10^{15},S_3=(0.6-0.5)\times 10^{15},S_4=(0.3-0.1)\times 10^{15},S_5=(0.3-0.1)\times 10^{15}$.

Brute-force attack refers to the situation where an attacker tries all possible key combinations until the correct key for decrypting the information is found. The size of the key space determines the number of possible key combinations. The larger the key space, the more difficult it is for the attacker to find the correct key through brute-force attempts. The key space designed for the novel discrete hyperchaotic map is $2^{238}$, significantly larger than the recommended minimum of $2^{128}$ for the key space, which can effectively resist brute-force attacks. Therefore, the algorithm has larger scale and complexity, and the proposed image encryption scheme can effectively resist external attacks and provide greater security.

4.2.2 Histogram analysis

In image encryption, histogram analysis is an important method to evaluate the encryption effect [63]. Figures 11a, c, e are the original images, and their corresponding image histograms are shown in Figures 11b, d, f, and their pixel value distribution can be visually seen. By comparing the encrypted histograms, as shown in Figures 11g, i, k, it can be observed that the encrypted image histograms should show more uniform distribution characteristics. The histogram of the decrypted image is obtained by the decryption algorithm as shown in Figures 11h, j, l. This balance indicates that confusing and dispersing the pixel information of the original image reduces its recognizability and improves security. That is, the attacker cannot obtain the histogram information of the plaintext image by statistically analyzing the histogram of the ciphertext image, indicating that the proposed algorithm has good diffusion and resistance to statistical attacks.

Figure 11

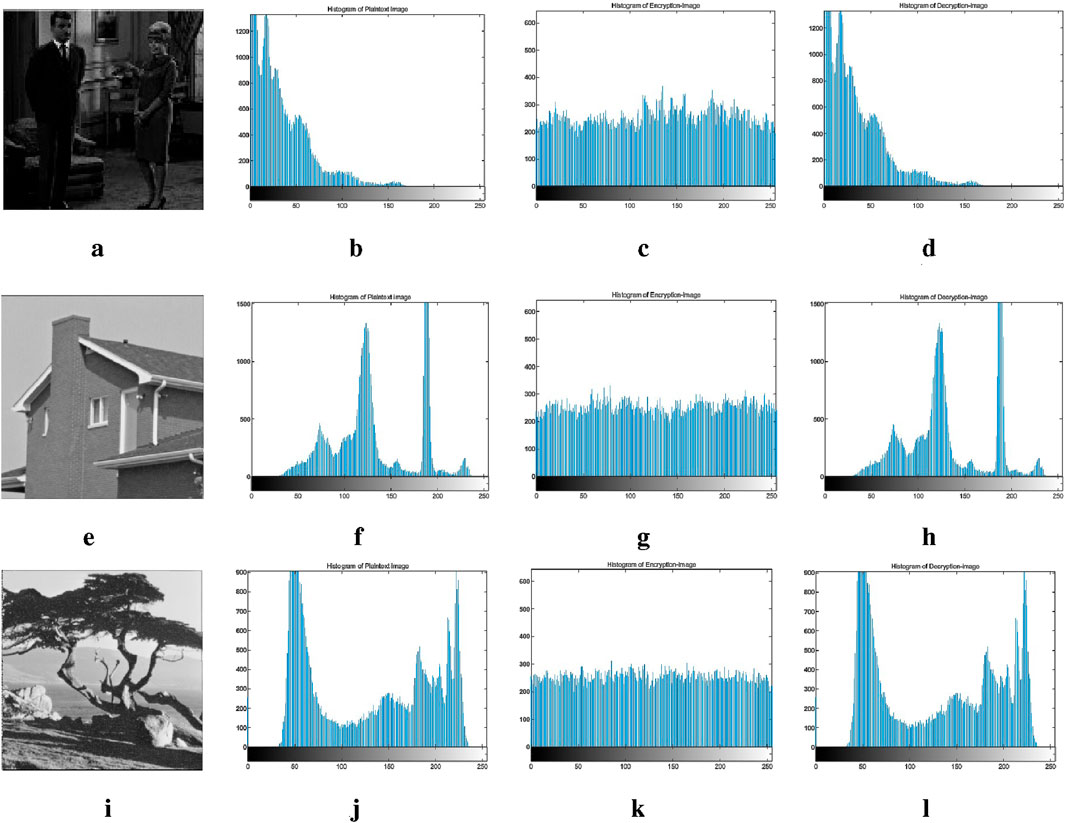
Figure 11. Histograms of plaintext and ciphertext images. (a) Plaintext-image. (b) Histogram of Plaintext-image. (c) Histogram of Encryption-image. (d) Histogram of Decryption-image. (e) Plaintext-image. (f) Histogram of Plaintext-image. (g) Histogram of Encryption-image. (h) Histogram of Decryption-image. (i) Plaintext image. (j) Histogram of Plaintext image. (k) Histogram of Encryption-image. (l) Histogram of Decryption-image.

The entropy of the histogram is also a key indicator to evaluate the effectiveness of image encryption. The higher the entropy value, the higher the complexity of the encrypted image information and the stronger the ability to resist various attacks, as shown in Figures 11d, h, i. In this study, the encrypted image generated by the new discrete hyperchaotic map has a high histogram entropy value, which shows the effectiveness and security of the encryption algorithm in practical applications.

4.2.3 Relevance analysis

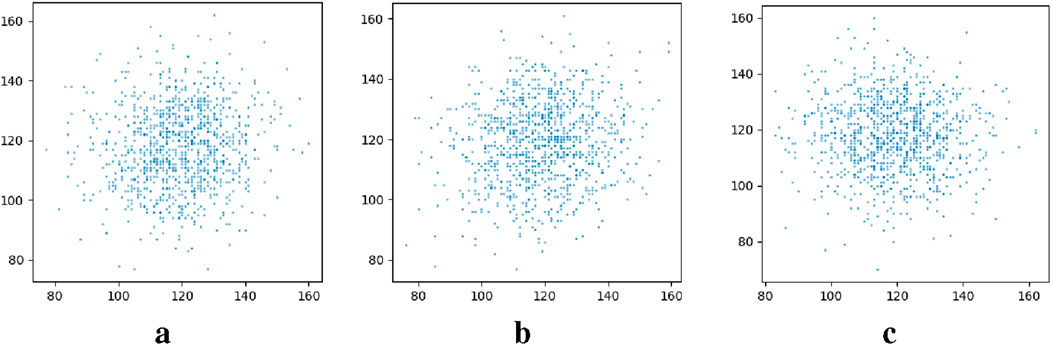
In the design and implementation of image encryption algorithms, correlation analysis is an important performance index. Low correlation means that there is almost no linear or non-linear relationship between the pixel values of the encrypted image, which effectively increases the difficulty of cracking. In order to evaluate the performance of the new discrete hyperchaotic map proposed in the process of image encryption, it is necessary to analyze the correlation of the images before and after encryption. Figures 12, 13 illustrate the correlation between the adjacent pixels of the plaintext image before image encryption and the ciphertext image after encryption, respectively.

Figure 12

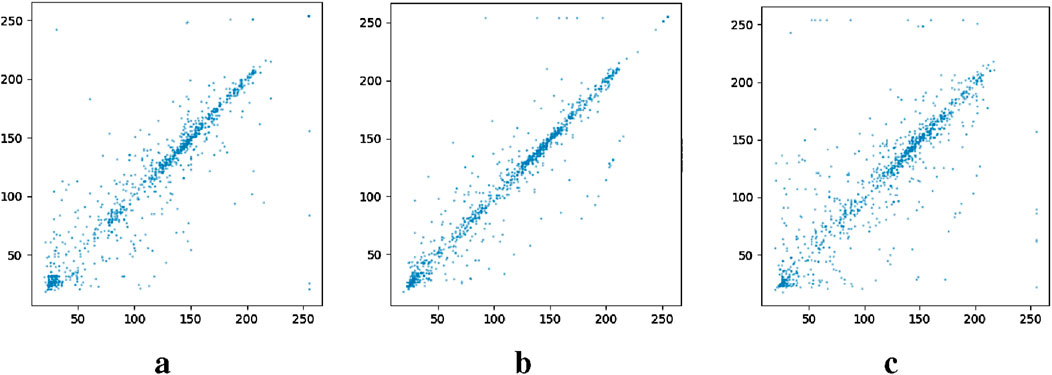
Figure 12. Correlation between adjacent pixels in a plaintext image. (a) Horizontal. (b) Vertical. (c) Diagonal.

Figure 13

Figure 13. Encrypted image adjacent pixel correlation. (a) Horizontal. (b) Vertical. (c) Diagonal.

The image is very strong, as shown in Figures 12a–c, and there is usually a correlation close to 1; However, the correlation between adjacent pixels in a ciphertext image is close to zero, as shown in Figures 13a–c. For different test images, different chaotic sequences are used for encryption, and the correlation difference between the encryption results can be observed, which further verifies the randomness of the new discrete hyperchaotic map, thus improving the security of the encrypted images.

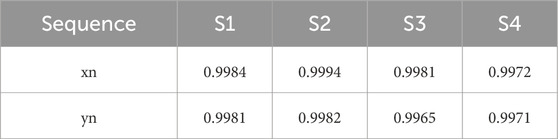
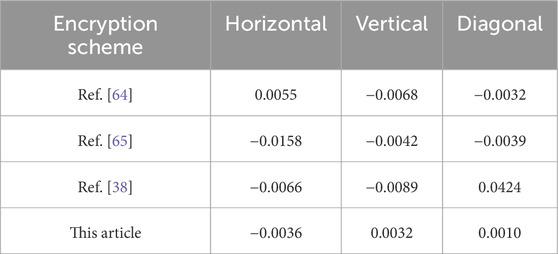
As can be seen from the correlation coefficient of the ciphertext image in Table 3, the correlation between adjacent pixels in the ciphertext image is close to 0, and they are almost uncorrelated. The experimental results show that the designed image encryption algorithm maintains a high encryption strength under the condition of low correlation. Compared with traditional chaotic encryption algorithms, this novel discrete hyperchaotic mapping effectively reduces the correlation between different pixels, thereby enhancing the security of the encrypted image. When compared with more advanced chaotic encryption algorithms, this algorithm also has obvious advantages in terms of processing speed. It can complete the encryption and decryption processes of images more rapidly. Moreover, when facing common attack methods such as differential attacks and statistical attacks, it demonstrates stronger attack resistance, providing a more reliable guarantee for the security of image data.

Table 3

Table 3. Correlation coefficient of ciphertext images.

4.2.4 Information entropy analysis

Information entropy is a basic concept of information theory. It is an important index for measuring the randomness and uncertainty of information. Generally, it is around 8.0, indicating that the encrypted image has good randomness in the pixel intensity distribution. In this study, a new encryption algorithm based on a discrete hyperchaotic map is used to compare the entropy of the original image and the encrypted image. It can be seen from Table 4 that after IES - CTG encryption processing, the information entropy of the ciphertext image is very close to the ideal value of 8, and compared to some existing schemes, it has certain advantages.

Table 4

Table 4. Information entropy of ciphertext images with different encryption schemes.

Furthermore, the variation law of the information entropy under different chaotic parameters is analyzed, and the information entropy performance of the encryption results is affected by adjusting the parameters of the chaotic system. Under the corresponding parameter settings, the increase in the entropy value shows significant sensitivity, which further verifies the effectiveness of chaos characteristics in enhancing the security of image encryption.

5 Conclusion

In this paper, we conduct in-depth research and discussion on a new type of discrete hyperchaotic map and its application in image encryption. By designing and analyzing a novel discrete hyperchaotic map model, we not only clarify its dynamic characteristics, but also reveal its advantages in generating high-quality chaotic sequences. Then, an image encryption algorithm based on a novel discrete hyperchaotic map design is implemented on the MATLAB platform. The key is used to scramble and diffuse the digital image to be encrypted at the pixel level to improve the security of the image. The experimental results show that the proposed encryption algorithm has significant performance advantages. By comparing images with different encryption effects, the security of encrypted images was evaluated using methods such as histogram analysis, information entropy calculation, and adjacent pixel correlation detection. The experimental results show that the encrypted image presents a good degree of visual chaos and the information entropy value is significantly improved, indicating that its security is better than that of traditional image encryption methods.

The new discrete hyperchaotic map and its application in image encryption have important theoretical value and practical significance. Future research can further explore the application potential of other chaos map models in different information security fields, to promote the progress and innovation of overall information encryption technology.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

FY: Supervision, Writing – review and editing, Project administration, Resources, Writing – original draft. YW: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Writing – original draft, Writing – review and editing. XW: Formal Analysis, Software, Validation, Writing – original draft. TH: Investigation, Supervision, Validation, Writing – original draft. SZ: Software, Supervision, Writing – original draft. JJ: Funding acquisition, Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by National Natural Science Foundation of China under Grant 62273141, and by the Guiding Science and Technology Plan Project of Changsha City under Grant kzd2501129.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Deng Q, Wang C, Yang Q. Chaotic dynamics of memristor-coupled tabu learning neuronal network. International Journal of Bifurcation and Chaos (2025) 35:2550053. doi:10.1142/S0218127425500531

CrossRef Full Text | Google Scholar

2. Yuan Y, Yu F, Tan B, Huang Y, Yao W, Cai S, et al. A class of n-d Hamiltonian conservative chaotic systems with three-terminal memristor: modeling, dynamical analysis, and fpga implementation. Chaos (2025) 35:013121. doi:10.1063/5.0238893

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Gao S, Zhang Z, Iu HHC, Ding S, Mou J, Erkan U, et al. A parallel color image encryption algorithm based on a 2d logistic-rulkov neuron map. IEEE Internet Things J (2025) 1. doi:10.1109/JIOT.2025.3540097

CrossRef Full Text | Google Scholar

4. Yu F, Wu C, Xu S, Yao W, Xu C, Cai S, Wang C. Color video encryption transmission in IoT based on memristive hopfield neural network. Signal, Image and Video Processing (2025) 19:77. doi:10.1007/s11760-024-03697-x

CrossRef Full Text | Google Scholar

5. Jin J, Wu M, Ouyang A, Li K, Chen C. A novel dynamic hill cipher and its applications on medical iot. IEEE Internet Things J (2025) 12:14297–308. doi:10.1109/JIOT.2025.3525623

CrossRef Full Text | Google Scholar

6. Yuan Z, Wu Y, Ou C, Zhong P, Zhao X, Ma M. Dynamical behavior of sw-sw neural networks. Chin J Phys (2025) 94:108–20. doi:10.1016/j.cjph.2024.12.031

CrossRef Full Text | Google Scholar

7. Luo D, Wang C, Deng Q, Sun Y. Dynamics in a memristive neural network with three discrete heterogeneous neurons and its application. Nonlinear Dyn (2025) 113:5811–24. doi:10.1007/s11071-024-10513-1

CrossRef Full Text | Google Scholar

8. Hua C, Cao X, Liao B. Real-time solutions for dynamic complex matrix inversion and chaotic control using ode-based neural computing methods. Comput Intelligence (2025) 41:e70042. doi:10.1111/coin.70042

CrossRef Full Text | Google Scholar

9. Yu F, Zhang S, Su D, Wu Y, Gracia YM, Yin H. Dynamic analysis and implementation of fpga for a new 4d fractional-order memristive hopfield neural network. Fractal and Fractional (2025) 9:115. doi:10.3390/fractalfract9020115

CrossRef Full Text | Google Scholar

10. Deng Q, Wang C, Sun Y, Yang G. Memristive multi-wing chaotic hopfield neural network for lidar data security. Nonlinear Dyn (2025) 113:17161–76. doi:10.1007/s11071-025-10982-y

CrossRef Full Text | Google Scholar

11. Feng W, Zhang J, Chen Y, Qin Z, Zhang Y, Ahmad M, et al. Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption. Expert Syst Appl (2024) 246:123190. doi:10.1016/j.eswa.2024.123190

CrossRef Full Text | Google Scholar

12. Lai Q, Yang L, Chen G. Design and performance analysis of discrete memristive hyperchaotic systems with stuffed cube attractors and ultraboosting behaviors. IEEE Trans Ind Electronics (2024) 71:7819–28. doi:10.1109/tie.2023.3299016

CrossRef Full Text | Google Scholar

13. Liu X, Mou J, Zhang Y, Cao Y. A new hyperchaotic map based on discrete memristor and meminductor: dynamics analysis, encryption application, and dsp implementation. IEEE Trans Ind Electronics (2023) 71:5094–104. doi:10.1109/tie.2023.3281687

CrossRef Full Text | Google Scholar

14. Yu F, Tan B, He T, He S, Huang Y, Cai S, et al. A wide-range adjustable conservative memristive hyperchaotic system with transient quasi-periodic characteristics and encryption application. Mathematics (2025) 13:726. doi:10.3390/math13050726

CrossRef Full Text | Google Scholar

15. Chen L, Yu M, Luo J, Mi J, Shi K, Tang S. Dynamic analysis and fpga implementation of a new linear memristor-based hyperchaotic system with strong complexity. Mathematics (2024) 12:1891. doi:10.3390/math12121891

CrossRef Full Text | Google Scholar

16. Ma X, Wang Z, Wang C. An image encryption algorithm based on tabu search and hyperchaos. Int J Bifurcation Chaos (2024) 34:2450170. doi:10.1142/s0218127424501700

CrossRef Full Text | Google Scholar

17. Zhu S, Deng X, Zhang W, Zhu C. Construction of a new 2d hyperchaotic map with application in efficient pseudo-random number generator design and color image encryption. Mathematics (2023) 11:3171. doi:10.3390/math11143171

CrossRef Full Text | Google Scholar

18. Yu F, Xu S, Xiao X, Yao W, Huang Y, Cai S, et al. Dynamics analysis, fpga realization and image encryption application of a 5d memristive exponential hyperchaotic system. Integration (2023) 90:58–70. doi:10.1016/j.vlsi.2023.01.006

CrossRef Full Text | Google Scholar

19. Hua Z, Zhou Y, Bao B. Two-dimensional sine chaotification system with hardware implementation. IEEE Trans Ind Inform (2019) 16:887–97. doi:10.1109/tii.2019.2923553

CrossRef Full Text | Google Scholar

20. Feng W, Wang Q, Liu H, Ren Y, Zhang J, Zhang S, et al. Exploiting newly designed fractional-order 3d lorenz chaotic system and 2d discrete polynomial hyper-chaotic map for high-performance multi-image encryption. Fractal and Fractional (2023) 7:887. doi:10.3390/fractalfract7120887

CrossRef Full Text | Google Scholar

21. Mostafaee J, Mobayen S, Vaseghi B, Vahedi M, Fekih A. Complex dynamical behaviors of a novel exponential hyper–chaotic system and its application in fast synchronization and color image encryption. Sci Prog (2021) 104:00368504211003388. doi:10.1177/00368504211003388

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Liu J, Li Z, Tang Y, Hu W, Wu J. 3d convolutional neural network based on memristor for video recognition. Pattern Recognition Lett (2020) 130:116–24. doi:10.1016/j.patrec.2018.12.005

CrossRef Full Text | Google Scholar

23. Hong Q, Jiang H, Xiao P, Du S, Li T. A parallel computing scheme utilizing memristor crossbars for fast corner detection and rotation invariance in the orb algorithm. IEEE Trans Comput (2025) 74:996–1010. doi:10.1109/tc.2024.3504817

CrossRef Full Text | Google Scholar

24. Yu F, He S, Yao W, Cai S, Xu Q. Bursting firings in memristive hopffeld neural network with image encryption and hardware implementation. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2025) 1–13. doi:10.1109/TCAD.2025.3567878

CrossRef Full Text | Google Scholar

25. Zhang S, Yao W, Xiong L, Wang Y, Tang L, Zhang X, et al. A hindmarsh–rose neuron model with electromagnetic radiation control for the mechanical optimization design. Chaos, Solitons and Fractals (2024) 187:115408. doi:10.1016/j.chaos.2024.115408

CrossRef Full Text | Google Scholar

26. Sun J, Zhai Y, Liu P, Wang Y. Memristor-based neural network circuit of associative memory with overshadowing and emotion congruent effect. IEEE Trans Neural Networks Learn Syst (2024) 36:3618–30. doi:10.1109/TNNLS.2023.3348553

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Xu Q, Fang Y, Feng C, Parastesh F, Chen M, Wang N. Firing activity in an n-type locally active memristor-based hodgkin–huxley circuit. Nonlinear Dyn (2024) 112:13451–64. doi:10.1007/s11071-024-09728-z

CrossRef Full Text | Google Scholar

28. Peng Y, Li M, Li Z, Ma M, Wang M, He S. What is the impact of discrete memristor on the performance of neural network: a research on discrete memristor-based bp neural network. Neural Networks (2025) 185:107213. doi:10.1016/j.neunet.2025.107213

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yao W, Fang J, Yu F, Xiong L, Tang L, Zhang J, et al. Electromagnetic radiation control for nonlinear dynamics of hopfield neural networks. Chaos (2024) 34:073149. doi:10.1063/5.0194928

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Deng W, Ma M. Analysis of the dynamical behavior of discrete memristor-coupled scale-free neural networks. Chin J Phys (2024) 91:966–76. doi:10.1016/j.cjph.2024.08.033

CrossRef Full Text | Google Scholar

31. Xu Q, Ding X, Chen B, Parastesh F, Ho-Ching IH, Wang N. A universal configuration framework for mem-element-emulator-based bionic firing circuits. IEEE Trans Circuits Syst Regular Pap (2024) 71:4120–30. doi:10.1109/tcsi.2024.3428857

CrossRef Full Text | Google Scholar

32. Lin H, Deng X, Yu F, Sun Y. Diversified butterfly attractors of memristive hnn with two memristive systems and application in iomt for privacy protection. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2025) 44:304–16. doi:10.1109/tcad.2024.3429410

CrossRef Full Text | Google Scholar

33. Hong Q, Xiao P, Fan R, Du S. Memristive neural network circuit design based on locally competitive algorithm for sparse coding application. Neurocomputing (2024) 578:127369. doi:10.1016/j.neucom.2024.127369

CrossRef Full Text | Google Scholar

34. Gao S, Iu HHC, Erkan U, Simsek C, Toktas A, Cao Y, et al. A 3d memristive cubic map with dual discrete memristors: design, implementation, and application in image encryption. IEEE Trans Circuits Syst Video Technology (2025) 1. doi:10.1109/TCSVT.2025.3545868

CrossRef Full Text | Google Scholar

35. Yu F, Su D, He S, Wu Y, Zhang S, Yin H. Resonant tunneling diode cellular neural network with memristor coupling and its application in police forensic digital image protection. Chin Phys B (2025) 34:050502. doi:10.1088/1674-1056/adb8bb

CrossRef Full Text | Google Scholar

36. Wan Q, Yang Q, Liu T, Chen C, Shen K. Single direction, grid and spatial multi-scroll attractors in hopfield neural network with the variable number memristive self-connected synapses. Chaos, Solitons and Fractals (2024) 189:115584. doi:10.1016/j.chaos.2024.115584

CrossRef Full Text | Google Scholar

37. Yu F, Xu S, Lin Y, Gracia YM, Yao W, Cai S. Dynamic analysis, image encryption application and fpga implementation of a discrete memristor-coupled neural network. Int J Bifurcation Chaos (2024) 34:2450068. doi:10.1142/s0218127424500688

CrossRef Full Text | Google Scholar

38. Liu X, Sun K, Wang H, He S. A class of novel discrete memristive chaotic map. Chaos, Solitons and Fractals (2023) 174:113791. doi:10.1016/j.chaos.2023.113791

CrossRef Full Text | Google Scholar

39. Tang Z, Zhang Y. Continuous and discrete gradient-zhang neuronet (gzn) with analyses for time-variant overdetermined linear equation system solving as well as mobile localization applications. Neurocomputing (2023) 561:126883. doi:10.1016/j.neucom.2023.126883

CrossRef Full Text | Google Scholar

40. Demirtaş M. A novel multiple grayscale image encryption method based on 3d bit-scrambling and diffusion. Optik (2022) 266:169624. doi:10.1016/j.ijleo.2022.169624

CrossRef Full Text | Google Scholar

41. Xiang Q, Gong H, Hua C. A new discrete-time denoising complex neurodynamics applied to dynamic complex generalized inverse matrices. The J Supercomputing (2025) 81:159–25. doi:10.1007/s11227-024-06601-z

CrossRef Full Text | Google Scholar

42. Peng Y, He S, Sun K. A higher dimensional chaotic map with discrete memristor. AEU-International J Electronics Commun (2021) 129:153539. doi:10.1016/j.aeue.2020.153539

CrossRef Full Text | Google Scholar

43. Liu X, Mou J, Yan H, Bi X. Memcapacitor-coupled Chebyshev hyperchaotic map. Int J Bifurcation Chaos (2022) 32:2250180. doi:10.1142/s0218127422501802

CrossRef Full Text | Google Scholar

44. Wang C, Li Y, Deng Q. Discrete-time fractional-order local active memristor-based hopfield neural network and its fpga implementation. Chaos, Solitons and Fractals (2025) 193:116053. doi:10.1016/j.chaos.2025.116053

CrossRef Full Text | Google Scholar

45. Di Marco M, Forti M, Pancioni L, Tesi A. New class of discrete-time memristor circuits: first integrals, coexisting attractors and bifurcations without parameters. Int J Bifurcation Chaos (2024) 34:2450001. doi:10.1142/s0218127424500019

CrossRef Full Text | Google Scholar

46. Zhong H, Li G, Xu X. A generic voltage-controlled discrete memristor model and its application in chaotic map. Chaos, Solitons and Fractals (2022) 161:112389. doi:10.1016/j.chaos.2022.112389

CrossRef Full Text | Google Scholar

47. Wang C, Luo D, Deng Q, Yang G. Dynamics analysis and fpga implementation of discrete memristive cellular neural network with heterogeneous activation functions. Chaos, Solitons and Fractals (2024) 187:115471. doi:10.1016/j.chaos.2024.115471

CrossRef Full Text | Google Scholar

48. Hamadneh T, Abbes A, Al-Tarawneh H, Gharib GM, Salameh WMM, Al Soudi MS, et al. On chaos and complexity analysis for a new sine-based memristor map with commensurate and incommensurate fractional orders. Mathematics (2023) 11:4308. doi:10.3390/math11204308

CrossRef Full Text | Google Scholar

49. Pan X. Research on discrete differential solution methods for derivatives of chaotic systems. AIMS Mathematics (2024) 9:33995–4012. doi:10.3934/math.20241621

CrossRef Full Text | Google Scholar

50. Peng S, Shi H, Li R, Xiang Q, Dai S, Li Y. Simulink modeling and analysis of a three-dimensional discrete memristor map. Symmetry (2024) 16:990. doi:10.3390/sym16080990

CrossRef Full Text | Google Scholar

51. Bao BC, Li H, Wu H, Zhang X, Chen M. Hyperchaos in a second-order discrete memristor-based map model. Electronics Lett (2020) 56:769–70. doi:10.1049/el.2020.1172

CrossRef Full Text | Google Scholar

52. Zheng J, Luo Z, Tang Z. An image encryption algorithm based on multichaotic system and dna coding. Discrete Dyn Nat Soc (2020) 2020:1–16. doi:10.1155/2020/5982743

CrossRef Full Text | Google Scholar

53. Lai Q, Lai C, Zhang H, Li C. Hidden coexisting hyperchaos of new memristive neuron model and its application in image encryption. Chaos, Solitons and Fractals (2022) 158:112017. doi:10.1016/j.chaos.2022.112017

CrossRef Full Text | Google Scholar

54. Banu SA, Amirtharajan R. A robust medical image encryption in dual domain: chaos-dna-iwt combined approach. Med and Biol Eng and Comput (2020) 58:1445–58. doi:10.1007/s11517-020-02178-w

CrossRef Full Text | Google Scholar

55. Li Y, You X, Lu J, Lou J. A joint image compression and encryption scheme based on a novel coupled map lattice system and dna operations. Front Inf Technology and Electron Eng (2023) 24:813–27.

Google Scholar

56. Ahmad I, Shin S. A novel hybrid image encryption–compression scheme by combining chaos theory and number theory. Signal Processing: Image Commun (2021) 98:116418. doi:10.1016/j.image.2021.116418

CrossRef Full Text | Google Scholar

57. Wei H, Wang X. Optical multiple-image authentication and encryption based on phase retrieval and interference with sparsity constraints. Opt and Laser Technology (2021) 142:107257. doi:10.1016/j.optlastec.2021.107257

CrossRef Full Text | Google Scholar

58. Hua Z, Zhang K, Li Y, Zhou Y. Visually secure image encryption using adaptive-thresholding sparsification and parallel compressive sensing. Signal Process. (2021) 183:107998. doi:10.1016/j.sigpro.2021.107998

CrossRef Full Text | Google Scholar

59. Xu Q, Sun K, Cao C, Zhu C. A fast image encryption algorithm based on compressive sensing and hyperchaotic map. Opt Lasers Eng (2019) 121:203–14. doi:10.1016/j.optlaseng.2019.04.011

CrossRef Full Text | Google Scholar

60. Chen W, Chen X. Optical multiple-image encryption based on multiplane phase retrieval and interference. J Opt (2011) 13:115401. doi:10.1088/2040-8978/13/11/115401

CrossRef Full Text | Google Scholar

61. Wei Z, Sixing X, Guilin W, Yonghong L, Qichang J. Multi-image optical encryption method of jtc system combining cgh and frequency shift. Infrared Laser Eng (2022) 51:20220175–1. doi:10.3788/irla20220175

CrossRef Full Text | Google Scholar

62. Zhang B, Liu L. A novel fast image encryption algorithm based on coefficient independent coupled exponential chaotic map. Physica Scripta (2024) 99:025249. doi:10.1088/1402-4896/ad1fc3

CrossRef Full Text | Google Scholar

63. Ning Y, Jin J, Li Z, Chen C, Ouyang A. A time-varying hill cipher for dynamic image cryptography. Tsinghua Sci Technology (2025). doi:10.26599/TST.2024.9010213

CrossRef Full Text | Google Scholar

64. Wu X, Wang D, Kurths J, Kan H. A novel lossless color image encryption scheme using 2d dwt and 6d hyperchaotic system. Inf Sci (2016) 349:137–53. doi:10.1016/j.ins.2016.02.041

CrossRef Full Text | Google Scholar

65. Xu M, Tian Z. A novel image cipher based on 3d bit matrix and Latin cubes. Inf Sci (2019) 478:1–14. doi:10.1016/j.ins.2018.11.010

CrossRef Full Text | Google Scholar