Monophasic and biphasic neurodynamics of bi-S-type locally active memristor

Inspired by the energy-efficient information processing of biological neural systems, this paper proposes an artificial memristive neuron to reproduce biological neuronal functions. By leveraging Chua’s unfolding theorem, we establish a bi-S-type locally active memristor mathematical model exhibiting negative differential resistance (NDR), which serve as fingerprints for local activity. A second-order neuronal circuit is constructed to emulate periodic spiking and excitability, while a third-order circuit extends functionality to chaotic oscillations and bursting behaviors. Besides, the constructed neuronal circuit generates biphasic action potential through voltage symmetry modulation, replicating bidirectional signal transmission akin to biological systems. Hardware emulation validates neurodynamics under varying stimuli from theoretical analyses, offering a unit module and theoretical reference for energy-efficient neuromorphic computing network.

1 Introduction

As information technology rapidly advances, traditional computing architectures face growing limitations in energy efficiency and computational complexity. Against this backdrop, neuromorphic computing has emerged as a novel computing paradigm [1, 2]. Its core concept is to emulate information processing mechanisms of biological systems by constructing brain-like computing structures to achieve energy-efficient computation [3, 4]. This brain-inspired approach demonstrates superior capabilities in adaptive learning, positioning it as a cornerstone for next-generation intelligent systems [5–7]. Central to this technology are neuroelectronic devices that emulate neuronal functions, which are fundamental units in the construction of neuromorphic computing systems [8, 9].

Current neuroelectronic implementations primarily employ Complementary Metal-Oxide-Semiconductor (CMOS) circuits, leveraging mature fabrication techniques to simulate membrane potential dynamics and action potential generation [10, 11]. However, CMOS-based neurons suffer from inherent limitations including complex circuit topologies and elevated power consumption hinder scalability in large neural networks [12]. Memristive devices present an alternative solution through their intrinsic nonlinearity and low-power operation [13], yet conventional passive memristors require auxiliary negative impedance converters to achieve neuronal dynamics, compromising system integration efficiency [14, 15]. These challenges have driven the exploration of locally active memristors (LAMs) [16, 17], whose negative differential resistance (NDR) enables weak signal amplification and action potential generation without external circuitry [18–20].

Recent advancements in LAM-based neuronal modeling demonstrate promising results. The FitzHugh-Nagumo circuit modifications using N-type LAMs successfully replicate biological spiking patterns [21, 22]. Enhanced LAM designs with ultra-robust NDR characteristics further enable hardware implementation of nine distinct neuronal firing modes [4]. However, these advancements remain primarily confined to monophasic action potential emulation. Emerging experimental evidence from sciatic nerve electrophysiology and myocardial fiber studies demonstrates that biphasic potentials constitute fundamental encoding mechanisms in neural systems [23–25], enabling sophisticated information processing [26]. Current neuromorphic platforms predominantly neglect this biphasic paradigm, impeding hardware-level implementation of biologically plausible neural networks.

Memristive neurons exhibit broad application potential in neuromorphic systems, including frequency-based classifiers for animal sound recognition [27], image protection systems [28, 29], and cyclic neural networks with self-adaptive synapses [30]. Notably, their implementation in artificial neural networks has achieved high-precision MNIST digit recognition and effective edge detection in image processing [31].

The structure of this work is as follows: section 2 characterizes the proposed bi-S-type LAM’s nonlinear dynamics; section 3 constructed a second-order neuronal circuit and demonstrates spiking regimes; Section 4 illustrates various monophasic neurodynamics, biphasic spikes, and symmetry behaviors in the third-order memristive neuron. Section 5 gives the circuit simulated validation.

2 Bi-S-type locally active memristor

Most nanoscale memristors fabricated using various materials exhibit characteristics of generic or extended memristors. Chua’s unfolding theorem provides a systematic method to construct generic memristor models [32]. A generic current-controlled memristor can be defined as

$\left\{\begin{array}{l}v=R_{\mathrm{m}}\left(x\right)i=\left({\displaystyle \sum _{k=0}^r}{d}_k{x}^k\right)i\\ \frac{dx}{dt}=f\left(x,i\right)={\displaystyle \sum _{k=0}^n}{\alpha }_k{x}^k+{\displaystyle \sum _{k=0}^m}{\beta }_k{i}^k+{\displaystyle \sum _{k=0}^p}{\displaystyle \sum _{l=0}^q}{\delta }_{kl}{i}^k{x}^l\end{array}\right.(1)$

where v, i, and x are the voltage, current, and state variable of the memristor, respectively; R_m (x) represents memristance; f (x, i) is the state-controlled equation; α_k, β_k, δ_kl, and d_k are tunable parameters.

Using Equation 1, we derive a memristor model characterized by

$\left\{\begin{array}{l}{v}_{\mathrm{m}}=R_{\mathrm{M}}\left(x\right)i_{\mathrm{m}}=\left(d_2{x}^2+d_0\right)i_{\mathrm{m}}=f_1\left(x,i_{\mathrm{m}}\right)\\ \frac{dx}{dt}={\delta }_0+{\alpha }_{1}x+{\beta }_2{i_{\mathrm{m}}}^2=f_2\left(x,i_{\mathrm{m}}\right)\end{array}\right.(2)$

with parameters: δ₀ = 3 × 10⁴, α₁ = −3 × 10³, β₂ = −8 × 10⁷, d₂ = 2, d₀ = 20.

2.1 Fingerprints of locally active memristor

Chua indicates that a pinched hysteresis loop in the voltage-current plane constitutes a definitive memristor signature [33]. The negative differential resistance (NDR) regions on the DC V-I curve serve as critical indicators of local activity in one-port memristors [34]. These are fingerprints of LAMs.

2.1.1 fingerprint 1: pinched hysteresis loop

Let us apply a sinusoidal voltage v = Asin(2πft) with amplitude A = 5 V and frequencies f = 2 kHz, 5 kHz, 200 kHz to the proposed model. The characteristics of input voltage v_m and response current i_m are depicted in Figure 1A. It shows that the loci plotted on the v_m-i_m plane is a pinched hysteresis loop at f = 2 kHz (dark red curve). The lobe area decreases progressively with increasing frequency (black curve: f = 5 kHz), collapsing to a linear blue line at f = 200 kHz, confirming memristive behavior.

Figure 1

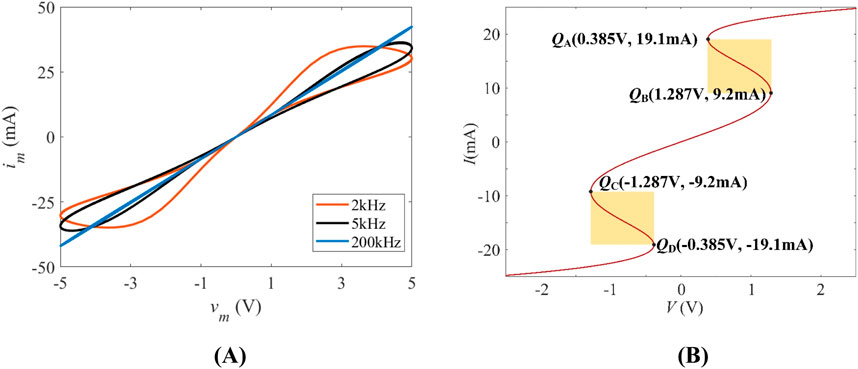
Figure 1. (A) Pinched hysteresis loops measured from Equation 2 on v_m-i_m plane for input voltages v_m with amplitude A = 5 V and frequencies f = 2 kHz, 5 kHz, 200 kHz; (B) DC V-I curve of the LAM with the shaded NDR regions.

2.1.2 fingerprint 2: negative differential resistance (NDR) regions

The DC V-I curve (Figure 1B), obtained by sweeping DC currents from −25 mA to 25 mA with the step size of 0.1 mA, reveals two NDR regions (yellow shading) corresponding to local activity. Signal amplification occurs at these operating points where V ∈ [0.385 V, 1.287 V] (I ∈ [9.2 mA, 19.1 mA]) and V ∈ [−1.287 V, −0.385 V] (I ∈ [−19.1 mA, −9.2 mA]).

However, the operating points Q (V, I) of the LAM exhibit instability when biased at V ∈ [–1.287 V, −0.385 V] ∪ [0.385 V, 1.287 V]. As shown in Figure 2 (left inset), three intersections (M₀, M₁, M₂) or (M₃, M₄, M₅) emerge at V = ±1 V: two stable (M₁, M₂ or M₄, M₅) and one unstable (M₀ or M₃), which is verified by the dynamic route with x-dx/dt. Then, stabilization was achieved by adding an appropriate resistor R₀ = 1 kΩ, and the obtained locally active voltages are V ∈ [R₀I_D + V_D, R₀I_C + V_C] ∪ [R₀I_B + V_B, R₀I_A + V_A], i.e., V ∈ [−19.485 V, −10.487 V] ∪ [10.487 V, 19.485 V] (Figure 2, right inset). Observe that single stable equilibria emerge under these two operating points.

Figure 2

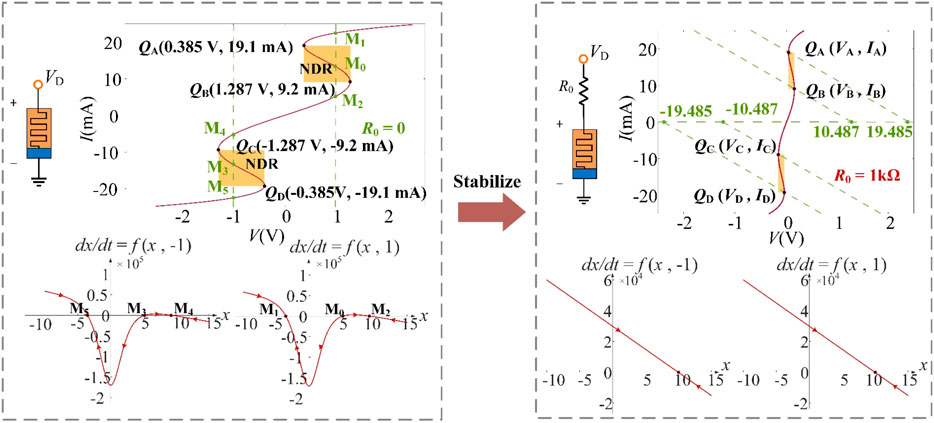
Figure 2. Stabilization mechanism: (left) unstable equilibria in the memristor without resistors; (right) stabilized operation with series resistor R₀.

2.2 Small-signal equivalent circuit of LAM

The small-signal equivalent circuit enables nonlinear dynamics prediction at arbitrary operating points. By applying Taylor series expansion to Equation 2 at operating point Q (V_Q, I_Q) under sufficiently small signals (ignoring higher-order terms), we obtain

$\left\{\begin{array}{l}△v=a_{11}\left(Q\right)△x+a_{12}\left(Q\right)△i\\ △\dot{x}=b_{11}\left(Q\right)△x+b_{12}\left(Q\right)△i\end{array}\right.(3)$

where Δv, Δi, and Δx denote small perturbations; a₁₁ = (δf₁/δx)|_Q = 2d₂I_QX_Q, a₁₂ = (δf₁/δi)|_Q = d₂X_Q² + d₀ = R_M(X), b₁₁ = (δf₂/δx)|_Q = α₁, b₁₂ = (δf₂/δi)|_Q = 2β₂I_Q. Here, the differential resistance R_D=(Δv/Δi)|_Q = a₁₁ (Δx/Δi) + a₁₂ = a₁₂ – (a₁₁b₁₂)/b₁₁, the equivalent resistance R_M = a₁₂.

Taking the Laplace transform of (Equation 3) yeilds

$\begin{array}{ll}\hfill & Z\left(s,Q\right)=\frac{\widehat{v}\left(s\right)}{\widehat{i}\left(s\right)}=\frac{a_{11}\left(Q\right)b_{12}\left(Q\right)}{s-b_{11}\left(Q\right)}+a_{12}\left(Q\right)\hfill \\ \hfill & =\frac{1}{\frac{s}{b_{11}\left(R_{\mathrm{M}}-R_{\mathrm{D}}\right)}+\frac{1}{R_{\mathrm{D}}-R_{\mathrm{M}}}}+R_{\mathrm{M}}=\frac{1}{C_{\mathrm{s}}s+\frac{1}{R_{\mathrm{s}}}}+R_{\mathrm{M}}\hfill \end{array}(4)$

Figure 3A illustrates the small-signal equivalent circuit of the LAM about an operating point: a parallel R_s-C_s network in series with R_M. Figure 3B shows parameter variations under V ∈ [10 V, 20 V]. Notably, negative capacitances (C_s < 0) occur at locally active voltages V ∈ [10.487 V, 19.485 V], which critically determine memristive characteristics for neuronal circuit design. Similar trends hold for V ∈ [–19.485 V, −10.487 V].

Figure 3

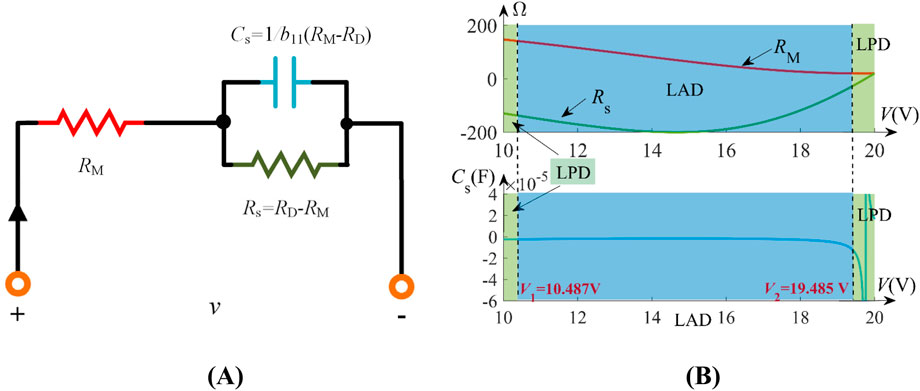
Figure 3. Small-signal analysis of the LAM: (A) the small-signal equivalent circuit of the LAM; (B) the values of R_M, C_s, and R_s varying with operating voltages over the range of V ∈ [10 V, 20 V].

3 LAM-based second-order neuron

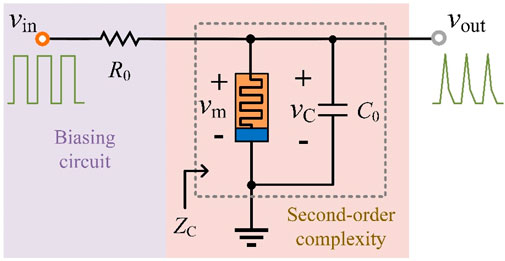
To construct a second-order neuronal circuit using the LAM, an external capacitor C₀ is required to compensate for the inductive behavior of the LAM in locally active domains (LADs). The proposed circuit includes excitation and response signals (v_in and v_out = v_C = v_m), a biasing resistor R₀, and capacitor C₀, as depicted in Figure 4.

Figure 4

Figure 4. LAM-based second-order neuronal circuit.

Frequency-domain analysis determines C₀. Substituting s = iω into the impedance function Z (s, Q) in Equation 4 yields

$Z\left(i\omega ,Q\right)=\text{Re}Z\left(i\omega ,Q\right)+\mathrm{i}\text{Im}Z\left(i\omega ,Q\right)=\left(R_{\mathrm{M}}+\frac{R_{\mathrm{s}}}{1+{R_{\mathrm{s}}}^2{C_{\mathrm{s}}}^2{\omega }^2}\right)+\mathrm{i}\frac{-{R_{\mathrm{s}}}^2{C}_{\mathrm{s}}\omega }{1+{R_{\mathrm{s}}}^2{C_{\mathrm{s}}}^2{\omega }^2}(5)$

The resonant frequency ω₀ occurs when Re [Z (iω, Q)] = 0. From Equation 5, the corresponding imaginary part can be calculated. For oscillation initiation, the critical capacitance satisfies:

$C_0=\frac{1}{{\omega }_0\text{Im}\left(i{\omega }_0,Q\right)}=-\frac{R_{\mathrm{s}}{C}_{\mathrm{s}}}{R_{\mathrm{s}}+R_{\mathrm{M}}}(6)$

3.1 Composite impedance function

The oscillation condition for the composite neuronal circuit is derived from its impedance function:

$Z_{\mathrm{C}}\left(s,Q\right)=\frac{1}{\frac{1}{Z\left(s,Q\right)}+C_{0}s}=\frac{R_{\mathrm{M}}s-R_{\mathrm{D}}{b}_{11}}{R_{\mathrm{M}}{C}_0{s}^2+\left(1-R_{\mathrm{D}}{C}_0{b}_{11}\right)s-b_{11}}(\mathrm{7a})$

with two poles

$\left\{\begin{array}{l}{p}_1=\frac{R_{\mathrm{D}}{C}_0{b}_{11}-1+\sqrt{{\left(1-R_{\mathrm{D}}{C}_0{b}_{11}\right)}^2+4R_{\mathrm{M}}{C}_0{b}_{11}}}{2R_{\mathrm{M}}{C}_0}\\ p_2=\frac{R_{\mathrm{D}}{C}_0{b}_{11}-1-\sqrt{{\left(1-R_{\mathrm{D}}{C}_0{b}_{11}\right)}^2+4R_{\mathrm{M}}{C}_0{b}_{11}}}{2R_{\mathrm{M}}{C}_0}\end{array}\right.(\mathrm{7b})$

Figure 5A maps three operational domains: Locally Passive Domains (LPD, yellow), Unstable Locally Active Domains (RHP, right-half plane, cyan), Stable Locally Active Domains (EOC, edge of chaos, green) based on Equations 6, 7a, 7b. These domains align with the memristor’s LAD and LPD characteristics. RHP requires simultaneous local activity and instability, while EOC demands local activity with asymptotic stability.

Figure 5

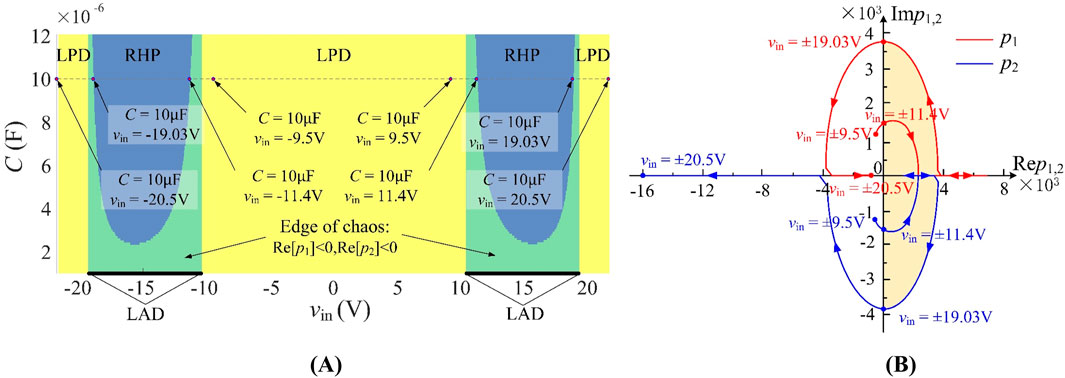
Figure 5. (A) The parameter distributions of LAD, LPD, and EOC on V_in-C plane; (B) poles trajectories with the change of voltage V_in at C = 10 μF.

The pole evolution analysis in Equation 7b under bias voltages v_in ∈ [–20.5 V, −9.5 V]∪[9.5 V, 20.5 V] and C = 10 μF reveals dynamic stability transitions, as depicted in Figure 5B. Red and blue curves represent the trajectories of p₁ and p₂, respectively, with oscillation occurring when v_in ∈ [–19.03 V, −11.4 V]∪[11.4 V, 19.03 V] (orange region). In this region, at least one pole is in the right-half plane (RHP). However, stability persists when p_{1, 2} ∈ LHP (left-half plane). Particularly, Hopf bifurcation emerges at v_in = ±11.4 V and ±19.03 V, characterized by conjugate complex pole pairs.

3.2 Periodic spikes

The state equations of the second-order neuronal circuit in Figure 4 are governed by

$\left\{\begin{array}{l}\frac{dx}{dt}={\delta }_0+{\alpha }_{1}x+{\beta }_2{\left(\frac{v_{\mathrm{m}}}{d_2{x}^2+d_0}\right)}^2\\ \frac{d{v}_{\mathrm{m}}}{dt}=\frac{1}{C_0}\left(\frac{v_{\text{in}}-v_{\mathrm{m}}}{R_0}-\frac{v_{\mathrm{m}}}{d_2{x}^2+d_0}\right)\end{array}\right.(8)$

where x and v_m represent memristor state and membrane potential, respectively.

With C₀ = 10 μF and initial condition [x (0), v_m (0)] = (0, 0), distinct neuromorphic behaviors emerge under varying stimuli v_in according to Equation 8. For stimuli v_in = 9.5 V (LPD) and 10.8 V (EOC), the trajectories converge from the initial point (0, 0) into (v_C, x) = (1.27, 8.19) and (1.29, 7.58), respectively, maintaining resting states as shown in Figure 6A. Increasing v_in to 18 V (see RHP domain in Figure 5A) triggers sustained periodic spikes with frequency f = 204 Hz, demonstrated by time-domain waveform of v_C and limit cycles in the x-v_out phase portrait (Figure 6B). We conclude that the neuron maintains quiescence when operating in the LPD or EOC domains, while inducing spikes under locally active operating points. Notably, spiking frequency modulation under varying v_in = 12 V, 14.5 V, 16.5 V, and 18.5 V replicates biological neural encoding mechanisms (Figure 6C). Besides, the neuron emulates excitatory and inhibitory response transitions, as illustrated in Figure 6D.

Figure 6

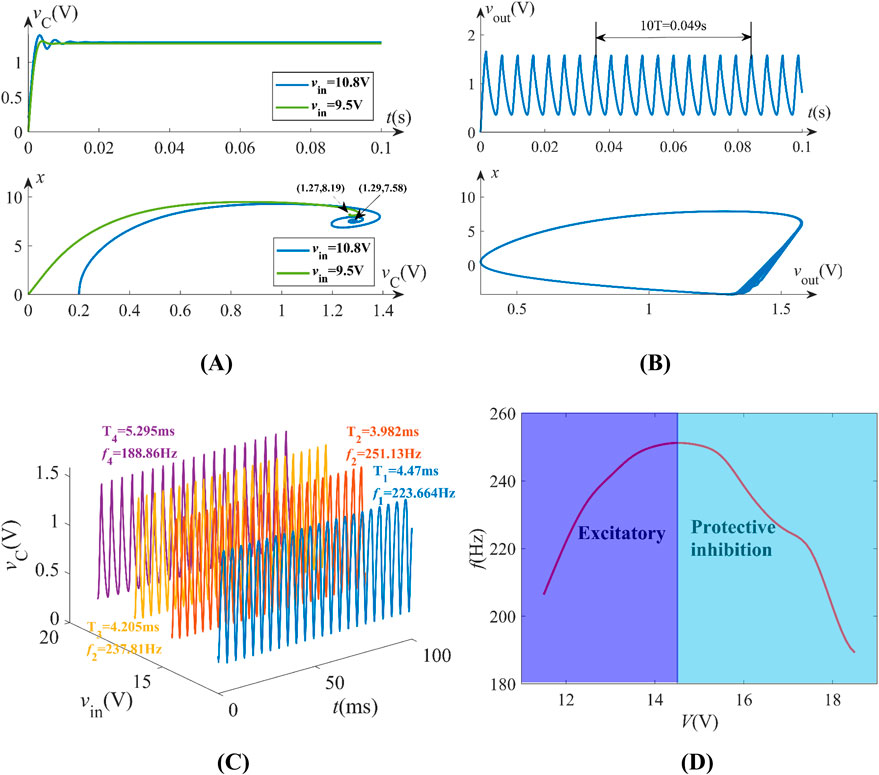
Figure 6. Neuromorphic behaviors under some typical voltages: (A) v_in = 9.5 V, 10.8 V, resting states; (B) v_in = 18 V, periodic spikes; (C) spiking frequency modulation; (D) excitatory and protective inhibition behaviors.

4 LAM-based third-order neuron

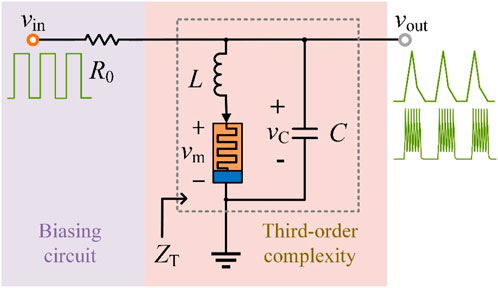
Second-order neurons cannot simulate complex neurodynamics such as chaos and bursting, then we construct a memristive neuron with third-order complexity, as shown in Figure 7, including an LAM, a capacitor, an inductor, a resistor, and a voltage source.

Figure 7

Figure 7. The circuit schematic of the third-order memristive neuron model.

4.1 Stability condition

The impedance function Z_T (s, Q) of third-order memristive neuron circuit is written as:

$Z_{\mathrm{T}}\left(s,Q\right)=\frac{1}{1/\left(Z\left(s,Q\right)+sL\right)+sC}=\frac{L{s}^2+\left(R_{\mathrm{M}}-b_{11}L\right)s-b_{11}{R}_{\mathrm{D}}}{LC{s}^3+\left(R_{\mathrm{M}}-L{b}_{11}\right)C{s}^2+\left(1-C{R}_{\mathrm{D}}{b}_{11}\right)s-b_{11}}(\mathrm{9a})$

whose three poles are

$\left\{\begin{array}{l}{p}_1=-\frac{R_{\mathrm{M}}-b_{11}L}{3L}+{}^3\sqrt{-\frac{q}{2}+\sqrt{\Delta }}+{}^3\sqrt{-\frac{q}{2}-\sqrt{\Delta }}\\ p_2=-\frac{R_{\mathrm{M}}-b_{11}L}{3L}+\left(\frac{-1+\sqrt{3}\mathrm{i}}{2}\right){}^3\sqrt{-\frac{q}{2}+\sqrt{\Delta }}+{\left(\frac{-1+\sqrt{3}\mathrm{i}}{2}\right)}^2{}^3\sqrt{-\frac{q}{2}-\sqrt{\Delta }}\\ p_3=-\frac{R_{\mathrm{M}}-b_{11}L}{3L}+{\left(\frac{-1+\sqrt{3}\mathrm{i}}{2}\right)}^2{}^3\sqrt{-\frac{q}{2}+\sqrt{\Delta }}+\omega {}^3\sqrt{-\frac{q}{2}-\sqrt{\Delta }}\end{array}\right.(\mathrm{9b})$

where $\Delta ={\left(\frac{\left(R_{\mathrm{M}}-b_{11}L\right)·\left(1-C{R}_{\mathrm{D}}{b}_{11}\right)}{6L^{2}C}-\frac{{\left(R_{\mathrm{M}}-b_{11}L\right)}^3}{27L^3}+\frac{b_{11}}{2LC}\right)}^2+\left(\frac{1-C{R}_{\mathrm{D}}{b}_{11}}{3LC}-\right.$${\left.\frac{{\left(R_{\mathrm{M}}-b_{11}L\right)}^2}{9L^2}\right)}^3$, $q=-\frac{\left(R_{\mathrm{M}}-b_{11}L\right)\left(1-C{R}_{\mathrm{D}}{b}_{11}\right)}{3L^{2}C}+\frac{2{\left(R_{\mathrm{M}}-b_{11}L\right)}^3}{27L^3}-\frac{b_{11}}{LC}$.

Based on Equation 9, the trajectory diagram of poles p₁,_2,3 within the range of 8.2 V ≤ V_in ≤ 20 V is depicted in Figure 8A, where blue, red, and yellow curves correspond to the trajectories of p₁, p₂, and p₃, respectively, with arrows denoting directionality as v_in increases. Oscillatory behavior occurs when Re p > 0, particularly within v_in ∈ [11.12 V, 19.38 V] where Hopf bifurcation emerges at v_in = 11.12 V and v_in = 19.38 V, characterized by conjugate complex poles (Im p = 0). For v_in ≤ 11.12 V, all poles reside in the left-half plane (LHP), driving the circuit to stable equilibrium. Conversely, right-half plane (RHP) poles dominate in the oscillatory regime, enabling sustained dynamics. Figures 8B,C confirm this operational range through Lyapunov exponent and bifurcation diagram analysis, demonstrating consistent periodic and chaotic domains in this range under L = 20 mH and C = 10 μF, where the chaotic ranges are v_in ∈ [–18.98 V, −18.89 V] ∪[18.89 V, 18.98 V].

Figure 8

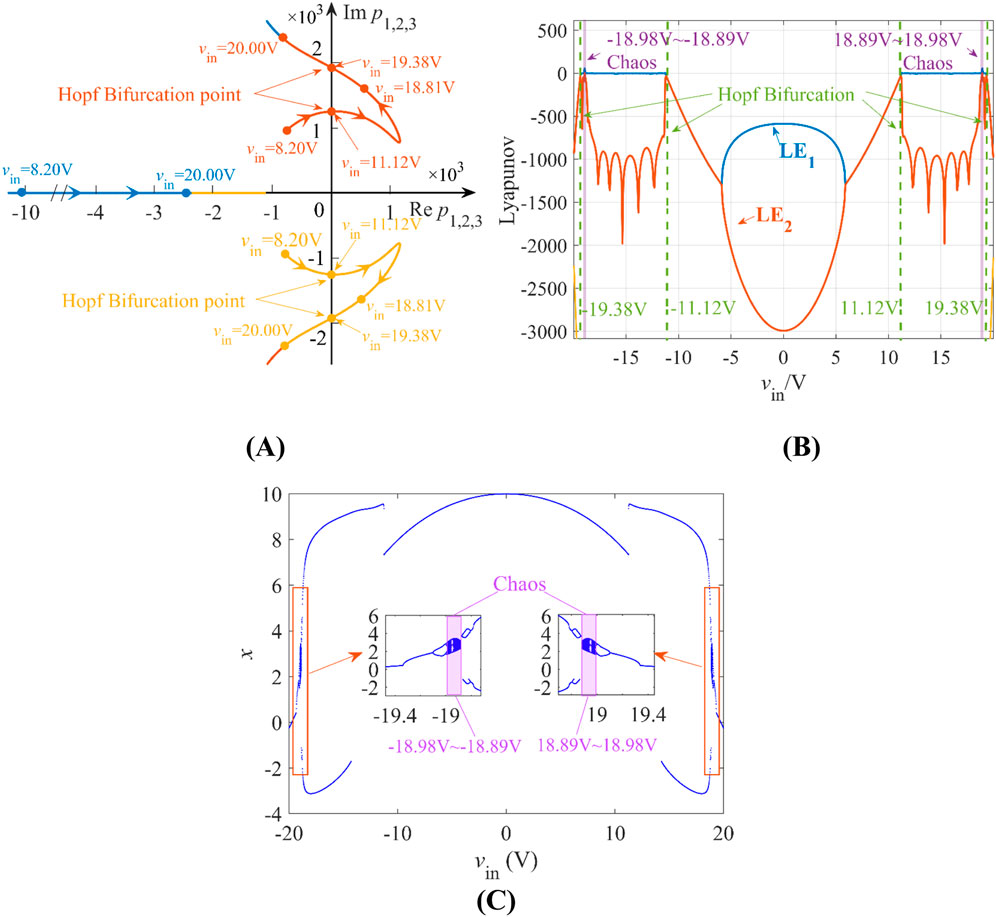
Figure 8. (A) Poles diagram with respect to biasing voltages v_in when L = 20 mH, C = 10 μF; (B) Lyapunov exponents under L = 20 mH, C = 10 μF; (C) bifurcation diagram with respect to v_in under L = 20 mH, C = 10 μF.

4.2 Monophasic neurodynamics

The third-order LAM-based neuronal circuit in Figure 7 is described by

$\left\{\begin{array}{l}\frac{\mathrm{d}x}{\mathrm{d}t}={\delta }_0+{\alpha }_{1}x+{\beta }_2{i_{\mathrm{L}}}^2\\ \frac{\mathrm{d}{v}_{\mathrm{C}}}{\mathrm{d}t}=\frac{1}{C}\left(\frac{v_{\text{in}}-v_{\text{out}}}{R_0}-i_{\mathrm{L}}\right)\\ \frac{\mathrm{d}{i}_{\mathrm{L}}}{\mathrm{d}t}=\frac{1}{L}\left(v_{\text{out}}-\left(d_2{x}^2+d_0\right)i_{\mathrm{L}}\right)\end{array}\right.(10)$

where x (memristor state), i_L (inductor current), and v_C (output voltage) define the neuron dynamics.

Under L = 20 mH and C = 10 μF, six monophasic neuromorphic behaviors emerge through parametric control of v_in based on Equation 10. At v_in = 19.3 V (RHP domain), subthreshold oscillations occur (Figure 9A). Reducing v_in to 18.5 V and 18.9 V within the RHP domain induces periodic spikes (Figure 9B) and chaotic dynamics (Figure 9C), respectively. Time-varying stimulation v_in = 9.9 t V (t ∈[1.2 s, 2.2 s]) triggers Class II excitability, maintaining constant spiking frequency despite voltage modulation (Figure 9D). For periodic square-wave inputs (T = 0.0625 s, A = 15 V), the neuron exhibits bursting patterns (Figure 9E). Besides, depolarizing after-potentials emerge under the parameter set of C = 0.5 μF, L = 20 mH and v_in = 15 V, mimicking post-spike membrane potential modulation (Figure 9F). These results demonstrate voltage-controlled emulation of biological neuronal encoding.

Figure 9

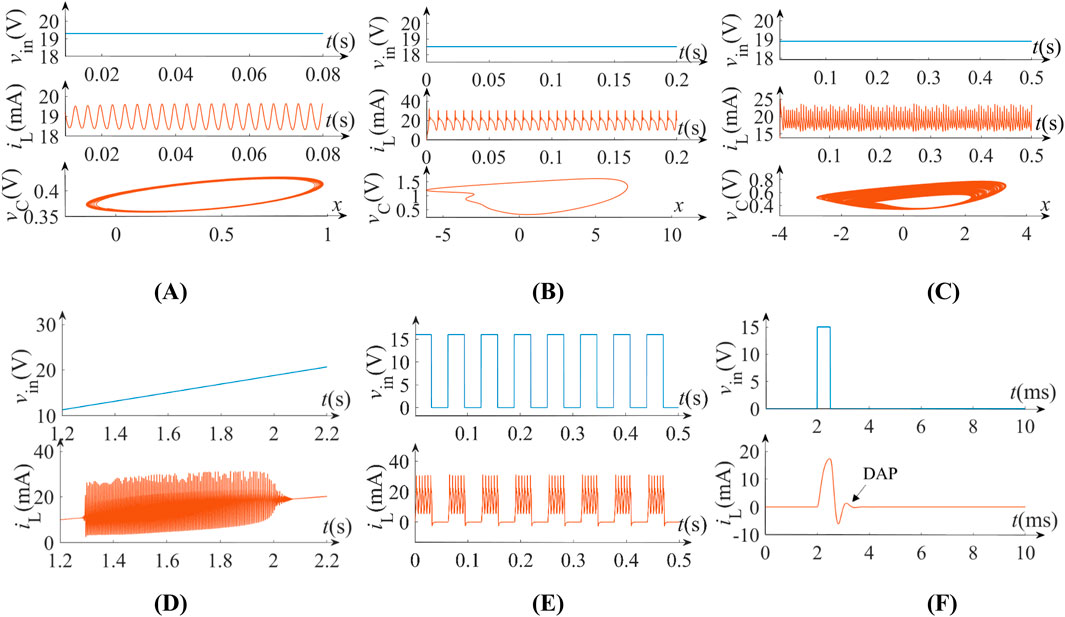
Figure 9. Monophasic neurodynamics under different input voltage v_in with C = 10 μF and L = 20 mH: (A) subthreshold oscillation; (B) periodic spiking; (C) chaos; (D) Class II excitability; (E) periodic bursting. (F) depolarizing after-potential with C = 0.5 μF, L = 20 mH and v_in = 15 V.

4.3 Biphasic spikes

The neuronal circuit in Figure 7 generates biphasic action potentials when driven by bipolar square-wave inputs (v_in = 16 V, D = 50%). As shown in Figures 10A a T= 10 ms periodic stimulus (blue waveform) induces single-cycle bidirectional spiking, characterized by counterphase positive and negative pulses in the inductor current i_L (red waveform). When we increase the period T of the input periodic square wave to 22.22 ms, 33.33 ms, 43.48 ms, 55.56 ms and 66.67 ms, the output waveform changes into two spikes, three spikes, four spikes, five spikes and six spikes in the upward direction and down direction in one period, as shown in Figures 10B–F.

Figure 10

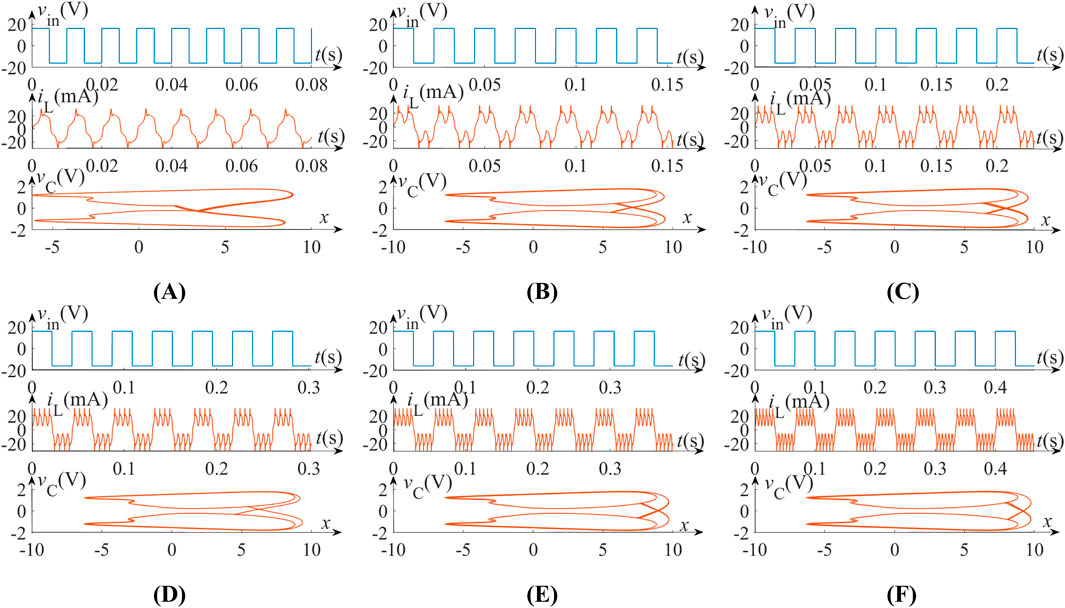
Figure 10. Biphasic action potentials generated by the neuron circuit, when driven by a bipolar periodic square wave with the amplitude v_in = 16 V, duty cycles D = 50% and various period T. (A) T = 10.00 ms; (B) T = 22.22 ms; (C) T = 33.33 ms; (D) T = 43.48 ms; (E) T = 55.56 ms; (F) T = 66.67 ms.

4.4 Symmetric behaviors

The third-order memristive neuron demonstrates voltage-polarity-dependent symmetry in neurodynamic behaviors, originating from the voltage symmetry in Figure 5A. This nonlinear symmetry allows symmetrical action potential generation: positive DC voltages (v_in > 0) induce upward-polarized spikes, while negative inputs (v_in < 0) produce downward-polarized counterparts, as depicted in Figure 11.

Figure 11

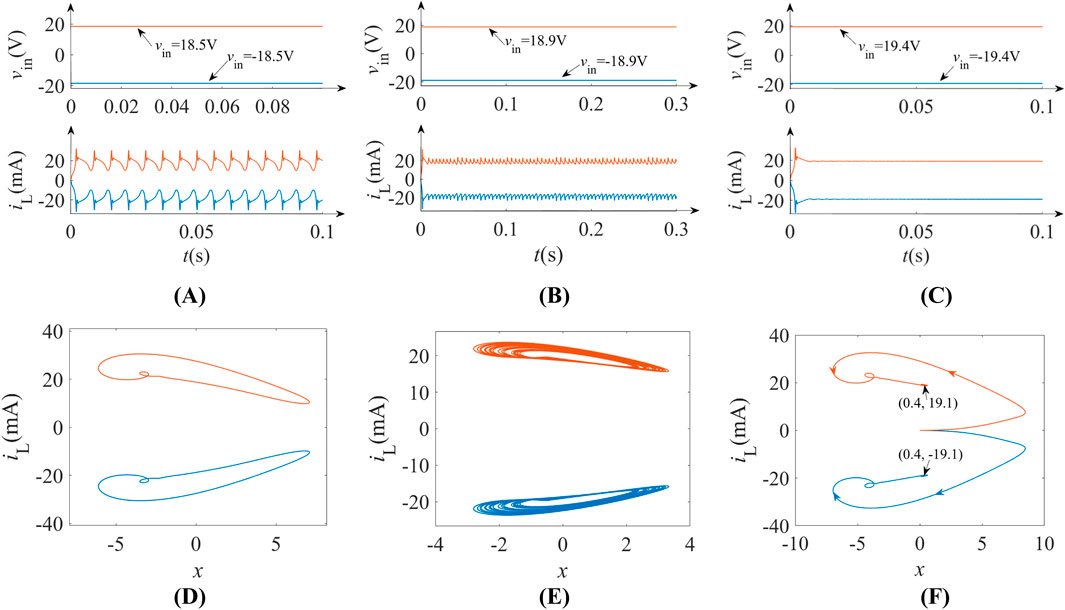
Figure 11. Voltage-polarity-modulated symmetric behaviors: (A) periodic spikes; (B) chaos; (C) resting states; (D) phase portraits of periodic spikes; (E) phase portraits of chaos; (F) phase portraits of resting states.

Under voltage excitation v_in = ±18.5 V, the inductor current i_L exhibits mirror-symmetric periodic spiking, i.e., upward polarization for positive bias (orange curve) versus downward polarization for negative bias (blue curve) in Figure 11A. Voltage modulation to ±18.9 V induces symmetrical chaotic dynamics with identical Lyapunov exponents but opposing phase-space trajectories, as shown in Figure 11B. Transient behavior analysis reveals bidirectional spike initiation: v_in = 19.4 V triggers upward spikes while v_in = −19.4 V generates downward equivalents, both returning to symmetrical resting potentials after undergoing 5 m (Figure 11C). The corresponding phase portraits of these three nonlinear behaviors are depicted in Figures 11D–F.

5 Circuit emulator

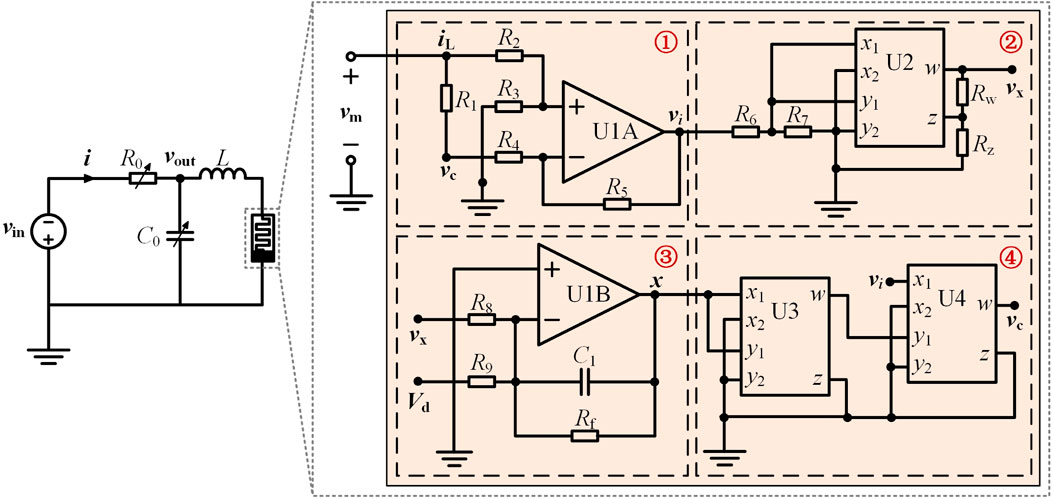
The circuit emulator of the memristive neuron with third-order complexity is constructed, as shown in Figure 12, which consists of two operational amplifiers (U1A and U1B), three analog multipliers (U1, U2, and U3), two capacitors (C₀ and C₁), one inductor L, and some resistors.

Figure 12

Figure 12. Circuit emulator schematic of the third-order memristive neuron.

As shown in Figure 12, the equivalent circuit of the locally active memristor comprises four functionally integrated modules: (1) Current sensing module ① monitors emulator input current in real-time, generating proportional output v_i; (2) analog multiplier arrays ② and ④ implement nonlinear term computations; (3) State equation solver ③ converts DC bias V_d into memristor state variable x through differential integration, that is, v_x = x; (4) Feedback integration completes the loop via R₁. Kirchhoff’s voltage and current laws govern this circuit architecture, yielding three coupled differential equations that mathematically describe electrophysiological dynamics of the memristive neuron, as

$\left\{\begin{array}{l}{C}_1\frac{\mathrm{d}x}{\mathrm{d}t}=-\left(\frac{V_{\mathrm{d}}}{R_9}+\frac{x}{R_{\mathrm{f}}}+\frac{R_{\mathrm{w}}+R_{\mathrm{z}}}{10R_{\mathrm{w}}{R}_8}{\left(\frac{R_7{R}_5{R}_1}{R_4\left(R_6+R_7\right)}{i}_{\mathrm{L}}\right)}^2\right)\\ C_0\frac{\mathrm{d}{v}_{\mathrm{C}}}{\mathrm{d}t}=\frac{v_{\text{in}}-v_{\mathrm{C}}}{R_0}-i_{\mathrm{L}}\\ L\frac{d{i}_{\mathrm{L}}}{dt}=v_{\mathrm{C}}-\left(\frac{R_1{R}_5{R}_{11}}{10R_4{R}_{10}}{x}^2+R_1\right)i_{\mathrm{L}}\end{array}\right.(11)$

where the circuit parameters are R₁ = 20 Ω, R₀ = R₂ = R₄ = R₆ = R₇ = R_w = 1 kΩ, R₃ = R₅ = R₈ = R₉ = 10 kΩ, R_z = 7 kΩ, R_f = 33.3 kΩ, C₁ = 10 nF, C₀ = 9.5 μF, L = 20 mH, and V_d = −3 V.

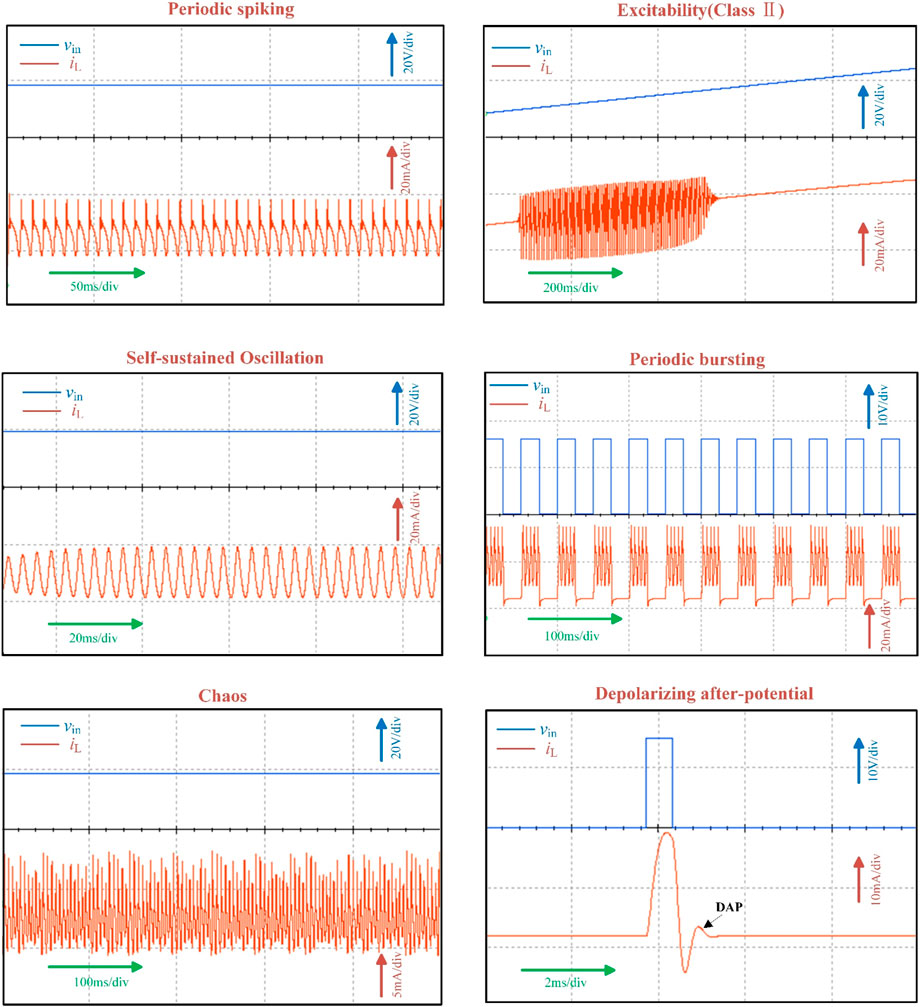
The circuit simulated results calculated via Equation 11 are shown in Figure 13, reproducing key neurodynamics including periodic spikes, class II excitability, self-sustained oscillations, bursting, chaos, and depolarizing after-potential. These results demonstrate quantitative agreement with theoretical predictions.

Figure 13

Figure 13. Circuit simulated neuromorphic dynamics under various biasing voltages.

6 Conclusion

This work constructs neuronal circuits leveraging a bi-S-type locally active memristor that amplifies weak signals through intrinsic local activity. The designed second-order circuit achieves voltage-modulated periodic spiking and adaptive inhibition, while the third-order extension emulates biological neural dynamics including monophasic and biphasic action potentials, chaos, and bursting, which are driven by memristive symmetry. The study of memristive neurons not only offers essential building blocks for neuromorphic computing architectures but also lays a theoretical reference for the development of more advanced and bio-realistic neural processing systems.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XW: Software, Writing – original draft, Formal Analysis, Validation. YD: Methodology, Writing – review and editing, Validation, Software, Funding acquisition. GW: Writing – review and editing, Supervision, Formal Analysis. ZZ: Writing – original draft, Formal Analysis, Software. YM: Writing – review and editing, Visualization. PJ: Investigation, Resources, Writing – review and editing. YL: Formal Analysis, Writing – review and editing, Funding acquisition.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported in part by the Zhejiang Provincial Natural Science Foundation of China under Grant LQ23F010018 and Y24F010007; in part by the National Natural Science Foundation of China under Grant 62301202 and 62171173.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kendall JD, Kumar S. The building blocks of a brain-inspired computer. Appl Phys Rev (2020) 7(1):011305. doi:10.1063/1.5129306

CrossRef Full Text | Google Scholar

2. Yuan R, Tiw PJ, Cai L, Yang ZY, Liu C, Zhang T, et al. A neuromorphic physiological signal processing system based on VO₂ memristor for next-generation human-machine interface. Nat Commun (2023) 14(1):3695. doi:10.1038/s41467-023-39430-4

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Park SO, Jeong H, Park J, Bae J, Choi S. Experimental demonstration of highly reliable dynamic memristor for artificial neuron and neuromorphic computing. Nat Commun (2022) 13(1):2888. doi:10.1038/s41467-022-30539-6

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Pei YF, Yang B, Zhang XM, He H, Sun Y, Zhao JH, et al. Ultra robust negative differential resistance memristor for hardware neuron circuit implementation. Nat Commun (2025) 16(1):48. doi:10.1038/s41467-024-55293-9

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Markovic D, Mizrahi A, Querlioz D, Grollier J. Physics for neuromorphic computing. Nat Rev Phys (2020) 2(9):499–510. doi:10.1038/s42254-020-0208-2

CrossRef Full Text | Google Scholar

6. Schuman CD, Kulkarni SR, Parsa M, Mitchell JP, Date P, Kay B. Opportunities for neuromorphic computing algorithms and applications. Nat Comput Sci (2022) 2(1):10–9. doi:10.1038/s43588-021-00184-y

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sun B, Guo T, Zhou GD, Ranjan S, Jiao YX, Wei L, et al. Synaptic devices based neuromorphic computing applications in artificial intelligence. Mater Today Phys (2021) 18:100393. doi:10.1016/j.mtphys.2021.100393

CrossRef Full Text | Google Scholar

8. Kumar S, Williams RS, Wang ZW. Publisher Correction: third-order nanocircuit elements for neuromorphic engineering. Nature (2020) 592(7853):E9. doi:10.1038/s41586-021-03349-x

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Yi W, Tsang KK, Lam SK, Bai XW, Crowell JA, Flores EA. Biological plausibility and stochasticity in scalable VO₂ active memristor neurons. Nat Commun (2018) 9:4661. doi:10.1038/s41467-018-07052-w

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Wu XY, Saxena V, Zhu KH, Balagopal S. A CMOS spiking neuron for brain-inspired neural networks with resistive synapses and in situ learning. IEEE Trans Circuits Syst Exp Briefs (2015) 62(11):1088–92. doi:10.1109/TCSII.2015.2456372

CrossRef Full Text | Google Scholar

11. Frenkel C, Lefebvre M, Legat JD, Bol D. A 0.086-mm² 12.7-pJ/SOP 64k-synapse 256-neuron online-learning digital spiking neuromorphic processor in 28-nm CMOS. IEEE Trans Biomed Circuits Syst (2019) 13(1):145–58. doi:10.1109/TBCAS.2018.2880425

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Natarajan A, Hasler J. Hodgkin-Huxley neuron and FPAA dynamics. IEEE Trans Biomed Circuits Syst (2018) 12(4):918–26. doi:10.1109/TBCAS.2018.2837055

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Strukov DB, Snider GS, Stewart DR, Williams RS. The missing memristor found. Nature (2008) 453(7250):80–3. doi:10.1038/nature08166

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Li YX, Wang SQ, Yang K, Yang YC, Sun Z. An emergent attractor network in a passive resistive switching circuit. Nat Commun (2024) 15(1):7683. doi:10.1038/s41467-024-52132-9

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Xie Q, Pan XQ, Wang Y, Luo WB, Zhao ZB, Tong JD, et al. Passive LiNbO₃ memristor with multilevel states for neuromorphic computing. IEEE Trans Electron Devices (2024) 71(10):6049–54. doi:10.1109/TED.2024.3450437

CrossRef Full Text | Google Scholar

16. Jin P, Wang G, Liang Y, Lu HHC, Chua LO. Neuromorphic dynamics of Chua corsage memristor. IEEE Trans Circuits Syst Reg Pap (2021) 68(11):4419–32. doi:10.1109/tcsi.2021.3121676

CrossRef Full Text | Google Scholar

17. Qin MH, Lai Q, Fortuna L, Zhao XW. Rich dynamics induced by memristive synapse in Chialvo neuron network. Nonlinear Dyn (2025) 113(13):17095–109. doi:10.1007/s11071-025-10996-6

CrossRef Full Text | Google Scholar

18. Kumar S, Strachan JP, Williams RS. Chaotic dynamics in nanoscale NbO₂ Mott memristors for analogue computing. Nature (2017) 548(7667):318–21. doi:10.1038/nature23307

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Tang D, Wang CH, Lin HR, Yu F. Dynamics analysis and hardware implementation of multi-scroll hyperchaotic hidden attractors based on locally active memristive Hopfield neural network. Nonlinear Dyn (2024) 112(2):1511–27. doi:10.1007/s11071-023-09128-9

CrossRef Full Text | Google Scholar

20. Shen H, Yu F, Kong XX, Mokbel AAM, Wang CH, Cai S. Dynamics study on the effect of memristive autapse distribution on Hopfield neural network. Chaos (2022) 32(8):083133. doi:10.1063/5.0099466

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Xu Q, Fang YJ, Wu HG, Bao H, Wang N. Firing patterns and fast-slow dynamics in an N-type LAM-based FitzHugh-Nagumo circuit. Chaos Solitons and Fractals (2024) 187:115376. doi:10.1016/j.chaos.2024.115376

CrossRef Full Text | Google Scholar

22. Xu Q, Wang YT, Lu HHC, Wang N, Bao H. Locally active memristor-based neuromorphic circuit: firing pattern and hardware experiment. IEEE Trans Circuits Syst Reg Pap (2023) 70(8):3130–41. doi:10.1109/TCSI.2023.3276983

CrossRef Full Text | Google Scholar

23. Yao L, Yu HM, Xiong QP, Sun W, Xu Y, Meng W, et al. Cordycepin decreases compound action potential conduction of frog sciatic nerve in vitro involving Ca²⁺-dependent mechanisms. Neural Plast (2015) 2015:1–7. doi:10.1155/2015/927817

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Dumitru D, King JC, van der Rijt W, Stegeman DF. The biphasic morphology of voluntary and spontaneous single muscle fiber action potentials. Muscle Nerve (1994) 17:1301–7. doi:10.1002/mus.880171109

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Someck S, Levi A, Sloin HE, Spivak L, Gattegno R, Stark E. Positive and biphasic extracellular waveforms correspond to return currents and axonal spikes. Commun Biol (2023) 6:950. doi:10.1038/s42003-023-05328-6

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Watanabe M, Otani NF, Gilmour RF. Biphasic restitution of action potential duration and complex dynamics in ventricular myocardium. Circ Res (1995) 76:915–21. doi:10.1161/01.res.76.5.915

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Chen P, Xiong X, Zhang B, Ye Y, Pan G, Lin P. Neuromorphic auditory classification based on a single dynamical electrochemical memristor. Neuromorphic Comput Eng (2024) 4:014012. doi:10.1088/2634-4386/ad33cc

CrossRef Full Text | Google Scholar

28. Yu F, He S, Yao W, Cai S, Xu Q. Quantitative characterization system for macroecosystem attributes and states. IEEE Trans Comput-aided Des Integr Circuits Syst (2025) 36:1–12. doi:10.13287/j.1001-9332.202501.031

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yu F, Dan S, He S, Wu Y, Zhang S, Yin H. Resonant tunneling diode cellular neural network with memristor coupling and its application in police forensic digital image protection. Chin Phys B (2025) 34:050502. doi:10.1088/1674-1056/adb8bb

CrossRef Full Text | Google Scholar

30. Lai Q, Guo S. Heterogeneous coexisting attractors, large-scale amplitude control and finite-time synchronization of central cyclic memristive neural networks. Neural Networks (2024) 178:106412. doi:10.1016/j.neunet.2024.106412

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wu Y, Li S, Ji Y, Weng Z, Xing H, Arauz L, et al. Enhancing memristor performance with 2D SnOx/SnS2 heterostructure for neuromorphic computing. Sci China Mater (2025) 68:581–9. doi:10.1007/s40843-024-3208-3

CrossRef Full Text | Google Scholar

32. Chua L. Resistance switching memories are memristors. Appl Phys A, Sol Surf. (2011) 102(4):765–83. doi:10.1007/s00339-011-6264-9

CrossRef Full Text | Google Scholar

33. Chua L. If it’s pinched it’s a memristor. Semicond Sci Technol (2013) 29(10):104001. doi:10.1088/0268-1242/29/10/104001

CrossRef Full Text | Google Scholar

34. Chua L. Everything you wish to know about memristors but are afraid to ask. Radioengineering (2015) 24(2):319–68. doi:10.13164/re.2015.0319

CrossRef Full Text | Google Scholar