Synergistic task-offloading in 6G edge networks based on propagation dynamics

In future 6G edge networks, Device-to-Device (D2D)-assisted Mobile Edge Computing (MEC) can fully utilize the idle resources of user terminals (UT) and alleviate the burden on backhaul links. However, the limited idle resources of UT and the over-reliance on D2D-assisted computation offloading may result in a large number of terminals experiencing task overload, which could lead to the risk of edge network paralysis. To address these issues, this paper establishes a Service-Auxiliary-Request-Healing $(SARH)$ task-offloading propagation model based on propagation dynamics theory. This model describes the dynamic transmission process of offloaded tasks in 6G edge networks and constructs two linear threshold functions to characterize the differences in task processing capabilities between UT and edge servers (ES). Furthermore, the proposed task-offloading propagation model is theoretically analyzed using edge compartment theory, and the propagation dynamics equations are established to derive the saddle point and critical conditions leading to task overload in a large number of UT, providing theoretical guidance for preventing network paralysis. Finally, simulation results show that the $SARH$ model effectively describes the task-offloading propagation process in edge networks, and by controlling key factors such as the proportion of UT selecting D2D-assisted MEC synergistic task-offloading, network connectivity density, and network degree distribution heterogeneity, network paralysis can be avoided.

1 Introduction

With the continuous development of the 6G mobile communication networks and the emerging Internet of Things (IoT), the rapid expansion of user terminals (UT) scale and the sharp increase in computation-intensive and latency-sensitive applications, such as immersive cloud augmented reality, holographic communication, autonomous driving, and digital twins [1, 2], have led to an explosive growth in mobile internet data traffic [3, 4]. This has heightened the demand for highly reliable network performance and ultra-low latency [5, 6]. To meet the increasingly stringent requirements of emerging intelligent applications, Device-to-Device (D2D)-assisted Mobile Edge Computing (MEC) technology has been identified as a key enabler to address the challenges faced by 6G edge networks [7–9], representing an essential component of the distributed architecture and ubiquitous edge intelligence envisioned in 6G [10–12]. By offloading complex computational tasks to nearby edge servers (ES) or neighboring UT, this approach can fully utilize the idle computational resources of UT, effectively improving the efficiency of task processing, and significantly reducing task processing delay and energy consumption [11, 13, 14], while also alleviating data traffic pressure on the backhaul link [15, 16]. Therefore, research on D2D-assisted MEC technology is of great significance for 6G edge synergistic networks.

With the widespread application of UT and their increasing intelligence, the MEC collaborative computing offloading model assisted by D2D technology has garnered significant attention from researchers. Hu et al. [12] proposed a fully distributed task offloading algorithm, SITOff, which leverages graph computation and attention mechanisms to enable efficient knowledge collaboration among mobile devices (MDs) in decentralized MEC (D-MEC) systems, thereby enhancing offloading performance without centralized control. Liu et al. [17] formulated a joint optimization scheme considering task offloading and computational resource allocation in D2D-assisted MEC networks by establishing a cost optimization model with multi-objective constraints, aiming to minimize task delay and terminal energy consumption. Dai et al. [18] proposed a collaborative offloading framework that integrates migration costs and offloading willingness into D2D-assisted MEC networks and studied a learning-based task collaboration offloading algorithm to achieve minimum system costs. Wang et al. [19] developed a DRL-based offloading framework, DMOEA, integrating entropy and attention mechanisms to model interactions between D2D cooperation and edge offloading. The framework adopts a multi-agent structure and attention mechanisms to achieve efficient and low-latency dynamic MEC offloading. Jiang et al. [20] introduced a hierarchical deep reinforcement learning (HDRL) framework that combines DQN and DDPG to jointly optimize computation offloading and resource allocation. By employing a multi-level actor-critic architecture, it effectively addresses mixed action spaces and device coordination, significantly reducing task latency. Saleem et al. [21] investigated the question of computational task execution delay and interference under shared resources, proposing a D2D-supported MEC framework and using the Joint Partial Offloading and Resource Allocation (JPORA) allocation scheme to minimize delay. Reference [22] presented a distributed D2D collaboration and task offloading framework that integrates the power-of-two-choices mechanism with a Stackelberg game. By incorporating mean field modeling and Lyapunov optimization, the framework jointly optimizes collaboration efficiency and pricing fairness in large-scale MEC systems.

Most studies mentioned above focus on minimizing task delay, reducing energy consumption, and enhancing network capacity. In 6G edge networks, an increasing number of UT are opting to offload computational tasks to surrounding UT. When a UT node receives an excessive number of offloading tasks, it may become overloaded, losing its ability to provide offloading services, and task processing delays may significantly increase, potentially leading to large-scale network paralysis. Moreover, due to the diversity and large scale of devices in 6G edge networks, challenges such as complex network topology and significant dynamic heterogeneity in service demands arise. Most existing studies lack a comprehensive analysis of the overall state of the network system and fail to consider the dynamic changes in task-offloading propagation in 6G edge synergistic computing networks, as well as the potential risk of network paralysis caused by excessive reliance on D2D-assisted computation offloading. Complex network propagation dynamics theory can reveal the characteristics and dynamic mechanisms of information dissemination within a network and provide insights into the overall state of the network. Therefore, from a system perspective, applying complex network propagation dynamics theory and models to analyze the dynamic task offloading patterns in 6G edge networks is an emerging approach and trend.

Several studies have applied propagation dynamics theory and models to disseminate information and content in networks [23–25]. These works explore the dynamic propagation behavior and patterns in mobile edge networks by applying established propagation dynamics models or constructing new information dissemination models. In [26], a contagious disease model is proposed to study the D2D propagation of malware in wireless IoT, providing a foundation for assisting in planning, designing, and defending such networks from a defender’s perspective. Lien et al. [27] derived a caching and content distribution strategy for edge mobile devices through analysis. An epidemic model was used to analyze the temporal evolution of information dissemination between mobile devices, with optimal control theory applied to cache deployment accordingly. Fan et al. [28] employed a propagation dynamics model to characterize content dissemination between user terminals in mobile edge networks and formulated a joint optimization problem for cache placement and base station resource allocation, maximizing user satisfaction. Hu et al. [29] investigated caching and data-sharing strategies in non-geostationary orbit satellite constellations, deriving the optimal data density threshold based on propagation dynamics and improving the water-filling algorithm and reinforcement learning techniques. Experimental results demonstrated that this strategy effectively reduced both energy consumption and service latency. Ren et al. [30] utilized the diffusion threshold model from propagation dynamics theory to describe the process of collaborative task offloading delivery among terminals in mobile edge networks and its effects. Zhang et al. [31] developed a 6G space-air-ground integrated multi-layer information propagation model based on propagation dynamics, analyzing the impact of network node degree, link relationships, and interference factors on information transmission while discussing key research challenges. Wang et al. [32] proposed an edge caching distribution strategy based on propagation dynamics to address the problem of decreasing cache success rates caused by the time-varying nature of content popularity. Simulation results confirmed that the proposed caching strategy improves cache success rates compared to baseline strategies. These studies leverage established models from propagation dynamics theory, such as epidemic models and threshold adoption models, to explore the dynamic propagation behavior and characteristics of information and content in mobile edge networks, and to propose related optimization algorithms and resource allocation schemes. However, most of the existing research does not consider the dynamic changes in task-offloading propagation and the complexity of network topology in the context of 6G edge synergistic computing networks.

Motivated by the aforementioned studies, and considering the dynamic variations in task-offloading propagation in 6G edge synergistic computing networks as well as the potential network paralysis caused by excessive reliance on D2D technology for computational offloading, this paper establishes a Service-Auxiliary-Request-Healing $(SARH)$ task-offloading propagation model based on propagation dynamics theory. This model is used to investigate the dynamic mechanisms of offloading propagation in 6G edge synergistic computing networks and to explore the topological structure rules and evolutionary mechanisms of the network.

The main contributions of this paper are summarized as follows:

(1) Based on propagation dynamics and threshold theory, this paper proposes a $SARH$ task-offloading propagation model to illustrate the dynamic process and behavioral characteristics of offloading propagation in 6G edge synergistic computing networks. Two types of state transition linear threshold functions are constructed to characterize the differences in task-handling capabilities and capacities between UT and ES.

(2) A theoretical analysis of the proposed $SARH$ task-offloading propagation model is conducted using edge-based compartmental theory. The propagation dynamics equations are established, and the saddle point is derived through mathematical methods. Critical conditions leading to network paralysis in 6G edge synergistic computing networks are identified, providing a theoretical reference to prevent edge network failures, which aids in the deployment of edge communication networks to ensure their stability.

(3) Simulation results demonstrate that the $SARH$ model effectively describes the task-offloading propagation process in 6G edge networks. Additionally, the study explores the effects of the proportion of initially $R$ state UT, the service capacity of individual $A$ state UT, the density of network connections, offloading propagation probability, and network degree distribution heterogeneity on the dynamic offloading propagation process in 6G edge synergistic computing networks. These findings lead to conclusions that can effectively prevent network paralysis, thereby enhancing the efficiency and stability of the network.

The rest of this paper is organized as follows: In Section 2, the System Model is introduced. Section 3 presents the theoretical analysis and derivations. Section 4 provides simulation results along with detailed discussions. In Section 5, the conclusion of this paper is proposed.

2 System model

2.1 6G edge synergistic computing network

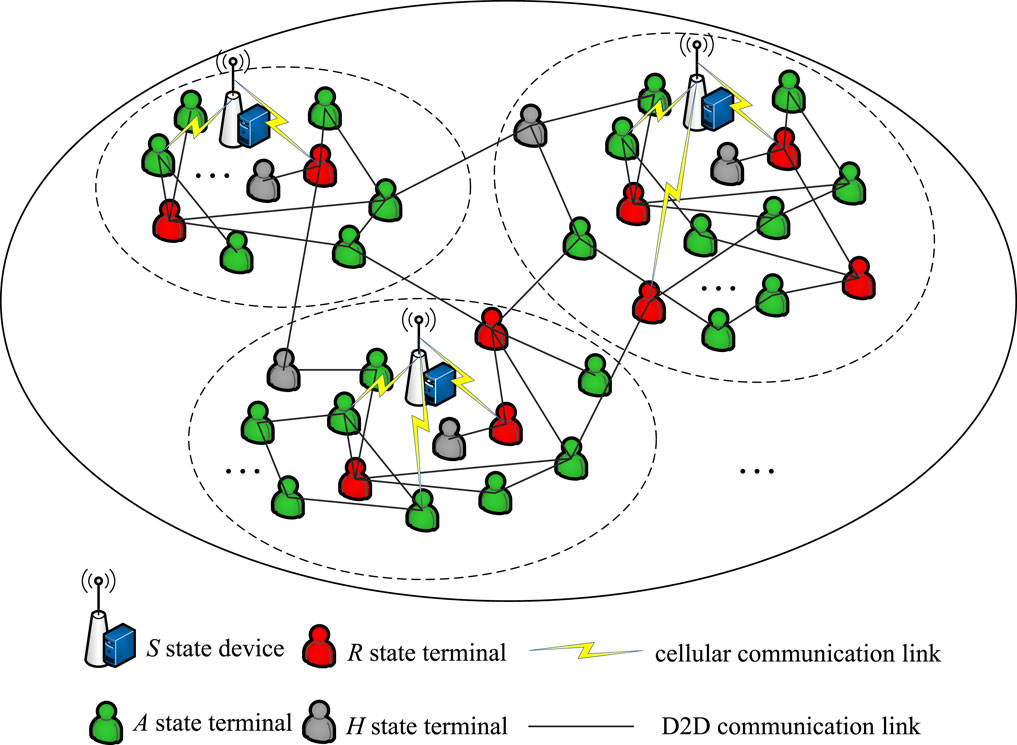
This paper considers a 6G edge synergistic computing network with a total of $N$ node devices and a degree distribution $P(k)$ as shown in Figure 1. In this network, there are four types of node devices: Service state $(S)$, Auxiliary state $(A)$, Request state $(R)$, and Healing state $(H)$. The definitions of these four types of node devices are as follows:

Figure 1

Figure 1. 6G edge synergistic computing network.

$S$ State: These refer to ES that have sufficient computing resources and capacity to provide offloading services for computational tasks, in addition to meeting their task requirements.

$A$ State: These are UT that can meet their task requirements and also provide computational task offloading services.

$R$ State: These UT experience task overload and need to initiate a synergistic computational task offloading request.

$H$ State: These are UT that have recovered from the request state through task offloading and can meet their task requirements. However, due to prior task overload, they are no longer willing to offer computational task offloading services for safety reasons.

In 6G edge synergistic computing networks, communication between two neighboring node devices can be classified into two types: one is D2D communication between UT, and the other is wireless cellular communication between UT and ES. State UT can offload computational tasks to neighboring UT, neighboring ES, or cloud servers for processing. For the sake of analytical simplicity, this paper stipulates that during the task-offloading propagation process within the entire network, each pair of neighboring $R$ state UT and $A$ state UT (or $S$ state devices) can only perform one synergistic computing task-offloading at a time, with each offloading corresponding to one computational task.

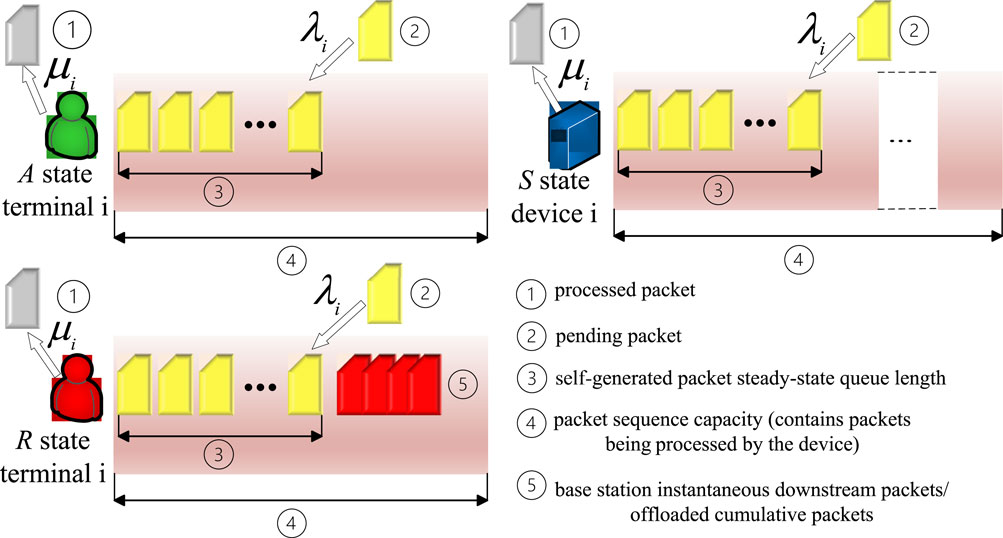
Regardless of the state of the node devices, potential computational tasks are categorized into two types: tasks generated by the device itself and tasks offloaded by neighboring UT. The task arrival and processing models for $S$ state devices, $A$ state terminals, and $R$ state terminals are illustrated in Figure 2. It is assumed that the computational resources required to process a single data packet are identical across all node devices, denoted as $W_0(cycles)$. The set of computational resources available to each node device is represented as $f(cycles/s)=\left\{f_1,f_2,,f_i,,f_N\right\}$, and the set of computational delays for processing a single data packet across the network is $t=\left\{t_1,t_2,,t_i,,t_N\right\}$, where $t_i=W_0/f_i$.

Figure 2

Figure 2. Illustration of task arrival and processing models for $S$ state devices, $A$ state terminals, and $R$ state terminals.

For the locally generated computational tasks, an $M/M/1/N$ queuing model is assumed with an arrival rate of ${\lambda }_i$ and a service rate of ${\mu }_i$. Here, the arrival rate ${\lambda }_i$ represents the number of data packets arriving at the node per second, while the service rate ${\mu }_i$ denotes the number of data packets the node can process per second. Accordingly, the service rate is given by ${\mu }_i=1/t_i$. Let $\rho =\lambda /\mu$, then, according to the queuing model, the steady-state queue length for the data packet sequence generated by the node device itself is $L_i=\rho /(1-\rho )$, where $L_i<N_p,N_q$, with $N_p$ and $N_q$ representing the maximum queue lengths that can be accommodated by each $S$ state device and $A$ state UT, respectively. For tasks offloaded from neighboring $R$ state UT, since the task-offloading transmission process is not stable or continuous, the task processing model differs from that for the node’s tasks. The specific handling mechanism is detailed in the $SARH$ task-offloading propagation model.

2.2 SARH task-offloading propagation model

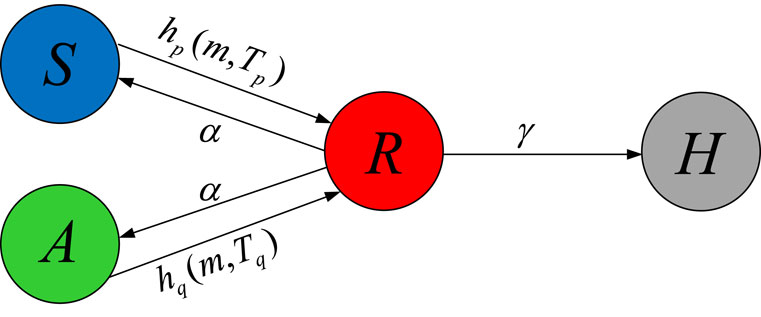
In the 6G edge synergistic computing network scenario, as shown in Figure 3, this paper establishes a $SARH$ model to describe the task-offloading propagation process. It is assumed that the network is in a stable state initially, with two types of node devices in the network: $S$ state and $A$ state. The proportions of $S$ state ES and $A$ state UT are denoted as $p$ and $q$, respectively, with $p+q=1$. At a certain time $t_0$, the base station in the network dispatched an excessive number of computational tasks, resulting in a proportion ${\rho }_0$ of UT experiencing task overload and subsequently transitioning to a $R$ state. In each time step, $R$ state UT may transmit offloading tasks to neighboring $A$ state UT or neighboring ES with a probability $\alpha$. For $A$ state UT, when the accumulated packet sequence exceeds the threshold, they will transition to the $R$ state with a probability $h_q(m,T_q)$. Similarly, $S$ state devices will transition to the $R$ state with a probability $h_p(m,T_p)$. It is generally assumed that ES can provide sufficient computing resources and system capacity, so $S$ state devices remain in the $S$ state. Meanwhile, each $R$ state UT can transition to the $H$ state with a probability $\gamma$, and no longer participate in the task-offloading propagation. The task-offloading propagation process terminates when there are no more $R$ state UT in the network, and the network reaches stability.

Figure 3

Figure 3. Schematic of the $SARH$ task-offloading propagation model.

For analysis, this paper proposes two linear threshold functions to describe the state transition threshold models for UT and ES. For $A$ state UT, the set of stable queue lengths of all UT in the network can be represented as $L_q=\{L_{q,1},\dots ,L_{q,n},\dots ,L_{q,qN}\}$, where the maximum value is denoted as $L_{q,\max }$. The threshold for the number of data packets that each $A$ state UT can accommodate is defined as $T{h}_q=N_q-L_{q,\max }$. The number of offloaded data packets received by the $A$ state UT must not exceed this threshold, otherwise, the terminal will undergo a state transition. Assuming that the number of data packets contained in each offloaded task $P$ satisfies $T{h}_q/(T_q+1)<P<T{h}_q/T_q$, this indicates that the $A$ state UT will not undergo a state transition as long as it receives no more than $T_q$ offloading tasks. Therefore, for $A$ state terminals, the following threshold function is used to represent the relationship between the state transition probability and the number of offloading tasks received:

$h_q\left(m,T_q\right)=\left\{\begin{array}{cc}0,\hfill & 0<m\le T_q\hfill \\ 1,\hfill & m>T_q\hfill \end{array}\right.(1)$

Let $m$ represent the number of computational tasks received by an $A$ state terminal within a time step, and let $h_q(m,T_q)$ denote the state transition probability of the $A$ state UT.

Similarly, for $S$ state devices, the set of stable queue lengths of all ES in the network can be represented as $L_p=\{L_{p,1},L_{p,2},\dots ,L_{p,n},\dots ,L_{p,pN}\}$, where the maximum value is denoted as $L_{p,\max }$. The threshold for the number of data packets that each $S$ state device can accommodate is defined as $T{h}_p=N_p-L_{p,\max }$, with $T{h}_p\gg T{h}_q$. The threshold $T_p$ for the number of offloading tasks that a $S$ state device can receive satisfies $T{h}_p/(T_p+1)<P<T{h}_p/T_p$, where $T_p$ is sufficiently large. Therefore, for service $S$ devices, the following threshold function is used to represent the relationship between the state transition probability and the number of offloading tasks received:

$h_p\left(m,T_p\right)=\left\{\begin{array}{cc}0,\hfill & 0<m\le T_p\hfill \\ 1,\hfill & m>T_p\hfill \end{array}\right.(2)$

$m$ is the number of computational tasks received by the $S$ state device in a time step, and $h_p(m,T_p)$ is the $S$ state device state transition probability.

3 Theoretical analysis

In this paper, $S(t)$, $A(t)$, $R(t)$ and $H(t)$ are used to represent the proportion of node devices in each state. Let $\theta (t)$ denote the probability that neighbor $i$ has not offloaded a task to the $S$ state device (or $A$ state terminal) $j$ before time $t$. If the node degree of $S$ state device (or $A$ state terminal) $j$, i.e., the number of neighboring nodes or devices, is $k_j$, then the probability that node $j$ has received offloaded tasks from $m$ neighbors before time $t$ can be expressed as:

${\varphi }_m\left(k_j,t\right)=C_{k_j}^m\cdot \theta {\left(t\right)}^{k_j-m}\cdot {\left(1-\theta \left(t\right)\right)}^m(3)$

For $A$ state terminal $j$, according to the linear threshold model, its state remains unchanged when it receives no more than $T_q$ offloaded tasks. Therefore, the probability that $A$ state terminal $j$ remains in the auxiliary state at time $t$ is:

$\begin{array}{cc}\hfill A\left(k_j,t\right)& ={\displaystyle \sum _{m=0}^{k_j}}{\varphi }_m\left(k_j,t\right)\cdot \prod _{l=0}^m\left[1-h_q\left(l,T_q\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{m=0}^{T_q}}{\varphi }_m\left(k_j,t\right)\hfill \end{array}(4)$

For a randomly selected $A$ state terminal $j$, given that the degree distribution of the network is $P(k)$, the probability that $A$ state terminals in the entire network do not undergo a state transition at time $t$ is:

${\eta }_q={\displaystyle \sum _{k_j=k_{\min }}^{k_{\max }}}P\left(k_j\right)\cdot A\left(k_j,t\right)(5)$

The proportion of user terminals in the $A$ state in the entire network at time $t$ is:

$A\left(t\right)=\left(1-{\rho }_0\right)\cdot q\cdot {\eta }_q(6)$

For $S$ state device $j$, according to the linear threshold model, its state remains unchanged when it receives no more than $T_p$ offloaded tasks. Therefore, the probability that $S$ state device $j$ remains in the service state at time $t$ is calculated as follows:

$\begin{array}{cc}\hfill S\left(k_j,t\right)& ={\displaystyle \sum _{m=0}^{k_j}}{\varphi }_m\left(k_j,t\right)\cdot \prod _{l=0}^m\left[1-h_p\left(l,T_p\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{m=0}^{T_p}}{\varphi }_m\left(k_j,t\right)\hfill \end{array}(7)$

For a randomly selected $S$ state device $j$, given that the degree distribution of the network is $P(k)$, the probability that $S$ state devices in the entire network maintain their original state at time $t$ is:

${\eta }_p={\displaystyle \sum _{k_j=k_{\min }}^{k_{\max }}}P\left(k_j\right)\cdot S\left(k_j,t\right)(8)$

The proportion of node devices in the service state in the entire network at time $t$ is:

$S\left(t\right)=\left(1-{\rho }_0\right)\cdot p\cdot {\eta }_p(9)$

Since both $A$ state UT and $S$ state ES participate in synergistic task-offloading and provide task-offloading services throughout the entire edge network and offloading propagation process, the roles and state transition mechanisms of $A$ state nodes and $S$ state nodes in the network are similar, with the only difference being their linear propagation thresholds. Therefore, for ease of subsequent analysis, the proportion of $A$ state UT at time $t$, $A(t)$, and the proportion of $S$ state ES at time $t$, $S(t)$, can be combined to obtain $SA(t)$:

$SA\left(t\right)=S\left(t\right)+A\left(t\right)=\left(1-{\rho }_0\right)\cdot \left[p{\eta }_p+q{\eta }_q\right](10)$

where ${\rho }_0$ represents the initial proportion of $R$ state UT. From the analysis, it can be seen that once $\theta (t)$ is obtained, $SA(t)$ can be determined.

Since neighbor node $i$ of $A$ state node $j$ (or $S$ state node $j$) can be in one of four possible states, $\theta (t)$ can be expressed as:

$\theta \left(t\right)={\psi }_S\left(t\right)+{\psi }_A\left(t\right)+{\psi }_R\left(t\right)+{\psi }_H\left(t\right)(11)$

${\psi }_S(t)$, ${\psi }_A(t)$, ${\psi }_R(t)$, and ${\psi }_H(t)$ represent the probabilities that neighbor node $i$ is in the $S$ state, $A$ state, $R$ state, or $H$ state, respectively, and has not offloaded a task to $A$ state (or $R$ state) node $j$ before time $t$. The detailed analysis is as follows:

If neighbor $i$ is an $A$ state terminal and has $k_i$ neighboring nodes, since node $j$ is an $A$ state terminal or $S$ state device, node $j$ will not offload tasks to node $i$. Therefore, node $i$ can only receive offloaded tasks from the remaining $k_i-1$ neighboring nodes. The probability that node $i$ has received $n$ offloaded tasks before time $t$ is:

${\phi }_n\left(k_i-1,t\right)=C_{k_i-1}^n\cdot \theta {\left(t\right)}^{k_i-1-n}\cdot {\left[1-\theta \left(t\right)\right]}^n(12)$

Considering that neighbor $i$ is an $A$ state node and the corresponding linear threshold model, the probability that neighbor $i$ receives $n$ offloaded tasks before time $t$ and does not undergo a state transition at time $t$ is calculated as follows:

$\begin{array}{cc}\hfill {\tau }_A\left(k_i,t\right)& ={\displaystyle \sum _{n=0}^{k_i-1}}{\phi }_n\left(k_i-1,t\right)\cdot \prod _{l=0}^n\left[1-h_q\left(l,T_q\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{n=0}^{T_q}}{\phi }_n\left(k_i-1,t\right)\hfill \end{array}(13)$

In a 6G edge synergistic computing network with a degree distribution of $P(k)$, the probability that node $j$ is a neighbor of node $i$ with degree $k_i$ is given by $k_{i}P(k_i)/⟨k⟩$, where $⟨k⟩$ is the average degree of the network. For a randomly selected node $i$, considering all possible values of $k_i$, the probability that node $i$ is an $A$ state terminal and does not undergo a state transition at time $t$ in the entire network is:

${\psi }_A\left(t\right)=\left(1-{\rho }_0\right)\cdot q\cdot \left[{\displaystyle \sum _{k_i=k_{\min }}^{k_{\max }}}\frac{k_{i}P\left(k_i\right)}{⟨k⟩}\cdot {\tau }_A\left(k_i,t\right)\right](14)$

If neighbor $i$ is a $S$ state device, and since node $j$ is either an $A$ state terminal or a $S$ state device, node $j$ will not offload tasks to node $i$. Therefore, node $i$ can only receive offloaded tasks from the remaining $k_i-1$ neighboring nodes. Considering that neighbor $i$ is a $S$ state node and the corresponding linear threshold model, the probability that neighbor $i$ receives $n$ offloaded tasks before time $t$ and does not undergo $a$ state transition at time $t$ is:

$\begin{array}{cc}\hfill {\tau }_S\left(k_i,t\right)& ={\displaystyle \sum _{n=0}^{k_i-1}}{\phi }_n\left(k_i-1,t\right)\cdot \prod _{l=0}^n\left[1-h_p\left(l,T_p\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{n=0}^{T_p}}{\phi }_n\left(k_i-1,t\right)\hfill \end{array}(15)$

For a randomly selected node $i$, considering all possible values of $k_i$, the probability that node $i$ is a $S$ state device and does not undergo a state transition at time $t$ in the entire network is:

${\psi }_S\left(t\right)=\left(1-{\rho }_0\right)\cdot p\cdot \left[{\displaystyle \sum _{k_i=k_{\min }}^{k_{\max }}}\frac{k_{i}P\left(k_i\right)}{⟨k⟩}\cdot {\tau }_S\left(k_i,t\right)\right](16)$

Similarly, since $A$ state nodes and $S$ state nodes have similar roles and state transition mechanisms in the network, differing only in their linear propagation thresholds, for ease of subsequent analysis, the probabilities of node $i$ being in either the $A$ state or the $S$ state and not undergoing a state transition at time $t$ can be combined. This yields ${\psi }_{S\text{A}}(t)$:

${\psi }_{SA}\left(t\right)=\left(1-{\rho }_0\right)\cdot {\displaystyle \sum _{k_i=k_{\min }}^{k_{\max }}}\frac{k_{i}P\left(k_i\right)}{⟨k⟩}\cdot \epsilon \left(k_i,t\right)(17)$

where, to simplify the equation, let $\epsilon (k_i,t)=p{\tau }_S(k_i,t)+q{\tau }_A(k_i,t)$.

Since $A$ state UT or $S$ state ES do not offload tasks, the probability that node $i$ remains in the $A$ or $S$ state (i.e., does not undergo a state transition) at time $t$ is the same as the probability that neighbor node $i$ is an $A$ state terminal or $S$ state device and has not offloaded tasks to the $A$ state (or $S$ state) node $j$ before time $t$.

If neighbor $i$ is a $R$ state terminal, we need to analyze the evolution equation for ${\psi }_R(t)$. When a $R$ state terminal $i$ offloads tasks to an $A$ state (or $S$ state) node $j$ with probability $\alpha$, the following equation can be obtained:

$\frac{d\theta \left(t\right)}{dt}=-\alpha {\psi }_R\left(t\right)(18)$

If neighbor $i$ is a $H$ state terminal, then within the time interval preceding time $t$, a $R$ state terminal may transition to the $H$ state with probability $\gamma$ after offloading propagation (but not offloading to node $j$). The evolution of ${\psi }_H(t)$ can be expressed by the following equation:

$\frac{d{\psi }_H\left(t\right)}{dt}=\gamma \left(1-\alpha \right){\psi }_R\left(t\right)(19)$

By combining Equation 18 and Equation 19 with the initial conditions $\theta (0)=1$ and ${\psi }_H(0)=0$, the following can be derived:

${\psi }_H\left(t\right)=\gamma \left[1-\theta \left(t\right)\right]\cdot \left(\frac{1}{\alpha }-1\right)(20)$

Substituting Equation 17 and Equation 20 into Equation 11 yields the following expression:

${\psi }_R\left(t\right)=-\left(1-{\rho }_0\right)\cdot {\displaystyle \sum _{k_i=k_{\min }}^{k_{\max }}}\frac{k_{i}P\left(k_i\right)}{⟨k⟩}\cdot \epsilon \left(k_i,t\right)-\gamma \left[1-\theta \left(t\right)\right]\cdot \left(\frac{1}{\alpha }-1\right)+\theta \left(t\right)(21)$

Substituting Equation 21 into Equation 18 allows the evolution of $\theta (t)$ to be re-expressed as follows:

$\frac{d\theta \left(t\right)}{dt}=\alpha \left(1-{\rho }_0\right)\cdot {\displaystyle \sum _{k_i=k_{\min }}^{k_{\max }}}\frac{k_{i}P\left(k_i\right)}{⟨k⟩}\cdot \epsilon \left(k_i,t\right)+\gamma \left(1-\alpha \right)-\left[\gamma +\alpha \left(1-\gamma \right)\right]\cdot \theta \left(t\right)(22)$

In the entire network, according to the propagation dynamics, the density change of each state can be described as follows:

$\frac{dH\left(t\right)}{dt}=\gamma R\left(t\right)(23)$

$\frac{dR\left(t\right)}{dt}=-\frac{dA\left(t\right)}{dt}-\frac{dS\left(t\right)}{dt}-\gamma R\left(t\right)(24)$

Therefore, by combining and iterating Equation 6, Equation 9, Equation 10, Equation 3, Equation 23 and Equation 24, the proportions and evolution trends of the node devices in the four states—$S(t)$, $A(t)$, $R(t)$ and $H(t)$—across the entire network at any given time can be computed.

According to the linear threshold model and the $SARH$ task-offloading propagation model, as $t\to \infty$, the system stabilizes, offloading propagation ceases, and only $A$ state, $S$ state, and $H$ state UT or ES remain in the network, with no $R$ state UT present. Thus, ${\left.\frac{d\theta (t)}{dt}\right|}_{t=\infty }\to 0$, from which the following can be derived:

$\begin{array}{c}\theta \left(\infty \right)=\frac{\alpha \left(1-{\rho }_0\right)\cdot {\displaystyle \sum _{k_i=k_{\min }}^{k_{\max }}}{k}_{i}P\left(k_i\right)\cdot \epsilon \left(k_i,t\right)+⟨k⟩\gamma \left(1-\alpha \right)}{⟨k⟩\gamma +\alpha \left(1-\gamma \right)⟨k⟩}\end{array}(25)$

By combining and iterating Equation 6, Equation 9, Equation 10, and Equation 25, along with $R(\infty )=0$, the values of $S(\infty )$, $A(\infty )$, $SA(\infty )$, and $H(\infty )$ can be determined. The phenomenon of behavioral adoption outbreaks, similar to social propagation processes, warrants attention [33–35]. Therefore, the critical condition for task overload leading to network failure due to a large number of UT in a short period can be determined by deriving the non-trivial solution of Equation 25. Let the function be as shown in Equation 26.

$y\left[\theta \left(\infty \right)\right]=\frac{\alpha \left(1-{\rho }_0\right)\cdot {\displaystyle \sum _{k_i=k_{\min }}^{k_{\max }}}{k}_{i}P\left(k_i\right)\cdot \epsilon \left(k_i,\infty \right)}{\langle k\rangle \gamma +\alpha \left(1-\gamma \right)\langle k\rangle }-\theta \left(\infty \right)+\frac{\gamma \left(1-\alpha \right)}{\gamma +\alpha \left(1-\gamma \right)}(26)$

From the analysis, it can be seen that the solution to the critical condition corresponds to the x-coordinate ${\theta }_c(\infty )$ of the point where the function Equation 26 is tangent to the horizontal axis. Here, ${\theta }_c(\infty )$ represents the probability that no offloaded tasks will be propagated to $A$ state (or $S$ state) node $j$ under the critical offloading propagation probability ${\alpha }_c$, once the network has stabilized. Therefore, the critical condition is defined as follows:

${\left.\frac{dy}{d\theta \left(\infty \right)}\right|}_{\theta \left(\infty \right)={\theta }_c\left(\infty \right)}=0(27)$

Solving Equation 27 yields the critical offloading probability:

${\alpha }_c=\frac{\gamma }{\mathrm{\Delta }+\gamma -1}(28)$

where,

$\begin{array}{c}\hfill \begin{array}{c}\mathrm{\Delta }=\left(1-{\rho }_0\right)\cdot {\displaystyle \sum _{k_i=k_{\min }}^{k_{\max }}}{\frac{k_{i}P\left(k_i\right)}{⟨k⟩}\cdot \left.\frac{d\epsilon \left(k_i,\infty \right)}{d\theta \left(\infty \right)}\right|}_{\theta \left(\infty \right)={\theta }_c\left(\infty \right)}\end{array}\end{array}(29)$

From the results of Equation 28 and Equation 29, it can be seen that the critical offloading propagation probability ${\alpha }_c$ is not only directly related to dynamic parameters such as the initial proportion of $R$ state UT ${\rho }_0$, the healing rate of $R$ state UT $\gamma$, and the maximum number of $R$ state UT $T_q$ that a single $A$ state UT can serve, but also depends on network structural parameters such as the average network degree $⟨k⟩$ and the network degree distribution $P(k)$.

4 Simulation results and analysis

4.1 Simulation settings

Considering a large number of nodes and the complex topology in 6G edge synergistic computing networks, extensive simulation and numerical analysis were conducted on both Erdos-Renyi $(ER)$ networks [36] and Scale-Free $(SF)$ networks [37] to verify the universality and applicability of the theoretical analysis. In $ER$ random networks, node degrees follow a Poisson distribution, i.e., $P(k)=e^{-⟨k⟩}⟨k⟩/k!$, where random connections are generated based on a probability mechanism, reflecting the characteristic of random node distribution. In $SF$ networks, the degree distribution follows a power-law, i.e., $P(k)\stackrel{̃}{}{k}^{-v}$, where the scale-free property highlights the phenomenon where a few nodes take on a large number of connections, which corresponds to the importance of certain key nodes in 6G edge synergistic computing networks. The parameter $v$ represents the degree distribution exponent of the $SF$ network, where the degree distribution is negatively correlated with $v$; the smaller the value of $v$, the more heterogeneous the network, leading to stronger network heterogeneity. The fixed parameters, including network size, offloading propagation probability, and the healing rate of $R$ state UT, are set as $N={10}^4$, $\alpha \in [\mathrm{0,1}]$ and $\gamma =1.0$, respectively. The network size of ${10}^4$ refers to 10,000 independent dynamic entities within the mobile edge network, including UT and ES. Based on the system model and the characteristics of practical mobile edge communication systems, it can be concluded that each $R$ state UT will ultimately be able to process its accumulated computational tasks through edge synergistic computing offloading, cloud computing offloading, or other offloading methods, thereby transitioning back to the idle state. However, due to prior experiences of task overload, for safety considerations and the inherent selfishness of UT, these terminals are no longer willing to provide computational task-offloading services and instead transition into the $H$ state. Therefore, this study assumes the healing rate of state UT as $\gamma =1.0$.

$H(\infty )$ represents the proportion of H state UT in the network when the entire network reaches a stable state after a sufficiently long period. It indirectly reflects the total number of R state nodes that experienced task overload and computation offloading requests throughout the entire synergistic task-offloading propagation process. A sudden surge in $H(\infty )$ at a certain moment indicates a large number of devices experiencing task overload within a short period, signifying a network paralysis scenario.

The parameters influencing the offloading propagation process can be categorized into dynamic parameters and network structural parameters. The dynamic parameters include the initial proportion of $R$ state UT ${\rho }_0$, the maximum number of $R$ state UT that a single $A$ state UT can serve $T_q$, the initial proportion of $A$ state UT $q$, and the maximum number of $R$ state UT that a single $S$ state ES can serve $T_p$. The network structural parameters include the average degree of $ER$ networks $⟨k⟩$ and the degree distribution exponent $v$ for $SF$ networks. The following sections will discuss the impact of these dynamic and network structural parameters on the offloading propagation process.

4.2 Results and discussion

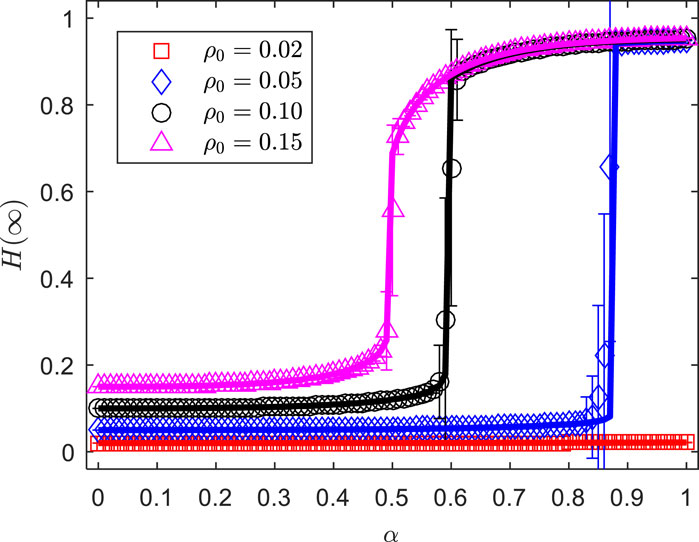
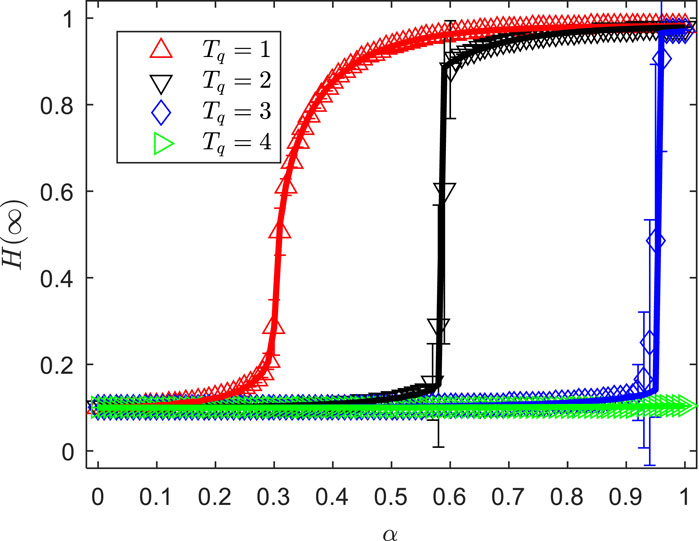
Figure 4 explores the variation of the proportion of UT in the final $H$ state, $H(\infty )$, with the offloading propagation probability, $\alpha$, as the initial proportion of $R$ state UT, ${\rho }_0$, changes in $ER$ networks. The other parameters are set as $N={10}^4$, $\alpha \in [\mathrm{0,1}]$, $\gamma =1.0$, $⟨k⟩=10$, $T_q=2$, $T_p=50$ and $q=0.95$. As observed in the figure, when the initial proportion of $R$ state UT is relatively small ${\rho }_0=0.02$, the proportion of UT in the final $H$ state, $H(\infty )$, shows almost no increase as the offloading propagation probability, $\alpha$, gradually increases. This indicates that the task-offloading process only affects a very small portion of $A$ state terminals that transition to $R$ state terminals, implying that the computational resources and capacity provided by the 6G edge synergistic computing network can handle the task-offloading of a certain proportion of $R$ state UT. However, when the initial proportion of $R$ state UT increases to a certain level ${\rho }_0=0.05,0.10$, the proportion of UT in the final $H$ state, $H(\infty )$, initially increases slowly within a certain range as the offloading propagation probability, $\alpha$, gradually increases. When $\alpha$ reaches a certain value, $H(\infty )$ experiences a sudden increase, reaching a significantly higher proportion. This phenomenon is referred to as a first-order discontinuous phase transition in the field of propagation dynamics [38], and the offloading propagation probability at which this sudden surge in $H(\infty )$ occurs is known as the critical offloading probability, ${\alpha }_c$. When such a first-order discontinuous phase transition occurs during the offloading process in the network, it indicates that a large number of $A$ state terminals in the network have quickly experienced task overload and resource shortages, transitioning to $R$ state terminals, which ultimately leads to network paralysis. It is worth noting that the larger the proportion of $R$ state UT selecting the D2D-assisted MEC synergistic task-offloading method $\alpha$, the more likely network paralysis will occur. A higher initial proportion of $R$ state UT ${\rho }_0$ indicates a greater volume of computational tasks that need to be offloaded in a short period at the initial stage, thus requiring a smaller $\alpha$ to cause network paralysis. Comparing the variation of $H(\infty )$ with $\alpha$ for ${\rho }_0=0.05$, ${\rho }_0=0.10$, and ${\rho }_0=0.15$ in Figure 5, it can be observed that the larger the initial proportion of $R$ state UT ${\rho }_0$, the smaller the critical offloading probability corresponding to network paralysis caused by task overload on a large number of $A$ UT. This demonstrates that the theoretical analysis results are consistent with the simulation outcomes.

Figure 4

Figure 4. The impact of the initial proportion of $R$ state user terminals ${\rho }_0$ on the variation of the proportion of final $H$ state user terminals $H(\infty )$ with the offloading propagation probability $\alpha$ in $ER$ networks.

Figure 5

Figure 5. The impact of the maximum number of $R$ state user terminals that a single $A$ state terminal can serve, $T_q$, on the variation of the proportion of terminal users in the final $H$ state, $H(\infty )$, with the offloading propagation probability, $\alpha$, in $ER$ networks.

Figure 5 shows the variation pattern of the proportion of UT in the final $H$ state, $H(\infty )$, with the offloading propagation probability, $\alpha$, as the maximum number of $R$ state UT that a single $A$ state UT can serve, $T_q$, changes. The other parameters are set as $N={10}^4$, $\alpha \in [\mathrm{0,1}]$, $\gamma =1.0$, $⟨k⟩=10$, ${\rho }_0=0.10$, $T_p=50$ and $q=0.98$. As observed in Figure 5, when a single $A$ state terminal can only serve one $R$ state terminal $T_q=1$, $H(\infty )$ gradually increases in a small range before reaching the critical offloading propagation probability, ${\alpha }_c$, at which point a discontinuous phase transition occurs, leading to network paralysis. As the maximum number of $R$ state terminals that a single $A$ state terminal can serve increases $T_q=2$ and $T_q=3$, the critical offloading propagation probability at which task overload causes a large number of $A$ state terminals to fail, resulting in network paralysis, also increases. Additionally, by comparing the variation trends of $H(\infty )$ with the offloading propagation probability $\alpha$ for $T_q=1$, $T_q=2$ and $T_q=3$, it can be observed that the stronger the task-offloading service capacity of a single $A$ state terminal, the greater the increase in the proportion of $H$ state terminals when the network stabilizes at the critical offloading propagation probability. However, when $T_q=4$, $H(\infty )$ increases slowly within a small range as $\alpha$ increases, and no matter how large $\alpha$ becomes, $H(\infty )$ will not undergo a discontinuous phase transition, meaning that network paralysis does not occur. From this, it can be inferred that the stronger the service capacity of a single $A$ state terminal, the larger the proportion of $R$ state terminals allowed to select mobile edge synergistic task-offloading before network paralysis occurs. If the service capacity of a single $A$ state terminal is sufficiently strong, the task-offloading capacity of the mobile edge synergistic computing network will be able to handle the task load, keeping the network in a stable state without the risk of paralysis. Simulation results indicate that if the proportion of user terminals opting for D2D-assisted MEC synergistic task-offloading remains below the critical offloading propagation probability, network paralysis can be avoided. Therefore, controlling the proportion of user terminals selecting D2D-assisted MEC synergistic task-offloading is essential to ensuring the stability and efficiency of the synergistic task-offloading network.

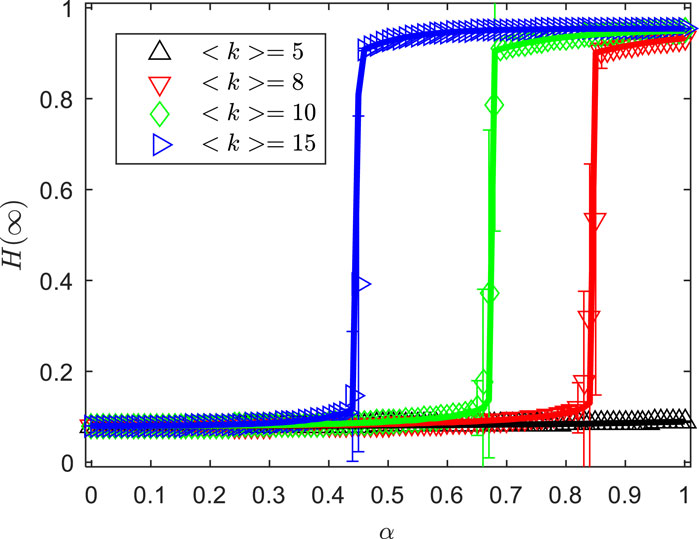
Figure 6 illustrates the growth trend and pattern of the proportion of terminal users in the final $H$ state, $H(\infty )$, with the offloading propagation probability, $\alpha$, as the network topology of the $ER$ network changes. The other parameters are set as $N={10}^4$, $\alpha \in [\mathrm{0,1}]$, $\gamma =1.0$, $T_q=2$, ${\rho }_0=0.08$, $T_p=50$ and $q=0.95$. As shown in Figure 6, when the average degree is relatively low $(⟨k⟩=5)$, the connections between the network nodes are sparse, and $H(\infty )$ shows almost no increase with increasing offloading propagation probability, $\alpha$, and no phase transition is observed. As the average degree increases ($⟨k⟩=8$, $⟨k⟩=10$, and $⟨k⟩=15$), $H(\infty )$ increases continuously within a small range as $\alpha$ increases, until a discontinuous phase transition occurs at the critical offloading propagation probability. Moreover, the larger the $⟨k⟩$, the smaller the critical offloading propagation probability at which the first-order discontinuous phase transition of $H(\infty )$ occurs. In practical mobile communication networks, the average degree $⟨k⟩$ represents the average number of communication links established by each dynamic entity (UT or ES) with $⟨k⟩$ other UT (or ES), enabling the transmission of offloaded computational tasks. A larger average degree $⟨k⟩$ means that, on average, each UT (or ES) has more communication links with neighboring devices, resulting in a more tightly connected network, which is more conducive to task offloading propagation. Under constant conditions of other parameters, a larger network average degree $⟨k⟩$ leads to faster and earlier global diffusion of task offloading, while reducing the maximum proportion of $R$ state UT allowed to choose mobile edge synergistic task-offloading. Therefore, controlling the average number of communication links (i.e., the network connectivity density) among devices (UT and ES) can help prevent network paralysis caused by task overloads from a large number of UT.

Figure 6

Figure 6. The variation curve of the proportion of users terminal in the final $H$ state, $H(\infty )$, with the offloading propagation probability, $\alpha$, under different average degree $⟨k⟩$ values in $ER$ networks.

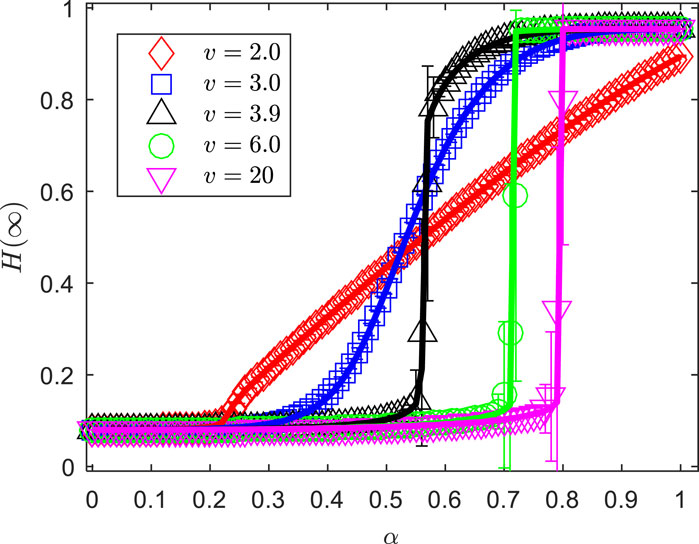
Figure 7 illustrates the impact of the degree distribution heterogeneity of the $SF$ network on the variation trend of the proportion of UT in the final $H$ state, $H(\infty )$, for the offloading propagation probability, $\alpha$. The other parameters are set as $N={10}^4$, $\alpha \in [\mathrm{0,1}]$, $\gamma =1.0$, $T_q=2$, ${\rho }_0=0.08$, $T_p=100$ and $q=0.95$. It can be observed from the figure that when the degree distribution exponents, $v$, are 2.0, 3.0, and 3.9, there are two trends in the growth of $H(\infty )$ as $\alpha$ increases: when the probability of $R$ state UT opting for D2D-assisted MEC synergistic task-offloading is relatively low, $H(\infty )$ decreases as $v$ increases; conversely, when the probability is relatively high, $H(\infty )$ increases with the growth of $v$. This is because, for scale-free networks with a power-law degree distribution (such as $SF$ networks), the smaller the degree distribution exponent $v$, the stronger the heterogeneity of the network’s degree distribution. In such networks, there is a large number of nodes with very small degrees and a few nodes with very large degrees. When the propagation probability is relatively low, the nodes with smaller degrees, which are more numerous, play a major role in information dissemination and are more likely to receive information fragments exceeding the threshold, thereby undergoing state transitions. However, as the propagation probability increases, the influence of high-degree nodes on the dissemination process gradually becomes more significant, reducing the probability of smaller-degree nodes adopting the behavior, ultimately resulting in a smaller propagation scale [39]. Additionally, it can be observed from the figure that as the degree distribution exponent $v$ increases, the variation trend of $H(\infty )$ with the offloading propagation probability $\alpha$ transitions from a second-order continuous phase transition to a first-order discontinuous phase transition. Through extensive simulations, a critical degree distribution exponent, $v_c=3.9$, was identified. When $v<v_c$, $H(\infty )$ exhibits continuous growth, while when $v>v_c$, $H(\infty )$ shows discontinuous growth. These two phenomena indicate that as the network becomes more uneven, deploying high-degree nodes as $S$ state devices can prevent the network from crashing prematurely due to task overload in a large number of UT. The higher the maximum proportion of $R$ state UT allowed to request D2D-assisted MEC synergistic task-offloading, the greater the network’s stability and efficiency.

Figure 7

Figure 7. The variation pattern of the proportion of terminal users in the final $H$ state, $H(\infty )$, with respect to the offloading propagation probability, $\alpha$, for different degree distribution exponents $v$ in $SF$ networks.

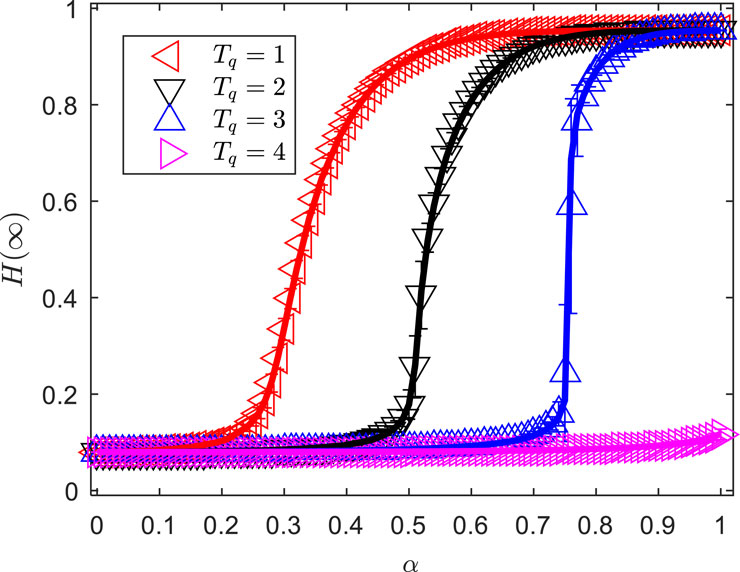
As shown in Figure 8, this paper further investigates the impact of the maximum number of $R$ state UT, $T_q$, that can be served by a single $A$ state UT on the proportion of final $H$ state UT, $H(\infty )$, as it changes with the task offloading propagation probability, $\alpha$, in a $SF$ network with a power-law degree distribution. When $T_q=1$, $T_q=2$, and $T_q=3$, $H(\infty )$ increases continuously with $\alpha$ within a small range, and starts to increase sharply at the critical offloading propagation probability. Moreover, as $T_q$ increases, the growth trend of $H(\infty )$ with $\alpha$ shifts from continuous to discontinuous, and the critical offloading propagation probability, at which $H(\infty )$ increases sharply, becomes larger. When $T_q=4$, $H(\infty )$ only increases continuously within a small range without a sudden increase as $\alpha$ rises. By comparing Figures 5, 8, it can be seen that the effect of $T_q$ on the variation of $H(\infty )$ with $\alpha$ in an $SF$ network is generally consistent with its effect in an $ER$ network. This demonstrates that, regardless of whether the network structure is $ER$ or $SF$, the stronger the service capability of a single $A$ state UT, the more stable the network becomes. Therefore, improving the task-offloading service capability of UT is an effective method to enhance the efficiency and stability of 6G edge synergistic computing networks.

Figure 8

Figure 8. The impact of offloading propagation probability $\alpha$ and the maximum number of $R$ state user terminals $T_q$ that can be served by a single $A$ state user terminal on the proportion of final $H$ state user terminals $H(\infty )$ in a $SF$ network with heterogeneous degree distribution.

5 Conclusion

This paper investigates the dynamics, evolutionary mechanisms, and influencing factors involved in task-offloading propagation within the context of a 6G edge synergistic computing network. Based on propagation dynamics theory, a $SARH$ task offloading propagation model is established. Furthermore, two types of state transition linear threshold functions are proposed to characterize the differences in task processing capabilities and capacities between UT and ES. Through mathematical methods, the saddle point of the dynamic equations is derived, and critical conditions leading to network paralysis in 6G edge synergistic computing networks are obtained. These findings provide theoretical insights into preventing paralysis in edge networks, contributing to the stable deployment of edge communication networks. Simulation results demonstrate that the proposed task-offloading propagation dynamics model effectively describes the behavior and characteristics of task-offloading in 6G edge synergistic computing networks. Additionally, through the analysis of simulation outcomes, several conclusions are drawn that help to avoid network paralysis, thereby enhancing network efficiency and stability. In future work, we aim to further improve the task-offloading propagation dynamics model based on this research, incorporating factors such as terminal selfishness and heterogeneous user behaviors to better align the model with real-world scenarios and accommodate more complex conditions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

CZ: Writing – original draft, Writing – review and editing. YZ: Writing – original draft, Writing – review and editing. XW: Writing – original draft, Writing – review and editing. XZ: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The work was supported in part by Sub Project of National Key Research and Development plan in 2020. NO. 2020YFC1511704, Beijing Information Science & Technology University. NO.2020KYNH212, NO. 2021CGZH302. Beijing Science and Technology Project (Grant No. Z211100004421009), and in part by the National Natural Science Foundation of China (Grant No.: 62301058).

Acknowledgments

We are grateful for the contributions made by Frontiers editorial staff members. We also thank the reviewers who provided valuable input for each manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Liu Y, Peng M, Shou G, Chen Y, Chen S. Toward edge intelligence: multiaccess edge computing for 5g and internet of things. IEEE Internet Things J (2020) 7:6722–47. doi:10.1109/JIOT.2020.3004500

CrossRef Full Text | Google Scholar

2. Vaezi M, Azari A, Khosravirad SR, Shirvanimoghaddam M, Azari MM, Chasaki D, et al. Cellular, wide-area, and non-terrestrial iot: a survey on 5g advances and the road toward 6g. IEEE Commun Surv and Tutorials (2022) 24:1117–74. doi:10.1109/COMST.2022.3151028

CrossRef Full Text | Google Scholar

3. Zhang Y, Gang Y, Wu P, Fan G, Xu W, Ai B, et al. Integrated sensing, communication, and computation in sagin: joint beamforming and resource allocation. IEEE Trans Cogn Commun Networking (2025) 1–doi. doi:10.1109/TCCN.2025.3577377

CrossRef Full Text | Google Scholar

4. Fan X, Chen H, Ni Z, Li G, Sun H, Yu J. Multi-agent collaborative caching strategies in dynamic heterogeneous d2d networks. IEEE Trans Vehicular Technology (2024) 73:7204–17. doi:10.1109/TVT.2023.3345863

CrossRef Full Text | Google Scholar

5. Tan C, Yu P, Li W, Zhou F, Wang Y, Xu S, et al. Self-adaptive and efficient training node selection for federated learning in b5g/6g edge network. In: NOMS 2023-2023 IEEE/IFIP network operations and management symposium. (2023) IEEE p. 1–5.

CrossRef Full Text | Google Scholar

6. Wang J, Hu Y, Zhu Y, Wang T, Schmeink A. Reliability-optimal offloading for mobile edge-computing in low-latency industrial iot networks. IEEE Trans Wireless Commun (2024) 23:12765–81. doi:10.1109/TWC.2024.3396161

CrossRef Full Text | Google Scholar

7. Liu W, Zhang H, Ding H, Yu Z, Yuan D. Recommendation based video caching and transcoding in mobile edge networks. IEEE Trans Vehicular Technology (2024) 73:6572–83. doi:10.1109/TVT.2023.3338231

CrossRef Full Text | Google Scholar

8. Wang D, Wang W, Gao H, Zhang Z, Han Z. Delay-optimal computation offloading in large-scale multi-access edge computing using mean field game. IEEE Trans Wireless Commun (2024) 23:1684–98. doi:10.1109/TWC.2023.3291198

CrossRef Full Text | Google Scholar

9. Kim M, Cho H, Cui Y, Lee J. Joint service caching and computing resource allocation for edge computing-enabled networks. IEEE Trans Wireless Commun (2023) 22:9029–44. doi:10.1109/TWC.2023.3267829

CrossRef Full Text | Google Scholar

10. Siriwardhana Y, Porambage P, Liyanage M, Ylianttila M. A survey on mobile augmented reality with 5g mobile edge computing: architectures, applications, and technical aspects. IEEE Commun Surv and Tutorials (2021) 23:1160–92. doi:10.1109/COMST.2021.3061981

CrossRef Full Text | Google Scholar

11. Zhao Y, Xiao A, Wu S, Jiang C, Kuang L, Shi Y. Adaptive partitioning and placement for two-layer collaborative caching in mobile edge computing networks. IEEE Trans Wireless Commun (2024) 23:8215–31. doi:10.1109/TWC.2023.3346885

CrossRef Full Text | Google Scholar

12. Hu Z, Niu J, Ren T, Liu X, Guizani M. Sitoff: enabling size-insensitive task offloading in d2d-assisted mobile edge computing. IEEE Trans Mobile Comput (2025) 24:1567–84. doi:10.1109/TMC.2024.3483951

CrossRef Full Text | Google Scholar

13. Fang T, Yuan F, Ao L, Chen J. Joint task offloading, d2d pairing, and resource allocation in device-enhanced mec: a potential game approach. IEEE Internet Things J (2022) 9:3226–37. doi:10.1109/JIOT.2021.3097754

CrossRef Full Text | Google Scholar

14. Li J, Ou W, Ouyang B, Ye S, Zeng L, Chen L, et al. Revisiting location privacy in mec-enabled computation offloading. IEEE Trans Inf Forensics Security (2025) 20:4396–407. doi:10.1109/TIFS.2025.3558593

CrossRef Full Text | Google Scholar

15. Wang X, Wang X, Wang C, Zeng R, Ma L, He Q, et al. Truthful online combinatorial auction-based mechanisms for task offloading in mobile edge computing. IEEE Trans Mobile Comput (2025) 24:6488–502. doi:10.1109/TMC.2025.3542135

CrossRef Full Text | Google Scholar

16. Wang L, Deng X, Zhang H, Wan S, Min G. Multitask-oriented efficient computational offloading orchestrator for iot applications in mobile-edge computing. IEEE Internet Things J (2025) 12:14096–108. doi:10.1109/JIOT.2025.3526984

CrossRef Full Text | Google Scholar

17. Liu Z, Fan J, Geng S, Qin P, Zhao X. Joint optimization of task offloading and computing resource allocation in mec-d2d network. In: 2022 IEEE 5th international conference on computer and communication engineering technology (CCET). (2022) IEEE p. 256–60.

Google Scholar

18. Dai X, Xiao Z, Jiang H, Alazab M, Lui JCS, Dustdar S, et al. Task co-offloading for d2d-assisted mobile edge computing in industrial internet of things. IEEE Trans Ind Inform (2023) 19:480–90. doi:10.1109/TII.2022.3158974

CrossRef Full Text | Google Scholar

19. Wang C, Chai X, Peng S, Yuan Y, Li G. Deep reinforcement learning with entropy and attention mechanism for d2d-assisted task offloading in edge computing. IEEE Trans Serv Comput (2024) 17:3317–29. doi:10.1109/TSC.2024.3495503

CrossRef Full Text | Google Scholar

20. Jiang W, Feng D, Sun Y, Feng G, Wang Z, Xia X-G. Joint computation offloading and resource allocation for d2d-assisted mobile edge computing. IEEE Trans Serv Comput (2023) 16:1–14. doi:10.1109/tsc.2022.3190276

CrossRef Full Text | Google Scholar

21. Saleem U, Liu Y, Jangsher S, Tao X, Li Y. Latency minimization for d2d-enabled partial computation offloading in mobile edge computing. IEEE Trans Vehicular Technology (2020) 69:4472–86. doi:10.1109/TVT.2020.2978027

CrossRef Full Text | Google Scholar

22. Wang X, Ye J, Lui JCS. Mean field graph based d2d collaboration and offloading pricing in mobile edge computing. IEEE/ACM Trans Networking (2024) 32:491–505. doi:10.1109/TNET.2023.3288558

CrossRef Full Text | Google Scholar

23. Xiao Y, He W, Yang T, Li Q. A dynamic information dissemination model based on user awareness and evolutionary games. IEEE Trans Comput Social Syst (2023) 10:2837–46. doi:10.1109/TCSS.2022.3201061

CrossRef Full Text | Google Scholar

24. Zhang Y, Zou L, Pan D. Cloud-edge collaboration dynamics information dissemination model for social internet of things. IEEE Trans Netw Sci Eng (2023) 10:1905–18. doi:10.1109/TNSE.2023.3236478

CrossRef Full Text | Google Scholar

25. Rashidi L, Dalili-Yazdi A, Entezari-Maleki R, Sousa L, Movaghar A. Modeling epidemic routing: capturing frequently visited locations while preserving scalability. IEEE Trans Vehicular Technology (2021) 70:2713–27. doi:10.1109/TVT.2021.3057541

CrossRef Full Text | Google Scholar

26. Chen M, Wang H, Han D, Chu X. Signaling-based incentive mechanism for d2d computation offloading. IEEE Internet Things J (2022) 9:4639–49. doi:10.1109/JIOT.2021.3107945

CrossRef Full Text | Google Scholar

27. Lien S-Y, Hung S-C, Hsu H. Latency control in edge information cache and dissemination for unmanned mobile machines. IEEE Trans Ind Inform (2018) 14:4612–21. doi:10.1109/TII.2018.2834619

CrossRef Full Text | Google Scholar

28. Fan S, Gao H, Tian H, Yang S. Evolutionary adaptation mechanism for edge caching under propagation dynamics. IEEE Internet Things J (2024) 11:15179–92. doi:10.1109/JIOT.2023.3347415

CrossRef Full Text | Google Scholar

29. Hu Z, Jiang Z, Zhao J, Li Y. Joint optimization of energy and delay in ngso satellite constellations: cached data sharing based on spreading dynamics. IEEE Trans Vehicular Technology (2023) 72:7884–99. doi:10.1109/TVT.2023.3241332

CrossRef Full Text | Google Scholar

30. Ren S, Xu X, Han S. Device-collaborative computation offloading in mobile edge networks based on propagation dynamics theory. In: 2023 2nd international joint conference on information and communication engineering (JCICE). (2023) IEEE p. 85–9.

Google Scholar

31. Zhang Y, Wang X, Gang Y, Wang J, Wu S, Zhang P, et al. 6g sagin information transmission model. IEEE Commun Mag (2025) 63:98–105. doi:10.1109/MCOM.001.2400351

CrossRef Full Text | Google Scholar

32. Wang X, Zhang Y, Zhang S. Epidemic dynamics edge caching strategy for 6g networks. Front Phys (2024) 12:1410472. doi:10.3389/fphy.2024.1410472

CrossRef Full Text | Google Scholar

33. Wang W, Tang M, Zhang H-F, Lai Y-C. Dynamics of social contagions with memory of nonredundant information. Phys Rev e (2015) 92:012820. doi:10.1103/physreve.92.012820

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Wang W, Tang M, Shu P, Wang Z. Dynamics of social contagions with heterogeneous adoption thresholds: crossover phenomena in phase transition. New J Phys (2016) 18:013029. doi:10.1088/1367-2630/18/1/013029

CrossRef Full Text | Google Scholar

35. Wang X, Lan Y, Xiao J. Measuring the hierarchical influence in social contagions and the emergence of crossover phase transitions. Physica A: Stat Mech its Appl (2019) 531:121721. doi:10.1016/j.physa.2019.121721

CrossRef Full Text | Google Scholar

36. Erdös P, Rényi A. On the evolution of random graphs. In: The structure and Dy-namics of networks. Princeton: Princeton University Press (2006). p. 38–82doi. doi:10.1515/9781400841356.38

CrossRef Full Text | Google Scholar

37. Zhang X. Model design of wireless sensor network based on scale-free network theory. In: 2009 5th international conference on wireless communications, networking and mobile computing. (2009) IEEE p. 1–4.

CrossRef Full Text | Google Scholar

38. Wang W, Shu P, Zhu Y-X, Tang M, Zhang Y-C. Dynamics of social contagions with limited contact capacity. Chaos: An Interdiscip J Nonlinear Sci (2015) 25:103102. doi:10.1063/1.4929761

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Zhu X, Wang W, Cai S, Stanley HE. Dynamics of social contagions with local trend imitation. Scientific Rep (2018) 8:7335. doi:10.1038/s41598-018-25006-6

PubMed Abstract | CrossRef Full Text | Google Scholar