Mind as music

Cognitive neuroscience typically develops hypotheses to explain phenomena that are localized in space and time. Specific regions of the brain execute characteristic functions, whose causes and effects are prompt; determining these functions in spatial and temporal isolation is generally regarded as the first step toward understanding the coherent operation of the whole brain over time. In other words, if the task of cognitive neuroscience is to interpret the neural code, then the first step has been semantic, searching for the meanings (functions) of localized elements, prior to exploring neural syntax, the mutual constraints among elements synchronically and diachronically. While neuroscience has made great strides in discovering the functions of regions of the brain, less is known about the dynamic patterns of brain activity over time, in particular, whether regions activate in sequences that could be characterized syntactically. Researchers generally assume that neural semantics is a precondition for determining neural syntax. Furthermore, it is often assumed that the syntax of the brain is too complex for our present technology and understanding. A corollary of this view holds that functional MRI (fMRI) lacks the spatial and temporal resolution needed to identify the dynamic syntax of neural computation. This paper examines these assumptions with a novel analysis of fMRI image series, resting on the conjecture that any computational code will exhibit aggregate features that can be detected even if the meaning of the code is unknown. Specifically, computational codes will be sparse or dense in different degrees. A sparse code is one that uses only a few of the many possible patterns of activity (in the brain) or symbols (in a human-made code). Considering sparseness at different scales and as measured by different techniques, this approach clearly distinguishes two conventional coding systems, namely, language and music. Based on an analysis of 99 subjects in three different fMRI protocols, in comparison with 194 musical examples and 700 language passages, it is observed that fMRI activity is more similar to music than it is to language, as measured over single symbols, as well as symbol combinations in pairs and triples. Tools from cognitive musicology may therefore be useful in characterizing the brain as a dynamical system.

Introduction

In 1895, radio communication emanated for the first time from the workshop of Guglielmo Marconi; since then radio signals have propagated 115 light years in all directions, passing through several thousand star systems. If alien astronomers happen to detect Marconi’s first tentative broadcast, and the myriad following, what could they infer about its source? After determining that the signals are neither random nor from natural sources, the distant astronomers might speculate that energies of the signal could be tokens in a language. But what could the sequences of the purported language mean? Back on earth, one might begin with semantics, looking for aspects of the signal that correlate with the local environment, but this intuitive path is not available off world. They must therefore attend to formal properties of the signal as a stream of possible language tokens, its syntax.

How will the analysis of “language-likeness” proceed? Let’s assume that the aliens have figured out how to individuate tokens, perhaps using gaps or some regular markers to parse the stream. From there, several formal, numerical, properties of the stream can be measured, characterizing the possible code prior to any insight into its meaning. For example, imagine a short passage of about 500 words. At one extreme, the passage might comprise 500 different words, each used just once. A coding like this is dense, in that all of the available symbol types are used with equal frequency. Alternatively, the passage might employ fewer symbols, using some frequently and others rarely. This would be a sparse code: the coding resources are scanty, with some symbols used repeatedly.

Sequences of real language fall between these two extremes. Considering the first 500 words of this paper, several words are used repeatedly; 301 distinct word types compose the passage. Most are used once, but several more than once – “the” leads the pack with 29 occurrences. The passage is relatively sparse (or if you prefer, semi-dense). We can similarly examine the characters: 3245 make up the passage, combinations of 56 different symbols (omitting spaces. The characters include capital and lowercase letters, numerals, and punctuation.) Lowercase “e” and “a” win, with 353 and 235 appearances. If the passage were spoken, we could do the same sort of analysis with its syllables or phonemes, with a similar general result. In these examples, then, we observe an unevenness in symbol token use. The coding schemes are relatively sparse. Many symbols are rarely used, but a few of them are used extensively.

Human languages are sparse (Zipf, 1949; Meadow and Wang, 1993)¹. Although sparseness is a contingent property, the idea of sparseness captures an intuition about natural language, namely, that in semantics and syntax languages must compromise between expressive power and learnability. Dense language streams, composed of unique tokens, each used exactly once, are possible but obviously increasingly impractical as streams lengthen: unlearnable, opaque to reasoning, generalization, and continuity, such fragile codes soon fail as communication. (As an exercise, the reader is invited to compose a unique-token essay of 500 words or more.) On the other hand, a language with few symbol types will be easy to learn but unwieldy. Specific contents will either require long expressions or be ambiguous. In practice, continuity and reasoning will be loose, equivocal, and unreliable. (Homework: write 500 words using a language you have studied for 1 week.)

In the 500 word example above, we considered the sparseness of words and characters in their individual occurrences, a property we will refer to as first-order sparseness. But we could parse the signal in different ways. For example, we can regard word pairs as our basic unit, breaking the current sentence into “for example,” “example we,” “we can,” etc. Sparseness could be measured for the occurring pairs of words, or for triples, quadruples, and beyond. Sparseness is thus a property of languages at many levels of analysis. First-order sparseness (of single symbols) characterizes the usage of basic units, while higher-order measures characterizes some of the constraints governing language as it unfolds in time, indicating mutual constraints between symbol pairs, triplets, and more. Thus, sparseness is one mark of syntax. It is a statistic that informs us that not everything goes, that limitations and constraints govern symbol choices and combinations. What seems at first to be an obscure statistical property can be a useful tool to discover some very basic properties of a signal stream.

The several dimensions of sparseness thus afford a window into the structure of a language independent of its semantics. Passages of different languages will have different profiles of sparseness at different levels, and can be compared along these different dimensions. Initially, no single level needs to be privileged. The alien astronomers can carve up the radio signal many different ways. If it is language (at least of the human type), they can expect to find sparseness, distinguishing the terran signal from noise. At that point, they can compare the mystery signal to signals in their own languages, and begin to understand the human world and mind.

The example is fanciful, but analogous to a mystery signal that ripples through real (earthly) science every day: the magnetic resonance (MR) signal emitted by brains in scanners around the world. Tuned to detect the right segment of the signal, these scanners detect brain metabolism, and thus indirectly measure large-scale effects of neural activity (Logothetis, 2002). Most of the effort of cognitive neuroscience focuses on the semantics of functional MR signals, rendered as sequences of three dimensional images or “volumes.” That is, the dominant issue of this science is the relationship between conditions outside the brain and those within, seeking the laws that synchronize our cognitive lives as behaving organisms with the neural machinery. The fable of the alien astronomers suggests a different way in, inviting an examination of formal, syntactic properties of the global MR signal streams over time. These are properties that are not necessarily linked to the semantics of brains. Sparseness provides a systematic way of characterizing a series of activity patterns, opening a new avenue in the study of the dynamic brain.

The connection between sparseness and most language codes also affords a bridge between functional brain imaging and classical cognitive science. There, the concept of language and linguistic codes applies beyond the realm of communication between individuals. According to classical cognitive science, language is a basic vehicle of all cognition: this is the foundation of computationalism (the view that cognition is computation, and the brain a particular kind of computer). More specifically, language is the controlling metaphor for the “language of thought hypothesis” (LOTH; Fodor, 1975, 2008). The evidence of LOTH turns on the necessary conditions for cognition – what computational resources must a brain have to display the behavioral capacities of human intelligence? In its strongest form, LOTH is not just a conjecture about the implementation of human language abilities, which at some level would have to be “language-like” in order to issue in language behavior. Rather, strong LOTH proposes a lingua franca for all cognition. Like a computer’s machine language, LOT, or “mentalese” is the medium for all neural computation. Strong LOTH further holds that mentalese is distinct from any natural language, that it can frame every actual or possible concept humans could entertain, and that it is innate (Fodor, 1975).

Initially, the hypothesis was defended with the claim that LOTH was the only available theory, and that as such one must embrace it and all of its implications. The renaissance in neural network modeling challenged the uniqueness of LOTH, while leaving intact the assumption that a representational system with language-like properties must underlie cognition (McClelland and Rumelhart, 1986; Rumelhart et al., 1986; Smolensky, 1988). Even so, cognitive neuroscience and LOTH theorizing have developed independently. Functional brain imaging has seemed to be the wrong technique to probe the language of thought (Petersen and Roskies, 2001; Coltheart, 2006; Roskies, 2009).

The fable of the alien astronomers, however, offers a glimmer of encouragement in the pursuit of the underlying “language” of cognition. Sparseness and other syntactic properties can be measured in a signal stream, without any knowledge of the semantics of the stream. We can look at functional MRI (fMRI) as a mystery signal, and compare it to various language examples. In this way, we measure language-likeness, even at the relatively fine level of comparison with particular natural languages.

All signals are sparse to some extent, however. One might wonder if the “discovery” that fMRI signals are sparse might be hollow. Language-likeness denotes a loose and ambiguous spectrum. Just as everything is a computer – under some description – so every sequence is language-like, to some extent. Any empirical result would thus leave the LOT hypothesis unmoved. To put it in other words, we could not discover that a signal was not language-like.

The alien astronomers and LOT theorists are overlooking an alternative, however. Not all sparse signals are instances of language. The other kind of signal stream that will have saturated our galactic neighborhood is music. Music is also sparse. If the aliens asked whether the signals received fell into distinct types, with distinguishable profiles of sparsity at different levels of analysis, could they determine whether a signal is language-like or music-like? When a human signal stream is parsed as words (in language) or tones (in music), it turns out that music and language are very different in sparsity at many levels – this is the first main finding of this paper. These syntactic distinctions lead then to a new analysis of fMRI signals, and to an alternative view of neural coding at the global level. The alternative to the Language of Thought is the Music of Thought, MOT rather than LOT.

The idea that the lingua franca of cognition is not a lingua at all is initially incredible, with aftershocks for semantics, method, and more. In the discussion, we will consider the implications of the Music of Thought hypothesis. But first, we will tour the empirical evidence. The landscape shared by LOT, MOT, and fMRI has never been mapped. This paper is an initial survey. In the next section, we will consider appropriate measures of sparseness and the units over which it can be measured. At several scales of analysis, music and language are distinct. Then, we will locate fMRI signals between the poles of language and music, using data from two studies involving nearly 100 subjects.

Materials and Methods

Sparsity and density are properties of any signal series, but coordinating language, brain, and music requires a common framework for comparison. Language tokens are sequential; MR signals are separable into multiple simultaneous signals. Music can go either way. Monophonic note sequences – melodies – are serial streams like language. But musical scores can also symbolize simultaneous or more complex signals.

The present analysis uses representative language streams as its model, and will seek ways to coordinate other types of signals with examples of language. Language, both spoken and written, can be parsed as words, discrete identifying tokens realized in a sequence². Music can be similarly parsed as notes, tokens usually represented in a score or something similar (e.g., a MIDI file). Melodies will be the target here, to allow comparison with language. The most “polyphonic,” however, is certainly the fMRI signal, spatially separable into thousands of sequential streams. For this analysis, fMRI data have been streamlined in two steps. First, we preprocessed each volume image series with independent component analysis (ICA; Calhoun et al., 2002, 2008). ICA is a statistical method that locates ensembles of voxels (pixels in the MR image) that vary together. In effect, ICA locates “supervoxels” of correlated brain activity. Sometimes the component brain regions determined by ICA are spatially contiguous, but often they involve multiple anatomic areas. ICA is relatively “data driven,” in that external hypotheses are not needed to separate time points as a basis for finding correlations. In many experiments, including those we have used here, 20 independent components preserve 80–95% of the variance in the original data³. Thus, ICA is an attractive method for initial data analysis.

Twenty simultaneous channels still do not compare with the serial signals of language and melody. We address this by further filtering the signal to comprise just the most active component at each time point⁴. Informally expressed, we locate the component (brain region) that is the most active “hot spot” from moment to moment, where that hot spot has been identified by ICA. Each component, then, is understood as a symbol type, with a distinct (but unknown) meaning. The image stream is thus rendered as a sequence of symbol tokens, where each symbol is a distributed brain region identified by ICA.

In this three-way comparison, the common measure of sparseness is the relative frequency of occurrence of different symbol tokens in the signal stream. As long as symbols can be distinguished (unambiguously assigned to types), sparseness can be determined.

Assumptions are unavoidable. They are more (or less) reasonable according to either conceptual or empirical standards. Conceptually, we ask whether words, notes, and hot spots are comparable concepts, occupying similar positions in the edifice of theory and intuition in their domains – issues we revisit in the discussion. However, these assumptions can also be tested for empirical adequacy. Conceptually, music and language are distinct. Whatever our approach, we want our methods to sort examples into these two types correctly. Music, however varied, should land in a different bin from language. If our methods sort correctly for known cases, then we can test MR series for their resemblance to either of the other two types. This will be our procedure here.

Empirical validity, then, is best tested against a variety of benchmarks. In this study, 194 musical examples from six musical traditions form one pole of the analysis. These include three folk traditions, African, British, and Chinese, and melodies of three composers, Stephen Foster, George Gershwin, and Franz Schubert⁵. The language examples include transcripts of spontaneous spoken language and written texts. The texts include compiled corpora in Chinese, Finnish, French, Spanish, and English. Transcripts include examples in Ingrian Finnish and English. Some sparseness measures are sensitive to the length of the sample tested. The language sources are each very long, so the statistical measures were taken over random starting-point windows of equivalent length to the MR signal series. One hundred samples were extracted and analyzed from each linguistic corpus⁶.

Music and language have been produced and transcribed for hundreds to thousands of years. Nonetheless, in 20 short years functional neuroimaging data have been gathered in thousands of experimental settings. For the present probe, we conducted a secondary analysis of a small subset: 18 subjects performing a simple auditory oddball task⁷; 17 individuals with schizophrenia performing the same task; and 64 subjects in the “rest” state, also known as Default Mode⁸. The auditory oddball task broadly activates cognitive processes of attention and perception, while the rest state affords an unconstrained window into cognitive processes in general (Stevens et al., 2005; Biswal et al., 2010). Schizophrenia data allows us to further interpret the results and take a first look at sparseness in individuals with mental illness (Garrity et al., 2007).

None of the experiments considered here involve either language or music as components of experimental tasks. If the subjects wander into verbal reflection or musical reminiscence, they do so “on their own time,” and not within the task demands of the experiment. The “rest state” data are particularly useful. In rest state experiments, subjects are unconstrained in their mental activity. Although the scanner is an unnatural environment, the subjects entertain a thought process that may sample the common ground of all cognition “in the wild.” In asking whether these data are music-like or language-like, then, we probe cognition in general.

The music and especially the language examples fail to completely represent the diversity of human production, nor do the fMRI protocols capture the many facets of human cognitive life. But for an initial probe, they sample some of the variety within and across cognition, musical traditions, and languages. Future analyses will seek the empirical borders of all three domains.

Another kind of diversity affects the measures of sparsity/density of symbol streams. Here there are two questions: How should sparseness be measured? And over what? Beginning with the second, initially sparseness is measured over tokens individually and independently. In other words, relative frequencies of words/notes/hotspots is the basis for the first measure, measured separately for each sample string. This will be termed “first-order sparseness.” In language and music, however, the order of symbols is meaningful and constrained by the systems of production. Sparseness is relevant with respect to sequences – of the possible sequences, syntax allows some and excludes others. Accordingly, we can consider ordered token pairs, triples, and quadruples. If a signal stream is randomly shuffled, individual (first-order) sparseness will be preserved, but higher-order sparseness destroyed. Pairs in the random sequence will occur by chance, resulting in uniform density.

The underlying idea of sparse representation is the uneven use of symbol types. A sparse system uses fewer symbols more often. So, if we measure the average frequency of all symbols in a stream, in a sparse stream some will be considerably greater than the mean, and others less. The distribution of symbol frequencies around the mean is the basis for sparsity measures. Beyond that, researchers disagree on the appropriate calculation. Here, we will circumnavigate the debate by using three different measures. The simplest is the coefficient of variation (CV), the SD divided by the mean (of symbol frequencies) – the normalized SD, in short. The second is the Gini coefficient, as adapted by Hurley and Rickard, who argue that the Gini coefficient best captures the concept of sparseness (Gini, 1921; Deaton, 1997; Rickard and Fallon, 2004; Hurley and Rickard, 2009)⁹. The Gini index, often used as a measure of income inequality, also measures the dispersion of values from the mean (e.g., rich and poor). The third method derives from the ratio of the L1 vector norm to the L2 vector norm. (This is the ratio of the sum of vector elements to the magnitude of the vector.) We will refer to this as the Hoyer coefficient, after its author (Hoyer, 2004)¹⁰.

Figure 1 displays a notional example. The bar charts represent the relative frequency of particular symbols in coding schemes ranging from the dense to the sparse. The three metrics are found beneath the examples. The three measures deliver proportionately similar results. For simplicity, then, the main paper presents the results using the Gini index¹¹.

FIGURE 1

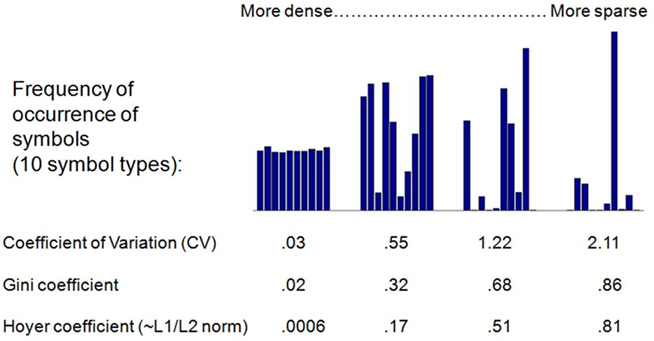
Figure 1. Examples of sparseness in four codings: The bars chart the frequency of symbol use in an imaginary coding scheme with 10 symbol types. In a dense coding scheme (left), the symbols are used with nearly equal frequency. In a sparse code, some symbols are used often, and others hardly at all.

In spite of common strategies for data formatting, the examples for analysis vary in some basic statistical properties, which affect the sparseness measures. These include the length of samples and the number of symbols in the “lexicon” of possible symbols for each sample. To control for these effects, sparseness measures for each sample were normalized by contrasting them with sparseness measures for statistically similar random data. These surrogate data samples provide a baseline for each sparseness estimate. Specifically, for each data sample, 1000 random surrogate samples were created, each matching their originals in number of symbol types and length of symbol stream. Sparsity was measured in the surrogates in the same manner as the original data, and the median of these surrogate measures used to normalize measurements on the original data. Accordingly, for each sparseness measure, a value of one indicates that the data were indistinguishable from random surrogates. A maximally dense code uses its symbols with equal frequency, so a random code is not maximally dense.

To summarize, the exploration here rests on a three-way comparison of 194 musical examples, 700 language examples, and 99 subjects in three experiments (in two laboratories). Sparsity/density will be measured over single symbols, and symbol pairs, triples, and quadruples, using three different methods for calculating sparseness. Thus, 12 comparisons will support the conclusions below.

Results

Figure 2 represents sparseness measures for the language and music examples, measured by the Gini coefficient, normalized by random baselines. Figure 2A depicts first-order sparseness, the unevenness of symbol use, comparing words, and notes. Triangles mark 95% confidence intervals; if intervals between triangles do not overlap, then the sample medians are significantly different at the p < 0.05 level. Individual subtypes overlap, but on the whole music and language are distinct by this measure (as they are by the other two sparseness measures as well). Music is more sparse, using some notes frequently and others rarely. Composed music is most sparse, while folk traditions are less so. Word usage in the language examples is more densely coded. Overall, word use varies less in frequency from most- to least-used words. Spoken and written examples are similar in specific languages. Finnish, a non-Indo-European language, is the most dense. Finnish has a complex grammar, conjugating verbs and running nouns and modifiers through a gauntlet of 14 or 15 cases. Each inflection means a different token, possibly driving Finnish language streams toward syntactic density.

FIGURE 2

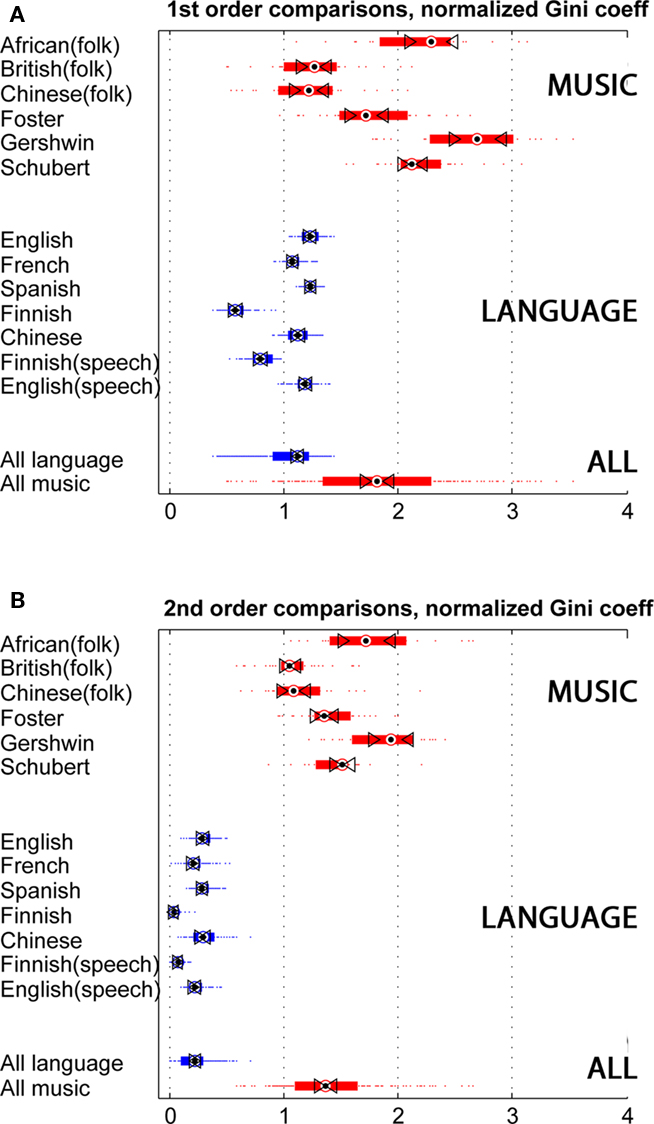
Figure 2. Sparseness in music and language examples, as measured by the Gini coefficient (normalized in comparison to statistically similar random surrogate data). Red: 194 melodies from six traditions; Blue: 700 texts, written, and transcribed. Colored bars span the 25th to the 75th percentile. Triangle markers span the 95% confidence interval. The bottommost bars represent aggregate medians in the two groups. (A) 1st order sparseness, i.e., sparsity/density of single symbols (words or tones). (B) 2nd order sparseness, i.e., sparsity/density of sequential pairs of symbols. Overall, the figure points to a robust and large difference in first- and especially second-order sparseness, as measured by the Gini coefficient.

Figure 2B depicts second-order sparseness in the same data, comparing pairs of notes and words. Music and language permit some transitions from symbol to symbol but exclude others, a constraint of syntax. Music is evidently more limited in its preferred or permitted transitions. Language is more open. Each word might be followed by many others, and there is comparatively little tendency to favor particular word pairs over others. This contrast sharpens in third- and fourth-order comparisons (not shown). In symbol choice and transitions, then, music is the sparser code.

Languages vary greatly in many features (consider Finnish and Chinese, for example). The musical landscape that includes African and Chinese folk traditions, Gershwin, and Schubert is likewise variegated. Yet sparseness seems to be a property of symbol streams that can distinguish language from music. Accordingly, sparseness measures can be applied to symbol streams whose domain is unknown, mapping their resemblance to one pole or the other. Figure 3 adds the fMRI data to the comparison. The brain data are similar in their medians and range, despite their different original sources. Healthy subjects and schizophrenia patients differ little. They all performed the same task, and possibly this explains why these two groups seem to differ from the resting subjects. A hypothesis for further testing is that specific tasks drive the brain toward sparser codings.

FIGURE 3

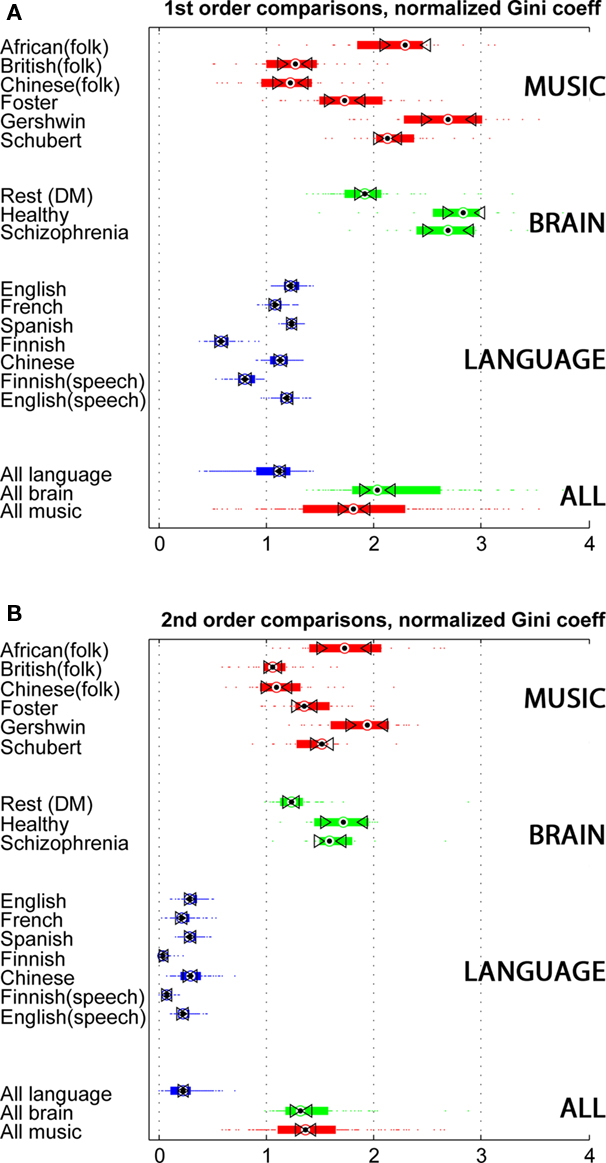
Figure 3. Three-way comparison of music, language, and fMRI data. The figure scheme is as in Figure 2. Green bars represent data from 99 subjects in three experiments. Healthy and Schizophrenia subjects both performed an “auditory oddball task,” consisting of identifying a target tone in a stream on non-target tones and distracting noises. The largest group comprises 64 subjects in the rest condition (also known as Default Mode). (A) 1st order sparseness, i.e., sparsity/density of single symbols. (B) 2nd order sparseness, i.e., sparsity/density of sequential pairs of symbols.

The striking observation, however, is the similarity of the brain data to music. Figure 3A depicts the first-order sparseness measures. The aggregate comparison of the three signal types is at the bottom of the figure. The musical examples tend to draw from their set of possible notes certain notes to the exclusion of others. In different musical traditions, these selections are different but share this statistical profile. The brain operates similarly, using areas of activity like notes in a melody, at least with respect to the density of usage of certain areas, and the relatively infrequent use of other areas. This similarity remains striking in the second-order analysis. Language is much denser in its use of symbol pairs. In music and in brain activity, transitions from one state to the next are constrained; certain transitions are preferred over others.

Sparseness measures using the CV and Hoyer coefficient are similar. Figure 4 plots the normalized sparsity values for the three data types, from first to fourth-order, for the three methods of measurement. In general, at the lower orders at least, music data resemble brain data; at higher-orders the brain and language data approach maximum density (where each sequence of symbols is used once). For ease of reference, we can combine these results (and others, developed below) by using the probability of the null hypothesis as a measure of similarity of groups, as calculated with the (Mann–Whitney) Wilcoxon rank sum test (a non-parametric comparison of group medians). Since the tested null hypothesis is that the groups are from the same population, a higher p value indicates greater group overlap, i.e., greater similarity. We can accordingly count instances where the rank sum statistic is higher for the brain–music comparison than for the other two comparisons (brain–language and music–language). Since we have three different measures at four orders, there are 12 cases to compile. For 10 of these, the closest resemblance was indeed between brain data and music¹². In these observations, by all three measures and among single symbols, pairs, and triples, the dynamics of the brain are more similar to the dynamics of music. Indeed, in all cases brain data and music data are more similar to each other than brain data and language.

FIGURE 4

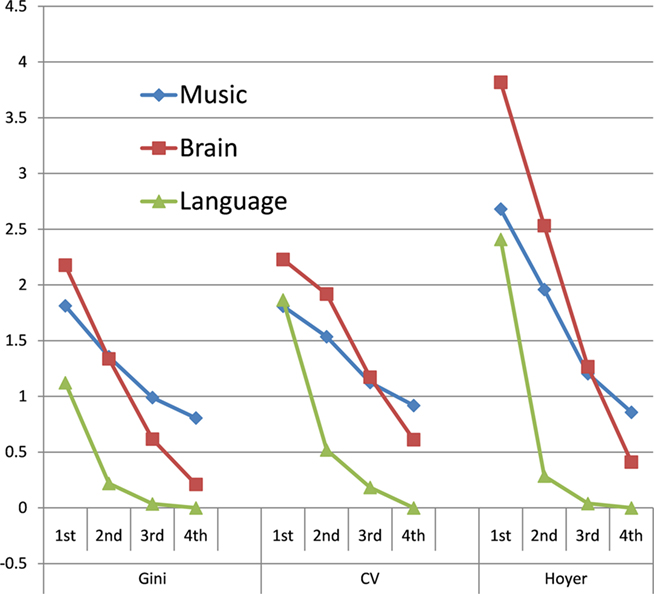
Figure 4. Normalized Sparseness measures for music, brain data, and language (median values). Single symbols (first order), pairs (second), triples, and quadruples and compared, as calculated with the Gini coefficient, the coefficient of variation, and the Hoyer index. For 10 of the 12 separate observations, the greatest similarity is between brain data and music. In all cases, brain data are more similar to music than they are to language, as measured by Wilcoxon rank sum probabilities (see text).

The figures above obscure another important contrast between the groups, which is displayed in Figure 5, a scatterplot of first- vs. second-order sparsity. All the data points are plotted individually, revealing a distinct pattern of dispersion with respect to sparsity for brains and melodies. Individual samples and subjects in the groups can have quite different sparseness values. The language samples, in contrast, cluster around characteristic sparseness for each one. Moreover, first and second-order sparseness is strongly correlated for individual melodies and subjects.

FIGURE 5

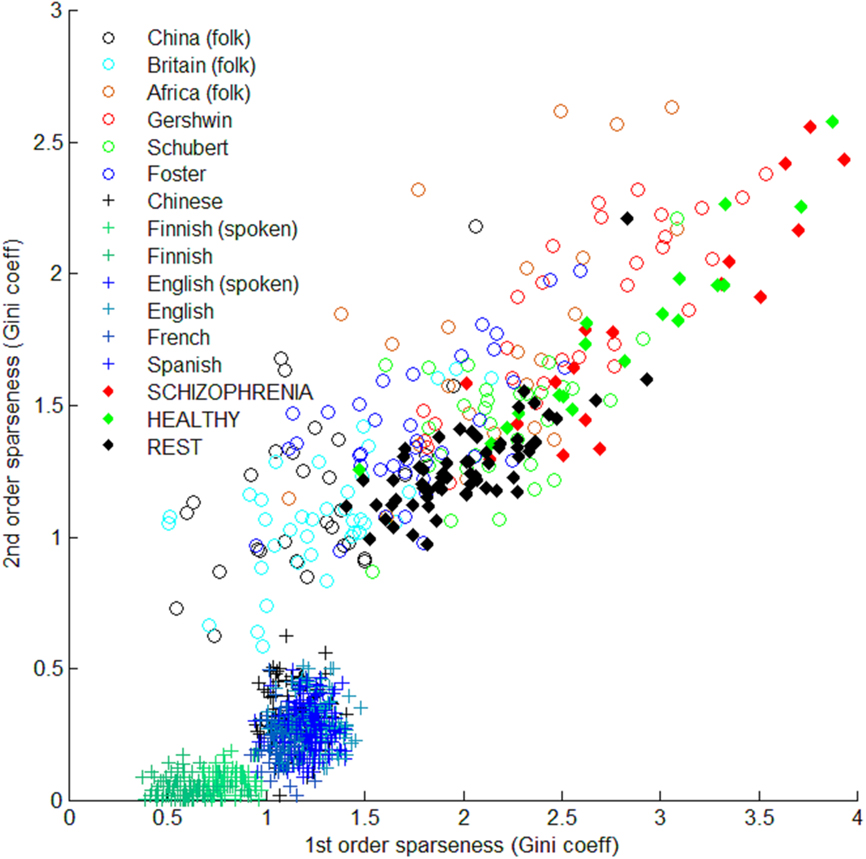
Figure 5. First-order sparseness (x axis) compared to second-order sparseness (y axis), representing sparseness measures for all examples and subjects individually. Crosses are language examples; Open circles are melodies; filled diamonds are brain scan data for each subject. Among the language cases, first and second-order sparseness values are nearly constant. Finnish examples, both spoken and written, are outliers, perhaps due to the complex grammar of the language. In music and brain data, first and second-order sparseness varies across melodies and subjects, and the two orders of sparseness seem to be strongly correlated.

The correlation between first-order and higher-order sparseness is not surprising. Streams with high first-order sparsity will use some symbols heavily, drawing from a short list of symbol types (notes, words, or hotspots). Thus, at the second level, pairs of symbols will often have the same initial element. This increases the likelihood of a match of both elements of the pair, even if the second is drawn randomly from the same (sparse) set of symbol types. Nonetheless, the similarity of the range of data points, and their distribution, seems not to be an artifact. The figure makes vivid a difference between language, on the one hand, and the other two data types. Music and brain activity are very similar in their mean sparseness. In this basic sense, brain activity is decisively more like music than language. However, within both groups, individual examples vary widely, and over a similar range. The differences between melodies can be bigger than the difference between music (in general) and texts. Likewise, the differences between individual subjects can be just as great. In the framework of this preliminary investigation, people differ from one another across a range similar to the range of music.

Discussion

Apples and Oranges?

The separate domains of language, music, and brain activity (as imaged with fMRI) each have their own “ontologies,” stable taxonomies of entities, and their properties. In language and music especially, categories like words and notes are taken for granted, along with the properties that we use to individuate them. In brain imaging, the ontology is not as stable, but generally depends on spatial or anatomical divisions within the brain. Any comparison across domains will depend on an analogy that coordinates elements of the separate domains. This is not unusual in science. The LOTH itself is an analogy, between the properties of natural and computational languages and the properties of a purported cognitive computational engine implemented in the brain. As a fruitful analogy deepens, it is promoted into a “model,” under which comparisons become more exact, and theorizing can be passed from the philosopher to the scientist. Can a different analogy, the Music of Thought hypothesis, gain any traction on a path from loose analogy to rigorous model? One way, perhaps the only way, to answer this question is to try, to use the analogy to generate and test hypotheses. Each of the initial steps on this long road will require choices among plausible alternatives. Here there are three domains in play, so the roadmap will be especially complex. Coordinating data from different sources inevitably raises questions of commensurability, so the first task in this discussion is to review the case for incommensurability. We need to take seriously the possibility that the three domains cannot be compared along the dimensions highlighted here.

The principle framework for coordinating the three domains is time. In every case, we are comparing a serial signal stream, examining the stream in “chunks” between about a 10th of a second (the fastest notes) and about 2 s (the fMRI images, spanning 1.5 s in the oddball task data, and 2 s in the Rest state data); this is the “second scale” of signal analysis. Speech and music signals lend themselves to the millisecond scale as well, but this information is lost in fMRI. However, even within this time window there is a fairly large spectrum of temporal windowing. Does this invalidate the comparison? We can reply to this worry both theoretically and empirically. Theoretically, at least regarding music and language, note and word share the honor of being the fundamental unit of symbolic interpretation. As such, they are the building blocks of syntax, making this the right level for syntactic comparison across the domains. Notes (single tones) and words are the items that humans learn and learn to manipulate. When signal streams are parsed, these are generally the smallest manageable chunks, the items most congenial to thinking about signals, learning them, and communicating them to others. Meanwhile, the signals recorded from the brain are undifferentiated, without the props of a conventional scheme for parsing and symbolizing the information passing among brain areas. The starting-point, then, is the arbitrary one of the finest resolution afforded, and that is in the second range. Since we cannot improve upon this, it makes sense to parse the symbol stream in the other two domains in a similar range.

That is the theoretical reply. However, the question of time scale can be examined empirically as well. To this end, the ICA data were mapped onto a pseudo image series at twice and four times their initial sampling frequency. [Between each pair of component vectors, an intermediate vector was interpolated, to create virtual TR of 0.75 s (oddball task) and 1 s (rest state data).] The aggregate measures were similar. At twice the sampling rate, singletons, pairs, and triplets are nonetheless most similar in Gini coefficients between brain data and music, and likewise for the other two measures, using the p value as a similarity measure. (86% of the 12 measures; in all cases brain data and music are more similar than brain data and language data.) When the intervals between images is halved again, to 0.375 and 0.5 s, these results are unchanged. While it would be ideal to collect functional MR images at these rates, in their absence the interpolation strategy may be the best approximation of the changing hemodynamic response.

Another “apples and oranges” objection distinguishes language from the other two domains. The language stream, considered lexically, is “monophonic,” using its coding resources sequentially. Music is often polyphonic, and symbolized as such. However, music is not exclusively polyphonic (and in world music polyphony is rare; Patel, 2007). Even among polyphonic traditions there are reasonable methods and conventions for isolating melody as salient in the symbol stream. For present purposes, serial language limits the comparison to sequential music, the melodies alone. The fMRI signal, however, is fundamentally polyphonic. Are we somehow violating the ontology of the data to reduce this multichannel signal to the progression of hot spots, jumping from one area of the brain to another?

Once again, language is our constraint. Its monophonic data are incommensurate with a polyphonic signal stream, so the only way we can meaningfully compare the two domains is by restricting data to a sequential representation. However, this study is not alone in funneling fMRI. Most of cognitive neuroscience aims at hypotheses that are “monophonic” in the same way, by seeking maximally activated regions that correspond to particular cognitive functions. This is the strategy of functional localization, where anatomical regions are probed for the specific conditions that provoke their activity. Studies that involve ICA look for the component or components that most strongly correlate with an experimental variable; non-ICA (“standard”) studies test the oscillations of voxels one by one, and group together those that follow the variable of interest. In general, the outcome is a hypothesis about a single region or network of regions, a hot spot turning on or off over time. Activity less than the threshold for hot spot detection drops out of consideration. Brain imagers realize that hot spots must be modulated, and indeed that ultimately cognition is all modulation, supported by highly distributed and variable networks of activity (Friston et al., 1995, 1996a,b,c; Friston, 2002; Price and Friston, 2005). Nonetheless, localist hypotheses continue to be confirmed in abundance; it is true that areas of the brain are associated with specific functions, even if that is less than the whole story. The isolation of hot spots used in this study, in short, conforms to the standard procedure of cognitive neuroscience.

Usually the language/music comparison is discussed theoretically, debating whether music just is a subtype of language (Kivy, 2002; Patel, 2007). So yet another challenge to this study would be to declare MOT to be a mere modification the LOT hypothesis. Sparseness may characterize the type of language the brain deploys, leaving the main claim, that there is a language of thought, unmoved.

Again there are both theoretical and empirical replies. In this instance, however, there is a real underlying issue concerning the boundaries of music and language. Music does share many properties with language, the most prominent being the syntactic property of compositionality (Lehrdahl and Jackendoff, 1996; Huron, 2006; Patel, 2007). Music, like language, has a grammar that permits some combinations and excludes others, and both domains involve procedures for building larger units out of smaller one. (Beyond these broad commonalities, however, there is great controversy over the degree of similarity between musical and linguistic syntax. See Patel, 2007 for discussion.) Like language, music has developed a diversity of subtypes, musical traditions that loosely govern local music dialects. Like language, children grow up within a tradition and become fluent in it – not necessarily virtuosos but able to recognize musical signals and detect syntactic violations. Like language, fluency has oral/aural and literate forms. Nearly everyone can hear music as music, but some can also read it and write it on the page. Theoretically, then, we could agree that music is a language subtype, but nonetheless it is distinct, apparently in a category separate from all (other) natural languages. Locating brain activity decisively in the category of music is nonetheless an important development for any version of a LOTH.

The music of thought hypothesis gains import when we consider the ways in which music is unlike language. Musical semantics fundamentally differs from linguistic semantics. Musical signal streams at all levels of analysis do not refer to items in the world in anything like the way that words and sentences do (Meyer, 1956; Narmour, 1990; Kivy, 2002). This point is underscored by the failures of every attempt to provide a semantics of music parallel to a semantics of language (Patel, 2007). “Program music” tells no stories without a program in hand, moving many philosophers and musicologists to link music to more general referents, like moods and bodily movement (Langer, 1942; Clarke, 2001). Even if these referents are external to the musical work, the vagueness of this denotation is in striking contrast to the specificity of syntax. The third movement of the Beethoven’s fifth symphony may convey triumphal elation (see E. M. Foster’s Howard’s End for an elaboration), and Beethoven no doubt entertained many alternative formulations of his meaning. His alternatives might have been vastly different but have little overall effect on the vaguely felt emotions of the audience. But if the second-chair French horn player plays a B where B-flat is written, in measure 446 of the symphony, every member of the audience will know, and will know it to be wrong. Overall, the syntax of music is fine-grained while its semantics is very coarse, according to any attempt to force the semantics to work like the semantics of language. This mismatch implies that music and language are deeply and interestingly distinct.

Empirically, music and language are fundamentally different as well, a corollary finding of the present study. Here we have measured a fundamental property of signal streams in hundreds of examples from the two domains. Within each domain, diverse subtypes have been included. The empirical measurements described above converge on the conclusion that in one conspicuous property, considered at several orders of organization, music and language are different. With the present data, that difference holds notwithstanding any theoretical declarations of affinities between music and language. However that spectrum of difference is interpreted, the brain data land at a point nearer to music.

Philosophers might take the apples and oranges objection in two other directions, both resting on the nature of music. First, most music (unlike language) is a form of art, and thus a beneficiary of the ballooning boundaries of art during the twentieth century. The main consequence of the previous century, in brief, is that in music (as in other arts), when the context is apt, anything goes (Danto, 1981). John Cage’s “4′33′,” featuring a performer striking no notes at all, is the limit case. Thus, any signal stream could be music, in the appropriate context, and the finding that a signal is “musical” is empty. The second objection also stems from the concept of music itself: Is not music necessarily audible? To both of these, we could offer philosophical rebuttals, but the objections could also be granted. The concept of music in play here need not be the inclusive philosophical concept, but rather the empirical territory of musical traditions, the ground bass of composition and performance against which the avant garde is measured. Similarly, the empirical study here is based on music as a signal without specifying its medium or component frequencies. The energy fluctuations detected by fMRI are of course not audible. If this excludes these signals from “real music,” then the study is probing a property of “music-likeness,” characteristic of signals in various media. The properties of signals resembling music can be compared along these formal dimensions.

The skeptic might persist, observing that music is a cultural artifact, shaped by convention over a few millennia, while the brain is the product of long evolution. It seems incredible, then, that any cultural process could also characterize the biological brain. In reply, however, note that language is also a cultural convention. But neither language nor music are entirely conventional. Science assumes that language was shaped by selection within evolutionary time. Music may be just as ancient and also adaptive (for sexual selection, for example). The two might stem from a common origin. In any case, it is no less incredible to regard language as the foundation of all cognition than to set music in that role. But also observe that the music in question is produced and shaped by the brain. It has the form it has in part because of the brains that produce it. From the structure of the effect we infer the structure of the cause. Again, this exactly parallels the argument for natural language as a model for the language of thought.

Caution is nonetheless warranted, on the grounds that the initial findings here may not generalize (and so, fail to replicate). Time will tell; however it does appear that the results are resilient across many variations in method, as discussed above¹³. The steps preceding the specific analyses in this paper are equally governed by various parameters. ICA, for example, involves numerous choices of algorithm, number of components, and more. Here we deliberately adopted “default” values typical of research studies using ICA. The existence of numerous ICA studies strongly suggests that the method (with its standard parameters) validly identifies functionally significant brain regions, which in turn conform to the present anatomical and functional understanding of the brain across mainstream cognitive neuroscience. The observations of this paper thus rest on the same foundations as many other papers. More important is the question of whether the properties tracked here generalize toward other properties of music. Sparseness is one dimension of music, and a very useful one in that it seems to demarcate music from language. In examining first, second, third, and fourth-order sparseness, we have taken a first look at the components of a signal stream and some of their relations. Where sparsity is found, we conclude that we are looking at a system with formal constraints. Empirically, not everything is allowed. But of course music is empirically characterized by many properties. Resembling music across four orders of sparseness might be an isolated finding about a signal type that in other respects has nothing in common with music.

Thus, a large project lies ahead, taking two general directions. First, we can search for further analogs of musical structure in brain activity¹⁴. Music from every tradition can be analyzed with respect to tonality, distribution of durations, rhythms, harmony among parts, and many more. These measures can be quantified, and compared to analogous features of brain signals. This study is underway. Second, the individual tones in most music have timbral properties, characterized by component sound frequencies (and other features). Functional MRI signals can be similarly treated, while recognizing (and adjusting for) frequency differences of about two orders of magnitude. In a separate paper (submitted), we show that the component frequencies of fMRI signals have music-like timbral structures: their partials (overtones) are sparse, as in music, and their greatest power is in the lowest frequency (the “1/f” power spectrum, typical of music; Voss and Clarke, 1976). Both of these explorations probe properties that lack obvious analogs in language, so these studies rely on contrasts with various forms of surrogate data.

These promissory comments suggest a possible consequence for cognitive science, pursuing the analogy of cognition and music. Cognitive musicologists, building on a long tradition of music theory, have at hand a toolbox of concepts to characterize musical signals and their perceptual effects. There are many general features of music that only music has – features that either do not apply to other signal streams (like language) or that clearly demarcate most music (for example, in contrast with various forms of noise). Some of these features are structural, like the interaction of timbre and tonality, but many of them are dynamic, characterizing the play of sound over time in musical signals (Sethares, 2005, 2007). Functional MRI “scores” could be explored with these tools as well. Since music is both structurally and dynamically complex, the musicologists’ tools may articulate the obscure multivariate dynamics of the brain.

Another domain of dynamics operating on complex structures is that of consciousness itself. The philosophical tradition of phenomenology has characterized conscious life as an interaction between the present moment and immediate memory and anticipation (Husserl, 1966/1928). This picture of consciousness is necessarily both structurally complex and temporally dynamic. According to Husserl, every object of perception or reflection is apprehended in a context of its past and possible future. Accordingly, in any act of perception, we also perceive that the object is a new arrival or something that has already been before us, a first occurrence or a repetition. This is fundamental to musical perception as well. Indeed, one of Husserl’s favorite examples is music (although he did not extend the analogy to consciousness in general).

The dynamics of music may offer a rich analogy with the dynamics of conscious life; the syntax of these two domains may be comparable (and discoverable in the brain). Moreover, the semantics of music can change our view of mind–world relations. Musical semantics is very specific, but internal to musical works themselves and music in general (Meyer, 1956; Narmour, 1990). That is, music is self-referential. What happens in the first measure of a musical piece is relevant to the “meaning” of every other measure. Thus, every time point of a piece of music is densely and specifically connected to every other time point (especially within time spans less than a minute; Levinson, 1997). Musical perception and cognition is the awareness of and reflection on the internal referents within music, as they unfold in time. The foundation of representation in music, then, is resemblance and difference. As noted above, detecting resemblances over time is fundamental to conscious experience. If we consider consciousness overall as musical, then its contents are readily characterized by the analogy. What a state of mind is “about” is a complex history and expectations of other experiences. Of course, the world exerts a continuous causal influence on the dynamics of consciousness, but there is no need on this model for a special relationship between mind and world. Semantics on this analogy need not be grounded in reference (cf. Fodor, 2008). Philosophers who worry about mind–world relations might welcome this simplification of the theory of representation (Lloyd, 1997). For the present, we offer this as an avenue for future exploration.

Conscious life, then, might be likened to the experience of a performer improvising at a keyboard: She is simultaneously the creator of the music, its performer, and its audience. But these elements are all combined in a single stream, a series of single acts of simultaneous creation and perception. And the improvisation weaves around a musical background, the causal influence of the body and world. However, we must remember that the music of mind will dwarf any actual music in its complexity. The polyphony of the brain is ultimately a counterpoint of millions of channels, and the temporal dynamism extends from milliseconds to years. Its articulations involve many more dimensions than the ear can discern. These are the articulations of full sensory and motor experience, along with the flow of reflection in all its forms.

Conclusion

Ancient philosophers (both Western and Eastern) held music to be the counterpart and equal to rhetoric and other practical arts. Their cultures were infused with music. This has not changed. Especially in the age of mass media, humans live in a world saturated with music. Yet cognitive science and philosophy have privileged sight over sound, and language over other forms of expression and communication. Without denying the importance of vision or language, there is room to expand the conceptual tools available to comprehend consciousness and its emergence from the activity of the brain. Here, just one dimension of music has been mined for quantifiable frameworks for coordinating music, language, and brain activity. The fMRI signal is different from both language and musical examples, but it is more similar to music. This is most true with respect to sparse coding of single tokens and consecutive pairs of tokens, and robust with respect to different measures of sparseness and with respect to a wide range of examples of music and language, applied to three experiments involving nearly 100 subjects. This could be a first step toward a novel framework for thinking about brain activity as the foundation of cognition and consciousness. For a new sound in cognitive science, we might do well to listen to the music of thought.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Thanks are due to research assistants Elsie Arce, Brian Castelluccio, Maria Niedernhuber, Amy Poon, and Amelia Wattenberger for their data analysis and discussion, and to the Trinity College Faculty Research Committee for ongoing support. This research could not have been undertaken without shared data, made available for secondary analysis, in this case by Abigail Garrity (University of Michigan) and Zang Yufeng (Beijing Normal University). The Rest State data are archived at the 1000 Connectomes database [Neuroimaging Informatics Tools and Resources Clearinghouse (NITRC), www.nitrc.org/projects/fcon_1000/]. Comments of referees for Frontiers in Theoretical and Philosophical Psychology were very helpful and much appreciated as well.

Footnotes

1. ^Sparsity in languages has been characterized more precisely with “Zipf’s law,” the observation that the frequency of occurrence of individual words in a language is inversely proportional to their ranking in the frequency distribution for the language, a relationship that holds in many domains outside of language as well (Zipf, 1949; Meadow and Wang, 1993). A Zipfian “power law” distribution of frequencies is clearly rather sparse.
2. ^The analysis here begins at the lexical (word) level, while higher-order comparisons analyze patterns and constraints in short word sequences, patterns that could reflect syntax and pragmatics. Of course other levels of language could be analyzed, an issue discussed below.
3. ^More specifically, images were registered, normalized, and spatially smoothed with SPM8 software. Spatial independent component analysis was conducted for each subject in this study using the infomax algorithm, implemented with GIFT software (http://icatb.sourceforge.net/). Data were initially reduced to 20 dimensions using principle component analysis, followed by independent component estimation. For each analysis, obvious artifacts (due to eye movement or whole head movement) were removed, and the analysis repeated, yielding the component time series used for the present study.
4. ^Maximum activity was identified as follows: Component magnitudes were normalized to fall between 1 and −1; at each time point, the component with the largest normalized magnitude was retained in the serial stream.
5. ^The musical examples are melodies collected in the KernScores database (http://kern.humdrum.org/), including 24 African folksongs, 38 British children’s songs, 30 Chinese folksongs, 38 songs by Stephen Foster, 29 by George Gershwin, and 35 by Franz Schubert. They range in length from 27 to 478 notes, with a mean length of 140 (SD = 94).
6. ^The language sources: English, French, and Spanish texts: Parallel translations of UN proceedings (http://www.uncorpora.org/); Finnish text: a compilation of news (Helsingin Sanomat), and Wikipedia articles in Finnish; Chinese text: subset of PH Corpus, from Xinhua News Agency, 1990–1991, compiled by Guo Jin (ftp://ftp.cogsci.ed.ac.uk/pub/chinese); Finnish speech transcription: “Language Contacts in the Northeastern Regions of the Baltic Sea,” compiled by Savijärvi et al. (1997; http://helmer.hit.uib.no/Ingrisk/ingrian.html); English speech transcription: Corpus of Spoken, Professional American-English (http://www.athel.com/cspatg.html).
7. ^In the auditory oddball paradigm, subjects listen to a steady series of tones with the task of pressing a button when a tone of a different, target frequency occurs. Distracting noises occur randomly among the tones as well. For details, see Garrity et al. (2007).
8. ^Functional MRI data: (1) The oddball task: 18 healthy control subjects (“Hc”), Olin Neuropsychiatry Research Center, Hartford, CT. For details, see Garrity et al. (2007) (TR = 1.5, no. timepoints = 248). (2) Oddball task, same protocol as (1): 17 schizophrenia patients (“Sz”), from Garrity et al. (2007). (3) “Rest” (Default Mode): 64 subjects (26 F, ages 18–26) from the 1000 Connectomes database (Neuroimaging Informatics Tools and Resources Clearinghouse (NITRC), www.nitrc.org/projects/fcon_1000/), a subset of data set Beijing_Zang (Zang, Y. F.; TR = 2; no. timepoints = 225).
9. ^The Gini index algorithm can be conceptualized by ranking the frequencies of occurrence of symbols in the signal stream and plotting the ranked values from least to greatest. If we normalize these values to fall between 0 and 1, we have an approximation of the “Lorenz curve” for the data. In a maximally dense/least sparse stream this is a straight line. The Gini index compares the data curve to the line expected in a perfectly dense coding scheme, measuring the area between the purely dense line and the actual data plot. See Hurley and Rickard (2009) for a contemporary discussion of this much-used measurement. Here, the calculation was implemented in the Matlab function ginicoeff by Oleg Komarov (http://www.mathworks.com/matlabcentral/fileexchange/26452-gini-coefficient), following (without mean normalization) the proposed simplification by Deaton (1997).
10. ^Specifically, 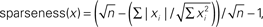where n is the dimensionality of x. See Hoyer (2004).
11. ^Hurley and Rickard (2009) write, “Intuitively, a sparse representation is one in which a small number of coefficients contain a large proportion of the energy.” They outline six criteria that a measure of sparseness should observe, described in terms of a distribution of wealth: (1) “Robin Hood”: moving wealth from rich to poor decreases sparsity; (2) Scaling: multiplying data values by a constant should not alter sparsity (i.e., sparseness is a relative measure); (3) “Rising Tide”: adding a constant to each coefficient decreases sparsity; (4) “Cloning”: If every member of a population is twinned, sparsity of the doubled population is not changed; (5) “Bill Gates”: Adding one or more very wealthy individuals increases sparsity; (6) “Babies”: Adding individuals with no wealth increases sparsity. The Gini coefficient observes these constraints, making it a reasonable measure of sparseness, which Rickard and Fallon (2004) successfully applied to assess various sparse representations of speech signals. For these reasons, we have adopted it for the main analysis in this paper.
12. ^The means (and medians) of the data locate brain and language as most similar for triples as well, so it could be argued that the brain–music link is only valid for single symbols and their pairs. However, mean and median, unlike the rank sum statistic, are insensitive to the dispersion from the mean, an important feature of these data.
13. ^Independent component analysis does not find brain regions of increased activity, but instead regions of coherent activity change over time. Accordingly, component magnitudes can be reversed in sign without changing the ICA results overall. Do these arbitrary sign changes affect the outcome here? In all of 50 simulations where component signs were randomly assigned, the qualitative results remained unchanged: Brain data resembled music more than language at all levels, as tested with the Gini coefficient.
14. ^We could, for example, further explore the relationship of brain data to Zipf’s law (see note 1). Among many options, here this issue was provisionally explored by (first) calculating an ideal Zipfian distribution for sequences of comparable length and number of symbol types, i.e., the symbol frequency distribution if the data conformed to Zipf’s law (with its ample empirical confirmation for natural languages). The Zipfian distribution was then compared to data in this study. In this case, language data most nearly resemble the ideal distribution. Music and brain data are not as similar to the Zipf distribution, and are most similar to each other at all four orders. This difference does not mean that music and brain data do not exhibit a distribution like Zipf’s law (or some other power law), but only that they do not match the ideal law as closely as the language data in this study. This intriguing comparison will be a topic of future study.

References

Biswal, B. B., Mennes, M., Zuo, X. N., Gohel, S., Kelly, C., Smith, S. M., Beckmann, C. F., Adelstein, J. S., Buckner, R. L., Colcombe, S., Dogonowski, A. M., Ernst, M., Fair, D., Hampson, M., Hoptman, M. J., Hyde, J. S., Kiviniemi, V. J., Kötter, R., Li, S. J., Lin, C. P., Lowe, M. J., Mackay, C., Madden, D. J., Madsen, K. H., Margulies, D. S., Mayberg, H. S., McMahon, K., Monk, C. S., Mostofsky, S. H., Nagel, B. J., Pekar, J. J., Peltier, S. J., Petersen, S. E., Riedl, V., Rombouts, S. A., Rypma, B., Schlaggar, B. L., Schmidt, S., Seidler, R. D., Siegle, G. J., Sorg, C., Teng, G. J., Veijola, J., Villringer, A., Walter, M., Wang, L., Weng, X. C., Whitfield-Gabrieli, S., Williamson, P., Windischberger, C., Zang, Y. F., Zhang, H. Y., Castellanos, F. X., and Milham, M. P. (2010). Toward discovery science of human brain function. Proc. Natl. Acad. Sci. U.S.A. 107, 4734–4739.

Pubmed Abstract | Pubmed Full Text

Calhoun, V. D., Adali, T., Pearlson, G. D., van Zijl, P. C., and Pekar, J. J. (2002). Independent component analysis of fMRI data in the complex domain. Magn. Reson. Med. 48, 180–192.

Pubmed Abstract | Pubmed Full Text

Calhoun, V. D., Kiehl, K. A., and Pearlson, G. D. (2008). Modulation of temporally coherent brain networks estimated using ICA at rest and during cognitive tasks. Hum. Brain Mapp. 29, 828–838.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Clarke, E. (2001). Meaning and specification of motion in music. Music. Sci. 5, 213–234.

Coltheart, M. (2006). What has functional neuroimaging told us about the mind (so far)? Cortex 42, 323–331.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Danto, A. (1981). The Transfiguration of the Commonplace: A Philosophy of Art. Cambridge, MA: Harvard University Press.

Deaton, A. (1997). Analysis of Household Surveys. Baltimore, MD: Johns Hopkins University Press.

Fodor, J. A. (1975). The Language of Thought. New York: Crowell.

Fodor, J. A. (2008). LOT 2: The Language of Thought Revisited. Oxford: Oxford University Press.

Friston, K. (2002). Beyond phrenology: what can neuroimaging tell us about distributed circuitry? Annu. Rev. Neurosci. 25, 221–250.

Pubmed Abstract | Pubmed Full Text

Friston, K., Frith, C., Fletcher, P., Liddle, P., and Frackowiak, R. (1996a). Functional topography: multidimensional scaling and functional connectivity in the brain. Cereb. Cortex 6, 156–164.

CrossRef Full Text

Friston, K., Price, C., Fletcher, P., Moore, R., Frackowiak, R., and Dolan, R. (1996b). The trouble with cognitive subtraction. Neuroimage 4, 97–104.

CrossRef Full Text

Friston, K. J., Price, C. J., Fletcher, P., Moore, C., Frackowiak, R. S., and Dolan, R. J. (1996c). The trouble with cognitive subtraction. Neuroimage 4, 97–104.

CrossRef Full Text

Friston, K., Frith, C., Frackowiak, R., and Turner, R. (1995). Characterizing dynamic brain responses with fMRI: a multivariate approach. Neuroimage 2, 166–172.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Garrity, A. G., Pearlson, G. D., McKiernan, K., Lloyd, D., Kiehl, K. A., and Calhoun, V. D. (2007). Aberrant “default mode” functional connectivity in schizophrenia. Am. J. Psychiatry 164, 450–457.

Pubmed Abstract | Pubmed Full Text

Gini, C. (1921). Measurement of inequality of incomes. Econ. J. 31, 124–126.

Hoyer, P. (2004). Non-negative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 5, 12.

Hurley, N., and Rickard, S. (2009). Comparing measures of sparsity. IEEE Trans. Inf. Theory 55, 18.

Huron, D. B. (2006). Sweet Anticipation: Music and the Psychology of Expectation. Cambridge, MA: MIT Press.

Husserl, E. (1966/1928). Zur Phänomenologie des inneren Zeitbewusstseins (Phenomenology of Inner Time Consciousness). The Hague: Martinus Nijhoff.

Kivy, P. (2002). Introduction to a Philosophy of Music. Oxford: Oxford University Press.

Langer, S. (1942). Philosophy in a New Key: A Study in the Symbolism of Reason, Right, and Art. Cambridge, MA: Harvard University Press.

Lehrdahl, F., and Jackendoff, R. (1996). A Generative Theory of Tonal Music. Cambridge, MA: MIT Press.

Levinson, G. (1997). Music in the Moment. Ithaca, NY: Cornell University Press.

Lloyd, D. (1997). Consciousness and its discontents. Commun. Cogn. 30, 273–285.

Logothetis, N. K. (2002). The neural basis of the blood-oxygen-level-dependent functional magnetic resonance imaging signal. Philos. Trans. R. Soc. Lond. B Biol. Sci. 357, 1003–1037.

Pubmed Abstract | Pubmed Full Text

McClelland, J., and Rumelhart, D. (1986). Parallel Distributed Processing: Explorations in Parallel Distributed Processing. Cambridge, MA: MIT Press.

Meadow, C. T., and Wang, J. (1993). An analysis of Zipf-Mandelbrot language measures and their application to artificial languages. J. Inform. Sci. 19, 247.

Meyer, L. B. (1956). Emotion and Meaning in Music. Chicago: University of Chicago Press.

Narmour, E. (1990). The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. Chicago: University of Chicago Press.

Patel, A. D. (2007). Music, Language, and the Brain. Oxford: Oxford University Press.

Petersen, S. E., and Roskies, A. L. (2001). “Visualizing human brain function,” in Frontiers of Life, Vol. 3, The Intelligent Systems, Part One: The Brain of Homo Sapiens, eds E. Bizzi, P. Calissano, and V. Volterra (New York: Academic Press), 87–109.

Price, C. J., and Friston, K. J. (2005). Functional ontologies for cognition: the systematic definition of structure and function. Cogn. Neuropsychol. 22, 262–275.

Pubmed Abstract | Pubmed Full Text

Rickard, S., and Fallon, M. (2004). “The Gini index of speech,” in Conference on Information Sciences and Systems, Princeton, NJ.

Roskies, A. L. (2009). Brain-mind and structure-function relationships: a methodological response to Coltheart. Philos. Sci. 76, 927–939.

Rumelhart, D., Smolensky, P., McClelland, J., and Hinton, G. (1986). “Schemata and sequential thought processes,” in Parallel Distributed Processing: Explorations in the Microstructure of Cognition, eds D. Rumelhart and J. McClelland (Cambridge, MA: MIT Press), 7–57.

Sethares, W. A. (2005). Tuning, Timbre, Spectrum, Scale. London: Springer.

Sethares, W. A. (2007). Rhythm and Transforms. Berlin: Springer.

Smolensky, P. (1988). On the proper treatment of connectionism. Behav. Brain Sci. 11, 1–23.

CrossRef Full Text

Stevens, M. C., Calhoun, V. D., and Kiehl, K. A. (2005). fMRI in an oddball task: effects of target-to-target interval. Psychophysiology 42, 636–642.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Voss, R., and Clarke, J. (1976). 1/f noise from systems in thermal equilibrium. Phys. Rev. Lett. 36, 42–45.

CrossRef Full Text

Zipf, G. (1949). Human Behavior and the Principle of Least Effort. Cambridge, MA: Addison-Wesley.