- 1Department of Psychology, Centre for Neuroscience in Education, University of Cambridge, Cambridge, United Kingdom
- 2Department of Developmental Psychology, University of Padua, Padua, Italy
We review how stress induction, time pressure manipulations and math anxiety can interfere with or modulate selection of problem-solving strategies (henceforth “strategy selection”) in arithmetical tasks. Nineteen relevant articles were identified, which contain references to strategy selection and time limit (or time manipulations), with some also discussing emotional aspects in mathematical outcomes. Few of these take cognitive processes such as working memory or executive functions into consideration. We conclude that due to the sparsity of available literature our questions can only be partially answered and currently there is not much evidence of clear associations. We identify major gaps in knowledge and raise a series of open questions to guide further research.
Introduction
Negative feelings and stressful situations can interfere to different degrees with success in mathematical tasks (Ashcraft and Kirk, 2001; Maloney and Beilock, 2012; Vukovic et al., 2013). Here, we systematically review the existing literature on the relationship between experiencing worrying/demanding situations (through stress induction), time pressure manipulations, math anxiety and strategy selection. Our main question is whether stressors in mathematics drive selection of more efficient strategies (i.e., providing the best accuracy within the constraints of the new situation) or whether they cause suboptimal strategy selection due to inducing interfering worrying thoughts.
Strategic behavior (i.e., deciding between two or more available options) is used in a wide range of problem solving domains, not only in the field of education (Pillutla and Murnighan, 1995; Hughes, 1998; Olthof et al., 2011). A wide body of research in the decision-making field states that individuals use a variety of strategies to make choices (Abelson and Levi, 1985). Similarly to in the arithmetic field, the selection of a particular strategy is contingent on many task- and context-related variables (Payne et al., 1988), suggesting that people can also adaptively change processing strategies appropriately when modest changes occur in the structure of the problems. Stress both influences and is influenced by strategy selection, resulting in quite a strong association between strategy selection and stress responses (Starcke and Brand, 2012).
In the mathematical domain, a wide body of research suggests that mathematics builds on several cognitive abilities (Passolunghi et al., 2008; Krajewski and Schneider, 2009; Geary, 2011) implemented by an extended neural network of the brain (Goswami and Szűcs, 2011; Fias et al., 2013; Szűcs et al., 2014). The flexibility and adaptability of strategic behavior coordinating these cognitive abilities (Verschaffel et al., 2009; Rittle-Johnson et al., 2012) is highly important as the correct execution of arithmetic problems typically involves a series of steps, which include adaptively switching between different arithmetic strategies in order to select and apply the most efficient one (Siegler and Shipley, 1995; Siegler and Lemaire, 1997). This choice can be influenced or driven by different factors. Some of these are linked to the features of the problem itself (such as the complexity of the algorithm in Imbo and LeFevre, 2010). Others are related to personal features of the solver in terms of both domain-specific aspects (such as their mathematical expertise and attitudes/emotions toward math; Baroody and Dowker, 2003) and domain-general aspects, i.e., broader cognitive and emotional factors (Devine et al., 2012; Mammarella et al., 2015).
Among cognitive factors, the process most widely explored and strongly related to the successful performance on arithmetical tasks is working memory (WM; for review see Raghubar et al., 2010; Bull and Lee, 2014; see also Passolunghi et al., 2008; Friso-Van Den Bos et al., 2013; Szűcs, 2016). WM is commonly analyzed as a predictor to explain mathematic outcomes at a later point in time, and the number of studies investigating this relationship has sharply increased in recent years (Bull et al., 2008; LeFevre et al., 2012; Li and Geary, 2013; Caviola et al., 2014; Cragg and Gilmore, 2014; Szűcs et al., 2014). This evidence supports the view that WM influences math achievement in different ways: it might help to keep track of relevant information (e.g., storage and retrieval of partial results) during a problem-solving process, as well as being involved in the successful selection and implementation of procedures (Barrouillet and Lépine, 2005; Swanson, 2006; Wu et al., 2008; Meyer et al., 2010).
While important for mathematical processes, WM is also highly sensitive to interference from stressors. Ashcraft and Kirk (2001) and Ashcraft and Krause (2007) found that cognitive processes can be negatively affected by the interference of negative emotions, such as math anxiety or pressured situations. This suggests how negative feelings might overload the WM system, thus resulting in a drop in performance (e.g., failing to achieve the result due the application of an inefficient strategy). Eysenck and colleagues tried to define the interaction between negative feelings and WM by developing the Attentional Control Theory (ACT, Eysenck and Calvo, 1992; Eysenck and Derakshan, 2011). According to this theory, anxiety affects participants' performance by disrupting their ability to control attention, making them more susceptible to distraction. This theory postulates that anxiety shifts the attention to task irrelevant stimuli by reducing cognitive resources allocated to the concurrent (relevant) task. This mechanism damages the subject's efficiency, whether the distracting stimuli are external (i.e., task-irrelevant stimuli) or internal (i.e., worrying thoughts; self-preoccupation). In summary, according to this model, anxiety affects the central executive component of WM processes, leading to a reduced cognitive performance in terms of decreased task efficiency and effectiveness, particularly on complex tasks (Ramirez and Beilock, 2011; Mammarella et al., 2017). Another important determinant of mathematical strategy selection is problem difficulty or complexity. The likelihood of choosing one strategy rather than another varies with problem features (Siegler, 1996; Lemaire and Callies, 2009). Increasing problem difficulty promotes the use of more advanced computational strategies, in order to maximize efficiency while still maintaining accuracy. The complexity of a problem can be manipulated in different ways (e.g., the type of algorithm, the number of digits in the operands, the presence or absence of a carrying procedure, etc.) resulting in different WM demands (Imbo and LeFevre, 2010). In fact, increasing the complexity of a problem can itself act as a stressor or modulate the effect of stress on math task execution. Efficiency usually decreases when carry or borrow problems have to be performed due to an increase in WM demand (Noël et al., 2001; Imbo et al., 2007; Caviola et al., 2012). Previous studies have also stated that negative emotional states (i.e., math anxiety) affect complex arithmetic performance more than simple arithmetic performance (Ashcraft, 1995; Devine et al., 2012).
Stressful situations can also be induced by manipulating the context in which the problem is presented, such as punishing poor performance with social consequences, in order to interfere with cognition (Beilock and Carr, 2001, 2005). In other words, taxing people's executive resources by increasing anxiety due to fear of negative consequences resulted in less efficient strategy use, and consequently poorer arithmetic performance.
In this review, we summarize the state of research about the relationship between cognitive stress and strategic behavior used to solve arithmetic tasks. The synthesis has been complicated by the use of different terms according to the specific line of research. In particular, studies on stress and math-related emotions each look at slightly different domains and consequently refer to them with slightly different terms. For example, “stress,” “negative emotions” and “anxiety” are labels which, in the mathematical research field, have often been used to describe similar states of mind that potentially can interfere with the execution of mathematical tasks (Stipek and Gralinski, 1991; Galla and Wood, 2012; Brunyé et al., 2013). In the first part of this article we present and discuss different conceptual and methodological approaches related to manipulating task complexity, focusing in particular on the different ways to trigger cognitive stress. In the second part we pay particular attention to time pressure manipulation, by highlighting its effect on strategy choice and cognitive processes and its relationship with emotional aspects, such as math anxiety.
Electronic Searches and Selection of Studies
An electronic search was conducted on principal databases (PsychINFO, Web of Science, PubMed, EBSCO, Scopus) for English published articles. No date restriction was used, and the keywords were: time pressure/time constraint/time limit/time deadline; strategy/strategy selection/strategy choice/strategy efficiency; problem solving/arithmetic/math/mathematics/calculation; emotional factors/cognitive stress/anxiety/math anxiety. The search has been done with the following combinations of terms: (time pressure OR time limit OR time constraint OR time deadline) AND (arithmetic OR math* OR calculation OR problem solving) AND (strateg*) AND (emot* OR stress OR anxiety). We used the wildcard * where alternative words like “strategic”/“strategy” or “emotion”/“emotional” might arise. As allowed by each database, the terms have been explored mainly in the title, abstract and keywords, and when possible through the entire full text.
Research was included in this review by following these inclusion criteria. First, since studies on this topic vary in their methodological design, we included those studies which clearly stated the manipulation of the execution time during the main task; second, if they considered how the time constraint affected participants' strategic behavior and consequently their results; and finally, if they have quantitatively measured emotional aspects related to math tasks. Studies aiming to highlight gender differences or that revealed different sample sizes according to gender were excluded, as well as research primarily focused on neuroimaging effects.
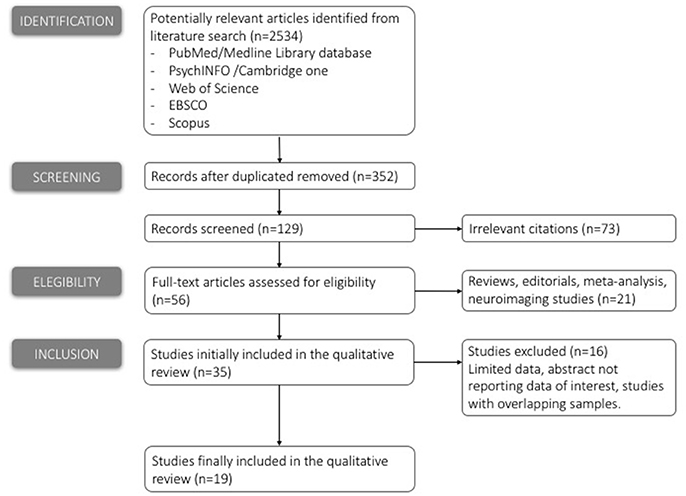
We considered papers published before December 2016. The initial inspection was independently completed by two reviewers (SC and EC): the electronic search identified 2,534 papers which matched the search terms. After deleting duplication 352 studies were selected. Titles and abstracts of the studies retrieved were then screened by two reviewers to identify studies that potentially met the criteria outlined above. The full text of the 129 remaining potentially eligible studies were then retrieved and independently assessed for eligibility by two reviewers: any disagreement between the two reviewers was resolved through discussion with a third reviewer (DS): 56 papers remained at this stage.
It is important to note that the inclusion criteria we used in the papers selection led us to exclude all the studies which applied a time limit constraint due to the experimental setting, i.e., studies which did not actually impose a direct time limit on the performance, but instead looked at results by setting a post-hoc deadline for responses (e.g., ERP studies for time course analysis of arithmetic information processing; Rosenberg-Lee et al., 2009; Hinault and Lemaire, 2016). A total of other 21 studies were excluded at this stage.
Finally, 35 studies attained the eligibility criteria. A pre-prepared Excel spreadsheet was used to record extracted data from the included studies for assessment of study quality and data synthesis. Study quality consisted of a risk of bias assessment: quality of individual studies was evaluated in terms of sample size and type (and number) of tasks reported for each domain (time limits/mathematical tasks/emotional factors). Where there was concern over the methodological quality of any studies, sensitivity analyses were conducted: only 19 met the selection criteria and were included in the present review (see Figure 1). Once the target articles had been agreed, the two independent reviewers (SC and EC), by using a customized scheme, extracted the relevant data. Besides participants' age, information about (1) experimental design and timing, including the type of arithmetical task and relative strategies, (2) emotional aspects and (3) the type of cognitive processes investigated (if present), were collected. We also noted whether studies included children (6–12 years), adolescents (13–17 years) or adults (18 years and above).
Regarding the experimental designs, we preferred not to use any restrictive classification of the mathematical tasks reported, but due to high heterogeneity, we report a description of the task itself. Specifically related to the “pressure” aspect, we tried to classify how pressure was induced in the experimental design, in particular whether (i) it was provided by inducing a time limit or by means of other manipulations (e.g., monetary incentives), (ii) in the case of time limits, we considered extensively the experimental methodology (e.g., number of conditions, time limit applied to stimuli presentations or response window).
Structure of the Review
The main goal of this review was to shed light on how stress induction, particularly time pressure manipulations, can interfere with or modulate strategy selection in arithmetical tasks. Additionally, we were also interested in whether this association could be moderated by emotional and cognitive factors.
The electronic search and the subsequent screening phases highlighted how stress induction or time pressure manipulation have been differentially implemented to trigger cognitive stress during math task execution. Indeed, among the 19 relevant articles identified, 8 papers applied social constraints to induce pressure. Eleven further studies implemented a time pressure manipulation to induce pressure.
In the subsequent section of this article (Social Stress Induction and Choking under Pressure Phenomenon), we first consider those papers which induce stress and “choking under pressure” via social manipulations which do not limit time available to solve tasks. In the next section (Time Pressure in Math: Strategy Selection), we consider tasks which engaged a time pressure manipulation. These two types of pressure manipulation are different in nature for a fundamental reason: regardless of “choking under pressure,” time pressure manipulations may render a previous strategy useless due to complexity. With only limited time available, rapid heuristic strategies can become optimal simply due to their speed. Finally, in Section Emotional Aspects and Stress Manipulation, we consider those studies which actually measure affective factors (such as mathematics anxiety). There is a paucity of such studies, making firm conclusions challenging: however, they are of importance in determining the role of pressure in math tasks (see Figure 2 for a graphic summary).
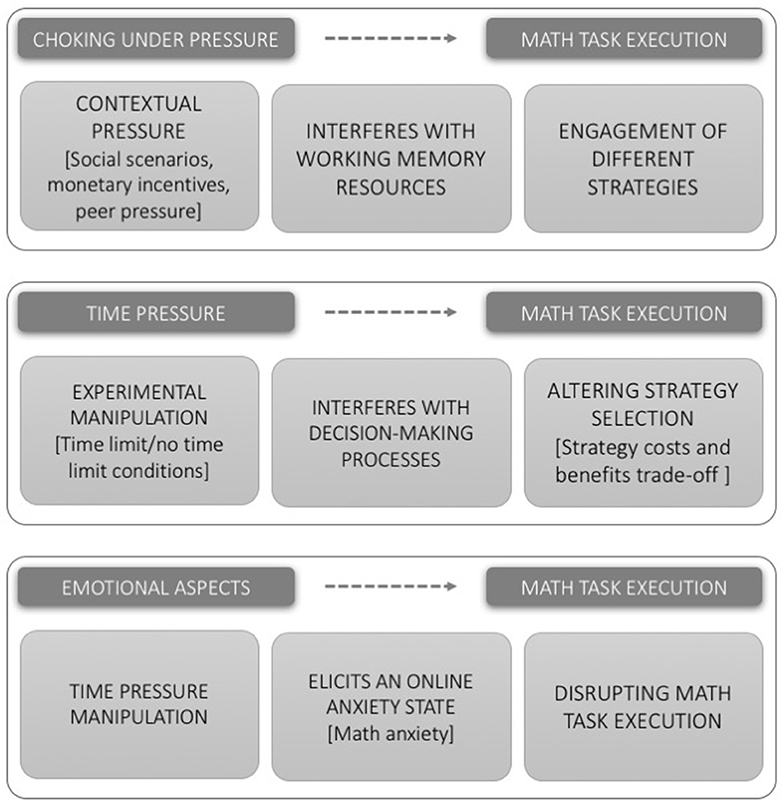
Figure 2. Graphic summary of the three principal mechanisms/relationships discussed in different sections of the manuscript.
The outcomes of the present review only partially resolve our initial questions and they can be understood more as open questions than evidence of clear associations. Each section concludes by raising a series of aspects in which this field of research may move forward.
Social Stress Induction and Choking under Pressure Phenomenon
As noted, cognitive stress may influence cognitive resources (Mazzoni and Cornoldi, 1993; Barrouillet et al., 2007) and consequently affects strategic behavior in different domains, such as mathematical learning, which often involves high-pressure tests. Especially in math, where stress and anxiety are common and there is a strong desire to perform well, people may fail to perform at their best level, despite having the required skill (Benny and Banks, 2015).
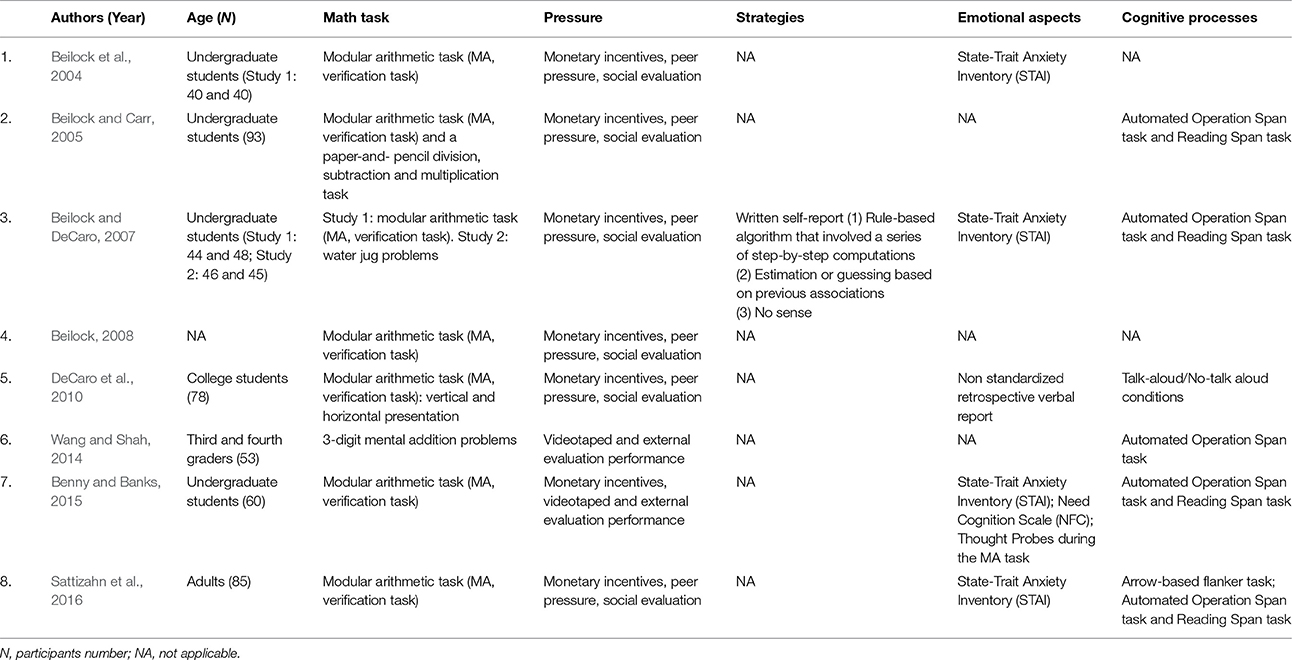
Surveying the literature regarding stress-induced performance in mathematical domain, one of the main topics referred to is the “choking under pressure” phenomenon. Choking, or worse performance than expected for one's level of ability, tends to happen in situations involving performance pressure (Baumeister, 1984; Lewis and Linder, 1997; Beilock and Carr, 2001). Table 1 summarizes this research.
The main hypothesis of this research field is that contextual pressure interferes with limited WM resources (Miyake and Shah, 1999; Jonides et al., 2008). According to this perspective, pressure is assumed to cause worrying off-task thoughts that result in overload of WM already engaged in the math task, similarly to math anxiety. Beilock and colleagues (Beilock et al., 2004; Beilock and Carr, 2005; Beilock and DeCaro, 2007; Beilock, 2008) investigated how individual differences in WM capacity relate to high and low pressure conditions defined by different social scenarios, such as monetary incentives or peer pressure, while subjects solve modular arithmetic problems (a complex task that can be solved by computation or estimation strategies). They found that participants with higher WM capacity were more disturbed by the pressure constraint than the subjects with less WM capacity, leading to a more significant lowering of arithmetic performance in those with higher WM capacity.
In subsequent research, Beilock and DeCaro (2007) tried to disentangle the issue of which strategy was engaged by analyzing the availability of WM resources and task complexity within a single study. In all their studies the authors manipulated the pressure condition by prompting commonly experienced pressures in everyday life, such as monetary reward, peer pressure, and social evaluation. The authors found that the difference in terms of performance between high- and low-WM participants was linked to the strategy selected to solve the problems: because high WM individuals typically use more WM-intensive strategies than low WM individuals, their strategies were affected more strongly by performance pressure (DeCaro et al., 2010). Similar results have also been reported in primary school children who had to solve mental arithmetic tasks (Wang and Shah, 2014). This data partially replicated previous findings but also added something new: the presence of a pressure condition (induced by simulating the recording of an evaluation video) affected children' math performance depending on their own cognitive resources and the specific task difficulty. In this study, high-pressure scenarios led to more errors when high WM children had to solve normal carry problems, whereas low WM children choked under pressure when they had to solve hidden carry problems, i.e., problems that can only be solved successfully through computational strategies. No such distinction emerged from individual differences in WM with simpler no-carry problems, regardless of the pressure. This effect seems to be strictly connected to the strategy selected and applied to solve the problem. According to the authors, these problems could be solved with two main strategies: computational strategies, that are WM demanding, or more heuristic and estimation strategies. Children' decision to use computational strategies or easier heuristics to solve problems is dependent on both task complexity and a subject's available working memory resources, influenced by the presence of pressure. In the pressure condition, low WM children were not able to rely on computationally demanding strategies to solve for hidden carry problems, so were forced to use the less demanding and also less accurate heuristic strategies. These results show that different strategies are optimal depending on the mental state induced by the problem context. When a factor reducing WM capacity is in place, students may be better to use less accurate but less WM-intensive strategies. On the other hand, when WM capacity is higher, more WM-intensive and higher accuracy strategies are more worthwhile (Beilock and DeCaro, 2007; Benny and Banks, 2015; DeCaro et al., 2016).
Recently, Sattizahn et al. (2016) replicated previous results demonstrating that adults with high WM resources performed significantly worse due to experiencing high pressure. They also tested individuals' variability in attentional control processes, finding that differences in attentional control influenced the effect of a pressure situation. Those with low attentional control suffered decreased performance under pressure, whereas those with high attentional control did not. This likely reflects that some individuals are able to prevent the interfering effect of pressure on their performance, whereas other with lower attentional control are not able to do this.
Although the above studies seem to answer a distinctive question (how can pressure influence math performance?), they differ in so many aspects, making it difficult to reach a certain answer. For example, all the above research aimed to analyze the effect of pressure on math, but none of them implemented a quantifiable manipulation of pressure with controlled conditions. Instead, they engaged social scenarios which could differentially affect each participant. Similarly, the mathematical tasks and cognitive measures considered vary widely across studies. In order to clarify findings in this domain it is important to systematically consider the role of task difficulty, the nature of the tasks themselves (those that allow for multiple strategies vs. those that do not), and the type of pressure manipulation used in the different studies. This leads to another question: how else can cognitive stress be induced in the math domain?
Time Pressure in Math: Strategy Selection
A large amount of literature from the decision-making field suggests that manipulating the time limit/pressure associated with a task has a very strong effect on the stressful nature of that particular task (e.g., Kerstholt, 1994; Ordóñez and Benson, 1997; Huber and Kunz, 2007; Young et al., 2012; Cone and Rand, 2014; Byrne et al., 2015). However, in the mathematical cognition field few studies have considered a time deadline as an important interference source and explicitly manipulated it by inserting in the experimental design at least two separate conditions; one with and one without a time limit.
One of the first studies on this topic attempted to simulate a computational model of automated and controlled processing during the execution of addition problems in trinary notation: Richardson and Hunt (1985) addressed the issue of how “problem solving sometimes takes place under severe real time constraints” by inserting a series of interruptions during stimulus presentation. Subsequent research has manipulated the time limit using more controlled experimental designs, across a variety of mathematical tasks, such as numerosity judgment (Luwel and Verschaffel, 2003) arithmetical problems (Kellogg et al., 1999; Campbell and Austin, 2002), probabilistic and proportional reasoning (Gillard et al., 2009; Agus et al., 2015), and algebraic concepts (McNeil et al., 2010; Chesney et al., 2013). A summary of the studies which implemented a time pressure manipulation is listed in Table 2.
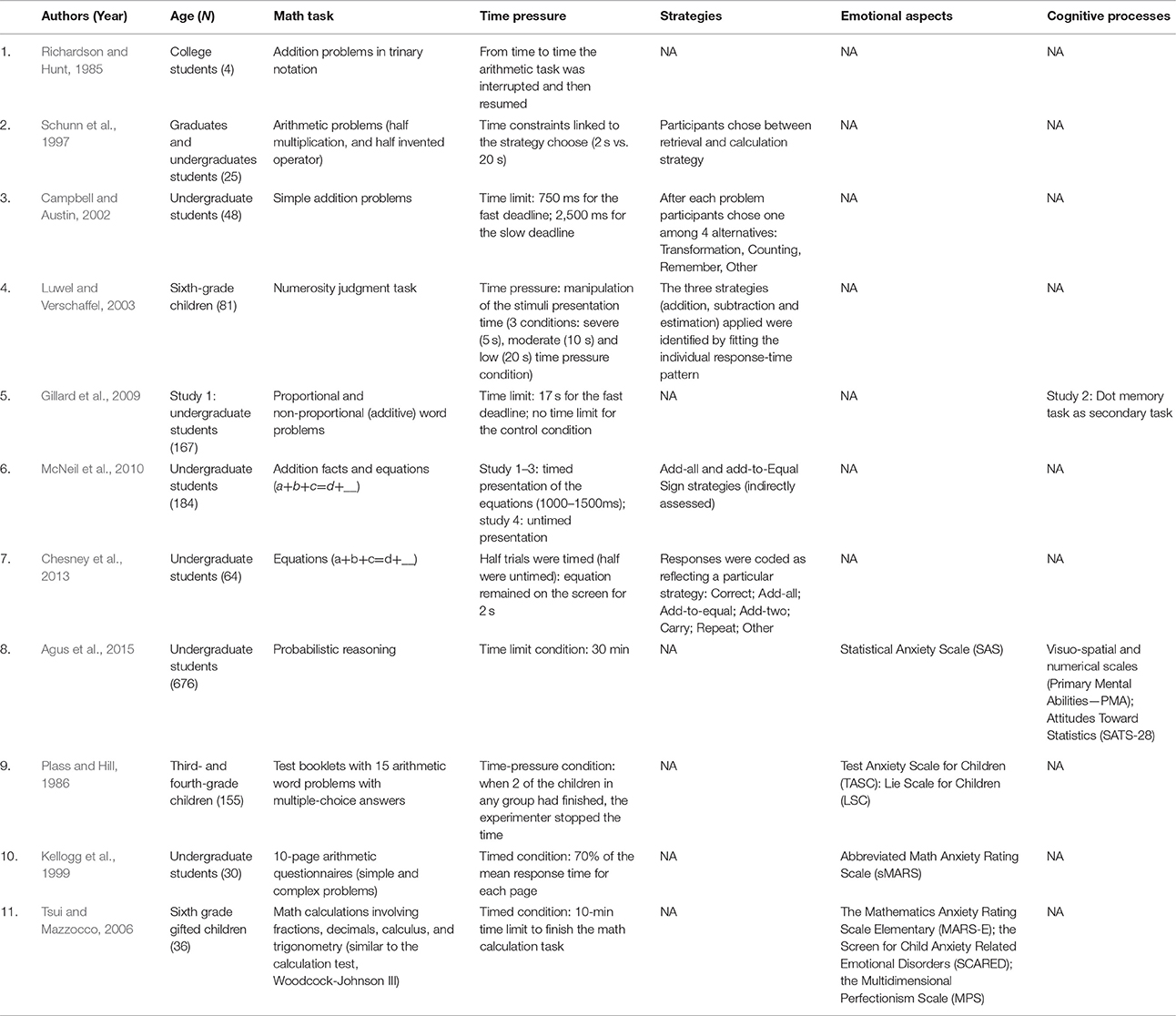
Table 2. Studies investigating strategy selection (positions 1–8) and emotional aspects (position 9–11) with time condition manipulation.
As in the decision-making domain, time pressure in mathematics has been manipulated primarily by limiting available time for each decision or choice. Several studies have shown that time pressure interferes with decision-making by altering strategy selection. The presence of a time constraint in any math or problem-solving situation can affect performance: the presence of time limits could either encourage students' engagement with the task or increase choice of the wrong strategy for that task (Beilock and DeCaro, 2007; Rieskamp and Hoffrage, 2008). Leaving an open time window to complete a task enables participants to get a greater amount of information by focusing attention on important task features, which results in the best strategy selection (Payne et al., 1988; Siegler and Lemaire, 1997; Rieskamp and Hoffrage, 2008; Heinze et al., 2009). According to this viewpoint, Gillard et al. (2009) manipulated time pressure by reducing the solution time or introducing a concurrent task, leading to a self-imposed time constraint to complete the main task (see for Rieskamp and Hoffrage, 2008). The authors compared heuristic (which engage faster and automatic processes) and analytic processes during the execution of proportional and non-proportional problems in university students in two different experiments. They found that limiting students' resources, by reducing their response time or loading their working memory system, resulted in an increase in the wrong choice of heuristic proportional solution strategy.
Thus, time pressure is one factor that influencing which strategy people select to deal with a particular math problem situation (Young et al., 2012; Alison et al., 2013). McNeil and colleagues investigated how time pressure can influence the strategies used by both adults and children to solve equation problems. They found that under time pressure, university students used the same typical arithmetic strategies applied by children to solve mathematical equivalence problems, demonstrating how people can shift from more complex to simpler strategies when they are under pressured conditions (Mcneil and Alibali, 2005; McNeil et al., 2010; Chesney et al., 2013). Similarly, Campbell and Austin (2002) used a time limit manipulation when adults were solving simple addition problems in order to alter their strategy choice. The author imposed a fast deadline (750 ms) to force adult participants to use a retrieval strategy, and a slower one (2,500 ms) to elicit use of procedural strategy (e.g., counting or transformation). Results indicated adaptive strategic behavior (Siegler and Lemaire, 1997) which was influenced by problem features. The fast deadline resulted in a small effect on retrieval strategy usage for smaller problems, where fact retrieval was used under both conditions. On the other hand, for larger problems, participants report decreased use of procedural strategies under the faster condition. The time pressure imposed by the fast deadline adaptively modified the participants' selection strategy increasing the attempts to solve larger problems by a retrieval strategy. For large problems under the time pressure condition, retrieval strategy was both faster and more accurate than a multistep procedure, making this an example of adaptive strategy selection.
A similar pattern of results has been found by Luwel and Verschaffel (2003) testing the estimation strategies of sixth graders under three different time pressure conditions. In this study, participants were asked to determine the number of filled blocks in a 10 × 10 grid as accurately and fast as possible, according to time pressure conditions, operated by introducing three temporal windows of stimulus presentation (5, 10, or 20 s). To accomplish the task, participants would engage three possible strategies, identified in prior studies, each of which is expected to elicit a specific pattern of response times (and deviation scores) as a function of the number of blocks present (Luwel et al., 2000, 2001). Analysis of the results revealed that children's performance was also affected by increasing time pressure on strategy repertoire, relative frequency of strategy use and efficiency of strategy execution, indicating that even at a young age children seem able to adapt their strategy use to the external task demands, in terms of coping with the given time restrictions (for a different pattern of results, see Schunn et al., 1997).
The overall results highlight that time pressure adjusts the strategy decision process generating a sort of strategy costs and benefits trade-off: when the available time is short and the task complexity is substantial (i.e., Campbell and Austin, 2002), strategies that can be applied rapidly represent the more appropriate choice. On the other hand, leaving an open time window to complete a task enables participants to get a greater amount of information by using a slower but more accurate strategy (Payne et al., 1988; Siegler and Lemaire, 1997; Rieskamp and Hoffrage, 2008; Heinze et al., 2009). A reduction in execution time allowed to solve a mathematical task can lead to a decrease of information that can be collected. The importance of reaction time analysis in the study of mathematical processes is widely acknowledged, above all in the domain of strategy selection (DeCaro et al., 2016). For example, it is worth noting that switching between complex and shortcut strategies incurs a cost to reaction time (e.g., Luwel et al., 2009; Schillemans et al., 2009; Lemaire and Lecacheur, 2010), but this can be directly tested only when the experimental paradigm requires there to be no time limit in place.
Emotional Aspects and Stress Manipulation
The negative emotional state and discomfort felt during performance of mathematical tasks is commonly referred to as math anxiety (Hembree, 1990; Ma, 1999; Ma and Xu, 2004). The current consensus is that math anxiety is negatively correlated with mathematical performance (Ashcraft, 2002; Devine et al., 2012; Carey et al., 2016; Hill et al., 2016). Most of the research measures math anxiety levels through self-report questionnaires detecting a sort of “offline” measure rather than testing anxiety levels while solving math problems (e.g., Trezise and Reeve, 2014, 2015). This assessment of math anxiety implicitly leads one to assume that it is an enduring anxiety (trait) rather than an anxiety state experienced whilst solving particular problems. On the other hand, manipulating time pressure during a mathematical task might elicit an online anxiety state that allows accurate analysis of how anxiety can disrupt or interfere with arithmetic task execution.
Although it seems to be widely recognized that providing a reasonable time for the accomplishment of a math test should be effective in reducing at least some of the disadvantage experienced by math anxious subjects (Faust et al., 1996; Ashcraft and Kirk, 2001), surprisingly little research directly includes a time condition manipulation. To our knowledge, only three studies involved a clear time pressure manipulation for testing the effect of math anxiety on mathematical tasks (see Table 2, studies numbered 9–11).
Plass and Hill (1986) analyzed the relation between problem solving ability, test anxiety and gender differences in 155 third- and fourth-grade primary school children. The sample was divided into three groups (low, middle, and high test-anxiety) either under time or no-time pressure conditions. Under time pressure, high- and middle-anxiety children performed worse than low-anxiety children of both genders. The removal of time pressure strongly improved performance for anxious boys but not for girls.
Tsui and Mazzocco (2006) examined the effects of math anxiety on math performance, under timed and untimed testing conditions in 36 sixth grade primary school children. They found a general pattern of reduced accuracy in math performance under the timed testing condition. This was influenced by participants' math anxiety level: higher anxiety children performed equally under timed and untimed testing conditions. Conversely, lower anxiety children had decreased math performance under timed condition. Although there was no main effect of gender on timed vs. untimed math performance, boys were equally accurate on timed and untimed testing, by contrast, girls showed a discrepancy in accuracy in favor of untimed conditions. They explain this pattern of results in terms of facilitating anxiety: according to the authors, the performance of gifted children with high math anxiety did not drop under time pressure because of math anxiety canceling out the negative effect of time pressure; effect that was present for lower math anxiety children.
These outcomes do not converge with Kellogg et al. (1999) who tested 30 undergraduate university students divided into three different groups according their math anxiety level. Participants were asked to solve a series of arithmetical tasks in both a timed and untimed condition. Kellogg et al. (1999) did not observe any difference between high and low anxiety individuals, although the timing manipulation negatively affected the arithmetic performance of both groups. The authors stated that time pressure manipulation had an additive effect with anxiety on arithmetic performance. Consequently, although “worry” may adversely affect the performance of highly anxious individuals (Eysenck and Calvo, 1992), it does not appear that the level of worry is differentially related to the amount of time assigned to perform a mathematical task. In other words, they concluded that time pressure was not a contributor to the worrisome thoughts that occupy individuals with high math anxiety during arithmetic testing.
In sum, there is some evidence that math anxiety interacts with timed or high-stakes conditions to cause a further performance decrement than usual. However, due to the paucity and heterogeneity of research both in terms of sample and tasks considered, these results do not allow us to conclude that increasing time pressure has a differential effect depending on math anxiety. Similarly, assuming causal relations between time pressure and inducing math anxiety currently does not have evidential support.
General Conclusions
This literature overview of the past 30 years focuses on the effect of stress and/or time pressure on math proficiency. It has revealed that, generally speaking, pressure has a great influence on both strategic and emotional aspects of task execution.
Research on choking and excelling under pressure has focused on tasks that demand many cognitive resources, especially working memory (Miyake and Shah, 1999; Jonides et al., 2008). Similarly, some research on math anxiety suggest that trait anxiety also reduces effective working memory capacity (Ashcraft and Kirk, 2001; Ashcraft and Krause, 2007). This suggests that anxiety impairs performance by overloading working memory. Specifically, pressure is expected to lead to worry, concern and other distracting thoughts about performance, which consume working memory resources (Beilock and Carr, 2005).
It has been widely assumed that people are equipped with a range of cognitive strategies which they adaptively select and apply according to the specific task and situation. Within this framework, pressure represents one factor that can influence which strategy people select to deal with a particular situation. Relatively little research has focused on the impact of time pressure on strategy selection in mathematics, principally aiming to show how time pressure interferes with the decision process in terms of strategy selection in mathematical domain. Results seem to suggest that time pressure generally acts as a stressor, causing suboptimal strategy selection. However, the causal mechanism of this is still unclear. It is not clear whether time pressure interferes with strategy selection or whether it simply renders the optimal strategy impossible, due to an overload of working memory resources.
Further research is needed to address this question, taking into account the huge variability of execution time linked to task type (e.g., simple vs. complex calculation or even verification vs. production task; Ashcraft, 1995; Rousselle and Noël, 2008). For example, the answer modality of a math task (verification vs. production) can strongly influence and drive the solution process itself, and consequently the strategies applied to solve the task. Sometimes, experimenters chose to adopt a verification mode (i.e., namely a choice among a series of alternatives) compared to a production task (i.e., participant is asked to produce/give the right answer) for time limit issues linked to the experimental setting or data analyses (e.g., ERP study for time course analysis of arithmetic information processing; time limit set up only during data analysis to identify outliers or specific retrieval answers). Within this perspective, the studies summarized in the “choking under pressure” section mainly reported verification tasks, conversely, the experiments listed in the other subsequent sections were often production tasks, making it harder to provide general conclusions based on this methodological aspect.
Similar considerations can be drawn regarding the relationship between time pressure and emotional aspects within the mathematical learning framework, leaving space for several open questions. Among them is whether time pressure can be always considered as a negative factor in terms of proficiency and math anxiety. To date the literature does not clearly answer this issue. Decreased performance under time pressure is not consistently observed in high or low math anxiety individuals. Previous problem-solving studies suggest that time constraints inhibit creative thinking; but more recent research indicates that time constraints can sometimes prove beneficial (Medeiros et al., 2014). An alternative explanation of this inconsistent pattern may be found in the social pressure literature by considering where individuals focus their attention during the performance. It may be important whether attention is directed on the process of performance or to the outcome of performance: these situational aspects of the attentional system may affect results. Pressure does not simply cause a reduction in executive resources; it changes one's motivational state, leading to failure or success with different types of tasks due to the availability of attentional resources during performance (see e.g., Markman et al., 2006; Worthy et al., 2009).
To sum, the present review demonstrates the need for a broader view of the effects of time pressure on math performance. Future research should systematically examine the effects of time pressure on math performance and strategy selection to develop a fuller framework of phenomena that drive choking or excelling under pressure.
Author Contributions
SC and DS developed the study concept. Literature review was conducted by SC and EC. SC and IM drafted the manuscript. DS provided critical revisions. All authors approved the final version of the manuscript for submission.
Funding
The project leading to this application has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 700031.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abelson, R. P., and Levi, A. (1985). Decision making and decision theory. Handb. Soc. Psychol. 1, 231–309.
Agus, M., Peró-Cebollero, M., Penna, M. P., and Guàrdia-Olmos, J. (2015). Comparing psychology undergraduates' performance in probabilistic reasoning under verbal-numerical and graphical-pictorial problem presentation format: what is the role of individual and contextual dimensions? Eur. J. Math. Sci. Technol. Educ. 11, 735–750. doi: 10.12973/eurasia.2015.1382a
Alison, L., Doran, B., Long, M. L., Power, N., and Humphrey, A. (2013). The effects of subjective time pressure and individual differences on hypotheses generation and action prioritization in police investigations. J. Exp. Psychol. 19, 83–93. doi: 10.1037/a0032148
Ashcraft, M. H. (1995). Cognitive psychology and simple arithmetic: a review and summary of new directions. Math. Cogn. 1, 3–34.
Ashcraft, M. H. (2002). Math anxiety: personal, educational, and cognitive consequences. Curr. Dir. Psychol. Sci. 11, 181–185. doi: 10.1111/1467-8721.00196
Ashcraft, M. H., and Kirk, E. P. (2001). The relationships among working memory, math anxiety, and performance. J. Exp. Psychol. 130, 224–237. doi: 10.1037/0096-3445.130.2.224
Ashcraft, M. H., and Krause, J. A. (2007). Working memory, math performance, and math anxiety. Psychon. Bull. Rev. 14, 243–248. doi: 10.3758/BF03194059
Baroody, A. J., and Dowker, A. (Eds.). (2003). The Development of Arithmetic Concepts and Skills: Constructive Adaptive Expertise. London, UK: Routledge.
Barrouillet, P., Bernardin, S., Portrat, S., Vergauwe, E., and Camos, V. (2007). Time and cognitive load in working memory. J. Exp. Psychol. Learn. Mem. Cogn. 33, 570–585. doi: 10.1037/0278-7393.33.3.570
Barrouillet, P., and Lépine, R. (2005). Working memory and children's use of retrieval to solve addition problems. J. Exp. Child Psychol. 91, 183–204. doi: 10.1016/j.jecp.2005.03.002
Baumeister, R. F. (1984). Choking under pressure: self-consciousness and paradoxical effects of incentives on skillful performance. J. Pers. Soc. Psychol. 46, 610–620. doi: 10.1037/0022-3514.46.3.610
Beilock, S. L. (2008). Math performance in stressful situations. Curr. Dir. Psychol. Sci. 17, 339–343. doi: 10.1111/j.1467-8721.2008.00602.x
Beilock, S. L., and Carr, T. H. (2001). On the fragility of skilled performance: what governs choking under pressure? J. Exp. Psychol. Gen. 130, 701–725. doi: 10.1037/0096-3445.130.4.701
Beilock, S. L., and Carr, T. H. (2005). When high-powered people fail: working memory and “Choking under Pressure” in math. Psychol. Sci. 16, 101–105. doi: 10.1111/j.0956-7976.2005.00789.x
Beilock, S. L., and DeCaro, M. S. (2007). From poor performance to success under stress: working memory, strategy selection, and mathematical problem solving under pressure. J. Exp. Psychol. Learn. Mem. Cogn. 33, 983–998. doi: 10.1037/0278-7393.33.6.983
Beilock, S. L., Kulp, C. A., Holt, L. E., and Carr, T. H. (2004). More on the fragility of performance: choking under pressure in mathematical problem solving. J. Exp. Psychol. Gen. 133, 584–600. doi: 10.1037/0096-3445.133.4.584
Benny, B., and Banks, J. B. (2015). Under pressure. J. Individ. Diff. 36, 93–100. doi: 10.1027/1614-0001/a000160
Brunyé, T. T., Mahoney, C. R., Giles, G. E., Rapp, D. N., Taylor, H. A., and Kanarek, R. B. (2013). Learning to relax: evaluating four brief interventions for overcoming the negative emotions accompanying math anxiety. Learn. Individ. Differ. 27, 1–7. doi: 10.1016/j.lindif.2013.06.008
Bull, R., Espy, K. A., and Wiebe, S. A. (2008). Short-term memory, working memory, and executive functioning in preschoolers: longitudinal predictors of mathematical achievement at age 7 years. Dev. Neuropsychol. 33, 205–228. doi: 10.1080/87565640801982312
Bull, R., and Lee, K. (2014). Executive functioning and mathematics achievement. Child Dev. Perspect. 8, 36–41. doi: 10.1111/cdep.12059
Byrne, K. A., Silasi-Mansat, C. D., and Worthy, D. A. (2015). Who chokes under pressure? The Big Five personality traits and decision-making under pressure. Pers. Individ. Dif. 74, 22–28. doi: 10.1016/j.paid.2014.10.009
Campbell, J. I. D., and Austin, S. (2002). Effects of response time deadlines on adults' strategy choices for simple addition. Mem. Cogn. 30, 988–994. doi: 10.3758/BF03195782
Carey, E., Hill, F., Devine, A., and Szücs, D. (2016). The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance. Front. Psychol. 6:1987. doi: 10.3389/fpsyg.2015.01987
Caviola, S., Mammarella, I. C., Cornoldi, C., and Lucangeli, D. (2012). The involvement of working memory in children's exact and approximate mental addition. J. Exp. Child Psychol. 112, 141–160. doi: 10.1016/j.jecp.2012.02.005
Caviola, S., Mammarella, I. C., Lucangeli, D., and Cornoldi, C. (2014). Working memory and domain-specific precursors predicting success in learning written subtraction problems. Learn. Individ. Differ. 36, 92–100. doi: 10.1016/j.lindif.2014.10.010
Chesney, D. L., McNeil, N. M., Brockmole, J. R., and Kelley, K. (2013). An eye for relations: eye-tracking indicates long-term negative effects of operational thinking on understanding of math equivalence. Mem. Cognit. 41, 1079–1095. doi: 10.3758/s13421-013-0315-8
Cone, J., and Rand, D. G. (2014). Time pressure increases cooperation in competitively framed social dilemmas. PLoS ONE 9:e115756. doi: 10.1371/journal.pone.0115756
Cragg, L., and Gilmore, C. (2014). Skills underlying mathematics: the role of executive function in the development of mathematics proficiency. Trends Neurosci. Educ. 3, 63–68. doi: 10.1016/j.tine.2013.12.001
DeCaro, M. S., Rotar, K. E., Kendra, M. S., and Beilock, S. L. (2010). Diagnosing and alleviating the impact of performance pressure on mathematical problem solving. Q. J. Exp. Psychol. 63, 1619–1630. doi: 10.1080/17470210903474286
DeCaro, M. S., Van Stockum, C. A., and Wieth, M. B. (2016). When higher working memory capacity hinders insight. J. Exp. Psychol. Learn. Mem. Cogn. 42, 39–49. doi: 10.1037/xlm0000152
Devine, A., Fawcett, K., Szűcs, D., and Dowker, A. (2012). Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behav. Brain Funct. 8:33. doi: 10.1186/1744-9081-8-33
Eysenck, M. W., and Calvo, M. G. (1992). Anxiety and performance: the processing efficiency theory. Cogn. Emot. 6, 409–434. doi: 10.1080/02699939208409696
Eysenck, M. W., and Derakshan, N. (2011). New perspectives in attentional control theory. Pers. Individ. Dif. 50, 955–960. doi: 10.1016/j.paid.2010.08.019
Faust, M. W., Ashcraft, M. H., and Fleck, D. E. (1996). Mathematics anxiety effects in simpe and complex addition. Math. Cogn. 2, 25–62. doi: 10.1080/135467996387534
Fias, W., Menon, V., and Szűcs, D. (2013). Multiple components of developmental dyscalculia. Trends Neurosci. Educ. 2, 43–47. doi: 10.1016/j.tine.2013.06.006
Friso-Van Den Bos, I., Van Der Ven, S. H. G., Kroesbergen, E. H., and Van Luit, J. E. H. (2013). Working memory and mathematics in primary school children: a meta-analysis. Educ. Res. Rev. 10, 29–44. doi: 10.1016/j.edurev.2013.05.003
Galla, B. M., and Wood, J. J. (2012). Emotional self-efficacy moderates anxiety-related impairments in math performance in elementary school-age youth. Pers. Individ. Dif. 52, 118–122. doi: 10.1016/j.paid.2011.09.012
Geary, D. C. (2011). Cognitive predictors of achievement growth in mathematics: a 5-year longitudinal study. Dev. Psychol. 47, 1539–1552. doi: 10.1037/a0025510
Gillard, E., Van Dooren, W., Schaeken, W., and Verschaffel, L. (2009). Proportional reasoning as a heuristic-based process g time constraint and dual task considerations. Exp. Psychol. 56, 92–99. doi: 10.1027/1618-3169.56.2.92
Goswami, U., and Szűcs, D. (2011). Educational neuroscience: developmental mechanisms: towards a conceptual framework. NeuroImage 57, 651–658. doi: 10.1016/j.neuroimage.2010.08.072
Heinze, A., Star, J. R., and Verschaffel, L. (2009). Flexible and adaptive use of strategies and representations in mathematics education. ZDM Int. J. Math. Educ. 41, 535–540. doi: 10.1007/s11858-009-0214-4
Hembree, R. (1990). The nature, effects, and relief of mathematics anxiety. J. Res. Math. Educ. 21, 33–46. doi: 10.2307/749455
Hill, F., Mammarella, I. C., Devine, A., Caviola, S., Passolunghi, M. C., and Szucs, D. (2016). Maths anxiety in primary and secondary school students: gender differences, developmental changes and anxiety specificity. Learn. Individ. Diff. 48, 45–53. doi: 10.1016/j.lindif.2016.02.006
Hinault, T., and Lemaire, P. (2016). What does EEG tell us about arithmetic strategies? A review. Int. J. Psychophysiol. 106, 115–126. doi: 10.1016/j.ijpsycho.2016.05.006
Huber, O., and Kunz, U. (2007). Time pressure in risky decision-making: effect on risk defusing. Psychol. Sci. 49, 415–426.
Hughes, C. (1998). Finding “four marbles: does preschoolers” strategic behavior predict later understanding of mind? Dev. Psychol. 34, 1326–1339. doi: 10.1037/0012-1649.34.6.1326
Imbo, I., and LeFevre, J.-A. (2010). The role of phonological and visual working memory in complex arithmetic for Chinese- and Canadian-educated adults. Mem. Cognit. 38, 176–185. doi: 10.3758/MC.38.2.176
Imbo, I., Vandierendonck, A., and Vergauwe, E. (2007). The role of working memory in carrying and borrowing. Psychol. Res. 71, 467–483. doi: 10.1007/s00426-006-0044-8
Jonides, J., Lewis, R. L., Nee, D. E., Lustig, C. A., Berman, M. G., and Moore, K. S. (2008). The mind and brain of short-term memory. Annu. Rev. Psychol. 59, 193–224. doi: 10.1146/annurev.psych.59.103006.093615
Kellogg, J. S., Hopko, D. R., and Ashcraft, M. H. (1999). The effects of time pressure on arithmetic performance. J. Anxiety Disord. 13, 591–600. doi: 10.1016/S0887-6185(99)00025-0
Kerstholt, J. H. (1994). The effect of time pressure on decision-making behaviour in a dynamic task environment. Acta Psychol. 86, 89–104. doi: 10.1016/0001-6918(94)90013-2
Krajewski, K., and Schneider, W. (2009). Exploring the impact of phonological awareness, visual-spatial working memory, and preschool quantity-number competencies on mathematics achievement in elementary school: findings from a 3-year longitudinal study. J. Exp. Child Psychol. 103, 516–531. doi: 10.1016/j.jecp.2009.03.009
LeFevre, J. A., Berrigan, L., Vendetti, C., Kamawar, D., Bisanz, J., Skwarchuk, S. L., et al. (2012). The role of executive attention in the acquisition of mathematical skills for children in Grades 2 through 4. J. Exp. Child Psychol. 114, 243–261. doi: 10.1016/j.jecp.2012.10.005
Lemaire, P., and Callies, S. (2009). Children's strategies in complex arithmetic. J. Exp. Child Psychol. 103, 49–65. doi: 10.1016/j.jecp.2008.09.007
Lemaire, P., and Lecacheur, M. (2010). Strategy switch costs in arithmetic problem solving. Mem. Cognit. 38, 322–332. doi: 10.3758/MC.38.3.322
Lewis, B. P., and Linder, D. E. (1997). Thinking about choking? Attentional processes and paradoxical performance. Pers. Soc. Psychol. Bull. 23, 937–944. doi: 10.1177/0146167297239003
Li, Y., and Geary, D. C. (2013). Developmental gains in visuospatial memory predict gains in mathematics achievement. PLoS ONE 8:e70160. doi: 10.1371/journal.pone.0070160
Luwel, K., Schillemans, V., Onghena, P., and Verschaffel, L. (2009). Does switching between strategies within the same task involve a cost? Br. J. Psychol. 100(Pt 4), 753–771. doi: 10.1348/000712609X402801
Luwel, K., and Verschaffel, L. (2003). Adapting strategy choices to situational factors: the effect of time pressure on children's numerosity judgement strategies. Psychol. Belg. 43, 269–295.
Luwel, K., Verschaffel, L., Onghena, P., and De Corte, E. (2001). Strategic aspects of children' s numerosity judgement. Eur. J. Psychol. Educ. 16, 233–255. doi: 10.1007/BF03173028
Luwel, K., Verschaffel, L., Onghena, P., and De Corte, E. (2000). Children's strategies for numerosity judgement in square grids of different sizes. Psychol. Belg. 40, 183–209.
Ma, X. (1999). A meta-analysis of the relationship between anxiety toward mathematics and achievement in mathematics. J. Res. Math. Educ. 30, 520–540. doi: 10.2307/749772
Ma, X., and Xu, J. (2004). The causal ordering of mathematics anxiety and mathematics achievement: a longitudinal panel analysis. J. Adolesc. 27, 165–179. doi: 10.1016/j.adolescence.2003.11.003
Maloney, E. A., and Beilock, S. L. (2012). Math anxiety: who has it, why it develops, and how to guard against it. Trends Cogn. Sci. 16, 404–406. doi: 10.1016/j.tics.2012.06.008
Mammarella, I. C., Caviola, S., Giofrè, D., and Borella, E. (2017). Separating math from anxiety: the role of inhibitory mechanisms. Appl. Neuropsychol. Child doi: 10.1080/21622965.2017.1341836. [Epub ahead of print].
Mammarella, I. C., Hill, F., Devine, A., Caviola, S., and Szűcs, D. (2015). Math anxiety and developmental dyscalculia: a study on working memory processes. J. Clin. Exp. Neuropsychol. 37, 878–887. doi: 10.1080/13803395.2015.1066759
Markman, A. B., Maddox, W. T., Worthy, D. A., and Markman, B. (2006). Choking and excelling under choking pressure. Psychol. Sci. 17, 944–948. doi: 10.1111/j.1467-9280.2006.01809.x
Mazzoni, G., and Cornoldi, C. (1993). Strategies in study time allocation: why is study time sometimes not effective? J. Exp. Psychol. Gen. 122, 47–60. doi: 10.1037/0096-3445.122.1.47
Mcneil, N. M., and Alibali, M. W. (2005). Why won't you change your mind? Knowledge of operational patterns hinders learning and performance on equations. Child Dev. 76, 883–899. doi: 10.1111/j.1467-8624.2005.00884.x
McNeil, N. M., Rittle-Johnson, B., Hattikudur, S., and Petersen, L. A. (2010). Continuity in representation between children and adults: arithmetic knowledge hinders undergraduates' algebraic problem solving. J. Cogn. Dev. 11, 437–457. doi: 10.1080/15248372.2010.516421
Medeiros, K. E., Partlow, P. J., and Mumford, M. D. (2014). Not too much, not too little: the influence of constraints on creative problem solving. Psychol. Aesthet. Creat. Arts 8, 198–210. doi: 10.1037/a0036210
Meyer, M. L., Salimpoor, V. N., Wu, S. S., Geary, D. C., and Menon, V. (2010). Differential contribution of specific working memory components to mathematics achievement in 2nd and 3rd graders. Learn. Individ. Differ. 20, 101–109. doi: 10.1016/j.lindif.2009.08.004
Miyake, A., and Shah, P. (1999). Models of Working Memory: Mechanisms of Active Maintenance and Executive Control. Cambridge University Press. doi: 10.1017/CBO9781139174909
Noël, M.-P., Désert, M., Aubrun, A., and Seron, X. (2001). Involvement of short-term memory in complex mental calculation. Mem. Cognit. 29, 34–42. doi: 10.3758/BF03195738
Olthof, T., Goossens, F. A., Vermande, M. M., Aleva, E. A., and van der Meulen, M. (2011). Bullying as strategic behavior: relations with desired and acquired dominance in the peer group. J. Sch. Psychol. 49, 339–359. doi: 10.1016/j.jsp.2011.03.003
Ordóñez, L., and Benson, I. I. L. (1997). Decisions under time pressure: how time constraint affects risky decision making. Organ. Behav. Hum. Decis. Process. 71, 121–140.
Passolunghi, M. C., Mammarella, I. C., and Altoè, G. M. (2008). Cognitive abilities as precursors of the early acquisition of mathematical skills. Dev. Neuropsychol. 33, 229–250. doi: 10.1080/87565640801982320
Payne, J. W., Bettman, J. R., and Johnson, E. (1988). Adaptive strategy selection in decision making. J. Exp. Psychol. Learn. Mem. Cogn. 14, 534–552. doi: 10.1037/0278-7393.14.3.534
Pillutla, M. M., and Murnighan, J. K. (1995). Being fair or appearing fair: strategic behavior in ultimatum bargaining. Acad. Manag. J. 38, 1408–1426. doi: 10.2307/256863
Plass, J. A., and Hill, K. T. (1986). Children's achievement strategies and test performance: the role of time pressure, evaluation anxiety, and sex. Dev. Psychol. 22, 31–36. doi: 10.1037/0012-1649.22.1.31
Raghubar, K. P., Barnes, M. A., and Hecht, S. A. (2010). Working memory and mathematics: a review of developmental, individual difference, and cognitive approaches. Learn. Individ. Differ. 20, 110–122. doi: 10.1016/j.lindif.2009.10.005
Ramirez, G., and Beilock, S. L. (2011). Writing about testing worries boosts exam performance in the classroom. Science 331, 211–213. doi: 10.1126/science.1199427
Richardson, M., and Hunt, E. (1985). “Problem solving under time-constraints,” in Paper Presented at the Mathematical Psychologymeeting, August, 1985, Univer-Sity of California (San Diego, CA), 58. Available Online at: http://eric.ed.gov/?id=ED260908
Rieskamp, J., and Hoffrage, U. (2008). Inferences under time pressure: how opportunity costs affect strategy selection. Acta Psychol. 127, 258–276. doi: 10.1016/j.actpsy.2007.05.004
Rittle-Johnson, B., Star, J. R., and Durkin, K. (2012). Developing procedural flexibility: are novices prepared to learn from comparing procedures? Brit. J. Educ. Psychol. 82, 436–455. doi: 10.1111/j.2044-8279.2011.02037.x
Rosenberg-Lee, M., Lovett, M. C., and Anderson, J. R. (2009). Neural correlates of arithmetic calculation strategies. Cogn. Affect. Behav. Neurosci. 9, 270–285. doi: 10.3758/CABN.9.3.270
Rousselle, L., and Noël, M.-P. (2008). Mental arithmetic in children with mathematics learning disabilities: the adaptive use of approximate calculation in an addition verification task. J. Learn. Disabil. 41, 498–513. doi: 10.1177/0022219408315638
Sattizahn, J. R., Moser, J. S., and Beilock, S. L. (2016). A closer look at who “Chokes Under Pressure.” J. Appl. Res. Mem. Cogn. 5, 470–477. doi: 10.1016/j.jarmac.2016.11.004
Schillemans, V., Luwel, K., Bultè, I., Onghena, P., and Verschaffel, L. (2009). The influence of previous strategy use on individuals' subsequent strategy choice: findings from a numerosity judgement task. Psychol. Belg. 49, 191–205. doi: 10.5334/pb-49-4-191
Schunn, C. D., Reder, L. M., Nhouyvanisvong, A., Richards, D. R., and Stroffolino, P. J. (1997). To calculate or not to calculate: a source activation confusion model of problem familiarity's role in strategy selection. J. Exp. Psychol. Learn. Mem. Cogn. 23, 3–29. doi: 10.1037/0278-7393.23.1.3
Siegler, R. S. (1996). Emerging Minds: The Process of Change in Children's Thinking. New York, NY: Oxford University Press.
Siegler, R. S., and Lemaire, P. (1997). Older and younger adults' strategy choices in multiplication: testing predictions of ASCM using the choice/no-choice method. J. Exp. Psychol. Gen. 126, 71–92. doi: 10.1037/0096-3445.126.1.71
Siegler, R. S., and Shipley, C. (1995). “Variation, selection, and cognitive change,” in Developing Cognitive Competence: New Approaches to Process Modeling, eds T. Simmon and G. Haldord (Hillsdale, NJ: Lawrence Erlbaum Associates), 31–76.
Starcke, K., and Brand, M. (2012). Decision making under stress: a selective review. Neurosci. Biobehav. Rev. 36, 1228–1248. doi: 10.1016/j.neubiorev.2012.02.003
Stipek, D. J., and Gralinski, J. H. (1991). Gender differences in children's achievement-related beliefs and emotional responses to success and failure in mathematics. J. Educ. Psychol. 83, 361–371. doi: 10.1037/0022-0663.83.3.361
Swanson, H. L. (2006). Cross-sectional and incremental changes in working memory and mathematical problem solving. J. Educ. Psychol. 98, 265–281. doi: 10.1037/0022-0663.98.2.265
Szűcs, D. (2016). Subtypes and comorbidity in mathematical learning disabilities: multidimensional study of verbal and visual memory processes is key to understanding. Prog. Brain Res. 227, 277–304. doi: 10.1016/bs.pbr.2016.04.027
Szűcs, D., Devine, A., Soltesz, F., Nobes, A., and Gabriel, F. (2014). Cognitive components of a mathematical processing network in 9-year-old children. Dev. Sci. 17, 506–524. doi: 10.1111/desc.12144
Trezise, K., and Reeve, R. A. (2015). Worry and working memory influence each other iteratively over time. Cogn. Emot. 9931, 1–16. doi: 10.1080/02699931.2014.1002755
Trezise, K., and Reeve, R. A. (2014). Working memory, worry, and algebraic ability. J. Exp. Child Psychol. 121, 120–136. doi: 10.1016/j.jecp.2013.12.001
Tsui, J., and Mazzocco, M. M. (2006). Effects of math anxiety and perfectionism on timed versus untimed math testing in mathematically gifted sixth graders. Roeper Rev. 29, 132–139. doi: 10.1080/02783190709554397
Verschaffel, L., Luwel, K., Torbeyns, J., and Van Dooren, W. (2009). Conceptualizing, investigating, and enhancing adaptive expertise in elementary mathematics education. Eur. J. Psychol. Educ. 24, 335–359. doi: 10.1007/BF03174765
Vukovic, R. K., Kieffer, M. J., Bailey, S. P., and Harari, R. R. (2013). Mathematics anxiety in young children: concurrent and longitudinal associations with mathematical performance. Contemp. Educ. Psychol. 38, 1–10. doi: 10.1016/j.cedpsych.2012.09.001
Wang, Z., and Shah, P. (2014). The effect of pressure on high- and low-working-memory students: an elaboration of the choking under pressure hypothesis. Brit. J. Educ. Psychol. 84, 226–238. doi: 10.1111/bjep.12027
Worthy, D. A., Markman, A. B., and Maddox, W. T. (2009). What is pressure? Evidence for social pressure as a type of regulatory focus. Psychon. Bull. Rev. 16, 344–349. doi: 10.3758/PBR.16.2.344
Wu, S. S., Meyer, M. L., Maeda, U., Salimpoor, V., Tomiyama, S., Geary, D. C., et al. (2008). Standardized assessment of strategy use and working memory in early mental arithmetic performance. Dev. Neuropsychol. 33, 365–393. doi: 10.1080/87565640801982445
Keywords: time constraints, arithmetic, problem solving, strategies, stress, math anxiety
Citation: Caviola S, Carey E, Mammarella IC and Szucs D (2017) Stress, Time Pressure, Strategy Selection and Math Anxiety in Mathematics: A Review of the Literature. Front. Psychol. 8:1488. doi: 10.3389/fpsyg.2017.01488
Received: 11 June 2017; Accepted: 17 August 2017;
Published: 01 September 2017.
Edited by:
Thomas J. Faulkenberry, Tarleton State University, United StatesReviewed by:
Krzysztof Cipora, University of Tübingen, GermanyDelphine Sasanguie, KU Leuven Kulak, Belgium
Copyright © 2017 Caviola, Carey, Mammarella and Szucs. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sara Caviola, c2MyMDE0QGNhbS5hYy51aw==
 Sara Caviola
Sara Caviola Emma Carey
Emma Carey Irene C. Mammarella
Irene C. Mammarella Denes Szucs
Denes Szucs